Найти пределы lim калькулятор: Решение пределов. Корни многочленов. Онлайн решение

калькулятор пределов – найти предел онлайн

Table of Contents:

• Какие есть ограничения?
• Как оценить лимиты?

Калькулятор пределов используется для оценки предельных функций по указанной переменной. Переменная может быть x, y или z. Предел калькулятор решает границы с шагами и показывает каждую фазу расчета.

Ниже вы найдете определение лимитов, как рассчитать лимиты без использования поиска лимитов, формулу лимитов и некоторые примеры для понимания лимитов.

Какие есть ограничения?

Идея предела функции жизненно важна для изучения исчисления. Он используется при описании некоторых важных теорий в исчислении, таких как определенный интеграл функции, производная функции и непрерывность.

Предел некоторой функция F (X) определяет поведение функции вблизи конкретной й значение. По сути, он не дает значения функции в точке x. n

Проверка наличия лимита

Чтобы проверить, существует ли предел для f (x) при x = a, мы проверяем,

Предел слева = Предел справа = f ( a)

Правило L’hospital

Где,

f ( а) = 0

г ( а) = 0

Потом,

Правило суммы пределов

Ограничивает правило продукта

Правило предельного частного

Правило ограничения власти

Постоянное правило ограничений

Предел постоянной функции равен постоянной.

Как оценить лимиты?

Оценщик пределов разработан специально для оценки пределов. Но мы объясним ручной метод оценки пределов. Пример ниже иллюстрирует метод из справочника с пошаговыми инструкциями.

Пример :
Evluate :

lim_{x→c ​}f(x)= L−−

Решение:

Шаг 1: Запишите значение. 2) -5 (2) +2 

= 8 + 8-10 + 2
= 8

так,

1 lim_x→2​(x³)+ 2 lim_x→2​(x²)− 5 lim_x→2​(x)+ lim_x→2​(x)+ 2−−

Вы можете использовать приведенный выше калькулятор правил l’hopital, чтобы проверить ответ любой функции ограничения.

Вот график, построенный для указанной выше функции.

Найти пределы функций (не используя правило Лопиталя). решение задачи Математический анализ с ответом

Пример 1

Найти пределы функций (не используя правило Лопиталя):

Пример 2

Найти пределы функций (не используя правило Лопиталя):

Пример 3

Найти пределы функций (не используя правило Лопиталя):

Пример 4

Найти пределы функций (не используя правило Лопиталя):

Пример 5

Найти пределы функций (не используя правило Лопиталя):

Пример 6

Найти пределы функций (не используя правило Лопиталя):

Пример 7

Найти пределы функций (не используя правило Лопиталя):

Пример 8

Найти пределы функций (не используя правило Лопиталя):

Пример 9

Найти пределы функций (не используя правило Лопиталя):

Пример 10

Найти пределы функций (не используя правило Лопиталя):

Пример 11

Найти пределы функций (не используя правило Лопиталя):

Пример 12

Найти пределы функций (не используя правило Лопиталя):

Пример 13

Найти пределы функций (не используя правило Лопиталя):

Пример 14

Найти пределы функций (не используя правило Лопиталя):

Пример 15

Найти пределы функций (не используя правило Лопиталя):

Пример 16

Вычислить пределы функций, не пользуясь правилом Лопиталя.

Пример 17

Вычислить пределы функций, не пользуясь правилом Лопиталя.

Пример 18

Вычислить пределы функций, не пользуясь правилом Лопиталя.

Пример 19

Вычислить пределы функций, не пользуясь правилом Лопиталя.

Пример 20

Вычислить пределы функций, не пользуясь правилом Лопиталя.

Пример 21

Вычислить предел функции, не пользуясь правилом Лопиталя.

Пример 22

Вычислить предел функции, не пользуясь правилом Лопиталя.

Пример 23

Вычислить предел функции, не пользуясь правилом Лопиталя.

Пример 24

Вычислить предел функции, не пользуясь правилом Лопиталя.

Пример 25

Вычислить предел функции, не пользуясь правилом Лопиталя.

Пример 26

Вычислить предел функции, не пользуясь правилом Лопиталя.

Пример 27

Вычислить предел функции, не пользуясь правилом Лопиталя.

Пример 28

Вычислить предел, не пользуясь правилом Лопиталя.

Пример 29

Вычислить предел, не пользуясь правилом Лопиталя.

Пример 30

Найти предел, не пользуясь правилом Лопиталя:

Пример 31

Найти предел, не пользуясь правилом Лопиталя:

Пример 32

Найти предел, не пользуясь правилом Лопиталя:

Пример 33

Найти предел, не пользуясь правилом Лопиталя:

Пример 34

Вычислить предел функций не пользуясь правилом Лопиталя.

Пример 35

Вычислить предел функции не пользуясь правилом Лопиталя.

 

Пример 36

Вычислить предел функции не пользуясь правилом Лопиталя.

‎App Store: Калькулятор лимита с шагами

Описание

Решатель предельных калькуляторов — это подарок всем, кто изучает математику, и тем, кто преподает математический анализ. Потому что этот калькулятор рассчитывает лимиты и показывает пошаговые результаты.

Этот онлайн-калькулятор пределов позволяет сразу найти предел любой сложной дифференцируемой функции. Вы можете получить подробное решение любой функции, заключенной в определенные границы, используя этот искатель пределов.

Что такое предел?

«Предел говорит нам о поведении конкретной функции вблизи точки, но не точно в этой точке».

Эта операция обеспечивает надежную поддержку при решении различных числовых задач. Воспользуйтесь этим приложением калькулятора пределов, чтобы выполнить ряд математических вычислений в кратчайшие сроки. Этот искатель пределов не только вычисляет границы, но и отображает разложение данной функции в ряд Тейлора.

Правило Лопиталя:
Это специальное правило предлагается для нахождения пределов точно так же, как 0/0 или ∞/∞. Наш калькулятор лимитов сразу же упрощает такие лимиты и предоставляет вам правильный способ выполнения расчетов.

Как найти предел сложных функций с помощью калькулятора пределов?

Поскольку пределы широко используются в математике, вы можете найти границы функции, в которых она сохраняет свою непрерывность.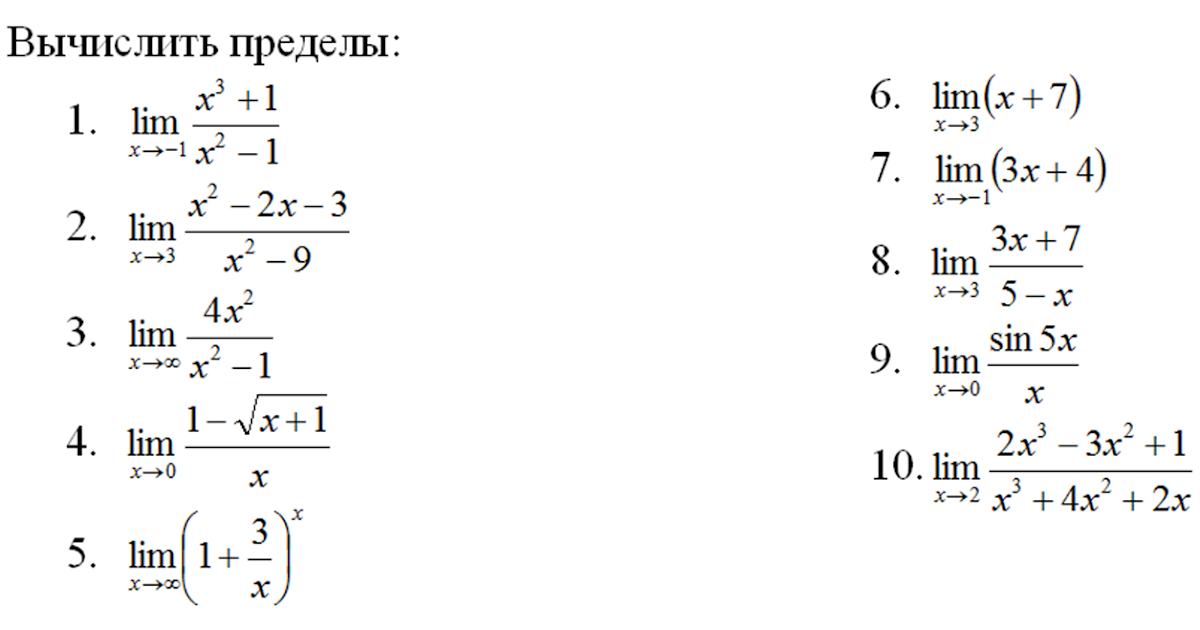 Что вам нужно сделать, так это ввести функцию в наш лимитный калькулятор с шагами, и он быстро определит характер функции. Найдем как!

Запишите функцию в указанное поле
Теперь выберите переменную, для которой вы хотите найти предел
Затем выберите точку, вблизи которой должен быть определен предел.
Из следующего выпадающего списка выберите направление предела, которое может быть как положительным, так и отрицательным.
Нажмите кнопку расчета, и калькулятор пределов предоставит пошаговый шаг решения на экране вашего устройства.

Возможности многопараметрического решателя:

Дружественный интерфейс
100% точные результаты
Пошаговые расчеты
Легко загружаемый PDF-файл всего решения для лучшего понимания проблемы

Простота в использовании
Удобная клавиатура для ввода любой сложной функции без каких-либо препятствий

Итак, используйте это приложение-калькулятор пределов, чтобы получить четкое представление о задачах исчисления, связанных с ограничениями.

5 апреля 2022 г.

Версия 1.0.2

— Исправление ошибки

— Добавление дополнительных функций
— Улучшение взаимодействия с пользователем

Рейтинги и обзоры

1 Рейтинг

Разработчик Асад Ахсан указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.

Данные, используемые для отслеживания вас

Следующие данные могут использоваться для отслеживания вас в приложениях и на веб-сайтах, принадлежащих другим компаниям:

Данные, связанные с вами

Следующие данные могут быть собраны и связаны с вашей личностью:

Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста.

Узнать больше

Информация

Продавец

Асад Ахсан

Размер

36,2 МБ

Категория

Образование

Возрастной рейтинг

4+

Авторское право

© 2022 eClixTech.

Цена

Бесплатно

• Сайт разработчика
• Тех. поддержка
• Политика конфиденциальности

Еще от этого разработчика

Вам также может понравиться

Как решать предельные значения с помощью калькулятора

Обновлено: 16. 07.2021

Учебное пособие по исчислению для чайников с онлайн-практикой

Изучить книгу Купить на Amazon

С помощью калькулятора можно решить большинство задач с предельным значением. Есть два основных метода. Например, предположим, что вы хотите оценить следующий предел:

Первый метод

Вот что вы делаете. Возьмите число, очень близкое к 5, и подставьте его в

x. Если у вас есть калькулятор Texas Instruments TI-84, выполните следующие действия:

1. Введите свой номер, например 4,9999, на главном экране.

2. Нажмите кнопку Sto (сохранить), затем кнопку x , а затем кнопку Enter .

   Сохраняет число в формате x.

3. Введите функцию:

4. Нажмите Enter.

   Результат 9,9999 очень близок к круглому числу 10, так что это и есть ваш ответ.

5. На всякий случай запишите 4,999999 в x .

   Выполните процедуру шага 2.

6. Прокрутите назад до функции, нажав 2nd , Enter , 2nd , Enter .

7. Нажмите Введите еще раз.

   Получится 9,999999 — даже ближе к 10. Если у вас все еще есть сомнения, попробуйте еще одно число.

8. Сохранить 4.99999999 в x , прокрутите вверх до функции и нажмите Введите .

   Результат, 10, подтверждает это. (Значение функции 4,99999999 на самом деле не равно 10, но оно настолько близко, что калькулятор округляет его до 10.)

Кстати, если вы используете другую модель калькулятора, вы, скорее всего, сможете добиться того же результата с помощью той же техники или чего-то очень близкого к ней.

Второй метод

Второй метод калькулятора заключается в создании таблицы значений:

1. В графическом режиме вашего калькулятора введите следующее:

2. Перейдите к «настройке стола» и введите число ограничения, 5, в качестве «начала стола».

3. Введите небольшое число, например 0,001, для ∆ Tbl .

   Это размер x- приращений в таблице.

4. Нажмите кнопку Tab le , чтобы создать таблицу.

5. Прокрутите вверх, чтобы увидеть пару цифр меньше 5.

   Вы должны увидеть таблицу значений, похожую на ту, что в этой таблице.

   Х	Д
   4,998	9,998
   4,999	9,999
   5	Ошибка
   5,001	10.001
   5,002	10.002
   5,003	10.003

Потому что y очень близко подходит к 10, так как x обнуляет 5 сверху и снизу, 10 является пределом.

Эти методы расчета полезны по ряду причин:

• Ваш калькулятор может дать вам ответы на предельные задачи, которые невозможно решить алгебраически.