Найти пределы онлайн с подробным решением: Решение пределов · oнлайн с подробным решением - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Решение высшей математики онлайн

‹– Назад

В этом разделе мы на основе изученных выше свойств бесконечно малых величин (то есть функций, имеющих предел, равный 0) выясним свойства функций, имеющих произвольное значение предела.

Теорема 2.8 Пусть функции и имеют пределы при одной и той же базе :

Тогда функция также имеет предел при базе , и этот предел равен сумме пределов слагаемых:

Доказательство. Равенство означает, в соответствии с теоремой 2.4, что величина — бесконечно малая; равенство — что — бесконечно малая. Поэтому по теореме 2.5 сумма

также является бесконечно малой. Теорема 2.4 утверждает, что тот факт, что разность бесконечно мала, означает, что ; это и требовалось доказать.

Замечание 2.2 В доказанной теореме не утверждается, что если существует предел суммы, то существуют и пределы слагаемых. Это неверно, что показывает простейший пример: пусть и . Тогда и предел , в то время как пределы при функций и не существуют.

Так что из несуществования пределов слагаемых не следует несуществование предела суммы.

Теорема 2.9 Пусть функции и имеют пределы при одной и той же базе :

Тогда функция также имеет предел при базе , и этот предел равен произведению пределов сомножителей:

Доказательство. Равенство означает, в соответствии с теоремой 2. 4, что величина — бесконечно малая; равенство — что — бесконечно малая. Поэтому и , откуда

или

Покажем, что в правой части этого равенства стоит бесконечно малая величина. Величина — бесконечно малая согласно следствию 2.3, а величина — бесконечно малая по теореме 2.7 (величина имеет предел, равный 0, и, следовательно, локально ограничена по теореме 2.6). Поскольку разность между функцией и постоянной бесконечно мала при базе , то по теореме 2.4; это и требовалось доказать.

Замечание 2.3 Сделаем замечание, аналогичное замечанию 2. 2: если существует предел произведения, то отсюда не следует, что существуют пределы каждого из сомножителей; доказанная теорема этого не утверждает. Приведём пример, который был уже разобран выше: функция при имеет предел, равный 0, однако предела при не существует (хотя другой множитель, , имеет предел при этой базе).

Так что из несуществования предела у какого-нибудь сомножителя не следует несуществование предела произведения.

Следствие 2.4 Пусть и (то есть — постоянная величина). Тогда существует предел функции , равный :

Доказательство. Для доказательства достаточно заметить, что, согласно примеру 2.4, , и применить теорему 2.9.

Доказанное следствие означает, что постоянный множитель можно выносить за знак предела, а также вносить под знак предела. Иными словами, умножение на постоянную и переход к пределу можно менять местами.

Следствие 2.5 Пусть функции имеют при базе пределы, равные соответственно , и — постоянные. Тогда

Доказательство. Оно состоит в последовательном -кратном применении теоремы 2.8 к слагаемым , предел которых, согласно предыдущему следствию, равен .

В качестве частного случая можно рассмотреть предел разности двух функций. Разность можно представить в виде и применить следствие 2.5 к этой сумме из двух слагаемых. Получим тогда, что

то есть что разность (как и сумма) сохраняется при переходе к пределу.

Замечание 2.4 Утверждение следствия 2.5, с алгебраической точки зрения, означает, что, во-первых, множество всех функций, заданных на фиксированном окончании базы и имеющих предел при базе — это линейное пространство, а во-вторых — что операция взятия предела — это линейное отображение линейного пространства в линейное пространство вещественных чисел . Попросту: переход к пределу сохраняет суммирование и умножение на постоянные.

Предел отношения двух функций , в отличие от суммы, разности и произведения, не обязательно равен отношению пределов числителя и знаменателя , даже если пределы и существуют. Дело в том, что предел знаменателя может равняться нулю, и отношение пределов тогда не имеет смысла, в то время как предел отношения при этом вполне может существовать. Приведём такой простейший пример:

Пример 2.15 Пусть , и взята база . Тогда, очевидно, , и отношение пределов не имеет смысла. При этом при и предел отношения существует: .

Оказывается, условия , которое обеспечивает то, что отношение пределов имеет смысл, — этого условия достаточно для того, чтобы предел отношения двух функций был равен отношению их пределов. Ниже мы докажем соответствующую теорему, а пока докажем такое вспомогательное утверждение.

Лемма 2.1 Пусть при некоторой базе существует предел . Тогда функция определена на некотором окончании этой базы и локально ограничена при этой базе.

Доказательство. Возьмём положительное число . По определению предела, в базе найдётся такое окончание , что при всех будет . Это неравенство можно привести к виду

(2.2)

При это неравенство означает, что ; так как , то и при всех и, следовательно, функция определена во всех точках окончания и удовлетворяет неравенству

При неравенство (2. 2) означает, что ; так как , то и при всех и, опять-таки, функция определена во всех точках окончания ; она удовлетворяет неравенству

В любом случае получаем, что функция определена во всех точках и при этих удовлетворяет неравенству , что означает локальную ограниченность функции при базе .

На основе этой леммы мы докажем обещанное выше утверждение о пределе отношения.

Теорема 2.10 Пусть при одной и той же базе существуют пределы и , причём . Тогда функция определена на некотором окончании базы , существует предел , и , то есть предел отношения равен отношению пределов числителя и знаменателя.

Доказательство. Представим отношение в виде , в котором и первый, и второй множители определены на некотором окончании базы (относительно второго множителя см. предыдущую лемму). Поэтому и исходное отношение имеет смысл при всех .

Утверждение о том, что , эквивалентно тому, что разность — бесконечно малая величина. Приводя эту разность к общему знаменателю, получим, что . Величина — постоянная и, следовательно (см. пример 2.11), локально ограничена; функция — тоже локально ограничена при базе (по предыдущей лемме). Значит, с учётом предложения 2.1 и теоремы 2.7, будет доказано, что величина бесконечно малая, если мы покажем, что бесконечно мала при базе величина . Найдём предел этой величины. По свойству линейности предела ( следствие 2.5)

Это означает, что величина бесконечно мала.

Замечание 2.5 Как и в случае пределов суммы и произведения, можно сделать замечание (аналогичное замечаниям 2.2 и 2.3): если существует предел отношения, то пределы числителя и знаменателя, вообще говоря, существовать не обязаны. Приведите сами пример, иллюстрирующий это утверждение.

Пример 2.16 Найдём предел

Разделим числитель и знаменатель дроби на старшую степень , то есть на , и получим предел

В этом пределе знаменатель стремится к 3, так как и (здесь мы применили теорему о пределе произведения для последнего слагаемого) и, следовательно, (здесь мы воспользовались линейностью предела). Поскольку предел знаменателя оказался не равен 0, то можно применить теорему о пределе отношения и получить, что

Предел числителя, равный 2, мы нашли аналогично пределу знаменателя, пользуясь линейностью предела.

Итак,

Заметим, что предел отношения многочленов оказался равен отношению коэффициентов при старшей степени , то есть, в данном случае, при .

Аналогично решаются и другие примеры на вычисление пределов отношения двух многочленов при , а также пределов отношения некоторых других функций, например, связанных с корнями из многочленов.

Пример 2.17 Найдём предел

Для этого поделим числитель и знаменатель дроби на (под знаком корня в знаменателе для этого придётся поделить на ):

Поскольку , то подкоренное выражение стремится к 4, а весь знаменатель — к . ⁶ Предел знаменателя оказался отличен от 0, поэтому предел отношения равен отношению пределов. Найдём предел числителя. Поскольку при всех (так как показатель степени отрицателен), то величина локально ограничена при базе и поскольку величина — бесконечно малая при этой базе, то произведение также бесконечно мало, то есть стремится к 0 при . Значит, предел числителя равен

а исходный предел —

Упражнение 2.5 Найдите пределы:

Ответ: ; ; .

Указания: поделите числитель и знаменатель дроби в первом примере на , во втором — на и в третьем — на . Во втором примере воспользуйтесь тем, что и — величины, ограниченные при всех (и, следовательно, локально ограниченные при любой базе).

Теорема 2.11 (теорема “о двух милиционерах”) Пусть даны три функции , и , при всех из некоторого окончания базы связанные неравенством

Пусть функции и имеют общий предел при базе :

Тогда функция также имеет предел при базе , равный тому же числу :

Доказательство. Согласно определению предела, для любого найдутся такие окончания базы и , что при выполняется неравенство

а при — неравенство

Значит, для окончания при всех выполняются неравенства

то есть

Это означает, что предел величины равен .

Рис.2.21.Два милиционера и и пьяный движутся в участок

(Происхождение названия теоремы таково: пусть график функции — это траектория движения первого милиционера в участок, график — второго милиционера туда же, а график — траектория движения нетрезвого гражданина, находящегося, в соответствии с неравенством

в любой момент между двумя милиционерами. Тогда и этот гражданин неизбежно придёт туда же, в участок .)

Теорема 2.12 (теорема о пределе неотрицательной величины) Пусть при всех из некоторого окончания базы и существует . Тогда . Иными словами, при переходе к пределу знак нестрогого неравенства сохраняется.

Доказательство. Если бы предел был отрицательным, то можно было бы взять и найти такое окончание базы , что при выполняется неравенство , откуда . Это же будет выполнено на некотором окончании , что противоречит предположению, что при всех . Противоречие доказывает, что отрицательным предел быть не может, то есть .

Следствие 2.6 Пусть при всех из некоторого окончания базы и существует . Тогда .

Доказательство. Для доказательства достаточно взять функцию , применить к ней доказанную только что теорему и воспользоваться тем, что знак минус можно вынести за знак предела (по свойству линейности предела).

Следствие 2.7 (переход к пределу в нестрогом неравенстве) Пусть при всех из некоторого окончания базы выполняется неравенство . Предположим, что существуют пределы и . Тогда (то есть значения пределов связаны тем же нестрогим неравенством, что и функции). То же верно для нестрогого неравенства .

Доказательство. Рассмотрим функцию . По условию теоремы, , причём

Применим к функции теорему о пределе неотрицательной величины и получим, что , то есть , что и требовалось доказать. Для другого нестрогого неравенства доказательство аналогично.

Замечание 2.6 Аналогичные утверждения для строгих неравенств ( и ) неверны. Для того, чтобы в этом убедиться, достаточно рассмотреть предел . Очевидно, он равен 0, хотя при любом из любого окончания базы величина строго положительна.

Рис.2.22.Предел строго положительной величины может оказаться равным 0

Напомним, что функция называется не убывающей на множестве , если для любых , таких что , выполняется неравенство , и не возрастающей на , если при и выполняется неравенство .

Теорема 2.13 (о пределе монотонной функции) Пусть рассматривается одна из баз , , , которую обозначим . Пусть функция не убывает на некотором окончании базы и ограничена сверху на этом окончании, то есть существует такая постоянная , что при всех . Тогда существует предел , причём .

Рис.2.23.Предел неубывающей ограниченной сверху функции

Доказательство этой теоремы достаточно сложно; оно основывается на довольно тонких свойствах системы вещественных чисел, а именно, на том, что у ограниченного снизу множества чисел , где числа ограничивают функцию сверху, существует точная нижняя грань ; она-то и будет пределом неубывающей функции.

Мы ограничимся здесь этим замечанием и поясняющим рисунком, а за подробным доказательством отошлём читателя к полному курсу математического анализа, например, книгам: Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления, т. 1 или С. М. Никольский, Курс математического анализа, т. 1.

Имеют место также утверждения, получающиеся из теоремы о пределе монотонной функции сменой знака функции или заменой координаты :

Следствие 2.8 Пусть рассматривается одна из баз , , , которую обозначим . Пусть функция не возрастает на некотором окончании базы и ограничена снизу на этом окончании, то есть существует такая постоянная , что при всех . Тогда существует предел , причём .

Рис.2.24.Предел невозрастающей ограниченной снизу функции

Следствие 2.9 Пусть рассматривается одна из баз , , которую обозначим . Пусть функция не убывает на некотором окончании базы и ограничена снизу на этом окончании, то есть существует такая постоянная , что при всех . Тогда существует предел , причём .

Рис.2.25.Предел неубывающей ограниченной снизу функции

Следствие 2.10 Пусть рассматривается одна из баз , , которую обозначим . Пусть функция не возрастает на некотором окончании базы и ограничена сверху на этом окончании, то есть существует такая постоянная , что при всех . Тогда существует предел , причём .

Рис.2.26.Предел невозрастающей ограниченной сверху функции

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Калькулятор с интегралами онлайн: Неопределенный интеграл — ЭкоДом: Дом своими руками

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

DiracDelta(x)

Дельта-функция Дирака

Heaviside(x)

Функция Хевисайда

Интегральные функции:

Si(x): Интегральный синус от x
Ci(x): Интегральный косинус от x
Shi(x): Интегральный гиперболический синус от x
Chi(x): Интегральный гиперболический косинус от x

В выражениях можно применять следующие операции:

Действительные числа: вводить в виде 7. 3; — возведение в степень
x + 7: — сложение
x — 6: — вычитание
15/7: — дробь

Другие функции:

asec(x): Функция — арксеканс от x
acsc(x): Функция — арккосеканс от x
sec(x): Функция — секанс от x
csc(x): Функция — косеканс от x
floor(x): Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
ceiling(x): Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
sign(x): Функция — Знак x
erf(x): Функция ошибок (или интеграл вероятности)
laplace(x): Функция Лапласа
asech(x): Функция — гиперболический арксеканс от x
csch(x): Функция — гиперболический косеканс от x
sech(x): Функция — гиперболический секанс от x
acsch(x): Функция — гиперболический арккосеканс от x

Постоянные:

pi: Число «Пи», которое примерно равно ~3. 14159..
e: Число e — основание натурального логарифма, примерно равно ~2,7183..
i: Комплексная единица
oo: Символ бесконечности — знак для бесконечности

Содержание

24 интеграл

Вы искали 24 интеграл? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и math44 интегралы, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «24 интеграл».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек

использовал еще в древности и с тех пор их применение только возрастает.

Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 24 интеграл,math44 интегралы,взятие интеграла онлайн,взять интеграл,взять интеграл онлайн,взять интеграл онлайн с решением,вычисление интеграл,вычисление интеграла,вычисление интегралов,вычисление интегралов онлайн калькулятор,вычисление интегралов онлайн с подробным решением,вычисление неопределенного интеграла онлайн,вычисление первообразной,вычислите интеграл онлайн с решением,вычислить интеграл,вычислить интеграл онлайн калькулятор с подробным решением,вычислить интеграл онлайн с подробным решением,вычислить интеграл онлайн с подробным решением бесплатно,вычислить интеграл онлайн с подробным решением калькулятор,вычислить интегралы онлайн с подробным решением,вычислить криволинейный интеграл онлайн,вычислить неопределенный интеграл онлайн с подробным решением,вычислить несобственный интеграл онлайн с подробным решением,вычислить онлайн с решением,вычислить повторный интеграл онлайн с решением,изменить порядок интегрирования онлайн калькулятор,изменить порядок интегрирования онлайн калькулятор с решением,интеграл 24,интеграл вычисление,интеграл как посчитать,интеграл онлайн калькулятор с подробным,интеграл онлайн с подробным решением,интеграл решение,интеграл частного,интегралов,интегралы калькулятор онлайн,интегралы онлайн с подробным решением,интегралы онлайн с решением,интегралы решать,интегралы решение,интегралы с подробным решением,интегральный калькулятор,интегрирование калькулятор,интегрирование по частям онлайн,интегрирование по частям онлайн калькулятор,интегрирование по частям онлайн с подробным решением,интегрирование рациональных дробей онлайн калькулятор,интегрировать онлайн,інтеграл,інтеграли,как интеграл посчитать,как посчитать интеграл,как решить интеграл,калькулятор вычисление интегралов онлайн,калькулятор интеграла,калькулятор интеграла онлайн,калькулятор интегралов,калькулятор интегралов онлайн,калькулятор интегралов онлайн с подробным,калькулятор интегралов онлайн с решением,калькулятор интегралы,калькулятор интегрирования,калькулятор интервалов,калькулятор онлайн вычисление интегралов,калькулятор онлайн интегралов,калькулятор онлайн интегрирование по частям,калькулятор определенных интегралов онлайн с подробным решением,калькулятор первообразной онлайн,калькулятор первообразных онлайн с решением,калькулятор с интегралами,криволинейные интегралы онлайн,криволинейный интеграл онлайн калькулятор,найти интеграл методом замены переменной онлайн,найти интеграл онлайн калькулятор,найти интегралы онлайн с подробным решением,найти неопределенные интегралы онлайн с полным решением,найти неопределенный интеграл онлайн калькулятор с подробным решением,найти неопределенный интеграл онлайн с подробным решением,найти первообразную онлайн,нахождение интеграла,нахождение интегралов,нахождение первообразной онлайн,неопределенный интеграл онлайн калькулятор с подробным решением,несобственный интеграл онлайн калькулятор,онлайн вычисление неопределенных интегралов,онлайн интегралы с пошаговым решением,онлайн калькулятор вычисление интегралов,онлайн калькулятор интеграл,онлайн калькулятор интеграла,онлайн калькулятор интегралов с подробным,онлайн калькулятор интегралы,онлайн калькулятор интегрирование рациональных дробей,онлайн калькулятор найти интеграл,онлайн калькулятор неопределенный интеграл,онлайн калькулятор решение интегралов с подробным решением,онлайн неопределенные интегралы,онлайн решение интегралов с подробным,онлайн решение интегралов с подробным решением,онлайн решение интегралов с подробным решением бесплатно,онлайн решение неопределенных интегралов с подробным решением,первообразная калькулятор,первообразная калькулятор онлайн,первообразная онлайн калькулятор,первообразная онлайн калькулятор с подробным решением,посчитать интеграл,посчитать интеграл онлайн с подробным решением,посчитать как интеграл,проинтегрировать онлайн,проинтегрировать уравнение онлайн,расчет интегралов,расчет интегралов онлайн,решать интегралы,решение интеграла,решение интеграла онлайн с подробным решением,решение интеграла с подробным решением онлайн,решение интегралов,решение интегралов калькулятор онлайн,решение интегралов онлайн калькулятор с подробным решением,решение интегралов онлайн с подробным решением,решение интегралов онлайн с подробным решением бесплатно,решение интегралов онлайн с подробным решением калькулятор,решение интегралов онлайн с решением,решение интегралов с подробным решением,решение интегралы,решение криволинейных интегралов онлайн,решение неопределенного интеграла онлайн с подробным решением,решение неопределенных интегралов онлайн с подробным решением,решения интегралов,решить интеграл онлайн с подробным,решить интеграл онлайн с подробным решением,решить интеграл онлайн с подробным решением бесплатно,решить интеграл онлайн с решением,решить интегралы онлайн с подробным решением,решить неопределенный интеграл онлайн,решить неопределенный интеграл онлайн с подробным решением,справочник веществ интеграл онлайн,сходимость интегралов онлайн.

На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 24 интеграл. Просто введите задачу в окошко и нажмите
«решить» здесь (например, взятие интеграла онлайн).

Решить задачу 24 интеграл вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо

сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

Интегральный калькулятор | Лучший интегральный калькулятор

Определение интегрального калькулятора

Интегральный калькулятор представляет собой математический инструмент, который позволяет легко вычислять интегралы . Интегральный онлайн-калькулятор обеспечивает быстрый и надежный способ решения различных интегральных задач.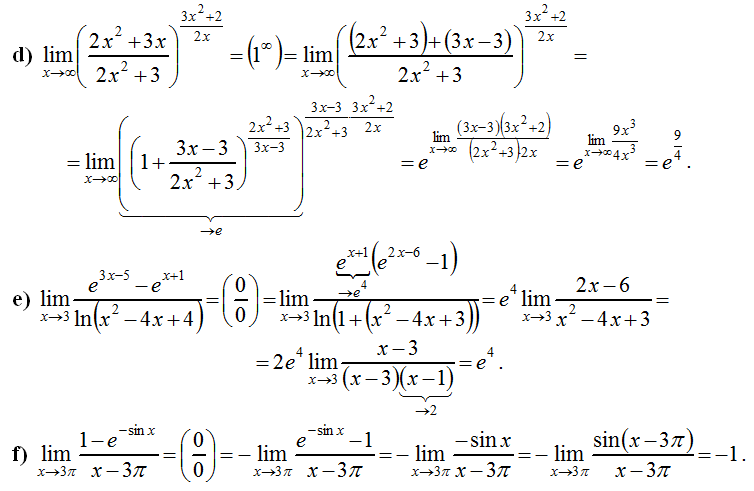 онлайн-калькулятор интеграции и его процесс отличается
от обратного
производный калькулятор, поскольку эти два являются основными понятиями исчисления.

Что такое интеграция?

Интегрирование находит дифференциальное уравнение математических интегралов. Интегральная функция дифференцирует и вычисляет площадь под кривой графика.

Определение интеграла помогает найти площадь, центральную точку, объем и т. д. Онлайн-калькулятор интеграции определение интеграла для нахождения площади под кривой следующим образом:

Где

F(x) — функция, а

А — площадь под кривой.

Что такое Integrand в калькуляторе интеграции?

Интегранд является интегралом
уравнения или формулы интегрирования, она обозначается как функция f(x). В калькуляторе интеграции вам нужно будет ввести значение, чтобы оно работало правильно.

Как интегральный калькулятор взаимодействует с интегральной записью?

Для интегрального уравнения

∫ 2x dx

∫ — символ интеграла, а 2x — функция, которую мы хотим интегрировать.

В этом интегральном уравнении dx является дифференциалом переменной x. Он подчеркивает, что переменная интеграции равна x. dx показывает направление вдоль оси x, а dy показывает направление вдоль оси y.

Интегральные символы и интегральные правила используются калькулятором интегралов для быстрого получения результатов.

Как вычислить интеграл?

Мы можем вычислить функцию за несколько простых шагов. Сначала разделите площадь на срезы и сложите ширину этих срезов с Δx. Тогда ответ будет не точен. (см. рис. 1)

Если сделать Δx много меньшей ширины и сложить все эти маленькие кусочки, то точность ответа станет лучше. (см. рисунок 2)

Если ширина ломтиков приближается к нулю, то ответ приближается к истинному или фактическому результату. Итак,

Теперь мы говорим, что dx означает, что ширина срезов Δx приближается к нулю.

Обратите внимание, что интеграл является обратной производной

Вычисляет ли калькулятор интегралов определенный интеграл и неопределенный интеграл?

Этот онлайн-калькулятор интегрирования позволит вам вычислять определенные интегралы и неопределенные интегралы. Вам просто нужно указать значения в поле ввода. Определенный интеграл имеет как начальное значение, так и конечное значение. Интеграл исчисления функции f(x) представляет собой площадь под кривой от x = a до x = b.

Неопределенный интеграл не имеет верхнего предела и нижнего предела функции f(x). Неопределенный интеграл также известен как первообразная.

Узнайте, как найти предел функциональности здесь.

Как вычислить двойные интегралы?

Одной из трудностей при вычислении двойных интегралов является определение пределов интегрирования. Пределы интегрирования в порядке dxdydxdy необходимы для определения пределов интегрирования для эквивалентного интегрального порядка dydxdydx.

Трудность при вычислении двойных интегралов заключается в определении пределов интегрирования. Пределы интегрирования в порядке dxdydxdy определяют пределы интегрирования для целочисленного порядка dydxdydx.

Предоставляет ли интегральный калькулятор шаги?

Наш калькулятор интегрального исчисления предоставляет вам шаги, чтобы вы могли увидеть, как был рассчитан ваш запрос. Вы можете еще больше расширить свои знания и понимание, просматривая пошаговый ответ.

Этот интегральный решатель очень эффективен для сложных задач интеграции, поскольку он обеспечивает быстрый ответ на сложные проблемы интеграции и решения.

Используйте калькулятор площади сектора, чтобы еще больше укрепить свои математические понятия, связанные с вычислением площади.

Как найти лучший интегральный калькулятор?

Calculatored имеет лучший калькулятор частных интегралов с точки зрения точности, скорости и результатов. Калькуляторные методы интегрального исчисления могут быть разными, но методы и концепции остаются теми же. Вы можете выполнить поиск по запросу calculateed или найти наш интегральный онлайн-калькулятор в Google.

Как использовать интегральный калькулятор с шагами?

Для основных примеров интеграции и решений очень эффективен калькулятор линейного интеграла. Калькулятор интеграции по частям прост и удобен в использовании. Все, что вам нужно сделать, это выполнить следующие шаги:

Шаг #1: Заполните интегральное уравнение, которое вы хотите решить.

Шаг № 2: Выберите переменную как X или Y.

Шаг № 3: Введите значение верхней границы.

Шаг №4: Введите значение нижней границы.

Шаг № 5: Нажмите кнопку «РАССЧИТАТЬ».

После того, как вы выполните указанные выше шаги и нажмете кнопку расчета, онлайн-калькулятор интеграции с шагами немедленно решит интеграл по частям. Вы увидите результаты антипроизводной, интегральных шагов, дерева синтаксического анализа и график результата.

Вы также можете заполнить примеры интегралов для решения интегралов для практики. Мы надеемся, что вы найдете полезную информацию об интегралах и их вычислениях.

Пожалуйста, оставьте свой ценный отзыв ниже. Удачи вам в обучении и расчетах. Ваше здоровье!

Внешние ресурсы:

История интегралов.
Интегральное уравнение.
Определенные интегралы и их вычисление
Неопределенный интеграл с решенными примерами.

Калькулятор и решатель тригонометрических интегралов

Получите подробные решения ваших математических задач с помощью нашего пошагового калькулятора тригонометрических интегралов

. Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. Проверьте все наши онлайн-калькуляторы здесь!

(◻)

—

◻/◻

◻ 07

20004 ◻ ^◻

√◻

√

^◻ √◻

^◻ √

∞

log

log _◻

lim

d/dx

D ^□_x

∫

∫ ^◻

|◻|

sin

cos

tan

cot

sec

csc

asin

acos

atan

acot

asec

acsc

sinh

cosh

tanh

coth

sech

csch

asinh

acosh

atanh

acoth

asech

acsch

Пример

Решенные проблемы

92dx$

Промежуточные шаги

Интеграл от константы равен произведению константы на переменную интеграла

$\frac{1}{4}x$

Интеграл $\frac{1}{4}\int1dx$ дает: $\frac{1}{4}x$

$\frac{1}{4}x$

Промежуточные шаги

Интеграл функции, умноженный на константу ($-2$), равен произведению константы на интеграл функции

$-\frac{1}{2}\int\cos\left(2x\right)dx$

Применить формулу: $\int\cos\left(ax\right)dx$$=\frac{1}{a}\sin\left(ax\right)$, где $a=2$

$ -\frac{1}{4}\sin\left(2x\right)$

Интеграл $\frac{1}{4}\int-2\cos\left(2x\right)dx$ дает: $-\frac{1}{4}\sin\left(2x\right) $

$-\frac{1}{4}\sin\left(2x\right)$

Умножить один член $\frac{1}{8}$ на каждый член многочлена $\left(x+\frac{1}{4}\sin\left(4x\right)\right)$ 92dx$, применяя интегрирование методом подстановки (также называемым U-подстановкой).

limits and continuity exam pdf

AlleVideosBilderBücherMapsNewsShopping

Suchoptionen

[PDF] Limits and Continuity Practice Test

mamackay.weebly.com › uploads › limits_and_continuity_practice_test

Limits and Continuity Practice Test. 1. Найдите предел. →0. 6 5−8 3. 9 3−6 5 а. 2. 3 б. −. 8. 9 в. 4. 3 д. −. 8. 3 эл. Несуществующий. 2. предел. →−∞.

[PDF] Ограничения и преемственность Глава 3: Проблемы практики/проверки

www.ms.uky.edu › конспекты лекций › Answers_Review_Chapter3

Пределы и преемственность. Глава 3: Практика/обзор проблем. Перечисленный ниже сборник задач содержит вопросы, взятые из предыдущих экзаменов MA123.

[PDF] Limits and Continuity Practice

Washingtonlee.apsva.us › wp-content › uploads › site › 2016/09 › Li…

Для приведенной ниже функции: a) Найдите значения x (если есть), при котором f(x) не является непрерывной. Обоснуйте свой ответ (ответы). * Какие разрывы являются устранимыми?

[PDF] Обзор экзамена AP по исчислению AB — Средняя школа Ранчо

rancho-hs.enschool.org › 1_ Пределы и непрерывность с ответами

26.08.2016 · Обзор экзамена AP по исчислению AB. Пределы и непрерывность. БОЛЬШОЙ ВЫБОР. … Определите предел алгебраически, если он существует.

[PDF] Пределы исчисления AP, непрерывность и дифференцируемость

www.slps.org › site › handlers › filedownload › FileName=01 Limits …

Знайте взаимосвязь между пределами и асимптотами (т.е. пределы, которые … Обсуждать непрерывность алгебраически и графически и знать ее отношение к пределу.

[PDF] Пределы и непрерывность — Австралийский институт математических наук

amsi.org.au › ESA_Senior_Years › PDF › Limits3a

Формальное определение предела обычно не изучается в средней школе. Стр. 5. Руководство для учителей – 11 и 12 классы •{5} математика. Это определение …

[PDF] Пределы и непрерывность

www.uobabylon.edu.iq › eprints › публикация_3_20403_1332

В этой главе мы покажем, как определять и вычислять пределы значений функции. Кали- … Одно из применений пределов — проверка функций на непрерывность.

[PDF] AP Исчисление Test Глава 2 Пределы и непрерывность Название

www.pleacher.com › mlessons › calctest › test2a

Напишите на своем листе полные определения для каждого из следующих пунктов: 9. Предел. 10. Преемственность. III. Определите пределы следующих функций, …

[PDF] AP-CALCULUS-BC-TEST-Limit-and-Continuity.pdf – SAT PREP

satprep.co.in › wp-content › uploads › 2021/04 › AP-CALCULUS-B…

SAT PREP. Задание: AP CALCULUS BC TEST (предел и непрерывность). Страница 2. Страница 3. Q2 и Q6 основаны на функции f, показанной на графике и определенной …

[PDF] Глава 2: Пределы и непрерывность — mellinamathclass. com

www.mellinamathclass.com › загрузки › Chapter_2_-_limits___contin…

Проверка непрерывности в указанных точках. Четко покажите три вещи, которые делают функцию непрерывной в точке. а. Z [ = 2[ − …

Ähnlichesuchanfragen

Пределы и непрерывность вопросы и ответы PDF

Пределы вопросы и ответы pdf

Пределы и непрерывность тест с ответами

Тест пределов с ответами

Исчисление Глава 1 Тест пределов и непрерывности Ответы

Тест пределов pdf

Практический тест пределов и непрерывности

Вопросы с несколькими вариантами ответов по пределам и непрерывности PDF

ap исчисление ab пределы обзорные рабочие листы 9000 с ответами AlleBilderVideosBücherMapsNewsShopping

suchoptionen

[PDF] AP CALCULUS AB LIMIT WORKSHEET #1 Найдите указанный лимит …

hadleysclasses.weebly.com › загрузки › limit_worksheets_with_answers

AP ВЫЧИСЛЕНИЕ AB. РАБОЧИЙ ЛИСТ №1. Найдите указанный предел. Какой метод наиболее подходит: Прямая замена, Численный,. Аналитический или графический?

[PDF] CALCULUS AB РАБОЧИЙ ЛИСТ 1 ПО ПРЕДЕЛАМ Выполните следующие действия на …

mrparrbccalculus.weebly.com › загрузки › calc_ab_-_worksheets_for_…

CALCULUS AB. РАБОЧИЙ ЛИСТ 1 ПО ПРЕДЕЛАМ. Работайте следующим образом на тетрадной бумаге. Нет калькулятора. 1. Даны графики f и g. Используйте их для оценки каждого предела …

[PDF] Обзорный лист главы 1 AP Calculus AB — школы города Бичвуд

www.beachwoodschools.org › Загрузки › AB_Ch2_Review_Sheet5

AP Calculus AB. Обзорный лист главы 1. Оцените каждое ограничение: 14). -2-. 15). 16). 17). Используйте следующую диаграмму, чтобы ответить #9-13:.

[PDF] Обзор лимитов KEY.pdf

www.dvusd.org › cms › lib011 › Centricity › Домен › Обзор лимитов…

AP Calculus AB. Обзор пределов (разделы 1.2-1.5, 2.1A и 3.5) … Для задач 3-18 оцените каждый предел БЕЗ КАЛЬКУЛЯТОРА, четко показав все шаги.

AP Исчисление AB Рабочие листы (CH. Обзоры) – Исчисление Д.Грэма

site.google.com › сайт › исчисление-рабочие листы

Список заданий, рабочих листов и Библий исчисления Д.Грэма. … AP Исчисление AB Рабочие листы (CH. Обзоры) … CH.1 LIMITS STUDY SHEET.doc.

[PDF] Расчет A Пределы и непрерывность Рабочий лист — AWS

mitycourses.s3.amazonaws.com › …

Ключ ответа. Название теста: РАБОЧИЙ ЛИСТ ПРЕДЕЛОВ И НЕПРЕРЫВНОСТИ. 1) -5. 2) 15. 3) -4. 4) 8. 5) 12. 6) -27. 7) Не существует. 8) Не существует.

[PDF] Рабочие листы AP Calculus-AB по темам

teshalemath.com › wp-content › uploads › 2018/10 › AP-Calc-Works…

Рабочие листы AP Calculus-AB по темам. Функции, ограничения и непрерывность. Дифференциация … Чтение графика положения – Ответьте на вопросы о движении, используя a.

[PDF] 201-103-RE – Расчет 1 РАБОЧИЙ ЛИСТ: ПРЕДЕЛЫ

cpb-us-w2.wpmucdn.com › dist › 2017/05 › Calculus-Review-1cnmf49

f Использовать график функции (х) ответить на каждый вопрос.