Найти производную y: Дифференцирование функции, заданной неявно

{2}}$

Полная таблица производных Решение производных онлайн

Читать дальше: производная корня икс, sqrt(x)’.

2, а также чему он равен. Это будет темой последнего раздела этого сообщения в блоге.

Но прежде чем мы углубимся в эту идею, давайте подытожим другое содержание лекций.

Лекция 4A

Я начинаю лекцию 4A с решения задач с экспоненциальными уравнениями.

Расчет 1, Урок 4A: Экспоненциальные задачи, линейное и экспоненциальное моделирование ВВП, композиция функций

Общий смысл решения таких задач таков. Учитывая две точки данных

и , ищем числа и такие, что график показательной функции проходит через эти точки.

Это означает, что мы хотим, чтобы

и оба были правдой. Деление первого уравнения на второе дает , предполагая . Затем это уравнение решается путем извлечения корня из обеих частей. Затем вы можете использовать одно из исходных уравнений для решения .

Другим важным моментом в лекции 4А является идея моделирования данных. Рассматриваются реальные данные о валовом внутреннем продукте (ВВП) США. Затем я графически сравниваю, какая модель лучше «подходит» для данных — линейная или экспоненциальная. Считается, что экспоненциальная модель лучше, потому что ее остатки (ошибки) более случайны. Это очень важная перспектива, если вы хотите использовать математические модели в реальной жизни.

Завершающим пунктом лекции 4А является композиция функций. Композиция функций означает, что мы применяем две функции в последовательности . Имея две функции

и соответствующие домены и кодомены, мы можем сформировать новую функцию. Эта функция определяется формулой . Другими словами, вывод подключается к . Это важная концепция как для более глубокого понимания функций, так и для идеи обратной функции.

Лекция 4B

Это приводит нас к лекции 4B, где я начинаю описывать обратные функции и их свойства.

Исчисление 1, лекция 4B: композиция функций, обратные функции, квадратичные функции

Сначала более подробно дается идея композиции функций на примере.

Отсюда определяются обратные функции для взаимно однозначных функций. Для заданной взаимно однозначной (инъективной) функции

ее обратная функция определяется так, чтобы удовлетворять двум свойствам относительно композиции. Оно должно удовлетворять всем в области . И оно должно удовлетворять всем в области (которая является диапазоном .

Еще один факт, который я подчеркиваю в этой лекции, заключается в том, что функции, которые не являются взаимно однозначными, иногда можно сделать таковыми путем соответствующего ограничения их доменов. В частности, области определения квадратичных функций можно соответствующим образом ограничить, используя метод завершения квадрата для записи их формул в вершинной форме.

Лекции 5A и 5B

Я начинаю лекцию 5A, используя систему компьютерной алгебры (CAS) Mathematica , чтобы построить график 92 в этом посте.

Calc 1, Lec 5A: Mathematica Plot, Обратный квадрат (заполнение квадрата), Введение в производные

Я также использую функцию под названием «Manipulate» в Mathematica , чтобы сделать анимацию графика

по мере увеличения .

Это соответствует горизонтальному переносу (сдвигу) «родительской» функции.

Отсюда я решаю физическую задачу о высоте объекта под действием силы тяжести, используя функцию, обратную квадратичному. Как уже упоминалось, метод завершения квадрата используется для преобразования квадратного числа в вершинную форму. Затем область определения сужается и по квадратичной формуле находится соответствующая обратная функция. 92 при произвольном значении x для измерения (мгновенной) скорости изменения функции в этой точке. Это также описывается как наклон касательной к графику

в этой точке.

Начните с выбора произвольного значения

. Тогда пусть будет ненулевым числом.

Это стандартное обозначение для изменение x . Мы действительно воображаем, что независимая переменная (вход) для функции

меняется с на . Если , то вход увеличивается и . Если , то вход убывает.

Для простоты предположим, что

. График не является линией, поэтому он не имеет постоянного наклона. Однако среднюю скорость изменения на закрытом интервале все же можно определить. Он определяется как наклон линии, соединяющей точки и .

Эта линия называется секущей к графику

. Его наклон равен . Для можно сделать следующее упрощение этого выражения.

.

Наглядное изображение секущей линии, приближающейся к касательной

Последнее равенство верно до тех пор, пока

, что мы и предполагаем. То, что мы только что сделали, можно визуализировать, как показано ниже.

Наклон секущей к графику между и равен . В этом визуальном элементе наклон упрощается до . По мере приближения к 0 этот наклон становится все ближе и ближе к 3.

Так что же тогда является производной ? Это предел наклонов этих секущих, поскольку

«уходят» в нуль.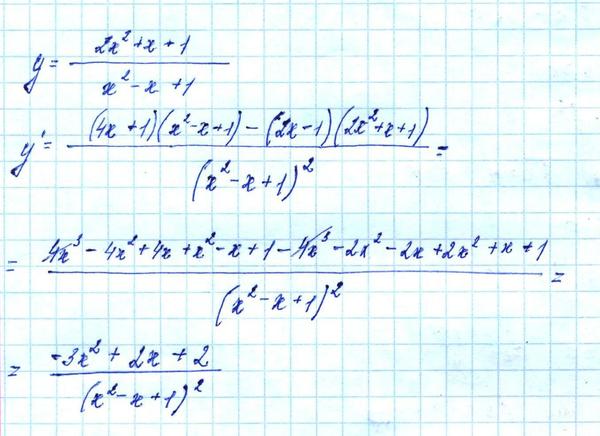 Этот предел, , если он существует , тогда определяется как наклон касательной к графику при заданном значении . Другими словами, в данной точке на графике касательной является линия, проходящая через эту точку с наклоном, равным только что описанному пределу .

Производная — это предел

Но что такое предел?

Мы уточним ограничения в следующем посте. На данный момент в данной ситуации просто подумайте об этом как о значениях

as становится все ближе и ближе к нулю, фактически не равняясь нулю (потому что тогда мы будем делить на ноль).

Начиная с

когда , этот предел можно найти, подумав о значениях когда близко к нулю.

Как происходит это мышление? Проще говоря, поскольку

является «хорошей» (непрерывной) функцией (предполагаемой «фиксированной»), мы можем просто подключиться, чтобы получить ответ.

Это производное от

! Условно мы пишем .

Сейчас вы вполне можете почесать затылок и сказать:

, но подождите минутку! Я думал, мы говорили

! Но мы вставили ноль в конце! Как же так?!?!?

Это, мой друг, часть сбивающей с толку тонкости ограничений. Как я уже сказал, мы углубимся в это в другом посте.

Не расстраивайтесь, если вы не сразу это понимаете. В конце концов, даже гениальные Исаак Ньютон и Готфрид Вильгельм Лейбниц не до конца понимали это в 1600-х годах. Полного понимания пришлось ждать, пока в 1800-х годах не появились Огюстен-Луи Коши и Карл Вейерштрасс.

Но не волнуйтесь! Вы можете «стоять на плечах этих гигантов». Вы действительно можете «получить это» с достаточной помощью и временем на размышления!

Калькулятор неявного дифференцирования с шагами

Введение в калькулятор неявного дифференцирования?

Калькулятор неявного дифференцирования — это онлайн-инструмент, с помощью которого можно вычислить любую производную функцию через x и y. Калькулятор неявной производной с шагами позволяет крупным производителям быстро освоить это, выполняя вычисления во время выполнения. Пошаговые результаты калькулятора неявной производной заставят вас выполнить конкретную задачу в рамках менуэта.

Интегрирование и дифференцирование обратны друг другу. Вы можете найти полезные калькуляторы интеграции на этом веб-сайте, а также полезные блоги.

Что такое неявное дифференцирование?

В исчислении слово неявный используется для функций, которые могут быть выражены как через x, так и через y. Неявное дифференцирование — это процесс, в котором мы находим производную зависимой переменной. Это делается с помощью

Раздельного дифференцирования каждого члена

Выражения производной зависимой переменной в виде символа 92 \right) = \frac{d}{dx} (1) $$

Этот веб-сайт предлагает другие полезные инструменты дифференцирования, например, вы можете использовать калькулятор дифференцирования на главной странице или калькулятор частных производных, чтобы получить мгновенное решение. вашей проблемы.

Преимущества использования калькулятора неявных функций

Всегда лучше использовать онлайн-инструмент, чем ручной метод. Вот некоторые из основных преимуществ калькулятора dy/dx с шагами:

1. Он экономит ваше время, которое вы тратите на выполнение ручных вычислений.
2. Неявный калькулятор прост и удобен в использовании.
3. Он обеспечивает точные и пошаговые результаты.
4. Вы можете увидеть график и возможные промежуточные шаги неявного дифференцирования.
5. Калькулятор неявной производной с шагами поможет вам попрактиковаться в Интернете, чтобы закрепить свои концепции.

Помимо этого калькулятора неявного дифференциала, вы также можете использовать калькулятор аппроксимации касательной для нахождения производной наклона или кривой.

Преимущества использования калькулятора dy dx

Использование калькулятора второй неявной производной с шагами для обучения и практики всегда полезно и разумно. Вот некоторые из основных преимуществ этого решателя неявного дифференцирования:

1. Он экономит ваше время, затрачиваемое на ручные вычисления.
2. Этот неявный калькулятор с шагами прост и удобен в использовании.
3. Вы можете попрактиковаться, чтобы закрепить свои концепции неявной дифференциации.
4. Дает пошаговые точные результаты.
5. Вы можете найти сюжет и возможные промежуточные шаги неявного дифференцирования.
6. Вам не нужна плата или подписка, чтобы использовать калькулятор производной неявной функции.

Связанный: Также найдите сопутствующие инструменты, такие как калькулятор производных частных, и бесплатно найдите производные с помощью калькулятора правил произведения.

Как пользоваться калькулятором неявной дифференциации?

Наш калькулятор неявного дифференцирования с шагами очень прост в использовании. Просто выполните следующие действия, чтобы получить точные результаты. Эти шаги:

1. Введите функцию в основной ввод или загрузите пример.

2. Выберите переменную, относительно которой вы хотите произвести оценку.

3. Подтвердите в предварительном просмотре правильность функции или переменной.

4. Нажмите кнопку “РАССЧИТАТЬ”, чтобы получить пошаговый ответ.

Надеемся, вам понравился наш калькулятор неявных функций. На этом веб-сайте есть и другие полезные онлайн-инструменты, которые вы можете использовать, такие как калькулятор третьей производной или калькулятор цепного правила с шагами. Такие инструменты могут сэкономить ваше время, которое вы тратите на ручные вычисления.

Часто задаваемые вопросы

Является ли неявное дифференцирование тем же, что и частичное дифференцирование?

При неявном дифференцировании функция дифференцируется по одной переменной, но в конце другая переменная исчезает.

В то время как при частичном дифференцировании функция дифференцируется одновременно по двум переменным. Используйте калькулятор неявных частных производных, чтобы получить точные результаты онлайн.

Что такое производная неявной функции?

Неявное дифференцирование, функция дифференцируется по одной переменной, рассматривая другую как функцию первой переменной. При оценке вторая переменная изолируется от решения. Вы можете использовать калькулятор производной неявной функции, чтобы получить мгновенные и точные результаты.

Что такое неявная функция дифференцирования?

Функция называется неявной функцией, если одна из ее переменных записана в виде функции другой переменной. Например, х ² +xy=0 является неявной функцией, поскольку одна переменная является зависимой, то есть функцией независимой переменной. Между тем, вы можете вычислить эти функции и уравнения, шаг за шагом используя калькулятор производной неявной функции.

Как найти производную неявной функции?

Мы можем легко дифференцировать неявную функцию. Например, чтобы найти y’ для xy=1, мы можем выполнить следующие шаги.