Таблички с формулами скорость время расстояние. Формулы прямолинейного равноускоренного движения
Планирование
Равномерное движение, это вдвижение спостоянной скоростью. То есть другимим словами, тело за одинаковые промежутки времени должно проходить одинаковое расстояние. Например, если машина будет за каждый час своего пути проезжать расстояние в 50 километров, то такое движение будет являться равномерным.
Обычно равномерное движение очень редко можно встретить в реальной жизни. За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.
Расчет скорости при равномерном движении
Скорость тела при равномерном движении будет вычисляться по следующей формуле.
- Скорость = путь / время.
Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.
- V=s/t.

Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.
Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.
Расчет скорости при неравномерном движении
При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.
Средняя скорость неравномерного движения вычисляется по формуле
- Vcp=S/t.
Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.
Расчет пути при равномерном движении
Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.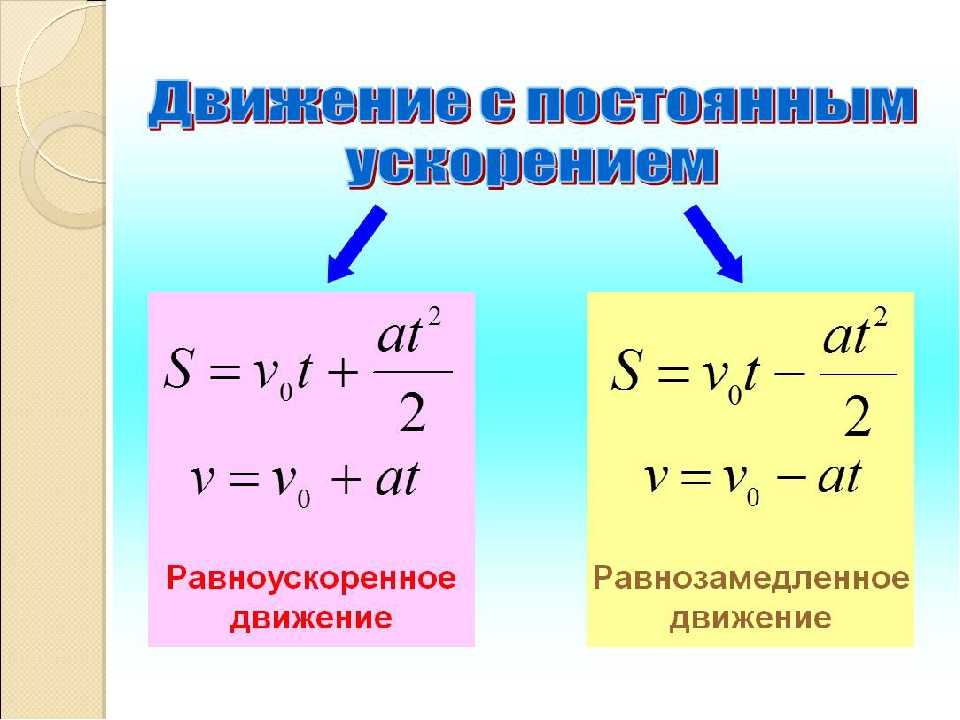
- S=V*t.
То есть, зная скорость и время движения, мы всегда сможем найти путь.
Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.
Расчет времени при равномерном движении
Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.
- t=S/V.
Полученные выше формулы будут справедливы, если тело совершало равномерное движение.
При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.
Расчет пути при неравномерном движении
Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.
- S=Vcp*t
Расчет времени при неравномерном движении
Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.
- t=S/Vcp.
Графиком равномерного движения, в координатах S(t) будет являться прямая линия.
Скорость – это величина, которая описывает быстроту перемещения объекта из точки А в точку Б. Обозначается латинской буквой V – сокращение от латинского velocitas – скорость. Скорость можно узнать, если известно время (t), в течение которого перемещался объект, и расстояние (S), которое объект преодолел.
Чтобы расчитать скорость, используйте формулу пути: V=S/t. Например, за 12 секунд объект продвинулся на 60 метров, значит его скорость равнялась 5 м/с (V=60/12=5).
Используйте одинаковые единицы измерения, если сравниваете скорость двух разных объектов. Основной единицей измерения скорости в международной системе единиц являются метры в секунду или сокращенно м/с. Также распространены километры в часы, километры в секунду, метры в минуту и метры в секунду. В англоязычных странах используются мили в секунду, мили в час, футы в секунду и футы в минуту.
В предложенном задании нас просят объяснить, как найти скорость, время и расстояние в задаче. Задачи с такими величинами относят к задачам на движение.
Задачи на движение
Всего в задачах на движение используются три основные величины, как правило, одна из которых, является неизвестной и её надо найти. Сделать это можно с помощью формул:
- Скорость. Скоростью в задаче называют величину, которая обозначает, какое расстояние проделал объект за единиц времени. Следовательно, она находится по формуле:
скорость = расстояние / время.
- Время. Временем в задаче называют величину, которая показывает, какое время затратил объект на путь при определённое скорости. Соответственно, оно находится по формуле:
время = расстояние / скорость.
- Расстояние. Расстоянием или путём в задаче называют величину, которая показывает, какое расстояние преодолел субъект при определённой скорости за какой-либо промежуток времени. Таким образом, оно находится по формуле:
расстояние = скорость * время.
Итог
Таким образом, подводим итог. Задачи на движения могут решаться по вышеуказанным формулам. В заданиях также может быть несколько движущихся объектов или несколько отрезков пути и времени. В таком случае решение будет состоять из нескольких отрезков, которые в итоге складываются или вычитываются в зависимости от условий.
Которое потребовалось на этот путь:
v=s/t, где:
v – это скорость,
s – длина пройденного пути, а
t – время
Примечание.
Предварительно, все единицы измерения следует привести к одной системе (желательно СИ).
Пример 1
Разогнавшись до максимальной скорости, автомобиль проехал один километр за полминуты, после чего затормозил и .
Определите максимальную скорость автомобиля.
Решение.
Так как после разгона автомобиль двигался на максимальной скорости, то ее по условиям задачи можно считать равномерной. Следовательно:
s=1 км,
t=0,5 мин.
Приводим единицы измерения времени и пройденного пути к одной системе (СИ):
1 км=1000 м
0,5 мин= 30 сек
Значит, максимальная скорость автомобиля:
1000/30=100/3=33 1/3 м/с, или приблизительно: 33,33 м/с
Для определения скорости тела при равноускоренном движении необходимо знать начальную скорость и величину или другие связанные параметры. Ускорение может быть и отрицательным (в этом случае это, фактически, торможение).
Скорость равна начальной скорости плюс ускорение, умноженное на время. В виде это записывается следующим образом:
v(t)= v(0)+аt, где:
v(t) – скорость тела в момент времени t
Чему была равна скорость кирпича в момент приземления?
Решение.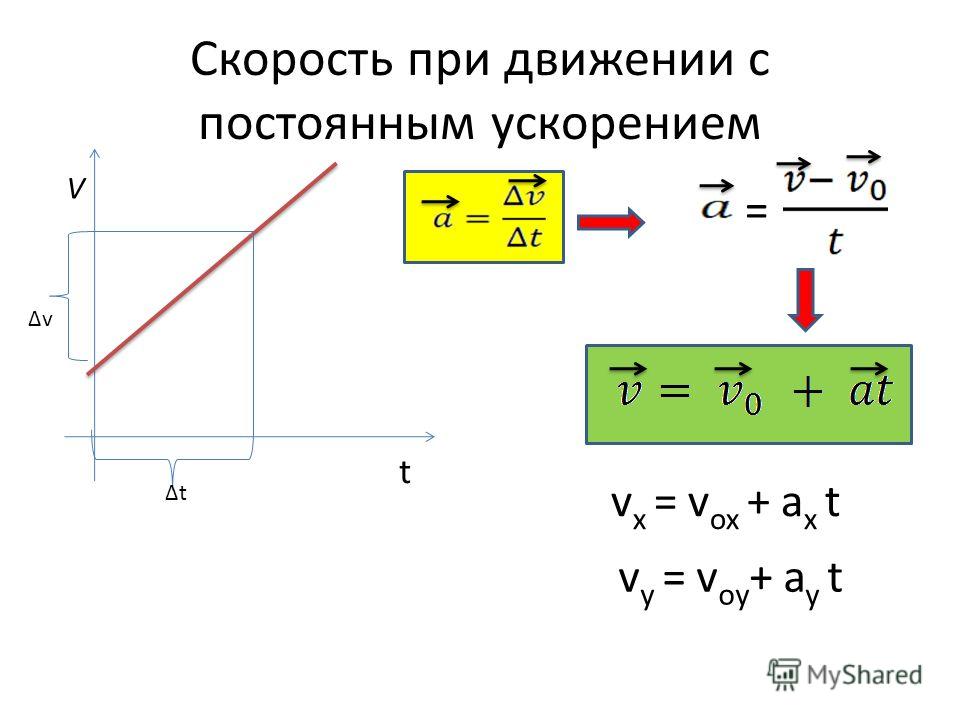
Так как направление начальной скорости и ускорения свободного падения совпадают, то скорость кирпича у поверхности земли будет равной:
Сопротивление в такого рода, как правило, не учитывается.
Скорость автомобиля постоянно меняется во время путешествия. Определением того, какая скорость у машины была в тот или иной момент пути, очень часто занимаются как сами автолюбители, так и компетентные органы. Тем более, что способов узнать скорость автомобиля огромное количество.
Инструкция
Самый простой способ определить скорость автомобиля знаком всем еще со школы. Для этого вам нужно зафиксировать количество километров, которое вы проехали, и время, за которое вы это расстояние преодолели. Рассчитывается скорость авто по : расстояние (км.) разделить на время (ч.). Так вы получите искомое число.
Вариант второй используется тогда, когда автомобиль резко остановился, но базовых замеров, как то время и расстояние, никто не проводил. В этом случае скорость автомобиля рассчитывают по его . Для подобных вычислений есть даже своя . Но использоваться она может только в том случае, если при торможении остался на дороге след.
Для подобных вычислений есть даже своя . Но использоваться она может только в том случае, если при торможении остался на дороге след.
Итак, формула следующим образом: начальная скорость автомобиля равна 0,5 х время нарастания торможения (м/с) х, установившееся замедление авто при торможении (м/с²) + корень из длины тормозного пути (м) х, установившееся замедление автомобиля при торможении (м/с²). Величина под названием «установившееся замедление авто при торможении» фиксированная и зависит только от того, какой асфальт имел место быть. В случае сухой дороги в формулу подставьте число 6,8 – оно прописано в ГОСТе, используемом для расчетов. Для мокрого асфальта данная величина будет равняться 5.
Как решать задачи на движение? Формула зависимости между скоростью, временем и расстоянием. Задачи и решения.
Формула зависимости времени, скорости и расстояния за 4 класс: как обозначается скорость, время, расстояние?
Люди, животные или машины могут двигаться с определенной скоростью.
- Путь – S
- Скорость – v
- Время – t
Если вы опаздываете в школу, вы можете этот же путь пройти за 20 минут, увеличив свою скорость. А значит, один и тот же путь может быть пройден за разное время и с различной скоростью.
Как зависит время прохождения пути от скорости?
Чем больше скорость, тем быстрее будет пройдено расстояние. И чем меньше скорость, тем больше времени понадобится для прохождения пути.
Как найти время, зная скорость и расстояние?
Для того, чтобы найти время, понадобившееся для прохождения пути, нужно знать расстояние и скорость. Если расстояние разделить на скорость — вы узнаете время. Пример такой задачи:
Если расстояние разделить на скорость — вы узнаете время. Пример такой задачи:
Задача про Зайца. Заяц убегал от Волка со скоростью 1 километр за минуту. Он пробежал до своей норы 3 километра. За какое время Заяц добежал до норы?
Как легко решать задачи на движение, где нужно найти расстояние, время или скорость?
- Внимательно прочитайте задачу и определите, что известно из условия задачи.
- Напишите на черновике эти данные.
- Также напишите, что неизвестно и что нужно найти
- Воспользуйтесь формулой для задач про расстояние, время и скорость
- Введите в формулу известные данные и решите задачу
Решение для задачи про Зайца и Волка.
- Из условия задачи определяем, что нам известно скорость и расстояние.
- Также из условия задачи определяем, что нам нужно найти время, которое нужно было зайцу, чтобы добежать до норы.
Пишем в черновик эти данные например так:
Время — неизвестно
Теперь запишем то же самое математическими знаками:
S — 3 километра
V — 1 км/мин
t — ?
Вспоминаем и записываем в тетрадь формулу для нахождения времени:
t = S: v
t = 3: 1 = 3 минуты
Как найти скорость, если известно время и расстояние?
Для то, чтобы найти скорость, если известно время и расстояние, нужно расстояние разделить на время. Пример такой задачи:
Пример такой задачи:
Заяц убегал от Волка и пробежал до своей норы 3 километра. Он преодолел это расстояние за 3 минуты. С какой скоростью бежал Заяц?
Решение задачи на движение:
- В черновик записываем, что нам известно расстояние и время.
- Из условия задачи определяем, что нужно найти скорость
- Вспоминаем формулу для нахождения скорости.
Формулы для решения таких задач показаны на картинке ниже.
Формулы для решения задач про расстояние, время и скорость
Подставляем известные данные и решаем задачу:
Расстояние до норы — 3 километра
Время, за которое Заяц добежал до норы — 3 минуты
Скорость — неизвестна
Запишем эти известные данные математическими знаками
S — 3 километра
t — 3 минуты
v — ?
Записываем формулу для нахождения скорости
v = S: t
Теперь запишем решение задачи цифрами:
v = 3: 3 = 1 км/мин
Как найти расстояние, если известно время и скорость?
Чтобы найти расстояние, если известно время и скорость нужно время умножить на скорость. Пример такой задачи:
Пример такой задачи:
Заяц убегал от Волка со скоростью 1 километр за 1 минуту. Чтобы добежать до норы ему понадобилось три минуты. Какое расстояние пробежал Заяц?
Решение задачи: Записываем в черновик, что нам известно из условия задачи:
Скорость Зайца — 1 километр за 1 минуту
Время, которое Заяц бежал до норы — 3 минуты
Расстояние — неизвестно
Теперь, то же самое запишем математическими знаками:
v — 1 км/мин
t — 3 минуты
S — ?
Вспоминаем формулу для нахождения расстояния:
S = v ⋅ t
Теперь запишем решение задачи цифрами:
S = 3 ⋅ 1 = 3 км
Как научиться решать более сложные задачи?
Чтобы научиться решать более сложные задачи нужно понять как решаются простые, запомнить какими знаками обозначаются расстояние, скорость и время. Если не получается запомнить математические формулы их нужно выписать на лист бумаги и всегда держать под рукой во время решения задач. Решайте с ребенком несложные задачи, которые можно придумать на ходу, например во время прогулки.
Решайте с ребенком несложные задачи, которые можно придумать на ходу, например во время прогулки.
Ребенок, который умеет решать задачи, может гордиться собой
Когда решают задачи про скорость, время и расстояние, очень часто делают ошибку, из-за того, что забыли перевести единицы измерения.
ВАЖНО: Единицы измерения могут быть любыми, но, если в одной задаче есть разные единицы измерения, переведите их одинаковые. Например, если скорость измерена в километрах за минуту, то расстояние обязательно должно быть представлено в километрах, а время в минутах.
Для любознательных : Общепринятая сейчас система мер называется метрической, но так было не всегда, и в старину на Руси использовали другие единицы измерения.
Задача про удава : Слоненок и мартышка мерили длину удава шагами. Они двигались навстречу друг другу. Скорость мартышка была 60 см за одну секунду, а скорость слоненка 20 см за одну секунду. На измерение они потратили 5 секунд. Какова длина удава? (решение под картинкой)
На измерение они потратили 5 секунд. Какова длина удава? (решение под картинкой)
Решение:
Из условия задачи определяем, что нам известно скорость мартышки и слоненка и время, которое им понадобилось для измерения длины удава.
Запишем эти данные:
Скорость мартышки — 60 см/сек
Скорость слоненка — 20 см/сек
Время — 5 секунд
Расстояние неизвестно
Запишем эти данные математическими знаками:
v1 — 60 см/сек
v2 — 20 см/сек
t — 5 секунд
S — ?
Запишем формулу для расстояние, если известна скорость и время:
S = v ⋅ t
Посчитаем, какое расстояние прошла мартышка:
S1 = 60 ⋅ 5 = 300 см
Теперь посчитаем, сколько прошел слоненок:
S2 = 20 ⋅ 5 = 100 см
Суммируем расстояние, которое прошла мартышка и расстояние, которое прошел слоненок:
S = S1 + S2 = 300 + 100 = 400 см
График зависимости скорости тела от времени: фото
Расстояние, преодолеваемое с разной скорость преодолевается за разное время. Чем больше скорость — тем меньше потребуется времени для передвижения.
Чем больше скорость — тем меньше потребуется времени для передвижения.
Таблица 4 класс: скорость, время, расстояние
В таблице ниже приведены данные для которых нужно придумать задачи, а потом их решить.
| № | Скорость (км/час) | Время (час) | Расстояние (км) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Вы можете пофантазировать и придумать задачи к таблице сами. Ниже наши варианты условия задач:
- Мама отправила Красную Шапочку к бабушке. Девочка постоянно отвлекалась и шла по лесу медленно, со скоростью 5 км/час. На путь она потратила 2 часа. Какое расстояние за это время прошла Красная Шапочка?
- Почтальон Печкин вез на велосипеде посылку со скоростью 12 км/час.
 Он знает, что расстояние между его домом и домом Дяди Федора 12 км. Помогите Печкину рассчитать, сколько времени понадобится на дорогу?
Он знает, что расстояние между его домом и домом Дяди Федора 12 км. Помогите Печкину рассчитать, сколько времени понадобится на дорогу? - Папа Ксюши купил автомобиль и решил отвезти семью на море. Машина ехала со скоростью 60 км/час и на дорогу было потрачено 4 часа. Какое расстояние между домом Ксюши и морским побережьем?
- Утки собрались в клин и полетели в теплые края. Птицы махали крыльями без устали 3 часа и преодолели за это время 300 км. Какой была скорость птиц?
- Самолет АН-2 летит со скоростью 220 км/час. Он вылетел из Москвы и летит в Нижний Новгород, расстояние между этими двумя городами 440 км. Сколько времени самолет будет в пути?
Ответы на приведенные задачи можно найти в таблице ниже:
| № | Скорость (км/час) | Время (час) | Расстояние (км) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Примеры решения задач на скорость, время, расстояние за 4 класс
Если в одной задаче есть несколько объектов движения, нужно научить ребенка рассматривать движение этих объектов отдельно и только потом вместе. Пример такой задачи:
Пример такой задачи:
Двое друзей Вадик и Тема решили прогуляться и вышли из своих домов навстречу друг другу. Вадик ехал на велосипеде, а Тема шел пешком. Вадик ехал со скоростью 10 км/час, а Тема шел со скоростью 5 км в час. Через час они встретились. Какое расстояние между домами Вадика и Темы?
Эту задачу можно решить используя формулу зависимости расстояния от скорости и времени.
S = v ⋅ t
Расстояние, которое проехал Вадик на велосипеде будет равно его скорости умноженной на время в пути.
S = 10 ⋅ 1 = 10 километров
Расстояние, которое прошел Тема считают аналогично:
S = v ⋅ t
Подставляем в формулу цифровые значения его скорости и времени
S = 5 ⋅ 1 = 5 километров
Расстояние, которое проехал Вадик нужно прибавить к расстоянию, которое прошел Тема.
10 + 5 = 15 километров
Как научиться решать сложные задачи, для решения которых требуется логически мыслить?
Развивать логическое мышление ребенка, нужно решая с ним простые, а затем и сложные логические задачи. Эти задачи могут состоять из нескольких этапов. Перейти с одного этапа на другой можно только в том случае, если решен предыдущий. Пример такой задачи:
Эти задачи могут состоять из нескольких этапов. Перейти с одного этапа на другой можно только в том случае, если решен предыдущий. Пример такой задачи:
Антон ехал на велосипеде со скоростью 12 км/час, а Лиза ехала на самокате со скоростью в 2 раза меньше, чем у Антона, а Денис шел пешком со скоростью в 2 раза меньше, чем у Лизы. Какова скорость Дениса?
Чтобы решить эту задачу нужно сначала узнать скорость Лизы и только после этого скорость Дениса.
Кто едет быстрее? Задача про друзей
Иногда в учебниках для 4 класса попадаются непростые задачи. Пример такой задачи:
Два велосипедиста выехали из разных городов навстречу друг другу. Один из них спешил и мчался со скоростью 12 км/час, а второй ехал не спеша со скоростью 8 км/час. Расстояние между городами из которых выехали велосипедисты 60 км. Какое расстояние проедет каждый велосипедист, перед тем как они встретятся? (решение под фото)
Решение:
- 12+8 = 20 (км/час) — это общая скорость двух велосипедистов, или скорость с которой они приближались друг к другу
- 60 : 20 = 3 (часа) — это время через которое велосипедисты встретились
- 3 ⋅ 8 = 24 (км) — это расстояние, которое проехал первый велосипедист
- 12 ⋅ 3 = 36 (км) — это расстояние, которое проехал второй велосипедист
- Проверка: 36+24=60 (км) — это расстояние, которое проехали два велосипедиста.
 2})\left(2\right).\]
2})\left(2\right).\]Кинематическое уравнение скорости при свободном падении
Свободное падение происходит с постоянным ускорением, что было установлено еще Галилеем, поэтому скорость в кинематике определяет уравнение для равнопеременного движения:
\[\overline{v}\left(t\right)={\overline{v}}_0+\overline{g}t\ \left(3\right).\]
Уравнение (3) показывает изменение вектора скорости $\overline{v}\left(t\right),$ где ${\overline{v}}_0$ – начальная скорость движения тела.
Используя это уравнение, и зная начальные условия движения тела можно найти скорость тела относительно избранной системы отсчета для любого момента времени.
Скорость тела, брошенного под углом к горизонту
Допустим, что тело бросили под углом $\alpha $ к горизонту. Ось X системы координат направим горизонтально, ось Y перпендикулярно горизонту вверх, тогда начальные условия движения для скорости данного тела запишем как:
\[\left\{ \begin{array}{c} v_x\left(t=0\ \right)=v_0{\cos \alpha ,\ } \\ v_y\left(t=0\ \right)=v_0{\sin \alpha \ } \end{array} \right.
 \left(4\right).\]
\left(4\right).\]Это означает, что тело бросили под углом $\alpha $ к горизонту с начальной скоростью ${\overline{v}}_0$. При этом проекции уравнения (3) дадут нам систему уравнений:
\[\left\{ \begin{array}{c} v_x\left(t\right)=v_0{\cos \alpha ,\ } \\ v_y\left(t\right)=v_0{\sin \alpha -gt\ } \end{array} \right.\left(5\right).\]
Формула скорости при свободном падении тела из состояния покоя
Начальные условия для скорости движения для тела, которое падает из состояния покоя, запишем так:
\[\left\{ \begin{array}{c} v_x\left(t=0\ \right)=0, \\ v_y\left(t=0\ \right)=0 \end{array} \right.\left(6\right).\]
В таком случае выражение (3) в проекции на ось Y, которую выберем вдоль направления движения (рис.1), тела будет выглядеть как:
\[\left\{ \begin{array}{c} v_y=-gt \end{array} \right.\left(7\right).\]
В момент падения скорость тела при свободном его падении с высоты $h$ равна:
\[v_{pad}=-\sqrt{2gh}\left(8\right).
 \]
\]Знак минус в формуле (8) означает, что скорость падения направлена против нашей оси Y.
Отметим, что тело, брошенное вертикально вверх движется до максимальной высоты подъема столько же времени, сколько оно потом падает с этой высоты до точки бросания.
Примеры задач с решением
Пример 1
Задание. Тело бросили вертикально вверх. Оно вернулось в точку бросания через $t’$ секунд. Какова начальная скорость тела?\textit{}
Решение. Сделаем рисунок.
Запишем уравнение для скорости движения тела в векторном виде:
\[\overline{v}\left(t\right)={\overline{v}}_0+\overline{g}t\ \left(1.1\right).\]
Найдем проекцию этого уравнения на ось Y:
\[v=v_0-gt\ \left(1.2\right).\]
В точке максимального подъема скорость тела равна нулю, следовательно:
\[0=v_0-g{t\ }_{pod}\to v_0=g{t\ }_{pod}\left(1.
 3\right).\]
3\right).\]Принимая во внимание, что время подъема равно времени спуска при отсутствии сил трения, имеем:
\[{t\ }_{pod}=\frac{t’}{2}\left(1.4\right).\]
Подставим (1.4) в (1.3), имеем:
\[v_0=g\frac{t’}{2}.\]
Ответ. $v_0=g\frac{t’}{2}$
Пример 2
Задание. Одно тело бросили вертикально вверх с начальной скоростью равной $v_0.$ В этот же момент времени вертикально вниз с начальной скоростью $v_0$ бросили второе тело. Высота, с которой бросили это тело равно высоте максимального подъема первого тела. Какова скорость первого и второго тел в момент встречи этих двух тел? Тела считайте материальными точками, сопротивление воздуха не учитывать.
Решение. Сделаем рисунок.
За основу решения задачи примем уравнение для скорости движения тела в поле тяжести Земли:
\[\overline{v}\left(t\right)={\overline{v}}_0+\overline{g}t\ \left(2.
 2_0}{2g}=v_0+\frac{v_0}{4}=\frac{5}{4}v_0.\]
2_0}{2g}=v_0+\frac{v_0}{4}=\frac{5}{4}v_0.\]Ответ. $v_1=\frac{3}{4}v_0,$ $v_2=\frac{5}{4}v_0$
Читать дальше: формула ускорения свободного падения.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
3 факта о времени с ускорением и расстоянием –
Здесь мы собираемся обсудить, как найти необходимое время для совершения прямолинейного движения.
Объект приобретает скорость, когда меняет свое положение со временем, и ускоряется, когда его скорость меняется со временем. Если мы знаем значение смещения и времени, мы можем найти скорость; аналогично можно найти ускорение. Теперь возникает вопрос, как найти время с ускорением и расстоянием? В основном, это зависит от вопроса и количества, указанного в вопросе. Мы можем узнать время линейного движения, если у нас есть следующие три типа комбинаций данных, заданных в вопросе,
- Ускорение, а также начальная и конечная скорость объекта
- Скорость и пройденное расстояние
- Скорость и ускорение
Предположим, вопрос предоставляет величину ускорения, начальную скорость и конечную скорость объекта.
 В этом случае лучший способ вычислить время, необходимое для завершения движения, — это решить первое кинематическое уравнение движения.
В этом случае лучший способ вычислить время, необходимое для завершения движения, — это решить первое кинематическое уравнение движения.Предположим, что автомобиль начинает движение с начальной скоростью (u) и конечной скоростью (v), которая в процессе движения ускоряется. Величина ускорения (а) в положительном направлении х. Теперь, чтобы узнать время, необходимое для совершения движения, воспользуемся первым уравнением кинематики. Первое кинематическое уравнение движения: Автомобиль, движущийся в направлении x
Изображение предоставлено: Videoplasty.com, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, через Wikimedia CommonsСледовательно,
u – начальная скорость автомобиля
v – конечная скорость автомобиля движение
а – Ускорение автомобиля
Когда заданы скорость и расстояние, пройденное объектом
Когда вопрос дает величину скорости и расстояние, которое преодолевает объект, мы можем быстро определить время, необходимое для этого движения.
 Мы знаем, что скорость — это скорость изменения смещения во времени. Математически записывается как
Мы знаем, что скорость — это скорость изменения смещения во времени. Математически записывается какСледовательно,
Используя приведенные выше формулы, мы можем рассчитать время, необходимое для завершения его движения.
Когда заданы скорость и ускорениеКогда объект движется с непрерывно изменяющейся скоростью, это означает, что объект ускоряется в движении с некоторой величиной (a). Мы знаем, что ускорение — это скорость изменения скорости во времени. Итак, если вопрос дает величину средней скорости и ускорения объекта, мы можем легко узнать время, необходимое для этого движения. Как известно,
Следовательно,
–
9 0005 Некоторые примеры
и часто задаваемые вопросы Велосипед начинает движение с начальной скоростью 30 м/с и ускорением 30 м/с 2 .После времени t, его скорость 90 м/сек. Сколько времени требуется велосипеду, чтобы набрать конечную скорость?Дано,
начальная скорость (u) – 30 м/с
конечная скорость (v) – 90 м/с
Ускорение – 30 м/с 2
Здесь мы задали начальную скорость, конечную скорость, а также ускорение велосипеда, затем используем первое кинематическое уравнение, чтобы найти вне времени,
Мы знаем, что первое кинематическое уравнение движения имеет вид 003
90 = 30 + 30t
Поэтому
t = 2 с
Следовательно, велосипеду требуется 2 с, чтобы развить скорость 90 м/с.
Автомобиль движется со скоростью 50 м/с. Сколько времени потребуется, чтобы преодолеть расстояние 500 км?
Дано, скорость автомобиля – 50 м/с
Пройденное расстояние – 500 км что скорость есть скорость изменения расстояния относительно время
т.е. скорость = расстояние/время
Время = расстояние/скорость
t = 10000 с
т.е. 0003
Автомобиль движется из положения А в положение со скоростью 30 м/с и ускорением 3 м/ в движении. Сколько времени нужно, чтобы добраться из пункта А в пункт Б?Мы знаем, что ускорение — это изменение скорости во времени.
Ускорение = скорость/время
Из приведенного выше уравнения мы можем найти время, необходимое для перемещения автомобиля из точки A в точку B.
Положив заданные значения, T = 10 сПоэтому автомобилю требуется 10 с, чтобы переместиться из A в B
Часто задаваемые вопросы Что такое прямолинейное движение объекта?когда объект совершает прямолинейное движение из точки А в точку В, то такое линейное движение называется прямолинейным движением.
В чем разница между скоростью и скоростью?
Скорость — это скалярная величина, а скорость — векторная величина. Скорость определяет величину, с которой движется объект, а скорость определяет величину и направление движения объектов. можно сказать, что скорость есть величина скорости.
Какие три кинематических уравнения движения?три кинематических уравнения выглядят следующим образом: 006
- v 2 = и 2 + 2as
где, s, a, t, u, v представляют перемещение, ускорение, начальную скорость, конечную скорость и время движения соответственно.
Что такое Средняя скорость объекта?средняя скорость – это отношение общего расстояния, пройденного при движении, к общему времени, необходимому для совершения движения. Формула средней скорости выглядит следующим образом:
Ускорение и время: значение и примеры
Вы когда-нибудь задумывались над тем, какие ощущения испытывает лифт, когда он разгоняется, а затем останавливается? Это рывковое ощущение связано с ускорением лифта и тем фактом, что оно непостоянно. Со временем, когда вы находитесь в подъемнике, ускорение подъемника будет меняться, и это изменение ускорения со временем и приводит к ощущению рывков. Читайте дальше для объяснений и примеров изменения ускорения со временем. 92.\)
Со временем, когда вы находитесь в подъемнике, ускорение подъемника будет меняться, и это изменение ускорения со временем и приводит к ощущению рывков. Читайте дальше для объяснений и примеров изменения ускорения со временем. 92.\)
Ускорение напрямую связано со временем в том смысле, что оно представляет собой скорость изменения скорости с течением времени. Эта скорость изменения может быть линейной или квадратичной зависимостью.
Если вы исследуете линейную зависимость с постоянным ускорением с заданными значениями для комбинации смещения, начальной скорости, конечной скорости, ускорения и времени, вы должны применить уравнения SUVAT и решить для своей неизвестной переменной в своем решении. Вы можете увидеть дальнейшее объяснение этого ниже.
Вы можете применять SUVAT к нескольким измерениям — например, при движении снаряда вы будете рассматривать движение в плоскостях \(x\) и \(y\) и разрешать каждую плоскость отдельно, используя SUVAT и тригонометрию. Для получения дополнительной информации см. Дополнительные снаряды.
Для получения дополнительной информации см. Дополнительные снаряды.
Если бы вам представили функцию, которая приводит к непостоянному ускорению — она может быть квадратичной, — вы бы применили дифференциальный или интегральный метод, так как взаимосвязь другая.
Большинство вопросов, оценивающих решение с помощью дифференциального или интегрального метода, будут касаться \(\mathrm{d} t\), что означает, что функции отслеживают изменение переменной во времени. Этими переменными могут быть положение, скорость или ускорение. На приведенном ниже рисунке показано, как это будет работать.
Рис. 1. График, показывающий соотношение между смещением, скоростью и ускорением.
Ускорение и уравнение времени
Глядя на график выше, вы видите, как связаны перемещение, скорость и ускорение, но как это записать математически?
Если у вас есть выражение для положения объекта, заданное как \(r,\), вы можете видеть, что скорость будет равна тому, как это положение изменяется со временем:
\[v=\frac{\mathrm{d} r}{\mathrm{d} t}. \] 92}.\]
\] 92}.\]
Это производные отношения, которые вы используете для оценки скорости и ускорения. Как видно из рисунка, если вы хотите работать в другом направлении, вы просто интегрируете:
\[v=\int a\, \mathrm{d} t\]\[r=\int v\, \mathrm {d} t.\]
Как вы можете видеть в приведенных выше формулах, все они относятся к \(dt\), что подчеркивает взаимосвязь между временем и этими другими переменными – они меняются со временем.
График ускорения и времени
График ускорения и времени можно использовать для определения изменения скорости за определенный период времени. Как вы видели выше, метод перехода от ускорения к скорости — это интегрирование по времени. В графическом формате это означает нахождение площади между линией и осью \(x\). Давайте посмотрим на рисунок ниже, чтобы контекстуализировать это.
Рис. 2. Пример графика ускорение-время.
Вы видели, как нахождение площади, ограниченной линией и осью, дает изменение скорости и как это связано с интегрированием, но давайте посмотрим, как это работает.
Сначала проверьте от \(0\) до \(1\) секунд. Вы видите значение оси \(y\) \(-3\), которое указывает на то, что скорость уменьшается, и, поскольку этот временной интервал равен одной секунде, вы можете понять, что в интервале скорость упала на \(3\text{ РС}\). Это подходит, так как площадь между линией и осью в этом интервале равна \(-3\cdot 1\).
Теперь посмотрим на интервал сразу после между \(1\) и \(3\) секундами. Здесь линия на оси x указывает на то, что скорость не меняется с течением времени – нет ускорения.
Давайте теперь посмотрим между \(5\) и \(7\) секундами – здесь область между линией и осью определяется:
\[a \Delta t= -2\cdot 2 = – 4\text{ м/с}.\]
Это означает, что скорость уменьшалась на \(-2\text{ м/с}\) в течение \(2\) секунд, поэтому скорость уменьшилась в общей сложности на \( 4\текст{ м/с}.\)
Давайте теперь посмотрим на пример вопроса, используя этот рисунок.
Что касается приведенного выше графика ускорение-время, каково изменение значений скорости в \(3\) и \(7\) секунд?
Решение
Глядя на график, вы можете увидеть два изменения ускорения за период времени. 2\) 92\) за \(2\) секунд. Это приводит к уменьшению \(4\text{ м/с}\). Следовательно, изменение значений скорости в \(3\) и \(7\) секунд равно \(0\text{ м/с}\).
2\) 92\) за \(2\) секунд. Это приводит к уменьшению \(4\text{ м/с}\). Следовательно, изменение значений скорости в \(3\) и \(7\) секунд равно \(0\text{ м/с}\).
Ускорение и время до скорости
Теперь вы увидели общий принцип перемещения между смещением, ускорением и временем, когда у вас есть функция, определяющая движение во времени с помощью методов интегрирования и дифференцирования. Давайте теперь посмотрим на пример, который реализует этот принцип на практике.
Частица имеет ускорение, которое меняется со временем:
\[a=3\sin(2t).\]
Если она стартует из состояния покоя, найдите ее скорость через 30 секунд.
Решение
Ваша методология настолько проста, насколько может быть такой вопрос. У вас есть один шаг преобразования — вы интегрируете ускорение, чтобы получить скорость — вы применяете начальные условия, а затем решаете за 30 секунд.
Шаг первый: интегрировать
\[\begin{align} v&=\int a\, \mathrm{d}t\\&=\int 3\sin(2t)\, \mathrm{d} t \\&=3\cdot \int \sin(2t)\, \mathrm{d} t\\&=3\left( -\frac{1}{2}\right) \cos(2t)+C\ \&=- \frac{3}{2}\cos(2t)+C \end{align}\]
Шаг второй: применить начальные условия и найти постоянную интегрирования
Вы знаете, что частица начинается с покоя, поэтому: \(v=0\) и \(t=0\).
\[\begin{align} v&=- \frac{3}{2}\cos(2t)+C\\ 0&=- \frac{3}{2}\cos(2\cdot 0)+C \\ 0&=\left[- \frac{3}{2}\cdot 1 \right] +C\\ \frac{3}{2}&=C. \end{align}\]
Поэтому
\[ v=- \frac{3}{2}\cos(2t)+ \frac{3}{2} . \]
Шаг третий: Рассчитайте скорость при \(t=30\)
Теперь вы берете выражение для скорости в терминах времени и подставляете свое значение времени.
\[\begin{align} v&=- \frac{3}{2}\cos(2t)+ \frac{3}{2} \\&=- \frac{3}{2}\cos( 2\cdot 30)+ \frac{3}{2} \\&=0.75\text{ м/с}\end{align}\]
Ускорение и время до расстояния
Теперь вы хорошо понимаете, как Чтобы найти решение вопроса, когда ускорение меняется со временем, вы можете дважды интегрировать его, чтобы увеличить расстояние, и вы графически изучили, как эта теория работает при переходе к скорости. 92}.\]
Сначала найдите скорость объекта через время \(t\), а затем найдите его положение через \(7\) секунд. Через \(1\) секунду объект имеет скорость \(6\text{ м/с}\) и прошел \(2,4\text{ м}\) через \(1,5\) секунд. 2}\, \mathrm{d} t\\&=4\ln|t|+C-\left[-\frac{2}{t}\ справа]\\&= 4\ln|t|+\frac{2}{t} +C. \конец{выравнивание}\]
2}\, \mathrm{d} t\\&=4\ln|t|+C-\left[-\frac{2}{t}\ справа]\\&= 4\ln|t|+\frac{2}{t} +C. \конец{выравнивание}\]
Вы знаете, что объект имеет скорость \(6\) м/с через \(1\) секунду, поэтому вы можете применить эти начальные условия: \(v=6\) и \(t=1.\)
\[\begin{align}v&= 4\ln|t|+\frac{2}{t} +C \\ 6&=4\ln|1|+ \frac{2}{1}+C \ \ 6&= 0+2+С\\4&=С. \end{align} \]
Поэтому
\[ v= 4\ln|t|+\frac{2}{t} +4.\]
Шаг второй: вычислить позицию через 7 секунд
Чтобы получить выражение для положения, вам нужно будет снова проинтегрировать – на этот раз от скорости до ускорения.
\[\begin{align} r&=\int v\, \mathrm{d} t \\ &=\int (4\ln|t|+\frac{2}{t} +4) \, \ mathrm{d} t\\&=\int 4\ln|t|dt+\int \frac{2}{t} \, \mathrm{d} t+ \int 4 \, \mathrm{d} t\\& = 4t\ln|t|-4t+2\ln|t|+4t+C\\&=4t\ln|t|+2\ln|t|+C\end{align}\]
Вы знаете объект прошел \(2,4\текст{м}\) через \(1,5\) секунд, поэтому вы можете применить начальные условия \(r=2,4\) и \(t=1,5\).

 Он знает, что расстояние между его домом и домом Дяди Федора 12 км. Помогите Печкину рассчитать, сколько времени понадобится на дорогу?
Он знает, что расстояние между его домом и домом Дяди Федора 12 км. Помогите Печкину рассчитать, сколько времени понадобится на дорогу? 2})\left(2\right).\]
2})\left(2\right).\] \left(4\right).\]
\left(4\right).\] \]
\] 3\right).\]
3\right).\] 2_0}{2g}=v_0+\frac{v_0}{4}=\frac{5}{4}v_0.\]
2_0}{2g}=v_0+\frac{v_0}{4}=\frac{5}{4}v_0.\]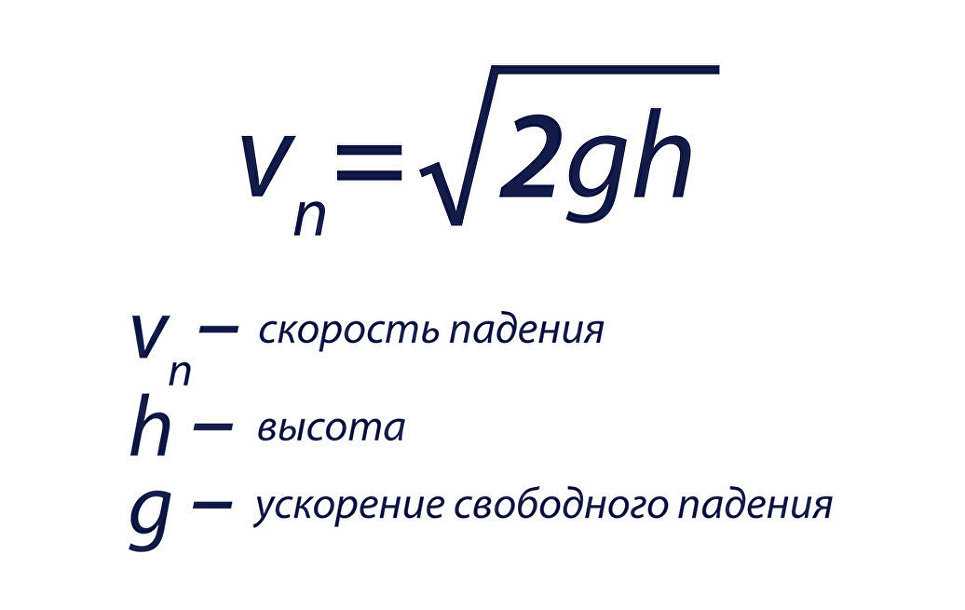 В этом случае лучший способ вычислить время, необходимое для завершения движения, — это решить первое кинематическое уравнение движения.
В этом случае лучший способ вычислить время, необходимое для завершения движения, — это решить первое кинематическое уравнение движения. Мы знаем, что скорость — это скорость изменения смещения во времени. Математически записывается как
Мы знаем, что скорость — это скорость изменения смещения во времени. Математически записывается как
