Напряжение через сопротивление: Электрическое сопротивление. Закон Ома для участка электрической цепи — урок. Физика, 8 класс.

Сила тока в резисторе. Определить силу тока в резисторе.

Один из способов определения силы тока в резисторе – это ее прямое измерение мультиметром. Измерения следует проводить в разрыве цепи после резистора следующим образом:

– выставить на тестере максимально допустимый диапазон,

– присоединить щупы прибора к месту разрыва цепи.

Применив закон Ома, искомую величину можно также определить расчетным путем:

где I – сила тока, U – напряжение, R – сопротивление (единицы измерения ампер (А), вольт (В), ом (Ом) соответственно).

В приборостроении и электротехнике применяются различные типы соединения и подключения резисторов, что обеспечивает разнообразие электротехнических свойств электрических схем.

Соединение элементов в одну цепь осуществляется следующими способами:

• последовательно;

• параллельно;

• смешанно.

Общие схемы типов соединений представлены на рисунке 1.

Рисунок 1. Типы соединений резисторов

Параллельным соединением принято считать соединение, при котором элементы цепи соединены так, что их начала могут соединиться в одной точке, а концы – в другой (см.рис.2)

Рисунок 2. Параллельное соединение резисторов

Потоку заряженных частиц при прохождении участка АВ предоставлено несколько вариантов пути, поэтому на каждом участке с резистором будет протекать ток, величиной, обратно пропорциональной сопротивлению резистора.

При увеличении нагрузки параллельного соединения, в случае подключения большого числа резисторов способом параллельного соединения в электрическую цепь, общее сопротивление цепи значительно уменьшится, за счет увеличения числа путей, предоставленных потоку заряженных частиц. Увеличение количества возможных вариантов движения влечет за собой уменьшение противодействия движению тока.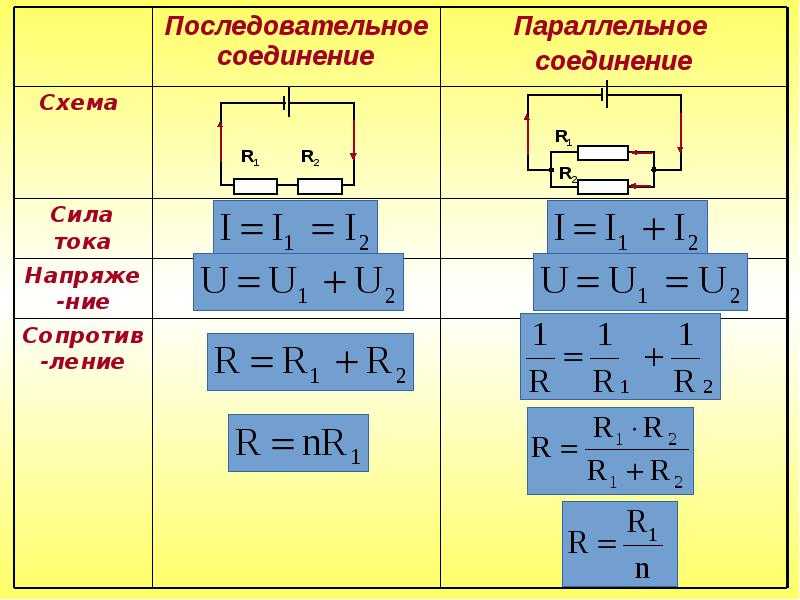

Как найти сопротивление параллельно соединенных резисторов?

Общее сопротивление резисторов в случае параллельного соединения определено по закону Ома в следующем соотношении:

и рассчитывается по формуле:

Для примера произведем расчет общего сопротивления для цепи из двух резисторов, обладающих сопротивлением R₁= R₂=7Ом (см. рис.3а)

R₁₂= 7*7/ (7+7) = 3,5Ом

Сопротивление на участке АВ _{(1– 2)} в 2 раза меньше R_{каждого из резисторов.}

При параллельном подсоединении к рассматриваемой цепи еще одного резистора, также обладающего аналогичным сопротивлением R₃=7Ом (см. рис.3б) общее сопротивление цепи рассчитывается с учетом предыдущих вычислений, где R₁₂= 3,5Ом

Rобщ= 3,5*7/ (3,5+7) = 2,33 Ом

R₁₂₃< R₃

Рисунок 3.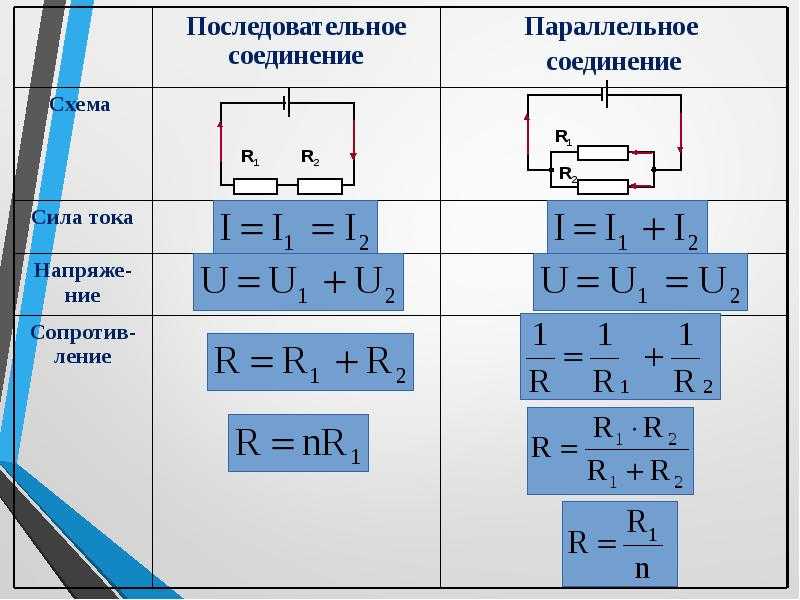 Увеличение цепи параллельного соединения резисторов

Из расчетов следует, что общее сопротивление (см. рис.3в) всегда будет меньше сопротивления любого параллельно включенного резистора. Такое условие обеспечивается равенством токов на входе и выходе узлов или групп параллельных резисторов и постоянством напряжения в сети.

Что такое последовательное соединение резисторов?

При последовательном соединении резисторы подсоединяются друг за другом, при этом конец предыдущего резистора соединен с началом последующего резистора (рисунок 4).

Рисунок 3. Последовательное соединение резисторов.

Потоку заряженных частиц при прохождении участка АВ предоставлен один путь, поэтому, чем больше резисторов подсоединено, тем большее сопротивление движущимся заряженным частицам они оказывают, то есть общее сопротивление участка цепи Rобщ возрастает.

Формула для расчета общего сопротивления при последовательном соединении имеет вид:

Как рассчитать напряжения на последовательно соединенных резисторах?

Последовательное соединение резисторов увеличивает общее сопротивление.

Ток во всех частях схемы будет одинаковым, при этом будет определяться падение напряжения на каждом резисторе.

Общее напряжение питания на резисторах, соединенных последовательно, равно сумме разностей потенциалов на каждом резисторе:

U_{Rобщ =}U_R1+ U_R2 + U_R3+ U_R4

Применив закон Ома, можно вычислить напряжение на каждом резисторе:

U_R1=I*R₁,_{UR2=I*R2, UR3=I*R3, U}

R4=I*R₄

Напряжение на участке АВ рассчитывается по формуле:

U_АВ=I* (R₁ + R₂+R₃+R₄)

А ток в цепи:

Резисторы, соединенные последовательно, применяются в электротехнике в качестве делителя напряжения.

Рисунок 5. Схема простейшего делителя напряжения

Регулируя сопротивление обоих резисторов можно выделить требуемую часть входящего напряжения. При необходимости деления напряжения на несколько частей к источнику напряжения подключается несколько последовательно соединенных резисторов.

Смешанное соединение резисторов

В электротехнике наиболее распространено использование различных комбинаций параллельного и последовательного подключения. Силу тока при смешанном соединении резисторов определяют путем разделения цепи на последовательно соединенные части. Однако для определения общего сопротивления в случае параллельного сопротивления различных частей следует применять соответствующую формулу.

Алгоритм расчета смешанного подключения аналогичен правилу расчета базовой схемы последовательного и параллельного подключения резисторов. В этом нет ничего нового: нужно правильно разложить предложенное решение на пригодные для расчета части.

Участки с элементами подключаются поочередно или параллельно. Гибридное резистивное соединение представляет собой комбинацию последовательного и параллельного. Эту комбинацию иногда называют последовательно-параллельным соединением.

На рисунке 6 представлена схема смешанного соединения резисторов.

Рисунок 6. Смешанное соединение резисторов.

На рисунке показано, что резисторы R₂ и R₃ соединены параллельно, а R₁, R₂₃ и R₄ последовательно.

Чтобы рассчитать сопротивление этого соединения, вся схема делится на простейшие части, начиная с параллельного или последовательного сопротивления. Тогда следующий алгоритм выглядит следующим образом:

1. Определите эквивалентное сопротивление части резистора, подключенной параллельно.

2. Если эти части содержат резисторы, включенные последовательно, сначала рассчитайте их сопротивление.

3. Вычислив эквивалентное сопротивление резистора, перерисовываем схему. Обычно схема получается из последовательного эквивалентного сопротивления.

4. Рассчитайте сопротивление цепи.

Другие способы подключения хорошо видны на примере, показанном на рисунке. Без специальных расчетов очевидно, что параллельное соединение резисторов создает несколько путей для тока. Следовательно, в одиночном контуре его сила будет меньше по сравнению с контрольными точками на входе и выходе. При этом напряжение на отметке остается неизменным.

Пример участка цепи для расчета сопротивления смешанного соединения показан на рисунке 5.

Рисунок 7. Общее сопротивление участка цепи со смешанным соединением резисторов.

Что такое напряжение, ток, сопротивление: разбираемся на примерах

Содержание

Не имея определенных начальных знаний об электричестве, тяжело себе представить, как работают электрические приборы, почему вообще они работают, почему надо включать телевизор в розетку, чтобы он заработал, а фонарику хватает маленькой батарейки, чтобы он светил в темноте.

И так будем разбираться во всем по порядку.

Электричество

Электричество – это природное явление, подтверждающее существование, взаимодействие и движение электрических зарядов. Электричество впервые было обнаружено еще в VII веке до н.э. греческим философом Фалесом. Фалес обратил внимание на то, что если кусочек янтаря потереть о шерсть, он начинает притягивать к себе легкие предметы. Янтарь на древнегреческом – электрон.

Вот так и представляю себе, сидит Фалес, трет кусок янтаря о свой гиматий (это шерстяная верхняя одежда у древних греков), а затем с озадаченным видом смотрит, как к янтарю притягиваются волосы, обрывки ниток, перья и клочки бумаги.

Данное явление называется статическим электричеством. Вы можете повторить данный опыт. Для этого хорошенько потрите шерстяной тканью обычную пластмассовую линейку и поднесите ее к мелким бумажным кусочкам.

Следует отметить, что долгое время это явление не изучалось. И только в 1600 году в своем сочинении «О магните, магнитных телах и о большом магните – Земле» английский естествоиспытатель Уильям Гилберт ввел термин – электричество. В своей работе он описал свои опыты с наэлектризованными предметами, а также установил, что наэлектризовываться могут и другие вещества.

Далее на протяжении трех веков самые передовые ученые мира исследуют электричество, пишут трактаты, формулируют законы, изобретают электрические машины и только в 1897 году Джозеф Томсон открывает первый материальный носитель электричества – электрон, частицу, благодаря которой возможны электрические процессы в веществах.

Электрон – это элементарная частица, имеет отрицательный заряд примерно равный -1,602·10^-19 Кл (Кулон). Обозначается е или е^–.

Напряжение

Чтобы заставить перемещаться заряженные частицы от одного полюса к другому необходимо создать между полюсами разность потенциалов или – Напряжение. Единица измерения напряжения – Вольт (В или V). В формулах и расчетах напряжение обозначается буквой V. Чтобы получить напряжение величиной 1 В нужно передать между полюсами заряд в 1 Кл, совершив при этом работу в 1 Дж (Джоуль).

Для наглядности представим резервуар с водой расположенный на некоторой высоте. Из резервуара выходит труба. Вода под естественным давлением покидает резервуар через трубу. Давайте условимся, что вода – это электрический заряд, высота водяного столба (давление) – это напряжение, а скорость потока воды – это электрический ток.

Таким образом, чем больше воды в баке, тем выше давление. Аналогично с электрической точки зрения, чем больше заряд, тем выше напряжение.

Начнем сливать воду, давление при этом будет уменьшаться. Т.е. уровень заряда опускается – величина напряжения уменьшается. Такое явление можно наблюдать в фонарике, лампочка светит все тусклее по мере того как разряжаются батарейки.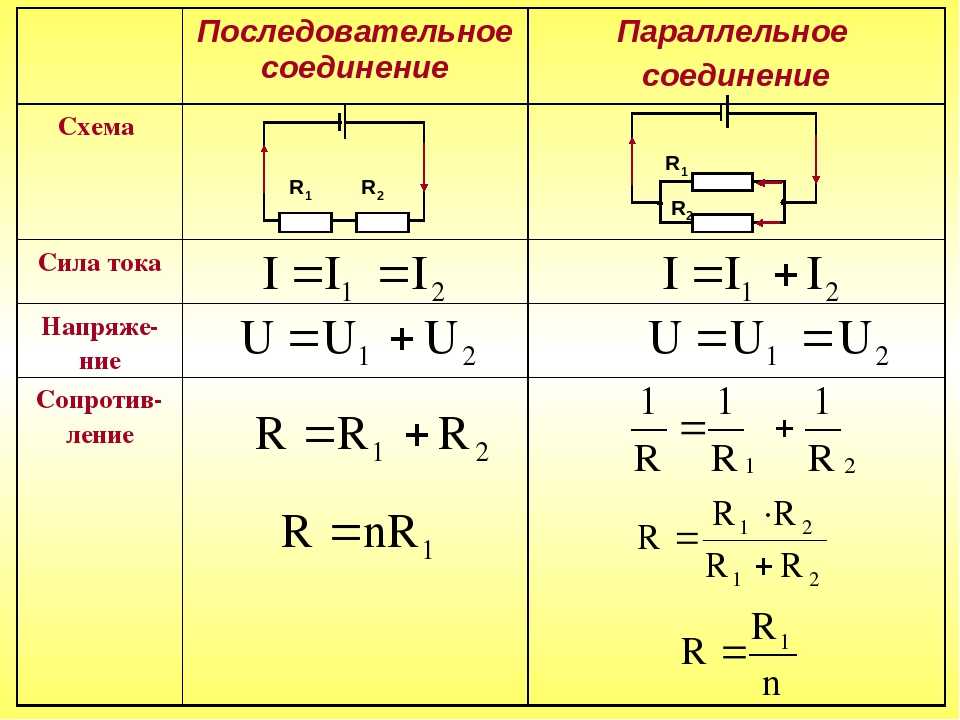 Обратите внимание, чем меньше давление воды (напряжение), тем меньше поток воды (ток).

 

Электрический ток

Электрический ток – это физический процесс направленного движения заряженных частиц под действием электромагнитного поля от одного полюса замкнутой электрической цепи к другому. В качестве частиц, переносящих заряд, могут выступать электроны, протоны, ионы и дырки. При отсутствии замкнутой цепи ток невозможен. Частицы способные переносить электрические заряды существуют не во всех веществах, те в которых они есть, называются проводниками и полупроводниками. А вещества, в которых таких частиц нет – диэлектриками.

Принято считать направление тока от плюса к минусу, при этом электроны движутся от минуса к плюсу!

Единица измерения силы тока – Ампер (А). В формулах и расчетах сила тока обозначается буквой I. Ток в 1 Ампер образуется при прохождении через точку электрической цепи заряда в 1 Кулон (6,241·10¹⁸ электронов) за 1 секунду.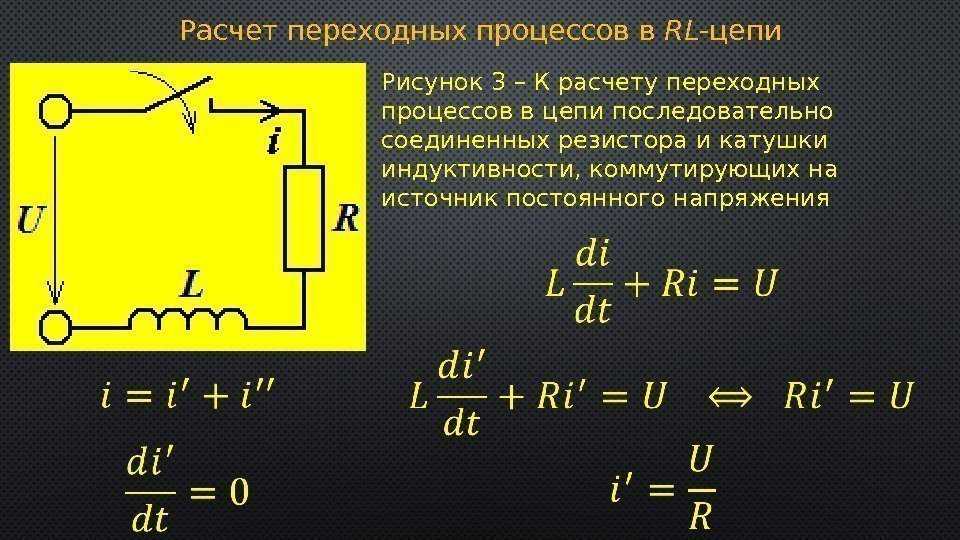

 

Вновь обратимся к нашей аналогии вода – электричество. Только теперь возьмем два резервуара и наполним их равным количеством воды. Отличие между баками в диаметре выходной трубы.

Откроем краны и убедимся, что поток воды из левого бака больше (диаметр трубы больше), чем из правого. Такой опыт – явное доказательство зависимости скорости потока от диаметра трубы. Теперь попробуем уравнять два потока. Для этого добавим в правый бак воды (заряд). Это даст большее давление (напряжение) и увеличит скорость потока (ток). В электрической цепи в роли диаметра трубы выступает сопротивление.

Проведенные эксперименты наглядно демонстрируют взаимосвязь между напряжением, током и сопротивлением. Подробнее о сопротивлении поговорим чуть позже, а сейчас еще несколько слов о свойствах электрического тока.

Если напряжение не меняет свою полярность, плюс на минус, и ток течет в одном направлении, то – это постоянный ток и соответственно постоянное напряжение. Если источник напряжения меняет свою полярность и ток течет то в одном направлении, то в другом – это уже переменный ток и переменное напряжение. Максимальные и минимальные значения (на графике обозначены как Io) – это амплитудные или пиковые значения силы тока. В домашних розетках напряжение меняет свою полярность 50 раз в секунду, т.е. ток колеблется то туда, то сюда, получается, что частота этих колебаний составляет 50 Герц или сокращенно 50 Гц. В некоторых странах, например в США принята частота 60 Гц.

Сопротивление

Электрическое сопротивление – физическая величина, определяющая свойство проводника препятствовать (сопротивляться) прохождению тока. Единица измерения сопротивления – Ом (обозначается Ом или греческой буквой омега Ω). В формулах и расчетах сопротивление обозначается буквой R. Сопротивлением в 1 Ом обладает проводник к полюсам которого приложено напряжение 1 В и протекает ток 1 А.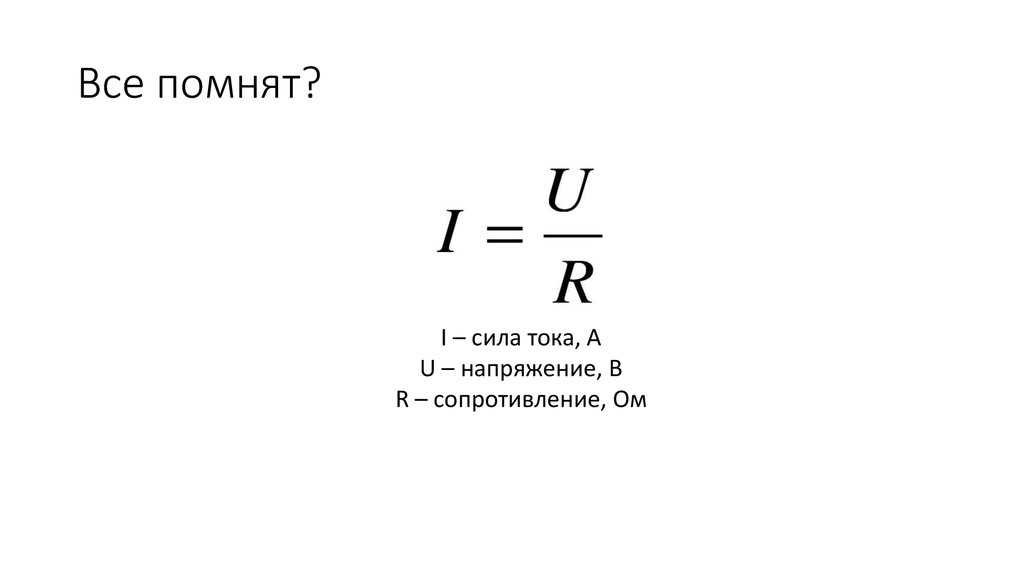

Проводники по-разному проводят ток. Их проводимость зависит, в первую очередь, от материала проводника, а также от сечения и длины. Чем больше сечение, тем выше проводимость, но, чем больше длина, тем проводимость ниже. Сопротивление – это обратное понятие проводимости.

На примере водопроводной модели сопротивление можно представить как диаметр трубы. Чем он меньше, тем хуже проводимость и выше сопротивление.

Сопротивление проводника проявляется, например, в нагреве проводника при протекании в нем тока. Причем, чем больше ток и меньше сечение проводника – тем сильнее нагрев.

 

Мощность

Электрическая мощность – это физическая величина, определяющая скорость преобразования электроэнергии. Например, вы не раз слышали: «лампочка на столько-то ватт». Это и есть мощность потребляемая лампочкой за единицу времени во время работы, т.е. преобразовании одного вида энергии в другой с некоторой скоростью.

Источники электроэнергии, например генераторы, также характеризуется мощностью, но уже вырабатываемой в единицу времени.

Единица измерения мощности – Ватт (обозначается Вт или W). В формулах и расчетах мощность обозначается буквой P. Для цепей переменного тока применяется термин Полная мощность, единица измерения – Вольт-ампер (В·А или V·A), обозначается буквой S.

И в завершение про Электрическую цепь. Данная цепь представляет собой некоторый набор электрических компонентов, способных проводить электрический ток и соединенных между собой соответствующим образом.

Что мы видим на этом изображении – элементарный электроприбор (фонарик). Под действием напряжения U (В) источника электроэнергии (батарейки) по проводникам и другим компонентам обладающих разными сопротивлениями R (Ом) от плюса к минусу течет электрический ток I (А) заставляющий светиться лампочку мощностью P (Вт). Не обращайте внимания на яркость лампы, это из-за плохого давления и малого потока воды батареек.

Фонарик, что представлен на фотографии, собран на базе конструктора «Знаток». Данный конструктор позволяет ребенку в игровой форме познать основы электроники и принцип работы электронных компонентов. Поставляется в виде наборов с разным количеством схем и разного уровня сложности.

Учебное пособие по физике: последовательные цепи

Как упоминалось в предыдущем разделе урока 4, два или более электрических устройства в цепи могут быть соединены последовательно или параллельно. Когда все устройства соединены с помощью последовательных соединений, цепь называется последовательной цепью . В последовательной цепи каждое устройство подключено таким образом, что существует только один путь, по которому заряд может пройти через внешнюю цепь. Каждый заряд, проходящий через петлю внешней цепи, будет последовательно проходить через каждый резистор.

В предыдущем разделе урока 4 было проведено краткое сравнение и противопоставление последовательной и параллельной цепей. В этом разделе было подчеркнуто, что добавление большего количества резисторов в последовательную цепь приводит к довольно ожидаемому результату в виде увеличения общей сопротивление. Поскольку в цепи есть только один путь, каждый заряд сталкивается с сопротивлением каждого устройства; поэтому добавление большего количества устройств приводит к увеличению общего сопротивления. Это повышенное сопротивление служит для уменьшения скорости протекания заряда (также известной как ток).

 

Эквивалентное сопротивление и ток

Заряды текут вместе по внешней цепи со скоростью, которая везде одинакова. Ток в одном месте не больше, чем в другом. Фактическая величина тока обратно пропорциональна величине общего сопротивления. Существует четкая зависимость между сопротивлением отдельных резисторов и общим сопротивлением набора резисторов. Что касается батареи, которая качает заряд, наличие двух 6-омных резисторов, соединенных последовательно, будет эквивалентно наличию в цепи одного 12-омного резистора. Наличие трех последовательно соединенных резисторов сопротивлением 6 Ом будет эквивалентно наличию в цепи одного резистора сопротивлением 18 Ом. А наличие четырех резисторов на 6 Ом последовательно было бы эквивалентно наличию в цепи одного резистора на 24 Ом.

Это концепция эквивалентного сопротивления. Эквивалентное сопротивление цепи представляет собой величину сопротивления, которая потребуется одному резистору, чтобы уравнять общий эффект набора резисторов, присутствующих в цепи. Для последовательных цепей математическая формула для расчета эквивалентного сопротивления (R _экв. ) выглядит следующим образом:

R _экв. = R ₁ + R ₂ + R ₃ + …

, где R ₁ , R ₂ и R ₃ — значения сопротивления отдельных резисторов, соединенных последовательно.

Больше практики

Создавайте, решайте и проверяйте свои собственные проблемы с помощью виджета Equivalent Resistance ниже. Составьте себе задачу с любым количеством резисторов и любых номиналов. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ.

Ток в последовательной цепи везде одинаков. Заряд НЕ накапливается и не начинает накапливаться в любом заданном месте, так что ток в одном месте больше, чем в других местах. Заряд НЕ расходуется резисторами так, что в одном месте его меньше, чем в другом. Заряды можно представить себе как марширующие вместе по проводам электрической цепи, везде марширующие с одинаковой скоростью. Ток — скорость, с которой течет заряд, — везде одинакова. Это то же самое на первом резисторе, что и на последнем резисторе, как и в батарее. Математически можно написать

I _{Аккумулятор} = I ₁ = I ₂ = I ₃ = …

, где I ₁ , I ₂ и I ₃ , Iccount Thurn. Thuousth Ara The Arach значения в отдельных местах резисторов.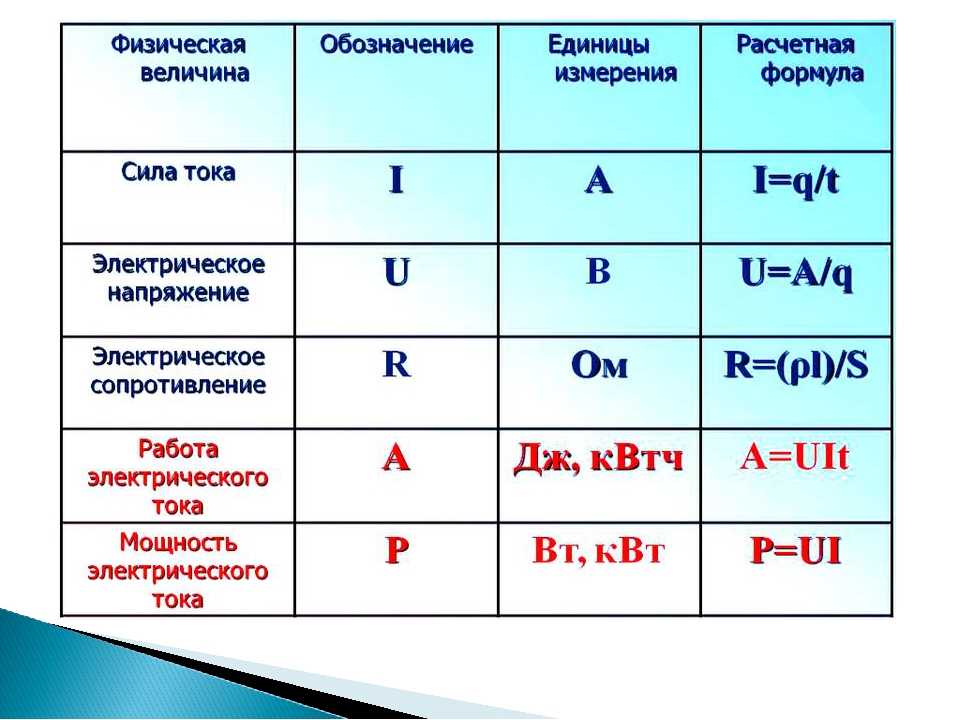

Эти значения тока легко рассчитать, если известно напряжение батареи и известны значения отдельных сопротивлений. Используя значения отдельных резисторов и приведенное выше уравнение, можно рассчитать эквивалентное сопротивление. А используя закон Ома (ΔV = I • R), можно определить ток в батарее и, следовательно, через каждый резистор, найдя соотношение напряжения батареи и эквивалентного сопротивления.

 

I _battery = I ₁ = I ₂ = I ₃ = ΔV _battery / R _eq

 

 

Electric Potential Difference and Voltage Drops

Как обсуждалось в Уроке 1, электрохимическая ячейка цепи подает энергию заряду для его перемещения через ячейку и создания разности электрических потенциалов на двух концах внешней цепи. Ячейка на 1,5 вольта создаст разность электрических потенциалов во внешней цепи 1,5 вольта. Это означает, что электрический потенциал на положительной клемме на 1,5 вольт больше, чем на отрицательной клемме. Когда заряд движется по внешней цепи, он теряет 1,5 вольта электрического потенциала. Эта потеря электрического потенциала называется падение напряжения . Это происходит, когда электрическая энергия заряда преобразуется в другие формы энергии (тепловую, световую, механическую и т. д.) внутри резисторов или нагрузок. Если электрическая цепь, питаемая от 1,5-вольтовой ячейки, оснащена более чем одним резистором, то суммарная потеря электрического потенциала составляет 1,5 вольта. На каждом резисторе есть падение напряжения, но сумма этих падений напряжения составляет 1,5 вольта – столько же, сколько номинальное напряжение источника питания. Эта концепция может быть выражена математически следующим уравнением:

ΔV _{батарея} = ΔV ₁ + ΔV ₂ + ΔV ₃ + …

Чтобы проиллюстрировать этот математический принцип в действии, рассмотрим две схемы, показанные ниже на диаграммах A и B.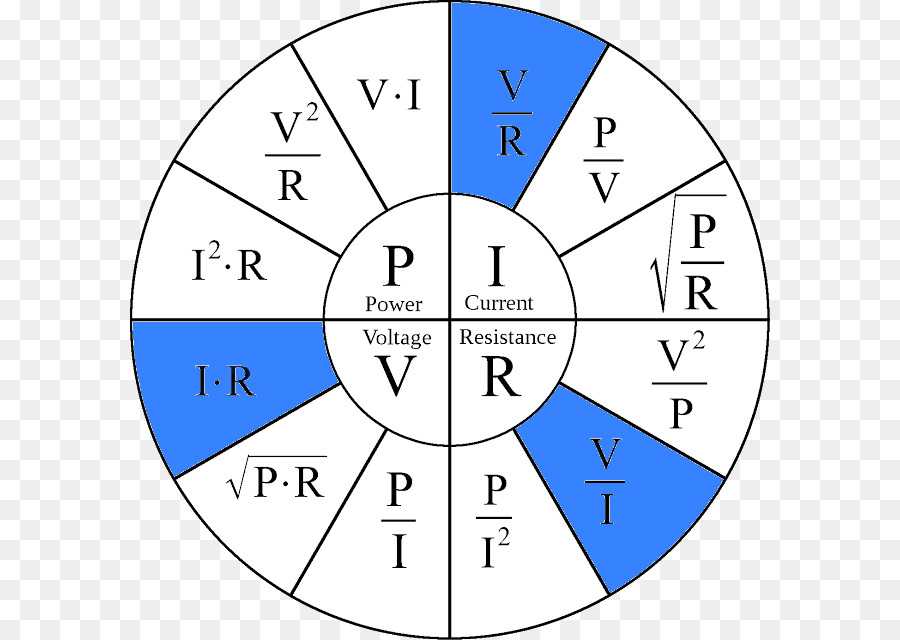 что вас попросили определить два неизвестных значения разности электрических потенциалов между лампочками в каждой цепи. Чтобы определить их значения, вам придется использовать приведенное выше уравнение. Батарея изображается своим обычным схематическим символом, а ее напряжение указывается рядом с ним. Определите падение напряжения для двух лампочек, а затем нажмите кнопку «Проверить ответы», чтобы убедиться, что вы правы.

 

 

 

Ранее в Уроке 1 обсуждалось использование диаграммы электрического потенциала. Диаграмма электрических потенциалов — это концептуальный инструмент для представления разности электрических потенциалов между несколькими точками электрической цепи. Рассмотрим принципиальную схему ниже и соответствующую ей диаграмму электрических потенциалов.

Схема, показанная на схеме выше, питается от 12-вольтового источника питания. В цепи последовательно соединены три резистора, каждый из которых имеет свое падение напряжения.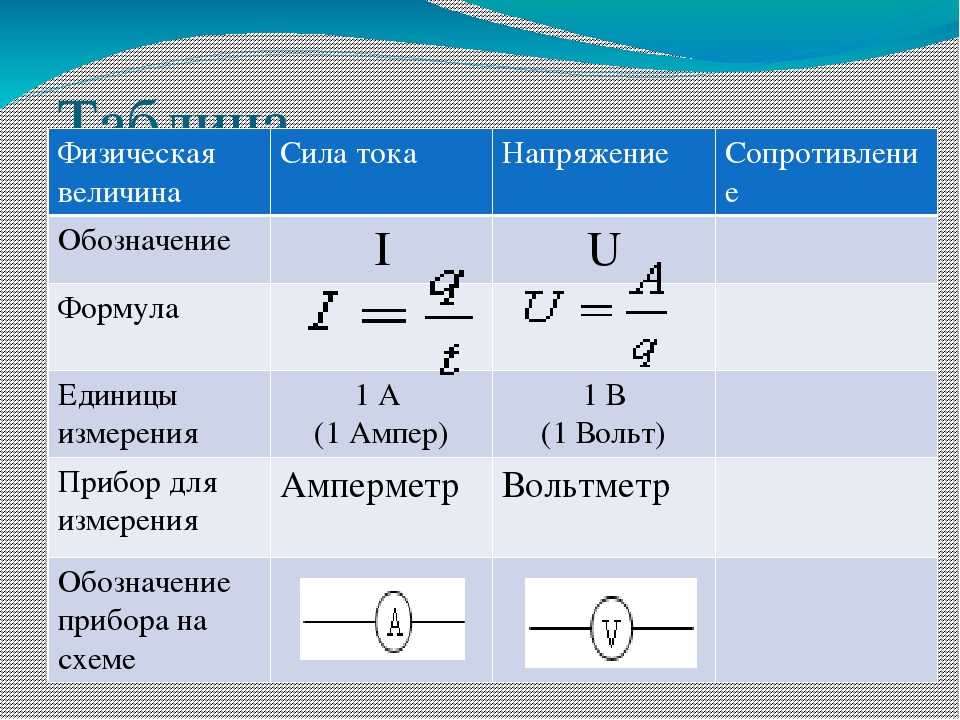 Отрицательный знак разности электрических потенциалов просто означает, что при прохождении через резистор происходит потеря электрического потенциала. Обычный ток направляется по внешней цепи от положительного вывода к отрицательному. Поскольку схематический символ источника напряжения использует длинную полосу для обозначения положительной клеммы, место А на схеме соответствует положительной клемме или клемме с высоким потенциалом. Место A находится под напряжением 12 вольт, а место H (отрицательная клемма) находится под напряжением 0 вольт. Проходя через аккумулятор, заряд приобретает 12 вольт электрического потенциала. А при прохождении через внешнюю цепь заряд теряет 12 вольт электрического потенциала, как показано на диаграмме электрических потенциалов, показанной справа от принципиальной схемы. Эти 12 вольт электрического потенциала теряются за три этапа, каждый из которых соответствует протеканию через резистор. При прохождении через соединительные провода между резисторами происходит небольшая потеря электрического потенциала из-за того, что провод оказывает относительно небольшое сопротивление потоку заряда. Поскольку точки А и В разделены проводом, они имеют практически одинаковый электрический потенциал 12 В. Когда заряд проходит через его первый резистор, он теряет 3 В электрического потенциала и падает до 9 В.V в точке C. Поскольку точка D отделена от точки C простым проводом, она имеет фактически тот же электрический потенциал 9 В, что и C. Когда заряд проходит через второй резистор, он теряет 7 В электрического потенциала и падает вниз. до 2 В в точке E. Поскольку точка F отделена от точки E простым проводом, она имеет фактически тот же электрический потенциал 2 В, что и E. Наконец, когда заряд проходит через последний резистор, он теряет 2 В электрического тока. потенциала и падает до 0 В в точке G. В точках G и H заряду не хватает энергии, и ему требуется повышение энергии, чтобы снова пройти через внешнюю цепь. Повышение энергии обеспечивается аккумулятором по мере того, как заряд перемещается от H к A.

В уроке 3 закон Ома (ΔV = I • R) был представлен как уравнение, связывающее падение напряжения на резисторе с сопротивлением резистора и током на резисторе. Уравнение закона Ома можно использовать для любого отдельного резистора в последовательной цепи. При объединении закона Ома с некоторыми принципами, уже обсуждавшимися на этой странице, возникает большая идея.

В последовательных цепях резистор с наибольшим сопротивлением имеет наибольшее падение напряжения.

Поскольку ток в последовательной цепи везде одинаков, значение I ΔV = I • R одинаково для каждого из резисторов последовательной цепи. Таким образом, падение напряжения (ΔV) зависит от изменения сопротивления. Везде, где сопротивление наибольшее, падение напряжения будет наибольшим на этом резисторе. Уравнение закона Ома можно использовать не только для прогнозирования того, что резистор в последовательной цепи будет иметь наибольшее падение напряжения, но и для расчета фактических значений падения напряжения.

Δ В 1 = I • R 1

Δ В 2 = I • R 2

Δ В 3 = I • R 3

 

Математический анализ последовательных цепей

Приведенные выше принципы и формулы можно использовать для анализа последовательной цепи и определения значений тока при и разности электрических потенциалов на каждом из резисторов в последовательной цепи. Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R _eq ), тока в батарее (I _tot ), а также падения напряжения и тока для каждого из трех резисторов.

 

Анализ начинается с использования значений сопротивления отдельных резисторов для определения эквивалентного сопротивления цепи.

R _eq = R ₁ + R ₂ + R ₃ = 17 Ом + 12 Ом + 11 Ом = 40 Ом

Теперь, когда известно эквивалентное сопротивление батареи можно определить с помощью уравнения закона Ома. При использовании уравнения закона Ома (ΔV = I • R) для определения тока в цепи важно использовать напряжение батареи для ΔV и эквивалентное сопротивление для R. Расчет показан здесь:

I _tot = ΔV _{батареи} / R _eq = (60 В) / (40 Ом) = 1,5 ампера

Значение тока 1,5 ампера — это ток в месте расположения батареи.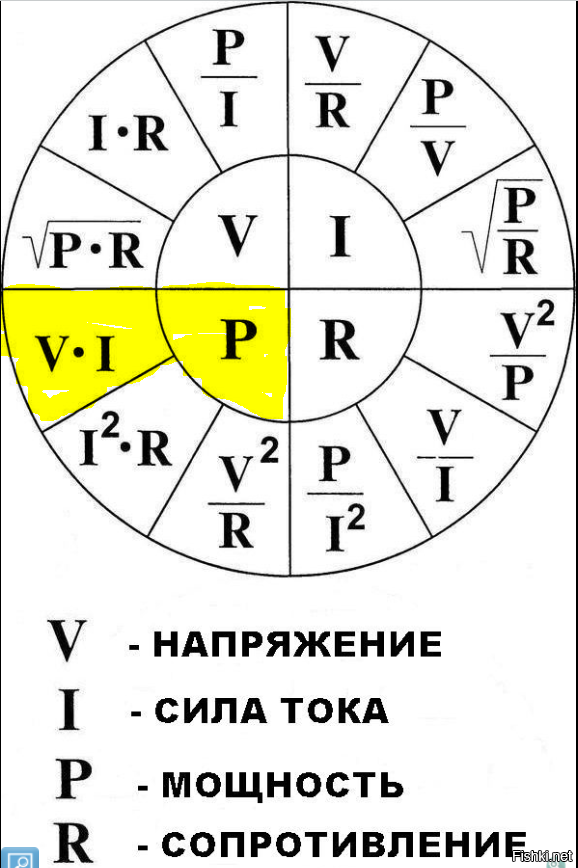 Для последовательной цепи без мест разветвления ток везде одинаков. Ток в месте расположения батареи такой же, как ток в каждом месте резистора. Следовательно, 1,5 ампера — это значение I ₁ , I ₂ и I ₃ .

I _{аккумулятор} = I ₁ = I ₂ = I ₃ = 1,5 А

Осталось определить три значения — падение напряжения на каждом из отдельных резисторов. Закон Ома снова используется для определения падения напряжения на каждом резисторе – это просто произведение тока на каждом резисторе (рассчитанного выше как 1,5 ампера) и сопротивления каждого резистора (указанного в условии задачи). Расчеты показаны ниже.

ΔV 1 = I 1 • R 1 ΔV 1 = (1,5 А) • (17 Ом) ΔV 1 = 25,5 В

ΔV 2 = I 2 • R 2 ΔV 2 = (1,5 А) • (12 Ом) ΔV 2 = 18 В

ΔV 3 = I 3 • R 3 ΔV 3 = (1,5 А) • (11 Ом) ΔV 3 = 16,5 В

В качестве проверки точности выполненных математических расчетов целесообразно проверить, удовлетворяют ли рассчитанные значения принципу, согласно которому сумма падений напряжения на каждом отдельном резисторе равна номинальному напряжению батареи.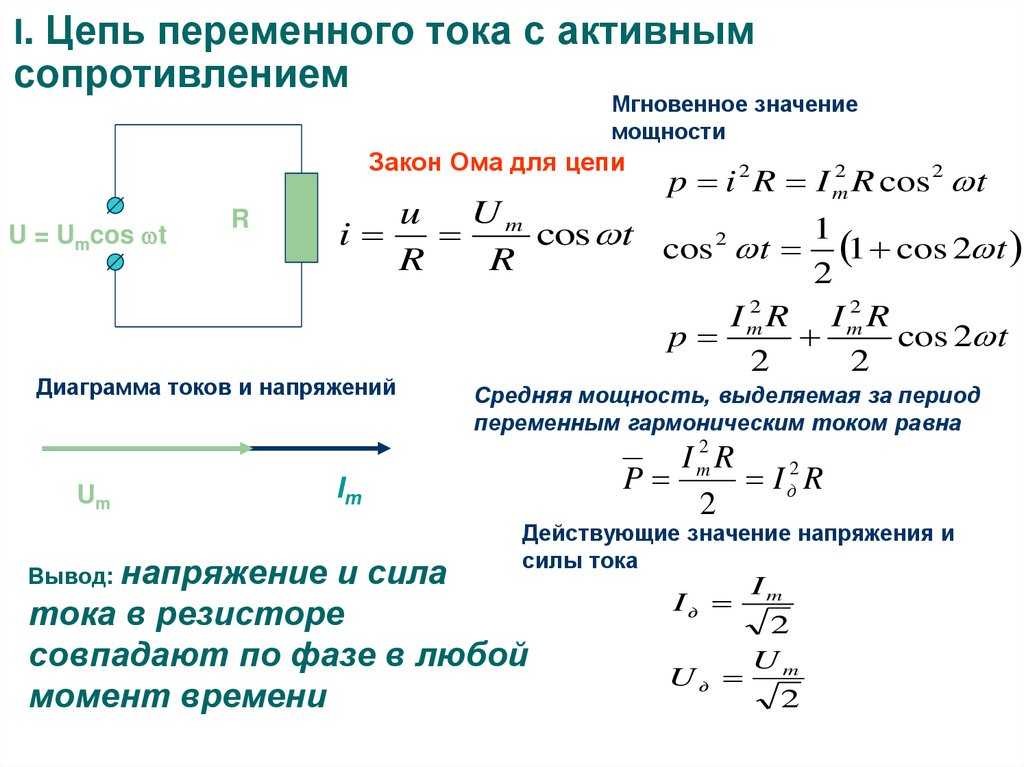 Другими словами, является ли ΔV _{батарея} = ΔV ₁ + ΔV ₂ + ΔV ₃ ?

Является ли батарея ΔV = ΔV ₁ + ΔV ₂ + ΔV ₃ ?

Является ли 60 В = 25,5 В + 18 В + 16,5 В?

Является ли 60 В = 60 В?

Да!!

 

Математический анализ этой последовательной цепи включал сочетание концепций и уравнений. Как это часто бывает в физике, отрыв понятий от уравнений при решении физической задачи — опасный поступок. Здесь необходимо учитывать понятия, что ток везде одинаков и что напряжение батареи эквивалентно сумме падений напряжения на каждом резисторе, чтобы завершить математический анализ. В следующей части урока 4 параллельные цепи будут проанализированы с использованием закона Ома и концепций параллельных цепей. Мы увидим, что подход смешивания понятий с уравнениями будет столь же важен для этого анализа.

 

 

Мы хотели бы предложить . ..

Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного конструктора цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Конструктор цепей постоянного тока предоставляет учащимся набор для создания виртуальных схем. Вы можете легко перетаскивать источники напряжения, резисторы и провода на рабочее место, располагать и соединять их так, как пожелаете. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Прикосновение к резистору или источнику напряжения позволяет изменить сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если только вы не используете его в ванной).

Посетите:  DC Circuit Builder

Проверьте свое понимание

1. Используйте свое понимание эквивалентного сопротивления, чтобы завершить следующие утверждения:

a. Два последовательно соединенных резистора сопротивлением 3 Ом обеспечат сопротивление, эквивалентное одному резистору сопротивлением _____ Ом.

б. Три последовательно соединенных резистора сопротивлением 3 Ом обеспечат сопротивление, эквивалентное одному резистору сопротивлением _____ Ом.

с. Три последовательно соединенных резистора сопротивлением 5 Ом обеспечат сопротивление, эквивалентное одному резистору _____ Ом.

д. Три резистора с сопротивлением 2 Ом, 4 Ом и 6 Ом включены последовательно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.

эл. Три резистора с сопротивлением 5 Ом, 6 Ом и 7 Ом включены последовательно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.

ф. Три резистора с сопротивлением 12 Ом, 3 Ом и 21 Ом включены последовательно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.

 

 

2. При увеличении количества резисторов в последовательной цепи общее сопротивление __________ (увеличивается, уменьшается, остается неизменным) и ток в цепи __________ (увеличивается, уменьшается, остается неизменным).

3. Рассмотрим следующие две схемы последовательных цепей. Для каждой диаграммы используйте стрелки, чтобы указать направление условного тока. Затем сравните напряжение и ток в обозначенных точках для каждой диаграммы.

 

 

4. Три одинаковые лампочки подключены к D-ячейке, как показано справа. Какое из следующих утверждений верно?

а. Все три лампочки будут иметь одинаковую яркость.

б. Лампочка между X и Y будет самой яркой.

в. Лампочка между Y и Z будет самой яркой.

д. Лампочка между Z и батареей будет самой яркой.

 

 

 

5. Три одинаковые лампочки подключены к батарейке, как показано справа. Какие корректировки можно внести в схему, чтобы увеличить ток, измеряемый в точке X? Перечислите все, что применимо.

а. Увеличьте сопротивление одной из лампочек.

б. Увеличьте сопротивление двух лампочек.

в. Уменьшите сопротивление двух лампочек.

д. Увеличьте напряжение батареи.

эл. Уменьшите напряжение батареи.

ф. Снимите одну из лампочек.

 

 

6. Три одинаковые лампочки подключены к батарейке, как показано справа. W, X, Y и Z обозначают местоположения вдоль цепи. Какое из следующих утверждений верно?

а. Разность потенциалов между X и Y больше, чем между Y и Z.

б. Разность потенциалов между X и Y больше, чем между Y и W.

в. Разность потенциалов между Y и Z больше, чем между Y и W.

д. Разность потенциалов между X и Z больше, чем между Z и W.

эл. Разность потенциалов между X и W больше, чем на аккумуляторе.

ф. Разность потенциалов между X и Y больше, чем между Z и W.

 

7. Сравните схемы X и Y ниже. Каждый питается от 12-вольтовой батареи. Падение напряжения на резисторе 12 Ом в цепи Y равно ____ падению напряжения на одном резисторе в цепи X.

a. меньше чем

б. больше

в. то же, что

 

 

 

8. Батарея 12 В, резистор 12 Ом и лампочка подключены, как показано на схеме X ниже. Резистор на 6 Ом добавляется к резистору на 12 Ом и лампочке, чтобы создать цепь Y, как показано на рисунке. Лампочка появится ____.

а. диммер в контуре X

б. диммер в цепи Y

в. одинаковая яркость в обоих контурах

 

 

9. Три резистора соединены последовательно. Если поместить в цепь с 12-вольтовым источником питания. Определить эквивалентное сопротивление, общий ток цепи, падение напряжения и ток на каждом резисторе.

 

 

Следующий раздел:

Как рассчитать падение напряжения на резисторе, подробное объяснение

Базовая электроника 0

Если вы ищете, как рассчитать падение напряжения на резисторе, то вот полная теория и практические примеры падения напряжения на резисторе.

Перед этим давайте освежим понятие закона Ома: (прокрутите вниз, если у вас все хорошо)

• Обычный способ показать поведение схемного устройства — это его характеристика.
• 
  Это график зависимости тока I, проходящего через устройство, от приложенного к нему напряжения V. Это устройство, резистор, имеет простую линейную характеристику В–I , показанную на рис. . выше.
• Эта линейная зависимость устройства выражается Законом Ома :
  V = IR
• Здесь коэффициент пропорциональности R известен как сопротивление устройства и равен наклону ВАХ. Единица сопротивления Ом, обозначение Ом . Любое устройство с линейной характеристикой VI можно рассматривать как резистивное по своей природе.

Каково падение напряжения на резисторе?

• Падение напряжения на резисторе — это не что иное, как значение напряжения на резисторе. Иногда его также называют «напряжение на резисторе» или просто «падение напряжения».
• Обычно обозначается как:
  ‘V(drop ) ’ или ‘Vr’ или ‘Vd’
  Для нескольких резисторов это записывается как Vr1, Vr2, Vr3 и т.д.

Как мы все знаем, резистор — это устройство, оказывающее сопротивление протекающему через него току. Затем, применив закон Ома, резистор создаст падение напряжения на резистивном устройстве, которое определяется как:

 В ( падение ) = I × R

, где I = ток через резистор в (А) амперах
R = сопротивление в (Ом) омах
В( падение ) = падение напряжения в (В) вольтах

Поэтапный расчет падения напряжения на сопротивлении:

Шаг 1: Упростите данную схему. Если, скажем, цепь полна резисторов, соединенных последовательно и параллельно, то переподключите ее, чтобы упростить. (см. практический пример ниже)

Шаг 2: Затем найдите эквивалентный резистор.
Для параллельного подключения: 1 / Треб. = 1 / R1 + 1 / R2 …
Для серии: Необх. = R1 + R2 + . . .

Шаг 3: Найдите ток через каждый резистор. (Ток через последовательный резистор одинаков, а ток через параллельные резисторы разный и зависит от его значения)

Шаг 4 : Примените формулу из закона Ома для расчета падения напряжения, В = IR

Один из способов — воспользоваться онлайн-инструментом «Калькулятор падения напряжения на резисторе».

Существует также другой способ найти падение напряжения, просто вы можете рассчитать его, используя формулу делителя напряжения

 

один резистор последовательно с батареей или источником питания, как показано на этой схеме.

В этой схеме падение напряжения на резисторе такое же, как и у источника питания. Это связано с тем, что оба компонента имеют общие потенциальные точки, разделенные между ними (точка A и точка B)

∴ Vs = Vdrop = 5 вольт (скажем)

Случай II:

Если есть два или больше резисторов последовательно с батареей, как показано на этой схеме.

В этой цепи мы должны рассчитать общий ток «I» через цепь.
I (общий) = V (питание) / R (эквивалент)

∴ I (общий) = 5 / 30 = 0,166 A

Тогда падение напряжения на R1 будет: Vr1 = I × R1
Падение напряжения на R2 будет: Vr2 = I × R2
Также падение напряжения на Rn будет: Vrn = I × Rn

—> Vr1 =I × R1 = 0,166 × 10 = 1,66 вольт       &         Vr2 = I × R2 = 0,166 × 20 = 3,33 вольта

 

Напряжение на параллельных резисторах:

Случай I:
Два резистора подключены параллельно к батарее или источнику питания, как показано на этой схеме.

В этой схеме падение напряжения на этих параллельных резисторах такое же, как и у источника питания.
Это связано с тем, что оба резистора имеют общие потенциальные точки (точка A и точка B), поэтому напряжение будет одинаковым, а ток будет разным.

∴Vs = Vdrop = Vr1 = Vr2 = 5 вольт   (скажем)

Случай II:
Один резистор соединен последовательно и два резистора с источником питания, как показано на этой схеме.

В этой схеме нам нужно рассчитать ток «I» через каждый компонент.

• i1 = I (всего) = Is  = V (предложение) / R (эквивалент), где R (эквивалент) = R1 + Rp
  где 1 / Rp = 1 / R2 + 1 / R3
  ∴ Rp = 12 Ом и R ( эквивалент ) = 22 Ом
• I2 = I1 * (R3/(R2+R3))
  I3 = I1 * (R2/(R2+R3))
77777777777773737737777377377377773773777377773773773777773777737377773773773737777773777377377377373773737377373737377373737н7н7н.
• Падение напряжения на R1 будет Vr1 = R1 * i1
  Падение напряжения на R2 будет Vr2 = R2 * i2
  Падение напряжения на R3 будет Vr3 = R2 * i3 Теперь i1 = V(питание) / R(эквивалент) = 5/22 = 0,227 А
  ∴ i1 = 0,227 А

  Падение напряжения на сопротивлении 10 Ом -> Vr1 = 10 * i1 = 10 × 0,227 В
  ∴ Vr1 = 2,27 В

  Теперь (R0/

  i1 *, i2) ∴ I2 = 0,1362 A

  Падение напряжения на 20 Ом -> VR2 = 20 * I2 = 20 × 0,1362 вольт
  ∴ VR2 = 2,724 Вольт

  , I1 * I1 * I1 * I1 * I1 * I1 /(R1+R2))
  ∴   i3 =0,09 А

  Падение напряжения на сопротивлении 30 Ом -> Vr2 = 30 * i2 = 30 × 0,09 Вольт
  ∴ VR3 = 2,7 Вольт

  Метод 2:

  • Найти I1 = В (Сповтвращение) / R (эквивалент) = 0,2274.