Формула напряжения тока. Найти электрическое напряжение, разность потенциалов. « ЭлектроХобби
Как известно у электрического напряжения должна быть своя мера, которая изначально соответствует той величине, что рассчитана для питания того или иного электротехнического устройства. Превышение или снижение величины этого напряжения питания негативно влияет на электрическую технику, вплоть до полного выхода ее из строя. А что такое напряжение? Это разность электрических потенциалов. То есть, если для простоты понимания его сравнить с водой, то это примерно будет соответствовать давлению. По научному электрическое напряжение — это физическая величина, показывающая, какую работу совершает на данном участке ток при перемещении по этому участку единичного заряда.
Наиболее распространенной формулой напряжения тока является та, в которой имеются три основные электрические величины, а именно это само напряжение, ток и сопротивление. Ну, а формула эта известна под названием закона Ома (нахождение электрического напряжения, разности потенциалов).
Звучит эта формула следующим образом — электрическое напряжение равно произведению силы тока на сопротивление. Напомню, в электротехнике для различных физических величин существуют свои единицы измерения. Единицей измерения напряжения является «Вольт» (в честь ученого Алессандро Вольта, который открыл это явление). Единица измерения силы тока — «Ампер», и сопротивления — «Ом». В итоге мы имеем — электрическое напряжение в 1 вольт будет равно 1 ампер умноженный на 1 ом.
Помимо этого второй наиболее используемой формулой напряжения тока является та, в которой это самое напряжение можно найти зная электрическую мощность и силу тока.
Звучит эта формула следующим образом — электрическое напряжение равно отношению мощности к силе тока (чтобы найти напряжение нужно мощность разделить на ток). Сама же мощность находится путем перемножения тока на напряжение. Ну, и чтобы найти силу тока нужно мощность разделить на напряжение. Все предельно просто. Единицей измерения электрической мощности является «Ватт».
Следовательно 1 вольт будет равен 1 ватт деленный на 1 ампер.
Ну, а теперь приведу более научную формулу электрического напряжения, которая содержит в себе «работу» и «заряды».
В этой формуле показывается отношение совершаемой работы по перемещению электрического заряда. На практике же данная формула вам вряд ли понадобится. Наиболее встречаемой будет та, которая содержит в себе ток, сопротивление и мощность (то есть первые две формулы). Но, хочу предупредить, что она будет верна лишь для случая применения активных сопротивлений. То есть, когда расчеты производятся для электрической цепи, у которой имеется сопротивления в виде обычных резисторов, нагревателей (со спиралью нихрома), лампочек накаливания и так далее, то приведенная формула будет работать. В случае использования реактивного сопротивления (наличии в цепи индуктивности или емкости) нужна будет другая формула напряжения тока, которая учитывает также частоту напряжения, индуктивность, емкость.
P.S.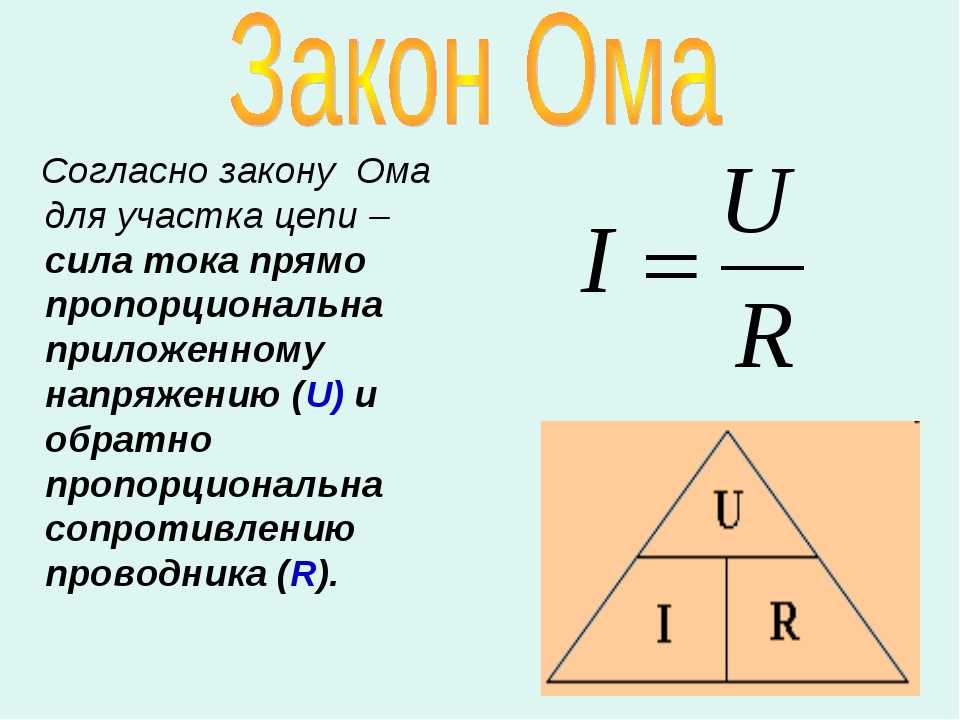
Формула закона Ома является фундаментальной, и именно по ней всегда можно найти одну неизвестную величину из двух известных (ток, напряжение, сопротивление). На практике закон ома будет применяться очень часто, так что его просто необходимо знать наизусть каждому электрику и электронику.
Как рассчитать силу тока, потребляемую бытовым прибором?
Главная » Познавательное
Познавательное
Автор Савельев Николай На чтение 3 мин Просмотров 1.8к. Опубликовано Обновлено
Если вам необходимо узнать силу тока, которую потребляет прибор, то вы можете воспользоваться одной из двух формул для расчета силы тока. Одна формула позволяет рассчитать силу тока, используя мощность и напряжение, а вторая используя сопротивление и напряжения.
Расчет через мощность
Чтобы рассчитать потребляемую силу тока, нужно разделить мощность (P) данного электрического устройства на напряжение (U), поступающее от источника питания.
Сила тока (I), протекающего по проводнику, измеряется в амперах (А). Эквивалентом напряжения в источнике питания является вольт (В). Наконец, мощность, производимая электричеством, измеряется в ваттах (Вт). Все эти измерения взаимосвязаны при расчете потребления электроэнергии.
Первым делом нужно выяснить мощность устройства. Любое устройство, потребляющее электрическую энергию, называется нагрузкой. Примерами нагрузок являются лампочка, электроплита, холодильник, кондиционер или любое другое устройство. Мощность в ваттах часто печатается на шильдике самого устройства, если на шильдике такой информации нет, то посмотрите в техническом паспорте или инструкции, которые обычно идут в комплекте. На худой конец, вы можете найти информацию в интернете, зная производителя и модель устройства.
Шильдик с комбоусилителя моей гитары. Источник: Собственное фотоНапряжение нам известно, обычно оно в пределах 220 — 230 В. Если ваш прибор питается от аккумулятора, то напряжение можно посмотреть на его корпусе.
Батареи типа «крона» имеют напряжение 9 вольт, а небольшие батарейки типов C, AA или AAA, работают от 1 до 3 вольт, в зависимости от размера и состава.
I=P/U
Формула расчета силы тока через мощность и напряжение
На примере комбоусилителя для моей электрогитары мы можем рассчитать потребляемую им силу тока следующим образом: 28 Вт / 230 В = 0,12 А.
Почему в российской розетке не 220, а 230 Вольт? Решил разобраться
Расчет через сопротивление
Электричество, протекающее по проводам, можно сравнить с водой, протекающей по руслу реки. Чем шире русло, тем меньше сопротивление и тем большее количество протекает по руслу за единицу времени. Протекание тока в проводнике ограничено сопротивлением тока, которое, в свою очередь, измеряется в Омах.
Источник: pixabayДля расчета силы тока через сопротивление, мы можем использовать закон Ома. Сопротивление приборов зачастую также указано на шильдике устройства.
Сопротивление же проводов, соединяющих розетку и прибор можно не учитывать и считать его бесконечно малым.
I = UR
Закон Ома
Закон Ома гласит, что напряжение равно силе тока, умноженной на сопротивление, поэтому, если вы разделите напряжение вашего источника питания на сопротивление нагрузки, вы найдете силу тока в амперах. Например, если мы подключим стиральную машину с сопротивлением 40 Ом к розетке 220 В, то выясним, что машинка потребляет ток, равный 5,5 А.
Остались вопросы? Пишите в комментариях, разберемся вместе!
Оцените автора
Что из нижеследующего представляет собой напряжение?A. \[\dfrac{\text{Выполненная работа}}{\text{Текущая}\!\!\times\!\!\text{ Время}}\] B. $\text{Выполненная работа}\!\!\ раз\!\!\text{ Зарядка}$ C. $\dfrac{\text{Проделанная работа}\!\!\times\!\!\text{ Текущее}}{\text{Время}}$ D. $ \text{Проделанная работа}\!\!\times\!\!\text{ Оплата }\!\!\times\!\!\text{ Time}$
Ответ
Подтверждено
236.
1k+ просмотров
Подсказка: Нам даны четыре уравнения, и нас просят найти, какое из данных уравнений представляет напряжение. У нас есть три отношения между выполненной работой и напряжением. Из этих трех соотношений мы можем составить уравнение для напряжения и найти, какое из них дано в вариантах. 9{2}}}{R}\times t$, где «W» — проделанная работа, «V» — напряжение, «R» — сопротивление, а «t» — время.
$W=VQ$, где «W» — проделанная работа, «V» — напряжение, а «Q» — заряд.
$W=VIT$, где «W» — проделанная работа, «V» — напряжение, «$I$» — ток, а «T» — время.
Полный пошаговый ответ:
В вопросе нам даны четыре отношения, и нас просят найти, какое из них представляет напряжение.
Во всех четырех приведенных отношениях мы видим, что «выполненная работа» является общей. 9{2}}=\dfrac{WR}{t}$
$\Rightarrow V=\sqrt{\dfrac{WR}{t}}$
То есть
\[\Rightarrow \text{Voltage}=\sqrt {\dfrac{\text{Проделанная работа}\!\!\times\!\!\text{ Сопротивление}}{\text{Время}}}\]
рассмотрим другое соотношение между выполненной работой и напряжением.
$W=VQ$, где W — проделанная работа, V — напряжение, Q — заряд.
Из этого уравнения мы получим выражение напряжения как
$\Rightarrow V=\dfrac{W}{Q}$, то есть
$\Rightarrow \text{Voltage=}\dfrac{\text{Выполнено}}{\text{Заряд}}$
Это соотношение также не указано в опциях.
Следовательно, мы можем рассмотреть другое отношение выполненной работы и напряжения.
$W=VIT$, где «W» — проделанная работа, «V» — напряжение, «$I$» — ток, а «T» — время.
Из этого уравнения выражение для напряжения может быть записано как
$\Rightarrow V=\dfrac{W}{I\times T}$, то есть
$\Rightarrow \text{Voltage=}\dfrac{\text {Выполнено}}{\text{Текущий}\!\!\times\!\!\text{ Время}}$
Поскольку это соотношение задано в опциях, мы можем сказать, что $\dfrac{\text{Выполненная работа}}{\text{Ток}\!\!\times\!\!\text{ Время}}$ представляет собой напряжение.
Итак, правильный ответ — «Вариант А».
Примечание: Напряжение, также известное как электродвижущая сила, представляет собой разность потенциалов электрического заряда между двумя точками электрической цепи.
Мы знаем, что напряжение также определяется как работа, совершаемая на единицу заряда при перемещении заряда между двумя точками в электрическом поле.
Недавно обновленные страницы
Большинство эубактериальных антибиотиков получены из биологии ризобия класса 12 NEET_UG
Биоинсектициды саламин были извлечены из класса 12 Biology NEET_UG
Какое из следующих утверждений, касающихся Baculovirussess, Neet_ug
. Какое из следующих утверждений, касающихся Baculoviruses, Neet_ug
. муниципальные канализационные трубы не должны быть непосредственно 12 класса биологии NEET_UG
Очистка сточных вод осуществляется микробами A B Удобрения 12 класса биологии NEET_UG
Иммобилизация фермента – это конверсия активного фермента класса 12 биологии NEET_UG
Большинство эубактериальных антибиотиков получают из биологического класса Rhizobium 12 NEET_UG
Саламиновые биоинсектициды были извлечены из биологического класса А 12 NEET_UG
12 класс биологии NEET_UG
Канализационные или городские канализационные трубы не должны быть напрямую 12 класс биологии NEET_UG
Очистка сточных вод выполняется микробами A B Удобрения 12 класс биологии NEET_UG
Иммобилизация фермента — это преобразование активного фермента класса 12 в биологии NEET_UG
Тенденции сомнения
Конденсатор i-v уравнение в действии
Конденсатор является одним из идеальных элементов схемы.
Давайте применим уравнение для конденсатора $i$-$v$, чтобы увидеть, что произойдет с напряжением, если мы добавим ток.
Автор Вилли Макаллистер.
Содержимое
- Реакция напряжения на импульс тока
- До импульса
- Во время импульса
- После импульса
- Всего ответов
- Имитационная модель
- Задача дизайна
Куда мы движемся
Постоянный ток, подаваемый в конденсатор, создает напряжение с прямолинейным нарастанием. Такое поведение предсказывается интегральной формой уравнения конденсатора $i$-$v$.
Обычное уравнение конденсатора $i$-$v$ представляет собой зависимость $i$ от $v$ в производной форме, 9{\,T} i\,dt + v_0$
$v_0$ – напряжение на конденсаторе в начале интеграла, при $t=0$.
Обозначение времени немного сложное,
Маленький $t$ — непрерывная временная переменная внутри интеграла.
Большой $T$ – это момент, когда вы хотите узнать напряжение на конденсаторе.
$i = \text C\,\dfrac{dv}{dt}$
$d$ — это исчисление для «дифференциала» или «маленького изменения в…». Например, $dt$ означает «мизерное изменение во времени». Когда вы видите его в соотношении, таком как $dv/dt$, это означает «крошечное изменение $v$ (напряжения) для каждого крошечного изменения $t$ (времени)». Выражение, подобное $dv/dt$, производная. Производная измеряет скорость изменения напряжения во времени (наклон напряжения в зависимости от времени). 9{\,T} i\,dt + v_0$
Петля $\int$ — еще один символ исчисления. Это интегральный признак. Его значение аналогично символу суммирования Sigma $\Sigma$. Интегрирование противоположно взятию производной.
В уравнении конденсатора знак интеграла означает, что вы складываете последовательность произведений $(i \times dt)$ или (current $\times$ крошечный интервал времени). Когда вы видите верхний и нижний пределы символа интеграла, это делает его определенным интегралом .
Это означает интегрировать по определенному диапазону $t$. Вы начинаете в момент времени $t=0$ и останавливаетесь в момент времени $t=T$. 9{\,T} i\,dt + v_0$
Текущий импульс имеет резкие изменения, поэтому мы собираемся найти $v(t)$ в трех отдельных фрагментах: до, во время и после текущего импульса.
Перед импульсом
Перед импульсом тока $(t < 0)$ ток не течет, поэтому на $\text C$ не накапливается заряд. Следовательно, $v_{(t<0)} = 0$. Нам даже не пришлось использовать уравнение.
Во время импульса
В любое время в течение импульса тока $(0 \lt t \lt 3\,\text{ms})$ протекает ток, на $\text C$ накапливается заряд, а напряжение возрастает. Примените уравнение конденсатора, чтобы найти, что происходит с напряжением, 9{\,T} i\,dt + v_0$
Обратите внимание на временные переменные. Маленький $t$ — это непрерывное время, переменная, которая интегрируется. Большой $T$ — это время, в течение которого может накапливаться заряд. Определенный интеграл пролистывает время $t$ от $0$ до некоторого времени накопления, большого $T$.
Чтобы найти напряжение в конце импульса, присвоим большой $T$ значение $3\,\text{ms}$.
$i$ постоянна (вершина импульса плоская) в течение этого времени, поэтому мы можем вынести ее за пределы интеграла. Мы сказали, что конденсатор начал с заряда $0$, поэтому $v_0$ равен нулю, и мы можем его не указывать. 9{-6}\,\text F} = 2000\,\text{вольт/сек}$
Для любой ширины импульса напряжение равно,
$v(T) = 2000 \,\text{вольт/сек } \,\cdot T$
Ширина нашего импульса $T = 3\,\text{ms}$, поэтому напряжение на конденсаторе возрастает до,
$v_{(T=3\,\text{ms })} = 2000 \,\text{вольт/сек} \,\cdot \,0,003 \,\text{сек} = 6\,\text{вольт}$
При постоянном токе $2\,\text {мА}$, напряжение на конденсаторе нарастает по прямой с наклоном $2000\,\text{вольт/сек}$. Напряжение начиналось с $0\,\text V$ и поднималось до $6\,\text{volts}$ после $3\,\text{ms}$.
После импульса
Эта часть довольно интересна, если вы не задумывались об этом раньше. После импульса ток падает до $0$.
Это означает, что заряд перестает накапливаться на конденсаторе. Это может показаться странным, но поскольку заряд не движется, заряду, накопленному на конденсаторе, некуда деваться, поэтому он остается на конденсаторе. Это означает, что мы должны ожидать, что напряжение на конденсаторе останется прежним. $q = \текст C\,v$. Константа $q$ подразумевает константу $v$.
Посмотрите, как математика фиксирует это, написав уравнение конденсатора после окончания импульса. 9{\,T} 0\,dt + 6$
Интеграл оценивается как $0$, и мы получаем,
$v(T) = 6\,\text V\quad$ для любого значения $T$.
После прекращения тока заряд сохраняется, поэтому напряжение на конденсаторе остается постоянным на уровне $6\,\text В$. Он остается там навсегда.
Общий ответ
Объединение трех фрагментов вместе дает нам $v(t)$ на нижнем графике,
Эта конфигурация схемы (источник тока, питающий конденсатор) имеет прозвище. Это называется интегратор , потому что он накапливает или интегрирует заряд с течением времени.
Он часто используется для создания пилообразного напряжения.
Имитационная модель
Найдите ток и напряжение с помощью этой имитационной модели. Откройте ссылку и щелкните TRAN в верхней строке меню, чтобы выполнить переходную симуляцию. Источник тока моделируется как одиночный ИМПУЛЬС. (Дважды щелкните текущий источник, чтобы увидеть, как он определяется.) Элементы управления масштабированием находятся в левой части окна и отображаются светло-серым цветом.
Вот еще одна имитационная модель с источником тока, определенным другим способом, как форма волны PWL (кусочно-линейная). Время и ток вводятся в виде списка разделенных запятыми пар [время, ток], например: -1 с, 0, 0 с, 0, 1 нс, 2 м, 3 мс, 2 м, 3 мс, 0, 5 с, 0.
Посмотрите, можете ли вы изменить форму кривой тока, чтобы напряжение на конденсаторе снизилось до $0\text V$ еще за $3\,\text{ms}$. Вы собираетесь сделать что-то похожее на это:
показать ответ Дважды щелкните текущий источник и введите это в PWL “список чередующихся значений времени и значений, разделенных запятыми”.