Научиться решать интегралы с нуля: Интегралы – Математика – Смотреть онлайн видео уроки для начинающих бесплатно!

Интегралы – Математика – Смотреть онлайн видео уроки для начинающих бесплатно!

В категории Интегралы собраны бесплатные онлайн видео уроки по этой теме. Интеграл (integer – целый) – это математический символ, который используется в исчислении, является аналогом операции суммирования. Интегрирование – это процесс нахождения интеграла функции, действие, обратное дифференцированию. Формально, это деление площади фигуры на прямоугольные полоски и нахождение предела сумм этих площадей. Определённый интеграл функции f (x) с нижним пределом а и верхним пределом b представляет собой площадь части графика функции, которая ограничена осью абсцисс, кривой у = f(x) и двумя прямыми х = а и х = b. Если значения а и b не заданы, то интеграл называется неопределенным. Изучение интегралов по видео урокам будет полезно как для начинающих, так и для более опытных математиков. Видеоуроки из рубрики Интегралы Вы можете смотреть бесплатно в любое удобное время. К некоторым видео урокам по интегралам приложены дополнительные материалы, которые можно скачать.

Приятного Вам обучения!

---

---

Новые · Лучшие · Популярные

---

Смотреть урок онлайн

Метод замены переменной при решении неопределенных интегралов

В этом видео уроке рассказывается о том, как использовать метод замены переменной при решении неопределенных интегралов. В первой части обучения будет рассмотрена схема применения данного метода. Метод замены переменной является основным методом решения неопределенных интегралов. Его еще часто называют методом подстановки. После изучения теоретической части, полученные знания будут применяться на практических заданиях. С этой целью, в данном видео уроке представлено решение нескольких примеров…

Смотреть урок онлайн

Простейшие интегралы. Решение с помощью таблицы

Это видео посвящено вопросу о том, как решать простые интегралы при помощи таблицы. Для начала вспомним определение первообразной. Функция F(x) является первообразной для функции f(x) на определенном промежутке, если для любого значения x данного промежутка справедливо равенство F (x)= f(x). Сформулируем определение неопределенного интеграла. Неопределённый интеграл – это совокупность всех первообразных функции f(x). При этом используется следующая запись: интеграл f(x)dx=F(x)+C, где f(x…

Смотреть урок онлайн

Определенный интеграл (11 класс). Понятие, решение примера

Видео урок «Определенный интеграл (11 класс). Понятие, решение примера» посвящен вопросу о понятии определенного интеграла как площади криволинейной трапеции. Пусть на отрезке ab задана непрерывная функция y=f(x). Попробуем определить площадь фигуры, границами которой являются: сверху – график функции y=f(x), по бокам – вертикальные прямые x=a и x=b, снизу – ось абсцисс. Образовавшаяся в результате фигура называется криволинейной трапецией. Для нахождения площади данной криволинейной трапеции. ..

Смотреть урок онлайн

Что такое интеграл

В этом видео мы поговорим об интеграле. Этим зверем из высшей математики часто пугают несчастных детей, но тебе, если ты посмотрел мои видео про производную и первообразную, этот серый волк будет совсем не страшен. Определенный интеграл равен всего лишь навсего разности первообразных, которая в свою очередь совпадает с площадью под графиком производной. За страшным словом скрывается простая суть: слово интеграл переводится как сумма. Помните – сумма прямоугольников. А действия по нахождению…

Смотреть урок онлайн

Решение интегралов с квадратичной функцией, примеры

Видео «Решение интегралов с квадратичной функцией, примеры» посвящено вопросу о том, как правильно выполнять интегрирование выражений, в состав которых входит квадратичная функция. Здесь дается алгоритм вычисления интеграла, который начинается с выделения полного квадрата квадратичной функции.

Затем выполняется замена переменной. Полученный упрощенный интеграл решается обычным способом. После того как интеграл вычислен, остается вернуться к первоначальным переменным. Кроме теоретического…

Смотреть урок онлайн

Несобственные интегралы 2 рода – от неограниченных (разрывных) функций

В этом онлайн уроке рассказывается о том, что собой представляют несобственные интегралы 2 рода – от неограниченных (разрывных) функций. Допустим, задана функция, которая непрерывна на определенном промежутке, причем её предел с одной стороны равен бесконечности, т.е. функция в этой точке терпит разрыв второго рода. При рассмотрении определенного интеграла с пределами соответствующими этому промежутку возникает вопрос, к какому значению он стремиться. В данном видео уроке будет рассмотрен…

Смотреть урок онлайн

Интегралы с бесконечными пределами (несобственные 1 рода)

Видео «Интегралы с бесконечными пределами (несобственные 1 рода)» посвящено вопросу о том, что такое интегралы с бесконечными пределами и каков их геометрический смысл, решение примера.

Допустим, что задан определенный интеграл от непрерывной функции с верхним пределом интегрирования равным B. Представим себе, что значение этого интеграла численно равно площади криволинейной трапеции. При увеличении значения предела B, площадь этой трапеции также увеличивается. Возникает вопрос, к какому…

Смотреть урок онлайн

Как найти объем тела вращения через вычисление определенного интеграла

В этом видео уроке рассказывается о том, как найти объем тела вращения через вычисление определенного интеграла. Допустим, дана криволинейная трапеция, которая ограничена сверху графиком непрерывной функции, а по бокам – вертикальными прямыми линиями. При вращении данной плоской фигуры вокруг оси абсцисс, образуется объемная фигура. С помощью определенного интеграла можно вычислить объем этого тела. Здесь будет представлена формула, по которой вычисляется объем тела вращения. В первом случае…

Смотреть урок онлайн

Как найти длину дуги кривой через вычисление определенного интеграла

Онлайн урок «Как найти длину дуги кривой через вычисление определенного интеграла» посвящен вопросу о методе, с помощью которого можно определить длину дуги кривой. Одним из приложений определенного интеграла является нахождение длин дуг кривых. Здесь будет представлена формула, с помощью которой можно найти длину дуги кривой. Для решения данной задачи с помощью этой формулы необходимо знать функцию, которой задана кривая и абсциссы точек, между которыми измеряется длина кривой. В данном видео…

Смотреть урок онлайн

Метод интегрирования по частям в определенном интеграле – формула, пример решения

Это видео посвящено вопросу о том, как использовать метод интегрирования по частям при решении определенного интеграла, формула, пример использования. Если вы уже освоили данный метод при решении неопределенных интегралов, то вам не составит труда научиться его использовать и для вычисления определенного интеграла. Также необходимо уметь применять формулу Ньютона-Лейбница. Здесь представлена формула, по которой будет проводиться вычисление интеграла. Применение метода интегрирования по частям.

..

---

1 2

Если у Вас есть качественные видео уроки, которых нет на нашем сайте, то Вы можете добавить их в нашу коллекцию. Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.

апреля 2020 | Уроки математики и физики для школьников и родителей

Урок 6. Определённый интеграл

ВИДЕО УРОК

Для того чтобы научиться решать определённые интегралы необходимо

1)  Уметь находить неопределённые интегралы.

2)  Уметь вычислить определённый интеграл.

В общем виде определённый интеграл записывается так:

По сравнению с неопределённым интегралом прибавились пределы интегрирования.

Нижний предел интегрирования обозначается буквой 

а.

Верхний предел интегрирования обозначается буквой  b.

Отрезок  [a; b]  называется отрезком интегрирования.

Определённый интеграл – это число. Решить определённый интеграл это значит найти число.

Находится определённый интеграл с помощью формулы Ньютона-Лейбница.

Этапы решения определённого интеграла.

1)  Сначала находим первообразную функцию

(неопределённый интеграл). Константа  С

  в определённом интеграле не добавляется.

Обозначение

является чисто техническим, и вертикальная палочка не несёт никакого математического смысла. Запись

нужна для подготовки применения формулы Ньютона-Лейбница.

2)  Подставляем значение верхнего предела в первообразную функцию

3)  Подставляем значение нижнего предела в первообразную функцию

4)  Находим разность (число)

F(b) – F(a).

Определённый интеграл существует не всегда.

ПРИМЕР:

Интеграла

не существует, поскольку отрезок интегрирования  

[–5; –2]  

не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными).

ПРИМЕР:

Интеграла

не существует, поскольку на отрезке интегрирования  [–2; 3]  тангенс терпит бесконечные разрывы в точках

х = –^π/₂,  х = ^π/₂.

Для того чтобы определённый интеграл существовал, достаточно чтобы подынтегральная функция была непрерывной на отрезке интегрирования.

Поэтому перед тем, как приступить к решению любого определённого интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования.

Определённый интеграл может быть равен отрицательному числу или нулю.

Нижний предел интегрирования может быть больше верхнего предела интегрирования.

ПРИМЕР:

Интеграл вычисляется по формуле Ньютона-Лейбница.

Свойства определённого интеграла.

1)  В определённом интеграле можно переставить верхний и нижний предел, сменив при этом знак.

ПРИМЕР:

В определённом интеграле

перед интегрированием целесообразно поменять пределы интегрирования на <<привычный>> порядок:

В таком виде интегрировать значительно удобнее.

2)  Свойства линейности.

где   k = const.

Это справедливо не только для двух, но и для любого количества функций.

ПРИМЕР:

Вычислить определённый интеграл:

РЕШЕНИЕ:

Выносим константу за знак интеграла:

Интегрируем по таблице с помощью формулы

Используем формулу Ньютона-Лейбница.

Сначала подставляем в  х³  верхний предел, зптем нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.

= ²/₃ (2³ – 1³) = ²/₃ (8 – 1) = ²/₃ ∙ 7 = ¹⁴/₃ = 4²/₃.

ПРИМЕР:

Вычислить определённый интеграл:

РЕШЕНИЕ:

ПРИМЕР:

Вычислить определённый интеграл:

РЕШЕНИЕ:

Используем свойства линейности определённого интеграла.

Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница.

Рассмотрим второй способ решения этого интеграла.

ПРИМЕР:

Вычислить определённый интеграл:

РЕШЕНИЕ:

Сначала используем правило линейности и проинтегрируем по таблице. Получается одна скобка с отчёркиванием пределов.

В первообразную функцию сначала подставим  4, затем  –2. А затем найдём разность. Перед тем, как использовать формулу Ньютона-Лейбница, полезно провести проверку и убедиться, что первообразная функция найдена правильно.
Так, применительно к рассматриваемому примеру, перед тем, как в первообразную функцию

подставлять верхний и нижний пределы, необходимо проверить правильно или нет, найден неопределённый интеграл. Дифференцируем:

Получена исходная подынтегральная функция, значит, неопределённый интеграл найден верно.

ПРИМЕР:

Вычислить определённый интеграл:

РЕШЕНИЕ:

Задания к уроку 6

Задание 2. Простейшие тригонометрические уравнения

Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока 

или 

посмотрите

ВИДЕО УРОК

 1. Решите уравнение:

 а)  (–1)^k ∙ ^π/₆ + ^πk/₂,  k ∈ Z;     

 б)  ±^π/₁₂ + πk,  k ∈ Z;     

 в)  (–1)^k ∙ ^π/₁₂ + πk,  k ∈ Z;     

 г)  ±^π/₆ + 2πk,  k ∈ Z.

 2. Решите уравнение:

sin 4х = –1.

 а)  –^π/₂ + 2πk,  k ∈ Z;     

 б)  –^π/₄ + πk,  k ∈ Z;     

 в)  –^π/₈ + ^πk/₂,  k ∈ Z;     

 г)  –^π/₈ + πk,  k ∈ Z.

 3. Найдите корни уравнения:

sin ^х/₂ = –1.

 а)  –^π/₂ + 2πk,  k ∈ Z;     

 б)  –^π/₄ + πk,  k ∈ Z;     

 в)  π + 4πk,  k ∈ Z;     

 г)  –π + 4πk,  k ∈ Z.

 4. Решите уравнение:

ctg х = 0.

 а)  πk,  k ∈ Z;     

 б)  ^π/₂ + πk,  k ∈ Z;     

 в)  2πk,  k ∈ Z;     

 г)  ^π/₂ + 2πk,  k ∈ Z.

 5. Какое уравнение не имеет корней ?

 6. Решите уравнение:

 а)  ±^π/₆ + πk,  k ∈ Z;     

 б)  ±^5π/₁₂ + πk,  k ∈ Z;     

 в)  (–1)^k+1 ∙ ^π/₁₂ + 2πk,  k ∈ Z;     

 г)  ^π/₆ + 2πk,  k ∈ Z.

 7. Решите уравнение:

cos ^х/₃ = 0.

 а)  ^π/₂ + πk,  k ∈ Z;     

 б)  ^π/₆ + ^πk/₃,  k ∈ Z;     

 в)  ^3π/₂ + 3πk,  k ∈ Z;     

 г)  ^3π/₂ + 6πk,  k ∈ Z.

 8. Сколько корней имеет уравнение ?

 а)  один корень;     

 б)  два корня;     

 в)  много корней;     

 г)  нет корней.

 9. Решите уравнение:

 а)  ±^2π/₃ + 2πk,  k ∈ Z;     

 б)  ±^π/₃ + 2πk,  k ∈ Z;     

 в)  ±^2π/₃ + 4πk,  k ∈ Z;     

 г)  ±^π/₃ + 4πk,  k ∈ Z.

10. Решите уравнение:

6 tg х – 12 = 0.

 а)  arctg 2 + πk,  k ∈ Z;     

 б)  ¹/₆ arctg 12 + ^πk/₆,  k ∈ Z;     

 в)  arctg 2 + 2πk,  k ∈ Z;     

 г)  –arctg 2 + πk,  k ∈ Z.

11. Решите уравнение:

cos x = 0.

 а)  ^π/₂ + πk,  k ∈ Z;     

 б)  πk,  k ∈ Z;     

 в)  2πk,  k ∈ Z;     

 г)  π + 2πk,  k ∈ Z.

12. Сколько корней имеет уравнение ?

sin х = sin 2.

 а)  один корень;     

 б)  два корня;     

 в)  много корней;     

 г)  нет корней.

Следующие Предыдущие Главная страница

Подписаться на: Сообщения (Atom)

Техники интеграции: примеры и типы

Прежде чем перейти к математике, вот шутка, чтобы поднять настроение (кто сказал, что математика не может быть смешной?):

---

Учитель: Что такое 3+3?

Бобби: 3!

Учитель: Да, Бобби, верно.

---

Шутки в сторону, вы, вероятно, сталкивались с факториалами в различных ситуациях. Обычно мы определяем факториалы следующим образом:

$$n! = n(n-1)…1$$

Это определение имеет смысл, если n — натуральное число, но не в том случае, если \(n\) — вещественное число любого другого типа. Математики, будучи математиками, решили, что такое положение вещей, откровенно говоря, неприемлемо. Итак, они придумали определения факториалов, которые позволяют вам делать такие вещи, как найти \(\pi!\). Одной из них является гамма-функция 9{-Икс} \; dx.$$

Это здорово, но ставит перед нами другую дилемму: как нам вычислить этот (честно говоря, несколько пугающий) интеграл? К счастью, существует множество методов интеграции, которые мы можем использовать для решения проблемы. Наиболее распространенными методами интегрирования являются:

• Степенное правило интегрирования

• Интегрирование подстановкой

• Тригонометрическая подстановка

• Интегрирование по частям3

  0023

  Интегрирование неполными дробями

• Интегрирование функций с использованием длинного деления

Их необходимо знать, но они не всегда помогут вам с интегралами, такими как гамма-функция. Существует слишком много методов интегрирования, чтобы их можно было полностью охватить в одной статье, но здесь вы увидите несколько наиболее известных методов решения проблемных интегралов. В частности, в этой статье будут рассмотрены степенное правило интегрирования, интегралы от обратных функций, подстановка Вейерштрасса и метод интегрирования Фейнмана. Подробнее о других техниках интеграции, перечисленных выше, читайте в соответствующих статьях. 9{4} + C.\]

Вы можете проверить, дифференцируя, что этот ответ правильный.

Другие общие методы

Некоторые общие методы интеграции включают в себя:

• Интеграция по замене

• Тригонометрическая замена

• Интеграция по деталям

• Интеграция по частям

• . Подразделение

Для получения дополнительной информации о каждом из них см. соответствующие статьи. 9{5/2}.\end{align}\]

Дополнительные методы интегрирования

Поиск новых методов интегрирования является почти кустарным делом среди математиков. Это связано с тем, что методы интеграции могут быть интересными, неожиданными и просто забавными, с которыми можно возиться. Детальное описание всех известных методов интеграции выходит за рамки этой статьи, но мы можем рассмотреть несколько примеров. В частности, мы рассмотрим интегралы обратных функций, технику тригонометрических интегралов и технику интегрирования Фейнмана. 9{-1}\) относительно линии \(y=x\), как показано на рисунке ниже.

Рис. 3. Наглядное доказательство интеграла обратной функции в виде площади.

Итак, как показано на рисунке выше, сумма наших интегралов равна площади прямоугольника, которая равна \(bf(b)\).

Теперь, если вы позволите \(a\) и \(c\) быть ненулевыми, все, что вы делаете геометрически, это вырезание прямоугольника с площадью \(af(a)\) из области, которую вы ищете как вы можете видеть на графике ниже.

Рис. 4. Наглядное доказательство интеграла обратной функции с ненулевым пределом интегрирования. 91} \лн(у) \; dy = 1. \]

Тригонометрические методы интегрирования

Тригонометрические функции встречаются во многих интегралах и могут быть весьма полезными даже в неожиданных местах. Дополнительные сведения о подстановке тригонометрических функций или о том, как интегрировать тригонометрические функции в целом, см. в статьях «Тригонометрическая подстановка», «Тригонометрические интегралы» и «Интегралы, приводящие к обратным тригонометрическим функциям». Здесь вы можете взглянуть на подстановку Вейерштрасса, интересный метод, используемый для оценки рациональных функций синуса и косинуса. Этот метод основан на подстановке \(u\), поэтому перед прочтением этого раздела может быть полезно прочитать статью «Интеграция путем подстановки». 92}\справа) \; du\\&= \int \frac{1}{u} \; du\\&= \ln|u| + C\\&= \ln\left|\tan\left(\frac{x}{2}\right)\right| + C.\end{align}\]

Метод интегрирования Фейнмана

Метод интегрирования Фейнмана представляет собой интересный метод интегрирования, который иногда также называют «дифференцированием под знаком интеграла». Техника Фейнмана позволяет использовать дифференцирование сложных интегралов для получения выражения, которое (будем надеяться!) легче интегрировать.

9b \frac{\partial}{\partial t} f(x, t) dx.\]

Используя основную теорему исчисления, проинтегрируйте \(I'(t)\), чтобы найти \(I (в)\).

Здесь выражение \(\frac{\partial}{\partial t}\) просто означает «дифференцировать выражение по \(t\), а не по \(x\)». Это называется частной производной ; вы увидите больше из них, если вы возьмете многомерное исчисление.

Примеры техники Фейнмана

9{t=1}\\&= \frac{\pi}{2}\left[\ln|2| – \ln|1|\right]\\&= \frac{\pi}{2}\ln(2).\end{align}\]

Как и в этом примере, вам часто нужно использовать интегрирование Фейнмана с другие методы интеграции.

Ричард Фейнман (1918–1988) был американским физиком-теоретиком, проделавшим значительную работу в области физики элементарных частиц и квантовой механики. Он был блестящим физиком, обладавшим даром ясно, элегантно и конкретно объяснять сложные понятия. Хотя он и не был автором метода интеграции, носящего его имя, он сыграл определенную роль в его популяризации. Вот что он сказал о технике:

«Я научился вычислять интегралы с помощью различных методов, показанных в книге, которую дал мне мой школьный учитель физики мистер Бейдер. Однажды он сказал мне остаться после занятий. «Фейнман, — сказал он, — ты слишком много говоришь и слишком много шумишь. Я знаю, почему. Тебе скучно. Так что я дам тебе книгу. , и изучите эту книгу, и когда вы узнаете все, что в этой книге, вы снова сможете говорить». … [В этой книге] показано, как дифференцировать параметры под знаком интеграла — это определенная операция. Оказывается, в университетах этому не очень учат; они не подчеркивают это. Но я понял, как использовать этот метод, и я использовал этот проклятый инструмент снова и снова. Так как я был самоучкой по этой книге, у меня были особые методы вычисления интегралов. … Так что я получил прекрасную репутацию в решении интегралов только потому, что мой набор инструментов отличался от всех остальных, и они опробовали на нем все свои инструменты, прежде чем дать задачу мне ». ¹

Методы интегрирования – основные выводы

• Общие методы интегрирования включают степенное правило для интегралов, интегрирование с помощью подстановки, тригонометрическую замену, интегрирование по частям, интегрирование с помощью частичных дробей и интегрирование функций с использованием деления в длину.
• Правило силы для интеграции — это правило, которое «отменяет» правило силы для дифференциации.
• Замена Вейерштрасса полезна для замены рациональных выражений тригонометрических функций.
• Интеграл функции может быть выражен через ее обратную.
• Техника интегрирования Фейнмана полезна для сложных интегралов, включающих дифференцирование под знаком интеграла.

---

Ссылки

1. Ричард Фейнман, вы, конечно, шутите, мистер Фейнман!, 1985.

Интегрирование в математике: определение, способы его расчета и примеры Что такое математическая интеграция?

Ключевые формулы интегрирования

Как вычислять интегралы

4 примера интеграции

Что такое интеграция в математике?

Что означает интегрирование в математике? Интеграция есть обратный процесс дифференциации. Интегрирование некоторой функции f(x)f(x)f(x) дает другую функцию, F(x)F(x)F(x). При дифференцировании эта функция F(x)F(x)F(x) возвращает исходную функцию f(x)f(x)f(x). По этой причине неопределенный интеграл часто называют первообразной. Точно так же мы также называем интеграцию антидифференцированием.

Чтобы освежить свои знания об интегралах, прочтите это руководство для начинающих по интегралам.

Давайте рассмотрим обозначения для интегрирования. Неопределенный интеграл действительнозначной функции f (x) f (x) f (x) по действительной переменной x записывается как:

∫f(x)dx=F(x)+C\int f(x)dx = F(x) + C∫f(x)dx=F(x)+C

• Символ ∫\ int∫ называется знаком интеграла.

• Функция f(x)f(x)f(x) называется подынтегральной функцией. Мы хотим найти первообразную этой функции.

• Буквы dxdxdx обозначают дифференциал dxdxdx. Дифференциал dxdxdx указывает на то, что мы интегрируем нашу функцию по переменной x.

• F(x)F(x)F(x) — первообразная функция, полученная в результате взятия интеграла. 2 + C = F(x)∫(2x)dx=x2+C=F(x). 92+100F(x)=x2+100, тогда F’(x)=2xF’(x) = 2xF’(x)=2x

Какую бы константу мы ни поставили в конце первообразной функции F(x)F(x)F(x), производная F’(x)F’(x)F’(x) всегда одна и та же; и F’(x)F’(x)F’(x) всегда равна исходной функции f(x)f(x)f(x).

Поскольку существует бесконечное число функций F(x)F(x)F(x), производная которых равна f(x)f(x)f(x), включение C дает нам способ выразить общее форма первообразной F (x) F (x) F (x), представляя семейство бесконечно многих функций.

Чтобы подробнее рассказать об первообразных производных, один из наших инструкторов, доктор Тим Шартье, расскажет о них более подробно:

Ключевые формулы интегрирования

Давайте рассмотрим наиболее важные правила интегрирования и некоторые стандартные интегралы. Хотя есть много правил, которые нужно запомнить, не отчаивайтесь. Многие следуют аналогичной схеме. Стоит потратить время, чтобы ознакомиться с ними всеми.

В следующих свойствах предположим, что fff и ggg — непрерывные функции. 9{-1}x + C∫1+x2dx​=tan−1x+C

∫sin⁡(ax)dx=−cos⁡(ax)a+C\int \sin{(ax)}dx = \frac{-\cos{(ax)}}{a}+C∫sin(ax) dx=a−cos(ax)​+C для некоторого действительного числа a

∫cos⁡(ax)dx=sin⁡(ax)a+C\int \cos{(ax)}dx = \frac{\sin{(ax)}}{a}+C∫cos(ax)dx= asin(ax)​+C для некоторого действительного числа a

Правило абсолютного значения

∫∣x∣dx=x∣x∣2+C\int |x|dx = \frac{x |x|}{2} + C∫∣x∣dx=2x∣x∣​+C

Доктор Тим Шартье объясняет эти правила подробнее здесь:

Как вычислять интегралы

Мы узнаем, как интегрировать, используя 4 разных метода. 4} dx∫x4x3−2x​dx. Обратите внимание, что, упростив и используя правило суммы, мы получаем: 9{2}}+C∫x4x3−2x​dx=ln∣x∣+x21​+C.

2. Интеграция по частям

Мы используем интегрирование по частям для вычисления интеграла от произведения функций.

Вот формула интегрирования по частям:

∫udv=uv−∫vdu\int udv = uv – \int vdu∫udv=uv−∫vdu

Интегрирование по частям включает в себя выбор одной функции под интегралом для представления u и одной функции для представления dv.

Вот несколько простых шагов:

1. Выберите uuu и dvdvdv, чтобы разделить заданную функцию на произведение функций.

2. Разделите uuu, чтобы найти dududu, и объедините dvdvdv, чтобы найти vvv.

3. Подставьте uuu, vvv и dududu в формулу интегрирования по частям.

4. Решите и упростите там, где это необходимо.

Как правило, вы выбираете uuu как термин, который легче всего различать, и выбираете dvdvdv как термин, который легче всего интегрировать.

Вместе сделаем один пример. Допустим, мы хотим вычислить ∫xcos⁡(3x)dx\int x \cos (3x) dx∫xcos(3x)dx.

Шаг 1

Давайте выберем dv=cos⁡(3x)dxdv = \cos (3x)dxdv=cos(3x)dx, поскольку у нас есть простая формула для интегрирования этой функции с использованием приведенных выше правил тригонометрии. Тогда u=xu = xu=x, так как это то, что осталось.

Шаг 2

Дифференцируя u, мы имеем dudx=d(x)dx=1\frac{du}{dx}=\frac{d(x)}{dx}=1dxdu=dxd(x)=1. После умножения обеих частей на дифференциал dxdxdx мы находим, что du=1dxdu = 1dxdu=1dx.

Теперь давайте интегрируем dvdvdv, чтобы найти vvv. Одна из приведенных выше тригонометрических формул дает нам простой ответ на этот вопрос. Итак, v = ∫dv = ∫cos⁡(3x)dx=sin⁡(3x)3v = \int dv = \int \cos (3x) dx = \frac{\sin{(3x)}}{3}v= ∫dv=∫cos(3x)dx=3sin(3x)​.

Шаг 3

Используя формулу интегрирования по частям, имеем:

∫udv=uv−∫vdu\int udv = uv – \int vdu∫udv=uv−∫vdu

∫xcos⁡(3x)dx=x⋅sin⁡(3x)3−∫sin⁡(3x) 3dx\int x \cos (3x) dx = x \cdot \frac{\sin{(3x)}}{3} – \int \frac{\sin{(3x)}}{3}dx∫xcos(3x )dx=x⋅3sin(3x)​−∫3sin(3x)​dx

=xsin⁡(3x)3−13⋅∫sin⁡(3x)dx= \frac{x\sin{(3x)}} {3} – \frac{1}{3} \cdot \int \sin{(3x)}dx=3xsin(3x)​−31​⋅∫sin(3x)dx

=xsin⁡(3x)3− 13⋅−cos⁡(3x)3= \frac{x\sin{(3x)}}{3} – \frac{1}{3} \cdot \frac{-\cos{(3x)}}{3 }=3xsin(3x)−31⋅3−cos(3x)​

=xsin⁡(3x)3+cos⁡(3x)9+C= \frac{x\sin{(3x)}}{3} + \frac{\cos{(3x)}}{9}+ C=3xsin(3x)​+9cos(3x)​+C

Итак, ∫xcos⁡(3x)dx=xsin⁡(3x)3+cos⁡(3x)9+C\int x \cos (3x) dx = \frac{x\sin{(3x)}}{3} + \frac{{\cos{(3x)}}}{9}+C∫xcos(3x)dx=3xsin(3x)​+9cos(3x) +С.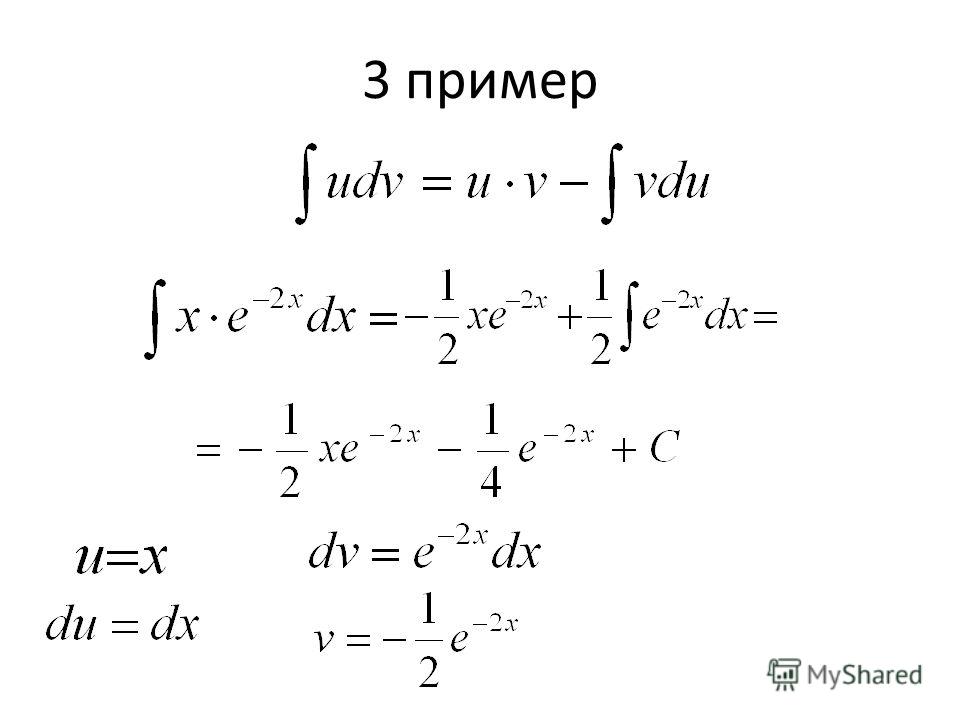

3. U-замена

U-подстановка распутывает цепное правило для производных. По этой причине u-подстановка также называется правилом обратной цепочки и используется для интеграции составных функций.

Если вы можете распознать как функцию, так и ее производную внутри одного и того же интеграла, это хороший признак того, что вы можете использовать u-подстановку. Функция, в которой вы можете использовать u-подстановку, будет выглядеть так:

∫f(g(x))g'(x)dx\int f(g(x))g'(x)dx∫f(g(x))g'(x)dx

Мы хотим подставим вместо подынтегрального выражения u=g(x)u = g(x)u=g(x) и du=g'(x)du = g'(x)du=g'(x) так, чтобы оно выглядело как это:

∫f(g(x))g'(x)dx=f(u)du\int f(g(x))g'(x)dx = f(u)du∫f(g(x) )g'(x)dx=f(u)du 92+5}+C∫(4x)e2x2+5dx=e2x2+5+C.

4. Интегрирование неполными дробями

Этот метод полезен для интегрирования рациональных функций. Рациональная функция — это функция, которая записывается как отношение двух полиномиальных функций. 2+92+9x+4} = \frac{2x}{(2x+1)(x+4)}2×2+9x+42x​=(2x+1)(x+4)2x​

=A2x+1+ Bx+4= \frac{A}{2x+1} + \frac{B}{x+4}=2x+1A​+x+4B​

=A(x+4)(2x+1)( x+4)+B(2x+1)(2x+1)(x+4)=\frac{A(x+4)}{(2x+1)(x+4)}+\frac{B( 2x+1)}{(2x+1)(x+4)}=(2x+1)(x+4)A(x+4)​+(2x+1)(x+4)B(2x+ 1)​

=Ax+4A+2Bx+B(2x+1)(x+4)=\frac{Ax+4A+2Bx+B}{(2x+1)(x+4)}=(2x +1)(x+4)Ax+4A+2Bx+B​

Теперь мы собираем члены x с одной стороны числителя и собираем постоянные члены с другой стороны числителя. Это позволяет нам отразить структуру исходного числителя подынтегрального выражения 2x+02x+02x+0.

2x(2x+1)(x+4)=(Ax+2Bx)+(4A+B)(2x+1)(x+4)\frac{2x}{(2x+1)(x+4) )} = \frac{(Ax+2Bx)+(4A+B)}{(2x+1)(x+4)}(2x+1)(x+4)2x​=(2x+1)(x +4)(Ax+2Bx)+(4A+B)​

Теперь мы можем найти A и B, составив два уравнения:

числитель новой рациональной функции.

Это уравнение уравнивает постоянные члены в числителе исходного подынтегрального выражения с постоянными членами в числителе новой рациональной функции. 92+9x+4} dx = \int (\frac{-2}{7(2x+1)}+\frac{8}{7(x+4)})dx∫2×2+9x+42x​dx= ∫(7(2x+1)−2​+7(x+4)8​)dx

=−27∫12x+1dx+87∫1x+4dx=\frac{-2}{7}\int \ frac{1}{2x+1}dx + \frac{8}{7}\int \frac{1}{x+4}dx=7−2​∫2x+11​dx+78​∫x+41 ​dx

= −2ln⁡(2x+1)2⋅7+8ln⁡(x+4)7+C=\frac{-2 \ln{(2x+1)}}{2 \cdot 7} + \frac{8 \ln{(x+4)}}{7} + C=2⋅7−2ln(2x+1)​+78ln(x+4)​+C

= −17ln⁡(2x+ 1)+87ln⁡(x+4)=-\frac{1}{7}\ln{(2x+1)} + \frac{8}{7} \ln{(x+4)}=-71 ​ln(2x+1)+78​ln(x+4)

=87ln⁡(x+4)−17ln⁡(2x+1)+C=\frac{8}{7} \ln{(x +4)} -\frac{1}{7}\ln{(2x+1)} + C=78​ln(x+4)−71​ln(2x+1)+C 93} + C=3×3−lnx​−9×31​+C

Пример 3

Вычислить ∫sin⁡(ln⁡x)xdx\int \frac{\sin{(\ln x)}}{x}dx∫xsin(lnx)​dx.

Решение : Мы можем решить эту проблему с помощью u-замены. Пусть u=ln⁡xu = \lnxu=lnx. Тогда du=1xdu = \frac{1}{x}du=x1​.

∫sin⁡(ln⁡x)xdx=∫sin⁡udu\int \frac{\sin{(\ln x)}}{x}dx = \int \sin{u}du∫xsin(lnx)​ dx=∫sinudu

=−cos⁡u+C=-\cos{u}+C=−cosu+C

=−cos⁡(ln⁡x)+C=-\cos{(\ln x) } + C=−cos(lnx)+C 92+10x+3} = \frac{x+1}{(x+3)(3x+1)}3×2+10x+3x+1​=(x+3)(3x+1)x+1​

=Ax+3+B3x+1= \frac{A}{x+3} + \frac{B}{3x+1}=x+3A​+3x+1B​

=A(3x+1) +B(x+3)(x+3)(3x+1)=\frac{A(3x+1)+B(x+3)}{(x+3)(3x+1)}=(x +3)(3x+1)A(3x+1)+B(x+3)​

=3Ax+A+Bx+3B(x+3)(3x+1)=\frac{3Ax+A+ Bx+3B}{(x+3)(3x+1)}=(x+3)(3x+1)3Ax+A+Bx+3B​

=3Ax+Bx+A+3B(x+3) (3x+1)=\frac{3Ax+Bx+A+3B}{(x+3)(3x+1)}=(x+3)(3x+1)3Ax+Bx+A+3B​

Теперь составим наши два уравнения. Один представляет термины x, а другой представляет константы. 92+10x+3}dx=\int(\frac1{4(x+3)}+\frac1{4(3x+1)})dx∫3×2+10x+3x+1​dx=∫(4(x +3)1​+4(3x+1)1​)dx

=14∫1x+3dx+14∫13x+1dx=\frac{1}{4}\int \frac{1}{x+3 }dx+\frac{1}{4}\int \frac{1}{3x+1}dx=41​∫x+31​dx+41​∫3x+11​dx

=14ln⁡(x+3 )+112ln⁡(3x+1)+C=\frac{1}{4} \ln{(x+3)}+\frac{1}{12} \ln{(3x+1)} + C= 41​ln(x+3)+121​ln(3x+1)+C

Исследуйте отмеченные наградами курсы For-Credit от Outlier

Outlier (от соучредителя MasterClass) собрал некоторые из лучшие в мире преподаватели, гейм-дизайнеры и режиссеры для создания будущего онлайн-колледжа.

Ознакомьтесь с этими родственными курсами:

Исчисление I

Изучите курс

Исчисление I

Математика изменений.

Изучить курс

Введение в статистику

Изучить курс

Введение в статистику

Как данные описывают наш мир.

Изучить курс

Введение в микроэкономику

Изучить курс

Введение в микроэкономику

Почему маленькие решения имеют большое влияние.