Неопределенность 0 в степени 0: Основные неопределенности пределов и их раскрытие

Почему 0 в степени 0 равно 1? — Обсуждай

Почему 0 в степени 0 равно 1? — Обсуждай

М(

Михаил (Москва)

Почему 0 в степени 0 равно 1? степень

2 года

838

61

0

Ответы

Elchin Tehmezov

Ноль в степени ноль равно нулю. Я знаком с методами как доказывают обратное. Все они не приемлемы. Вот внизу ролик поставили. Человек вычитывает степень числа которое приближается к нулю. Итог приближается к единице. Но во первых это не ноль, на самом деле это бесконечность. Ибо число приближается к нулю бесконечно. Значит тот число в его степени бесконечно приближается к единице. Но то число никогда не станет нулем, и степень ни когда не станет единицей. По этому такой подход не верный. Если использовать логарифму, получается то же самое.

Ничего если возвести на степень ни чего, то ничего не будет происходить. Ибо нет какого либо числа, над чем можно работать. Ноль- на самом деле не число а дополнение, без которого математика просто не работает. А само по себе, это ни что. То есть нуля нет.

2 года

0

Elchin Tehmezov

А в калькуляторах и т.п. вычисляется один по простой причине. Компьютер не понимает всего этого. Он понимает только это – есть сигнал, нет сигнала. Есть 1 нет 0- так приятно принимать. Но само число ноль должно выводится на экран, а значит должен иметь сигнал. Если нет сигнала, то монитор ничего не покажет. Ибо не получает данных. Компьютер не может вычислить, и показывает единицу. Ноль не может выдать, так как получил несколько сигналов для вычисление. Компьютер не понимает ничего из того что мы говорим или пишем. Он понимает только две вещи – есть электричество, нет электричество.

0=0/0. А 0/0 не обязательно единица, это неопределенность, ведь на 0 делить нельзя))) это работает для выражения «а в степени b, где a и b стремятся к 0».

2 года

0

АВ

Александра Воронцова

Из всего, что нагуглила в интернете, самое доступное для нематематиков обьяснение нашла вот это: “отображение пустого множества в пустое, а оно единственно”. Такое литературное выражение хоть как-то (с трудом), но можно переварить.

2 года

0

ЗБ

Зинаида Бадяева

Глубоко ошибаетесь – в математике -это неопределенность такого типа и доказывается эта единица с помощью известных теорем из теории пределов высшей математики совсем не просто не для математиков !

2 года

0

АР

Алексей Райтман

Математический парадокс,любое число в степени ноль,равно единице,в случае с нолем,ответ считается неочевидным. Просто математический закидон.

2 года

0

Михаил Киранов

Значит так решили принять.
А вообще-то это одна из неопределённостей. Но всё зависит от того, что является этим нулём.

2 года

0

Дмитрий Кузнецов

Известно, что абсолютно любое число в нулевой степени равно единице.Если правильно помню,класс 2-3….

2 года

0

RW

Rion West

Это чисто символически. В нуле эта функция разрывается и не имеет значения

2 года

0

Ла

Лариса

Математики всего мира ещё не пришли к единому мнению по этому вопросу.

2 года

0

ЛЗ

Любовь Золотарева

Любое число или выражение в нулевой степени равно 1(правило).

2 года

0

TS

Timur Sa

Потому что это не так. значение 0 в степени 0 – не определено

2 года

0

Александр Патрушев

Ноль – число, а любое число в нулевой степени равно единице.

2 года

0

Ех

Ехидна

Хороший вопрос…. Ответ думаю только один – “Потому что”))))

2 года

0

ВМ

В М

Все просто. Это и есть великая тайна сотворения мира. = 0!

2 года

0

ЛС

Лиана Сафарли

Любое число в нулевой степени равно единице.

2 года

0

~E

~ Eva Lansca ~

Насколько я помню , число в степени ноль = 1

2 года

0

ИЕ

Ина Ева

Поавило тако, любое число в нулевой – один

2 года

0

Ан

Андрей

Потому, что сахар сладкий, но всегда один

2 года

0

ДА

Дмитрий Арбузов

В мире абсурда всё стремится к единице.

2 года

0

Виктор Бабенко

0 чести, 0 совести = 1 депутат , логично

2 года

0

Следующая страница

Виды и правила раскрытия неопределенностей (Таблица)

Вид неопределенности	Правило раскрытия
1.	1.1. Чтобы раскрыть неопределенность вида , заданную отношением двух многочленов, надо и числитель и знаменатель почленно разделить на переменную величину в наибольшей степени.
	1.2. Для раскрытия неопределенности вида , заданную отношением иррациональных функций, надо и числитель и знаменатель почленно разделить на переменную величину в наибольшей степени с учетом степеней корней.
2.	2.1. Для того, чтобы определить предел дробно-рациональной функции в случае, когда при x → a числитель и знаменатель дроби имеют пределы, равные  нулю, надо числитель и знаменатель дроби разделить на x – a и перейти к пределу. Если и после этого числитель и знаменатель новой дроби имеют пределы, равные  нулю при x → a, то надо произвести повторное деление на x – a.
	2.2. Чтобы раскрыть неопределенность вида , в которой числитель или знаменатель иррациональны, следует надлежащим образом избавиться от иррациональности, умножив и числитель и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби. В случае квадратных корней и числитель и знаменатель дроби умножаются на сопряженное выражение тому, которое содержит иррациональность и применяется формула a2 – b2 = (a – b)(a + b) . В случае кубических корней и числитель и знаменатель дроби умножаются на неполный квадрат суммы или разности и применяется формула a3 ± b3 = (a ± b)(a2 ± ab + b2).
3.	3.1. Неопределенность вида , получающаяся в результате алгебраической суммы иррациональных выражений, устраняется или приводится к типу 1 путем домножения и деления на одно и то же выражение, приводящее к формулам сокращенного умножения. В случае квадратных корней разность домножается на сопряженное выражение и применяется формула a2 – b2 = (a – b)(a + b) . В случае кубических корней функция домножается на неполный квадрат суммы или разности и применяется формула a3 ± b3 = (a ± b)(a2 ± ab + b2).
	3.2. Неопределенность вида , получающаяся в результате алгебраической суммы двух дробей, устраняется или сводится к типу 2  путем приведения дробей к общему знаменателю. Пусть: , . Тогда:
4. Замечательные пределы	4.1. Первый замечательный предел  (неопределенность ). В случае, когда под знаком предела стоят тригонометрические функции, дающие неопределенность , используется первый замечательный предел: . Его различные формы:      ,     ,     ,   ,          ,   ,          .
	4.2. Второй замечательный предел (неопределенность ):    . Его различные формы: ,    ,      , ,
5.	5.1. Неопределенность вида   сводится либо к неопределенности типа 1 , либо к неопределенности типа 2  путем перемещения в знаменатель одного из сомножителей. Пусть , . Тогда:
6.      ,	6.1. Неопределенности вида ,   сводятся к неопределенности типа 5  путем логарифмирования.

Как рассчитать неопределенность | Наука

Обновлено 26 октября 2020 г.

Ли Джонсон

Количественная оценка уровня неопределенности в ваших измерениях является важной частью науки. Ни одно измерение не может быть идеальным, и понимание ограничений точности ваших измерений помогает гарантировать, что вы не сделаете на их основе необоснованных выводов. Основы определения неопределенности довольно просты, но объединение двух неопределенных чисел усложняется. Хорошая новость заключается в том, что существует множество простых правил, которым вы можете следовать, чтобы скорректировать свои неопределенности независимо от того, какие расчеты вы делаете с исходными числами.

TL;DR (слишком длинное; не читал)

Если вы добавляете или вычитаете величины с неопределенностями, вы добавляете абсолютные неопределенности. Если вы умножаете или делите, вы добавляете относительную неопределенность. Если вы умножаете на постоянный коэффициент, вы умножаете абсолютные неопределенности на тот же коэффициент или ничего не делаете с относительными неопределенностями. Если вы берете мощность числа с неопределенностью, вы умножаете относительную неопределенность на число в степени.

Оценка неопределенности в измерениях

Прежде чем комбинировать или делать что-либо с вашей неопределенностью, вы должны определить неопределенность исходного измерения. Часто это связано с некоторым субъективным суждением. Например, если вы измеряете диаметр мяча с помощью линейки, вам нужно подумать о том, насколько точно вы действительно можете прочитать измерение. Вы уверены, что измеряете от края мяча? Насколько точно вы можете прочитать линейку? Это типы вопросов, которые вы должны задавать при оценке неопределенностей.

В некоторых случаях можно легко оценить неопределенность. Например, если вы взвешиваете что-то на весах, измеряющих с точностью до 0,1 г, то вы можете с уверенностью оценить погрешность измерения ±0,05 г. Это связано с тем, что измерение 1,0 г действительно может составлять от 0,95 г (округление в большую сторону) до чуть менее 1,05 г (округление в меньшую сторону). В других случаях вам придется оценить его как можно лучше на основе нескольких факторов.

• Значащие цифры: Как правило, абсолютные погрешности указываются только до одной значащей цифры, за исключением случаев, когда первая цифра равна 1. Из-за значения неопределенности нет смысла указывать вашу оценку с большей точностью, чем ваша неопределенность. Например, измерение 1,543 ± 0,02 м не имеет никакого смысла, потому что вы не уверены во втором десятичном знаке, поэтому третий по сути бессмысленен. Правильный результат: 1,54 м ± 0,02 м.

Абсолютная и относительная погрешности

Указание вашей погрешности в единицах исходного измерения, например, 1,2 ± 0,1 г или 3,4 ± 0,2 см, дает «абсолютную» погрешность. Другими словами, он явно сообщает вам величину, на которую исходное измерение может быть неверным. Относительная неопределенность дает неопределенность в процентах от исходного значения. Вычислите это с помощью:

\text{Относительная неопределенность} = \frac{\text{абсолютная неопределенность}}{\text{наилучшая оценка}} × 100\%

Таким образом, в приведенном выше примере:

\text{Относительная неопределенность} = \frac{0,2 \text{ см}}{3,4\text{ см}} × 100\% = 5,9\%

Таким образом, значение может быть указывается как 3,4 см ± 5,9%.

Сложение и вычитание неопределенностей

Вычислите общую неопределенность при сложении или вычитании двух величин с их собственными неопределенностями путем сложения абсолютных неопределенностей. Например:

(3,4 ± 0,2 \text{ см}) + (2,1 ± 0,1 \text{ см}) = (3,4 + 2,1) ± (0,2 + 0,1) \text{ см} = 5,5 ± 0,3 \text{ см} \\ (3,4 ± 0,2 \text{ см}) – (2,1 ± 0,1 \text{ см}) = (3,4 – 2,1) ± (0,2 + 0,1) \text{ см} = 1,3 ± 0,3 \text{ см } 92 ± 10\%

\frac{(3,4 \text{ см} ± 5,9\%)}{(1,7 \text{ см} ± 4,1 \%)} = \frac{3,4}{1,7} ± (5,9 + 4.1)\% = 2,0 ± 10%

Умножение на константу

Если вы умножаете число с неопределенностью на постоянный коэффициент, правило зависит от типа неопределенности. Если вы используете относительную неопределенность, это остается прежним:

(3,4 \text{ см} ± 5,9\%) × 2 = 6,8 \text{ см} ± 5,9\%

Если вы используете абсолютные неопределенности , вы умножаете неопределенность на тот же коэффициент: 93 ± 9\%

Вы следуете тому же правилу для дробных степеней.

Неопределенность и ошибки: формула и расчет

Когда мы измеряем такое свойство, как длина, вес или время, мы можем внести ошибки в наши результаты. Ошибки, которые создают разницу между реальным значением и тем, которое мы измерили, являются результатом того, что что-то идет не так в процессе измерения.

Причинами ошибок могут быть используемые инструменты, люди, считывающие значения, или система, используемая для их измерения.

Если, например, термометр с неправильной шкалой регистрирует один дополнительный градус каждый раз, когда мы используем его для измерения температуры, мы всегда будем получать результат, отличающийся на этот один градус.

Из-за разницы между реальным значением и измеренным, наши измерения будут иметь некоторую погрешность. Таким образом, когда мы измеряем объект, фактическое значение которого мы не знаем, работая с прибором, выдающим ошибки, фактическое значение находится в «диапазоне неопределенности».

Разница между неопределенностью и ошибкой

Основное различие между ошибками и неопределенностями заключается в том, что ошибка представляет собой разницу между фактическим значением и измеренным значением, а неопределенность представляет собой оценку диапазона между ними, представляющую надежность измерение. В этом случае абсолютная неопределенность будет представлять собой разницу между большим значением и меньшим.

Простой пример — значение константы. Допустим, мы измеряем сопротивление материала. Измеренные значения никогда не будут одинаковыми, потому что измерения сопротивления различаются. Мы знаем, что есть принятое значение 3,4 Ом, и, измерив сопротивление дважды, мы получим результаты 3,35 и 3,41 Ом.

Ошибки дали значения 3,35 и 3,41, а диапазон от 3,35 до 3,41 является диапазоном неопределенности.

Возьмем другой пример, в данном случае измерение гравитационной постоянной в лаборатории.

Стандартное ускорение свободного падения составляет 9,81 м/с ² . В лаборатории, проведя некоторые эксперименты с маятником, мы получили четыре значения g: 9,76 м/с ² , 9,6 м/с ² , 9,89 м/с ² и 9,9 м/с ² . Разница в значениях является продуктом ошибок. Среднее значение 92\]

Какова стандартная ошибка среднего?

Стандартная ошибка среднего значения — это значение, которое говорит нам, насколько велика ошибка наших измерений по сравнению со средним значением. Для этого нам нужно сделать следующие шаги:

1. Вычислить среднее значение всех измерений.
2. Вычтите среднее значение из каждого измеренного значения и возведите результаты в квадрат.
3. Сложите все вычтенные значения.
4. Разделите результат на квадратный корень из общего количества выполненных измерений.

Давайте рассмотрим пример.

Вы измерили вес предмета четыре раза. Известно, что объект весит ровно 3,0 кг с точностью менее одного грамма. Ваши четыре измерения дают вам 3,001 кг, 2,997 кг, 3,003 кг и 3,002 кг. Получите ошибку среднего значения.

Сначала вычисляем среднее значение:

\[\frac{3,001 кг + 2,997 кг + 3,003 кг + 3,002 кг}{4} = 3,00075 кг\]

Так как измерения имеют только три значащих цифры после запятой , мы принимаем значение 3.000 кг. Теперь нам нужно вычесть среднее значение из каждого значения и возвести результат в квадрат: 92 = 0,000009 кг\)

Все наши результаты равны 0, так как мы берем только три значащие цифры после запятой. Когда мы разделим это на квадратный корень выборок, который равен \(\sqrt4\), мы получим:

\(\text{Стандартная ошибка среднего} = \frac{0}{2} = 0\)

В этом случае стандартная ошибка среднего \((\сигма x\)) почти ничто.

Что такое калибровка и допуск?

Допуск — это диапазон между максимальным и минимальным допустимым значением измерения. Калибровка — это процесс настройки измерительного прибора таким образом, чтобы все измерения находились в допустимых пределах.

Для калибровки прибора его результаты сравниваются с другими приборами с более высокой точностью и точностью или с объектом, значение которого имеет очень высокую точность.

Одним из примеров является калибровка весов.

Чтобы откалибровать весы, вы должны измерить вес, который, как известно, имеет приблизительное значение. Допустим, вы используете массу в один килограмм с возможной погрешностью в 1 грамм. Допуск составляет диапазон от 1,002 кг до 0,998 кг. Весы постоянно дают меру 1,01 кг. Измеренный вес превышает известное значение на 8 граммов, а также превышает допустимый диапазон. Весы не проходят калибровочный тест, если вы хотите измерять вес с высокой точностью.

Как сообщается о неопределенности?

При проведении измерений необходимо сообщать о неопределенности. Это помогает тем, кто читает результаты, узнать о возможных вариациях. Для этого после символа ± добавляется диапазон неопределенности.

Допустим, мы измерили значение сопротивления 4,5 Ом с погрешностью 0,1 Ом. Сообщаемое значение с его неопределенностью составляет 4,5 ± 0,1 Ом.

Мы находим значения неопределенности во многих процессах, от производства до проектирования и архитектуры, механики и медицины.

Что такое абсолютные и относительные ошибки?

Погрешности измерений бывают абсолютными и относительными. Абсолютные ошибки описывают отличие от ожидаемого значения. Относительные ошибки измеряют разницу между абсолютной ошибкой и истинным значением.

Абсолютная ошибка

Абсолютная ошибка – это разница между ожидаемым значением и измеренным. Если мы произведем несколько измерений значения, мы получим несколько ошибок. Простой пример — измерение скорости объекта.

Допустим, мы знаем, что мяч, движущийся по полу, имеет скорость 1,4 м/с. Мы измеряем скорость, вычисляя время, необходимое мячу для перемещения из одной точки в другую с помощью секундомера, что дает нам результат 1,42 м/с.

Абсолютная погрешность вашего измерения составляет 1,42 минус 1,4.

\(\text{Абсолютная погрешность} = 1,42 м/с – 1,4 м/с = 0,02 м/с\)

Относительная погрешность

Относительная погрешность сравнивает величины измерений. Это показывает нам, что разница между значениями может быть большой, но она мала по сравнению с величиной значений. Давайте возьмем пример абсолютной ошибки и посмотрим на ее значение по сравнению с относительной ошибкой.

Вы используете секундомер для измерения мяча, движущегося по полу со скоростью 1,4 м/с. Вы подсчитываете, сколько времени потребуется мячу, чтобы преодолеть определенное расстояние, и делите длину на время, получая значение 1,42 м/с.

\(\text{Относительная ошибка} = \frac{|1,4 м/с – 1,42 м/с|}{1,4 м/с} = 0,014\)

\(\text{Абсолютная ошибка} = 0,02 м/ s\)

Как видите, относительная ошибка меньше абсолютной ошибки, потому что разница мала по сравнению со скоростью.

Другой пример разницы в масштабе — ошибка на спутниковом снимке. Если ошибка изображения имеет значение 10 метров, это много по человеческим меркам. Однако, если изображение имеет размеры 10 километров в высоту и 10 километров в ширину, ошибка в 10 метров невелика.

Относительная погрешность также может быть указана в процентах после умножения на 100 и добавления символа процента %.

Отображение неопределенностей и ошибок

Неопределенности отображаются в виде столбцов на графиках и диаграммах. Полосы простираются от измеренного значения до максимально и минимально возможного значения. Диапазон между максимальным и минимальным значением является диапазоном неопределенности. См. следующий пример столбцов неопределенности:

Рис.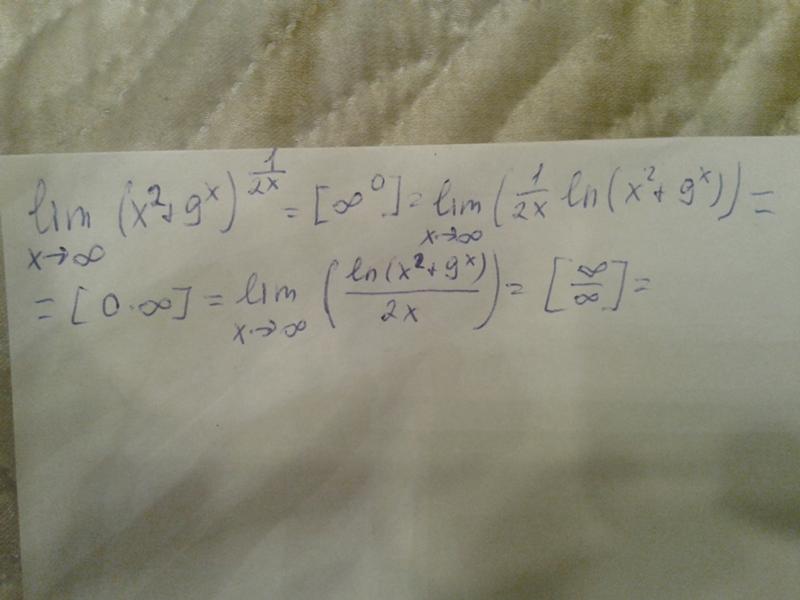 1. График, показывающий точки среднего значения каждого измерения. Полосы, отходящие от каждой точки, показывают, насколько могут отличаться данные. Источник: Мануэль Р. Камачо, StudySmarter.

См. следующий пример с несколькими измерениями:

Вы выполняете четыре измерения скорости мяча, движущегося на 10 метров, скорость которого уменьшается по мере продвижения. Вы отмечаете 1-метровые деления, используя секундомер, чтобы измерить время, которое требуется мячу, чтобы пройти между ними.

Вы знаете, что ваша реакция на секундомер составляет около 0,2 м/с. Измерив время секундомером и разделив его на расстояние, вы получите значения, равные 1,4 м/с, 1,22 м/с, 1,15 м/с и 1,01 м/с.

Поскольку реакция на секундомер задерживается, что приводит к погрешности 0,2 м/с, ваши результаты составляют 1,4 ± 0,2 м/с, 1,22 ± 0,2 м/с, 1,15 ± 0,2 м/с и 1,01 ± 0,2 м/с. с.

График результатов может быть представлен следующим образом:

Рисунок 2. График показывает приблизительное представление. Точки представляют фактические значения 1,4 м/с, 1,22 м/с, 1,15 м/с и 1,01 м/с. Столбцы представляют погрешность ±0,2 м/с.

Как распространяются неопределенности и ошибки?

Каждое измерение имеет ошибки и погрешности. Когда мы выполняем операции со значениями, взятыми из измерений, мы добавляем эти неопределенности к каждому расчету. Процессы, посредством которых неопределенности и ошибки изменяют наши расчеты, называются распространением неопределенности и распространением ошибок, и они вызывают отклонение от фактических данных или отклонение данных.

Здесь есть два подхода:

1. Если мы используем процентную ошибку, нам нужно вычислить процентную ошибку каждого значения, используемого в наших вычислениях, а затем сложить их вместе.
2. Если мы хотим знать, как неопределенности распространяются на расчеты, нам нужно выполнить расчеты, используя наши значения с учетом и без учета неопределенностей.

Разница заключается в распространении неопределенности в наших результатах.

См. следующие примеры:

Допустим, вы измерили ускорение свободного падения как 9,91 м/с ² , и вы знаете, что ваше значение имеет погрешность ± 0,1 м/с ² .

Вы хотите рассчитать силу, создаваемую падающим объектом. Объект имеет массу 2 кг с погрешностью 1 грамм или 2 ± 0,001 кг.

Чтобы рассчитать распространение с использованием процентной погрешности, нам необходимо рассчитать погрешность измерений. Рассчитаем относительную ошибку для 9,91 м/с ² с отклонением (0,1 + 92} = 0,01\)

Умножая на 100 и прибавляя знак процента, получаем 1%. Если затем мы узнаем, что масса 2 кг имеет погрешность в 1 грамм, мы вычисляем и для нее процентную ошибку, получая значение 0,05%.

Чтобы определить процент распространения ошибки, мы складываем обе ошибки.

\(\text{Error} = 0,05\% + 1\% = 1,05\%\)

Чтобы рассчитать распространение неопределенности, нам нужно рассчитать силу как F = m * g. Если мы вычислим силу без неопределенности, мы получим ожидаемое значение. 92)\]

Мы можем округлить это число до двух значащих цифр и получить 19,83 ньютона. Теперь мы вычитаем оба результата.

\[\text{Неопределенность = |Сила – Сила с неопределенностями|} = 0,21\]

Результат выражается как «ожидаемое значение ± значение неопределенности».

\[\text{Сила} = 19,62 \pm 0,21 Ньютона\]

Если мы используем значения с неопределенностями и ошибками, мы должны сообщить об этом в наших результатах.

Отчет о неопределенностях

Чтобы сообщить результат с неопределенностями, мы используем вычисленное значение, за которым следует неопределенность. Мы можем поместить количество в круглые скобки. Вот пример того, как сообщать о неопределенностях.

Мы измеряем силу, и, согласно нашим результатам, погрешность силы составляет 0,21 ньютона.

\[\text{Сила} = (19,62 \pm 0,21) ньютонов\]

Наш результат равен 19,62 ньютона, что может варьироваться плюс-минус 0,21 ньютона.

Распространение неопределенностей

См. следующие общие правила распространения неопределенностей и расчета неопределенностей. Для любого распространения неопределенности значения должны иметь одни и те же единицы измерения.

Сложение и вычитание: если значения добавляются или вычитаются, общее значение неопределенности является результатом сложения или вычитания значений неопределенности. Если у нас есть измерения (A±a) и (B±b), результатом их сложения будет A+B с полной неопределенностью (±a)+(±b).

Допустим, мы добавляем два куска металла длиной 1,3 м и 1,2 м. Погрешности составляют ± 0,05 м и ± 0,01 м. Суммарное значение после их добавления составляет 1,5 м с погрешностью ± (0,05 м + 0,01 м) = ± 0,06 м.

Умножение на точное число: общее значение неопределенности вычисляется путем умножения неопределенности на точное число.

Допустим, мы вычисляем площадь круга, зная, что площадь равна \(A = 2 \cdot 3,1415 \cdot r\). Мы вычисляем радиус как r = 1 ± 0,1 м. Неопределенность равна \(2 \cdot 3,1415 \cdot 1 \pm 0,1 м\), что дает нам значение неопределенности 0,6283 м.

Деление на точное число: процедура такая же, как и при умножении. В этом случае мы делим неопределенность на точное значение, чтобы получить общую неопределенность.

Если мы имеем длину 1,2 м с погрешностью ± 0,03 м и разделим ее на 5, неопределенность составит \(\pm \frac{0,03}{5}\) или ±0,006.

Отклонение данных

Мы также можем рассчитать отклонение данных, вызванное неопределенностью, после выполнения расчетов с использованием данных. Отклонение данных изменяется, если мы складываем, вычитаем, умножаем или делим значения. Отклонение данных использует символ «δ».

• Отклонение данных после вычитания или сложения: для расчета отклонения результатов нам необходимо вычислить квадратный корень из квадратов неопределенностей: 92}{B}}\]

  Если у нас есть более двух значений, нам нужно добавить больше терминов.

  Округление чисел

  Когда ошибки и неопределенности либо очень малы, либо очень велики, удобно удалить члены, если они не изменяют наши результаты. Когда мы округляем числа, мы можем округлять их в большую или меньшую сторону.

  При измерении значения гравитационной постоянной на Земле наше значение равно 9,81 м/с ² , а погрешность составляет ± 0,10003 м/с ² . Значение после запятой изменяет наши измерения на 0,1 м/с ² ; Однако последнее значение 0,0003 имеет настолько малую величину, что его эффект будет едва заметен. Поэтому мы можем округлить, удалив все после 0,1.

  Округление целых и десятичных дробей

  Чтобы округлить числа, нам нужно решить, какие значения важны в зависимости от величины данных.

  Существует два варианта округления чисел: округление в большую или меньшую сторону. Вариант, который мы выбираем, зависит от числа после цифры, которая, по нашему мнению, является наименьшим значением, важным для наших измерений.

  • Округление: мы исключаем числа, которые мы считаем ненужными. Простой пример — округлить 3,25 до 3,3.
  • Округляя в меньшую сторону: снова отбрасываем числа, которые считаем не нужными. Например, округление 76,24 до 76,2 в меньшую сторону.
  • Правило округления в большую и меньшую сторону: по общему правилу, когда число заканчивается любой цифрой от 1 до 5, оно будет округлено в меньшую сторону. Если цифра заканчивается между 5 и 9, она будет округлена в большую сторону, а 5 всегда округляется в большую сторону. Например, 3,16 и 3,15 становятся 3,2, а 3,14 становятся 3,1.

  Глядя на вопрос, вы часто можете сделать вывод, сколько десятичных разрядов (или значащих цифр) необходимо. Допустим, вам дан график с числами, имеющими только два знака после запятой. В этом случае вы также должны будете включать два десятичных знака в свои ответы.

  Округление величин с неопределенностями и ошибками

  Когда у нас есть измерения с ошибками и неопределенностями, значения с более высокими ошибками и неопределенностями устанавливают значения общей неопределенности и ошибки. Другой подход требуется, когда вопрос требует определенного количества десятичных знаков.

  Допустим, у нас есть два значения (9,3 ± 0,4) и (10,2 ± 0,14). Если мы добавим оба значения, нам также необходимо добавить их неопределенности. Сложение обоих значений дает нам общую неопределенность как | 0,4 | + | 0,14 | или ± 0,54. Округление 0,54 до ближайшего целого числа дает нам 0,5, поскольку 0,54 ближе к 0,5, чем к 0,6.

  Таким образом, результат сложения обоих чисел и их неопределенностей и округления результатов составляет 19,5 ± 0,5m.

  Допустим, вам нужно умножить два значения, и оба имеют неопределенность. Вам будет предложено рассчитать общую распространенную ошибку. Величины A = 3,4 ± 0,01 и B = 5,6 ± 0,1. Вопрос просит вас рассчитать ошибку, распространенную до одного десятичного знака.

  Сначала вы вычисляете процентную ошибку обоих:

  \(\text{B процентная ошибка} = \frac{|5.6-5.7|}{5.6} \cdot 100 = 1.78 \%\)

  \(text {Ошибка в процентах} = \frac{|3.