Но Кроме того, отношение действительно D NT=it(6.20) §(x) * Oh — §(I) 236 Глава 6. Людмила Фирмаль
Основная теорема о дифференцируемых функциях Теорема 6.9 дает форму o правила раскрытия неопределенности — Отношение двух функций для вычисления пределов по отношению к этой точке, полученное из этих функций, уменьшающих вычисление пределов в точке А. D o K a z a t e l s T V o. сходим {Xn}к a и делаем его произвольной последовательностью значений аргументов, состоящей из чисел, отличных от a. определим функции/(x) и§
(x) в точке a и сравним эту точку с нулем. В таком определении функции/(x) и y'(x) дополняются точками A, то есть всюду в окрестности B точки a, смежной всюду в множестве SB. Фактически, непрерывность во всех точках/(x) и§(x) окрестности b точки a вытекают из их Дифференцируемости в этих точках, за исключением самой точки a, и непрерывность и расстояние между точками a и B одинаковы.
сделали … D х) г(х).. Г'(ч ) И T1’=и T1. Данные-А Е (Х)данные в’ (Х)данны姻(х ) П р и М е р ы одна) N Т ДГ- * о 1-поп х Н т 5Ш Х Два. Икс Два. * 2) следующие пределы рассчитываются путем применения правила Лопиталя дважды: Н т ч ы X-8SH X НЗ х — >0 1-поп х Zx2 = НОВЫЙ ЗАВЕТ х — >0 81P X §Икс Один. Шесть. Х 238CH. 6. Основная теорема о дифференцируемых функциях 3) предел рассчитывается путем применения правила Лопиталя три раза п т т——————-= и т—————- = и Т h»o h3+2soz-2h — > — o2h-2 81ph h — >0 12ha2-2 х поп =11•1Т—2-4-х— — =1, Р2. X —
неопределенности формы-y-для случая предела точки a.as ну и предел X — > — OO [- Sy], точно такой же результат в случае правой [левой]точки a Теперь мы знаем, что теорема 6. 1 2) Расчет P t————— u — — — — — — — (этот пример из- H — >0°I P —— Икс Случай 2). Применяя правило Лопиталя, мы получаем Н т Один. 81P—— Икс =Н т
1 2) Расчет P t————— u — — — — — — — (этот пример из- H — >0°I P —— Икс Случай 2). Применяя правило Лопиталя, мы получаем Н т Один. 81P—— Икс =Н т
Смотрите также:
Методическое пособие по математическому анализу
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Предел функции, суммы ряда. Ограниченность функции, замечательные пределы, односторонние и бесконечные пределы, необходимые и достаточные условия существования предела функции в точке. Правила вычисления. Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers поддержка сайта: Zavarka Team | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||
Неопределенности пределов
Очень часто при вычислении пределов функций в какой-либо точке в результате упрощения получаются выражения, не несущие какой-либо информации об этой функции. Такие выражения носят название неопределённостей.
Виды неопредлённостей
$\frac{0}{0}$ — деление нуля на нуль;
$\frac{\infty}{\infty}$ — деление бесконечности на бесконечность;
$0 \cdot \infty$ — умножение нуля на бесконечность;
$1^{\infty}$ — единица, возведённая в степень бесконечности;
$(\infty-\infty$) — разность бесконечностей;
$0^0$ — нуль в нулевой степени;
$\infty^0$ — бесконечность в степени 0.
 2}{x}=lim_{x\to 0} x=0$.
2}{x}=lim_{x\to 0} x=0$.Наиболее универсальным способом для раскрытия неопределённостей является правило Лопиталя, но к нему не всегда возможно прибегнуть. Как было упомянуто выше, его возможно применять лишь к двум видам неопределённостей, тогда как остальные необходимо для начала привести к одной из форм основных неопределённостей.
В целом, при раскрытии неопредлённостей возможно использовать различные тождественные преобразования, замечательные пределы и замену одного бесконечно малого выражения на другое, подобное ему.
Готовые работы на аналогичную тему
Рассмотрим подробнее замену бесконечно малых выражений на аналогичное.
Таблица эквивалентных бесконечно малых выражений
Если две переменные $α$ и $β$ сходятся к нулю в одной точке и предел их отношения в этой точке равен единице, то эти переменные называются эквивалентными бесконечно малыми переменными.
Таблица эквивалентных бесконечно малых функций:
$x~sin x$;
$x~arcsin x$;
$x ~ tg x$;
$x ~ arctg x$;
$x ~ ln(1+x)$;
$1-cos x ~ \frac{x^2}{2}$;
$ a^x-1 ~ x ln a$;
$e^x-1 ~ x$;
$(1+x)^a-1 ~ ax$.
 2}=-\frac{1}{6}$
2}=-\frac{1}{6}$Раскрытие неопределённости, содержащей бесконечность в числителе и знаменателе
Для того чтобы раскрыть такую неопределённость, сначала находят в выражении старшую степень при переменной, а затем делят на эту переменную числитель и знаменатель.
Раскрытие неопределённости, содержащей нуль в числителе и знаменателе
При возникновении такого случая сначала производят разложение на множители числителя и знаменателя, а затем осуществляют сокращение дроби.
Правило Лопиталя для раскрытия неопределённостей
Данное правило является главным методом для вычисления неопределённостей вида $\frac{0}{0}$ и $\frac{\infty}{\infty}$. Суть метода состоит в том, чтобы вместо предела отношения двух функций находить предел производных двух функций:
$lim_{x\to c} \frac{f(x)}{g(x)}=lim_{x\to c} \frac{f’(x)}{g’(x)}$
Использование производных позволяет упростить выражения и найти, к чему стремится данный предел.
С помощью этого правила можно находить не только неопределённости, про которые сказано выше, но также и другие.
 {-\infty}$ эквивалентно выражению $\frac{1}{0}$.
{-\infty}$ эквивалентно выражению $\frac{1}{0}$.04. Основные элементарные функции. Пределы элементарных функций. Свойства пределов
К основным элементарным функциям относятся:
1) степенная функция y=xn
2) показательная функция y=ax
3) логарифмическая функция y=logax
4) тригонометрические функции y=sin x, y=cos x, y=tg x, y=ctg x
5) обратные тригонометрические функции y=arcsin x, y=arccos x, y=arctg x, y=arcctg x.
Предел элементарной функции в точке ее определения равен частному значению функции в этой точке
Это свойство функций и называется непрерывностью в точке х0.
Функции, полученные из основных элементарных с помощью конечного числа арифметических действий и конечного числа композиций, называются элементарными.
При вычислении пределов функций обычно пользуются следующими основными теоремами о пределах:
1. , где С-константа 2. Константа выносится изпод знака предела.
Если пределы существуют и конечны, то
3.
 Предел суммы (разности) равен сумме (разности) пределов.
Предел суммы (разности) равен сумме (разности) пределов.4.
5. , если
Предел произведения равен произведению пределов. Предел частного равен частному пределов.
Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводит к неопределенностям.
Например, зная лишь, что Нельзя сказать заранее, чему равен
Говорят, что имеет место Неопределенность вида
Элементарными приемами раскрытия неопределенностей являются:
1) сокращение на множитель, создающий неопределенность
2) деление числителя и знаменателя на старшую степень аргумента (для отношения многочленов при x®¥)
3) применение эквивалентных бесконечно малых и бесконечно больших
4) использование двух замечательных пределов:
Первый замечательный предел
Второй замечательный предел,
А также следующие свойства (*)
если , т. е. .
если , т. е. .
если а , т.
 е. .
е. .если А , т. е. .
Рассмотрим конкретные примеры пределов:
1. Найдем
Воспользуемся свойством предела суммы:
Воспользуемся свойствами о пределе константы и выносе константы за знак предела:
Так как под знаком предела у нас находятся основные элементарные функции, подставляем вместо х его предельное значение 1 и получаем: Z1=3+2+5=10
2.Найдем
Под знаком предела стоит композиция основных элементарных функций – элементарная функция. Подставляем вместо х его предельное значение равное 3, получаем в числителе бесконечно большую, а в знаменателе бесконечно малую функцию.
3. Найдем
Так как Существует и конечен, Существует, конечен и не равен 0, то
4. Найдем
Подстановка предельного значения в знаменатель дает предел, равный нулю. Следовательно мы имеем отношение константы к бесконечно малой (соотношения *) { c/0}
5.
 Найдем
НайдемПодстановка предельного значения приводит к неопределенности. Затем делим на старшую степень х~х2.
6. Найдем
Подстановка предельного значения аргумента приводит к неопределенности типа . Так как под знаком предела стоит отношение двух многочленов, то разделим числитель и знаменатель на старшую степень аргумента, т. е. на х4.
поскольку при x®¥ функции являются бесконечно малыми.
7. Рассмотрим неопределенность вида {¥ -¥}
При раскрытии неопределенности этого вида достаточно домножить и разделить выражение под знаком предела на сопряженное ему выражение
8. Неопределенность вида {0/0}.
При подстановке предельного значения получается неопределенность вида {0/0}. Это вызвано тем, что и многочлен в числителе и многочлен в знаменателе имеют –1 своим корнем. Следовательно, надо сократить дробь на критический множитель х+1 выделив его предварительно:
Подставляем предельное значение и пользуясь свойствами пределов, получаем:
9.
 Найдем
НайдемИмеем неопределенность вида {0/0} в тригонометрическом выражении. Раскроем ее с помощью первого замечательного предела, но в первом замечательном пределе знаменатель дроби и аргумент синуса должны совпадать. Следовательно, домножим и разделим на 5х, чтобы получить
так как при То первый сомножитель стремится к единице и
10. Найдем
Z10 содержит неопределенность {0/0} в тригонометрическом выражении. Попытаемся обратиться к первому замечательному пределу. Для этого надо числитель заменить выражением, содержащим синус по известной тригонометрической формуле cos двойного угла:
11. Найдем
Здесь неопределенность {0/0}, к которой приводит предел выражения, содержащего обратные тригонометрические функции. Сделаем замену переменных. Возьмем за новую переменную arcsin(x-1), тогда мы получим выражение подобное первому замечательному пределу: (y=arcsin(x-1)).
Заметим, что при то есть ,
12.
 Найдем .
Найдем .Здесь имеет место неопределенность типа {1¥}
При раскрытии неопределенностей такого вида пользуются вторым замечательным пределом.
Т. к. при То положим
Обратимся теперь подробнее к вопросу о непрерывности функций.
Вопросы для самоконтроля:
1. Что такое функция? Ее область определения и область значений.
2. Что такое сложная функция?
3. Дайте определение предела функции в т. х0 слева, справа, вообще определение предела.
4. Какие свойства пределов Вы знаете?
5. Какие бесконечно малые называются бесконечно малыми одного порядка?
6. Какие бесконечно малые называются эквивалентными бесконечно малыми?
< Предыдущая Следующая > Правила Лопиталя | Математика, которая мне нравится
Швейцарский математик Иоганн I Бернулли (1667-1748) после успешного окончания Базельского университета, путешествуя по Европе, в 1690 году приезжает в Париж.
 В литературном салоне философа Никола Мальбранша (1638-1715) Иоганн знакомится с французским математиком маркизом Гийомом Франсуа Антуаном де Лопиталем (1661-1704). В ходе оживленной беседы Лопиталь удивился, как легко, “как бы играя”, юнец Бернулли решал трудные задачи по новому исчислению. Поэтому Лопиталь попросил прочитать ему несколько лекций. Устные беседы понравились Лопиталю, и он за приличный гонорар стал получать материалы в письменном виде. Заметим, что общеизвестное теперь “правило Лопиталя” для раскрытия неопределенностей также было передано ему Иоганном. Уже в 1696 году появился знаменитый трактат Лопиталя “Введение в анализ бесконечно малых для понимания кривых линий”. Вторая часть курса, изложенного Иоганном I Бернулли, была опубликована лишь в 1742 году и называлась “Математические лекции о методе интегралов и другие; написаны для знаменитого маркиза Госпиталия; годы 1691–1692”. В 1921 году были обнаружены рукописные копии лекций, написанные рукой Иоганна I Бернулли, оригиналы которых были переданы Лопиталю в 1691–1692 гг.
В литературном салоне философа Никола Мальбранша (1638-1715) Иоганн знакомится с французским математиком маркизом Гийомом Франсуа Антуаном де Лопиталем (1661-1704). В ходе оживленной беседы Лопиталь удивился, как легко, “как бы играя”, юнец Бернулли решал трудные задачи по новому исчислению. Поэтому Лопиталь попросил прочитать ему несколько лекций. Устные беседы понравились Лопиталю, и он за приличный гонорар стал получать материалы в письменном виде. Заметим, что общеизвестное теперь “правило Лопиталя” для раскрытия неопределенностей также было передано ему Иоганном. Уже в 1696 году появился знаменитый трактат Лопиталя “Введение в анализ бесконечно малых для понимания кривых линий”. Вторая часть курса, изложенного Иоганном I Бернулли, была опубликована лишь в 1742 году и называлась “Математические лекции о методе интегралов и другие; написаны для знаменитого маркиза Госпиталия; годы 1691–1692”. В 1921 году были обнаружены рукописные копии лекций, написанные рукой Иоганна I Бернулли, оригиналы которых были переданы Лопиталю в 1691–1692 гг. Из них ученые неожиданно обнаружили, что Лопталь в своем “Анализе” почти не отступал от лекций своего молодого учителя.
Из них ученые неожиданно обнаружили, что Лопталь в своем “Анализе” почти не отступал от лекций своего молодого учителя. Теорема (Коши). Пусть функции и непрерывны на , дифференцируемы на и . Тогда :
Доказательство. Рассмотрим функцию
выберем так, чтобы выполнялись все условия теоремы Ролля, т.е. .
По теореме Ролля существует :
Первое правило Лопиталя
Определение. Пусть функции , непрерывны на , дифференцируемы в , причем . Пусть . Тогда говорят, что отношение при представляет собой неопределенность вида .
Теорема. Если при указанных условиях существует
то и
Пусть конечно. По выберем : в интервале выполняется неравенство
Применим теорему Коши к отрезку , где . Существует :
и, значит,
Это и означает, что .

В случае, когда бесконечно, неравенство (1) заменяется на
или
в зависимости от знака . В остальном доказательство не меняется.Второе правило Лопиталя
Определение. Пусть функции , непрерывны и дифференцируемы в , причем . Пусть . Тогда говорят, что отношение при представляет собой неопределенность вида .
Теорема. Если при указанных условиях существует
то и
Доказательство. Пусть конечно. По выберем : в интервале выполняется неравенство
Определим функцию из условия
Имеем
при . Применим к отрезку теорему Коши. Получим, что существует :
Для тех , для которых
Так как произвольно мало, то
В случае, когда , неравенство (2) заменяется на
а неравенство (4) — на неравенство
имеющим место при , достаточно близких к в силу (3).

Аналогично рассматривается случай .
Делить на ноль — это норма. Часть 1 / Хабр
Часть 1. Вобще-то уже все поделили до нас!
Часть 2. Истина где-то рядомГоворят, можно поделить на ноль если определить результат деления на ноль. Просто нужно расширить алгебру. По странному стечению обстоятельств найти хоть какой-то, а лучше понятный и простой, пример такого расширения не удается. Чтобы исправить интернет нужна либо демонстрация одного из способов такого расширения, либо описание почему это не возможно.
Статья написана в продолжение тренда:
Disclaimer
Цель данной статьи — объяснить «человеческим языком», как работают фундаментальные основы математики, структурировать знания и восстановить упущенные причинно-следственные связи между разделами математики. Все рассуждения являются философскими, в части суждений расходятся с общепринятыми (следовательно, не претендует на математическую строгость). Статья рассчитана на уровень читателя «сдал вышку много лет назад».

Понимание принципов арифметики, элементарной, общей и линейной алгебры, математического и нестандартного анализа, теории множеств, общей топологии, проективной и аффинной геометрии — желательно, но не обязательно.
В ходе экспериментов ни одна бесконечность не пострадала.
Пролог
Выход «за рамки» — это естественный процесс поиска новых знаний. Но не всякий поиск приносит новое знание и следовательно пользу.
1. Вобще-то уже все поделили до нас!
1.1 Аффинное расширение числовой прямой
Начнем с того, с чего начинают, наверное, все искатели приключений при делении на ноль. Вспомним график функции
.
Слева и справа от нуля функция уходит в разные стороны «небытия». В самом нуле вообще “омут” и ничего не видно.
Вместо того, чтобы бросаться в «омут» с головой, посмотрим что туда втекает и что оттуда вытекает. Для этого воспользуемся пределом — основным инструментом математического анализа. Основная “фишка” в том, что предел позволяет идти к заданной точке так близко, как это возможно, но не “наступить на нее”.

ОригиналХорошо, «оградку» поставили. Уже не так страшно. У нас есть два пути к «омуту». Зайдем слева — крутой спуск, справа — крутой подъем. Сколько к “оградке” не иди, ближе она не становится. Пересечь нижнее и верхнее «небытие» никак не выходит. Возникают подозрения, может мы идем по кругу? Хотя нет, числа-то меняются, значит не по кругу. Пороемся в сундучке с инструментами математического анализа еще. Кроме пределов с «оградкой» в комплекте идет положительная и отрицательная бесконечности. Величины совершенно абстрактные (не являются числами), хорошо формализованы и готовы к употреблению! Это нам подходит. Дополним наше «бытие» (множество вещественных чисел) двумя бесконечностями со знаком.
Математическим языком:Именно это расширение позволяет брать предел при аргументе стремящемся к бесконечности и получить бесконечность в качестве результата взятия предела.
Есть два раздела математики которые описывают одно и тоже используя разную терминологию.

С геометрической точки зрения выполнено аффинное расширение числовой прямой. То есть привычная последовательность вещественных чисел “сжата” так, чтобы можно было оперировать границами этой последовательности. В качестве границ (условных) введены две абстрактные бесконечно большие величины. Расширение аффинное, но это не значит что оно пришло из Греции, это значит что сохраняется относительное положение точек (в нашем случае чисел) на прямой. Отсюда и следует, что сохраняются отношения “больше” и ”меньше” как для чисел между собой, так и в сравнении с границами.
С точки зрения общей топологии выполнена двухточечная компактификация числовой прямой путем добавления двух идеализированных точек (бесконечностей с противоположным знаком).
1.2 Проективное расширение числовой прямой
Прогуливаясь по графику
, у нас есть только два пути к нулю (слева и справа). В конце каждого пути стоит небольшая «оградка». По странному стечению обстоятельств одна и та же «оградка» оказалась и на дне и на вершине «бытия».
 Если мы хотим чтобы пути сошлись, то за «оградкой» нам нужен телепорт из одного конца «бытия» в другой. Мы уже такие телепорты видали. Не проблема.
Если мы хотим чтобы пути сошлись, то за «оградкой» нам нужен телепорт из одного конца «бытия» в другой. Мы уже такие телепорты видали. Не проблема.Попробуем состыковать обе границы «бытия» так, как это делали наши предки. Перейдем на одно измерение выше. Отобразим одномерную линию на двумерной плоскости.
После стыковки наличие двух знаковых бесконечностей теряет смысл. Вместо них можно ввести одну общую точку пересечения, беззнаковую бесконечность.
Эта стыковка очень похожа на линию перемены даты находящуюся (в основном), между часовыми поясами UTC+12 и UTC-12 в Тихом океане. Именно там находится телепорт из сегодня во вчера и из сегодня в завтра. У нас же телепорт из сверхмалых в сверхбольшие.
Математическим языком:
По факту это самостоятельное расширение, проведенное над исходным множеством вещественных чисел. Данное расширение не основывается на рассмотренном ранее аффинном расширении.
С геометрической точки зрения выполнено проективное расширение числовой прямой (есть информация на wolfram.
 com). То есть введена идеализированная точка которая соединяет оба конца вещественной прямой. Так как расширение не аффинное, сравнение вещественных чисел с бесконечностью не определено.
com). То есть введена идеализированная точка которая соединяет оба конца вещественной прямой. Так как расширение не аффинное, сравнение вещественных чисел с бесконечностью не определено.С точки зрения общей топологии выполнена одноточечная компактификация числовой прямой путем добавления идеализированной точки (бесконечности без знака).
Аналогичным расширением над полем комплексных чисел является широко известная в математических кругах Сфера Римана.
Хорошо, избавились от знака минус. Однако в нуле у нас
разрыв второго родаи устранимой точкой разрыва его нельзя считать по определению. Нарушается требование «конечности» предела. Соответственно мы не можем судить о равенстве предела справа и слева.
Но так как приближение к бесконечности выполняется по одинаковым правилам, мы можем утверждать что пределы слева и справа совпадают. Соответственно мы можем принять наш разрыв за точку устранимого разрыва в бесконечности.
Математическим языком:
Посмотрим внимательнее, как мы оперируем бесконечно большими и малыми величинами.
 При операциях мы часто пренебрегаем малыми низшего порядка попросту отбрасывая их при записи результата.
При операциях мы часто пренебрегаем малыми низшего порядка попросту отбрасывая их при записи результата.
Аналогичная ситуация при нахождении производных
Отбрасывая «мелочевку» мы теряем информацию! Это хорошо видно на примере взятия пределов. Рассмотрим две функции, которые стремятся к положительной бесконечности при стремлении аргумента к нулю справа.
Однако одинаковая запись результата взятия предела не свидетельствует о их равенстве. Данные бесконечности разного порядка и это подтверждается отсутствием конечного предела в отношении одной функции к другой.
В нестандартном анализе такие упрощения не допустимы. Поле вещественных чисел расширяется путем введения гиперреальных чисел. Бесконечно малые представлены в виде привычного значения — ноль, но в довесок хранится вся выкинутая “мелочевка”. Для бесконечно больших потенциальная бесконечность (две или одна — неважно), разбивается на множество актуальных бесконечностей. С одной стороны мы усложняем (теряем возможность поглощения/пренебрежения). С другой стороны мы приобретаем возможность сравнения бесконечно малых и бесконечно больших величин. А это значит что мы можем рассматривать бесконечности как числа.
С другой стороны мы приобретаем возможность сравнения бесконечно малых и бесконечно больших величин. А это значит что мы можем рассматривать бесконечности как числа.Для функции актуальные бесконечности слева и справа от нуля равны (по модулю, т.е. не учитывая знак), так как:
- с обеих сторон путь (количество элементов, которые нужно пройти) от нуля до бесконечности одинаков;
- алгоритм приближения (формула в виде дроби) одинаков;
- знак минус в алгоритме не влияет на скорость или ускорение приближения к бесконечности.
Стоит отметить что указанные критерии условны и не приведены к формальным определениям нестандартного анализа.Для дальнейших рассуждений понятие актуальной бесконечности нам больше не потребуется. Мы возвращаемся в привычный мир где будем оперировать понятием бесконечность, подразумевая потенциальную бесконечность.
Хорошо, пределы совпадают. Теперь, похоже, все готово для устранения разрыва между ними.

В математической модели, использующей
проективное расширение числовой прямой, деление на ноль определено.
Создается впечатление что наша задача решена. Однако не будем спешить, посмотрим к каким последствиям это привело. В дополнение к делению в системе определены следующие операции (напомним, что бесконечность беззнаковая).
Практически все они с дополнительными условиями, это настораживает. Но не будем спешить, лучше посмотрим на список
неопределенныхопераций:
Посмотрим как будет вести себя дистрибутивный закон. Подставим в него определенные значения и выполним требуемые операции.
Как следствие, часть тождеств перестает вести себя так как мы привыкли. Однако, они не исчезли бесследно. Дистрибутивный закон работает только справа налево (т.е. в случае, когда правая часть равенства определена). Это один из ярких примеров негативных последствий. Другие же тождества сохранилась в
более-менее устойчивойформе.
Подытожим:
- Изменилось привычное поведение тождеств.
 Чтобы ими оперировать, нужно не забывать про новые дополнительные условия.
Чтобы ими оперировать, нужно не забывать про новые дополнительные условия. - Искажено привычное поведение нуля. Мы привыкли рассуждать, если ноль раз взять что-либо, то будет ноль. Однако в данной алгебраической системе произведение нуля на бесконечность не определено. Соответственно алгебраическое выражение с переменными, в котором встречается например такая запись , не может быть упрощено в одностороннем порядке.
- Исчезает возможность привычного сравнения. Сравнение на больше-меньше определено только на части пространства. Например, сравнение вещественных чисел с бесконечностью не определено.
- Полученная алгебраическая структура не поле в терминах общей алгебры. Нарушается дистрибутивный закон (показано выше). Так же не существует обратного элемента для бесконечности (произведение этого элемента и бесконечности должно дать единицу). Последние можно рассматривать как следствие неопределенности деления бесконечности на бесконечность. Но все же следует понимать что это грубое упрощение.
 Строгое определение обратного элемента не связано с операцией деления.
Строгое определение обратного элемента не связано с операцией деления.
В сухом остатке. Старые подходы перестали работать. Сложность системы, в виде кучи “если”, “для всех, кроме” и т.п., возросла. У нас было только две неопределенности 1/0 и 0/0 (мы не рассматривали степенные операции), стало пять. Раскрытие одной неопределенности породило еще больше неопределенностей.
1.2 Колесо
На введении беззнаковой бесконечности все не остановилось. Для того чтобы выбраться из неопределенностей нужно второе дыхание.
Итак, у нас есть множество вещественных чисел и две неопределенности 1/0 и 0/0. Для устранения первой мы выполнили проективное расширение числовой прямой (то есть ввели беззнаковую бесконечность). Попробуем разобраться со второй неопределенностью вида 0/0. Сделаем аналогично. Дополним множество чисел новым элементом, представляющим вторую неопределенность.
Определение операции деления основано на умножении. Это нам не подходит.
 Отвяжем операции друг от друга, но сохраним привычное поведение для вещественных чисел. Определим унарную операцию деления, обозначаемую знаком “/”.
Отвяжем операции друг от друга, но сохраним привычное поведение для вещественных чисел. Определим унарную операцию деления, обозначаемую знаком “/”.Доопределим операции.
Данная структура называется «Колесом» (
Wheel). Термин был взят из-за схожести с топологической картинкой проективного расширения числовой прямой и точки 0/0.
Вроде все неплохо выглядит, но дьявол кроется в деталях:
- Умножение ∞ либо ⊥ на ноль не дает ноль. Это приводит к тому, что в общем случае.
- Для ∞ и ⊥ отсутствуют обратные элементы по обеим бинарным операциям. Это значит, что по умножению в общем случае. Как следствие, нет возможности ввести бинарную операцию деления покрывающую все пространство.
- Симметричная ситуация по сложению, в общем случае.
Чтобы устаканить все особенности, дополнительно к расширению множества элементов прилагается бонус в виде не одного, а двух тождеств, описывающих дистрибутивный закон.
Математическим языком:С точки зрения общей алгебры мы оперировали полем.
 А в поле, как известно, определены всего две операции (сложение и умножение). Понятие деления выводится через обратные, а если еще глубже, то единичные элементы. Внесенные изменения превращают нашу алгебраическую систему в моноид как по операции сложения (с нулем в качестве нейтрального элемента), так и по операции умножения (с единицей в качестве нейтрального элемента).
А в поле, как известно, определены всего две операции (сложение и умножение). Понятие деления выводится через обратные, а если еще глубже, то единичные элементы. Внесенные изменения превращают нашу алгебраическую систему в моноид как по операции сложения (с нулем в качестве нейтрального элемента), так и по операции умножения (с единицей в качестве нейтрального элемента).В трудах первооткрывателей не всегда используются символы ∞ и ⊥. Вместо этого можно встретить запись в виде /0 и 0/0.
Мир уже не так прекрасен, не правда ли? Все же не стоит спешить. Проверим, справятся ли новые тождества дистрибутивного закона с нашим расширенным множеством
.
На этот раз результат намного лучше.
Подытожим:
- Все операции хорошо определены и нет возможности «вывалиться за борт».
- Элементарная алгебра является частным случаем колеса. Если мы отбросим надстройки ∞ и ⊥ (то есть снова сможем утверждать что и ), то все формулы выродятся в привычные.

- По ощущениям все что было “не определено” (Undefined) при проективном расширении было обозначено символом . Данный объект так же поглощает все с чем столкнется как и “не определено”. Все щели, где появились неопределенности при проективном расширении, были заткнуты данным объектом.
В сухом остатке. Алгебра работает отлично. Однако за основу было взято понятие «не определено» которое стали считать чем-то существующим и оперировать им. Однажды кто-нибудь скажет, что все плохо и нужно разбить данное «не определено» еще на несколько “не определено”, но помельче. Общая алгебра скажет: “Без проблем, Бро!”.
Примерно так постулированы дополнительные (j и k) мнимые единицы в
кватернионах.
Стоит отметить, существуют и другие алгебраические системы с делением. Например, «луга» (common meadows). Они чуть проще, так как не расширяют пространство, вводя новые элементы. Цель достигается как в колесах, трансформацией операций сложения и умножения, а так же отказом от бинарного деления.

Возможность «передвигать неизвестные» для математики норма. Но все эти обертки не дают ответа на главный вопрос, что же там внутри?
Полезная литератураНеопределённость в задачах моделирования и управления сложных, слабо формализуемых многокомпонентных систем
%PDF-1.5 % 2 0 obj > /Metadata 4 0 R /Pages 5 0 R /StructTreeRoot 6 0 R /Type /Catalog >> endobj 4 0 obj > stream
- IEEE application/pdf
- Неопределённость в задачах моделирования и управления сложных, слабо формализуемых многокомпонентных систем 2020-05-23T13:36:26+03:00Microsoft® Word 20102020-05-24T19:57:52+03:00Microsoft® Word 2010uuid:0d8104f9-a74c-406d-82bb-37f0cbc3b638uuid:7a1ceca4-4d56-4252-b114-2b7c3bfc8a3b endstream endobj 15 0 obj > stream x=َ$q8k,{̴!~(ymX>>x?~o?ǟ>}?]חw~.
- 1.
ρ – MES.
- 2.
\ (H {({\ rm {A}} | {\ rm {B}})} _ {\ rho} = – {\ mathrm {log} \,} _ {2} {d} _ {\ rm {A}}} \).
- 3.
\ ({E} _ {{\ rm {R}}} (\ rho) = {\ mathrm {log} \,} _ {2} {d} _ {{\ rm {A}}} \).
- 4.
\ ({E} _ {{\ rm {F}}} (\ rho) = {\ mathrm {log} \,} _ {2} {d} _ {{\ rm {A}}} \).

- 5.
ρ имеет спектральное разложение \ (\ rho = {\ sum} _ {s} {\ lambda} _ {s} \ left | {{{\ Psi}}} _ {s} \ right \ rangle \ left \ langle {{{\ Psi}}} _ {s} \ right | \) такая, что все \ (\ left | {{{\ Psi}}} _ {s} \ right \ rangle \) являются MES, а \ ({\ mathrm {tr}} _ {{\ rm {A}}} (\ left | {{{\ Psi}}} _ {s} \ right \ rangle \ left \ langle {{{\ Psi}}}} _ {s} \ right |) \) имеют взаимно ортогональные носители.
- 1.
ρ – MES.
- 2.
\ (H {({\ rm {A}} | {\ rm {B}})} _ {\ rho} = – {\ mathrm {log} \,} _ {2} {d} _ {\ rm {A}}} \).
- 3.
\ ({E} _ {{\ rm {R}}} (\ rho) = {\ mathrm {log} \,} _ {2} {d} _ {{\ rm {A}}} \).
- 4.
\ ({E} _ {{\ rm {F}}} (\ rho) = {\ mathrm {log} \,} _ {2} {d} _ {{\ rm {A}}} \).
- 5.
ρ имеет спектральное разложение \ (\ rho = {\ sum} _ {s} {\ lambda} _ {s} \ left | {{{\ Psi}}} _ {s} \ right \ rangle \ left \ langle {{{\ Psi}}} _ {s} \ right | \) такая, что все \ (\ left | {{{\ Psi}}} _ {s} \ right \ rangle \) являются MES, а \ ({\ mathrm {tr}} _ {{\ rm {A}}} (\ left | {{{\ Psi}}} _ {s} \ right \ rangle \ left \ langle {{{\ Psi}}}} _ {s} \ right |) \) имеют взаимно ортогональные носители.
- 1.
ρ – MES.
- 2.
\ (H {({\ rm {A}} | {\ rm {B}})} _ {\ rho} = – {\ mathrm {log} \,} _ {2} {d} _ {\ rm {A}}} \).
- 3.
\ ({E} _ {{\ rm {R}}} (\ rho) = {\ mathrm {log} \,} _ {2} {d} _ {{\ rm {A}}} \).
- 4.
\ ({E} _ {{\ rm {F}}} (\ rho) = {\ mathrm {log} \,} _ {2} {d} _ {{\ rm {A}}} \).
- 5.
ρ имеет спектральное разложение \ (\ rho = {\ sum} _ {s} {\ lambda} _ {s} \ left | {{{\ Psi}}} _ {s} \ right \ rangle \ left \ langle {{{\ Psi}}} _ {s} \ right | \) такая, что все \ (\ left | {{{\ Psi}}} _ {s} \ right \ rangle \) являются MES, а \ ({\ mathrm {tr}} _ {{\ rm {A}}} (\ left | {{{\ Psi}}} _ {s} \ right \ rangle \ left \ langle {{{\ Psi}}}} _ {s} \ right |) \) имеют взаимно ортогональные носители.
- 1.
ρ – MES.
- 2.
\ (H {({\ rm {A}} | {\ rm {B}})} _ {\ rho} = – {\ mathrm {log} \,} _ {2} {d} _ {\ rm {A}}} \).
- 3.
\ ({E} _ {{\ rm {R}}} (\ rho) = {\ mathrm {log} \,} _ {2} {d} _ {{\ rm {A}}} \).
- 4.
\ ({E} _ {{\ rm {F}}} (\ rho) = {\ mathrm {log} \,} _ {2} {d} _ {{\ rm {A}}} \).
- 5.
ρ имеет спектральное разложение \ (\ rho = {\ sum} _ {s} {\ lambda} _ {s} \ left | {{{\ Psi}}} _ {s} \ right \ rangle \ left \ langle {{{\ Psi}}} _ {s} \ right | \) такая, что все \ (\ left | {{{\ Psi}}} _ {s} \ right \ rangle \) являются MES, а \ ({\ mathrm {tr}} _ {{\ rm {A}}} (\ left | {{{\ Psi}}} _ {s} \ right \ rangle \ left \ langle {{{\ Psi}}}} _ {s} \ right |) \) имеют взаимно ортогональные носители.
- Основные операции выполняются так же, как и с другими экспоненциальными числами.
 Kdz)P/4==w5OlzQ{8.THF_j iqx0bՃ>(.e}”z.;Lu
Kdz)P/4==w5OlzQ{8.THF_j iqx0bՃ>(.e}”z.;LuСостояния с нулевой неопределенностью при наличии квантовой памяти
Максимально запутанные состояния
Чтобы установить наши основные результаты, сначала нам нужно лучше понять MES. Двудольное состояние ρ в гильбертовом пространстве \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}) }} \) размерности d A × d B является MES, если мы можем создать каждое состояние на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) от до локальными операциями и классической связью (LOCC) 27 .{{d} _ {{\ rm {B}}} – 1} \) являются вычислительными базами \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \) и \ ( {{\ mathcal {H}}} _ {{\ rm {B}}} \) соответственно. MES не обязательно является чистым, как поясняется в следующей лемме, по существу доказанной в ref. 28 ; см. дополнительную информацию для независимого доказательства.
Лемма 1 Пусть ρ – двудольное состояние на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{ \ rm {B}}} \) с d A ≤ d B .Тогда следующие утверждения эквивалентны .
Здесь H (A∣B) ρ = S ( ρ ) – S ( ρ B ) – условная энтропия A для данного B, где S ( ρ ) и S ( ρ B ) – энтропии фон Неймана ρ и \ ({\ rho} _ {{\ rm {B}}}: = {\ mathrm {tr }} _ {{\ rm {A}}} (\ rho) \) соответственно. E R ( ρ ) и E F ( ρ ) – относительная энтропия запутанности и запутанности образования 27 . {\ prime}} \) будет поддержкой ρ В .{\ prime} \ right \ rangle \) является чистым MES в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{ {\ rm {B}}} _ {1}} \), а τ – оператор плотности полного ранга на \ ({{\ mathcal {H}}} _ {{{\ rm {B}}} _ {2}} \). Таким образом, все MES на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) эквивалентны под локальными операциями Боба.
{\ prime}} \) будет поддержкой ρ В .{\ prime} \ right \ rangle \) является чистым MES в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{ {\ rm {B}}} _ {1}} \), а τ – оператор плотности полного ранга на \ ({{\ mathcal {H}}} _ {{{\ rm {B}}} _ {2}} \). Таким образом, все MES на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) эквивалентны под локальными операциями Боба.
Следствие 1 Все MES на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B }}} \) с d A ≤ d B могут быть преобразованы друг в друга локальными операциями на \ ({{\ mathcal {H}}} _ {{\ rm { B}}} \) .{m} \). Тогда прогнозирование результата O x сводится к прогнозированию результата проективного измерения на основе \ ({{\ mathcal {B}}} _ {x} \). Когда эти наблюдаемые несовместимы (не коммутируют друг с другом), в целом Боб не может с уверенностью предсказать результат измерения, даже если он знает полное классическое описание состояния системы, которое характеризуется матрицей плотности ρ A . { 2} \).
{ 2} \).
Ситуация иная, если Боб имеет квантовую память с гильбертовым пространством \ ({{\ mathcal {H}}} _ {{\ rm {B}}}}) и может создать запутанное состояние ρ на суставе system \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \), как показано на Рис. . 1. Предположим, Алиса выбирает базис \ ({{\ mathcal {B}}} _ {x} \) (observable O x ), тогда Боб может выполнить обобщенное измерение, характеризуемое положительным оператором – оценочная мера (POVM) \ ({\ {{{{\ Pi}}} _ {xk} \}} _ {k} \) в его подсистеме \ ({{\ mathcal {H}}} _ {{\ rm {B}}} \), где Π x k соответствует угадыванию результата k с учетом базы измерения \ ({\ mathcal {B}}} _ {x} \) Алисы.Средняя вероятность успеха составляет ∑ x p x / m с
$$ {p} _ {x} = \ sum _ {k} {\ mathrm {tr}} \, [\ rho (\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | \ otimes \ Pi_ {xk})] = \ sum _ { k} {\ mathrm {tr}} \, ({\ rho} _ {xk} \ Pi_ {xk}), $$
(2)
, где \ ({\ rho} _ {xk} = \ left \ langle {\ psi} _ {xk} \ right | \ rho \ left | {\ psi} _ {xk} \ right \ rangle \) субнормализованы уменьшенные состояния Боба. Обратите внимание, что p x также является вероятностью того, что POVM \ ({\ {{{{\ Pi}}}} _ {xk} \}} _ {k} \) может успешно различить ансамбль состояний
Обратите внимание, что p x также является вероятностью того, что POVM \ ({\ {{{{\ Pi}}}} _ {xk} \}} _ {k} \) может успешно различить ансамбль состояний
$$ {\ mathscr {S}} (\ rho, {{\ mathcal {B}}} _ {x}) = \ {\ left \ langle \ psi \ right | \ rho \ left | \ psi \ right \ rangle \: \ \ left | \ psi \ right \ rangle \ in {{\ mathcal {B}}} _ {x} \}. $$
(3)
Максимум средней вероятности предположения по всем POVM может быть определен с помощью полуопределенного программирования, и этот максимум определяется состоянием ρ и базисным набором \ ({\ mathscr {B}} \) (или наблюдаемым набором \ ({\ mathscr {O}} \)) Алисы.
Рис. 1: Связь между нулевой неопределенностью и максимальной запутанностью в игре на неопределенность. Выполняя подходящие измерения (в зависимости от наблюдаемых Алисой) своей квантовой памяти, Боб может лучше предсказать результаты измерений Алисы. {m} \) для Алисы совместное состояние ρ Алисы и Боба является ZUS, если Боб может с уверенностью предсказать результат измерения Алисы с помощью подходящего измерения в зависимости от выбора Алисы.Учитывая ZUS, вероятность угадывания p x для каждого измерения Алисы может достигать максимума 1, а условная энтропия H ( O x B) равна 0. Напротив. с минимальными состояниями неопределенности и интеллектуальными состояниями 14,15,16 , ZUS не только минимизируют неопределенность, но также полностью устраняют неопределенность. Более того, здесь определение не зависит от какой-либо конкретной меры неопределенности.
{m} \) для Алисы совместное состояние ρ Алисы и Боба является ZUS, если Боб может с уверенностью предсказать результат измерения Алисы с помощью подходящего измерения в зависимости от выбора Алисы.Учитывая ZUS, вероятность угадывания p x для каждого измерения Алисы может достигать максимума 1, а условная энтропия H ( O x B) равна 0. Напротив. с минимальными состояниями неопределенности и интеллектуальными состояниями 14,15,16 , ZUS не только минимизируют неопределенность, но также полностью устраняют неопределенность. Более того, здесь определение не зависит от какой-либо конкретной меры неопределенности.
Чтобы оценить важность запутанности для построения ZUS, рассмотрим пример с двумя наблюдаемыми, в этом случае отношение неопределенности в уравнении.{-1}) + H {({\ rm {A}} | {\ rm {B}})} _ {\ rho}. $$
(4)
Здесь условная энтропия H (A∣B) ρ показывает влияние запутанности на уменьшение неопределенности. { -1}), $$
{ -1}), $$
(5)
, где второй получен в исх.{2} = 1 / {d} _ {{\ rm {A}}} \) для всех j , k 35 . Тогда у нас есть c = 1/ d A и
$$ {E} _ {{\ rm {F}}} (\ rho) = {E} _ {{\ rm {R}} } (\ rho) = – H {({\ rm {A}} | {\ rm {B}})} _ {\ rho} = {\ mathrm {log} \,} _ {2} {d} _ {{\ rm {A}}}, $$
(6)
, что означает, что d B ≥ d A и ρ является MES по лемме 1, и в этом случае ρ действительно является ZUS.К сожалению, это рассуждение в целом не работает. Чтобы решить эту проблему, нам нужен совершенно другой образ мышления.
Ключевые наблюдения о ZUS
Боб может предсказать результат измерения на основе \ ({\ mathcal {B}}} _ {x} \) с уверенностью, если и только если ансамбль \ ({\ mathscr {S}} (\ rho, {{\ mathcal {B}}} _ {x}) \), определенный в уравнении. (3) отлично различимо, то есть все состояния в \ ({\ mathscr {S}} (\ rho, {{\ mathcal {B}}} _ {x}) \) имеют взаимно ортогональные опоры. {m} \) тогда и только тогда, когда каждый ансамбль \ ({\ mathscr {S}} (\ rho, {{\ mathcal {B}}} _ {x}) \) отлично различим.Следующие три предложения являются простыми следствиями этих наблюдений.
Предложение 1 Предположим, что ρ – это ZUS, тогда любое состояние, поддерживаемое при поддержке ρ, является ZUS .
Предложение 2 Предположим, что ρ 1 и ρ 2 – это два ZUS на \ ({{\ mathcal {H}}} _ {{\ rm {A}}) } \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) . Если \ ({\ mathrm {tr} \,} _ {{\ rm {A}}} ({\ rho} _ {1}) \) и \ ({\ mathrm {tr} \,} _ {{\ rm {A}}} ({\ rho} _ {2}) \) имеют ортогональные опоры, тогда любая выпуклая смесь ρ 1 и ρ 2 является ZUS .
Предложение 3 Предположим, что ρ – двудольное состояние на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) и Λ – это полностью положительное и сохраняющее след (CPTP) отображение (квантовый канал) из системы B в систему \ (\ tilde {{\ rm {B}}}} \) . Тогда ρ является ZUS, если (1 \ (\ otimes \) Λ ) (ρ) равно .
Здесь предложения 1 и 2 связаны с тем фактом, что смесь квантовых состояний может только уменьшить различимость, если у приведенных состояний Боба нет ортогональных носителей.Предложение 3 следует из того простого факта, что квантовые операции не могут улучшить различимость. Два состояния ρ 1 и ρ 2 на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ { {\ rm {B}}} \) эквивалентны, если они могут быть превращены друг в друга локальными операциями над \ ({{\ mathcal {H}}} _ {{\ rm {B}}} \). В этом случае ρ 1 является ZUS по отношению к \ ({\ mathscr {B}} \), если ρ 2 является. В соответствии с этими локальными операциями ZUS делятся на эквивалентные классы.{m} \) в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \), нам сначала нужно точно определить ключевое свойство базисного набора. Граф переходов \ (G ({\ mathscr {B}}) \) из \ ({\ mathscr {B}} \) представляет собой -дробный граф размером м с м d A вершин, которые являются во взаимно однозначном соответствии с состояниями базиса (одинаковые состояния в разных базах соответствуют разным вершинам). Две разные вершины являются смежными, если соответствующие состояния не ортогональны, то есть вероятность перехода между двумя состояниями отлична от нуля.Граф \ (G ({\ mathscr {B}}) \) кодирует структуру несовместимости базисного набора \ ({\ mathscr {B}} \), которая имеет решающее значение для изучения ZUS и квантовой проверки, как мы увидим ниже. потом.
Базисный набор \ ({\ mathscr {B}} \) неприводим, если граф переходов \ (G ({\ mathscr {B}}) \) связан, и в этом случае проекторы на базисные состояния генерируют все операторная алгебра на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \). Любой базисный набор, состоящий из m ≥ 2 взаимно несмещенных базисов (или общих случайных баз), является неприводимым, поскольку граф переходов представляет собой полный m -раздельный граф, как показано на рис.2.
Рис. 2: Граф переходов трех взаимно несмещенных базисов для кубита, который соответствует собственным базам трех матриц Паули.Две вершины одного цвета связаны с двумя состояниями в одном базисе. Этот граф переходов связан, поэтому соответствующий базис неприводим.
Базисный набор \ ({\ mathscr {B}} \) приводим, если граф переходов \ (G ({\ mathscr {B}}) \) не связан. В этом случае базисный набор можно рассматривать как прямую сумму базисных наборов, определенных на меньших подпространствах.{m} \) неприводимо для \ ({{\ mathcal {H}}} _ {{\ rm {A}}, a} \).
Соедините ZUS с MES
Теперь мы готовы представить наши основные результаты по ZUS и MES, как показано на рис. 1. Во-первых, мы проясним, когда Боб может предсказать результат одного проективного измерения Алисы. Следующая лемма, доказанная в дополнительной информации, является ступенькой к пониманию ZUS при наличии квантовой памяти.
Лемма 2 Предположим, что \ (\ rho = \ left | {{\ Psi}} \ right \ rangle \ left \ langle {{\ Psi}} \ right | \) является двудольным чистым состоянием на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) и \ ({ \ mathcal {B}} \) является ортонормированной базой для \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \) .Тогда ансамбль \ ({\ mathscr {S}} (\ rho, {\ mathcal {B}}) \) отлично различим тогда и только тогда, когда \ ({\ mathcal {B}} \) является собственным основанием \ ({\ rho} _ {{\ rm {A}}} = {\ mathrm {tr} \,} _ {{\ rm {B}}} (\ rho) \).
Обратите внимание, что Боб может предсказать результат измерения Алисы на основе \ ({\ mathcal {B}} \) с уверенностью, если и только если ансамбль \ ({\ mathscr {S}} (\ rho, {\ mathcal {B}) }) \), определенные в формуле. (3) отлично различимы. По лемме 2 это так, если и только если ρ A диагональна относительно базиса \ ({\ mathcal {B}} \).Следовательно, чистое состояние ρ является ZUS относительно базисного набора \ ({\ mathscr {B}} \) тогда и только тогда, когда ρ A диагонально относительно каждого базиса в \ ({\ mathscr {B }} \). Когда \ ({\ mathscr {B}} \) неприводимо, оказывается, только MES могут удовлетворять этому условию. Основываясь на этом наблюдении, мы можем вывести следующую теорему, доказанную в дополнительной информации.
Теорема 1 Предположим, что \ ({\ mathscr {B}} \) – неприводимый базис в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ ) .Тогда двудольное (чистое или смешанное) состояние ρ на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm { B}}} \) является ZUS по отношению к \ ({\ mathscr {B}} \) iff d B ≥ d A и ρ является MES .
По теореме 1 и лемме 1 каждый ZUS относительно \ ({\ mathscr {B}} \) является тензорным произведением чистого MES и вспомогательного состояния. Кроме того, для достижения нулевой неопределенности измерения Боба на опоре B однозначно определяются аналогом Алисы, как показано в дополнительном примечании E.Все ZUS относительно \ ({\ mathscr {B}} \) могут быть превращены друг в друга локальными операциями над \ ({{\ mathcal {H}}} _ {{\ rm {B}}} \) и таким образом образуют единый эквивалентный класс. Если d A ≤ d B <2 d A , то все ZUS чистые и могут быть превращены друг в друга с помощью унитарных преобразований на \ ({{\ mathcal {H}}} _ {{\ rm {B}}} \). Эти результаты сохраняются, пока граф переходов \ (G ({\ mathscr {B}}) \) связан, даже если \ ({\ mathscr {B}} \) состоит только из двух почти идентичных оснований, так что соответствующие наблюдаемые являются только слабо несовместимыми, что определяется количественно коммутатором или устойчивостью к несовместимости 36,37,38 .
Теорема 1 устанавливает простую и точную связь между нулевой неопределенностью и максимальной запутанностью, которая не зависит от конкретной неопределенности и мер запутанности. Эта связь предлагает свежий взгляд на понимание принципа неопределенности при наличии квантовой памяти 8 . Это также может пролить свет на взаимодополняемость неопределенности и реальности, учитывая тесную связь между обозначениями неопределенности и реальности 7,30,31,32 .
ZUS относительно приводимых базисных наборов
Затем мы определяем ZUS относительно приводимых базисов \ ({\ mathscr {B}} \).
Теорема 2 Предположим, что \ ({\ mathscr {B}} \) – это набор ортонормированных базисов в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \) и имеет g неприводимых компонентов с компонентными подпространствами \ ({{\ mathcal {H}}} _ {{\ rm {A}}, a} \) , компонентные проекторы P a , и ранги компонентов r a для = 1 , 2 , … , г. Пусть ρ – двудольное состояние на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) и \ (\ rho_a = (P_a \ otimes 1_B) \ rho (P_a \ otimes 1_B) \) .Тогда ρ является ZUS относительно \ ({\ mathscr {B}} \) , если выполняются следующие три условия: r a ≤ d B всякий раз, когда \ (\ mathrm {tr} \, ({\ rho} _ {a})> 0 \) ; каждый ρ a с \ (\ mathrm {tr} \, ({\ rho} _ {a})> 0 \) является (субнормализованным) MES на \ ({{\ mathcal { H}}} _ {{\ rm {A}}, a} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) ; все \ ({\ mathrm {tr} \,} _ {{\ rm {A}}} ({\ rho} _ {a}) \) имеют взаимно ортогональные опоры .{a} \) и, кроме того, все \ ({\ mathrm {tr} \,} _ {{\ rm {A}}} ({\ rho} _ {a}) \) имеют взаимно ортогональные опоры. Обратите внимание, что согласованность между различными подпространствами компонентов бесполезна для построения ZUS. Кроме того, размер d B из \ ({{\ mathcal {H}}} _ {{\ rm {B}}}}) должен удовлетворять \ ({d} _ {{\ rm {B}) }} \ ge {r} _ {\ min} \) для построения ZUS, где \ ({r} _ {\ min} = \ mathop {\ min} \ nolimits_ {1 \ le a \ le g} {r} _ {a} \) – минимальный ранг компонента. Когда нижняя граница насыщена, каждый ZUS является чистым MES на \ ({{\ mathcal {H}}} _ {{\ rm {A}}, a} \ otimes {{\ mathcal {H}}} _ { {\ rm {B}}} \), где \ ({{\ mathcal {H}}} _ {{\ rm {A}}, a} \) – компонентное подпространство размерности \ ({r} _ { \ min} \).Кроме того, \ ({r} _ {\ min} \) определяет минимальную запутанность, необходимую для построения ZUS, как показано в разделе “Методы”.
В случае чистых состояний ZUS допускают гораздо более простую характеризацию, как показано в следующем следствии.
Следствие 2 Двудольное чистое состояние \ (\ left | {{\ Psi}} \ right \ rangle \) в \ ({{\ mathcal {H}}} _ {{\ rm {A }}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) является ZUS по отношению к \ ({\ mathscr {B}} \) , если и только если сокращенное состояние ρ A – это взвешенная сумма компонентных проекторов в \ ({\ mathscr {P}} ({\ mathscr {B}}) \).
Следствие 2 является частным случаем теоремы 2 и также следует из леммы 2 и дополнительной леммы 2. Здесь ρ A является взвешенной суммой компонентных проекторов тогда и только тогда, когда ρ A диагонально относительно каждого базиса. \ ({\ mathcal {B}} \) в \ ({\ mathscr {B}} \) (см. дополнительное примечание C). Как следствие следствия 2, приведенное состояние ρ A любого (чистого или смешанного) ZUS ρ относительно \ ({\ mathscr {B}} \) является взвешенной суммой компонентных проекторов в \ ({\ mathscr {P}} ({\ mathscr {B}}) \), учитывая, что любой ZUS является выпуклой смесью чистых ZUS.{{d} _ {{\ rm {A}}} – 1} \ left | jj \ right \ rangle / \ sqrt {{d} _ {{\ rm {A}}}} \) таким образом: Боб сначала создает MES в своей лаборатории, а затем отправляет одну частицу запутанной пары Алисе через квантовый канал. Чтобы проверить результирующее состояние ρ , они могут выполнять тесты на основе коррелированных локальных проективных измерений, так что только целевое состояние может пройти все тесты с уверенностью 39,40,41,42,43 . {m} \) в котором \ ({{\ mathcal {B}}} _ {x} \) выбрано с вероятностью μ x > 0.{*} \ right | $$
(8)
– тестовый проектор. Обратите внимание, что \ (\ left | {{\ Phi}} \ right \ rangle \) является собственным состоянием \ (P ({{\ mathcal {B}}} _ {x}) \) и Ω с собственным значением 1, и поэтому может с уверенностью пройти каждое испытание. Кроме того, \ (\ left | {{\ Phi}} \ right \ rangle \) можно надежно проверить с помощью этого протокола, если и только если максимальное собственное значение Ω невырождено, то есть проходное собственное подпространство Ω имеет размерность 1 40, 41,42,43 . Это так, если и только если базисный набор \ ({\ mathscr {B}} \) неприводим по следующей теореме, доказанной в дополнительной информации.{m} {\ mu} _ {x} = 1 \) . Тогда вырождение максимального собственного значения 1 Ω равно количеству компонент связности графа переходов \ (G ({\ mathscr {B}}) \) . Это собственное значение невырождено тогда и только тогда, когда базис \ ({\ mathscr {B}} \) неприводим .
Затем предположим, что Боб нечестен. Тогда Алиса не сможет различать состояния, эквивалентные локальным операциям Боба. Тем не менее, она все еще может проверить MES \ (\ left | {{\ Phi}} \ right \ rangle \) с точностью до эквивалентности.Благодаря теореме 1 описанная ранее игра в неопределенность фактически обеспечивает протокол проверки всякий раз, когда базисный набор \ ({\ mathscr {B}} \) Алисы неприводим. Обратите внимание, что Боб может пройти каждый тест (угадать каждый результат измерения) Алисы с уверенностью, только если подготовленное состояние ρ является MES. Удивительно, но требования к базам измерения Алисы остаются неизменными, когда Боб становится нечестным. Кроме того, измерения Боба, необходимые для достижения максимальной вероятности угадывания, по существу однозначно определяются аналогом Алисы.{*} \) с вероятностью μ x > 0 для x = 1, 2,…, m и вернуть результат. Затем Алиса выполняет проективное измерение на \ ({{\ mathcal {B}}} _ {x} \ in {\ mathscr {B}} \), и тест считается пройденным, если она получает тот же результат, что и Боб. В качестве альтернативы Алиса может выбрать POVM с двумя исходами \ (\ {\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right |, {1} _ { {\ rm {A}}} – \ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | \} \), если Боб получает результат k .{*} \). Тогда вероятность того, что Боб пройдет тест, составляет
$$ \ sum _ {k} \ left \ langle {\ psi} _ {xk} \ right | {\ sigma} _ {xk} \ left | {\ psi} _ {xk} \ right \ rangle, \ quad {\ sigma} _ {xk} = {\ mathrm {tr}} _ {{\ rm {B}}} [\ rho ({1} _ {{\ rm {A }}} \ otimes \ Pi_ {xk})], $$
(9)
, который является вариантом уравнения. (2). Субнормализованные состояния σ x k удовлетворяют условию нормализации ∑ k σ x k = ρ A ансамбля и образуют ρ A для каждого x . {m} \) с \ ({{\ mathcal {B}}} _ {x} = {\ {\ left | {\ psi} _ {xk} \ right \ rangle \}} _ {k} \) – это неприводимый набор ортонормированных базисов в . \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \) .Предположим \ ({\ {{\ {{\ sigma} _ {xk} \}} _ {k} \}} _ {x} \) – сборка для ρ А , что удовлетворяет \ ({\ sum} _ {k} \ left \ langle {\ psi} _ {xk} \ right | {\ sigma} _ {xk} \ left | {\ psi} _ {xk} \ right \ rangle = 1 \) для каждого x. Тогда ρ А полностью перемешан, а \ ({\ sigma} _ {xk} = \ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | / {d} _ {{\ rm {A}}} \) для каждого x и k.
Здесь условие \ ({\ sum} _ {k} \ left \ langle {\ psi} _ {xk} \ right | {\ sigma} _ {xk} \ left | {\ psi} _ {xk} \ right \ rangle = 1 \) означает, что сборка \ ({\ {{\ {{\ sigma} _ {xk} \}} _ {k} \}} _ {x} \) может с уверенностью пройти каждый тест Алисы . В силу теоремы 1 мы можем далее показать, что совокупность \ ({\ {{\ {\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | / {d} _ {{\ rm {A}}} \}} _ {k} \}} _ {x} \) может быть сгенерировано только MES, как указано в следующей теореме и доказано в Дополнительной Информация.
Теорема 4 Учитывая базис \ ({\ mathscr {B}} \) в лемме 3, предположим, что ρ – двудольное состояние на \ ({{\ mathcal {H}}} _ {{ \ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) , который может генерировать сборку \ ({\ {{\ {\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | / {d} _ {{\ rm {A}}} \}} _ {k} \}} _ {x} \) по замерам Боба. Тогда d B ≥ d A , а ρ – MES и ZUS по отношению к \ ({\ mathscr {B}} \).
Благодаря лемме 3 и теореме 4 тесты Алисы могут проверять совокупность \ ({\ {{\ {\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | / {d} _ {{\ rm {A}}} \}} _ {k} \}} _ {x} \), который, в свою очередь, может проверять MES всякий раз, когда \ ({\ mathscr {B}} \) неприводимо. Кроме того, теорема 4 предлагает общий рецепт построения ансамблей, характерных для MES. Эти результаты устанавливают тесную связь между соотношениями неопределенностей, квантовой запутанностью и квантовым управлением, которые представляют внутренний интерес для фундаментальных исследований.Между тем, эти результаты поучительны для изучения подготовки удаленного состояния 21,22 и полу-аппаратно-независимого самотестирования 18,23,24,25,26 .
Состояния с нулевой неопределенностью при наличии квантовой памяти
Максимально запутанные состояния
Чтобы установить наши основные результаты, сначала нам нужно лучше понять MES. Двудольное состояние ρ в гильбертовом пространстве \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}) }} \) размерности d A × d B является MES, если мы можем создать каждое состояние на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) от до локальными операциями и классической связью (LOCC) 27 .{{d} _ {{\ rm {B}}} – 1} \) являются вычислительными базами \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \) и \ ( {{\ mathcal {H}}} _ {{\ rm {B}}} \) соответственно. MES не обязательно является чистым, как поясняется в следующей лемме, по существу доказанной в ref. 28 ; см. дополнительную информацию для независимого доказательства.
Лемма 1 Пусть ρ – двудольное состояние на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{ \ rm {B}}} \) с d A ≤ d B .Тогда следующие утверждения эквивалентны .
Здесь H (A∣B) ρ = S ( ρ ) – S ( ρ B ) – условная энтропия A для данного B, где S ( ρ ) и S ( ρ B ) – энтропии фон Неймана ρ и \ ({\ rho} _ {{\ rm {B}}}: = {\ mathrm {tr }} _ {{\ rm {A}}} (\ rho) \) соответственно. {\ prime}} \) будет поддержкой ρ В .{\ prime} \ right \ rangle \) является чистым MES в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{ {\ rm {B}}} _ {1}} \), а τ – оператор плотности полного ранга на \ ({{\ mathcal {H}}} _ {{{\ rm {B}}} _ {2}} \). Таким образом, все MES на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) эквивалентны под локальными операциями Боба.
Следствие 1 Все MES на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B }}} \) с d A ≤ d B могут быть преобразованы друг в друга локальными операциями на \ ({{\ mathcal {H}}} _ {{\ rm { B}}} \) .{m} \). Тогда прогнозирование результата O x сводится к прогнозированию результата проективного измерения на основе \ ({{\ mathcal {B}}} _ {x} \). Когда эти наблюдаемые несовместимы (не коммутируют друг с другом), в целом Боб не может с уверенностью предсказать результат измерения, даже если он знает полное классическое описание состояния системы, которое характеризуется матрицей плотности ρ A . { 2} \).
Ситуация иная, если Боб имеет квантовую память с гильбертовым пространством \ ({{\ mathcal {H}}} _ {{\ rm {B}}}}) и может создать запутанное состояние ρ на суставе system \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \), как показано на Рис. . 1. Предположим, Алиса выбирает базис \ ({{\ mathcal {B}}} _ {x} \) (observable O x ), тогда Боб может выполнить обобщенное измерение, характеризуемое положительным оператором – оценочная мера (POVM) \ ({\ {{{{\ Pi}}} _ {xk} \}} _ {k} \) в его подсистеме \ ({{\ mathcal {H}}} _ {{\ rm {B}}} \), где Π x k соответствует угадыванию результата k с учетом базы измерения \ ({\ mathcal {B}}} _ {x} \) Алисы.Средняя вероятность успеха составляет ∑ x p x / m с
$$ {p} _ {x} = \ sum _ {k} {\ mathrm {tr}} \, [\ rho (\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | \ otimes \ Pi_ {xk})] = \ sum _ { k} {\ mathrm {tr}} \, ({\ rho} _ {xk} \ Pi_ {xk}), $$
(2)
, где \ ({\ rho} _ {xk} = \ left \ langle {\ psi} _ {xk} \ right | \ rho \ left | {\ psi} _ {xk} \ right \ rangle \) субнормализованы уменьшенные состояния Боба.Обратите внимание, что p x также является вероятностью того, что POVM \ ({\ {{{{\ Pi}}}} _ {xk} \}} _ {k} \) может успешно различить ансамбль состояний
$$ {\ mathscr {S}} (\ rho, {{\ mathcal {B}}} _ {x}) = \ {\ left \ langle \ psi \ right | \ rho \ left | \ psi \ right \ rangle \: \ \ left | \ psi \ right \ rangle \ in {{\ mathcal {B}}} _ {x} \}. $$
(3)
Максимум средней вероятности предположения по всем POVM может быть определен с помощью полуопределенного программирования, и этот максимум определяется состоянием ρ и базисным набором \ ({\ mathscr {B}} \) (или наблюдаемым набором \ ({\ mathscr {O}} \)) Алисы.
Рис. 1: Связь между нулевой неопределенностью и максимальной запутанностью в игре на неопределенность.Выполняя подходящие измерения (в зависимости от наблюдаемых Алисой) своей квантовой памяти, Боб может лучше предсказать результаты измерений Алисы. {m} \) для Алисы совместное состояние ρ Алисы и Боба является ZUS, если Боб может с уверенностью предсказать результат измерения Алисы с помощью подходящего измерения в зависимости от выбора Алисы.Учитывая ZUS, вероятность угадывания p x для каждого измерения Алисы может достигать максимума 1, а условная энтропия H ( O x B) равна 0. Напротив. с минимальными состояниями неопределенности и интеллектуальными состояниями 14,15,16 , ZUS не только минимизируют неопределенность, но также полностью устраняют неопределенность. Более того, здесь определение не зависит от какой-либо конкретной меры неопределенности.
Чтобы оценить важность запутанности для построения ZUS, рассмотрим пример с двумя наблюдаемыми, в этом случае отношение неопределенности в уравнении.{-1}) + H {({\ rm {A}} | {\ rm {B}})} _ {\ rho}. $$
(4)
Здесь условная энтропия H (A∣B) ρ показывает влияние запутанности на уменьшение неопределенности. { -1}), $$
(5)
, где второй получен в исх.{2} = 1 / {d} _ {{\ rm {A}}} \) для всех j , k 35 . Тогда у нас есть c = 1/ d A и
$$ {E} _ {{\ rm {F}}} (\ rho) = {E} _ {{\ rm {R}} } (\ rho) = – H {({\ rm {A}} | {\ rm {B}})} _ {\ rho} = {\ mathrm {log} \,} _ {2} {d} _ {{\ rm {A}}}, $$
(6)
, что означает, что d B ≥ d A и ρ является MES по лемме 1, и в этом случае ρ действительно является ZUS.К сожалению, это рассуждение в целом не работает. Чтобы решить эту проблему, нам нужен совершенно другой образ мышления.
Ключевые наблюдения о ZUS
Боб может предсказать результат измерения на основе \ ({\ mathcal {B}}} _ {x} \) с уверенностью, если и только если ансамбль \ ({\ mathscr {S}} (\ rho, {{\ mathcal {B}}} _ {x}) \), определенный в уравнении. (3) отлично различимо, то есть все состояния в \ ({\ mathscr {S}} (\ rho, {{\ mathcal {B}}} _ {x}) \) имеют взаимно ортогональные опоры. {m} \) тогда и только тогда, когда каждый ансамбль \ ({\ mathscr {S}} (\ rho, {{\ mathcal {B}}} _ {x}) \) отлично различим.Следующие три предложения являются простыми следствиями этих наблюдений.
Предложение 1 Предположим, что ρ – это ZUS, тогда любое состояние, поддерживаемое при поддержке ρ, является ZUS .
Предложение 2 Предположим, что ρ 1 и ρ 2 – это два ZUS на \ ({{\ mathcal {H}}} _ {{\ rm {A}}) } \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) . Если \ ({\ mathrm {tr} \,} _ {{\ rm {A}}} ({\ rho} _ {1}) \) и \ ({\ mathrm {tr} \,} _ {{\ rm {A}}} ({\ rho} _ {2}) \) имеют ортогональные опоры, тогда любая выпуклая смесь ρ 1 и ρ 2 является ZUS .
Предложение 3 Предположим, что ρ – двудольное состояние на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) и Λ – это полностью положительное и сохраняющее след (CPTP) отображение (квантовый канал) из системы B в систему \ (\ tilde {{\ rm {B}}}} \) . Тогда ρ является ZUS, если (1 \ (\ otimes \) Λ ) (ρ) равно .
Здесь предложения 1 и 2 связаны с тем фактом, что смесь квантовых состояний может только уменьшить различимость, если у приведенных состояний Боба нет ортогональных носителей.Предложение 3 следует из того простого факта, что квантовые операции не могут улучшить различимость. Два состояния ρ 1 и ρ 2 на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ { {\ rm {B}}} \) эквивалентны, если они могут быть превращены друг в друга локальными операциями над \ ({{\ mathcal {H}}} _ {{\ rm {B}}} \). В этом случае ρ 1 является ZUS по отношению к \ ({\ mathscr {B}} \), если ρ 2 является. В соответствии с этими локальными операциями ZUS делятся на эквивалентные классы.{m} \) в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \), нам сначала нужно точно определить ключевое свойство базисного набора. Граф переходов \ (G ({\ mathscr {B}}) \) из \ ({\ mathscr {B}} \) представляет собой -дробный граф размером м с м d A вершин, которые являются во взаимно однозначном соответствии с состояниями базиса (одинаковые состояния в разных базах соответствуют разным вершинам). Две разные вершины являются смежными, если соответствующие состояния не ортогональны, то есть вероятность перехода между двумя состояниями отлична от нуля.Граф \ (G ({\ mathscr {B}}) \) кодирует структуру несовместимости базисного набора \ ({\ mathscr {B}} \), которая имеет решающее значение для изучения ZUS и квантовой проверки, как мы увидим ниже. потом.
Базисный набор \ ({\ mathscr {B}} \) неприводим, если граф переходов \ (G ({\ mathscr {B}}) \) связан, и в этом случае проекторы на базисные состояния генерируют все операторная алгебра на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \). Любой базисный набор, состоящий из m ≥ 2 взаимно несмещенных базисов (или общих случайных баз), является неприводимым, поскольку граф переходов представляет собой полный m -раздельный граф, как показано на рис.2.
Рис. 2: Граф переходов трех взаимно несмещенных базисов для кубита, который соответствует собственным базам трех матриц Паули.Две вершины одного цвета связаны с двумя состояниями в одном базисе. Этот граф переходов связан, поэтому соответствующий базис неприводим.
Базисный набор \ ({\ mathscr {B}} \) приводим, если граф переходов \ (G ({\ mathscr {B}}) \) не связан. В этом случае базисный набор можно рассматривать как прямую сумму базисных наборов, определенных на меньших подпространствах.{m} \) неприводимо для \ ({{\ mathcal {H}}} _ {{\ rm {A}}, a} \).
Соедините ZUS с MES
Теперь мы готовы представить наши основные результаты по ZUS и MES, как показано на рис. 1. Во-первых, мы проясним, когда Боб может предсказать результат одного проективного измерения Алисы. Следующая лемма, доказанная в дополнительной информации, является ступенькой к пониманию ZUS при наличии квантовой памяти.
Лемма 2 Предположим, что \ (\ rho = \ left | {{\ Psi}} \ right \ rangle \ left \ langle {{\ Psi}} \ right | \) является двудольным чистым состоянием на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) и \ ({ \ mathcal {B}} \) является ортонормированной базой для \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \) .Тогда ансамбль \ ({\ mathscr {S}} (\ rho, {\ mathcal {B}}) \) отлично различим тогда и только тогда, когда \ ({\ mathcal {B}} \) является собственным основанием \ ({\ rho} _ {{\ rm {A}}} = {\ mathrm {tr} \,} _ {{\ rm {B}}} (\ rho) \).
Обратите внимание, что Боб может предсказать результат измерения Алисы на основе \ ({\ mathcal {B}} \) с уверенностью, если и только если ансамбль \ ({\ mathscr {S}} (\ rho, {\ mathcal {B}) }) \), определенные в формуле. (3) отлично различимы. По лемме 2 это так, если и только если ρ A диагональна относительно базиса \ ({\ mathcal {B}} \).Следовательно, чистое состояние ρ является ZUS относительно базисного набора \ ({\ mathscr {B}} \) тогда и только тогда, когда ρ A диагонально относительно каждого базиса в \ ({\ mathscr {B }} \). Когда \ ({\ mathscr {B}} \) неприводимо, оказывается, только MES могут удовлетворять этому условию. Основываясь на этом наблюдении, мы можем вывести следующую теорему, доказанную в дополнительной информации.
Теорема 1 Предположим, что \ ({\ mathscr {B}} \) – неприводимый базис в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ ) .Тогда двудольное (чистое или смешанное) состояние ρ на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm { B}}} \) является ZUS по отношению к \ ({\ mathscr {B}} \) iff d B ≥ d A и ρ является MES .
По теореме 1 и лемме 1 каждый ZUS относительно \ ({\ mathscr {B}} \) является тензорным произведением чистого MES и вспомогательного состояния. Кроме того, для достижения нулевой неопределенности измерения Боба на опоре B однозначно определяются аналогом Алисы, как показано в дополнительном примечании E.Все ZUS относительно \ ({\ mathscr {B}} \) могут быть превращены друг в друга локальными операциями над \ ({{\ mathcal {H}}} _ {{\ rm {B}}} \) и таким образом образуют единый эквивалентный класс. Если d A ≤ d B <2 d A , то все ZUS чистые и могут быть превращены друг в друга с помощью унитарных преобразований на \ ({{\ mathcal {H}}} _ {{\ rm {B}}} \). Эти результаты сохраняются, пока граф переходов \ (G ({\ mathscr {B}}) \) связан, даже если \ ({\ mathscr {B}} \) состоит только из двух почти идентичных оснований, так что соответствующие наблюдаемые являются только слабо несовместимыми, что определяется количественно коммутатором или устойчивостью к несовместимости 36,37,38 .
Теорема 1 устанавливает простую и точную связь между нулевой неопределенностью и максимальной запутанностью, которая не зависит от конкретной неопределенности и мер запутанности. Эта связь предлагает свежий взгляд на понимание принципа неопределенности при наличии квантовой памяти 8 . Это также может пролить свет на взаимодополняемость неопределенности и реальности, учитывая тесную связь между обозначениями неопределенности и реальности 7,30,31,32 .
ZUS относительно приводимых базисных наборов
Затем мы определяем ZUS относительно приводимых базисов \ ({\ mathscr {B}} \).
Теорема 2 Предположим, что \ ({\ mathscr {B}} \) – это набор ортонормированных базисов в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \) и имеет g неприводимых компонентов с компонентными подпространствами \ ({{\ mathcal {H}}} _ {{\ rm {A}}, a} \) , компонентные проекторы P a , и ранги компонентов r a для = 1 , 2 , … , г. Пусть ρ – двудольное состояние на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) и \ (\ rho_a = (P_a \ otimes 1_B) \ rho (P_a \ otimes 1_B) \) .Тогда ρ является ZUS относительно \ ({\ mathscr {B}} \) , если выполняются следующие три условия: r a ≤ d B всякий раз, когда \ (\ mathrm {tr} \, ({\ rho} _ {a})> 0 \) ; каждый ρ a с \ (\ mathrm {tr} \, ({\ rho} _ {a})> 0 \) является (субнормализованным) MES на \ ({{\ mathcal { H}}} _ {{\ rm {A}}, a} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) ; все \ ({\ mathrm {tr} \,} _ {{\ rm {A}}} ({\ rho} _ {a}) \) имеют взаимно ортогональные опоры .{a} \) и, кроме того, все \ ({\ mathrm {tr} \,} _ {{\ rm {A}}} ({\ rho} _ {a}) \) имеют взаимно ортогональные опоры. Обратите внимание, что согласованность между различными подпространствами компонентов бесполезна для построения ZUS. Кроме того, размер d B из \ ({{\ mathcal {H}}} _ {{\ rm {B}}}}) должен удовлетворять \ ({d} _ {{\ rm {B}) }} \ ge {r} _ {\ min} \) для построения ZUS, где \ ({r} _ {\ min} = \ mathop {\ min} \ nolimits_ {1 \ le a \ le g} {r} _ {a} \) – минимальный ранг компонента. Когда нижняя граница насыщена, каждый ZUS является чистым MES на \ ({{\ mathcal {H}}} _ {{\ rm {A}}, a} \ otimes {{\ mathcal {H}}} _ { {\ rm {B}}} \), где \ ({{\ mathcal {H}}} _ {{\ rm {A}}, a} \) – компонентное подпространство размерности \ ({r} _ { \ min} \).Кроме того, \ ({r} _ {\ min} \) определяет минимальную запутанность, необходимую для построения ZUS, как показано в разделе “Методы”.
В случае чистых состояний ZUS допускают гораздо более простую характеризацию, как показано в следующем следствии.
Следствие 2 Двудольное чистое состояние \ (\ left | {{\ Psi}} \ right \ rangle \) в \ ({{\ mathcal {H}}} _ {{\ rm {A }}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) является ZUS по отношению к \ ({\ mathscr {B}} \) , если и только если сокращенное состояние ρ A – это взвешенная сумма компонентных проекторов в \ ({\ mathscr {P}} ({\ mathscr {B}}) \).
Следствие 2 является частным случаем теоремы 2 и также следует из леммы 2 и дополнительной леммы 2. Здесь ρ A является взвешенной суммой компонентных проекторов тогда и только тогда, когда ρ A диагонально относительно каждого базиса. \ ({\ mathcal {B}} \) в \ ({\ mathscr {B}} \) (см. дополнительное примечание C). Как следствие следствия 2, приведенное состояние ρ A любого (чистого или смешанного) ZUS ρ относительно \ ({\ mathscr {B}} \) является взвешенной суммой компонентных проекторов в \ ({\ mathscr {P}} ({\ mathscr {B}}) \), учитывая, что любой ZUS является выпуклой смесью чистых ZUS.{{d} _ {{\ rm {A}}} – 1} \ left | jj \ right \ rangle / \ sqrt {{d} _ {{\ rm {A}}}} \) таким образом: Боб сначала создает MES в своей лаборатории, а затем отправляет одну частицу запутанной пары Алисе через квантовый канал. Чтобы проверить результирующее состояние ρ , они могут выполнять тесты на основе коррелированных локальных проективных измерений, так что только целевое состояние может пройти все тесты с уверенностью 39,40,41,42,43 . {m} \) в котором \ ({{\ mathcal {B}}} _ {x} \) выбрано с вероятностью μ x > 0.{*} \ right | $$
(8)
– тестовый проектор. Обратите внимание, что \ (\ left | {{\ Phi}} \ right \ rangle \) является собственным состоянием \ (P ({{\ mathcal {B}}} _ {x}) \) и Ω с собственным значением 1, и поэтому может с уверенностью пройти каждое испытание. Кроме того, \ (\ left | {{\ Phi}} \ right \ rangle \) можно надежно проверить с помощью этого протокола, если и только если максимальное собственное значение Ω невырождено, то есть проходное собственное подпространство Ω имеет размерность 1 40, 41,42,43 . Это так, если и только если базисный набор \ ({\ mathscr {B}} \) неприводим по следующей теореме, доказанной в дополнительной информации.{m} {\ mu} _ {x} = 1 \) . Тогда вырождение максимального собственного значения 1 Ω равно количеству компонент связности графа переходов \ (G ({\ mathscr {B}}) \) . Это собственное значение невырождено тогда и только тогда, когда базис \ ({\ mathscr {B}} \) неприводим .
Затем предположим, что Боб нечестен. Тогда Алиса не сможет различать состояния, эквивалентные локальным операциям Боба. Тем не менее, она все еще может проверить MES \ (\ left | {{\ Phi}} \ right \ rangle \) с точностью до эквивалентности.Благодаря теореме 1 описанная ранее игра в неопределенность фактически обеспечивает протокол проверки всякий раз, когда базисный набор \ ({\ mathscr {B}} \) Алисы неприводим. Обратите внимание, что Боб может пройти каждый тест (угадать каждый результат измерения) Алисы с уверенностью, только если подготовленное состояние ρ является MES. Удивительно, но требования к базам измерения Алисы остаются неизменными, когда Боб становится нечестным. Кроме того, измерения Боба, необходимые для достижения максимальной вероятности угадывания, по существу однозначно определяются аналогом Алисы.{*} \) с вероятностью μ x > 0 для x = 1, 2,…, m и вернуть результат. Затем Алиса выполняет проективное измерение на \ ({{\ mathcal {B}}} _ {x} \ in {\ mathscr {B}} \), и тест считается пройденным, если она получает тот же результат, что и Боб. В качестве альтернативы Алиса может выбрать POVM с двумя исходами \ (\ {\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right |, {1} _ { {\ rm {A}}} – \ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | \} \), если Боб получает результат k .{*} \). Тогда вероятность того, что Боб пройдет тест, составляет
$$ \ sum _ {k} \ left \ langle {\ psi} _ {xk} \ right | {\ sigma} _ {xk} \ left | {\ psi} _ {xk} \ right \ rangle, \ quad {\ sigma} _ {xk} = {\ mathrm {tr}} _ {{\ rm {B}}} [\ rho ({1} _ {{\ rm {A }}} \ otimes \ Pi_ {xk})], $$
(9)
, который является вариантом уравнения. (2). Субнормализованные состояния σ x k удовлетворяют условию нормализации ∑ k σ x k = ρ A ансамбля и образуют ρ A для каждого x . {m} \) с \ ({{\ mathcal {B}}} _ {x} = {\ {\ left | {\ psi} _ {xk} \ right \ rangle \}} _ {k} \) – это неприводимый набор ортонормированных базисов в . \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \) .Предположим \ ({\ {{\ {{\ sigma} _ {xk} \}} _ {k} \}} _ {x} \) – сборка для ρ А , что удовлетворяет \ ({\ sum} _ {k} \ left \ langle {\ psi} _ {xk} \ right | {\ sigma} _ {xk} \ left | {\ psi} _ {xk} \ right \ rangle = 1 \) для каждого x. Тогда ρ А полностью перемешан, а \ ({\ sigma} _ {xk} = \ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | / {d} _ {{\ rm {A}}} \) для каждого x и k.
Здесь условие \ ({\ sum} _ {k} \ left \ langle {\ psi} _ {xk} \ right | {\ sigma} _ {xk} \ left | {\ psi} _ {xk} \ right \ rangle = 1 \) означает, что сборка \ ({\ {{\ {{\ sigma} _ {xk} \}} _ {k} \}} _ {x} \) может с уверенностью пройти каждый тест Алисы . В силу теоремы 1 мы можем далее показать, что совокупность \ ({\ {{\ {\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | / {d} _ {{\ rm {A}}} \}} _ {k} \}} _ {x} \) может быть сгенерировано только MES, как указано в следующей теореме и доказано в Дополнительной Информация.
Теорема 4 Учитывая базис \ ({\ mathscr {B}} \) в лемме 3, предположим, что ρ – двудольное состояние на \ ({{\ mathcal {H}}} _ {{ \ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) , который может генерировать сборку \ ({\ {{\ {\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | / {d} _ {{\ rm {A}}} \}} _ {k} \}} _ {x} \) по замерам Боба. Тогда d B ≥ d A , а ρ – MES и ZUS по отношению к \ ({\ mathscr {B}} \).
Благодаря лемме 3 и теореме 4 тесты Алисы могут проверять совокупность \ ({\ {{\ {\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | / {d} _ {{\ rm {A}}} \}} _ {k} \}} _ {x} \), который, в свою очередь, может проверять MES всякий раз, когда \ ({\ mathscr {B}} \) неприводимо. Кроме того, теорема 4 предлагает общий рецепт построения ансамблей, характерных для MES. Эти результаты устанавливают тесную связь между соотношениями неопределенностей, квантовой запутанностью и квантовым управлением, которые представляют внутренний интерес для фундаментальных исследований.Между тем, эти результаты поучительны для изучения подготовки удаленного состояния 21,22 и полу-аппаратно-независимого самотестирования 18,23,24,25,26 .
Состояния с нулевой неопределенностью при наличии квантовой памяти
Максимально запутанные состояния
Чтобы установить наши основные результаты, сначала нам нужно лучше понять MES. Двудольное состояние ρ в гильбертовом пространстве \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}) }} \) размерности d A × d B является MES, если мы можем создать каждое состояние на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) от до локальными операциями и классической связью (LOCC) 27 .{{d} _ {{\ rm {B}}} – 1} \) являются вычислительными базами \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \) и \ ( {{\ mathcal {H}}} _ {{\ rm {B}}} \) соответственно. MES не обязательно является чистым, как поясняется в следующей лемме, по существу доказанной в ref. 28 ; см. дополнительную информацию для независимого доказательства.
Лемма 1 Пусть ρ – двудольное состояние на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{ \ rm {B}}} \) с d A ≤ d B .Тогда следующие утверждения эквивалентны .
Здесь H (A∣B) ρ = S ( ρ ) – S ( ρ B ) – условная энтропия A для данного B, где S ( ρ ) и S ( ρ B ) – энтропии фон Неймана ρ и \ ({\ rho} _ {{\ rm {B}}}: = {\ mathrm {tr }} _ {{\ rm {A}}} (\ rho) \) соответственно. {\ prime}} \) будет поддержкой ρ В .{\ prime} \ right \ rangle \) является чистым MES в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{ {\ rm {B}}} _ {1}} \), а τ – оператор плотности полного ранга на \ ({{\ mathcal {H}}} _ {{{\ rm {B}}} _ {2}} \). Таким образом, все MES на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) эквивалентны под локальными операциями Боба.
Следствие 1 Все MES на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B }}} \) с d A ≤ d B могут быть преобразованы друг в друга локальными операциями на \ ({{\ mathcal {H}}} _ {{\ rm { B}}} \) .{m} \). Тогда прогнозирование результата O x сводится к прогнозированию результата проективного измерения на основе \ ({{\ mathcal {B}}} _ {x} \). Когда эти наблюдаемые несовместимы (не коммутируют друг с другом), в целом Боб не может с уверенностью предсказать результат измерения, даже если он знает полное классическое описание состояния системы, которое характеризуется матрицей плотности ρ A . { 2} \).
Ситуация иная, если Боб имеет квантовую память с гильбертовым пространством \ ({{\ mathcal {H}}} _ {{\ rm {B}}}}) и может создать запутанное состояние ρ на суставе system \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \), как показано на Рис. . 1. Предположим, Алиса выбирает базис \ ({{\ mathcal {B}}} _ {x} \) (observable O x ), тогда Боб может выполнить обобщенное измерение, характеризуемое положительным оператором – оценочная мера (POVM) \ ({\ {{{{\ Pi}}} _ {xk} \}} _ {k} \) в его подсистеме \ ({{\ mathcal {H}}} _ {{\ rm {B}}} \), где Π x k соответствует угадыванию результата k с учетом базы измерения \ ({\ mathcal {B}}} _ {x} \) Алисы.Средняя вероятность успеха составляет ∑ x p x / m с
$$ {p} _ {x} = \ sum _ {k} {\ mathrm {tr}} \, [\ rho (\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | \ otimes \ Pi_ {xk})] = \ sum _ { k} {\ mathrm {tr}} \, ({\ rho} _ {xk} \ Pi_ {xk}), $$
(2)
, где \ ({\ rho} _ {xk} = \ left \ langle {\ psi} _ {xk} \ right | \ rho \ left | {\ psi} _ {xk} \ right \ rangle \) субнормализованы уменьшенные состояния Боба.Обратите внимание, что p x также является вероятностью того, что POVM \ ({\ {{{{\ Pi}}}} _ {xk} \}} _ {k} \) может успешно различить ансамбль состояний
$$ {\ mathscr {S}} (\ rho, {{\ mathcal {B}}} _ {x}) = \ {\ left \ langle \ psi \ right | \ rho \ left | \ psi \ right \ rangle \: \ \ left | \ psi \ right \ rangle \ in {{\ mathcal {B}}} _ {x} \}. $$
(3)
Максимум средней вероятности предположения по всем POVM может быть определен с помощью полуопределенного программирования, и этот максимум определяется состоянием ρ и базисным набором \ ({\ mathscr {B}} \) (или наблюдаемым набором \ ({\ mathscr {O}} \)) Алисы.
Рис. 1: Связь между нулевой неопределенностью и максимальной запутанностью в игре на неопределенность.Выполняя подходящие измерения (в зависимости от наблюдаемых Алисой) своей квантовой памяти, Боб может лучше предсказать результаты измерений Алисы. {m} \) для Алисы совместное состояние ρ Алисы и Боба является ZUS, если Боб может с уверенностью предсказать результат измерения Алисы с помощью подходящего измерения в зависимости от выбора Алисы.Учитывая ZUS, вероятность угадывания p x для каждого измерения Алисы может достигать максимума 1, а условная энтропия H ( O x B) равна 0. Напротив. с минимальными состояниями неопределенности и интеллектуальными состояниями 14,15,16 , ZUS не только минимизируют неопределенность, но также полностью устраняют неопределенность. Более того, здесь определение не зависит от какой-либо конкретной меры неопределенности.
Чтобы оценить важность запутанности для построения ZUS, рассмотрим пример с двумя наблюдаемыми, в этом случае отношение неопределенности в уравнении.{-1}) + H {({\ rm {A}} | {\ rm {B}})} _ {\ rho}. $$
(4)
Здесь условная энтропия H (A∣B) ρ показывает влияние запутанности на уменьшение неопределенности. { -1}), $$
(5)
, где второй получен в исх.{2} = 1 / {d} _ {{\ rm {A}}} \) для всех j , k 35 . Тогда у нас есть c = 1/ d A и
$$ {E} _ {{\ rm {F}}} (\ rho) = {E} _ {{\ rm {R}} } (\ rho) = – H {({\ rm {A}} | {\ rm {B}})} _ {\ rho} = {\ mathrm {log} \,} _ {2} {d} _ {{\ rm {A}}}, $$
(6)
, что означает, что d B ≥ d A и ρ является MES по лемме 1, и в этом случае ρ действительно является ZUS.К сожалению, это рассуждение в целом не работает. Чтобы решить эту проблему, нам нужен совершенно другой образ мышления.
Ключевые наблюдения о ZUS
Боб может предсказать результат измерения на основе \ ({\ mathcal {B}}} _ {x} \) с уверенностью, если и только если ансамбль \ ({\ mathscr {S}} (\ rho, {{\ mathcal {B}}} _ {x}) \), определенный в уравнении. (3) отлично различимо, то есть все состояния в \ ({\ mathscr {S}} (\ rho, {{\ mathcal {B}}} _ {x}) \) имеют взаимно ортогональные опоры. {m} \) тогда и только тогда, когда каждый ансамбль \ ({\ mathscr {S}} (\ rho, {{\ mathcal {B}}} _ {x}) \) отлично различим.Следующие три предложения являются простыми следствиями этих наблюдений.
Предложение 1 Предположим, что ρ – это ZUS, тогда любое состояние, поддерживаемое при поддержке ρ, является ZUS .
Предложение 2 Предположим, что ρ 1 и ρ 2 – это два ZUS на \ ({{\ mathcal {H}}} _ {{\ rm {A}}) } \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) . Если \ ({\ mathrm {tr} \,} _ {{\ rm {A}}} ({\ rho} _ {1}) \) и \ ({\ mathrm {tr} \,} _ {{\ rm {A}}} ({\ rho} _ {2}) \) имеют ортогональные опоры, тогда любая выпуклая смесь ρ 1 и ρ 2 является ZUS .
Предложение 3 Предположим, что ρ – двудольное состояние на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) и Λ – это полностью положительное и сохраняющее след (CPTP) отображение (квантовый канал) из системы B в систему \ (\ tilde {{\ rm {B}}}} \) . Тогда ρ является ZUS, если (1 \ (\ otimes \) Λ ) (ρ) равно .
Здесь предложения 1 и 2 связаны с тем фактом, что смесь квантовых состояний может только уменьшить различимость, если у приведенных состояний Боба нет ортогональных носителей.Предложение 3 следует из того простого факта, что квантовые операции не могут улучшить различимость. Два состояния ρ 1 и ρ 2 на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ { {\ rm {B}}} \) эквивалентны, если они могут быть превращены друг в друга локальными операциями над \ ({{\ mathcal {H}}} _ {{\ rm {B}}} \). В этом случае ρ 1 является ZUS по отношению к \ ({\ mathscr {B}} \), если ρ 2 является. В соответствии с этими локальными операциями ZUS делятся на эквивалентные классы.{m} \) в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \), нам сначала нужно точно определить ключевое свойство базисного набора. Граф переходов \ (G ({\ mathscr {B}}) \) из \ ({\ mathscr {B}} \) представляет собой -дробный граф размером м с м d A вершин, которые являются во взаимно однозначном соответствии с состояниями базиса (одинаковые состояния в разных базах соответствуют разным вершинам). Две разные вершины являются смежными, если соответствующие состояния не ортогональны, то есть вероятность перехода между двумя состояниями отлична от нуля.Граф \ (G ({\ mathscr {B}}) \) кодирует структуру несовместимости базисного набора \ ({\ mathscr {B}} \), которая имеет решающее значение для изучения ZUS и квантовой проверки, как мы увидим ниже. потом.
Базисный набор \ ({\ mathscr {B}} \) неприводим, если граф переходов \ (G ({\ mathscr {B}}) \) связан, и в этом случае проекторы на базисные состояния генерируют все операторная алгебра на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \). Любой базисный набор, состоящий из m ≥ 2 взаимно несмещенных базисов (или общих случайных баз), является неприводимым, поскольку граф переходов представляет собой полный m -раздельный граф, как показано на рис.2.
Рис. 2: Граф переходов трех взаимно несмещенных базисов для кубита, который соответствует собственным базам трех матриц Паули.Две вершины одного цвета связаны с двумя состояниями в одном базисе. Этот граф переходов связан, поэтому соответствующий базис неприводим.
Базисный набор \ ({\ mathscr {B}} \) приводим, если граф переходов \ (G ({\ mathscr {B}}) \) не связан. В этом случае базисный набор можно рассматривать как прямую сумму базисных наборов, определенных на меньших подпространствах.{m} \) неприводимо для \ ({{\ mathcal {H}}} _ {{\ rm {A}}, a} \).
Соедините ZUS с MES
Теперь мы готовы представить наши основные результаты по ZUS и MES, как показано на рис. 1. Во-первых, мы проясним, когда Боб может предсказать результат одного проективного измерения Алисы. Следующая лемма, доказанная в дополнительной информации, является ступенькой к пониманию ZUS при наличии квантовой памяти.
Лемма 2 Предположим, что \ (\ rho = \ left | {{\ Psi}} \ right \ rangle \ left \ langle {{\ Psi}} \ right | \) является двудольным чистым состоянием на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) и \ ({ \ mathcal {B}} \) является ортонормированной базой для \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \) .Тогда ансамбль \ ({\ mathscr {S}} (\ rho, {\ mathcal {B}}) \) отлично различим тогда и только тогда, когда \ ({\ mathcal {B}} \) является собственным основанием \ ({\ rho} _ {{\ rm {A}}} = {\ mathrm {tr} \,} _ {{\ rm {B}}} (\ rho) \).
Обратите внимание, что Боб может предсказать результат измерения Алисы на основе \ ({\ mathcal {B}} \) с уверенностью, если и только если ансамбль \ ({\ mathscr {S}} (\ rho, {\ mathcal {B}) }) \), определенные в формуле. (3) отлично различимы. По лемме 2 это так, если и только если ρ A диагональна относительно базиса \ ({\ mathcal {B}} \).Следовательно, чистое состояние ρ является ZUS относительно базисного набора \ ({\ mathscr {B}} \) тогда и только тогда, когда ρ A диагонально относительно каждого базиса в \ ({\ mathscr {B }} \). Когда \ ({\ mathscr {B}} \) неприводимо, оказывается, только MES могут удовлетворять этому условию. Основываясь на этом наблюдении, мы можем вывести следующую теорему, доказанную в дополнительной информации.
Теорема 1 Предположим, что \ ({\ mathscr {B}} \) – неприводимый базис в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ ) .Тогда двудольное (чистое или смешанное) состояние ρ на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm { B}}} \) является ZUS по отношению к \ ({\ mathscr {B}} \) iff d B ≥ d A и ρ является MES .
По теореме 1 и лемме 1 каждый ZUS относительно \ ({\ mathscr {B}} \) является тензорным произведением чистого MES и вспомогательного состояния. Кроме того, для достижения нулевой неопределенности измерения Боба на опоре B однозначно определяются аналогом Алисы, как показано в дополнительном примечании E.Все ZUS относительно \ ({\ mathscr {B}} \) могут быть превращены друг в друга локальными операциями над \ ({{\ mathcal {H}}} _ {{\ rm {B}}} \) и таким образом образуют единый эквивалентный класс. Если d A ≤ d B <2 d A , то все ZUS чистые и могут быть превращены друг в друга с помощью унитарных преобразований на \ ({{\ mathcal {H}}} _ {{\ rm {B}}} \). Эти результаты сохраняются, пока граф переходов \ (G ({\ mathscr {B}}) \) связан, даже если \ ({\ mathscr {B}} \) состоит только из двух почти идентичных оснований, так что соответствующие наблюдаемые являются только слабо несовместимыми, что определяется количественно коммутатором или устойчивостью к несовместимости 36,37,38 .
Теорема 1 устанавливает простую и точную связь между нулевой неопределенностью и максимальной запутанностью, которая не зависит от конкретной неопределенности и мер запутанности. Эта связь предлагает свежий взгляд на понимание принципа неопределенности при наличии квантовой памяти 8 . Это также может пролить свет на взаимодополняемость неопределенности и реальности, учитывая тесную связь между обозначениями неопределенности и реальности 7,30,31,32 .
ZUS относительно приводимых базисных наборов
Затем мы определяем ZUS относительно приводимых базисов \ ({\ mathscr {B}} \).
Теорема 2 Предположим, что \ ({\ mathscr {B}} \) – это набор ортонормированных базисов в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \) и имеет g неприводимых компонентов с компонентными подпространствами \ ({{\ mathcal {H}}} _ {{\ rm {A}}, a} \) , компонентные проекторы P a , и ранги компонентов r a для = 1 , 2 , … , г. Пусть ρ – двудольное состояние на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) и \ (\ rho_a = (P_a \ otimes 1_B) \ rho (P_a \ otimes 1_B) \) .Тогда ρ является ZUS относительно \ ({\ mathscr {B}} \) , если выполняются следующие три условия: r a ≤ d B всякий раз, когда \ (\ mathrm {tr} \, ({\ rho} _ {a})> 0 \) ; каждый ρ a с \ (\ mathrm {tr} \, ({\ rho} _ {a})> 0 \) является (субнормализованным) MES на \ ({{\ mathcal { H}}} _ {{\ rm {A}}, a} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) ; все \ ({\ mathrm {tr} \,} _ {{\ rm {A}}} ({\ rho} _ {a}) \) имеют взаимно ортогональные опоры .{a} \) и, кроме того, все \ ({\ mathrm {tr} \,} _ {{\ rm {A}}} ({\ rho} _ {a}) \) имеют взаимно ортогональные опоры. Обратите внимание, что согласованность между различными подпространствами компонентов бесполезна для построения ZUS. Кроме того, размер d B из \ ({{\ mathcal {H}}} _ {{\ rm {B}}}}) должен удовлетворять \ ({d} _ {{\ rm {B}) }} \ ge {r} _ {\ min} \) для построения ZUS, где \ ({r} _ {\ min} = \ mathop {\ min} \ nolimits_ {1 \ le a \ le g} {r} _ {a} \) – минимальный ранг компонента. Когда нижняя граница насыщена, каждый ZUS является чистым MES на \ ({{\ mathcal {H}}} _ {{\ rm {A}}, a} \ otimes {{\ mathcal {H}}} _ { {\ rm {B}}} \), где \ ({{\ mathcal {H}}} _ {{\ rm {A}}, a} \) – компонентное подпространство размерности \ ({r} _ { \ min} \).Кроме того, \ ({r} _ {\ min} \) определяет минимальную запутанность, необходимую для построения ZUS, как показано в разделе “Методы”.
В случае чистых состояний ZUS допускают гораздо более простую характеризацию, как показано в следующем следствии.
Следствие 2 Двудольное чистое состояние \ (\ left | {{\ Psi}} \ right \ rangle \) в \ ({{\ mathcal {H}}} _ {{\ rm {A }}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) является ZUS по отношению к \ ({\ mathscr {B}} \) , если и только если сокращенное состояние ρ A – это взвешенная сумма компонентных проекторов в \ ({\ mathscr {P}} ({\ mathscr {B}}) \).
Следствие 2 является частным случаем теоремы 2 и также следует из леммы 2 и дополнительной леммы 2. Здесь ρ A является взвешенной суммой компонентных проекторов тогда и только тогда, когда ρ A диагонально относительно каждого базиса. \ ({\ mathcal {B}} \) в \ ({\ mathscr {B}} \) (см. дополнительное примечание C). Как следствие следствия 2, приведенное состояние ρ A любого (чистого или смешанного) ZUS ρ относительно \ ({\ mathscr {B}} \) является взвешенной суммой компонентных проекторов в \ ({\ mathscr {P}} ({\ mathscr {B}}) \), учитывая, что любой ZUS является выпуклой смесью чистых ZUS.{{d} _ {{\ rm {A}}} – 1} \ left | jj \ right \ rangle / \ sqrt {{d} _ {{\ rm {A}}}} \) таким образом: Боб сначала создает MES в своей лаборатории, а затем отправляет одну частицу запутанной пары Алисе через квантовый канал. Чтобы проверить результирующее состояние ρ , они могут выполнять тесты на основе коррелированных локальных проективных измерений, так что только целевое состояние может пройти все тесты с уверенностью 39,40,41,42,43 . {m} \) в котором \ ({{\ mathcal {B}}} _ {x} \) выбрано с вероятностью μ x > 0.{*} \ right | $$
(8)
– тестовый проектор. Обратите внимание, что \ (\ left | {{\ Phi}} \ right \ rangle \) является собственным состоянием \ (P ({{\ mathcal {B}}} _ {x}) \) и Ω с собственным значением 1, и поэтому может с уверенностью пройти каждое испытание. Кроме того, \ (\ left | {{\ Phi}} \ right \ rangle \) можно надежно проверить с помощью этого протокола, если и только если максимальное собственное значение Ω невырождено, то есть проходное собственное подпространство Ω имеет размерность 1 40, 41,42,43 . Это так, если и только если базисный набор \ ({\ mathscr {B}} \) неприводим по следующей теореме, доказанной в дополнительной информации.{m} {\ mu} _ {x} = 1 \) . Тогда вырождение максимального собственного значения 1 Ω равно количеству компонент связности графа переходов \ (G ({\ mathscr {B}}) \) . Это собственное значение невырождено тогда и только тогда, когда базис \ ({\ mathscr {B}} \) неприводим .
Затем предположим, что Боб нечестен. Тогда Алиса не сможет различать состояния, эквивалентные локальным операциям Боба. Тем не менее, она все еще может проверить MES \ (\ left | {{\ Phi}} \ right \ rangle \) с точностью до эквивалентности.Благодаря теореме 1 описанная ранее игра в неопределенность фактически обеспечивает протокол проверки всякий раз, когда базисный набор \ ({\ mathscr {B}} \) Алисы неприводим. Обратите внимание, что Боб может пройти каждый тест (угадать каждый результат измерения) Алисы с уверенностью, только если подготовленное состояние ρ является MES. Удивительно, но требования к базам измерения Алисы остаются неизменными, когда Боб становится нечестным. Кроме того, измерения Боба, необходимые для достижения максимальной вероятности угадывания, по существу однозначно определяются аналогом Алисы.{*} \) с вероятностью μ x > 0 для x = 1, 2,…, m и вернуть результат. Затем Алиса выполняет проективное измерение на \ ({{\ mathcal {B}}} _ {x} \ in {\ mathscr {B}} \), и тест считается пройденным, если она получает тот же результат, что и Боб. В качестве альтернативы Алиса может выбрать POVM с двумя исходами \ (\ {\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right |, {1} _ { {\ rm {A}}} – \ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | \} \), если Боб получает результат k .{*} \). Тогда вероятность того, что Боб пройдет тест, составляет
$$ \ sum _ {k} \ left \ langle {\ psi} _ {xk} \ right | {\ sigma} _ {xk} \ left | {\ psi} _ {xk} \ right \ rangle, \ quad {\ sigma} _ {xk} = {\ mathrm {tr}} _ {{\ rm {B}}} [\ rho ({1} _ {{\ rm {A }}} \ otimes \ Pi_ {xk})], $$
(9)
, который является вариантом уравнения. (2). Субнормализованные состояния σ x k удовлетворяют условию нормализации ∑ k σ x k = ρ A ансамбля и образуют ρ A для каждого x . {m} \) с \ ({{\ mathcal {B}}} _ {x} = {\ {\ left | {\ psi} _ {xk} \ right \ rangle \}} _ {k} \) – это неприводимый набор ортонормированных базисов в . \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \) .Предположим \ ({\ {{\ {{\ sigma} _ {xk} \}} _ {k} \}} _ {x} \) – сборка для ρ А , что удовлетворяет \ ({\ sum} _ {k} \ left \ langle {\ psi} _ {xk} \ right | {\ sigma} _ {xk} \ left | {\ psi} _ {xk} \ right \ rangle = 1 \) для каждого x. Тогда ρ А полностью перемешан, а \ ({\ sigma} _ {xk} = \ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | / {d} _ {{\ rm {A}}} \) для каждого x и k.
Здесь условие \ ({\ sum} _ {k} \ left \ langle {\ psi} _ {xk} \ right | {\ sigma} _ {xk} \ left | {\ psi} _ {xk} \ right \ rangle = 1 \) означает, что сборка \ ({\ {{\ {{\ sigma} _ {xk} \}} _ {k} \}} _ {x} \) может с уверенностью пройти каждый тест Алисы . В силу теоремы 1 мы можем далее показать, что совокупность \ ({\ {{\ {\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | / {d} _ {{\ rm {A}}} \}} _ {k} \}} _ {x} \) может быть сгенерировано только MES, как указано в следующей теореме и доказано в Дополнительной Информация.
Теорема 4 Учитывая базис \ ({\ mathscr {B}} \) в лемме 3, предположим, что ρ – двудольное состояние на \ ({{\ mathcal {H}}} _ {{ \ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) , который может генерировать сборку \ ({\ {{\ {\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | / {d} _ {{\ rm {A}}} \}} _ {k} \}} _ {x} \) по замерам Боба. Тогда d B ≥ d A , а ρ – MES и ZUS по отношению к \ ({\ mathscr {B}} \).
Благодаря лемме 3 и теореме 4 тесты Алисы могут проверять совокупность \ ({\ {{\ {\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | / {d} _ {{\ rm {A}}} \}} _ {k} \}} _ {x} \), который, в свою очередь, может проверять MES всякий раз, когда \ ({\ mathscr {B}} \) неприводимо. Кроме того, теорема 4 предлагает общий рецепт построения ансамблей, характерных для MES. Эти результаты устанавливают тесную связь между соотношениями неопределенностей, квантовой запутанностью и квантовым управлением, которые представляют внутренний интерес для фундаментальных исследований.Между тем, эти результаты поучительны для изучения подготовки удаленного состояния 21,22 и полу-аппаратно-независимого самотестирования 18,23,24,25,26 .
Состояния с нулевой неопределенностью при наличии квантовой памяти
Максимально запутанные состояния
Чтобы установить наши основные результаты, сначала нам нужно лучше понять MES. Двудольное состояние ρ в гильбертовом пространстве \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}) }} \) размерности d A × d B является MES, если мы можем создать каждое состояние на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) от до локальными операциями и классической связью (LOCC) 27 .{{d} _ {{\ rm {B}}} – 1} \) являются вычислительными базами \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \) и \ ( {{\ mathcal {H}}} _ {{\ rm {B}}} \) соответственно. MES не обязательно является чистым, как поясняется в следующей лемме, по существу доказанной в ref. 28 ; см. дополнительную информацию для независимого доказательства.
Лемма 1 Пусть ρ – двудольное состояние на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{ \ rm {B}}} \) с d A ≤ d B .Тогда следующие утверждения эквивалентны .
Здесь H (A∣B) ρ = S ( ρ ) – S ( ρ B ) – условная энтропия A для данного B, где S ( ρ ) и S ( ρ B ) – энтропии фон Неймана ρ и \ ({\ rho} _ {{\ rm {B}}}: = {\ mathrm {tr }} _ {{\ rm {A}}} (\ rho) \) соответственно. {\ prime}} \) будет поддержкой ρ В .{\ prime} \ right \ rangle \) является чистым MES в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{ {\ rm {B}}} _ {1}} \), а τ – оператор плотности полного ранга на \ ({{\ mathcal {H}}} _ {{{\ rm {B}}} _ {2}} \). Таким образом, все MES на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) эквивалентны под локальными операциями Боба.
Следствие 1 Все MES на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B }}} \) с d A ≤ d B могут быть преобразованы друг в друга локальными операциями на \ ({{\ mathcal {H}}} _ {{\ rm { B}}} \) .{m} \). Тогда прогнозирование результата O x сводится к прогнозированию результата проективного измерения на основе \ ({{\ mathcal {B}}} _ {x} \). Когда эти наблюдаемые несовместимы (не коммутируют друг с другом), в целом Боб не может с уверенностью предсказать результат измерения, даже если он знает полное классическое описание состояния системы, которое характеризуется матрицей плотности ρ A . { 2} \).
Ситуация иная, если Боб имеет квантовую память с гильбертовым пространством \ ({{\ mathcal {H}}} _ {{\ rm {B}}}}) и может создать запутанное состояние ρ на суставе system \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \), как показано на Рис. . 1. Предположим, Алиса выбирает базис \ ({{\ mathcal {B}}} _ {x} \) (observable O x ), тогда Боб может выполнить обобщенное измерение, характеризуемое положительным оператором – оценочная мера (POVM) \ ({\ {{{{\ Pi}}} _ {xk} \}} _ {k} \) в его подсистеме \ ({{\ mathcal {H}}} _ {{\ rm {B}}} \), где Π x k соответствует угадыванию результата k с учетом базы измерения \ ({\ mathcal {B}}} _ {x} \) Алисы.Средняя вероятность успеха составляет ∑ x p x / m с
$$ {p} _ {x} = \ sum _ {k} {\ mathrm {tr}} \, [\ rho (\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | \ otimes \ Pi_ {xk})] = \ sum _ { k} {\ mathrm {tr}} \, ({\ rho} _ {xk} \ Pi_ {xk}), $$
(2)
, где \ ({\ rho} _ {xk} = \ left \ langle {\ psi} _ {xk} \ right | \ rho \ left | {\ psi} _ {xk} \ right \ rangle \) субнормализованы уменьшенные состояния Боба.Обратите внимание, что p x также является вероятностью того, что POVM \ ({\ {{{{\ Pi}}}} _ {xk} \}} _ {k} \) может успешно различить ансамбль состояний
$$ {\ mathscr {S}} (\ rho, {{\ mathcal {B}}} _ {x}) = \ {\ left \ langle \ psi \ right | \ rho \ left | \ psi \ right \ rangle \: \ \ left | \ psi \ right \ rangle \ in {{\ mathcal {B}}} _ {x} \}. $$
(3)
Максимум средней вероятности предположения по всем POVM может быть определен с помощью полуопределенного программирования, и этот максимум определяется состоянием ρ и базисным набором \ ({\ mathscr {B}} \) (или наблюдаемым набором \ ({\ mathscr {O}} \)) Алисы.
Рис. 1: Связь между нулевой неопределенностью и максимальной запутанностью в игре на неопределенность.Выполняя подходящие измерения (в зависимости от наблюдаемых Алисой) своей квантовой памяти, Боб может лучше предсказать результаты измерений Алисы. {m} \) для Алисы совместное состояние ρ Алисы и Боба является ZUS, если Боб может с уверенностью предсказать результат измерения Алисы с помощью подходящего измерения в зависимости от выбора Алисы.Учитывая ZUS, вероятность угадывания p x для каждого измерения Алисы может достигать максимума 1, а условная энтропия H ( O x B) равна 0. Напротив. с минимальными состояниями неопределенности и интеллектуальными состояниями 14,15,16 , ZUS не только минимизируют неопределенность, но также полностью устраняют неопределенность. Более того, здесь определение не зависит от какой-либо конкретной меры неопределенности.
Чтобы оценить важность запутанности для построения ZUS, рассмотрим пример с двумя наблюдаемыми, в этом случае отношение неопределенности в уравнении.{-1}) + H {({\ rm {A}} | {\ rm {B}})} _ {\ rho}. $$
(4)
Здесь условная энтропия H (A∣B) ρ показывает влияние запутанности на уменьшение неопределенности. { -1}), $$
(5)
, где второй получен в исх.{2} = 1 / {d} _ {{\ rm {A}}} \) для всех j , k 35 . Тогда у нас есть c = 1/ d A и
$$ {E} _ {{\ rm {F}}} (\ rho) = {E} _ {{\ rm {R}} } (\ rho) = – H {({\ rm {A}} | {\ rm {B}})} _ {\ rho} = {\ mathrm {log} \,} _ {2} {d} _ {{\ rm {A}}}, $$
(6)
, что означает, что d B ≥ d A и ρ является MES по лемме 1, и в этом случае ρ действительно является ZUS.К сожалению, это рассуждение в целом не работает. Чтобы решить эту проблему, нам нужен совершенно другой образ мышления.
Ключевые наблюдения о ZUS
Боб может предсказать результат измерения на основе \ ({\ mathcal {B}}} _ {x} \) с уверенностью, если и только если ансамбль \ ({\ mathscr {S}} (\ rho, {{\ mathcal {B}}} _ {x}) \), определенный в уравнении. (3) отлично различимо, то есть все состояния в \ ({\ mathscr {S}} (\ rho, {{\ mathcal {B}}} _ {x}) \) имеют взаимно ортогональные опоры. {m} \) тогда и только тогда, когда каждый ансамбль \ ({\ mathscr {S}} (\ rho, {{\ mathcal {B}}} _ {x}) \) отлично различим.Следующие три предложения являются простыми следствиями этих наблюдений.
Предложение 1 Предположим, что ρ – это ZUS, тогда любое состояние, поддерживаемое при поддержке ρ, является ZUS .
Предложение 2 Предположим, что ρ 1 и ρ 2 – это два ZUS на \ ({{\ mathcal {H}}} _ {{\ rm {A}}) } \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) . Если \ ({\ mathrm {tr} \,} _ {{\ rm {A}}} ({\ rho} _ {1}) \) и \ ({\ mathrm {tr} \,} _ {{\ rm {A}}} ({\ rho} _ {2}) \) имеют ортогональные опоры, тогда любая выпуклая смесь ρ 1 и ρ 2 является ZUS .
Предложение 3 Предположим, что ρ – двудольное состояние на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) и Λ – это полностью положительное и сохраняющее след (CPTP) отображение (квантовый канал) из системы B в систему \ (\ tilde {{\ rm {B}}}} \) . Тогда ρ является ZUS, если (1 \ (\ otimes \) Λ ) (ρ) равно .
Здесь предложения 1 и 2 связаны с тем фактом, что смесь квантовых состояний может только уменьшить различимость, если у приведенных состояний Боба нет ортогональных носителей.Предложение 3 следует из того простого факта, что квантовые операции не могут улучшить различимость. Два состояния ρ 1 и ρ 2 на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ { {\ rm {B}}} \) эквивалентны, если они могут быть превращены друг в друга локальными операциями над \ ({{\ mathcal {H}}} _ {{\ rm {B}}} \). В этом случае ρ 1 является ZUS по отношению к \ ({\ mathscr {B}} \), если ρ 2 является. В соответствии с этими локальными операциями ZUS делятся на эквивалентные классы.{m} \) в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \), нам сначала нужно точно определить ключевое свойство базисного набора. Граф переходов \ (G ({\ mathscr {B}}) \) из \ ({\ mathscr {B}} \) представляет собой -дробный граф размером м с м d A вершин, которые являются во взаимно однозначном соответствии с состояниями базиса (одинаковые состояния в разных базах соответствуют разным вершинам). Две разные вершины являются смежными, если соответствующие состояния не ортогональны, то есть вероятность перехода между двумя состояниями отлична от нуля.Граф \ (G ({\ mathscr {B}}) \) кодирует структуру несовместимости базисного набора \ ({\ mathscr {B}} \), которая имеет решающее значение для изучения ZUS и квантовой проверки, как мы увидим ниже. потом.
Базисный набор \ ({\ mathscr {B}} \) неприводим, если граф переходов \ (G ({\ mathscr {B}}) \) связан, и в этом случае проекторы на базисные состояния генерируют все операторная алгебра на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \). Любой базисный набор, состоящий из m ≥ 2 взаимно несмещенных базисов (или общих случайных баз), является неприводимым, поскольку граф переходов представляет собой полный m -раздельный граф, как показано на рис.2.
Рис. 2: Граф переходов трех взаимно несмещенных базисов для кубита, который соответствует собственным базам трех матриц Паули.Две вершины одного цвета связаны с двумя состояниями в одном базисе. Этот граф переходов связан, поэтому соответствующий базис неприводим.
Базисный набор \ ({\ mathscr {B}} \) приводим, если граф переходов \ (G ({\ mathscr {B}}) \) не связан. В этом случае базисный набор можно рассматривать как прямую сумму базисных наборов, определенных на меньших подпространствах.{m} \) неприводимо для \ ({{\ mathcal {H}}} _ {{\ rm {A}}, a} \).
Соедините ZUS с MES
Теперь мы готовы представить наши основные результаты по ZUS и MES, как показано на рис. 1. Во-первых, мы проясним, когда Боб может предсказать результат одного проективного измерения Алисы. Следующая лемма, доказанная в дополнительной информации, является ступенькой к пониманию ZUS при наличии квантовой памяти.
Лемма 2 Предположим, что \ (\ rho = \ left | {{\ Psi}} \ right \ rangle \ left \ langle {{\ Psi}} \ right | \) является двудольным чистым состоянием на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) и \ ({ \ mathcal {B}} \) является ортонормированной базой для \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \) .Тогда ансамбль \ ({\ mathscr {S}} (\ rho, {\ mathcal {B}}) \) отлично различим тогда и только тогда, когда \ ({\ mathcal {B}} \) является собственным основанием \ ({\ rho} _ {{\ rm {A}}} = {\ mathrm {tr} \,} _ {{\ rm {B}}} (\ rho) \).
Обратите внимание, что Боб может предсказать результат измерения Алисы на основе \ ({\ mathcal {B}} \) с уверенностью, если и только если ансамбль \ ({\ mathscr {S}} (\ rho, {\ mathcal {B}) }) \), определенные в формуле. (3) отлично различимы. По лемме 2 это так, если и только если ρ A диагональна относительно базиса \ ({\ mathcal {B}} \).Следовательно, чистое состояние ρ является ZUS относительно базисного набора \ ({\ mathscr {B}} \) тогда и только тогда, когда ρ A диагонально относительно каждого базиса в \ ({\ mathscr {B }} \). Когда \ ({\ mathscr {B}} \) неприводимо, оказывается, только MES могут удовлетворять этому условию. Основываясь на этом наблюдении, мы можем вывести следующую теорему, доказанную в дополнительной информации.
Теорема 1 Предположим, что \ ({\ mathscr {B}} \) – неприводимый базис в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ ) .Тогда двудольное (чистое или смешанное) состояние ρ на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm { B}}} \) является ZUS по отношению к \ ({\ mathscr {B}} \) iff d B ≥ d A и ρ является MES .
По теореме 1 и лемме 1 каждый ZUS относительно \ ({\ mathscr {B}} \) является тензорным произведением чистого MES и вспомогательного состояния. Кроме того, для достижения нулевой неопределенности измерения Боба на опоре B однозначно определяются аналогом Алисы, как показано в дополнительном примечании E.Все ZUS относительно \ ({\ mathscr {B}} \) могут быть превращены друг в друга локальными операциями над \ ({{\ mathcal {H}}} _ {{\ rm {B}}} \) и таким образом образуют единый эквивалентный класс. Если d A ≤ d B <2 d A , то все ZUS чистые и могут быть превращены друг в друга с помощью унитарных преобразований на \ ({{\ mathcal {H}}} _ {{\ rm {B}}} \). Эти результаты сохраняются, пока граф переходов \ (G ({\ mathscr {B}}) \) связан, даже если \ ({\ mathscr {B}} \) состоит только из двух почти идентичных оснований, так что соответствующие наблюдаемые являются только слабо несовместимыми, что определяется количественно коммутатором или устойчивостью к несовместимости 36,37,38 .
Теорема 1 устанавливает простую и точную связь между нулевой неопределенностью и максимальной запутанностью, которая не зависит от конкретной неопределенности и мер запутанности. Эта связь предлагает свежий взгляд на понимание принципа неопределенности при наличии квантовой памяти 8 . Это также может пролить свет на взаимодополняемость неопределенности и реальности, учитывая тесную связь между обозначениями неопределенности и реальности 7,30,31,32 .
ZUS относительно приводимых базисных наборов
Затем мы определяем ZUS относительно приводимых базисов \ ({\ mathscr {B}} \).
Теорема 2 Предположим, что \ ({\ mathscr {B}} \) – это набор ортонормированных базисов в \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \) и имеет g неприводимых компонентов с компонентными подпространствами \ ({{\ mathcal {H}}} _ {{\ rm {A}}, a} \) , компонентные проекторы P a , и ранги компонентов r a для = 1 , 2 , … , г. Пусть ρ – двудольное состояние на \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) и \ (\ rho_a = (P_a \ otimes 1_B) \ rho (P_a \ otimes 1_B) \) .Тогда ρ является ZUS относительно \ ({\ mathscr {B}} \) , если выполняются следующие три условия: r a ≤ d B всякий раз, когда \ (\ mathrm {tr} \, ({\ rho} _ {a})> 0 \) ; каждый ρ a с \ (\ mathrm {tr} \, ({\ rho} _ {a})> 0 \) является (субнормализованным) MES на \ ({{\ mathcal { H}}} _ {{\ rm {A}}, a} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) ; все \ ({\ mathrm {tr} \,} _ {{\ rm {A}}} ({\ rho} _ {a}) \) имеют взаимно ортогональные опоры .{a} \) и, кроме того, все \ ({\ mathrm {tr} \,} _ {{\ rm {A}}} ({\ rho} _ {a}) \) имеют взаимно ортогональные опоры. Обратите внимание, что согласованность между различными подпространствами компонентов бесполезна для построения ZUS. Кроме того, размер d B из \ ({{\ mathcal {H}}} _ {{\ rm {B}}}}) должен удовлетворять \ ({d} _ {{\ rm {B}) }} \ ge {r} _ {\ min} \) для построения ZUS, где \ ({r} _ {\ min} = \ mathop {\ min} \ nolimits_ {1 \ le a \ le g} {r} _ {a} \) – минимальный ранг компонента. Когда нижняя граница насыщена, каждый ZUS является чистым MES на \ ({{\ mathcal {H}}} _ {{\ rm {A}}, a} \ otimes {{\ mathcal {H}}} _ { {\ rm {B}}} \), где \ ({{\ mathcal {H}}} _ {{\ rm {A}}, a} \) – компонентное подпространство размерности \ ({r} _ { \ min} \).Кроме того, \ ({r} _ {\ min} \) определяет минимальную запутанность, необходимую для построения ZUS, как показано в разделе “Методы”.
В случае чистых состояний ZUS допускают гораздо более простую характеризацию, как показано в следующем следствии.
Следствие 2 Двудольное чистое состояние \ (\ left | {{\ Psi}} \ right \ rangle \) в \ ({{\ mathcal {H}}} _ {{\ rm {A }}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) является ZUS по отношению к \ ({\ mathscr {B}} \) , если и только если сокращенное состояние ρ A – это взвешенная сумма компонентных проекторов в \ ({\ mathscr {P}} ({\ mathscr {B}}) \).
Следствие 2 является частным случаем теоремы 2 и также следует из леммы 2 и дополнительной леммы 2. Здесь ρ A является взвешенной суммой компонентных проекторов тогда и только тогда, когда ρ A диагонально относительно каждого базиса. \ ({\ mathcal {B}} \) в \ ({\ mathscr {B}} \) (см. дополнительное примечание C). Как следствие следствия 2, приведенное состояние ρ A любого (чистого или смешанного) ZUS ρ относительно \ ({\ mathscr {B}} \) является взвешенной суммой компонентных проекторов в \ ({\ mathscr {P}} ({\ mathscr {B}}) \), учитывая, что любой ZUS является выпуклой смесью чистых ZUS.{{d} _ {{\ rm {A}}} – 1} \ left | jj \ right \ rangle / \ sqrt {{d} _ {{\ rm {A}}}} \) таким образом: Боб сначала создает MES в своей лаборатории, а затем отправляет одну частицу запутанной пары Алисе через квантовый канал. Чтобы проверить результирующее состояние ρ , они могут выполнять тесты на основе коррелированных локальных проективных измерений, так что только целевое состояние может пройти все тесты с уверенностью 39,40,41,42,43 . {m} \) в котором \ ({{\ mathcal {B}}} _ {x} \) выбрано с вероятностью μ x > 0.{*} \ right | $$
(8)
– тестовый проектор. Обратите внимание, что \ (\ left | {{\ Phi}} \ right \ rangle \) является собственным состоянием \ (P ({{\ mathcal {B}}} _ {x}) \) и Ω с собственным значением 1, и поэтому может с уверенностью пройти каждое испытание. Кроме того, \ (\ left | {{\ Phi}} \ right \ rangle \) можно надежно проверить с помощью этого протокола, если и только если максимальное собственное значение Ω невырождено, то есть проходное собственное подпространство Ω имеет размерность 1 40, 41,42,43 . Это так, если и только если базисный набор \ ({\ mathscr {B}} \) неприводим по следующей теореме, доказанной в дополнительной информации.{m} {\ mu} _ {x} = 1 \) . Тогда вырождение максимального собственного значения 1 Ω равно количеству компонент связности графа переходов \ (G ({\ mathscr {B}}) \) . Это собственное значение невырождено тогда и только тогда, когда базис \ ({\ mathscr {B}} \) неприводим .
Затем предположим, что Боб нечестен. Тогда Алиса не сможет различать состояния, эквивалентные локальным операциям Боба. Тем не менее, она все еще может проверить MES \ (\ left | {{\ Phi}} \ right \ rangle \) с точностью до эквивалентности.Благодаря теореме 1 описанная ранее игра в неопределенность фактически обеспечивает протокол проверки всякий раз, когда базисный набор \ ({\ mathscr {B}} \) Алисы неприводим. Обратите внимание, что Боб может пройти каждый тест (угадать каждый результат измерения) Алисы с уверенностью, только если подготовленное состояние ρ является MES. Удивительно, но требования к базам измерения Алисы остаются неизменными, когда Боб становится нечестным. Кроме того, измерения Боба, необходимые для достижения максимальной вероятности угадывания, по существу однозначно определяются аналогом Алисы.{*} \) с вероятностью μ x > 0 для x = 1, 2,…, m и вернуть результат. Затем Алиса выполняет проективное измерение на \ ({{\ mathcal {B}}} _ {x} \ in {\ mathscr {B}} \), и тест считается пройденным, если она получает тот же результат, что и Боб. В качестве альтернативы Алиса может выбрать POVM с двумя исходами \ (\ {\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right |, {1} _ { {\ rm {A}}} – \ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | \} \), если Боб получает результат k .{*} \). Тогда вероятность того, что Боб пройдет тест, составляет
$$ \ sum _ {k} \ left \ langle {\ psi} _ {xk} \ right | {\ sigma} _ {xk} \ left | {\ psi} _ {xk} \ right \ rangle, \ quad {\ sigma} _ {xk} = {\ mathrm {tr}} _ {{\ rm {B}}} [\ rho ({1} _ {{\ rm {A }}} \ otimes \ Pi_ {xk})], $$
(9)
, который является вариантом уравнения. (2). Субнормализованные состояния σ x k удовлетворяют условию нормализации ∑ k σ x k = ρ A ансамбля и образуют ρ A для каждого x . {m} \) с \ ({{\ mathcal {B}}} _ {x} = {\ {\ left | {\ psi} _ {xk} \ right \ rangle \}} _ {k} \) – это неприводимый набор ортонормированных базисов в . \ ({{\ mathcal {H}}} _ {{\ rm {A}}} \) .Предположим \ ({\ {{\ {{\ sigma} _ {xk} \}} _ {k} \}} _ {x} \) – сборка для ρ А , что удовлетворяет \ ({\ sum} _ {k} \ left \ langle {\ psi} _ {xk} \ right | {\ sigma} _ {xk} \ left | {\ psi} _ {xk} \ right \ rangle = 1 \) для каждого x. Тогда ρ А полностью перемешан, а \ ({\ sigma} _ {xk} = \ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | / {d} _ {{\ rm {A}}} \) для каждого x и k.
Здесь условие \ ({\ sum} _ {k} \ left \ langle {\ psi} _ {xk} \ right | {\ sigma} _ {xk} \ left | {\ psi} _ {xk} \ right \ rangle = 1 \) означает, что сборка \ ({\ {{\ {{\ sigma} _ {xk} \}} _ {k} \}} _ {x} \) может с уверенностью пройти каждый тест Алисы . В силу теоремы 1 мы можем далее показать, что совокупность \ ({\ {{\ {\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | / {d} _ {{\ rm {A}}} \}} _ {k} \}} _ {x} \) может быть сгенерировано только MES, как указано в следующей теореме и доказано в Дополнительной Информация.
Теорема 4 Учитывая базис \ ({\ mathscr {B}} \) в лемме 3, предположим, что ρ – двудольное состояние на \ ({{\ mathcal {H}}} _ {{ \ rm {A}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {B}}} \) , который может генерировать сборку \ ({\ {{\ {\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | / {d} _ {{\ rm {A}}} \}} _ {k} \}} _ {x} \) по замерам Боба. Тогда d B ≥ d A , а ρ – MES и ZUS по отношению к \ ({\ mathscr {B}} \).
Благодаря лемме 3 и теореме 4 тесты Алисы могут проверять совокупность \ ({\ {{\ {\ left | {\ psi} _ {xk} \ right \ rangle \ left \ langle {\ psi} _ {xk} \ right | / {d} _ {{\ rm {A}}} \}} _ {k} \}} _ {x} \), который, в свою очередь, может проверять MES всякий раз, когда \ ({\ mathscr {B}} \) неприводимо. b [/ latex] (где « b » – целое число, а « a » – любое действительное число), например [латекс] 6 .{23} [/ латекс].
Ключевые термины
- Научная нотация : способ записи чисел, которые слишком велики или слишком малы для удобной записи в стандартной форме.
- целое число : элемент бесконечного числового множества {…, -3, -2, -1,0,1,2,3,…}.
- Порядок величины : Порядок величины – это класс масштаба или величины любой величины, где каждый класс содержит значения фиксированного отношения к предшествующему ему классу.b [/ latex] (где « b » – целое число, а « a » – любое действительное число). При записи в научных обозначениях включайте только значащие цифры в действительное число, « a ». Важные цифры представлены в другом разделе.
Чтобы выразить число в экспоненциальном представлении, вы перемещаете десятичный разряд вправо, если число меньше нуля, или влево, если число больше нуля. Например, в 456000 десятичная дробь находится после последнего нуля, поэтому, чтобы выразить это в научных обозначениях, вам нужно будет переместить десятичную дробь между 4 и 5.5 [/ латекс]. Имейте в виду, что нули не включаются в « a », потому что они не являются значащими цифрами.
Для перехода между экспоненциальным представлением и десятичными дробями десятичная точка перемещается на количество пробелов, указанное экспонентой. Отрицательная экспонента говорит вам переместить десятичную запятую вправо, а положительная экспонента говорит вам, что нужно переместить ее влево.
Научная нотация: Введение – YouTube : Научитесь преобразовывать числа в научную систему и обратно.Научная запись – это способ выразить очень большие и очень маленькие числа с показателем степени десяти. Его также иногда называют экспоненциальной записью. Это видео включает в себя объяснение и руководство, а также практические примеры и примеры задач.
Примеры научного обозначения:
- 0,0001 = 1 x 10 -4
- 0,0256 = 2,56 x 10 -2
- 4759000 = 4,759 x 10 6
- 5000 = 5 x 10 3
Другой способ записать это выражение, которое можно увидеть на калькуляторах и компьютерных программах, – использовать E для представления «умноженного на десять в степени.Пример показан здесь:
Научная запись для числа Авогадро : Вот пример научной записи на калькуляторе. 6.02E23 означает то же самое, что и 6.02 x 10 23 .
Научная нотация позволяет проводить сравнения между порядками величин. Как видно выше, в научных обозначениях используется основание 10, и если одно число на порядок больше другого, оно в 10 раз больше. Например, 4,759 x 10 6 на 3 порядка больше, чем 5 x 10 3 ; она на 8 порядков больше 2.{-5} [/ латекс]
Основные операции : Основные операции, такие как умножение и сложение, выполняются так же, как и с экспонентами.
значащие цифры
Значащие цифры – это цифры, которые влияют на точность числа.
Цели обучения
Применять знание значащих цифр в научных расчетах
Ключевые выводы
Ключевые моменты
- Значащие цифры – это любые ненулевые цифры или нули в ловушке.Они не включают нули в начале и в конце.
- При переходе между десятичным и научным представлением поддерживайте одинаковое количество значащих цифр.
- Окончательный ответ в задаче умножения или деления должен содержать то же количество значащих цифр, что и исходное число с наименьшим количеством значащих цифр.
- В дополнение к вычитанию окончательный ответ должен содержать то же количество десятичных знаков, что и исходное число с наименьшим количеством десятичных знаков.
Ключевые термины
- Значащие цифры : Цифры, которые несут значение числа и способствуют его точности.
Пи : Этот калькулятор показывает восемь значащих цифр числа Пи.
Значащие цифры числа – это цифры, которые влияют на точность этого числа. Числа, которые не вносят никакой точности и не должны считаться значимыми:
- начальные или конечные нули (это заполнители)
- цифра, которые вводятся в результате вычислений, которые придают числу большую точность, чем позволяют исходные данные.
Правила определения значимости числа
- Все ненулевые цифры считаются значащими. Например, у 91 две значащие цифры (9 и 1), а у 123,45 пять значащих цифр (1, 2, 3, 4 и 5).
- Нули, появляющиеся между двумя ненулевыми цифрами (захваченные нули), имеют значение. Пример: 101.12 имеет пять значащих цифр: 1, 0, 1, 1 и 2.
- Начальные нули (нули перед ненулевыми числами) не имеют значения.Например, 0,00052 состоит из двух значащих цифр: 5 и 2.
- Завершающие нули (нули после ненулевых чисел) в числе без десятичной дроби обычно не имеют значения (подробнее см. Ниже). Например, у 400 есть только одна значащая цифра (4). Завершающие нули не считаются значимыми.
- Завершающие нули в числе, содержащем десятичную точку, имеют значение. Например, 12.2300 имеет шесть значащих цифр: 1, 2, 2, 3, 0 и 0. Число 0.000122300 по-прежнему имеет только шесть значащих цифр (нули перед 1 не имеют значения).Кроме того, 120.00 состоит из пяти значащих цифр, так как у него три нуля в конце. Это соглашение поясняет точность таких чисел. Например, если измерение с точностью до четырех десятичных разрядов (0,0001) задано как 12,23, то это измерение можно понимать как имеющее только два десятичных знака точности. Указание результата как 12,2300 дает понять, что измерение является точным до четырех десятичных знаков (в данном случае шести значащих цифр).
- У числа 0 одна значащая цифра.Следовательно, любые нули после десятичной точки также имеют значение. Пример: 0.00 состоит из трех значащих цифр.
- Любые числа в экспоненциальном представлении считаются значимыми. Например, 4,300 x 10 -4 имеет 4 значащих цифры.
Условные обозначения, касающиеся значимых цифр
Значение конечных нулей в числе, не содержащем десятичной точки, может быть неоднозначным. Например, не всегда может быть ясно, является ли число вроде 1300 точным с точностью до ближайшей единицы (и просто случайно оказывается точным кратным сотне) или отображается только до ближайшей сотни из-за округления или неопределенности.Для решения этой проблемы существуют различные соглашения:
- Полоса может быть помещена над последней значащей цифрой, показывая, что любые конечные нули, следующие за ней, не имеют значения. Например, 1300 с полосой, помещенной над первым 0, будет иметь три значащих цифры (с полосой, указывающей, что число является точным с точностью до ближайшей десяти).
- Последняя значащая цифра числа может быть подчеркнута; например, «2000» состоит из двух значащих цифр.
- После числа можно поставить десятичную точку.Например, «100». указывает, в частности, что имеются в виду три значащие цифры.
- В сочетании числа и единицы измерения неоднозначности можно избежать, выбрав подходящий префикс единицы измерения. Например, количество значащих цифр в массе, указанной как 1300 г, неоднозначно, в то время как в массе 13 гг или 1,3 кг оно намного яснее.
При преобразовании десятичной формы в экспоненциальную всегда поддерживайте одинаковое количество значащих цифр.Например, 0,00012 состоит из двух значащих цифр, поэтому правильным научным обозначением для этого числа будет 1,2 x 10- 4 .
При умножении и делении чисел количество используемых значащих цифр определяется исходным числом с наименьшим количеством значащих цифр. При сложении и вычитании окончательное число следует округлить до десятичной точки наименее точного числа.
Примеры:
1,423 x 4,2 = 6,0, поскольку 1,423 имеет 4 значащие цифры и 4.2 состоит только из двух значащих цифр, окончательный ответ также должен состоять из двух значащих цифр.
234,67 – 43,5 = 191,2, поскольку 43,5 имеет один десятичный знак, а 234,67 – два десятичных знака, окончательный ответ должен содержать только один десятичный знак.
Другой способ определить сиг-инжир: правила Тихого океана и правила Атлантики
Может быть сложно запомнить все правила, касающиеся значащих цифр и того, является ли каждый ноль значащим или несущественным. Вот еще один способ определения значащих цифр (фиг): правила Тихого и Атлантического океана.
Если в числе присутствует десятичная дробь, используйте тихоокеанское правило (обратите внимание на двойные P). Тихий океан находится слева от Соединенных Штатов, поэтому начните с левой стороны числа. Начните считать сиг-инжир с первого ненулевого числа и продолжайте до конца числа. Например, поскольку в 0,000560 присутствует десятичная дробь, начните с левой стороны числа. Не начинайте считать сиг-инжир до первого ненулевого числа (5), затем считайте до конца числа. Следовательно, в этом номере 3 сиг-инжира (5,6,0).
Если число не имеет десятичной дроби (десятичная дробь отсутствует), используйте атлантическое правило (опять же, обратите внимание на двойные A). Поскольку Атлантический океан находится на правой стороне Соединенных Штатов, начните с правой стороны числа и начните считать сиг-инжир с первого ненулевого числа. Например, поскольку в 2900 нет десятичной дроби, начните с правой стороны числа и начните отсчет подписей с первого ненулевого числа (9). Итак, в этом числе два сиг-инжира (2,9).
Значительные цифры – проще простого! – YouTube : пусть вас не смущают значащие цифры.Это будет иметь смысл с этим видео. В видео представлены значащие числа и обсуждается, как округлить для умножения и деления, используя значащие числа.
Точные числа
Точные числа – это определенные числа или результат подсчета, в отличие от измеренных чисел.
Цели обучения
Распознавать точные и измеренные числа
Ключевые выводы
Ключевые моменты
- В точном числе нет никакой неопределенности.
- Точные числа не могут быть упрощены и имеют бесконечное количество значащих цифр.
- Измеряемые числа имеют ограниченное количество значащих цифр.
Ключевые термины
- Точные числа : Эти числа либо определенные числа, либо результат подсчета. У них бесконечное количество значащих цифр.
Точные числа
Точные числа – это либо определенные числа, либо результат подсчета. Например, дюжина определяется как 12 предметов, а фунт определяется как 16 унций.Точное число может быть выражено только одним способом и не может быть далее упрощено. Точные числа имеют бесконечное количество значащих цифр, но часто встречаются как целые числа.
Точные числа : На этой картинке ровно два стула. Количество стульев считается, а не измеряется, поэтому мы полностью уверены, сколько стульев.
Примеры точных чисел:
- Преобразования в американской системе (например, фунты в унции, количество футов в миле, количество дюймов в футе и т. Д.).
- Преобразование в метрической системе (например, килограммы в граммы, количество метров в километре, количество сантиметров в метре).
- Слова на и процентов означают ровно из одной или ста соответственно.
- Счетные числа точные: на фотографии два стула. На полке пятнадцать книг. Лекцию посетили 87 человек.
Измеренные числа
Напротив, измеряемые числа всегда имеют ограниченное количество значащих цифр.Масса, указанная в 0,5 грамма, должна быть известна с точностью до десятых долей грамма, а не до сотых долей грамма.
Каждый раз, когда вы что-то измеряете, возникает некоторая неопределенность. Например, вес конкретного образца составляет 0,825 г, но на самом деле он может составлять 0,828 г или 0,821 г, потому что здесь присутствует неотъемлемая погрешность. С другой стороны, поскольку точные числа не измеряются, у них нет неопределенности и бесконечного числа значащих цифр.
Измеряемые числа : Масса – это пример измеренного числа.Когда масса указывается как 0,5237 г, как показано на этой шкале, это более точно, чем масса, указанная как 0,5 г.
Примеры измеряемых чисел:
- Диаметр монеты, например 10,2 мм.
- Вес объекта, например 8,887 грамма.
- Длина ручки, например 12 см.
Точность, прецизионность и погрешность
Точность – это насколько близко измеренное значение к истинному значению, тогда как точность выражает воспроизводимость.
Цели обучения
Опишите разницу между точностью и прецизионностью и определите источники ошибок в измерениях
Ключевые выводы
Ключевые моменты
- Точность означает, насколько точно измеренное значение величины соответствует ее «истинному» значению.
- Прецизионность выражает степень воспроизводимости или соответствия между повторными измерениями.
- Чем больше измерений вы сделаете и чем выше точность, тем меньше будет ошибка.
Ключевые термины
- систематическая ошибка : неточность, вызванная дефектами прибора.
- Точность : Степень близости между измерениями величины и ее фактическим (истинным) значением.
- Точность : Также называется воспроизводимостью или повторяемостью, это степень, в которой повторные измерения в неизменных условиях показывают одинаковые результаты.
Точность и прецизионность
Точность – это насколько измерение близко к правильному значению для этого измерения.Точность измерительной системы означает, насколько близко согласие между повторными измерениями (которые повторяются в одних и тех же условиях). Измерения могут быть как точными, так и точными, точными, но не точными, точными, но не точными, или ни тем, ни другим.
Высокая точность, низкая точность : В этом случае все попадания расположены близко к центру, но ни одно не расположено близко друг к другу; это пример точности без точности.
Низкая точность, высокая точность : В этом «яблочко» все попадания расположены близко друг к другу, но не в центре «яблочка»; это пример точности без точности.
Точность иногда разделяют на:
- Повторяемость – отклонение, возникающее, когда прилагаются все усилия для поддержания постоянных условий за счет использования одного и того же инструмента и оператора и повторения измерений в течение короткого периода времени.
- Воспроизводимость – отклонения, возникающие при использовании одного и того же процесса измерения разными приборами и операторами в течение более длительных периодов времени.
Точность и прецизионность – YouTube : это легкое для понимания введение в точность и прецизионность.
Ошибка
Все измерения подвержены ошибкам, что увеличивает неопределенность результата. Ошибки можно классифицировать как ошибку человека или техническую ошибку. Возможно, вы переносите небольшой объем из одной пробирки в другую, но не полностью набираете ее во вторую пробирку, потому что вы ее пролили: это человеческая ошибка.
Техническую ошибку можно разделить на две категории: случайная ошибка и систематическая ошибка. Случайная ошибка, как следует из названия, происходит периодически, без распознавания закономерностей.Систематическая ошибка возникает при неисправности прибора. Например, шкала может быть неправильно откалибрована и показывать 0,5 г, когда на ней ничего нет. Следовательно, все измерения будут завышены на 0,5 г. Если вы не учтете это в своих измерениях, ваше измерение будет содержать некоторую погрешность.
Как точность, точность и ошибка соотносятся друг с другом?
Случайная погрешность будет меньше с более точным прибором (измерения выполняются с меньшими приращениями) и с большей повторяемостью или воспроизводимостью (точностью).Рассмотрим обычный лабораторный эксперимент, в котором вы должны определить процентное содержание кислоты в образце уксуса, наблюдая за объемом раствора гидроксида натрия, необходимым для нейтрализации данного объема уксуса. Вы проводите эксперимент и получаете значение. На всякий случай повторите процедуру с другим идентичным образцом из той же бутылки с уксусом. Если вы действительно проделали это в лаборатории, вы будете знать, что маловероятно, что второе испытание даст тот же результат, что и первое.Фактически, если вы проведете несколько повторных (то есть идентичных во всех отношениях) испытаний, вы, вероятно, получите разрозненные результаты.
Как указано выше, чем больше измерений будет выполнено, тем ближе мы сможем узнать истинное значение величины. С помощью нескольких измерений (повторений) мы можем оценить точность результатов, а затем применить простую статистику, чтобы оценить, насколько близко среднее значение было бы к истинному значению, если бы в системе не было систематической ошибки. Среднее значение меньше отклоняется от «истинного значения» по мере увеличения количества измерений.
Ошибка и процент ошибки – YouTube : Как рассчитать ошибку и процент ошибки.
Измерение с нулевой погрешностью измерения примитивная величина
Новая версия Международного словаря метрологии (далее VIM) [1], в примечании 2 к позиции 2.1 указывает, что понятие «измерение» включает в себя подсчет объектов. Этот факт, хотя и очевидный для некоторых авторов [2, 3], имеет большое значение для настоящих и будущих формулировок текстов, касающихся метрологии, чистой или прикладной.
В книгах и статьях по аналитической химии, клиническим лабораторным наукам или любой другой науке, в которой необходимы измерения (вероятно, все науки), было принято утверждать, что все измерительные системы и, следовательно, все измерения вызывают метрологические ошибки, по крайней мере, случайные.Однако после принятия того, что подсчет является мерой, следует соответствующим образом применить вышеприведенное утверждение.
Таким образом, когда измеряется отдельная величина, имеющая вид величины «количество объектов», и измерения (подсчет) выполняются путем визуального осмотра всей системы (без использования ее выборки), неопределенность измерения равно нулю (пример: результат измерения количества пальцев конкретной руки человека равен 5). Такое разъяснение в статьях или книгах может помочь в международном процессе гармонизации метрологических концепций.
С другой, совершенно иной точки зрения, явное признание того, что понятие «измерение» включает в себя подсчет объектов, как упомянуто выше, может привести к некоторым концептуальным изменениям. В текущей версии VIM указано (в примечании 3 к позиции 1.4), что «количество объектов», которое является основной величиной, связанной с процессом подсчета, «может рассматриваться как базовая величина в любой системе количеств. ». Однако, поскольку определение VIM «базового количества» – это «количество в традиционно выбранном подмножестве данной системы количеств, где никакое количество подмножества не может быть выражено в терминах других», если «количество объектов» рассматривалось как Базовая величина в Международной системе количеств, текущая базовая величина «количество вещества» – количество элементарных объектов [атомов или молекул], деленное на константу Авогадро [4] – будет производной величиной.
Возможно, было бы удобно рассматривать «количество объектов» как «примитивную величину», которую можно было бы определить как «количество, которое выражает количество объектов данного вида в системе, независимо от системы величин, принимаемых во внимание. учетная запись”.
Информация об авторе
Принадлежность
Laboratori Clínic, Hospital Universitari de Bellvitge, 08907 L’Hospitalet de Llobregat, Каталония, Испания
Xavier Fuentes-Arderiu
Корреспондент
Автор для переписки Ксавье Фуэнтес-Ардериу.Об этой статье
Цитируйте эту статью
Fuentes-Arderiu, X. Измерение с нулевой неопределенностью измерения – примитивная величина. Accred Qual Assur 16, 103 (2011). https://doi.org/10.1007/s00769-010-0745-y
Скачать цитату
Поделиться этой статьей
Все, с кем вы поделитесь следующей ссылкой, смогут прочитать это содержание:
Получить ссылкуИзвините, Ссылка для совместного использования в настоящее время недоступна для этой статьи.
Предоставлено инициативой по обмену контентом Springer Nature SharedIt
Ключевые слова
- Визуальный осмотр
- Пояснение
- Неопределенность измерений
- Концептуальное изменение
- Международный процесс
4.8: Другие свойства Particle-in-a-Box
Теперь, когда у нас есть математические выражения для волновых функций и энергии для частицы в коробке, мы можем ответить на ряд интересных вопросов.Ответы на эти вопросы используют квантовую механику для предсказания некоторых важных и общих свойств электронов, атомов, молекул, газов, жидкостей и твердых тел.
Какая наименьшая энергия у электрона? Самый низкий уровень энергии – это \ (E_1 \), и важно понимать, что эта самая низкая энергия не равна нулю. Эта конечная (т.е. ни нулевая, ни бесконечная) энергия называется энергией нулевой точки, а движение, связанное с этой энергией, называется движением нулевой точки. Любая система, ограниченная некоторой областью пространства, называется связанной.Энергия нулевой точки и движение являются проявлением волновых свойств и принципа неопределенности Гейзенберга и являются общими свойствами связанных квантово-механических систем. Положение и импульс частицы нельзя определить точно. Согласно принципу неопределенности Гейзенберга произведение неопределенностей, то есть стандартных отклонений этих величин, должно быть больше или равно / 2. Если бы энергия была равна нулю, то импульс был бы точно равен нулю, что нарушило бы принцип неопределенности Гейзенберга, если бы неопределенность положения не была бы бесконечной.Тогда система вообще не будет локализована в пространстве, что мы обнаружим, что это верно для случая свободной частицы, которая не связана. Неопределенность положения связанной системы не бесконечна, поэтому неопределенность импульса не может быть нулевой, как это было бы, если бы энергия была равна нулю.
Где электрон?
Упражнение \ (\ PageIndex {1} \)
Воспользуйтесь решением упражнения \ (\ PageIndex {15} \), чтобы написать несколько предложений, отвечающих на этот вопрос о местонахождении электрона.Что вы поймете из построенных вами графиков распределения вероятностей при очень больших n по сравнению с n = 1?
Упражнение \ (\ PageIndex {2} \)
Используйте общую форму волновой функции частицы в коробке sin (kx) для любого n, чтобы найти математическое выражение для значения математического ожидания положения \ (\ left \ langle x \ right \ rangle \) для прямоугольника длины L. Как \ (\ left \ langle x \ right \ rangle \) зависит от n? Вычислите интеграл.
Упражнение \ (\ PageIndex {3} \)
Рассчитайте вероятность обнаружения электрона на L / 2 в диапазоне от \ (\ dfrac {L} {2} – \ dfrac {L} {200} \) до \ (\ dfrac {L} {2} + \ dfrac {L} {200} \) для n = 1 и n = 2.Поскольку длина интервала L / 100 мала по сравнению с L, вы можете получить приблизительный ответ без интегрирования.
Каков импульс электрона в ящике?
Волновые функции типа “частица в ящике” не являются собственными функциями оператора импульса.
Упражнение \ (\ PageIndex {4} \)
Покажите, что волновые функции типа “частица в ящике” не являются собственными функциями оператора импульса.
Пример \ (\ PageIndex {1} \)
Хотя волновые функции не являются собственными функциями импульса, мы можем вычислить математическое ожидание импульса.L_0 \ sin (\ dfrac {n \ pi x} {L}) \ cos (\ dfrac {n \ pi x} {L}) dx \]
\ [= 0 \]
Может показаться, что электрон не имеет импульса, что неверно, потому что мы знаем, что энергия никогда не равна нулю. Фактически, энергия, которую мы получили для частицы в коробке, является полностью кинетической энергией, потому что мы установили потенциальную энергию равной 0.
Поскольку кинетическая энергия – это квадрат импульса, деленный на удвоенную массу, легко понять, как средний импульс может быть равен нулю, а кинетическая энергия – конечной.{-ikx} \) по формуле Эйлера. Покажите, что собственные значения импульса для этих двух функций равны p = + ħk и -k.
Интерпретация этих результатов физически интересна. Экспоненциальные волновые функции в линейной комбинации для синусоидальной функции представляют два противоположных направления, в которых может двигаться электрон. Один экспоненциальный член представляет движение влево, а другой член представляет движение вправо. Электроны движутся, у них есть кинетическая энергия и импульс, но средний импульс равен нулю.
Является ли тот факт, что средний импульс электрона равен нулю, а среднее положение L / 2, нарушает принцип неопределенности Гейзенберга? Нет, конечно, нет, потому что принцип неопределенности Гейзенберга относится к неопределенности импульса и положения, а не к средним значениям.
Количественные значения этих неопределенностей могут быть получены для сравнения с пределом, установленным принципом неопределенности Гейзенберга для произведения неопределенностей в импульсе и положении.2–2} \ label {4-34} \]
и стандартное отклонение импульса на
\ [\ sigma _p = \ dfrac {n \ pi \ hbar} {L} \ label {4-35} \]
Даже для n = 1, наименьшего значения для n, σx конечно и пропорционально L. По мере увеличения L увеличивается неопределенность положения электрона. С другой стороны, когда L увеличивается, σp уменьшается, но произведение никогда не равно нулю; и действует принцип неопределенности.
Упражнение \ (\ PageIndex {6} \)
Оцените произведение σx σp для n = 1 и общего n.2 \)? Что этот результат подразумевает о значении квантования энергии для бейсбольных мячей в коробке между насыпью для подачи и домашней пластиной? Какое значение имеет квантовая механика для игры в бейсбол в мире, где h настолько велико, что бейсбольные мячи проявляют квантовые эффекты?
- Насколько важно квантование для макроскопических объектов?
- Как можно определить относительные энергии волновых функций путем исследования?
Первая производная функции – это скорость изменения функции, а вторая производная – это скорость изменения скорости изменения, также известная как кривизна.Функция с большой второй производной меняется очень быстро. Поскольку вторая производная волновой функции встречается в гамильтоновом операторе, который используется для вычисления энергии с помощью уравнения Шредингера, волновая функция, имеющая более резкую кривизну, чем другая, то есть более крупные вторые производные, должна соответствовать состоянию, имеющему более высокую энергию. Волновая функция с большим количеством узлов, чем другая в той же области пространства, должна иметь более резкую кривизну и большие вторые производные и, следовательно, должна соответствовать более высокому энергетическому состоянию.
Упражнение \ (\ PageIndex {9} \)
Определите взаимосвязь между количеством узлов в волновой функции и ее энергией, изучив графики, которые вы построили в упражнении \ (\ PageIndex {15} \). Узел – это точка, в которой амплитуда проходит через ноль. Что означает наличие множества узлов о форме волновой функции?
.


 2. Чтобы раскрыть неопределенность вида , в которой числитель или знаменатель иррациональны, следует надлежащим образом избавиться от иррациональности, умножив и числитель и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби. В случае квадратных корней и числитель и знаменатель дроби умножаются на сопряженное выражение тому, которое содержит иррациональность и применяется формула
2. Чтобы раскрыть неопределенность вида , в которой числитель или знаменатель иррациональны, следует надлежащим образом избавиться от иррациональности, умножив и числитель и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби. В случае квадратных корней и числитель и знаменатель дроби умножаются на сопряженное выражение тому, которое содержит иррациональность и применяется формула 

 2}{x}=lim_{x\to 0} x=0$.
2}{x}=lim_{x\to 0} x=0$. 2}=-\frac{1}{6}$
2}=-\frac{1}{6}$ {-\infty}$ эквивалентно выражению $\frac{1}{0}$.
{-\infty}$ эквивалентно выражению $\frac{1}{0}$. Предел суммы (разности) равен сумме (разности) пределов.
Предел суммы (разности) равен сумме (разности) пределов. е. .
е. . Найдем
Найдем Найдем
Найдем Найдем .
Найдем . В литературном салоне философа Никола Мальбранша (1638-1715) Иоганн знакомится с французским математиком маркизом Гийомом Франсуа Антуаном де Лопиталем (1661-1704). В ходе оживленной беседы Лопиталь удивился, как легко, “как бы играя”, юнец Бернулли решал трудные задачи по новому исчислению. Поэтому Лопиталь попросил прочитать ему несколько лекций. Устные беседы понравились Лопиталю, и он за приличный гонорар стал получать материалы в письменном виде. Заметим, что общеизвестное теперь “правило Лопиталя” для раскрытия неопределенностей также было передано ему Иоганном. Уже в 1696 году появился знаменитый трактат Лопиталя “Введение в анализ бесконечно малых для понимания кривых линий”. Вторая часть курса, изложенного Иоганном I Бернулли, была опубликована лишь в 1742 году и называлась “Математические лекции о методе интегралов и другие; написаны для знаменитого маркиза Госпиталия; годы 1691–1692”. В 1921 году были обнаружены рукописные копии лекций, написанные рукой Иоганна I Бернулли, оригиналы которых были переданы Лопиталю в 1691–1692 гг.
В литературном салоне философа Никола Мальбранша (1638-1715) Иоганн знакомится с французским математиком маркизом Гийомом Франсуа Антуаном де Лопиталем (1661-1704). В ходе оживленной беседы Лопиталь удивился, как легко, “как бы играя”, юнец Бернулли решал трудные задачи по новому исчислению. Поэтому Лопиталь попросил прочитать ему несколько лекций. Устные беседы понравились Лопиталю, и он за приличный гонорар стал получать материалы в письменном виде. Заметим, что общеизвестное теперь “правило Лопиталя” для раскрытия неопределенностей также было передано ему Иоганном. Уже в 1696 году появился знаменитый трактат Лопиталя “Введение в анализ бесконечно малых для понимания кривых линий”. Вторая часть курса, изложенного Иоганном I Бернулли, была опубликована лишь в 1742 году и называлась “Математические лекции о методе интегралов и другие; написаны для знаменитого маркиза Госпиталия; годы 1691–1692”. В 1921 году были обнаружены рукописные копии лекций, написанные рукой Иоганна I Бернулли, оригиналы которых были переданы Лопиталю в 1691–1692 гг. Из них ученые неожиданно обнаружили, что Лопталь в своем “Анализе” почти не отступал от лекций своего молодого учителя.
Из них ученые неожиданно обнаружили, что Лопталь в своем “Анализе” почти не отступал от лекций своего молодого учителя. 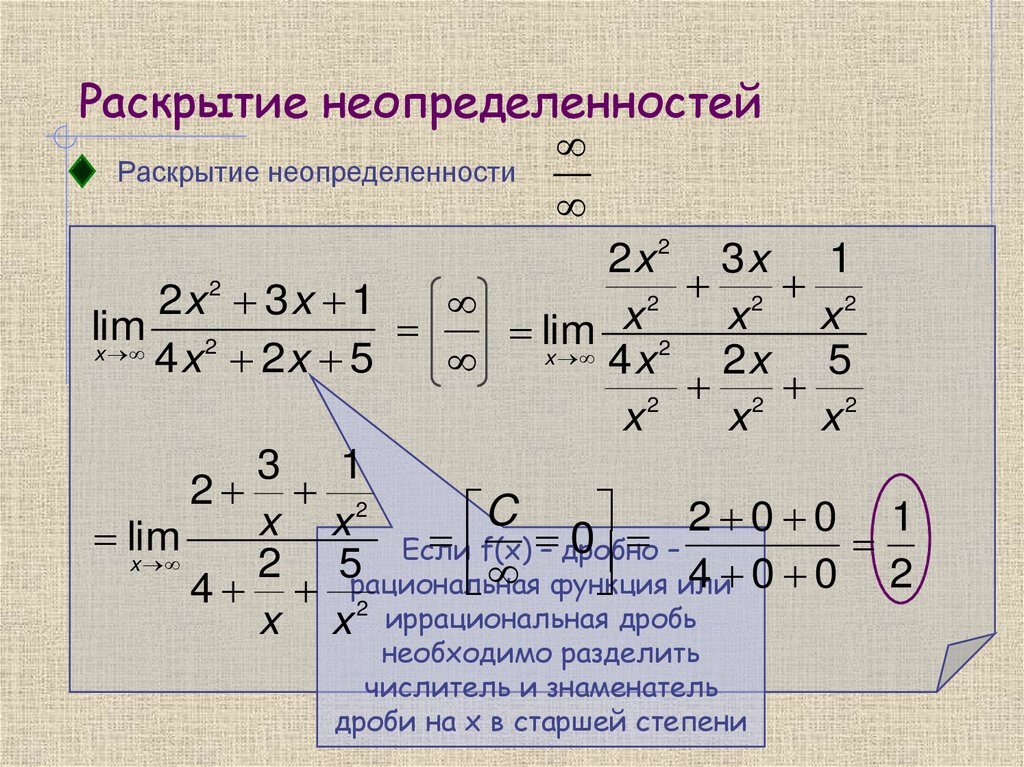




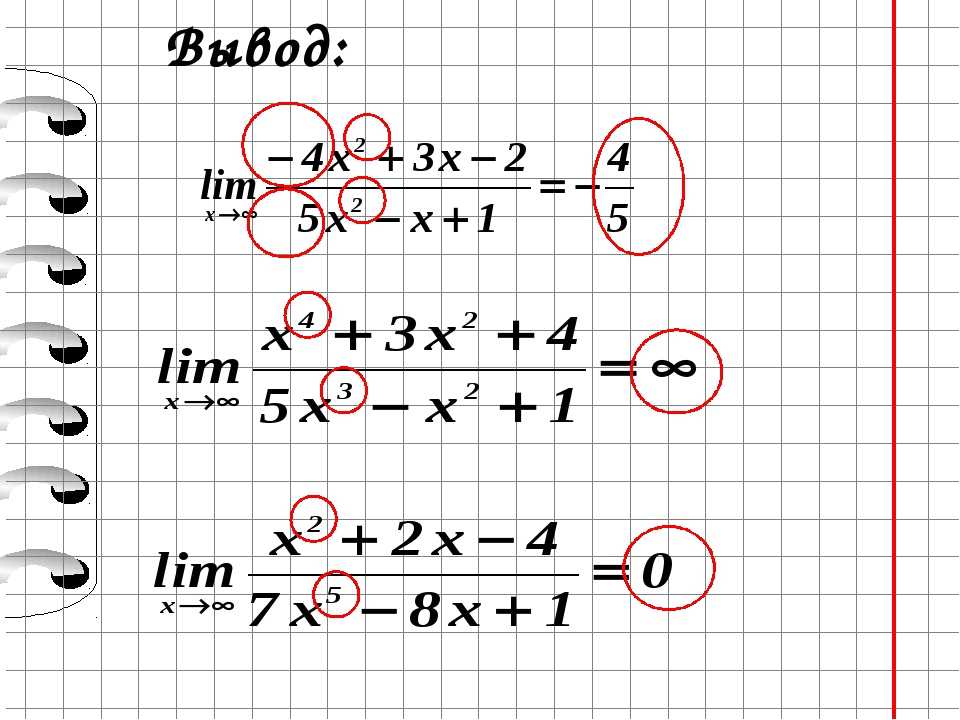 Если мы хотим чтобы пути сошлись, то за «оградкой» нам нужен телепорт из одного конца «бытия» в другой. Мы уже такие телепорты видали. Не проблема.
Если мы хотим чтобы пути сошлись, то за «оградкой» нам нужен телепорт из одного конца «бытия» в другой. Мы уже такие телепорты видали. Не проблема. com). То есть введена идеализированная точка которая соединяет оба конца вещественной прямой. Так как расширение не аффинное, сравнение вещественных чисел с бесконечностью не определено.
com). То есть введена идеализированная точка которая соединяет оба конца вещественной прямой. Так как расширение не аффинное, сравнение вещественных чисел с бесконечностью не определено. При операциях мы часто пренебрегаем малыми низшего порядка попросту отбрасывая их при записи результата.
При операциях мы часто пренебрегаем малыми низшего порядка попросту отбрасывая их при записи результата. С другой стороны мы приобретаем возможность сравнения бесконечно малых и бесконечно больших величин. А это значит что мы можем рассматривать бесконечности как числа.
С другой стороны мы приобретаем возможность сравнения бесконечно малых и бесконечно больших величин. А это значит что мы можем рассматривать бесконечности как числа.
 Чтобы ими оперировать, нужно не забывать про новые дополнительные условия.
Чтобы ими оперировать, нужно не забывать про новые дополнительные условия. Строгое определение обратного элемента не связано с операцией деления.
Строгое определение обратного элемента не связано с операцией деления. Отвяжем операции друг от друга, но сохраним привычное поведение для вещественных чисел. Определим унарную операцию деления, обозначаемую знаком “/”.
Отвяжем операции друг от друга, но сохраним привычное поведение для вещественных чисел. Определим унарную операцию деления, обозначаемую знаком “/”.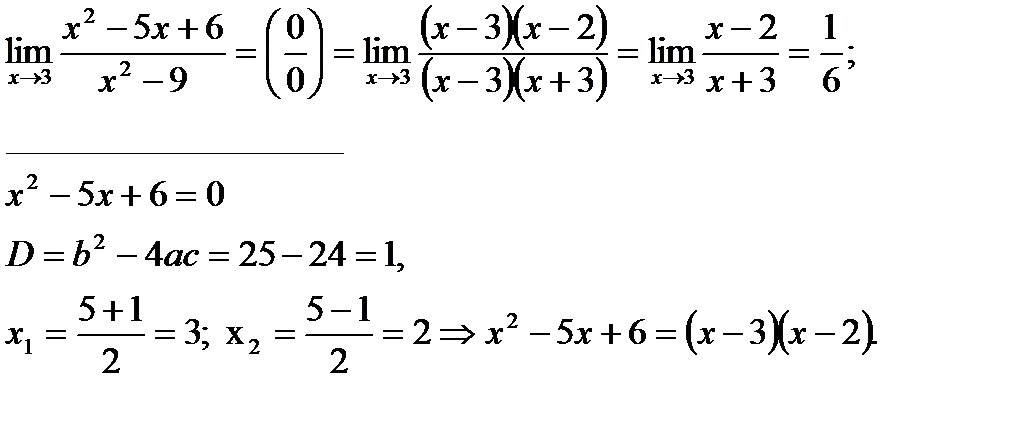 А в поле, как известно, определены всего две операции (сложение и умножение). Понятие деления выводится через обратные, а если еще глубже, то единичные элементы. Внесенные изменения превращают нашу алгебраическую систему в моноид как по операции сложения (с нулем в качестве нейтрального элемента), так и по операции умножения (с единицей в качестве нейтрального элемента).
А в поле, как известно, определены всего две операции (сложение и умножение). Понятие деления выводится через обратные, а если еще глубже, то единичные элементы. Внесенные изменения превращают нашу алгебраическую систему в моноид как по операции сложения (с нулем в качестве нейтрального элемента), так и по операции умножения (с единицей в качестве нейтрального элемента).

