Главная
Неопределенности пределов: Основные неопределенности пределов и их раскрытие

Неопределенности пределов: Основные неопределенности пределов и их раскрытие

Физики использовали квантовую запутанность, чтобы дойти до пределов принципа неопределенности

Георгий Голованов

Почти век назад физик Вернер Гейзенберг, изучавший законы квантовой механики, сформулировал фундаментальные ограничения точности измерения определенных свойств микроскопических объектов. Однако, как выяснила международная команда исследователей, те же законы способны значимо повысить точность до уровня, который ранее не представлялся возможным. Новый метод может оказаться полезен для широкого спектра технологий, от медицины до квантовой коммуникации.

«Мы смогли раздвинуть границы варианта „принципа неопределенности“ Гейзенберга в некоторых обстоятельствах, указав на то, что для других сценариев могут быть необходимы другие принципы неопределенности», — заявили исследователи Лоркан Конлон и Сиед Ассад на страницах издания The Conversation.

Изучать свойства микроскопических, квантовых объектов вроде электронов или фотонов намного сложнее, чем больших. Машина, например, не изменит цвет или скорость, если мы узнаем ее точное расположение в пространстве. А вот у электронов все устроено именно так. Другими словами, отдельные свойства квантовых объектов соединены друг с другом. Измерение одного воздействует на другое.

Связь между этими свойствами — прямое проявление принципа неопределенности Гейзенберга. Невозможно одновременно измерить два сопряженных свойства квантового объекта с желаемой степенью точности: чем больше ты знаешь об одном, тем меньше знаешь о другом. Хотя этот принцип накладывает ограничение на измерения, на практике очень сложно приблизиться к пределу точности измерения одного из свойств. Тем не менее, это важно и для науки, и для развития новых технологий.

Команда ученых из разных стран разработала метод более точного определения сопряженных свойств квантовых объектов. В его основе лежит квантовая запутанность. Когда два объекта спутаны между собой, их свойства можно измерить с большей точностью, чем в случае незапутанных объектов.

Для создания двух идентичных квантовых объектов и их последующего спутывания ученые использовали квантовые компьютеры, способные управлять этими объектами с высокой точностью.  Измерив спутанные объекты, исследователи подтвердили верность своей гипотезы: в результате этого процесса снижается уровень помех в измерениях, а значит — повышается точность.

В теории, можно также запутать и измерить три и более квантовых системы. Это позволило бы добиться еще больше точности. Однако экспериментально доказать это предположение ученые пока не сумели.

Недавно физики из Брукхейвенской национальной лаборатории США наткнулись в ходе исследований на совершенно новый тип квантового феномена, который связывает частицы на любом расстоянии. В экспериментах с ускорителем частиц это явление дало им возможность рассмотреть во всех подробностях внутренности ядер атомов.

Пределы с иррациональностями. Примеры раскрытия неопределённостей. Первая часть.

Высшая математика » Пределы » Пределы с иррациональностями » Первая часть

Первая часть

Вторая часть

Третья часть

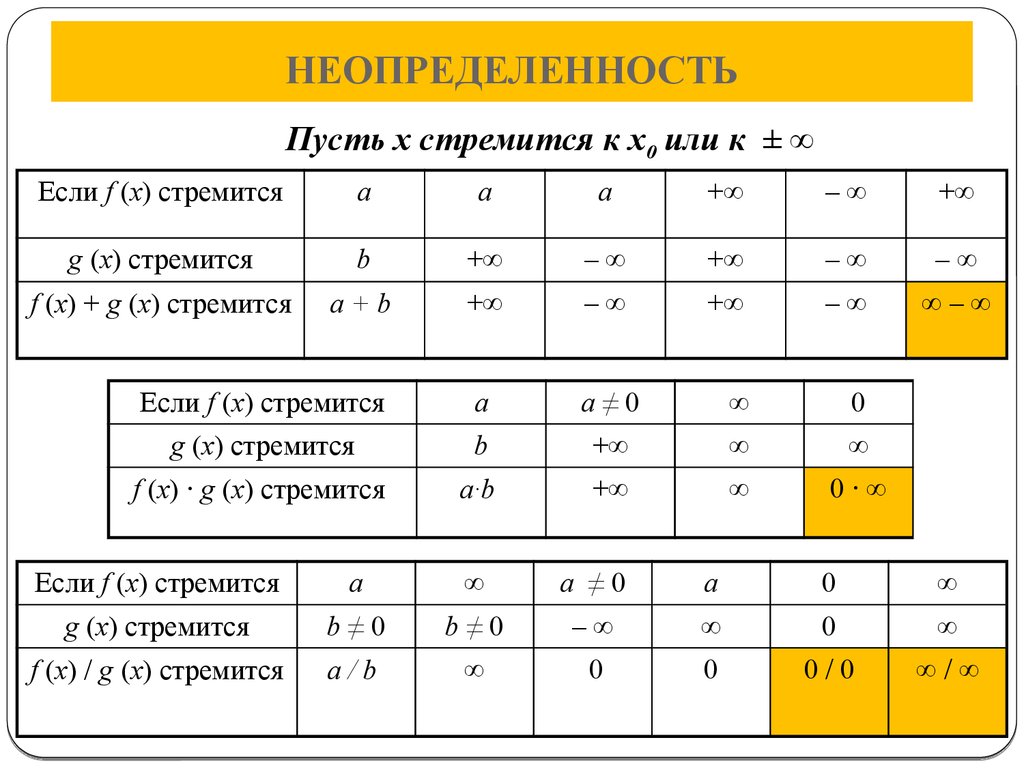
Пределы, содержащие иррациональности (или, попросту говоря, корни) крайне популярны у составителей типовых расчётов и контрольных работ по высшей математике. Обычно рассматриваются три группы неопределённостей:

В данной теме мы рассмотрим все три перечисленные выше группы пределов с иррациональностями. Начнём с пределов, содержащих неопределенность вида $\frac{0}{0}$.

Схема решения стандартных примеров такого типа обычно состоит из двух шагов:

  • Избавляемся от иррациональности, вызвавшей неопределенность, домножая на так называемое “сопряжённое” выражение;
  • При необходимости раскладываем выражение в числителе или знаменателе (или и там и там) на множители;
  • Сокращаем множители, приводящие к неопределённости, и вычисляем искомое значение предела.
    2+bx+c=a\cdot(x-x_1)\cdot(x-x_2) \end{equation} $$

    Формул (1)-(5) вполне хватит для решения стандартных задач, к которым мы сейчас и перейдём.

    Пример №1

    Найти $\lim_{x\to 3}\frac{\sqrt{7-x}-2}{x-3}$.

    Решение

    Найдём отдельно пределы числителя и знаменателя:

    $$ \begin{aligned} & \lim_{x\to 3}(\sqrt{7-x}-2)=\sqrt{7-3}-2=\sqrt{4}-2=0;\\ & \lim_{x\to 3} (x-3)=3-3=0. \end{aligned} $$

    В заданном пределе мы имеем неопределённость вида $\frac{0}{0}$. Раскрыть эту неопределённость нам мешает разность $\sqrt{7-x}-2$. Для того, чтобы избавляться от подобных иррациональностей, применяют умножение на так называемое “сопряжённое выражение”. Как действует такое умножение мы сейчас и рассмотрим. Умножим $\sqrt{7-x}-2$ на $\sqrt{7-x}+2$:

    $$(\sqrt{7-x}-2)(\sqrt{7-x}+2)$$

    Чтобы раскрыть скобки применим формулу №1, подставив в правую часть упомянутой формулы $a=\sqrt{7-x}$, $b=2$:

    $$(\sqrt{7-x}-2)(\sqrt{7-x}+2)=(\sqrt{7-x})^2-2^2=7-x-4=3-x. $$

    Как видите, если умножить числитель на $\sqrt{7-x}+2$, то корень (т.е. иррациональность) в числителе исчезнет. Вот это выражение $\sqrt{7-x}+2$ и будет сопряжённым к выражению $\sqrt{7-x}-2$. Однако мы не вправе просто взять и умножить числитель на $\sqrt{7-x}+2$, ибо это изменит дробь $\frac{\sqrt{7-x}-2}{x-3}$, стоящую под пределом. Умножать нужно одовременно и числитель и знаменатель:

    $$ \lim_{x\to 3}\frac{\sqrt{7-x}-2}{x-3}= \left|\frac{0}{0}\right|=\lim_{x\to 3}\frac{(\sqrt{7-x}-2)\cdot(\sqrt{7-x}+2)}{(x-3)\cdot(\sqrt{7-x}+2)}$$

    Теперь вспомним, что $(\sqrt{7-x}-2)(\sqrt{7-x}+2)=3-x$ и раскроем скобки. А после раскрытия скобок и небольшого преобразования $3-x=-(x-3)$ сократим дробь на $x-3$:

    $$ \lim_{x\to 3}\frac{(\sqrt{7-x}-2)\cdot(\sqrt{7-x}+2)}{(x-3)\cdot(\sqrt{7-x}+2)}= \lim_{x\to 3}\frac{3-x}{(x-3)\cdot(\sqrt{7-x}+2)}=\\ =\lim_{x\to 3}\frac{-(x-3)}{(x-3)\cdot(\sqrt{7-x}+2)}= \lim_{x\to 3}\frac{-1}{\sqrt{7-x}+2} $$

    Неопределенность $\frac{0}{0}$ исчезла. 2-3x+6}-\sqrt{5x-9}}=-6$.

    В следующей (второй) части рассмотрим ещё пару примеров, в которых сопряжённое выражение будет иметь иной вид, нежели в предыдущих задачах. Главное, помните, что цель использования сопряжённого выражения – избавиться от иррациональности, вызывающей неопределённость.

    Первая часть

    Вторая часть

    Третья часть

    Вернуться к списку тем

    Задать вопрос на форуме

    Записаться на занятия

    Онлайн-занятия по высшей математике

    Пределы неопределенности | Ватт с этим?

    Любопытные вещи

    4 года назад

    Уиллис Эшенбах

    Гостевой пост Уиллиса Эшенбаха

    высота поверхности моря может быть. Комментатор сказал:

    Ионосферная задержка действительно является проблемой. Для Джейсона они оценивают его с помощью двухчастотного метода. Как и в большинстве случаев в мире спутниковых данных о повышении уровня моря, в их оценке задержки, вероятно, есть некоторая ошибка, но трудно понять, почему любые ошибки не устраняются или не разрешаются в течение очень большого количества измерений с постоянным смещением. в их оценке уровня моря, что не должно влиять на оценку повышения уровня моря.

    Имейте в виду, что спутники производят более 1000 измерений каждую секунду и перемещают свою «целевую точку» примерно на 8 км (я думаю) вбок каждую секунду. Многие вещи действительно усредняются со временем.

    Я подумал, что должен написать об этом распространенном недоразумении.

    В основе лежит простая математика. Неопределенность среднего (также называемого «средним») группы чисел равна стандартному отклонению чисел (показатель того, насколько разбросаны числа), деленному на квадратный корень из числа имеющихся чисел. . На математическом языке это

    , где сигма (σ) — стандартное отклонение, а N — количество анализируемых чисел.

    Очевидно, что по мере увеличения числа измерений неопределенность среднего значения уменьшается. Это все математика, которая была хорошо изучена на протяжении сотен лет. И именно на этом основании комментатор утверждает, что повторными измерениями мы можем получить очень и очень хорошие результаты со спутников.

    В этом прологе позвольте мне показать пределы этого надежного математического принципа в реальном мире.

    Предположим, я хочу измерить длину кредитной карты.

    Итак, я заставляю десять тысяч человек использовать линейку на чертеже для измерения длины кредитной карты в миллиметрах. Почти все они дают измерение длины где-то между 85 мм и 86 мм.

    Это дало бы нам стандартное отклонение их ответов порядка 0,3 мм. И использование приведенной выше формулы для неопределенности среднего дает нам:

    Теперь… поднимите руку, если вы думаете, что мы только что точно измерили длину кредитной карты с точностью до трех тысячных миллиметра.

    Конечно нет. И ответ не улучшился бы, если бы у нас был миллион измерений.

    Размышление над всем этим привело к еще одному из моих многочисленных эмпирических правил, а именно: наблюдения.

    Следуя этому эмпирическому правилу, если вы измеряете, скажем, температуру с точностью до градуса, независимо от того, сколько измерений у вас есть, ваше среднее значение будет действительным с точностью до ближайшей десятой доли градуса… но не до ближайшей сотой доли градуса.

    степень.

    Как и в любом эмпирическом правиле, могут быть исключения… но в целом я думаю, что это правда. Например, следуя моему эмпирическому правилу, я бы сказал, что мы могли бы использовать повторные измерения, чтобы получить оценку длины кредитной карты с точностью до ближайшей десятой доли миллиметра… но я не думаю, что мы можем измерить ее с точностью до сотой доли. миллиметра независимо от того, сколько раз мы владеем линейкой.

    С наилучшими пожеланиями в ночь дождей,

    w.

    Моя общая просьба: когда вы комментируете, пожалуйста, цитируйте точные слова, которые вы имеете в виду, чтобы мы могли избежать недоразумений.

    1 1 голос

    Рейтинг статьи

    Нравится:

    Нравится Загрузка…

    2.5.8.1. Расчет пересмотренной неопределенности

    2.5.8.1. Расчет пересмотренной неопределенности
    2. Характеристика процесса измерения
    2.5. Анализ неопределенностей
    2.5.8. Лечение нескорректированного смещения

    2.5.8.1.

    Расчет пересмотренной неопределенности

    Определение смещения и скорректированное измерение     		Если смещение равно \(\delta\) и скорректированное измерение определяется $$ Y_{cor} = Y – \delta ,$$ исправленное значение \(Y\) имеет обычный расширенный интервал неопределенности, который симметричен относительно неизвестного истинного значения для процесса измерения и имеет следующий тип: $$ Y_{cor} – U \, \le \, \mbox{True} \, \mbox{Value} \, \le \, Y_{cor} + U $$
    Определение асимметричного интервала неопределенности для учета нескорректированное измерение Если поправка на смещение не внесена, неопределенность интервал загрязнен влиянием члена смещения следующим образом: $$ Y – (U + \delta) \, \le \, \mbox{True} \, \mbox{Value} \, \le \, Y + (U – \delta) $$ и может быть переписан в терминах верхней и нижней конечных точек, которые асимметричный относительно истинного значения; а именно, $$ Y – U_- \, \le \, \mbox{True} \, \mbox{Value} \, \le \, Y + U_+ $$
    Условия связи между смещением и U Приведенное выше определение может привести к отрицательному пределу неопределенности; например. , если смещение положительное и больше \(U\), верхняя конечная точка становится отрицательным. Требование, чтобы пределы неопределенности больше или равно нулю для всех значений гарантий смещения неотрицательные пределы неопределенности и принимается за счет несколько более широкие интервалы неопределенности. Это приводит к следующему набор ограничений на пределы неопределенности: $$ U_- = \left\{ \begin{массив}{ll} U + \delta & \mbox{if } \,\, U + \delta >
    0 \\ 0 & \mbox{if } \,\, U + \delta \le 0 \\ \end{массив} \right. $$

    $$ U_+ = \left\{ \begin{массив}{ll} U – \delta & \mbox{if } \,\, U – \delta > 0 \\ 0 & \mbox{if } \,\, U – \delta \le 0 \end{массив} \right. $$

    Ситуация, когда смещение точно неизвестно, но должно быть по оценкам
    		Если смещение точно неизвестно, его величина оценивается по формуле повторные измерения, по разреженным данным или по теоретическим соображений, а стандартное отклонение оценивается по повторяющимся измерений или из предполагаемого распределение.

    Оставить комментарий