Раскрытие неопределенностей в пределах
Рассмотрим теперь способы избавления от истинных неопределенностей типа . Первый способ следующий. Если при вычислении возникают указанные выше неопределенности, то можно попробовать тождественно преобразовать выражение, задающее функцию , таким образом, чтобы неопределенности (при подстановке в преобразованное выражение) уже не возникало. Вся сложность этого способа в том, как научиться находить такое тождественное преобразование. Однако для определенных классов функций и типов получающихся неопределенностей такие преобразования известны. Рассмотрим некоторые из них.
1.
Предел отношения многочленов: .
В этом случае можно попытаться
разложить многочлены числителя и
знаменателя на множители, затем сократить
общие множители. Вспомним некоторые способы
разложения многочленов на множители:
а) формулы сокращенного
умножения: , , ;
б)
вынесение за скобки общего множителя
;
в) разложение квадратного трехчлена: ,
где и − корни квадратного уравнения .
Пример 1. = = = ;
Пример 2. = = ;
Пример 3. ={находим корни квадратного уравнения : , , а потому } = = .
2. Предел отношения многочленов на бесконечности: .
В этом случае неопределенность исчезает, если разделить числитель и знаменатель на старшую степень знаменателя (т.е. на , так как в знаменателе многочлен степени n).
Пример 4. {если формально подставить в выражение после знака предела, то в дробях , , , и получится ; в соответствии с рассмотренным выше «первым правилом псевдонеопределенности» это означает стремление этих дробей к 0, что в дальнейшем обозначим для наглядности значком } = .
Пример 5. = = = . Пример 6. = = = .
3. Пределы с корнями: .
В числителе и/или
в знаменателе стоит сумма или разность
выражений, содержащих корни (квадратные,
кубичные …). В случае квадратных корней
можно домножить числитель и знаменатель
на так называемое сопряженное выражение
к числителю и/или знаменателю (сумму
или разность корней домножить на их
разность или сумму соответственно),
после этого воспользоваться формулой
разности квадратов: .
Если же участвуют корни третьей степени,
то домножать числитель и знаменатель
необходимо на неполный квадрат
суммы-разности корней для образования
формулы суммы-разности кубов: .
После применения этих формул корни
исчезают, либо входят уже в такие
выражения, которые не ведут к
неопределенности при вычислении предела.
В случае квадратных корней
можно домножить числитель и знаменатель
на так называемое сопряженное выражение
к числителю и/или знаменателю (сумму
или разность корней домножить на их
разность или сумму соответственно),
после этого воспользоваться формулой
разности квадратов: .
Если же участвуют корни третьей степени,
то домножать числитель и знаменатель
необходимо на неполный квадрат
суммы-разности корней для образования
формулы суммы-разности кубов: .
После применения этих формул корни
исчезают, либо входят уже в такие
выражения, которые не ведут к
неопределенности при вычислении предела.
Пример 7. = {квадратный корень содержится в числителе в разности , поэтому домножим числитель и знаменатель на соответствующую сумму и применим формулу } = = = = = = {после сокращения на } = ={подставляя } = .

Пример 9. = {кубичный корень содержится в числителе в сумме , поэтому домножим числитель и знаменатель на неполный квадрат разности и применим формулу } = = = = .
Мы прошли лишь некоторые приемы избавления от неопределенностей в пределах. Подобных приемов гораздо больше, но все они «работают» лишь для конкретных классов функций и видах неопределенности. В дальнейшем (после прохождения производных) будет дан практически универсальный прием избавления от неопределенностей в пределах (так называемое «правило Лопиталя»).
Виды неопределенностей и методы их разрешения
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Виды неопределенностей и методы их разрешения.
Существует несколько видов неопределенностей
0
0
0
,
,
0
,
1
,
,
,
0
.
0
Неопределенность вида
(бесконечность деленная
на бесконечность).
Выражение под знаком предела представляет собой
частное многочленов любой степени.
Pn ( x)
f ( x)
Qm ( x)
Для
раскрытия
такого
вида
неопределенности
необходимо:
1. разделить все слагаемые числителя и знаменателя на
переменную х в старшей степени;
2. рассмотреть предел каждого слагаемого.
три случая:
а). Степень многочлена числителя равна степени
многочлена знаменателя.
10 8
3x 2 10 x 8
3 2
2 2
2
2
3x 10 x 8 lim x
x x 3
x
x lim
lim 2
.
 x 2
x 2x
5 4
x 5x 4
x x 5 x 4
1
2
x
x
x2 x2 x2
На основании теоремы о пределе частного, суммы
(разности) рассмотрим предел каждого слагаемого
10
lim
0;
x x
8
lim 2 0;
x x
5
lim 0;
x x
4
lim 2 0.
x x
3 1
2 x3 3x 1
2 0 0 2
x
x
lim 3
lim
;
2
x 3 x x 5
3 0 0 3
x 3 1 5
x x3
5 1
7 2 4
7 x4 5×2 1
7 0 0 7
x
x
lim 4
lim
;
3
x 6 x 5 x 8
6 0 0 6
x 6 5 8
x x4
б).
Степень многочлена числителя больше степени
многочлена знаменателя
5 7
3x 2 5 x 7
3
2
2
2
2
2
3x 5 x 7
3
x
x
x
x
x
lim
lim
lim
x
2 1
x
2x 1
0
x
2x 1
2
2
x x2
x
x
x5 6 x3 11x 2 5
5 5 5
5
3
2
5
x 6 x 11x 5 lim x
x
x
x
lim
x
4
2
2
3
x
x
8x
x
3x x 8 x
5 5
5
x
x
x
lim
x
6 11 5
3 5
2
x
x
x 1
0
3 1 8
3 4
x x
x
1
в).
 степень
степеньмногочлена числителя меньше степени
многочлена знаменателя
2 x 4 4 x3 x 2
6 6
6
2 x 4 4 x3 x 2
lim
x
x
x
lim 6
6
5
4
5
4
x
4 x 5 x 3x
x
4
x 4 x 5 x 3x x 4
x6
x6
x6 x6 x6
2 4 1
3 4
2
0
x
x
x
lim
0
x
5 3 1 4 4
4 2 5 6
x
x
x
x
Предел отношения двух многочленов при х
0 при n m
Pn ( x) a1
lim
при n m
x Q ( x )
m
a2
при n m
1. если степень многочлена числителя меньше степени
многочлена знаменателя, по предел равен нулю.
2. если степень многочлена числителя равна степени
многочлена знаменателя, то предел равен отношению
коэффициентов при старшей степени переменной;
3. если степень многочлена числителя больше степени
многочлена знаменателя, по предел равен бесконечности;
2. Неопределенность вида
0 .
0
Метод раскрытия неопределенности такого вида зависит
от выражения стоящего под знаком предела, как правило
выделяют два частных случая:
а).

рациональной функцией:
2
x 4 0
lim 3
x 2 x 8
0
Для решения задачи необходимо
формулами сокращенного умножения:
воспользоваться
a2 b2 a b a b a3 b3 a b a 2 ab b 2 .
Разложим числитель и знаменатель на множители:
x 2 x 2
x2 4 0
lim 3
lim
2
x
2
x 2 x 8
x 2 x 2x 4
0
x 2
2 2
1
lim 2
2
.
x 2 x 2 x 4
2 2 2 4 3
Если числитель и знаменатель дробно-рациональной
функции являются многочленами второй степени, то для
раскрытия неопределенности необходимо разложить и
числитель и знаменатель на множители:
2
x2 4 x 5 0
bx c a x x1 x x2
lim 2
;
x 1 x 2 x 3
0
Для решения задачи необходимо
1. Определить корни числителя и знаменателя
x2 4 x 5 0
b D
x1,2
2a
x2 5
x1 1
x2 2 x 3 0
x1 1
D b2 4ac
x2 3
2. Разложить многочлен на множители
x 4 x 5 ( x 1)( x 5)
2
x 2 2 x 3 ( x 1)( x 3)
x 1 x 5
x2 4x 5 0
x 5 3
lim 2
lim
lim
.

x 1 x 2 x 3
0 x 1 x 1 x 3 x 1 x 3 2
Рассмотрим пример:
3 x 2 10 x 8 0
lim
x 4 x 2 5 x 4
0
Вычислим корни многочлена числителя и знаменателя,
разложим числитель и знаменатель на множители:
2
x1 4; x 2 .
3
x2 5x 4 0;
x1 4; x2 1.
2
2
3(
x
4)(
x
)
3(
x
)
3 x 2 10 x 8
3 lim
3
lim
lim 2
x 4 ( x 4)( x 1)
x 4 ( x 1)
x 4 x 5 x 4
3 x 2 3( 4) 2 14
x 4 ( x 1)
4 1
3
lim
б). выражение стоящее под знаком предела, содержит
дробно-иррациональную функцию
В этом случае для раскрытия неопределенности
умножают и числитель и знаменатель на выражение
сопряженное к иррациональному выражению и используют
формулу сокращенного умножения
a b a b a 2 b 2 .
Например, знаменатель дроби является иррациональным
выражением
( x 3)( x 2 8 x )
x 3
0 lim
lim
x 3
x 3
( x 2 8 x )( x 2 8 x )
x 2 8 x 0
( x 3)( x 2 8 x )
( x 3)( x 2 8 x )
lim
lim
x 3
x 3
x 2 8 x
( x 2) (8 x)
( x 3)( x 2 8 x )
( x 3)( x 2 8 x )
lim
lim
x
3
x 3
2( x 3)
2x 6
x 2 8 x
3 2 8 3
lim
5
x 3
2
2
Рассмотрим пример, когда числитель дроби является
иррациональным выражением
2 x 2 x
2 x 2 x
2 x 2 x 0
lim
lim
x
0
x 0
x
x 2 x 2 x
0
lim
x 0
x
lim
x 0
x
2 x 2 x
Пример:
2 x 2 x
lim
x 0
2x
2 x 2 x
x
lim
x 0
2 x 2 x
2 x 2 x
2
2
1
2 x 2 x 2 2
2
2 x
0
lim
x 4 3 2 x 1
0
В этом случае и числитель и знаменатель содержат
иррациональные выражения.

2 x
(2 x )(2 x )(3 2 x 1)
0
lim
lim
x 4 3 2 x 1
x
4
(3 2 x 1)(3 2 x 1)(2 x )
0
(4 x)(3 2 x 1)
(4 x)(3 2 x 1)
lim
lim
x 4 (9 (2 x 1))(2
x
4
x)
(9 2 x 1)(2 x )
(4 x)(3 2 x 1)
(4 x)(3 2 x 1)
lim
lim
x 4 (8 2 x )(2
x 4 2(4 x )(2
x)
x)
3 2 4 1 3
4
2(2 4)
Первый замечательный предел
sin x 0
lim
1
x 0
x
0
lim
x 0
sin x
x
1,
1. lim
x 0 sin x
x
Если выражение, стоящее под знаком предела содержит
тригонометрические
функции,
то
для
раскрытия
неопределенности
используют
формулу
первого
замечательного предела.
Формулы, используемые при решении
x
1 cos x 2sin
2
2
sin х cos х 1
2
2sin х cos х sin 2 х
2
Рассмотрим пример
sin 2 x 0 lim 2sin 2 x 2lim sin 2 x 2 1 2
lim
x 0
x 0 7 2 x
7 7
7 2x
x 0
7x
0
1 cos5 x
x 0 1 cos3 x
lim
5x
2sin
2
lim
x 0
3x
2sin 2
2
2
5x
sin
2
lim
x 0
3x
sin 2
2
2
2
5x
5 x 3x 3x 5 x 5 x
25
x
sin sin
25
2
2
2
2
2
2
4
lim
lim
2
x 0 5 x
9
5x
3x
3 x 3 x 3 x x 0 9 x
sin
sin
4
2
2
2
2 2 2
cos 7 x
limsin 3 x ctg 7 x 0 limsin 3 x
lim sin 3 x
x 0
x 0
sin 7 x x 0 sin 7 x
sin 3x 3x 7 x
lim
x 0 3 x
sin 7 x 7 x
3x 3
lim
x 0 7 x
7
lim tg 5 x ctg 6 x 0 lim
x 0
x 0
sin 5 x cos 6 x
cos5 x sin 6 x
sin 5 x 5 x 6 x
5х 5
lim
lim
x 0 5 x
sin 6 x 6 x x 0 6 х 6
arctg 4 x 0
arctg 4 x 4
4 А
lim
lim
lim
2
x 0
x 0 x
x
0 x 0 4 x x
0
2
1 cos12 x 0
2sin
6x
2
lim
1 cos12 x 2sin 6 x lim
x 0
x 0 x sin x
x sin x
0
2sin 6 x sin 6 x 6 x 6 x lim 72 x 72
lim
x 0
x
x 0
6 x 6 x x sin x
2sin 3 x cos3 x
2sin 3x 3x 5 x
1 cos 6 x 0
lim
lim 2
lim
2
2
x
0
x 0
x 0 x sin 5 x
x sin 5 x
3x sin 5 x 5 x x
0
2 3x
6
lim
2
2
x 0 5 x x
x 0 5 x
lim
3.
 Неопределенность вида
Неопределенность вида1
Для
раскрытия
неопределенностей
применяется второй замечательный предел:
lim 1
x
x
такого
1
x
1
e,
x
lim(1 x) e
x 0
Рассмотрим пример:
2x 3
lim
x 3 x 4
2x 3
lim
x 3 x 4
x 1
x 1
2x
lim
x 3 x
2x
xlim
3 x
x 1
x 1
2
3
2
3
0
вида
Пример:
3x 5
lim
x 3 x 7
2 x 1
12
3x 7
lim
x
3x 7 3x 7
3x 7 7 5
lim
x
3x 7
2 x 1
1
lim 1
x
3x 7
12
2 x 1
2 x 1
1
lim 1
x
3x 7
12
3 x 7 12
(2 x 1)
12 3 x 7
lim e
x
12(2 x 1)
3 x 7
е
lim
x
24 x 12
3 x 7
e8
24 x 12 24
так как lim
8
3
x 3 x 7
Пример:
2 x2 3
lim 2
x 2 x 3
2 x 2 1
3x
2 x2 3 3 3
lim
2
x
2x 3
2 x 2 1
3x
2 x2 3
6
lim 2
2
x 2 x 3
2
x
3
1
lim 1 2
x
2x 3
6
e
2(2 x 2 1)
lim
x x (2 x 2 3)
2 x 2 1
2x
e
2 x 2 1
3x
6
lim
1 2
x
2
x
3
1
lim 1 2
x
2 x 3
6
4 x 2 1
lim
x 2 x3 3
e
2
x x
lim
2 x 2 1
3x
2 x 2 3 6 2 x 2 1
6 2 x 2 3 3 x
e б .
 м. 1
м. 1Пример
3x 2 5
lim 2
x 3 x 7
5 x 4 2
2x
2
3
x
7 7 5
1 lim
2
x
3
x
7
1
lim 1 2
x
3
x
7
12
5 x4 2
2x
3 x 2 7 12 5 x 4 2
12 3 x 2 7 2 x
lim e 10 x e
x
10 x
lim
e
e
0
x
lim e
x
60 x 4 24
6 x3 14 x
Пример:
5x 7
lim
x 5 x 4
6 x 2 1
5x 4 4 7
1 lim
x
5x 4
3
5x 4
lim
x 5 x 4
5x 4
6 x 2 1
6 x 2 1
5 x 4
3
3
lim 1
x
5x 4
3
(6 x 2 1)
5 x 4
e
3(6 x 2 1)
lim
x
5 x 4
18 x
lim
2
x 5
18 x 3 e
e 0
lim
e x 5 x 4
18 x
lim
x 5
e
e
Пример:
lim(2 x)
2x
1 x
x 1
1 lim(1 1 x)
x 1
lim (1 (1 x))
x 1
1
1 x
1 x 2 x
1 1 x
2x
1 x
(1 x))
lim(1
x 1
e
lim 2 x
x 1
e
2
Пример:
lim(7 2 x)
x 3
2
x 3
1 lim(1 6 2 x)
x 3
2
x 3
2x
1 x
lim(1 (6 2 x))
2
x 3
x 3
1
6 2 x
lim (1 (6 2 x)
x 3
e
2(3 x ) 2
lim
x 3
1
x 3
e
6 2 x 2
1 x 3
4( x 3)
lim
x 3
x 3
e
4
Пример:
lim(2 x 3) ln( x 2) ln x
x
Для решения задач данного типа, необходимо
преобразовать выражение стоящее под знаком предела,
используя свойства логарифмической функции.

a
ln a ln b ln
Решение.
b
ln a k ln a
k
x 2
x 3) ln
lim(2 x 3) ln( x 2) ln x lim(2
x
x
x
2 x 3
x 2
x 2
ln lim
lim ln
x
x
x
x
2
ln lim 1
x
x
ln e
4 x 6
x x
lim
2 x 3
1
x
2
1
ln lim 1
x
x
2
ln e 4
4
2 x 3
2
(2 x 3)
x
4. Неопределенность вида
lim( 9 x 4 x 3 x)
2
x
Замечание: данный вид неопределенности возможен
только при x
Выражение, стоящее под знаком предела представляет
собой разность бесконечно больших величин , для раскрытия
неопределенности такого вида, необходимо умножить и
разделить исходное выражение на сопряженное выражение и
привести к виду
Решение.
lim( 9 x 2 4 x 3 x)
x
lim
( 9 x 2 4 x 3x)( 9 x 2 4 x 3x)
( 9 x 2 4 x 3 x)
x
lim
lim
2
x
2
x
9 x 4 x 3x
9 x 4 x 3x
9×2 4x 9×2
4x
4x
4x
4 2
lim
lim
x
9 x 2 3x x 3 x 3 x 6 3
Задача о непрерывном начислении процентов
Первоначальный вклад в банк составил Q0 денежных
единиц.

Банк выплачивает ежегодно р% годовых.
Определить размер вклада Qt через t лет.
Решение.
1. Простые проценты – размер вклада ежегодно
p
увеличивается на одну и туже величину
Q0
100
За год Q Q 1 p
1
0
100
2p
За два года
Q2 Q0 1
100
pt
Q
Q
1
За t лет
t
0
100
2. Сложные проценты – размер вклада ежегодно
увеличивается в одно и то же число раз равное
p
1
100
Таким образом
p
Q1 Q0 1
100
p
Q2 Q0 1
100
2
p
Qt Q0 1
100
t
При начислении процентов n раз в году и ежегодном
приросте р% процент начисления за 1 – часть года составит
n
p
%
n
Размер вклада за t лет при nt начислениях составить
nt
p
Q lim Q0 1
n
100
n
Рассмотрим начисление процентов каждое полугодие ( n=2),
квартал (n=4), ежемесячно (n=12), непрерывно ( n ).
Размер вклада за t лет составит
pt
100 n 100
p
nt
pt
1
p
lim Q0 1
Qt lim Q0 1
Q0 e100
n
100n n 100n
p
=е
Полученная
формула
выражает
показательный
(экспоненциальный) закон роста вклада (при р>0).

Замечание. В практических финансово-кредитных
операциях непрерывно начисление применяется редко.
Этот метод применяется при анализе сложных
финансовых вопросов, таких как обоснование и выбор
инвестиционных решений.
English Русский Правила
Неопределенности в измерениях и почему они важны
Перейти к содержимому
Вы когда-нибудь видели неопределенности в своем сертификате калибровки или слышали, как кто-то говорит о неопределенностях, и задавались вопросом, что они означают? Знаете ли вы, как использовать эту информацию и/или знаете, как она может повлиять на ваши данные измерений?
На самом базовом уровне неопределенность является констатацией качества сообщаемых данных. Даже после того, как все ошибки измерения были приняты во внимание, все еще остаются неизбежные сомнения относительно того, насколько точно измерение отражает измеряемую величину.
Чтобы лучше объяснить это, давайте рассмотрим простой пример. Если вы измеряете длину детали с помощью штангенциркуля и показание составляет 8,52 дюйма, это не представляет истинную длину , это измеренная длина . К сожалению, в реальных приложениях у вас нет способа узнать истинную длину, но если вы оцените неопределенность измерения традиционными способами, вы будете знать, что сделанное вами измерение будет иметь очень высокую вероятность того, что оно будет лежать в пределах определенной неопределенности.
Если вы измеряете длину детали с помощью штангенциркуля и показание составляет 8,52 дюйма, это не представляет истинную длину , это измеренная длина . К сожалению, в реальных приложениях у вас нет способа узнать истинную длину, но если вы оцените неопределенность измерения традиционными способами, вы будете знать, что сделанное вами измерение будет иметь очень высокую вероятность того, что оно будет лежать в пределах определенной неопределенности.
Расширенная неопределенность измерения обычно сообщается с доверительной вероятностью 95%, когда коэффициент охвата или k =2. Это просто означает, что вы берете объединенную погрешность измерения и умножаете ее на 2 . Итак, для нашего примера, если определено, что расширенная погрешность измерения составляет ± 0,2 дюйма, то вы можете быть уверены, что истинное значение находится где-то в диапазоне 0,4 дюйма или, в данном случае, между 8,32–8,72 дюйма.
Чтобы определить совокупную неопределенность ваших результатов, вы должны учесть все источники неопределенности, которые могут повлиять на ваши измерения. Источники погрешности включают спецификацию или допуск используемого стандарта, погрешность калибровки поставщика, сертифицировавшего стандарт, повторяемость и воспроизводимость процесса измерения, факторы окружающей среды, разрешение тестируемого устройства и многое другое, в зависимости от типа используемого оборудования. . Все источники неопределенности можно разделить на две категории: тип A и тип B.
Источники погрешности включают спецификацию или допуск используемого стандарта, погрешность калибровки поставщика, сертифицировавшего стандарт, повторяемость и воспроизводимость процесса измерения, факторы окружающей среды, разрешение тестируемого устройства и многое другое, в зависимости от типа используемого оборудования. . Все источники неопределенности можно разделить на две категории: тип A и тип B.
- Тип A относится к случайным эффектам, которые можно рассчитать через стандартные отклонения повторных измерений. Эти источники неопределенности связаны с повторяемостью и воспроизводимостью. Источники типа А можно улучшить, проанализировав и улучшив процессы измерения.
- Источники типа B относятся к неопределенностям, которые не возникают в результате анализа повторных измерений. Обычно они указываются в сертификатах калибровки эталонных материалов, которые вы используете для калибровки оборудования, или предоставляются производителем оборудования в руководстве или в спецификациях продукта.

Источники после их идентификации объединяются на основе их предполагаемого влияния на общую неопределенность посредством анализа бюджета неопределенности. Это довольно сложный процесс оценки и объединения всех факторов неопределенности в таблице для нахождения суммарного значения неопределенности. Если вы хотите глубже погрузиться в этот процесс, не стесняйтесь обращаться к одному из наших экспертов по измерениям, который может предоставить дополнительную информацию об анализе неопределенности.
Итак, почему неопределенность имеет значение?
Краткий ответ заключается в том, что измерения нельзя сравнивать без погрешностей. Обычно используемый пример — измерение струны. Если вы дадите кусок веревки трем разным людям и попросите их измерить ее без дополнительных инструкций, все они сделают это немного по-разному. Можно положить нить рядом с линейкой и прочитать результат. Следующий может держать веревку вертикально и использовать рулетку для определения длины.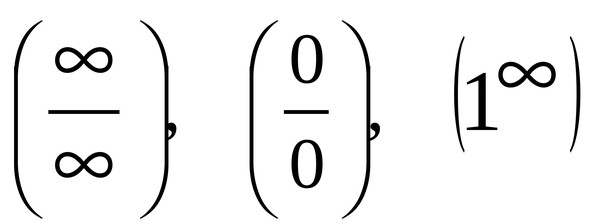 А третий может положить струну рядом с калиброванной линейкой, растянуть струну на всю длину и измерить ее 5 раз, а затем взять среднее значение своих 5 результатов. Как вы можете себе представить, все трое получат немного разные измерения. Последние, вероятно, будут иметь самые низкие неопределенности, потому что их протокол сводит к минимуму влияние случайной ошибки и предвзятости в процессе измерения. По сути, без неопределенностей нельзя сравнивать результаты измерений «яблоки с яблоками».
А третий может положить струну рядом с калиброванной линейкой, растянуть струну на всю длину и измерить ее 5 раз, а затем взять среднее значение своих 5 результатов. Как вы можете себе представить, все трое получат немного разные измерения. Последние, вероятно, будут иметь самые низкие неопределенности, потому что их протокол сводит к минимуму влияние случайной ошибки и предвзятости в процессе измерения. По сути, без неопределенностей нельзя сравнивать результаты измерений «яблоки с яблоками».
Неопределенности важны при определении того, находится ли измеряемая деталь или вещество в пределах допуска. Например, подумайте о примере с суппортом из предыдущего примера. Предположим, что измеряемая вами деталь имеет допуск от 8,4 до 8,6 дюймов, и для вашего процесса критически важно, чтобы деталь находилась в пределах допуска. На основании расширенной неопределенности измерения, представленной в предыдущем примере, деталь может быть неприемлемой. Хотя есть вероятность того, что деталь находится в пределах досягаемости, также высока вероятность того, что деталь имеет размер всего 8,32 дюйма или 8,72 дюйма. Вам нужно будет либо переоценить свой процесс, скорректировать допуск, либо использовать другой инструмент с меньшей неопределенностью. Как правило, вы хотите убедиться, что ваши расширенные погрешности измерения меньше, чем допуск процесса или устройства, и что они достаточно малы, чтобы гарантировать, что они не влияют на достоверность результатов калибровки (т.е. , скорректировано и др.).
Вам нужно будет либо переоценить свой процесс, скорректировать допуск, либо использовать другой инструмент с меньшей неопределенностью. Как правило, вы хотите убедиться, что ваши расширенные погрешности измерения меньше, чем допуск процесса или устройства, и что они достаточно малы, чтобы гарантировать, что они не влияют на достоверность результатов калибровки (т.е. , скорректировано и др.).
At Cross, делая заявления о соответствии, мы используем «принцип общего риска», что означает, что мы не принимаем во внимание неопределенность измерения при заявлении о соответствии. Однако мы предпринимаем шаги, чтобы свести к минимуму неопределенность и избежать проблем, связанных с допусками, при калибровке оборудования. В наших процедурах калибровки мы требуем коэффициента точности испытаний (TAR) 4:1. Это означает, что используемый эталон как минимум в 4 раза более точен, чем допуск точности тестируемого устройства. Иногда невозможно достичь минимального TAR 4:1. В этих случаях мы оцениваем расширенную неопределенность, чтобы убедиться, что результаты измерений остаются достоверными, или рассматриваем возможность аутсорсинга в другую лабораторию с большей неопределенностью. Кроме того, когда мы калибруем оборудование, мы настраиваем его в пределах 70% допуска. Это означает, что если мы обнаружим, что ваше оборудование находится в допустимых пределах, но находится на верхнем или нижнем пределе без уважительной причины, мы настроим оборудование так, чтобы его показания были ближе к середине допустимого диапазона. Подобная практика помогает снизить риск, связанный с неопределенностью измерений, и гарантировать, что вероятность ложного принятия (PFA) представляет «приемлемый риск» для клиента и поставщика продуктов и услуг.*
Кроме того, когда мы калибруем оборудование, мы настраиваем его в пределах 70% допуска. Это означает, что если мы обнаружим, что ваше оборудование находится в допустимых пределах, но находится на верхнем или нижнем пределе без уважительной причины, мы настроим оборудование так, чтобы его показания были ближе к середине допустимого диапазона. Подобная практика помогает снизить риск, связанный с неопределенностью измерений, и гарантировать, что вероятность ложного принятия (PFA) представляет «приемлемый риск» для клиента и поставщика продуктов и услуг.*
Теперь, когда вы знаете больше о погрешностях, вы можете заметить, что они не указаны во всех ваших сертификатах калибровки. Как правило, только аккредитованные сертификаты калибровки включают данные о неопределенности. Свяжитесь с нами сегодня, чтобы узнать больше о наших уровнях калибровки и о том, что данные о неопределенности могут означать для вашего процесса. Наши специалисты по измерениям могут помочь вам определить, какой уровень обслуживания необходим для вашей системы качества.
* Концепция PFA при оформлении заявлений о соответствии и определении приемлемого риска является сложным, что подчеркивается в новых стандартах ISO 17025: 2017. Ожидайте, что мы рассмотрим эту тему более подробно в следующей статье.
Узнайте, как наша группа по прецизионным измерениям может помочь улучшить качество, повысить эффективность и снизить риски.
- 855.889.0092
МагазинКрест
Подпишитесь на нашу рассылку, чтобы получать отраслевые новости, образовательные материалы и обновления продуктов так, как вам удобно.
Загрузите нашу последнюю версию W9
Свяжитесь с нашей командой
Держать крепко! Были Идет поиск… Идет поиск… Идет поиск…
Мы просматриваем тысяч страниц, чтобы найти самую актуальную информацию.
А пока наслаждайтесь этими забавными фактами…
Знаете ли вы… Группа точных измерений в компании Cross была основана в 1939 году дедом нашего нынешнего генерального директора, Джимом Кингом. Это целая куча калибровки!
Это целая куча калибровки!
Знаете ли вы… Отпечаток пальца весит около 50 микрограммов. Мы знаем, мы взвесили это! Остаток, оставшийся от пальца, может повлиять на результаты взвешивания, поэтому мы надеваем перчатки при калибровке весов. Для справки, лист к бумаге примерно 4,5 грамма, это 4,5 миллиона мкг.
Знаете ли вы, что… Cross Company является ESOP (План владения акциями сотрудников). Наш ESOP начался в 1979 году, а с 2006 года мы на 100 % принадлежат сотрудникам! Узнайте больше о нашем ESOP и о том, как это приносит пользу как членам команды, так и нашим клиентам.
Знаете ли вы… Компания Cross значительно выросла с момента своего основания в 1954 году. За эти годы мы приобрели 26 компаний! Сегодня наши пять групп обладают опытом во всем, от промышленной автоматизации до точных измерений, а также отраслевыми знаниями, начиная с 19 века.39.
Как справиться с неопределенностью – HelpGuide.
 org
orgРоль неопределенности в жизни
Неопределенность окружает нас повсюду, и сегодня она как никогда актуальна. Будь то глобальная пандемия, экономика или ваши финансы, здоровье и отношения, многое из того, что ждет вас впереди в жизни, остается неопределенным. Тем не менее, как человеческие существа, мы жаждем безопасности. Мы хотим чувствовать себя в безопасности и контролировать свою жизнь и благополучие. Страх и неуверенность могут оставить вас в состоянии стресса, беспокойства и бессилия над направлением вашей жизни. Это может истощить вас эмоционально и заманить в ловушку бесконечных «а что, если» и наихудших сценариев того, что может принести завтрашний день.
Мы все разные в том, насколько неопределенность мы можем терпеть в жизни. Некоторым людям нравится рисковать и жить непредсказуемой жизнью, в то время как другие находят случайность жизни глубоко огорчительной. Но у всех нас есть предел. Если вы чувствуете себя подавленным неуверенностью и беспокойством, важно знать, что вы не одиноки; многие из нас находятся в одной лодке. Также важно понимать, что независимо от того, насколько беспомощным и безнадежным вы себя чувствуете, есть шаги, которые вы можете предпринять, чтобы лучше справляться с неконтролируемыми обстоятельствами, уменьшить тревогу и с большей уверенностью встретить неизвестное.
Также важно понимать, что независимо от того, насколько беспомощным и безнадежным вы себя чувствуете, есть шаги, которые вы можете предпринять, чтобы лучше справляться с неконтролируемыми обстоятельствами, уменьшить тревогу и с большей уверенностью встретить неизвестное.
Поговорите с лицензированным терапевтом
Крупнейшая в мире терапевтическая служба. 100% онлайн. Получите консультацию профессионального, лицензированного и проверенного терапевта менее чем за 48 часов.
Получите скидку 20%
Профессиональная онлайн-терапия и инструменты, основанные на проверенных стратегиях когнитивно-поведенческой терапии. Получите мгновенную помощь вместе с вашим собственным персонализированным набором инструментов для терапии.
Получите скидку 20%
Раскрытие информации о партнерских программах
Учимся справляться с неопределенностью
Хотя мы, возможно, и не хотим этого признавать, неопределенность — естественная и неизбежная часть жизни. Очень мало в нашей жизни является постоянным или абсолютно определенным, и хотя мы можем контролировать многие вещи, мы не можем контролировать все, что с нами происходит. Как показала пандемия коронавируса, жизнь может меняться очень быстро и очень непредсказуемо. В один день все может быть просто прекрасно, а в следующий вы внезапно заболеете, потеряете работу или обнаружите, что изо всех сил пытаетесь накормить стол или обеспечить свою семью.
Очень мало в нашей жизни является постоянным или абсолютно определенным, и хотя мы можем контролировать многие вещи, мы не можем контролировать все, что с нами происходит. Как показала пандемия коронавируса, жизнь может меняться очень быстро и очень непредсказуемо. В один день все может быть просто прекрасно, а в следующий вы внезапно заболеете, потеряете работу или обнаружите, что изо всех сил пытаетесь накормить стол или обеспечить свою семью.
Чтобы справиться со всей этой неопределенностью, многие из нас используют тревогу как инструмент, чтобы попытаться предсказать будущее и избежать неприятных сюрпризов. Из-за беспокойства может показаться, что у вас есть некоторый контроль над неопределенными обстоятельствами. Вы можете полагать, что это поможет вам найти решение ваших проблем или подготовит вас к худшему. Может быть, если вы достаточно долго будете мучиться над проблемой, просто обдумаете каждую возможность или прочитаете каждое мнение в Интернете, вы найдете решение и сможете контролировать результат. К сожалению, ничего из этого не работает. Хроническое беспокойство не может дать вам больше контроля над неконтролируемыми событиями; это просто лишает вас удовольствия в настоящем, истощает вашу энергию и не дает вам спать по ночам. Но есть более здоровые способы справиться с неопределенностью — и это начинается с корректировки вашего мышления.
К сожалению, ничего из этого не работает. Хроническое беспокойство не может дать вам больше контроля над неконтролируемыми событиями; это просто лишает вас удовольствия в настоящем, истощает вашу энергию и не дает вам спать по ночам. Но есть более здоровые способы справиться с неопределенностью — и это начинается с корректировки вашего мышления.
[Читайте: Как перестать беспокоиться]
Следующие советы помогут вам:
- Сосредоточьтесь на том, чтобы контролировать то, что находится под вашим контролем.
- Испытайте свою потребность в уверенности.
- Научитесь лучше терпеть и даже принимать неизбежную неопределенность жизни.
- Уменьшите уровень беспокойства и стресса.
Совет 1. Действуйте над тем, что вы можете контролировать
В настоящее время в жизни многое неясно, и многие вещи остаются вне вашего контроля. Но хотя вы не можете контролировать распространение вируса, восстановление экономики или получение зарплаты на следующей неделе, вы не совсем бессильны. Какими бы ни были ваши страхи или личные обстоятельства, вместо того, чтобы беспокоиться о неконтролируемом, постарайтесь переориентировать свой разум на принятие мер в отношении тех аспектов, которые находятся под вашим контролем.
Какими бы ни были ваши страхи или личные обстоятельства, вместо того, чтобы беспокоиться о неконтролируемом, постарайтесь переориентировать свой разум на принятие мер в отношении тех аспектов, которые находятся под вашим контролем.
Например, если вы потеряли работу или доход в это трудное время, вы все еще можете контролировать, сколько энергии вы тратите на поиск работы в Интернете, отправку резюме или общение в сети со своими контактами. Точно так же, если вы беспокоитесь о своем здоровье или недавнем диагнозе, например, вы все равно можете принять меры, снизив уровень стресса, обратившись за поддержкой к близким и справившись со своими симптомами.
Сосредоточив внимание на тех аспектах проблемы, которые вы можете таким образом контролировать, вы переключитесь с неэффективного беспокойства и размышлений на активное решение проблемы. Конечно, все обстоятельства разные, и вы можете обнаружить, что в некоторых ситуациях вы можете контролировать только свое отношение и эмоциональную реакцию.
[Читать: Преодоление опасной для жизни болезни или серьезного нарушения здоровья]
Активно справляться со своими эмоциями
Когда обстоятельства выходят из-под вашего контроля, страх и негативные эмоции могут легко захлестнуть вас. Вы можете думать, что если сдерживать свои чувства, пытаться сделать храброе лицо или заставлять себя быть позитивным, то это даст наилучший результат. Но отрицание или подавление своих эмоций только усилит стресс и тревогу и сделает вас более уязвимыми для депрессии или эмоционального выгорания.
Когда вы ничего не можете поделать с ситуацией, вы все равно можете активно противостоять своим эмоциям, даже самым негативным и пугающим. Позволив себе испытать неуверенность таким образом, вы сможете уменьшить стресс, лучше смириться со своими обстоятельствами и обрести чувство спокойствия, сталкиваясь с трудностями.
Совет 2: бросьте вызов своей потребности в уверенности
Хотя неопределенность и перемены — неотъемлемая часть жизни, мы часто принимаем определенные меры, чтобы справиться с дискомфортом, который они могут принести.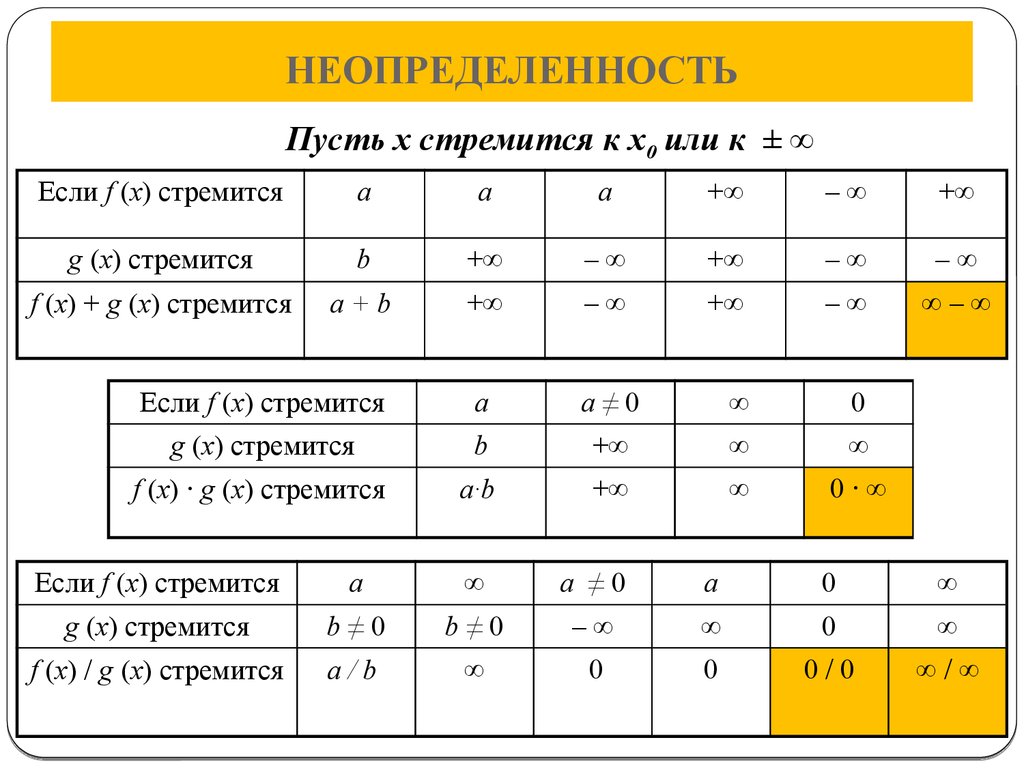 Помимо беспокойства по поводу всех возможных сценариев, вы можете:
Помимо беспокойства по поводу всех возможных сценариев, вы можете:
Чрезмерно искать поддержки у других . Вы постоянно спрашиваете друзей или близких, принимаете ли вы правильное решение, бесконечно ищете информацию в Интернете или ищете совета у экспертов, чтобы избавиться от неопределенности в своей жизни.
Микроуправление людьми . Вы отказываетесь делегировать задачи другим, ни на работе, ни дома. Вы даже можете попытаться заставить окружающих вас людей измениться, сделать их поведение более предсказуемым для вас.
Промедление . Не принимая решений, вы надеетесь избежать неопределенности, которая неизбежно последует. Вы найдете способы отсрочить или отсрочить действие — или даже вообще избегать определенных ситуаций — в попытке предотвратить плохие вещи.
Неоднократно проверять вещи . Вы снова и снова звоните или пишете своей семье, друзьям или детям, чтобы убедиться, что они в безопасности. Вы проверяете и перепроверяете электронные письма, тексты или формы перед отправкой, перепроверяете списки, чтобы убедиться, что вы не пропустили ничего, что могло бы повлиять на предсказуемость будущего.
Вы проверяете и перепроверяете электронные письма, тексты или формы перед отправкой, перепроверяете списки, чтобы убедиться, что вы не пропустили ничего, что могло бы повлиять на предсказуемость будущего.
Как бросить вызов такому поведению
Вы можете бросить вызов поведению, которое вы выбрали для облегчения дискомфорта от неопределенности, задав себе следующие вопросы:
- Каковы преимущества уверенности? Каковы недостатки? Жизнь может измениться в одно мгновение, она полна неожиданных событий и сюрпризов, но это не всегда плохо. На каждый неприятный сюрприз, такой как дорожно-транспортное происшествие или серьезный медицинский диагноз, есть и хорошие вещи, которые случаются ни с того ни с сего — предложение о работе мечты, неожиданное повышение зарплаты или неожиданный телефонный звонок от старого друга. Возможности часто возникают из-за неожиданностей, и необходимость столкнуться с неопределенностью в жизни также может помочь вам научиться адаптироваться, преодолевать трудности и повышать свою устойчивость.
 Это может помочь вам вырасти как личности.
Это может помочь вам вырасти как личности. - В чем вы можете быть абсолютно уверены в жизни? Есть ли у кого-нибудь работа на всю жизнь, гарантия крепкого здоровья или абсолютная уверенность в завтрашнем дне? Такое поведение, как беспокойство, микроуправление и прокрастинация, создают иллюзию некоторого контроля над ситуацией, но что они меняют на самом деле? Правда в том, что как бы вы ни старались планировать и готовиться к каждому возможному исходу, жизнь найдет способ удивить вас. Все, что на самом деле делает стремление к определенности, лишь подпитывает тревогу и тревогу.
- Вы предполагаете, что плохие вещи произойдут только потому, что результат неясен? Какова вероятность, что они будут? Когда вы сталкиваетесь с неопределенностью, легко переоценить вероятность того, что случится что-то плохое, и недооценить свою способность справиться, если это произойдет. Но учитывая, что вероятность того, что случится что-то плохое, низка даже в эти нестабильные времена, можно ли жить с этим небольшим шансом и вместо этого сосредоточиться на более вероятных результатах? Спросите своих друзей и семью, как они справляются с неопределенностью в определенных обстоятельствах.
 Не могли бы вы сделать то же самое?
Не могли бы вы сделать то же самое?
Борясь со своей потребностью в уверенности, вы можете начать избавляться от негативного поведения, уменьшить стресс и беспокойство и высвободить время и энергию для более практических целей.
Совет 3. Научитесь принимать неопределенность
Как бы вы ни старались избавиться от сомнений и непостоянства в своей жизни, правда в том, что вы и так ежедневно принимаете неопределенность. Каждый раз, когда вы переходите улицу, садитесь за руль автомобиля или едите еду на вынос или в ресторане, вы принимаете определенный уровень неопределенности. Вы верите, что движение остановится, вы не попадете в аварию и все, что вы едите, безопасно.
Вероятность того, что в таких обстоятельствах произойдет что-то плохое, невелика, поэтому вы принимаете риск и идете дальше, не требуя определенности. Если вы религиозны, вы также, вероятно, принимаете некоторые сомнения и неуверенность как часть своей веры.
Когда вас одолевают иррациональные страхи и беспокойства, бывает трудно логически мыслить и точно взвешивать вероятность того, что произойдет что-то плохое. Чтобы помочь вам стать более терпимым и принять неопределенность, могут помочь следующие шаги:
Определите свои триггеры неопределенности . Большая часть неуверенности, как правило, возникает сама по себе, например, из-за чрезмерного беспокойства или пессимистического взгляда. Однако некоторая неопределенность может быть вызвана внешними источниками, особенно в такие моменты. Чтение статей в СМИ, посвященных наихудшим сценариям, проведение времени в социальных сетях среди слухов и полуправды или просто общение с встревоженными друзьями — все это может подпитывать ваши собственные страхи и неуверенность. Вот почему так много людей начинают панически покупать, когда приходят плохие новости — они видят, как это делают другие, и это подпитывает их собственные страхи. Распознав свои триггеры, вы можете предпринять действия, чтобы избежать или уменьшить воздействие на них.
Распознавайте, когда чувствуете потребность в уверенности . Обратите внимание, когда вы начинаете беспокоиться и бояться ситуации, начинаете беспокоиться о том, что, если, или чувствуете, что ситуация намного хуже, чем она есть на самом деле. Ищите физические признаки того, что вы испытываете тревогу. Вы можете заметить напряжение в шее или плечах, одышку, появление головной боли или чувство пустоты в желудке. Найдите минутку, чтобы сделать паузу и признать, что вы жаждете уверенности или гарантии.
[Читайте: Тревожные расстройства и тревожные атаки]
Позвольте себе почувствовать неуверенность . Вместо того, чтобы предпринимать тщетные попытки получить контроль над неконтролируемым, позвольте себе испытать дискомфорт неопределенности. Как и все эмоции, если вы позволите себе чувствовать страх и неуверенность, они в конечном итоге пройдут. Сосредоточьтесь на настоящем моменте и своем дыхании и позвольте себе просто чувствовать и наблюдать неуверенность, которую вы испытываете.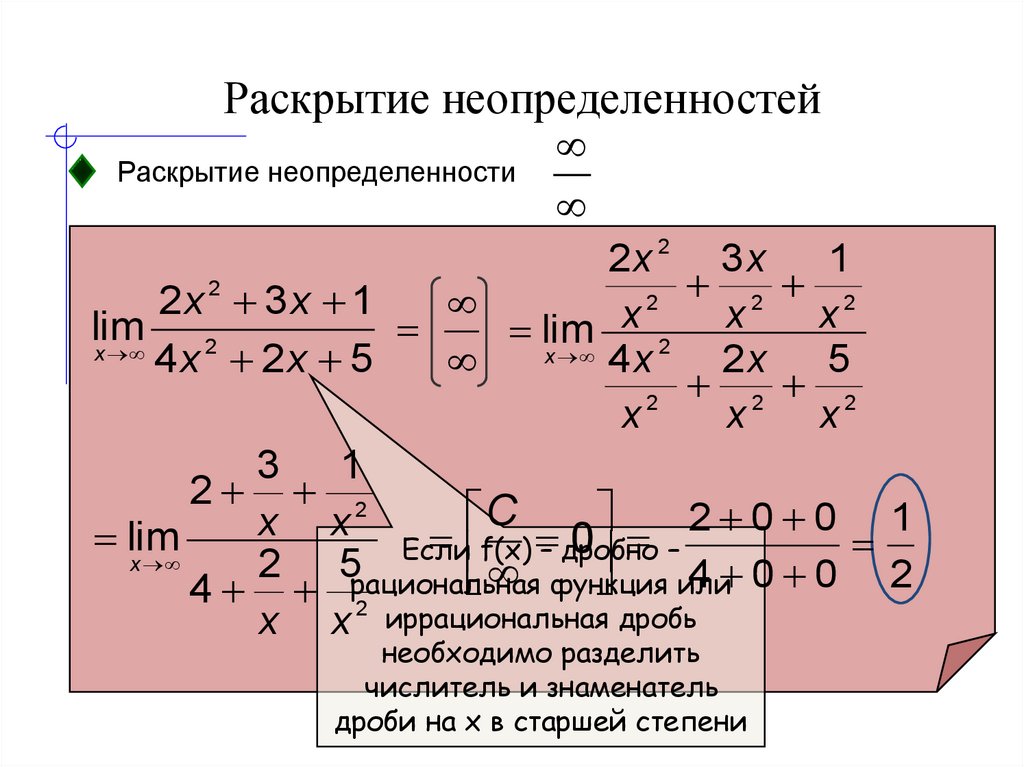 Сделайте несколько медленных глубоких вдохов или попробуйте медитацию, чтобы закрепиться в настоящем.
Сделайте несколько медленных глубоких вдохов или попробуйте медитацию, чтобы закрепиться в настоящем.
Отпустить . Отвечайте на мысли, которые приходят вам в голову, признавая, что вы не гадалка; вы не знаете, что произойдет. Все, что вы можете сделать, это отпустить ситуацию и принять неопределенность как часть жизни.
Переключи внимание . Сосредоточьтесь на решаемых проблемах, приняв меры по тем аспектам проблемы, которые вы можете контролировать, или просто вернитесь к тому, что вы делали. Когда ваш разум возвращается к беспокойству или возвращается чувство неуверенности, снова сосредоточьтесь на настоящем моменте и собственном дыхании.
Принятие неопределенности не означает отсутствия плана
Принятие неопределенности не означает, что у вас не должно быть плана на случай некоторых непредвиденных жизненных обстоятельств. Всегда полезно иметь некоторые сбережения на случай непредвиденных расходов, держать под рукой набор для подготовки, если вы живете в районе, подверженном риску землетрясений или ураганов, или иметь план на случай, если вы или ваш близкий заболеете. Но вы не можете подготовиться ко всем возможным сценариям. Жизнь слишком случайна и непредсказуема.
Но вы не можете подготовиться ко всем возможным сценариям. Жизнь слишком случайна и непредсказуема.
Совет 4: Сосредоточьтесь на настоящем
Неопределенность часто связана с беспокойством о будущем и обо всех плохих вещах, которые вы можете предвидеть. Это может вызвать у вас чувство безнадежности и депрессии по поводу предстоящих дней, преувеличить масштабы проблем, с которыми вы сталкиваетесь, и даже парализовать вас от принятия мер для решения проблемы.
Один из самых надежных способов не беспокоиться о будущем — сосредоточиться на настоящем. Вместо того, чтобы пытаться предсказать, что может произойти, переключите свое внимание на то, что происходит прямо сейчас. Будучи полностью подключенным к настоящему, вы можете прервать негативные предположения и катастрофические прогнозы, проходящие в вашем уме.
Вы можете научиться целенаправленно сосредотачивать свое внимание на настоящем с помощью осознанности. При регулярной практике внимательность может помочь изменить вашу озабоченность будущими заботами на более сильное понимание настоящего момента, а также поможет успокоить ваш разум, снять стресс и улучшить общее настроение.
Вы можете начать практику осознанности, следуя аудиомедитации или включив ее в программу упражнений, например ходьбу. Использование осознанности, чтобы оставаться сосредоточенным на настоящем, может потребовать настойчивости. Поначалу вы можете обнаружить, что ваше внимание продолжает возвращаться к вашим будущим страхам и беспокойствам, но продолжайте в том же духе. Каждый раз, когда вы снова сосредотачиваете свое внимание на настоящем, вы укрепляете новую умственную привычку, которая может помочь вам освободиться от неуверенности.
Совет 5. Справляйтесь со стрессом и беспокойством
Принятие мер по снижению общего уровня стресса и беспокойства может помочь вам прервать нисходящую спираль негативных мыслей, обрести внутреннее спокойствие и лучше справляться с неопределенностью в вашей жизни.
Двигайся . Физические упражнения — это естественное и эффективное средство для снятия стресса и снятия беспокойства.
