Неопределенный интеграл формулы: Найти неопределённый интеграл: начала начал, примеры решений

11.1.1. Основные формулы и свойства неопределенного интеграла.

Главная » 11 класс. Алгебра. » 11.1.1. Основные формулы и свойства неопределенного интеграла

Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 4.1k. Опубликовано 9 сентября 2012

Все простейшие формулы интегралов будут иметь вид:

∫f (x) dx=F (x)+C, причем, должно выполняться равенство:

(F (x)+C)’=f (x).

Формулы интегрирования можно получить обращением соответствующих формул дифференцирования.

Действительно,

Показатель степени n может быть  и дробным. Часто приходится находить неопределенный интеграл от функции у=√х. Вычислим интеграл от функции f (x)=√x, используя формулу 1).

Запишем этот пример в виде формулы 2).

Так как (х+С)’=1, то ∫dx=x+C.

3) ∫dx=x+C.

Заменяя 1/х² на х^-2, вычислим интеграл от 1/х².

А можно было получить этот ответ обращением известной формулы дифференцирования:

Запишем наши рассуждения в виде формулы 4).

Умножив обе части полученного равенства на 2, получим формулу 5).

Найдем интегралы от основных тригонометрических функций, зная их производные: (sinx)’=cosx; (cosx)’=-sinx; (tgx)’=1/cos²x; (ctgx)’=-1/sin²x. Получаем формулы интегрирования 6) — 9).

6) ∫cosxdx=sinx+C;

7) ∫sinxdx=-cosx+C;

После изучения показательной и логарифмической функций, добавим еще несколько формул.

Основные свойства неопределенного интеграла.

I. Производная неопределенного интеграла равна подынтегральной функции.

(∫f (x) dx)’=f (x).

II. Дифференциал неопределенного интеграла равен подынтегральному выражению.

d∫f (x) dx=f (x) dx.

III. Неопределенный интеграл от дифференциала (производной) некоторой функции равен сумме этой функции и произвольной постоянной С.

∫dF (x)=F (x)+C  или   ∫F'(x) dx=F (x)+C.

Обратите внимание: в I, II и III свойствах знаки дифференциала и интеграла (интеграла и дифференциала) «съедают» друг друга!

IV. Постоянный множитель подынтегрального выражения можно вынести за знак интеграла.

∫kf (x) dx=k·∫f (x) dx, где k – постоянная величина, не равная нулю.

V.  Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций.

∫(f (x)±g (x)) dx=∫f (x) dx±∫g (x) dx.

VI. Если F (x) есть первообразная для f (x), а k и b — постоянные величины, причем, k≠0, то (1/k)·F (kx+b) есть первообразная для f (kx+b). Действительно, по правилу вычисления производной сложной функции имеем:

Можно записать:

неопределенный интеграл

( 1 оценка, среднее 5 из 5 )

Формулы. Справочный материал. Неопределенный интеграл

Первообразная

(1) F(x) называется первообразной для f(x) на заданном промежутке, если и

Неопределенный интеграл

(2) С – произвольная постоянная

Свойства неопределенного интеграла

(3)

(4)

(5)

(6)

(7)

(8)

Таблица интегралов

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

Метод интегрирования с помощью замены переменной

(33) Метод подведения под знак дифференциала:

(34)

(35)

Метод интегрирования по частям

(36)

(37)

Интегрирование рациональных дробей

(38)

– многочлены.

Сводится к сумме интегралов от простейших рациональных дробей методом неопределенных коэффициентов

Интегрирование простейших рациональных дробей

(39) Простейшая дробь 1-го типа:

(40) Простейшая дробь 2-го типа:

(41) Простейшая дробь 3-го типа:

(42) Простейшая дробь 4-го типа:

(43)

(44)

Интегралы от некоторых рациональных дробей

(45)

(46)

(47)

(48)

(49)

(50)

(51)

(52)

(53)

(54)

(55)

(56)

(57)

(58)

(59)

(60)

(61)

(62)

(63)

(64)

Интегралы от некоторых иррациональных функций

(65)

(66)

(67)

(68)

(69)

(70)

(71)

(72)

Интегралы от некоторых показательных и логарифмических функции

(73)

(74)

(75)

(76)

(77)

(78)

(79)

(80) ;

(81)

(82)

Интеграл от некоторых тригонометрических функций

(83)

(84)

(85)

(86)

(87)

(88)

(89)

(90)

(91)

(92)

(93)

(94)

(95)

(96)

(97)

(98)

(99)

(100)

(101)

(102)

Связь определенного и неопределенного интеграла

1. Если непрерывна на отрезке, то функция

– одна из первообразных для , то есть

(2) – произвольная постоянная

Формула Ньютона-Лейбница

(3)

Свойства определенного интеграла

(4)

(5)

(6)

(7) (аддитивность)

(8) – постоянная

(9)

(10) Если – четная, то

(11) Если – нечетная, то

Оценки значения определенного интеграла (a<b)

(12)

(13)

(14)

(15)

(16) Если непрерывна на отрезке , то

(теорема о среднем)

Метод интегрирования с помощью замены переменной

(17)

(18)

Метод интегрирования по частям

(19)

(20)

Вычисление площадей, длин дуг и объемов с помощью определенного интеграла

(21) Вычисление площади криволинейной трапеции, ограниченной графиком непрерывной функции ,и прямыми

(22) Вычисление площади криволинейной трапеции, ограниченной графиком функции, заданной в параметрической форме

(23) Вычисление площади криволинейного сектора, ограниченного графиком непрерывной функции и лучами(в полярных координатах):

(24) Вычисление длины дуги кривой, заданной непрерывной функцией , имеющей непрерывную производную,:

(25) Вычисление длины дуги кривой, заданной функцией в параметрической форме

(26) Вычисление длины дуги кривой, заданной функцией , имеющей непрерывную производную в области определения

(27) Вычисление объема тела вращения, образованного криволинейной трапецией, ограниченной графиком непрерывной неотрицательной функции и прямымипри вращении вокруг оси ОХ:

(28) Вычисление объема тела через площадь поперечного сечения , перпендикулярного оси ОХ:

(29) Вычисление площади поверхности тела вращения, образованного графиком непрерывной, имеющей непрерывную производную, неотрицательной функции при вращении вокруг оси ОХ в области определения:

(30) Вычисление площади поверхности тела вращения, образованного графиком функции, заданной в параметрической форме

(31) вычисление площади поверхности тела вращения, образованного графиком непрерывной, имеющей непрерывную производную, функции в области определения, при вращении вокруг оси ОХ:

5.

1: Неопределенный интеграл – Mathematics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

54786

• Майкл Коррал
• Schoolcraft College

Производные появляются во многих физических явлениях, таких как движение объектов. Вспомним, например, что, зная функцию положения \(s(t)\) объекта, движущегося по прямой линии в момент времени \(t\), можно найти скорость \(v(t)=s'(t )\) и ускорение \(a(t)=v'(t)\) объекта в момент времени \(t\) путем взятия производных. Предположим, что ситуация была обратной: если задана функция скорости, как бы вы нашли функцию положения, или задана функция ускорения, как бы вы нашли функцию скорости?

В этом случае вычисление производной не поможет, так как нужен обратный процесс: вместо дифференцирования нужен способ выполнения антидифференцирования , т. е. вычисление первопроизводной .

Дифференциация относительно проста. Вы изучили производные многих классов функций (например, многочлены, тригонометрические функции, экспоненциальные и логарифмические функции), и с помощью различных правил дифференцирования вы можете вычислять производные сложных выражений, включающих эти функции (например, суммы, степени, произведения, частные) . Однако антидифференциация — это отдельная история. 92 + C\) — производная которой также оказывается \(f(x) = 2x\)? К счастью, ответ отрицательный:

.

Чтобы доказать это, рассмотрим функцию \(H(x) = F(x) – G(x)\), определенную для всех \(x\) в общей области \(I\) функции \(F\) и \(G\). Поскольку \(F'(x) = G'(x) = f(x)\), то

\[H'(x) ~=~ F'(x) ~-~ G'(x) ~=~ f(x) ~-~ f(x) ~=~ 0\] для всех \(x\ ) в \(I\), поэтому \(H(x)\) является постоянной функцией на \(I\), как было показано в разделе 4.4 о теореме о среднем значении. Таким образом, существует константа \(С\) такая, что 92 + C\), где \(C\) — константа общего положения.

Таким образом, функции имеют не одну первообразную, а целое семейство первообразных, отличающихся только константой. Следующие обозначения облегчают выражение всего этого:

.

Большой S-образный символ перед \(f(x)\) называется знаком интеграла . Хотя неопределенный интеграл \(\int f(x)~\dx\) представляет всех первообразных \(f(x)\), этот интеграл можно рассматривать как отдельный объект или функцию в своем собственном праве, чья производная равна \(f'(x)\):

Вам может быть интересно, что представляет собой знак интеграла в неопределенном интеграле и почему включено бесконечно малое число \(\dx\). Это связано с тем, что представляет бесконечно малая величина: бесконечно малая «часть» количества. Для первообразной \(F(x)\) функции \(f(x)\) инфинитезимальная (или дифференциальная) \(d\!F\) определяется формулой \(d\!F = F'( х)\,\dx = f(x)\,\dx\), и поэтому

\[F(x) ~=~ \int\,f(x)~\dx ~=~ \int\,d\!F ~.\] Таким образом, знак интеграла действует как символ суммирования: он суммирует бесконечно малые «кусочки» \(d\!F\) функции \(F(x)\) в каждом \(x\), так что в сумме они составляют всю функцию \(F(x)\).

Думайте об этом как о обычном символе суммирования \(\Sigma\), используемом для дискретных сум; знак интеграла \(\int\) вместо этого принимает сумму континуума бесконечно малых величин.

Нахождение (или вычисление ) неопределенного интеграла функции называется интегрированием функции, а интегрированием является антидифференцированием.

Пример \(\PageIndex{1}\): antideriv1

Добавьте сюда текст.

Решение

Вычислить \(\displaystyle\int\,0~\dx\).

Решение: Поскольку производная любой постоянной функции равна 0, то \(\int\,0~\dx = C\), где \(C\) — общая константа.

Примечание. С этого момента \(C\) будет просто считаться универсальной константой, без необходимости каждый раз указывать это явно.

Пример \(\PageIndex{1}\): antideriv2

Добавьте сюда текст.

Решение

Вычислить \(\displaystyle\int\,1~\dx\).

Решение: Поскольку производная \(F(x) = x\) равна \(F'(x) = 1\), то \(\int\,1~\dx = x + C\). 9{-1}\), то можно проинтегрировать любую степень \(x\):

Следующие правила для неопределенных интегралов являются прямым следствием правил для производных:

Приведенные выше правила легко доказать. Например, первое правило является простым следствием постоянного кратного правила для производных: если \(F(x) = \int\,f(x)~\dx\), то

\[\ddx(k\,F(x)) ~=~ k\,\ddx(F(x)) ~=~ k\,f(x) \quad\Стрелка вправо\quad \int\,k\ ;f(x)~\dx ~=~ k\,F(x) ~=~ k\,\int\,f(x)~\dx ~.\quad\checkmark\] Остальные правила доказываются аналогично и остаются в качестве упражнений. Повторное использование приведенных выше правил вместе с формулой мощности показывает, что любой многочлен можно интегрировать почленно — фактически любую конечную сумму функций можно интегрировать таким образом: 92 + 100\), измеряется в футах.

Решение: Когда объект падает в момент времени \(t=0\), единственной силой, действующей на него, является гравитация, заставляющая объект двигаться вниз с известной постоянной скоростью 32 фута/с ² . Таким образом, ускорение объекта \(a(t)\) в момент времени \(t\) равно \(a(t) = -32\). Если \(v(t)\) – скорость объекта в момент времени \(t\), то \(v'(t) = a(t)\), а это означает, что

\[v(t) ~=~ \int a(t)~\dt ~=~ \int -32~\dt ~=~ -32t ~+~ C\] для некоторой константы \(C\). Константа \(C\) здесь равна 92 ~+~ 100\] для всех \(t \ge 0\).

Формула для \(s(t)\) в примере

Пример \(\PageIndex{1}\): гравитация

Добавьте сюда текст.

Решение

можно обобщить следующим образом: обозначим начальное положение объекта в момент времени \(t=0\) через \(s_0\), пусть \(v_0\) – начальная скорость объекта (положительная, если брошено вверх, отрицательный, если его бросают вниз), и пусть \(g\) представляет собой (положительное) постоянное ускорение под действием силы тяжести. По первому закону Ньютона единственное ускорение, сообщаемое телу 92 + v_0(0) + С = С\). Подводя итог:

Обратите внимание, что единицы измерения не указаны — они просто должны быть согласованы. В метрических единицах \(g = 9,8\) м/с ² , а \(g = 32\) фут/с ² в английских единицах.

Представление о неопределенном интеграле как о сумме всех бесконечно малых «частей» функции — с целью извлечения этой функции — обеспечивает удобный способ интегрирования дифференциального уравнения для получения решения. Ключевая идея состоит в том, чтобы преобразовать дифференциальное уравнение в 9{kt}\) для некоторой константы \(A\). Можно предположить, что \(y(t) > 0\) для всех \(t\).

Решение: Поместите члены \(y\) слева и члены \(t\) справа, т.е. разделите переменные:

\[\frac{\dy}{y} ~=~ k\,\dt\] Теперь проинтегрируйте обе части (обратите внимание, как функция \(y\) обрабатывается как переменная ):

\[\begin{align} \int\,\frac{\dy}{y} ~&=~ \int k\,\dt\

\[6pt] \ln\,y + C_1 ~&=~ kt + C_2 \quad\text{($C_1$ и $C_2$ — константы)}\\ \ln\,y ~&=~ kt + C \quad\text{(объединить $C_1$ и $C_2$ в константу $C$)}\\ y ~&=~ e^{kt+C} ~=~ e^{kt} \cdot e^C ~ =~ A e^{kt}\end{aligned}\], где \(A = e^C\) — константа. Обратите внимание, что это формула радиоактивного распада из раздела 2.3.

Пример \(\PageIndex{1}\): intidealgas

Добавьте сюда текст.

Решение

Вспомним из раздела 3.6 уравнение дифференциальных

\[\dfrac{\dP}{P} ~+~ \dfrac{\dV}{V} ~=~ \dfrac{\dT}{T}\] относительно давления \(P\), объема \( V\) и температура \(T\) идеального газа. Проинтегрируйте это уравнение, чтобы получить исходный закон идеального газа \(PV = RT\), где \(R\) – константа. .

Решение: Интегрирование обеих частей уравнения дает 9С\) является константой.

Формулы интегрирования в этом разделе зависели от того, что уже были известны производные определенных функций, а затем «работали в обратном направлении» от их производных для получения исходных функций. Без этих предварительных знаний вы были бы сведены к догадкам или, возможно, к распознаванию паттерна из какой-то производной, с которой вы столкнулись. Вскоре будет представлен ряд методов интегрирования, но есть много неопределенных интегралов, для которых не существует простой замкнутой формы (например, \(\int e^{x^2}\,\dx\) и \(\int \sin( х^2)\,\dx\)). 2}{ 2g}\).

---

1. В этом случае предполагается, что функция \(f\) дифференцируема в точке \(x\). Если нет, то точки, в которых \(f\) не дифференцируемы, можно исключить, не влияя на интеграл.
2. Доказательство и более полное обсуждение всего этого см. в главах 1-2 в Knopp, MI, Theory of Area , Chicago: Markham Publishing Co., 1969. В книге делается попытка точно определить, что на самом деле означает «площадь». , включая прямоугольник (показывая согласие с интуитивным понятием ширины, умноженной на высоту).↩
3. Теорема может быть доказана для более слабого условия, что \(f\) просто непрерывно на \(\ival{a}{b}\). См. стр. 173-175 у Parzynski, W.R. and P.W. Zipse, Introduction to Mathematical Analysis , New York: McGraw-Hill, Inc., 1982. ↩
4. Создан физиком П.А.М. Дирак (1902-1984), получивший Нобелевскую премию по физике в 1933 году. Функция не является ни вещественной, ни непрерывной в \(x=0\). «График» на рисунке [fig:dirac], возможно, вводит в заблуждение, поскольку \(\infty\) не является фактической точкой на оси \(y\). Одна из интерпретаций состоит в том, что \(\delta\) представляет собой абстракцию мгновенного импульса или всплеска из что-то , с предшествующим и последующим ничего . Чтобы узнать больше об этой увлекательной и полезной функции, см. §15 в Dirac, P.A.M., The Principles of Quantum Mechanics , 4-е изд., Оксфорд, Великобритания: Oxford University Press, 1958.↩
5. См. стр. 140-141 в Buck, RC, Advanced Calculus , 2nd ed., New York: McGraw-Hill Book Co., 1965. ↩

---

Эта страница под названием 5.1: The Indefinite Integral распространяется под лицензией GNU General Public License 3.0 и была создана, изменена и/или курирована Майклом Корралом.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Майкл Коррал

   Лицензия

   GNU GPL

   Показать страницу TOC

   нет

2. Теги

   На этой странице нет тегов.

5.4: Неопределенные интегралы и теорема о чистом изменении

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4474

Цели обучения

• Применение основных формул интегрирования.
• Объясните значение теоремы о чистом изменении.
• Используйте теорему о чистых изменениях для решения прикладных задач.
• Применить интегралы от нечетных и четных функций.

В этом разделе мы используем некоторые основные формулы интегрирования, изученные ранее, для решения некоторых ключевых прикладных задач. Важно отметить, что эти формулы представлены в терминах неопределенных интегралов. Хотя определенные и неопределенные интегралы тесно связаны между собой, следует помнить о некоторых ключевых различиях. Определенный интеграл — это либо число (когда пределы интегрирования — константы), либо отдельная функция (когда один или оба предела интегрирования — переменные). Неопределенный интеграл представляет собой семейство функций, каждая из которых отличается на константу. По мере того, как вы будете лучше знакомиться с интегрированием, вы почувствуете, когда использовать определенные интегралы и когда использовать неопределенные интегралы. Вы, естественно, выберете правильный подход к данной проблеме, не слишком задумываясь об этом. Однако до тех пор, пока эти концепции не закрепятся в вашем уме, тщательно подумайте, нужен ли вам определенный интеграл или неопределенный интеграл, и убедитесь, что вы используете правильную запись, основанную на вашем выборе. 92 – 3x\справа) \, dx = −\frac{10}{3} \nonumber \]

Теорема о чистом изменении

Теорема о чистом изменении рассматривает интеграл скорости изменения . В нем говорится, что при изменении количества новое значение равно первоначальному значению плюс интеграл скорости изменения этого количества. Формула может быть выражена двумя способами. Второй более знаком; это просто определенный интеграл.

Теорема о чистом изменении

Новое значение изменяющейся величины равно первоначальному значению плюс интеграл скорости изменения: 9b_aF'(x)dx=F(b)−F(a). \label{Net2} \]

Вычитание \(F(a)\) из обеих частей уравнения \ref{Net1} дает уравнение \ref{Net2}. Поскольку это эквивалентные формулы, какую из них мы используем, зависит от приложения.

Значение теоремы о чистом изменении заключается в результатах. Чистое изменение может быть применено к площади, расстоянию и объему, и это лишь некоторые из приложений. Чистое изменение учитывает отрицательные величины автоматически, без необходимости писать более одного интеграла. Чтобы проиллюстрировать это, давайте применим теорему о чистом изменении к скорость функция, результатом которой является смещение.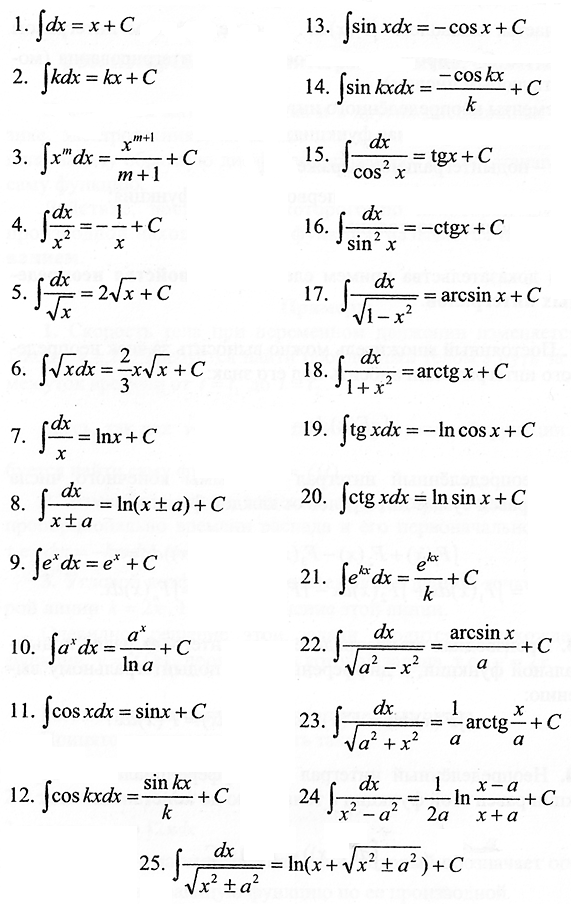

Мы рассмотрели простой пример этого в разделе «Определенный интеграл». Предположим, что автомобиль движется прямо на север (в положительном направлении) со скоростью 40 миль в час между 14:00 и 14:00. и 16:00, затем машина движется на юг со скоростью 30 миль в час между 16:00 и 16:00. и 17:00 Мы можем изобразить это движение, как показано на рисунке \(\PageIndex{1}\).

Рисунок \(\PageIndex{1}\): График показывает зависимость скорости от времени для заданного движения автомобиля.

Как и прежде, мы можем использовать определенные интегралы для расчета чистого перемещения, а также общего пройденного расстояния. 95_430\,дт=80+30=110. \nonumber \]

Таким образом, между 14:00 и 17:00 машина проехала в общей сложности 110 миль.

Подводя итог, чистое перемещение может включать как положительные, так и отрицательные значения. Другими словами, функция скорости учитывает как расстояние вперед, так и расстояние назад. Чтобы найти чистое смещение, проинтегрируйте функцию скорости по интервалу. С другой стороны, общее пройденное расстояние всегда положительно. Чтобы найти общее расстояние, пройденное объектом независимо от направления, нам нужно проинтегрировать абсолютное значение функции скорости. 92}{2}−5(3)\right]−0=\frac{27}{2}−15=\frac{27}{2}−\frac{30}{2}=−\frac{3 {2}. \nonumber \]

Чистое водоизмещение равно \( −\frac{3}{2}\) м (рис. \(\PageIndex{2}\)).

Рисунок \(\PageIndex{2}\): График показывает зависимость скорости от времени для частицы, движущейся с линейной функцией скорости.

Пример \(\PageIndex{3}\): определение общего пройденного расстояния

Используйте пример \(\PageIndex{2}\) для нахождения общего расстояния, пройденного частицей, в соответствии с функцией скорости \(v(t) =3t−5\) м/с за интервал времени \([0,3].\)

Решение

Общее пройденное расстояние включает как положительные, так и отрицательные значения. Следовательно, мы должны проинтегрировать абсолютное значение функции скорости, чтобы найти общее пройденное расстояние.

Чтобы продолжить пример, используйте два интеграла, чтобы найти общее расстояние. Сначала найдите \(t\)-пересечение функции, так как именно там происходит деление интервала. Приравняйте уравнение к нулю и решите относительно \(t\). Таким образом,

\[ \begin{align*} 3t−5 &=0 \\[4pt] 3t &=5 \\[4pt] t &=\frac{5}{3}. \end{выравнивание*}\] 94}{4}\right]−0 \\[4pt] &=10−\frac{16}{4} \\[4pt] &=6. \end{align*} \nonumber \]

Таким образом, моторная лодка использует \(6\) галлонов бензина за \(2\) часа.

Пример \(\PageIndex{5}\): Начало главы: Ледяные лодки

Как мы видели в начале главы, лучшие гонщика на ледяной лодке могут развивать скорость, в пять раз превышающую скорость ветра. Однако Эндрю – средний ледоход, поэтому он развивает скорость, равную только удвоенной скорости ветра.

Рисунок \(\PageIndex{3}\): (кредит: модификация работы Картера Брауна, Flickr)

Предположим, однажды утром Эндрю выводит свой ледоход, когда все утро дует легкий бриз со скоростью \(5\) в час. Однако, когда Эндрю настраивает свою ледяную лодку, ветер начинает усиливаться. В течение первых получаса его катания на лодке скорость ветра увеличивается в соответствии с функцией \(v(t)=20t+5.\). Во вторые полчаса прогулки Эндрю остается стабильным со скоростью \(15\) миль в час. Другими словами, скорость ветра определяется как

\[ v(t)=\begin{cases}20t+5, & \text{for } 0≤t≤\frac{1}{2}\\15, & \text{for} \frac{1}{2}≤t≤1\end{cases} \nonumber \] 91_{1/2} \\[4pt]
&=\left(\frac{20}{4}+5\right)−0+(30−15) \\[4pt]
&=25. \end{align*}\]

Эндрю находится в 25 милях от начальной точки через 1 час.

Упражнение \(\PageIndex{3}\)

Предположим, что вместо того, чтобы оставаться устойчивым в течение вторых получасов прогулки Эндрю, ветер начинает стихать в соответствии с функцией \(v(t)=−10t+ 15.\) Другими словами, скорость ветра определяется как

\[ v(t)=\begin{cases}20t+5, & \text{for } 0≤t≤\frac{1}{2} \\−10t+15, &\text{для } \frac{1}{2}≤t≤1\end{случаев}. \номер\]

В этих условиях, как далеко от исходной точки находится Андрей через 1 час?

Подсказка

Не забывайте, что ледяная лодка Эндрю движется в два раза быстрее ветра.

Ответить

\(17,5\) ми

Интегрирование четных и нечетных функций

Мы видели в разделе «Функции и графики», что четная функция — это функция, в которой \(f(−x)=f(x)\) для всех \(x\) в области — то есть график кривой не изменится при замене \(x\) на \(−x\). Графики четных функций симметричны относительно оси \(y\). нечетная функция – это функция, в которой \(f(-x)=-f(x)\) для всех \(x\) в области, а график функции симметричен относительно начала координат.

Интегралы четных функций, когда пределы интегрирования от \(−a\) до \(a\), включают две равные площади, потому что они симметричны относительно оси \(y\). Интегралы нечетных функций, когда пределы интегрирования равны \([−a,a],\), оцениваются как нуль, потому что площади выше и ниже оси \(x\) равны.

Интегралы четных и нечетных функций 98−2)\,dx\) и убедиться в справедливости формулы интегрирования четных функций.

Решение

Симметрия показана на графиках на рисунке \(\PageIndex{4}\). На графике (а) показана область под кривой и над осью \(х\). Нам нужно сильно увеличить этот график, чтобы увидеть регион. На графике (b) показана область над кривой и под осью \(x\). Знаковая область этой области отрицательна. Оба представления иллюстрируют симметрию относительно оси \(y\) четной функции. У нас есть 92_{0}=\frac{512}{3}−4=\frac{500}{3} \nonumber \]

Так как \( 2⋅\frac{500}{3}=\frac{1000}{ 3},\) мы проверили формулу для четных функций на данном конкретном примере.

Рисунок \(\PageIndex{4}\): На графике (a) показана положительная площадь между кривой и осью \(x\), а на графике (b) показана отрицательная площадь между кривой и осью \(x).