Решаем неравенство с тангенсом – Сайт Александра Бабаева
Как с косинусом и синусом, решать неравенства с тангенсом мы будем с помощью единичной окружности.
Клише для решений неравенства с тангенсомАлгоритм решения неравенств с тангенсом:
- перерисовываем клише, изображённое на вышестоящем рисунке;
- на линии тангенса отмечаем $a$ и проводим до этой точки из начала координат прямую;
- точка пересечения этой прямой с полуокружностью будет закрашенной, если неравенство нестрогое и не закрашенное, если строгое;
- область будет находится снизу от прямой и до окружности, если неравенство содержит знак “$>$”, и снизу прямой и до окружности, если неравенство содержит знак “$<$”;
- для нахождения точки пересечения, достаточно найти арктангенс $a$, т.е. $x_{1}={\rm arctg} a$;
- в ответ выписывается полученный промежуток, добавляя к концам $+ \pi n$.
Примеры решения неравенств с помощью алгоритма.
Пример 1: Решить неравенство:
${\rm tg}{x} \leq 1.
- Копируем клише.
- Отметим на линии тангенса координату $1$.
- Проводим до этой точки из начала координат прямую.
- Отметим точку пересечения. Она будет закрашенной, так как неравенство нестрогое.
- Знак неравенства $\leq$, а, значит, закрашиваем область снизу от прямой, т.е. больший “кусок пирога”.
- Находим точку пересечения: $x_{1}={\rm arctg}{1}=\frac{\pi}{4}$.
Таким образом, решение примет вид:
$x \in \left(-\frac{\pi}{2} + \pi n; \frac{\pi}{4} + \pi n\right], \ n \in Z.$
Важно! Точки $-\frac{\pi}{2}$ и $\frac{\pi}{2}$ у тангенса всегда (независимо от знака неравенства)
Пример 2: Решить неравенство:
${\rm tg}{x} > – \sqrt{3}.$
Отмечаем на линии тангенса точку $- \sqrt{3}$ и проводим прямую из начала координат до неё. Точка пересечения этой прямой с полуокружностью будет не закрашенной, так как неравенство строгое. Область будет находится выше прямой и до окружности, так как знак неравенства $>$. найдём точку пересечения:
найдём точку пересечения:
$x_{1} = {\rm arctg}{\left(-\sqrt{3}\right)} = -\frac{\pi}{3}.$
Таким образом, ответом будет:
$x \in \left(-\frac{\pi}{3} + \pi n; \frac{\pi}{2} + \pi n\right), \ n \in Z.$
Пример 3:
${\rm tg}{\left(2x-\frac{\pi}{3}\right)} + \sqrt{3} > 0.$
Сейчас применить алгоритм нельзя. Этот пример похож на пример 3 неравенства с синусом или косинусом. И действовать нужно аналогично. Сначала перенесём всё, что не содержит тригонометрической функции в правую часть.
${\rm tg}{\left(2x-\frac{\pi}{3}\right)} > – \sqrt{3}.$
Теперь же, чтобы применить алгоритм, делаем замену переменной. Всё, что стоит под тригонометрической функцией, обозначаем за новую переменную:
$t=2x-\frac{\pi}{3}$
и получаем неравенство
${\rm tg}{t} > – \sqrt{3},$
которое мы уже решили в примере 2:
$t \in \left(-\frac{\pi}{3} + \pi n; \frac{\pi}{2} + \pi n\right).$
Возвращаемся к исходной переменной:
$\left(2x-\frac{\pi}{3}\right) \in \left(-\frac{\pi}{3} + \pi n; \frac{\pi}{2} + \pi n\right). $
$
Последнее равносильно системе неравенств
$\left\{\begin{array}{c} 2x-\frac{\pi}{3} > -\frac{\pi}{3} + \pi n, \\ 2x-\frac{\pi}{3} < \frac{\pi}{2}+\pi n, \end{array} \right.$
решив которую мы получим ответ. Действительно,
$\left\{\begin{array}{c} 2x > \pi n, \\ 2x < \frac{5 \pi}{6} + \pi n, \end{array} \right.$
$\left\{\begin{array}{c} x > \frac{\pi n}{2}, \\ x < \frac{5\pi}{12}+\frac{\pi n}{2}. \end{array} \right. $
И окончательно получаем:
$x \in \left(\frac{\pi n}{2}; \frac{5\pi}{12} + \frac{\pi n}{2}\right), \ n \in Z.$
Калькулятор онлайн – Решение тригонометрических неравенств
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Тригонометрические неравенства
Неравенства вида \( \sin x > a \) и \( \sin x
Пусть дано простейшее неравенство \( \sin x > a \).
1) При \(-1
Из данного рисунка видно, что в этом случае решение неравенства будет таким:
$$ x \in (\arcsin a + 2\pi k; \;\; \pi – \arcsin a + 2\pi k), k \in \mathbb{Z} $$
3) При \(а 4) При \(а = -1 \) решением неравенства является любое действительное число, отличное от \( -\frac{\pi}{2} + 2\pi k, \; k \in \mathbb{Z} \)
Пусть дано простейшее неравенство \( \sin x
1) При \(-1
Из данного рисунка видно, что в этом случае решение неравенства будет таким:
$$ x \in (\pi – \arcsin a + 2\pi k; \;\; 2\pi + \arcsin a + 2\pi k), k \in \mathbb{Z} $$
2) При \(а > 1 \) решением неравенства является любое действительное число: \( x \in \mathbb{R} \)
3) При \(а = 1 \) решением неравенства является любое действительное число, отличное от \( \frac{\pi}{2} + 2\pi k, \; k \in \mathbb{Z} \)

Неравенства вида \( \cos x > a \) и \( \cos x
Пусть дано простейшее неравенство \( \cos x > a \).
1) При \(-1
Из данного рисунка видно, что в этом случае решение неравенства будет таким:
$$ x \in (-\arccos(a) + 2\pi k; \;\; \arccos a + 2\pi k), \; k \in \mathbb{Z} $$
2) При \( a \geqslant 1\) неравенство не имеет решений.
3) При \(а
4) При \(а = -1\) решением неравенства является любое действительное число, отличное от \( \pi + 2\pi k, \; k \in \mathbb{Z} \)
Пусть дано простейшее неравенство \( \cos x
1) При \(-1
Из данного рисунка видно, что в этом случае решение неравенства будет таким:
$$ x \in (\arccos a + 2\pi k; \;\; 2\pi – \arccos a + 2\pi k), \; k \in \mathbb{Z} $$
2) При \(a > 1\) решением неравенства является любое действительное число: \( x \in \mathbb{R} \)
3) При \(a \leqslant -1\) неравенство не имеет решений.
4) При \(a = 1\) решением неравенства является любое действительное число, отличное от \( 2\pi k, \; k \in \mathbb{Z} \)
Неравенства вида \( tg \;x > a \) и \( tg \;x
Пусть дано простейшее неравенство \( tg \;x > a \).
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.
Из данного рисунка видно, что при любом \(a \in \mathbb{R} \) решение неравенства будет таким:
$$ x \in \left(arctg \;a + \pi k; \;\; \frac{\pi}{2} + \pi k \right), \; k \in \mathbb{Z} $$
Пусть дано простейшее неравенство \( tg \;x
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.
Из данного рисунка видно, что при любом \(a \in \mathbb{R} \) решение неравенства будет таким:
Неравенства вида \( ctg \;x > a \) и \( ctg \;x
Пусть дано простейшее неравенство \( ctg \;x > a \).
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.
Из данного рисунка видно, что при любом \(a \in \mathbb{R} \) решение неравенства будет таким:
$$ x \in ( \pi k; \;\; arcctg \;a + \pi k ), \; k \in \mathbb{Z} $$
Пусть дано простейшее неравенство \( ctg \;x
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.
Из данного рисунка видно, что при любом \(a \in \mathbb{R} \) решение неравенства будет таким:
$$ x \in ( arcctg \; a + \pi k; \;\; \pi + \pi k ), \; k \in \mathbb{Z} $$
Решение тригонометрических неравенств
ПРИМЕР 1. Решим неравенство \( \sin x > \frac{1}{2} \).Так как \( -1 $$ x \in \left( \arcsin \frac{1}{2} + 2\pi k; \;\; \pi – \arcsin \frac{1}{2} + 2\pi k \right), \; k \in \mathbb{Z} $$
Так как \( \arcsin \frac{1}{2} = \frac{\pi}{6} \), то решение можно переписать в виде
$$ x \in \left(\frac{\pi}{6} + 2\pi k; \;\; \frac{5\pi}{6} + 2\pi k \right), \; k \in \mathbb{Z} $$
ПРИМЕР 2. Решим неравенство \( \sin \;x
Так как \( -1
$$ x \in \left(\pi – \arcsin \left( -\frac{2}{3} \right) + 2\pi k; \;\; 2\pi + \arcsin \left( -\frac{2}{3} \right) + 2\pi k \right), \; k \in \mathbb{Z} $$
Решим неравенство \( \sin \;x
Так как \( -1
$$ x \in \left(\pi – \arcsin \left( -\frac{2}{3} \right) + 2\pi k; \;\; 2\pi + \arcsin \left( -\frac{2}{3} \right) + 2\pi k \right), \; k \in \mathbb{Z} $$
Воспользовавшись равенством \( \arcsin(-a) = -\arcsin a \), перепишем решение в виде
$$ x \in \left(\pi + \arcsin \frac{2}{3} + 2\pi k; \;\; 2\pi – \arcsin \frac{2}{3} + 2\pi k \right), \; k \in \mathbb{Z} $$
ПРИМЕР 3. Решим неравенство \( \cos x > \frac{1}{2} \).
Так как \( -1
$$ x \in \left(-\frac{\pi}{3} + 2\pi k; \;\; \frac{\pi}{3} + 2\pi k \right), \; k \in \mathbb{Z} $$
ПРИМЕР 4. Решим неравенство \( \cos x
Так как \( -1
$$ x \in (\arccos(-0{,}3) + 2\pi k; \;\; 2\pi – \arccos(-0{,}3) + 2\pi k), k \in \mathbb{Z} $$
Воспользовавшись равенством \( \arccos(-a) = \pi – \arccos a \), перепишем решение в виде
$$ x \in (\pi-\arccos 0{,}3 + 2\pi k; \;\; \pi + \arccos 0{,}3 + 2\pi k), \; k \in \mathbb{Z} $$
ПРИМЕР 5.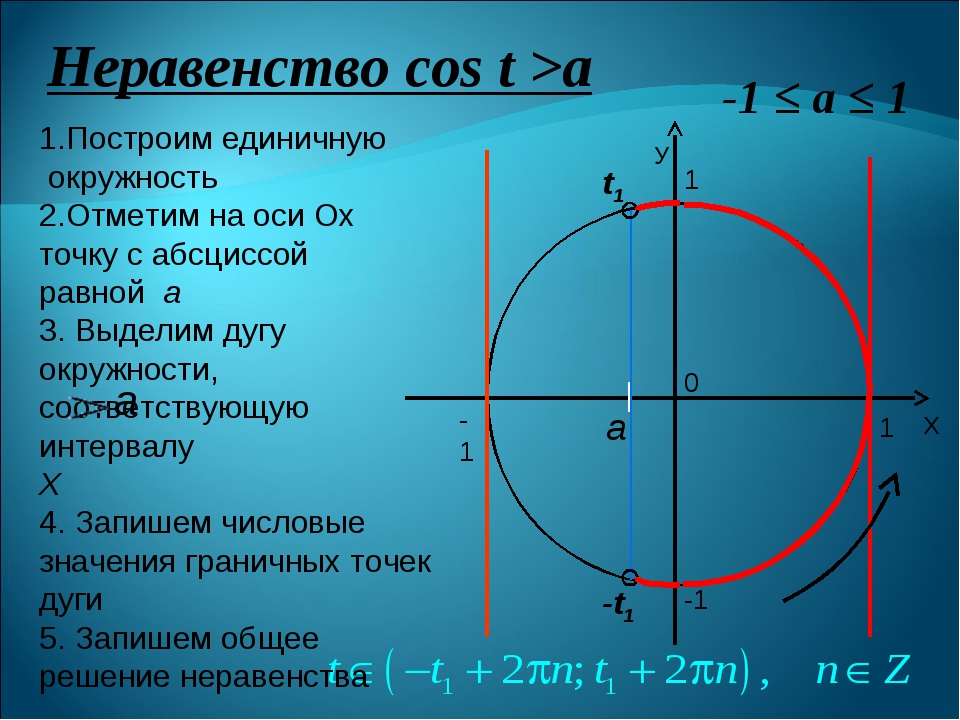 Решим неравенство \( tg \;x > 1 \).
Решим неравенство \( tg \;x > 1 \).
Очевидно, что решение неравенства будет таким:
$$ x \in \left(\frac{\pi}{4} + \pi k; \;\; \frac{\pi}{2} + \pi k\right), \; k \in \mathbb{Z} $$
ПРИМЕР 6. Решим неравенство \( tg \;x
Очевидно, что решение неравенства будет таким:
$$ x \in \left(-\frac{\pi}{2} + \pi k; \;\; arctg \left( -\frac{1}{2} \right) + \pi k\right), \; k \in \mathbb{Z} $$
Воспользовавшись равенством \( arctg(-a) = -arctg \; a \), перепишем решение в виде
$$ x \in \left(-\frac{\pi}{2} + \pi k; \;\; -arctg \frac{1}{2} + \pi k\right), \; k \in \mathbb{Z} $$
ПРИМЕР 7. Решим неравенство \( ctg \;x > \frac{\sqrt{3}}{3} \).
Очевидно, что решение неравенства будет таким:
$$ x \in \left( \pi k; \;\; \frac{\pi}{3} + \pi k \right), \; k \in \mathbb{Z} $$
ПРИМЕР 8. Решим неравенство \( ctg \;x
Очевидно, что решение неравенства будет таким:
$$ x \in \left( arcctg \left( -\frac{5}{4} \right) + \pi k; \;\; \pi + \pi k \right), \; k \in \mathbb{Z} $$
Воспользовавшись равенством \( arcctg(-a) = \pi – arcctg \;a \), перепишем решение в виде
$$ x \in \left( \pi – arcctg \frac{5}{4} + \pi k; \;\; \pi + \pi k \right), \; k \in \mathbb{Z} $$
или в виде
$$ x \in \left( – arcctg \frac{5}{4} + \pi n; \;\; \pi n \right), \; n \in \mathbb{Z} $$
Урок 50.
 тригонометрические неравенства – Алгебра и начала математического анализа – 10 класс
тригонометрические неравенства – Алгебра и начала математического анализа – 10 классАлгебра и начала математического анализа, 10 класс
Урок №50. Тригонометрические неравенства.
Перечень вопросов, рассматриваемых в теме
- решение простейших тригонометрических неравенств с помощью тригонометрической окружности;
- решение тригонометрических неравенств, сводимых к квадратным;
- решение тригонометрических неравенств методом интервалов.
Глоссарий по теме
- Синусом угла называется ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол . Обозначается
- Косинусом угла называется абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол . Обозначается
- Тангенсом угла называется отношение к
Угол может выражаться и в градусах и в радианах.
- Арккосинусом числа называется такое число α, что: .
 Арккосинус числа m обозначают: .
Арккосинус числа m обозначают: . - Арксинусом числаназывается такое число α, что: и . Арксинус числа m обозначают:.
- Арктангенсом числа m называется такое число α, что: и . Арктангенс числа m обозначают: .
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни под ред. А.Б. Жижченко. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-022250-1, сс. 334-337.
Шахмейстер А.Х. Тригонометрия. М.: Издательство МЦНМО : СПб.: «Петроглиф» : «Виктория плюс», 2013. – 752 с.: илл. ISBN 978-5-4439-0050-6, сс. 353-367.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru
Теоретический материал для самостоятельного изучения
1. Рассмотрим простейшие тригонометрические неравенства.
Начнем рассматривать с неравенства .
Из рисунка 1 видно, что если a>1, то решений данное неравенство не имеет.
Рисунок 1 – Точки пересечения прямой y=a (a>1) с тригонометрической окружностью
Если a=1, то решений такое неравенство также не имеет (рис.2). Однако, если мы изменим знак на (получим неравенство , то решением его будет множество точек, в которых . Это числа .
Рисунок 2 – Общие точки прямой y=1 с тригонометрической окружностью
Рассмотрим теперь значение (рис.3).
Рисунок 3 – Решение неравенства
Видим, что множество решений данного неравенства представляет собой дугу, начало которой в точке (1) , конец в точке (2) N(π – arcsina) . В зависимости от знака неравенство (строгое оно или нестрогое) промежуток представляет собой интервал или отрезок. Далее множество промежутков получается прибавлением :
(для строгого неравенства) – множество интервалов;
(для нестрогого неравенства) – множество отрезков.
Если значение a= – 1,то получим следующую картинку (рис. 4):
4):
Рисунок 4 – Общие точки прямой y= – 1 с тригонометрической окружностью
Видно. что если неравенство нестрогое, то решением неравенства является любое действительное число. Если неравенство строгое, то решением неравенства является любое действительное число, кроме чисел вида .
Наконец, если , то решением неравенства является любое действительное число.
Решение неравенства рассмотрим более коротко.
Очевидно, что если , то решением неравенства является любое действительное число.
Если , то решением неравенства является любое действительное число, а решением неравенства является любое действительное число, за исключением чисел вида .
Если , то решением неравенства являются числа вида , а неравенство решений не имеет. То же самое можно сказать о решении неравенств и в случае .
Случай рассмотрим более подробно (рис. 5).
Рисунок 5 – Решение неравенства
Решение неравенства для :
(для строгого неравенства) – множество интервалов;
(для нестрогого неравенства) – множество отрезков.
2. Теперь рассмотрим решение неравенств и .
Рассуждая по аналогии с неравенствами относительно синуса, можем сделать вывод, что для неравенство решений не имеет, а решением неравенства является любое действительное число.
Для неравенство решений не имеет, а решением неравенства является любое действительное число.
Рассмотрим случай более подробно.
Рассмотрим решение неравенства (рис. 6).
Рисунок 6 – Решение неравенства
Множество решений этого неравенства:
.
Теперь рассмотрим неравенство (рис. 7).
Рисунок 7 – Решение неравенства
Множество решений этого неравенства:
.
3. Теперь рассмотрим решение простейших неравенств и .
Сначала рассмотрим неравенство (рис. 8).
Рисунок 8 – Решение неравенства
Множество решений этого неравенства:
.
Соответственно, множество решений неравенства :
.
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Решите неравенство. Заполните пропуски
Решение:
Ведем новую переменную: .
Вспомогательное неравенство имеет вид:
, .
Вернемся к исходной переменной: .
Второе неравенство решений не имеет. Решением первого неравенства является:
.
Ответ: .
Пример 2.
Решите неравенство. Найдите коэффициенты
Решение:
Выразим
Рисунок 9 – решение неравенства
Ответ:
Урок по теме “Решение тригонометрических неравенств”
– Переходим к более сложным тригонометрическим неравенствам,
решение которых будет сводиться к решению простейших тригонометрических неравенств. Рассмотрим примеры.
(Решение неравенств на доске под руководством учителя).
№1. cos22x – 2cos2x 0.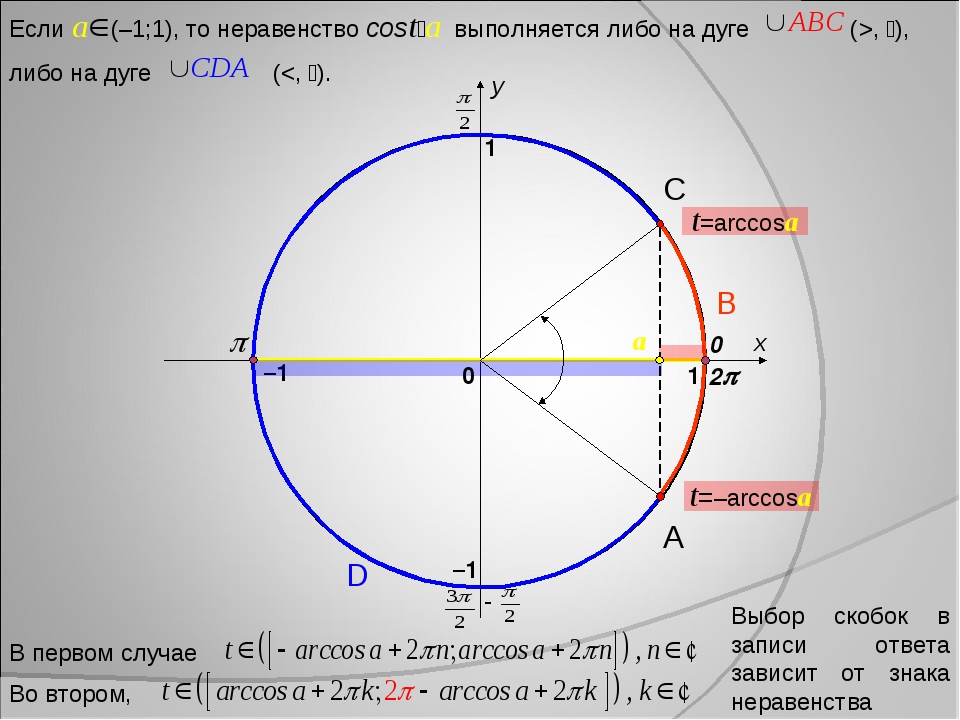
(Вспомним прием решения тригонометрических уравнений вынесением общего множителя за скобку).
cos2x(cos2x – 2) 0.
Замена: cos2x = t, 1; t(t – 2) 0; Второе неравенство не удовлетворяет условию 1.
cos2x 0. (Решить неравенство самостоятельно. Проверить ответ).
Ответ: + p n< х< + p n, n Z.
№2. 6sin2x – 5sinx + 1 0.
(Вспомним прием решения тригонометрических уравнений заменой переменной. У доски решает ученик с комментариями).
Замена sinx = t, 1. 6t2 – 5t +1 0, 6(t – )(t – ),
Ответ: + 2p n х
+ 2p n, -p -arcsin+ 2p k х arcsin+ 2p
k, n, k Z.
№3. sinx + cos2x> 1.
(Обсуждаем варианты решения. Вспоминаем фомулу косинуса двойного угла. Класс решает самостоятельно, один ученик – на индивидуальной доске с последующей проверкой).
sinx + cos2x – 1> 0, sinx – 2sin2x> 0, sinx(1 – 2sinx) > 0,
Ответ:
2p n< x< + 2p n, + 2p n< x< p + 2p n, n Z.
Проанализировать ситуации, когда ответ к решению квадратного неравенства записываем в виде совокупности двух неравенств, а когда – в виде системы. Полезна следующая схема:
00025165926425165824000000000012516582401
№4. coscosx – sinsinx< -.
(Обсуждение. К доске вызываются по
одному ученику на каждый шаг решения,
комментируются этапы. Учитель проверяет запись у
учеников, работающих на месте).
К доске вызываются по
одному ученику на каждый шаг решения,
комментируются этапы. Учитель проверяет запись у
учеников, работающих на месте).
cos(x + ) < -, cost< -.
+ 2p n< t< + 2p n, n Z,
+ 2p n< x + < + 2p n, n Z,
+ 2p n< x< + 2p n, n Z.
Ответ:
+ 2p n < x < + 2p n, n Z.
№5. Определите все а, при каждом из которых неравенство
4sinx + 3cosx а имеет хотя бы одно решение.
(Вспомнить алгоритм решения
тригонометрического уравнения с нормирующим
множителем. Решение записано на кодоскопной
ленте. Открываю его поэтапно по мере рассуждений. Дифференцированная работа).
Дифференцированная работа).
4sinx + 3cosx а, М = = 5. Разделим обе части неравенства на 5: sinx + cosx . Так как ()2 + ()2 = 1, то существует такой угол , что cos = , а sin = . Перепишем предыдущее неравенство в виде: sin(x + ) . Последнее неравенство, а, значит, и исходное неравенство имеет хотя бы одно решение при каждома таком, что -1, то есть при каждом а -5. Ответ: а -5.
Решение простейших тригонометрических неравенств – online presentation
Решениепростейших
тригонометрических
неравенств
Все сложные тригонометрические неравенства решаются
простейшие
тригонометрические
решаются
сВсе
помощью
тех же
алгоритмов, что инеравенства
тригонометрические
одним
и темконце
же способом:
уравнения, но
в самом
приходится решать
простейшие тригонометрические неравенства.

1. Выделяем на единичной окружности дугу, координаты точек
которой удовлетворяют нашему неравенству.
2. Определяем начальную точку движения по этой дуге, исходя
из того, что мы «умеем» двигаться только в положительном
направлении, то есть против часовой стрелки (от меньшего
числа к большему)
3. Двигаясь по выделенной дуге в положительном направлении,
определяем конечную точку движения.
4. После того, как мы определили начальную и конечную точку
движения по дуге, записываем решение неравенства и ответ.
̶ 4π
—
3 2π
—
̶—
5π 3π 3
4 —
̶ 7π 5π 4
— —
6 6
Числа
на
единичной
окружности,
которые
π
могут
2
1
3
̶ π -1
2
2
2
участвовать
в записи
̶—
5π 7π
решения
6 —
6 5π
неравенства
̶—
3π —
4
4π
4
—
̶ 2π 3
—
3
π
̶ 3π
— y—
2
2
1
̶ 5π
—
3
π
̶—
7π
—
3 π 4
—
̶ 11π
4 π —
— 6
6
3
2 2
2
1
2
+
0
1
2
1
2
-1
2
2
3
2
̶ π 3π
— —
2 2
2
2
31
2
0
̶ 2π
2π
x
̶
11π —
̶ π
—
6
6
7π
̶ π
— —
4 4
5π
— ̶ π
3 —
3
Алгоритм решения неравенства sin x a
Изобразить единичную окружность, отметить число у = a (sinα = y)
y
Провести прямую у = a
Выделить дугу окружности,
соответствующую знаку сравнения
(обход – строго против часовой
стрелки).

Записать числовые значения
граничных точек дуги.
Учитывая, что начало дуги –
меньшее значение.
х1
a
х2
х
0
y
sin x > a
х2
Записать решение неравенства
х 1 + 2πn
sin x
a
0
Записать ответ
х1
х
На оси Оу отмечаем значение
1.
и проводим прямую у =
2
2
2
0 ,7
2
3.
Выделяем
нижнюю часть
окружности
(обход – строго
против часовой
стрелки).
Подписываем
полученные точки.
Обязательно
учитываем, что
начало дуги –
меньшее значение
5
4
2
2
2
sin x ≤ 0,7
2.
y
2
sin x
2
О
4
2
x
4. Записываем решение:
5
2 k x
2 k , k Z
4
4
6. sin x > 0,5
sin x > 0,5y
1
5π ̸ 6
π̸6
0,5
0
-1
x
5
x 2 n;
2 n , n Z
6
6
На Оу отмечаем значение
1.
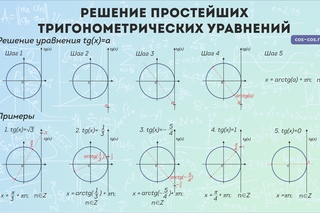
и проводим прямую у =
3
0,8
2
3
2
2
Подписываем
полученные точки.
Обязательно
учитываем, что
начало дуги –
меньшее значение.
sin x ≥ – 0,8
3.
y
Выделяем верхнюю
часть окружности
(обход – строго против
часовой стрелки).
2.
3
sin x
2
4
3
3
2
О
x
3
2
3
2 k x
4. Записываем решение:
4
2 k , k Z
3
sin x > – 1,3
y
x R
1
0
-1
○ – 1,3
x
9. sinx ≤ 0,4
yx1 = π ̶ arcsin 0,4
1
0,4
x1
sin x ≤ 0,4
π
0
x2 = 2 π + arcsin 0,4
x2
t 0 = arcsin 0,4
2π
x
x1 + 2πk ≤ x ≤ x2 + 2πk, kϵZ
-1
x ϵ [ π ̶ arcsin 0,4 + 2πk;
2 π + arcsin 0,4 +2πk], kϵZ
Алгоритм решения неравенства cos x > a или cos x
Изобразить единичную окружность, отметить число x = a (cosα = x)
Провести прямую x = a
Выделить дугу окружности,
соответствующую знаку сравнения
(обход – строго против часовой
стрелки).
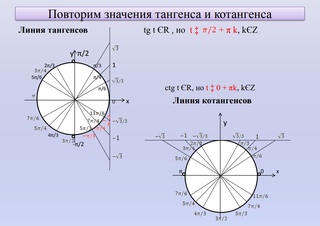
Записать числовые значения
граничных точек дуги.
Учитывая, что начало дуги –
меньшее значение.
y
cos x > a
0
х
х2
a
х1
y
cos x
х1
Записать решение неравенства Записать
ответ
х2
х 1 + 2πn
a
0
х
1.
На Ох отмечаем значение
2
0,7
2
2
2
и проводим прямую х =
2
cos x
2
y
2
2.
3.
Выделяем правую
часть окружности
(обход – строго
против часовой
стрелки).
Подписываем
полученные точки.
Обязательно
учитываем, что
начало дуги –
меньшее значение.
3
4
cos x ≥ – 0,7
3
4
2
2
О
2
4. Записываем решение:
x
3
3
2 k x
2 k , k Z
4
4
1.
На Оx отмечаем значение
1
и проводим прямую х =
2
1
2
y
2
2.
3.
Выделяем левую
часть окружности
(обход – строго
против часовой
стрелки).

Подписываем
полученные точки.
Обязательно
учитываем, что
начало дуги –
меньшее значение.
1
cos x
2
3
cos x ≤ 0,5
О
1
2
2
x
5
3 4. Записываем решение:
5
2 k x
2 k , k Z
3
3
x R
cos х
y
cos х
-1
0
1,1
1
x
cos x ≥ 0
2
y
2
2 k x
2
2 ,
x
-1
1
0
2
Алгоритм решения неравенства tg x ≤ a
Изобразить
Показать единичную
точки, в которых
окружность
не определён
и провести
тангенс
линию тангенсов
Выделить
часть
На линии нижнюю
тангенсов
отметить
линии
поскольку
число тангенсов,
a и провести
луч через
решаем
неравенство
со знаком ≤
эту точку
и центр окружности
y
2
а
х2
Выделить соответствующие дуги
окружности (обход совершаем
против часовой стрелки)
Подписать полученные точки на
одной из дуг (вторая получается из
неё: к концам +π).
 Учесть , что
Учесть , чтоначало дуги – меньшее значение
Записать решение неравенства
х 1 + πn
-1
0
2
х1
Записать ответ.
1
x
tg x ≤ 1
x (
2
k ;
4
y
2
4
1
k ], k Z
-1
0
5
4
2
1
x
проводим луч через эту точку и
центр окружности
2. Выделяем нижнюю часть
линии тангенсов,
поскольку решаем
неравенство со знаком ≤ .
3.
4.
Выделяем
соответствующую
часть окружности
(обход совершаем
против часовой
стрелки).
y
3 1,7
2
3
Подписываем полученные
точки. Обязательно
учитываем, что
начало дуги – меньшее
значение
tgx 3
3 1 ,7
2
О
2
tg x ≤ 1,7
На линии тангенсов отмечаем
1.
x
5. Записываем решение:
2
k x
3
k , k Z
На линии тангенсов отмечаем
значение 1
проводим луч через эту точку и
центр окружности
2.

3.
4.
Выделяем верхнюю часть
линии тангенсов, поскольку
решаем неравенство со
знаком ≥ .
Выделяем
соответствующую
часть окружности
(обход – строго
против часовой
стрелки).
Подписываем полученные
точки. Обязательно
учитываем, что начало
дуги – меньшее значение
y
2
4
1
4
2
О
tgx 1
tg x≥ 1
1.
x
2
5. Записываем решение:
k x
2
k , k Z
таблица=а тангенсов корень из 3
поисковые фразы формулы ар
Почта (не публикуется) *
Таким образом, решение неравенства tgx<-1 есть открытый промежуток (-п/2+пn; -п/4+пn).
Решить неравенство tgx<-1
Рассмотрим конкретный пример решения неравенства с тангенсом.
Решение неравенства tgx<-a аналогично решению неравенства tgx<a с той разницей, что arcg (-a)=-arctg a.
В этом случае решению неравенства tgx<a соответствует часть линии тангенсов, расположенная ниже a. Соответственно, поскольку промежуток мы всегда записываем от меньшего к большему, в этом случае решение начинается от -п/2 и идет к arctg a.
Соответственно, поскольку промежуток мы всегда записываем от меньшего к большему, в этом случае решение начинается от -п/2 и идет к arctg a.
Чтобы решить неравенствоP tgx>-a, рассуждаем так же как и для неравенства tgx>a. Поскольку arctg (-a)=-arctg a, только этим и отличается ответ.
Если неравенство нестрогое, точку с arctg a включаем в ответ (на рисунке ее заштриховываем, в ответ записываем с квадратной скобкой). Точка п/2 в ответ никогда не включается, поскольку не входит в область определения тангенса (точка выколотая, скобка круглая).
Для решения неравенства tgx>a вполне достаточно полуокружности от -п/2 до п/2. Но если требуется найти, к примеру, решение системы неравенств с тангенсом и синусом, то нужна вся окружность.
На линии тангенсов значениям тангенсов, большим a, соответствует часть, расположенная выше точки а. Заштриховываем соответствующий луч. Теперь проводим прямую через точку О — начало отсчета- и точку а на линии тангенсов. Она пересекает окружность в точке arctg a. Соответственно, на окружности решению неравенства tgx>a соответствует дуга от точки arctg a до п/2. Чтобы учесть все решения (а их с учетом периодичности тангенса — бесконечное множество), к каждому концу интервала прибавляем пn, где n — целое число (n принадлежит Z).
Соответственно, на окружности решению неравенства tgx>a соответствует дуга от точки arctg a до п/2. Чтобы учесть все решения (а их с учетом периодичности тангенса — бесконечное множество), к каждому концу интервала прибавляем пn, где n — целое число (n принадлежит Z).
Для решения нам потребуется чертеж единичной окружности и . Радиус единичной окружности равен 1, поэтому, откладывая на линии тангенсов отрезки, длина которых равна радиусу, получаем соответственно точки, в которых тангенс равен 1, 2, 3 и т.д., а вниз — -1,-2,-3 и т.д.
Рассмотрим решение тригонометрических неравенств вида tgx>a и tgx<a на единичной окружности.
Знание — сила. Познавательная информация
Презентация Решение простейших тригонометрических неравенств.
- Презентации
- Презентация Решение простейших тригонометрических неравенств.
Автор публикации: Скурлатова О.В.
Дата публикации: 31.07.2016
Краткое описание:
1
Воробьев Леонид Альбертович, г.Минск Тема : Решение простейших тригонометрических неравенств. Г. Тамбов2
sint cost t x y 0 1 0 1 sint – ордината точки поворота cost – абсцисса точки поворота (под «точкой поворота» следует понимать – «точку единичной тригонометрической окружности, полученной при повороте на t радиан от начала отсчета»)Благодаря этой рекламе сайт может продолжать свое существование, спасибо за просмотр.3
x y 0 1 0 1 –1 –1 a 1 a –1 Аналогично, неравенство sint<,a , при a–1 также не имеет решений. Неравенство sint>,a, при a 1 не имеет решений. На окружности не существует точек поворота, ординаты которых больше единицы. На окружности не существует точек поворота, ординаты которых меньше минус единицы.4
x y 0 1 0 1 –1 –1 a 1 a –1 Если знак неравенства нестрогий, то неравенство sint a, при a 1 выполняется, при5
x y 0 1 0 1 t=arcsina t=–arcsina a –1 –1 2 A D B C Выбор скобок в записи ответа зависит от знака неравенства Дугу CBA можно записать в виде промежутка [(arcsina+2n, –arcsina+2n)], n, а дугу ADC – в виде промежутка [(–arcsina+2k, arcsina+2+2k)], k,6
Пример. Решите неравенство sin(2x–3)>,–0,5. Решение. Выполняем рисунок: или
Решите неравенство sin(2x–3)>,–0,5. Решение. Выполняем рисунок: или7
x y 0 1 0 1 –1 –1 a –1 a 1 Для неравенство cost>,a, при a 1 и cost<,a, при a –1 проведите рассуждения самостоятельно (под руководством учителя). tØ8
x y 0 1 0 1 –1 –1 a 1 a –1 Если знак неравенства нестрогий, то неравенство cost a, при a 1 выполняется, при9
x y 0 1 1 –1 –1 2 A D B C Выбор скобок в записи ответа зависит от знака неравенства 0 t=arccosa t=–arccosa a10
Пример. Решите неравенство . Решение. Выполняем рисунок: или11
x y 1 0 1 –1 0 линия тангенсов a Так как E(tg)=, то неравенство tgta всегда имеет решение. –1 Значению tgt=a соответствуют числа t (величины углов поворота в радианной мере), попадающие в две точки тригонометрического круга. Для неравенств tgt>,a или tgta получаем две дуги. Обе они могут быть записаны в виде промежутка: Для неравенств tgt<,a или tgta получаем две дуги. 0 Обе они могут быть записаны в виде промежутка: Выбор скобок в записи ответа зависит от знака неравенства12
x y 1 0 1 –1 0 линия котангенсов a –1 Проследите за ходом решения и выведите общие формулы для неравенств: Так как E(tg)=, то неравенство сtgta всегда имеет решение. 0 ctgt>,a ctgta ctgt<,a ctgta
0 ctgt>,a ctgta ctgt<,a ctgta13
Пример. Решите неравенство x y 1 0 1 –1 0 линия тангенсов –1 0 Получаем:Неравенства точного для касательной функции с приложениями
Этот раздел посвящен формулировке и доказательству основных результатов, касающихся некоторых неравенств для касательной функции. Точнее, имеем следующее.
Теорема 1
для p ∈ (−∞, 4/ π 2 ], пусть Y ( т ) = exp ( т детская кроватка т – 1) и B p ( т ) определяется на (0, π /2) по (1.9).
- (i) Если p ≤ 2/15 ≈ 0,13333, то функция т ↦ Y ( т ) / B p ( т ) строго убывает на интервале (0, π /2). Следовательно, , для всех т ∈ (0, π /2)
αp (π / 2) (1 − pt2) 1 / (3p)
3,1
с лучшими коэффициентами 1 и α p ( π /2) определяется (2.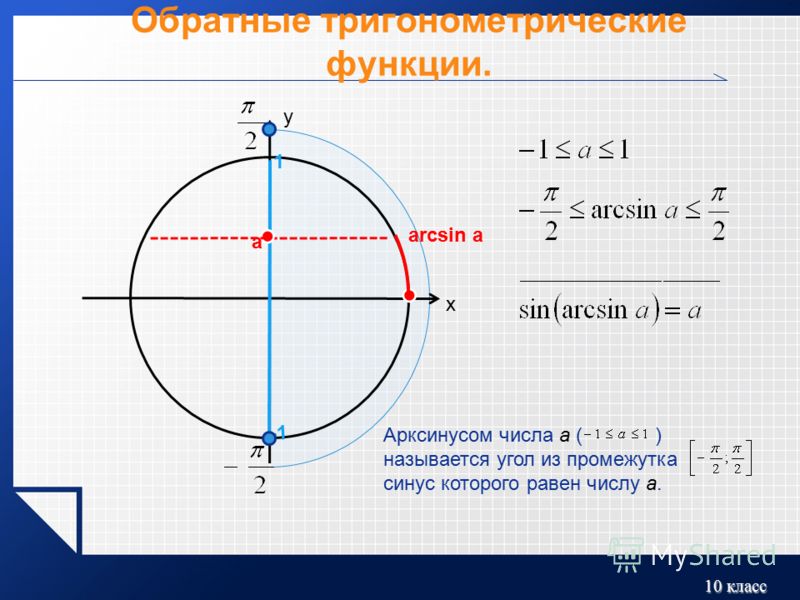 6).
6). - (ii) Если p ≥ 4 / (3 π 2 ) ≈ 0,13509, , то функция т ↦ Y ( т ) / B p ( т ) строго увеличивается на (0, π /2), и, следовательно, , для всех t ∈ (0, π /2),
(1 − pt2) 1 / (3p)
3,2
с лучшими коэффициентами 1 и α p ( π /2) определяется (2.6). - (iii) Если 2/15 < p <4 / (3 π 2 ), , то есть т 0 ∈ (0, π /2) так, что функция т ↦ Y ( т ) / B p ( т ) строго увеличивается на (0, т 0 ) и уменьшается на ( т 0 , π /2), и, следовательно, , для всех t ∈ (0, π /2),
мин (αp (π / 2), 1) (1 − pt2) 1 / (3p)
3.
с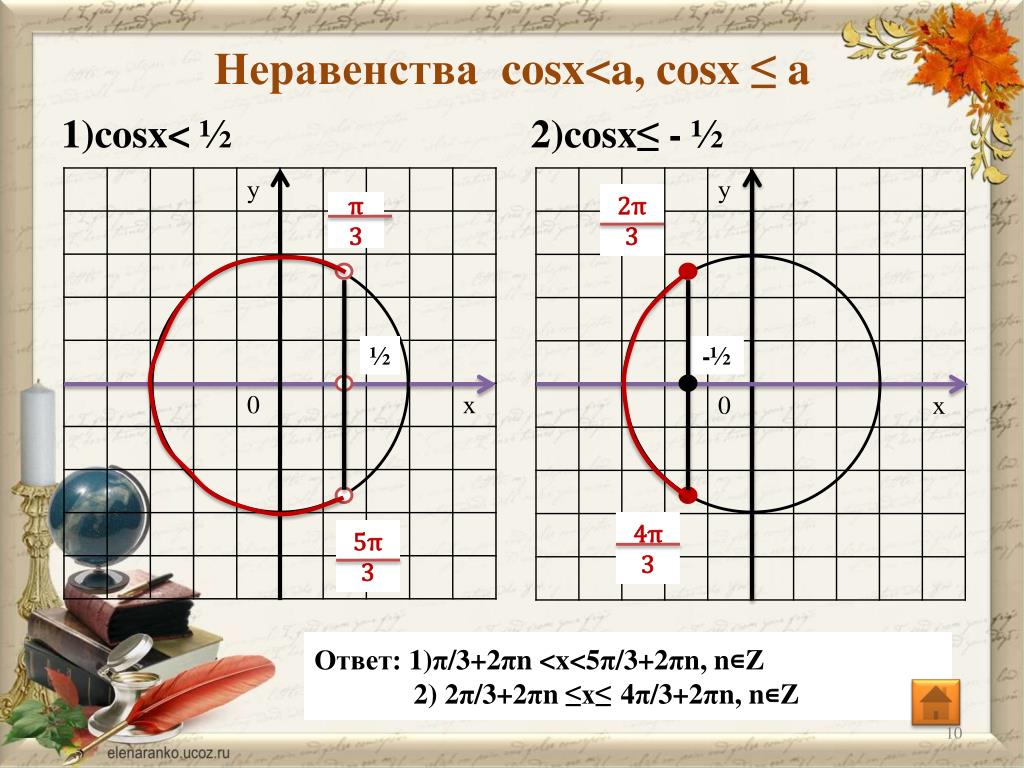 3
3βp = t0cott0−1 (1 − pt02) 1 / (3p),
где т 0 – единственное решение уравнениязатраты int − tsin2t + 2t3 (1 − pt2) = 0
3,4
по (0, π /2).
Когда p ∈ [ p 0 , 4 / (3 π 2 )), двойное неравенство (3.2) остается верным для всех . t ∈ (0, π /2). В частности, , , когда p = p 0 , имеем
(1 − p0t2) 1 / (3p0) 3,5 с лучшими константами 1 и β p 0 ≈ 1.0002. Пусть f (t) = lnY (t) −lnBp (t) = {ttant − 1−13pln (1 − pt2), если p ≠ 0, ttant − 1 + t23, если p = 0. 3,6 Результат дифференцирования f ′ (t) = costint − tsin2t + 2t3 (1 − pt2) = 3t2 (t − costint) 3 (1 − pt2) sin2t (p − 3t − 3costsint − 2tsin2t3t2 (t− sintcost)) = 3t2 (t − costint) 3 (1 − pt2) sin2t [p − g (t)], , где g ( t ) определяется формулой (2. Обратите внимание на то, что ( t – cos t sin t ) = [2 t – sin (2 t )] / 2> 0 для t ∈ (0, π /2 ) и (1 – p t 2 )> 0 для p ∈ (−∞, 4/ π 2 ] и t ∈ (0, π /2), легко видеть, что для всех t ∈ (0, π /2), sgn f ′ ( t ) = sign ( p – g ( t ) ). 3,7 Как показано в лемме 4, функция g строго возрастает с (0, π /2) на (2/15, 4 / (3 π 2 )). Теперь мы можем выделить три случая, чтобы доказать требуемый результат. Случай 1 : p ≤ min t ∈ (0, π /2) g ( t ) = 2/15. Тогда получаем f ′ ( t ) ≤ 0 для t ∈ (0, π /2), что означает, что f строго убывает на (0, π /2). lnαp (π2) = f (π2 -) , что эквивалентно двойному неравенству (3.1), выполняемому для всех t ∈ (0, π /2) с лучшими коэффициентами 1 и α p . Случай 2 : p ≥ max t ∈ (0, π /2) g ( t ) = 4 / (3 π 2 ). Аналогично, f ′ ( t )> 0 для t ∈ (0, π /2), что означает, что двойное неравенство (3.2) выполняется для всех t ∈ (0, π /2) с лучшими коэффициентами 1 и α p ( π /2). Случай 3 : 2/15 < p <4 / (3 π 2 ). Так как t ↦ p – g ( t ): = g 1 ( t ) строго убывает на (0, π /2) с g1 (0+ ) = p − 215> 0 и g1 (π2 -) = p − 43π2 <0, , мы находим, что существует t 0 ∈ (0, π /2), такое что g 1 ( t )> 0 для t ∈ (0, t 0 ) и g 1 ( t ) <0 для t ∈ ( t 0 , π /2). min (0, lnαp (π / 2)) = min (f (0 +), f (π2 -)) для всех t ∈ (0, π /2), то есть (3.3) выполняется для всех t ∈ (0, π /2), где β p = Y ( т 0 ) / B п ( т 0 ). Когда p ∈ [ p 0 , 4 / (3 π 2 )), по лемме 5 имеем α p ≥ 1, и отсюда следует, что 0 < f ( t ) ≤ f ( t 0 ) = ln β p , , то есть двойное неравенство (3.2) все еще сохраняется для t ∈ (0, π /2). В частности, для p = p 0 ≈ 0. Принимая p = 2/15 ≈ 0,13333, 1/8, 1/9, 0 и → −∞ соответственно. Тогда по части (i) теоремы 1 и монотонности p ↦ B p ( t ) и p ↦ α p ( π /2) B p ( t ) из леммы 5, сразу получаем следующий вывод. для t ∈ (0, π /2), неравенства e − 1 <α0e − t2 / 3 <α1 / 9 (1 − t29) 3 <α1 / 8 (1 − t28) 8/3 <α2 / 15 (1−2t215) 5/2 3.8 трюмов с лучшими коэффициентами α2 / 15 = e − 1 (1 − π230) −5 / 2≈0,99742, α1 / 8 = e − 1 (1 − π232) −8 / 3≈0,98356, α1 / 9 = e − 1 (1− π236) −3≈0,96200, α0 = eπ2 / 12−1≈0,83733. Аналогично, принимая p = 4 / (3 π 2 ) ≈ 0.13509, 1/7, 1/6, 1/3 и 4/ π 2 соответственно, имеем следующее. Этот раздел посвящен формулировке и доказательству основных результатов, касающихся некоторых неравенств для касательной функции. Точнее, имеем следующее. для p ∈ (−∞, 4/ π 2 ], пусть Y ( т ) = exp ( т детская кроватка т – 1) и B p ( т ) определяется на (0, π /2) по (1.9). αp (π / 2) (1 − pt2) 1 / (3p) 3,1 (1 − pt2) 1 / (3p) 3,2 мин (αp (π / 2), 1) (1 − pt2) 1 / (3p) 3. βp = t0cott0−1 (1 − pt02) 1 / (3p), затраты int − tsin2t + 2t3 (1 − pt2) = 0 3,4 Когда p ∈ [ p 0 , 4 / (3 π 2 )), двойное неравенство (3.2) остается верным для всех . t ∈ (0, π /2). В частности, , , когда p = p 0 , имеем (1 − p0t2) 1 / (3p0) 3,5 с лучшими константами 1 и β p 0 ≈ 1.0002. Пусть f (t) = lnY (t) −lnBp (t) = {ttant − 1−13pln (1 − pt2), если p ≠ 0, ttant − 1 + t23, если p = 0. 3,6 Результат дифференцирования f ′ (t) = costint − tsin2t + 2t3 (1 − pt2) = 3t2 (t − costint) 3 (1 − pt2) sin2t (p − 3t − 3costsint − 2tsin2t3t2 (t− sintcost)) = 3t2 (t − costint) 3 (1 − pt2) sin2t [p − g (t)], , где g ( t ) определяется формулой (2. Обратите внимание на то, что ( t – cos t sin t ) = [2 t – sin (2 t )] / 2> 0 для t ∈ (0, π /2 ) и (1 – p t 2 )> 0 для p ∈ (−∞, 4/ π 2 ] и t ∈ (0, π /2), легко видеть, что для всех t ∈ (0, π /2), sgn f ′ ( t ) = sign ( p – g ( t ) ). 3,7 Как показано в лемме 4, функция g строго возрастает с (0, π /2) на (2/15, 4 / (3 π 2 )). Теперь мы можем выделить три случая, чтобы доказать требуемый результат. Случай 1 : p ≤ min t ∈ (0, π /2) g ( t ) = 2/15. Тогда получаем f ′ ( t ) ≤ 0 для t ∈ (0, π /2), что означает, что f строго убывает на (0, π /2). lnαp (π2) = f (π2 -) , что эквивалентно двойному неравенству (3.1), выполняемому для всех t ∈ (0, π /2) с лучшими коэффициентами 1 и α p . Случай 2 : p ≥ max t ∈ (0, π /2) g ( t ) = 4 / (3 π 2 ). Аналогично, f ′ ( t )> 0 для t ∈ (0, π /2), что означает, что двойное неравенство (3.2) выполняется для всех t ∈ (0, π /2) с лучшими коэффициентами 1 и α p ( π /2). Случай 3 : 2/15 < p <4 / (3 π 2 ). Так как t ↦ p – g ( t ): = g 1 ( t ) строго убывает на (0, π /2) с g1 (0+ ) = p − 215> 0 и g1 (π2 -) = p − 43π2 <0, , мы находим, что существует t 0 ∈ (0, π /2), такое что g 1 ( t )> 0 для t ∈ (0, t 0 ) и g 1 ( t ) <0 для t ∈ ( t 0 , π /2). min (0, lnαp (π / 2)) = min (f (0 +), f (π2 -)) для всех t ∈ (0, π /2), то есть (3.3) выполняется для всех t ∈ (0, π /2), где β p = Y ( т 0 ) / B п ( т 0 ). Когда p ∈ [ p 0 , 4 / (3 π 2 )), по лемме 5 имеем α p ≥ 1, и отсюда следует, что 0 < f ( t ) ≤ f ( t 0 ) = ln β p , , то есть двойное неравенство (3.2) все еще сохраняется для t ∈ (0, π /2). В частности, для p = p 0 ≈ 0. Принимая p = 2/15 ≈ 0,13333, 1/8, 1/9, 0 и → −∞ соответственно. Тогда по части (i) теоремы 1 и монотонности p ↦ B p ( t ) и p ↦ α p ( π /2) B p ( t ) из леммы 5, сразу получаем следующий вывод. для t ∈ (0, π /2), неравенства e − 1 <α0e − t2 / 3 <α1 / 9 (1 − t29) 3 <α1 / 8 (1 − t28) 8/3 <α2 / 15 (1−2t215) 5/2 3.8 трюмов с лучшими коэффициентами α2 / 15 = e − 1 (1 − π230) −5 / 2≈0,99742, α1 / 8 = e − 1 (1 − π232) −8 / 3≈0,98356, α1 / 9 = e − 1 (1− π236) −3≈0,96200, α0 = eπ2 / 12−1≈0,83733. Аналогично, принимая p = 4 / (3 π 2 ) ≈ 0.13509, 1/7, 1/6, 1/3 и 4/ π 2 соответственно, имеем следующее. Этот раздел посвящен формулировке и доказательству основных результатов, касающихся некоторых неравенств для касательной функции. Точнее, имеем следующее. для p ∈ (−∞, 4/ π 2 ], пусть Y ( т ) = exp ( т детская кроватка т – 1) и B p ( т ) определяется на (0, π /2) по (1.9). αp (π / 2) (1 − pt2) 1 / (3p) 3,1 (1 − pt2) 1 / (3p) 3,2 мин (αp (π / 2), 1) (1 − pt2) 1 / (3p) 3. βp = t0cott0−1 (1 − pt02) 1 / (3p), затраты int − tsin2t + 2t3 (1 − pt2) = 0 3,4 Когда p ∈ [ p 0 , 4 / (3 π 2 )), двойное неравенство (3.2) остается верным для всех . t ∈ (0, π /2). В частности, , , когда p = p 0 , имеем (1 − p0t2) 1 / (3p0) 3,5 с лучшими константами 1 и β p 0 ≈ 1.0002. Пусть f (t) = lnY (t) −lnBp (t) = {ttant − 1−13pln (1 − pt2), если p ≠ 0, ttant − 1 + t23, если p = 0. 3,6 Результат дифференцирования f ′ (t) = costint − tsin2t + 2t3 (1 − pt2) = 3t2 (t − costint) 3 (1 − pt2) sin2t (p − 3t − 3costsint − 2tsin2t3t2 (t− sintcost)) = 3t2 (t − costint) 3 (1 − pt2) sin2t [p − g (t)], , где g ( t ) определяется формулой (2. Обратите внимание на то, что ( t – cos t sin t ) = [2 t – sin (2 t )] / 2> 0 для t ∈ (0, π /2 ) и (1 – p t 2 )> 0 для p ∈ (−∞, 4/ π 2 ] и t ∈ (0, π /2), легко видеть, что для всех t ∈ (0, π /2), sgn f ′ ( t ) = sign ( p – g ( t ) ). 3,7 Как показано в лемме 4, функция g строго возрастает с (0, π /2) на (2/15, 4 / (3 π 2 )). Теперь мы можем выделить три случая, чтобы доказать требуемый результат. Случай 1 : p ≤ min t ∈ (0, π /2) g ( t ) = 2/15. Тогда получаем f ′ ( t ) ≤ 0 для t ∈ (0, π /2), что означает, что f строго убывает на (0, π /2). lnαp (π2) = f (π2 -) , что эквивалентно двойному неравенству (3.1), выполняемому для всех t ∈ (0, π /2) с лучшими коэффициентами 1 и α p . Случай 2 : p ≥ max t ∈ (0, π /2) g ( t ) = 4 / (3 π 2 ). Аналогично, f ′ ( t )> 0 для t ∈ (0, π /2), что означает, что двойное неравенство (3.2) выполняется для всех t ∈ (0, π /2) с лучшими коэффициентами 1 и α p ( π /2). Случай 3 : 2/15 < p <4 / (3 π 2 ). Так как t ↦ p – g ( t ): = g 1 ( t ) строго убывает на (0, π /2) с g1 (0+ ) = p − 215> 0 и g1 (π2 -) = p − 43π2 <0, , мы находим, что существует t 0 ∈ (0, π /2), такое что g 1 ( t )> 0 для t ∈ (0, t 0 ) и g 1 ( t ) <0 для t ∈ ( t 0 , π /2). min (0, lnαp (π / 2)) = min (f (0 +), f (π2 -)) для всех t ∈ (0, π /2), то есть (3.3) выполняется для всех t ∈ (0, π /2), где β p = Y ( т 0 ) / B п ( т 0 ). Когда p ∈ [ p 0 , 4 / (3 π 2 )), по лемме 5 имеем α p ≥ 1, и отсюда следует, что 0 < f ( t ) ≤ f ( t 0 ) = ln β p , , то есть двойное неравенство (3.2) все еще сохраняется для t ∈ (0, π /2). В частности, для p = p 0 ≈ 0. Принимая p = 2/15 ≈ 0,13333, 1/8, 1/9, 0 и → −∞ соответственно. Тогда по части (i) теоремы 1 и монотонности p ↦ B p ( t ) и p ↦ α p ( π /2) B p ( t ) из леммы 5, сразу получаем следующий вывод. для t ∈ (0, π /2), неравенства e − 1 <α0e − t2 / 3 <α1 / 9 (1 − t29) 3 <α1 / 8 (1 − t28) 8/3 <α2 / 15 (1−2t215) 5/2 3.8 трюмов с лучшими коэффициентами α2 / 15 = e − 1 (1 − π230) −5 / 2≈0,99742, α1 / 8 = e − 1 (1 − π232) −8 / 3≈0,98356, α1 / 9 = e − 1 (1− π236) −3≈0,96200, α0 = eπ2 / 12−1≈0,83733. Аналогично, принимая p = 4 / (3 π 2 ) ≈ 0.{2}}. \ end {align} $$ Сравнение неравенств $$ LY (t)> ZH (t)> BS_ {1} (t)> \ max \ bigl (ZS (t), Z (t), BS_ {2} (t) \ bigr) $$ (4,2) трюм для \ (t \ in (0, \ pi / 2) \). Кроме того, , \ (ZS (t) \), \ (Z (t) \) и \ (BS_ {2} (t) \) не сопоставимы между собой на все \ (t \ in (0, \ pi / 2) \).{2}}} Это завершает доказательство. □ Из приведенного выше предложения мы видим, что точная нижняя оценка в (4.1) превосходит оценки, указанные в (1.2), (1. Аналогично, сравнивая пределы при \ (t = 0 \) и \ (t = \ pi / 2 \), мы находим точную верхнюю границу в (4.{2}} \ biggr). Неравенство $$ \ frac {\ sin t} {t} <\ frac {2+ \ cos t} {3}, \ quad t \ in \ biggl (0, \ frac {\ pi} {2} \ biggr), $$ верно из-за статьи Куса и Гюйгенса (см. , например, [19]), которое теперь известно как неравенство Куса (см. , например, [8, 20–23]). . Некоторые уточнения и обобщения неравенства Куса можно найти в [8, 21, 22, 24–29].{2}} \ quad \ textit {for} x \ in (\ pi, 2 \ pi). \ end {align} $$ (4,7) Кроме того, , два двойных неравенства резкие . В [12], следствие 12, Ян и др. $$ \ sqrt {\ exp \ biggl (\ frac {t} {\ tan t} -1 \ biggr)} < \ frac {\ sin t} {t} <\ exp \ biggl (\ frac {t} {\ tan (t / 2)} -2 \ biggr).{1 / (6r)} \ end {align} $$ (4.8) трюм для \ (t \ in (0, \ pi / 2) \) с лучшими константами \ (s = 1 / \ sqrt {2} \), \ (r = 1/15 \) и $$ \ begin {выровнено} & \ lambda_ {s} = \ frac {2} {\ pi \ exp (\ sqrt {2} \ pi \ cot (\ sqrt {2} \ pi / 4) -1) } \ ок0.{2} = 2/15 \), и тогда \ (r = 1/15 \) и \ (\ rho_ {r} \) также являются лучшими. Это завершает доказательство. □ Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org. Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу. Чтобы отправить уведомление, выполните следующие действия: Вы должны включить следующее: Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса – изображению, ссылке, тексту и т. Отправьте жалобу нашему уполномоченному агенту по адресу: Чарльз Кон
Varsity Tutors LLC Или заполните форму ниже: 506 J. -L. Чжао, К. -М. Луо, Б. -Н. Guo, F. Qi [5] Guo, B. -N. и Qi, F. логарифмически полная монотонность степенно-экспоненциальной функции, Politehn.Univ. Bucharest Sci. Бык. Сер. Приложение A Appl. M ath. Phys. 72 (2), 21–30, 2010. [6] Guo, B.-N. и Qi, F. Уточнение и обобщение неравенства Карлсона для функции косинуса arc , Hacet. J. Math. Стат. 39 (3), 403–409, 2010. [7] Kuang, J. -C. Чангыонг Будженгши (Прикладные неравенства), 3-е изд. (Shandong Science и Technology Press, город Цзинань, провинция Шаньдун, Китай, 2004 г.). (на китайском языке) [8] Митринович Д.С. Аналитические неравенства (Springer-Verlag, New York, Heidelberg, Berlin, 1970). [9] Ци, Ф. и Го, Б. -Н. Уточнение и обобщение неравенства Шафера для синусоидальной функции arc , Integral Transforms Spec. Функц. 23 (2), 129–134, 2012; Доступно в Интернете по адресу http://dx.doi.org/10.1080/10652469.2011.564578. [10] Ци, Ф., Ню, Д. -У. дана и связанных с ним проблем, J.Неравно. Человек 2009 (2009), ID статьи 271923, 52 страниц, 2009; Доступно в Интернете по адресу http://dx.doi.org/10.1155/2009/271923. [11] Ци, Ф., Чжан, С.-Кв. и Го, Б. -Н. Уточнение и обобщение неравенства Шафера для функции арктангенса, J. Inequal. Прил. 2009 (2009), ID статьи 930294, 9 страниц, 2009; Доступно в Интернете по адресу http://dx.doi.org/10.1155/2009/930294. [12] Стекин С.Б. Некоторые замечания о тригонометрических многочленах, Успехи матем.Наук. (N.S.) 10 1 (63), 159–166, 1955. [13] Zhao, J. -L., Wei, C. -F., Guo, B. -N. и Qi, F. Уточнение и обобщение двойного неравенства Карлсона для функции арккосинуса, Hacet. J. Math. Стат. 41 (2), 201–209, 2012. [14] Zhu, L. и Hua, J. -K. Уточнение неравенств Беккера-Штарка, J. Inequal. Заявл. 2010 (2010), ID статьи 931275, 4 страницы, 2010; Доступно в Интернете по адресу http://dx. Simply Science – это бесплатная персонализированная платформа для обучения детей в возрасте от 6 до 12 классов на основе STEM. Мы – веб-сайт открытого обучения, который побуждает детей понимать концепции и логику в удобном для них темпе, предлагая помощь с помощью интерактивной навигации. Развивайте способности решения проблем, творческий подход к дизайну, логику и наблюдательность, не выходя из дома, бесплатно! Наш контент создан специально для привлечения маленьких умов и их любопытства.Разделенные на темы, вы можете выбрать интересующую вас тему и просто узнать все, что вы хотели знать о ней. Упорядоченный, умный и интерактивный с помощью примеров, аналогий и моделирования, Simply Science гарантирует, что вы приложите максимум усилий для мышления! Оцените свою способность обрабатывать информацию. Раскройте науку, математику и их загадки с помощью наших уникальных технологий, основанных на исследованиях на основе тем. Отправляйтесь в новый мир с нашими темами полного погружения, наполненными забавными, увлекательными видео, викторинами и персонализированной лентой контента. В то время как формальное школьное и институциональное обучение сосредоточено на языках, когнитивном развитии и многих других вещах, Simply Science является вспомогательной идеей учебного плана, обучая учащихся в 6 и 12 классах по естествознанию, технологиям, инженерному делу. Узнавайте что-то новое каждый день, занимайтесь интересами и отвечайте на вопросы, которые всегда заставляли вас задуматься! Педагогика Simply Science поощряет вас исследовать, вводить новшества и применять полученные концепции в повседневной жизни, от базовых концепций до подробных бесед. Наша модель на основе темы гарантирует, что тема охватывает все темы в дисциплинах, которые она затрагивает – математику, науку и технологии, биологию и химию и все, что между ними. Межотраслевое обучение с сокровищницей ресурсов – мы считаем, что каждый молодой ум должен иметь доступ к связанным и равным возможностям обучения. Доказательство
 5).
5). .Следовательно, мы можем вывести следующее наблюдение:
.Следовательно, мы можем вывести следующее наблюдение: Это указывает на то, что f строго возрастает на (0, t 0 ) и убывает на ( t 0 , π /2). Следовательно, получаем, что
Это указывает на то, что f строго возрастает на (0, t 0 ) и убывает на ( t 0 , π /2). Следовательно, получаем, что 13484, решение уравнения (3.4) для t дает t 0 ≈ 1,26254, и, следовательно, β p 0 ≈ 1.0002. На этом мы завершаем доказательство. □
13484, решение уравнения (3.4) для t дает t 0 ≈ 1,26254, и, следовательно, β p 0 ≈ 1.0002. На этом мы завершаем доказательство. □ Следствие 1

Точные неравенства для касательной функции с приложениями
Теорема 1
 6).
6). 3
3 Доказательство
 5).
5). .Следовательно, мы можем вывести следующее наблюдение:
.Следовательно, мы можем вывести следующее наблюдение: Это указывает на то, что f строго возрастает на (0, t 0 ) и убывает на ( t 0 , π /2). Следовательно, получаем, что
Это указывает на то, что f строго возрастает на (0, t 0 ) и убывает на ( t 0 , π /2). Следовательно, получаем, что 13484, решение уравнения (3.4) для t дает t 0 ≈ 1,26254, и, следовательно, β p 0 ≈ 1.0002. На этом мы завершаем доказательство. □
13484, решение уравнения (3.4) для t дает t 0 ≈ 1,26254, и, следовательно, β p 0 ≈ 1.0002. На этом мы завершаем доказательство. □ Следствие 1

Точные неравенства для касательной функции с приложениями
Теорема 1
 6).
6). 3
3 Доказательство
 5).
5). .Следовательно, мы можем вывести следующее наблюдение:
.Следовательно, мы можем вывести следующее наблюдение: Это указывает на то, что f строго возрастает на (0, t 0 ) и убывает на ( t 0 , π /2). Следовательно, получаем, что
Это указывает на то, что f строго возрастает на (0, t 0 ) и убывает на ( t 0 , π /2). Следовательно, получаем, что 13484, решение уравнения (3.4) для t дает t 0 ≈ 1,26254, и, следовательно, β p 0 ≈ 1.0002. На этом мы завершаем доказательство. □
13484, решение уравнения (3.4) для t дает t 0 ≈ 1,26254, и, следовательно, β p 0 ≈ 1.0002. На этом мы завершаем доказательство. □ Следствие 1

Предложение 1
Замечание 2
 3), (1.4), (1.5) и (1.7).
3), (1.4), (1.5) и (1.7). Замечание 3
Замечание 6
Замечание 7
 доказал, что для \ (t \ in (0, \ pi / 2) \),
доказал, что для \ (t \ in (0, \ pi / 2) \), Решение тригонометрических уравнений и неравенств
 Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors. д. – относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. – относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105 (PDF) Замечания к неравенствам для касательной функции
 Свойство логарифмически абсолютно монотонных функций и
Свойство логарифмически абсолютно монотонных функций и и Го, Б. -Н. Усовершенствования, обобщения и приложения неравенства Jor-
и Го, Б. -Н. Усовершенствования, обобщения и приложения неравенства Jor- doi.org/10.1155/2010/931275.
doi.org/10.1155/2010/931275. Персонализированная обучающая платформа для учащихся K6-K12
Бесплатная Персонализированная обучающая платформа для студентов
Обучение на основе тем
Знайте свой IQ и SQ
 Применяйте рассуждения и науку с помощью быстрого бесплатного теста IQ и SQ. Определите свои сильные и слабые стороны и сосредоточьтесь на своих интересах, чтобы построить свой научный коэффициент, который пробуждает ваше любопытство и облегчает изучение STEM.Наши IQ и SQ указывают на формирующую оценку по естествознанию и математике, которая может продвинуть вас вперед и раскрыть новый потенциал.
Применяйте рассуждения и науку с помощью быстрого бесплатного теста IQ и SQ. Определите свои сильные и слабые стороны и сосредоточьтесь на своих интересах, чтобы построить свой научный коэффициент, который пробуждает ваше любопытство и облегчает изучение STEM.Наши IQ и SQ указывают на формирующую оценку по естествознанию и математике, которая может продвинуть вас вперед и раскрыть новый потенциал. Технологии позволяют обучаться
Лучшая платформа для внеклассных занятий STEM для учащихся
 и математика.Благодаря междисциплинарному подходу, мероприятиям и ресурсам, ориентированным на воздействие, это идеальное занятие для молодых умов после школы.
и математика.Благодаря междисциплинарному подходу, мероприятиям и ресурсам, ориентированным на воздействие, это идеальное занятие для молодых умов после школы. Комплексные темы обучения для детей от 9 до 18 лет
Интерактивный и увлекательный контент и виртуальная помощь

