Нерешаемые уравнения: «Бывают ли нерешаемые системы двух уравнений с двумя неизвестными?» — Яндекс Кью

5 -x + 0•y = a

и продублируйте два раза, чтобы система получилась.

Вы, кстати, можете уже дважды заметить, что всегда достаточно одного уравнения и одной неизвестной, потому что если такое есть, то и два уравнения с двумя неизвестными тоже есть

3) Нерешаемое уравнение можно также истолковать в алгоритмическом смысле. Вопрос будет звучать так. Существуют ли уравнения, корни которых нельзя выразить не то, что в элементарных функциях, нельзя их в принципе найти никаким алгоритмом? Это так называемая 10-ая проблема Гильберта. И да, такие уравнения тоже существуют. Решение 10-ой проблемы было окончательно получено в 1970 году.

4) Под нерешаемым уравнением (системой) с большой натяжкой можно также понимать уравнение (или систему), которое на данный момент не решено. В том смысле, что математики не знают, как его решить. Но это скорее всего тогда не нерешаемое уравнение, а неизвестно, решаемое или нет. Если про систему или уравнение известно и доказано, что решение найти невозможно, то это скорее предыдущий описанный случай.

Нет оценок  ·

191

Комментировать ответ…Комментировать…

Вы знаете ответ на этот вопрос?

Поделитесь своим опытом и знаниями

Войти и ответить на вопрос

уравнения Навье-Стокса, гипотеза Ходжа, гипотеза Римана. Задачи тысячелетия

Нерешаемые задачи — это 7 интереснейших математических проблем. Каждая из них была предложена в свое время известными учеными, как правило, в виде гипотез. Вот уже много десятилетий над их решением ломают головы математики во всем мире. Тех, кто добьется успеха, ждет вознаграждение в миллион американских долларов, предложенное институтом Клэйя.

Предыстория

В 1900 году великий немецкий математик-универсал Дэвид Гильберт, представил список из 23-х проблем.

Исследования, осуществленные с целью их решения, оказали огромное влияние на науку 20 века. На данный момент большинство из них уже перестали быть загадками. В числе нерешенных или решенных частично остались:

• проблема непротиворечивости арифметических аксиом;
• общий закон взаимности на пространстве любого числового поля;
• математическое исследование физических аксиом;
• исследование квадратичных форм при произвольных алгебраических числовых коэффициентах;
• проблема строгого обоснования исчислительной геометрии Федора Шуберта;
• и пр.

Неисследованными являются: проблема распространения на любую алгебраическую область рациональности известной теоремы Кронекера и гипотеза Римана.

Институт Клэйя

Под таким названием известна частная некоммерческая организация, штаб-квартира которой находится в Кембридже, штат Массачусетс. Она была основана в 1998 году гарвардским математиком А. Джеффи и бизнесменом Л. Клэйем. Целью деятельности института является популяризация и развитие математических знаний. Для ее достижения организация выдает премии ученым и спонсирует многообещающие исследования.

В начале 21 столетия Математический институт Клэйя предложил премию тем, кто решит проблемы, которые известны, как самые сложные нерешаемые задачи, назвав свой список Millennium Prize Problems. Из «Списка Гильберта» в него вошла только гипотеза Римана.

Задачи тысячелетия

В список института Клэйя изначально входили:

• гипотеза о циклах Ходжа;
• уравнения квантовой теории Янга — Миллса;
• гипотеза Пуанкаре;
• проблема равенства классов Р и NP;
• гипотеза Римана;
• уравнения Навье Стокса, о существовании и гладкости его решений;
• проблема Берча — Свиннертон-Дайера.

Эти открытые математические проблемы представляют огромный интерес, так как могут иметь множество практических реализаций.

Что доказал Григорий Перельман

В 1900 году известный ученый-философ Анри Пуанкаре предположил, что всякое односвязное компактное 3-мерное многообразие без края гомеоморфно 3-мерной сфере. Ее доказательство в общем случае не находилось в течение века. Лишь в 2002-2003 годах петербургский математик Г. Перельман опубликовал ряд статей с решением проблемы Пуанкаре. Они произвели эффект разорвавшейся бомбы. В 2010 году гипотеза Пуанкаре была исключена из списка «Нерешенные задачи» института Клэйя, а самому Перельману было предложено получить полагающееся ему немалое вознаграждение, от которого последний отказался, не объяснив причин своего решения.

Самое понятное объяснение того, что удалось доказать российскому математику, можно дать, представив, что на бублик (тор), натягивают резиновый диск, а затем пытаются стянуть края его окружности в одну точку. Очевидно, что это невозможно. Другое дело, если произвести этот эксперимент с шаром. В таком случае вроде бы трехмерная сфера, получившаяся из диска, окружность которого стянули в точку гипотетическим шнуром, будет трехмерной в понимании обычного человека, но двумерной с точки зрения математики.

Пуанкаре предположил, что трехмерная сфера является единственным трехмерным «предметом», поверхность которой можно стянуть в одну точку, а Перельману удалось это доказать. Таким образом, список «Нерешаемые задачи» сегодня состоит из 6 проблем.

Теория Янга-Миллса

Эта математическая проблема была предложена ее авторами в 1954-м году. Научная формулировка теории имеет следующий вид: для любой простой компактной калибровочной группы квантовая пространственная теория, созданная Янгом и Милльсом, существует, и при этом имеет нулевой дефект массы.

Если говорить на языке, понятном для обычного человека, взаимодействия между природными объектами (частицами, телами, волнами и пр.) делятся на 4 типа: электромагнитное, гравитационное, слабое и сильное. Уже много лет физики пытаются создать общую теорию поля. Она должна стать инструментом для объяснения всех этих взаимодействий. Теория Янга-Миллса — это математический язык, с помощью которого стало возможно описать 3 из 4-х основных сил природы. Она не применима к гравитации. Поэтому нельзя считать, что Янгу и Миллсу удалось создать теорию поля.

Кроме того, нелинейность предложенных уравнений делает их крайне сложными для решения.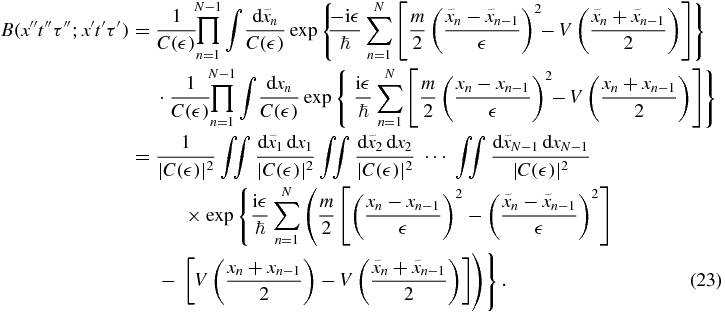 При малых константах связи их удается приближенно решить в виде ряда теории возмущений. Однако пока непонятно, как можно решить эти уравнения при сильной связи.

Уравнения Навье-Стокса

С помощью этих выражений описываются такие процессы, как воздушные потоки, течение жидкостей и турбулентность. Для некоторых частных случаев аналитические решения уравнения Навье-Стокса уже были найдены, однако сделать это для общего пока никому не удалось. В то же время, численное моделирование для конкретных значений скорости, плотности, давления, времени и так далее позволяет добиться прекрасных результатов. Остается надеяться, что у кого-нибудь получится применить уравнения Навье-Стокса в обратном направлении, т. е. вычислить с их помощью параметры, либо доказать, что метода решения нет.

Задача Берча — Свиннертон-Дайера

К категории «Нерешенные задачи» относится и гипотеза, предложенная английскими учеными из Кембриджского университета. Еще 2300 лет назад древнегреческий ученый Эвклид дал полное описание решений уравнения x2 + y2 = z2.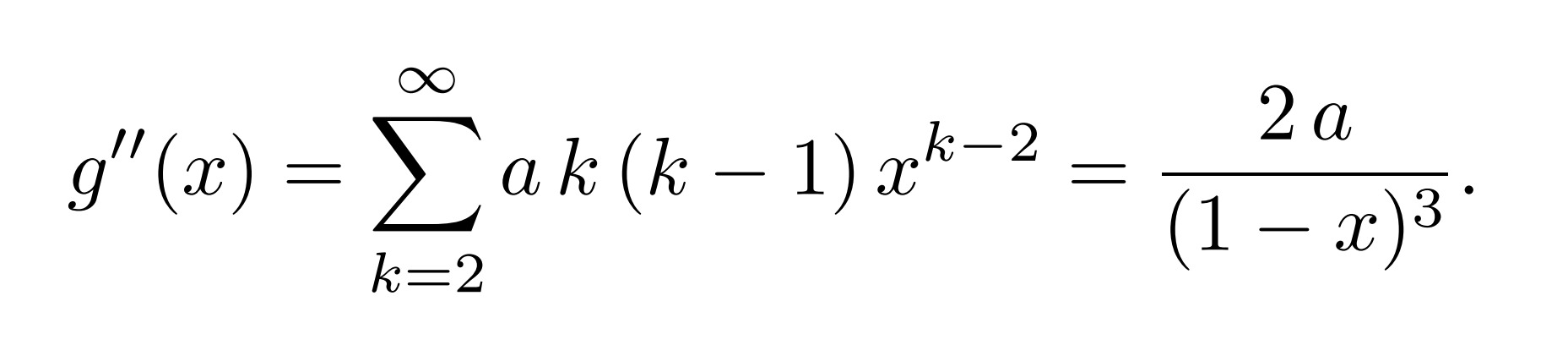

Если для каждого из простых чисел посчитать количество точек на кривой по его модулю, получится бесконечный набор целых чисел. Если конкретным образом «склеить» его в 1 функцию комплексной переменной, тогда получится дзета-функция Хассе-Вейля для кривой третьего порядка, обозначаемая буквой L. Она содержит информацию о поведении по модулю всех простых чисел сразу.

Брайан Берч и Питер Свиннертон-Дайер выдвинули гипотезу относительно эллиптических кривых. Согласно ей, структура и количество множества ее рациональных решений связаны с поведением L-функции в единице. Недоказанная на данный момент гипотеза Берча — Свиннертон-Дайера зависит от описания алгебраических уравнений 3 степени и является единственным сравнительно простым общим способом расчета ранга эллиптических кривых.

Чтобы понять практическую важность этой задачи, достаточно сказать, что в современной криптографии на эллиптических кривых основан целый класс асимметричных систем, и на их применении основаны отечественные стандарты цифровой подписи.

Равенство классов p и np

Если остальные «Задачи тысячелетия» относятся к чисто математическим, то эта имеет отношение к актуальной теории алгоритмов. Проблема, касающаяся равенства классов р и np, известная также, как проблема Кука-Левина, понятным языком может быть сформулирована следующим образом. Предположим, что положительный ответ на некий вопрос можно проверить достаточно быстро, т. е. за полиномиальное время (ПВ). Тогда правильно ли утверждение, что ответ на него можно довольно быстро отыскать? Еще проще эта задача звучит так: действительно ли решение задачи проверить не труднее, чем его найти? Если равенство классов р и np будет когда-либо доказано, то все проблемы подбора можно будет решать за ПВ. На данный момент многие специалисты сомневаются в истинности этого утверждения, хотя не могут доказать обратное.

Гипотеза Римана

Вплоть до 1859 года не было выявлено какой-либо закономерности, которая описывала бы, как распределяются простые числа среди натуральных. Возможно, это было связано с тем, что наука занималась другими вопросами. Однако к середине 19 столетия ситуация изменилась, и они стали одними из наиболее актуальных, которыми начала заниматься математика.

Гипотеза Римана, появившаяся в этот период — это предположение о том, что в распределении простых чисел существует определенная закономерность.

Сегодня многие современные ученые считают, что если она будет доказана, то придется пересмотреть многие фундаментальные принципы современной криптографии, составляющие основу значительной части механизмов электронной коммерции.

Согласно гипотезе Римана, характер распределения простых чисел, возможно, существенно отличается от предполагаемого на данный момент. Дело в том, что до сих пока не было обнаружено какой-либо системы в распределения простых чисел. Например, существует проблема «близнецов», разность между которыми равна 2. Этими числами являются 11 и 13, 29. Другие простые числа образуют скопления. Это 101, 103, 107 и др. Ученые давно подозревали, что подобные скопления существуют и среди очень больших простых чисел. Если их найдут, то стойкость современных криптоключей окажется под вопросом.

Гипотеза о циклах Ходжа

Эта нерешенная до сих пор задача сформулирована в 1941 году. Гипотеза Ходжа предполагает возможность аппроксимации формы любого объекта путем «склеивания» вместе простых тел большей размерности. Этот способ был известен и успешно применяется достаточно давно. Однако не известно, до какой степени можно производить упрощение.

Теперь вы знаете, какие нерешаемые задачи существуют на данный момент. Они являются предметом исследования тысяч ученых во всем мире. Остается надеяться, что в ближайшее время они будут решены, а их практическое применение поможет человечеству выйти на новый виток технологического развития.

10 математических уравнений, которые никогда не были решены

Математика сыграла важную роль во многих изобретениях и теориях, которые изменили жизнь. Но все еще есть некоторые математические уравнения, которые ускользнули от внимания даже величайших умов, таких как Эйнштейн и Хокинс. Другие уравнения, однако, просто слишком велики для вычисления. Так что по какой-то причине эти загадочные проблемы так и не были решены. Но что это такое?

Как и все мы, вы, вероятно, ожидаете следующего уровня сложности в этих математических задачах. Удивительно, но это не так. Некоторые из этих уравнений даже основаны на понятиях начальной школы и легко понятны — просто неразрешимы.

1. Гипотеза Римана

Уравнение: σ (n) ≤ Hn +ln (Hn)eHn

• Где n — натуральное число
• Hn – n-я гармоника номер
• σ(n) — сумма натуральных чисел, делящихся на n

Например, если n = 4, то σ(4)=1+2+4=7 и h5 = 1+1/2+1/3+1/4. Решите это уравнение, чтобы доказать или опровергнуть следующее неравенство n≥1? Верно ли это для всех n≥1?

Эта задача называется “Элементарная версия гипотезы Римана Лагариаса”. Математический фонд Клэя предлагает за ее решение цену в миллион долларов.

2. Гипотеза Коллатца

Уравнение: 3n+1

• где n — натуральное число n/2
• , где n — целое неотрицательное число
.

Докажите конец ответа, перебирая 1,4,2,1,4,2,1,…, если n — положительное целое число. Это повторяющийся процесс, и вы будете повторять его с новым значением n, которое получите. Если ваше первое n = 1, то ваши последующие ответы будут 1, 4, 2, 1, 4, 2, 1, 4… бесконечно. И если n = 5, ответы будут 5,16,8,4,2,1, остальное будет другим циклом со значениями 1, 4 и 2.

Это уравнение было составлено в 1937 году человеком по имени Лотар Коллатц, поэтому его называют гипотезой Коллатца.

3. Гипотеза Эрдеша-Стросса

Уравнение: 4/n=1/a+1/b+1/c

• где n≥2
• a, b и c — положительные целые числа.

Целью этого уравнения является проверка того, можем ли мы доказать, что если n больше или равно 2, то можно записать 4*n как сумму трех положительных единичных дробей.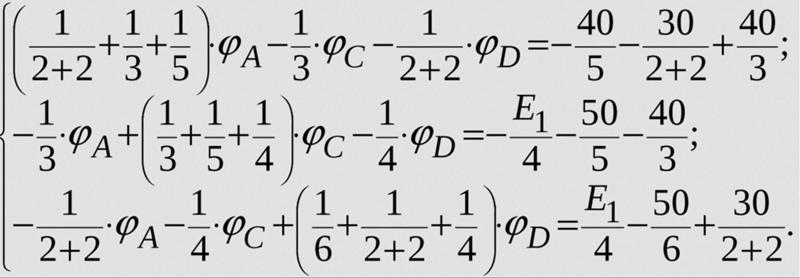

Это уравнение было сформировано в 1948 двумя мужчинами по имени Пол Эрдёш и Эрнст Штраус, поэтому его называют гипотезой Эрдёша-Штрауса.

4. Уравнение четыре

Уравнение: Используйте 2(2∧127)-1 – 1, чтобы доказать или опровергнуть, является ли это простым числом или нет?

Выглядит довольно прямолинейно, не так ли? Вот небольшой контекст проблемы.

Возьмем простое число 2. Итак, 22 – 1 = 3, что также является простым числом. 25 – 1 = 31, что также является простым числом, поэтому 27−1=127. 2127 -1=170141183460469231731687303715884105727 — тоже простое число.

5. Гипотеза Гольдбаха

Уравнение: Докажите, что x + y = n

• где x и y — любые два простых числа
• n равно ≥ 4 ​​

Эта проблема, как бы относительно проста она ни звучала, никогда не была решена. Решение этой задачи принесет вам бесплатный миллион долларов. Это уравнение было впервые предложено Гольдбахом, отсюда и название «гипотеза Гольдбаха».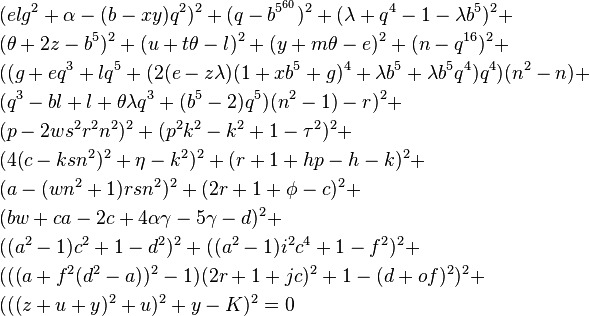

Если вы все еще не уверены, выберите любое четное число, например 6, его также можно выразить как 1 + 5, то есть два простых числа. То же самое касается 10 и 26.

6. Уравнение шесть

Уравнение: Докажите, что (K)n = JK1N(q)JO1N(q)

• Где O = unknot (мы имеем дело с теорией узлов)
• (K)n  =  Кашаевский инвариант K для любого K или узла
• JK1N(q) числа K равно N-цветному многочлену Джонса
• У нас также есть объем предположения как (EQ3)
• Здесь объем (K) = гиперболический объем

Это уравнение пытается изобразить связь между квантовыми инвариантами узлов и гиперболической геометрией узловых дополнений. Хотя это уравнение относится к математике, вы должны быть знакомы с физикой, чтобы понять его концепцию.

7. Гипотеза Уайтхеда

Уравнение: G = (S | R)

• , когда комплекс CW K (S | R) асферичен
• , если π2 (K (S | R)) = 0

Что вы делаете в этом уравнении, так это доказываете утверждение, сделанное мистером Уайтхедом в 1941 году в алгебраической топологии, что каждый подкомплекс асферического комплекса CW, который является связным и в двух измерениях, также является сферическим. Это было названо в честь человека, гипотезы Уайтхеда.

8. Уравнение восемь

Уравнение: (EQ4)

• Где Γ = вторая счетная локально компактная группа
• И индексы * и r = 0 или 1.

Это уравнение является определением морфизма и называется сборочной картой. Ознакомьтесь с сокращенной C*-алгеброй, чтобы лучше понять концепцию, связанную с этим уравнением.

9. Константа Эйлера-Маскерони

Уравнение: y=limn→∞(∑m=1n1m−log(n))

Выясните, является ли y рациональным или иррациональным в приведенном выше уравнении. Чтобы полностью понять эту проблему, вам нужно еще раз взглянуть на рациональные числа и их концепции. Символ y известен как константа Эйлера-Маскерони и имеет значение 0,5772.

Это уравнение было рассчитано почти до половины триллиона цифр, но до сих пор никто не смог сказать, является ли оно рациональным числом или нет.

10. Уравнение 10

Уравнение: π + e

Найдите сумму и определите, является ли она алгебраической или трансцендентной. Чтобы понять этот вопрос, вам нужно иметь представление об алгебраических действительных числах и о том, как они работают. Число пи или π возникло в 17 веке и является трансцендентным наряду с e. а как же их сумма? До сих пор это никогда не было решено.

Заключение

Как вы можете видеть из приведенных выше уравнений, есть несколько кажущихся простыми математических уравнений и теорий, которые так и не были опровергнуты. Проходят десятилетия, а эти проблемы остаются нерешенными. Если вы ищете головоломку, поиск решений этих проблем даст вам возможность заработать деньги.

См. 11 комментариев ниже.

Топ-5 неразрешимых математических задач за всю историю

Амина Решма Последнее обновление: 15 июля 2022 г., 6:06 EST

3 мин Чтение

Сложные математические задачи, несомненно, самые сложные, и многие из них остаются нерешенными. Мы всегда выполняем расчеты в погоне за более глубокими числовыми знаниями, несмотря на все достижения, которых мы достигли в мире математики за последнее время.

Например, суперкомпьютер, решивший задачу о сумме трех кубов, не давал покоя математикам 65 лет.

Математические задачи ставили нас в тупик на протяжении веков, и хотя некоторые головоломки могут казаться неразрешимыми для человека или машины, кто-то неизбежно решит их… или нет. Время покажет. Тем не менее, читайте дальше, чтобы узнать, являетесь ли вы математическим умом, который может решить самые неразрешимые математические задачи всех времен.

1. Разделение сепаратрис

Движущийся маятник может качаться из стороны в сторону или вращаться по непрерывному кругу. Сепаратриса — это точка перехода одного типа движения в другой, и ее можно вычислить в большинстве простых ситуаций. Однако, когда маятник толкают с почти постоянной скоростью, математика разваливается.

Может ли такая сепаратриса быть описана уравнением? ^{1 ​​}

2. Гипотеза Коллатца

 Гипотеза Коллатца в первую очередь касается последовательностей, начинающихся с любого положительного целого числа.

В нем говорится, что если мы начинаем с любого положительного числа, такого как n, то каждый член получается следующим образом:

• Если предыдущий член четный, следующий член составляет половину предыдущего члена, то есть n/ 2.
• Если предыдущий член нечетный, следующий член в 3 раза больше предыдущего плюс 1, то есть 3n+1. ⁵

Благодаря плодовитому математику Теренсу Тао недавно появились новости о прогрессе в решении этого 82-летнего вопроса. Хотя история прорыва Тао обнадеживает, проблема еще не решена полностью. В некотором смысле недавняя работа Тао близка к решению гипотезы Коллатца. Однако, как позже объяснил Тао, он вряд ли сможет адаптировать свои методы для получения полного решения проблемы. Это может привести к тому, что математики будут работать над ней десятилетиями. ²

3. Гипотеза Римана

Гипотеза Римана — одна из самых важных открытых проблем во всей математике. Он имеет далеко идущие последствия в различных областях математики, но в то же время он прост. Согласно гипотезе Римана, « все интересные решения уравнения

   ζ(s) = 0

лежат на некоторой вертикальной прямой». ³

Было проверено 10 000 000 000 000 решений, доказывающих, что каждое интересное решение действительно проливает свет на многие тайны, связанные с распределением простых чисел. Она настолько сложная, что стала самой сложной математической задачей, а также одной из задач тысячелетия, за решение которой присужден приз в 1 миллион долларов.

3

4. Уравнения Навье-Стокса

Уравнения Навье-Стокса — еще одна задача на премию тысячелетия с призом в 1 миллион долларов. Уравнения, разработанные в 1822 году, используются для описания движения вязких жидкостей, таких как воздух, проходящий через крыло самолета, или вода, вытекающая из крана. Однако бывают случаи, когда трудно сказать, не работают ли уравнения или вообще не дают ответа. Многие математики пытались, но не смогли решить эту задачу.

1 ​​

5. ГПИО ГПИОНТУРЫ БИРЕЧ И СВИННРТОНА

Описание всех решений в целых числах x, y, z для алгебрейских уравнений, таких как x + 2 . ^{2 всегда очаровывал математиков. Евклид дал полное решение этого уравнения, но это становится чрезвычайно трудным для более сложных уравнений, и не существует общего метода определения, когда такие уравнения имеют целочисленное решение. Гипотеза была развита в 1960-х годов британскими математиками Брайаном Берчем и Питером Суиннертоном-Дайером, и его точная формулировка очень техническая и со временем эволюционировала. 4}

Ссылки:

1. 5 самых сложных нерешенных математических задач в мире | Новый ученый. (н.д.). Получено 8 июня 2022 г. с https://www.newscientist.com/article/2193080-5-of-the-worlds-toughest-unsolved-maths-problems/
2. Простая математическая задача, которую мы все еще не можем решить Решить | Журнал Кванта. (н.д.). Получено 8 июня 2022 г. с https://www.quantamagazine.org/why-mathematicians-still-cant-solve-the-collatz-conjecture-202009.22/
3. Гипотеза Римана | Математический институт Клэя. (н.д.). Получено 8 июня 2022 г. с https://www.claymath.org/millennium-problems/riemann-hypothesis
4. Гипотеза Берча и Суиннертона-Дайера | Математический институт Клэя. (н.д.). Получено 8 июня 2022 г. с https://www.claymath.org/millennium-problems/birch-and-swinnerton-dyer-conjecture
5. Гипотеза Коллатца: простейшая гипотеза в математике, которую никто никогда не доказывал. (н.д.). Проверено 9 июня., 2022 г., с https://www.secretsofuniverse.in/collatz-conjecture/

Математика, Мир математики

Вам также может понравиться

Наука и математика: идеальное сочетание

Естествознание и математика — очень взаимосвязанные темы. Импликация одного автоматически подразумевает подразумеваемые части другого.