7 математических загадок тысячелетия. Просто о сложном
Только для мыслящих людей!
“Я знаю только то, что ничего не знаю, но другие не знают и этого”
(Сократ, древнегреческий философ)
НИКОМУ не дано владеть вселенским разумом и знать ВСЁ. Тем не менее, у большинства ученых, да и тех, кто просто любит размышлять и исследовать, всегда есть стремление узнать больше, разгадать загадки. Но остались ли еще неразгаданные темы у человечества? Ведь, кажется, все уже ясно и нужно только применять полученные веками знания?
НЕ стоит отчаиваться! Еще остались нерешенные проблемы из области математики, логики, которые в 2000 году эксперты Математического института Клэя в Кембридже (Массачусетс, США) объединили в список, так называемые, 7 загадок тысячелетия (Millennium Prize Problems). Эти проблемы волнуют ученых всей планеты. С тех пор и по сей день любой человек может заявить, что нашел решение одной из задач, доказать гипотезу и получить от бостонского миллиардера Лэндона Клэя (в честь которого и назван институт) премию.
Итак, вы готовы узнать о математических загадках?
Уравнения Навье – Стокса (сформулированы в 1822 году)
Область: гидроаэродинамика
Уравнения о турбулентных, воздушных потоках, а также течении жидкостей известны как уравнения Навье – Стокса. Если, к примеру, плыть по озеру на чем-либо, то неизбежно вокруг возникнут волны. Это касается и воздушного пространства: при полете на самолете в воздухе также будут образовываться турбулентные потоки.
Данные уравнения как раз производят описание процессов движения вязкой жидкости и являются стержневой задачей всей гидродинамики. Для некоторых частных случаев уже найдены решения, в которых части уравнений отбрасываются, как не влияющие на конечный результат, но в общем виде решения этих уравнений не найдены.
Гипотеза Римана (сформулирована в 1859 году)
Область: теория чисел
Известно, что распределение простых чисел (Которые делятся только на себя и на единицу: 2,3,5,7,11…) среди всех натуральных чисел не подчиняется никакой закономерности.
Над этой проблемой задумался немецкий математик Риман, который сделал свое предположение, теоретически касающееся свойств имеющейся последовательности простых чисел. Уже давно известны так называемые парные простые числа – простые числа-близнецы, разность между которыми равна 2, например 11 и 13, 29 и 31, 59 и 61. Иногда они образуют целые скопления, например, 101, 103, 107, 109 и 113.
Проблема Пуанкаре (сформулирована в 1904 году. Решена в 2002 году.)
Область: топология или геометрия многомерных пространств
Суть проблемы заключается в топологии и состоит в том, что если натягивать резиновую ленту, к примеру, на яблоко (сферу), то будет теоретически возможным сжать ее до точки, медленно перемещая без отрыва от поверхности ленту.
Представитель ленинградской геометрической школы Григорий Яковлевич Перельман является лауреатом премии тысячелетия математического института Клэя (2010 г.) за решение проблемы Пуанкаре. От знаменитой Фильдсовской премии он отказался.
Гипотеза Ходжа (сформулирована в 1941 году)
Область: алгебраическая геометрия
В реальности существуют множество как простых, так и куда более сложных геометрических объектов. Чем сложнее объект, тем труднее его изучать. Сейчас учеными придуман и вовсю применяется подход, основанный на использовании частей одного целого (“кирпичики”) для изучения этого объекта, как пример – конструктор. Зная свойства «кирпичиков», становится возможным подступиться и к свойствам самого объекта.
Гипотеза Ходжа в данном случае связана с некоторыми свойствами как «кирпичиков», так и объектов.
Уравнения Янга – Миллса (сформулированы в 1954 году)
Область: геометрия и квантовая физика
Физики Янг и Миллс описывают мир элементарных частиц. Они, обнаружив связь между геометрией и физикой элементарных частиц, написали свои уравнения в области квантовой физики. Тем самым был найден путь к объединению теорий электромагнитного, слабого и сильного взаимодействий.
На уровне микрочастиц возникает «неприятный» эффект: если на частицу действуют несколько полей сразу, их совокупный эффект уже нельзя разложить на действие каждого из них поодиночке. Это происходит по причине того, что в этой теории друг к другу притягиваются не только частицы материи, но и сами силовые линии поля.
Гипотеза Берча и Свиннертон-Дайера (сформулирована в 1960 году)
Область: алгебра и теория чисел
Гипотеза связана с уравнениями эллиптических кривых и множеством их рациональных решений. В доказательстве теоремы Ферма эллиптические кривые заняли одно из важнейших мест. А в криптографии они образуют целый раздел имени себя, и на них основаны некоторые российские стандарты цифровой подписи.
Проблема Кука (сформулирована в 1971 году)
Область: математическая логика и кибернетика
Ее еще называют “Равенство классов P и NP”, и она является одной из наиболее важных задач теории алгоритмов, логики и информатики.
Может ли процесс проверки правильности решения какой-либо задачи длиться дольше, чем время, затраченное на само решение этой задачи (независимо от алгоритма проверки)?
На решение одной и той же задачи, порой, нужно разное количество времени, если изменить условия и алгоритмы.
Основным вопросом является: все или не все задачи, которые можно легко и быстро проверить, можно также легко и быстро решить?
Математика, как может показаться многим, не так далека от реальности. Она является тем механизмом, с помощью которого можно описать наш мир и многие явления. Математика всюду. И прав был В.О. Ключевский, который изрек:
И в заключение….
Одну из самых популярных теорем математики – Великую (Последнюю) теорему Ферма: аn + bn = cn – не могли доказать 358 лет! И только в 1994 году британец Эндрю Уайлз смог дать ей решение.
Так что, дерзайте, великие умы!
Задачи тысячелетия.
Просто о сложном / ХабрПривет, хабралюди!
Сегодня я бы хотел затронуть такую тему как «задачи тысячелетия», которые вот уже десятки, а некоторые и сотни лет волнуют лучшие умы нашей планеты.
После доказательства гипотезы (теперь уже теоремы) Пуанкаре Григорием Перельманом, основным вопросом, который заинтересовал многих, был: «А что же он собственно доказал, объясните на пальцах?
Равенство классов P и NP
Все мы помним из школы квадратные уравнения, которые решаются через дискриминант. Решение этой задачи относится к
классу P (Polynomial time)— для нее существует быстрый (здесь и далее под словом «быстрый» подразумевается как выполняющийся за полиномиальное время) алгоритм решения, который и заучивается.
Также существуют NP-задачи (Non-deterministic Polynomial time), найденное решение которых можно быстро проверить по определенному алгоритму.
Таких задач много, но основным вопросом является, все или не все задачи которые можно легко и быстро проверить можно также легко и быстро решить? Сейчас для некоторых задач не найдено быстрого алгоритма решения, и неизвестно существует ли такой вообще.
На просторах интернета также встретил такую интересную и прозрачную формулировку:
Допустим, что вы, находясь в большой компании, хотите убедиться, что там же находится ваш знакомый. Если вам скажут, что он сидит в углу, то достаточно будет доли секунды, чтобы, бросив взгляд, убедиться в истинности информации. В отсутствие этой информации вы будете вынуждены обойти всю комнату, рассматривая гостей.
В данном случае вопрос стоит все тот же, есть ли такой алгоритм действий, благодаря которому даже не имея информации о том, где находится человек, найти его так же быстро, как будто зная где он находится.
Данная проблема имеет большое значение для самых различных областей знаний, но решить ее не могут уже более 40 лет.
Гипотеза Ходжа
В реальности существуют множество как простых так и куда более сложных геометрических объектов. Очевидно, что чем сложнее объект тем более трудоемким становится его изучение. Сейчас учеными придуман и вовсю применяется подход, основная идея которого заключается в том, чтобы вместо самого изучаемого объекта использовать простые
«кирпичики»с уже известными свойствами, которые склеиваются между собой и образуют его подобие, да-да, знакомый всем с детства конструктор. Зная свойства «кирпичиков», становится возможным подступиться и к свойствам самого объекта.
Гипотеза Ходжа в данном случае связана с некоторыми свойствами как «кирпичиков» так и объектов.
Гипотеза Римана
Всем нам еще со школы известны простые числа которые делятся только на себя и на единицу
(2,3,5,7,11…). С давних времен люди пытаются найти закономерность в их размещении, но удача до сих пор так никому и не улыбнулась. В результате ученые применили свои усилия к функции распределения простых чисел, которая показывает количество простых чисел меньше или равных определенного числа. Например для 4 — 2 простых числа, для 10 — уже 4 числа.
Гипотеза Риманакак раз устанавливает свойства данной функции распределения.
Многие утверждения о вычислительной сложности некоторых целочисленных алгоритмов, доказаны в предположении верности этой гипотезы.
Теория Янга — Миллса
Уравнения квантовой физики описывают мир элементарных частиц. Физики Янг и Миллс, обнаружив связь между геометрией и физикой элементарных частиц, написали свои уравнения, объединяющие теории электромагнитного, слабого и сильного взаимодействий. Одно время теория Янга-Миллса рассматривалась лишь как математический изыск, не имеющий отношения к реальности.
Однако, позже теория начала получать экспериментальные подтверждения, но в общем виде она все еще остается не решенной.
На основе теории Янга-Миллса построена стандартная модель физики элементарных частиц в рамках которой был предсказан и не так давно обнаружен нашумевший бозон Хиггса.
Существование и гладкость решений уравнений Навье — Стокса
Течение жидкостей, воздушные потоки, турбулентность. Эти, а также множество других явлений описываются уравнениями, известными как
уравнения Навье — Стокса. Для некоторых частных случаев уже найдены решения, в которых как правило части уравнений отбрасываются как не влияющие на конечный результат, но в общем виде решения этих уравнений неизвестны, и при этом даже неизвестно, как их решать.
Гипотеза Бёрча — Свиннертон-Дайера
Для уравнения x
2+ y
2= z
2 в свое время еще Эвклид дал полное описание решений, но для более сложных уравнений поиск решений становится чрезвычайно трудным, достаточно вспомнить историю доказательства знаменитой теоремы Ферма, чтобы убедиться в этом.
Данная гипотеза связана с описанием алгебраических уравнений 3 степени — так называемых эллиптических кривых и по сути является единственным относительно простым общим способом вычисления ранга, одного из важнейших свойств эллиптических кривых.
В доказательстве теоремы Ферма эллиптические кривые заняли одно из важнейших мест. А в криптографии они образуют целый раздел имени себя, и на них основаны некоторые российские стандарты цифровой подписи.
Гипотеза Пуанкаре
Думаю если не все, то большинство точно о ней слышали. Чаще всего встречается, в том числе и на центральных СМИ, такая расшифровка как «
резиновую ленту натянутую на сферу можно плавно стянуть в точку, а натянутую на бублик — нельзя». На самом деле эта формулировка справедлива для гипотезы Тёрстона, которая обобщает гипотезу Пуанкаре, и которую в действительности и доказал Перельман.
Частный случай гипотезы Пуанкаре говорит нам о том, что любое трехмерное многообразие без края (вселенная, например) подобно трехмерной сфере.
А общий случай переводит это утверждение на объекты любой мерности. Стоит заметить, что бублик, точно так же как вселенная подобна сфере, подобен обычной кофейной кружке.
Заключение
В настоящее время математика ассоциируется с учеными, имеющими странный вид и говорящие о не менее странных вещах. Многие говорят о ее оторванности от реального мира. Многие люди как младшего, так и вполне сознательного возраста говорят, что математика ненужная наука, что после школы/института, она нигде не пригодилась в жизни.
Но на самом деле это не так — математика создавалась как механизм с помощью которого можно описать наш мир, и в частности многие наблюдаемые вещи. Она повсюду, в каждом доме. Как сказал В.О. Ключевский: «Не цветы виноваты, что слепой их не видит».
Наш мир далеко не так прост, как кажется, и математика в соответствии с этим тоже усложняется, совершенствуется, предоставляя все более твердую почву для более глубокого понимания существующей реальности.
Хочу учиться – нерешенные задачи
Главная страница – » Задачи человечества
ЗАДАЧИ МАТЕМАТИКИ, НЕ РЕШЕННЫЕ ЧЕЛОВЕЧЕСТВОМ
Задачи Гильберта
23 важнейших проблем математики были представлены величайшим немецким математиком Давидом Гильбертом на Втором Международном конгресе математиков в Париже в 1990 году.
Тогда эти проблемы (охватывающие основания математики, алгебру, теорию чисел, геометрию, топологию, алгебраическую геометрию, группы Ли, вещественный и комплексный анализ, дифференциальные уравнения, математическую физику, вариационное исчисление и теорию вероятностей, не были решены. На данный момент решены 16 проблем из 23. Ещё 2 не являются корректными математическими проблемами (одна сформулирована слишком расплывчато, чтобы понять, решена она или нет, другая, далёкая от решения, — физическая, а не математическая). Из оставшихся 5 проблем две не решены никак, а три решены только для некоторых случаев
Задачи Ландау
До сих пор существует много открытых вопросов, связанных с простыми числами (простое число – это число, которое имеет отлько два делителя: единицу и само это число). Наиболее важные вопросы были перечислены Эдмундом Ландау на Пятом Междунанародном математическом конгресе:
Первая проблема Ландау (проблема Гольдбаха): верно ли, что каждое чётное число, большее двух, может быть представлено в виде суммы двух простых чисел, а каждое нечётное число, большее 5, может быть представлено в виде суммы трёх простых чисел?
Вторая проблема Ландау: бесконечно ли множество «простых близнецов» — простых чисел, разность между которыми равна 2?
Третья проблема Ландау (гипотеза Лежандра): верно ли, что для всякого натурального числа n между и всегда найдётся простое число?
Четвёртая проблема Ландау: бесконечно ли множество простых чисел вида , где n — натуральное число?
Задачи тысячелетия (Millennium Prize Problems)
Это семь математических задач, за решение каждой из которых инcтитут Клея предложил приз в 1 000 000 долларов США.
Вынося на суд математиков эти семь задач, иститут Клея сравнил их с 23 задачами Д.Гильберта, которые оказали большое влияние на на математику ХХ века. Из 23 проблем Гильберта большинство уже решены, и только одна — гипотеза Римана — вошла в список задач тысячелетия. По состоянию на декабрь 2012 года только одна из семи проблем тысячелетия (гипотеза Пуанкаре) решена. Приз за её решение присуждён российскому математику Григорию Перельману, который от него отказался.
Вот список этих семи задач:
№1. Равенство классов P и NP
Если положительный ответ на какой-то вопрос можно быстро проверить (используя некоторую вспомогательную информацию, называемую сертификатом), то верно ли, что и сам ответ (вместе с сертификатом) на этот вопрос можно быстро найти? Задачи первого типа относятся к классуц NP, второго — классу Р. Проблема равенства этих классов является одной из важнейших проблем теории алгоритмов.
№2.
Гипотеза ХоджаВажная проблема алгебраической геометрии. Гипотеза описывает классы комогологий на комплексных проективных многообразиях, реализуемые алгебраическими подмногообразиями.
№3. Гипотеза Пуанкаре (доказана Г.Я.Перельманом)
Cчитается наиболее известной проблемой топологии. Говоря более просто, она утверждает, что всякий 3D «объект», обладающий некоторыми свойствами трёхмерной сферы (например, каждая петля внутри него должна быть стягиваема), обязан быть сферой с точностью до деформации. Премия за доказательство гипотезы Пуанкаре присуждена российскому математику Г.Я.Перельману, опубликовавшему в 2002 году серию работ, из которых следует справедливость гипотезы Пуанкаре.
№4. Гипотеза Римана
Гипотеза гласит, что все нетривиальные (то есть имеющие ненулевую мнимую часть) нули дзета-функции Римана имеют действительную часть 1/2. Гипотеза Римана была восьмой в списке проблем Гильберта.
№5. Теория Янга — Миллса
Задача из области физики элементарных частиц.
Требуется доказать, что для любой простой компактной калибровочной группы G квантовая теория Янга — Миллса для четырехмарного пространства существует и имеет ненулевой дефект массы. Это утверждение соответствует экспериментальным данным и численному моделированию, однако доказать его до сих пор не удалось.
№6. Существование и гладкость решений уравнений Навье — Стокса
Уравнения Навье — Стокса описывают движение вязкой жидкости. Одна из важнейших задач гидродинамики.
№7. Гипотеза Бёрча — Свиннертон-Дайера
Гипотеза связана с уравнениями эллиптических кривых и множеством их рациональных решений.
на главную
7 ЗАДАЧ ТЫСЯЧЕЛЕТИЯ — I-NURE
Кто из вас хочет стать миллионером? Для этого не нужно покупать лотерейный билет или грабить банк. Математический институт Клэя в США готов с радостью выплатить миллион тем, кто просто решит хотя бы одну из их математических задач.
Звучит настолько просто, что вы уже готовы набросать решение любой из них? А давайте-ка сначала узнаем так ли просты эти задачки…
Как обычно, немного истории…
В начале 20 века знаменитый немецкий математик Давид Гильберт на одной из конференций представил миру 26 открытых математических проблем, требующих хорошенько пораскинуть мозгами. К концу столетия 20 из них были решены математиками всего мира. Последней, кстати, была теорема Ферма, знакомая многим из курса линейной алгебры и аналитической геометрии.
Новый список задач, представленный американским институтом Клэя в 1998 году, стал в несколько раз «скромнее» – всего 7 задач – но, как видно, и намного сложнее, ведь за 21 год существования, лишь одна из них была решена…
Так что собой представляют эти 7 задач?
Каждая из них касается какой-либо из областей математики: от теории алгоритмов до топологии и математической физики. И пусть некоторые на первый взгляд могут показаться простыми, но не просто же так за решение любой из них присуждается 1 миллион долларов! Но, пожалуй, начнем описание с той самой единственной решенной задачи.
Итак…
1. Гипотеза Пуанкаре
Область изучения – топология.
Эта гипотеза доказана в 2002 году российским математиком Григорием Перльманом. Очень часто можно встретить и другое название этой знаменитой задачи – «проблема бублика». Гипотеза утверждает следующее: всякий трёхмерный объект, обладающий некоторыми свойствами трёхмерной сферы, обязан быть сферой с точностью до деформации. Сама же история решения этой задачи тысячелетия прямо-таки, как сюжет фильма: гениальный математик из Санкт-Петербурга на несколько лет обрывает все связи с внешним миром, а потом триумфально возвращается с решением одной из 7 задач, навсегда занося своё имя в историю мировой науки! Что ещё более любопытно: от награды в 1 миллион долларов Григорий Перльман отказался.
2. Равенство классов P и NP
Область изучения – теория алгоритмов.
Перед вами два класса: P и NP.
P – это множество задач, которые компьютер может решить за полиномиальное время, т.е. довольно быстро. NP – это класс задач, правильность ответа, которых можно быстро проверить.
Для простоты понимания вот вам пример: у вас есть по одной монетке номиналом 2, 3, 5, 6 и 7. Ваша задача – оплатить покупку без сдачи на сумму 21 денежной единицы. Можно ли набрать из этих монет сумму, равную 21? Задача решается методом перебора, и вот плавно мы подходим к вопросу одной из задач тысячелетия: равны ли классы N и NP? Многие ученые уверены в отрицательном ответе, но доказать свою точку зрения так пока никто и не смог. Только вот что будет, если окажется, что P=NP?..
3. Уравнение Навье-Стокса
Область – гидродинамика.
Задача, которая может быть известна некоторым по фильму «Одарённая». В решении данного уравнения заложена одна из сложнейших проблем современной физики – проблема турбулентности. Турбулентность хоть и является довольно распространённым явлением, но до сих пор остаётся почти неизученной, отчего и совершенно непредсказуемой.
Помимо самого уравнения, задача ставит перед нами и такой вопрос: если известно состояние жидкости в определённый момент времени и характеристики её движения – существует ли решение, которое будет верно для всего будущего времени? Так что, помимо проблемы турбулентности, решение этой задачи помогло бы метеорологам делать более точные прогнозы погоды, а нам – всегда вовремя брать с собой зонтик.
4. Гипотеза Римана
Область – теория чисел.
Задача, посвященная нашим любимым простым числам. Если проследить их последовательность в общем строю всех чисел, то можно прийти к тому, что какой-либо закономерности их распределения нет.
Немецкий математик Бернхард Риман предложил гипотезу, которая утверждает, что все нетривиальные нули дзета-функции распределения простых чисел лежат на прямой линии. Гипотеза Римана уже была проверена для 10 триллионов решений, но полное доказательство ещё не было подтверждено, но математики утверждают, что уже совсем близко подошли к решению этой задачи тысячелетия.
5. Гипотеза Ходжа
Область – алгебраическая геометрия.
«На любом невырожденном проективном комплексном алгебраическом многообразии любой класс Ходжа представляет собой рациональную линейную комбинацию классов алгебраических циклов». Так звучит формулировать данной гипотезы. Немного запутанно, да?
Суть в чем: в мире нас окружают простые и сложные объекты. И, вполне логично, что сложные объекты можно описать с помощью определённого количества простых. Основная идея гипотезы состоит в том, чтобы выяснить, до какой степени мы можем приближаться к форме сложного объекта, склеивая вместе простые тела возрастающей размерности.
6. Теория Янга-Миллса
Область – физика элементарных частиц.
Физики Янг Чжэньнин и Роберт Миллс обнаружили связь между геометрией и физикой элементарных частиц и написали уравнения, объединяющие теории электромагнитного, слабого и сильного воздействия, что до этого казалось невозможным.
По сути, уравнения теории Янга-Миллса пытаются предсказать поведение элементарных частиц и дать общее описание 3 из 4 фундаментальных взаимодействий. Проведённые эксперименты полностью подтверждают выдвинутую теорию, однако полное обоснование до сих пор так и не найдено.
И наконец…
7. Гипотеза Бёрча-Свиннертон-Дайера
Область – алгебраическая геометрия. Снова.
Гипотеза связана с описанием алгебраических уравнений 3 степени – эллиптических кривых – и является единственным простым общим способом ранга эллиптических кривых.
Суть задачи такова: множество решений эллиптической кривой связано с поведением L-функции, которая вычисляется, как и дзета-функция гипотезы Римана, и количество рациональных решений бесконечно тогда, когда функция равна 0.
Главный вопрос: возможно ли вообще решить все задачи тысячелетия?
Как говорится: нет ничего невозможного! Терпение, труд и отличная математическая база всё перетрут.
Кто знает, дорогие студенты ХНУРЭ, может быть именно вы благодаря своим знаниям разрешите оставшиеся 6 задач тысячелетия? И это касается не только тех, кто обучаться по профилю «Прикладная математика», а студентов всех факультетов ВУЗа. Так что, достаём листочки и начинаем решать – за кем будущее, как не за нами?
По материалам: Wikipedia.org, naked-science.ru, habr.com
Карина Темчур
уравнения Навье-Стокса, гипотеза Ходжа, гипотеза Римана. Задачи тысячелетия
Нерешаемые задачи — это 7 интереснейших математических проблем. Каждая из них была предложена в свое время известными учеными, как правило, в виде гипотез. Вот уже много десятилетий над их решением ломают головы математики во всем мире. Тех, кто добьется успеха, ждет вознаграждение в миллион американских долларов, предложенное институтом Клэйя.
Предыстория
В 1900 году великий немецкий математик-универсал Дэвид Гильберт, представил список из 23-х проблем.
Исследования, осуществленные с целью их решения, оказали огромное влияние на науку 20 века. На данный момент большинство из них уже перестали быть загадками. В числе нерешенных или решенных частично остались:
- проблема непротиворечивости арифметических аксиом;
- общий закон взаимности на пространстве любого числового поля;
- математическое исследование физических аксиом;
- исследование квадратичных форм при произвольных алгебраических числовых коэффициентах;
- проблема строгого обоснования исчислительной геометрии Федора Шуберта;
- и пр.
Неисследованными являются: проблема распространения на любую алгебраическую область рациональности известной теоремы Кронекера и гипотеза Римана.
Институт Клэйя
Под таким названием известна частная некоммерческая организация, штаб-квартира которой находится в Кембридже, штат Массачусетс. Она была основана в 1998 году гарвардским математиком А. Джеффи и бизнесменом Л. Клэйем. Целью деятельности института является популяризация и развитие математических знаний.
Для ее достижения организация выдает премии ученым и спонсирует многообещающие исследования.
В начале 21 столетия Математический институт Клэйя предложил премию тем, кто решит проблемы, которые известны, как самые сложные нерешаемые задачи, назвав свой список Millennium Prize Problems. Из «Списка Гильберта» в него вошла только гипотеза Римана.
Задачи тысячелетия
В список института Клэйя изначально входили:
- гипотеза о циклах Ходжа;
- уравнения квантовой теории Янга — Миллса;
- гипотеза Пуанкаре;
- проблема равенства классов Р и NP;
- гипотеза Римана;
- уравнения Навье Стокса, о существовании и гладкости его решений;
- проблема Берча — Свиннертон-Дайера.
Эти открытые математические проблемы представляют огромный интерес, так как могут иметь множество практических реализаций.
Что доказал Григорий Перельман
В 1900 году известный ученый-философ Анри Пуанкаре предположил, что всякое односвязное компактное 3-мерное многообразие без края гомеоморфно 3-мерной сфере.
Ее доказательство в общем случае не находилось в течение века. Лишь в 2002-2003 годах петербургский математик Г. Перельман опубликовал ряд статей с решением проблемы Пуанкаре. Они произвели эффект разорвавшейся бомбы. В 2010 году гипотеза Пуанкаре была исключена из списка «Нерешенные задачи» института Клэйя, а самому Перельману было предложено получить полагающееся ему немалое вознаграждение, от которого последний отказался, не объяснив причин своего решения.
Самое понятное объяснение того, что удалось доказать российскому математику, можно дать, представив, что на бублик (тор), натягивают резиновый диск, а затем пытаются стянуть края его окружности в одну точку. Очевидно, что это невозможно. Другое дело, если произвести этот эксперимент с шаром. В таком случае вроде бы трехмерная сфера, получившаяся из диска, окружность которого стянули в точку гипотетическим шнуром, будет трехмерной в понимании обычного человека, но двумерной с точки зрения математики.
Пуанкаре предположил, что трехмерная сфера является единственным трехмерным «предметом», поверхность которой можно стянуть в одну точку, а Перельману удалось это доказать.
Таким образом, список «Нерешаемые задачи» сегодня состоит из 6 проблем.
Теория Янга-Миллса
Эта математическая проблема была предложена ее авторами в 1954-м году. Научная формулировка теории имеет следующий вид: для любой простой компактной калибровочной группы квантовая пространственная теория, созданная Янгом и Милльсом, существует, и при этом имеет нулевой дефект массы.
Если говорить на языке, понятном для обычного человека, взаимодействия между природными объектами (частицами, телами, волнами и пр.) делятся на 4 типа: электромагнитное, гравитационное, слабое и сильное. Уже много лет физики пытаются создать общую теорию поля. Она должна стать инструментом для объяснения всех этих взаимодействий. Теория Янга-Миллса — это математический язык, с помощью которого стало возможно описать 3 из 4-х основных сил природы. Она не применима к гравитации. Поэтому нельзя считать, что Янгу и Миллсу удалось создать теорию поля.
Кроме того, нелинейность предложенных уравнений делает их крайне сложными для решения.
При малых константах связи их удается приближенно решить в виде ряда теории возмущений. Однако пока непонятно, как можно решить эти уравнения при сильной связи.
Уравнения Навье-Стокса
С помощью этих выражений описываются такие процессы, как воздушные потоки, течение жидкостей и турбулентность. Для некоторых частных случаев аналитические решения уравнения Навье-Стокса уже были найдены, однако сделать это для общего пока никому не удалось. В то же время, численное моделирование для конкретных значений скорости, плотности, давления, времени и так далее позволяет добиться прекрасных результатов. Остается надеяться, что у кого-нибудь получится применить уравнения Навье-Стокса в обратном направлении, т. е. вычислить с их помощью параметры, либо доказать, что метода решения нет.
Задача Берча — Свиннертон-Дайера
К категории «Нерешенные задачи» относится и гипотеза, предложенная английскими учеными из Кембриджского университета. Еще 2300 лет назад древнегреческий ученый Эвклид дал полное описание решений уравнения x2 + y2 = z2.
Если для каждого из простых чисел посчитать количество точек на кривой по его модулю, получится бесконечный набор целых чисел. Если конкретным образом «склеить» его в 1 функцию комплексной переменной, тогда получится дзета-функция Хассе-Вейля для кривой третьего порядка, обозначаемая буквой L. Она содержит информацию о поведении по модулю всех простых чисел сразу.
Брайан Берч и Питер Свиннертон-Дайер выдвинули гипотезу относительно эллиптических кривых. Согласно ей, структура и количество множества ее рациональных решений связаны с поведением L-функции в единице. Недоказанная на данный момент гипотеза Берча — Свиннертон-Дайера зависит от описания алгебраических уравнений 3 степени и является единственным сравнительно простым общим способом расчета ранга эллиптических кривых.
Чтобы понять практическую важность этой задачи, достаточно сказать, что в современной криптографии на эллиптических кривых основан целый класс асимметричных систем, и на их применении основаны отечественные стандарты цифровой подписи.
Равенство классов p и np
Если остальные «Задачи тысячелетия» относятся к чисто математическим, то эта имеет отношение к актуальной теории алгоритмов. Проблема, касающаяся равенства классов р и np, известная также, как проблема Кука-Левина, понятным языком может быть сформулирована следующим образом. Предположим, что положительный ответ на некий вопрос можно проверить достаточно быстро, т. е. за полиномиальное время (ПВ). Тогда правильно ли утверждение, что ответ на него можно довольно быстро отыскать? Еще проще эта задача звучит так: действительно ли решение задачи проверить не труднее, чем его найти? Если равенство классов р и np будет когда-либо доказано, то все проблемы подбора можно будет решать за ПВ. На данный момент многие специалисты сомневаются в истинности этого утверждения, хотя не могут доказать обратное.
Гипотеза Римана
Вплоть до 1859 года не было выявлено какой-либо закономерности, которая описывала бы, как распределяются простые числа среди натуральных.
Возможно, это было связано с тем, что наука занималась другими вопросами. Однако к середине 19 столетия ситуация изменилась, и они стали одними из наиболее актуальных, которыми начала заниматься математика.
Гипотеза Римана, появившаяся в этот период — это предположение о том, что в распределении простых чисел существует определенная закономерность.
Сегодня многие современные ученые считают, что если она будет доказана, то придется пересмотреть многие фундаментальные принципы современной криптографии, составляющие основу значительной части механизмов электронной коммерции.
Согласно гипотезе Римана, характер распределения простых чисел, возможно, существенно отличается от предполагаемого на данный момент. Дело в том, что до сих пока не было обнаружено какой-либо системы в распределения простых чисел. Например, существует проблема «близнецов», разность между которыми равна 2. Этими числами являются 11 и 13, 29. Другие простые числа образуют скопления. Это 101, 103, 107 и др.
Ученые давно подозревали, что подобные скопления существуют и среди очень больших простых чисел. Если их найдут, то стойкость современных криптоключей окажется под вопросом.
Гипотеза о циклах Ходжа
Эта нерешенная до сих пор задача сформулирована в 1941 году. Гипотеза Ходжа предполагает возможность аппроксимации формы любого объекта путем «склеивания» вместе простых тел большей размерности. Этот способ был известен и успешно применяется достаточно давно. Однако не известно, до какой степени можно производить упрощение.
Теперь вы знаете, какие нерешаемые задачи существуют на данный момент. Они являются предметом исследования тысяч ученых во всем мире. Остается надеяться, что в ближайшее время они будут решены, а их практическое применение поможет человечеству выйти на новый виток технологического развития.
Проблемы тысячелетия понятным языком: imit_omsu — LiveJournal
«Кажется, что-то слышал об этом» — самый популярный ответ от собеседников на вопрос о задачах тысячелетия.
Хотите немного разобраться в запутанной сети математических проблем, чтобы не сгорать от стыда в разговоре с преподавателями? Тогда смелее читайте дальше!
Первое, о чем стоит вам сообщить: список из 7 проблем был определен Математическим институтом Клэя в 2000 году, а за решение каждой из них американский институт готов выплатить 1 миллион долларов.
Свое историческое начало задачи берут еще 1900 году, когда в Париже на II Международном конгрессе математиков Давид Гильберт выступил с докладом, в котором сформулировал 23 проблемы, нуждающиеся, по его мнению, в разрешении. Именно они в дальнейшем и определили многие ключевые направления развития математики в XX веке. Случилось так, что к началу XXI века многие проблемы из списка были либо решены, либо вычернуты из-за нечёткой постановки задачи.
После Гильберта обновлением списка занялся математик Стивен Смейл. На тот момент он состоял из 18 нерешенных задач, однако более широкой огласке предалась его альтернативная версия, составленная институтом Клэя, о которой далее и пойдет речь.
Второе, о чем стоит знать, так это о том, что задач всего 7, одна из них уже считается решенной, а 6 остальных, соответственно, находятся в «подвешенном» состоянии. К примеру, гипотеза Римана перекочевала ещё из списка 1900 года, и с тех самых пор остается нерешенной.
Ну а теперь предлагаю начать знакомство с каждой из них!
На сегодняшний день гипотеза Пуанкаре считается единственной решенной задачей тысячелетия из списка. Она была сформулирована еще в 1904 году математиком Анри Пуанкаре. Данная задача — одна из наиболее известных проблем топологии. Её суть состояла в том, что если каждая замкнутая петля стягивается в точку, то ваша поверхность представляет собой деформированную сферу. Возьмём тор (тот же бублик). Если мы начнем чуть-чуть мять и растягивать резиновую сферу, тор мы никак не получим.
Почему нет? Потому что с бубликами не всё так просто. Чтобы из сферы получить тор, её надо или порвать, или растянуть и склеить, а значит, тор — не деформированная сфера.
По итогу имеем, что на поверхности сферы все петли стягиваются в точку, а на поверхности тора — нет.
После того, как в 2002-2003 годах задача была решена Григорием Перельманом, автором серии работ, подтверждающих справедливость данной гипотезы, проблема предалась широкой огласке. Многие СМИ объясняли суть задачи простыми словами: «резиновую ленту, натянутую на сферу можно плавно стянуть в точку, а натянутую на бублик — нельзя». Однако, данная формулировка больше подходит для описания гипотезы Тёрстона — обобщения гипотезы Пуанкаре. Но это уже совсем другая история. 🙂
Если возвращаться к истории петербургского математика Григория Перельмана, то выясняется, что премия института Клэя за доказательство гипотезы Пуанкаре была присуждена ему только в 2010 году. Однако, после того, как у него попытались отобрать лавры первооткрывателя, Перельман отказался от получения денежного вознаграждения.
Григорий ПерельманРавенство классов P и NP (1971 г.
)В узких кругах эта задача известна как «Пробема Кука» и «Проблема перебора». Отношения между классами P и NP рассматриваются в разделе теории алгоритмов, и вот уже почти полвека как великие умы человечества не могут найти чёткого доказательства для этой проблемы. Может быть это получится у вас? 🙂 А для того, чтобы разобраться в постановке задачи, вам нужно знать, что из себя представляют классы P и NP.
Итак, в теории алгоритмов класс P (polynomial) опеределяют как множество задач, имеющих быстрые алгоритмы решения, время работы которых напрямую зависит от размера входных данных. Главное, что осуществляется такой алгоритм за полиномиальное время. Примерами задач из класса P являются известные ещё со школьной скамьи такие простейшие арифметические операции, как сложение, умножение, деление, взятие остатка от деления (естественно, все операции целочисленные).
Класс NP (not-deterministic polinomial) в свою очередь включает в себя множество задач разрешимости, решение которых можно проверить на машине Тьюринга за время, не превосходящее значения некоторого многочлена, зависящего, опять же, от размера входных данных.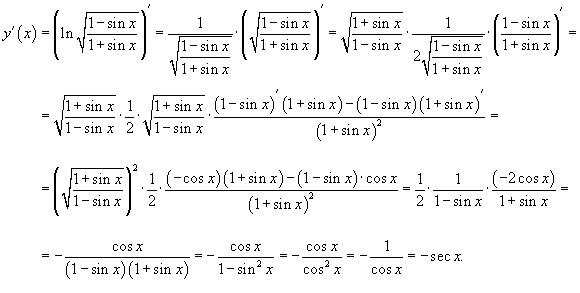
Подобных задач разрешимости очень много, но основной вопрос они поднимают, по большей части, один и тот же: «все ли задачи, которые можно быстро проверить, можно столь же быстро решить?» На данный момент, для некоторых задач не найдено не то что быстрого алгоритма решения, даже неизвестно существует ли такой алгоритм вообще!
Если данная проблема когда-нибудь обретёт аргументированное доказательство, то это здорово улучшит качество нашей жизни, ведь она имеет большое значение для самых различных областей знаний. Однако, на данный момент времени предполагается, что классы P и NP не равны, поскольку далеко не все задачи, решения которых легко проверяемы, могут быть легко решаемы.
P = NP?Гипотеза Римана (1859 г.)Эта задача из области теории чисел, уже третья из списка проблем тысячелетия, была сформулирована немецким математиком Бернхардом Риманом еще в XIX веке, но по сей день так и остается нерешенной.
s + … — обращается в ноль.
А нам известно, что нулевое значение она имеет, когда s — отрицательное четное число. В таких случаях мы получаем, так называемые, «тривиальные» нули дзета-функции. Кроме того, благодаря некоторым выкладкам Римана стало известно, что другие нули появляются, если s — комплексное число, действительная часть которого равна 1/2.
Что сейчас известно о ходе решения задачи: расчёты, проведённые с использованием суперкомпьютеров и для невероятно громадных простых чисел, подтверждают справедливость гипотезы Римана. Она доказана примерно для 10 трлн первых решений, но в общем виде пока нет. А поскольку простые числа играют немаловажную роль в работе криптографических алгоритмов, то после доказательства данной гипотезы нас ожидает значительный прогресс в сфере шифрования и безопасности интернета.
Действительная (красная) и мнимая (синяя) компоненты дзета-функцииСуществование и гладкость решений уравнений Навье — Стокса (1822 г.
)Спешу познакомить вас с ещё одной проблемой тысячелетия, но на сей раз из области математической физики (гидродинамики). Эта задача известна миру на протяжении практически 200 лет, но до сих пор остается нерешенной. Суть загадки состоит в том, чтобы доказать, что решение данных уравнений существует и является гладкой функцией.
Задача, возникшая на стыке математики и классической физики, вырастает из научных трудов XIX в., в которых учёные стали формулировать строгие законы, описывающие движение жидкостей. Полученные уже тогда уравнения Навье — Стокса остаются одними из важнейших в гидродинамике и аэродинамике. С их помощью можно вычислить скорость потока с учётом вязкости, сжимаемости, плотности, давления, потому сами уравнения используются повсеместно.
На первый взгляд может показаться, будто всё уже на своих местах и доказывать нечего, однако решить уравнения Навье — Стокса в общем виде до сих пор никому не удалось, а все расчёты, которые ведутся на данный момент, рассматривают лишь отдельные, частные случаи.
Эта проблема особенно актуальна в наше время, ведь решение уравнений помогло бы раскрыть многие тайны о природе течения жидкостей, воздушных потоков и турбулентности. Современные технологии, от самолетов и подлодок до ветряных электростанций и автомобилей, повсеместно сталкиваются с последним явлением, и тот факт, что оно остается плохо изученным, делает турбулентость плохо просчитываемой и практически непредсказуемой.
Из последних новостей о проблеме тысячелетия известно, что в 2014 году к решению приблизился казахстанский математик Мухтарбай Отелбаев, однако в его расчётах была найдена ошибка.
Дифференциальные уравнения движения Навье-СтоксаГипотеза Ходжа (1941 г.)Одна из самых важных задач алгебраической геометрии, сформулированная в 1941 году, заключается в том, что для проективных алгебраических многообразий (неприводимых замкнутых подмножеств многомерного проективного пространства над алгебраически замкнутым полем, ну это 1-й курс точно уже знает!) класс Ходжа представляет собой рациональную линейную комбинацию классов алгебраических циклов.
Все равно ничего не понятно…
Иными словами, в реальности существуют множество как простых, так и сложных геометрических объектов, и чем сложнее объект, тем более трудоёмким становится процесс его изучения. Но для простоты исследования свойств различных сложных геометрических объектов, ученые отдельно изучают свойства частички одного целого. Данный метод активно используется математиками ещё с XX века.
Гипотеза Ходжа непосредственно связана как со свойствами составных частей, так и со свойствами целых объектов. На сегодняшний день в алгебраической геометрии это является достаточно серьёзной проблемой. Ещё бы, отыскать точные методы для анализа сложных предметов и форм на основании анализа его простых частей, а после склеивания вместе таких частиц (по возрастающей размерности) составить некий «портрет» о свойствах самого объекта.
Метод оказался эффективным при описании разнообразных объектов, встречающихся в математике. При этом геометрические обоснования метода оставались весьма смутными: в некоторых случаях возникала необходимость в прибавлении частей, не имеющих никакого геометрического истолкования.
Известно, что на данный момент времени удалось доказать гипотезу Ходжа удалось только для некоторых частных случаев. Более общее доказательство пока не найдено, впрочем, как и не найдено доказательство обратного — что гипотеза неверна.
Список проблем тысячелетия продолжает ещё одна задача из области алгебраической геометрии, которая была выдвинута в начале 1960-х английскими учёными из Кембриджского университета. Её суть заключается в том, чтобы описать все возможные решения алгебраических уравнений с несколькими переменными, сложнее, чем уравнение школьной параболы.
Юрий Матиясевич
Кроме того, не стоит забывать о том, что переменные в них обязательно должны быть целочисленными, как и решения, а значит, сами уравнения могут считаться диофантовыми. Однако, ещё в 1970 году советский математик Юрий Матиясевич, будучи аспирантом, показал, что универсального решения диофантовых уравнений не существует, сделав финальный шаг в доказательстве неразрешимости задачи о существовании решений у произвольного диофантова уравнения, ответив тем самым на вопрос десятой проблемы Гильберта.
При рассмотрении частного случая, когда решения уравнений образуют абелево многообразие, Бёрч и Свиннертон-Дайер выдвинули предположение о том, что множество решений эллиптической кривой связано с поведением L-функции в окрестности единицы.
Что же такое L-функция? Это некоторая комплексная функция L(s), заданная при условии, что вещественная часть числа s > 1. Свойства данной функции на всей комплексной плоскости в основном определяются свойствами уже известной нам дзета-функции (см. «Гипотеза Римана»). То есть, в случае, если дзета-функция в точке 1 принимает значение равное нулю, мы получаем бесконечное число решений. Если же значение L(1) не равно нулю, то получаем конечное число рациональных решений, и это доказал математик Виктор Колывагин.
Есть некоторая вероятноятность, что ответы на гипотезу Бёрча – Свиннертон-Дайера будут получены только в частном виде, поскольку первый случай так и остается неподкрепленным какой-либо доказательной базой.
3 + 877*x
Перейдем к заключающей проблеме тысячелетия, пришедшей из слияния таких областей науки как физика элементарных частиц и геометрия. Еще в 1954 году физики Янг и Миллс написали уравнения, применимые в области квантовой физики, объединяющие в себе описание нескольких фундаментальных взаимодействий природы — электромагнитного, слабого и сильного.
На данный момент теория Янга — Миллса подтвердилась экспериментальным путем только для электрослабого и сильного взаимодействий. Но все попытки решить уравнения, описывающие все три взаимодейстия одновременно, оборачивались неудачей, однако рассчётные эксперименты показывают, что шанс всё-таки есть.
Известно, что на основе теории Янга-Миллса была построена стандартная модель физики элементарных частиц — некий «код» нашей Вселенной, состоящий из кварков, лептонов и калибровочных бозонов, из которых, в свою очередь, слеплено всё, что существует во Вселенной. (-24) доли секунды, в Швейцарии построили Большой Адронный Коллайдер. В нем разгоняют банчи (иными словами, сгустки) протонов и сталкивают друг с другом. Подробнее эту тему лучше изучать самостоятельно, но ни в коем случае не пытайтесь повторить это дома!
Сейчас же уравнения Янга — Миллса приняты учеными-физиками во всем мире. Несмотря на это, предсказать массы элементарных частиц экспериментальным путем в рамках их теории так и не удалось, ровно как и решить проблему в общем виде.
Специально для ЖЖ матфака, с большим желанием пробудить в вас стремление к новому, ранее неизведанному, Садуллаева Надежда.
Миллион долларов за дырку от бублика Российский математик решил проблему Пуанкаре, но премию получать не спешит: Lenta.ru
Ученые считают, что 38-летний российский математик Григорий Перельман предложил верное решение проблемы Пуанкаре. Об этом на научном фестивале в Эксетере (Великобритания) заявил профессор математики Стэнфордского университета Кит Девлин.
Проблема (ее также называют задачей или гипотезой) Пуанкаре относится к числу семи важнейших математических проблем, за решение каждой из которых Математический институт Клэя (Clay Mathematics Institute) назначил премию в один миллион долларов. Именно это и привлекло столь широкое внимание к результатам, полученным Григорием Перельманом, сотрудником лаборатории математической физики Санкт-Петербургского отделения Математического института имени Стеклова .
Ученые всего мира узнали о достижениях Перельмана из двух препринтов (статей, предваряющих полноценную научную публикацию), размещенных автором в ноябре 2002-го и марте 2003 года на сайте архива предварительных работ Лос-Аламосской научной лаборатории.
Согласно правилам, принятым Научным консультативным советом института Клэя, новая гипотеза должна быть опубликована в специализированном журнале, имеющем “международную репутацию”. Кроме того, по правилам Института, решение о выплате приза принимает, в конечном счёте, “математическое сообщество”: доказательство не должно быть опровергнуто в течение двух лет после публикации.
Проверкой каждого доказательства занимаются математики в разных странах мира.
Проблема Пуанкаре
Родился 13 июня 1966 года в Ленинграде, в семье служащих. Окончил знаменитую среднюю школу № 239 с углубленным изучением математики. В 1982 году в составе команды советских школьников участвовал в Международной математической олимпиаде, проходившей в Будапеште. Был без экзаменов зачислен на матмех Ленинградского государственного университета. Побеждал на факультетских, городских и всесоюзных студенческих математических олимпиадах. Получал Ленинскую стипендию. Окончив университет, Перельман поступил в аспирантуру при Санкт-Петербургском отделении Математического института им.В.А.Стеклова. Кандидат физико-математических наук. Работает в лаборатории математической физики.
Проблема Пуанкаре относится к области так называемой топологии многообразий – особым образом устроенных пространств, имеющих разную размерность. Двухмерные многообразия можно наглядно представить себе, например, на примере поверхности трехмерных тел – сферы (поверхности шара) или тора (поверхности бублика).
Легко вообразить, что произойдет с воздушным шариком, если его деформировать (изгибать, скручивать, тянуть, сжимать, пережимать, сдувать или надувать). Ясно, что при всех вышеперечисленных деформациях шарик будет изменять свою форму в широких пределах. Однако мы никогда не сможем превратить шарик в бублик (или наоборот) без нарушения непрерывности его поверхности, то есть не разрывая. В этом случае топологи говорят, что сфера (шарик) негомеоморфна тору (бублику). Это означает, что данные поверхности невозможно отобразить одну на другую. Говоря простым языком, сфера и тор различны по своим топологическим свойствам. А поверхность воздушного шарика при всевозможных его деформациях гомеоморфна сфере, равно как поверхность спасательного круга – тору. Иными словами, любая замкнутая двумерная поверхность, не имеющая сквозных отверстий, обладает теми же топологическими свойствами, что и двухмерная сфера.
ТОПОЛОГИЯ, раздел математики, занимающийся изучением свойств фигур (или пространств), которые сохраняются при непрерывных деформациях, таких, например, как растяжение, сжатие или изгибание.
Непрерывная деформация – это деформация фигуры, при которой не происходит разрывов (т.е. нарушения целостности фигуры) или склеиваний (т.е. отождествления ее точек).
ТОПОЛОГИЧЕСКОЕ ПРЕОБРАЗОВАНИЕ одной геометрической фигуры на другую – есть отображение произвольной точки Р первой фигуры на точку Р` другой фигуры, которое удовлетворяет следующим условиям: 1) каждой точке Р первой фигуры должна соответствовать одна и только одна точка Р` второй фигуры, и наоборот; 2) Отображение должно быть взаимно непрерывно. Например, имеются две точки Р и N, принадлежащие одной фигуре. Если при движении точки Р к точке N расстояние между ними стремится к нулю, то расстояние между точками Р` и N` другой фигуры тоже должно стремиться к нулю, и наоборот.
ГОМЕОМОРФИЗМ. Геометрические фигуры, переходящие одна в другую при топологических преобразованиях, называются гомеоморфными. Окружность и граница квадрата гомеоморфны, так как их можно перевести друг в друга топологическим преобразованием (т.е. изгибанием и растяжением без разрывов и склеиваний, например, растяжением границы квадрата на описанную вокруг него окружность).
Область, в которой любую замкнутую простую (т.е. гомеоморфную окружности) кривую можно стянуть в точку, оставаясь все время в этой области, называется односвязной, а соответствующее свойство области – односвязностью. Если же некоторую замкнутую простую кривую этой области нельзя стянуть в точку, оставаясь все время в этой области, то область называется многосвязной, а соответствующее свойство области – многосвязностью.
Проблема Пуанкаре утверждает то же самое для трехмерных многообразий (для двухмерных многообразий, таких как сфера, это положение было доказано еще в XIX веке). Как заметил французский математик, одно из важнейших свойств двухмерной сферы состоит в том, что любая замкнутая петля (например, лассо), лежащая на ней, может быть стянута в одну точку, не покидая при этом поверхности. Для тора это справедливо не всегда: петля, проходящая через его отверстие, стянется в точку либо при разломе тора, либо при разрыве самой петли. В 1904 году Пуанкаре высказал предположение, что если петля может стягиваться в точку на замкнутой трехмерной поверхности, то такая поверхность гомеоморфна трехмерной сфере.
Доказательство этой гипотезы оказалось чрезвычайно сложной задачей.
Сразу уточним: упомянутая нами формулировка проблемы Пуанкаре говорит вовсе не о трехмерном шаре, который мы можем представить себе без особого труда, а о трехмерной сфере, то есть о поверхности четырехмерного шара, который представить себе уже гораздо труднее. Но в конце 1950-х годов неожиданно выяснилось, что с многообразиями высоких размерностей работать гораздо легче, чем с трех- и четырехмерными. Очевидно, отсутствие наглядности – далеко не главная трудность, с которой сталкиваются математики в своих исследованиях.
Задача, подобная проблеме Пуанкаре, для размерностей 5 и выше была решена в 1960 году Стивеном Смэйлом (Stephen Smale), Джоном Стэллингсом (John Stallings) и Эндрю Уоллесом (Andrew Wallace). Подходы, использованные этими учеными, оказались, однако, неприменимы к четырехмерным многообразиям. Для них проблема Пуанкаре была доказана лишь в 1981 году Майклом Фридманом (Michael Freedman). Трехмерный же случай оказался самым сложным; его решение и предлагает Григорий Перельман.
Необходимо отметить, что у Перельмана есть соперник. В апреле 2002 года профессор математики британского университета Саутгемптон Мартин Данвуди предложил свой метод решения проблемы Пуанкаре и теперь ожидает вердикт от института Клэя.
Специалисты считают, что решение проблемы Пуанкаре позволит сделать серьезный шаг в математическом описании физических процессов в сложных трехмерных объектах и даст новый импульс развитию компьютерной топологии. Метод, который предлагает Григорий Перельман, приведет к открытию нового направления в геометрии и топологии. Петербургский математик вполне может претендовать на премию Филдса (аналог Нобелевской премии, которую по математике не присуждают).
Между тем, некоторые находят поведение Григория Перельмана странным. Вот что пишет британская газета “Гардиан”: “Скорее всего, подход Перельмана к разгадке проблемы Пуанкаре верный. Но не все так просто. Перельман не предоставляет доказательств того, что работа издана в качестве полноценной научной публикации (препринты таковой не считаются).
А это необходимо, если человек хочет получить награду от института Клэя. Кроме того, он вообще не проявляет интереса к деньгам”.
Видимо, для Григория Перельмана, как для настоящего ученого, деньги – не главное. За решение любой из так называемых “задач тысячелетия” истинный математик продаст душу дьяволу.
Список тысячелетия
ЖЮЛЬ АНРИ ПУАНКАРЕ. Фото с сайта www.ibmh.msk.su
Lenta.ru
8 августа 1900 года на международном математическом конгрессе в Париже математик Дэвид Гилберт (David Hilbert) изложил список проблем, которые, как он полагал, предстояло решить в ХХ веке. В списке было 23 пункта. Двадцать один из них на данный момент решены. Последней решенной проблемой из списка Гилберта была знаменитая теорема Ферма , с которой ученые не могли справиться в течение 358 лет. В 1994 году свое решение предложил британец Эндрю Уайлз. Оно и оказалось верным.
По примеру Гилберта в конце прошлого века многие математики пытались сформулировать подобные стратегические задачи на ХХI век.
Один из таких списков приобрел широкую известность благодаря бостонскому миллиардеру Лэндону Клэю (Landon T. Clay). В 1998 году на его средства в Кембридже (Массачусетс, США) был основан Математический институт Клэя (Clay Mathematics Institute) и установлены премии за решение ряда важнейших проблем современной математики. 24 мая 2000 года эксперты института выбрали семь проблем – по числу миллионов долларов, выделенных на премии. Список получил название Millennium Prize Problems:
1. Проблема Кука (сформулирована в 1971 году)
Допустим, что вы, находясь в большой компании, хотите убедиться, что там же находится ваш знакомый. Если вам скажут, что он сидит в углу, то достаточно будет доли секунды, чтобы, бросив взгляд, убедиться в истинности информации. В отсутствие этой информации вы будете вынуждены обойти всю комнату, рассматривая гостей. Это говорит о том, что решение какой-либо задачи часто занимает больше времени, чем проверка правильности решения.
ДЭВИД ГИЛБЕРТ.
Фото с сайта www.krugosvet.ru
Lenta.ru
Стивен Кук сформулировал проблему: может ли проверка правильности решения задачи быть более длительной, чем само получение решения, независимо от алгоритма проверки. Эта проблема также является одной из нерешенных задач из области логики и информатики. Ее решение могло бы революционным образом изменить основы криптографии, используемой при передаче и хранении данных.
2. Гипотеза Римана (сформулирована в 1859 году)
Некоторые целые числа не могут быть выражены как произведение двух меньших целых чисел, например 2, 3, 5, 7 и так далее. Такие числа называются простыми и играют важную роль в чистой математике и ее приложениях. Распределение простых чисел среди ряда всех натуральных чисел не подчиняется никакой закономерности. Однако немецкий математик Риман высказал предположение, касающееся свойств последовательности простых чисел. Если гипотеза Римана будет доказана, то это приведет к революционному изменению наших знаний в области шифрования и к невиданному прорыву в области безопасности Интернета.
3. Гипотеза Берча и Свиннертон-Дайера (сформулирована в 1960 году)
Связана с описанием множества решений некоторых алгебраических уравнений от нескольких переменных с целыми коэффициентами. Примером подобного уравнения является выражение x2 + y2 = z2. Эвклид дал полное описание решений этого уравнения, но для более сложных уравнений поиск решений становится чрезвычайно трудным.
4. Гипотеза Ходжа (сформулирована в 1941 году)
В ХХ веке математики открыли мощный метод исследования формы сложных объектов. Основная идея заключается в том, чтобы использовать вместо самого объекта простые “кирпичики”, которые склеиваются между собой и образуют его подобие. Гипотеза Ходжа связана с некоторыми предположениями относительно свойств таких “кирпичиков” и объектов.
5. Уравнения Навье – Стокса (сформулированы в 1822 году)
ПРОФЕССОР МАРТИН ДАНВУДИ, ТАКЖЕ ПРЕДЛОЖИВШИЙ РЕШЕНИЕ ПРОБЛЕМЫ ПУАНКАРЕ. Фото с сайта www.maths.soton.ac.uk |
Если плыть в лодке по озеру, то возникнут волны, а если лететь в самолете, в воздухе возникнут турбулентные потоки. Предполагается, что эти и другие явления описываются уравнениями, известными как уравнения Навье – Стокса. Решения этих уравнений неизвестны, и при этом даже неизвестно, как их решать. Необходимо показать, что решение существует и является достаточно гладкой функцией. Решение этой проблемы позволит существенно изменить способы проведения гидро- и аэродинамических расчетов.
6. Проблема Пуанкаре (сформулирована в 1904 году)
Если натянуть резиновую ленту на яблоко, то можно, медленно перемещая ленту без отрыва от поверхности, сжать ее до точки. С другой стороны, если ту же самую резиновую ленту соответствующим образом натянуть вокруг бублика, то никаким способом невозможно сжать ленту в точку, не разрывая ленту или не ломая бублик. Говорят, что поверхность яблока односвязна, а поверхность бублика – нет.
Доказать, что односвязна только сфера, оказалось настолько трудно, что математики ищут правильный ответ до сих пор.
7. Уравнения Янга – Миллса (сформулированы в 1954 году)
Уравнения квантовой физики описывают мир элементарных частиц. Физики Янг и Миллс, обнаружив связь между геометрией и физикой элементарных частиц, написали свои уравнения. Тем самым они нашли путь к объединению теорий электромагнитного, слабого и сильного взаимодействий. Из уравнений Янга – Миллса следовало существование частиц, которые действительно наблюдались в лабораториях во всем мире, поэтому теория Янга – Миллса принята большинством физиков несмотря на то, что в рамках этой теории до сих пор не удается предсказывать массы элементарных частиц.
Михаил Витебский
самых сложных математических задач и уравнений
Наряду с гипотезой Гольдбаха гипотеза о простых числах-близнецах является самой известной в теории чисел — или изучении натуральных чисел и их свойств, часто с участием простых чисел.
Поскольку вы знаете эти числа с начальной школы, формулировать предположения несложно.
Когда два простых числа имеют разность 2, они называются простыми числами-близнецами. Таким образом, 11 и 13 являются простыми числами-близнецами, как и 599 и 601. Итак, это факт Теории чисел дня 1, что существует бесконечно много простых чисел.Итак, бесконечно ли много простых чисел-близнецов ? Гипотеза о простых числах-близнецах утверждает, что да.
Давайте углубимся. Первое в паре простых чисел-близнецов, за одним исключением, всегда на 1 меньше, чем кратное 6. Таким образом, второе простое число всегда на 1 больше, чем кратное 6. Вы поймете почему, если будете готовы следуйте немного опрометчивой теории чисел.
Все простые числа после 2 нечетные. Четные числа всегда на 0, 2 или 4 больше, чем кратные 6, а нечетные числа всегда на 1, 3 или 5 больше, чем кратные 6.Ну, одна из этих трех возможностей для нечетных чисел вызывает проблему. Если число на 3 больше, чем кратное 6, то оно имеет множитель 3.
Наличие множителя 3 означает, что число не является простым (за исключением самого числа 3). И именно поэтому каждое третье нечетное число не может быть простым.
Как твоя голова после этого абзаца? А теперь представьте головную боль всех, кто пытался решить эту проблему за последние 170 лет.
Хорошая новость заключается в том, что за последнее десятилетие мы добились многообещающего прогресса.Математикам удавалось решать все более и более близкие версии гипотезы о простых числах-близнецах. Это была их идея: как доказать, что существует бесконечно много простых чисел с разницей в 2? Как насчет того, чтобы доказать, что существует бесконечно много простых чисел с разницей в 70 000 000? Это было умно доказано в 2013 году Итаном Чжаном из Университета Нью-Гэмпшира.
В течение последних шести лет математики улучшали это число в доказательстве Чжана с миллионов до сотен. Уменьшение его до 2 будет решением гипотезы о простых числах-близнецах.Самое близкое, к чему мы подошли — с учетом некоторых тонких технических предположений — это 6.
Время покажет, будет ли последний шаг от 6 к 2 прямо за углом, или эта последняя часть будет бросать вызов математикам еще десятилетиями.
6 обманчиво простых математических задач, которые никто не может решить
Все мы знаем, что математика очень сложна. На самом деле настолько сложно, что буквально целая страница Википедии посвящена нерешенным математическим задачам, несмотря на то, что некоторые из величайших умов мира работают над ними круглосуточно.
Но, как отмечает Эвери Томпсон в Popular Mechanics , , по крайней мере, с самого начала, некоторые из этих задач кажутся удивительно простыми — настолько простыми, что их может понять любой человек, обладающий базовыми знаниями математики… включая нас. К сожалению, оказывается, что доказать их немного сложнее.
Вдохновившись списком Томпсона, мы составили собственный список обманчиво простых математических задач, чтобы расстроить (и, надеюсь, вдохновить) вас.
Гипотеза о простых числах-близнецах
Простые числа — это волшебные единороги, которые делятся только на себя и на 1.
Насколько нам известно, существует бесконечное число простых чисел, и математики постоянно работают над поиском следующего по величине простого числа. номер.
Но существует ли бесконечное количество пар простых чисел, отличающихся на два, например 41 и 43? По мере того, как простые числа становятся все больше и больше, эти простые числа-близнецы все труднее найти, но теоретически они должны быть бесконечными… проблема в том, что никто еще не смог это доказать.
Проблема с движущимся диваном
Клаудио Роккини
Это то, с чем большинство из нас сталкивалось раньше – вы переезжаете в новую квартиру и пытаетесь взять с собой свой старый диван. Но, конечно же, вам придется маневрировать за углом, прежде чем вы сможете удобно расположиться на нем в своей гостиной.
Вместо того, чтобы сдаться и просто купить погремушку, сейчас математики хотят знать: какой самый большой диван вы могли бы разместить вокруг угла в 90 градусов, независимо от формы, без изгиба? (Хотя они смотрят на все это с двухмерной точки зрения.
)
Томпсон объясняет:
“Самая большая площадь, которая может поместиться за углом, называется – я не шучу – константой дивана.
Никто точно не знает, насколько он велик, но у нас есть довольно большие диваны, которые работают, поэтому мы знаем, что он должен быть как минимум таким же большим, как они. У нас также есть несколько диванов, которые не работают, поэтому они должны быть меньше, чем те. Все вместе мы знаем, что константа дивана должна быть между 2,2195 и 2,8284».
Держу пари, Росс из друзей хотел бы, чтобы кто-нибудь сказал ему это.
Friends/NBC
Гипотеза Коллатца
XKCD
Гипотеза Коллатца — одна из самых известных нерешенных математических задач, потому что она настолько проста, что ее можно объяснить ребенку младшего школьного возраста, и они Вероятно, вы будете достаточно заинтригованы, чтобы попытаться найти ответ для себя.
Вот как это делается: выберите номер, любой номер.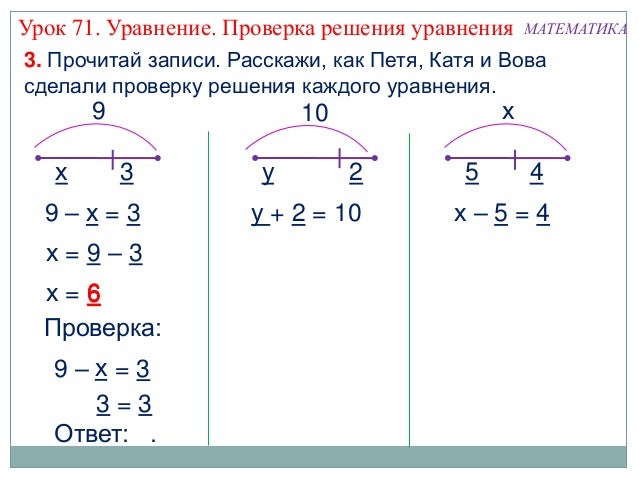
Если четное, разделите на 2. Если нечетное, умножьте на 3 и прибавьте 1.Теперь повторите эти шаги еще раз с новым номером. В конце концов, если вы продолжите, вы в конечном итоге будете получать 1 каждый раз (попробуйте сами, мы подождем).
Как бы просто это ни звучало, это действительно работает. Но проблема в том, что хотя математики и доказали, что это так с миллионами чисел, они не нашли ни одного числа, которое не соответствовало бы правилам.
«Возможно, что существует какое-то действительно большое число, которое вместо этого стремится к бесконечности, или, может быть, число, которое застревает в цикле и никогда не достигает 1», — объясняет Томпсон.«Но никому никогда не удавалось доказать это наверняка».
Гипотеза Била
Гипотеза Била в основном выглядит так…
z — все положительные целые числа (целые числа больше 0), то A, B и C должны иметь общий простой делитель.
Общий простой делитель означает, что каждое из чисел должно делиться на одно и то же простое число.
Таким образом, числа 15, 10 и 5 имеют общий простой делитель 5 (все они делятся на простое число 5).
Пока что все просто, и это похоже на то, что вы бы решили в средней школе по алгебре.
Но вот проблема. Математикам никогда не удавалось решить гипотезу Била, где x, y и z больше 2.
Например, давайте воспользуемся нашими числами с общим простым множителем 5, полученным ранее….
5 1 + 10 1 = 15 1 = 15 1 8 , но 5 2
В настоящее время есть премия на 1 миллион долларов США по предложению для тех, кто может предложить рецензируемое доказательство этой гипотезы… так что вычисляйте.
Задача о вписанном квадрате
Клаудио Роккини
Для этого требуется небольшой рисунок. На листе бумаги нарисуйте петлю — она не обязательно должна быть какой-то заданной формы, просто замкнутая петля, которая не пересекается сама с собой.
Согласно гипотезе о вписанном квадрате, внутри этой петли вы должны нарисовать квадрат, все четыре угла которого касаются петли, как на диаграмме выше.
Звучит просто… но с математической точки зрения существует множество возможных форм петель, и в настоящее время невозможно сказать, сможет ли квадрат касаться их всех.
«Это уже было решено для ряда других форм, таких как треугольники и прямоугольники, — пишет Томпсон, — но квадраты сложны, и до сих пор формальное доказательство ускользало от математиков».
Гипотеза Гольдбаха
Подобно гипотезе о простых числах-близнецах, гипотеза Гольдбаха — еще один известный и, казалось бы, простой вопрос о простых числах. Это звучит так: всякое ли четное число больше 2 является суммой двух простых чисел?
Кажется очевидным, что ответ будет положительным, ведь 3 + 1 = 4, 5 + 1 = 6 и так далее.По крайней мере, такова была первоначальная гипотеза немецкого математика Кристиана Гольдбаха еще в 1742 году.
целые числа больше 4 можно представить в виде суммы двух простых чисел.
И все же, несмотря на столетия попыток, до сих пор никому не удалось доказать, что так будет всегда. В начале 2000-х за это даже рекламировалась премия, но она осталась невостребованной.
Реальность такова, что по мере того, как мы продолжаем вычислять все большие и большие числа, мы можем в конце концов найти число, которое не является суммой двух простых чисел… или такое число, которое бросает вызов всем правилам и логике, которые у нас есть до сих пор. И вы можете быть уверены, что математики не перестанут искать, пока не найдут его.
Примечание редактора (19 мая 2021 г.): В более ранней версии этой статьи приводился неверный пример гипотезы Гольдбаха. Это было разъяснено, чтобы объяснить, как гипотеза изменилась с момента ее возникновения.
10 математических уравнений, которые никогда не были решены
Математика сыграла важную роль во многих изобретениях и теориях, изменивших жизнь.
Но все еще есть некоторые математические уравнения, которые ускользнули от внимания даже величайших умов, таких как Эйнштейн и Хокинс. Другие уравнения, однако, просто слишком велики для вычисления. Так что по какой-то причине эти загадочные проблемы так и не были решены. Но что это такое?
Как и все мы, вы, вероятно, ожидаете следующего уровня сложности в этих математических задачах.Удивительно, но это не так. Некоторые из этих уравнений даже основаны на понятиях начальной школы и легко понятны — просто неразрешимы.
1. Гипотеза Римана
Уравнение: σ (n) ≤ Hn +ln (Hn)eHn
- Где n — целое положительное число
- Hn – номер n-й гармоники
- σ(n) — сумма натуральных чисел, делящихся на n
Например, если n = 4, то σ(4)=1+2+4=7 и h5 = 1+1/2+1/3+1/4. Решите это уравнение, чтобы доказать или опровергнуть следующее неравенство n≥1? Верно ли это для всех n≥1?
Эта проблема называется элементарной версией гипотезы Римана Лагариаса, и Математический фонд Клэя предлагает за ее решение цену в миллион долларов.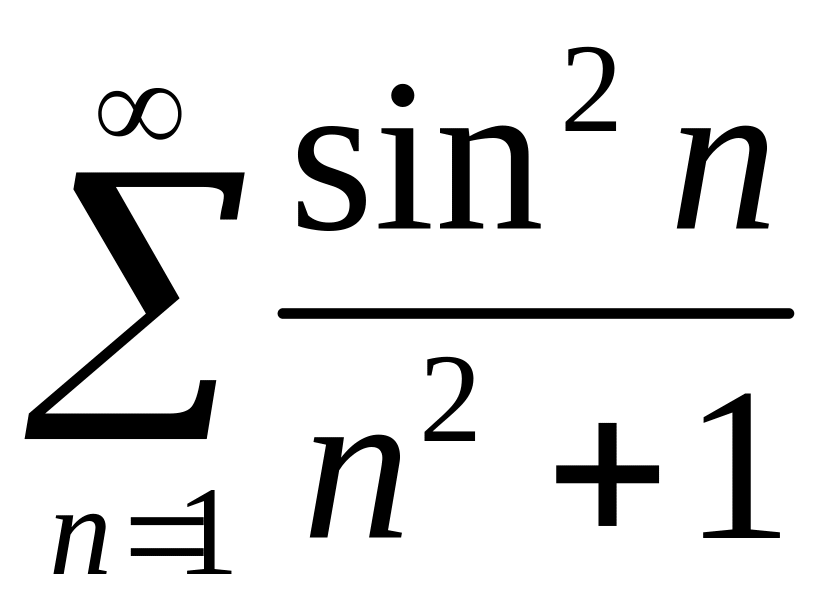
2. Гипотеза Коллатца
Уравнение: 3n+1
- где n — целое положительное число n/2
- , где n — целое неотрицательное число .
Докажите конец ответа, циклически перебирая 1,4,2,1,4,2,1,…, если n — положительное целое число. Это повторяющийся процесс, и вы будете повторять его с новым значением n, которое получите. Если ваше первое n = 1, то ваши последующие ответы будут 1, 4, 2, 1, 4, 2, 1, 4… бесконечно. И если n = 5, ответы будут 5,16,8,4,2,1, остальное будет другим циклом со значениями 1, 4 и 2.
Это уравнение было составлено в 1937 году человеком по имени Лотар Коллатц, поэтому его называют гипотезой Коллатца.
3. Гипотеза Эрдеша-Стросса
Уравнение: 4/n=1/a+1/b+1/c
- где n≥2
- a, b и c — положительные целые числа.
Целью этого уравнения является проверка того, можем ли мы доказать, что если n больше или равно 2, то можно записать 4*n как сумму трех положительных единичных дробей.
Это уравнение было составлено в 1948 году двумя людьми по имени Пауль Эрдёш и Эрнст Штраус, поэтому его называют гипотезой Эрдёша-Стросса.
4. Уравнение четыре
Уравнение: Используйте 2(2∧127)-1 – 1, чтобы доказать или опровергнуть, является ли это простым числом или нет?
Выглядит довольно прямолинейно, не так ли? Вот небольшой контекст проблемы.
Возьмем простое число 2. Итак, 22 – 1 = 3, что также является простым числом. 25 – 1 = 31, что также является простым числом, поэтому 27−1=127. 2127 −1=170141183460469231731687303715884105727 также является простым числом.
5. Гипотеза Гольдбаха
Уравнение: Докажите, что x + y = n
- где x и y — любые два простых числа
- n равно ≥ 4
Эта проблема, как бы относительно проста она ни звучала, так и не была решена.Решение этой задачи принесет вам бесплатный миллион долларов. Это уравнение было впервые предложено Гольдбахом, отсюда и название «гипотеза Гольдбаха».
Если вы все еще не уверены, выберите любое четное число, например 6, его также можно выразить как 1 + 5, то есть два простых числа. То же самое касается 10 и 26.
6. Уравнение шесть
Уравнение: Докажите, что (K)n = JK1N(q)JO1N(q)
Это уравнение пытается изобразить связь между квантовыми инвариантами узлов и гиперболической геометрией узловых дополнений.Хотя это уравнение относится к математике, вы должны быть знакомы с физикой, чтобы понять его концепцию.
7. Гипотеза Уайтхеда
Уравнение: G = (S | R)
- когда комплекс CW K (S | R) асферичен
- , если π2 (K (S | R)) = 0
Что вы делаете в этом уравнении, так это доказываете утверждение, сделанное г-ном Уайтхедом в 1941 году в алгебраической топологии, что каждый подкомплекс асферического комплекса CW, который является связным и в двух измерениях, также является сферическим.Это было названо в честь человека, гипотезы Уайтхеда.
8. Уравнение восемь
Уравнение: (EQ4)
Это уравнение является определением морфизма и называется картой сборки.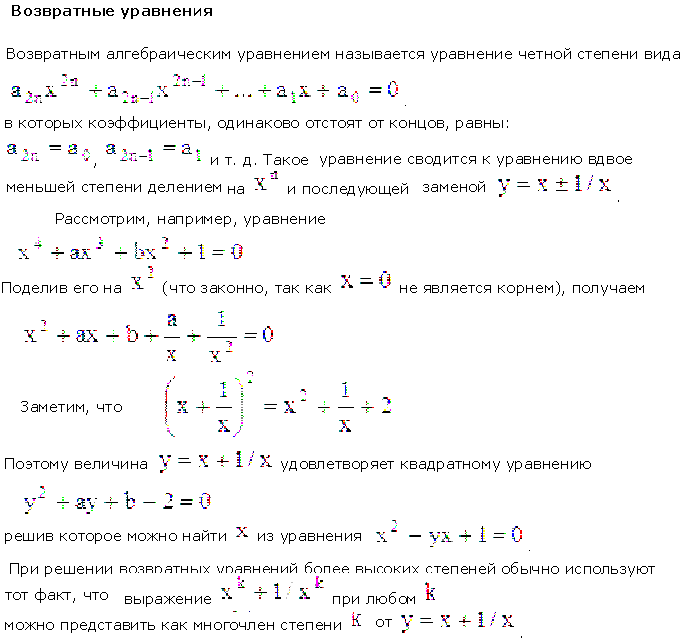
Ознакомьтесь с сокращенной C*-алгеброй, чтобы лучше понять концепцию, связанную с этим уравнением.
9. Константа Эйлера-Маскерони
Уравнение: y=limn→∞(∑m=1n1m−log(n))
Выясните, является ли y рациональным или иррациональным в приведенном выше уравнении. Чтобы полностью понять эту проблему, вам нужно еще раз взглянуть на рациональные числа и их понятия.Символ y известен как константа Эйлера-Маскерони и имеет значение 0,5772.
Это уравнение было рассчитано почти до половины триллиона цифр, но до сих пор никто не смог сказать, является ли оно рациональным числом или нет.
10. Уравнение 10
Уравнение: π + e
Найдите сумму и определите, является ли она алгебраической или трансцендентной. Чтобы понять этот вопрос, вам нужно иметь представление об алгебраических действительных числах и о том, как они работают. Число пи или π возникло в 17 веке и является трансцендентным наряду с e.а как же их сумма? До сих пор это никогда не было решено.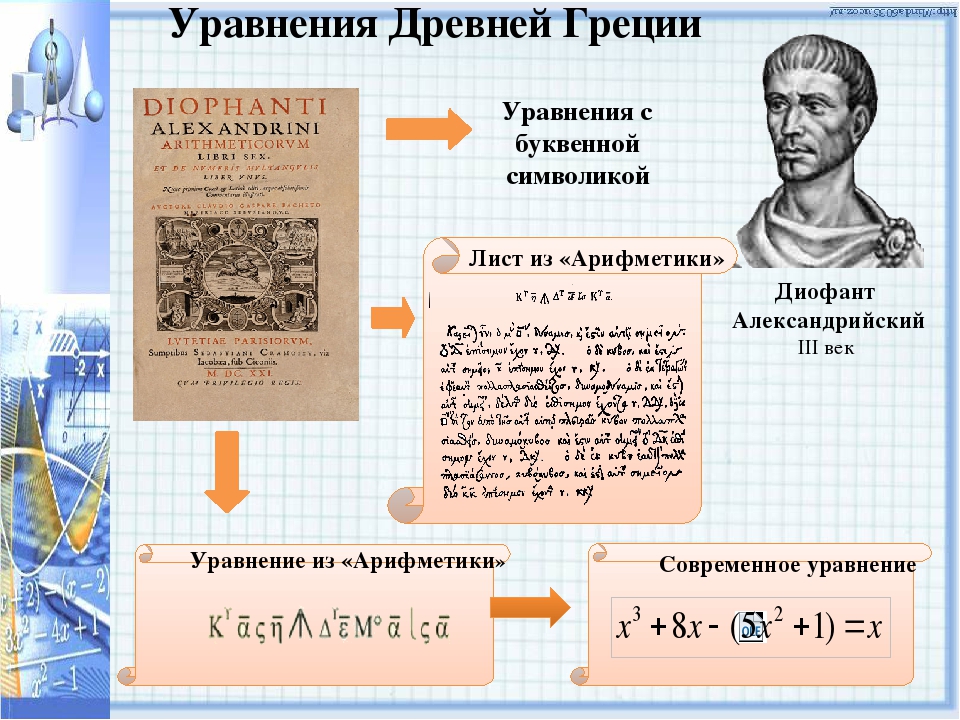
Заключение
Как вы можете видеть из приведенных выше уравнений, есть несколько, казалось бы, простых математических уравнений и теорий, которые так и не были опровергнуты. Проходят десятилетия, а эти проблемы остаются нерешенными. Если вы ищете головоломку, поиск решений этих проблем даст вам возможность заработать деньги.
Будьте первым, кто оставит комментарий ниже.
Если вы сможете решить одну из этих 6 основных математических задач, вы выиграете приз в размере 1 миллиона долларов | The Independent
В 2000 году Математический институт Клэя объявил задачи Премии тысячелетия.Это был сборник из семи наиболее важных математических задач, которые до сих пор остаются нерешенными.
Отражая важность проблем, Институт предложил приз в размере 1 миллиона долларов каждому, кто сможет предоставить строгое, проверенное экспертами решение любой из проблем.
В то время как одна из задач, гипотеза Пуанкаре, была успешно решена в 2006 году (математик, решивший ее, Григорий Перельман, столь же лихо отказался и от премии в миллион долларов, и от заветной Филдсовской медали), остальные шесть проблем остаются нерешенными.
.
Вот шесть математических задач, настолько важных, что решение любой из них стоит 1 миллион долларов.
P против NP
(Getty Images/iStockphoto)
Некоторые проблемы просты, а некоторые трудны.
В мире математики и компьютерных наук существует множество задач, которые мы знаем, как запрограммировать компьютер для «быстрого» решения — элементарная арифметика, сортировка списка, поиск в таблице данных. Эти проблемы могут быть решены за «полиномиальное время», сокращенно «П.” Это означает, что количество шагов, необходимых для сложения двух чисел или сортировки списка, растет с увеличением размера чисел или длины списка.
Но есть еще одна группа задач, для которых легко проверить, действительно ли или не возможное решение проблемы верно, но мы не знаем, как эффективно найти решение.Нахождение простых множителей большого числа – такая проблема – если у меня есть список возможных множителей, я могу умножить их вместе и посмотреть, получу ли я свой первоначальный номер.
Но не существует известного способа быстро найти множители произвольно большого числа. Действительно, безопасность Интернета зависит от этого факта.
По историческим и техническим причинам задачи, решение которых можно быстро проверить, называются решаемыми за «недетерминированное полиномиальное время» или «NP».
Любая проблема в P автоматически попадает в NP — если я могу быстро решить проблему, я могу так же быстро проверить возможное решение, просто решив проблему и посмотрев, соответствует ли ответ моему возможному решению.Суть вопроса P vs NP заключается в том, верно ли обратное: если у меня есть эффективный способ проверить решения проблемы, существует ли эффективный способ найти эти решения?
Большинство математиков и программистов считают, что ответ отрицательный. Алгоритм, который мог бы решать задачи NP за полиномиальное время, имел бы умопомрачительные последствия для большей части математики, естественных наук и технологий, и эти последствия настолько не от мира сего, что они дают основания сомневаться в том, что это возможно.
Конечно, доказательство того, что такого алгоритма не существует, само по себе невероятно сложная задача. Для того чтобы сделать такое заявление о такого рода проблемах, вероятно, потребуется гораздо более глубокое понимание природы информации и вычислений, чем мы имеем сейчас, и почти наверняка это будет иметь глубокие и далеко идущие последствия.
Прочтите официальное описание P vs NP от Математического института Клэя здесь.
Уравнения Навье-Стокса
Удивительно трудно объяснить, что происходит, когда вы добавляете сливки в утренний кофе.
Уравнения Навье-Стокса представляют собой гидродинамическую версию трех законов движения Ньютона. Они описывают, как будет развиваться поток жидкости или газа при различных условиях. Точно так же, как второй закон Ньютона дает описание того, как скорость объекта будет изменяться под действием внешней силы, уравнения Навье-Стокса описывают, как скорость потока жидкости будет изменяться под действием внутренних сил, таких как давление и вязкость, а также внешних сил.
силы, подобные гравитации.
Уравнения Навье-Стокса представляют собой систему дифференциальных уравнений.Дифференциальные уравнения описывают, как конкретная величина изменяется во времени при заданных начальных начальных условиях, и они полезны при описании всех видов физических систем. В случае уравнений Навье-Стокса мы начинаем с некоторого начального потока жидкости, а дифференциальные уравнения описывают, как этот поток развивается.
Решение дифференциального уравнения означает нахождение некоторой математической формулы, позволяющей определить, какой на самом деле будет интересующая вас величина в любой конкретный момент времени, на основе уравнений, описывающих изменение величины.Многие физические системы, описываемые дифференциальными уравнениями, такие как вибрация гитарной струны или поток тепла от горячего объекта к холодному, имеют хорошо известные решения этого типа.
Однако уравнения Навье-Стокса сложнее. С математической точки зрения инструменты, используемые для решения других дифференциальных уравнений, оказались здесь бесполезными.
Физически жидкости могут вести себя хаотично и турбулентно: дым, исходящий от свечи или сигареты, обычно течет плавно и предсказуемо, но быстро превращается в непредсказуемые вихри и завихрения.
Возможно, такое турбулентное и хаотичное поведение означает, что уравнения Навье-Стокса не могут быть точно решены во всех случаях. Возможно, удастся сконструировать некую идеализированную математическую жидкость, которая, следуя уравнениям, в конце концов станет бесконечно турбулентной.
Любой, кто сможет построить способ решения уравнений Навье-Стокса во всех случаях или показать пример, в котором уравнения не могут быть решены, получит Премию тысячелетия за эту задачу.
Прочтите официальное описание уравнений Навье-Стокса, данное Институтом математики Клэя.
Теория Янга-Миллса и квантовая массовая щель
Математика и физика всегда были взаимовыгодны. Развитие математики часто открывало новые подходы к физической теории, а новые открытия в физике стимулировали более глубокие исследования лежащих в их основе математических объяснений.
Квантовая механика была, пожалуй, самой успешной физической теорией в истории.Материя и энергия ведут себя совершенно по-разному в масштабе атомов и субатомных частиц, и одним из величайших достижений 20-го века стало теоретическое и экспериментальное понимание этого поведения.
Одной из основных основ современной квантовой механики является теория Янга-Миллса, которая описывает квантовое поведение электромагнетизма, а также слабых и сильных ядерных взаимодействий в терминах математических структур, возникающих при изучении геометрических симметрий. Предсказания теории Янга-Миллса были подтверждены бесчисленными экспериментами, и эта теория является важной частью нашего понимания того, как собираются атомы.
Несмотря на этот физический успех, теоретические математические основы теории остаются неясными. Одна из представляющих особенный интерес проблема — это «массовый разрыв», который требует, чтобы определенные субатомные частицы, которые в некотором роде аналогичны безмассовым фотонам, имели положительную массу.
Разрыв масс является важной частью того, почему ядерные силы чрезвычайно сильны по сравнению с электромагнетизмом и гравитацией, но имеют чрезвычайно короткие радиусы действия.
Таким образом, задача Премии тысячелетия состоит в том, чтобы показать общую математическую теорию, стоящую за физической теорией Янга-Миллса, и получить хорошее математическое объяснение разницы масс.
Прочтите официальное описание Математического института Клэя теории Янга-Миллса и проблемы массового разрыва здесь.
Гипотеза Римана
Возвращаясь к древним временам, простые числа — числа, которые делятся только на себя и на 1 — были объектом восхищения математиков. На фундаментальном уровне простые числа являются «кирпичиками» целых чисел, поскольку любое целое число можно однозначно разбить на произведение простых чисел.
Учитывая центральную роль простых чисел в математике, вопросы о том, как простые числа распределяются вдоль числовой прямой, то есть насколько далеко друг от друга простые числа, являются активными областями интереса.
К 19 веку математики открыли различные формулы, дающие приблизительное представление о среднем расстоянии между простыми числами. Что остается, однако, неизвестным, так это то, насколько близко к этому среднему остается истинное распределение простых чисел, то есть есть ли части числовой прямой, где «слишком много» или «слишком мало» простых чисел в соответствии с этими формулами среднего.
Гипотеза Римана ограничивает эту возможность, устанавливая границы того, насколько далеко от среднего может отклоняться распределение простых чисел. Гипотеза эквивалентна и обычно формулируется в терминах того, лежат ли все решения уравнения, основанного на математической конструкции, называемой «дзета-функцией Римана», вдоль определенной линии в плоскости комплексных чисел. Действительно, изучение таких функций, как дзета-функция, стало отдельной областью математических интересов, что делает гипотезу Римана и связанные с ней проблемы еще более важными.
Как и в некоторых других задачах Премии Тысячелетия, существуют серьезные доказательства того, что Гипотеза Римана верна, но строгое доказательство остается неуловимым.
На сегодняшний день вычислительные методы показали, что около 10 триллионов решений уравнения дзета-функции укладываются в требуемую линию, а контрпримеры не найдены.
Конечно, с математической точки зрения, 10 триллионов примеров истинности гипотезы абсолютно не заменяют полного доказательства этой гипотезы, оставляя гипотезу Римана одной из открытых проблем Премии тысячелетия.
Прочтите официальное описание гипотезы Римана Института математики Клэя здесь.
Гипотеза Бёрча и Суиннертона-Дайера
Одним из старейших и широчайших объектов математического изучения являются диофантовые уравнения, или полиномиальные уравнения, для которых мы хотим найти решения в целых числах. Классический пример, который многие могут вспомнить из школьной геометрии, — пифагорейские тройки, или наборы из трех целых чисел, удовлетворяющие теореме Пифагора x2 + y2 = z2.
В последние годы алгебраисты уделяют особое внимание изучению эллиптических кривых, которые определяются особым типом диофантовых уравнений.
Эти кривые имеют важные приложения в теории чисел и криптографии, и поиск целочисленных или рациональных решений для них является основной областью исследований.
Одним из самых ошеломляющих математических достижений за последние несколько десятилетий стало доказательство Эндрю Уайлсом классической Великой теоремы Ферма, утверждающее, что версий пифагорейских троек с большей степенью не существует.Доказательство этой теоремы Уайлсом явилось следствием более широкого развития теории эллиптических кривых.
Гипотеза Берча и Суиннертона-Дайера предоставляет дополнительный набор аналитических инструментов для понимания решений уравнений, определяемых эллиптическими кривыми.
Прочтите официальное описание гипотезы Бёрча и Суиннертона-Дайера, данное Институтом математики Клэя.
Гипотеза Ходжа
Математическая дисциплина алгебраической геометрии, вообще говоря, является изучением многомерных форм, которые могут быть определены алгебраически как множества решений алгебраических уравнений.
В качестве очень простого примера вы можете вспомнить из курса алгебры в средней школе, что уравнение y = x2 приводит к параболической кривой, когда решения этого уравнения вычерчиваются на листе миллиметровой бумаги. Алгебраическая геометрия имеет дело с многомерными аналогами такого рода кривых, когда рассматриваются системы множественных уравнений, уравнения с большим количеством переменных и уравнения на плоскости комплексных чисел, а не действительные числа.
20-й век стал свидетелем расцвета сложных методов для понимания кривых, поверхностей и гиперповерхностей, которые являются предметами алгебраической геометрии.Сложные для воображения формы можно сделать более понятными с помощью сложных вычислительных инструментов.
Гипотеза Ходжа предполагает, что некоторые типы геометрических структур имеют особенно полезный алгебраический аналог, который можно использовать для лучшего изучения и классификации этих форм.
Прочтите официальное описание гипотезы Ходжа Институтом математики Клэя здесь.
Подробнее:
• Сколько зарабатывают самые высокооплачиваемые работники 20 профессий
• Семь устаревших «правил» мужского стиля, которые теперь можно игнорировать
• 16 навыков, которым трудно научиться, но они окупятся навсегда
Прочтите оригинальную статью на Business Insider UK.© 2017. Следите за новостями Business Insider UK в Твиттере.
Эти математические задачи ошеломили математиков по всему миру
Вы, наверное, видели фильм 1997 года «Умница Уилл Хантинг», получивший премию «Оскар», с участием покойного Робина Уильямса, Мэтта Деймона и Бена Аффлека. Вкратце, фильм сосредоточен вокруг вымышленного, измученного гения Уилла Хантинга. Несмотря на свой интеллект и эйдетическую память, Хантинг работает скромным уборщиком в Массачусетском технологическом институте в Кембридже, штат Массачусетс.
Однажды он замечает математическую задачу на доске в коридоре, поставленную профессором Джеральдом Ламбо, обладателем медали Филдса.
По сюжету, на решение этой математической задачи у двух профессоров Массачусетского технологического института ушло два года. Уилл Хантинг решает проблему всего за один день, анонимно. В конце концов, профессор обнаруживает, что решение принадлежит Хантингу, и сюжет начинается. Эта история упоминалась и даже упоминалась в мемах бесчисленное количество раз в математическом сообществе. Однако случалось ли когда-нибудь что-то подобное?
Умница Уилл Хантинг: Математическая городская легенда
Существует городская легенда, немного похожая на эту историю.Как гласит история, студент опаздывает на экзамен. Торопясь сдать экзамен, он без лишних вопросов и раздумий записывает задачи, написанные на классной доске. Он справляется с экзаменационными вопросами, причем последняя математическая задача представляет собой лишь немного более сложную задачу, чем обычно, но он справляется и представляет свои результаты. Позже той же ночью ему безумно звонит профессор и сообщает, что он должен был решить только первые несколько задач.
Последним вопросом на доске была нерешенная математическая задача.
Хотя детали немного отличаются, эта городская легенда основана на истории молодого Джорджа Бернарда Данцига, американского ученого-математика, внесшего вклад в промышленную инженерию, исследование операций, информатику, экономику и статистику.
Как упоминалось ранее, есть несколько математических задач, которые до сих пор не решены. Некоторые из этих задач выглядят обманчиво простыми, а другие похожи на чужой язык. Как бы то ни было, они существуют, постоянно напоминая нам, что существуют идеи о природе нашей реальности, которые нам еще только предстоит понять.
Если вы сможете решить любую из этих математических задач, сообщите нам об этом, так как некоторые из них сопровождаются призом в миллион долларов. Это может быть ваш момент Уилла Хантинга.
Уравнения Навье-Стокса
Возможно, вы не знаете об этой математической задаче. Тем не менее, вы, вероятно, знакомы с принципами, которые он описывает.
Уравнения Навье-Стокса, названные в честь французского инженера и физика Клода-Луи Навье и англо-ирландского физика и математика Джорджа Габриэля Стокса, представляют собой набор дифференциальных уравнений в частных производных, которые используются для объяснения движения вязких жидких веществ.Эти уравнения можно использовать для описания воздуха, проходящего через крыло самолета, или воды, вытекающей из крана в кухонной раковине. Однако есть проблема. Уравнения терпят неудачу в определенных ситуациях, и математики точно не знают, почему.
Уравнения Навье-Стокса действительны только до тех пор, пока репрезентативный масштаб физической длины данной системы намного больше, чем длина свободного пробега молекул, составляющих жидкость. То есть буквальное пространство для маневра, предоставляемое частицам в жидкости, должно быть больше, чем коробка, в которой они находятся.Есть люди, которые якобы решили эту загадку только для того, чтобы позже отказаться от своих ответов. Если вы чувствуете, что у вас есть идея, как решить эту проблему, это может стоить вашего времени.
Уравнение Навье-Стокса — одна из семи задач тысячелетия, списка математических задач, за правильное решение которых присуждается приз в 1 миллион долларов каждая.
Гипотеза Коллатца
Источник: xkcdЭта задача подпадает под категорию обманчиво простой, хотя на самом деле люди рвали на себе волосы, пытаясь решить ее.Самое смешное, что вы, вероятно, могли бы объяснить это своему младшему брату или сестре. Смотреть. Выберите число, любое число. Если вы выбрали четное число, разделите его на 2.
СМОТРИТЕ ТАКЖЕ: 5 ИЗВЕСТНЫХ УЧЕНЫХ, КОТОРЫЕ БОРЬБИЛИСЬ С МАТЕМАТИКОЙ
Если ваше число нечетное, разделите его на три и прибавьте 1. С новым числом повторите те самые шаги. Интересно, что независимо от пути вы в конечном итоге получите число 1. Математики неоднократно доказывали, что гипотеза Коллатца верна.Они не нашли ни одного номера, который бы не нарушал правила. Что ускользнуло от них, так это объяснение почему. В этом году Марин Хеул, ученый-компьютерщик из Университета Карнеги-Меллона, объявил, что планирует решить эту неразрешимую математическую задачу с помощью компьютеризированной техники доказательства, называемой SAT-решением.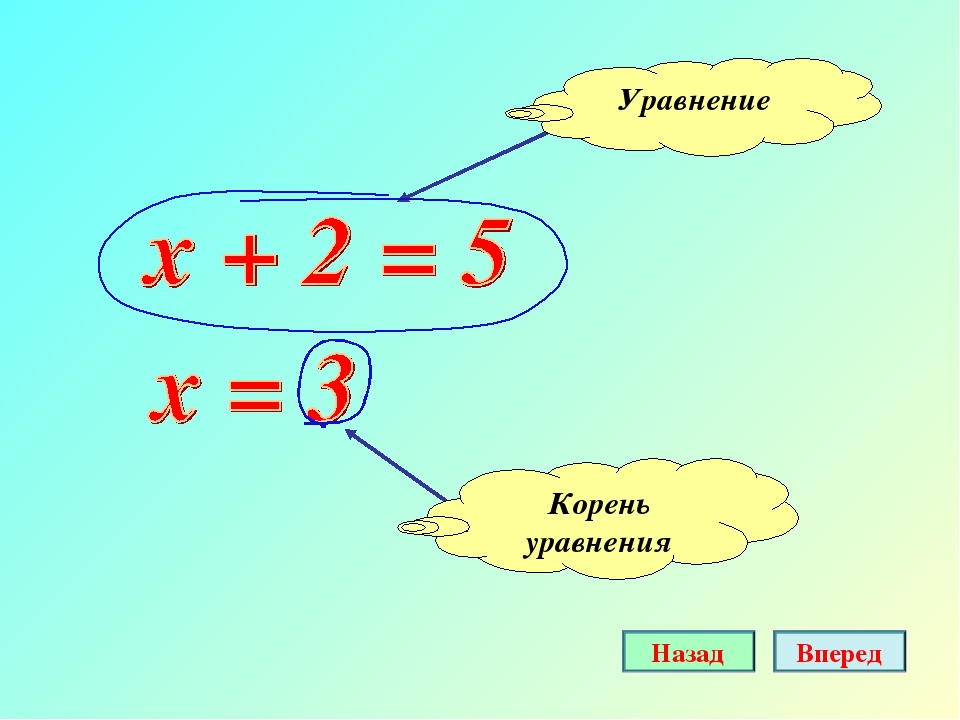
z.2 – нельзя. Ответ на эту математическую дилемму также принесет вам приз в размере 1 миллиона долларов.
Проблема с движущимся диваном
Да, мы говорим о том самом старом диване, который сейчас стоит в вашей гостиной. Процесс перемещения мебели непосредственно вдохновляет эту математическую задачу. Независимо от того, въезжаете ли вы или выезжаете, вам нужно найти способ перенести диван через коридор. Эта нерешенная проблема геометрии задает простой вопрос: какой самый большой диван вы могли бы разместить вокруг угла в 90 градусов, независимо от формы, без изгиба?
Важно знать, что математики смотрят на эту проблему только через призму двух измерений.Интересно, что по сей день математики понятия не имеют о границах константы дивана, самой большой области, которая может поместиться за углом. Подумайте об этом в следующий раз, когда ваш сосед по комнате скажет, что он не сможет поставить этот диван Ikea в вашу квартиру.
Математике еще многое предстоит нам показать.
Математика очаровательна хотя бы тем простым фактом, что однажды доказанная истина закрепится навечно. Конечно, вы можете экспериментировать с новой концепцией, расширять ее или даже манипулировать ею, но основная идея остается неизменной.Это «романтика математики», — говорит физик-теоретик, математик и теоретик струн Брайан Грин в своей книге « до конца времен ». Грин утверждает, что математика – это «творчество, ограниченное логикой, а набор аксиом диктует, как можно манипулировать идеями и комбинировать их, чтобы выявить непоколебимые истины».
Если наши исследования Вселенной чему-то и научили нас, так это тому, что существуют непоколебимые истины, которые еще предстоит открыть. Будете ли вы решить их?
Вы можете стать миллионером, если решите любое из этих математических уравнений
Эти задачи были выбраны научным консультативным советом.
Решение каждой проблемы может принести вам 1 миллион долларов (7,4 крор рупий). Единственное предостережение заключается в том, что решение должно быть тщательно проверено и тщательно проверено.
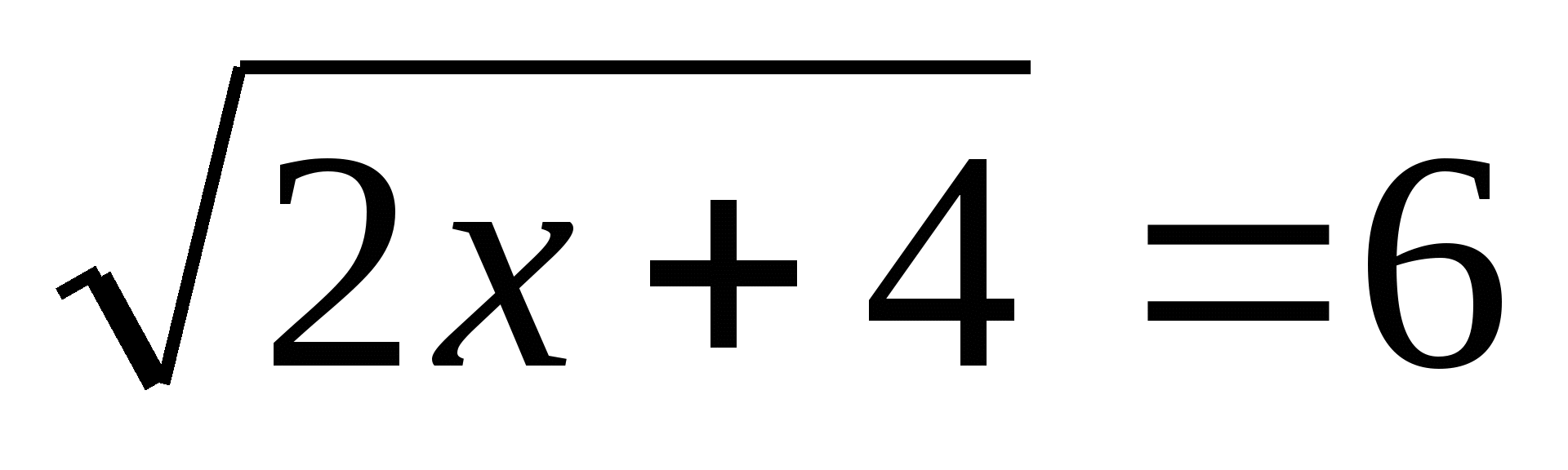
Еще в 2000 году Математический институт Клэя в США объявил задачи Премии тысячелетия, сборник из семи нерешенных математических задач. Институт также приготовил огромный денежный приз для тех, кто решит их. Эти проблемы были отобраны научно-консультативным советом. По данным правления, эти уравнения «много лет сопротивлялись решению».Излишне говорить, что эти задачи смехотворно сложны, и именно поэтому они были выбраны. Но это не означает, что эти уравнения не могут быть решены.
Одну из них, гипотезу Пуанкаре, решил в 2006 году математик Григорий Перельман. Тем не менее, есть еще шесть нераскрытых дел. Исследователи и математики надеются, что кто-то в конце концов решит оставшиеся уравнения и выиграет денежный приз. Решение каждой проблемы может принести вам 1 миллион долларов (7 рупий).4 крор). Единственное предостережение заключается в том, что решение должно быть тщательно проверено и тщательно проверено.
Если вы тоже признанный гений или считаете себя гением математики, вы тоже можете попробовать свои силы в этих головоломках и получить награду в миллион долларов.
Давайте взглянем на шесть нерешенных математических уравнений, которые стоят огромной денежной суммы.
- Уравнения Навье-Стокса : Это уравнение регулирует поток жидкостей, таких как вода и воздух. Хотя нет доказательств уравнения для таких вопросов, как «существуют ли решения?» и «уникальны ли они?», математики и физики считают, что объяснение турбулентности в современной струе можно найти, если разобраться в уравнениях Навье-Стокса.
- Ян-Миллс и массовый разрыв : Многие эксперименты и компьютерное моделирование в прошлом предполагали существование массового разрыва. Физики обнаружили, что, хотя классические волны распространяются со скоростью света, квантовые частицы имеют положительную массу. Однако до сих пор это свойство не было понято с теоретической точки зрения.
- Гипотеза Римана : Это нерешенное числовое уравнение дает результаты о распределении простых чисел.
- Гипотеза Берча и Суиннертона-Дайера : Она признана одной из самых сложных математических задач для решения.
Это связано с теорией чисел. - Гипотеза Ходжа : Эта проблема связана с алгебраической геометрией, связанной с алгебраической топологией неособого комплексного алгебраического многообразия.
- P vs NP : Это уравнение связано с информатикой и подчиняется правилу, согласно которому, если решение задачи легко проверить на правильность, значит, и проблема должна быть легко решена.Хотя P — это набор относительно простых задач, а NP — это набор очень сложных уравнений, тогда P=NP будет означать, что у сложных задач будут относительно простые решения.
Это связано с теорией чисел.Читайте все последние новости, экстренные новости и новости о коронавирусе здесь
Нерешенные проблемы
Задачи тысячелетия — это семь задач по математике, сформулированных Математическим институтом Клэя в 2000 году. Они не решаются десятилетиями. Головокружительные задачи настолько важны и известны, что за каждый правильный ответ предлагается награда в 1 миллион долларов.
Это семь величайших нерешенных математических загадок нашего времени. Каждая из них существует уже давно, хорошо известна в математике и сопротивлялась попыткам решения лучших математических умов мира.Самой последней из семи проблем тысячелетия является проблема P vs. NP, которая была разработана в 1970 году. Гипотеза Римана, связанная с закономерностью простых чисел, остается нерешенной, несмотря на то, что впервые была поднята в 1859 году. Гипотеза Римана единственная проблема, которую математики хотели бы решить больше всего.
По состоянию на июнь 2013 года шесть проблем остаются нерешенными. Гипотезу Пуанкаре, единственную решенную на сегодняшний день задачу о премии тысячелетия, решил Григорий Перельман, но в 2010 году он отказался от награды в 1 миллион долларов.
- Семь задач:
- P по сравнению с NP
Вопрос заключается в том, может ли алгоритм для всех задач, для которых алгоритм может быстро проверить данное решение (то есть за полиномиальное время), также быстро найти это решение. Первый описывает класс задач, называемый NP, а второй описывает P.Вопрос в том, все ли проблемы в NP есть и в P. - Гипотеза Ходжа
Гипотеза Ходжа состоит в том, что для проективных алгебраических многообразий циклы Ходжа являются рациональными линейными комбинациями алгебраических циклов. - Гипотеза Пуанкаре (доказана)
В топологии сфера с двумерной поверхностью существенно характеризуется тем, что она односвязна. Верно также и то, что всякая двумерная поверхность, одновременно компактная и односвязная, топологически является сферой.Гипотеза Пуанкаре состоит в том, что это верно и для сфер с трехмерными поверхностями. Вопрос давно решен для всех измерений выше трех. Решение этой задачи для трех занимает центральное место в задаче классификации трехмерных многообразий. - Гипотеза Римана
Гипотеза Римана состоит в том, что все нетривиальные нули аналитического продолжения дзета-функции Римана имеют действительную часть 1/2. - Существование Янг-Миллса и массовая щель
В физике классическая теория Янг-Миллса является обобщением теории электромагнетизма Максвелла, согласно которой хромо-электромагнитное поле само несет заряды. - Существование и гладкость Навье-Стокса
Уравнения Навье-Стокса описывают движение жидкостей. Хотя они были найдены в 19 веке, они до сих пор недостаточно изучены. Проблема состоит в том, чтобы продвинуться к математической теории, которая даст представление об этих уравнениях. - Гипотеза Берча и Суиннертона-Дайера
Гипотеза Берча и Суиннертона-Дайера касается определенного типа уравнений, определяющих эллиптические кривые над рациональными числами.Гипотеза состоит в том, что существует простой способ определить, имеют ли такие уравнения конечное или бесконечное число рациональных решений.
Первый описывает класс задач, называемый NP, а второй описывает P.Вопрос в том, все ли проблемы в NP есть и в P.
Так что удачи в решении проблем Миллениума. Помните, если вы решите одну из оставшихся шести задач, отправьте свое решение мистеру П., и он позаботится о том, чтобы переслать его для вас в Математический институт Клэя!! (-:
Вот пара анекдотов про Гипотезу Римана:
Математик спросил гадалку: “Скажи мне, доказательства нерешенных теорем находятся на небесах?”
«У меня есть хорошие и плохие новости», — отвечает она.