Как определить фазу и ноль мультиметром
Очень часто при выполнении в квартире, доме, гараже или на даче ремонтных либо монтажных работ, связанных с электричеством, возникает необходимость отыскать ноль и фазу. Это нужно для правильного подключения розеток, выключателей, осветительных приборов. Большинство людей, даже если они не имеют специального технического образования, представляют себе, что для этого есть специальные индикаторы. Мы рассмотрим вкратце этот метод, а также расскажем вам об ещё одном приборе, без которого не обходится ни один профессиональный электрик. Поговорим о том, как определить фазу и ноль мультиметром.
Содержание
- Понятия ноля и фазы
- Простейшие способы
- По цветовому исполнению жил
- Индикаторной отвёрткой
- Мультиметр. Что это за прибор?
- Как использовать прибор?
- Несколько правил по использованию мультиметра
Понятия ноля и фазы
Перед тем, как определить фазу ноль, хорошо бы вспомнить самую малость физики и разобраться, что это за понятия и зачем их находят в розетке.
Все электросети (и бытовые, и промышленные) подразделяются на два типа – с постоянным и переменным током. Со школы помним, что ток – это передвижение электронов в определённом порядке. При постоянном токе электроны передвигаются в каком-то одном направлении. При переменном токе это направление постоянно меняется.
Нас больше интересует переменная сеть, которая состоит из двух частей:
- Рабочей фазы (как правило, её называют просто «фазой»). На неё подаётся рабочее напряжение.
- Пустой фазы, именуемой в электричестве «нулём». Она необходима, чтобы создать замкнутую сеть для подключения и работы электрических приборов, служит также для заземления сети.
Когда мы включаем приборы в однофазную сеть, то особой важности нет, где именно пустая или рабочая фаза. А вот когда монтируем в квартире электрическую проводку и подсоединяем её к общей домовой сети, это знать необходимо.
Разница между нолем и фазой на видео:
youtube.com/embed/bwDhRtp0kGg?feature=oembed” frameborder=”0″ allowfullscreen=””> Простейшие способы
Существует несколько способов, как найти фазу и ноль. Рассмотрим их вкратце.
По цветовому исполнению жил
Наиболее простым, но в то же время и самым ненадёжным способом, является определение фазы и ноля по цветам изоляционных оболочек проводников. Как правило, фазная жила имеет чёрное, коричневое, серое или белое цветовое исполнение, а ноль делают голубым либо синим. Чтобы вы были в курсе, бывают ещё жилы зелёные или жёлто-зелёные, так обозначаются проводники защитного заземления.
В этом случае никаких приборов не нужно, глянули на цвет провода и определили – фаза это или ноль.
Но почему этот метод самый ненадёжный? А нет никакой гарантии, что во время монтажа электрики соблюдали цветовую маркировку жил и ничего не перепутали.
Цветовая маркировка проводов на следующем видео:
Индикаторной отвёрткой
Более правдивым методом является применение индикаторной отвёртки.
Она состоит из не токопроводящего корпуса и встроенных в него резистора с индикатором, который представляет собой обыкновенную неоновую лампочку.
Например, при подключении выключателя главное не перепутать ноль с фазой, так как этот коммутационный аппарат работает только на разрыв фазы. Проверка индикаторной отвёрткой заключается в следующем:
- Отключите общий вводной автомат на квартиру.
- Зачистите ножом проверяемые жилы от изоляционного слоя на 1 см. Разведите их между собой на безопасное расстояние, чтобы полностью исключить возможность соприкосновения.
- Подайте напряжение, включив вводной автомат.
- Жалом отвёртки прикоснитесь к оголённым проводникам. Если при этом загорится индикаторное окошко, значит, провод соответствует фазному. Отсутствие свечения говорит о том, что найденный провод – нулевой.
- Нужную жилу наметьте маркером либо кусочком изоленты, после чего снова отключите общий автомат и проведите подсоединение коммутационного аппарата.
Более сложные и точные проверки выполняются с помощью мультиметра.
Поиск фазы индикаторной отверткой и мультиметром на видео:
Мультиметр. Что это за прибор?
Мультиметр (электрики его ещё называют тестером) представляет собой комбинированный прибор для электрических измерений, который объединил в себе множество функций, основные из которых омметр, амперметр, вольтметр.
Эти приборы бывают разными:
- аналоговыми;
- цифровыми;
- переносными лёгкими для каких-то базовых измерений;
- сложными стационарными с большим количеством возможностей.
С помощью мультиметра можно не только определить землю, ноль или фазу, но и померить на участке цепи ток, напряжение, сопротивление, проверить электрическую цепь на целостность.
Прибор представляет собой дисплей (или экран) и переключатель, который можно устанавливать в различные позиции (вокруг него находится восемь секторов).
В самом верху (в центре) имеется сектор «OFF», когда переключатель установлен в это положение, значит, прибор выключен. Чтобы выполнять замеры напряжения понадобится установить переключатель в сектора «ACV» (для переменного напряжения) и «DCV» (для постоянного напряжения).
В комплект мультиметра входят ещё два измерительных щупа – чёрный и красный. Чёрный щуп подсоединяется в нижнее гнездо с маркировкой «СОМ», такое подключение является постоянным и используется при проведении любых измерений. Красный щуп в зависимости от замеров вставляется в среднее или верхнее гнездо.
Как использовать прибор?
Выше мы рассмотрели, как найти при помощи индикаторной отвёртки фазный провод, а вот различить ноль и землю при помощи такого инструмента не получится. Тогда давайте поучимся, как проверить жилы мультиметром.
Подготовительный этап выглядит точно так же, как и для работы с индикаторной отвёрткой. При отключенном напряжении зачистите концы жил и обязательно их разведите, чтобы не спровоцировать случайного прикосновения и возникновения короткого замыкания.
- Выберите на приборе измерительный предел переменного напряжения выше 220 В. Как правило, имеется отметка со значением 750 В на режиме «ACV», установите переключатель на это положение.
- На приборе имеется три гнезда, куда вставляются измерительные щупы. Найдём среди них тот, который обозначен буквой «V» (то есть для измерения напряжения). Вставьте в него щуп.
- Прикасайтесь щупом к зачищенным жилам и смотрите на экран прибора. Если вы видите небольшое значение напряжения (до 20 В), значит, вы касаетесь фазного провода. В случае, когда на экране нет никаких показаний, вы нашли ноль мультиметром.
Для определения «земли» зачистите небольшой участок на любом металлическом элементе домашних коммуникаций (это могут быть водопроводные или отопительные трубы, батареи).
В этом случае у нас будут задействованы два гнезда «СОМ» и «V», вставьте в них измерительные щупы.
Прибор установите в режим «ACV», на значение 200 В.У нас есть три провода, среди них нужно отыскать фазу, ноль и землю. Одним щупом коснитесь зачищенного места на трубе или батарее, вторым дотроньтесь до проводника. Если на экране высвечивается показание порядка 150-220 В, значит, вы нашли фазный провод. Для нулевого провода при аналогичных замерах показание колеблется в пределах 5-10 В, при прикосновении к «земле» на экране ничего не будет отображаться.
Наметьте каждую жилу маркером или изолентой, а чтобы удостовериться в правильности выполненных измерений, сделайте теперь замеры относительно друг друга.
Прикоснитесь двумя щупами к фазному и нулевому проводникам, на экране должна появиться цифра в пределах 220 В. Фаза с землёй дадут немного меньшее показание. А если прикоснуться к нулю и земле, то на экране будет значение от 1 до 10 В.
Несколько правил по использованию мультиметра
Перед тем, как определить фазу и ноль мультиметром, ознакомьтесь с несколькими правилами, которые необходимо соблюдать при работе с прибором:
- Никогда не пользуйтесь мультиметром во влажной среде.
- Не применяйте неисправные измерительные щупы.
- В момент проведения замеров не меняйте измерительные пределы и не переставляйте положение переключателя.
- Не измеряйте параметры, значение которых выше чем верхний измерительный предел прибора.
Как замерять напряжение мультиметром – на следующем видео:
Обратите внимание на важный нюанс в использовании мультиметра. Поворотный переключатель изначально всегда необходимо устанавливать на максимальное положение, чтобы избежать повреждения электронного прибора. А уже в дальнейшем, если показания оказываются ниже, переключатель переставляется на низкие отметки для получения максимально точных замеров.
Как определить фазу и ноль
При выполнении ремонтно-строительных работ важным этапом является подключение помещений и зданий к системе электроснабжения. В этом случае, кроме электропроводки, устанавливается большое количество другого оборудования, в том числе розеток и выключателей.
При выполнении подключений довольно часто возникает вопрос, как определить фазу и ноль, а также заземляющий проводник в электрической сети. Определить назначение каждого проводника возможно с помощью нескольких простых и доступных способов рассмотренных ниже.
Содержание
Как определить фазу и ноль индикаторной отверткой
Наиболее простым и распространенным способом, позволяющим точно определить фазу и ноль, является использование индикаторной отвертки. Данная операция не представляет каких-либо сложностей и требует лишь соблюдения определенного алгоритма действий.
Решая вопрос, как определить где фаза, а где ноль, прежде всего необходимо обесточить линию и отключить автомат, через который питается домашняя электросеть. После отключения следует зачистить проверяемые провода, сняв примерно 1-2 см изоляции. Далее проводники разводятся между собой на безопасное расстояние. Это необходимо сделать, чтобы исключить возможность короткого замыкания при случайном соприкосновении после подачи напряжения.
После всех подготовительных мероприятий можно приступать к определению фазы и нуля. Предварительно следует включить автомат и подать напряжение в сеть.
Непосредственная проверка фазы и нуля тестером осуществляется следующим образом. Индикатор зажимается между большим и средним пальцем. При этом нельзя касаться пальцами открытой, неизолированной части жала отвертки во избежание удара электрическим током.
Указательный палец должен касаться круглого металлического выступа, расположенного в конце рукоятки. После этого жало отвертки прикладывается к зачищенным концам проводников. Если тестер коснулся фазного проводника, в этом случае загорается светодиод. Следовательно, второй провод является нулевым. Нулевой провод определяется когда индикаторная лампочка не загорелась изначально.
Как определить фазу и ноль мультиметром
Кроме индикаторной отвертки, определение фазы и нуля может быть выполнено с помощью мультиметра. В этом случае также необходима зачистка проводников, подлежащих проверке.
Предварительно следует обесточить электрическую сеть путем выключения автомата. Таким образом исключается вероятность короткого замыкания при случайном соприкосновении проводников фазы и нуля. Сами провода нужно немного раздвинуть. После этого автомат следует снова включить.
Далее на мультиметре устанавливается предельная величина для измерений переменного напряжения, составляющая более 220 В. Затем нужно посмотреть, какую маркировку имеют гнезда со щупами прибора. Щуп в гнезде СОМ не подходит для определения фазы, следовательно, использоваться будет оставшийся щуп, обозначенный символом V. Определившись со щупами, можно приступать к определению назначения проводов.
Нужно взять щуп, коснуться им одного из проводов в розетке и посмотреть на показания мультиметра. При отображении данных с небольшим значением напряжения (менее 20 В), провод будет считаться фазным. Если же измерительный прибор показывает нулевое значение, то и сам провод соответственно будет нулевым.
Для измерений может использоваться любой тип мультиметра – с цифровым табло или стрелочный.
Точность измерений мультиметром значительно выше, чем индикаторной отверткой. При определение фазы и нуля мультиметром запрещается одновременно касаться фазного и заземляющего провода. Такие действия могут вызвать короткое замыкание и травматические ожоги.
Как определить фазу и ноль без приборов
Довольно часто возникают ситуации, когда отсутствует индикаторная отвертка и мультиметр, а выяснить назначение проводов нужно, чтобы не останавливать электромонтажные работы. В таких случаях приходится решать проблему, определения фазы и ноля без прибора.
Наиболее простым способом считается определение назначения проводов по их маркировке и по цвету изоляции. Данная методика приносит положительный результат лишь тогда, когда проводка выполнена с соблюдением всех технических правил. В этом случае цвет изоляции прямо указывает на принадлежность того или иного провода.
В желто-зеленый цвет окрашивается заземляющий провод, а нулевой проводник чаще всего бывает голубого или синего цвета.
Для фазного проводника выбирается черный, белый или коричневый провод. Правильность подключения можно проверить визуально, не только в щитке, но и в распределительных коробках, в люстре и других точках.
Второй способ определения фазы и нуля, предполагает использование так называемой контрольной лампочки. Можно воспользоваться обычной лампой накаливания и двумя отрезками проводов, по 50 см длиной каждый. Жилы проводов через патрон подключаются к лампочке и конструкция готова к работе. Одним концом провода нужно коснуться трубы отопления, а другим – проверяемых проводов. Если во время прикосновения лампочка загорается, значит этот провод является фазным.
Данный способ в домашних условиях считается опасным в связи с высокой вероятностью поражения электрическим током. Его нельзя применять, когда в сети присутствует предельное напряжение. Более безопасным является использование неоновых лампочек, позволяющих с не меньшей точностью определить назначение проводов.
-2}}{1-0.9{j\omega}))}$$, но мне трудно понять, как его использовать и что такое фазовая характеристика. Можете ли вы привести пример того, как рассчитать фазовую характеристику определенного угла?- фаза
- бесконечная импульсная характеристика
- передаточная функция
- z-преобразование
- величина
$\endgroup$
4
$\begingroup$ 9{j\omega})$ ведет себя.
Что касается фазы, обратите внимание, что ваша формула (отношение мнимой и действительной частей) на самом деле является тангенсом фазы, а не самой фазой. Прежде всего ясно, что фаза должна быть нулевой при постоянном токе (т.е. $z=1$) и при Найквисте (т.е. $z=-1$). Кроме того, полная фазовая характеристика равна фазе числителя минус фаза знаменателя. Итак, если вы вычислите фазовую характеристику одного нуля (для одного полюса вы получите то же самое с отрицательным знаком), вы можете составить общую фазу, просто суммируя эти частичные фазы для каждого полюса и нуля.
Качественно для каждого полюса вы получаете уменьшающийся вклад в фазу (с максимальным уменьшением на частоте полюса), а для каждого нуля вы получаете возрастающий вклад в фазу (с максимальным увеличением на частоте нуля). 9{-j{\pi\более 2}}=-i$. Выражение для величины оценивается как $3,3793$ под этим углом.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Калькулятор фазового сдвига
Создано Maciej Kowalski, PhD кандидатом
Отредактировано Анной Щепанек, PhD и Стивеном Вудингом
Последнее обновление: 11 октября 2022 г.
Содержание:- сдвиг
- Как найти амплитуду
- Как найти период
- Как найти фазовый сдвиг
- Как найти вертикальный сдвиг
- Пример: использование калькулятора фазового сдвига амплитуды периода
- Часто задаваемые вопросы
Добро пожаловать в Omni калькулятор фазового сдвига , где мы изучим тригонометрические функции и как вычислить их фазовый сдвиг. На самом деле, мы рассмотрим больше: мы также объясним, как найти амплитуду и как найти период . На деле оказывается, что огромный класс функций ведет себя практически одинаково, а различия сводятся к описанию тех самых значений, о которых говорилось выше; амплитуда, период и фазовый сдвиг.
ну до вертикальное смещение , по крайней мере.
Амплитуда, период, фазовый сдвиг и сдвиг по вертикали
Как мы упоминали выше, здесь мы сосредоточимся на тригонометрических функциях : более конкретно на синусе и косинусе. Тем не менее, важно помнить, что многие понятия являются более общими , особенно понятия горизонтального переноса или вертикального сдвига.
Прежде всего, давайте посмотрим на картинку, показывающую , где амплитуда, период, фазовый сдвиг и вертикальный сдвиг отображаются на графике (обратите внимание, что такое же изображение появляется в верхней части калькулятора фазового сдвига Omni).
Мы можем записать такие функции с помощью формулы (иногда называемой уравнением фазового сдвига или формулой фазового сдвига ):
f(x)=A⋅sin(Bx−C)+Df(x) = A\cdot\sin(Bx-C)+Df(x)=A⋅sin(Bx−C)+D
или
f(x) = A\cdot\cos(Bx-C) +Д |
|---|
для произвольных действительных чисел AAA, BBB, CCC, DDD, но с ненулевыми AAA и BBB (иначе это не была бы тригонометрическая функция).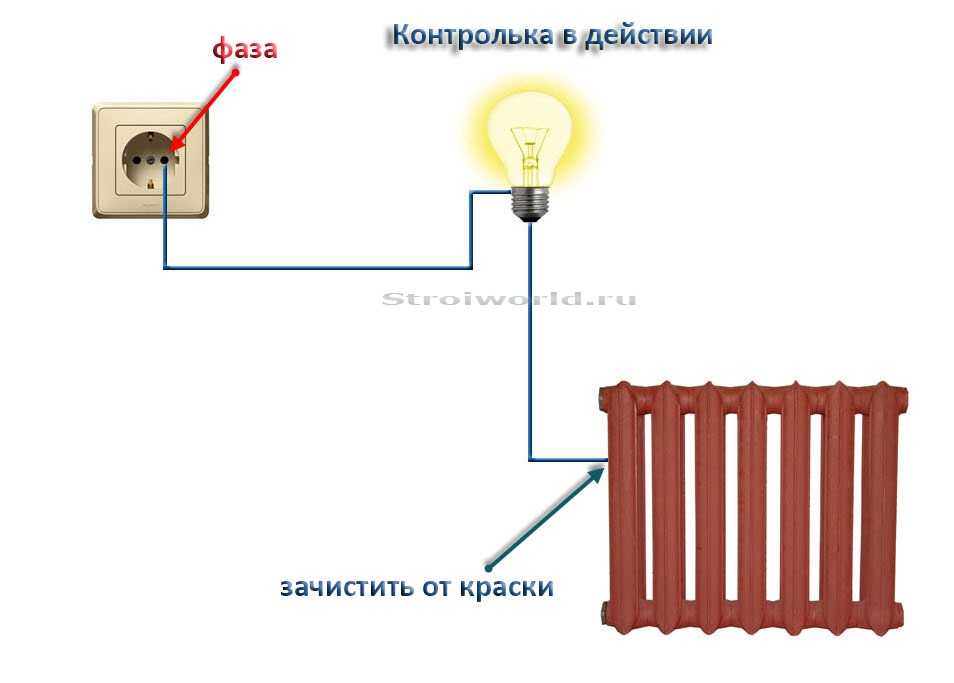
Очевидно, эти четыре числа определяют амплитуду, период, фазовый сдвиг и сдвиг по вертикали . В какой-то степени картина показывает, как они влияют на график. Тем не менее, было бы полезно поддержать визуальные эффекты некоторыми определениями.
- Амплитуда показывает, как далеко (в любом направлении) значения отходят от центральной линии графика. Для простого синуса или косинуса его значение равно 111, так как центральная линия находится в точке 000, а значения функции находятся в диапазоне от -1-1-1 до 111.
- Период — длина по горизонтальной оси, после которой функция начинает повторяться. Другими словами, (бесконечный) граф — это просто набор копий длины периода, склеенных вместе на концах . Для простого синуса или косинуса период равен 2π2\pi2π, поскольку sin(0)=sin(2π)=sin(4π)=…\sin(0) = \sin(2\pi) = \ sin(4\pi) = …sin(0)=sin(2π)=sin(4π)=… и части между ними точно такие же (и аналогично для косинуса).
- Фазовый сдвиг (также называемый сдвиг по горизонтали или сдвиг по горизонтали ) описывает, насколько далеко по горизонтали график сместился от обычного синуса или косинуса. Таким образом, значение равно 000, если две функции не изменены.
- Вертикальный сдвиг (также называемый вертикальным сдвигом ) описывает, насколько вертикально график сместился от обычного синуса или косинуса. Другими словами, это близнец фазового сдвига, который касается перпендикулярного направления . В частности, значение снова равно 000, если обе функции остаются неизменными.
Итак, мы узнали, что такое фазовый сдвиг, а также три сопутствующих значения. Разделы ниже описывают , как вычислить каждый из них на основе обозначений из приведенной выше формулы фазового сдвига. Сначала мы покажем , как найти амплитуду .
Введенные нами понятия получили широкое распространение при изучении колебательных и гармонических движений.
Короче говоря, эти явления — лучшие друзья тригонометрии. Вы можете найти связь на нашем калькуляторе тригонометрии или узнать больше о различных функциях, которые постоянно появляются, когда вы анализируете маятник, на калькуляторе тригонометрических функций или на более конкретном калькуляторе косинуса и калькуляторе синуса!
Как найти амплитуду
Мы знаем, что функции синуса и косинуса имеют значения в диапазоне от −1-1−1 до 111. Более того, этот простой факт не меняет , если мы подставим sin(x )\sin(x)sin(x) или cos(x)\cos(x)cos(x) для sin(Bx−C)\sin(Bx – C)sin(Bx−C) или cos( Bx−C)\cos(Bx – C)cos(Bx−C) для ненулевого BBB и произвольного CCC. На самом деле, это потому, что функция f(x)=Bx−Cf(x) = Bx – Cf(x)=Bx−C является тогда биекцией (т. е. взаимно однозначным соответствием) на пространство вещественные числа.
Теперь давайте посмотрим, что произойдет, если мы добавим DDD, то есть если у нас есть sin(Bx−C)+D\sin(Bx – C) + Dsin(Bx−C)+D или cos(Bx−C) +D\cos(Bx – C) + Dcos(Bx−C)+D вместо этого.
Так как первая часть дает что-то между -1-1-1 и 111, все это будет между -1+D-1 + D-1+D и 1+D1 + D1+D (см. Как найти вертикальную сдвиг для сравнения). Это означает, что 90 107 центральная линия приходится на 90 108 DDD, а амплитуда по-прежнему равна 111, потому что значения отклоняются на 111 от DDD.
Следовательно, единственное, что может повлиять на амплитуду в формулах фазового сдвига A⋅sin(Bx−C)+DA\cdot\sin(Bx – C) + DA⋅sin(Bx−C)+D и A⋅cos (Bx−C)+DA\cdot\cos(Bx – C) + DA⋅cos(Bx−C)+D — это ненулевое AAA. И действительно, поскольку sin(Bx−C)\sin(Bx-C)sin(Bx−C) и cos(Bx−C)\cos(Bx-C)cos(Bx−C) все это время находятся между −1-1−1 и 111, множитель AAA изменяет этот диапазон на −1⋅A=−A-1\cdot A = -A−1⋅A=−A и 1⋅A=A1 \cdot A = A1⋅ А=А.
Да, вы уже догадались: амплитуда уравнений фазового сдвига A⋅sin(Bx−C)+DA \cdot\sin(Bx – C) + DA⋅sin(Bx−C)+D и A⋅cos(Bx−C)+DA \cdot\cos (Bx – C) + DA⋅cos(Bx−C)+D просто равно AAA.
Как найти период
Напомним, что функции синуса и косинуса имеют периоды, равные 2π2\pi2π, т. е. имеем sin(x+2π)=sin(x)\sin(x + 2\ pi) = \sin(x)sin(x+2π)=sin(x) и cos(x+2π)=cos(x)cos(x + 2\pi) = cos(x)cos(x+2π) =cos(x) для любого xxx. В частности, это дает: x\!+\!2\pi)\!+\!D\!=\!A\!\cdot\!\sin(x)\!+\!DA⋅sin(x+2π)+D=A ⋅sin(x)+D
и
A ⋅ cos(x + 2π) + D = A ⋅ cos(x) ccot+\!\ +\!2\pi)\!+\!D\!=\!A\!\cdot\!\cos(x)\!+\!DA⋅cos(x+2π)+D=A⋅cos( x)+D
Итак, мы видим, что AAA и DDD в формуле фазового сдвига не влияют на период . Действительно, все сводится к тому, что происходит внутри тригонометрических функций . И еще:
sin(x−C+2π)=sin(x−C)\sin(x – C + 2\pi) = \sin(x – C)sin(x−C+2π)= sin(x−C)
И:
cos(x−C+2π)=cos(x−C)\cos(x – C + 2\pi) = cos(x – C)cos(x− C+2π)=cos(x−C)
По тем же правилам, что и выше, поэтому это не CCC или , который выполняет эту работу.
Таким образом, с отброшенными тремя вариантами должен быть четвертый : BBB.
Мы снова обратимся к комментарию, который мы начали с , чтобы понять, почему и как BBB влияет на периодичность в уравнениях фазового сдвига A⋅sin(Bx−C)+DA \cdot \sin(Bx – C) + DA⋅sin (Bx−C)+D и A⋅cos(Bx−C)+DA \cdot \cos(Bx – C) + DA⋅cos(Bx−C)+D. В конце концов:
sin(Bx)=sin(Bx+2π)=sin(B⋅(x+2πB))\begin{split} \sin(Bx) &= \sin(Bx + 2\pi)\\ & = \sin(B \cdot (x + \frac{2\pi}{B})) \end{split}sin(Bx)=sin(Bx+2π)=sin(B⋅(x+B2π))
Таким образом, при добавлении каждых 2π/B2\pi/B2π/B к аргументу xxx, мы возвращаемся в то же место , и функция повторяется (и аналогично для косинуса).
Всего период уравнения фазового сдвига равен 2π/B2\pi/B2π/B.
Наши ежедневные знания о волнах обычно отдают приоритет частоте за период; однако это почти одно и то же. Узнайте почему на частотном калькуляторе Omni
Как найти фазовый сдвиг
По определению фазовый сдвиг описывает горизонтальный перенос функции по отношению к обычному sin(x)\sin(x)sin(x) или cos(x)\cos(x)cos(x ).
Таким образом, базовые функции имеют его равным 000. На самом деле, если мы сравним их графики:
… мы заметим, что мы можем получить, переведя другие (на самом деле взаимные кофункции имеют много общего). Чтобы быть точным, мы имеем:
sin(x+pi2)=cos(x) \sin(x+\frac{pi}{2})=\cos(x) sin(x+2pi)=cos(x)
И:
cos(x−pi2)=sin(x)\cos(x-\frac{pi}{2})=\sin(x) cos(x−2pi)=sin(x )
В приведенном выше примере уже показано, где в A⋅sin(Bx−C)+DA \cdot\sin(Bx – C) + DA⋅sin(Bx−C)+D и A⋅cos(Bx−C )+DA \cdot\cos(Bx – C) + DA⋅cos(Bx−C)+D следует искать значения, отвечающие за фазовые сдвиги. Однако, в отличие от амплитуды и периода, на этот раз нам понадобятся две из четырех букв .
В общем случае (т.е. не только в уравнениях фазового сдвига) получаем горизонтальный перенос произвольной функции f(x)f(x)f(x) путем вычисления f(x−a)f(x – a)f(x−a): сдвиг графика на aaa к право. Другими словами, мы заменяем каждое вхождение xxx на x−ax – ax−a в формуле для f(x)f(x)f(x).
Например, применение преобразования к sin(x)\sin(x)sin(x) дает sin(x−a)\sin(x – a)sin(x−a), но, скажем, для cos (3x+1)\cos(3x+1)cos(3x+1) мы получим:
cos(3(x−a)+1)=cos(3x−3a+1)\begin{ расколоть} &\cos(3(х-а)+1)\\ &=\cos(3x-3a+1) \end{split}cos(3(x−a)+1)=cos(3x−3a+1)
т.е. нельзя забывать о множителях, стоящих перед xxx.
В нашем случае формула фазового сдвига дает:
A⋅sin(Bx−C)+D=A⋅sin(B⋅(x−CB))+D\begin{split} A\cdot&\sin(Bx-C)+D\\ =A\cdot&\sin\left(B\cdot\left(x-\frac{C}{B}\right)\right)+D \end{split}A⋅=A⋅sin(Bx−C)+Dsin(B⋅(x−BC))+D
, что равно фазовому сдвигу C/BC/BC/B ( вправо) функции A⋅sin(Bx)A \cdot\sin(Bx)A⋅sin(Bx). Конечно, мы можем повторить вышеописанное и для косинуса.
Подводя итог, чтобы вычислить фазовый сдвиг уравнения фазового сдвига, нужно найти C/BC/BC/B.
Как найти вертикальный сдвиг
Это легко , особенно теперь, когда мы узнали, что такое фазовый сдвиг, амплитуда и период и как их вычислить.
Давайте опираться на то, что мы уже узнали.
Мы знаем, что в формулах фазового сдвига A⋅sin(Bx−C)+DA \cdot\sin(Bx – C) + DA⋅sin(Bx−C)+D и A⋅cos(Bx−C )+DA \cdot\cos(Bx – C) + DA⋅cos(Bx−C)+D, AAA определяет, насколько сильно колеблются значения по обе стороны от центральной линии. BBB указывает, насколько далеко мы расширяем выпуклости графика и, как результат, как быстро мы можем повторять значения. Кроме того, вместе с CCC они описывают, сдвинули ли мы функцию влево или вправо и насколько.
Очевидно, горизонтальное смещение не влияет на вертикальное смещение : ведь это два перпендикулярных направления. С другой стороны, амплитуда только говорит нам, как далеко по вертикали простирается график, но не сдвигает его на . В общем, у нас осталась только одна буква : DDD.
DDD в уравнениях фазового сдвига точно соответствует вертикальному сдвигу . Он определяет диапазон функции, т. е. насколько далеко от обычной версии без DDD мы сдвигаем график.
На этом теоретическая часть на сегодня завершена. Пришло время посмотреть как вычислить фазовый сдвиг на красивом примере . И знаешь, что? Мы также покажем, как найти период, амплитуду и сдвиг по вертикали. В конце концов, почему бы и нет? Больше математических расчетов = больше удовольствия!
Пример: использование калькулятора фазового сдвига амплитуды периода
Давайте посмотрим , как найти амплитуду, период, фазовый сдвиг и вертикальный сдвиг функции f(x)=0,5⋅sin(2x−3)+4f(x) = 0,5 \cdot\sin(2x – 3) + 4f(x)=0,5⋅sin(2x−3)+4. Во-первых, мы позволим калькулятору фазового сдвига Omni говорить за вас.
В верхней части нашего инструмента нам нужно выбрать функцию, которая появляется в нашей формуле. В нашем случае мы выбираем « синус » под « Тригонометрическая функция в f ». Это вызовет символическое представление такого уравнения фазового сдвига : f(x)=A⋅sin(Bx−C)+Df(x) = A \cdot\sin(Bx – C) + Df(x )=A⋅sin(Bx−C)+D.
Оглядываясь назад на то, что у нас есть, мы вводим:
A=0.5B=2C=3D=4\begin{split} А&=0,5\\ В&=2\\ С&=3\\ Д&=4 \end{split}ABCD=0.5=2=3=4
(Обратите внимание, что еще до того, как мы введем значения, калькулятор фазового сдвига отображает график функции sin(x)\sin(x)sin( x). Это потому, что инструмент понимает без указания определенных значений как отсутствие чисел в соответствующих местах в формуле . Таким образом, он вообще не считывает ввод как A=1A = 1A=1, B=1B = 1B= 1, C=0C = 0C=0 и D=0D = 0D=0, что дает:
1⋅sin(1⋅x−0)+0=sin(x)1 \cdot \sin(1\cdot x – 0) + 0 = \sin(x)1⋅sin(1⋅x−0 )+0=sin(x)
В тот момент, когда мы даем последнее значение, , график функции появляется под вместе с амплитудой, периодом, фазовым сдвигом и вертикальным сдвигом ниже. Также обратите внимание, что при необходимости вы можете перейти в расширенный режим калькулятора, чтобы найти значение функции в любой точке x0x_0x0.
Теперь объясним как найти фазовый сдвиг и все остальные значения самостоятельно .
Для этого достаточно вспомнить четыре раздела выше, чтобы вычислить, что:
- Амплитуда равна A=0,5A = 0,5A=0,5;
- Период равен 2π/B=2π/2=π2\pi / B = 2\pi / 2 = \pi2π/B=2π/2=π;
- Фазовый сдвиг равен C/B=3/2=1,5C / B = 3/2 = 1,5C/B=3/2=1,5; и
- Вертикальное смещение равно D=4D = 4D=4.
В общем, график выглядит так :
Пара пустяков, не так ли? Обязательно поиграйте с калькулятором фазового сдвига, чтобы увидеть как различные коэффициенты влияют на график . А когда вам это наскучит, переходите к другим тригонометрическим калькуляторам Omni и приготовьтесь получить еще больше удовольствия от !
Часто задаваемые вопросы
Как рассчитать фазовый сдвиг?
Чтобы вычислить фазовый сдвиг функции вида A × sin(Bx - C) + D или A × cos(Bx - C) + D , необходимо:
- Определить
В. - Определить
С. - Разделить
С/Б. - Помните , что если результат:
- Положительный , график сдвинут вправо.
- Отрицательный , график смещен влево.
- Наслаждайтесь игрой , обнаружив фазовый сдвиг.
Как найти фазовый сдвиг по графику?
Чтобы найти фазовый сдвиг по графику , нужно:
- Определить , является ли это сдвинутым синусом или косинусом.
- Посмотрите на график справа от вертикальной оси.
- Найдите первый:
- Пик , если коэффициент перед функцией положительный; или
- Корыто , если коэффициент отрицательный.
- Рассчитать расстояние от вертикальной линии до этой точки.
- Если бы функция была синусоидальной, вычесть из этого расстояния
π/2. - Наслаждайтесь игрой , найдя фазовый сдвиг по графику.
Как найти амплитуду, период и фазовый сдвиг?
Нахождение амплитуды, периода и фазового сдвига функции вида A × sin(Bx - C) + D или A × cos(Bx - C) + D выполняется следующим образом:
- Амплитуда равна
A; - Период равно
2π/B; и - Фазовый сдвиг равен
C/B.
Как графически отображать триггерные функции с фазовым сдвигом?
Чтобы построить график триггерных функций с фазовым сдвигом , вам необходимо:
- Определить , что такое триггерная функция.
- Фокус на точку
(0,0)на плоскости. - Если фазовый сдвиг:
- Положительный , двигаться вправо.
- Негатив , двигаться влево.
- Переместите на расстояние, определяемое фазовым сдвигом.
- Точка, в которую вы приземлитесь, является вашей отправной точкой .
- Нарисуйте график несмещенной функции, как если бы точка была
(0,0). - Наслаждайтесь игрой , построив график триггерной функции с фазовым сдвигом.
Сдвиг по горизонтали и фазе — это одно и то же?
Что касается тригонометрических функций, да . Обычно мы оставляем за собой термин “фазовый сдвиг ” для триггерных функций. Другими словами, у нас может быть горизонтальный сдвиг любого графика или функции . Тем не менее, когда это на самом деле тригонометрический сдвиг, мы можем эквивалентно назвать этот сдвиг по горизонтали фазовым сдвигом.