Нормальное и касательное ускорение: Тангенциальное и нормальное ускорение — урок. Физика, 10 класс.

Что характеризует собой касательное ускорение?

Величина ускорения равна:

a = an 2 + aτ 2 .

Направление ускорения определяется углом β между вектором a и

главной нормалью:

β = arctg aτ . an

Касательное ускорение существует лишь при неравномерном движении и характеризует изменение скорости по величине.

При каком движении точки равно нулю касательное ускорение, и при каком – нормальное?

Касательное ускорение равно нулю (aτ = 0), при равномерном движении точки.

Нормальное ускорение равно нулю (an = 0) в случае прямолинейного движения точки.

Как классифицируются движения точки по ускорениям?

Если во всё время движения касательное ускорение равно нулю aτ = v = 0 , то движение называется равномерным.

Если касательное ускорение точки во всё время движения постоянно aτ = const , то движение называется равнопеременным.

Как определяются проекции ускорения на неподвижные оси декартовых координат?

Проекции ускорения на неподвижные оси равны первым производным по времени от проекций скоростей на соответствующие оси или вторым производным от соответствующих координат точки:

22

ax = vx = x , ay = vy = y , az = vz = z .

Как определяется модуль и направление ускорения при координатном способе задания движения точки?

Модуль ускорения определяется через проекции:

a = ax 2 + ay 2 + az 2 .

Направление ускорения a определяется направляющими косинусами:

cos(a, x) = aax , cos(a, y) = aay , cos(a, z) = aaz .

Что характеризует собой нормальное ускорение?

Нормальное ускорение существует лишь при криволинейном движении

ихарактеризует изменение направления скорости.

Вкакие моменты времени нормальное ускорение в криволинейном движении может обратиться в нуль?

Нормальное ускорение в данный момент времени может быть равно ну-

лю an = 0 в том случае, когда в данный момент скорость точки обраща-

ется в нуль (точка меняет направление движения), или, когда движущаяся точка находится в точке перегиба своей траектории ρ = ∞.

В какие моменты времени касательное ускорение в неравномерном движении может обратиться в нуль?

Если в данный момент времени aτ = 0 , то в этот момент величина ско-

рости достигает максимума или минимума.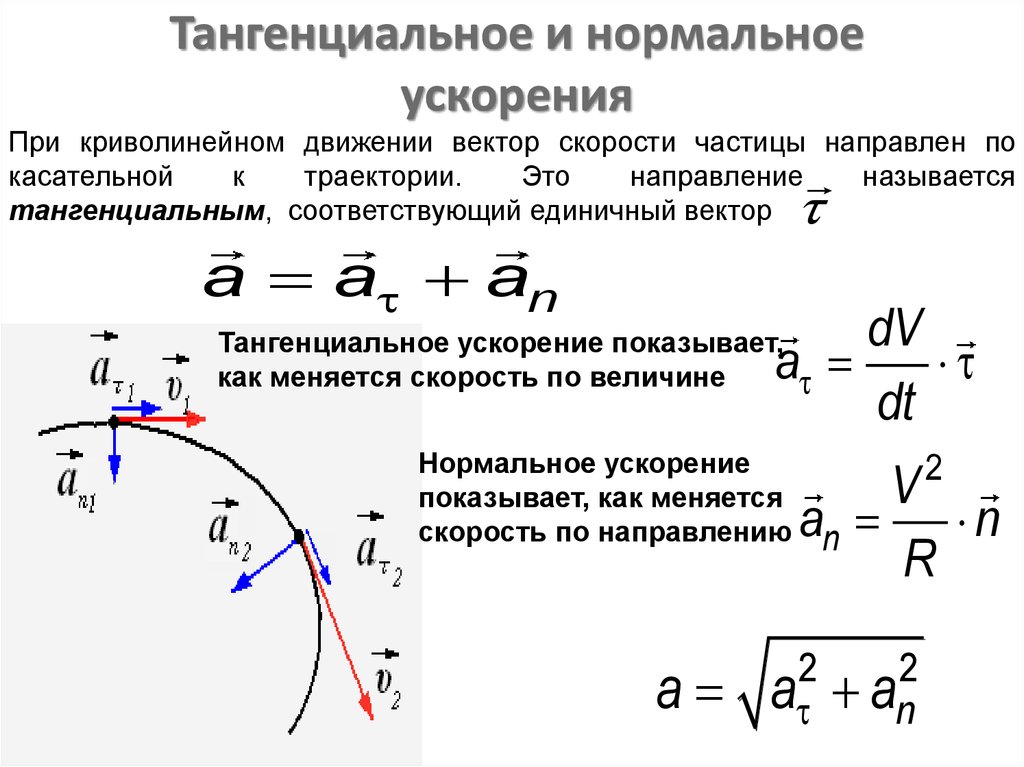

Если aτ = 0 в течение некоторого промежутка времени, то на этом ин-

тервале времени численная величина скорости постоянна и движение является равномерным криволинейным, а ускорение направлено по главной нормали.

23

Чем отличается график пути от графика движения точки?

Графиком движения точки называется график зависимости её дуговой координаты s от времени t .

Путь, пройденный точкой за некоторый промежуток времени, представляет собой сумму абсолютных значений элементарных перемещений за этот промежуток времени, т. е. линия этого графика непрерывно поднимается вверх независимо от направления движения.

Как по графику движения определить алгебраическую величину скорости точки?

Для определения скорости точки в любой момент времени следует провести касательную к графику движения в соответствующей точке, определить угол α наклона этой касательной к оси t и определить скорость

v = tg (α).

Как по графику скорости определить алгебраическую величину касательного ускорения точки?

Для определения касательного ускорения точки следует провести касательную к графику скорости в соответствующей точке и найти угол наклона β этой касательной к оси t . Тангенс угла β определяет алгеб-

раическую величину касательного ускорения: aτ = tg (β ).

В каком случае полное ускорение точки в течение некоторого промежутка времени может быть равно нулю.

Полное ускорение может быть равно нулю a = 0, когда точка движется относительно выбранной системы отсчёта равномерно и прямолинейно.

Назовите основные виды движения твёрдого тела.

24

Различают пять видов движения твёрдого тела: поступательное, вращательное, плоскопараллельное (плоское), сферическое и общий случай движения твёрдого тела.

Какое движение твёрдого тела называется поступательным?

Поступательным движением твёрдого тела называется такое движение, при котором любая прямая, соединяющая две точки тела, движется параллельно самой себе.

Все точки твёрдого тела, движущегося поступательно, описывают тождественные и параллельные между собой траектории и в каждый момент времени имеют геометрически равные скорости и ускорения.

Какое движение твёрдого тела называется вращательным?

Вращательным называется такое движение твёрдого тела, при котором остаются неподвижными все его точки, лежащие на прямой, называемой осью вращения.

При этом все остальные точки движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на этой оси.

Как определяется положение вращающегося тел?

Положение вращающегося тела в любой момент времени определяется углом поворота ϕ , являющегося функцией времени t .

ϕ = f (t) .

Это уравнение представляет собой уравнение вращательного движения тела.

Какая величина называется угловой скоростью?

Величина, характеризующая быстроту изменения угла поворота ϕ с те-

чением времени, называется угловой скоростью тела

25

Касательное и нормальное ускорение

Криволинейное движение – движение мат.точек, траектории которых представляют собой не прямые, а кривые линии. Криволинейное движение – это всегда движение с ускорением , даже если по модулю скорость постоянна. Кр. движ. с постоянным ускорением всегда происходит в той плоскости, в которой наход-ся векторы ускорения и начальные скорости точки.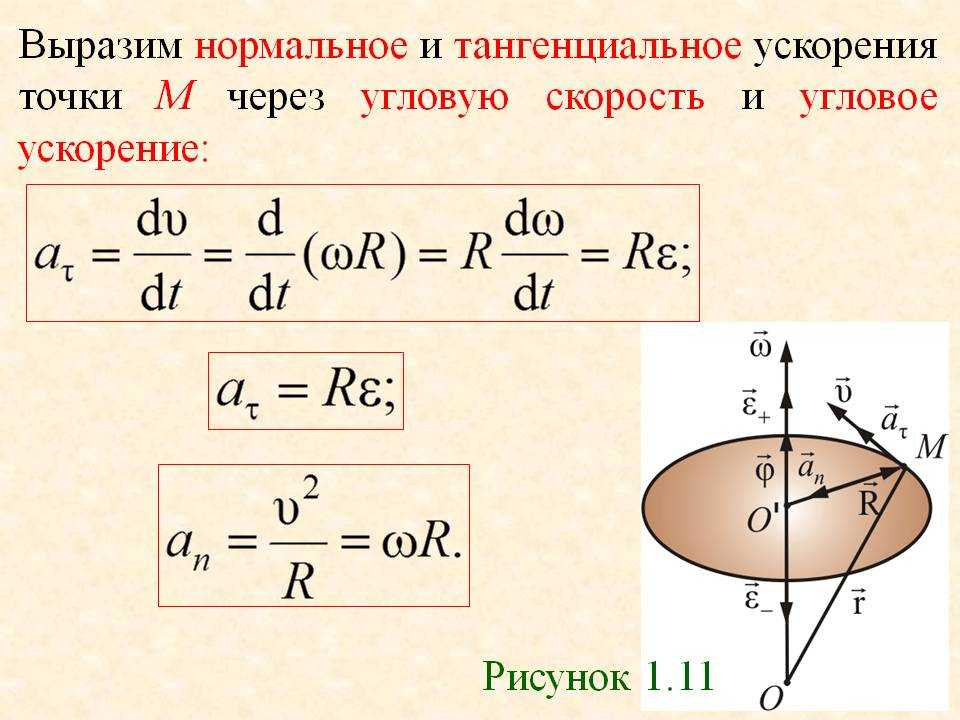 В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции v_xи v_y ее скорости на оси Ox и Oy и координаты x и  y точки в любой момент времени t определяется по формулам

 

частным случаем криволинейного движения – является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением

где r – радиус окружности.

Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости. При криволинейном движении ускорение можно представить как сумму нормальной  и тангенциальной  составляющих: ,

 – нормальное (центростремительное) ускорение, направлено к центру кривизны траектории и характеризует изменение скорости по направлению:

v – мгновенное значение скорости,   r – радиус кривизна траектории в данной точке.

 – тангенциальное (касательное) ускорение, направлено по касательной к траектории и характеризует изменение скорости по модулю. Полное ускорение, с которым движется материальная точка, равно: .

Кроме центростремительного ускорения, важнейшими характе­ристиками равномерного движения по окружности являются период и частота обращения.

Уравнение движения тела, движение с постоянным ускорением Пусть тело движется равномерно вдоль оси О_х системы координат, связанной с телом отсчета. Тогда уравнение движения тела имеет вид х = x₀+v_x·t. Пусть тело движется равноускоренно в положительном направлении О_х выбранной системы координат. Тогда уравнение движения тела имеет вид (1.16): x=x

0+v_0x·t+a_xt²/2.Движение с постоянным ускорением называют равноускоренным. Движение с постоянным ускорением подчиняется закону:  ; .

Равноускоренное движение — движение, при котором вектор ускорения остаётся неизменным по модулю и направлению.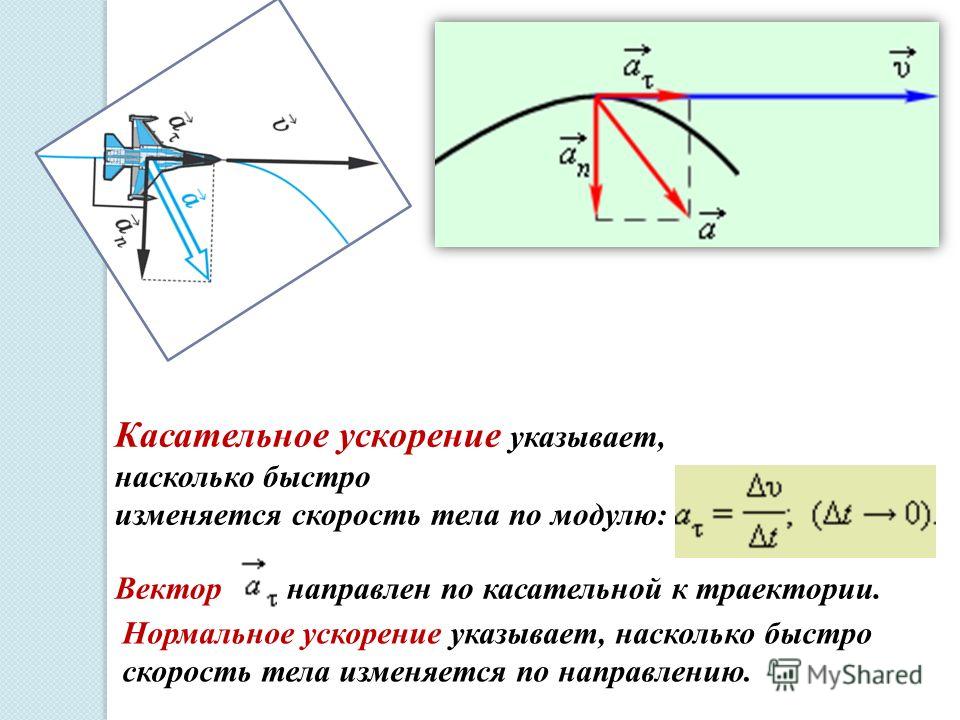

Вращательное движение, угловая скорость и ускорение

Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна. Характеристики вращательного движения: При равномерном вращении (T оборотов в секунду),Частота вращения — число оборотов тела в единицу времени. , Период вращения — время одного полного оборота. Период вращения

T и его частота ν связаны соотношением T = 1 / ν. Линейная скорость точки, находящейся на расстоянии R от оси вращения , Угловая скорость вращения тела . Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси: , где: m_i — масса i-й точки, r_i — расстояние от i-й точки до оси. Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении. Кинетическая энергия вращательного движения где I _z — момент инерции тела относительно оси вращения. ω — угловая скорость

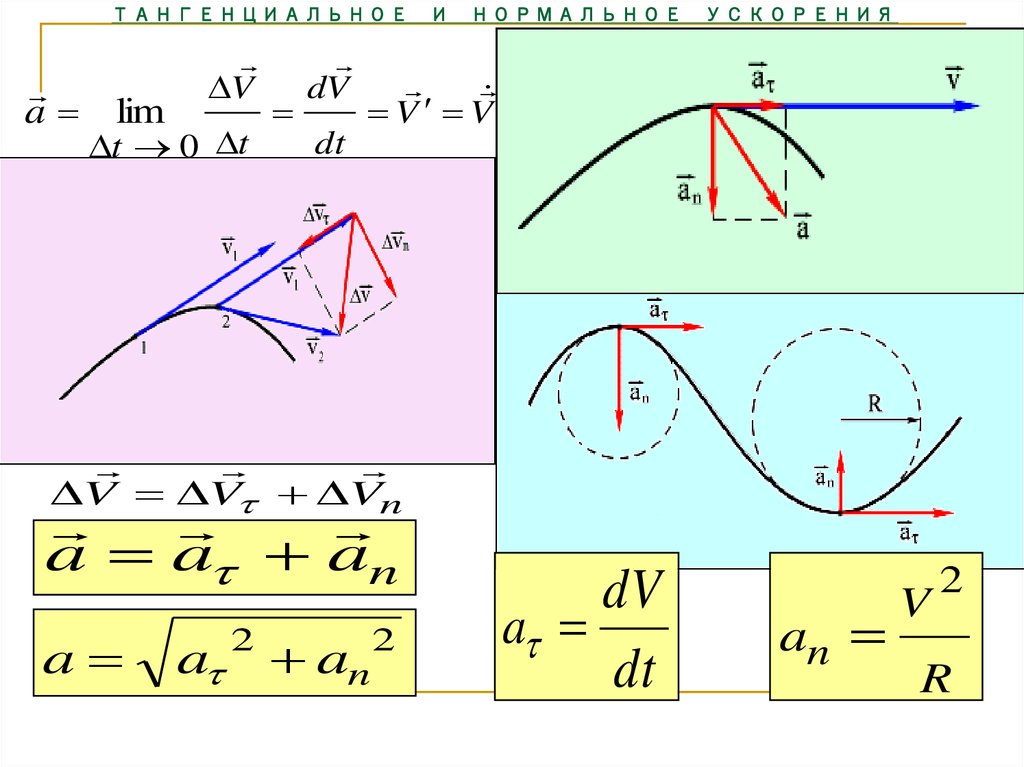
Углова́я ско́рость — векторная величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

w_z=dфи/dt (рад/с). . Угловая скорость представляет собой вектор, направление которого связывают с направлением оси вращения тела Угловое ускорение — производная по времени от вектора угловой скорости ω (соответственно вторая производная по времени от угла поворота)

Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.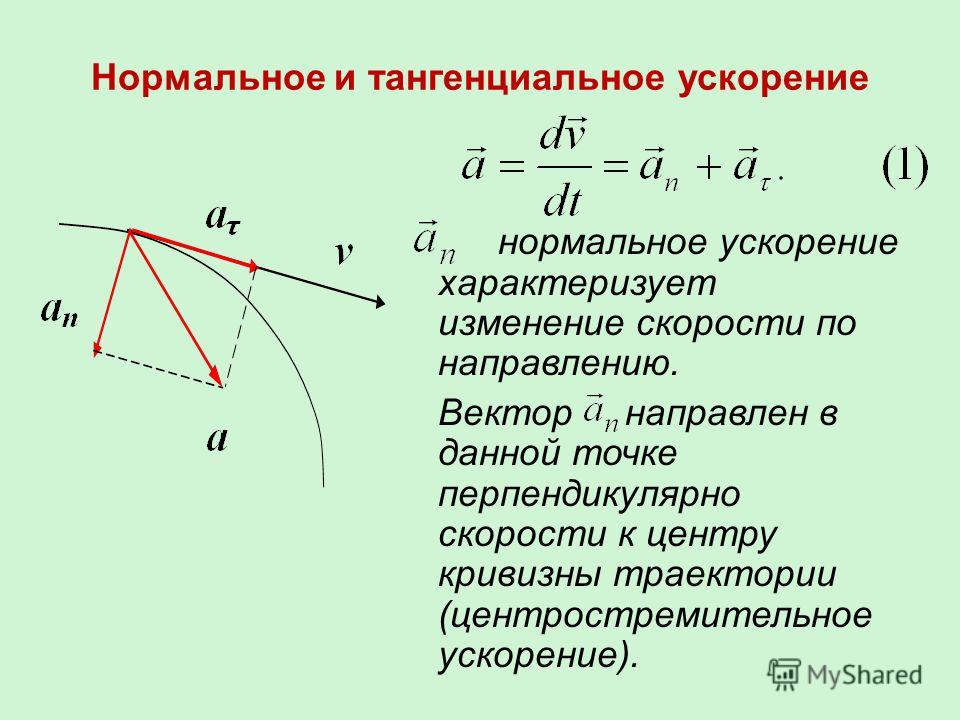

Вектор углового ускорения α направлен вдоль оси вращения (в сторону при ускоренном вращении и противоположно  — при замедленном).При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости ω по времени^[2], то есть a=dw/dt.

Нормальная и тангенциальная составляющие ускорения

спросил 5 лет, 2 месяца назад

Изменено 5 лет, 2 месяца назад

Просмотрено 13 тысяч раз

$\begingroup$

Меня попросили решить на тесте следующую задачу:

92}{р}$. Я не уверен, является ли это нормальной или тангенциальной составляющей ускорения или нет. Если это одно из этих двух, то как вычислить другое? Каковы способы их различения?

• ускорение

$\endgroup$

$\begingroup$

При постоянной скорости имеется только нормальное ускорение (от водителя к центру окружности). 2/r. Тангенциальная составляющая равна нулю.

$\endgroup$

$\begingroup$

Тангенциальное ускорение — это ускорение, параллельное круговой траектории. Поскольку скорость (эта скорость также в тангенциальном направлении) автомобилиста постоянна, тангенциальное ускорение отсутствует.

Нормальное ускорение — это ускорение перпендикулярно траектории; здесь центростремительное ускорение.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Доказательство – Тангенциальная и нормальная составляющие ускорения

Нагрузка.

Бесплатные отработанные решения

Видео исчисления

Брюс освещает каждое доказательство

Загрузка данных

Загрузка наборов данных в форме электронной таблицы

Вращающиеся графики

Просмотр и вращение трехмерных графиков

Математические графики

Печать собственных рабочих листов

Предыдущий Следующий

Глава Глава 1 Глава 2 Глава 3 Глава 4 Глава 5 Глава 6 Глава 7 Глава 8 Глава 9 Глава 10 Глава 11 Глава 12 Глава 13 Глава 14 Глава 15 Глава 160005

VideoProof – Acceleration VectorProof – Касательные и нормальные компоненты ускоренияКасательные и нормальные векторы – Обзор Касательные векторы и нормальные векторы – Скорость и ускорение – ОбзорНахождение тангенциальной составляющей ускорения – AНахождение тангенциальной составляющей ускорения – BНахождение нормальной составляющей ускорения – AНахождение нормальной составляющей ускорения – В