. Односторонние пределы: Асимптоты графика функции.
Пример 1. Найти односторонние пределы функции в точке :
1) , ; 2)
Решение. 1. Вычислим пределы функции в точке слева и справа, т.е.
и .
При .
Значит .
При .
Значит .
2. При функция задана формулой .
Поэтому
,
При функция задана формулой т.е.
Значит .
Пример 2. С помощью односторонних предметов показать, что функция не имеет предела в точке.
Решение. При имеем и функция принимает вид
.
Поэтому .
При имеем и функцию .
Поэтому .
Получим, что оба
односторонних предела функции в точке
существуют,
однако они различны, поэтому не существует.
Пример 3. Найти асимптоты графика функции .
Решение. Вертикальных асимптот данная функция не имеет, потому что она определена для любых . Для того чтобы найти горизонтальные асимптоты надо рассмотреть пределы функции на бесконечности:
.
Получили, что – горизонтальная асимптота (ось ).
Будем искать наклонные асимптоты в виде .
Согласно формулам (25), (26) вычисляем:
.
Так как , значит наклонных асимптот у графика нет.
Пример 4. Найти асимптоты графика функции
.
Решение.
и
Вычисляем: ;
Поэтому прямая является вертикальной асимптотой графика функции.
Ищем горизонтальную асимптоту. Поскольку
,
то горизонтальных
асимптот нет.
Выясним наличие наклонных асимптот. По формулам (25) и (26) находим
.
Получим, что – наклонная асимптоты.
. Непрерывность функции. Классификация
точек разрыва.
Пример 1. Пользуясь определением непрерывности доказать, что функция непрерывна всюду на .
Решение. Докажем непрерывность этой функции в произвольной точке .
Пусть – приращение аргумента в точке . Соответствующее приращение функции имеет вид:
Вычислим предел приращения функции, когда приращение аргумента стремится к нулю:
.
Получили, что , что и означает непрерывность функции на всей числовой прямой, т.к. – произвольная действительная точка.
Пример 2. Найти точки разрыва функции и исследовать их характер. Построить схематический чертеж графиков этих функций в окрестности точек разрыва
Решение.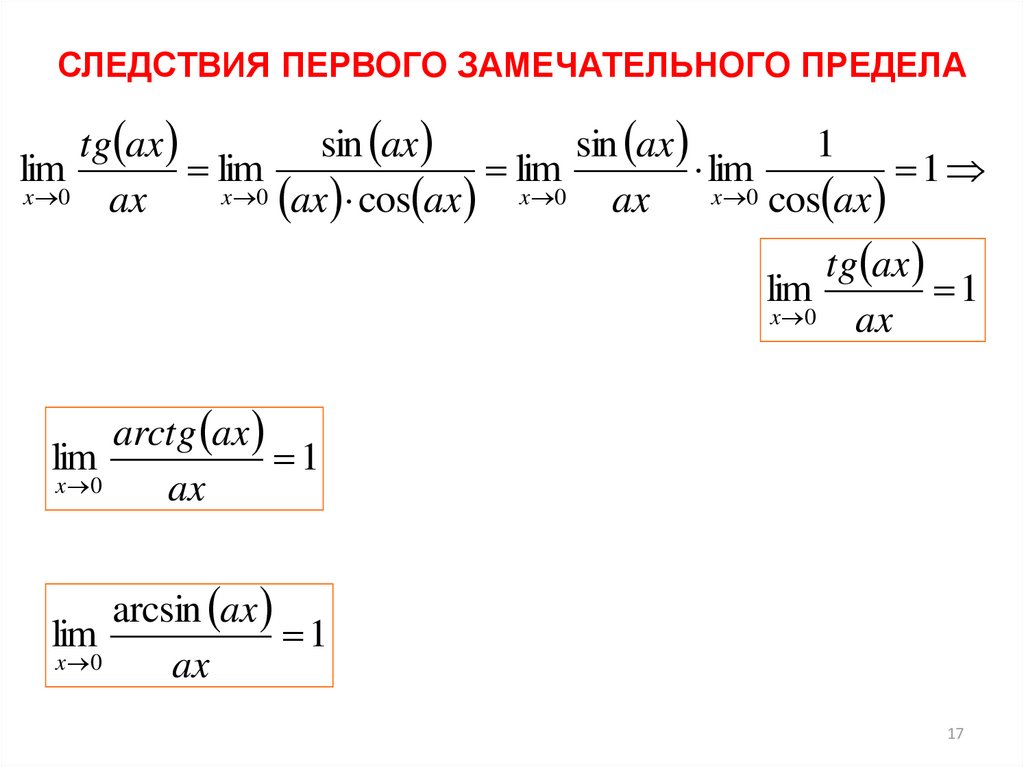
Функция определена на всей числовой прямой,
кроме
. Данная
функция является элементарной,
следовательно она является непрерывной
в каждой точке своей области определения.
Поэтому единственной точкой разрыва
является точка
,
в которой функция не определена. Для
определения типа разрыва в этой точке
вычислим односторонние пределы функции:
; .
Приходим к выводу, что – точка разрыва II рода (бесконечного скачка).
График функции в окрестности точки представлен на
2. .Точкой разрыва данной функции является точка .
Вычислим односторонние пределы заданной функции в точке .
Получили, что оба односторонних предела существуют (и конечны), но не равны между собой. Поэтому – точка разрыва I рода (скачка) – рис.2. Заметим, что скачок равен:
.
Пример 3. Дана функция
Исследовать ее на
непрерывность и разрыв.
Построить
график.
Решение. На промежутках заданы аналитические выражения элементарных функций, которые определены и, следовательно, непрерывны на каждом промежутке. Поэтому точками «подозрительными на разрыве», являются точки и .
Вычислим односторонние пределы функции в точке .
Так как при , то
.
Так как при , то
.
Вычислим значение функции в точке :
.
Получим, что выполнены условия непрерывности функции в точке . Поэтому в точке разрыва функции нет.
Вычислим односторонние пределы функции в точке .
Так как при , то
.
Так как при , то
.
Получили, что – точка разрыва I рода (скачка). Значит, функция непрерывна всюду на числовой прямой кроме точки. в которой она имеет скачок, равный 1.
Ошибка
Перейти к основному содержанию
Вся размещенная на ресурсе информационная продукция предназначена для детей, достигших возраста шестнадцати лет (16+)
Извините, не удалось найти запрашиваемый Вами файл
Подробнее об этой ошибке
Перейти на.
..
Перейти на…Новостной форумКомплексные числа (с приложениями к задачам электротехники)Лекционный материал по теме «Комплексные числа»Разбор типовых задач задач по теме «Комплексные числа»Примеры решения задач по теме «Комплексные числа»КОМПЛЕКСНЫЕ ЧИСЛАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийТеория функций комплексного переменного. Операционное исчислениеПрезентация по теме «Комплексные числа»Дополнительный материал к темеОсновы линейной алгебры с приложениями в других разделах математикиЛекционный материал по теме «Матрицы. Определители»Лекционный материал по теме «Системы линейных алгебраических уравнений (СЛАУ). Применение СЛАУ в экономике»Лекционный материал по теме «Линейные операторы»Примеры решения по теме «Системы линейных алгебраических уравнений»ЛИНЕЙНАЯ АЛГЕБРАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийЛинейная алгебра для экономистовМатрицы. ОпределителиВекторная алгебра.Аналитическая геометрияЛекционный материал по теме «Векторная алгебра.
Интегрирование рациональных дробей (неопределенный интеграл)Практическое занятие 5. Определенный интегралПримеры решения задач по теме «Неопределенный интеграл»Примеры решения задач по теме «Определенный интеграл»ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙТест «Таблица основных неопределенных интегралов»Тест «Интегрирование функций одной переменной»1. Неопределенный интеграл. Основы интегрирования2. Интегрирование иррациональных выражений 3. Интегрирование тригонометрических выражений 4. Определенный интегралДифференциальное исчисление функций нескольких переменныхЛекционный материал по теме «Функции нескольких переменных»Примеры решения задач по теме «Функции нескольких переменных»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХТест «Дифференциальное исчисление функций нескольких переменных»1. Функции нескольких переменныхПрименение функций нескольких переменных в экономикеОбыкновенные дифференциальные уравненияОбыкновенные дифференциальные уравнения и их приложенияДифференциальные уравнения первого порядкаДифференциальные уравнения высших порядковСистемы дифференциальных уравнений и устойчивость их решенийЛекционный материал по теме «Дифференциальные уравнения 1-го порядка»Лекционный материал по теме «Дифференциальные уравнения высших порядков»Примеры решения задач по теме «Дифференциальные уравнения»ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯТест «Обыкновенные дифференциальные уравнения»1.
Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»Примеры решения задач по теме «Ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Теория вероятностей (случайные события)Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий.
Основные теоремы о вероятности»Лекционный материал по теме «Дискретные случайные величины»Лекционный материал по теме «Непрерывные случайные величины»Лекционный материал по теме «Числовые характеристики случайных величин»Лекционный материал по теме «Моменты и другие характеристики распределений»Лекционный материал по теме «Нормальное распределение»Практическое занятие 1. КомбинаторикаПрактическое занятие 2. Действия над событиями. Вероятность событияПрактическое занятие 3. Теоремы умножения и сложения вероятностей событийПрактическое занятие 4. Формула полной вероятности Практическое занятие 5. Схема Бернулли. Локальная и интегральная теоремы ЛапласаПрактическое занятие 6. Дискретные случайные величины. Числовые характеристикиПрактическое занятие 7. Непрерывные случайные величины. Классические законы распределения НСВПримеры решения задач по теме «Комбинаторика»Примеры решения задач по теме «Классическое определение вероятности»Примеры решения задач по теме «Теоремы сложения и умножения»Примеры решения задач по теме «Формула полной вероятности.
Формулы Байеса»Примеры решения задач по теме «Схема независимых испытаний Бернулли»Примеры решения задач по теме «Дискретные случайные величины»Примеры решения задач по теме «Основные числовые характеристики дискретных случайных величин»Примеры решения задач по теме “Непрерывные случайные величины”Примеры решения задач по теме “Основные числовые характеристики непрерывных случайных величин”Примеры решения задач по теме “Классические законы распределения дискретных случайных величин”Примеры решения задач по теме “Классические законы распределения непрерывных случайных величин”Таблица значений функции ЛапласаТЕОРИЯ ВЕРОЯТНОСТЕЙТест по разделу “Случайные события”Тест по теме “Числовые характеристики случайных величин”Тест по теме “Дискретные случайные величины”Тест по теме “Непрерывные случайные величины”Основные подходы к определению вероятностиАлгебра событий. Основные теоремы о вероятностиТеория вероятностей (Лыткина Е.М.,Чихачев А.С., 2013)Математическая статистикаОсновы математической статистикиМатематическая статистика: практикумПримеры решения задач по математической статистикиМАТЕМАТИЧЕСКАЯ СТАТИСТИКАТест по разделу “Математическая статистика”.
Тема “Статистическое распределение. Точечные и интервальные оценки параметров распределения”Тест по разделу “Математическая статистика”. Тема “Статистические гипотезы. Корреляционный и регрессионный анализ”Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Лекционный материал по теме «Системы массового обслуживания»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу “Случайные события”*Тест по теме “Дискретные случайные величины”*Тест по теме “Непрерывные случайные величины”*Тест по теме “Числовые характеристики случайных величин”*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа.
Дифференциальное исчисление функций нескольких переменныхКонтрольная работа. Неопределенный интеграл (методы интегрирования)Контрольная работа. Неопределенный интеграл (интегрирование рациональных дробей)Контрольная работа. Определенный интегралКонтрольная работа. Обыкновенные дифференциальные уравненияКонтрольная работа 1. Теория вероятностей (случайные события)Контрольная работа 2. Теория вероятностей (характеристики дискретной случайной величины)Контрольная работа 3. Теория вероятностей (характеристики непрерывной случайной величины)Контрольная работа 4. Теория вероятностей (классические законы распределения дискретной случайной величины)Контрольная работа 5. Теория вероятностей (классические законы распределения непрерывной случайной величины)Экзамен Математика (2 семестр). СОД.1,2,3-19-1 (И,З)ЭКЗАМЕН. Математика (3 семестр)_СОД.1,2,3-19 (з)2.4: Односторонние пределы — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 8221
Мы мягко ввели понятие предела, аппроксимировав их значения графически и численно.
Далее последовало строгое определение предела вместе с, по общему признанию, утомительным методом их оценки. В предыдущем разделе мы дали нам инструменты (которые мы называем теоремами), которые позволяют нам с большей легкостью вычислять пределы. Главными среди результатов были факты, что полиномы и рациональные, тригонометрические, экспоненциальные и логарифмические функции (и их суммы, произведения и т. д.) ведут себя «хорошо». В этом разделе мы строго определяем, что мы подразумеваем под «хорошо».
В разделе 1.1 мы исследовали три способа, при которых пределы функций не существовали:
- Функция приближалась к разным значениям слева и справа,
- Функция неограниченно растет, и
- Функция колеблется.
В этом разделе мы подробно изучим концепции, лежащие в основе #1, введя односторонний предел . Мы начнем с формальных определений, которые очень похожи на определение предела, данное в разделе 1.2, но обозначения немного отличаются, и “\(x\neq c\)” заменяется либо “\(x
” 9-} f(x) = L,\]
означает, что для любого \(\epsilon > 0\) существует \(\delta > 0\) такое, что для всех \(x Правый предел Пусть \(I\) — открытый интервал, содержащий \(c\), и пусть \(f\) — функция, определенная на \(I\), за исключением, возможно, точки \(c\ ). Предел \(f(x)\), как \(x\) приближается к \(c\) из справа, равен 9-\) означает, что мы смотрим на значения \(x\) слева от \(c\). Обозначение не имеет ничего общего с положительными или отрицательными значениями \(x\) или \(c\). Аналогичное утверждение верно для оценки правых пределов; там мы рассматриваем только значения \(x\) справа от \(c\), т. е. \(x>c\). Мы можем использовать теоремы из предыдущих разделов, чтобы помочь нам оценить эти пределы; мы просто ограничиваем наш взгляд одной стороной \(c\). Мы тренируемся оценивать левые и правые пределы на ряде примеров. Фраза «если и только если» означает, что два утверждения эквивалентны : они либо оба истинны, либо оба ложны. Если предел равен \(L\), то левый и правый пределы оба равны \ (L\).Если предел не равен \(L\), то хотя бы один из левого и правого пределов не равен \(L\) (может даже не существовать) Один Что следует учитывать в примерах 17-20, так это то, что значение функции может быть/не быть равным значению (значениям) ее левого/правого пределов, даже если эти пределы совпадают.-} f(x)=1.\) Глядя на график, становится ясно, что левый и правый пределы \(f\), когда \(х\) приближается к 1, равно 0. Таким образом, также ясно, что предел равен 0; т. е. \(\lim\limits_{x\to 1} f(x) = 0\). Также ясно сказано, что \(f(1) = 1\). Пример 20: Оценка пределов кусочно определенной функции 9+} f(x) =\lim\limits_{x\to 1} f(x) =f(1) = 1.\] В примерах 17-20 нас попросили найти оба \( \lim\limits_ {х\к 1}f(x)\) и \(f(1)\). Рассмотрим следующую таблицу: \[\begin{array}{ccc} & \lim\limits_{x\to 1}f(x) & f(1) \\ \hline \text{Пример 17} & \text {не существует} & 1 \\ \text{Пример 18} & 1 & \text{не определено} \\ \text{Пример 19} & 0 & 1 \\ \text{Пример 20} & 1 & 1 \\ \end{array}\] Только в примере 20 и функция, и предел существуют и согласуются друг с другом. Это кажется «хорошим», на самом деле это кажется «нормальным». 2.4: One-Sided Limits распространяется под лицензией CC BY-NC-SA и был создан, изменен и/или курирован LibreTexts. 9 Диагностические тесты
308 практических тестов
Вопрос дня
Карточки
Learn by Concept ← Предыдущая 1 2 3 4 5 6 7 8 9 … 41 42 Следующая → Исчисление 2 Помощь »
Ограничения »
Нахождение пределов и односторонние пределы Какой график является возможным эскизом функции , обладающей следующими характеристиками: Возможные ответы: Такого графика не существует. Правильный ответ: Объяснение: Поскольку возможна вертикальная асимптота в точке . При приближении слева график должен стремиться к . При приближении справа график стремится к . Единственным графом, который делает это, является . Сообщить об ошибке На приведенном выше графике показана схема функции . Находить . Возможные ответы: Не существует Правильный ответ: 300239 00224
+}f(x) = L.\]
9+} f(x)\)
\(\text{РИСУНОК 1.23}\): График \(f\) в примере 19.
Это на самом деле важная ситуация, которую мы исследуем в следующем разделе, озаглавленном «Непрерывность». Короче говоря, непрерывная функция — это функция, в которой, когда функция приближается к значению как \(x\rightarrow c\) (т. е. когда \(\lim\limits_{x\to c} f(x) = L\)), она на самом деле достигает этого значения в \(c\). Такие функции ведут себя хорошо, поскольку они очень предсказуемы. Поиск пределов и односторонних пределов
Все ресурсы исчисления 2
Нам нужно посмотреть на поведение функции, когда она стремится слева. Поэтому ответ такой.
Сообщить об ошибке
График выше является эскизом . Находить .
Возможные ответы:
Не существует
Правильный ответ:
90 Объяснение: Предел не существует, так как односторонние пределы не равны; , тогда как .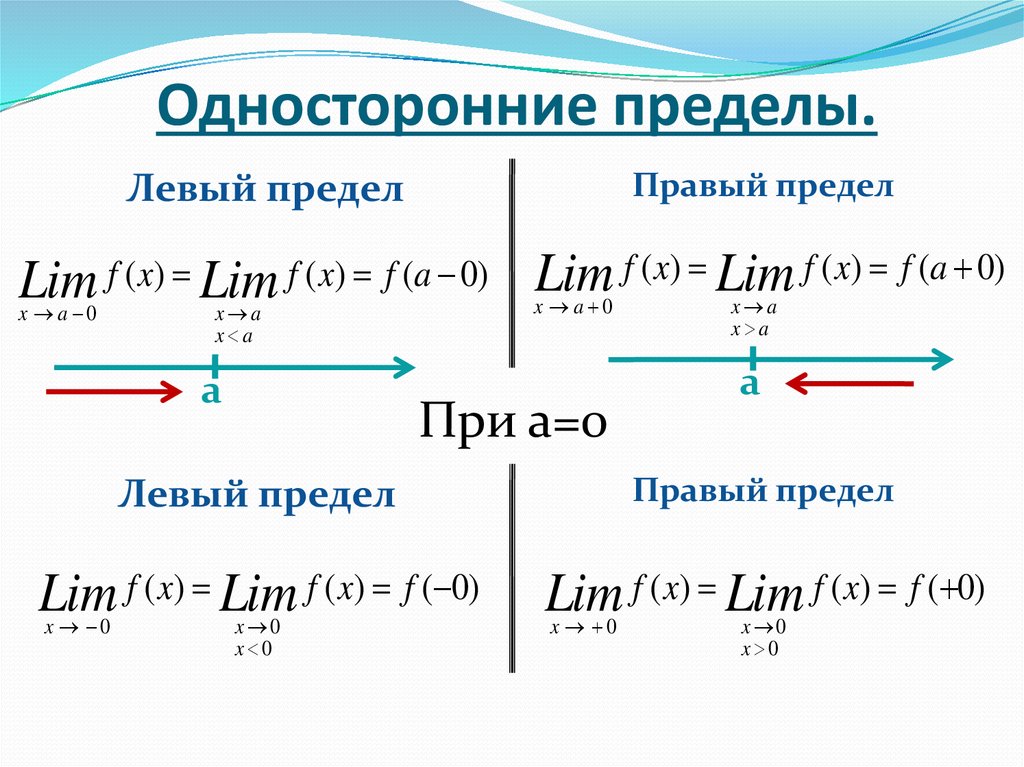
Сообщить об ошибке
Определите значение .
Возможные ответы:
Правильный ответ:
Объяснение:
Выражение указывает, что все точки в домене равны 5, поскольку абсолютное значение отрицает отрицательные значения.
Поиск предела по мере приближения графика к левой стороне графика. Поскольку абсолютное значение отрицательного числа пять равно пяти, график приближается к пяти слева.
Правильный ответ .
Сообщить об ошибке
Оценить следующий предел.
Возможные ответы:
Предела не существует Объяснение:
Этот предел можно решить с помощью простой обработки выражения внутри предела:
Сообщить об ошибке
Вычислить предел:
Возможные ответы:
Правильный ответ:
Объяснение:
Рассмотрим домен функции.
Поскольку это уравнение является многочленом, x не ограничен никаким значением. Таким образом, способ оценки этого предела состоял бы в том, чтобы просто включить значение, к которому x приближается, в предельное уравнение.
Сообщить об ошибке
Оценить лимит:
Возможные ответы:
Правильный ответ:
Объяснение:
Рассмотрим домен функции. Поскольку это уравнение является многочленом, x не ограничен никаким значением. Таким образом, способ оценки этого предела состоял бы в том, чтобы просто включить значение, к которому x приближается, в предельное уравнение.
Сообщить об ошибке
Оценить лимит:
Возможные ответы:
Правильный ответ:
Пояснение:
Предельной ситуацией в этом уравнении будет знаменатель.
Подставьте значение, к которому x приближается, в знаменатель, чтобы увидеть, будет ли знаменатель равен 0. В этом вопросе знаменатель не будет равен нулю, когда x=-2; поэтому мы продолжаем вставлять значение x во все уравнение.
Сообщить об ошибке
Оценить лимит:
Возможные ответы:
Правильный ответ:
Пояснение:
Предельной ситуацией в этом уравнении будет знаменатель. Подставьте значение, к которому x приближается, в знаменатель, чтобы увидеть, будет ли знаменатель равен 0. В этом вопросе знаменатель не будет равен нулю, когда x=0; поэтому мы продолжаем вставлять значение x во все уравнение.
Сообщить об ошибке
Оценить лимит:
Возможные ответы:
Правильный ответ:
Пояснение:
Предельной ситуацией в этом уравнении будет знаменатель.