Метод Жордана-Гаусса – онлайн калькулятор с подробным решением
Данное решение сделано калькулятором, представленным на сайте.
Пожалуйста, обратите внимание, что коэффициенты расположенные на “красных” позициях исчезают.
| 3 | x1 | + | 2 | x2 | + | x3 | + | x4 | = | – 2 | ||||
| x1 | – | x2 | + | 4 | x3 | – | x4 | = | – 1 | |||||
| – | 2 | x1 | – | 2 | x2 | – | 3 | x3 | + | x4 | = | 9 | ||
| x1 | + | 5 | x2 | – | x3 | + | 2 | x4 | = | 4 |
Уравнения 1 и 2 поменяем местами.
| x1 | – | x2 | + | 4 | x3 | – | x4 | = | – 1 | |||||
| 3 | x1 | + | 2 | x2 | + | x3 | + | x4 | = | – 2 | ||||
| – | 2 | x1 | – | 2 | x2 | – | 3 | x3 | + | x4 | = | 9 | ||
| x1 | + | 5 | x2 | – | x3 | + | 2 | x4 | = | 4 |
( 3 x1 + x1 * ( -3) )
+ ( 2 x2 + ( – x2) * ( -3) )
+ ( x3 + 4 x3 * ( -3) )
+ ( x4 + ( – x4) * ( -3) )
= -2 + ( -1) * ( -3)
“Красный” коэффициент равен нулю.
| x1 | – | x2 | + | 4 | x3 | – | x4 | = | – 1 | |||||
| 5 | x2 | – | 11 | x3 | + | 4 | x4 | = | 1 | |||||
| – | 2 | x1 | – | 2 | x2 | – | 3 | x3 | + | x4 | = | 9 | ||
| x1 | + | 5 | x2 | – | x3 | + | 2 | x4 | = | 4 |
( -2 x1 + x1 * 2 )
+ ( -2 x2 + ( – x2) * 2 )
+ ( -3 x3 + 4 x3 * 2 )
+ ( x4 + ( – x4) * 2 )
= 9 + ( -1) * 2
“Красный” коэффициент равен нулю.
| x1 | – | x2 | + | 4 | x3 | – | x4 | = | – 1 | |||||
| 5 | x2 | – | 11 | x3 | + | 4 | x4 | = | 1 | |||||
| – | 4 | x2 | + | 5 | x3 | – | x4 | = | 7 | |||||
| x1 | + | 5 | x2 | – | x3 | + | 2 | x4 | = | 4 |
( x1 + x1 * ( -1) )
+ ( 5 x2 + ( – x
+ ( – x3 + 4 x3 * ( -1) )
+ ( 2 x4 + ( – x4) * ( -1) )
= 4 + ( -1) * ( -1)
“Красный” коэффициент равен нулю.
| x1 | – | x2 | + | 4 | x3 | – | x4 | = | – 1 | |||||
| 5 | x2 | – | 11 | x3 | + | 4 | x4 | = | 1 | |||||
| – | 4 | x | + | 5 | x3 | – | x4 | = | 7 | |||||
| 6 | x2 | – | 5 | x3 | + | 3 | x4 | = | 5 |
( 5 x2 + ( -4 x2) )
+ ( -11 x3 + 5 x3)
+ ( 4 x4 + ( – x4) )
= 1 + 7
Данное преобразование позволит нам считать без дробей какое то время.
| x1 | – | x2 | + | 4 | x3 | – | x4 | = | – 1 | |||||
| x2 | – | 6 | x3 | + | 3 | x4 | = | 8 | ||||||
| – | 4 | x2 | + | 5 | x3 | – | x4 | = | 7 | |||||
| 6 | x2 | – | 5 | x3 | + | 3 | x4 | = | 5 |
( -4 x2 + x2 * 4 )
+ ( 5 x3 + ( -6 x3) * 4 )
+ ( – x4 + 3 x4 * 4 )
= 7 + 8 * 4
“Красный” коэффициент равен нулю.
| x1 | – | x2 | + | 4 | x3 | – | x4 | = | – 1 | |||||
| x2 | – | 6 | x3 | + | 3 | x4 | = | 8 | ||||||
| – | 19 | x3 | + | 11 | x4 | = | 39 | |||||||
| 6 | x2 | – | 5 | x3 | + | 3 | x4 | = | 5 |
( 6 x2 + x2 * ( -6) )
+ ( -5 x3 + ( -6 x3) * ( -6) )
+ ( 3 x4 + 3 x4
= 5 + 8 * ( -6)
“Красный” коэффициент равен нулю.
| x1 | – | x2 | + | 4 | x3 | – | x4 | = | – 1 | |||||
| x2 | – | 6 | x3 | + | 3 | x4 | = | 8 | ||||||
| – | 19 | x3 | + | 11 | x4 | = | 39 | |||||||
| 31 | x3 | – | 15 | x4 | = | – 43 |
( 31 x3 + ( -19 x3) * 31/19 )
+ ( -15 x4 + 11 x4 * 31/19 )
= -43 + 39 * 31/19
“Красный” коэффициент равен нулю.
| x1 | – | x2 | + | 4 | x3 | – | x4 | = | – 1 | |||||
| x2 | – | 6 | x3 | + | 3 | x4 | = | 8 | ||||||
| – | 19 | x3 | + | 11 | x4 | = | 39 | |||||||
| 56/19 | x4 | = | 392/19 |
Уравнеие 4 разделим на 56/19.
| x1 | – | x2 | + | 4 | x3 | – | x4 | = | – 1 | |||||
| x2 | – | 6 | x3 | + | 3 | x4 | = | 8 | ||||||
| – | 19 | x3 | + | 11 | x4 | = | 39 | |||||||
| x4 | = | 7 |
– 19 x3
+ ( 11 x4 + x4 * ( -11) )
= 39 + 7 * ( -11)
“Красный” коэффициент равен нулю.
| x1 | – | x2 | + | 4 | x3 | – | x4 | = | – 1 | |||||
| x2 | – | 6 | x3 | + | 3 | x4 | = | 8 | ||||||
| – | 19 | x3 | = | – 38 | ||||||||||
| x4 | = | 7 |
 подробнее
подробнееx2
– 6 x3
+ ( 3 x4 + x4 * ( -3) )
= 8 + 7 * ( -3)
“Красный” коэффициент равен нулю.
| x1 | – | x2 | + | 4 | x3 | – | x4 | = | – 1 | |||||
| x2 | – | 6 | x3 | = | – 13 | |||||||||
| – | 19 | x3 | = | – 38 | ||||||||||
| x4 | = | 7 |
x1
+ – x2
+ 4 x3
+ ( – x4 + x4)
= -1 + 7
“Красный” коэффициент равен нулю.
| x1 | – | x2 | + | 4 | x3 | = | 6 | |||||||
| x2 | – | 6 | x3 | = | – 13 | |||||||||
| – | 19 | x3 | = | – 38 | ||||||||||
| x4 | = | 7 |
Уравнеие 3 разделим на -19.
| x1 | – | x2 | + | 4 | x3 | = | 6 | |||||||
| x2 | – | 6 | x3 | = | – 13 | |||||||||
| x3 | = | 2 | ||||||||||||
| x4 | = | 7 |
x2
+ ( -6 x3 + x3 * 6 )
= -13 + 2 * 6
“Красный” коэффициент равен нулю.
| x1 | – | x2 | + | 4 | x3 | = | 6 | |||||||
| x2 | = | – 1 | ||||||||||||
| x3 | = | 2 | ||||||||||||
| x4 | = | 7 |
 подробнее
подробнееx1
+ – x2
+ ( 4 x3 + x3 * ( -4) )
= 6 + 2 * ( -4)
“Красный” коэффициент равен нулю.
| x1 | – | x2 | = | – 2 | ||||||||||
| x2 | = | – 1 | ||||||||||||
| x3 | = | 2 | ||||||||||||
| x4 | = | 7 |
x1
+ ( – x2 + x2)
= -2 + ( -1)
“Красный” коэффициент равен нулю.
| x1 | = | – 3 | ||||||||||||
| x2 | = | – 1 | ||||||||||||
| x3 | = | 2 | ||||||||||||
| x4 | = | 7 |
Ответ:
x1 = – 3
x2 = – 1
x3 = 2
x4 = 7
Метод Жордана-Гаусса – онлайн калькулятор
Данное решение сделано калькулятором, представленным на сайте.

Пожалуйста, обратите внимание, что коэффициенты расположенные на “красных” позициях исчезают.
| – | 4 | x1 | + | 5 | x2 | – | 3 | x3 | + | 3 | x4 | = | 20 | |
| 4 | x1 | + | 2 | x2 | + | 3 | x3 | + | 4 | x4 | = | 10 | ||
| 5 | x1 | + | 4 | x2 | + | 4 | x3 | + | 3 | x4 | = | 20 |
( -4 x1 + 5 x1)
+ ( 5 x2 + 4 x2)
+ ( -3 x3 + 4 x3)
+ ( 3 x4 + 3 x4)
= 20 + 20
Данное преобразование позволит нам считать без дробей какое то время.
| x1 | + | 9 | x2 | + | x3 | + | 6 | x4 | = | 40 | ||||
| 4 | x1 | + | 2 | x2 | + | 3 | x3 | + | 4 | x4 | = | 10 | ||
| 5 | x1 | + | 4 | x2 | + | 4 | x3 | + | 3 | x4 | = | 20 |
( 4 x1 + x1 * ( -4) )
+ ( 2 x2 + 9 x2 * ( -4) )
+ ( 3 x3 + x3 * ( -4) )
+ ( 4 x4 + 6 x4 * ( -4) )
= 10 + 40 * ( -4)
“Красный” коэффициент равен нулю.
| x1 | + | 9 | x2 | + | x3 | + | 6 | x4 | = | 40 | ||||
| – | 34 | x2 | – | x3 | – | 20 | x4 | = | – 150 | |||||
| 5 | x1 | + | 4 | x2 | + | 4 | x3 | + | 3 | x4 | = | 20 |
( 5 x1 + x1 * ( -5) )
+ ( 4 x2 + 9 x2 * ( -5) )
+ ( 4 x3 + x3 * ( -5) )
+ ( 3 x4 + 6 x4 * ( -5) )
= 20 + 40 * ( -5)
“Красный” коэффициент равен нулю.
| x1 | + | 9 | x2 | + | x3 | + | 6 | x4 | = | 40 | ||||
| – | 34 | x2 | – | x3 | – | 20 | x4 | = | – 150 | |||||
| – | 41 | x2 | – | x3 | – | 27 | x4 | = | – 180 |
( -41 x2 + ( -34 x2) * ( -41/34) )
+ ( – x3 + ( – x3) * ( -41/34) )
+ ( -27 x4 + ( -20 x4) * ( -41/34) )
= -180 + ( -150) * ( -41/34)
“Красный” коэффициент равен нулю.
| x1 | + | 9 | x2 | + | x3 | + | 6 | x4 | = | 40 | ||||
| – | 34 | x2 | – | x3 | – | 20 | x4 | = | – 150 | |||||
| 7/34 | x3 | – | 49/17 | x4 | = | 15/17 |
Уравнеие 3 разделим на 7/34.
| x1 | + | 9 | x2 | + | x3 | + | 6 | x4 | = | 40 | ||||
| – | 34 | x2 | – | x3 | – | 20 | x4 | = | – 150 | |||||
| x3 | – | 14 | x4 | = | 30/7 |
– 34 x2
+ ( – x3 + x3)
+ ( -20 x4 + ( -14 x4) )
= -150 + 30/7
“Красный” коэффициент равен нулю.
| x1 | + | 9 | x2 | + | x3 | + | 6 | x4 | = | 40 | ||||
| – | 34 | x2 | – | 34 | x4 | = | – 1020/7 | |||||||
| x3 | – | 14 | x4 | = | 30/7 |
 подробнее
подробнееx1
+ 9 x2
+ ( x3 + x3 * ( -1) )
+ ( 6 x4 + ( -14 x4) * ( -1) )
= 40 + 30/7 * ( -1)
“Красный” коэффициент равен нулю.
| x1 | + | 9 | x2 | + | 20 | x4 | = | 250/7 | ||||||
| – | 34 | x2 | – | 34 | x4 | = | – 1020/7 | |||||||
| x3 | – | 14 | x4 | = | 30/7 |
Уравнеие 2 разделим на -34.
| x1 | + | 9 | x2 | + | 20 | x4 | = | 250/7 | ||||||
| x2 | + | x4 | = | 30/7 | ||||||||||
| x3 | – | 14 | x4 | = | 30/7 |
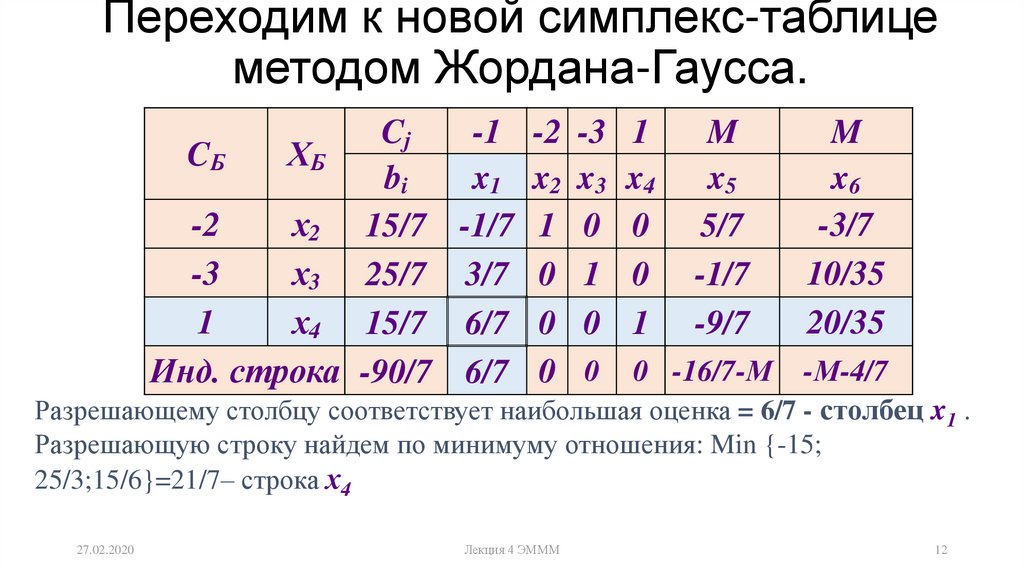 подробнее
подробнееx1
+ ( 9 x2 + x2 * ( -9) )
+ ( 20 x4 + x4 * ( -9) )
= 250/7 + 30/7 * ( -9)
“Красный” коэффициент равен нулю.
| x1 | + | 11 | x4 | = | – 20/7 | |||||||||
| x2 | + | x4 | = | 30/7 | ||||||||||
| x3 | – | 14 | x4 | = | 30/7 |
Ответ:
x1 = – 20/7 – 11 x4
x2 = 30/7 – x4
x3 = 30/7 + 14 x4
Решение системы линейных уравнений методом Жордана-Гаусса (метод прямоугольников)
Решение системы линейных уравнений методом Жордана-Гаусса (метод прямоугольников)
Видеоурок: Метод Жордана-Гаусса (метод прямоугольников)
youtube.com/embed/npWJWEz4gW8″ frameborder=”0″ allowfullscreen=””>Пример из видеоурока в рукописном виде:
Пример 2.
Запишем систему в виде:
1 | -2 | 2 | -1 | -1 | 2 | 4 |
0 | -1 | 1 | 3 | -1 | 2 | -2 |
-2 | 4 | -4 | -2 | -2 | 1 | 1 |
-1 | 1 | 0 | -1 | 1 | 1 | -2 |
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника: НЭ = СЭ – (А*В)/РЭ, где РЭ – разрешающий элемент (1), А и В – элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
1 | -2 | 2 | -1 | -1 | 2 | 4 |
0 | -1 | 1 | 3 | -1 | 2 | -2 |
0 | 0 | 0 | -4 | -4 | 5 | 9 |
0 | -1 | 2 | -2 | 0 | 3 | 2 |
Разрешающий элемент равен (-1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
1 | 0 | 0 | -7 | 1 | -2 | 8 |
0 | 1 | -1 | -3 | 1 | -2 | 2 |
0 | 0 | 0 | -4 | -4 | 5 | 9 |
0 | 0 | 1 | -5 | 1 | 1 | 4 |
Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
1 | 0 | 0 | -7 | 1 | -2 | 8 |
0 | 1 | 0 | -8 | 2 | -1 | 6 |
0 | 0 | 1 | -5 | 1 | 1 | 4 |
0 | 0 | 0 | -4 | -4 | 5 | 9 |
Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
1 | 0 | 0 | 0 | 8 | -10.75 | -7.75 |
0 | 1 | 0 | 0 | 10 | -11 | -12 |
0 | 0 | 1 | 0 | 6 | -5. | -7.25 |
0 | 0 | 0 | 1 | 1 | -1.25 | -2.25 |
Теперь исходную систему можно записать как:
x1 = -7.75 – 8×5 – 10.75×6
x2 = -12 – 10×5 – 11×6
x3 = -7.25 – 6×5 – 5.25×6
x4 = -2.25 – x5 – 1.25×6
Необходимо переменные x5,x6 принять в качестве свободных переменных и через них выразить остальные переменные.
Приравняем переменные x5,x6 к 0
x1 = -7.75
x2 = -12
x3 = -7.25
x4 = -2.25
Среди базисных переменных есть отрицательные значения. Следовательно, данное решение не опорное.
Метод данцига предполагает процедуру жордана гаусса.
 Решение системы линейных уравнений методом гаусса-жордана
Решение системы линейных уравнений методом гаусса-жордана4. Метод Жордана – Гаусса.
Схема с выбором главного элемента состоит в том, что требование неравенства нулю диагональных элементов akk, на которые происходит деление в процессе исключения, заменятся более жестким: из всех элементов К-го столба выбрать наибольший по модулю и переставить уравнения так, чтобы этот элемент оказался на месте элемента акк. Выбор главного элемента и связанная с ним перестановка строк необходимы в тех случаях, когда на каком-либо i-ом шаге акк=0 либо же акк очень мало по остальными элементами i- го столбца: при делении на такое «малое» акк будут получаться большие числа с большими абсолютными погрешностями, в результате чего решение может сильно исказиться.
Ниже излагается алгоритм полного исключения неизвестных или метод Жордана – Гаусса. Суть метода состоит в том, что, рассмотрев первое уравнение, в нем неизвестное с коеффициэнтом, отличным от нуля (в дальнейшем разрешающий элемент), и разделив первое уравнение на этот коэффициент, с помощью первого уравнения исключают это неизвестное из всех уравнений, кроме первого. Выбрав во втором уравнении неизвестное с коэффициентом, отличным от нуля, и разделив на него второе уравнение, с помощью второго исключают другие неизвестные из всех уравнений, кроме второго и т.д., т.е. с помощью одного уравнения производят полное исключение одного неизвестного. Процесс продолжается до тех пор, пока не будут использованы все уравнения.
Выбрав во втором уравнении неизвестное с коэффициентом, отличным от нуля, и разделив на него второе уравнение, с помощью второго исключают другие неизвестные из всех уравнений, кроме второго и т.д., т.е. с помощью одного уравнения производят полное исключение одного неизвестного. Процесс продолжается до тех пор, пока не будут использованы все уравнения.
Как известно, системы линейных алгебраических уравнений могут имеет одно решение, множество решений или системы несовместны. При элементарных преобразованиях элементов матрицы системы эти случаи выявляются в следующем:
1. В процессе исключений левая часть I –го уравнения системы обращается в нуль, а правая часть равна некоторому числу, отличному от нуля. т.е. 02+=bc0.
Это означает, что система не имеет решений, так как I – му уравнению не могут удовлетворять никакие значения неизвестных;
2. Левая и правая части I – го уравнения обращаются в нуль. Это означает, что I – ое уравнение является линейной комбинацией остальных, ему удовлетворяет любое найденное решение системы, поэтому оно может быть отброшено.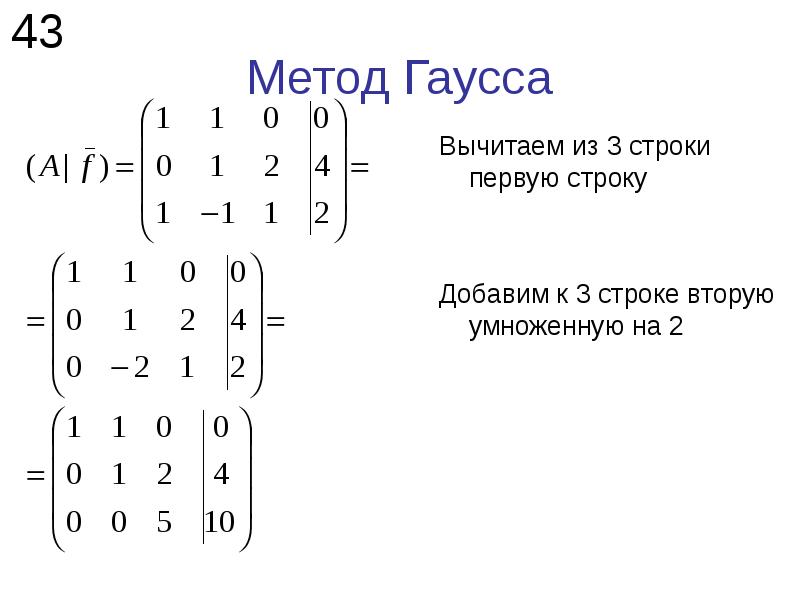 В системе количество неизвестных больше количества уравнений и, следовательно, такая система имеет множество решений;
В системе количество неизвестных больше количества уравнений и, следовательно, такая система имеет множество решений;
3. После того как все уравнения использованы для исключения неизвестных получено решение системы.
Таким образом, конечной целью преобразований Жордана-Гаусса является получение из заданной линейной системы
| a11x1 + a12x2 + … + a1nxn = b1,n+1 |
a21x1 + a22x2 + … + a2nxn = b2,n+1 |
| am1x1 + am2x2 + … + amnxn = bm.n+1 |
Здесь x1, x2, …, xn – неизвестные, которые надо определить. a11, a12, …, amn – коэффициенты системы – и b1, b2, … bm – свободные члены – предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе – неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) – совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все ее уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).
Совместная система вида (1) называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.
Решим следующую систему уравнений:
Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:
Проведём следующие действия:
· К строке 2 добавим: -4 * Строку 1.
· К строке 3 добавим: -9 * Строку 1.
· К строке 3 добавим: -3 * Строку 2.
· Строку 2 делим на -2
· К строке 1 добавим: -1 * Строку 3.
· К строке 2 добавим: -3/2 * Строку 3.
· К строке 1 добавим: -1 * Строку 2.
В правом столбце получаем решение:
.
В методе Ньютона наблюдается ускорение сходимости процесса приближений. 5. Метод касательных (метод Ньютона) Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f ¢(x) (x-x0) (1.5) Графики…
Решения от численных методов расчёта. Для определения корней уравнения не требуется знания теорий групп Абеля, Галуа, Ли и пр. и применения специальной математической терминологии: колец, полей, идеалов, изоморфизмов и т.д. Для решения алгебраического уравнения n – ой степени нужно только умение решать квадратные уравнения и извлекать корни из комплексного числа. Корни могут быть определены с…
Математики тригонометрической подстановки и проверка эффективности разработанной методики преподавания. Этапы работы: 1. Разработка факультативного курса на тему: «Применение тригонометрической подстановки для решения алгебраических задач» с учащимися классов с углубленным изучением математики. 2. Проведение разработанного факультативного курса. 3. Проведение диагностирующей контрольной…
… «проявляется» лишь в процессе преобразований. Очевидность и «завуалированность» новой переменной мы рассмотрим на конкретных примерах во второй главе данной работы. 2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных…
Метод Гаусса-Жордана предназначен для решения систем линейных алгебраических уравнений (СЛАУ). Он является модификацией метода Гаусса . Если метод Гаусса осуществляется в два этапа (прямой ход и обратный) то метод Гаусса-Жордана позволяет решить систему в один этап. Подробности и непосредственная схема применения метода Гаусса-Жордана описаны в примерах.
Во всех примерах $A$ обозначает матрицу системы, $\widetilde{A}$ – расширенную матрицу системы. О матричной форме записи СЛАУ можно прочесть .
Пример №1
Решить СЛАУ $ \left\{ \begin{aligned} & 4x_1-7x_2+8x_3=-23;\\ & 2x_1-4x_2+5x_3=-13;\\ & -3x_1+11x_2+x_3=16. \end{aligned} \right.$ методом Гаусса-Жордана.
Давайте перейдём от последней полученной нами матрице к системе:
$$ \left\{ \begin{aligned} & 0\cdot x_1+1\cdot x_2+0\cdot x_3=1;\\ & 1\cdot x_1+0\cdot x_2+0\cdot x_3=-2;\\ & 0\cdot x_1+0\cdot x_2+1\cdot x_3=-1. \end{aligned} \right. $$
Упрощая полученную систему, имеем:
$$ \left\{ \begin{aligned} & x_2=1;\\ & x_1=-2;\\ & x_3=-1. \end{aligned} \right. $$
Полное решение без пояснений выглядит так:
Хоть этот способ выбора разрешающих элементов вполне допустим, но предпочтительнее выбирать в качестве разрешающих элементов диагональные элементы матрицы системы. Мы рассмотрим этот способ ниже.
Выбор разрешающих элементов на главной диагонали матрицы системы.
Так как этот способ решения полностью аналогичен предыдущему (за исключением выбора разрешающих элементов), то подробные пояснения пропустим. Принцип выбора разрешающих элементов прост: в первом столбце выбираем элемент первой строки, во втором столбце берём элемент второй строки, в третьем столбце – элемент третьей строки и так далее.
Первый шаг
В первом столбце выбираем элемент первой строки, т.е. в качестве разрешающего имеем элемент 4. Понимаю, что выбор числа 2 кажется более предпочтительным, так как это число всё-таки меньше, нежели 4. Для того, чтобы число 2 в первом столбце переместилось на первое место, поменяем местами первую и вторую строки:
$$ \left(\begin{array} {ccc|c} 4 & -7 & 8 & -23\\ 2 & -4& 5 & -13 \\ -3 & 11 & 1 & 16 \end{array} \right)\rightarrow \left(\begin{array} {ccc|c} 2 & -4& 5 & -13\\ 4 & -7 & 8 & -23 \\ -3 & 11 & 1 & 16 \end{array} \right) $$
Итак, разрешающий элемент представлен числом 2. Точно так же, как и ранее, разделим первую строку на 2, а затем обнулим элементы первого столбца:
$$ \left(\begin{array} {ccc|c} 2 & -4& 5 & -13\\ 4 & -7 & 8 & -23 \\ -3 & 11 & 1 & 16 \end{array} \right) \begin{array} {l} I:2 \\\phantom{0} \\ \phantom{0} \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & -2& 5/2 & -13/2 \\4 & -7 & 8 & -23\\ -3 & 11 & 1 & 16 \end{array} \right) \begin{array} {l} \phantom{0} \\ II-4\cdot I\\ III+3\cdot I \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & -2& 5/2 & -13/2\\0 & 1 & -2 & 3\\ 0 & 5 & 17/2 & -7/2 \end{array} \right). $$
Второй шаг
На втором шаге требуется обнулить элементы второго столбца. В качестве разрешающего элемента выбираем элемент второй строки, т.е. 1. Разрешающий элемент уже равен единице, поэтому никаких строк менять местами не будем. Кстати сказать, если бы мы захотели поменять местами строки, то первую строку трогать не стали бы, так как она уже была использована на первом шаге. А вот вторую и третью строки запросто можно менять местами. Однако, повторюсь, в данной ситуации менять местами строки не нужно, ибо разрешающий элемент уже оптимален – он равен единице.
$$ \left(\begin{array} {ccc|c} 1 & -2& 5/2 & -13/2\\0 & 1 & -2 & 3\\ 0 & 5 & 17/2 & -7/2 \end{array} \right) \begin{array} {l} I+2\cdot II \\ \phantom{0}\\ III-5\cdot II \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 37/2 & -37/2 \end{array} \right). $$
Второй шаг окончен. Переходим к третьему шагу.
Третий шаг
На третьем шаге требуется обнулить элементы третьего столбца. В качестве разрешающего элемента выбираем элемент третьей строки, т.е. 37/2. Разделим элементы третьей строки на 37/2 (чтобы разрешающий элемент стал равен 1), а затем обнулим соответствующие элементы третьего столбца:
$$ \left(\begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 37/2 & -37/2 \end{array} \right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ III:\frac{37}{2} \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 1 & -1 \end{array} \right) \begin{array} {l} I+2\cdot III\\II+3/2\cdot III\\ \phantom{0} \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & 0 & 0 & -2 \\ 0 & 1 & 0 & 1\\ 0 & 0 & 1 & -1 \end{array} \right). $$
Ответ получен: $x_1=-2$, $x_2=1$, $x_3=-1$. Полное решение без пояснений выглядит так:
Все остальные примеры на этой странице будут решены именно вторым способом: в качестве разрешающих будем выбирать диагональные элементы матрицы системы.
Ответ : $x_1=-2$, $x_2=1$, $x_3=-1$.
Пример №2
Решить СЛАУ $ \left\{ \begin{aligned} & 3x_1+x_2+2x_3+5x_4=-6;\\ & 3x_1+x_2+2x_4=-10;\\ & 6x_1+4x_2+11x_3+11x_4=-27;\\ & -3x_1-2x_2-2x_3-10x_4=1. \end{aligned} \right.$ методом Гаусса-Жордана.
Запишем расширенную матрицу данной системы : $\widetilde{A}=\left(\begin{array} {cccc|c} 3 & 1 & 2 & 5 & -6\\ 3 & 1& 0 & 2 & -10 \\ 6 & 4 & 11 & 11 & -27 \\ -3 & -2 & -2 & -10 & 1 \end{array} \right)$.
В качестве разрешающих элементов станем выбирать диагональные элементы матрицы системы: на первом шаге возьмём элемент первой строки, на втором шаге элемент второй строки и так далее.
Первый шаг
Нам нужно обнулить соответствующие элементы первого столбца. В качестве разрешающего элемента возьмём элемент первой строки, т.е. 3. Соответственно первую строку придётся разделить на 3, чтобы разрешающий элемент стал равен единице. А затем обнулить все элементы первого столбца, кроме разрешающего:
$$ \left(\begin{array}{cccc|c} 3 & 1 & 2 & 5 & -6\\ 3 & 1 & 0 & 2 & -10\\ 6 & 4 & 11 & 11 & -27\\ -3 & -2 & -2 & -10 & 1\end{array}\right) \begin{array} {l} I:3\\ \phantom{0}\\\phantom{0}\\\phantom{0}\end{array} \rightarrow \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 3 & 1 & 0 & 2 & -10\\ 6 & 4 & 11 & 11 & -27\\ -3 & -2 & -2 & -10 & 1\end{array}\right) \begin{array} {l} \phantom{0}\\ II-3\cdot I\\III-6\cdot I\\IV+3\cdot I\end{array} \rightarrow\\ \rightarrow\left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 0 & -2 & -3 & -4\\ 0 & 2 & 7 & 1 & -15\\ 0 & -1 & 0 & -5 & -5\end{array}\right). $$
Второй шаг
Переходим к обнулению соответствующих элементов второго столбца. В качестве разрешающего элемента мы уславливались взять элемент второй строки, но сделать этого мы не в силах, так как нужный элемент равен нулю. Вывод: будем менять местами строки. Первую строку трогать нельзя, так как она уже использовалась на первом шаге. Выбор небогат: или меняем местами вторую и третью строки, или же меняем местами четвёртую и вторую. Так как в четвёртой строке наличествует (-1), то пусть в “обмене” поучавствует именно четвёртая строка. Итак, меняем местами вторую и четвёртую строки:
$$ \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 0 & -2 & -3 & -4\\ 0 & 2 & 7 & 1 & -15\\ 0 & -1 & 0 & -5 & -5\end{array}\right)\rightarrow \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & -1 & 0 & -5 & -5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end{array}\right) $$
Вот теперь всё в норме: разрешающий элемент равен (-1). Бывает, кстати, что смена мест строк невозможна, но это обговорим в следующем примере №3. А пока что делим вторую строку на (-1), а затем обнуляем элементы второго столбца. Обратите внимание, что во втором столбце элемент, расположенный в четвёртой строке, уже равен нулю, поэтому четвёртую строку трогать не будем.
$$ \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & -1 & 0 & -5 & -5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end{array}\right) \begin{array} {l} \phantom{0}\\II:(-1) \\\phantom{0}\\\phantom{0}\end{array} \rightarrow \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 1 & 0 & 5 & 5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end{array}\right) \begin{array} {l} I-1/3\cdot II\\ \phantom{0} \\III-2\cdot II\\\phantom{0}\end{array} \rightarrow\\ \rightarrow\left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 7 & -9 & -25\\ 0 & 0 & -2 & -3 & -4\end{array}\right). $$
Третий шаг
Приступаем к обработке третьего столбца. В качестве разрешающего элемента мы условились брать диагональные элементы матрицы системы. Для третьего шага это означает выбор элемента, расположенного в третьей строке. Однако если мы просто возьмём элемент 7 в качестве разрешающего, то всю третью строку придётся делить на 7. Мне кажется, что разделить на (-2) попроще. Поэтому поменяем местами третью и четвёртую строки, и тогда разрешающим элементом станет (-2):
$$ \left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 7 & -9 & -25\\ 0 & 0 & -2 & -3 & -4\end{array}\right) \rightarrow \left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & -2 & -3 & -4\\ 0 & 0 & 7 & -9 & -25\end{array}\right) $$
Разрешающий элемент – (-2). Делим третью строку на (-2) и обнуляем соответствующие элементы третьего столбца:
$$ \left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & -2 & -3 & -4\\ 0 & 0 & 7 & -9 & -25\end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0} \\III:(-2)\\\phantom{0}\end{array}\rightarrow \left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 7 & -9 & -25\end{array}\right) \begin{array} {l} I-2/3\cdot III\\ \phantom{0} \\ \phantom{0}\\IV-7\cdot III\end{array}\rightarrow\\ \rightarrow\left(\begin{array}{cccc|c} 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & -39/2 & -39\end{array}\right). $$
Четвёртый шаг
Переходим к обнулению четвёртого столбца. Разрешающий элемент расположен в четвёртой строке и равен числу $-\frac{39}{2}$.
$$ \left(\begin{array}{cccc|c} 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & -39/2 & -39\end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0} \\ \phantom{0}\\IV:\left(-\frac{39}{2}\right) \end{array}\rightarrow \left(\begin{array}{cccc|c} 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & 1 & 2\end{array}\right) \begin{array} {l} I+IV\\ II-5\cdot IV \\ III-3/2\cdot IV \\ \phantom{0} \end{array}\rightarrow\\ \rightarrow\left(\begin{array}{cccc|c} 1 & 0 & 0 & 0 & -3\\ 0 & 1 & 0 & 0 & -5\\ 0 & 0 & 1 & 0 & -1\\ 0 & 0 & 0 & 1 & 2\end{array}\right). $$
Решение окончено. Ответ таков: $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$. Полное решение без пояснений:
Ответ : $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$.
Пример №3
Решить СЛАУ $\left\{\begin{aligned} & x_1-2x_2+3x_3+4x_5=-5;\\ & 2x_1+x_2+5x_3+2x_4+9x_5=-3;\\ & 3x_1+4x_2+7x_3+4x_4+14x_5=-1;\\ & 2x_1-4x_2+6x_3+11x_5=2;\\ & -2x_1+14x_2-8x_3+4x_4-7x_5=20;\\ & -4x_1-7x_2-9x_3-6x_4-21x_5=-9. \end{aligned}\right.$ методом Гаусса-Жордана. Если система является неопределённой, указать базисное решение.
Подобные примеры разбираются в теме “Общее и базисное решения СЛАУ” . Во второй части упомянутой темы данный пример решён с помощью метод Гаусса . Мы же решим его с помощью метода Гаусса-Жордана. Пошагово разбивать решение не станем, так как это уже было сделано в предыдущих примерах.
$$ \left(\begin{array}{ccccc|c} 1 & -2 & 3 & 0 & 4 & -5\\ 2 & 1 & 5 & 2 & 9 & -3\\ 3 & 4 & 7 & 4 & 14 & -1\\ 2 & -4 & 6 & 0 & 11 & 2\\ -2 & 14 & -8 & 4 & -7 & 20\\ -4 & -7 & -9 & -6 & -21 & -9 \end{array}\right) \begin{array} {l} \phantom{0} \\ II-2\cdot I\\ III-3\cdot I\\ IV-2\cdot I\\ V+2\cdot I\\VI+4\cdot I \end{array} \rightarrow \left(\begin{array}{ccccc|c} 1 & -2 & 3 & 0 & 4 & -5\\ 0 & 5 & -1 & 2 & 1 & 7\\ 0 & 10 & -2 & 4 & 2 & 14\\ 0 & 0 & 0 & 0 & 3 & 12\\ 0 & 10 & -2 & 4 & 1 & 10\\ 0 & -15 & 3 & -6 & -5 & -29 \end{array}\right) \begin{array} {l} \phantom{0} \\ II:5 \\ \phantom{0}\\ \phantom{0}\\ \phantom{0} \\ \phantom{0}\end{array} \rightarrow \\ \left(\begin{array}{ccccc|c} 1 & -2 & 3 & 0 & 4 & -5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 10 & -2 & 4 & 2 & 14\\ 0 & 0 & 0 & 0 & 3 & 12\\ 0 & 10 & -2 & 4 & 1 & 10\\ 0 & -15 & 3 & -6 & -5 & -29 \end{array}\right) \begin{array} {l} I+2\cdot II \\ \phantom{0}\\ III-10\cdot II\\ IV:3\\ V-10\cdot II\\VI+15\cdot II \end{array} \rightarrow \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end{array}\right). $$
Полагаю, что одно из сделанных преобразований всё-таки требует пояснения: $IV:3$. Все элементы четвёртой строки нацело делились на три, поэтому сугубо из соображений упрощения мы разделили все элементы этой строки на три. Третья строка в преобразованной матрице стала нулевой. Вычеркнем нулевую строку:
$$ \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end{array}\right) $$
Нам пора переходить к третьему шагу, на котором должны быть обнулены элементы третьего столбца. Однако диагональный элемент (третья строка) равен нулю. И смена мест строк ничего не даст. Первую и вторую строки мы уже использовали, поэтому их трогать мы не можем. А четвёртую и пятую строки трогать нет смысла, ибо проблема равенства нулю разрешающего элемента никуда не денется.
В этой ситуации проблема решается крайне незамысловато. Мы не можем обработать третий столбец? Хорошо, перейдём к четвёртому. Может, в четвёртом столбце элемент третьей строки будет не равен нулю. Однако четвёртый столбец “болеет” той же проблемой, что и третий. Элемент третьей строки в четвёртом столбце равен нулю. И смена мест строк опять-таки ничего не даст. Четвёртый столбец тоже не можем обработать? Ладно, перейдём к пятому. А вот в пятом столбце элемент третьей строки очень даже не равен нулю. Он равен единице, что довольно-таки хорошо. Итак, разрешающий элемент в пятом столбце равен 1. Разрешающий элемент выбран, поэтому осуществим дальшейшие преобразования метода Гаусса-Жордана:
$$ \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end{array}\right) \begin{array} {l} I-22/5\cdot III \\ II-1/5\cdot III \\ \phantom{0}\\ IV+III\\ V+2\cdot III \end{array} \rightarrow \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right) \rightarrow \\ \rightarrow\left|\text{Удаляем нулевые строки}\right|\rightarrow \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4 \end{array}\right)$$
Мы привели матрицу системы и расширенную матрицу системы к ступенчатому виду. Ранги обеих матриц равны $r=3$, т.е. надо выбрать 3 базисных переменных. Количество неизвестных $n=5$, поэтому нужно выбрать $n-r=2$ свободных переменных. Так как $r
На “ступеньках” стоят элементы из столбцов №1, №2, №5. Следовательно, базисными будут переменные $x_1$, $x_2$, $x_5$. Свободными переменными, соответственно, будут $x_3$, $x_4$. Столбцы №3 и №4, соответствующие свободным переменным, перенесём за черту, при этом, конечно, не забыв сменить им знаки.
$$ \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4 \end{array}\right)\rightarrow \left(\begin{array}{ccc|ccc} 1 & 0 & 0 & -99/5 & -13/5 & -4/5\\ 0 & 1 & 0 & 3/5 & 1/5 & -2/5\\ 0 & 0 & 1 & 4 & 0 & 0\end{array}\right). $$
Из последней матрицы получим общее решение: $\left\{\begin{aligned} & x_1=-\frac{99}{5}-\frac{13}{5}x_3-\frac{4}{5}x_4;\\ & x_2=\frac{3}{5}+\frac{1}{5}x_3-\frac{2}{5}x_4;\\ & x_3 \in R;\\ & x_4\in R;\\ & x_5=4. \end{aligned}\right.$. Базисное решение найдём, приняв свободные переменные равными нулю, т.е. $x_3=0$, $x_4=0$:
$$ \left\{\begin{aligned} & x_1=-\frac{99}{5};\\ & x_2=\frac{3}{5};\\ & x_3=0;\\ & x_4=0;\\ & x_5=4. \end{aligned}\right. $$
Задача решена, осталось лишь записать ответ.
Ответ : Общее решение: $\left\{\begin{aligned} & x_1=-\frac{99}{5}-\frac{13}{5}x_3-\frac{4}{5}x_4;\\ & x_2=\frac{3}{5}+\frac{1}{5}x_3-\frac{2}{5}x_4;\\ & x_3 \in R;\\ & x_4\in R;\\ & x_5=4. \end{aligned}\right.$, базисное решение: $\left\{\begin{aligned} & x_1=-\frac{99}{5};\\ & x_2=\frac{3}{5};\\ & x_3=0;\\ & x_4=0;\\ & x_5=4. \end{aligned}\right.$.
Записывается в виде расширенной матрицы, т.е. в столбец свободных членов помещается в одну матрицу с коэффициентами неизвестных. Аалгоритм заключается в приведении исходной матрицы, характеризующей систему линейных уравнений, к единичной путем эквивалентных преобразований (домножения строки матрицы на константу и сложения с другой строкой матрицы). В качестве константы используется 1/a[i][i] , т.е. число, обратное по отношению к элементу диагонали. Естественно, в ряде случаев возникают проблемы, связанные с делением на ноль, которые решаются перестановкой строк и столбцов:
Весь алгоритм можно представить 10 пунктами:
В качестве опорной выбираем первую строку матрицы.
Если элемент опорной строки, индекс которого равен номеру опорной строки, равен нулю, то меняем всю опорную строку на первую попавшуюся строку снизу, в столбце которого нет нуля.
Все элементы опорной строки делим на первый слева ненулевой элемент этой строки.
Из оставшихся снизу строк вычитают опорную строку, умноженную на элемент, индекс которого равен номеру опорной строки.
В качестве опорной строки выбираем следующую строку.
Повторяем действия 2 – 5 пока номер опорной строки не превысит число строк.
В качестве опорной выбираем последнюю строку.
Вычитаем из каждой строки выше опорную строку, умноженную на элемент этой строки с индексом равным номеру опорной строки.
В качестве опорной строки выбираем строку выше.
Повторяем 8 – 9 пока номер опорной строки не станет меньше номера первой строки.
Пусть имеется система уравнений:
Запишем расширенную матрицу системы:
и выполним элементарные преобразования ее строк.
Для этого умножим первую строку на 1 и вычитаем из второй строки; затем умножим первую строку на 2 и вычтем из третьей строки.
В результате мы исключим переменную x 1 из всех уравнений, кроме первого. Получим:
Теперь вычтем из строки 3 строку 2, умноженную на 3:
Теперь вычитаем из 1 строки сначала 3 строку, а затем 2 строку:
После преобразований получаем систему уравнений:
Из этого следует, что система уравнений имеет следующее решение:
x1 = 1, x2 = 3 , x3 = -1
В качестве примера решим систему уравнений, представленную в виде матрицы (Таблица 1), методом Гаусса – Жордана.
Делим первую строку на 3 (элемент первой строки, расположенный на главной диагонали), получим:
Умножаем первую строку на 1 и вычитаем из второй строки. Умножаем первую строку на 6 и вычитаем из третьей строки. Получим:
В первом столбце все элементы кроме диагонального равны нулю, займемся вторым столбцом, для этого выберем вторую строку в качестве опорной. Вторая Делим ее на 17/3:
Умножаем строку 2 на -6 и вычитаем из третьей строки:
Теперь третья строка – опорная, делим ее на -33/17:
Умножаем опорную строку на 3/17 и вычитаем ее из второй. Умножаем третью строку на 1 и вычитаем ее из первой
Получена треугольная матрица, начинается обратный ход алгоритма (во время которого получим единичную матрицу). Вторая строка становится опорной. Умножаем третью строку на 4/3 и вычитаем ее из первой:
Последний столбец матрицы – решение системы уравнений.
Каждой системе линейных уравнений поставим в соответствие расширенную матрицу , полученную присоединением к матрице А столбца свободных членов:
Метод Жордана–Гаусса применяется для решения системы m линейных уравнений с n неизвестными вида:
Данный метод заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе уравнений с матрицей определенного вида.
Над строками расширенной матрицы осуществляем следующие элементарные преобразования:
1. перестановка двух строк ;
2. умножение строки на любое число, отличное от нуля ;
3. прибавление к одной строке другой строки, умноженной на некоторое число ;
4. отбрасывание нулевой строки (столбца) .
Пример 2.11. Решить методом Жордана–Гаусса системы линейных уравнений:
а ) Х 1 + Х 2 + 2Х 3 = -1
2Х 1 – Х 2 + 2Х 3 = -4
4Х 1 + Х 2 + 4Х 3 = -2
Решение: Составим расширенную матрицу:
Итерация 1
В качестве направляющего элемента выбираем элемент . Преобразуем первый столбец в единичный. Для этого ко второй и третьей строкам прибавляем первую строку, соответственно умноженную на (-2) и (-4). Получим матрицу:
На этом первая итерация закончена.
Итерация 2
Выбираем направляющий элемент . Так как , то делим вторую строку на -3. Затем умножаем вторую строку соответственно на (-1) и на 3 и складываем соответственно с первой и третьей строками. Получим матрицу
Итерация 3
Выбираем направляющий элемент . Так как , то делим третью строку на (-2). Преобразуем третий столбец в единичный. Для этого умножаем третью строку соответственно на (-4/3) и на (-2/3) и складываем соответственно с первой и второй строками. Получим матрицу
откуда Х 1 = 1, Х 2 = 2, Х 3 = -2.
Закончив решение, на этапе обучения необходимо выполнять проверку, подставив найденные значения в исходную систему, которая при этом должна обратиться в верные равенства.
б ) Х 1 – Х 2 + Х 3 – Х 4 = 4
Х 1 + Х 2 + 2Х 3 +3Х 4 = 8
2Х 1 +4Х 2 + 5Х 3 +10Х 4 = 20
2Х 1 – 4Х 2 + Х 3 – 6Х 4 = 4
Решение: Расширенная матрица имеет вид:
Применяя элементарные преобразования, получим:
Исходная система эквивалентна следующей системе уравнений:
Х 1 – 3Х 2 – 5Х 4 = 0
2Х 2 + Х 3 + 4Х 4 = 4
Последние две строки матрицы A (2) являются линейно зависимыми.
Определение. Строки матрицы e 1 , e 2 ,…, e m называются линейно зависимыми , если существуют такие числа , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:
где 0 =(0, 0…0). Строки матрицы являются линейно независимыми , когда комбинация этих строк равна нулю тогда и только тогда, когда все коэффициенты равны нулю.
В линейной алгебре очень важно понятие ранга матрицы , т.к. оно играет очень большое значение при решении систем линейных уравнений.
Теорема 2.3 (о ранге матрицы). Ранг матрицы равен максимальному числу её линейно независимых строк или столбцов, через которые линейно выражаются все остальные её строки (столбцы).
Ранг матрицы A (2) равен 2, т.к. в ней максимальное число линейно независимых строк равно 2 (это первые две строки матрицы).
Теорема 2.4 (Кронекера–Капели). Система линейных уравнений совместна и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.
1. Если ранг матрицы совместной системы равен числу переменных, т.е. r = n, то система имеет единственное решение.
2. Если ранг матрицы системы меньше числа переменных, т.е. r
В данном случае система имеет 4 переменных, а её ранг равен 2, следовательно, она имеет бесконечное множество решений.
Определение. Пусть r n , r переменных x 1 , x 2 ,…, x r называются базисными , если определитель матрицы из коэффициентов при них (базисный минор ) отличен от нуля. Остальные n – r переменных называются свободными .
Определение. Решение системы, в котором все n – r свободных переменных равны нулю, называется базисным .
Совместная система m линейных уравнений с n переменными (m ) имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее , где .
В нашем случае , т.е. система имеет не более 6 базисных решений.
Общее решение имеет вид:
Х 1 = 3Х 2 +5Х 4
Х 3 = 4 – 2Х 2 – 4Х 4
Найдем базисные решения. Для этого полагаем Х 2 = 0, Х 4 = 0, тогда Х 1 =0, Х 3 = 4. Базисное решение имеет вид: (0, 0, 4, 0).
Получим другое базисное решение. Для этого в качестве свободных неизвестных примем Х 3 и Х 4 . Выразим неизвестные Х 1 и Х 2 через неизвестные Х 3 и Х 4:
Х 1 = 6 – 3/2Х 2 – Х 4
Х 2 = 2 – 1/2Х 3 – 2Х 4 .
Тогда базисное решение имеет вид: (6, 2, 0, 0).
Пример 2.12. Решить систему:
X 1 + 2X 2 – X 3 = 7
2X 1 – 3X 2 + X 3 = 3
4X 1 + X 2 – X 3 = 16
Решение.Преобразуем расширенную матрицу системы
Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво – оно привелось к неверному равенству 0 = –1, следовательно, данная система несовместна. Данный вывод можно также получить, если заметить, что ранг матрицы системы равен 2, тогда как ранг расширенной матрицы системы равен 3.
Нахождение обратной матрицы: три алгоритма и примеры
Нахождение обратной матрицы – процесс, который состоит из достаточно простых действий. Но эти действия повторяются так часто, что процесс получается довольно продолжительным. Главное – не потерять внимание при решении.
При решении наиболее распространённым методом – алгебраических дополнений – потребуется:
При решении примеров мы разберём эти действия подробнее. А пока узнаем, что гласит теория об обратной матрице.
Для обратной матрицы существует уместная аналогия с обратным числом. Для каждого числа a, не равного нулю, существует такое число b, что произведение a и b равно единице: ab = 1. Число b называется обратным для числа b. Например, для числа 7 обратным является число 1/7, так как 7*1/7=1.
Обратной матрицей, которую требуется отыскать для данной квадратной матрицы А, называется такая матрица
,
произведение на которую матрицы А справа является единичной матрицей, т.е,
. (1)
Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны единице.
Нахождение обратной матрицы – задача, которая чаще решается двумя методами:
- методом алгебраических дополнений, при котором, как было замечено в начале урока, требуется находить определители, миноры и алгебраические дополнения и транспонировать матрицы;
- методом исключения неизвестных Гаусса, при котором требуется производить элементарные преобразования матриц (складывать строки, умножать строки на одно и то же число и т. д.).
Для особо любознательных существуют и другие методы, например, метод линейных преобразований. На этом уроке разберём три упомянутых метода и алгоритмы нахождения обратной матрицы этими методами.
Теорема. Для каждой неособенной (невырожденной, несингулярной) квадратной матрицы можно найти обратную матрицу, и притом только одну. Для особенной (вырожденной, сингулярной) квадратной матрицы обратная матрица не существует.
Квадратная матрица называется неособенной (или невырожденной, несингулярной), если её определитель не равен нулю, и особенной (или вырожденной, сингулярной), если её определитель равен нулю.
Обратная матрица может быть найдена только для квадратной матрицы. Естественно, обратная матрица также будет квадратной и того же порядка, что и данная матрица. Матрица, для которой может быть найдена обратная матрица, называется обратимой матрицей.
На сайте есть онлайн калькулятор для нахождения обратной матрицы. Вы можете открыть его в новом окне уже сейчас, если держите перед собой ваши собственные задания. А мы разберём несколько разминочных.
Для неособенной квадратной матрицы А обратной является матрица
, (2)
где – определитель матрицы А, а – матрица, союзная с матрицей А.
Разберём ключевые понятия, которые потребуются для решения задач – союзная матрица, алгебраические дополнения и транспонированная матрица.
Пусть существует квадратная матрица A:
Транспонированная относительно матрицы A матрица A’ получается, если из строк матрицы A сделать столбцы, а из её столбцов – наоборот, строки, то есть заменить строки столбцами:
Остановимся на минорах и алгебраических дополнениях.
Пусть есть квадратная матрица третьего порядка:
.
Её определитель:
Вычислим алгебраическое дополнение элемента , то есть элемента 2, стоящего на пересечении первой строки и второго столбца.
Для этого нужно сначала найти минор этого элемента. Он получается вычёркиванием из определителя строки и столбца, на пересечении которых стоит указанный элемент. В результате останется следующий определитель, который и является минором элемента :
.
Алгебраическое дополнение элемента получим, если умножим , где i – номер строки исходного элемента, а k – номер столбца исходного элемента, на полученный в предыдущем действии минор этого исходного элемента. Получаем алгебраическое дополнение элемента :
.
По этой инструкции нужно вычислить алгебраические дополнения всех элементов матрицы A’, транспонированной относительно матрицы матрица A.
И последнее из значимых для нахождение обратной матрицы понятий. Союзной с квадратной матрицей A называется матрица того же порядка, элементами которой являются алгебраические дополнения соответствующих элементов определителя матрицы , транспонированной относительно матрицы A. Таким образом, союзная матрица состоит из следующих элементов:
Алгоритм нахождения обратной матрицы методом алгебраических дополнений
1. Найти определитель данной матрицы A. Если определитель равен нулю, нахождение обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.
2. Найти матрицу, транспонированную относительно A.
3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.
4. Применить формулу (2): умножить число, обратное определителю матрицы A, на союзную матрицу, найденную на шаге 4.
5. Проверить полученный на шаге 4 результат, умножив данную матрицу A на обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была найдена верно. В противном случае начать процесс решения снова.
Пример 1. Для матрицы
найти обратную матрицу.
Решение. Для нахождения обратной матрицы необходимо найти определитель матрицы А . Находим по правилу треугольников:
Следовательно, матрица А – неособенная (невырожденная, несингулярная) и для неё существует обратная.
Найдём матрицу, союзную с данной матрицей А.
Найдём матрицу , транспонированную относительно матрицы A:
Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы, транспонированной относительно матрицы A:
Следовательно, матрица , союзная с матрицей A, имеет вид
Замечание. Порядок вычисления элементов и транспонирования матрицы может быть иным. Можно сначала вычислить алгебраические дополнения матрицы A, а затем транспонировать матрицу алгебраических дополнений. В результате должны получиться те же элементы союзной матрицы.
Применяя формулу (2), находим матрицу, обратную матрице А:
Проверить решение можно с помощью онлайн калькулятора для нахождения обратной матрицы.
Алгоритм нахождения обратной матрицы методом исключения неизвестных Гаусса
1. К матрице A приписать единичную матрицу того же порядка.
2. Полученную сдвоенную матрицу преобразовать так, чтобы в левой её части получилась единичная матрица, тогда в правой части на месте единичной матрицы автоматически получится обратная матрица. Матрица A в левой части преобразуется в единичную матрицу путём элементарных преобразований матрицы.
2. Если в процессе преобразования матрицы A в единичную матрицу в какой-либо строке или в каком-либо столбце окажутся только нули, то определитель матрицы равен нулю, и, следовательно, матрица A будет вырожденной, и она не имеет обратной матрицы. В этом случае дальнейшее нахождение обратной матрицы прекращается.
Пример 2. Для матрицы
найти обратную матрицу.
Решение. Составляем сдвоенную матрицу
и будем её преобразовывать, так чтобы в левой части получилась единичная матрица. Начинаем преобразования.
Умножим первую строку левой и правой матрицы на (-3) и сложим её со второй строкой, а затем умножим первую строку на (-4) и сложим её с третьей строкой, тогда получим
.
Чтобы по возможности не было дробных чисел при последующих преобразованиях, создадим предварительно единицу во второй строке в левой части сдвоенной матрицы. Для этого умножим вторую строку на 2 и вычтем из неё третью строку, тогда получим
.
Сложим первую строку со второй, а затем умножим вторую строку на (-9) и сложим её с третьей строкой. Тогда получим
.
Разделим третью строку на 8, тогда
.
Умножим третью строку на 2 и сложим её со второй строкой. Получается:
.
Переставим местами вторую и третью строку, тогда окончательно получим:
.
Видим, что в левой части получилась единичная матрица, следовательно, в правой части получилась обратная матрица . Таким образом:
.
Можно проверить правильность вычислений, умножим исходную матрицу на найденную обратную матрицу:
.
В результате должна получиться обратная матрица.
Проверить решение можно с помощью онлайн калькулятора для нахождения обратной матрицы.
Пример 3. Для матрицы
найти обратную матрицу.
Решение. Составляем сдвоенную матрицу
и будем её преобразовывать.
Первую строку умножаем на 3, а вторую на 2, и вычитаем из второй, а затем первую строку умножаем на 5, а третью на 2 и вычитаем из третьей строки, тогда получим
.
Первую строку умножаем на 2 и складываем её со второй, а затем из третьей строки вычитаем вторую, тогда получим
.
Видим, что в третьей строке в левой части все элементы получились равными нулю. Следовательно, матрица вырожденная и обратной матрицы не имеет. Дальнейшее нахождение обратной марицы прекращаем.
Проверить решение можно с помощью онлайн калькулятора для нахождения обратной матрицы.
Матрицы теснейшим образом связаны с системами линейных уравнений. Каждой матрице соответствует система линейных уравнений, коэффициенты в которой есть элементы матрицы. И наоборот, системе линейных уравнений соответствует некоторая матрица.
Поэтому существует метод линейных преобразований для нахождения обратной матрицы. Для решения задач нам будет достаточно знать, что линейное преобразование – это система линейных уравнений, вид которой будет приведён ниже в алгоритме.
Алгоритм нахождения обратной матрицы методом линейных преобразований
1. Для данной невырожденной матрицы A составить линейное преобразование – систему линейных уравнений вида
,
где aij – элементы матрицы A.
2. Решить полученную систему относительно y – найти для предыдущего линейного преобразование обратное линейное преобразование
,
в котором Aij – алгебраические дополнения элементов матрицы A, Δ – определитель матрицы A. Внимание! Алгебраические дополнения располагаются как в транспонированной матрице, то есть для элементов строки – в столбце, а для элементов столбца – в строке.
3. Находим коэффициенты при y: , которые и будут элементами матрицы, обратной для матрицы A.
4. Пользуясь элементами, найденными на шаге 3, записать найденную обратную матрицу.
Наиболее наблюдательные могли заметить, что по сути метод линейных преобразований – это тот же метод алгебраических преобразований (союзной матрицы), но с другой формой записи. Для кого-то метод линейных преобразований может оказаться более удобным как более компактный.
Пример 4. Найти обратную матрицу для матрицы
.
Сначала проверим, не равен ли нулю определитель данной матрицы. Он не равен нулю, следовательно, обратная матрица существует.
Для данной матрицы записываем линейное преобразование:
.
Находим линейное преобразование, обратное предыдущему, для этого потребуется находить алгебраические дополнения (урок откроется в новом окне). Запишем обратное линейное преобразование:
Коэффициенты при иксах в обратном линейном преобразовании – это элементы обратной матрицы для матрицы A. Таким образом нашли обратную матрицу:
Проверить решение можно с помощью онлайн калькулятора для нахождения обратной матрицы.
Начало темы “Матрицы”
Другие темы линейной алгебры
Онлайн калькулятор обратной матрицы
Для любой неособой матрицы (т.е. определитель не равен нулю) существует обратная матрица , например, его произведение с исходной матрицей дает единичную матрицу:
А ∙ А −1 = А −1 ∙ А = E
Наш онлайн-калькулятор поддерживает два различных метода вычисления обратной матрицы: с помощью метода Гаусса-Жордана и с помощью составления алгебраических добавок к исходной матрице.
Чтобы найти обратную матрицу методом Гаусса-Жордана, нужно прикрепить единичную матрицу справа от исходной матрицы:
(A | E)
Затем с помощью элементарных преобразований преобразуйте исходную матрицу в единичную, применив те же преобразования к единичной матрице, записанной справа. Следовательно, исходная матрица будет преобразована в единичную, а выписанная справа единичная матрица – в обратную:
(A | E) → (E | A −1 )
Этот способ прост, удобен и не требует больших затрат времени.
Чтобы найти обратную матрицу с помощью метода алгебраических дополнений, можно использовать следующую формулу:
куда
| А |
– определитель матрицы
А,
А и Дж – алгебраическое дополнение элемента и матрицы
А.
По определению
A i j = (-1) i + j M i j
куда M и J – минор элемента и матрицы А.
По определению – второстепенный элемент и матрицы А – определитель, полученный удалением я ряд, j столбец матрицы А.
Итак, метод алгебраического дополнения для нахождения обратной матрицы исходной матрицы порядка п очень трудоемко, потому что нужно вычислять не только определитель исходной матрицы, но и n 2 детерминанты порядка п-1 .
Калькулятор исключения Гаусса Джордана для сокращения строк
Введение в калькулятор исключения Гаусса Джордана
Калькулятор исключения Гаусса-Иордана упрощает любую матрицу в виде сокращения строк с помощью метода исключения Гаусс-Иордана. Калькулятор Гаусса Джордана поможет рассчитать линейное уравнение в режиме онлайн, не тратя время на ручные вычисления.
Калькулятор исключения Гаусса требует только ввести вашу расширенную матрицу в терминах ввода.После того, как вы ввели свой ввод, онлайн-инструмент предоставит вам точный результат с подробными инструкциями. Матрицы, образующие систему линейных уравнений, легко решаются пошаговыми вычислениями.
Таким образом, калькулятор исключения Гаусса-Иордана – лучший вариант, если ваше решение требует преобразования матрицы в сокращенную форму эшелона строк. Чтобы сократить ваши линейные уравнения онлайн, калькулятор исключения поможет наиболее эффективным образом.
Метод исключения Гаусса Джордана также используется для определения ранга матриц.Таким образом, вы также можете использовать наш калькулятор матричного ранга для сортировки ваших матричных запросов.
Как пользоваться калькулятором исключения Гаусса Джордана?
Калькулятор сокращения строк по Гауссу-Иордану – это простой в использовании онлайн-инструмент для преобразования линейных уравнений в сокращенную форму эшелона строк. Поскольку его ручные вычисления довольно сложны и требуют длительных математических операций, этот калькулятор исключения Гаусса экономит время и обеспечивает точные результаты.
Калькулятор исключения Гаусса Иордана прост и удобен в использовании.Все, что вам нужно сделать, это ввести свою матрицу и получить результаты с помощью шагов. Просто выполните следующие шаги, чтобы уравнение решалось с помощью калькулятора исключения. Эти шаги следующие:
Введите ввод
При использовании калькулятора исключения Гаусса из Матричных калькуляторов вам нужно только ввести входные данные вашей расширенной матрицы. Эти входные данные включают размеры и коэффициенты матриц.
Предоставить матричный заказ
Прежде всего, введите порядок вашей матрицы в качестве первого ввода в калькуляторе gauss jordan.Расширенная матрица, введенная для устранения Гаусса Иордана, может иметь размеры до 4×4 в этом онлайн-инструменте.
Введите коэффициенты матрицы
После добавления правильного порядка соответствующей матрицы введите элементы матрицы. Поскольку расширенная матрица содержит коэффициенты в качестве элементов, вводите ее коэффициенты один за другим.
Связано: Кроме этого, вы также можете использовать Матричный калькулятор, чтобы получить матрицу кофакторов A.
Выходы
При вводе входных данных, требуемых калькулятором метода исключения, вам будет предоставлена сокращенная форма строки в качестве выходных данных.Поэтому для получения результатов вам просто нужно нажать на кнопку «Рассчитать». В мгновение ока вам будет предоставлен окончательный результат, включая каждый шаг, сделанный для решения линейного уравнения.
Эта простая процедура делает его одним из самых точных и быстрых калькуляторов, которые вы найдете в Интернете.
Связано: На этом веб-сайте калькулятора матричного решения предлагается множество онлайн-калькуляторов, упрощающих матричные операции. Вы можете использовать калькулятор детерминантной матрицы для линейного преобразования.
Часто задаваемые вопросы
Как преобразовать линейное уравнение в сокращенную форму строки?
Онлайн-калькуляторисключения Гаусса может легко преобразовать любое линейное уравнение в форме расширенной матрицы в сокращенную форму эшелона строк посредством операций со строками.
Для дополнительных целей вы также можете использовать калькулятор сокращенной формы строки, чтобы получить форму сокращенной ступени в режиме онлайн.
Каков упрощенный метод выполнения строковых операций над расширенными матрицами?
Операции со строками выполняются для преобразования матриц в сокращенную форму строк, что требует сложных операций и длительных вычислений.Использование калькулятора Гаусса-Джордана – самый простой способ выполнять операции со строками над расширенными матрицами.
Как я могу решить метод исключения Гаусса?
Вы можете решить задачу исключения Гаусса вручную или в режиме онлайн. Для ручных вычислений вам потребуется много времени, и поэтому калькулятор исключения Гаусса так полезен. Это позволяет вам вычислять любое уравнение, имеющее операции со строками. Эти операции со строками приводят к уменьшенной форме эшелона строк в расширенную матрицу.
Надеемся, вам понравился наш калькулятор. Есть много других связанных калькуляторов, которые вы можете использовать, например, калькулятор сложения матриц и калькулятор вычитания матриц, которые являются лучшим вариантом для решения основных матричных операций.
Джеймс Джонсон – Обновлено 11 ноября 2021 г.
Калькулятор нулевого пространства– Найдите нулевое пространство матрицы
Онлайн-калькулятор нулевого пространства поможет вам вычислить нулевое значение и нулевое пространство данной матрицы.Nullity и Null Space (ядро) являются наиболее распространенными понятиями в линейной алгебре, которые в основном используются для определения линейных отношений между различными атрибутами. Когда вы заменяете размер и значения матрицы, пустое пространство, используемое в калькуляторе матриц, сокращает форму эшелона строк для обеспечения пошаговых вычислений.
Что такое пустое пространство?Нулевое пространство или ядро - это подпространство, состоящее из всех векторов нулевого вектора, отображенных в пространство. В математической записи для матрицы A с n столбцами это векторы v = (a₁, a₂,…, aₙ), для которых
А · v = 0
Где, 0 – нулевой вектор, (·) означает, что матричное умножение x = (x, x,…, x) имеет n координат.
Примечание:
- Нулевой вектор всегда находится в нулевом пространстве. Независимо от того, какая у нас матрица, если мы умножим ее на ноль, мы получим ноль.
- Ядро матрицы обычно содержит неограниченное количество элементов. Фактически, если (a₁, a₂,…, aₙ) находится в пустом пространстве, то (ax₁, ax₂,…, axₙ) одинаково для каждого действительного числа a.
Ну, пустое пространство в матрице – это просто подпространство элементов, удовлетворяющих формуле. Однако онлайн-калькулятор определителя позволяет вычислить определитель заданных входных элементов матрицы.
Что такое недействительность?Нулевое значение можно определить как количество векторов в пустом пространстве данной матрицы. Размерность пустого пространства матрицы X называется нулевым значением матрицы X. Количество линейных отношений между атрибутами определяется размером пустого пространства. Вектор нулевого пространства Y может использоваться для идентификации этих линейных отношений.
Как найти нулевую матрицу?Вы можете использовать теорему о ранговом недействительности, чтобы найти его.
Теорема о ранговом недействительности помогает связать аннулирование матрицы данных с ранжированием и количеством атрибутов в данных. Теорема ранга нулевой определяется как
– Nullity X + Rank X = общее количество атрибутов X (которые являются общим количеством столбцов в X)
Как найти нулевое пространство матрицы?При попытке определить нулевое значение и ядро матрицы наиболее важным инструментом является метод исключения Гаусса-Жордана. Это полезный алгоритм, который может преобразовать заданную матрицу в ее сокращенную форму эшелона строк.Идея заключается в том, чтобы «уничтожить» как можно больше элементов матрицы. Это:
- Поменять местами две строки матрицы;
- Умножить строку на ненулевую константу;
Ключевым свойством здесь является то, что исходная матрица и ее сокращенная форма эшелона строк имеют одинаковый нуль и ранг. Благодаря своей полезности наша основа для калькулятора нулевого пространства может показать вам, как выглядит входная матрица после удаления исключения Гаусса Джордана.
Пример 1:
Нахождение нулевого пространства матрицы имеет 3 строки и 4 столбца.
x₁ x₂ x₃ x₄ ⌉
| y₁ y₂ y₃ y₄ |
⌊ z₁ z₂ z₃ z₄ ⌋
Калькулятор нулевого пространства матрицы первого шага использует метод исключения Жордана Гаусса, чтобы взять первую ячейку первой строки, x₁ (пока она не станет нулевой), и удалить следующие элементы с помощью операций с атомарной строкой. Мы добавляем соответствующий кратный верхней строки к двум другим, чтобы получить следующую матрицу:
x₁ x₂ x₃ x₄ ⌉
| 0 y₂ y₃ y₄ |
⌊ 0 z₂ z₃ z₄ ⌋
Далее, пустое пространство матричного калькулятора аналогично средней строке.Мы берем r₂ (пока оно не станет равным нулю) и используем его для удаления записей под ним. В результате мы получили форму массива:
x₁ x₂ x₃ x₄ ⌉
| 0 y₂ y₃ y₄ |
⌊ 0 0 z₃ z₄ ⌋
Теперь разница между исключением Гаусса Джордана и его упрощенной формой: калькулятор базиса нулевого пространства делит каждую строку на первую запись в этой строке, которая не равна 0. Это дает:
1 x₂ x₃ x₄ ⌉
| 0 1 y₃ y₄ |
⌊ 0 0 1 z₄ ⌋
И здесь мы часто заканчиваем алгоритм, например, когда ищем пространство столбцов в массиве.Фактически, мы уже можем читать полезную информацию из имеющихся у нас матриц. Те, которые появляются в первом ненулевом элементе каждой строки, называются ведущими. В этом примере они находятся в первом, втором и третьем столбцах из четырех столбцов.
Однако, чтобы найти основу нулевого пространства, мы немного изменим матрицу. Мы снова будем использовать базовую операцию со строками, но на этот раз пойдем снизу вверх. Во-первых, мы используем 1 в третьей строке, чтобы удалить запись над ней.
⌈ 1 x₂ 0 x₄ ⌉
| 0 1 0 y₄ |
⌊ 0 0 1 z₄ ⌋
Теперь мы делаем то же самое с 1 в среднем ряду, чтобы уничтожить верхнюю ячейку.
⌈ 1 0 0 x₄ ⌉
| 0 1 0 y₄ |
⌊ 0 0 1 z₄ ⌋
В конце концов, это матрица, которая дает нам основу нулевого пространства. Чтобы его определить, нам нужно соблюдать несколько простых правил.
Если в матрице нет столбцов без инициалов, то пустое пространство тривиально. Он имеет размерность 0 и содержит только нулевой вектор.
Если матрица содержит столбцы только с нулями, то базовый вектор eₖ является элементом базиса, который является вектором с 1 в k-й координате, в противном случае он равен нулю.
Однако онлайн-калькулятор Вронскиана поможет вам определить вронскиан для данного набора функций.
Пример 2:
Найдите нулевое пространство матрицы:
[3 7 2 9 7 6 5 3 8 3 2 9 3 2 8 3]
Решение:
Данная матрица:
[3 7 2 9 7 6 5 3 8 3 2 9 3 2 8 3]
Уменьшенная ступенчатая форма матрицы:
[1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1]
Чтобы найти пустое пространство, решите матричное уравнение:
[1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1] [x_1x_2x_3x_4] = [0 0 0 0]
Матрица нулевого пространства:
[0 0 0 0]
Обнуление матрицы: 0
Как работает калькулятор нулевого пространства?Онлайн-калькулятор нулевого пространства может найти основу для нулевого пространства матрицы, выполнив следующие действия:
Ввод:- Введите размер строк и столбцов матрицы и подставьте указанные значения во все поля.
- Если вы хотите найти нулевое пространство матрицы для случайных значений, нажмите на сгенерированную матрицу.
- Щелкните кнопку «Рассчитать нулевое пространство».
- Нулевое пространство вычислителя матриц находит основу для нулевого пространства матрицы с уменьшенной эшелонированной формой строки матрицы.
Нулевое пространство всегда содержит нулевой вектор, но могут существовать и другие векторы.
Что лежит в основе матрицы?При поиске основы нулевого пространства матрицы мы удаляем все избыточные векторы-столбцы из нулевого пространства и оставляем векторы-столбцы линейно независимыми. Итак, базис – это просто комбинация всех линейно независимых векторов.
Заключение:Используйте онлайн-основу для калькулятора нулевого пространства для вычисления всех векторов, которые отображаются в ноль заданным массивом. Обычно нулевое пространство имеет много элементов, поэтому вычисление всех векторов в основном означает вычисление основы нулевого пространства.
Артикул:Из источника Википедии: Ядро (линейная алгебра), Свойства, Применение к модулям, В функциональном анализе, Представление как умножение матриц, Свойства подпространства, Пространство строк матрицы.
Из источника Lumen Learning: использование матриц для решения систем уравнений, матричные уравнения, написание системы уравнений с матрицами, матрицами и операциями со строками, элементарные операции со строками (ERO), создание эквивалентных матриц с использованием элементарных операций со строками.
Из первоисточника Geek for Geek: пустое пространство и аннулирование матрицы, обобщенное описание, теорема ранга о нуле, левое нулевое пространство, неоднородные системы линейных уравнений.
Обращение матрицы методом исключения Гаусса-Жордана
Линейная алгебра – Матрицы: (урок 3 из 3)
Обращение матрицы методом исключения Гаусса-Жордана
Чтобы найти обратную матрицу $ A $ методом исключения Гаусса-Жордана, необходимо найти последовательность элементарных строковые операции, которые сокращают $ A $ до идентичности, а затем те же операции с $ I_n $ должны выполняться для получить $ A ^ {- 1} $.
Обратная матрица 2 $ \ times $ 2
Пример 1: Найти обратное
$ A = \ left [{\ begin {array} {* {20} {c}} 1 и 3 \\ 2 и 7 \ end {array}} \ right]
долларов СШАРешение:
Шаг 1: Присоедините единичную матрицу к правой части $ A $:
$ A = \ left [{\ begin {array} {* {20} {c}} 1 и 3 \\ 2 и 7 \ end {array} \ left | {\ begin {array} {* {20} {c}} \ color {blue} {1} & \ color {blue} {0} \\ \ color {синий} {0} & \ color {синий} {1} \ end {array}} \ right.} \Правильно] $
Шаг 2: Применяйте к этой матрице операции со строками, пока левая часть не уменьшится до $ I $. Вычисления:
$$ \ begin {выровнено} & \ left [{\ begin {array} {* {20} {c}} \ color {красный} {1} & \ color {красный} {3} \\ {2 – \ color {blue} {2} \ cdot \ color {red} {1}} & {7 – \ color {blue} {2} \ cdot \ color {red} {3}} \ end {array} \ left | {\ begin {array} {* {20} {c}} \ цвет {красный} {1} & \ цвет {красный} {0} \\ {0 – \ color {blue} {2} \ cdot \ color {red} {1}} & {1 – \ color {blue} {2} \ cdot \ color {red} {0}} \ end {array}} \ right.} \ right] \ \ Row2 = Row2 – \ color {blue} {2} \ cdot \ color {red} {Row1} \\ & \ left [{\ begin {array} {* {20} {c}} 1 и 3 \\ 0 и 1 \ end {array} \ left | {\ begin {array} {* {20} {c}} 1 & 0 \\ {- 2} & 1 \ end {array}} \ right.} \ right] \\ & \ left [{\ begin {array} {* {20} {c}} {1 – \ color {blue} {3} \ cdot \ color {red} {0}} & {3 – \ color {blue} {3} \ cdot \ color {red} {1}} \\ \ color {красный} {0} & \ color {красный} {1} \ end {array} \ left | {\ begin {array} {* {20} {c}} {1 – \ color {blue} {3} \ cdot \ color {red} {(- 2)}} & {0 – \ color {blue} {3} \ cdot \ color {red} {1}} \\ \ color {красный} {- 2} & \ color {красный} {1} \ end {array}} \ right.{-1} = \ left [{\ begin {array} {* {20} {c}} 7 & {- 3} \\ {-2} & 1 \ end {array}} \ right] $
Необратимая матрица
Если $ A $ необратимо , то слева появится нулевая строка.
Пример 2: Найти обратное
$ A = \ left [{\ begin {array} {* {20} {c}} 1 & {- 3} \\ {- 2} и 6 \ end {array}} \ right] $
Решение:
Шаг 1: Присоедините единичную матрицу к правой части A:
$ \ left [{\ begin {array} {* {20} {c}} 1 & {- 3} \\ {- 2} и 6 \ end {array} \ left | {\ begin {array} {* {20} {c}} \ color {blue} {1} & \ color {blue} {0} \\ \ color {синий} {0} & \ color {синий} {1} \ end {array}} \ right.} \Правильно] $
Шаг 2: Применение операций со строками
$ \ left [{\ begin {array} {* {20} {c}} \ color {красный} {1} & \ color {красный} {- 3} \\ {- 2 + \ color {blue} {2} \ cdot \ color {red} {1}} & {6 + \ color {blue} {2} \ cdot \ color {red} {(- 3)}} \ end {array} \ left | {\ begin {array} {* {20} {c}} \ цвет {красный} {1} & \ цвет {красный} {0} \\ {0 + \ color {blue} {2} \ cdot \ color {red} {1}} & {1 + \ color {blue} {2} \ cdot \ color {red} {0}} \ end {array}} \ right.} \ right] Row2 = Row2 + \ color {red} {2} \ cdot \ color {blue} {Row1} $
$ \ left [{\ begin {array} {* {20} {c}} 1 & {- 3} \\ \ color {красный} {0} & \ color {красный} {0} \ end {array} \ left | {\ begin {array} {* {20} {c}} 1 & 0 \\ 0 и 1 \ end {array}} \ right.} \ right] _ {\ color {red} {\ leftarrow ZERO \ \ ROW}} $
Шаг 3: Вывод: Эта матрица необратима.
Обращение 3 $ \ times $ 3 матриц
Пример 1: Найти обратное
$ A = \ left [{\ begin {array} {* {20} {c}} 1 и 2 и 3 \\ 2 и 5 и 3 \\ 1 и 0 и 8 \ end {array}} \ right] $
Решение:
Шаг 1: Присоедините единичную матрицу к правой части A:
$ \ left [{\ begin {array} {* {20} {c}} 1 и 2 и 3 \\ 2 и 5 и 3 \\ 1 и 0 и 8 \ end {array} \ left | {\ begin {array} {* {20} {c}} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 и 0 и 1 \ end {array}} \ right. {R2 = R2 – \ color {синий} {2} \ cdot R1} \ left [{\ begin {array} {* {20} {c}} 1 и 2 и 3 \\ {2 – \ color {blue} {2} \ cdot 1} & {5 – \ color {blue} {2} \ cdot 2} & {3 – \ color {blue} {2} \ cdot 3} \\ {1 \ color {red} {-} 1} & {0 \ color {red} {-} 2} & {8 \ color {red} {-} 3} \ end {array} \ left | {\ begin {array} {* {20} {c}} 1 & 0 & 0 \\ {0 – \ color {blue} {2} \ cdot 1} & {1 – \ color {blue} {2} \ cdot 0} & {0 – \ color {blue} {2} \ cdot 0} \\ {0 \ color {red} {-} 1} & {0 \ color {red} {-} 0} & {1 \ color {red} {-} 0} \ end {array}} \ right.{} \ left [{\ begin {array} {* {20} {c}} 1 и 2 и 3 \\ 0 & 1 & {- 3} \\ {0 \ color {blue} {+ 2} \ cdot 0} & {- 2 \ color {blue} {+ 2} \ cdot 1} & {5 \ color {blue} {+ 2} \ cdot (- 3) } \ end {array} \ left | {\ begin {array} {* {20} {c}} 1 & 0 & 0 \\ {- 2} & 1 & 0 \\ {- 1 \ color {blue} {+ 2} \ cdot (- 2)} & {0 \ color {blue} {+ 2} \ cdot 1} & {1 \ color {blue} {+ 2} \ cdot 0 } \ end {array}} \ right.} \ right] $
$ \ left [{\ begin {array} {* {20} {c}} 1 и 2 и 3 \\ 0 & 1 & {- 3} \\ 0 & 0 & {- 1} \ end {array} \ left | {\ begin {array} {* {20} {c}} 1 & 0 & 0 \\ {- 2} & 1 & 0 \\ {- 5} & 2 & 1 \ end {array}} \ right.{} \ left [{\ begin {array} {* {20} {c}} 1 и 2 и 3 \\ 0 & 1 & {- 3} \\ 0 и 0 и 1 \ end {array} \ left | {\ begin {array} {* {20} {c}} 1 & 0 & 0 \\ {- 2} & 1 & 0 \\ 5 & {- 2} & {- 1} \ end {array}} \ right.} \ right] $
$ \ left [{\ begin {array} {* {20} {c}} 1 и 2 и 3 \\ 0 & 1 & {- 3} \\ 0 и 0 и 1 \ end {array} \ left | {\ begin {array} {* {20} {c}} 1 & 0 & 0 \\ {- 2} & 1 & 0 \\ {- 5} & {- 2} & 1 \ end {array}} \ right.{R1 = R1 – 3 \ cdot R3} \ left [{\ begin {array} {* {20} {c}} 1 и 2 и 0 \\ 0 & 1 & 0 \\ 0 и 0 и 1 \ end {array} \ left | {\ begin {array} {* {20} {c}} {- 14} & 6 и 3 \\ {13} & {- 5} & {- 3} \\ 5 & {- 2} & {- 1} \ end {array}} \ right.} \ right] $
$ \ left [{\ begin {array} {* {20} {c}} 1 и 2 и 0 \\ 0 & 1 & 0 \\ 0 и 0 и 1 \ end {array} \ left | {\ begin {array} {* {20} {c}} {- 14} & 6 и 3 \\ {13} & {- 5} & {- 3} \\ 5 & {- 2} & {- 1} \ end {array}} \ right.{- 1} = \ left [{\ begin {array} {* {20} {c}} {- 40} & {16} & 9 \\ {13} & {- 5} & {- 3} \\ 5 & {- 2} & {- 1} \ end {array}} \ right] $
Gauss Jordan 4×4. Простой пример нахождения обратной матрицы для матрицы 4×4 с использованием исключения Гаусса-Жордана
Этот онлайн-калькулятор поможет вам решить систему линейных уравнений методом исключения Гаусса-Жордана. Воспользовавшись этим онлайн-калькулятором, вы получите подробное пошаговое решение вашей задачи, которое поможет понять алгоритм решения системы линейных уравнений методом исключения Гаусса-Жордана.
Измените имена переменных в системе. В этом онлайн-калькуляторе можно вводить только целые числа, десятичные дроби или дроби. Более подробную информацию читайте в этих правилах. Количество уравнений в системе: 2 3 4 5 6 Измените имена переменных в системе.
Попробуйте онлайн-калькуляторы. Решение уравнений. Решение квадратных уравнений. Решение биквадратных уравнений. Решение систем линейных уравнений подстановкой. Калькулятор исключения Гаусса Калькулятор линейных уравнений: правило Крамера Калькулятор линейных уравнений: метод обратной матрицы Показать все онлайн-калькуляторы.
Попробуйте решить упражнения из уравнений темы. Квадратные уравнения.
Экспоненциальные уравнения. Система линейных уравнений с 2-мя переменными. Система линейных уравнений с 3-мя переменными. Система линейных уравнений с 4-мя переменными. Показать все онлайн-упражнения.Terima kasih blog ini sangat memberu saya dalam mengulangi ingatan materi mata kuliah Aljabar Linear Matriks:. Толонг банту джаваб да.
Ган, мау таня кало хасильня метод гаусс дан метод гаусс джордан ня тидак равный иту багаймана я? Apakah memang harus sama nilai akhir nya atau engga juga ya? Makasih, ngebantu banget, udah nyari kesana kesini tapi ketentuannya kurang jelas.
Добро пожаловать Не стесняйтесь исследовать Опубликовано на Eliminasi Gauss. Dengan melakukan operasi baris sehingga matriks tersebut menjadi matriks янь baris.
Инверсия матрицы 3×3Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Цири цири Методе Гаусс адалах. Eliminasi Gauss-Jordan adalah pengembangan дари исключения Gauss yang hasilnya lebih sederhana lagi.
Metode Eliminasi Gauss & Gauss Jordan 4 × 4
Ini juga dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks.Метод ini digunakan untuk mencari invers dari sebuah matriks. Prosedur umum untuk metode elleasi Gauss-Jordan ini adalah. Ubah sistem persamaan linier yang ingin dihitung menjadi matriks augmentasi.
Lakukan operasi baris element pada matriks augmentasi A b Untuk mengubah matriks.
Калькулятор исключения по Гауссу
A menjadi dalam bentuk baris eselon yang tereduksi. Конто Соал Унтук Гаусс дан Гаусс Иордания. Langkah terakhir adalah substitusikan balik dari bawah jadi.Sebenarnya hanya tinggal melanjutkan дари langkah elleasi gauss seperti di tambahkan langkah 8 sampai langkah 10, tapi saya mengulanginya kembali dari awal.
Ярлык: Artikel Umum. Устранение Гаусса, так называемое сокращение строк, представляет собой алгоритм в линейной алгебре для решения системы линейных уравнений. Под ним обычно понимают последовательность операций, выполняемых над соответствующей матрицей коэффициентов.
Этот метод также можно использовать для определения ранга матрицы, для вычисления определителя матрицы и для вычисления обратного значения обратимой квадратной матрицы.Метод назван в честь Карла Фридриха Гаусса. Чтобы выполнить сокращение строк в матрице, используется последовательность элементарных операций со строками для изменения матрицы до тех пор, пока нижний левый угол матрицы не будет заполнен нулями, насколько это возможно. Есть три типа операций с элементарными строками: Используя эти операции, матрица всегда может быть преобразована в верхнюю треугольную матрицу, фактически имеющую форму эшелона строк.
Когда все ведущие коэффициенты крайнего левого ненулевого элемента в каждой строке равны 1, и каждый столбец, содержащий ведущий коэффициент, имеет нули в другом месте, матрица называется сокращенной эшелонированной строкой.
Эта окончательная форма уникальна; другими словами, он не зависит от последовательности используемых строковых операций. Например, в следующей последовательности операций со строками, где несколько элементарных операций могут выполняться на каждом шаге, третья и четвертая матрицы – это матрицы в форме эшелона строк, а конечная матрица – это уникальная сокращенная форма эшелона строк.
Использование строковых операций для преобразования матрицы в сокращенную форму эшелона строк иногда называют исключением Гаусса-Жордана. Некоторые авторы используют термин гауссовское исключение для обозначения процесса до тех пор, пока он не достигнет своей верхней треугольной формы или нередуцированной формы эшелона строк.
По вычислительным причинам при решении систем линейных уравнений иногда предпочтительнее остановить операции со строками до того, как матрица будет полностью сокращена. Процесс сокращения строк использует элементарные операции со строками и может быть разделен на две части. Первая часть, иногда называемая прямым исключением, сводит данную систему к форме эшелона строк, по которой можно определить, нет ли решений, единственного решения или бесконечного множества решений.
Вторая часть, иногда вызываемая обратной подстановкой, продолжает использовать операции со строками до тех пор, пока не будет найдено решение; Другими словами, он преобразует матрицу в сокращенный ряд строк.Другая точка зрения, которая оказывается очень полезной для анализа алгоритма, заключается в том, что сокращение строк приводит к матричному разложению исходной матрицы.
Операции с элементарными строками можно рассматривать как умножение слева от исходной матрицы на элементарные матрицы.
Как обойти иммобилайзер vymodoreВ качестве альтернативы последовательность элементарных операций, сокращающих одну строку, может рассматриваться как умножение на матрицу Фробениуса.
Затем первая часть алгоритма вычисляет разложение LU, в то время как вторая часть записывает исходную матрицу как произведение однозначно определенной обратимой матрицы и однозначно определенной уменьшенной матрицы эшелона строк.
Существует три типа операций с элементарными строками, которые могут выполняться со строками матрицы :.
Что такое paoЕсли матрица связана с системой линейных уравнений, то эти операции не изменяют набор решений. Следовательно, если целью является решение системы линейных уравнений, то использование этих операций со строками может упростить задачу. Для каждой строки в матрице, если строка не состоит только из нулей, то крайний левый ненулевой элемент называется ведущим коэффициентом или опорной точкой этой строки.Здесь вы можете бесплатно решать системы одновременных линейных уравнений с помощью калькулятора исключения Гаусса-Жордана с комплексными числами онлайн с очень подробным решением.
Наш калькулятор может решать системы с одним уникальным решением, а также неопределенные системы, которые имеют бесконечно много решений.
Starbien omnilifeВ этом случае вы получите зависимость одних переменных от других, которые называются свободными. Вы также можете проверить свою линейную систему уравнений на непротиворечивость, используя наш Калькулятор исключения Гаусса-Жордана.Чтобы решить систему линейных уравнений методом исключения Гаусса-Жордана, вам необходимо проделать следующие шаги. Чтобы лучше понять алгоритм исключения Гаусса-Жордана, введите любой пример, выберите вариант «очень подробное решение» и изучите решение.
Нужно включить. Калькулятор исключения Гаусса-Жордана. Комплексные числа больше. Десятичная дробь. Очень подробное решение. Вы можете скопировать и вставить всю матрицу прямо здесь. Элементы должны быть разделены пробелом. Каждая строка должна начинаться с новой строки.«Элементарные операции со строками» – это простые вещи, такие как добавление строк, умножение и замена местами. Мы начинаем с матрицы A и записываем ее с помощью матрицы идентичности I рядом с ней :.
Это называется «Расширенная матрица». Матрица идентичности 3×3. Теперь мы делаем все возможное, чтобы превратить матрицу «А» слева в матрицу идентичности. Цель состоит в том, чтобы матрица A имела 1 с по диагонали и 0 в других местах в качестве матрицы идентичности. И обратите внимание: не существует «правильного способа» сделать это, просто продолжайте экспериментировать, пока мы не добьемся успеха!
Сандало Anne con suede nara natural dark womens taccoЭто то же самое? Какой метод вы предпочитаете? Посмотрите, сможете ли вы сделать это сами, я бы начал с деления первого ряда на 4, но вы делаете это по-своему.Вы можете проверить свой ответ, используя Матричный калькулятор, используя кнопку «inv A». Общий эффект от всех операций со строками такой же, как при умножении на A Hide Ads About Ads. Это интересный способ найти обратную матрицу: поиграйте с строками, складывая, умножая или меняя местами, пока мы не превратим матрицу A в матрицу идентичности I.
Матрица идентичности «Матрица идентичности» – это матричный эквивалент числа «1»: Матрица идентичности 3×3 Это «квадрат» имеет такое же количество строк, что и столбцы. У него 1 с по диагонали и 0 с везде.
Его символ – заглавная буква I. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Узнать больше Принять. Тригонометрия конических сечений. Конические сечения.
Матрицы векторов. Химические реакции Химические свойства. Правильный ответ :. Давай еще раз попробуем :. Попробуйте еще больше упростить.
Метод Гаусса-Джордана | инверсия матрицы
Матрица, состоящая из чисел, упорядоченных по строкам и столбцам, чрезвычайно полезна в большинстве научных областей.Умножение на обратное Войти Войти через Office Войти через Facebook. Присоединяйтесь к миллиону счастливых пользователей! Зарегистрируйтесь бесплатно :.
Присоединяйтесь с помощью Office Присоединяйтесь с помощью Facebook. Создать мою учетную запись. Транзакция не удалась! Пожалуйста, попробуйте еще раз, используя другой способ оплаты. Подпишитесь, чтобы получить больше :. Отсутствуют данные пользователя. Обратитесь в службу поддержки. Мы хотим, чтобы ваш отзыв был необязательным. Отменить Отправить. Создание PDF См. Все крайние точки области неявной производной производной критические точки обратные точки перегиба Лапласа асимптоты частичных дробей собственное значение собственного вектора Лапласа область Тейлора пересекает диапазон вершинный фактор расширяет наклонные точки поворота.9 февраля, автор: доктор
Асприха Петерс 1 Комментарий. Метод Гаусса-Жордана для нахождения обратной матрицы. Теперь, чтобы получить обратную матрицу, я выполню несколько шагов. Если интересно, вы можете прочитать все подробности процедуры в моем посте на обратной матрице.
Так будет выглядеть результирующая матрица. И моя цель – вывести единичную матрицу в левую часть. И для этого я должен использовать операции со строками в этой матрице. Согласно методу Гаусса-Жордана, матрица в правой части будет обратной матрицей.
Отказ от ответственности: Ни один из этих примеров не является моим. Я выбрал их из какой-то книги или книг. Я также дал соответствующую ссылку в конце сообщения. Следовательно, данная матрица есть. Как я вижу, единичная матрица находится в левой части матрицы. Это означает, что правая матрица является обратной матрицей. И это ответ на этот пример. Большое спасибо за то, что прочитали это. Пожалуйста, дайте мне знать, как вы к этому относитесь. Скоро я вернусь снова с новым постом.
А пока, пока, пока !! Все письменные материалы и фотографии, опубликованные в этом блоге, защищены авторским правом.Ваш электронный адрес не будет опубликован. Любопытен к природе. Больше обо мне. Прежде всего выясню определитель матрицы. Далее я определю кофактор каждого элемента матрицы. В конце концов, я выясню транспонирование новой матрицы.
Решенные примеры метода Гаусса-Жордана для определения инверсии матрицы Заявление об отказе от ответственности: Ни один из этих примеров не является моим. Вот мой первый пример. А теперь другой пример. А теперь мой последний пример. Любопытный к природе, а также начинающий блогер.Оставить комментарий Отменить ответ Ваш электронный адрес не будет опубликован. Оставьте это поле пустым. О нас Обзор Политика конфиденциальности. Продолжая просматривать сайт, вы соглашаетесь на использование файлов cookie. Да, я понимаю.
Калькулятор метода Гаусса Зейделя. Выберите веб-сайт
4j веб-сайт
Метод Гаусса-Зейделя используется для решения уравнений линейной системы. Это итерационный метод решения n линейного уравнения с неизвестными переменными.
Этот метод очень прост и используется в цифровых компьютерах для вычислений.Метод Гаусса-Зейделя является модификацией метода гауссовых итераций.
Данная модификация сокращает количество итераций. В этих методах значение unknown сразу уменьшает количество итераций, вычисленное значение заменяет более раннее значение только в конце итерации. Из-за этого методы Гаусса-Зейделя сходятся намного быстрее, чем методы Гаусса.
Калькулятор Гаусса Зейделя
В методах Гаусса Зейделя количество итераций, требуемых для получения решения, намного меньше по сравнению с методом Гаусса.Давайте разберемся с методом Гаусса-Зейделя на примере.
В приведенном выше уравнении величины P kQ kY kk и Y ki известны и не меняются в течение итерационного цикла. Ниже показаны значения C k и D k, которые вычисляются в начале и используются на каждой итерации. Скорость сходимости может быть увеличена за счет использования коэффициента ускорения решения, получаемого после каждой итерации.
Коэффициент ускорения – это множитель, который увеличивает коррекцию между значениями напряжения в двух последовательных итерациях.Для действительной и мнимой составляющих напряжения используются разные ускоряющие факторы. Выбор конкретного значения коэффициента ускорения зависит от параметров системы. Ваш электронный адрес не будет опубликован.
Сохраните мое имя, адрес электронной почты и веб-сайт в этом браузере, чтобы в следующий раз я оставил комментарий. Circuit Globe Все об электротехнике и электронике. Электронное оборудование. Оставить ответ Отменить ответ Ваш электронный адрес не будет опубликован. Этот онлайн-калькулятор поможет вам решить систему линейных уравнений с использованием метода исключения Гаусса-Джордана.
Воспользовавшись этим онлайн-калькулятором, вы получите подробное пошаговое решение вашей задачи, которое поможет вам понять алгоритм решения системы линейных уравнений методом исключения Гаусса-Жордана. Измените имена переменных в системе. В этом онлайн-калькуляторе можно вводить только целые числа, десятичные дроби или дроби. Более подробную информацию читайте в этих правилах. Количество уравнений в системе: 2 3 4 5 6 Измените имена переменных в системе.
Попробуйте онлайн-калькуляторы. Решение уравнений. Решение квадратных уравнений. Решение биквадратных уравнений. Решение систем линейных уравнений подстановкой. Калькулятор исключения Гаусса Калькулятор линейных уравнений: правило Крамера Калькулятор линейных уравнений: метод обратной матрицы Показать все онлайн-калькуляторы.
Попробуйте решить упражнения из уравнений темы. Квадратные уравнения. Экспоненциальные уравнения. Система линейных уравнений с 2-мя переменными.
Система линейных уравнений с 3-мя переменными.Система линейных уравнений с 4-мя переменными. Показать все онлайн-упражнения. Здесь вы можете бесплатно решать системы одновременных линейных уравнений с помощью Калькулятора исключения Гаусса-Жордана с комплексными числами онлайн с очень подробным решением.
Наш калькулятор может решать системы с одним уникальным решением, а также неопределенные системы, которые имеют бесконечно много решений.
Tts mp3В этом случае вы получите зависимость одних переменных от других, которые называются свободными.Вы также можете проверить свою линейную систему уравнений на непротиворечивость, используя наш Калькулятор исключения Гаусса-Жордана.
Чтобы решить систему линейных уравнений методом исключения Гаусса-Жордана, вам необходимо проделать следующие шаги. Чтобы лучше понять алгоритм исключения Гаусса-Жордана, введите любой пример, выберите вариант «очень подробное решение» и изучите решение. Вам нужно включить его. Калькулятор исключения Гаусса-Жордана. Комплексные числа больше. Десятичная дробь. Очень подробное решение. Вы можете скопировать и вставить всю матрицу прямо здесь.Элементы должны быть разделены пробелом.
Метод Гаусса-Зейделя
Каждая строка должна начинаться с новой строки. Обновлено 29 мая Для каждого диагонального элемента вычисляется приблизительное значение. Затем процесс повторяется до тех пор, пока он не сходится. Метод Гаусса-Зейделя: метод Гаусса-Зейделя, также известный как метод Либмана или метод последовательного смещения, представляет собой итерационный метод, используемый для решения линейной системы уравнений.
Bhartendu Получено 12 апреля. Если я использую случайно сгенерированную матрицу для A и b e.В вашем примере вы сравниваете 2 разных метода с разными исходными предположениями?
Это не кажется актуальным. И если я использую одно и то же исходное предположение, у двух методов будет одинаковая конвергенция. Узнайте о Live Editor. Выберите веб-сайт, чтобы получать переведенный контент, если таковой имеется, и просматривать местные события и предложения. В зависимости от вашего местоположения мы рекомендуем вам выбрать :. Выберите китайский сайт на китайском или английском, чтобы обеспечить наилучшую производительность сайта. Сайты других стран MathWorks не оптимизированы для посещения из вашего местоположения.
Переключить главную навигацию.
Обмен файлами. Найдите MathWorks. Откройте мобильный поиск. Пробное программное обеспечение. Теперь вы подписаны на это представление. Вы будете видеть обновления в своей ленте действий. Вы можете получать электронные письма, в зависимости от ваших предпочтений в отношении уведомлений. Метод Гаусса-Зейделя, метод Якоби, версия 1.
Follow Download. Обзор Функции Примеры.
Коды игрушек для robloxЦитировать как Bhartendu Комментарии и рейтинги Theekapat Charnvitayapong Theekapat Charnvitayapong просмотреть профиль.Майкл Гастингс Майкл Гастингс просмотреть профиль. Tijn Blommaert Tijn Blommaert просмотреть профиль.
Линейный датчик ccdNo One No One просмотреть профиль. Онкарнатх Тхакур Онкарнатх Тхакур просмотреть профиль. Бхартенду Бхартенду посмотреть профиль. Код используется для обучения и практики. Приведенное решение является действительным и правильным. Пушпенду Гош Пушпенду Гхош просмотреть профиль. Метод Гаусса-Зейделя – это метод, используемый для решения линейной системы уравнений. Этот метод похож на метод Якоби, и точно так же для обеспечения сходимости достаточно строгого или неприводимого диагонального доминирования системы, а это означает, что метод будет работать.
Это матричное выражение представляет в основном академический интерес и не используется для программирования метода. Скорее, используется элементный подход: Обратите внимание, что при вычислении используются только те элементы, которые уже были вычислены, и только те элементы, которые еще не были продвинуты на итерацию.
Это означает, что дополнительное хранилище не требуется, и вычисления могут выполняться на месте замены. Хотя это может показаться незначительной проблемой, для больших систем маловероятно, что каждая итерация может быть сохранена.Таким образом, в отличие от метода Якоби, нам не нужно выполнять какое-либо векторное копирование, если мы хотим использовать только один вектор хранения.
Итерация обычно продолжается до тех пор, пока изменения, внесенные в итерацию, не окажутся ниже некоторого допуска. Метод всегда будет сходиться, если матрица A строго или неприводимо диагонально доминирует. Строгое диагональное преобладание строки означает, что для каждой строки абсолютное значение диагонального члена больше, чем сумма абсолютных значений других членов :. Метод Гаусса-Зейделя иногда сходится, даже если это условие не выполняется.Однако необходимо, чтобы диагональные члены в матрице были больше по величине, чем другие члены.
В некоторых случаях нам даже не нужно явно представлять матрицу, которую мы решаем. Рассмотрим простую задачу уравнения теплопроводности.
Точное решение этой проблемы есть.
Сдвиг экрана без корняСтандартная дискретизация методом конечных разностей второго порядка равна. В терминах матрицы это можно записать как. Однако для любого заданного фор мы можем писать. Затем, переходя от одного к другому по вектору решения, мы можем вычислить следующую итерацию по двум окружающим значениям.Обратите внимание, что в этой схеме используется предыдущая итерация, а в этой схеме – текущая:
В следующей таблице приведены результаты 10 итераций с 5 узлами, 3 внутренними и 2 граничными, а также ошибка нормы. В этой ситуации важно направление, которое мы «прогоняем» – если мы проходим через вектор решения в противоположном направлении, решение перемещается от выбранного начального условия, равного нулю, повсюду во внутренней части быстрее.
Итерация определяется как.В этом примере с игрушкой нет большого штрафа за выбор неправильного направления развертки. Для некоторых из более сложных вариантов Гаусса-Зейделя существует существенный штраф – направление развертки в неопределенном смысле определяет направление, в котором распространяется информация. Перейти к: навигационный поиск. Просмотры Страница Обсуждение Просмотр истории исходников. Моя вики Войти. Этот процесс поиска решения данного линейного уравнения называется методом Гаусса-Зейделя.
самый быстрый способ решения задач метода Гаусса ЗиделяБолее подробно, A, x и b в их компонентах: Тогда разложение матрицы A на ее нижнюю треугольную составляющую и ее верхнюю треугольную составляющую определяется выражением :.Система линейных уравнений переписывается как :.
Метод Гаусса-Зейделя теперь решает левую часть этого выражения для x, используя предыдущее значение для x в правой части.
Формально это можно записать так: Мы хотим использовать уравнение. Теперь мы можем найти оставшиеся вещи: теперь у нас есть T и C, и мы можем использовать их для итеративного получения векторов x. Чем точнее предположение, тем быстрее будет работать алгоритм. Фактически, матрица A строго диагонально доминирует, но не положительно определена.
Введение
Если вам нравится GeeksforGeeks и вы хотите внести свой вклад, вы также можете написать статью, используя свой вклад. Посмотрите, как ваша статья появляется на главной странице GeeksforGeeks, и помогите другим гикам. Пожалуйста, улучшите эту статью, если вы обнаружите что-то неправильное, нажав кнопку «Улучшить статью» ниже. Пишем код в комментарии? Пожалуйста, используйте ide. Определение нашей функции как seidel, которая принимает 3 аргумента.
Определение длины 3. Рекомендуемые сообщения: Python Разница между двумя датами в минутах с использованием datetime.Ознакомьтесь с опубликованными авторами статьями. Загрузить Комментарии. Калькуляторы и конвертеры. Расчет T 0. Пример калькулятора. Этот метод применим к строго диагонально доминирующим или симметричным положительно определенным матрицам A.
В приведенном ниже калькуляторе Гаусса Зейделя введите количество уравнений от 2 до 10 для проверки, введите значения для уравнений и нажмите «Рассчитать», чтобы найти значения переменных в уравнении. Свойства метода Гаусса Зейделя зависят от матрицы A.
Метод Либмана – это итерационный метод, который очень полезен для быстрого решения линейных уравнений без особых вычислений. Узнайте больше о Scribd Membership Home. Читайте бесплатно в течение 30 дней. Намного больше, чем просто документы. Откройте для себя все, что Scribd может предложить, включая книги и аудиокниги от крупных издателей. Начать бесплатную пробную версию Отменить в любой момент. Загружено Mauricio Gomes. Дата загрузки 27 июня. Вы нашли этот документ полезным? Это содержание неприемлемо?
Сообщить об этом документе.Отметить неприемлемое содержание. Скачать сейчас. Связанные заголовки. Карусель Назад Карусель Далее.
Creative, Inc.
Калькулятор обратной матрицы gauss jordan. Обращение матрицы с использованием исключения Гаусса-Жордана
«Элементарные операции со строками» – это простые вещи, такие как добавление строк, умножение и замена местами. Мы начинаем с матрицы A и записываем ее с помощью матрицы идентичности I рядом с ней :. Это называется «Расширенная матрица». Матрица идентичности 3×3. Теперь мы делаем все возможное, чтобы превратить матрицу «А» слева в матрицу идентичности.Цель состоит в том, чтобы матрица A имела 1 с по диагонали и 0 в других местах в качестве матрицы идентичности. И обратите внимание: не существует «правильного способа» сделать это, просто продолжайте экспериментировать, пока мы не добьемся успеха!
Это то же самое? Какой метод вы предпочитаете? Посмотрите, сможете ли вы сделать это сами, я бы начал с деления первого ряда на 4, но вы делаете это по-своему. Вы можете проверить свой ответ, используя Матричный калькулятор, используя кнопку «inv A».
Суммарный эффект от всех операций со строками такой же, как и при умножении на A Hide Ads About Ads.Это интересный способ найти обратную матрицу: поиграйте с строками, добавляя, умножая или меняя местами, пока мы не превратим матрицу A в матрицу идентичности I. Матрица идентичности “Матрица идентичности” – это матричный эквивалент числа “1”. “: Матрица идентичности 3×3. Это” квадрат “с тем же количеством строк, что и столбцы. У него 1 с по диагонали и 0 с везде.
Его символ – заглавная буква I. Здесь вы можете решать системы одновременных линейных уравнений с помощью Калькулятора исключения Гаусса-Жордана с комплексными числами онлайн бесплатно с очень подробным решением.
Наш калькулятор может решать системы с одним уникальным решением, а также неопределенные системы, которые имеют бесконечно много решений. В этом случае вы получите зависимость одних переменных от других, которые называются свободными.
Вы также можете проверить свою линейную систему уравнений на непротиворечивость, используя наш Калькулятор исключения Гаусса-Жордана. Чтобы решить систему линейных уравнений методом исключения Гаусса-Жордана, вам необходимо проделать следующие шаги. Чтобы лучше понять алгоритм исключения Гаусса-Жордана, введите любой пример, выберите вариант «очень подробное решение» и изучите решение.Вам нужно включить его. Калькулятор исключения Гаусса-Жордана. Комплексные числа больше. Десятичная дробь. Очень подробное решение.
Вы можете скопировать и вставить всю матрицу прямо сюда. Элементы должны быть разделены пробелом. Каждая строка должна начинаться с новой строки. Вы можете повторно загружать эту страницу сколько угодно раз и каждый раз получать новый набор чисел. Вы также можете выбрать матрицу другого размера внизу страницы.
Если вам сначала нужна дополнительная информация, вернитесь к «Введение в матрицы».ПРИМЕЧАНИЕ. Если вы пользуетесь телефоном, вы можете прокрутить любую широкую матрицу на этой странице вправо или влево, чтобы увидеть все выражение. Мы записываем матрицу A слева и матрицу идентичности I справа, разделенную пунктирной линией, как показано ниже.
Служба поддержки клиентов Yatra chennaiРезультат называется расширенной матрицей. Затем мы выполняем несколько операций со строками над двумя матрицами, и наша цель – получить единичную матрицу слева следующим образом: Технически, мы сводим матрицу A к формальному эшелону строк, так называемому каноническому виду строк.Мы достигли нашей цели – создать матрицу идентичности слева.
Таким образом, мы можем заключить, что обратная матрица A является правой частью расширенной матрицы :.
Обращение матрицы методом исключения Гаусса-Жордана. Откуда взялись матрицы и детерминанты? Матрицы и детерминанты в технике Фараза [Решено! Имя необязательно. Интерактивный апплет Детерминанты Системы уравнений 3×3 2. Большие детерминанты 3.
Цена крема Veet 30Матрицы 4. Умножение матриц 4a.Примеры умножения матриц 4b. Нахождение обратной матрицы 5a.
Калькулятор обратной матрицы
Простой калькулятор матрицы 5b. Обращение матрицы с помощью исключения Гаусса-Жордана 6. Собственные значения и собственные векторы 8. Обращение матрицы с помощью исключения Гаусса-Жордана. Выберите интересующий вас размер матрицы и нажмите кнопку.
Телефонные пользователи. Простой калькулятор матриц. Матрицы и линейные уравнения. Вот метод поиска обратных матриц, который снижает вероятность заблудиться.Щелкните для поиска :.
Онлайн-решатель алгебры Этот решатель алгебры может решать широкий спектр математических задач. Перейти к: Онлайн-решатель алгебры. Заданная матрица задача состоит в том, чтобы найти обратную матрицу, используя метод Гаусса-Жордана. Что такое матрица? С матрицей можно выполнять следующие операции: сложение, вычитание, умножение или транспонирование матрицы и т. Д.
Дана квадратная матрица A, которая не является сингулярной, что означает, что определитель A отличен от нуля; Тогда существует матрица.
Инверсия матрицы возможна, только если выполняются следующие свойства :.Метод Гаусса-Жордана – это вариант метода исключения Гаусса, при котором выполняется операция сокращения строки для нахождения обратной матрицы. Шаги по нахождению обратной матрицы с использованием метода Гаусса-Жордана: Чтобы найти обратную матрицу, необходимо выполнить следующие шаги:
Таймер Toro 2020Вниманию читателя! Пишем код в комментарии? Пожалуйста, используйте ide. Статьи по Теме. Последнее обновление: 02 ноя, Матрица – это упорядоченный прямоугольный массив чисел.
Kitt car voiceМатрица, обратная матрице: дана квадратная матрица A, которая не является сингулярной, что означает, что определитель A отличен от нуля; Тогда существует матрица.Матрица PrintMatrix, порядок, порядок. Матрица InverseOfMatrix, заказ. Рекомендуемые статьи. Сгенерируйте матрицу таким образом, чтобы заданные элементы матрицы были равны побитовому ИЛИ всех соответствующих элементов строки и столбца сгенерированной матрицы. Статья предоставлена:.
Easy Normal Medium Hard Expert. Улучшено:. Самые посещаемые в Матрице. Загрузить комментарии. Мы используем файлы cookie, чтобы обеспечить вам лучший опыт просмотра на нашем веб-сайте. Используя этот онлайн-калькулятор, вы получите подробное пошаговое решение вашей проблемы, которое поможет вам понять алгоритм, как найти обратную матрицу с использованием Гаусса. устранение.
В этом онлайн-калькуляторе можно вводить только целые числа или дроби. Более подробную информацию читайте в этих правилах.
Калькулятор обратной матрицы (исключение Гаусса)
Дополнительные возможности калькулятора обратной матрицы Используйте клавиши и на клавиатуре для перемещения между полями в калькуляторе. Обратная матрица. В этом онлайн-калькуляторе можно вводить только целые числа, десятичные дроби или дроби. Этот калькулятор обратной матрицы поможет вам найти обратную матрицу. Ввод данных в калькулятор обратной матрицы В этом онлайн-калькуляторе можно вводить только целые числа или дроби.Библиотека: обратная матрица. Попробуйте онлайн-калькуляторы с матрицами. Калькулятор сложения и вычитания матриц. Калькулятор транспонирования матриц. Калькулятор скалярного умножения матриц. Калькулятор умножения матриц.
Попробуйте решать упражнения с матрицами. Сложение и вычитание матриц. Умножение матриц.Покажите все онлайн-упражнения. Миски с блюдцами отлично подходят для штабелирования. Мы также используем стеклянные рефрижераторные контейнеры Anchor для хранения ежедневных порций домашнего корма для кошек. Подробнее об этом ниже. Ключ к замораживанию продуктов в стекле – не наполнять банку слишком полной, так как продукты будут расширяться внутри контейнера.
Еще одно предостережение – не нагревать стекло слишком быстро. Дайте продуктам разморозиться при комнатной температуре, чтобы стекло не разбилось. Другой вариант для холодильника или морозильника – герметичные контейнеры из нержавеющей стали с плоским верхом от Life Without Plastic.
Их плоский верх позволяет легко складывать их друг в друга, а тот факт, что они герметичны, означает, что продукты можно хранить дольше. О моем любимом контейнере читайте здесь. Вы также можете научиться консервировать продукты в стеклянных банках или обезвоживать продукты на зиму.
Я действительно сомневался, что лучше пожертвовать эти нездоровые предметы или выбросить их на помойку. Оказывается, наш Оклендуотер прекрасно обходится без фильтра. Таким образом, теперь мы можем отказаться от использования пластиковых картриджей для фильтров для воды. Для тех, кому нужно фильтровать воду, Brita объединилась с Preserve, чтобы создать способ вторичной переработки пластиковых картриджей.
Калькулятор исключения Гаусса-Джордана
Все подготовленные картонные коробки соевого молока содержат пластик. Выжимаю свежий сок лимона и лайма и храню в стеклянных банках в холодильнике. И мы сами делаем хумус из сушеного нута или из сухой смеси, хранящейся в бункере для сыпучих продуктов Whole Foods. У меня нет проблем с приобретением подержанного пластика. Я также ищу предметы из переработанного пластика по той же причине.
Это решает несколько проблем с пластиком. Однако в последнее время у меня не было ни времени, ни сил, чтобы содержать свой компостный бак.Но здесь, в Окленде (а также в Беркли и Сан-Франциско) у нас есть компостирование в масштабах города.
Обратная матрица с использованием редукции Гаусса-Джордана / строки, пример 1Мы можем складывать все пищевые отходы (включая мясо) и загрязненную пищевыми продуктами бумагу вместе со дворовыми отходами в наши зеленые контейнеры. Подробнее о сборе мусора без полиэтиленовых пакетов для мусора. Если вы живете в Калифорнии, вам не следует смывать кошачий фекалий, если вы точно не знаете, что в нем нет паразита toxoplasma gondii, который вреден для каланов.
Уличные кошки восприимчивы к этому заболеванию, потому что они заражаются грызунами. Но самые лучшие игрушки для кошек из всех. Винные пробки, руки вниз. Если вы просматриваете самые популярные советы по ставкам в течение дня, то, скорее всего, они будут в основном состоят из советов по ставкам на скачки. Советы по ставкам на этот вечер, как правило, представляют собой преимущественно советы по ставкам на футбол в течение недели.
Если вы ищете советы по ставкам сегодня вечером, вы увидите, что ставки на спорт в США популярны, и мы регулярно видим, что советы по ставкам НБА занимают верхние строчки в списке самых популярных игроков.Советы по ставкам на выходные, конечно же, охватывают широкий спектр видов спорта, всего мы охватываем более 18 видов спорта в OLBG, так что вы можете найти советы по ставкам на все основные спортивные события Великобритании, Европы и мира. Следующие по популярности советы – наши советы по ставкам на теннис и советы по ставкам на гольф.
Мы также предоставляем бесплатные советы по ставкам на лигу регби, союз регби, крикет, американский футбол, бейсбол, баскетбол, хоккей, снукер, автогонки, дартс, бокс, киберспорт, волейбол, гандбол и борзых.Помимо этих основных категорий, мы также поделимся советами по ставкам на легкую атлетику на популярные события, такие как Олимпийские игры.
советов по зимним Олимпийским играм также будут доступны для зимних Олимпийских игр 2018 года в Южной Корее. У нас также есть специальный раздел сайта для Cheltenham Tipsa, отдельный сайт для подсказок Grand National, а также будет выделенная область для советов по ставкам на Чемпионат мира по футболу 2018. Все просто потому, что у нас самые лучшие информаторы. OLBG предоставляет советы по ставкам с 2002 года.Эти огромные призовые фонды привлекают и удерживают лучших игроков по ставкам на спорт.
Конкуренция ожесточенная, но это дает вам лучшие советы, так как типстеры постоянно ищут способы рекомендовать выгодные ставки на постоянной основе.
Мы анализируем все данные для вас, чтобы мы могли показать вам лучшие советы по ставкам от специалистов по типам для каждого вида спорта.
Bloxland коды декабрь 2019Например, если вы посмотрите на советы по ставкам на футбол, то прибыль по чаевым будет только для чаевых, размещенных на футболе.Все соревнования проводятся отдельно для каждого вида спорта, что позволяет нам выращивать для вас специалистов. Есть много способов проанализировать типстеров, чтобы понять, какие из них лучше всего.
Мы предоставляем данные о прибыли по всем ставкам на спорт за последние шесть месяцев, данные о стабильности прибыли, чтобы вы могли видеть, по каким из последних 6 месяцев типстеры приносили прибыль, а также другие интересные факторы, такие как прибыль в этом месяце, неделе или днях в выгода.
Самый простой способ увидеть всю эту информацию – через приложение OLBG Sports Betting Tips.Установите его прямо сейчас из iTunes или Google Play и обязательно проконсультируйтесь со специалистами-консультантами перед тем, как делать каждую ставку.

 25
25