Новости математического портала mathforyou.net
19/07/19:
Добавлен калькулятор выделения полного квадрата
Данный калькулятор позволяет выделить полный квадрат для любого квадратного полинома.
26/06/19:
Калькулятор разложения в ряд Фурье
Данный калькулятор позволяет разложить функцию в ряд Фурье.
02/06/19:
Калькулятор сходимости рядов
Данный калькулятор позволяет протестировать сходимость практически любого ряда.
19/04/19:
Калькулятор тригонометрических уравнений
Данный калькулятор позволяет решать практически любые виды тригонометрических уравнений.
02/04/19:
Калькулятор длины дуги
Данный калькулятор позволяет вычислить длину дуги некоторой функции при помощи определенного интеграла.
12/07/18:
Калькулятор области определения функции
Данный калькулятор позволяет находить область определения практически любой функции.
15/05/18:
Калькулятор СЛУ методом подстановки
Данный калькулятор позволяет решать системы линейных алгебраических уравнений методом подстановки с описанием подробного
решения на русском языке.
17/04/18:
Калькулятор СЛУ методом Крамера
Данный калькулятор позволяет решать системы линейных алгебраических уравнений методом Крамера с описанием подробного
решения на русском языке.
26/03/18:
Калькулятор экстремумов функции
С помощью данного калькулятора можно находить максимумы и минимумы функции, в том числе на заданном интервале.
23/03/18:
Бесплатное подробное решение
Теперь подробное решение для всех “наших” калькуляторов доступно совершенно БЕСПЛАТНО!
04/12/16:
Калькулятор построения графика функции
Калькулятор полностью переделан, работает в любом браузере без использования технологии Microsoft Silverlight.
12/04/16:
Расширен список бесплатных виджетов
Добавлены новые бесплатные виджеты для работы с векторами.
18/03/16:
Добавлен онлайн калькулятор для разложения вектора по базису
C помощью данного онлайн калькулятора можно бесплатно разложить вектор по заданному базису.
16/03/16:
Добавлен онлайн калькулятор для проверки образует ли система векторов базис
C помощью данного онлайн калькулятора можно бесплатно проверить образует ли система векторов базис.
C помощью данного онлайн калькулятора можно бесплатно проверить компланарность векторов.
10/03/16:
Добавлен онлайн калькулятор для проверки коллинеарности векторов
C помощью данного онлайн калькулятора можно бесплатно проверить коллинеарность векторов.
06/03/16:
Добавлен онлайн калькулятор для проверки ортогональности векторов
C помощью данного онлайн калькулятора можно бесплатно проверить ортогональность векторов.
02/03/16:
Добавлен онлайн калькулятор вычисления объёма тетраэдра, построенного на векторах
C помощью данного онлайн калькулятора можно бесплатно вычислить объём треугольной пирамиды (тетраэдра), построенной на векторах.
02/03/16:
Добавлен онлайн калькулятор вычисления объёма параллелепипеда, построенного на векторах
C помощью данного онлайн калькулятора можно бесплатно вычислить объём параллелепипеда, построенного на векторах.
C помощью данного онлайн калькулятора можно бесплатно вычислить площадь параллелограмма, построенного на векторах.
01/03/16:
Добавлен онлайн калькулятор вычисления площади треугольника, построенного на векторах
C помощью данного онлайн калькулятора можно бесплатно вычислить площадь треугольника, построенного на векторах.
29/02/16:
Добавлен онлайн калькулятор умножения вектора на скаляр
26/02/16:
Добавлен онлайн калькулятор вычисления проекции вектора
C помощью данного онлайн калькулятора можно бесплатно вычислить проекцию вектора на направление другого вектора.
24/02/16:
Добавлен онлайн калькулятор направляющих косинусов вектора
C помощью данного онлайн калькулятора можно бесплатно вычислить направляющие косинусы вектора с подробным описанием хода решения на русском языке.
19/02/16:
Добавлен онлайн калькулятор угла между векторами
C помощью данного онлайн калькулятора можно бесплатно вычислить угол между двумя векторами с подробным описанием хода решения на русском языке.
19/02/16:
Добавлен онлайн калькулятор модуля (длины) вектора
C помощью данного онлайн калькулятора можно бесплатно вычислить модуль (длину) вектора с подробным описанием хода решения на русском языке.
16/02/16:
Добавлен онлайн калькулятор разности векторов
C помощью данного онлайн калькулятора можно бесплатно вычислить разность векторов с подробным описанием хода решения на русском языке.
16/02/16:
Добавлен онлайн калькулятор смешанного произведения векторов
C помощью данного онлайн калькулятора можно бесплатно вычислять смешанное произведение векторов с подробным описанием хода решения на русском языке.
12/02/16:
Добавлены онлайн калькуляторы скалярного произведения векторов и векторного произведения векторов
04/02/16:
Добавлен калькулятор решения уравнений онлайн
С помощью данного калькулятора, построенного на основе системы Wolfram Alpha LLC можно решать уравнения практически любых видов.
04/02/16:
Добавлен калькулятор онлайн решения неравенств
03/02/16:
Добавлен калькулятор вычисления характеристического полинома матрицы
Теперь можно вычислить характеристический полином матрицы онлайн с бесплатным описанием подробного хода решения на русском языке.
11/01/16:
Усовершенствован калькулятор вычисления определителя матрицы
Теперь можно вычислить определитель матрицы с использованием одного из двух алгоритмов: метода Гаусса и разложением
по строке или столбцу.
05/01/16: Добавлены калькуляторы вычисления cледа матрицы, транспонирования матрицы, вычисления верхнетреугольной матрицы, вычисления ранга матрицы и вычисления определителя матрицы с описанием подробного хода решения на английском языке.
02/12/15:
Добавлен калькулятор сложения векторов
На сайте появился новый раздел с калькуляторами, предназначенными для работы с векторами.
На данный момент доступен калькулятор сложения векторов. Постепенно, мы
будем добавлять новые калькуляторы для осуществления операций над векторами.
12/10/15:
Улучшен алгоритм решения кубического уравнения
В основе решения как и прежде, лежит формула Кардано, однако теперь, решение стало более подробным. Кроме того,
появилась возможность вводить дроби и параметры в качестве коэффициентов уравнения.
15/09/15:
Добавлен калькулятор вычисления корня n-ой степени из комплексного числа
Используя данные калькулятор, Вы можете вычислить корень n-ой степени из комплексного числа с использованием формулы Муавра
11/09/15:
Добавлен калькулятор конвертации формы записи комплексного числа
Теперь Вы можете найти перевести комплексное число заданное в одной из форм (алгебраической, тригонометрической или показательной) в другую форму онлайн.
Все вычисления проводятся в символьном виде, поэтому в калькулятор можно вводить не только числа или дроби, но и параметры.
08/09/15:
Добавлен калькулятор вычисления степени комплексного числа онлайн
Теперь Вы можете найти степень комплексного числа, заданного в алгебраической, тригонометрической или показательной формах.
Все вычисления проводятся в
символьном виде, поэтому в калькулятор можно вводить не только числа или дроби, но и параметры.
19/05/15:
Расширены возможности личного кабинета пользователя
Начиная с этого момента, все задания введенные Вами в калькуляторы, а также купленные подробные
решения будут доступны в личном кабинете и Вы всегда сможете просмотреть их заново, если потребуется!
07/05/15:
Добавлена возможность использовать виджеты для своего сайта
Просто скопируйте код виджета на свой сайт и получите возможность пользоваться нашими калькуляторами совершенно бесплатно!
Каталог виджетов будет постепенно обновляться. Никаких навыков программирования при этом не требуется!
22/04/15:
Улучшен алгоритм вычисления корней квадратного уравнения
Теперь, на нашем сайте квадратные уравнения решаются в символьном, т.
е. в качестве коэффициентов Вы можете вводить не только
числа, но и дроби!
09/02/15:
Добавлен калькулятор вычисления площади криволинейной трапеции
На нашем сайте Вы можете вычислить площадь криволинейной трапеции онлайн, образованной пересечением двух графиков функций.
12/01/15:
Добавлены калькуляторы вычисления асимптот функции онлайн
На нашем сайте появилась возможность вычисления горизонтальных, вертикальных и наклонных
асимптот к функции онлайн.
14/12/14:
Добавлен калькулятор вычисления суммы ряда онлайн
Теперь Вы можете легко вычислить сумму практически любого ряда онлайн с помощью нашего калькулятора.
27/06/14:
Улучшения
Исправлены мелкие ошибки, улучшена стабильность работы сайта!
17/04/14:
Возможность ввода выражений в строку
Для некоторых сервисов мы добавили возможность ввода выражений двумя способами: “обычным” – когда ввод
осуществляется с клавиатуры в строку или “улучшенным” – когда ввод осуществляется с использованием панели
математического ввода.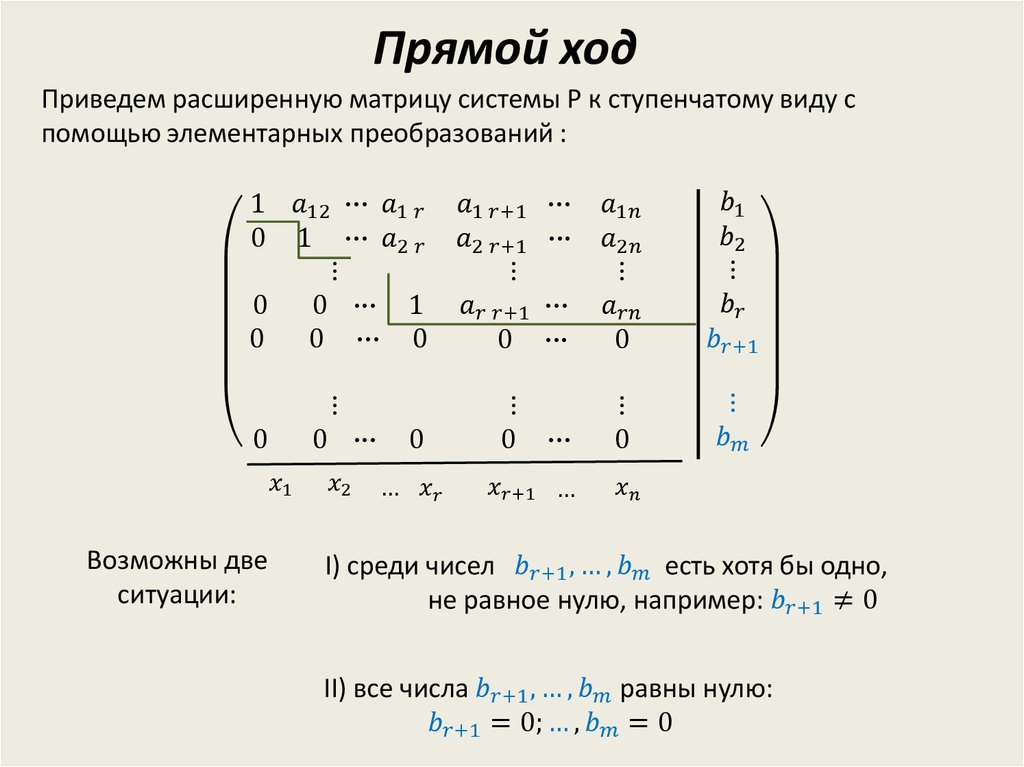
29/09/13:
Добавлена возможность поделиться ссылкой на введеное выражение
Если у Вас возникли проблемы с вводом своей задачи в наш онлайн калькулятор, кто-то другой может осуществить
ввод данных за Вас и отправить Вам ссылку. Вам нужно будет только перейти по ссылке и нажать кнопку равно для
получения решения!
17/08/13:
Улучшен формат отображения подробного решения для всех сервисов
Теперь математические формулы в комментариях к подробному решению отображаются четко, на одной линии с
текстом!
17/08/13:
Улучшен сервис решения производных
На нашем сайте появилась возможность вычислять подробное решение для производных высоких порядков
(до 5 порядке включительно!)
17/08/13:
Добавлено подробное решение пределов
Теперь вы можете получить подробное решение пределов на русском языке! Наш онлайн калькулятор пределов
находится на начальной стадии развития, но даже сейчас он может вычислять подробное решения для большого
количества различных пределов!
3/06/13:
Добавлен онлайн сервис вычисления производной неявной функции
Теперь на нашем сайте появилась возможность вычислять производную функции, заданной неявно.
24/05/13:
Добавлен онлайн сервис вычисления частных производных
Теперь на нашем сайте появилась возможность вычислять частные производные онлайн. Сервис позволяет
вычислять также смешанные производные и производные высоких порядков. Пример подробного решения, выдаваемого
новым сервисом, представлен здесь.
18/05/13:
Добавлен онлайн сервис вычисления параметрической производной
У нас на сайте появилась возможность найти производную от функции заданной параметрически с подробным решением.
26/04/13:
Добавлен пример подробного разложения дроби в сумму дробей
Теперь, вы можете ознакомиться с примером пошагового решения задачи разложения рациональной дроби в сумму элементарных дробей, и, если вам понравится, то купить пошаговое
решение своей задачи за минимальную цену.
12/04/13:
Добавлена теория по неопределенному интегралу
Мы добавили теоретическую информацию по свойствам неопределенного интеграла и по методу замены переменной.
12/04/13:
Улучшен алгоритм интегрирования
Мы существенно улучшили метод интегрирования по частям, используемый в нашем онлайн сервисе.
Теперь осуществляется поддержка большего количества интегралов.
14/03/13:
Добавлены примеры подробного решения производной и неопределенного интеграла
Теперь, вы можете ознакомиться с примерами пошаговых решений неопределенного интеграла и производной, и, если вам понравится, то купить пошаговое
решение своей задачи за минимальную цену.
13/03/13:
Улучшена стабильность и производительность алгоритма пошагового решения неопределенного интеграла
Теперь наш онлайн сервис работает быстро и более стабильно, а также поддерживает решение все большего количества интегралов.
(1/2) пошаговое решение теперь точно такое же, как в учебниках по высшей математике!
10/01/13:
Система ввода теперь доступна для решения определенных интегралов онлайн
Теперь, с помощью новой системы ввода выражений, вы сможете легко, быстро и БЕСПЛАТНО! вычислять определенные интегралы онлайн!
18/11/12:
Введена система регистрации
Введены базовые принципы системы регистрации, которая позволяет производить регистрацию и авторизацию пользователей.
В дальнейшем планируется произвести персонализацию сайта под каждого пользователя, таким образом вы сможете
настроить сайт под себя.
2/10/12:
Добален новый онлайн сервис: Решение линейных уравнений
Теперь вы можете получить бесплатное подробное решение линейных уравнений в режиме онлайн
1/10/12:
Новая форма ввода выражений доступна для вычисления предела онлайн
Панель ввода математических выражений теперь доступна для сервиса: Вычисление предела онлайн!
27/09/12:
Добавлен сервис построения уравнения нормали к графику функции
Теперь вы можете построить уравнение нормали к графику функции совершенно БЕСПЛАТНО!
20/09/12:
Добавлена справка по система ввода математических выражений
Потратьте всего 5 минут, прочитайте справку и вы поймете как пользоваться нашей уникальной системой ввода математических выражений
19/09/12:
Новая система ввода математических выражений
Для сервиса вычисление производной создана новая система ввода выражений, которая не позволит вам совершить ошибку!
19/09/12:
Подробное решение производной на русском языке совершенно БЕСПЛАТНО
Теперь подробное решение производной доступно на русском языке совершенно БЕСПЛАТНО.
15/09/12:
Новая система ввода математических выражений
Для сервиса неопределенного интеграла создана новая система ввода выражений, которая не позволит вам совершить ошибку!
15/09/12:
Подробное решение неопределенного интеграла на русском языке совершенно БЕСПЛАТНО
Теперь подробное решение неопределенного интергала доступно на русском языке совершенно БЕСПЛАТНО.
21/06/12:
Добавлена возможность решения любых дифференциальных уравнений
Теперь Вы можете решить любое дифференциальное уравнение в режиме онлайн у нас на сайте.
21/06/12:
Добавлена возможность разложения дроби в сумму простейших (элементарных) дробей
Теперь Вы можете разложить правильную дробь в сумму простейших (элементарных) дробей.
13/05/12:
Добавлена подробная справка по вводу математических выражений
Если у вас возникли проблемы с вводом математических выражений, вы всегда можете обратиться к справке.
15/04/12:
Улучшен алгоритм пошагового вычисления производной
Теперь подробное решение выводится в таком виде, как-будто бы решал человек.
17/03/12:
Добавлено пошаговое решение неопределенного интеграла и предела
Теперь Вы можете вычислить неопределенный интеграл и предел, получив при этом пошаговое решение совершенно бесплатно!
11/02/12:
Добавлено пошаговое решение производной
Теперь Вы можете вычислить производную, получив при этом пошаговое решение совершенно бесплатно!
09/02/12:
Перенос всех сервисов на html
Вся библиотека формул теперь доступна без использования технологии Microsoft Silverlight.
05/02/12:
Перенос всех сервисов на html
Все сервисы (кроме построения графиков) теперь доступны без использования технологии Microsoft Silverlight.
22/01/12:
Перенос некоторых сервисов на html
Некоторые сервисы из раздела Операции над матрицами теперь доступны без использования технологии Microsoft Silverlight.
18/12/11:
Перенос некоторых сервисов на html
Все сервисы из раздела дифференциального и интегрального исчисления теперь доступны без использования
технологии Microsoft Silverlight. Тоже самое касается решения кубических уравнений и уравнений произвольной степени.
08/12/11:
Добавлена возможность сохранения изображения построенных графиков в файл
Теперь Вы можете сохранять изображения полученных графики в файл (bmp, jpeg, png).
08/12/11:
Перенос некоторых сервисов на html
Многие сервисы (вычисление предела, производной, неопределенного интеграла, разложение функции в ряд Тейлора и решение квадратных уравнений)
теперь доступны без использования технологии Microsoft Silverlight. Т.е. теперь Вы можете использовать их с мобильного телефона!
27/11/11:
Добавлены новые формулы по пределам
На страничке пределы в разделе Библиотека формул
Вы можете ознакомиться с основными свойствами, формулами и приёмами нахождения пределов.
27/11/11:
Добавлен новый онлайн сервис – уравнение касательной к графику функции
Для получения уравнения касательной к графику функции Вам необходимо ввести функцию и абсциссу точки в
которой нужно получить уравнение касательной.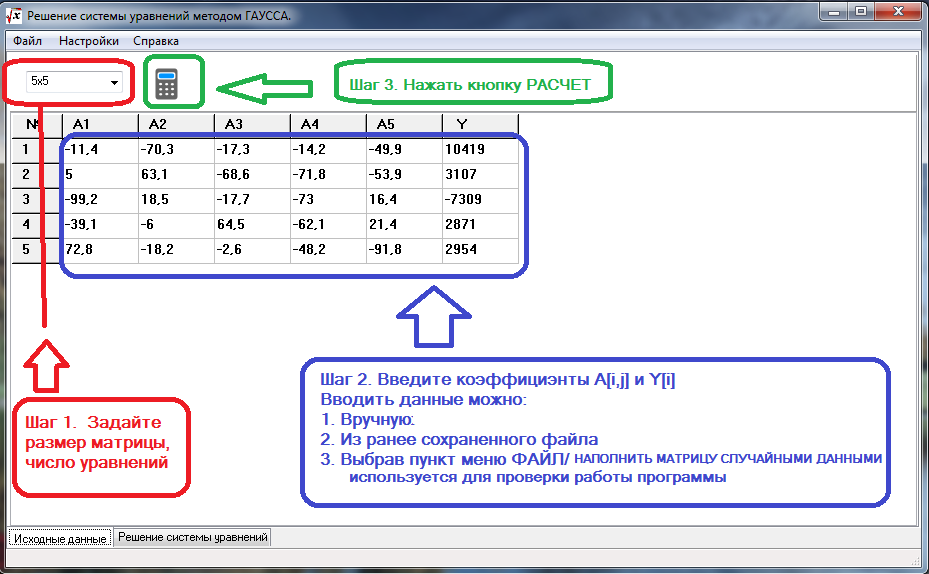
Далее программа выдаст Вам результат.
27/11/11:
Добавлен новый онлайн сервис – разложение функции в ряд Тейлора (Маклорена)
Для вычисления разложения функции в ряд Тейлора (Маклорена) Вам необходимо ввести функцию и точку в окрестности
которой нужно разложить функцию. Вы можете также указать порядок степени до которой выполнять разложение.
Далее программа выдаст Вам результат.
27/11/11:
Улучшен сервис – вычисление неопределенного интеграла
Теперь, при вычислении неопределенного интеграла Вы можете получить подробное, пошаговое
решение. Однако, это работает только в некоторых случаях, если шагов не очень много.
27/11/11:
Добавлена страничка новостей
На страничке новостей, Вы можете проследить историю развития проекта mathforyou.
net с момента его создания.
16/11/11:
Добавлен новый онлайн сервис – вычисление предела
Для вычисления предела Вам нужно всего лишь ввести функцию и точку к которой стремится
переменная этой функции. Далее программа выдаст Вам результат.
13/11/11:
Создана страница и
группа
нашего сайта ВКонтакте. Приглашаем всех желающих на
страничку нашего сайта
ВКонтакте, где можно задать интересующие вопросы, получить помощь в решении задач по математике, выдвинуть предложения по улучшению
онлайн сервисов, и т.д.
11/11/11:
Добавлен новый онлайн сервис – вычисление определенного интеграла
Для вычисления определенного интеграла Вам необходимо ввести функцию и пределы интегрирования.
Далее программа выдаст Вам результат.
06/11/11:
Добавлен новый онлайн сервис – вычисление неопределенного интеграла
Для вычисления неопределенного интеграла Вам необходимо всего лишь ввести функцию. Далее программа выдаст Вам результат.
03/11/11:
Добавлен новый онлайн сервис – вычисление производной
Для вычисления производной Вам необходимо всего лишь ввести функцию. Далее программа выдаст Вам результат.
31/05/11:
Улучшен сервис решения систем линейных уравнений
В отличие от большинства онлайн сервисов на других сайтах, которые могут решать СЛАУ лишь при условии, когда количество уравнений равно количеству переменных,
наш онлайн сервис позволяет решать совершенно любые СЛАУ. Т.е. не важно сколько у Вас уравнений и сколько переменных, Вы все равно получите решение.
Рассмотрены
варианты, когда имеется бесконечное множество решений. В этом случае программа автоматически определяет базисные и небазисные переменные, и соответствующим образом
выражает конечный результат.
Для получения решения Вам нужно выбрать количество уравнений, количество переменных и ввести данные. Далее программа сама проанализирует различные варианты и выдаст
Вам подробное решение.
02/05/11:
Добавлен новый сервис: вычисление собственных чисел и собственных векторов матрицы
Для нахождения собственных чисел квадратной матрицы, Вам необходимо ввести матрицу и нажать кнопку получить решение. Далее программа выдаст Вам пошаговое решение в
котором на первом этапе будет получен характеристический полином, затем будут найдены его корни (собственные числа) и собственные вектора.
21/04/11:
Запущен новый математический портал mathforyou.
net
Математический портал онлайн решений задач по математике mathforyou.net – некоммерческий проект, призванный помочь школьникам и студентам в освоении некоторых разделов математики путем решения задач в режими онлайн.
Метод гаусса решения слау. Решение систем линейных уравнений методом гаусса
Пусть задана система линейных алгебраических уравнений, которую необходимо решить (найти такие значения неизвестных хi, что обращают каждое уравнение системы в равенство).
Мы знаем, что система линейных алгебраических уравнений может:
1) Не иметь решений (бытьнесовместной ).
2) Иметь бесконечно много решений.
3) Иметь единственное решение.
Как мы помним,правило Крамера и матричный методнепригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений , который в каждом случае приведет нас к ответу! Сам алгоритм метода во всех трёх случаях работает одинаково.
Если в методах Крамера и матричном необходимы знания определителей, то для применения метода Гаусса необходимо знание только арифметических действий, что делает его доступным даже для школьников начальных классов.
Преобразования расширенной матрицы (это матрица системы – матрица, составленная только из коэффициентов при неизвестных, плюс столбец свободных членов) системы линейных алгебраических уравнений в методе Гаусса:
1) с троки матрицыможно переставлять местами.
2) если в матрице появились (или есть) пропорциональные (как частный случай – одинаковые) строки, то следуетудалить из матрицы все эти строки кроме одной.
3) если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить .
4) строку матрицы можноумножить (разделить) на любое число,отличное от нуля.
5) к строке матрицы можноприбавить другую строку, умноженную на число , отличное от нуля.
В методе Гаусса элементарные преобразования не меняют решение системы уравнений.
Метод Гаусса состоит из двух этапов:
- «Прямой ход» – с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду: элементы расширенной матрицы, расположенные ниже главной диагонали, равны нулю (ход «сверху-вниз»). Например, к такому виду:
Для этого выполним следующие действия:
1) Пусть мы рассматриваем первое уравнение системы линейных алгебраических уравнений и коэффициент при х 1 равен К. Второе, третье и т.д. уравнения преобразуем следующим образом: каждое уравнение (коэффициенты при неизвестных, включая свободные члены) делим на коэффициент при неизвестном х 1 , стоящий в каждом уравнении, и умножаем на К. После этого из второго уравнения (коэффициенты при неизвестных и свободные члены) вычитаем первое. Получаем при х 1 во втором уравнении коэффициент 0. Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х 1 не будут иметь коэффициент 0.
2) Переходим к следующему уравнению. Пусть это будет второе уравнение и коэффициент при х 2 равен М. Со всеми «нижестоящими» уравнениями поступаем так, как описано выше. Таким образом, «под» неизвестной х 2 во всех уравнениях будут нули.
3) Переходим к следующему уравнению и так до тех пора, пока не останется одна последняя неизвестная и преобразованный свободный член.
- «Обратный ход» метода Гаусса – получение решения системы линейных алгебраических уравнений (ход «снизу-вверх»). Из последнего «нижнего» уравнения получаем одно первое решение – неизвестную х n . Для этого решаем элементарное уравнение А*х n = В. В примере, приведенном выше, х 3 = 4. Подставляем найденное значение в «верхнее» следующее уравнение и решаем его относительно следующей неизвестной. Например, х 2 – 4 = 1, т.е. х 2 = 5. И так до тех пор, пока не найдем все неизвестные.
Пример.
Решим систему линейных уравнений методом Гаусса, как советуют некоторые авторы:
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Смотрим на левую верхнюю «ступеньку».
Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Поступим так:
1 шаг . К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).
2 шаг . Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
3 шаг . Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
4 шаг . К третьей строке прибавили вторую строку, умноженную на 2.
5 шаг . Третью строку разделили на 3.
Признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23) , и, соответственно, 11x 3 = 23, x 3 = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Выполняем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:
x 3 = 1
x 2 = 3
x 1 + x 2 – x 3 = 1, следовательно x 1 + 3 – 1 = 1, x 1 = –1
Ответ 😡 1 = –1, x 2 = 3, x 3 = 1.
Решим эту же систему по предложенному алгоритму. Получаем
4 2 –1 1
5 3 –2 2
3 2 –3 0
Разделим второе уравнение на 5, а третье – на 3.
Получим:
4 2 –1 1
1 0.6 –0.4 0.4
1 0.66 –1 0
Умножим второе и третье уравнения на 4, получим:
4 2 –1 1
4 2,4 –1.6 1.6
4 2.64 –4 0
Вычтем из второго и третьего уравнений первое уравнение, имеем:
4 2 –1 1
0 0.4 –0.6 0.6
0 0.64 –3 –1
Разделим третье уравнение на 0,64:
4 2 –1 1
0 0.4 –0.6 0.6
0 1 –4.6875 –1.5625
Умножим третье уравнение на 0,4
4 2 –1 1
0 0.4 –0.6 0.6
0 0.4 –1.875 –0.625
Вычтем из третьего уравнения второе, получим «ступенчатую» расширенную матрицу:
4 2 –1 1
0 0.4 –0.6 0.6
0 0 –1.275 –1.225
Таким образом, так как в процессе вычислений накапливалась погрешность, получаем х 3 = 0,96 или приблизительно 1.
х 2 = 3 и х 1 = –1.
Решая таким образом, Вы никогда не запутаетесь в вычислениях и не смотря на погрешности вычислений, получите результат.
Такой способ решения системы линейных алгебраических уравнений легко программируем и не учитывает специфические особенности коэффициентов при неизвестных, ведь на практике (в экономических и технических расчетах) приходиться иметь дело именно с нецелыми коэффициентами.
Желаю успехов! До встречи на занятиях! Репетитор Дмитрий Айстраханов .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Одним из универсальных и эффективных методов решения линейных алгебраических систем является метод Гаусса , состоящий в последовательном исключении неизвестных.
Напомним, две системы называются эквивалентными (равносильными), если множества их решений совпадают. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой и наоборот. Эквивалентные системы получаются приэлементарных преобразованиях уравнений системы:
умножение обеих частей уравнения на число отличное от нуля;
прибавление к некоторому уравнению соответствующих частей другого уравнения, умноженных на число отличное от нуля;
перестановка двух уравнений.
Пусть дана система уравнений
Процесс решения этой системы по методу
Гаусса состоит из двух этапов.
На первом
этапе (прямой ход) система с помощью
элементарных преобразований приводится
к ступенчатому , илитреугольному виду, а на
втором этапе (обратный ход) идет
последовательное, начиная с последнего
по номеру переменного, определение
неизвестных из полученной ступенчатой
системы.
Предположим, что коэффициент данной
системы
,
в противном случае в системе первую
строку можно поменять местами с любой
другой строкой так, чтобы коэффициент
прибыл отличен от нуля.
Преобразуем систему, исключив неизвестное во всех уравнениях, кроме первого. Для этого умножим обе части первого уравнения наи сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения наи сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалентную систему
Здесь
– новые значения коэффициентов и
свободных членов, которые получаются
после первого шага.
Аналогичным образом, считая главным
элементом
,
исключим неизвестноеиз всех уравнений системы, кроме первого
и второго.
Продолжим этот процесс, пока
это возможно, в результате получим
ступенчатую систему
,
где
,
,…,–
главные элементы системы
.
Если в процессе приведения системы к
ступенчатому виду появятся уравнения
,
т. е. равенства вида
,
их отбрасывают, так как им удовлетворяют
любые наборы чисел
.
Если же при
появится уравнение вида,
которое не имеет решений, то это
свидетельствует о несовместности
системы.
При обратном ходе из последнего уравнения
преобразованной ступенчатой системы
выражается первое неизвестное
через все остальные неизвестные
,
которые называютсвободными . Затем выражение переменнойиз последнего уравнения системы
подставляется в предпоследнее уравнение
и из него выражается переменная
.
Аналогичным образом последовательно
определяются переменные
.
Переменные
,
выраженные через свободные переменные,
называютсябазисными (зависимыми).
В результате получается общее решение
системы линейных уравнений.
Чтобы найти частное решение системы, свободным неизвестным
в общем решении придаются произвольные
значения и вычисляются значения
переменных
.
Технически удобнее подвергать элементарным преобразованиям не сами уравнения системы, а расширенную матрицу системы
.
Метод Гаусса – универсальный метод,
который позволяет решать не только
квадратные, но и прямоугольные системы,
в которых число неизвестных
не равно числу уравнений
.
Достоинство этого метода состоит
также в том, что в процессе решения мы
одновременно исследуем систему на
совместность, так как, приведя расширенную
матрицу
к ступенчатому виду, легко определить
ранги матрицыи расширенной матрицы
и применитьтеорему Кронекера –
Капелли .
Пример 2.1 Методом Гаусса решить систему
Решение . Число уравнений
и число неизвестных
.
Составим расширенную матрицу системы,
приписав справа от матрицы коэффициентов
столбец свободных членов.
Приведём матрицу к треугольному виду; для этого будем получать «0» ниже элементов, стоящих на главной диагонали с помощью элементарных преобразований.
Чтобы получить «0» во второй позиции первого столбца, умножим первую строку на (-1) и прибавим ко второй строке.
Это преобразование запишем числом (-1) против первой строки и обозначим стрелкой, идущей от первой строки ко второй строке.
Для получения «0» в третьей позиции первого столбца, умножим первую строку на (-3) и прибавим к третьей строке; покажем это действие с помощью стрелки, идущей от первой строки к третьей.
.
В полученной матрице, записанной второй в цепочке матриц, получим «0» во втором столбце в третьей позиции. Для этого умножили вторую строку на (-4) и прибавили к третьей. В полученной матрице вторую строку умножим на (-1), а третью – разделим на (-8). Все элементы этой матрицы, лежащие ниже диагональных элементов – нули.
Так как , система является совместной и
определенной.
Соответствующая последней матрице система уравнений имеет треугольный вид:
Из последнего (третьего) уравнения
.
Подставим во второе уравнение и получим
.
Подставим
и
в первое уравнение, найдём
.
Решение систем линейных уравнений методом Гаусса. Пусть нам требуется найти решение системы из n линейных уравнений с n неизвестными переменными
определитель основной матрицы которой отличен от нуля.
Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается x 1 из всех уравнений системы, начиная со второго, далее исключается x 2 из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменная x n . Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метода Гаусса . После завершения прямого хода метода Гаусса из последнего уравнения находитсяx n , с помощью этого значения из предпоследнего уравнения вычисляется x n-1 , и так далее, из первого уравнения находится x 1 .
Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса .
Кратко опишем алгоритм исключения неизвестных переменных.
Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменную x 1 из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на , и так далее, к n-ому уравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет вид
где , а .
К такому же результату мы бы пришли, если бы выразили x 1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x 1 исключена из всех уравнений, начиная со второго.
Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке
Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на , и так далее, к n-ому уравнению прибавим второе, умноженное на .
Система уравнений после таких преобразований примет вид
где , а . Таким образом, переменная x 2 исключена из всех уравнений, начиная с третьего.
Далее приступаем к исключению неизвестной x 3 , при этом действуем аналогично с отмеченной на рисунке частью системы
Так продолжаем прямой ход метода Гаусса пока система не примет вид
С этого момента начинаем обратный ход метода Гаусса: вычисляем x n из последнего уравнения как , с помощью полученного значения x n находим x n-1 из предпоследнего уравнения, и так далее, находим x 1 из первого уравнения.
Пример.
Решите систему линейных уравнений методом Гаусса.
Еще с начала XVI-XVIII веков математики усиленно начали изучать функции, благодаря которым так много в нашей жизни изменилось. Компьютерная техника без этих знаний просто не существовала бы. Для решения сложных задач, линейных уравнений и функций были созданы различные концепции, теоремы и методики решения.
Одним из таких универсальных и рациональных способов и методик решения линейных уравнений и их систем стал и метод Гаусса. Матрицы, их ранг, детерминант – все можно посчитать, не используя сложных операций.
Что представляет собой СЛАУ
В математике существует понятие СЛАУ – система линейных алгебраических уравнений. Что же она собой представляет? Это набор из m уравнений с искомыми n неизвестными величинами, обычно обозначающимися как x, y, z, или x 1 , x 2 … x n, или другими символами. Решить методом Гаусса данную систему – означает найти все искомые неизвестные. Если система имеет одинаковое число неизвестных и уравнений, тогда она называется системой n-го порядка.
Наиболее популярные методы решения СЛАУ
В учебных заведениях среднего образования изучают различные методики решения таких систем. Чаще всего это простые уравнения, состоящие из двух неизвестных, поэтому любой существующий метод для поиска ответа на них не займет много времени. Это может быть как метод подстановки, когда из одного уравнения выводится другое и подставляется в изначальное.
Или метод почленного вычитания и сложения. Но наиболее легким и универсальным считается метод Гаусса. Он дает возможность решать уравнения с любым количеством неизвестных. Почему именно эта методика считается рациональной? Все просто. Матричный способ хорош тем, что здесь не требуется по несколько раз переписывать ненужные символы в виде неизвестных, достаточно проделать арифметические операции над коэффициентами – и получится достоверный результат.
Где используются СЛАУ на практике
Решением СЛАУ являются точки пересечения прямых на графиках функций. В наш высокотехнологический компьютерный век людям, которые тесно связаны с разработкой игр и прочих программ, необходимо знать, как решать такие системы, что они представляют и как проверить правильность получившегося результата. Наиболее часто программисты разрабатывают специальные программы-вычислители линейной алгебры, сюда входит и система линейных уравнений. Метод Гаусса позволяет высчитать все существующие решения. Также используются и другие упрощенные формулы и методики.
Критерий совместимости СЛАУ
Такую систему можно решить только в том случае, если она совместима. Для понятности представим СЛАУ в виде Ax=b. Она имеет решение, если rang(A) равняется rang(A,b). В этом случае (A,b) – это матрица расширенного вида, которую можно получить из матрицы А, переписав ее со свободными членами. Выходит, что решить линейные уравнения методом Гаусса достаточно легко.
Возможно, некоторые обозначения не совсем понятны, поэтому необходимо рассмотреть все на примере. Допустим, есть система: x+y=1; 2x-3y=6. Она состоит всего из двух уравнений, в которых 2 неизвестные. Система будет иметь решение только в том случае, если ранг ее матрицы будет равняться рангу расширенной матрицы. Что такое ранг? Это число независимых строк системы. В нашем случае ранг матрицы 2. Матрица А будет состоять из коэффициентов, находящихся возле неизвестных, а в расширенную матрицу вписываются и коэффициенты, находящиеся за знаком «=».
Почему СЛАУ можно представить в матричном виде
Исходя из критерия совместимости по доказанной теореме Кронекера-Капелли, систему линейных алгебраических уравнений можно представить в матричном виде.
Применяя каскадный метод Гаусса, можно решить матрицу и получить единственный достоверный ответ на всю систему. Если ранг обычной матрицы равняется рангу ее расширенной матрицы, но при этом меньше количества неизвестных, тогда система имеет бесконечное количество ответов.
Преобразования матриц
Прежде чем переходить к решению матриц, необходимо знать, какие действия можно проводить над их элементами. Существует несколько элементарных преобразований:
- Переписывая систему в матричный вид и осуществляя ее решение, можно умножать все элементы ряда на один и тот же коэффициент.
- Для того чтобы преобразовать матрицу в канонический вид, можно менять местами два параллельных ряда. Канонический вид подразумевает, что все элементы матрицы, которые расположены по главной диагонали, становятся единицами, а оставшиеся – нулями.
- Соответствующие элементы параллельных рядов матрицы можно прибавлять один к другому.
Метод Жордана-Гаусса
Суть решения систем линейных однородных и неоднородных уравнений методом Гаусса в том, чтобы постепенно исключить неизвестные.
Допустим, у нас есть система из двух уравнений, в которых две неизвестные. Чтобы их найти, необходимо проверить систему на совместимость. Уравнение методом Гаусса решается очень просто. Необходимо выписать коэффициенты, находящиеся возле каждого неизвестного в матричный вид. Для решения системы понадобится выписать расширенную матрицу. Если одно из уравнений содержит меньшее количество неизвестных, тогда на место пропущенного элемента необходимо поставить «0». К матрице применяются все известные методы преобразования: умножение, деление на число, прибавление соответствующих элементов рядов друг к другу и другие. Получается, что в каждом ряду необходимо оставить одну переменную со значением «1», остальные привести к нулевому виду. Для более точного понимания необходимо рассмотреть метод Гаусса на примерах.
Простой пример решения системы 2х2
Для начала возьмем простенькую систему алгебраических уравнений, в которой будет 2 неизвестных.
Перепишем ее в расширенную матрицу.
Чтобы решить данную систему линейных уравнений, требуется проделать всего две операции. Нам необходимо привести матрицу к каноническому виду, чтобы по главной диагонали стояли единицы. Так, переводя с матричного вида обратно в систему, мы получим уравнения: 1x+0y=b1 и 0x+1y=b2, где b1 и b2 – получившиеся ответы в процессе решения.
- Первое действие при решении расширенной матрицы будет таким: первый ряд необходимо умножить на -7 и прибавить соответственно отвечающие элементы ко второй строке, чтобы избавиться от одного неизвестного во втором уравнении.
- Так как решение уравнений методом Гаусса подразумевает приведение матрицы к каноническому виду, тогда необходимо и с первым уравнением проделать те же операции и убрать вторую переменную. Для этого вторую строку отнимаем от первой и получаем необходимый ответ – решение СЛАУ. Или, как показано на рисунке, вторую строку умножаем на коэффициент -1 и прибавляем к первой строке элементы второго ряда. Это одно и то же.
Как видим, наша система решена методом Жордана-Гаусса. Переписываем ее в необходимую форму: x=-5, y=7.
Пример решения СЛАУ 3х3
Предположим, что у нас есть более сложная система линейных уравнений. Метод Гаусса дает возможность высчитать ответ даже для самой, казалось бы, запутанной системы. Поэтому, чтобы более глубоко вникнуть в методику расчета, можно переходить к более сложному примеру с тремя неизвестными.
Как и в прежнем примере, переписываем систему в вид расширенной матрицы и начинаем приводить ее к каноническому виду.
Для решения этой системы понадобится произвести гораздо больше действий, чем в предыдущем примере.
- Сначала необходимо сделать в первом столбце один единичный элемент и остальные нули. Для этого умножаем первое уравнение на -1 и прибавляем к нему второе уравнение. Важно запомнить, что первую строку мы переписываем в изначальном виде, а вторую – уже в измененном.
- Далее убираем эту же первую неизвестную из третьего уравнения. Для этого элементы первой строки умножаем на -2 и прибавляем их к третьему ряду. Теперь первая и вторая строки переписываются в изначальном виде, а третья – уже с изменениями. Как видно по результату, мы получили первую единицу в начале главной диагонали матрицы и остальные нули. Еще несколько действий, и система уравнений методом Гаусса будет достоверно решена.
- Теперь необходимо проделать операции и над другими элементами рядов. Третье и четвертое действие можно объединить в одно. Нужно разделить вторую и третью строку на -1, чтобы избавиться от минусовых единиц по диагонали. Третью строку мы уже привели к необходимому виду.
- Дальше приведем к каноническому виду вторую строку. Для этого элементы третьего ряда умножаем на -3 и прибавляем их ко второй строчке матрицы. Из результата видно, что вторая строка тоже приведена к необходимой нам форме. Осталось проделать еще несколько операций и убрать коэффициенты неизвестных из первой строки.
- Чтобы из второго элемента строки сделать 0, необходимо умножить третью строку на -3 и прибавить ее к первому ряду.
- Следующим решающим этапом будет прибавление к первой строке необходимые элементы второго ряда. Так мы получаем канонический вид матрицы, а, соответственно, и ответ.
Для этого элементы первой строки умножаем на -2 и прибавляем их к третьему ряду. Теперь первая и вторая строки переписываются в изначальном виде, а третья – уже с изменениями. Как видно по результату, мы получили первую единицу в начале главной диагонали матрицы и остальные нули. Еще несколько действий, и система уравнений методом Гаусса будет достоверно решена.
Как видно, решение уравнений методом Гаусса довольно простое.
Пример решения системы уравнений 4х4
Некоторые более сложные системы уравнений можно решить методом Гаусса посредством компьютерных программ. Необходимо вбить в существующие пустые ячейки коэффициенты при неизвестных, и программа сама пошагово рассчитает необходимый результат, подробно описывая каждое действие.
Ниже описана пошаговая инструкция решения такого примера.
В первом действии в пустые ячейки вписываются свободные коэффициенты и числа при неизвестных. Таким образом, получается такая же расширенная матрица, которую мы пишем вручную.
И производятся все необходимые арифметические операции, чтобы привести расширенную матрицу к каноническому виду. Необходимо понимать, что не всегда ответ на систему уравнений – это целые числа.
Иногда решение может быть из дробных чисел.
Проверка правильности решения
Метод Жордана-Гаусса предусматривает проверку правильности результата. Для того чтобы узнать, правильно ли посчитаны коэффициенты, необходимо всего-навсего подставить результат в изначальную систему уравнений. Левая сторона уравнения должна соответствовать правой стороне, находящейся за знаком “равно”. Если ответы не совпадают, тогда необходимо пересчитывать заново систему или попробовать применить к ней другой известный вам метод решения СЛАУ, такой как подстановка или почленное вычитание и сложение. Ведь математика – это наука, которая имеет огромное количество различных методик решения. Но помните: результат должен быть всегда один и тот же, независимо от того, какой метод решения вы использовали.
Метод Гаусса: наиболее часто встречающиеся ошибки при решении СЛАУ
Во время решения линейных систем уравнений чаще всего возникают такие ошибки, как неправильный перенос коэффициентов в матричный вид.
Бывают системы, в которых отсутствуют в одном из уравнений некоторые неизвестные, тогда, перенося данные в расширенную матрицу, их можно потерять. В результате при решении данной системы результат может не соответствовать действительному.
Еще одной из главных ошибок может быть неправильное выписывание конечного результата. Нужно четко понимать, что первый коэффициент будет соответствовать первому неизвестному из системы, второй – второму, и так далее.
Метод Гаусса подробно описывает решение линейных уравнений. Благодаря ему легко произвести необходимые операции и найти верный результат. Кроме того, это универсальное средство для поиска достоверного ответа на уравнения любой сложности. Может быть, поэтому его так часто используют при решении СЛАУ.
Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений.
В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.
О методе
При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.