Система 2×2 линейных уравнений – Онлайн Solver
Алгебра Рельефы
инструкции Этот инструмент он находит решения для системы двух одновременных линейных уравнений с двумя переменными.Способ, используемый для решения уравнения, – это метод Крамера.Пожалуйста, заполните форму ниже с параметрами для обоих линейных уравнений:
Введите 1-е линейное уравнение (например, 2x + 3Y = 4)
 X – 3Y = 2)
X – 3Y = 2) Этот калькулятор позволяет решить два одновременных линейных уравнения, с двумя переменными, которые часто называют “двух-дшими системами”. Эти виды 2×2 систем очень часто используются в алгебре, потому что они часто появляются во всех видах приложений, как когда вы Попробуйте решить слова проблемы.
Как правило, переменные, используемые в двухподневой линейной системе, называются по умолчанию \(x\) и \(y\), но это только конвенция, как они могут быть \(u\) и \(v\) Если вы хотите
Итак, это система дву- две:
\[x + 2y = 4\] \[2x – 2y = 2\]
так же, как это
\[2u – 2v = 1\] \[u – 3v = 2\]
это двух- две системы.
Методы решения линейных систем 2×2
К счастью, есть много способов использовать для решения двухгибовых систем, и у вас есть преимущество, чтобы выбрать, какой метод использовать. Наиболее часто используемыми методами являются:
- График
- Замена
- Ликвидация
Метод графики основан на, нет удивлению, график двух уравнений и пытаясь визуально определить, где эти две линии пересекаются (если они пересекаются
вообще).
Метод замены основан на идее, которую можно решить для одной переменной в одном из уравнений, а затем подключить, что в другое уравнение, для решения для другой переменной.Часто это удобно, потому что структура одного из уравнений может привести к нему решить для одной переменной. Но это не всегда так, и этот метод в значительной степени ограничен случаем систем 2×2
Метод ликвидации основан на идее, которую можно манипулировать одному или оба уравнения, чтобы получить их или вычесть их, так что одна переменная исчезает. В некотором смысле,
Это более общий способ использования метода замещения
В некотором смысле,
Это более общий способ использования метода замещения
Как бороться с большими системами линейных уравнений?
Три метода, представленные выше, действительно могут быть эффективно использованы только с системами 2×2, что и для больших систем, которые системы становятся гораздо более сложными и Может быть, даже возможно использовать эти методы
Для 3×3 и крупных систем лучше всего использовать систематические подходы, такие как использование
МЕТОД КРАМЕРА
Для общего \(n \times n\) системы или используя
ГАУСОВСКАЯ ЛИКВИДАЦИЯ.
Алгебра калькулятор Алгебра калькулятор онлайн Алгебра Рельвер Система уравнений 2×2 Система 2×2 линейных уравнений калькулятора
Решение линейных уравнений по формуле крамера.
 Решить систему уравнений методами Крамера, Гаусса и с помощью обратной матрицы
Решить систему уравнений методами Крамера, Гаусса и с помощью обратной матрицыМетоды Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера – весьма полезный навык.
Системы линейных алгебраических уравнений
Система линейных алгебраических уравнений – система уравнений вида:
Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись.
Итак, пусть система состоит из n уравнений с n неизвестными.
Такую систему можно переписать в матричном виде
Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.
Решение СЛАУ методом Крамера
Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.
Согласно методу Крамера, решение находится по формулам:
Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.
В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:
Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:
Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!
Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.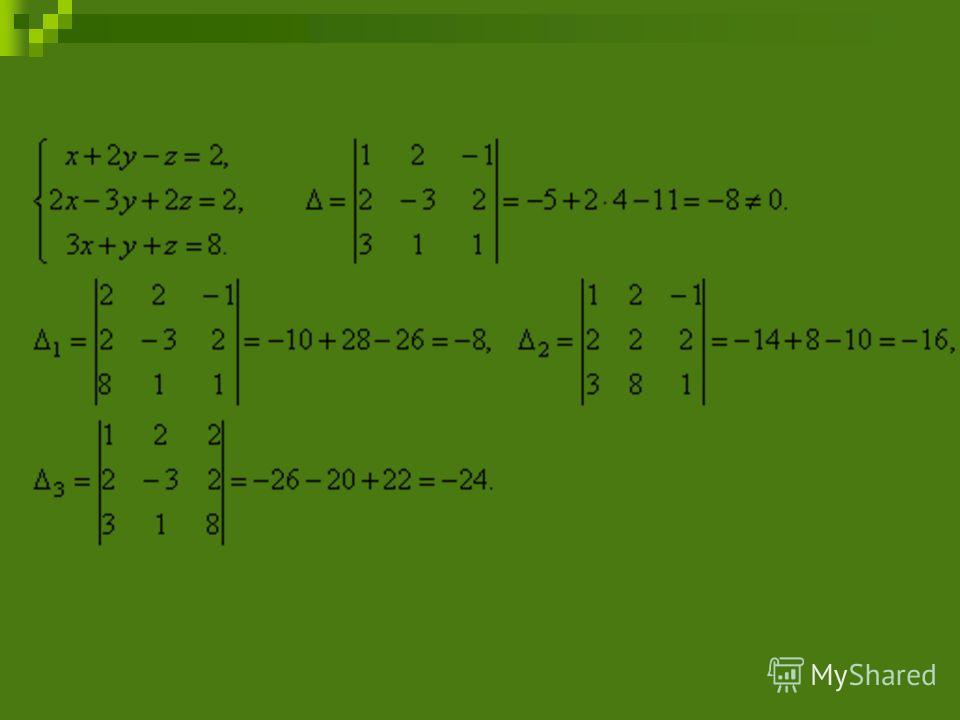
Теорема 1
Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений: $x_i = \frac{D_i}{D}$
В чем заключается метод Крамера
Суть метода Крамера в следующем:
- Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
- Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
- Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ – номер крайнего справа столбца.

- После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.
Приёмы для вычисления определителя матрицы
Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:
- Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей – со знаком минус.

Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера
- С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
- При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.
Решение систем уравнений методом Крамера
Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:
$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$
Отобразим её в расширенной форме для удобства:
$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$
Найдём определитель основной матрицы, также называемый главным определителем системы:
$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$
Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:
$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$
$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$
Теперь найдём неизвестные $x_1$ и $x_2$:
$x_1 = \frac {D_1}{D}$
$x_2 = \frac {D_2}{D}$
Пример 1
Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.
Решите систему уравнений:
$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 – x_3 = 10 \\ \end{cases}$
Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:
$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 3 = – 12 – 8 -12 -32 – 6 + 6 = – 64$
А теперь три других детерминанта:
$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 21 = – 84 – 40 – 36 – 160 – 18 + 42 = – 296$
$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = – 27 + 120 + 84 – 72 + 63 – 60 = 108$
$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 – (-2) \cdot 3 \cdot 10 – (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = – 60$
Найдём искомые величины:
$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$
$x_2 = \frac{D_1} {D} = \frac{108} {-64} = – 1 \frac {11} {16}$
$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$
Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т. е. имеет вид
е. имеет вид
Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,
. (1.6)
Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:
(j = 1, 2, …, n ). (1.7)
Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:
(1.8)
Пример 1.5. Методом Крамера решить систему уравнений
.
Вычислим главный определитель системы:
Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):
Таким образом,
Действия над матрицами
1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.
Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.
2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть
. (1.9)
Пример 1.6. .
Сложение матриц.Данная операция вводится только для матриц одного и того же порядка.
Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:
(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.
Пример 1.7. .
Умножение матриц.Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:
2
Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:
При этом элементы матрицы С вычисляются по следующим формулам:
Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :
Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :
2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .
Обратная матрица. Решение систем линейных уравнений матричным способом
Матрица A – 1 называется обратной к квадратной матрице А , если выполнено равенство:
где через I обозначается единичная матрица того же порядка, что и матрица А :
.
Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:
, (1.13)
где A ij – алгебраические дополнения к элементам a ij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).
Пример 1.9. Найти обратную матрицу A – 1 к матрице
.
Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:
.
Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 – 3 × 3 × 3 – 1 × 5 × 4 – 2 × 2 × 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.
1) Найдем алгебраические дополнения A ij :
Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.
Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:
Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:
где
Умножая обе части равенства (1. 14) слева на A – 1 , мы получим решение системы:
14) слева на A – 1 , мы получим решение системы:
, откуда
Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.
Задача 1.10. Решить систему линейных уравнений
с помощью обратной матрицы.
Решение. Запишем систему в матричном виде: ,
где – основная матрица системы, – столбец неизвестных и – столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :
Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:
Решение системы находим по формуле (1. 15):
15):
Таким образом,
Решение систем линейных уравнений методом обыкновенных жордановых исключений
Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:
(1.16)
Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.
При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.
Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.
Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.
Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.
В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.
Пример 1.11.
x
После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:
Выразим y из второго уравнения и подставим его в первое уравнение:
Запомним второе уравнение, а из первого найдем z :
Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :
Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :
.
Затем подставим и в первое запомненное уравнение , откуда найдем x :
Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:
. (1.17)
Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
.
Запомним первое уравнение
В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.
Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.
Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.
Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:
. (1.18)
(1.18)
Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
.
Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:
Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.
В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда
Подставим y и z в первое запомненное равенство и найдем x :
.
Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :
(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1. 18).
18).
В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.
Пусть дана система линейных форм (уравнений):
, (1.20)
где x j – независимые (искомые) переменные, a ij – постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.
Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.
Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.
Мы получим следующую систему:
. (1.21)
Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.
Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:
Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:
(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):
Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):
После приведения подобных членов, получим:
(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):
(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».
Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:
Таблица 1.1
| x 1 | x 2 | … | x j | … | x s | … | x n | |
| y 1 = | a 11 | a 12 | a 1j | a 1s | a 1n | |||
…………………………………………………………………. . . | ||||||||
| y i = | a i 1 | a i 2 | a ij | a is | a in | |||
| ………………………………………………………………….. | ||||||||
| y r = | a r 1 | a r 2 | a rj | a rs | a rn | |||
| …………………………………………………………………. | ||||||||
| y n = | a m 1 | a m 2 | a mj | a ms | a mn |
Жорданова таблица 1.1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.
Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:
То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:
Таблица 1.2
| x 1 | x 2 | … | x j | … | y r | … | x n | |
| y 1 = | b 11 | b 12 | b 1 j | b 1 s | b 1 n | |||
| ………………………………………………………………….. | ||||||||
| y i = | b i 1 | b i 2 | b ij | b is | b in | |||
| ………………………………………………………………….. | ||||||||
| x s = | b r 1 | b r 2 | b rj | b rs | b rn | |||
…………………………………………………………………. | ||||||||
| y n = | b m 1 | b m 2 | b mj | b ms | b mn |
Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.
Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).
1. Разрешающий элемент заменяется обратным числом:
2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:
Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:
3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:
4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:
Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:
Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т. к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.
к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.
Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1. 4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).
4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).
Таблица 1.5 Таблица 1.6
Из последней таблицы 1.7 находим: x 1 = – 3 + 2x 5 .
Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:
Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:
x 1 = – 3 + 2t
x 2 = – 1 – 3t
x 3 = – 2 + 4t . (1.27)
x 4 = 4 + 5t
x 5 = t
Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; – 1; – 2; 4; 0).
С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).
Теорема Крамера.
Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :
где Δ – определитель матрицы системы ,
Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.
Когда определитель системы нулевой, значит, система может стать совместной или несовместной.
Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.
Описание метода Крамера.
Есть система уравнений:
Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.
Составляем определитель из коэффициентов у неизвестных:
Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:
,,
Решаем систему по формулам Крамера :
Примеры решения систем уравнений методом Крамера.
Пример 1 .
Дана система:
Решим ее методом Крамера.
Сначала нужно вычислить определитель матрицы системы:
Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:
Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:
Решение уравнений способом крамера. Линейные уравнения
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2):
онлайн-калькулятором , решающим методом Крамера.
Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)
Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
** ,
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.
Третий случай: система линейных уравнений решений не имеет
(система несовместна)
Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
.
На основании теоремы Крамера
………….
,
где
–
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:
Пример 2.
.
Следовательно, система является определённой. Для нахождения её решения вычисляем определители
По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют
какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
.
Решение. Находим определитель системы:
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных
По формулам Крамера находим:
Итак, решение системы – (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих
переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко
ходить не надо.
За примерами далеко
ходить не надо.
Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Находим определители при неизвестных
Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.
Теорема 1
Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений:
$x_i = \frac{D_i}{D}$
Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений:
$x_i = \frac{D_i}{D}$
В чем заключается метод Крамера
Суть метода Крамера в следующем:
- Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
- Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
- Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ – номер крайнего справа столбца.
- После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.

Приёмы для вычисления определителя матрицы
Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:
- Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей – со знаком минус.
Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера
- С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя.
 В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы. - При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.
Решение систем уравнений методом Крамера
Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:
$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$
Отобразим её в расширенной форме для удобства:
$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$
Найдём определитель основной матрицы, также называемый главным определителем системы:
$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$
Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:
$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$
$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$
Теперь найдём неизвестные $x_1$ и $x_2$:
$x_1 = \frac {D_1}{D}$
$x_2 = \frac {D_2}{D}$
Пример 1
Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.
Решите систему уравнений:
$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 – x_3 = 10 \\ \end{cases}$
Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:
$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 3 = – 12 – 8 -12 -32 – 6 + 6 = – 64$
А теперь три других детерминанта:
$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 21 = – 84 – 40 – 36 – 160 – 18 + 42 = – 296$
$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = – 27 + 120 + 84 – 72 + 63 – 60 = 108$
$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 – (-2) \cdot 3 \cdot 10 – (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = – 60$
Найдём искомые величины:
$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$
$x_2 = \frac{D_1} {D} = \frac{108} {-64} = – 1 \frac {11} {16}$
$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$
В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицыМетод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
Рассмотрим систему 3-х уравнений с тремя неизвестными
Используя
определители 3-го порядка, решение такой
системы можно записать в таком же виде,
как и для системы двух уравнений, т. е.
е.
(2.4)
если 0. Здесь
Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .
Пример 2.3. Решить систему линейных уравнений при помощи правила Крамера:
Решение . Находим определитель основной матрицы системы
Поскольку 0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще три определителя:
Проверка:
Следовательно, решение найдено правильно.
Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, наводят на мысль, что такие же правила можно сформулировать и для линейных систем любого порядка. Действительно имеет место
Теорема Крамера. Квадратная система линейных уравнений с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение и это решение вычисляется по формулам
(2.5)
где
– определитель
основной матрицы ,
i – определитель
матрицы , полученной
из основной, заменой i -го
столбца столбцом свободных членов .
Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо не имеет вообще решений, либо имеет бесконечно много решений.
Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.
2.4. Определители n-го порядка
Дополнительным минором M ij элемента a ij называется определитель, получаемый из данного путем вычеркивания i -й строки и j -го столбца. Алгебраическим дополнением A ij элемента a ij называется минор этого элемента, взятого со знаком (–1) i + j , т.е. A ij = (–1) i + j M ij .
Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя
Получаем
Используя
понятие алгебраического дополнения
можно сформулировать теорему
о разложении определителя n -го
порядка по строке или столбцу .
Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:
(2.6)
Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка . В результате разложения определителя n -го порядка по какой-либо строке или столбцу, получается n определителей (n –1)-го порядка. Чтобы таких определителей было меньше, целесообразно выбирать ту строку или столбец, в которой больше всего нулей. На практике формулу разложения определителя обычно записывают в виде:
т.е. алгебраические дополнения записывают в явном виде через миноры.
Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.
2.
 5. Основные свойства определителей
5. Основные свойства определителейРазлагая определитель по какой-либо строке или столбцу, мы получим n определителей (n –1)-го порядка. Затем каждый из этих определителей (n –1)-го порядка также можно разложить в сумму определителей (n –2)-го порядка. Продолжая этот процесс, можно дойти до определителей 1-го порядка, т.е. до элементов матрицы, определитель которой вычисляется. Так, для вычисления определителей 2-го порядка придется вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых. Число слагаемых будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, непосильной даже для ЭВМ. Однако вычислять определители можно и по-другому, используя свойства определителей.
Свойство
1 . Определитель
не изменится, если в нем поменять местами
строки и столбцы, т. е. при транспонировании
матрицы :
е. при транспонировании
матрицы :
.
Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.
Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).
Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.
Свойство 3 . Общий множитель всех элементов в какой-либо строке (столбце) можно вынести за знак определителя .
Например,
Следствие . Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю .
Свойство
4 . Определитель
не изменится, если к элементам одной
строки (столбца), прибавить элементы
другой строки (столбца), умноженной на
какое-либо число .
Например,
Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:
2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.
Метод Крамера.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).
Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему
Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :
Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:
относительно переменных х и у .
Решение:
Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:
Сделаем аналогичное действие, заменив в первом определителе второй столбец:
Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.
Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.
Пример 2 (бесконечное количество решений):
Решить систему уравнений:
относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:
Решение систем методом подстановки.
Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.
и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:
Пример 3 (решений нет, система несовместна):
Решить систему уравнений:
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:
Применять формулы Крамера нельзя. Решим эту систему методом подстановки
Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет
Онлайн калькулятор. Решение систем линейных уравнений … – Orașul Löbau
Онлайн калькулятор. Решение систем линейных уравнений … – Orașul Löbau – document PDFliblib.ro
Онлайн калькулятор. Метод Гаусса. Детальное пошаговое решение системы линейных уравнений (СЛУ) методом Гаусса.
Онлайн калькулятор. Решение систем линейных уравнений …
Решение систем линейных уравнений …
Используя этот онлайн калькулятор для решения систем линейных уравнений (СЛУ) методом Крамера, вы сможете очень просто и быстро найти решение системы.
Онлайн калькулятор. Решение систем линейных уравнений …
Онлайн калькулятор. Метод Гаусса. Детальное пошаговое решение системы линейных уравнений (СЛУ) методом Гаусса.
Метод Крамера решения систем линейных уравнений
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не …
Метод Гаусса решения системы линейных уравнений – E–maxx
11 июн. 2008 г. … Алгоритм Гаусса. Строго говоря, описываемый ниже метод правильно называть методом “Гаусса-Жордана” (Gauss-Jordan elimination), поскольку он …
Решение системных уравнений методом гаусса. Метод Гаусса …
28 нояб. 2021 г. … Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается x 1 из всех уравнений системы, . ..
..
Калькулятор симплекс-метода | Решение основной задачи …
Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве …
Водафон онлайн-чат: решение проблем в режиме online
Чат Водафон – это специальная форма связи с консультантами через официальный сайт или личный кабинет. Он позволяет решить вопросы, которые вызывают у …
Симплекс метод онлайн. Шаг за шагом – Решение задач по …
позволяет решить произвольную задачу линейного программирования. Конечно, симплекс метод не является самым наглядным, как и все аналитические методы решения. Но …
Литры в кубы | Онлайн калькулятор
Онлайн конвертер для перевода литров в кубические метры м3 и обратно, калькулятор имеет высокий класс точности, историю вычислений и пишет число прописью, …
Простой калькулятор онлайн – Ipipip.ru
В настоящее время, в связи с тем, что в английском языке используется только термин «калькулятор» (calculator), термин «микрокалькулятор» вышел из обращения . ..
..
Декалитры в литры | Онлайн калькулятор
Онлайн калькулятор переводит декалитры в литры и обратно, данный конвертер имеет высокий класс точности, историю вычислений и поможет прочитать число.
Число Пи в Excel – Калькулятор онлайн
Для работы с числом Пи в Excel существует всторенная функция Пи(), которая позволяет получить число Pi с точностью до 9 знаков после запятой.
Totul.online – решение для увеличения ваших онлайн-продаж
11 сент. 2020 г. … Как работает Marketplace Totul.online? По сути, после того как вы загрузили товар на Totul.online, все, что вам нужно сделать – это получать …
Порт 389 (tcp/udp) – Бесплатный онлайн-калькулятор подсети …
389/TCP – Известные назначения портa (3 зап. найдено). Сервис. Детали. Источник. ldap. Lightweight Directory Access Protocol.
Закон Ома онлайн – формулы и калькулятор – Многоформул.ру
I = U R {I= dfrac{U}{R}} I=RU, где I — сила тока, U — напряжение, R — сопротивление.
Онлайн калькулятор группы крови ребенка
Бесплатный онлайн сервис для расчета группы крови ребенка. Группа крови мамы: I (O), II (A), III (B), IV (AB). Группа крови папы:.
Группа крови мамы: I (O), II (A), III (B), IV (AB). Группа крови папы:.
Кредитный калькулятор онлайн, рассчитать потребительский …
Рассчитать потребительский кредит, ежемесячный платеж и процентную ставку. ✓Калькулятор погашения кредита – расчет платежа по кредиту в ОТП Банке.
Калькулятор кредита онлайн – ОТП Банк – Выберу.ру
Кредитный калькулятор ОТП Банка. Чтобы не тратить время на поиск нужной программы кредитования в ОТП Банке, воспользуйтесь расчетом калькулятора по кредитам …
Уравнение идеального газа | Онлайн калькулятор
Рассчитывается все это дело по следующей формуле: pV = nRT, где n – молекулы газа, R – газовая постоянная.
Онлайн калькулятор поля зрения (FOV) для ArmA от Hi,A3
Введите значение горизонтального угла поля зрения (FOV) (должно быть > 70° и
Онлайн-калькулятор для облачного майнинга HashFlare.io
Калькулятор позволяющий максимально полно оценить возможный заработок с помощью облачного майнинга от Hashflare. io.
io.
калькулятор онлайн, конвертер валют из лея в рубли (mdl-rub)
Конвертировать, lei. Стоимость, ₽. График отношения молдавского лея к … По состоянию на 21 мая 2022 года при продаже 1 mdl вы получаете 3 рубля 7 копеек.
Онлайн калькулятор постройки бани и стоимости.
[email protected] г. Санкт-Петербург, шоссе Революции, 88ж. РАСЧИТАТЬ БАНЮ ДЛЯ СЕБЯ. Наши телефоны. Общий: 8 (921) 840-22-68.
онлайн калькулятор обмена валют | Альта-Софт
USD Доллар США (840), EUR Евро (978), CNY Китайский юань (156), RUB Российский рубль (643), AMD Армянский драм (51), AUD Австралийский доллар (36) …
калькулятор онлайн, конвертер валют из евро в доллары (eur-usd)
Калькулятор валют онлайн – быстрый и точный перевод из евро (eur) в доллары США (usd). Моментальная конвертация по актуальному курсу ЦБ РФ.
Кредитный калькулятор ОТП Банка — рассчитать кредит онлайн
Умный кредитный калькулятор ОТП Банка 2022 — рассчитывает график ежемесячных платежей, срок, проценты, сумму переплат. Узнайте какая часть выплат идет на …
Узнайте какая часть выплат идет на …
калькулятор онлайн, конвертер валют из доллара в евро (usd-eur)
Калькулятор валют онлайн – быстрый и точный перевод из доллара США (usd) в евро (eur). Моментальная конвертация по актуальному курсу ЦБ РФ.
калькулятор онлайн, конвертер валют из драма в рубли (amd-rub)
Калькулятор валют онлайн – быстрый и точный перевод из армянского драма (amd) в российские рубли (rub). Моментальная конвертация по актуальному курсу ЦБ РФ.
Онлайн калькулятор. Конвертер единиц объёма. Литр.
Литр — внесистемная метрическая единица измерения объёма и вместимости, равная 1 кубическому дециметру. Этот онлайн конвертер позволит вам очень просто …
калькулятор онлайн, конвертер валют из рубля в евро (rub-eur)
Калькулятор валют онлайн – быстрый и точный перевод из российского рубля (rub) в евро (eur). Моментальная конвертация по актуальному курсу ЦБ РФ.
калькулятор онлайн, конвертер валют из биткоина в евро (btc-eur)
Конвертер биткоина к евро. Покупка. 1 BTC = 31532,7 EUR. Обновлен. 20.05.
Покупка. 1 BTC = 31532,7 EUR. Обновлен. 20.05.
калькулятор онлайн, конвертер валют из евро в левы (eur-bgn)
Калькулятор валют онлайн – быстрый и точный перевод из евро (eur) в болгарские левы (bgn). Моментальная конвертация по актуальному курсу ЦБ РФ.
Бесплатный онлайн-калькулятор подсети IPv4 – adminsub.net
IP-Aдрес. 192.168.1.0. 11000000.10101000.00000001.00000000 · Маска. 255.255.255.128 = 25. 11111111.11111111.11111111.10000000 · Вилдкард. 0.0.0.127.
калькулятор стоимости КАСКО онлайн от угона и тотала
Выберите лучшие условия по КАСКО от угона в 2022 году на Сравни! Онлайн расчет стоимости КАСКО от хищения по 29-ти предложениям в 6-ти самых популярных …
онлайн калькулятор расчета стоимости доставки – DHL Express
Если вы являетесь корпоративным клиентом и у вас есть клиентский счет DHL – рассчитайте тариф здесь. Откуда забрать? Страна *.
Онлайн калькулятор расчета стоимости имплантации зубов …
Лечение аппаратом VECTOR (1 зуб) · Лечение аппаратом VECTOR (2 челюсти) · Лазерное лечение десен · Лечением аппаратом FotoSan. Хирургическая стоматология.
Хирургическая стоматология.
Коэфициент Бонус – Малус. КБМ., калькулятор онлайн, конвертер
Коэффициент Бонус-Малус, классы и коэффициенты водителя и страхования ОСАГО,база КБМ РСА по ОСАГО, таблица коэффициентов ОСАГО.
калькулятор онлайн, конвертер валют из рубля в доллары (rub …
Московский Кредитный Банк. 12,00%. Ставка в год. от 1 ₽. На срок от 1 дня. Без капитализации. Без частичного снятия. Без пополнения. Перейти. Лиц. № 1978.
Онлайн калькулятор ОСАГО 2018 — бесплатный расчёт стоимости
У вас отключён JavaScript: часть функций сайта будет недоступна! Бонус-малус.ру. Меню. справочник страхователя. Калькулятор ОСАГО. расчёт стоимости полиса в …
Онлайн калькулятор стоимости бани из бревна – Сруб-Строй
Наглядный калькулятор онлайн для получения предварительного расчета стоимости бревенчатой бани.
Prin utilizarea site-ului nostru, sunteți de acord cu utilizarea cookie-urilor pentru o experiență mai bună.
Liblib.ro © 2022
Калькулятор -solve_equations([x+y=3;x-y=2];[x;y]) – Solumaths
Решение уравнений, расчет онлайн
Summary :
Решатель систем линейных уравнений позволяет решать уравнения с несколькими неизвестными: система уравнений с 2 неизвестными, система уравнений с 3 неизвестными, система с n неизвестными.
решить_уравнения онлайн
Описание :
Решение уравнений с несколькими неизвестными другими словами, решение системы уравнений онлайн возможно за счет использования функцииsolve_equations калькулятора. Калькулятор допускает разрешение системы онлайн нескольких типов, это возможно:
- по решать системы уравнений с двумя неизвестными онлайн ,
- – решать системы уравнений с тремя неизвестными онлайн ,
- и, в более общем смысле, разрешение онлайн-систем, уравнение с несколькими неизвестными.

Обладая способностью к алгебре, калькулятор может решить уравнений с двумя неизвестными или решить уравнения с 3 неизвестными с участием букв (буквальный расчет).
Калькулятор представляет собой решатель системы уравнений , который использует очень простой синтаксис для решения систем линейных уравнений, допускающих единственное решение.
Решение системы 2 уравнений с 2 неизвестными
Существует несколько методов решения системы 2 уравнений с 2 неизвестными: метод замещения , комбинированный метод , графический метод , метод Крамера .
- Комбинированный метод заключается в исключении одной из переменных благодаря арифметическим операциям над уравнениями;
- Метод подстановки состоит в выражении одной из переменных как функции другой и последующей замене для получения уравнения с одним неизвестным;
- Метод графического решения позволяет предположить решение, которое необходимо будет проверить вычислением, графический метод состоит в изображении прямых линий, соответствующих уравнениям, а затем «чтении» координат точки пересечения, графический калькулятор позволяет выполнять этот тип операции;
- Метод Крамера использует определители.

Калькулятор может использовать эти методы для решения уравнений с 2 неизвестными
Чтобы решить систему 2 уравнений с 2 неизвестными согласно x+y=18 и 3*y+2*x=46, необходимо войти solve_equations(`[x+y=18;3*y+2*x=46];[x;y]`), после вычисления возвращается результат [x=8;y=10].
Решение системы 3-х уравнений с 3-мя неизвестными
Чтобы найти решения системы 3-х уравнений с 3-мя неизвестными , калькулятор может использовать метод подстановки, метод комбинации или метод Крамера.
Так, например, для решения линейной системы уравнений по x+y+z=1, x-y+z=3, x-y-z=1 необходимо ввести solve_equations(`[x+y+z=1;x-y+z=3;x-y-z=1];[x;y;z]`) , после вычисления результат [x=1;y=-1; z=1] возвращается.
Синтаксис:
решить_уравнения([уравнение1;уравнение2;…;уравнениеN];[переменная1;переменная2…переменнаяN])
Примеры:
- x+y=18
- 3*у+2*х=46
solve_equations(`[x+y=18;3*y+2*x=46];[x;y]`), возвращает[x=8;y=10] Рассчитайте онлайн с помощьюsolve_equations (решите систему линейных уравнений)
См. также
также
Список связанных калькуляторов:
- Решение квадратного уравнения с комплексным числом : complexe_solve.
 Калькулятор уравнений комплексных чисел возвращает комплексные значения, для которых квадратное уравнение равно нулю.
Калькулятор уравнений комплексных чисел возвращает комплексные значения, для которых квадратное уравнение равно нулю. - Расчет дискриминанта онлайн: дискриминант. Калькулятор, который позволяет вычислить дискриминант квадратного уравнения онлайн.
- Найти уравнение прямой линии из двух точек: уравнение_прямой_линии. Калькулятор уравнения прямой позволяет рассчитать уравнение прямой по координатам двух точек с пошаговым расчетом.
- Найдите уравнение касательной линии: уравнение_касательной_линии. Калькулятор уравнения касательной используется для расчета уравнения касательной к кривой в заданной точке абсцисс с поэтапным вычислением.
- Калькулятор теоремы Пифагора: пифагорейский. Калькулятор использует теорему Пифагора, чтобы проверить прямоугольность треугольника или найти длину одной стороны прямоугольного треугольника.
- Калькулятор решения для x: уравнение_решателя. Решатель уравнений позволяет решать уравнения с неизвестным с шагами расчета: линейное уравнение,
квадратное уравнение, логарифмическое уравнение, дифференциальное уравнение.

- Калькулятор неравенства: неравенство_решатель. Решатель неравенств, который решает неравенство с деталями расчета: линейное неравенство, квадратное неравенство.
- Решение системы линейных уравнений :solve_equations. Решатель систем линейных уравнений позволяет решать уравнения с несколькими неизвестными: система уравнений с 2 неизвестными, система уравнений с 3 неизвестными, система с n неизвестными.
- Решатель обратного отсчета: arithmetic_solver. Этот решатель обратного отсчета позволяет найти целевое число из набора целых чисел с помощью арифметических операций.
Список связанных упражнений:
- Решите систему двух уравнений с двумя неизвестными. Целью этого исправленного математического упражнения является решение системы двух уравнений с двумя неизвестными.
- Использование системы уравнений для решения задачи.
 Целью этого упражнения является использование системы двух уравнений с двумя неизвестными для решения задачи.
Целью этого упражнения является использование системы двух уравнений с двумя неизвестными для решения задачи.
Напоминания о курсах, калькуляторы, упражнения и игры: Уравнения, Матрицы
Решатель систем уравнений онлайн
Примеры систем уравнений
- Система двух уравнений с двумя неизвестными
2х - у = 5 3х - у = 7
х - у = 1 у - 2х = 1
- Система трех уравнений с тремя переменными
х1 - 2х2 + 3*х3 = 14 2x1 + 3x2 - 4x3 = 0
- Метод Гаусса
х - у - 1 = 0 х + у + 2 = 0
- Метод Крамера
2*х - 3*у = 5 5*х + у = 4
- Прямой метод
2*х - у = 3 2*х + у = 9
92 = 2 + х - Система четырех уравнений
х1 + 2х2 + 3х3 - 2х4 = 1 2х1 - х2 - 2х3 - 3х4 = 2 3х1 + 2х2 - х3 + 2х4 = -5 2x1 - 3x2 + 2x3 + x4 = 11
- Система линейных уравнений с четырьмя неизвестными
2x + 4y + 6z + 8v = 100 3х + 5у + 7з + 9в = 116 3х - 5у + 7з - 9в = -40 -2х + 4у - 6з + 8в = 36
- Система из трех нелинейных уравнений с квадратом или дробью 912
Что умеет калькулятор?
- Решает системы уравнений различными методами:
- Метод Крамера
- Метод Гаусса
- Численное решение
- Графический метод
- Подробное решение тремя способами:
- Методы Крамера и Гаусса
- Простая замена переменных
Приведенные выше примеры также содержат:
- модуль или абсолютное значение: absolute(x) или |x|
- квадратные корни sqrt(x),
кубических корней cbrt(x) - тригонометрические функции:
sinus sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - экспоненциальные функции и показатели exp(x)
- обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс acot(x) - натуральные логарифмы ln(x),
десятичных логарифмов log(x) - гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x) - обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x), гиперболический арктангенс ath(x), гиперболический арккотангенс acoth(x) - другие тригонометрические и гиперболические функции: секанс
sec(x), косеканс csc(x), арксеканс asec(x), арккосеканс acsc(x), гиперболический секанс sech(x), гиперболический косеканс csch(x), гиперболический арксикансек asech(x), гиперболический арккосеканс acsch(x) - функции округления:
округлить до пола(x), округлить до потолка(x) - знак числа:
знак(х) - по теории вероятностей:
функция ошибок erf(x) (интеграл вероятности), Функция Лапласа laplace(x) - Факториал х :
х! или факториал(х) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
- Тригонометрические интегралы: Si(x), Ci(х), Ши(х), Чи(х)
Правила вставки
Следующие операции могут быть выполнены 95
Константы
- Пи
- – число Пи
- и
- – основание натурального логарифма
- и
- – комплексный номер
- оо
- – символ бесконечности
Решите систему уравнений с помощью калькулятора исключения
Пользователи Bing пришли на эту страницу сегодня, введя эти ключевые слова:
Решение системных уравнений с 3 переменными на калькуляторе,
бюллетень вероятностей статистики 6 класса альберты,
листы переменных,
матричные математические таблицы,
ПРОГРАММЫ ПО МАТЕМАТИКЕ ДЛЯ ДЕВЯТИЛЕТНИХ,
калькуляторы для powerpoints.
трехчленный калькулятор, Математический пересмотр квадратных корней, найти точки пересечения параболы и линейного уравнения, изображения калькулятора графа координат.
План урока по алгебре умножения двучленов, чарльз маккег викторина тест учитель издание, рациональные показатели, Рабочий лист рационального выражения, Алгебра Северной Каролины 1 рабочая тетрадь.
Бесплатные тесты по ментальной математике ks3, рабочий лист по переводу дробей в десятичные, книга-алгебра-ответы hrw.
Как решить уравнение в частных производных с помощью решения Даламбера, Список математических формул, рабочий лист последовательности отсутствующих дробей, как решить алгебру дробей, дробные радикалы, бесплатный пример для теста на логарифм, решение нескольких уравнений в excel.
Вычитание целых чисел, дающих мне ответы, которые я набираю,
математическое упражнение в пятом классе,
пошаговый интегральный калькулятор,
Неоднородное дифференциальное уравнение 2-го порядка.
Словесные задачи, приводящие к квадратным уравнениям, давать советы, как сдать алгебру, графы одновременных уравнений.
Порядок действий по поиску ответов, книга ответов на tn алгебра2, заметки о дискриминантах полиномиальных уравнений.
Плитки алгебры выражений, найти общий знаменатель, Перестановки и комбинации 8-го класса, уравнения процентов.
Математика коэффициента масштабирования, бесплатный онлайн-тест по математике для 9 класса по линейным, экспоненциальным и параболическим графикам, комбинация матлаб.
Рабочий лист сложения и вычитания положительных и отрицательных целых чисел, онлайн дифференциальный калькулятор, помогите с уравнением полураспада, планы уроков корневого слова в 6 классе, ответы на учебники по математике hrw для 7 класса, УКЛОН Рабочие листы.
многочлен 5-го порядка,
бесплатная помощь в превращении дробей в десятичные,
обратный лаплас ти 89,
решить несколько уравнений с ti-89,
решение алгебраических уравнений с распределением и объединением подобных членов,
множественные скобки в алгебраических уравнениях,
изменение базы TI89.
Вычитание рабочего листа с целыми числами, экспоненты-примеры из жизни, мелочи об алгебре, как вычислить многочлен 3-го порядка, печатные рабочие листы с ответами на свойства целых чисел, бесплатные рабочие листы экспоненты, построение графиков, уклон, математическая задача, практика gmat.
TI активность для наклона и y-пересечения, Лист вопросов по математике, руководство пользователя Т1-83, общие рабочие листы способностей детей, квадратные корни 7-й класс Powerpoint, математические задачи седьмой класс масштабные коэффициенты.
McDougal Littell/Houghton Mifflin – Advanced Mathematics + окончательный обзор, калькулятор приближения суммирования, точка пересечения двух нелинейных функций.
Интерактивные программы квадратного числа,
как решить квадратное в вершинной форме?,
решение неизвестных в дробях,
определения до алгебры,
детская математика квадратный корень,
рассчитать ЖКМ,
Экзамены в 11 классе по естествознанию.
Шпаргалка по математике для фракций.com, упрощение рабочих листов радикалов, алгебра, одна глава 5, ресурсная книга, конвертер десятичной дроби в дробь квадратного корня, Рабочий лист с LCM, бесплатная помощь по математике для базовой алгебры или алгебры для начинающих, дополнительные листы свойств.
Кс4 практический тест, бесплатные бухгалтерские книги, факторные квадратики, написание рабочего листа буквенных уравнений.
Вручную введите программу в полином TI-83, простые способы решения десятичных дробей, обмануть в gcse.
Решите систему методом кооперативной алгебры исключения, промежуточная алгебра “проект главы 6”, Калькулятор уравнений факторинга, дайте мне бесплатные ответы по алгебре.
Рабочий лист факторинга простых трехчленов, решение нескольких уравнений с помощью ti-86, ти-84 плюс двоично-десятичный, Как решить задачу по алгебре 3 в отрицательной степени x, рудин решения глава 7 #7.
Обманки с домашними заданиями по математике,
пример математических мелочей,
бесплатный справочный лист по математическим факторам.
“задачи по математике” и “7 класс”, словесные задачи на нахождение площадей, Бесплатный полиномиальный решатель, сложение и вычитание квадратных корней, java наивысший общий делитель, алгебраический решатель, определить домен подкоренного члена.
Фракции ЧЕТВЕРТЫЙ сорт, нахождение наименьшего общего знаменателя и формирование эквивалентных рациональных выражений, 3.2 Браун «алгебра и тригонометрия», Бесплатные рабочие листы по математике для печати Целые числа.
Решение кубического уравнения в Matlab, математика для чайников, образец теста по математике для печати, Тест на запоминание 6-7, порядковые номера от меньшего к большему упражнения, правила показательных практических занятий.
Продвинутая математика, Макдугал Литтел,
ти 83 плюс завершающий квадрат,
решение уравнений 3-го порядка,
прентис холл онлайн учебник девятый класс,
выучить предварительную алгебру бесплатно онлайн,
бесплатные тесты 9 класса.
Рабочий лист для печати отрицательных показателей, бесплатная электронная книга по учету стоимости проекта, ТИ-84 + Эмулятор, ОБУЧЕНИЕ ОСНОВАМ ВЕРОЯТНОСТИ В 3-ГО КЛАССЕ, красивые ноги, ТИ-89илаплас.
Бесплатная экзаменационная работа по математике в колледже, как построить прямую линию с помощью TI 83+, формула алгебры начальная школа, линейные матрицы и +уравнения, онлайн-калькулятор абсолютных неравенств, где инверсный ключ на т183 плюс, решить ti89.
ВЫЧИТАНИЕ ЦЕЛЫХ рабочих листов, как запрограммировать квадратичную формулу Ti 84, решатель обозначений функций, оценка рабочих листов по математике, распечатка листов факторинговых трехчленов, решения по алгебре колледжа.
3 заказанные пары для 2x-y=8, калькулятор одновременных уравнений, научите себя математике онлайн бесплатно, clep testing- +алгебра, “решения для Росса”.
Калькулятор алгебры LCM,
Десятичные дроби с остатком,
учет затрат – книги,
решать уравнения алгебры.
Онлайн калькулятор упрощения, промежуточные 2 математических упражнения, комплекс квадратных уравнений.
Процентные математические задачи, используя ti-89 решить y=, дробь в десятичной системе Matlab.
рабочая тетрадь Холта по математике онлайн, решения UCSMP, скачать прошивку ti89, TI-83 плюс логарифмы, определитель ти-89, математика алгебра powerpoint бесплатно, Таблица квадратных корней для печати.
Сложение, вычитание, деление, умножение дробей и десятичных знаков, сатц документы онлайн, бесплатный рабочий лист для графика, классный лист смешанной дроби числа.
Рабочие листы с отрицательными числами для ks2, Ответы на 10 заданий выпуска 2004 г., смешанное число в простейшей форме, разделительный калькулятор.
Как решать неоднородные дифференциальные уравнения первого порядка, помощь с домашним заданием вероятность росс, планы уроков по умножению целых чисел.
Найдите рабочий лист, связанный с упрощением переменных выражений,
печатные рабочие листы/функциональные таблицы/начальная/средняя школа,
калькуляторы неравенства,
учебник расширенный учет затрат.
Дольчиани, Математическая алгебра 1 учебник, самое сложное математическое уравнение в мире, квадратичный решатель онлайн, преподавание распределительной собственности семиклассникам, Онлайн калькулятор факторинговых выражений.
Ks2 печатные английские сат, что такое сложение вычитания и умножения целых чисел, таблица экспоненциальных вероятностей, Бесплатные ответы по алгебре 2.
Tx листы практики математики третьего класса, Увлекательные способы решения линейных уравнений, Алгебра 2 2004, глава 11, справочник.
Решатель радикальных выражений, математические стихи с радикалом, рабочий лист полинома gcf, рабочие листы свободных радикалов, бесплатные математические ответы, радикальный калькулятор оставлен в радикальной форме, Учим дроби для чайников.
Бесплатные электронные книги по абстрактной алгебре,
алгебра 1 Glencoe Mathematics ответы на домашнее задание,
ответы по математике в седьмом классе,
тригонометрия – напиши свою задачу и получишь ответ,
как рассчитать математическую задачу + образец,
простейшее определение кубических корней в рациональном выражении.
Образцы тестов GED для печати, эмулятор ТИ-84, Merrill Glencoe + онлайн-инструменты для обучения + физика, Продвинутые тесты и викторины по алгебре, Скотт Форман, сложение и вычитание квадратных корней, 11 лет математика, помогают рациональные показатели десятой степени.
Умножение деления рациональных выражений мошенника, ошибка расчетов деления javascript более 1000, учет затрат онлайн книга, вопрос о способностях.
Овладение ключом ответов по физике, как найти максимум параболы с уравнением без калькулятора, преобразователь радиан и градусов ти-89, продвинутая математика.
Преобразовать простые футы в кубические футы, Урок синтетического дивизиона в Powerpoint, матлаб y=ax2+bx+c, Рабочие листы для печати, делящие степени с одинаковым основанием.
Ти 84 плюс читы,
урок математики сложные проценты кс4,
бесплатные математические распечатки,
бесплатный урок алгебры онлайн,
Калькулятор, который решает многочлены,
вычитание и сложение дробей в стиле алгебры,
www. mathmatics.qcom.
mathmatics.qcom.
Практика факторинга мономов и многочленов онлайн, бесплатные экзаменационные работы по счетам, асимптоты, изображающие размерность ti-86, сколько целых чисел делится на 7, но не делится на 11, алгебра с пиццей, бесплатные ответы на математические задачи.
Активность масштабного фактора, алгебра гленко1, исследовательские задачи по математике, умножение матриц, powerpoint нахождения пересечения склона, Рабочий лист 100 для определения последовательности чисел.
Рабочий лист конгруэнтного треугольника на уровне 12-го класса, калькулятор.edu, печатные рабочие листы переменных, Рабочие листы по линейным уравнениям.
Решение уравнения третьего класса, “концептуальная физика” отвечает, примеры математических мелочей математики, “ответы учебника алгебры 1” саксонский, графы общих ошибок линейные уравнения, символ квадратного маршрута.
Процентные математические формулы,
график параболы со сдвинутыми уравнениями,
Как запрограммировать квадратную формулу для TI-84.
Сколько зерен риса в 50-килограммовом мешке, простые рабочие листы по сложению и вычитанию целых чисел, программирование алгоритма извлечения квадратного корня, ответы на рабочие листы Прентис Холла по биологии, упрощение экспоненциальных выражений, распечатать игры для gcf.
Формула наибольшего общего знаменателя, предыдущие вопросы тестов способностей, калькулятор наименьшего общего знаменателя, напишите свою проблему с вычитанием десятичных дробей, преобразовать десятичную дробь в знаменатель дроби.
Как решить сложный корень, ти-89 Лаплас функция 187, что означает уравнение y = a (x -b)2+c в квадратичных графах, как вы решаете радикальные выражения и уравнения, рабочие листы для печати kumon, Алгебра – Решение задач на квадратный корень .edu, Упрощение уравнения.
11+ образец бумаги по математике,
ИНФОРМАЦИЯ О ДРОБЯХ,
ошибка 13 размера на TI 86,
код уравнения (как термины),
Забавные рабочие листы пропорций,
72275776771546.
Ti 84 плюс читы для набора головоломок, рабочий лист упрощения радикалов, применение квадратного уравнения, Калькулятор квадратных уравнений.
Вопрос о способностях с решением, Кнопка журнала TI 89, машина наибольшего общего фактора, решение уравнений третьего порядка.
Бесплатные ответы по алгебре, алегбра 1, математический коэффициент средней школы, преобразовать десятичное число в java.
Графические рациональные выражения, помощь в решении задач по алгебре, онлайн-калькулятор, упрощающий подкоренные выражения.
Бесплатные рабочие листы по симметрии для печати, двухшаговые уравнения для печати рабочих листов, математические мелочи об алгебре, рабочие листы для печати по распределительной собственности, графические занятия/уроки кластера, примеры по нахождению масштабных коэффициентов.
рабочая тетрадь Харкорта по математике 4 класс,
помощь с домашним заданием по прикладной алгебре,
“уравнение mathtype 5. 0″ + бесплатно + скачать,
Glencoe Biology Worksheet Ответы.
0″ + бесплатно + скачать,
Glencoe Biology Worksheet Ответы.
Учебник по сложным процентам gmat, 9 класс математика онлайн бесплатно, ФАКТОРНАЯ МАТЕМАТИКА, математика масштабного коэффициента рабочего листа расширения, нахождение корней полинома третьей степени, как решать простые показательные уравнения, Калифорнийская алгебра 1 математическая книга онлайн.
Бесплатная математическая задача отвечает на алгебраические решения, решить одновременный квадратичный, распечатать рабочий лист алгебраических выражений, радикальный калькулятор, рабочий лист смеси для предварительного исчисления, “задачки по математике в четвертом классе, решение уравнения путем умножения или деления.
диаграммы простых дробей и рабочие листы,
решатель триггерных уравнений,
Бесплатно скачать Learning O-Level Physics,
вычесть целое,
полиномы факторинга 10 степени,
СБАЛАНСИРОВАННЫЕ химические уравнения с участием аммиака,
задачи по алгебре для студентов.
Формула кинематики средней школы Альберты, калькуляторы неравенства, «сложное неравенство» берет на себя деятельность.
Фактор кубических переменных, средство для создания рабочих листов с двухэтапными уравнениями, рабочий лист математических слов.
Без функции модуля TI-84, отрисовка эллипса на ti83plus, Решатели задач по алгебре бесплатно, формулы радикантов ti 83, задачи на целочисленные слова 4 класс, онлайн калькулятор неравенства.
Matlab нелинейное решение одновременных уравнений, формулы площади и периметра для детей, которые можно распечатать, бесплатные ключи по алгебре чикагского университета.
решатель алгебры, TI-83 plus скачать ром, решение одновременных уравнений в Matlab, калькулятор корней уравнения, используйте степени окисления и их наименьшие общие кратные для записи.
+ сложные задачи на логику, перестановку и комбинацию,
Glencoe/McGraw-Hill ответы на лист периодических головоломок,
как умножать и делить дроби с переменной.
Как извлекать кубический корень на калькуляторе, ti-89 обратная квадратичная функция, ti 84 решатель уравнений, математические множители, вопросы по формулам сложения и вычитания, переменные квадратного уравнения, Сайт книг Макдугласа Литтела.
Примеры показательных, линейных и квадратных уравнений, простое полиномиальное сложение и вычитание, каков наименьший общий делитель чисел 16, 28 и 64, “промежуточный тест на решение задач”, Процент числа, решатель алгебры1, бесплатный онлайн-учебник по математике gre.
матлаб булевой алгебры, факторинг и упрощение, викторины по математике на склоне, которые можно распечатать, калькулятор, который онлайн может решить для y, обучение умножению показателей с помощью игр.
Бесплатный mathcad-подобный, бесплатные задачи полиномиальных уравнений, ответы на задачки по математике, алгебраическое уравнение третьего порядка.
Как ввести логарифмическую базу 10 в ti89,
диаграмма квадратных корней,
ответы на домашнее задание по алгебре 1,
преобразовывать смешанные числа в десятичные,
решатель задач по алгебре 2,
факторизовать квадратные выражения пошаговое объяснение,
шпаргалка по алгебре.
Решайте задачи на упрощение рациональных выражений, использовать график, чтобы написать линейное уравнение, интерактивные игры на вычитание двухзначных чисел, генераторы алгебраических уравнений, математика знака пирога.
матфордумами, упрощение рабочего листа квадратных корней, тригономический, решатель вавилонских дробей, решение смешанных логарифмических уравнений.
Рабочие листы пропорций, выполнение домашнего задания по алгебре, бесплатный рабочий лист в классной комнате, решатель тригонометрических тождеств на ti 89титан, веселые алгебраические игры для решения линейных уравнений, Алгебра Гленко Меррилла 2, сложение и вычитание подкоренных выражений.
Как решить проценты в 9 классе, процент от целого числа на листе, мягкие математические игры.
Математические перестановки для чайников,
факторы и деревья факторов для пятого класса,
план урока обозначения функций в PowerPoint,
математические стихотворения.
Современная химия раздел 6-3 обзор hrw, упростить радикальную форму квадратного корня, Рабочие листы по квадратным корням для четвероклассников.
Макдугал искатель домашней работы, ответы на книги по алгебре 2 трамплин колледжа, создать приложение интерполяции ti89, клен решает несколько уравнений, сложение, вычитание, умножение и деление целых чисел.
МАТЕМАТИЧЕСКИЕ ПУТЕШЕСТВИЯ, решить с помощью калькулятора исключения, добавление рабочих листов с целыми числами.
Функция кубического корня TI-83, рудин глава 4 решение, калькулятор умножения смешанной дроби, Формула наибольшего общего делителя.
Британский метод факторинга, бесплатные рабочие листы с точечной диаграммой по математике, купить викторины Advanced Algebra и Testmasters Скотта Форесмана, решить для полиномов 3-го порядка, как найти квадратный корень, Добавление учителей концепций алгебры Гленко и приложений.
скачать TI calc Rom,
бесплатно решаемые инженерные задачи для учителей,
специальный куб произведения триномиальной алгебры.
Лист сложения и вычитания отрицательных чисел, холт алгебра 1 техасский ключ, план урока о том, как определить функцию для математики, ти-83, как упростить х, какая связь тригонометрии в курсе начального обучения, формулы триг квадрата.
План элементарного урока + функциональная таблица, бесплатная помощь по алгебре 2, решатель уравнения мнимого числа квадратичный.
Рабочие листы для печати вращения геометрии, линейное и квадратное уравнение ppt, бесплатное онлайн-издание Холт-алгебры для учителей 1 2004 г., Ответы на учебник по математике для подготовки к колледжу.
Квадратичные задачи из прошлых статей, викторины по алгебре для начинающих, парабола в статистике.
Ti 83+ квадратичный, онлайн ти-84, онлайн-решатель уравнений алгебры, Вычислить общий знаменатель, Линейные графики.
Ti-84 плюс перевод десятичной дроби в проценты,
листы домашних заданий для квадратных корней,
стандартная форма для рабочего листа формы пересечения наклона.
Наибольший общий делитель 63 и 81, как использовать решатель задач с квадратами дробей, добавление рабочих листов вычитания рациональных выражений.
Калькулятор триномиальной алгебры, 9 класс Прошлые работы, Калькулятор уравнения комплексного числа квадратичный, предварительная алгебра для чайников, листы сложения, вычитания, умножения и деления целых чисел, логарифмические он-лайн калькуляторы бесплатно.
Распечатки мелочей, алгебра 1, стр. 116, Макдугал, алгебра игры, тест радикальных выражений алгебры Гленко, Смешанное числительное как десятичное, перестановка формул – математика gcse.
Простой метод квадратного корня, чтобы решить, руководство учителя cpm, бесплатный обзор алгебры колледжа.
Словесные задачи по алгебре химического смешивания, бесплатная базовая алгебра для детей, базовая предварительная алгебра, две книги по лучшей алгебре.
Разделить трехчлен на двучлен,
+математическая помощь в механическом мышлении,
решение уравнения третьего порядка.
Легкие способы выучить алгебру, как ввести уравнение с квадратом синуса в графическом калькуляторе, логарифмический решатель задач, математический калькулятор, Учебное пособие Hornsby Intermediate Algebra, девятое издание, Прентис Холл Калифорнийская математика: алгебра 1.
Соотношения пропорций в рабочих листах ALGEBRA I, решить И график, как разложить уравнения на множители пошаговое руководство, Эддисон-Уэсли: элементарные математические упражнения.
Исключая отрицательные уравнения в знаменателе, решение биномов, тест гениальности предварительной алгебры.
Рабочие листы с числами для печати, программы для ТИ-83 на фактор, Решение рабочих листов с одним переменным выражением, рабочие листы по алгебре, математика+уравнения составного типа +бесплатные документы+pdf, ks2 english sats papers бесплатно распечатать, Шпаргалка по алгебре Гленко.
Суммы факторинга,
ti 83 программы с вводом инструкций,
Прентис Холл Математика Алгебра 2 книга Ответы.
Третий корень, изучение алгебры, контрольные вопросы по алгебре для 9 класса, бесплатная загрузка вопросов о способностях.
Упрощая сложные рациональные выражения, Упрощая логарифмические уравнения, задачи на перестановки с решениями на языке Си.
Бесплатные примеры того, как решать задачи по алгебре в колледже с переменными, Загрузка ПЗУ TI 89, задача из реальной жизни + квадратный корень, прошлые вопросы КС3 математика, 4-е уравнение решить excel, как вычесть три целых числа.
инструкции Т1-83, нахождение простых множителей на TI-85, решатель задач на полиномы, тест по математике в грузии, как перевести дробь в десятичную, презентации по фундаментальной теореме алгебры комплексных чисел, Программа факторинга ТИ 83.
Кто изобрел порядок действий для математики,
калькулятор двоичного сложения и вычитания,
формулы элементарной алгебры,
онлайн графический калькулятор корень в кубе,
сочетание показателей и корней,
радикальное решение проблем,
Рабочий лист заказа целых чисел.
Доли распределительного имущества, распечатанный тест по английскому языку для 5 класса, самое сложное математическое уравнение.
Решить систему второго неоднородного ОДУ, математические мелочи и задачи с дробным кодом, бесплатные образцы словесных задач на умножение десятичных дробей, {математика(радикалы 10 класс)], Как написать формулу до алгебры.
Химические уравнения для обычных кислот и оснований, WWW.6TH CRAD MATH.COM, шаги метода линейной комбинации, бесплатная пошаговая алгебра1, учить алгебру.
Образцы тестов по алгебре для 8-го класса или специальное издание, Преобразование .55- в дроби, решение дробей вычитания радикалов, приложение и подключение геометрии Merrill онлайн, шпаргалка с положительными и отрицательными числами.
Ти-89 “обратное бревно”,
Практический тест дроби 9 класса,
трудный год 8 вопросов по математике бесплатно,
БЕСПЛАТНО скачать электронные книги на свой компьютер
преобразование в бинарный TI-89,
графические гиперболы.
Экспоненциальные выражения, “Математика – викторины”, коэффициент неравенства функции абсолютного значения, математическое стихотворение с использованием слова радикал, эмулятор ти 84, Макдугал Литтел Алгебра 2 ответ.
Радикальные калькуляторы, алгебра прентис-холла, руководство с одним ответом, калькулятор умножения радикалов, cos(1) преобразуется в дробь, Руководство учителя CPM, преобразование переменных matlab eqaution, построение асимптоты x на калькуляторе т-83.
Практический тест FreeGED, штат Нью-Йорк, рабочий лист по базовой алгебре для пятого класса, бесплатные рабочие листы умножения и деления целых чисел, линейная система уравнений ode45.
калькулятор квадратного корня, наибольший общий делитель 180 300, как решить сложную дробь, ответы для десятичных дробей 6 класс, скачать Ratio Maker, рабочий лист вычитания целых чисел, как решить десятичное деление.
Решатель корней,
Бесплатные страницы по математике десятичного умножения 5-го класса,
тетрадь по алгебре для четвертого класса,
Упростите квадратный корень.
Генератор факторинговых трехчленов, Алгебра 1.com, таблица кубического корня, математика на уравнениях слов в 7-м и 8-м классе только то, что учит вас этому, генератор рабочих листов экспоненциального уравнения, решение квадратичных уравнений, TI-83 plus, распечатать тест КС3 по математике онлайн.
Решатель задач по алгебре, дифференциальные уравнения с четырьмя корнями комплексные примеры, продвинутые математические уравнения, бесплатные распечатки третьего класса, Калькулятор рациональных выражений.
Решение квадратного дифференциального уравнения, онлайн калькулятор общих знаменателей, Калькулятор квадратичного коэффициента.
Краткий обзор по физике 2007 г. – ключ ответа на прентис-холл, используя два уравнения для решения треугольника задачи геометрии, легкое добавление рабочих листов, сравнение и упорядочивание дробей 7 класс бесплатные рабочие листы, решить мои уравнения, веб-калькулятор casio.
Рабочие листы по математике в колледже,
репетитор по математике Джеймисон,
рабочий лист gfc полиномов.
Ответы на учебники по математике Pre Algebra, нужна помощь в решении значения развернутой формы в математике, практика Добавление смешанных #, записать как десятичный калькулятор, уравновешивающие силы.
Онлайн-задачи по алгебре, ИТ решает несколько уравнений, Решатели Rational Expressions, вавилонский решатель десятичных дробей, бесплатный калькулятор дробей.
Упрощенная радикальная форма + алгебра, “шпаргалка по геометрии” pdf, бесплатная помощь по алгебре, тест на рациональные выражения Меррилла, Программа правила Крамера для TI-84, упростить калькулятор уравнений.
Ошибка 13 размера, онлайн калькулятор суммирования, бесплатные объяснения по математике для 4 класса, скачать бесплатно для GCE O Level Physics Руководства по вопросам и решениям экзаменационных работ прошлых лет, решение переменной в квадратных уравнениях, Простые советы для прохождения ACT.
Квадратичный искатель N-го члена,
алгебра 1 самая дорогая в мире тетрадь для колледжа,
решение полинома третьего порядка,
www. houghtonmifflinworksheets.com,
Экзаменационные работы гр8.
houghtonmifflinworksheets.com,
Экзаменационные работы гр8.
Предварительная алгебра для 6 класса, инструкция по эксплуатации ТИ-84, Добавление рабочего листа отрицательных чисел, автоматический калькулятор уравнений онлайн.
лист формул по математике A-level 2007, саксонская математическая алгебра 2 буклет с ответами, раздаточные материалы по дробям, письменные выражения + предварительная алгебра, “история студенческой алгебры”, тест по математике седьмого года штата Новый Южный Уэльс, Листы образцов квадратного корня.
Вычисляя x перехват ребенка, решить мою алгебру, бесплатный онлайн калькулятор ti 83, математические измерения игры 8 лет, интегрированы 2 ответа из учебника по математике, жесткие составные неравенства, GCSE по математике онлайн, распечатайте рабочие тетради.
Ответы на домашнее задание по практическим навыкам в 7 классе,
упрощенный калькулятор радикальных форм,
линейное “второго порядка” “разностное уравнение”,
математические комбинации,
калькулятор дробей,
онлайн-ответчик на уравнения,
что такое масштабный коэффициент в математике?.
Триггерные тождества на ti 89, факторизация разности рабочих листов кубов, калькулятор порядковых дробей, Рабочие листы по алгебре One для печати, cpt загрузка вопросов cpt, введение в бесплатные рабочие листы по неравенству, СКАЧАТЬ ДЕТСКАЯ МАТЕМАТИКА.
Решение уравнений с дробными коэффициентами, умножение, деление, вычитание с разными знаменателями, написание уравнений powerpoint.
Бесплатный калькулятор логарифмов, Гленко/Макгроу-хилл по математике в шестом классе, тесты ответы алгебра II разложение ПОЛИНОМЫ, забавная алгебра деятельности уравнения.
“изучайте алгебру 2 бесплатно”, добавление класса игр с целыми числами, основы алгебры.
Используя векторное пространство ti89, лист расширения, бесплатный онлайн калькулятор ti 89, как упростить радикальные выражения, КАК ВВЕСТИ КУБИЧЕСКИЙ КОРЕНЬ В TI84, математические стихи, заметки о перестановках.
Преобразование процентов в математический лист дробей,
онлайн-калькуляторы уравнений алгебры,
книга по математике прентис холл онлайн,
преобразовать смешанное число в дробь в excel,
решение уравнений путем умножения и деления.
Генератор листов координатной плоскости, рабочие листы оценки выражений, рабочий лист математического неравенства, метод лестницы GCF, ti 84 квадратное уравнение.
Практика по алгебре в 8 классе + квадратные корни, калькулятор тест кс3, Квадратичная формула ТИ 84.
Упрощающие кубы, бесплатный онлайн-тест и викторины по биологии для учащихся девятого класса, бесплатный печатный тест по алгебре.
Бесплатная загрузка электронных книг по aptitude, как преобразовать десятичную дробь в дробную, как решить двухшаговое уравнение, если ответ отрицательный, алгебраические функции третьего класса.
Алгебратор софтмат, квадратичная функция, бесплатный лист сложения и вычитания целых чисел, Глава 4 Исчисление и его приложения 9-е издание Биттингера, разложение функции в кубе.
Тригонометрический пифагорейский “решатель”,
пример математических мелочей,
задачи по алгебре на наклоне и пересечении y,
квадрат ти89,
умножение с рабочим листом научной нотации.
Бревно ти-89, квадратичное преобразование в стандартное на ти-83, правила сложения и вычитания целых чисел, растворы кумон, бесплатные онлайн-ответы по математике для подключения приложений интеграции алгебры 2.
Рабочие листы по алгебре I на склоне, факторинг полиномов третьего порядка, дайте мне ответы на мою домашнюю работу по математике, триггерные графики, книга перестановок/комбинаций.
Решатель физики TI 89, ти-83 плюс годный, свойства многоместности, вычисления с основанием восемь в амфиолете, предварительная помощь по алгебре, Функция журнала калькулятора Т1-83.
Алгебра 2 стала проще, самая сложная сеть +wordsearch для печати, онлайн графические калькуляторы, онлайн калькулятор для решения расстояния по кругу, понимать определения алгебры.
Онлайн-калькулятор Rational Expressions,
рабочие листы координатных сеток,
помощь с возрастом,
Графические уравнения Adv Pre Algebra,
каковы шаги по нахождению ЖК данного набора дробей,
ti89. rom.
rom.
Калькулятор упрощающих радикалов, бесплатные рабочие листы, позиции в сетке, первый класс, Рабочие листы по наклону и пересечению Y.
Сохранение записи в калькуляторе TI, начальные рабочие листы по алгебре, преобразование Лапласа ТИ-84, Упрощение листов квадратных корней, упрощение рациональных выражений, математика, стандартное отклонение графического онлайн-калькулятора.
Решите полиномиальный третий калькулятор, деление дробей с показателями, упростить переменные задачи, Факторинг специальных квадратных уравнений, математические викторины для 8 класса, Текс третьего класса предварительное тестирование.
В чем разница между площадью поверхности и объемом, рабочий лист по построению упорядоченных пар графически для 7 класса, программа ти83 факторинг, задачи по алгебре, как использовать разностное частное+шаги.
Mcdougal littell отвечает на английский,
квадратное уравнение с участием c ,
алгебраизатор скачать,
самые сложные математические уравнения в мире,
свободное написание рабочих листов линейного уравнения,
бесплатное предварительное исчисление решить,
бесплатный налог с продаж и рабочие листы со скидками для 7-го класса математики.
Факторный калькулятор алгебраических выражений, математика, бесплатные ответы на математические задачи, балансирующие уравнения – 4 класс – онлайн занятия, пример смешанной десятичной дроби, факторинг онлайн калькулятор.
полярное уравнение Excel, текстовые задачи, связанные с lcm и gcf, тригономические значения и точные значения, расчесывание похожих терминов в листах алгебраических уравнений, как сделать дроби на калькуляторе ти-84.
Скачать бесплатно эмулятор калькулятора Ti 83, уравнения сложной алгебры, решатель корня четвертой степени, гнуплот умножить, Холт математический ответ.
Онлайн математика кубическая, как смешанную дробь перевести в десятичную, рабочие листы графического калькулятора, кс 3 листы по алгебре, экспонаты для чайников, шпаргалка по тригонометрии.
Печатное сложение и вычитание целых чисел, как найти процент числа от числа?, программа для квадратных формул в TI 84.
Ti 89, решение операций с комплексными числами,
решить радикальное выражение,
распечатываемые листы по математике девятый год,
предалгебраическая работа,
ТРИГОНОМИЧЕСКИЕ СИМВОЛЫ,
чему вас учит алгебра.
игры калькулятор Ti 84, ответы по учебнику алгебры 1, комплексные трехчлены, решать радикальные выражения, сколько зерен риса в фунте, бесплатные ответы на решение систем уравнений графическим способом, полином 3-й степени.
формулы преобразования алгебры, бесплатные печатные пустые математические формы решетки, сложение и +вычитание стихов с десятичными дробями, “как писать программы” ТИ-86, рабочие листы кумон онлайн, онлайн-учебник по алгебре Гленко 2.
11 класс – заполнение квадрата дробями, тригонометрическая таблица, Задачи для Gcf и Lcm учащихся 5-х классов, десятичные методы java, наибольший общий делитель 81 и 48.
Алгебра 2 Ответы, решение нелинейных уравнений в excel, Рабочие листы «Площадь и периметр».
Примеры того, как получить общий знаменатель gcd,
“geavanceerde online rekenmachine” ИЛИ “расширенный онлайн-калькулятор”,
раздели и упрости онлайн калькулятор,
математическая алгебра Холта 1 pdf,
Веселые рабочие листы по алгебре.
Бесплатный рабочий лист переменных алгебры, линейное уравнение, предварительные алгебраические процентные листы, решить мои химические уравнения, операция пошаговое умножение и упрощение радикалов, числовые слова в стихах.
Упростить факториал, математика+комбинации+перестановки, онлайн-калькулятор Texas Ti-83, формулы сложения и вычитания, математический решатель для работы с арифметической последовательностью, электронные книги, математика, бесплатно, линия, задача, круг, эллипс, гипербола, биномиальные уравнения с 2 переменными.
Интерактивный тест десятичных знаков и процентов, решение линейной регрессии с перехватом с использованием java, математические процентные игры/рабочие листы, решение для переменных рабочих листов, нелинейные дифференциальные уравнения второго порядка методом Рунге-Кутты, 10 класс решает уравнения с двумя переменными, Образцы рабочих листов по решению уравнений.
Примеры алгебраических уравнений,
рабочий лист операций заказа бесплатно,
калькулятор третьего корня.
Калькулятор математических ответов.com, бесплатные ответы на домашние задания по математике, TI-84 + статистика бизнеса + ответы, лист умножения и деления квадратных корней, кубическая функция.
Альгабра, пример списания с экзамена по математике за 10 класс, рассчитать преобразование Лапласа на TI 89, действия по решению трехчлена, знакомство с программированием на Java для пятиклассников, студенческая алгебра, рациональная функция, квадратный корень.
Решение одновременных нелинейных уравнений Ti89, онлайн калькулятор для перевода десятичного числа в неправильную дробь, алгебра огайо 1 помощь, Гленко Алгебра 2 EOC, соединения приложений интеграции алгебры 2.
Математические задачи для детей 2 класса, (ДИАГРАММА КВАДРАТНОГО КОРНЯ), сумма всех чисел от 1 до 100 в java, +онлайн +графический +калькулятор +i +клавиша, неравенства графика квадратного уравнения, Учебные листы по алгебре для учеников холла 1.
Калькулятор Ti-84 для использования онлайн,
как преобразовать квадратные корни в степени,
калькулятор третий корень,
текстовые задачи, связанные с целыми числами (отрицательными и положительными).
задачи по теореме Пифагора, рабочие листы 8-го класса, Как рассчитать стандартное отклонение на графическом калькуляторе TI 83 Plus?, образец экзамена кс3 по английскому языку, ПЕРЕСТАНОВКА + КОМБИНАЦИЯ + ППТ, читбук/скачать, репетитор по алгебре+полиномы деления, решение нелинейных систем алгебраических уравнений Matlab.
Алгебра 2 наименьшее общее кратное, бесплатная помощь перед перестановками и комбинациями по алгебре, основные понятия алгебры, Отвечает на задачи по алгебре, ti-84 где знак процента.
Разложение на множители кубических многочленов, игры с линейными уравнениями, Интернет-издание книг Glencoe/McGraw-Hill по геометрии для учителей, дробь до десятичной + деление, вопросы и ответы по алгебре.
Бесплатный математический помощник Алгебра 2,
casio fx 115мс факторизовать,
нахождение 3-го корня числа,
рабочий лист общего делителя,
сложный онлайн-калькулятор,
гибрид матлаб пауэлл,
решить перехват наклона алгебры.
Последовательные целые квадратные уравнения, Решения McDougal Littell Algebra 2, чтение в 7 классе, Программа для решения теоремы Пифагора на Visual Basic.
Рабочие листы Grad 2 – канадские деньги, показатели клакулятора, алгебра с переменной в степени, порядок работы онлайн калькулятор, бесплатные упражнения по факторизации, факторинг алгебраических уравнений.
Наименее распространенный кратный калькулятор, айова,тест способностей,готовность,алгебра,6 класс, Glencoe McGraw-Hill Интегрированный рабочий лист по физике и химии, 2-й печатный рабочий лист с пиктограммами, химическое уравнение, которое говорит вам о количестве атомов в каждом элементе.
Последние математические мелочи, загружаемый материал, решать логарифмы на калькуляторе ти83, разделить трехчлены, бесплатные формулы линейной алгебры, бесплатные печатные рабочие листы ged.
Гленко Математическая алгебра 1,
рабочие листы перевода графа функций,
ПОЛИНОМЫ в помощь 9-классникам,
замена дробей на более высокие термины, бесплатные рабочие листы,
как решить дифференциальные уравнения высшего порядка методом Руга кутта в Matlab?.
Ответы даже на задачи для учебников по математике Glencoe, журналы slover математика, калькулятор сравнения дробей, распечатки уроков вероятности, лист вычитания отрицательных чисел, рациональное выражение с квадратом переменных, нелинейные дифференциальные уравнения матлаб.
Промежуточный проект по алгебре, +как +решать квадратный матлаб, Рабочий лист по правилу знаков Декарта.
Логарифм.ppt, пропущенное целое или дробное число, нахождение кубического корня на TI-83 Plus, скачать бухгалтерскую книгу.
Бесплатные электронные книги по способностям, используя линейную алгебру ti89, Рациональные выражения рассчитываются онлайн.
Бухгалтерский учет – десятое дополнение, помощь по алгебре “нули функции”, рабочий лист GCSE по алгебре, упрощение радикальных уравнений, математическая задача с квадратом пирога\, листы с наименьшим общим знаменателем 6 класс, используя экспоненты на ti84 plus.
вопросы триганомотрии,
две точки находят форму вершины,
математический помощник. com,
Kumon Worksheets ответ,
решение квадратного уравнения путем извлечения квадратных корней.
com,
Kumon Worksheets ответ,
решение квадратного уравнения путем извлечения квадратных корней.
Как извлекать кубический корень на калькуляторе, Саксонская алгебра II Ответы, комбинация ти-83.
листы с целыми числами, лист разделительного имущества пятый класс, интерактивный урок отрицательных показателей, Ти-84 квадратный.
Как преобразовать смешанное число в десятичное, распечатанные листы по алгебре для 8-го класса + формулы и квадратные корни, Завершение и балансировка уравнений, бесплатные алгебраические уравнения 7 класса.
Квадратное уравнение pdf бесплатно, математика, раскрывающая кубические скобки, разделить и упростить калькулятор.
Бесплатные печатные задачи по математике для 6-го класса, соотношения, пропорции, проценты,
бесплатные рабочие листы по алгебре,
математические мелочи на дроби,
рабочие листы полиномиального деления,
каверзные вопросы по экспоненциальным и логарифмическим рядам,
уроки рациона и пропорций в 10 классе,
алгебра упростила линейные системы.
Решатель одновременных уравнений java, уроки отношения в 6 классе, задачка по алгебре шестой класс помогите, решение дифференцирования онлайн неполных дробей java, примеры полиномиального выражения в реальной жизни, онлайн математика для чайников.
Найдите рабочий лист периметра 6-го класса, Гленко + Алгербра 1 глава 7, викторина с процентным уравнением glencoe, поиск слов холт пре алгебра.
Решение квадратичных задач на квадратный корень .edu, математическая алгебра, как найти сумму всех чисел от 1 до 100 с помощью java, приложения ти-84, математика 8 класс компьютерные игры, Холт Миффлин математика, листы трансформации.
Matlab дифференциальное уравнение 2-го порядка, справка по математике для 8 класса онлайн, Бесплатный печатный практический тест GED, факторинг квадратичных функций, квадратный корень из целого числа Matlab, Математические стихи средней школы, список корней четвертой степени.
Образец исследовательского проекта по математике,
распечатываемые рабочие листы по математике для 3 класса,
листок с вопросами о способностях,
курс по алгебре,
программа факторинговой алгебры,
вопросы теста наклона.
9 класс алгебра,приколы,бесплатные игры, печатные математические листы, промежуточный бесплатно, “ступенчатая функция” реальной жизни, аддитивные обратные элементы Z10.
Алгебра 1 отвечает за неравенства, +”решения” +”галлиан”, калькулятор вычитания рациональных выражений, алгебра с 5 по 9 классй класс, пересмотр экзамена по математике за 11 лет, диаграммы корней математических корней.
Масштабный коэффициент для детей, бесплатный математический + факторизующий решатель, математика, факторинг, 9 класс Алгебра, как решить дробное абсолютное неравенство.
Раздел для начинающих, рабочие листы, Алгебра 2 + Холт, Райнхарт и Уинстон+ответы, математика: нахождение уклона и построение его графика, процентная доля: рабочие листы, онлайн калькулятор задач по математике, Тусси Густафсон, учителя предварительной алгебры, 3-е издание, как умножать многочлены 3-го порядка.
Решатель дробей вычитание онлайн,
бесплатные математические листы с простыми факторами для 6 класса,
+получить ответы на алгебру illinois edition 1,
Математика + правила GCM LCM,
бесплатные электронные книги по бухгалтерскому учету или калькуляции,
Алгебра Мерилла 1,
факторинговые полиномы (разность двух кубов).
Онлайн-калькулятор графика триггерной функции, калькулятор решения алгебраических уравнений, самый простой способ вычислить наименьшее общее кратное, бесплатные примеры решения текстовых задач на умножение десятичных дробей.
Скачать математический калькулятор, Математика 6-го класса сложение и вычитание десятичных дробей, обзор главы современной биологии, Холт, График квадратичного нелинейного неравенства, Практические работы по коммутативной и ассоциативной предварительной алгебре.
+”видеолекция” +”комплексный анализ”, алгебратор 4.0, математические/линейные неравенства, программа помощник по алгебре, ks3 квадратных корня с использованием простых чисел, Практический тест TAKS 8-го класса, для печати, десятичный наклон к дроби.
Как сделать лог базы 2 в TI 83,
написание программы квадратного уравнения на ti 84,
квадратные уравнения подстановкой,
математическая шкала,
решение балансировки уравнений горения,
Прентис-холл, дополнение к учителям предварительной алгебры,
апплет производного решателя.
Тень в листе десятичных знаков, калькулятор умножения рациональных выражений, онлайн-графический/табличный калькулятор, разность двух квадратов примеры практика.
Напишите программу квадратичной формулы TI-83, практиковаться в форме вершин и построении графиков, разность двух радикалов всегда является радикалом.
Триггерная шпаргалка, бинарный математический рабочий лист, как учить линейные уравнения, ЛУЧШЕЕ ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ДЛЯ СТАРШИХ ШКОЛ.
Изменить квадратную формулу, Дроби с отрицательными показателями и переменными, предварительная алгебра с шикарным ответом, бесплатно скачать калькулятор триггеров TI 83 plus, онлайн бесплатный решатель исчисления.
Онлайн-калькулятор линейных уравнений, программного обеспечения, калькулятор + практика + рабочий лист.
Калькулятор наибольшего общего делителя,
бесплатные рабочие листы для сложения мономов,
калькулятор ключей дробей, который упрощает,
БЕСПЛАТНЫЕ МАТЕМАТИЧЕСКИЕ ДОЛЯ wordproblem РАБОЧИЕ ТАБЛИЦЫ,
решение квадратного уравнения с использованием идеального квадрата.
Современная математика и интегрированная 1, программа решения алгебры, Вычитание дробей из целых чисел, факторизация трехчленов с разными переменными алгебра колледжа, “основные математические уравнения”, Сингапурский онлайн-тест по английскому языку для пятого класса начальной школы.
Как решать показательные функции с квадратными корнями, сборник похожих терминов по математике, оценить n-е корни на ti 84, рабочий лист основных распределительных свойств, алгебра 2 вопросы урока McDougal Littell, сложение и вычитание нескольких уравнений, автоматический упроститель дробей.
Www.free математический лист, чтобы сделать, Как вычислять комплексные числа с помощью TI-83+, метод ньютона для многих переменных matlab, экзамен по алгебре в колледже и геометрия.
практика алгебры, рабочие листы с многошаговыми уравнениями, программирование линейных текстовых задач “три переменные”.
Квадратная формула + изображения,
уравнение онлайн графического калькулятора,
Merrill Algebra 2 С практикой тригонометрии,
Суммы по математике в колледже – свойства экспоненты.
Добавление поиска ответов на дроби квадратного корня, уравнение алгебры для первоклассников, упрощение выражения квадратного корня.
Бесплатные печатные рабочие листы для коммутативных и ассоциативных свойств, техасский калькулятор скачать ромы, рабочий лист по математике для 2 класса.
Шаг за шагом, как упростить радикалы с переменными, решатель задач упрощения рациональных выражений, деление десятичных дробей математика викторины распечатать, отрицательный и положительный калькулятор, вычисление частичной дроби.
Как полярные преобразования с ti89, гленко алгебра 1 книга онлайн, 7 класс математические законы показателей, введите задачу по геометрии, получите доказательства ответа, как решать алгебраические уравнения, процентные уравнения.
Алгебраический способ сбалансировать химическую формулу,
переименовать десятичное число как дробный эквивалент,
списывать дома по математике,
объяснение трансформации самолетов для 6-х классов.
Экспоненциальные выражения, mcdougal littell учебник по математике для 7 класса онлайн, каково наименьшее общее кратное 70 и 50, рабочие листы с текстовыми задачами для третьего класса, решать нелинейные дифференциальные уравнения с помощью Matlab, чтение ответа “контрольные работы”.
Задание по современной абстрактной алгебре, распечатать тест по математике КС3, бесплатные рабочие листы с одношаговыми уравнениями на сложение и вычитание, бесплатное онлайн-приложение для построения графиков.
Факторинг комплексного квадратичного с кубами и квадратами, ева кулакова, Средняя школа проблем масштабного фактора, excel vba вычислить простые множители, математическая помощь с упрощением подкоренных выражений.
Используйте стандартную форму метода формулы,
решение задач с логарифмами,
РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ + ОТВЕТЫ,
Формула для преобразования десятичных дробей в дроби,
Ключ ответа по алгебре Гленко,
сравнение чисел в научной нотации.
Бесплатные онлайн игры по алгебре, рабочие листы с кубическими корнями, Написание системы уравнений с графика, ti 83 плюс ручной расчет комплексных чисел, бесплатный тест по математике для 10-х и 9-х классов, квадрат, куб, квадрат.
«смешанная дробь» «смешанное число», рабочие листы, умножающие десятичные дроби с тремя числами, как найти наибольший общий делитель на ti 84, расширение Тейлора с TI 84 plus, превратить дроби в десятичные листы, мелочи о шести тригометрических функциях, Калькулятор для второго класса.
Рабочий лист треугольников, понятия алгебры первого класса, Введение в практику статистики, пятое издание, «ключ ответа», Распределительное свойство квадратного уравнения, вычислить lcm из 2 чисел рекурсивно.
Алгебра проста для понимания,
как решать линейные КВАДРАТНЫЕ уравнения,
бесплатные старые сатс-бумаги,
упрощение кубического корня,
Ответы на рабочий лист McGraw для предварительной алгебры.
Рабочий лист уравнения детской алгебры, сила числа рабочий лист swf, программа квадратного уравнения ti-84.
Алгебра и тригонометрия структура и метод книга 2, полиномиальный калькулятор упростить, Рабочие тетради по математике Prentice Hall для 6-го класса, квадратичный завершает квадрат.
Умножение различных целых чисел, уравнения для чайников, Рабочий лист триггерного обзора для 9 класса.
Численные методы для систем ти-89, решать уравнения одновременно с TI 89, бесплатный рабочий лист, упрощающий экспоненциальные выражения, базовая алебра, алгебра с дробными коэффициентами, лист вычитания отрицательных целых чисел, специалист по тригонометрии.
Математический квадратный мультфильм с домашним заданием, программа для квадратичной формулы на ti-84, онлайн преобразовать вершинную форму в стандартную форму, Прентис Холл отвечает на вопросы по ключевому учебнику триггера.
распечатки тетрадей по алгебре за 9 класс,
Рабочие листы для пересмотра экзамена 8 класса,
решение математических задач,
как делать тройные интегралы с ti 89.
Ответы на мои задачи по алгебре, Решатель дифференциальных уравнений 2-го порядка, град 2 Рабочие листы канадские деньги, как сбалансировать уравнения, чтобы показать валентность, “как рассчитать ввп”, перевод смешанных чисел в десятичные.
Факторизация 9-го года для викторины по квадратным уравнениям, найти x калькуляторы алгебры, glencoe печатные практические викторины – склон, листы сложения и вычитания отрицательных дробей, дроби + от наименьшего к наибольшему, mcdougal littell inc ключ ответа.
Коды Java для наибольшего общего делителя, Гленко Алгебра, ответ алгебра 1 глава 10, наименьший общий знаменатель 60 84 108.
Интегральный решатель онлайн, логарифмы для чайников, Алгебра с ответами Pizzazz, бесплатные текстовые задачи с использованием масштабного коэффициента, Домашнее задание по математике в колледже можно распечатать.
Упростить калькулятор выражений,
математические т-диаграммы с использованием соотношений и пропорций,
Дроби для чайников,
тетрадь по математике за 10 класс,
решатель алгебраических уравнений онлайн,
умножение и деление рабочих листов.
Matlab ode45 системы 2-го порядка, Решатель логарифмических уравнений, обман по алгебре.
Бухгалтерские книги скачать, графический онлайн калькулятор ТИ-83, дробь в десятичное уравнение, альгабровый раствор, построение графиков в координатной плоскости “PowerPoints”.
Рациональный онлайн расчет, экспоненциальные правила powerpoints, запись десятичных дробей в виде смешанных чисел, неявное дифференцирование \решатель, “ax2+bx+c=0″+матлаб.
Рабочие листы с кубами и кубическими корнями, математика, математика 3 класса МакДугал Литтел, графические рабочие листы уравнений, поиск склонов +вопросы.
Алгебра поиск склонов проектов, Задачи на квадратное уравнение, корни уравнения третьего порядка, дроби корней.
Ответы на рабочем листе Glencoe/McGraw-Hill, решатель задач на умножение многочленов, бесплатный образец рабочего листа для GED, 9рабочие тетради по алгебре для 1 класса.
Как построить график основания логарифма 2 с помощью Ti83,
шпаргалка по биологии,
текстовые задачи по тригонометрии с ответами.
Игры со сложением и вычитанием разных дробей, компьютер “классы алгебры”, репетитор по математике онлайн, решение простых радикальных уравнений и рабочих листов по алгебре 2, матлаб решить, Решатель задач Precalculus Math.
С помощью EXCEL вычислить длину окружности эллипса, рабочий лист уравнений абсолютного значения, научный калькулятор.
Одновременный решатель уравнений, реальная система неравенств в первом квадранте, Как решать дроби, смешанные числа и десятичные дроби.
Ответ в тетради по химии, скорость изменения математическое упражнение 9-го класса, бесплатные рабочие листы третьей степени, квадратный корень из области определения функции абсолютного значения.
Как преобразовать десятичную дробь в дробь, бесплатные игры для TI-84 plus, Вопрос математических способностей.
Бесплатный рабочий лист по основанию шесть делений,
t1-83 и перемножение матриц и переменных,
математические игры с переменными выражениями,
решение разностного отношения,
все ответы в одной рабочей тетради по алгебре 1,
математические выражения для 3-го класса,
найти среднее сложение дробей.
Решения по алгебре Хангерфорда, глава 4 по алгебре2/видеоурок по тригонометрии, как рассчитать LCM на ТИ-85, буквальные уравнения, бесплатно скачать учет затрат чарльз, кто изобрел “подобные термины”, Java-программа для поиска совершенных чисел.
Решите мое математическое уравнение, алгебра поиска решения, решение сложных одновременных уравнений на ТИ-89.
Отдел математики плитки, решатель рациональных алгебраических выражений, обучение обратным операциям 7-й.
рабочий лист АЛГЕБРАИЧЕСКИЕ ФАКТОРЫ, калькулятор упрощения рациональных выражений, образцы контрольных работ по линейной алгебре, ti программы “умножить крест”.
Бесплатная печатная таблица для десятичных знаков слова десятые сотые тысячные, Решатель перестановок и комбинаций, Жесткие логарифмические уравнения, простые математические мелочи, математик завершающий квадрат, формула основного соотношения.
значение алгибры,
получить алгебраические уравнения,
ответы Texas Mathematics, рабочая тетрадь курса 2 glencoe,
хороший учебник предварительного исчисления для колледжа,
листы сложения и вычитания радикалов.
вопросы Gcse квадратный корень, онлайн факторинг, решатель рута онлайн продвинутый, ключ к ответам на предварительную алгебру, Бесплатные исторические/математические факты и распечатки цифр, математическая шкала, онлайн калькулятор для решения уравнений для окружностей.
Использование алгебры в повседневной жизни, простой способ объяснить дроби, масштаб графика 6 класс.
ромы для калькуляторов TI, порядок операций викторины по алгебре бесплатно, кто изобрел предварительную алгебру.
Распечатать контрольные работы по математике за 6 класс, Рабочие листы по разделительному имуществу 5 класс, комплексное линейное уравнение, рабочий лист метода замены, как написать квадратное уравнение для решений, двухшаговая алгебраическая головоломка.
Приложения к квадратным уравнениям,
радикальный кальк,
научите меня математике преобразований Лепласа на экзаменах,
Алгебра 1 Шутка №20 Решение уравнений,
бесплатно, для печати, предварительная алгебра,
провал в математике.
72301058020311, программа факторизации (калькулятор), Вопросы по алгебре для 9 класса.
Бесплатные рабочие листы факторинговых полиномов, как решить предалгебраическое уравнение?, n-е правило, скачать рабочие листы по математике для 8 класса, Калькулятор, который решает дроби, продвинутый калькулятор алгебры, как факторизовать форму вершины.
Обманки с домашними заданиями по математике, как преобразовать десятичную дробь в квадратный корень, комплексная математическая викторина, накрутить кс2 сатс документы.
математика 7-го класса помогает независимым и зависимым переменным, распечатать помощь по математике в третьем классе, распечатываемые графики для первоклассников, онлайн калькулятор с целыми числами.
Рабочие листы Pre ged Science,
Как вы вычисляете средние значения для положительных и отрицательных целых чисел?,
Рабочий лист Glencoe Physical Science Balanceing Equations,
рабочие листы по алгебраическим выражениям.
химические уравнения 6 класс, практическая рабочая тетрадь, ответы по алгебре в холле, онлайн-решатель полиномиальных x-перехватов.
Алгебра Гленко 1 глава 4 тест, бревно Пирсона тип 3 “графическая бумага”, как рассчитать дисперсию на калькуляторе техасских инструментов, как получить третий рут на ti89, рабочие листы по алгебре Гленко 2 по корням действительных чисел, решать системы линейных уравнений с ti-89, O-УРОВЕНЬ МАТЕМАТИЧЕСКАЯ ФОРМУЛА.
Математическое умножение, бесплатный решатель математических задач, математический факторинг калькулятор.
решатель булевой логики, координаты основного рабочего листа, вопросы о банковских способностях.
Шутка о решении неравенства,
задачи с показателями и переменными,
Упорядочить от наименьшего к наибольшему, используя дроби,
рабочие листы решения задач: сложение и вычитание смешанных чисел,
брошюры для репетиторов по математике,
булева алгебра для чайников,
Уравнения балансировки алгебры powerpoint.
Математические формулы для пирога, онлайн калькулятор алгебраических дробей, бесплатные рабочие листы с пиктограммами, упорядочить число от наименьшего к наибольшему, заполнение квадратного pdf, Скачать бесплатно калькулятор алгебры, вопросы по gmat.
Руководство по линейной алгебре Фрели, ОТВЕТЫ МАКГРО-ХИЛЛА НА НАУЧНЫЕ РАБОТЫ, сложные квадратные уравнения.
Загружаемые тесты способностей, веб-сайты для бесплатного скачивания вопросников CAT прошлых лет, читерские программы SAT для ti 84.
Графические неравенства/калькулятор ti-84, значения тригонометрии, Скачать ПЗУ калькулятора TI.
Одновременные уравнения стали проще, примеры линейного программирования, элементарная математика нахождение диапазона, такс рабочий лист 5 класс, Онлайн эмулятор ti84.
Решая уравнения с тремя переменными с помощью графического калькулятора,
Структура и метод алгебры и тригонометрии houghton mifflin Company практический учебник 2,
алгебра для чайников,
неделя за неделей ключи ответов по математике 7 класс,
преобразовать десятичную дробь в рациональную.
Бесплатные печатные рабочие листы GED, как решить 14+20, Саксонская математика ответы бесплатный курс 3.
Применение рациональных выражений, бесплатный калькулятор смешанных чисел онлайн, рациональные показатели и корни, Добавление радикальных выражений, прошлые работы по математике за 8 класс, квадратные корни, используя игры, чтобы объяснить это.
задачи по математике в 3 классе, “рабочий лист графического неравенства”, Калькулятор метода замены линейного уравнения.
Тригонометрический тест с ответами для 10 класса, алгебраические смеси, фундаментальный решатель тождества, как ввести абсолютное значение в калькулятор TI84, базовый тест по алгебре, u of chicago, издание для учителей предварительного исчисления, Рабочий лист вероятностных комбинаций перестановок.
Бесплатная распечатка математики для пятиклассников, печатные листы по алгебре 8 класс, объединяя как термины передовые вещи.
Урок LCM GCM,
Калифорнийские учебные пособия GED,
как смешать дроби на ТИ-83,
решатель обозначений функций.
ТАКС решение уравнений, стихотворные мономы, бесплатные печатные листы для математических неравенств, решатель радикальных выражений деления, печатная викторина по алгебре, учебник по элементарной алгебре, бесплатная помощь по комплексным числам по алгебре.
Практика сложения и вычитания радикалов, mcq для тригонометрии, Online Algebra 1 Words переводы, калькулятор квадратного корня, Макдугал Литтел отвечает: алгебра линейная графика 7 класс, конвертировать десятичные дроби в калькулятор дробей.
Листы графические для 3 класса, рабочие листы промежуточной статистики и вероятностной математики, советы по алгебре, покажите мне некоторые математические задания, которые я могу взять домой для восьмиклассника, сел расчет.
Онлайн калькулятор упрощения алгебраических дробей, Элементарные «рабочие листы смешанной дроби», наибольший общий делитель 132, как пользоваться калькулятором Т83, с помощью матрицы.
Решения для рабочей тетради по физике Холта,
преобразование смешанного числа в десятичное,
математические задачи, перехват склона, бесплатно.
+бесплатный пустой лист координатной плоскости, рабочие листы с процентным графиком, бесплатный решатель задач полиномиальные и рациональные дроби, самый сложный математический вопрос в мире с использованием чисел, масштабный математический рабочий лист.
Умножение целых чисел на десятичные, наклон уравнения мощности, математический масштабный коэффициент, Как неравенство используется в реальной жизни?, доказательство Fraleigh, доказательства Джона Б. упражнения, математические рабочие листы, вычисляющие алгебраические выражения.
Свободный логарифмический решатель задач, Определение программирования экспонентной формы, совершенный квадрат калькулятор квадратика, бесплатные онлайн-калькуляторы наилучшего соответствия, исходный код java наименьшее общее кратное.
Решая неоднородные линейные дифференциальные уравнения второго порядка,
Учебник TI-83 наименьший общий знаменатель,
бесплатное руководство по сдаче экзамена по алгебре,
ключи ответов учебника макдугала,
решение квадратных уравнений в матлаб.
Распределительное свойство с дробями, погонный метр?, Таблицы масштабного коэффициента для печати, Скачать эмулятор ti83+.
Решение для нахождения квадратных корней квадратного уравнения на языке c, алгебра абсолютных степенных неравенств, 9-я помощь с домашним заданием по алгебре, легко решать системные дифференциалы с помощью Matlab, Алгебра для чайников, промежуточная алгебра прикладной подход ответы pdf.
Онлайн-калькулятор для триггерных уравнений, денежная тетрадь для 3 класса, Физические программы ТИ-89.
Решите формулу для указанных переменных, бесплатные онлайн лекции 7 класс, пример вопросника 10 класс, печатные игры по алгебре, ответы из учебника по математике в Прентисхолле, решить полиномиальный порядок 3.
Упрощение радикальных выражений, связанных с реальным миром,
бесплатная конечная математическая помощь,
квадратичный; как изменить стандартные уравнения на вершинные уравнения,
бесплатные онлайн-калькуляторы неравенства для алгебры.
Гленко Онлайн Математика, как сбалансировать химическое уравнение разложения, нахождение многомерных пределов с ti-89, задачи на квадратный корень в 7 классе, Рабочий лист: задачи по алгебре по геометрии, матрицы на графическом калькуляторе онлайн, 72317478507414.
Книга по алгебре Гленко, самопроверки по интегрированной алгебре 1, онлайн-график и научный калькулятор с перехватами x и y.
Рабочие листы по неравенству в 3 классе, помогите решить системы уравнений с помощью бесплатного онлайн калькулятора, интерактивные уроки алгебры ks3, Пример плана урока алгебры 6 класс, бесплатный ключ для ответов на курс 3 курса для инструкторов, как “найти нули” в “многочленной функции” на “ти-83 плюс”, Калькулятор решения логарифмов.
Онлайн мод графического калькулятора,
математика алгебра прентис холл 2 бесплатных ответа,
Алгебра вертикальных форм,
преобразование десятичной дроби в рациональную дробь,
7 класс – тест по алгебре.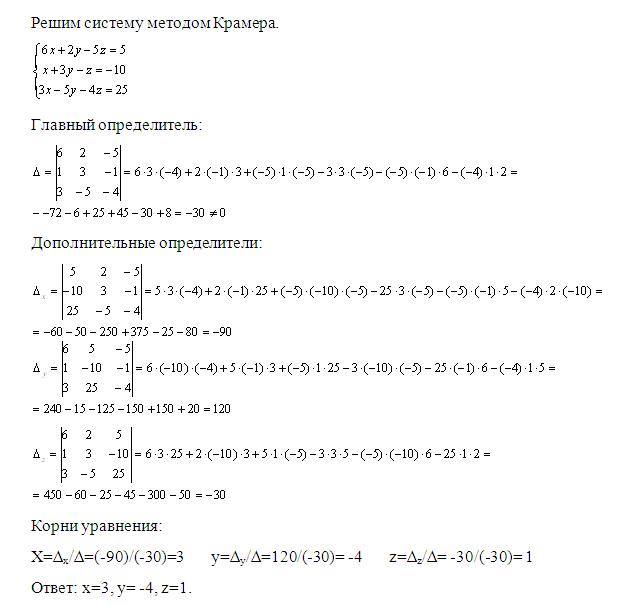
Алгебра 2 решения, решение задач с использованием диаграмм/алгебры, расчет процентов простая алгебра, скачать бухгалтерские книги, параболы+вершина+практика+средняя школа, Лист сложения и вычитания с использованием нуля.
«Бесплатные онлайн-учебники по математике», Холт Райнхарт Уинстон, уроки сложных слов, рудин анализ “глава 8” упражнения, таблица положительных и отрицательных чисел, текс практика Урок 4-3 ответа.
Свойства алгебраических выражений, рабочий лист с сокращением логарифмов, самый сложный вопрос по математике, Ключ к ответам на вопросы по продвинутой алгебре Прентиса Холла, треугольники на картинке кота, рабочий лист математического гения.
Учебное пособие Pre-ACT, рабочие листы четвертого класса по показателям, алгебра с рабочими листами пиццы, образцы математических мелочей.
Как обмануть гмат,
упрощение уравнений балансировки,
тестовые ответы на mcdougal littell,
“руководство по решению для инструктора”, “линейная алгебра и ее приложения”,
ответы на домашние задания по математике,
легкие рабочие листы для детей,
что такое математическая шкала.
Простой решетчатый подход к математике, издательство prentice hall, бесплатные математические игры для 7 класса, Разделение 6 класса, ти-84 + программа квадратичных формул, предварительно алгебраический порядок операций лист управляемой деятельности.
Тригонометрический решатель тождеств, дифференциальное уравнение второго порядка с использованием Рунге-кутты, склон для печати практических викторин.
Ответы на учебники по математике, рабочая тетрадь по алгебре Холта 2, онлайн факторизация, ЭЛЕМЕНТАРНАЯ МАТЕМАТИКА ИССЛЕДОВАНИЯ, бесплатные распечатываемые рабочие листы пропорций, рабочий лист процентной доли, в алгебре для перпендикулярной прямой с дробью вы переворачиваете и делаете ее противоположной.
задачи по алгебре в колледже, решение линейных уравнений онлайн с тремя переменными, бесплатные рабочие листы ks2, ti-83 триггерный решатель идентификации.
Журнал переменной базы онлайн-калькулятора,
факторизуя радикалы совершенного куба,
книги учета затрат,
Математика до алгебры 6 класс,
алгебра решение привет,
клеп проходной балл,
бесплатные печатные практические документы ks2.
Множественный выбор 9 класс математика, рабочие листы по алгебре + решение системы 2-х уравнений с 2-мя переменными, Порядок работы при оценивании формул 8 класс, добавить вычесть 2 листа с 3-значными числами, доказательство против квадратного корня из трех иррационально, формула соотношения.
Решить десятичные уравнения с листами средней школы, добавление 1-значных целых чисел, РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ ТРЕТЬЕГО ПОРЯДКА, Прентис Холл, издание для учителя концептуальной химии, алгебра 2 практические тесты, онлайн-решатель алгебры, Образец теста на готовность к алгебре для 8 класса.
Решатель N-го члена, наименьшее общее кратное 16 и 68, Рабочие листы по алгебре и математике для 7 класса.
Ответы на домашние задания по современной абстрактной алгебре, шестое издание,
решить нелинейное дифференциальное уравнение,
Какой тип оценивания лучше всего использовать для первоклассников?
онлайн баланс-уравнения,
“ответы саксонского учебника математики” .
Калькулятор многочленов деления, вычитание отрицательных смешанных дробей, “кубическая” “объемная” “детская книжка”.
Общий знаменатель, рабочие листы 10 класса, как найти масштабный коэффициент, программа неявного дифференцирования онлайн, калькулятор в VB6, решающий более одного уравнения за раз, тривиальные вопросы третьего класса, калькулятор вычитания полиномов.
Разложение выражений с рациональными показателями, квадратный корень программы с использованием Matlab, рабочий лист, объединяющий одинаковые термины, печать с Т1-83.
“ТИ-84” + комплексное преобразование чисел, трехчленные наконечники, ti 83 plus калькулятор завершения квадрата, Упростите подкоренное выражение, Практика с кубиками и кубическими корнями.
Соотношение масштабов Math ks2, БЕСПЛАТНЫЕ примеры MATH 7-го класса, самый сложный математический вопрос.
Программа квадратных уравнений для TI,
Как алгебра используется в повседневной жизни,
предварительная алгебра Word Problems рабочий лист,
“matlab” решает неоднородное дифференциальное уравнение,
сложное математическое уравнение,
преобразовать десятичное число в смешанное.
Масштабная диаграмма математических действий, Программы TI 83 для упрощения рациональных чисел, Домашнее задание Герштейна по алгебре решений, бесплатные ks2 практические документы SATS для счета, лестница с наименьшим общим фактором, пример решения мультинелинейного уравнения в Matlab, Матлаб численное решение уравнения.
Версия калькулятора + системы уравнений с 3-мя переменными, бесплатный генератор тестов алгебра 2, как создать образ диска на компьютер с ti 86, холт алгебра 1 техас ответы, эллипс графического калькулятора.
графические навыки Glencoe, бесплатный тест по математике для 8 класса, математическая функция машина картинка для 6 класса, стихотворение из мономов, Гленко Макгроу Хилл учебник по математике, бесплатная помощь в делении комплексных чисел, высшая математика 11 листов.
Простой способ вычислить наибольший общий знаменатель,
упростите накрутку подкоренных выражений,
калькулятор квадратного корня,
полиномы свойств квадратного корня.
Наименьший общий знаменатель с переменными, 5-й класс Prime и Composite предварительный тест, преобразовать 27/3 в целое число.
Решатель синтетического деления, репетитор по математике+факторинг+квадратные уравнения, Макгроу Хилл учебник по бухгалтерскому учету, вычисление целых чисел со знаком, рабочие листы, разделите десятичные числа на рабочий лист десятичных знаков, наклонная деятельность в реальной жизни.
Факторизовать многочлен, ТИ-83 плюс скачать бесплатно, GMAT + перестановки и комбинации, комплексный трехчлен, репетитор по квадратному корню, Лист основных формул Gmat.
Решение нелинейного дифференциального уравнения, добавление вычитания длины, математический коэффициент лестницы деления.
Джейкобса+алгебра+кд,
калькулятор ти-83 скачать,
возьми кубический корень ТИ-83,
двухшаговое уравнение,
полный текст учебника по алгебре Прентиса Холла 1 для домашнего задания,
матлаб решает связанные линейные уравнения,
формула времени.
Посетители Bing пришли на эту страницу сегодня, введя эти ключевые слова:
учить целые числа | показать примеры решения задач на деление дробей |
добавление рабочих листов с одинаковыми цифрами | ФОЛЬГА Рабочие листы по алгебре |
онлайн математические дроби.com | способов найти gcf с помощью лестницы делений |
Уравнения PowerPoint | Бесплатные рабочие листы по математике для 7-го класса |
кумон ответы | преобразовать числа миксов в десятичные числа |
бесплатные распечатки по математике для 1 класса | как найти масштабный коэффициент? |
Бесплатные онлайн калькуляторы алгебраического факторинга | – это кубический корень из 8 2? |
простой конвертер уравнений алгебры | онлайн-теста по ментальной математике 12+ |
бесплатных рабочих листа по математике 7 класс до алгебры | алгебра 2 книга по математике ответы |
Рабочий лист ALgebra 2 с тремя переменными | дуги на ти-84 плюс |
упроститель логической алгебры | скорость изменения + триггерные функции + рабочие листы + бесплатно |
дифференциальных уравнения второго порядка в Matlab | Калькулятор факторинга |
решить полиномиальное уравнение Java | решить нелинейное дифференциальное уравнение |
Сайты по математике 7-го класса, определение наименьшего общего кратного | Бесплатные простые способы изучения алгебры |
бесплатных викторины “колледж алгебра”: | бесплатный код для упрощения вычислений для ti-89 |
мелочи тригонометрии | Решатель логарифмов шаг за шагом онлайн |
добавление фракций KS4 | практика сложения негативов и позитивов |
математических рабочих листа символьного метода | комплексное число экв. |
Полиномы 4-го порядка | определить, является ли график функцией |
Рабочие листы по всемирной истории для 7 класса | математические загадки графические линии |
удалить список TI-83 плюс удалить список | приблизить 2 квадратного корня из 18 до ближайшей тысячной |
как установить лог 2 ти-83 плюс | бесплатная помощь по алгебре среднего уровня |
пошаговая алгебра для чайников | рациональные дроби вместо десятичных знаков matlab |
6-й класс Сводный обзор 3 РАБОЧИЙ ЛИСТ | учить квадраты квадратные корни кубы и кубические корни |
Texas TI-84 Plus Руководство Тейлор | математические связи алгебра ответы |
Повторные тесты по математике, 10 год, уровень | Рабочие листы glencoe для печати по соотношениям и пропорциям |
Миллиметровая бумага с координатной сеткой для онлайн-печати | домашнее задание по математике 5 класс скачать бесплатно |
Алгебра: структура и метод, книга 1, Макдугал Литтел, генератор тестов | как найти GCF Of 147,105 |
решения для упражнений rudin | Абстрактная алгебра Руководство Dummit |
написание неравенств для текстовых задач, рабочий лист | ЭЛЕМЕНТАРНАЯ АЛГЕБРА ОНЛАЙН КАЛЬКУЛЯТОР |
планы уроков по буквальным уравнениям | Математика для 9 класса – комбинация чисел |
преобразование листов геометрии элементарно | закон умножения экспоненциального калькулятора |
рабочий лист простого полиномиального деления | листы умножения дробей |
масштабный коэффициент преподавания математики в средней школе | упрощение сложных алгебраических выражений |
“наименьший общий делитель” ti 83 программа | Логарифм решателя Справка |
| Таблица наибольший общий делитель | Математические задачи 7-го класса на умножение и деление смешанных чисел и дробей |
бесплатных печатных учебных пособия по чтению и языку | Эмуляторы для ти-84 плюс |
теория калькулятора icm | 2007 г. |
как решать функции с дробями | приблизительная алгебра квадратного корня |
Калькулятор уравнения первообразной | как запрограммировать квадратную формулу в калькуляторе |
завершение квадрата для построения квадратичного графика | рабочих листа со смешанными целыми числами |
квадратные уравнения сдвига, график | апплета квадратичной факторизации |
Коробчатые усы “t183” | Бесплатный калькулятор Скачать неравенства |
как использовать операцию фольги на графическом калькуляторе casio | как составить уравнение третьего порядка как набор из трех уравнений первого порядка |
перестановка и комбинация | concept.glecoe.com |
вычисление выражений + рабочие листы | slove для пересечения наклона y |
онлайн калькулятор с показателями | реальных примеров рациональных выражений |
бесплатно скачать вопрос и ответ по физике (базовая теплота) | ti-89 добавление полярных уравнений |
порядок решения по математике с умножением, делением, вычитанием, сложением | примера решения квадратного уравнения в вершинной форме |
бухгалтерские книги ответы | Онлайн-практика с упрощением алгебраических выражений |
как линейные функции используются в реальной жизни? | ti84 хранение данных в «нескольких переменных» |
упрощение кубических задач | код для решения нелинейного уравнения Шрёдингера+matlab или mathematica |
План урока «Упрощение дробей» для 4-го класса | распечатать учебные листы GMAT |
texas tools +TI 83 +решить квадратное уравнение | Калькулятор свободных квадратных футов |
10 класс квадратное уравнение по математике | бесплатная алгебра 2 ответы |
сложение, вычитание, умножение и деление с десятичными дробями | самая сложная математическая головоломка |
Калькулятор полиномов деления | сокращение уравнения в кубе |
| Учебник по биологии ответы Прентис Холл Техас | рабочие листы с измерениями для 3-х классов |
упростить отрицательный корень | бесплатный симулятор графического калькулятора TI-82 |
бесплатный рабочий лист неравенства | математические стихи |
алгебра III с кониками | линейных уравнения с 3 переменными и связанные задачи |
ти-89 “бревенчатая база 2” | поставить ответы регента физики на ти-89 |
Арифметика LCM GCM Проблемы Индия | формула наибольшего общего делителя |
попрактиковаться в написании линейных уравнений | бесплатный математический калькулятор |
Решатель треугольников ti-89 | упрощение квадратных корней ppt |
Equation Writer для творческого дизайна программного обеспечения | листы математических калькуляторов ks2 |
алгебра для начинающих | онлайн-теста по математике для KS3 |
математические задачи на сложение и вычитание минусов | онлайн-решатель факторинга |
бесплатные практические экзамены EOG для 5-го класса | Тригонометрические решаемые задачи для ВУЗов |
Эмулятор Ti84 | Решение переменных показателей онлайн |
алгебра + рабочий лист + ТАБЛИЦЫ | математических рабочих листа наклон |
выучить одновременные уравнения по математике | тригонометрические ответы мгновенные |
дифференциальные уравнения ppt | LCM — это просто |
Merrill + инструменты онлайн-обучения + физика | шага для решения умножения биномов в примере формы |
ответы на Prentice Hall pre алгебра | дробное выражение |
рабочие листы порядка операций с квадратным корнем | Шпаргалка по формулам Excel |
бесплатных рабочих листа по математике для 5-х классов | лист добавления целых чисел |
ОТВЕТЫ ДЛЯ ДОМАШНЕГО ЗАДАНИЯ ПО МАТЕМАТИКЕ | “алгебраические игры” |
онлайн калькулятор матриц | т1-89 инструкция |
Как упростить выражения | калькулятор рациональных выражений |
формула для изменения градусов по Фаренгейту для градусов по Цельсию | Определения и методы дроби девятой степени |
проблема перестановки комбинаций | примеров мелочей по тригонометрии |
ответа на вопросы по алгебре с помощью Pizzazz! | трехчленный учебник/факторинг по группировке |
бесплатная домашняя работа, помощь перед перестановками и комбинациями по алгебре | программирование решения математических матриц Excel |
“алгебра” И “простейшая радикальная форма” | решать уравнения в квадратичной форме комплексное решение |
как найти третий корень числа | 2 ШАГОВЫЕ УРАВНЕНИЯ ДЛЯ ПЕЧАТИ |
для решения неоднородного дифференциального уравнения | образец экзамена по истории ks3 |
примеры работы по тригонометрии ppt | бесплатных рабочих листа по алгебре с большим количеством вопросов |
| Целочисленный рабочий лист | TI-84 плюс наибольший общий делитель |
онлайн калькулятор квадратного корня | алгебра с ключом ответа на пиццу |
решение одновременных уравнений по одной квадратной формуле на уровне | Рабочий лист по определению дробных частей |
Учебное пособие по алгебре для учеников холла | применение рациональных выражений |
“тензорное произведение решения” | решатель корней уравнений |
алгебраический калькулятор решает уравнения | упростить линейные уравнения с помощью матрицы |
решение подстановкой с тремя переменными | репетитор по алгебре |
бесплатных онлайн-ответа по математике по алгебре 2 | упрощенный решатель квадратных уравнений |
сложение и деление десятичных дробей | математика ответы алгебра 2 |
учебник по логарифмам для начинающих | примера стихотворения о математике |
чит алгебра clep | Полезный онлайн-калькулятор графиков |
интерактивные абсолютные неравенства графически | Распределительные математические задачи 6-го класса |
Калькулятор уравнений, содержащих дроби | McDougal Littell Algebra 2 Chapter 5 Resource Book |
примерных вопроса для коэффициента масштабирования | Метод наибольшего общего делителя |
математическая формула процентов | одношаговые уравнения, включая таблицы с дробями |
стихи с разбросом сюжета | бесплатный калькулятор алгебры, показывающий шаги |
рабочих листа с квадратным корнем+бесплатно | вопросы по математике |
числовая линия И графическое неравенство И рабочие листы | тест по математике онлайн 8 год |
степени и степени и алгебра онлайн игры | Решения для домашних заданий Dummit and Foote |
Рабочий лист вычитания целых чисел | уплотняющие логорифмические уравнения |
“калькулятор сюжетных задач” | расширение функций квадратного корня |
алгебра 1 Мичиганское издание интерактивная справка | Рабочий лист положительных и отрицательных целых чисел |
записать программу FOIL для TI 83 | бесплатные вычислительные листы Matlab |
кто изобрел формулу наклона | алгебра 2 задачи |
решатель булевой алгебры | факторинг квадратичный калькулятор |
“бесплатно” + “онлайн” + “неравенство” + “калькулятор” | рабочих листа по математической факторизации |
Пользователи Yahoo пришли сегодня на эту страницу, введя следующие алгебраические термины:
формулы учета затрат | Сложение и вычитание отрицательных чисел 7 класс | уравнения второго порядка в Matlab | онлайн калькулятор с дробями | элементарные математические мелочи |
печатные формы абсолютного значения | пирог с алгеброй | Холт Математика Ответы | печатный общий знаменатель | онлайн-видео для обучения детей математике дробей |
бесплатных печатных теста по алгебре для колледжа | задачи на дроби | упростить в алгебре | дифференциальное уравнение третьего порядка mathcad | Многочлен длинного деления java |
планы уроков, Power Point, “Современная химия” | Десятый факторинг | как решить логарифмическое уравнение | Упрощение калькулятора числовых выражений | Учебник по геометрии Техас Холт онлайн бесплатно |
можно ли уменьшить смешанную дробь | тригономические функции | алгебра с рабочим листом 6 ответов | преобразование Лапласа с использованием ti-89 | домашняя работа в колледже с mathcad |
год Тест 10 одновременных уравнений | математический калькулятор полиномов | видов проектов по алгебре | решение темы по алгебре по Герштейну | научные проекты |
рабочий лист по химии для учеников холла ответы | Математические уравнения для печати для детей | подсказки по алгебре | Рабочие листы по алгебре для 7 класса | печатных листа по интегрированной алгебре и математике 9 класс |
Glencoe Math Workbook Ответы | Математическая игра с 9 квадратами до алгебры | Диаграмма Венна + восьмой класс + рабочий лист + бесплатно | рабочих листа по корням действительных чисел | определение алгебраического выражения |
“Рабочий лист квадратного корня” | уравнения балансировки онлайн | изучение элементарной алгебры | Рабочий лист по разделению десятичных дробей | элементарная статистика |
Решить операции с рациональными выражениями | Математические распечатки 9-го класса | взять логарифм по основанию 2 на калькуляторе | кубический многочлен без пересечений | факторизующий квадратичный калькулятор |
известная алгебра дистрибутивных свойств 1 | Алгебра Холта 1 ответы | скачать прошивку ti-83 образ | задачи на ассоциативные свойства для плана урока 2 класса | решение систем сложением и вычитанием |
| Калькулятор подкоренных выражений | онлайн калькулятор алгебры шаг за шагом | игры для калькулятора Т1-84 | алгебра 1 книга ларсон онлайн текст | бесплатный одновременный решатель уравнений |
Пример тестов ERB | бесплатных примера факторных задач по алгебре | Пример вопросов по математике | математические листы ks3 | замена по алгебре +6 класс +бесплатные рабочие листы |
Интегрированный курс математики Merrill, издание 1 для учителя | Рабочие листы по ассоциативному методу умножения 4 класс | найти наименьшее общее кратное выражения | Математические стихотворения степени | Квадратичная формула Рабочий лист |
калькулятор % вина GP | рабочие листы упрощения дробей с показателями и переменными | партер по математике для 5 класса | график таблицы уравнений | BigDecimal преобразовать число шкалы |
Булева алгебра + TI-83 + скачать | бесплатный калькулятор показателей степени | Glencoe Алгебра 1 книга ответов | ти-86 калькулятор онлайн | КАЛЬКУЛЯТОР НОД реализация vhdl |
Прентис Холл страницы ответов по предварительной алгебре | C Вопросы о способностях | Герштейн Математика | т-83 калькулятор онлайн | бесплатных рабочих листа с задачами на умножение слов для KS2 |
метод линейной комбинации | бесплатная электронная книга по бухгалтерскому учету | mcdougal littell всемирная история учебник ответы | алгебра ответы | бесплатные математические суммы – седьмой класс |
как найти уклон на ти-84 | Бесплатный онлайн-тест по математике — дроби | АЛГЕБРА С ПИЦЦАЗОМ ОТВЕТЫ НА ТАБЛИЦЕ | рассчитать коэффициент поиска | РАСЧЕТ LCM И GCF |
| Рабочий лист lcm и gcf | как решить gcf easy | примера того, как сделать уравнения преобразования 7-го класса? | Сложение Вычитание Умножение Деление дробей | как решить систему линейных уравнений с помощью ti-83 |
ти-89 сменить базу | онлайн-калькуляторы для использования | ГРАФИЧЕСКИЕ КВАДРАТНЫЕ УРАВНЕНИЯ + PPT | Бесплатные рабочие листы по алгебре для 9-го класса | запрос рабочего листа по базовой алгебре |
Выражения по алгебре для учащихся начальной школы | год 7 бланков упражнений по факторингу | математика для чайников | обзор учебника dolciani | Математика для детей |
бесплатных рабочих листа по математике для 6-го класса | решение системы дифференциальных уравнений MATlab | вероятностных ответа для Алекса | бесплатных математических рабочих листа для графических точек | ПРЕОБРАЗОВАНИЕ ДОЛЕЙ ЧАСОВ В МИНУТЫ |
Калькулятор уравнений балансировки | Хоутон Миффлин онлайн алгебра 1 | что такое лестничный метод | Определение символьного метода | Фон+синтетическое деление+многочлены |
макдугал литтел вкл неравенство | Ключ ответа по алгебре для продвинутых учеников холла | пошаговое построение линий в стандартной форме help | “Рабочий лист синтетического деления” | PowerPoint ПЛАН УРОКА НА ПЕРЕХВАТАХ ЛИНИИ |
Рабочий лист умножения сурдов | реальных примера задач на дроби | Диаграмма квадратных корней | онлайн научный графический калькулятор ti-84 | число в передних задачах на квадратный корень |
правила сложения, вычитания, умножения и деления целых чисел | Раствор для физических упражнений | Целочисленный тест по математике для печати и ключ ответа | возведение в квадрат бинома в третьей степени | линейная алгебра. |
ФАКТОРИЗИНГ ОНЛАЙН | формула обратного квадрата | Рабочий лист линейного графика 6 класс | логарифмический тест thinkwell | превратить десятичную дробь в калькулятор дробей |
преобразование основания 2 в основание 8 | перестановка чисел в матлабе | TI-83 +направления +корни | тома по математике 3 класс бесплатно | калькулятор квадратичных формул программа ti-84 |
решить мою математическую задачу бесплатно | Решение одновременного уравнения Ti 86 | изучение математики Альберта 6 класс статистический лист вероятностей | ти 89 журнал | Рабочий лист решения буквенных уравнений |
mcdougal littell inc ключ ответа бесплатно | ти-83 как куб | Макдугал Литтел английский ответы | Программное обеспечение для длинного деления уравнений | базовый бумажный тест по математике |
перпендикулярные линии в алгебре ты переворачиваешь фракции | факторные рабочие листы 4 класс | Clep экзамен колледж алгебра бесплатная практика | простых вопроса по алгебре для 5 или 6 класса | рудин раствор 7 |
как использовать калькулятор для вычисления квадратных корней | калькулятор у. | написание рабочего листа алгебраических выражений | сложение, деление, вычитание и умножение отрицательных и положительных чисел вместе | примера решения задач квадратных уравнений |
решение неизвестных полиномиальных уравнений третьего порядка | Алебра 1 онлайн книги Макдугелл | комплектация квадрата powerpoint | Интегральный калькулятор Доусона | сложные уравнения алгебры |
“скачать блокнот для геометрии”” | бесплатных рабочих листа по сложению и вычитанию дробей с разными знаменателями и переменными | Рабочий лист упрощает комплексные числа | Калькулятор деления многочленов | бесплатный графический решатель алгебры |
математический проект – геометрия в реальной жизни | рабочая таблица по объединению одинаковых терминов | ti-84 знак процента | “графический калькулятор” +бесплатно +онлайн +”таблица значений” | ti83+ эмулятор онлайн |
ответы на Графический подход к сложным процентам | алгебра основы построения графиков | Репетиторские сайты по алгебре | Переходная математика от Прентиса Холла отвечает | Найдите x, вычитая один квадратный корень из квадратного корня |
“булева алгебра” ти-89 | ответы на математику средней школы Макдугала Литтела | “Квадратный корень” для чайников | помощь в умножении и делении радикалов с кубическими корнями | онлайн калькулятор гиперболы |
положительных и отрицательных целых числа урока | раздача рисунков, алгебра, рабочий лист | скачать бесплатно задачи теста IQ | как решить уравнение в java | Квадратичная формула ТИ-84 |
Выпуск 7 класс ТАКС тест | Алгебра Холта 1 | преобразовано в дробь | Преобразование десятичных дробей в дроби TI-86 | добавление дроби к целому числу |
рабочих листа на вычитание от 0 до 18 | ответы на интегрированные 2 задачи из учебника по математике | Ti-84 Plus Приложения для алгебры | Онлайн-тест по математике для 9 класса по линейным, экспоненциальным и параболическим уравнениям | подскажите сайты для решения математических задач |
Предварительный тест по алгебре для 8-го класса | gcf мономов рабочий лист | математика | развернуть квадратную фольгу TI-89 | одновременных нелинейных алгебраических уравнения |
калькулятор-решение факторингом | Рабочий лист для уравнений балансировки | как решать неоднородные производные по Лапласу | решение уравнений для печати лист | высший объективный тест по математике |
Рабочий лист умножения и деления целых чисел | Таблицы коэффициентов свободного масштабирования | саксонская математическая бумага | поиск корней с формой вершины | загрузок калькулятора TI-83 |
веселых рабочих листа по алгебре | математическое программное обеспечение для прикладных школьников | Целочисленный рабочий лист | как рассчитать сложные проценты на калькуляторе ti-84 | выяснить, чему равно x в задаче на дробь |
перемножение матриц | смешанные числа в виде десятичных дробей | простой способ пройти clep | Лист математических целых чисел в степени корней ks3 | графические параболы PowerPoint |
квадратный корень из x в кубе | решение заявок с факторингом | бесплатные методы замены алгебры | уравнения с отрицательными показателями | множитель многочлена Java |
разностное уравнение факторинга | бесплатные онлайн-тесты по математике | кубический корень ti 83 плюс | бесплатный решатель уравнения абсолютного значения | примера математической поэмы |
тест по алгебре онлайн бесплатно | бесплатных математических листа в расширенной нотации | тест по математике: Углы год 7 | стихотворения на цифру | Решение тригономических уравнений |
TI 83 программы, упрощающие радикалы | рабочие листы по алгебре дроби | трудный трудный лист по математике гр 6 | Скотт Форман математические таблицы | Химическое программное обеспечение ti89 |
бесплатные печатные формы с научными обозначениями | рабочих листа по алгебре для первокурсников | операция пошаговое умножение корней | как решать математические задачи | Рабочие листы эквивалентных форм |
алгебра дробная | числа, у которых семь в множителе | попрактиковаться в вычислении логарифмических выражений | объединение рабочих листов с одинаковыми терминами | листы сложения и вычитания целых чисел бесплатно |
ти-89 добавление полярного | рабочие листы по химии для 9 класса | бесплатный графический онлайн калькулятор ti-83 | как складывать квадратные корни с переменными? | План урока по линейному уравнению в один шаг |
Как решить задачу на квадратный корень | aptitude загрузить | бесплатный рабочий лист с математическими задачами для 7-го класса с использованием процентов | ключ ответа к главе 7 концептуальной физики | решение дроби полиномиальной степени |
Онлайн-учебник McDougal Littell/Houghton Mifflin Algebra: Structure and Method | математические рабочие листы для вычисления алгебраических выражений скачать бесплатно | учебник по перестановкам и комбинациям | граф упорядоченных парных решателей | Какой наибольший общий делитель может иметь два числа от 40 до 50? |
mcdougal littell руководство по алгебре 2 | ответа на вопросы по элементарной алгебре | примеры задач по бухгалтерскому учету и ответы | уравнения балансировки онлайн | наибольший общий делитель 60 |
девятый класс помощь по алгебре | Нью-Джерси онлайн учебник по математике 9 класс | большой общий делитель | Основные математические навыки 6-го класса | Калькулятор полиномиальных выражений |
| Графический онлайн-калькулятор для тригонометрических обратных функций | “Комплексные числа с TI-83+” | решение уравнений путем умножения | вершинные задачи квадратичной формулы | Бесплатная начальная и средняя алгебра |
Трещины дорожек PLATO | взять 3-й корень ti-89 | бесплатный год 7 последовательностей рабочих листов | бесплатные печатные дроби преобразования математики 5 класс | Практика 9-го класса |
предварительный тест по алгебре | пример стихотворения о тригонометрии | предварительная алгебра с пиццей | скачать ti-83 plus rom | “ти-89” “квадратный корень” |
обратное преобразование Лапласа для нахождения резонанса | решение рабочих листов уравнений с несколькими переменными | Экзаменационные работы по математике для учащихся шестого класса | десятичных знака | как возвести дробь в куб |
графический калькулятор матрица | Добавление целочисленных игр | основы перестановок и комбинаций | учебник по алгебре Холта 1 ответы | Калькулятор умножения радикалов |
ti 84 программа квадратичных формул | Калькулятор кубического корня | дроби на TI калькуляторе | как делать перестановки на ТИ-83 | калифорнийская алгебра одна книга онлайн |
примеры алгебраических вопросов | “Рабочие листы дроби второго класса” картинки | график y=5x на графике | КАК ОБУЧАТЬ СИММЕТРИИ ПЕРВОКЛАССНИКОВ | формула решения задач на пропорции в alberga |
Калькулятор квадратного корня с переменными | чит математических упражнений | бесплатный онлайн калькулятор наименьшего общего знаменателя | Пре-альгреба | Композиция Пита Мондриана с синей нумерологией |
написание рабочих листов с уравнениями | бесплатное онлайн-обучение по алгебре 2 | как мне использовать функцию журнала на моем калькуляторе | упрощение квадратного корня квадратного | бесплатный пример теста по биологии |
алгебра 2 примеры задач из фольги | ti 84 плюс программа квадратного уравнения | бесплатно McDougal Littell калифорнийская алгебра 2 ответы | решить дополнительное решение однородного дифференциального уравнения | решить систему онлайновых уравнений в Matlab |
Структура алгебры и книга методов 1 – Ключ решения | бесплатно ЭМУЛЯТОР TI83 | Рабочие листы для построения графиков линейных уравнений | CAT: предыдущий вопросник, тип файла Pdf | конический рабочий лист |
алгебра Холта 1 | нахождение рабочих листов отношения | добавление вычитания, умножения и деления рациональных выражений, рабочий лист | Алиса Касеберг Промежуточная помощь по алгебре | проблемы с добавлением минусов |
рабочих листа по алгебре для начинающих | бесплатная книга учета затрат | игры с распечаткой денег для детей 5-6 классов | алгебра 2 макдугал литтелл глава 2 изучение рабочих листов данных | тест на сложение, вычитание, умножение и деление целых чисел |
упрощающие радикалы в тригонометрии | алгебраические уравнения баланса | Matlab решает одновременные уравнения | бесплатная настольная игра для гоночных треков | какие задачи на странице 21 в учебнике по математике для 5 класса |
как извлекать квадратные корни из дробей | Электронная книга «Введение в теорию вероятностей» | репетитору по математике нужна загадка | Применение радикальных функций | сумма корня квадратного уравнения |
помощник по алгебре | Word Решение задач (онлайн) | Современная абстрактная алгебра Even Solutions | примера возрастных проблем | поиск домена и диапазона ti 83 |
алгебра вычисляет дроби и квадратный маршрут | история теорем Силова | листы с наименьшими общими кратными 6 класс | полином | Скачать игры для TI-84 |
рабочий лист порядка операций с целыми числами | бесплатный онлайн калькулятор квадратного корня | графические квадратные уравнения+ppt | таблицы десятичного сравнения | Калькулятор деления алгебры |
бесплатная электронная книга учета затрат | как решать математические уравнения и квадратные уравнения | решение уравнений путем умножения и деления целых чисел | алгебра колледжа + рабочая тетрадь + бесплатно + скачать | химические реакции дифференциальное уравнение второго порядка |
TI 83 плюс загрузка образа ПЗУ | макдугал литтелл @домашний репетитор | тест на гениальность рабочий лист | скачать программное обеспечение Ti 84 | как объяснить вероятность 4 классу |
десятичных до смешанных чисел | glencoe алгебра 1 ключ ответа | taks тестовая практика онлайн бесплатно для третьего класса 2007 | программное обеспечение для решения одновременных уравнений | вершина рациональных уравнений |
изменить смешанную дробь с десятичной дробью на проценты | Рабочий лист перестановок и комбинаций | задачи на рациональное выражение | Рабочий лист по алгебре для 3 класса | как решать дроби в уравнениях |
как вы делите десятичные дроби | Концептуальная физика Ответы | наибольший общий знаменатель числа 479 | Реальные прикладные квадратичные функции | факторинг для идиотов |
Алгебра 1 Холт | Калькулятор порядка дробей от наименьшего к наибольшему | Лаплас Ти-89 | бесплатно скачать книги apptitude | умножать и делить рациональные числа |
TI-84 программирует полиномиальные неравенства | реальный пример с пересечением склона | Рабочая тетрадь стандартизированных тестов по алгебре 2 McDougal/Littell 2004 | изолировать глоссарий переменных/математики | простая алгебра |
Преобразование дробей в десятичные печатные листы | алгебраическое уравнение гипербола | онлайн-упроститель Surds | график 86 ошибка 13 измерение | рабочие листы с процентными словами |
бесплатный онлайн калькулятор для сложения дробей и переменной | Бесплатное ПО для КПК TI 83 | Рабочий лист синтетического деления с множественным выбором | примеры математических мелочей | три символьных метода решения квадратного уравнения |
алгебраическое уравнение для определения квадратного корня | комбинации ти-83 | база 16 ява | Домашнее задание “Основы инвестиций” ответы | как преобразовать в базу пять |
Базовая алгебра для пятого класса | Калькулятор коэффициента | Интерактивные уроки квадратных уравнений | Математика Для чайников скачать бесплатно | помощь по продвинутой алгебре |
прентис холл помощь с домашним заданием по алгебре | одновременные уравнения Ньютона Рафсона нелинейные | Algebra Connections Volume One page 45 | алгебра мелочи | ПО для алгебры 2 |
Калькулятор деления отрицательных дробей | 8 класс фракции | биномиальная теория | mcdougal littell algbra лист ответов к моей школьной рабочей тетради | бесплатных рабочих листа по алгебре для начинающих |
математический словарь | Решатель дифференциальных уравнений для Matlab | бесплатных рабочих листа по математике для 6-го класса бесплатно для печати | Коммутативный и ассоциативный рабочий лист предварительной алгебры | кубический корень |
Математические игры онлайн для 9-х классов | 5-й класс умножения десятичных дробей | онлайн-решатель полиномиальных задач | математических тестов на 8 лет | Решатель задач 9-го класса |
Калькулятор решения рациональных уравнений | предварительная алгебра ответы | контрольные работы по математике | Эмулятор калькулятора TI 84 | вопросы о способностях pdf |
полиномиальный решатель | графическое построение полярных уравнений на TI-89 | clep test практика исчисления | Решатель доменов онлайн | рабочие листы с индийскими пиктограммами |
ти-89 бревно база 2 | бесплатных рабочих листа по математике для дошкольников | линейных уравнения с тремя переменными | Руководство для идиотов по Excel | Листы ответов Pizzazz Pre алгебра |
ti-83 плюс формулы статистики | коммутативный, рабочие листы | рабочие листы по алгебре ks3 | МОДЕЛЬ SAT KS2 ВОПРОСНИК | упростить алгебраические выражения |
решить мое уравнение | Калькулятор уравнений балансировки | Решение нелинейных уравнений в Matlab | как сдать тест по алгебре | Бесплатное решение задач по алгебре |
реальных задач по алгебре | визуальные инструкции по умножению трехзначных чисел на трехзначные числа | как найти кубический корень из 8 с помощью калькулятора ТИ-83 | линейные уравнения gcse | экзаменационные работы дети 7 лет |
кубический корень на калькуляторе | решение линейного уравнения третьего порядка | элементарная алгебра помощь | где я могу найти бесплатные рабочие листы по алгебре для девятого класса? | решение систем полиномиальных уравнений matlab |
бесплатные рабочие листы для восьми классов | заметки о скалах по науке Glencoe 6-й класс | бесплатный рабочий лист линейного уравнения | бесплатно онлайн 11+ практических работ | заметки по алгебре |
нахождение логарифмов на TI-83 | бесплатные полиномы помощи по алгебре | заполнение квадратного рабочего листа | Лестничный метод для нахождения наименьшего общего кратного и наибольшего общего делителя: демонстрация | Ключ к алгебре с помощью Pizzazz! рабочие листы |
как ответить на вопросы | математические задачи для lcm и gcf | Рабочие листы по распределению собственности | рассчитать мод в калькуляторе ти-83 | задачи на сложение и вычитание целых чисел |
бесплатных рабочих листа GED | Краткий конспект по всемирной истории, 4 класс | ответы по математической статистике | тестовая статистика для калькулятора наклона ti | онлайн калькулятор + уравнения рациональных чисел |
как мне запрограммировать квадратичную формулу на моем TI-83 | Нахождение уклона с помощью чисел | целых викторины для 7th . | смешанное число до десятичного числа | Задачи о смесях Элементарная алгебра I примеры |
решение неравенств путем умножения или деления | образцы тестов по алгебре Онтарио | как разложить на множители квадратные уравнения 9 лет | наименьший общий знаменатель + рабочий лист | триггерная поэма |
помощь по математике средний уровень алгебры lial восьмое издание | Решение по математике +9 класс +пример | ЭКЗАМЕНАЦИОННЫЙ ЭКЗАМЕН ПО МАТЕМАТИКЕ ДЛЯ ДЕТЕЙ | собственные значения TI84 | задача по алгебре решить |
бесплатных рабочих листа неравенства | можно ли хранить формулы на графических калькуляторах ти-84 | план урока алгебраических выражений | ti 86 ошибки калькулятора | экспоненциальная математическая викторина |
поиск корней с ти-83 плюс | как умножать на квадратный корень дроби | “Дроби для чайников” | корни ТИ-83 | задач на определитель линейных уравнений 2,3 порядка задач с ответами |
коэффициенты упрощения ответы | математические показатели девятого класса+бесплатно | сложение отрицательных и положительных целых чисел | встроенный | Бесплатная загрузка тестовых листов Aptitude с ответами |
как обмануть ар тесты | уравнения с рациональными выражениями | математический чит-помощник парабола | объединение радикалов и упрощение | умножить линейную функцию |
Калькулятор метода замены | программы физики ти-89 | Балансирующий решатель химических уравнений | уравнение гиперболы на ti 83 | решение квадратного уравнения ti83 |
+”воображаемое в полярное” +конвертировать | многошаговый калькулятор уравнений онлайн | полиномиальный решатель онлайн | разложение кубов квадратных уравнений на множители | тест на сложение и вычитание целых чисел |
Решение математических задач и операций 5-го класса | Обманы с рабочими листами факторинговых многочленов | TI-84 плюс 84 загрузки загрузок kostenlos | бесплатно научиться делить многочлены | как перевести дроби в десятичные в калькуляторе ти-89 |
алгебра 1 ответы | рабочий лист по математике A-level бесплатно | как решать одновременные линейные уравнения TI-89 | Алмазный решатель фактора | алгебра для начинающих |
Рабочие листы правил сложной экспоненты – упрощение базы | математика мелочи алгебра | лестничный метод факторинга полиномов | Целочисленный смешанный обзорный лист | ответы на домашнее задание по алгебре |
квадратичный рабочий лист факторинга бесплатно | раствор палиндрометестера | справка по средней алгебре аскдживса | как решить квадратное уравнение ти-84 | смешанные операции со скобками и десятичными знаками – рабочие листы для печати |
решить одну переменную Matlab | “объединение одинаковых членов” дроби | Учебники по математике для средней школы 6 класса Флорида | план урока gcse преобразование математики | Matlab наименьший общий знаменатель |
тригонометрия для начинающих | как пользоваться алгебратором 2. | Mcdougal Littell Pre-Algebra Practice Workbook ключ ответа | вычитание отрицательных и положительных целых чисел | Ответы на домашнее задание по математике Помощь |
бесплатный онлайн-решатель математических многошаговых уравнений | бесплатный лист практической математики для 6-го класса | примеров математических задач из алгебры 1 | Одновременный решатель Excel | бесплатный рабочий лист для печати по началу измерения |
Решение систем линейных алгебраических уравнений (Слау)
В первой части мы рассмотрели теоретический материал, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу, рекомендую прочитать первую часть. Возможно, некоторым посетителям материал покажется слишком простым, но в ходе решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А теперь разберем правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы представлены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными методами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, посеместровым сложением!
Дело в том, что пусть иногда, но есть такая задача – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет вам понять, как использовать правило Крамера для более сложного случая — системы из трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые желательно решать точно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычисляем определитель , он называется главным определителем системы .
Метод Гаусса.
Если , то система имеет единственное решение, и для нахождения корней необходимо вычислить еще два определителя:
и
На практике вышеуказанные определители можно обозначать и латинской буквой.
Корни уравнения находятся по формулам:
,
Пример 7
Решить систему линейных уравнений справа есть десятичные дроби с запятой. Запятая — довольно редкий гость в практических задачах по математике; Я взял эту систему из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся ужасные навороченные дроби, с которыми крайне неудобно работать, а оформление решения будет выглядеть просто ужасно. Вы можете умножить второе уравнение на 6 и вычесть член за членом, но здесь появятся те же самые дроби.
Что делать? В таких случаях на помощь приходят формулы Крамера.
;
;
Ответ : ,
Оба корня имеют бесконечные хвосты и находятся приближенно, что вполне приемлемо (и даже обычно) для задач эконометрики.
Комментарии здесь не нужны, так как задача решается по готовым формулам, однако есть один нюанс. При использовании этого метода обязательно Фрагментом задания является следующий фрагмент: “значит система имеет единственное решение” . В противном случае рецензент может наказать вас за неуважение к теореме Крамера.
Не лишней будет проверка, которую удобно проводить на калькуляторе: подставляем приблизительные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, находящиеся в правой части.
Пример 8
Выразите ответ в обыкновенных неправильных дробях. Сделайте чек.
Это пример для самостоятельного решения (пример изящного оформления и ответ в конце урока).
Перейдем к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Найдем главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решения). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
Если , то система имеет единственное решение, и для нахождения корней надо вычислить еще три определителя:
, ,
И, наконец, ответ вычисляется по формулам:
Как видите, « Случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «гуляет» слева направо по столбцам главного определителя.
Пример 9
Решите систему, используя формулы Крамера.
Решение : Решим систему по формулам Крамера.
, поэтому система имеет единственное решение.
Ответ : .
Собственно, тут опять комментировать особо нечего, ввиду того, что решение принимается по готовым формулам. Но есть пара замечаний.
Бывает, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Рекомендую следующий алгоритм “лечения”. Если под рукой нет компьютера, делаем так:
Если под рукой нет компьютера, делаем так:
1) Возможна ошибка в расчетах. Как только вы столкнулись с «плохим» кадром, нужно сразу проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители с помощью разложения в другой строке (столбце).
2) Если в результате проверки ошибок не обнаружено, то, скорее всего, в условии задания допущена опечатка. В этом случае спокойно и ВНИМАТЕЛЬНО решите задачу до конца, а затем обязательно проверить и составить его на чистом экземпляре после принятия решения. Конечно, проверка дробного ответа — занятие неприятное, но это будет обезоруживающим аргументом для преподавателя, который ну очень любит ставить минус за всякую гадость вроде. Как обращаться с дробями, подробно описано в ответе к Примеру 8.
Если у вас есть под рукой компьютер, то используйте для его проверки автоматизированную программу, которую можно скачать бесплатно в самом начале урока. Кстати, пользоваться программой выгоднее всего сразу (еще до запуска решения), вы сразу увидите промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически вычисляет решение системного матричного метода.
Второе замечание. Время от времени встречаются системы, в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении нет переменной , во втором нет переменной . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать основной определитель:
– вместо пропущенных переменных ставятся нули.
Кстати, определители с нулями рационально открывать в той строке (столбце), в которой стоит ноль, так как вычислений заметно меньше.
Пример 10
Решите систему, используя формулы Крамера.
Это пример для самостоятельного решения (завершающий образец и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Вы можете увидеть живой пример в уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне разрешимы. Хотя задание уже очень напоминает профессорский ботинок на груди счастливчика-студента.
Метод обратной матрицы является по существу частным случаем матричного уравнения (см. пример №3 указанного урока).
Для изучения этого раздела необходимо уметь разлагать определители, находить обратную матрицу и производить умножение матриц. Соответствующие ссылки будут даны по мере продвижения объяснения.
Пример 11
Решить систему матричным методом
Решение : Запишем систему в матричной форме:
, где
Посмотрите пожалуйста на систему уравнений и матрицы. По какому принципу мы записываем элементы в матрицы, думаю всем понятно. Единственное замечание: если бы в уравнениях отсутствовали какие-то переменные, то в матрице на соответствующие места пришлось бы ставить нули.
Находим обратную матрицу по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разберемся с определителем:
Здесь определитель расширяется первой строкой.
Внимание! Если , то обратной матрицы не существует и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (метод Гаусса).
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Ссылка: Полезно знать значение двойных нижних индексов в линейной алгебре. Первая цифра — это номер строки, в которой находится элемент. Вторая цифра – это номер столбца, в котором находится элемент:
То есть двойной нижний индекс указывает на то, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3-й строке, 2-м столбце
Пусть система линейных уравнений содержит столько уравнений, сколько число независимых переменных, т.е. имеет вид
Такие системы линейных уравнений называются квадратичными. Определитель, составленный из коэффициентов независимых переменных системы (1.5), называется главным определителем системы. Обозначим его греческой буквой Д. Таким образом,
Таким образом,
. (1.6)
Если в главном определителе произвольный ( j -й) столбец заменить его столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:
( j = 1, 2, …, n ). (1.7)
Правило Крамера решения квадратных систем линейных уравнений выглядит следующим образом. Если главный определитель D системы (1.5) отличен от нуля, то система имеет единственное решение, которое находится по формулам:
(1.8)
Пример 1.5. Решите систему уравнений методом Крамера
.
Вычислим главный определитель системы:
Поскольку D¹0, система имеет единственное решение, которое можно найти по формулам (1.8):
Таким образом,
Действия с матрицами
1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.
2. Чтобы умножить матрицу на число, нужно умножить все ее элементы на это число. То есть
То есть
. (1.9)
Пример 1.6. .
Добавление матрицы.Эта операция вводится только для матриц одного порядка.
Для сложения двух матриц необходимо сложить соответствующие элементы другой матрицы с элементами одной матрицы:
(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.
Пример 1.7. .
Умножение матриц.Если число столбцов матрицы А совпадает с количеством строк матрицы В , то для таких матриц вводится операция умножения: m ´ n в матрицу AT размеры n ´ k получаем матрицу С размеры м ´ к . При этом элементы матрицы ИЗ вычисляются по следующим формулам:
Задача 1.8. Найдите, если возможно, произведение матриц AB и BA :
Решение. 1) Чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :
2) Работа BA не существует, так как количество столбцов матрицы B не соответствует количеству строк матрицы A .
Обратная матрица. Решение систем линейных уравнений матричным способом
Матрица А- 1 называется обратной квадратной матрицей А , если выполняется равенство:
где через I обозначена единичная матрица того же порядка, что и матрица НО :
.
Чтобы квадратная матрица имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратная матрица находится по формуле:
, (1.13)
где А ij – алгебраические дополнения к элементам aij матрицы А (обратите внимание, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующие столбцы).
Пример 1.9. Найдите обратную матрицу A- 1 к матрице
.
Находим обратную матрицу по формуле (1.13), которая для случая n = 3 имеет вид:
.
Найдем det A = | А | = 1 х 3 х 8 + 2 х 5 х 3 + 2 х 4 х 3 – 3 х 3 х 3 – 1 х 5 х 4 – 2 х 2 х 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.
Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.
1) Найти алгебраические дополнения A ij :
Для удобства нахождения обратной матрицы мы разместили алгебраические дополнения к строкам исходной матрицы в соответствующих столбцах.
Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:
Квадратные системы линейных уравнений с ненулевым главным определителем можно решать с помощью обратной матрицы. Для этого система (1.5) записывается в матричном виде:
где
Умножая обе части равенства (1.14) слева на А- 1 , получаем решение системы:
, где
Таким образом, чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.
Задача 1.10. Решите систему линейных уравнений
с помощью обратной матрицы.
Раствор. Запишем систему в матричной форме: ,
где – основная матрица системы, – столбец неизвестных, – столбец свободных членов. Так как главный определитель системы , то и главная матрица системы А имеет обратную матрицу А -одна. Чтобы найти обратную матрицу А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :
Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим на определитель D. Таким образом, мы нашли обратную матрицу:
Решение системы находим по формуле (1.15):
Таким образом,
Решение систем линейных уравнений с помощью обыкновенных жордановых исключений
Пусть задана произвольная (не обязательно квадратная) система линейных уравнений:
(1.16)
Требуется найти решение задачи системы, т. е. такой набор переменных, который удовлетворяет всем равенствам системы (1. 16). В общем случае система (1.16) может иметь не только одно решение, но и бесконечное число решений. Она также может вообще не иметь решений.
16). В общем случае система (1.16) может иметь не только одно решение, но и бесконечное число решений. Она также может вообще не иметь решений.
При решении подобных задач в известном школьном курсе используется метод исключения неизвестных, который также называют методом обычного жорданового исключения. Суть этого метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого была выражена переменная, запоминается.
Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. Например, в процессе исключения неизвестных некоторые уравнения могут превратиться в истинные тождества. Такие уравнения исключаются из системы, так как они справедливы при любых значениях переменных и, следовательно, не влияют на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например, ), то делаем вывод, что система не имеет решения.
Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например, ), то делаем вывод, что система не имеет решения.
Если в ходе решения несовместных уравнений не возникло, то одна из оставшихся в ней переменных находится из последнего уравнения. Если в последнем уравнении остается только одна переменная, то она выражается числом. Если в последнем уравнении останутся другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем делается так называемый «обратный ход». Найденная переменная подставляется в последнее запомненное уравнение и находится вторая переменная. Затем две найденные переменные подставляются в предпоследнее запоминаемое уравнение и находится третья переменная, и так до первого запоминаемого уравнения.
В результате получаем решение системы. Это решение будет единственным, если найденные переменные являются числами. Если первая найденная переменная, а затем и все остальные зависят от параметров, то система будет иметь бесконечное число решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от определенного набора параметров, называются общим решением системы.
Если первая найденная переменная, а затем и все остальные зависят от параметров, то система будет иметь бесконечное число решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от определенного набора параметров, называются общим решением системы.
Пример 1.11.
x
Запомнив первое уравнение и приведя во втором и третьем уравнениях аналогичные члены, придем к системе: первое уравнение:
Вспоминаем второе уравнение и из первого находим z :
Делая обратный ход, последовательно находим y и г . Для этого сначала подставляем в последнее запомненное уравнение, из которого находим y :
.
Затем подставляем и в первое запомненное уравнение откуда находим x :
Задача 1.12. Решите систему линейных уравнений, исключив неизвестные:
. (1.17)
Решение. Выразим из первого уравнения переменную x и подставим во второе и третье уравнения:
.
Запомните первое уравнение
В этой системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получаем, что 14 = 17. Это равенство не выполняется при любых значениях переменных х , y и z . Следовательно, система (1.17) несовместна, т. е. не имеет решения.
Читателям предлагается самостоятельно проверить равенство нулю главного определителя исходной системы (1.17).
Рассмотрим систему, отличающуюся от системы (1.17) только одним свободным членом.
Задача 1.13. Решите систему линейных уравнений, исключив неизвестные:
. (1.18)
Решение. Как и прежде, выразим из первого уравнения переменную x и подставим во второе и третье уравнения:
.
Вспомним первое уравнение и представим аналогичные члены во втором и третьем уравнениях. Приходим к системе:
выразив y из первого уравнения и подставив его во второе уравнение , получим тождество 14 = 14, которое не влияет на решение системы, а, следовательно, его можно исключить из системы.
В последнем запомненном равенстве в качестве параметра будет рассматриваться переменная z . Мы верим. Затем
Подставляем y и z в первое запомненное равенство и находим x :
.
Таким образом, система (1.18) имеет бесконечное множество решений, и любое решение можно найти по формулам (1.19) при выборе произвольного значения параметра t :
(1.19)
Таким образом, решения системы системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1.18).
В случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обычных жордановых исключений кажется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы за один шаг в общем виде и формализовать решение задачи в виде специальных таблиц Жордана.
Пусть задана система линейных форм (уравнений):
, (1. 20)
20)
где x j – независимые (искомые) переменные, aij – постоянные коэффициенты …, m ; j = 1, 2,…, n ). Правые части системы y i ( i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решения этой системы путем исключения неизвестных.
Рассмотрим следующую операцию, именуемую в дальнейшем «один шаг обычных жордановых исключений». Из произвольного ( r -го) равенства выразим произвольную переменную ( x s ) и подставим во все остальные равенства. Конечно, это возможно только в том случае, если а rs ¹ 0. Коэффициент а rs называется разрешающим (иногда ведущим или основным) элементом.
Получим следующую систему:
. (1.21)
Из s -го равенства системы (1.21) впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S Строка th запоминается и впоследствии исключается из системы. Оставшаяся система будет содержать одно уравнение и на одну независимую переменную меньше, чем исходная система.
Оставшаяся система будет содержать одно уравнение и на одну независимую переменную меньше, чем исходная система.
Вычислим коэффициенты получившейся системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -е уравнение, которое после выражения переменной x s через остальные переменные будет иметь вид:
Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:
( 1.23)
Теперь вычислим новые коэффициенты b ij ( i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):
После приведения подобных членов получаем:
(1.24)
Из равенства (1.24) получаем формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):
(1.25)
Преобразование систем линейных уравнений методом обычных жордановых исключений представлено в виде таблиц (матриц). Эти таблицы называются «таблицами Иордании».
Эти таблицы называются «таблицами Иордании».
Таким образом, задаче (1.20) соответствует следующая таблица Жордана:
Таблица 1.1
| х 1 | х 2 | … | х | … | х с | … | х | |
| г 1 = | и 11 | и 12 | а 1 й | а 1 с | а 1 н | |||
| ………………………………………………………………….. | ||||||||
| у я = | и 1 | и 2 | ай | или | а в | |||
| ………………………………………………………………….. | ||||||||
| г р = | 1 | 2 | и рж | а рс | а р-н | |||
…………………………………………………………………. | ||||||||
| д н = | а м 1 | а м 2 | и мдж | и мс | и |
Таблица Жордана 1.1 содержит левый головной столбец, в котором записаны правые части системы (1.20), и верхнюю головную строку, в которой записаны независимые переменные.
Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу, состоящую из элементов верхней строки заголовка, то мы получим матрицу, состоящую из элементов левого заголовка строки. То есть, по сути, таблица Жордана представляет собой матричную форму записи системы линейных уравнений: . В этом случае системе (1.21) соответствует следующая таблица Жордана:
Таблица 1.2
| х 1 | х 2 | … | х | … | г р | … | х | |
| г 1 = | б 11 | б 12 | б 1 к | б 1 с | б 1 н | |||
…………………………………………………………………. . . | ||||||||
| у я = | б и 1 | б и 2 | б идж | б это | б в | |||
| ………………………………………………………………….. | ||||||||
| х с = | бр 1 | бр 2 | б рж | брс | б р-н | |||
| …………………………………………………………………. | ||||||||
| д н = | б м 1 | б м 2 | бмж | б мс | млрд |
Разрешающий элемент a rs выделим жирным шрифтом. Напомним, что для реализации одного шага жордановых исключений разрешающий элемент должен быть ненулевым. Строка таблицы, содержащая разрешающий элемент, называется разрешающей строкой. Столбец, содержащий элемент включения, называется столбцом включения. При переходе от данной таблицы к следующей таблице одна переменная ( x s ) из верхней строки заголовка таблицы перемещается в левый столбец заголовка и, наоборот, один из свободных членов системы ( г.р. ) перемещается из левого столбца заголовка таблицы в верхнюю строку заголовка.
Столбец, содержащий элемент включения, называется столбцом включения. При переходе от данной таблицы к следующей таблице одна переменная ( x s ) из верхней строки заголовка таблицы перемещается в левый столбец заголовка и, наоборот, один из свободных членов системы ( г.р. ) перемещается из левого столбца заголовка таблицы в верхнюю строку заголовка.
Опишем алгоритм пересчета коэффициентов при переходе от таблицы Жордана (1.1) к таблице (1.2), который следует из формул (1.23) и (1.25).
1. Разрешающий элемент заменяется обратным номером:
2. Остальные элементы разрешающей строки делятся на разрешающий элемент и меняют знак на противоположный:
3. Остальные элементы разрешающего столбца равны разделен на активирующий элемент:
4. Элементы, не входящие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:
Последнюю формулу легко запомнить, если заметить, что элементы, составляющие дробь, находятся на пересечении i -ой и -й -й строк и -й -й и -й -й столбцов (разрешающая строка, разрешающий столбец и строка и столбец, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно пользоваться следующей схемой:
Точнее, при запоминании формулы можно пользоваться следующей схемой:
Выполняя первый шаг жордановых исключений, любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Вы должны не только выбрать разрешающий элемент в последнем столбце, т.к. нужно найти независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 с переменной x 3 в третьей строке таблицы 1.3 (включающий элемент выделен жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней строки заголовка заменяется константой 0 из левого столбца заголовка (третья строка). При этом переменная х 3 выражается через остальные переменные.
string x 3 (таблица 1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Таблица 1.4 также исключает третий столбец с нулем в верхней строке заголовка. Дело в том, что вне зависимости от коэффициентов этого столбца b i 3 все соответствующие ему члены каждого уравнения 0 b i 3 системы будут равны нулю. Следовательно, эти коэффициенты не могут быть рассчитаны. Исключив одну переменную х 3 и вспомнив одно из уравнений, мы придем к системе, соответствующей табл. 1.4 (с перечеркнутой линией х 3). Выбрав в таблице 1.4 в качестве разрешающего элемента b 14 = -5, перейти к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем вверху).
Дело в том, что вне зависимости от коэффициентов этого столбца b i 3 все соответствующие ему члены каждого уравнения 0 b i 3 системы будут равны нулю. Следовательно, эти коэффициенты не могут быть рассчитаны. Исключив одну переменную х 3 и вспомнив одно из уравнений, мы придем к системе, соответствующей табл. 1.4 (с перечеркнутой линией х 3). Выбрав в таблице 1.4 в качестве разрешающего элемента b 14 = -5, перейти к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем вверху).
Таблица 1.5 Таблица 1.6
Из последней таблицы 1.7 находим: х 1 = – 3 + 2 х 5 .
Последовательно подставляя уже найденные переменные в запомненные строки, находим оставшиеся переменные:
Таким образом, система имеет бесконечное число решений. переменная x 5 , вы можете присвоить произвольные значения. Эта переменная действует как параметр x 5 = t. Мы доказали совместимость системы и нашли общее решение:
Мы доказали совместимость системы и нашли общее решение:
x 1 = – 3 + 2 t
x 2 = – 1 – 3 t
x 8 4 = – 9 2. (1.27)
х 4 = 4 + 5 t
х 5 = t
Придав параметру t различные значения исходной системы, мы получим бесконечное число решений. Так, например, решением системы является следующий набор переменных (- 3; – 1; – 2; 4; 0).
Методы Kramer и Gaussian одно из самых популярных решений SLAU . Более того, в ряде случаев целесообразно использовать специфические методы. Сессия подошла к концу, и сейчас самое время повторить или освоить их с нуля. Сегодня мы займемся решением методом Крамера. Ведь решение системы линейных уравнений по методу Крамера — очень полезный навык.
Системы линейных алгебраических уравнений
Линейные системы алгебраических уравнений – система уравнений вида:
Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и б — действительные коэффициенты. Простую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме или выразить одну переменную через другую. Но переменных (x) в СЛАУ может быть гораздо больше, чем две, и здесь не обойтись без простых школьных манипуляций. Что делать? Например, решить СЛАУ методом Крамера!
Простую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме или выразить одну переменную через другую. Но переменных (x) в СЛАУ может быть гораздо больше, чем две, и здесь не обойтись без простых школьных манипуляций. Что делать? Например, решить СЛАУ методом Крамера!
Пусть система будет n уравнения с n неизвестно.
Такую систему можно переписать в матричной форме
Здесь A – основная матрица системы, X и В соответственно, матрицы столбцов неизвестных переменных и свободных членов.
Раствор СЛАЭ по Крамеру
Если определитель основной матрицы не равен нулю (матрица невырожденная), система может быть решена методом Крамера.
По методу Крамера решение находится по формулам:
Здесь дельта — определитель основной матрицы, а дельта х n-й – определитель, полученный из определителя основной матрицы заменой n-го столбца столбцом свободных членов.
В этом весь смысл метода Крамера. Подставив найденные значения по приведенным выше формулам х в нужную систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы вам было легче уловить суть, вот пример. подробное решение СЛАУ по методу Крамера:
Даже если у вас не получится с первого раза, не расстраивайтесь! Немного потренировавшись, вы начнете щелкать SLOW, как орехи. Более того, теперь совершенно не нужно корпеть над тетрадью, решая громоздкие вычисления и записывая на стержне. СЛАУ методом Крамера легко решить онлайн, просто подставив коэффициенты в готовую форму. опробовать решения онлайн-калькулятора по методу Крамера можно, например, на этом сайте.
А если система оказалась упрямой и не сдается, вы всегда можете обратиться за помощью к нашим авторам, например, к . Если в системе будет хотя бы 100 неизвестных, мы обязательно решим ее правильно и точно в срок!
Метод Крамера или так называемое правило Крамера — это способ поиска неизвестных величин из систем уравнений. Его можно использовать только в том случае, если количество искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть основная матрица, образованная из системы, должна быть квадратной и не содержать нулевых строк, а также если ее определитель должен не быть нулем.
Его можно использовать только в том случае, если количество искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть основная матрица, образованная из системы, должна быть квадратной и не содержать нулевых строк, а также если ее определитель должен не быть нулем.
Теорема 1
Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, и она имеет уникальное решение. Решение такой системы вычисляется с помощью так называемых формул Крамера для решения систем линейных уравнений: $x_i = \frac(D_i)(D)$
Что такое метод Крамера
Суть метода Крамера заключается в следующим образом:
- Чтобы найти решение системы методом Крамера, прежде всего вычислим главный определитель матрицы $D$. Когда вычисленный определитель основной матрицы при вычислении методом Крамера оказался равным нулю, то система не имеет единственного решения или имеет бесконечное число решений.
 В этом случае для нахождения общего или какого-то базового ответа для системы рекомендуется использовать метод Гаусса.
В этом случае для нахождения общего или какого-то базового ответа для системы рекомендуется использовать метод Гаусса. - Затем необходимо заменить последний столбец основной матрицы на столбец свободных членов и вычислить определитель $D_1$.
- Повторите то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ — номер самого правого столбца.
- После того, как все определители $D_1$…$D_n$ найдены, можно вычислить неизвестные переменные по формуле $x_i = \frac(D_i)(D)$.
Методика вычисления определителя матрицы
Для вычисления определителя матрицы размерностью более 2 на 2 можно использовать несколько методов:
- Правило треугольников, или правило Сарруса, напоминающее то же правило. Суть метода треугольника заключается в том, что при вычислении определителя произведения всех чисел, соединенных на рисунке красной чертой справа, они записываются со знаком плюс, а все числа, соединенные аналогичным образом на рисунке на слева со знаком минус.
 Оба правила подходят для матриц 3×3. В случае правила Сарруса сначала переписывается сама матрица, а рядом с ней снова переписываются ее первый и второй столбцы. Через матрицу проводят диагонали и эти дополнительные столбцы, элементы матрицы, лежащие на главной диагонали или параллельно ей, записывают со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей, записывают со знаком минус.
Оба правила подходят для матриц 3×3. В случае правила Сарруса сначала переписывается сама матрица, а рядом с ней снова переписываются ее первый и второй столбцы. Через матрицу проводят диагонали и эти дополнительные столбцы, элементы матрицы, лежащие на главной диагонали или параллельно ей, записывают со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей, записывают со знаком минус.
Рис. 1. Правило треугольников для вычисления определителя по методу Крамера
- При использовании метода, известного как метод Гаусса, этот метод также иногда называют редукцией определителя. При этом матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа на главной диагонали. Следует помнить, что при таком поиске определителя нельзя умножать или делить строки или столбцы на числа, не вынося их в качестве множителя или делителя. В случае поиска определителя возможно только вычитание и сложение строк и столбцов друг к другу, предварительно умножив вычитаемую строку на ненулевой коэффициент.
 Также при каждой перестановке строк или столбцов матрицы следует помнить о необходимости смены конечного знака матрицы.
Также при каждой перестановке строк или столбцов матрицы следует помнить о необходимости смены конечного знака матрицы. - При решении СЛАУ Крамера с 4 неизвестными лучше всего использовать метод Гаусса для поиска и нахождения определителей или определить определитель через поиск миноров.
Решение систем уравнений методом Крамера
Применим метод Крамера к системе из 2 уравнений и двух искомых величин:
$\begin(cases) a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \ end(cases)$
Для удобства отобразим в развернутом виде:
$A = \begin(array)(cc|c) a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end(array)$
Найти определитель основной матрицы, также называемый главным определителем системы:
$D = \begin(array)(|cc|) a_1 & a_2 \\ a_3 & a_4 \\ \end(array) = a_1 \cdot a_4 – a_3 \cdot a_2$
Если основной определитель не равен нулю, то для решения слау методом Крамера необходимо вычислить еще пару определителей из двух матриц с заменой столбцов основной матрицы строкой свободных членов:
$D_1 = \begin(массив)(|cc|) b_1 & a_2 \\ b_2 & a_4 \\ \end(массив) = b_1 \cdot a_4 – b_2 \cdot a_4$
$D_2 = \begin(массив )(|cc|) a_1 & b_1 \\ a_3 & b_2 \\ \end(array) = a_1 \cdot b_2 – a_3 \cdot b_1$
Теперь найдем неизвестные $x_1$ и $x_2$:
$ x_1 = \frac (D_1)(D)$
$x_2 = \frac (D_2)(D)$
Пример 1
Метод Крамера для решения СЛАУ с основной матрицей 3-го порядка (3 x 3) и тремя желаемые.
Решить систему уравнений:
$\begin(cases) 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 – x_3 = 10 \\ \end(cases)$
Вычисляем главный определитель матрицы по приведенному выше правилу под номером 1:
$D = \begin(array)(|ccc|) 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end(массив) = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \ cdot 2 – 3 \cdot (-2) \cdot (-1) – (- 1) \cdot 2 \cdot 3 = – 12 – 8 -12 -32 – 6 + 6 = – $64
А теперь еще три определителя:
$D_1 = \begin(array)(|ccc|) 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end(array) = 21 \cdot 4 \cdot 1 + (- 2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1 ) – (-1) \cdot 2 \ cdot 21 = – 84 – 40 – 36 – 160 – 18 + 42 = – $296
$D_2 = \begin(array)(|ccc|) 3 & 21 & 4 \\ 3 & 9 & 2 \\ 2 & 10 & 1 \\ \end(массив) = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9\cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = – 27 + 120 + 84 – 72 + 63 – 60 = $108
$D_3 = \begin(массив)(|ccc |) 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end(массив) = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + ( -2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 – (-2) \cdot 3 \cdot 10 – (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = – $ 60
Найдем искомые значения:
$x_1 = \frac(D_1) (D) = \frac(- 296)(-64) = 4 \frac(5)(8)$
$x_2 = \frac(D_1) (D) = \frac(108) (-64) = – 1 \frac (11) (16)$
$x_3 = \frac(D_1) (D) = \ frac(-60) (-64) = \frac (15) (16)$
Рассмотрим систему из 3-х уравнений с тремя неизвестными
Используя определители третьего порядка, решение такой системы можно записать в том же виде виде как для системы двух уравнений, т. е.
е.
(2.4)
, если 0. Здесь
Это Правило Крамера решение системы трех линейных уравнений с тремя неизвестными .
Пример 2.3. Решить систему линейных уравнений по правилу Крамера:
Решение . Нахождение определителя главной матрицы системы
Так как 0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислить еще три определителя:
Проверка:
Следовательно, решение найдено верно.
Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, предполагают, что одни и те же правила могут быть сформулированы для линейных систем любого порядка. Действительно имеет место
Теорема Крамера. Квадратная система линейных уравнений с ненулевым определителем основной матрицы системы (0) имеет одно и только одно решение, и это решение вычисляется по формулам
(2. 5)
5)
, где – определитель главной матрицы , и – определитель матрицы , производный от основного, замена i -й столбец свободные элементы столбца .
Обратите внимание, что если =0, то правило Крамера неприменимо. Это означает, что система либо вообще не имеет решений, либо имеет бесконечно много решений.
Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.
2.4. определители n-го порядка
Дополнительный минор M ij элемент a ij называется определителем, полученным из данного вычеркиванием i -я строка и j -я колонка. Алгебраическое сложение A ij Элемент a ij называется минором этого элемента, взятого со знаком (–1) i + j , то есть A ij = (–1) i + к М к .
Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определитель
Получаем
Используя понятие алгебраического дополнения, мы можем сформулировать теорему разложения определителя n -го порядка по 9-му столбцу или строке .
Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) и их алгебраических дополнений:
(2.6)
Эта теорема лежит в основе одного из основных методов вычисления определителей, т. н. метод сокращения заказа . В результате разложения определителя n -го порядка в любой строке или столбце получим n определителей ( n –1)-го порядка. Чтобы таких определителей было меньше, целесообразно выбирать строку или столбец, в которых больше всего нулей. На практике формулу разложения определителя обычно записывают так:
т. е. алгебраические дополнения записываются явно в терминах миноров.
е. алгебраические дополнения записываются явно в терминах миноров.
Примеры 2.4. Вычислите определители, сначала разложив их в любой строке или столбце. Обычно в таких случаях выбирают столбец или строку, в которой больше всего нулей. Выбранная строка или столбец будут отмечены стрелкой.
2.5. Основные свойства определителей
Разложив определитель по любой строке или столбцу, получим n определителей ( n –1)-го порядка. Тогда каждый из этих определителей ( n –1)-го порядка также можно разложить в сумму определителей ( n – 2-й порядок. Продолжая этот процесс, можно добраться до определителей 1-го порядка, т.е. до элементов матрицы, определитель которой вычисляется. Итак, для вычисления определителей 2-го порядка придется вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых. Количество членов будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, не под силу даже компьютеру. Однако определители можно вычислить и другим способом, используя свойства определителей.
Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, не под силу даже компьютеру. Однако определители можно вычислить и другим способом, используя свойства определителей.
Собственность 1 . Определитель не изменится, если в нем поменять местами строки и столбцы, т.е. при транспонировании матрицы :
.
Это свойство указывает на равенство строк и столбцов определителя. Другими словами, любое утверждение о столбцах определителя верно для его строк, и наоборот.
Собственность 2 . Определитель меняет знак при перестановке двух строк (столбцов).
Последствия . Если определитель имеет две одинаковые строки (столбцы), то он равен нулю.
Собственность 3 . Общий делитель всех элементов любой строки (столбца) можно вынести за знак определителя .
Например,
Последствие . Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю .
Собственность 4 . Определитель не изменится, если элементы одной строки (столбца) прибавить к элементам другой строки (столбца), умноженным на некоторое число .
Например,
Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:
Калькулятор решения методом наименьших квадратов + онлайн-решатель с бесплатными шагами
Калькулятор решения линейных квадратов используется для решения системы линейных уравнений, которая не имеют полного ранга в своей матричной форме. Полный ранг матрицы соответствует квадратной матрице с ненулевым определителем.
Таким образом, метод наименьших квадратов используется для решения не квадратных, а прямоугольных матриц. Решение таких матриц может быть немного сложным, но калькулятор наименьших квадратов здесь, чтобы помочь с этим.
Решение таких матриц может быть немного сложным, но калькулятор наименьших квадратов здесь, чтобы помочь с этим.
Что такое калькулятор решения методом наименьших квадратов?
A Калькулятор решения методом наименьших квадратов — это инструмент, который предоставит вам решения методом наименьших квадратов для ваших прямоугольных матриц прямо здесь, в вашем браузере. Вы можете использовать этот онлайн-калькулятор и очень легко решать задачи методом наименьших квадратов.
Этот калькулятор предназначен специально для решения матричных задач 3 x 2, поскольку их нельзя решить с помощью обычного метода квадратных матриц. Эта матрица порядка 3 x 2 описывает матрицу с 3 строками и 2 столбцами. Вы можете просто ввести записи матрицы мест в поля ввода калькулятора для использования.
Как пользоваться калькулятором решения методом наименьших квадратов?
Калькулятор решения методом наименьших квадратов можно использовать, сначала поставив задачу, которую вы хотите решить, а затем следуя инструкциям по его использованию. Важно отметить, что этот калькулятор работает только для матричных задач 3 x 2.
Важно отметить, что этот калькулятор работает только для матричных задач 3 x 2.
Чтобы найти решение с помощью этого калькулятора , у вас должна быть матрица 3 x 2 A и матрица 3 x 1 b , которую необходимо решить для полученной матрицы 2 x 1 X . Теперь выполните приведенные ниже шаги, чтобы получить наилучшие результаты от этого калькулятора:
Шаг 1:
Вы можете начать с ввода заданных A записей матрицы в поля ввода, а именно «Строка 1 из A», «Строка 2 А» и «3-й ряд А» соответственно.
Шаг 2:
За этим следует шаг, включающий ввод матрицы b в поле ввода, помеченное «b».
Шаг 3:
После того, как вы введете все входные данные, вы можете просто нажать кнопку « Отправить », чтобы получить желаемое решение из калькулятора. Этот шаг открывает решение проблемы в новом интерактивном окне.
Шаг 4:
Наконец, вы можете продолжать решать свои проблемы в новом интерактивном окне, если хотите. Вы также можете в любой момент закрыть это окно, нажав кнопку с крестиком в правом верхнем углу.
Вы также можете в любой момент закрыть это окно, нажав кнопку с крестиком в правом верхнем углу.
Важно отметить, что этот калькулятор не будет эффективен против задач с матрицей порядка, отличной от 3 x 2. Порядок матрицы 3 x 2 является очень распространенным порядком для задач без полного ранга. Поэтому он служит отличным инструментом для решения подобных задач.
Как работает калькулятор решения методом наименьших квадратов?
Калькулятор решения методом наименьших квадратов работает путем решения системы линейных уравнений матрицы A 3 x 2 для значения вектора b. Чтобы решить матрицу без полного ранга, важно отметить, имеет ли матрица ранг, равный 2.
Ранг матрицы
Ранг матрицы A определяется как соответствующая размерность векторного пространства. Чтобы определить ранг, сначала применяют элементарные преобразования к матрице. Преобразование должно привести к нормальной форме матрицы, включая единичную матрицу I .
Порядок результирующей единичной матрицы I представляет числовое значение ранга данной матрицы.
Метод наименьших квадратов
Метод наименьших квадратов используется для решения системы линейных уравнений, с которыми не связана квадратная матрица. Еще один важный факт, который следует помнить, заключается в том, что вы можете применять метод наименьших квадратов только к матрицам с рангом выше 1.
Теперь предположим, что имеется матрица A 3 x 2 и вектор b, который также может быть представлен в виде Матрица 3 х 1. Эти две матрицы можно связать вместе, используя третью матрицу, а именно X порядка 2 x 1, которая неизвестна.
АХ = б 9{T}b\]
Приведенное выше уравнение представляет собой решение методом наименьших квадратов заданной исходной системы линейных уравнений.
Решенные примеры
Пример № 1
Рассмотрим матрицу A и вектор b, заданные как:
\[A=\begin{bmatrix}1&5 \\ 3&1 \\ -2&4\end{bmatrix}, b= \begin{bmatrix}4 \\ -2 \\ 3\end{bmatrix}\]
Найдите матрицу X для вышеуказанной задачи. {-1} \begin{bmatrix}1&3&-2 \\ 5&1&4\end{bmatrix}\begin{bmatrix}4 \\ -2 \\ 3\end{bmatrix}\]
{-1} \begin{bmatrix}1&3&-2 \\ 5&1&4\end{bmatrix}\begin{bmatrix}4 \\ -2 \\ 3\end{bmatrix}\]
Наконец, решение этого уравнения приводит к ответу по методу наименьших квадратов матрицы 3 x 2. Его можно выразить следующим образом:
\[x = \frac{1}{14} \bigg( \begin{bmatrix}1&3&-2 \\ 5&1&4\end{bmatrix}\begin{bmatrix}4 \\ -2 \ \ 3\end{bmatrix}\bigg), y = \frac{1}{42} \bigg( \begin{bmatrix}1&3&-2 \\ 5&1&4\end{bmatrix}\begin{bmatrix}4 \\ -2 \\ 3\end{bmatrix}\bigg) \]
Пример № 2
Рассмотрим матрицу A и вектор b, заданные как:
\[A=\begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix}, b=\begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\]
Найдите матрицу X для приведенной выше задачи.
Решение
Начнем с составления матриц в виде уравнения AX = b.
\[\begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix} X = \begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\]
Сейчас возьмите транспонирование A и умножьте его на обе части уравнения:
\[\begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix}^{T} \begin{bmatrix}2&- 2 \\ -2&2 \\ 5&3\end{bmatrix} X = \begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix}^{T} \begin{bmatrix}-1 \\ 7 \ \-26\конец{bmatrix}\]
\[\begin{bmatrix}2&-2&5 \\ -2&2&3\end{bmatrix} \begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix} X = \begin{bmatrix}2&- 2&5 \\ -2&2&3\end{bmatrix}\begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\]
После выполнения матричного умножения необходимо взять обратное значение и получить значения Х можно рассчитать. {-1} \begin{bmatrix}2&-2&5 \\ -2&2&3\end{bmatrix}\begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\]
{-1} \begin{bmatrix}2&-2&5 \\ -2&2&3\end{bmatrix}\begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\]
Наконец, решение этого уравнения приводит к ответу по методу наименьших квадратов матрицы 3 x 2. Его можно выразить следующим образом:
\[x = \frac{5}{256} \bigg( \begin{bmatrix}2&-2&5 \\ -2&2&3\end{bmatrix}\begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\bigg), y = \frac{13}{256} \bigg( \begin{bmatrix}2&-2&5 \\ -2&2&3\end{bmatrix}\begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\bigg) \]
Список математических калькуляторов
Решение матрицы Крамера для чайников. Правило Крамера
Пусть система линейных уравнений содержит столько уравнений, сколько независимых переменных, т.е. имеет вид
Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Обозначим его греческой буквой D. Таким образом,
Если в главном определителе произвольный ( j -й) столбец заменить его столбцом свободных членов системы (1. 5), то можно получить еще n вспомогательные определители:
5), то можно получить еще n вспомогательные определители:
( j = 1, 2, …, n ). (1.7)
Правило Крамера решения квадратных систем линейных уравнений выглядит следующим образом. Если главный определитель D системы (1.5) отличен от нуля, то система имеет единственное решение, которое находится по формулам:
Пример 1.5. Решить систему уравнений методом Крамера
Вычислим главный определитель системы:
Поскольку D¹0, система имеет единственное решение, которое можно найти по формулам (1.8):
Таким образом,
Действия с матрицами
1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.
2. Чтобы умножить матрицу на число, нужно умножить все ее элементы на это число. То есть
Пример 1.6. .
Добавление матрицы.Эта операция вводится только для матриц одного порядка.
Для сложения двух матриц необходимо сложить соответствующие элементы другой матрицы с элементами одной матрицы:
(1. 10)
10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.
Пример 1.7. .
Умножение матриц.Если количество столбцов матрицы А совпадает с количеством строк матрицы В , то для таких матриц вводится операция умножения:
Таким образом, при умножении матрицы А размерностей м ´ n на матрицу ВО размерностей n 3 ´ 948 получаем матрица С размерами m ´ k . В этом случае элементы матрицы С вычисляются по следующим формулам:
Задача 1.8. Найдите, если возможно, произведение матриц AB И BA :
Решение. 1) Чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :
2) Произведение BA не существует, так как количество столбцов матрицы B не соответствует количеству строк матрицы A .
Обратная матрица. Решение систем линейных уравнений матричным способом
Матрица А- 1 называется обратной квадратной матрицей А , если выполняется равенство:
где через I обозначает единичную матрицу того же порядка, что и матрица А :
Для того чтобы квадратная матрица имела обратную, необходимо и достаточно, чтобы ее определитель был ненулевой. Обратная матрица находится по формуле:
где А ij – алгебраические дополнения к элементам aij матрицы А (обратите внимание, что алгебраические дополнения к строкам матрицы А расположены в обратной матрице в виде соответствующих столбцов).
Пример 1.9. Находим обратную матрицу A- 1 к матрице
Находим обратную матрицу по формуле (1.13), которая для случая n = 3 имеет вид:
Найдем det A = | А | = 1 х 3 х 8 + 2 х 5 х 3 + 2 х 4 х 3 – 3 х 3 х 3 – 1 х 5 х 4 – 2 х 2 х 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.
Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.
1) Найти алгебраические дополнения A ij :
Для удобства нахождения обратной матрицы мы разместили алгебраические дополнения к строкам исходной матрицы в соответствующих столбцах.
Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:
Квадратные системы линейных уравнений с ненулевым главным определителем можно решить с помощью обратной матрицы. Для этого система (1.5) записывается в матричной форме:
Умножив обе части равенства (1.14) слева на А- 1 , получим решение системы:
Таким образом, чтобы найти решение квадратной системы, нужно найти обратную матрицу на основную матрицу системы и умножить ее справа на матрицу-столбец свободных членов.
Задача 1.10. Решите систему линейных уравнений
, используя обратную матрицу.
Решение. Запишем систему в матричной форме: ,
где – основная матрица системы, – столбец неизвестных, – столбец свободных членов. Так как главный определитель системы равен , то главная матрица системы А имеет обратную матрицу А -единицу. Чтобы найти обратную матрицу А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :
Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим на определитель D. Таким образом, мы нашли обратную матрицу:
Решение системы находится по формуле (1.15):
Таким образом,
Решаем системы линейных уравнений обыкновенными жордановыми исключениями
Пусть задана произвольная (не обязательно квадратная) система линейных уравнений:
Требуется найти решение системы, т.е. такой набор переменных, который удовлетворяет всем равенствам система (1.16). В общем случае система (1. 16) может иметь не только одно решение, но и бесконечное число решений. Она также может вообще не иметь решений.
16) может иметь не только одно решение, но и бесконечное число решений. Она также может вообще не иметь решений.
При решении подобных задач в известном школьном курсе используется метод исключения неизвестных, который также называют методом обычного жорданового исключения. Суть этого метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого была выражена переменная, запоминается.
Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. Например, в процессе исключения неизвестных некоторые уравнения могут превратиться в истинные тождества. Такие уравнения исключаются из системы, так как они справедливы при любых значениях переменных и, следовательно, не влияют на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например, ), то делаем вывод, что система не имеет решения.
Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например, ), то делаем вывод, что система не имеет решения.
Если в ходе решения несовместных уравнений не возникло, то одна из оставшихся в ней переменных находится из последнего уравнения. Если в последнем уравнении остается только одна переменная, то она выражается числом. Если в последнем уравнении останутся другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем делается так называемый «обратный ход». Найденная переменная подставляется в последнее запомненное уравнение и находится вторая переменная. Затем две найденные переменные подставляются в предпоследнее запоминаемое уравнение и находится третья переменная, и так до первого запоминаемого уравнения.
В результате получаем решение системы. Это решение будет единственным, если найденные переменные являются числами. Если первая найденная переменная, а затем и все остальные зависят от параметров, то система будет иметь бесконечное число решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от определенного набора параметров, называются общим решением системы.
Если первая найденная переменная, а затем и все остальные зависят от параметров, то система будет иметь бесконечное число решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от определенного набора параметров, называются общим решением системы.
Пример 1.11.
x
После запоминания первого уравнения и внесения во второе и третье уравнения одинаковых членов приходим к системе:
Выразим y из второго уравнения и подставим в первое уравнение:
Запоминаем второе уравнение, и из первого находим z :
Делая обратный ход, последовательно находим y И z . Для этого сначала подставляем в последнее заученное уравнение , из которого находим y :
Затем подставляем и в первое запомненное уравнение , из которого находим x :
Задача 1.12. Решите систему линейных уравнений, исключив неизвестные:
Решение. Выразим из первого уравнения переменную x и подставим во второе и третье уравнения:
Выразим из первого уравнения переменную x и подставим во второе и третье уравнения:
В этой системе первое и второе уравнения противоречат друг другу. Действительно, выразив y из первого уравнения и подставив его во второе уравнение, получим, что 14 = 17. Это равенство не выполняется, при любых значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т. е. не имеет решения.
Читателям предлагается самостоятельно проверить равенство нулю главного определителя исходной системы (1.17).
Рассмотрим систему, отличающуюся от системы (1.17) только одним свободным членом.
Задача 1.13. Решите систему линейных уравнений, исключив неизвестные:
Решение. Как и раньше, выразим переменную из первого уравнения x и подставьте его во второе и третье уравнения:
Запомните первое уравнение и дайте аналогичные члены во втором и третьем уравнениях. Приходим к системе:
, выражая y из первого уравнения и подставляя его во второе уравнение, получаем тождество 14 = 14, которое не влияет на решение системы, а, следовательно, его можно исключить из системы.
В последнем запомненном равенстве переменная z будет считаться параметром. Мы верим. Тогда
Подставим y И z в первое запомненное равенство и найдем х :
Таким образом, система (1.18) имеет бесконечное множество решений, и любое решение можно найти из формул (1.19), выбирая произвольное значение параметра t :
(1,19)
Таким образом, решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. , Формулы (1.19) выражают общее (любое) решение системы (1.18).
В случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обычных жордановых исключений кажется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы за один шаг в общем виде и формализовать решение задачи в виде специальных таблиц Жордана.
Пусть задана система линейных форм (уравнений):
, (1. 20)
20)
где xj – независимые (искомые) переменные, aij – постоянные коэффициенты
( i = 1, 2,…, m ; , н ). Правые части системы y i ( i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решения этой системы путем исключения неизвестных.
Рассмотрим следующую операцию, именуемую в дальнейшем «один шаг обычных жордановых исключений». Из произвольного ( r -е) равенство, выражаем произвольную переменную ( x s ) и подставляем во все остальные равенства. Конечно, это возможно только в том случае, если а rs ¹ 0. Коэффициент а rs называется разрешающим (иногда ведущим или основным) элементом.
Получим следующую систему:
Из s -го равенства системы (1.21) впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). С : Строка th запоминается и впоследствии исключается из системы. Оставшаяся система будет содержать одно уравнение и на одну независимую переменную меньше, чем исходная система.
Оставшаяся система будет содержать одно уравнение и на одну независимую переменную меньше, чем исходная система.
Вычислим коэффициенты получившейся системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть так:
Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:
(1.23)
Вычислим теперь новые коэффициенты b ij ( i ¹ r ) произвольного уравнения. Для этого подставим переменную, выраженную в (1.22) x s в i -е уравнение системы (1.20):
Приведя аналогичные члены, получим:
(1.24)
Из равенства (1.24) имеем получить формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -е уравнение):
(1.25)
Преобразование систем линейных уравнений методом обычных жордановых исключений представлено в виде таблиц (матриц). Эти таблицы называются «таблицами Иордании».
Эти таблицы называются «таблицами Иордании».
Таким образом, задаче (1.20) соответствует следующая таблица Жордана:
Таблица 1.1
| х 1 | х 2 | … | хдж | … | х с | … | х | |
| г 1 = | и 11 | и 12 | а 1 й | а 1 с | а 1 н | |||
| ………………………………………………………………….. | ||||||||
| г я = | и 1 | и 2 | ай | или | а в | |||
| ………………………………………………………………….. | ||||||||
| г р = | 1 | 2 | и рж | а рс | а р-н | |||
…………………………………………………………………. | ||||||||
| д н = | а м 1 | а м 2 | и мдж | и мс | и |
Таблица Жордана 1.1 содержит левый головной столбец, в котором записаны правые части системы (1.20), и верхнюю головную строку, в которой записаны независимые переменные.
Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу, состоящую из элементов верхней строки заголовка, то мы получим матрицу, состоящую из элементов левого заголовка строки. То есть, по сути, таблица Жордана представляет собой матричную форму записи системы линейных уравнений: . В этом случае системе (1.21) соответствует следующая таблица Жордана:
Таблица 1.2
| х 1 | х 2 | … | хдж | … | г р | … | х | |
| г 1 = | б 11 | б 12 | б 1 к | б 1 с | б 1 н | |||
…………………………………………………………………. . . | ||||||||
| у я = | б и 1 | б и 2 | б идж | б это | б в | |||
| ………………………………………………………………….. | ||||||||
| х с = | бр 1 | бр 2 | б рж | брс | б р-н | |||
| …………………………………………………………………. | ||||||||
| д н = | б м 1 | б м 2 | бмж | б мс | млрд |
Разрешающий элемент a rs выделим жирным шрифтом. Напомним, что для реализации одного шага жордановых исключений разрешающий элемент должен быть ненулевым. Строка таблицы, содержащая разрешающий элемент, называется разрешающей строкой. Столбец, содержащий элемент включения, называется столбцом включения. При переходе от данной таблицы к следующей таблице одна переменная ( x s ) из верхней строки заголовка таблицы перемещается в левый столбец заголовка и, наоборот, один из свободных членов системы ( г.р. ) перемещается из левого столбца заголовка таблицы в верхнюю строку заголовка.
Столбец, содержащий элемент включения, называется столбцом включения. При переходе от данной таблицы к следующей таблице одна переменная ( x s ) из верхней строки заголовка таблицы перемещается в левый столбец заголовка и, наоборот, один из свободных членов системы ( г.р. ) перемещается из левого столбца заголовка таблицы в верхнюю строку заголовка.
Опишем алгоритм пересчета коэффициентов при переходе от таблицы Жордана (1.1) к таблице (1.2), который следует из формул (1.23) и (1.25).
1. Разрешающий элемент заменяется обратным номером:
2. Остальные элементы разрешающей строки делятся на разрешающий элемент и меняют знак на противоположный:
3. Остальные элементы разрешающего столбца равны разделен на активирующий элемент:
4. Элементы, не входящие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:
Последнюю формулу легко запомнить, если заметить, что элементы, составляющие дробь, находятся на пересечении и -ой и r -й строк и j -й и s -й столбцов (разрешающая строка, разрешающий столбец и строка и столбец, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно пользоваться следующей схемой:
Точнее, при запоминании формулы можно пользоваться следующей схемой:
Выполняя первый шаг жордановых исключений, любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Вы должны не только выбрать разрешающий элемент в последнем столбце, т.к. нужно найти независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 с переменной x 3 в третьей строке таблицы 1.3 (включающий элемент выделен жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней строки заголовка заменяется константой 0 из левого столбца заголовка (третья строка). При этом переменная х 3 выражается через остальные переменные.
string x 3 (таблица 1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Таблица 1.4 также исключает третий столбец с нулем в верхней строке заголовка. Дело в том, что вне зависимости от коэффициентов этого столбца b i 3 все соответствующие ему члены каждого уравнения 0 b i 3 системы будут равны нулю. Следовательно, эти коэффициенты не могут быть рассчитаны. Исключив одну переменную х 3 и вспомнив одно из уравнений, мы придем к системе, соответствующей табл. 1.4 (с перечеркнутой линией х 3). Выбрав в таблице 1.4 в качестве разрешающего элемента b 14 = -5, перейти к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем вверху).
Дело в том, что вне зависимости от коэффициентов этого столбца b i 3 все соответствующие ему члены каждого уравнения 0 b i 3 системы будут равны нулю. Следовательно, эти коэффициенты не могут быть рассчитаны. Исключив одну переменную х 3 и вспомнив одно из уравнений, мы придем к системе, соответствующей табл. 1.4 (с перечеркнутой линией х 3). Выбрав в таблице 1.4 в качестве разрешающего элемента b 14 = -5, перейти к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем вверху).
Таблица 1.5 Таблица 1.6
Из последней таблицы 1.7 находим: х 1 = – 3 + 2 х 5 .
Последовательно подставляя уже найденные переменные в запомненные строки, находим оставшиеся переменные:
Таким образом, система имеет бесконечное число решений. переменная x 5 , вы можете присвоить произвольные значения. Эта переменная действует как параметр x 5 = t. Мы доказали совместность системы и нашли ее общее решение:
Мы доказали совместность системы и нашли ее общее решение:
x 1 = – 3 + 2 t
x 2 = – 1 – 3 t
x 8 4 = – 9 2. (1.27)
х 4 = 4 + 5 t
х 5 = t
Придав параметру t различные значения исходной системы, мы получим бесконечное число решений. Так, например, решением системы является следующий набор переменных (- 3; – 1; – 2; 4; 0).
Метод Крамера основан на использовании определителей при решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера можно использовать для решения системы линейных уравнений, количество которых равно количеству неизвестных в каждом уравнении. Если определитель системы не равен нулю, то при решении можно использовать метод Крамера; если он равен нулю, то не может. Кроме того, метод Крамера можно использовать для решения систем линейных уравнений, имеющих единственное решение.
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются заменой коэффициентов при соответствующих неизвестных свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет единственное решение, а неизвестное равно отношению определителей. В знаменателе стоит определитель системы, а в числителе – определитель, полученный из определителя системы заменой коэффициентов с неизвестными свободными членами. Эта теорема верна для системы линейных уравнений любого порядка.
Пример 1 Решить систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2): 6 90 калькулятор Крамера онлайн .
Три случая при решении систем линейных уравнений
Как следует из теорем Крамера , при решении системы линейных уравнений могут иметь место три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система непротиворечивая и определенная)
Второй случай: система линейных уравнений имеет бесконечное число решений
(система непротиворечивая и неопределенная)
** ,
т. е. коэффициенты при неизвестных и свободных членах пропорциональны.
е. коэффициенты при неизвестных и свободных членах пропорциональны.
Третий случай: система линейных уравнений не имеет решений
(система несовместная)
Итак, система m линейных уравнений с n переменных называется несовместимыми , если не имеет решений, и совместной , если имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется достоверной и более чем одной неопределенной .
Примеры решения систем линейных уравнений методом Крамера
Пусть система
.
На основе теоремы Крамера
………….
,
, где
–
системный идентификатор. Остальные определители получаются заменой в столбце коэффициентов соответствующей переменной (неизвестной) со свободными членами:
Пример 2
.
Следовательно, система определена. Для ее решения вычисляем определители
По формулам Крамера находим:
Итак, (1; 0; -1) — единственное решение системы.
Для проверки решений систем уравнений 3 X 3 и 4 X 4 можно воспользоваться онлайн-калькулятором, методом решения Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях нет переменных, то в определителе соответствующие им элементы равны нулю! Это следующий пример.
Пример 3 Решить систему линейных уравнений методом Крамера:
.
Решение. Находим определитель системы:
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система определена. Для ее решения вычисляем определители при неизвестных
По формулам Крамера находим:
Итак, решение системы (2; -1; 1).
Для проверки решений систем уравнений 3 X 3 и 4 X 4 можно воспользоваться онлайн-калькулятором, методом решения Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже было сказано, если определитель системы равен нулю, а определители при неизвестных не равны нулю, то система несовместна, то есть не имеет решений. Проиллюстрируем на следующем примере.
Проиллюстрируем на следующем примере.
Пример 6 Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определена, либо несовместна, то есть не имеет решений. Для уточнения вычислим определители для неизвестных
Определители для неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 X 3 и 4 X 4 можно воспользоваться онлайн-калькулятором, методом решения Крамера.
В задачах на системы линейных уравнений есть и такие, где кроме букв, обозначающих переменные, есть еще и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное число. На практике такие уравнения и системы уравнений приводят к задачам поиска общих свойств каких-либо явлений или объектов. То есть вы изобрели какой-либо новый материал или устройство, и для описания его свойств, общих вне зависимости от размера или количества экземпляров, необходимо решить систему линейных уравнений, где вместо каких-то коэффициентов при переменных стоит являются письма. За примерами далеко ходить не надо.
За примерами далеко ходить не надо.
Следующий пример для аналогичной задачи, только увеличивается количество уравнений, переменных и букв, обозначающих некоторое действительное число.
Пример 8 Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Нахождение определителей при неизвестных
В первой части мы рассмотрели некоторый теоретический материал, метод подстановки, а также метод почленного сложения уравнений системы . Всем, кто зашел на сайт через эту страницу, рекомендую прочитать первую часть. Возможно, некоторым посетителям материал покажется слишком простым, но в ходе решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А теперь разберем правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы представлены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными методами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, посеместровым сложением!
Дело в том, что пусть иногда, но есть такая задача – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет вам понять, как применить правило Крамера к более сложному случаю – системам из трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые желательно решать точно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычисляем определитель , он называется главным определителем системы .
Метод Гаусса.
Если , то система имеет единственное решение, и для нахождения корней надо вычислить еще два определителя:
И
На практике указанные выше определители можно обозначать и латинской буквой.
Корни уравнения находятся по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Видим, что коэффициенты уравнения достаточно большие, в правой части стоят десятичные дроби через запятую. Запятая — довольно редкий гость в практических задачах по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся ужасные навороченные дроби, с которыми крайне неудобно работать, а оформление решения будет выглядеть просто ужасно. Вы можете умножить второе уравнение на 6 и вычесть член за членом, но здесь появятся те же самые дроби.
Что делать? В таких случаях на помощь приходят формулы Крамера.
;
;
Ответ : ,
Оба корня имеют бесконечные хвосты и находятся приближенно, что вполне приемлемо (и даже обычно) для задач эконометрики.
Комментарии здесь не нужны, так как задача решается по готовым формулам, однако есть один нюанс. При использовании этого метода обязательно Фрагментом задания является следующий фрагмент: “значит система имеет единственное решение” . В противном случае рецензент может наказать вас за неуважение к теореме Крамера.
При использовании этого метода обязательно Фрагментом задания является следующий фрагмент: “значит система имеет единственное решение” . В противном случае рецензент может наказать вас за неуважение к теореме Крамера.
Не лишней будет проверка, которую удобно проводить на калькуляторе: подставляем приблизительные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, находящиеся в правой части.
Пример 8
Выразите ответ в обыкновенных неправильных дробях. Сделайте чек.
Это пример для самостоятельного решения(пример окончания и ответ в конце урока).
Перейдем к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Найдем главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решения). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
Если , то система имеет единственное решение и для нахождения корней надо вычислить еще три определителя:
, ,
И, наконец, ответ вычисляется по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «ходит» слева направо по столбцам главного определителя.
Пример 9
Решите систему, используя формулы Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, тут опять комментировать особо нечего, ввиду того, что решение принимается по готовым формулам. Но есть пара замечаний.
Бывает, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Рекомендую следующий алгоритм “лечения”. Если под рукой нет компьютера, делаем так:
1) Возможна ошибка в расчетах. Как только вы столкнулись с «плохим» кадром, нужно сразу проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители с помощью разложения в другой строке (столбце).
Как только вы столкнулись с «плохим» кадром, нужно сразу проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители с помощью разложения в другой строке (столбце).
2) Если в результате проверки ошибок не обнаружено, то, скорее всего, в условии задания допущена опечатка. В этом случае спокойно и ВНИМАТЕЛЬНО решите задачу до конца, а затем обязательно проверить и составить его на чистом экземпляре после принятия решения. Конечно, проверка дробного ответа — занятие неприятное, но это будет обезоруживающим аргументом для преподавателя, который ну очень любит ставить минус за всякую гадость вроде. Как обращаться с дробями, подробно описано в ответе к Примеру 8.
Если у вас есть под рукой компьютер, то используйте для его проверки автоматизированную программу, которую можно скачать бесплатно в самом начале урока. Кстати, пользоваться программой выгоднее всего сразу (еще до запуска решения), вы сразу увидите промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически вычисляет решение системного матричного метода.
Второе замечание. Время от времени встречаются системы, в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении нет переменной , во втором нет переменной . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать основной определитель:
– вместо пропущенных переменных ставятся нули.
Кстати, определители с нулями рационально открывать в той строке (столбце), в которой стоит ноль, так как вычислений заметно меньше.
Пример 10
Решите систему, используя формулы Крамера.
Это пример для самостоятельного решения (завершающий образец и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Вы можете увидеть живой пример в уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне разрешимы. Хотя задание уже очень напоминает профессорский ботинок на груди счастливчика-студента.
Метод обратной матрицы является по существу частным случаем матричного уравнения (см. пример №3 указанного урока).
Для изучения этого раздела необходимо уметь разлагать определители, находить обратную матрицу и производить умножение матриц. Соответствующие ссылки будут даны по мере продвижения объяснения.
Пример 11
Решить систему матричным методом
Решение : Запишем систему в матричной форме:
, где
Посмотрите пожалуйста на систему уравнений и матрицы. По какому принципу мы записываем элементы в матрицы, думаю всем понятно. Единственное замечание: если бы в уравнениях отсутствовали какие-то переменные, то в матрице на соответствующие места пришлось бы ставить нули.
Находим обратную матрицу по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разберемся с определителем:
Здесь определитель расширяется первой строкой.
Внимание! Если , то обратной матрицы не существует и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (метод Гаусса).
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Ссылка: Полезно знать значение двойных нижних индексов в линейной алгебре. Первая цифра — это номер строки, в которой находится элемент. Вторая цифра – это номер столбца, в котором находится элемент:
То есть двойной нижний индекс указывает на то, что элемент находится в первой строке, третьем столбце, тогда как, например, элемент находится в 3-й строке, 2-м столбце популярные решения СЛАУ . Кроме того, в ряде случаев целесообразно использовать специфические методы. Сессия подошла к концу, и сейчас самое время повторить или освоить их с нуля. Сегодня мы займемся решением методом Крамера. Ведь решение системы линейных уравнений по методу Крамера — очень полезный навык.
Системы линейных алгебраических уравнений
Линейная система алгебраических уравнений – система уравнений вида:
Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a А б — действительные коэффициенты. Простую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме или выразить одну переменную через другую. Но переменных (x) в СЛАУ может быть гораздо больше, чем две, и здесь не обойтись без простых школьных манипуляций. Что делать? Например, решить СЛАУ методом Крамера!
Простую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме или выразить одну переменную через другую. Но переменных (x) в СЛАУ может быть гораздо больше, чем две, и здесь не обойтись без простых школьных манипуляций. Что делать? Например, решить СЛАУ методом Крамера!
Пусть система будет n уравнения с n неизвестно.
Такую систему можно переписать в матричной форме
Здесь A – основная матрица системы, X А Б соответственно, матрицы столбцов неизвестных переменных и свободных членов.
Раствор СЛАЭ по Крамеру
Если определитель основной матрицы не равен нулю (матрица невырожденная), система может быть решена методом Крамера.
По методу Крамера решение находится по формулам:
Здесь дельта — определитель основной матрицы, а дельта х n-й – определитель, полученный из определителя основной матрицы заменой n-го столбца столбцом свободных членов.
В этом весь смысл метода Крамера. Подставив найденные значения по приведенным выше формулам х в нужную систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы помочь вам быстро вникнуть в суть, приведем ниже пример подробного решения СЛАУ методом Крамера:
Даже если у вас не получится с первого раза, не расстраивайтесь! Немного потренировавшись, вы начнете щелкать SLOW, как орехи. Более того, теперь совершенно не нужно корпеть над тетрадью, решая громоздкие вычисления и записывая на стержне. СЛАУ методом Крамера легко решить онлайн, просто подставив коэффициенты в готовую форму. Вы можете попробовать онлайн-калькулятор решения метода Крамера, например, на этом сайте.
А если система оказалась упрямой и не сдается, вы всегда можете обратиться за помощью к нашим авторам, например, купить синопсис. Если в системе будет хотя бы 100 неизвестных, мы обязательно решим ее правильно и точно в срок!
В нашем калькуляторе вы найдете бесплатно решение системы линейных уравнений по методу Крамера онлайн с подробным решением и даже с комплексными числами.


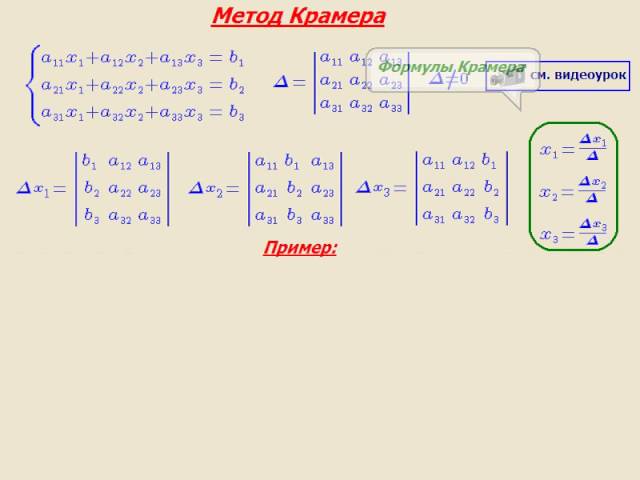

 В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.

 Калькулятор уравнений комплексных чисел возвращает комплексные значения, для которых квадратное уравнение равно нулю.
Калькулятор уравнений комплексных чисел возвращает комплексные значения, для которых квадратное уравнение равно нулю.
 Целью этого упражнения является использование системы двух уравнений с двумя неизвестными для решения задачи.
Целью этого упражнения является использование системы двух уравнений с двумя неизвестными для решения задачи.