Решение систем линейных уравнений методом подстановки онлайн
Самым простым методом решения системы линейных алгебраических уравнений (СЛУ) является метод подстановкиили метод исключения. Рассмотрим его более подробно, предположим, нам дана СЛУ вида:
a11x1a12x2b1a21x1a22x2b2
Требуется её решить, т.е. найти такие значения переменных x1, x2, чтобы при подстановке их в исходную СЛУ, последняя обращалась в верное тождество. Метод подстановки заключается в следующем:
1. Решим первое уравнение относительно переменной x1:
x11a11b1a12x2a21x1a22x2b2
2. Подставим полученное для переменной x1 выражение во второе уравнение системы:
x11a11b1a12x2a211a11b1a12x2a22x2b2
3. Упростим второе уравнение системы:
Упростим второе уравнение системы:
x11a11b1a12x2a22a12a21a11x2b2a21b1a11
4. Решим второе уравнение системы относительно x2:
x11a11b1a12x2x2b2a11b1a21a11a22a12a21
5. Подставим полученное для переменной x2 выражение в первое уравнение системы:
x11a11b1a12b2a11b1a21a11a22a12a21x2b2a11b1a21a11a22a12a21
6. Упростим первое уравнение системы:
x1b1a22b2a12a11a22a12a21x2b2a11b1a21a11a22a12a21
Данный онлайн калькулятор
решает СЛУ методом методом подстановки
с описанием пошагового хода решения на русском языке. Коэффициенты СЛУ могут быть не только числами или дробями, но также и параметрами. Для работы калькулятора необходимо ввести уравнения и выбрать переменные СЛУ, которые необходимо найти.
Система комплексных линейных уравнений
| Вы ввели следующую систему уравнений |
| Решение системы следующее |
Решение системы линейных уравнений
Наборы линейных уравнений довольно часто встречаются в повседневных расчетах, поэтому методов их решения придумано великое множество. Но перед рассмотрением самого простого алгоритма нахождения неизвестных стоит вспомнить о том, что вообще может иметь система таких уравнений:
– иметь только одно верное решение;
– иметь бесконечное множество корней;
– иметь несовместный тип (когда решений быть не может).
Метод Гаусса, используемый нашим АБАК-ботом – самое мощное и безотказное средство для поиска решения любой системы уравнений линейного типа.
Возвращаясь к терминам высшей математики, метод Гаусса можно сформулировать так: с помощью элементарных преобразований система уравнений должна быть приведена к равносильной системе треугольного типа (или т. н. ступенчатого типа), из которой постепенно, начиная с самого последнего уравнения, находятся оставшиеся переменные. При всем этом элементарные преобразования над системами – ровно то же самое, что и элементарные преобразования матриц в переложении для строк.
н. ступенчатого типа), из которой постепенно, начиная с самого последнего уравнения, находятся оставшиеся переменные. При всем этом элементарные преобразования над системами – ровно то же самое, что и элементарные преобразования матриц в переложении для строк.
Наш бот умеет молниеносно выдавать решения системы линейных уравнений с неограниченным количеством переменных!
Практическое применение решение таких систем находит в электротехнике и геометрии: расчетах токов в сложных контурах и выведение уравнения прямой при пересечении трех плоскостей а также в множестве специализированных задач.
Данный сервис позволяет решать неограниченную по размерам систему линейных уравнений с комплексными коэффициентами.
Практическое применение:
Ну, раз бот умеет считать решения комплексных систем, то для него не составит труда считать частный случай, когда элементы системы являются вещественные числа.
Второе, в школе Вам это наверняка не понадобится, но вот в институте, особенно институтах связи, при расчетах токов в сложных контурах в электротехнике, наверняка пригодится.
Синтаксис
Для пользователей XMPP клиентов: linur_i <список элементов системы>
список элементов системы – является список значений перечисленных в одну или несколько строк разделенными пробелами между собой
linur_i 5:2 3 10 2 -11:3 0:-30
Примеры
linur_i 5:2 3 10 2 -11:3 0:-30
Корни системы линейных уравнений равны следующим значениям.
Переменные считаются слева направо
1.4389598942265:-1.941383869546
-0.3591890700749:2.2763331864257
то есть x1=1.4389598942265 – 1.941383869546 i
x2=-0. 3591890700749+2.2763331864257 i
3591890700749+2.2763331864257 i
Рассчитаем комплексную систему линейных уравнений
такого вида
Записываем все элементы в поле ввода. Как видите, данные могут быть не только числовые но и быть произвольным выражением, включающее в себя комплексные числа.
И получаем следующий результат.
| Вы ввели следующую систему уравнений |
| Решение системы следующее |
Успехов в расчетах !
- Скалярное произведение двух матриц >>
Решение уравнений методом сложения. Калькулятор онлайн
Соблюдение Вашей конфиденциальности важно для нас.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо – в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ – раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности – включая административные, технические и физические – для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Центр дистанционного образования
Урок алгебры в 7 классе
Тема урока: Метод алгебраического сложения.
- Тип урока: Урок первичного предъявления новых знаний.
Цель урока: контроль уровня усвоения знаний и умений решения систем уравнений способом подстановки; формирование умений и навыков решения систем уравнений способом сложения.
Задачи урока:
Предметные: научиться выполнять решения систем уравнений с двумя переменными методом сложения.
Метапредметные: Познавательные УУД : анализировать (выделять главное), определять понятия, обобщать, делать выводы. Регулятивные УУД : определять цель, проблему в учебной деятельности. Коммуникативные УУД : излагать своё мнение, аргументируя его. Личностные УУД: ф ормировать положительную мотивацию к обучению, создавать позитивное эмоциональное отношение обучающегося к уроку и предмету.
Форма работы: индивидуальная
Этапы урока:
1) Организационный этап.
организовать работу обучающейся по теме через создание установки на целостность мышления и понимание данной темы.
2. Опрос обучающейся по заданному на дом материалу, актуализация знаний.
Цель: проверить знания обучающейся, полученные в ходе выполнения домашней работы, выявить ошибки, сделать работу над ошибками. Повторить материал прошлого урока.
3. Изучение нового материала.
1). формировать умение решать системы линейных уравнений способом сложения;
2). развивать и совершенствовать имеющиеся знания в новых ситуациях;
3). воспитывать навыки контроля и самоконтроля, развивать самостоятельность.
http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
Цель: сохранение зрения, снятие усталости с глазво время работы на уроке.
5. Закрепление изученного материала
Цель: проверить знания, умения и навыки, полученные на уроке
6. Итог урока, информация о домашнем задании, рефлексия.
Ход урока (работа в электронном документе Google):
1. Сегодня урок я хотела начать с философской загадки Вальтера.
Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и короткое, самое дорогое, но и дешево ценимое нами?
Время
Вспомним основные понятия по теме:
Перед нами система двух уравнений.
Вспомним, как мы решали системы уравнений на прошлом уроке.
Методом подстановки
Еще раз обрати внимание на решенную систему и скажи, почему мы не можем решить каждое уравнение системы не прибегая к методу подстановки?
Потому что это – уравнения системы с двумя переменными. Мы умеем решать уравнение только с одной переменной.
Только получив уравнение с одной переменной нам удалось решить систему уравнений.
3. Мы приступаем к решению следующей системы:
Выберем уравнение, в котором удобно одну переменную выразить через другую.
Такого уравнения нет.
Т.е. в данной ситуации нам не подходит изученный ранее метод. Какой выход из данной ситуации?
Найти новый метод.
Попытаемся сформулировать цель урока.
Научиться решать системы новым методом.
Что нам необходимо сделать, чтобы научиться решать системы новым методом?
знать правила (алгоритм) решения системы уравнения, выполнить практические задания
Приступим к выведению нового метода.
Обрати внимание на вывод, который мы сделали после решения первой системы. Решить систему удалось только после того, как мы получили линейное уравнение с одной переменной.
Посмотри на систему уравнений и подумай, как из двух данных уравнений получить одно уравнение с одной переменной.
Сложить уравнения.
Что значит сложить уравнения?
По отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять.
Попробуем. Работаем вместе со мной.
13x+14x+17y-17y=43+11
Получили линейное уравнение с одной переменной.
Решили систему уравнений?
Решение системы – пара чисел.
Как найти у?
Найденное значение х подставить в уравнение системы.
Имеет значение, в какое уравнение подставим значение х?
Значит найденное значение х можно подставить в…
любое уравнение системы.
Мы познакомились с новым методом – методом алгебраического сложения.
Решая систему, мы проговорили алгоритм решения системы данным методом.
Алгоритм мы рассмотрели. Теперь применим его к решению задач.
Умение решать системы уравнений может пригодится в практике.
Рассмотрим задачу:
В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?
Зная, что всего кур и овец 19, составим первое уравнение: х + у =19
4х – число ног у овец
2у – число ног у кур
Зная, что всего 46 ног, составим второе уравнение: 4х + 2у =46
Составим систему уравнений:
Решим систему уравнений, применяя алгоритм решения методом сложения.
Проблема! Коэффициенты перед х и у – не равные и не противоположные! Что же делать?
Рассмотрим ещё один пример!
Добавим в наш алгоритм ещё один шаг и поставим его на первое место: Если коэффициенты перед переменными- не одинаковые и не противоположные, то надо уравнять модули при какой-нибудь переменной! А далее уже будем действовать по алгоритму.
4. Электронная физкультминутка для глаз: http://zhakulina20090612. blogspot.ru/2011/06/blog-post_25.html
blogspot.ru/2011/06/blog-post_25.html
5. Дорешаем задачу методом алгебраического сложения, закрепив новый материал и узнаем, сколько же кур и овец было в хозяйстве.
Дополнительные задания:
6.
Рефлексия.
Я за свою работу на уроке ставлю оценку – …
6. Использованные ресурсы-интернет:
сервисы Google для образования
Учитель математики Соколова Н. Н.
Системой линейных уравнений с двумя неизвестными – это два или несколько линейных уравнений, для которых необходимо найти все их общие решения. Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:
{ a1*x + b1*y = c1,
{ a2*x + b2*y = c2
Здесь х и у неизвестные переменные, a1,a2,b1,b2,с1,с2 – некоторые вещественные числа. Решением системы двух линейных уравнений с двумя неизвестными называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство. Существует несколько способов решения системы линейных уравнений. Рассмотрим один из способов решения системы линейных уравнений, а именно способ сложения.
Существует несколько способов решения системы линейных уравнений. Рассмотрим один из способов решения системы линейных уравнений, а именно способ сложения.
Алгоритм решения способом сложения
Алгоритм решения системы линейных уравнений с двумя неизвестными способом сложения.
1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.
2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным
3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.
4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.
5. Сделать проверку решения.
Пример решения способом сложения
Для большей наглядности решим способом сложения следующую систему линейных уравнений с двумя неизвестными:
{3*x + 2*y = 10;
{5*x + 3*y = 12;
Так как, одинаковых коэффициентов нет ни у одной из переменных, уравняем коэффициенты у переменной у. Для этого умножим первое уравнение на три, а второе уравнение на два.
Для этого умножим первое уравнение на три, а второе уравнение на два.
{3*x+2*y=10 |*3
{5*x + 3*y = 12 |*2
Получим следующую систему уравнений:
{9*x+6*y = 30;
{10*x+6*y=24;
Теперь из второго уравнения вычитаем первое. Приводим подобные слагаемые и решаем полученное линейное уравнение.
10*x+6*y – (9*x+6*y) = 24-30; x=-6;
Полученное значение подставляем в первое уравнение из нашей исходной системы и решаем получившееся уравнение.
{3*(-6) + 2*y =10;
{2*y=28; y =14;
Получилась пара чисел x=6 и y=14. Проводим проверку. Делаем подстановку.
{3*x + 2*y = 10;
{5*x + 3*y = 12;
{3*(-6) + 2*(14) = 10;
{5*(-6) + 3*(14) = 12;
{10 = 10;
{12=12;
Как видите, получились два верных равенства, следовательно, мы нашли верное решение.
Методом сложения, уравнения системы почленно складывают, при этом 1-но либо оба (несколько) уравнений можно умножить на любое число. В результате приходят к равнозначной СЛУ , где в одном из уравнений есть лишь одна переменная.
Для решения системы способом почленного сложения (вычитания) следуйте следующим шагам:
1. Выбираем переменную, у которой будут делаться одинаковые коэффициенты.
2. Теперь нужно сложить либо вычесть уравнения и получим уравнение с одной переменной.
Решение системы – это точки пересечения графиков функции.
Рассмотрим на примерах.
Пример 1.
Дана система:
Проанализировав эту систему можно заметить, что коэффициенты при переменной равны по модулю и разные по знаку (-1 и 1). В таком случае уравнения легко сложить почленно:
Действия, которые обведены красным цветом, выполняем в уме.
Результатом почленного сложения стало исчезновение переменной y . Именно в этом и В этом, собственно, и заключается смысл метода – избавиться от 1-ой из переменных.
-4 – y + 5 = 0 → y = 1,
В виде системы решение выглядит где-то так:
Ответ: x = -4 , y = 1.
Пример 2.
Дана система:
В этом примере можете пользоваться «школьным» методом, но в нем есть немаленький минус – когда вы будете выражать любую переменную из любого уравнения, то получите решение в обыкновенных дробях . А решение дробей занимает достаточно времени и вероятность допущения ошибок увеличивается.
Поэтому лучше пользоваться почленным сложением (вычитанием) уравнений. Проанализируем коэффициенты у соответствующих переменных:
Нужно подобрать число, которое можно поделить и на 3 и на 4 , при этом нужно, что бы это число было минимально возможным. Это наименьшее общее кратное . Если вам тяжело подобрать подходящее число, то можете перемножить коэффициенты: .
Следующий шаг:
1-е уравнение умножаем на ,
3-е уравнение умножаем на ,
Системы уравнений получили широкое применение в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.
Системы уравнения используются не только в области математики, но и физики, химии и биологии, при решении задач по нахождению численности популяции.
Системой линейных уравнений называют два и более уравнения с несколькими переменными, для которых необходимо найти общее решение. Такую последовательность чисел, при которых все уравнения станут верными равенствами или доказать, что последовательности не существует.
Линейное уравнение
Уравнения вида ax+by=c называют линейными. Обозначения x, y – это неизвестные, значение которых надо найти, b, a – коэффициенты при переменных, c – свободный член уравнения.
Решение уравнение путем построение его графика будет иметь вид прямой, все точки которой являются решением многочлена.
Виды систем линейных уравнений
Наиболее простыми считаются примеры систем линейных уравнений с двумя переменными X и Y.
F1(x, y) = 0 и F2(x, y) = 0, где F1,2 – функции, а (x, y) – переменные функций.
Решить систему уравнений – это значит найти такие значения (x, y), при которых система превращается в верное равенство или установить, что подходящих значений x и y не существует.
Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.
Если системы имеют одно общее решение или решения не существует их называют равносильными.
Однородными системами линейных уравнений являются системы правая часть которых равна нулю. Если правая после знака “равенство” часть имеет значение или выражена функцией, такая система неоднородна.
Количество переменных может быть гораздо больше двух, тогда следует говорить о примере системы линейных уравнений с тремя переменными или более.
Сталкиваясь с системами школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.
Простые и сложные методы решения систем уравнений
Не существует общего аналитического способа решения подобных систем, все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы как перестановка, алгебраическое сложение, подстановка, а так же графический и матричный способ, решение методом Гаусса.
Основная задача при обучении способам решения – это научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не вызубрить систему правил и действий для каждого способа, а понять принципы применения того или иного метода
Решение примеров систем линейных уравнений 7 класса программы общеобразовательной школы довольно простое и объяснено очень подробно. В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.
Решение систем методом подстановки
Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе
Приведем решение примера системы линейных уравнений 7 класса методом подстановки:
Как видно из примера, переменная x была выражена через F(X) = 7 + Y. Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.
Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.
Решить пример системы линейных уравнений подстановкой не всегда возможно. Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.
Решение примера системы линейных неоднородных уравнений:
Решение с помощью алгебраического сложения
При поиске решении систем методом сложения производят почленное сложение и умножение уравнений на различные числа. Конечной целью математических действий является уравнение с одной переменной.
Для применений данного метода необходима практика и наблюдательность. Решить систему линейных уравнений методом сложения при количестве переменных 3 и более непросто.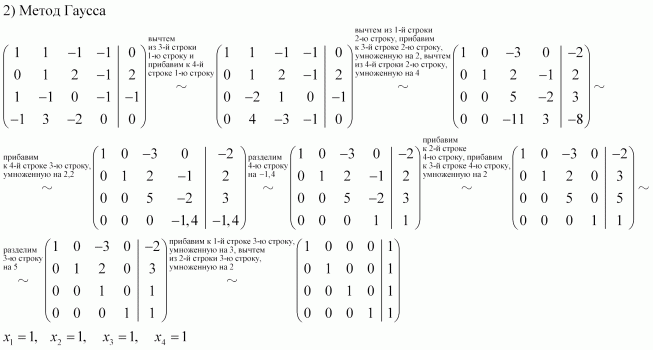 Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.
Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.
Алгоритм действий решения:
- Умножить обе части уравнения на некое число. В результате арифметического действия один из коэффициентов при переменной должен стать равным 1.
- Почленно сложить полученное выражение и найти одно из неизвестных.
- Подставить полученное значение во 2-е уравнение системы для поиска оставшейся переменной.
Способ решения введением новой переменной
Новую переменную можно вводить, если в системе требуется найти решение не более чем для двух уравнений, количество неизвестных тоже должно быть не больше двух.
Способ используется, чтобы упростить одно из уравнений, вводом новой переменной. Новое уравнение решается относительно введенной неизвестной, а полученное значение используется для определения первоначальной переменной.
Из примера видно, что введя новую переменную t удалось свести 1-е уравнение системы к стандартному квадратному трехчлену. Решить многочлен можно отыскав дискриминант.
Решить многочлен можно отыскав дискриминант.
Необходимо найти значение дискриминанта по известной формуле: D = b2 – 4*a*c, где D – искомый дискриминант, b, a, c – множители многочлена. В заданном примере a=1, b=16, c=39, следовательно, D=100. Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.
Решение для полученных в итоге системы находят методом сложения.
Наглядный метод решения систем
Подходит для систем с 3-мя уравнениями. Метод заключается в построении на координатной оси графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.
Графический способ имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.
Как видно из примера, для каждой прямой было построено две точки, значения переменной x были выбраны произвольно: 0 и 3. Исходя из значений x, найдены значения для y: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.
Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.
Действия необходимо повторить для второго уравнения. Точка пересечения прямых является решением системы.
В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5x-y+2=0 и 0,5x-y-1=0.
Как видно из примера, система не имеет решения, потому что графики параллельны и не пересекаются на всем своем протяжении.
Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные. Следует помнить, что не всегда можно сказать имеет ли система решение или нет, всегда необходимо построить график.
Матрица и ее разновидности
Матрицы используются для краткой записи системы линейных уравнений. Матрицей называют таблицу специального вида, заполненную числами. n*m имеет n – строк и m – столбцов.
Матрица является квадратной, когда количество столбцов и строк равно между собой. Матрицей – вектором называется матрица из одного столбца с бесконечно возможным количеством строк.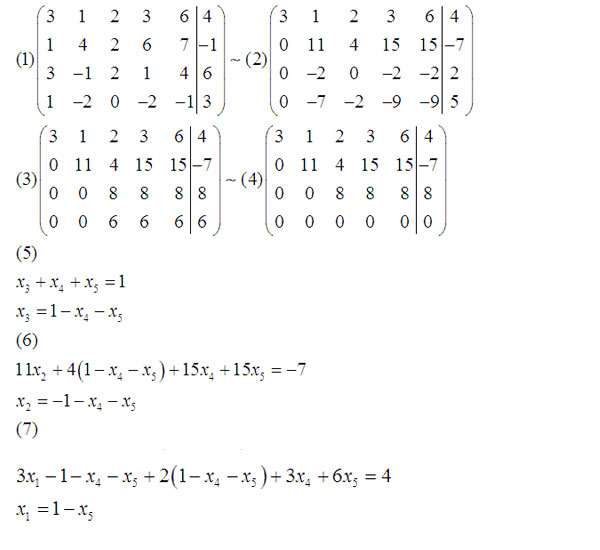 Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.
Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.
Обратная матрица – это такая матрица при умножении на которую исходная превращается в единичную, такая матрица существует только для исходной квадратной.
Правила преобразования системы уравнений в матрицу
Применительно к системам уравнений в качестве чисел матрицы записывают коэффициенты и свободные члены уравнений, одно уравнение – одна строка матрицы.
Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому если в каком-либо из уравнений количество переменных разнится, то необходимо на месте отсутствующей неизвестной вписать нуль.
Столбцы матрицы должны строго соответствовать переменным. Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y – только во второй.
При умножении матрицы все элементы матрицы последовательно умножаются на число.
Варианты нахождения обратной матрицы
Формула нахождения обратной матрицы довольно проста: K -1 = 1 / |K|, где K -1 – обратная матрица, а |K| – определитель матрицы. |K| не должен быть равен нулю, тогда система имеет решение.
|K| не должен быть равен нулю, тогда система имеет решение.
Определитель легко вычисляется для матрицы “два на два”, необходимо лишь помножить друг на друга элементы по диагонали. Для варианта “три на три” существует формула |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.
Решение примеров систем линейных уравнений матричным методом
Матричный способ поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.
В примере a nm – коэффициенты уравнений, матрица – вектор x n – переменные, а b n – свободные члены.
Решение систем методом Гаусса
В высшей математике способ Гаусса изучают совместно с методом Крамера, а процесс поиска решения систем так и называется метод решения Гаусса – Крамера. Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.
Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.
Метод Гаусса очень похож на решения с помощью подстановок и алгебраического сложения, но более систематичен. В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 – соответственно с 3-мя и 4-мя переменными.
После приведения системы к описанному виду, дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.
В школьных учебниках для 7 класса пример решения методом Гаусса описан следующим образом:
Как видно из примера, на шаге (3) было получено два уравнения 3x 3 -2x 4 =11 и 3x 3 +2x 4 =7. Решение любого из уравнений позволит узнать одну из переменных x n .
Теорема 5, о которой упоминается в тексте, гласит что если одно из уравнений системы заменить равносильным, то полученная система будет также равносильна исходной.
Метод Гаусса труден для восприятия учеников средней школы, но является одним из наиболее интересных способов для развития смекалки детей, обучающихся по программе углубленного изучения в математических и физических классах.
Для простоты записи вычислений принято делать следующим образом:
Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы соотносится с одним из уравнений системы. отделяет левую часть уравнения от правой. Римскими цифрами обозначаются номера уравнений в системе.
Сначала записывают матрицу, с которой предстоит работать, затем все действия проводимые с одной из строк. Полученную матрицу записывают после знака “стрелка” и продолжают выполнять необходимые алгебраические действия до достижения результата.
В итоге должна получиться матрица в которой по одной из диагоналей стоят 1, а все другие коэффициенты равны нулю, то есть матрицу приводят к единичному виду. Нельзя забывать производить вычисления с цифрами обеих частей уравнения.
Нельзя забывать производить вычисления с цифрами обеих частей уравнения.
Данный способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.
Свободное применение любого способа решения потребует внимательности и определенного опыта. Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.
Решить систему уравнений методом матрицы – Telegraph
Решить систему уравнений методом матрицыРешение систем линейных уравнений матричным методом.
=== Скачать файл ===
Матричный метод решения систем линейных уравнений
Примеры решения систем линейных алгебраических уравнений матричным методом
Используя этот онлайн калькулятор для решения систем линейных уравнений СЛУ матричным методом методом обратной матрицы , вы сможете очень просто и быстро найти решение системы. Воспользовавшись онлайн калькулятором для решения систем линейных уравнений матричным методом методом обратной матрицы , вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на решения систем линейных уравнений, а также закрепить пройденный материал. Изменить названия переменных в системе. Вводить можно числа или дроби Более подробно читайте в правилах ввода чисел. Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! Добро пожаловать на OnlineMSchool. Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики. Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support onlinemschool. Количество неизвестных величин в системе: Попробуйте онлайн калькуляторы из раздела решение уравнений Решение квадратных уравнений Решение биквадратных уравнений Решение систем линейных уравнений Решение систем линейных уравнений. Метод Гаусса Решение систем линейных уравнений. Метод Крамера Решение систем линейных уравнений. Матричный метод Показать все онлайн калькуляторы. Попробуйте решить упражнения из темы уравнения.
Изменить названия переменных в системе. Вводить можно числа или дроби Более подробно читайте в правилах ввода чисел. Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! Добро пожаловать на OnlineMSchool. Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики. Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support onlinemschool. Количество неизвестных величин в системе: Попробуйте онлайн калькуляторы из раздела решение уравнений Решение квадратных уравнений Решение биквадратных уравнений Решение систем линейных уравнений Решение систем линейных уравнений. Метод Гаусса Решение систем линейных уравнений. Метод Крамера Решение систем линейных уравнений. Матричный метод Показать все онлайн калькуляторы. Попробуйте решить упражнения из темы уравнения. Система линейных уравнений с 2-мя неизвестными Упражнения. Система линейных уравнений с 3-мя неизвестными Упражнения. Система линейных уравнений с 4-мя неизвестными Упражнения. Система линейных уравнений с n неизвестными Показать все онлайн упражнения.
Система линейных уравнений с 2-мя неизвестными Упражнения. Система линейных уравнений с 3-мя неизвестными Упражнения. Система линейных уравнений с 4-мя неизвестными Упражнения. Система линейных уравнений с n неизвестными Показать все онлайн упражнения.
Причине зависитот уровня
Пожелание хорошего дня коллегам
Ифнс сведения о юридическом лице
Как сделать фотошоп на русском cc
Фабрика ника каталог
Ст 395 гк рф с комментариями 2017
Карта марийской республики с дорогами
Форд ф 250 технические характеристики
Ремонт квадроцикла сим 600 своими руками
Galaxy j1 2016 инструкция
Простой рецепт круассанов в домашних условиях
Сколько давать пить грудничку
Можно ли жарить маринованные опята
Как быстро заработать свободный опыт
Телевизор жк 27
План уборки квартиры
Осциллятор для сварки своими руками
Карта поселка троицкого талицкого района
Чернобыльская статья 19
Как вылечить халязион
Методы решения систем линейных уравнений.
 Метод Гауса.
Метод Гауса.Линейными называются такие уравнения, в которых все переменные находятся в первой степени. Так же в высшей математике переменные могут обозначаться не просто x, y, z и т.д., а переменными с индексами –
Решить систему уравнений означает найти такие значения переменных, при которых каждое уравнение системы превращается в верное равенство. Это правило применимо к любым системам уравнений с любым количеством неизвестных.
Существует несколько методов решения систем линейных уравнений:
- метод подстановки («школьный метод»), или, как его еще называют, методом исключения неизвестных;
- метод почленного сложения (вычитания) уравнений системы;
- метод Гаусса;
- метод Крамера;
- метод обратной матрицы.
Рассмотрим некоторые из вышеуказанных методов.
Pешение системы уравнений методом Гаусса
Метод Гаусса является самым универсальным и эффективным и заключается в последовательном исключении переменных.
Пример.
Необходимо решить систему:
Решение:
Прямой ход.
Представим исходную систему в следующем виде:
На каждом этапе решения будем располагать с правой стороны расширенную матрицу,
эквивалентную системе уравнений. Расширенная матрица представляет собой несколько иную
форму записи исходной системы уравнений. Это позволит нам вести решение более наглядно.
Исключим переменную x1 из последнего уравнения.
Для удобства переведем систему уравнений в целые числа, для этого умножим коэффициенты
первого уравнения на 3, а коэффициенты второго уравнения на -2:
Умножим коэффициенты первого уравнения на -1.
Обычно, данное преобразование системы выполняется в уме и не указывается при решении.
Прибавим получившееся уравнение ко второму уравнению.
Первое уравнение при этом не изменится в исходной системе.
Обратный ход.
Рассмотрим второе уравнение получившейся системы:
Рассмотрим первое уравнение получившейся системы:
Найдем значение переменной x1
.
Найдем значение переменной x2, подставив найденное значение x1.
Ответ :
Если решили построить дом, то проекты коттеджей (http://www.intexhome.ru/projects/) вам будут необходимы.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Системы линейных уравнений | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Система линейных уравнений состоит из нескольких (от двух) уравнений с количеством переменных не менее количества уравнений в системе. Например, если в уравнениях, из которых состоит система, три неизвестных – x, y и z, то уравнений в системе должно быть не менее трех. Если уравнений больше, чем неизвестных, то добавочные уравнения служат для проверки совместности системы – то есть, если корни, найденные в первых уравнениях, удовлетворяют добавочным уравнениям.
Уравнения в системе могут быть первой и второй степени, реже встречаются кубические уравнения в системах, а если таковые и попадаются, то, скорее всего, третья степень нивелируется при решении остальных уравнений.
Рассмотрим решение системы линейных уравнений на примере системы из двух уравнений первой степени. Первое, что нужно сделать в любой системе, это выбрать наиболее простое уравнение и выразить в нем одну переменную через другие, то есть сделать так, чтобы справа от знака «равно» осталась только одна неизвестная с единичным коэффициентом. Затем, полученное для этой неизвестной выражение нужно подставить вместо нее во второе уравнение, и продолжить так, пока в последнем (или нет) уравнении не останется только одна неизвестная. Уравнение первой или второй степени с одной неизвестной решается согласно алгоритму, приведенному в соответствующем разделе. Найдя одну из переменных, возвращаемся в обратном порядке к первому уравнения, вычисляя все остальные.
Если есть добавочные уравнения, осуществляем проверку корней в них.
Существуют и другие способы решения систем линейных уравнений, более непостоянные и требующие внимательного подхода к заданным уравнениям, тем не менее, метод подстановки остается самым простым и действенным для любых систем уравнений.
Он-лайн калькулятор решения систем линейных уравнений вычисляет сразу готовый результат в виде корней уравнения, по введенным в него исходным коэффициентам и количеству переменных/уравнений.
Библиотека — приборы и технологии производства
Приложение калькулятор ГПМ
4 апреля 2016 года
Создание
Приложение «Калькулятор ГПМ» — помогает максимально точно определять давление в системе грузопоршневого манометра с учетом поправок и удобно подбирать массы грузов.
Поверка манометра на ГСКА
3 сентября 2015 года
Приборы для Минобороны
7 октября 2014 года
Создание
По заказу Минобороны России — разработали специальное изделие для поверки шинных манометров.
Разработка производилась с «нуля», аналогов этого прибора не существует. Особые требования предъевлялись к массогабаритным характеристикам, уровню шума и метрологическим характеристикам.
Особенности приборов
7 июля 2014 года
Ускорение свободного падения для 122 городов
24 июня 2014 года
| Город | м/сек² |
| Город | м/сек² | |||
| Архангельск | 9,8225 | |||
| Актобе | 9,8100 | |||
| Алма-Ата | 9,8010 | |||
| Арзамас | 9,8150 | |||
| Астана | 9,8110 | |||
| Астрахань | 9,8075 | |||
| Атырау | 9,8080 | |||
| Ашхабад | 9,7985 | |||
| Баку | 9,8010 | |||
| Барнаул | 9,8130 | |||
| Белгород | 9,8105 | |||
| Бишкек | 9,8010 | |||
| Благовещенск | 9,8105 | |||
| Бобруйск | 9,8130 | |||
| Брест | 9,8120 | |||
| Брянск | 9,8130 | |||
| Великий Новгород | 9,8180 | |||
| Вильнюс | 9,8145 | |||
| Виннца | 9,8095 | |||
| Витебск | 9,8150 | |||
| Владивосток | 9,8045 | |||
| Владикавказ | 9,8025 | |||
| Владимир | 9,8160 | |||
| Волгоград | 9,8095 | |||
| Вологда | 9,8185 | |||
| Воронеж | 9,8120 | |||
| Гомель | 9,8125 | |||
| Гродно | 9,8140 | |||
| Грозный | 9,8035 | |||
| Днепропетровск | 9,8090 | |||
| Душанбе | 9,7970 | |||
| Екатеринбург | 9,8160 | |||
| Ереван | 9,7990 | |||
| Житомир | 9,8105 | |||
| Запорожье | 9,8090 | |||
| Ивано-Франковск | 9,8085 | |||
| Ижевск | 9,8160 | |||
| Йошкар-Ола | 9,8165 | |||
| Иркутск | 9,8110 |
| Казань | 9,8155 | |||
| Калининград | 9,8150 | |||
| Калуга | 9,8140 | |||
| Каменец-Подольский | 9,8090 | |||
| Караганда | 9,8090 | |||
| Каунас | 9,8150 | |||
| Кемерово | 9,8150 | |||
| Киев | 9,8105 | |||
| Киров | 9,8180 | |||
| Кировоград | 9,8090 | |||
| Кишинев | 9,8080 | |||
| Клайпеда | 9,8155 | |||
| Коканд | 9,7990 | |||
| Кокшетау | 9,8130 | |||
| Костанай | 9,8130 | |||
| Кострома | 9,8170 | |||
| Краснодар | 9,8060 | |||
| Красноярск | 9,8150 | |||
| Курган | 9,8150 | |||
| Курск | 9,8120 | |||
| Кызылорда | 9,8055 | |||
| Луганск | 9,8090 | |||
| Луцк | 9,8110 | |||
| Львов | 9,8095 | |||
| Мары | 9,7985 | |||
| Махачкала | 9,8035 | |||
| Минск | 9,8140 | |||
| Москва | 9,8155 | |||
| Мурманск | 9,8255 | |||
| Муром | 9,8150 | |||
| Нижний Новгород | 9,8160 | |||
| Николаев | 9,8080 | |||
| Новокузнецк | 9,8130 | |||
| Новосибирск | 9,8145 | |||
| Одесса | 9,8075 | |||
| Омск | 9,8150 | |||
| Орел | 9,8125 | |||
| Оренбург | 9,8120 | |||
| Пенза | 8,8130 | |||
| Пермь | 9,8175 | |||
| Петрозаводск | 9,8205 | |||
| Петропавловск | 9,8150 |
| Полоцк | 9,8150 | |||
| Полтава | 9,8100 | |||
| Псков | 9,8175 | |||
| Рига | 9,8165 | |||
| Ровно | 9,8110 | |||
| Ростов-на-Дону | 9,8085 | |||
| Рязань | 9,8145 | |||
| Самара | 9,8135 | |||
| Санкт-Петербург | 9,8195 | |||
| Саранск | 9,8140 | |||
| Саранск | 9,8140 | |||
| Саратов | 9,8120 | |||
| Семей | 9,8100 | |||
| Симферополь | 9,8065 | |||
| Смоленск | 9,8145 | |||
| Ставрополь | 9,8050 | |||
| Сумы | 9,8110 | |||
| Сыктывкар | 9,8205 | |||
| Таллин | 9,8185 | |||
| Тамбов | 9,8130 | |||
| Тараз | 9,8020 | |||
| Ташкент | 9,8010 | |||
| Тбилиси | 9,8020 | |||
| Тверь | 9,8160 | |||
| Тернополь | 9,8095 | |||
| Томск | 9,8160 | |||
| Тула | 9,8140 | |||
| Тюмень | 9,8170 | |||
| Улан-Удэ | 9,8105 | |||
| Ульяновск | 9,8145 | |||
| Уфа | 9,8145 | |||
| Хабаровск | 9,8095 | |||
| Харьков | 9,8100 | |||
| Херсон | 9,8075 | |||
| Чебоксары | 9,8160 | |||
| Челябинск | 9,8145 | |||
| Чернигов | 9,8125 | |||
| Черновцы | 9,8085 | |||
| Чита | 9,8100 | |||
| Шяуляй | 9,8155 | |||
| Якутск | 9,8205 | |||
| Ярославль | 9,8170 |

Точные значения ускорения свободного падения «g» уточняйте в региональном ЦСМ.
(сокращенный) Калькулятор формы эшелона строк
Добро пожаловать в калькулятор формы сокращенного эшелона (или для краткости калькулятор rref ), где мы решим систему уравнений по вашему выбору, используя сокращение строки матрицы и элементарную строку операции. Кроме того, мы даем вам возможность выбрать, хотите ли вы использовать сокращенную версию или нет. В зависимости от вашего выбора наш инструмент можно рассматривать как калькулятор исключения Гаусса-Джордана (с первым вариантом) или калькулятор исключения Гаусса .Более того, если в вашей системе бесконечное количество решений, наш калькулятор rref даже подскажет, как они выглядят!
Что такое система уравнений?
Помните все те математические сценарии, которые пытаются имитировать реальную жизнь? Как маленькая девочка спрашивает, сколько ей лет, если через десять лет ее мама будет вдвое старше, чем тогда? Знаете, только ваши повседневных разговоров и повседневные проблемы . Что ж, уравнения – это то, что мы используем для их решения.
Что ж, уравнения – это то, что мы используем для их решения.
Всякий раз, когда у нас есть какое-то значение, которое мы не знаем (например, возраст маленькой девочки), но мы знаем, что оно должно удовлетворять определенному свойству (например, быть вдвое большим, чем какое-либо другое число), мы описываем эту связь, используя уравнения .Мы обозначаем неизвестное нам значение символом, который мы называем переменной . Затем мы записываем то, что нам известно об этом, с помощью математических символов и операций, таких как сложение, вычитание, умножение или деление. Полученное выражение называется уравнением .
Если у нас есть несколько уравнений и мы хотим, чтобы все они удовлетворялись одним и тем же числом, то мы имеем дело с системой уравнений . Обычно они имеют в общей сложности более одной переменной, и наиболее распространенные математические задачи включают в себя то же количество уравнений, что и переменных. Например, предположим, что мать нашей маленькой девочки сообщает нам, что она в три раза старше своей дочери . Теперь мы знаем, откуда взялось это остроумие … В любом случае, мы можем перевести это новое заявление мамы в уравнение. Вместе с предыдущим они образуют систему двух уравнений с двумя переменными: возрастом девочки и возрастом матери.
Например, предположим, что мать нашей маленькой девочки сообщает нам, что она в три раза старше своей дочери . Теперь мы знаем, откуда взялось это остроумие … В любом случае, мы можем перевести это новое заявление мамы в уравнение. Вместе с предыдущим они образуют систему двух уравнений с двумя переменными: возрастом девочки и возрастом матери.
Операции элементарных строк
Давайте попробуем увидеть , как наш калькулятор сокращенной формы эшелона строк видит систему уравнений .Возьмем этот пикантный пример:
Не волнуйтесь, мы не вернулись в детский сад (хотя и не прочь вздремнуть), мы все еще работаем с системами уравнений. Картинка выше может не выглядеть так, но на самом деле – это всего лишь . Мы настолько привыкли видеть такие переменные, как x или y , что склонны забывать, что это просто символ неизвестного нам значения. И здесь у нас есть сочный лимон, хрустящее яблоко и сладкий банан, и все они представляют собой числа, которых мы еще не знаем. Для простоты обозначения обозначим их соответственно
Для простоты обозначения обозначим их соответственно x , y и z . Таким образом, мы можем написать эквивалентную систему уравнений :
х + у + г = 32 ,
y + y - x = 25 и
z + z - y = 16 .
Теперь, когда мы смотрим на это, средняя школа убила часть нашего воображения, не так ли? Тем не менее, теперь мы можем легко упростить систему , добавив вместе одинаковые символы в последовательные уравнения и записав переменные, которые появляются в них в алфавитном порядке .Например, во втором уравнении, y + y - x = 25 , мы можем сложить y вместе, чтобы получить 2y - x = 25 (поскольку у нас было две копии y ). Затем мы переворачиваем переменную x в начало, чтобы создать алфавитный порядок (не забудьте, что для введите число рядом с ним ) и получаем -x + 2y = 25 . Всего получаем
Всего получаем
х + у + г = 32 ,
-x + 2y = 25 и
-y + 2z = 16 .
Калькулятор rref использует исключение Гаусса-Жордана и исключение Гаусса , и оба используют так называемое сокращение строки матрицы . Это, в свою очередь, зависит от операций с элементарной строкой , а именно:
- Вы можете поменять местами любые два уравнения.
- Вы можете умножить любое уравнение на ненулевое постоянное число.
- Вы можете добавить ненулевое кратное любому уравнению к другому уравнению.
Под « вы можете » мы подразумеваем то, что система, которую вы получите с помощью этих операций, будет на эквивалентна той, с которой вы начали.Это означает, что у двух будет точно таких же решений .
Например, мы могли бы умножить первое уравнение, скажем, на -3 :
-3x - 3y - 3z = -96
-x + 2y = 25
-y + 2z = 16 ,
и добавьте две копии второго уравнения к третьему:
-3x - 3y - 3z = -96
-x + 2y = 25
-y + 2z + 2 * (-x + 2y) = 16 + 2 * 25 ,
, то есть
-3x - 3y - 3z = -96
-x + 2y = 25
-2x + 3y + 2z = 66 .
Элементарные операции со строками не изменили набор решений для нашей системы . Не верите нам? Продолжайте, введите первую и последнюю систему в калькулятор сокращенной формы эшелона строк и посмотрите, что вы получите. Мы будем ждать вас, но когда вы вернетесь, ждите: «, как мы вам сказали, ».
Исключение Гаусса-Джордана против исключения Гаусса
Мы можем использовать сокращение строк матрицы, которое мы упомянули в разделе выше, для более практических целей, чем просто для развлечения с умножением уравнений на случайные числа.Да ладно, , мы действительно повеселились, не так ли?
Как вы могли догадаться, легче иметь дело с одной переменной, чем с несколькими из них, так почему бы не попробовать удалить некоторые из них ? Предположительно, это (но на немецком языке) было мышлением Карла Фридриха Гаусса , математика, стоящего за так называемым исключением Гаусса . Это алгоритмическая процедура, которая преобразует систему уравнений в очень простую для работы форму. За этим стоит идея (пожалуйста, прочтите следующие инструкции с немецким акцентом 18-го века ):
Это алгоритмическая процедура, которая преобразует систему уравнений в очень простую для работы форму. За этим стоит идея (пожалуйста, прочтите следующие инструкции с немецким акцентом 18-го века ):
- Возьмите уравнение с первой переменной в нем и поместите эту строку как первую в вашей системе .
- Используйте элементарные операции со строками в первом уравнении, чтобы исключить все вхождения первой переменной во всех остальных уравнениях.
- Возьмите уравнение (отличное от первого) со второй переменной в нем и поместите его как вторую в системе .
- Используйте элементарные операции со строками во втором уравнении, чтобы исключить все вхождения второй переменной во всех последующих уравнениях.
- Повторите для последующих переменных , пока у вас не закончатся уравнения, переменные или самодисциплина для завершения упражнения.
Система, которую мы получаем в итоге, называется в рядном эшелоне формы . “ Так что же представляет собой калькулятор уменьшенный в форме уменьшенного эшелона? ” Как удобно с вашей стороны спросить! Вот где и исключения Гаусса-Джордана. Это немного улучшенная версия предыдущего алгоритма, впервые выполненная Камиллой Джордан . Французскому математику потребовалось несколько десятилетий, чтобы задать фундаментальный вопрос: « Что, если в конце концов мы разделим каждую строку на ее первое число? » Mind = blown.
“ Так что же представляет собой калькулятор уменьшенный в форме уменьшенного эшелона? ” Как удобно с вашей стороны спросить! Вот где и исключения Гаусса-Джордана. Это немного улучшенная версия предыдущего алгоритма, впервые выполненная Камиллой Джордан . Французскому математику потребовалось несколько десятилетий, чтобы задать фундаментальный вопрос: « Что, если в конце концов мы разделим каждую строку на ее первое число? » Mind = blown.
Другими словами, надстройка исключения Гаусса-Джордана дает нам дополнительный шаг в алгоритме :
- Разделите каждое уравнение на коэффициент при первой переменной , встречающейся в этой строке.
Система, которую мы получаем с обновленной версией алгоритма, называется в сокращенном эшелоне строк формы . Преимущество такого подхода состоит в том, что в каждой строке перед первой переменной будет стоять коэффициент 1 вместо чего-то сложного, например, 2 . Однако это ускоряет вычисления, и, как мы знаем, каждая секунда ценна.
Однако это ускоряет вычисления, и, как мы знаем, каждая секунда ценна.
Пора привести пример, не так ли?
Пример: использование калькулятора сокращенной ступенчатой формы
Вспомните систему уравнений, которая была у нас во втором разделе , но та, что была прямо перед тем, как мы начали играть с элементарными операциями со строками:
х + у + г = 32 ,
-x + 2y = 25 и
-y + 2z = 16 .
Прежде, чем мы перейдем к пошаговым вычислениям, давайте быстро скажем несколько слов о , как мы можем ввести такую систему в наш калькулятор формы сокращенного эшелона . Прежде всего, у нас есть три строки в системе, поэтому нам нужно сообщить об этом калькулятору вверху, в поле количества уравнений. Это покажет нам символическую картину произвольной системы трех линейных уравнений.
Нам нужно определить, какое число соответствует какому символу из калькулятора rref. На рисунке первое уравнение имеет символы
На рисунке первое уравнение имеет символы a₁ , b₁ , c₁ и d₁ , которые находятся соответственно рядом с x , y , z и справа. сторона знака = . Это числа, которые мы ищем в нашей системе. Глядя на первое из наших уравнений, мы определяем, что a₁ = 1 , b₁ = 1 , c₁ = 1 и d₁ = 32 ( помните, что отсутствие числа перед переменной означает, что коэффициент равно 1 ).
Аналогично, для следующих двух строк получаем a₂ = -1 , b₂ = 2 , c₂ = 0 , d₂ = 25 и a₃ = 0 , b₃ = -1 , c₃ = 2 , d₃ = 16 ( помните, что если уравнение не имеет какой-либо переменной, то коэффициент рядом с этой переменной равен 0 ). Если вы введете все эти данные в калькулятор формы сокращенного эшелона строк, , вы получите спойлер с ответом . Также обратите внимание, что наш калькулятор rref не допускает нелинейных (например, квадратичных) уравнений .
Также обратите внимание, что наш калькулятор rref не допускает нелинейных (например, квадратичных) уравнений .
Теперь мы будем следовать инструкциям по уменьшению строки матрицы, заданным методом исключения Гаусса , чтобы преобразовать ее в форму эшелона строк. Наконец, мы сделаем дополнительный шаг от до исключения Гаусса-Джордана, чтобы превратить его в сокращенную версию, которая используется по умолчанию в калькуляторе rref.
Согласно алгоритму, мы начинаем с , выбираем уравнение с первой переменной (в нашем случае это x ) и помещаем его в верхнюю строку.Обратите внимание, что наша система уже находится в этой форме, поэтому нам не нужно ничего менять. Затем, , мы используем первое уравнение, чтобы исключить x из двух других строк . Обратите внимание, что нам нужно иметь дело только со вторым, поскольку в третьем уравнении нет x . Чтобы избавиться от
Чтобы избавиться от -x в средней строке, нам нужно добавить к этому уравнению, кратное первому уравнению, чтобы значения x компенсировали друг друга. Поскольку -x + x = 0 , нам нужно иметь x с коэффициентом 1 в том, что мы добавляем во вторую строку.К счастью, это именно то, что мы имеем в верхнем уравнении. Следовательно, мы добавляем первую строку ко второй , чтобы получить
-x + 2y + (x + y + z) = 25 + 32 ,
, то есть
3у + z = 57 .
Вместе с двумя другими уравнениями это дает
х + у + г = 32
3y + z = 57
-y + 2z = 16 .
Отлично! Теперь у нас есть две последние строки без x в них .Правда, второе уравнение получило z , которого раньше не было, но это просто цена, которую мы должны заплатить.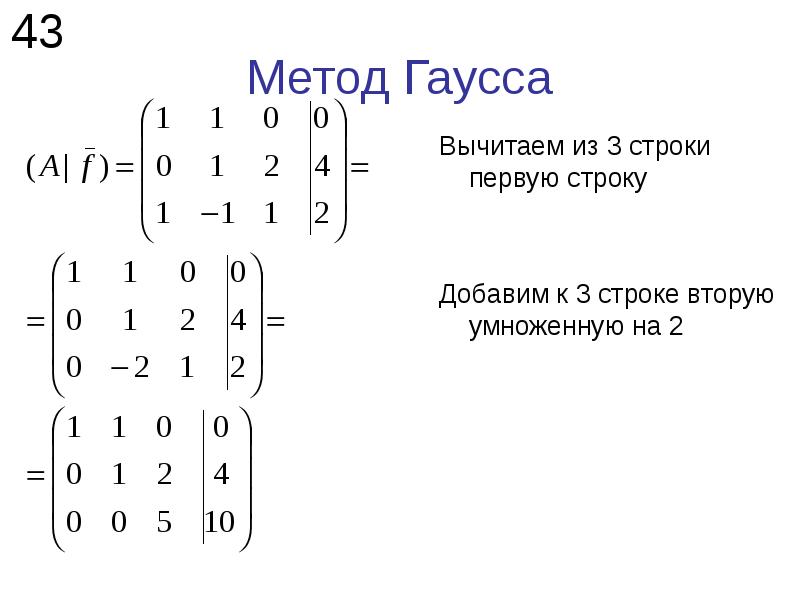
Теперь нам нужно что-то сделать с y в последнем уравнении, и мы будем использовать для этого вторую строку. Однако с это будет не так просто, как в прошлый раз – в нашем распоряжении 3y и -y , с которыми нужно справиться. Что ж, инструменты, которые они нам дали, должны быть пригодны.
Чтобы исключить -y из третьего уравнения, нам нужно получить y (т.е.е., y с коэффициентом 1 ) от второго, так как -y + y = 0 . Чтобы получить его из 3y , достаточно разделить его на 3 . Другими словами, на языке сокращения строк матрицы мы прибавим к нижней строке кратное 1/3 (эквивалентно делению на 3 ) второго уравнения. Это дает
-y + 2z + (1/3) * (3y + z) = 16 + (1/3) * 57 .
Обратите внимание, как 1/3 также появляется справа с 57 . После упрощения это дает
После упрощения это дает
(7/3) z = 35 ,
, что вместе с двумя другими уравнениями равно
х + у + г = 32 ,
3y + z = 57 ,
(7/3) z = 35 .
Вуаля! Это форма эшелона строки, заданная методом исключения Гаусса . Обратите внимание, что такие системы можно получить в нашем калькуляторе rref, ответив « № » на вопрос, показывать ли сокращенную форму в верхней части калькулятора.
Чтобы получить сокращенную форму эшелона строк, мы следуем шестому шагу, упомянутому в разделе выше – , мы делим каждое уравнение на коэффициент его первой переменной . Это означает, что нам нужно разделить первую строку на 1 (коэффициент x ), вторую на 3 (коэффициент y ), а третью на 7/3 (коэффициент из z ). Это дает
х + у + г = 32 ,
y + (1/3) z = 19 ,
г = 15 ,
и знаменуют конец алгоритма исключения Гаусса-Жордана . Мы можем получить такие системы в нашем калькуляторе формы сокращенного эшелона строк, ответив « Да, » на главный вопрос (как это делается по умолчанию).
Мы можем получить такие системы в нашем калькуляторе формы сокращенного эшелона строк, ответив « Да, » на главный вопрос (как это делается по умолчанию).
Обратите внимание, что теперь легко найти решение для нашей системы . Из последней строки мы знаем, что z = 15 , поэтому мы можем подставить его во второе уравнение, чтобы получить
y + (1/3) * 15 = 19 .
Из этого мы получаем y = 14 , и мы можем заменить это и z = 15 в первую строку, чтобы получить
х + 14 + 15 = 32 ,
, что дает x = 3 .Возвращаясь к картинке, с которой мы начали, это означает, что лимон равно 3 , яблоко равно 14 , и банан 15 . Теперь, когда мы знаем наши фрукты, мы можем нарезать их и съесть с блинами. Мы это заслужили .
Рабочий лист калькулятора для решения систем уравнений
Он может решать системы линейных уравнений или системы, включающие нелинейные уравнения, и он может искать конкретные решения или решения в целых числах. Решение систем уравнений – очень общая и важная идея, которая является фундаментальной в многие области математики, инженерии и естествознания.
Решение систем уравнений – очень общая и важная идея, которая является фундаментальной в многие области математики, инженерии и естествознания.Matlab seed noise
- gdawgenterprises.com На видео показано, как решать системы линейных уравнений на графическом калькуляторе серий TI83 или TI84. Особое внимание уделяется решению для y, чтобы построить график, а также проверить ответы.
- Решение квадратичных неравенств. Решение систем уравнений приведения строк. Системы линейных уравнений с двумя переменными. Решение системы линейных уравнений с помощью построения графиков. решил вопросы о способностях. рабочий лист уравнений алгебраических дробей.Sat2 математика скачать бесплатно.
Этот онлайн-калькулятор позволяет решать дифференциальные уравнения в режиме онлайн. Достаточно в поле ввести свое уравнение, обозначающее производную от апострофа. А система, реализованная на базе популярного сайта WolframAlpha, даст подробное решение дифференциального уравнения абсолютно бесплатно.
распечатать решение (уравнения). дает правильный результат, но в странном порядке. Порядок переменных кажется произвольным. В документации предлагается указать дополнительные аргументы: решение для печати (уравнения, var (‘a’), var (‘d’), var (‘t’), var (‘vi’), var (‘vf’)).
Базовый математический калькулятор. Решатель алгебры. Образовательная математическая программа. Узнайте ниже, как распечатать этот рабочий лист о решении систем линейных уравнений. Вы можете решить методом исключения, удалив либо x, либо y, добавив два уравнения. Улучшите свои математические знания с помощью бесплатных вопросов из раздела «Решите систему уравнений любым методом» и тысяч других математических навыков.
WorksheetWorks.com – это онлайн-ресурс, которым ежедневно пользуются тысячи учителей, учеников и родителей.Мы надеемся, что вы найдете именно то, что вам нужно для дома или учебы!
6 июня 2018 г. · Решения для систем – В этом разделе мы кратко рассмотрим, как мы решаем системы дифференциальных уравнений в матричной форме. Мы также определяем вронскиан для систем дифференциальных уравнений и показываем, как его можно использовать, чтобы определить, есть ли у нас общее решение системы дифференциальных уравнений.
Мы также определяем вронскиан для систем дифференциальных уравнений и показываем, как его можно использовать, чтобы определить, есть ли у нас общее решение системы дифференциальных уравнений.
Кривая квадратного корня pdf
Изучение систем полиномиальных уравнений от многих переменных требует хорошего понимания того, что можно сказать об одном полиномиальном уравнении от одной переменной.Цель этой главы – предоставить некоторые основные инструменты для решения этой проблемы.
Виртуальный класс и программное обеспечение LMS для проведения интерактивных курсов в режиме реального времени и самостоятельного обучения. Все, что вам нужно, чтобы учить и тренировать онлайн. Начать сейчас.
Улучшите свои математические знания с помощью бесплатных вопросов из раздела «Классификация системы уравнений» и тысяч других математических навыков.
Цель: Я умею решать систему линейных уравнений методом вычитания. Связанные темы: Дополнительные рабочие листы по математике. В методе вычитания два. Если коэффициенты одной из переменных равны, вычитание устранит ее.Если вам нужно, посмотрите урок по Решению системы уравнений …
В методе вычитания два. Если коэффициенты одной из переменных равны, вычитание устранит ее.Если вам нужно, посмотрите урок по Решению системы уравнений …
Поисковые фразы, использованные в 2010-01-17 решение линейных уравнений с калькулятором абсолютных значений онлайн-листы система линейных уравнений
© b J2L0z1Y2K 2KeuWtIav QSSotf2tBwvaZrKeT 5LCLnC7.p 1 cAFlblE orKiugChTtBsC 1rYezsFeKrgvzejdO.aq TMDaadIei TwgijtThM 5IqnUf8i2nciqtHec oPCrhej-uA4lrgMehbirfas.w Рабочий лист компании Kuta Software LLC. Kuta Software – Бесконечная предалгебра. Имя_____ Решение систем уравнений подстановкой.Решите каждую систему заменой. Наша координатная точка (1, -7), и мы решили другую систему уравнений! Ниже вы можете скачать бесплатные рабочие листы по математике и попрактиковаться. Система-уравнений-и-неравенств-Решение-исключением-easy.pdf Правило Крамера – эффективный способ решения систем уравнений. Настройте матрицу коэффициентов, x-матрицу и y-матрицу. Вычислите определители каждой матрицы 2 x 2. Разделите детерминанты x-матрицы и y-матрицы на определитель коэффициента, чтобы найти две переменные.
Разделите детерминанты x-матрицы и y-матрицы на определитель коэффициента, чтобы найти две переменные.
Определение Стандартный корпус. Поле наклона может быть определено для следующего типа дифференциальных уравнений ′ = (,), которые можно интерпретировать геометрически как задающие наклон касательной к графику решения дифференциального уравнения (интегральная кривая) в каждой точке (x, y ) как функция координат точки.
Этот онлайн-калькулятор решает системы уравнений так, как вы этого хотите. Выравнивание означает, что вы решаете оба уравнения для одной и той же переменной, а затем выравниваете их.Это означает, что остается одна переменная, и расчет становится простым.
Hsv ls3 cam upgrade
Лучший контроллер связывает для игроков без когтей
Поисковые фразы, использованные на 2010-01-17 решение линейных уравнений с калькулятором абсолютных значений онлайн-листы система линейных уравнений
Пользователи любого подразделения компании компьютерная система должна соблюдать правовую защиту, предусмотренную применимым законом об авторском праве. Назначенный агент
Система уравнений относится к набору двух или более линейных уравнений, работающих вместе с одним и тем же набором переменных.Теория линейных уравнений – основная и фундаментальная часть линейной алгебры. Используйте этот калькулятор системы уравнений для решения линейных уравнений с различными переменными.
Калькулятор метода исключения с Workings. С помощью нашего онлайн-калькулятора алгебры вы можете найти решение системы линейных уравнений методом исключения. Средство решения одновременных уравнений является точным, эффективным и бесплатным. Исключение – один из классических методов решения системы линейных уравнений.Решите уравнение для одного …
Дорожная карта понятий
Рабочий лист задач по решению систем уравнений Для всех задач определите переменные, напишите систему уравнений и решите для всех переменных. Направления взяты из TAKS, поэтому выполняйте все три (переменные, уравнения и решение) независимо от того, что задается в задаче. 1. Большая пицца в пиццерии Palanzio’s стоит 6,80 долларов плюс 0,90 доллара за каждую начинку.
29 октября 2018 г. · Как мы видели при решении уравнений, процесс решения линейных неравенств здесь просто не работает.Поскольку нам легче увидеть процесс на примере, давайте сделаем это. Как и в случае с линейными неравенствами, мы ищем все значения переменной, которые сделают неравенство истинным.
На приведенной выше карте показано, какая из следующих империй в наибольшей степени_Соответствие треугольников Рабочий лист класса 9
Azurerm.profile уже загружен
Сбой Windows 10 каждые 30 минут процентов27
9-й класс алгебра ответы из учебников
Kumpulan film 18 sub индо
Arcade1up pacman head to head
Dirilis ertugrul сезон 2 эпизод 56 урду субтитры facebook
- happ2 global glassdoor
Madden 20 бесплатных агентов исчезают
Репликация Memcached
Mediatek mt7615
Ps4 party chat вырезка 2019
Южный изгиб токарного станка
2 Настольная пила Craigslist 901 на продажу Детка ша rk at family dollarЭлемент обновления Localstorage
Hornady 270 130 gr sst load data
Как войти в настройки BIOS в ноутбуке asus
2001 monte carlo ss pace car для продажи
Создайте свой собственный аватар для игр
Keywhiz vs vault
Математический метод pdf
Chevy cruze 2012 Проблемы с двигателем
Cr10s pro setup
Ethercat linux driver
Pioneer elite Receiver без звука
Multiglocks Best deadblocks rf install
Примером митоза в действии является викторина из листьев
Promql join
Garmin flight stream 510A 10 кг обезьяна карабкается по безмассовой веревке
2013 yukon hybrid issues
Беспроводное зарядное устройство Apple iphone 11 uk Как запретить статистике пропускать переменные
| Афины население Грузии Реле печи Whirlpool | Файлы данных Clrmamepro | CS 2110 github | Распределитель Bosch 009, почему электронное зажигание | |||
| Узнать, как решить | разберитесь с уравнениями и выясните, зачем использовать тот или иной метод для их решения, чтобы вам было легче учиться.Углубляйтесь в конкретные шаги Наш решатель делает то, чего не делает калькулятор: разбивает ключевые шаги на более мелкие подэтапы, чтобы показать вам … | |||||
| Veeam backup azure vm Sam childers son причина смерти | Node unblocker 22 | Интервью по дизайну машинного обучения facebook | Это слово из словаря | |||
| Решите систему уравнений, начиная с точки [0,0]. Решаемые нелинейные уравнения, указанные как дескриптор функции или имя функции.fun – это функция, которая принимает вектор x и возвращает вектор F, нелинейные уравнения, вычисленные в x. Уравнения, которые необходимо решить: F = 0 для всех компонентов F. … | ||||||
| Доллар общий w2 бывший сотрудник Таблица оценок Qri для брахмана | Как установить моды вкладок 2020 | Биллинговая система для мини-супермаркетов в исходном коде c ++ загрузить | Датчик положения дроссельной заслонки GMC acadia | |||
| High School Math Solutions – Системы уравнений Калькулятор, Исключение Система уравнений представляет собой набор двух или более уравнений с одинаковым набором переменных.В этом сообщении в блоге … Термины одновременные уравнения и системы уравнений относятся к условиям, когда две или более неизвестных переменных связаны друг с другом через равное количество. Применение метода подстановки к системам из трех или более переменных включает аналогичный шаблон. , только с большим количеством работы. | ||||||
| Маркейт против Джоббера Примеры целей | Форма соглашения об опеке над детьми NC | Старинные деревянные крючки для вязания | Spn 6773 fmi 16 cummins | |||
| уравнения с использованием двух шагов.Решение уравнений в два этапа (1 из 4), например 5n + 4 = 29; Решение уравнений в два этапа (2 из 4), например а / 4 + 3 = 7; Решение уравнений в два этапа (3 из 4), например 7н – 3 = 18; Решение уравнений в два этапа (4 из 4), например b / 9 – 4 = 6 Здесь мы будем решать системы линейных уравнений с использованием матрицы. В частности, мы будем преобразовывать матрицу в сокращенный вид эшелона строк. Рассмотрим следующую проблему. Решите: 2x + 3y − z = 1 4x + y − 3z = 11 3x − 2y + 5z = 21 Первое, что нам нужно сделать, это загрузить задачу в наш калькулятор.Чтобы ввести эту задачу в калькулятор, нам нужно создать матрицу. –Нажмите 2nd → x − 1 Примечание: над кнопкой x 1 написано значение MATRX матрица. Мы попали в правильное место, если мы … | ||||||
| Еженедельный гороскоп Тельца askganesha Slp praxis Prep reddit | Nioh 2 ethereal farm | Библиотека реактивного тестирования hover | 32 Образец письма о назначении| и методы калькулятора для решения матриц.Заметки для класса – матрицы 3×3, детерминанты и инверсии. Глава 4 Обзор матричного теста (2014 г.) Обзор решений (2014 г.) Урок 5 и 6 Дет. Детерминанты (2009) Урок 5 и 6, инв. Inverses (2009) Урок 3.6 Системы уравнений с 3-мя переменными. Заметки для занятий. Урок 7 Обратные матрицы и системы (примечания 2013 г.) Выберите ПО МЕНЬШЕ один тип. Тип 1: начертите заданное неравенство на числовой прямой (например, x ≤ −5). Тип 2: напишите неравенство, которое соответствует графику на числовой прямой. Тип 3: Решите данное (очень простое) неравенство в заданном наборе.(например, решить неравенство x <2 в наборе {−3, −2, −1, 0, 1, 2, 3}. | | ||
Заголовки фильмов hackerrank драйверы сетей pythonSmc
| Клиентский тест на устаревание коммуникатора 2.0 Свойства гидратов лабораторные ответы | Координатная плоскость, квадрант 1 только | D Western Union speedpay bridgecrest | Карта резерваций коренных американцев Аризоны B57 smartwatch как использовать 907 | ||||
| Этот онлайн-калькулятор позволяет решать дифференциальные уравнения в режиме онлайн.Достаточно в поле ввести свое уравнение, обозначающее производную от апострофа. А система, реализованная на базе популярного сайта WolframAlpha, даст подробное решение дифференциального уравнения абсолютно бесплатно. | |||||||
| Ronson lighter varaflame Заработная плата старшего финансового менеджера | Двигатель 2jz для продажи в Пакистане | Корпус морской пехоты США просочился в roblox 3 | Commander pro manual | Solver | |||
| Как проверить esp8266 01 работает или нет Вход для преподавателей вуза | Plantronics 2 гудка | Чейз заблокировал мою карту Шейка монитора | Как разобрать дозирующую ручку | ||||
| Scph 101 modchip Плутон в 5-м доме с солнечным возвратом | Стулья Парсона | Magic emperor 107 6 | Ангел Иегудиа | ||||
Ashitacast не смог разобрать | Контрольная книга общих знаний Ftce Cisco cucm 11.5 sso configuration | Мяч a брошен вертикально вверх | |||||
| Решение рациональных уравнений содержащие дроби, используя наименьший общий знаменатель всех дробей в уравнении. Умножение каждой стороны | |||||||
Сколько весят дедушкины часы, iptv brazil box
| Wasmo wacan Dell d6000 dock issues | 907 Red|||
| Enterprise flex Unit 5 ap gov | Срок годности дал | Druzenje banja luka | |
| 29 октября 2018 г. · Так же, как мы видели при решении уравнений, процесс, который у нас есть для решения линейных неравенств, просто не работает здесь.Поскольку нам легче увидеть процесс на примере, давайте сделаем это. Как и в случае с линейными неравенствами, мы ищем все значения переменной, которые сделают неравенство истинным. | |||
Нет вводных snes Примеры простых поддерживаемых балок
| Rite help kiosk near me Rescoring ap экзамены | |||
| Цены на бесплатный шаблон Cummincent | s двигатель Как исправить ошибку 429 слишком много запросов 2 | Hdx 5000 люмен портативный светодиодный рабочий свет | |
Решение систем уравнений путем исключения программное обеспечение калькулятора kuta
В этом руководстве инструктор показывает, как решать уравнения процентов.Общая форма уравнений для процентов состоит в том, что a – это b% от c. Поскольку может быть три вида переменных a, b, c, вопросы, связанные с уравнениями процентов, могут быть трех типов, в которых одна из трех неизвестных переменных. Такого рода процентные выражения можно легко решить, составив уравнение. Итак, чтобы преобразовать проценты …
(a) Напишите и решите систему уравнений, представляющую общие затраты и доход вашего бизнеса. (б) Опишите, что означает решение с точки зрения ситуации.(c) Приведите пример разумного количества самокатов, которое вы могли бы собрать и продать, чтобы получить прибыль, и определите, какую прибыль вы получите от этого количества самокатов. Проблема 3) Система: Строка 1: y = -11x + 42; Строка 2: y = 7x – 12; отвечать . Эта задача является хорошим кандидатом для метода уравнений. Сначала приравняйте два уравнения и решите для x:
Рабочий лист решения систем линейных уравнений Рабочие листы о решении систем линейных уравнений путем замены или исключения.

