Решить систему методом зейделя онлайн. Метод зейделя решения слау
1. Преобразовать систему к виду одним из описанных способов.
2. Задать начальное приближение решения произвольно или положить , а также малое положительное число (точность). Положить .
3. Произвести расчеты по формуле (1)или (2) и найти .
(1)
4. Если выполнено условие окончания , процесс завершить и в качестве приближенного решения задачи принять . Иначе положить и перейти к пункту 3.
Решение систем нелинейных уравнений (СНУ).
Запишем систему n нелинейных уравнений с n неизвестными (СНУ) в общем виде:
f 1 (x 1 , x 2 , …, x n) = 0
f 2 (x 1 , x 2 , …, x n) = 0 (5.1)
f n (x 1 , x 2 , …, x n) = 0
Эту систему можно записать в компактной, операторной форме:
вектор-функция
вектор неизвестных
Решением системы называется набор значений
,(векторX *),
при которых все функции f i
равны 0 (система (5.
1) обращается в
тождество.)
СНУ могут иметь единственное решение, множество решений или вообще не иметь его. Поэтому численное решение СНУ проводят в два этапа:
1 этап – отделение решений.
2 этап – уточнение всех или только нужных решений.
Отделить решения – значит установить количество решений, определить приближенные значения каждого из них или указать область, в которой решение существует и является единственным.
Задача отделения решений достаточно просто решается только для системы двух уравнений с двумя неизвестными.
f 1 (x 1 , x 2) = 0
f 2 (x 1 , x 2) = 0
Для этого необходимо в координатах (x 1 , x 2) построить кривые
f 1 (x 1 ,х 2) = 0, f 2 (x 1 ,х 2) = 0.
Точки пересечения этих кривых являются решениями системы
Имеется два решения.
D 1 – область существования первого решения.
D 1 = {a 1
Графическое отделение решений СНУ.
Для систем с большим числом неизвестных (n 3) удовлетворительных общих методов определения области существования решения нет.
Отделение решений позволяет:
Выявить число решений и область существования каждого из них.
Проанализировать возможность применения выбранного метода решения СНУ в каждой области.
Выбрать начальное приближение решения X (0) из области его существования, так что X (0) D.
При отсутствии информации об области существования решения СНУ выбор начального приближения X (0) проводиться методом проб и ошибок (методом “тыка”).
Постановка задачи.
Требуется
решить систему нелинейных уравнений
.
Убедиться в существовании решения и количестве корней, а также выбрать нулевое приближение в случае системы двух уравнений с двумя неизвестными можно, построив графики функций в удобных координатах. В случае сложных функций можно посмотреть поведение аппроксимирующих их полиномов. Для трех и более неизвестных, а также для комплексных корней, удовлетворительных способов подбора начального приближения нет.
Метод простых итераций.
Как и в случае одного уравнения, метод простых итераций заключается в замене исходной системы уравнений
f 1 (x 1 , x 2 , …, x n) = 0
f 2 (x 1 , x 2 , …, x n) = 0
f n (x 1 , x 2 , …, x n) = 0 (5.1)
эквивалентной системой X=Φ(X) –(5.3) и построении итерационной последовательности
(5.4)-X (k) = Φ(X (k -1)) , где k=1,2,3,… – номер итерации,которая при k→∞ сходится к точному решению.
Здесь
– итерирующая вектор-функция, X (0)
D
– начальное приближение решения.
В развернутом виде формула итерационного процесса (выражение для вычисления очередного k-го приближения решения) имеет вид:
x i. (k) = φ i (x 1 (k-1) , x 2 (k-1) , … , x n (k-1)), .(5.5)
Условие окончания расчета
δ≤ε (5.6)
где ε заданная точность решения;
δ = (5.7)
Итерационный процесс (5.5) сходиться к точному решению, если в окрестности решения соблюдаются условия сходимости:
Таким образом, для уточнения решения СНУ методом простых итераций нужно найти такое эквивалентное преобразование (5.1) в (5.3), чтобы в области существования решения выполнялись условия (5.9) или (5.10).
В простейшем случае эквивалентную систему можно получать как.
Метод Зейделя (второе название – Гаусса-Зейделя) – это классический интернациональный метод, при помощи которого можно решать различные системы Сейчас мы расскажем об этом более детально.
Суть работы
Данный способ является своеобразной упрощенной модификацией метода Якоби.
Инновация состоит в том, что новое значение (і) используется сразу же после получения, а не после очередной итерации. Помимо этого, четко определены условия сходимости и окончания, нарушение которых приведет к неправильному ответу уравнения. Метод Зейделя, пример которого мы предоставили на картинке, не только упрощает процесс решения, но также ускоряет его. Поэтому он активно используется программистами для создания и решения сложных систем.
Метод Зейделя. “Паскаль”
Ни одна программист не обходится без математических формул и уравнений. А это значит, что метод Зейделя активно используется в программе “Паскаль” для получения опыта роботы с базовыми элементами. Выглядит все довольно-таки просто: в листе программы создается новый документ, с самого начала вводится условие уравнения и его границы, затем объясняются дополнительные сменные элементы (при условии их наличия), после этого прописывается проверка на совместимость. Если она положительна, то выводится сам алгоритм решения, а уже потом вывод могут включать несколько этапов решения, каждая часть которого имеет свой алгоритм, обязательные составные, сменные элементы и базовые формулы.
Все это записывается исключительно на английском языке, без возможных аналогов. Решение уравнения будет выводиться в виде готовой формулы или числа после сохранения всех данных.
“С++”
Метод Зейделя также широко используется в программе “С++”, но здесь все совсем иначе, чем в “Паскале”. Уравнение в “С++” начинается не с условия всей задачи, а с условия окончания, которое прописывается в три-четыре этапа с конечным выводом результата. Далее прописывается сам ход решения при помощи данного метода, детально описывая все неизвестные, после чего выводится формула для того, чтобы доказать равенство между двумя результатами уравнения. Условием есть то, что каждое значение предыдущего является необходимым для решения последующего. Учетные записи здесь также ведутся на английском языке, который заменить невозможно. “С++” значительно сложнее “Паскаля”, поэтому, не имея базовых знаний, ее не следует использовать изначально.
Подведем итоги
Итак, метод Зейделя – это специальный способ, благодаря которому можно решать системы линейных уравнений любой сложности.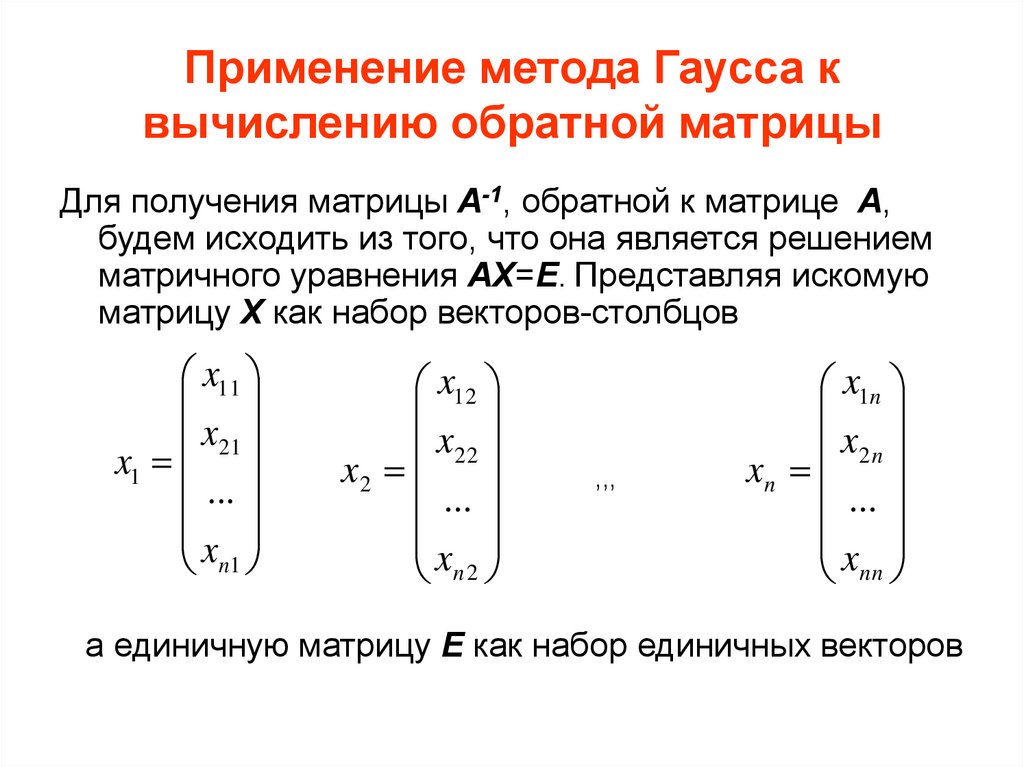
Чаще всего он является базовым для таких программ, как “Паскаль” и “С++”. Это своеобразная улучшенная модификация метода Якоби, которая исключает вариант использования дополнительных формул, но при этом имеет четкие условия сходимости и окончания. Строго установленные критерии упрощают весь процесс работы, так как в случае невыполнения одного из условий программа, будь то или “Паскаль”, или “С++”, просто-напросто откажется от дальнейшего решения задачи.
Одним из самых распространенных итерационных методов, отличающийся простотой и легкостью программирования, является метод Гаусса –Зейделя .
Проиллюстрируем сначала этот метод па примере решения системы
Предположим, что диагональные элементы а 11, а 22, а 33отличны от нуля (в противном случае можно переставить уравнения). Выразим неизвестные х 1, х 2и х 3 соответственно из первого, второго и третьего уравнений системы (2.27):
(2.28)
(2.29)
(2.30)
Зададим некоторые начальные (нулевые) приближения значений неизвестных: Подставляя эти значения в правую часть выражения (2.
Используя это значение для x 1 и приближение для х3 , находим из (2.29) первое приближение для х2 :
И наконец, используя вычисленные значения находим с помощью выражения (2.30) первое приближение для х 3:
На этом заканчивается первая итерация решения системы (2.28) – (2.30). Теперь с помощью значений х 1(1), х 2(1)и х 3(1)можно таким же способом провести вторую итерацию, в результате которой будут найдены вторые приближения к решению:
Приближение с номером k можно вычислить, зная приближение с номером k – 1, как
Итерационный процесс продолжается до тех пор, пока значения х 1(k), х 2(k)и х 3(k)не станут близкими с заданной погрешностью к значениям х 1(k-1), х 2(k-1)и х 3(k-1).
Пример.
Решить с помощью метода Гаусса – Зейделя следующую систему уравнений:
Легко проверить, что решение данной системы следующее: х 1 = х 2 = х
Решение . Выразим неизвестные х 1, х 2и х 3соответственно из первого, второго и третьего уравнений:
В качестве начального приближения (как это обычно делается) примем х 1= 0, х 2 = 0, х 3 = 0. Найдем новые приближения неизвестных:
Аналогично вычислим следующие приближения:
Итерационный процесс можно продолжать до получения малой разности между значениями неизвестных в двух последовательных итерациях.
Рассмотрим теперь систему п линейных уравнений с п неизвестными. Запишем ее в виде
Здесь также будем предполагать, что все диагональные элементы отличны от нуля. Тогда в соответствии с методом Гаусса – Зейделя
Итерационный процесс продолжается до тех пор, пока все значения не станут близкими к , т.
е. критерием завершения итераций является одно из условий (2.21) – (2.24).
Для сходимости итерационного процесса (2.31) достаточно, чтобы модули диагональных коэффициентов для каждого уравнения системы были не меньше сумм модулей всех остальных коэффициентов (преобладание диагональных элементов):
(2.32)
При этом хотя бы для одного уравнения неравенство должно выполняться строго. Эти условия являются достаточными для сходимости метода, но они не являются необходимыми, т.е. для некоторых систем итерации сходятся и при нарушении условий (2.32).
Алгоритм решения системы п линейных уравнений методом Гаусса – Зейделя представлен на рис.2.6. В качестве исходных данных вводят п, коэффициенты и правые части уравнений системы, погрешность ε, максимально допустимое число итераций М, а также начальные приближения переменных xi (i =1,2,…,n ).Отметим, что начальные приближения можно не вводить в компьютер, а полагать их равными некоторым значениям (например, нулю).
Критерием завершения итераций выбрано условие (2.22), в котором через δ обозначена максимальная абсолютная величина разности и :
Для удобства чтения структурограммы объясним другие обозначения: k – порядковый номер итерации; i – номер уравнения, а также переменного, которое вычисляется в соответствующем цикле; j – номер члена вида или в правой части соотношения (2.31). Итерационный процесс прекращается либо при δ , либо при k = М. В последнем случае итерации не сходятся, о чем выдается сообщение. Для завершения цикла, реализующего итерационный процесс, используется переменная l , которая принимает значения 0, 1 и 2, соответственно, при продолжении итераций, при выполнении условия δ и при выполнении условия k = М .
Рис. 2.6. Алгоритм решения системы n линейных уравнений методом Гаусса–Зейделя
Отчет по
ЧИСЛЕНННЫМ МЕТОДАМ
Выполнил: студент
Сулейманова Д.
И.
Проверила: доцент каф. хим.
кибернетики Кошкина Л.Ю.
Казань, 2012
Тема 1. «Численное решение систем линейных алгебраических уравнений». 3
Постановка задачи. 3
Прямые (точные) методы.. 3-4
Итерационные методы.. 5
Листинг программ. 4
Результаты.. 5
Выводы.. 5
Список литературы.. 5
ТЕМА 2. «ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ»
Постановка задачи
Решить систему линейных алгебраических уравнений:
| 0,5 | 1,7 | 0,3 | -0,24 | |
| 1,6 | 1,5 | -2,3 | 4,3 | |
| 3,7 | -2,5 | 3,2 | 6,5 |
0,5х 1 +1,7х 2 +0,3х 3 =-0,24
1,6х 1 +1,5х 2 -2,3х 3 =4,3
3,7х 1 -2,5х 2 +3,2х 3 =6,5
Для решения уравнения использовали следующие методы:
1. метод обратной матрицы,
2. метод Крамера,
3.
метод Гаусса,
4. метод простых итераций,
5. метод Гаусса-Зейделя.
Решение:
Прямые (точные) методы
1) Метод обратной матрицы: (х=А -1 *В – формула данного метода, где В-вектор свободных членов, А -1 -обратная функция)
А) Для реализации данного метода в электронных таблицах воспользовались математической функцией =МОБР(А1:С3) для определения коэффициента А:
0,3
Ввод n, a, b
Прямой ход
Обратный ход
Выбор главного элемента и перестановка уравнений
1) Метод простых итераций:
А) Выразим х 1 , х 2 , х 3 из уравнений главного определителя, тогда получим:
x 1 =(b 1 -a 12 x 2 -a 13 x 3)/a 11
x 2 =(b 2 -a 21 x 1 -a 23 x 3)/a 22
x 3 =(b 3 -a 31 x 1 -a 32 x 2)/a 33
Б) Зададим начальное (нулевое) приближение x 1 (0) , x 2 (0) , x 3 (0) .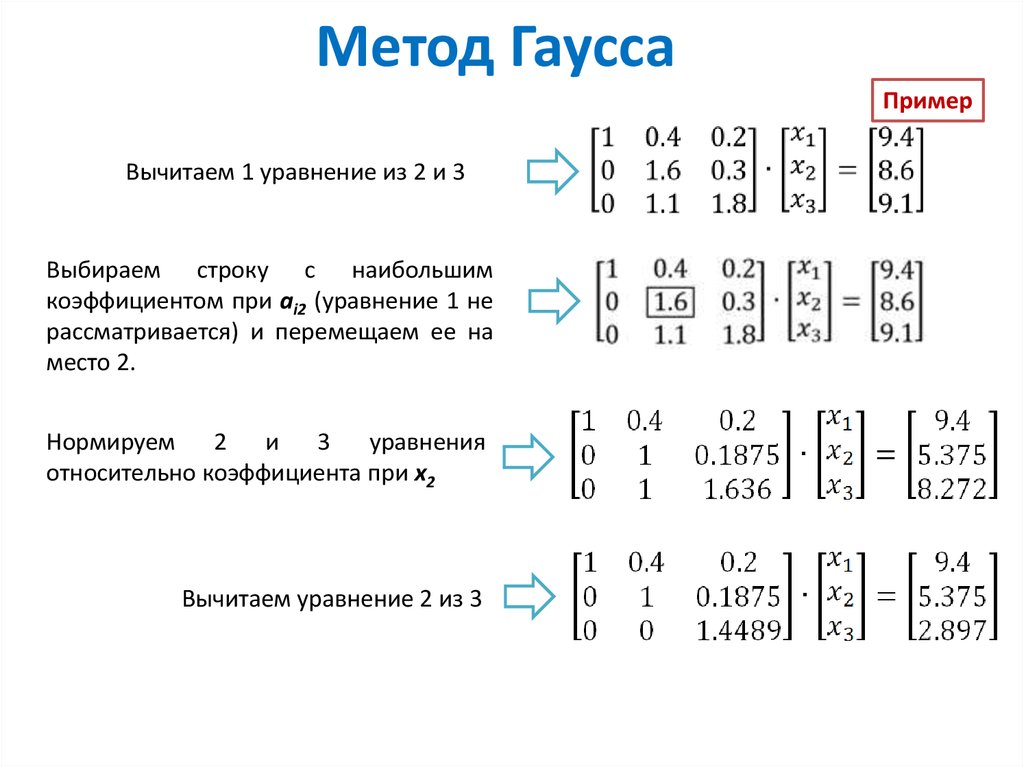
Подставляя их, получаем новое приближение.
В) Обозначим k-номер итерации, тогда для n уравнений итерационные формулы можно записать так:
x i (k) = (k-1))
Итерации проводятся до тех пор, пока не будет выполнено условие
|x i (k)-x i (k-1) |
2) Метод Гаусса-Зейделя:
Этот метод представляет собой модификацию метода простых итераций, когда на k-той итерации при j
x i (k) = (k) – (k-1))
Итерационный процесс продолжается до тех пор, пока не будет выполнено условие
|x i (k)-x i (k-1) |
Если условие не выполняется, итерации повторяются, приняв x i (k-1) = x i (k)
Алгоритм метода Гаусса-Зейделя
n-количество уравнений; e-точность; a(n,n)-массив коэффициентов; b(n)-массив свободных членов; x(n)-массив решения. Вводится начальное приближение x(n).
Листинг программ
Sub metod_g()
Dim a(1 To 3, 1 To 3)
a(i, j) = Worksheets(“Лист2”).Cells(i, j).
Value
b(i) = Worksheets(“Лист2”).Cells(i, 5).Value
For k = 1 To n – 1
For i = k + 1 To n
If Abs(a(i, k)) > Abs(a(g, k)) Then g = i
z = a(g, j): a(g, j) = a(k, j): a(k, j) = z
z = b(g): b(g) = b(k): b(k) = z
For i = k + 1 To n
m = a(i, k) / a(k, k)
For j = k + 1 To n
a(i, j) = a(i, j) – m * a(k, j)
b(i) = b(i) – m * b(k)
x(n) = b(n) / a(n, n)
For i = n – 1 To 1 Step -1
For j = i + 1 To n
s = s + a(i, j) * x(j)
x(i) = (b(i) – s) / a(i, i)
Worksheets(“Лист2”).Cells(i, 9).Value = x(i)
Sub MPI_SLAY()
Dim a(1 To 3, 1 To 3)
x2 = (b(2) – a(2, 1) * x10 – a(2, 3) * x30) / a(2, 2)
x3 = (b(3) – a(3, 1) * x10 – a(3, 2) * x20) / a(3, 3)
Loop While c > e
With Worksheets(“Лист2”)
Range(“J1”).Value = x1
Range(“J2”).Value = x2
Range(“J3”).Value = x3
Range(“J5”).Value = k
Sub GausZeid()
Dim a(1 To 3, 1 To 3)
a(i, j) = Worksheets(“Лист3”).
Cells(i, j).Value
b(i) = Worksheets(“Лист3”).Cells(i, 5).Value
x10 = 0: x20 = 0: x30 = 0
x1 = (b(1) – a(1, 2) * x20 – a(1, 3) * x30) / a(1, 1)
x2 = (b(2) – a(2, 1) * x1 – a(2, 3) * x30) / a(2, 2)
x3 = (b(3) – a(3, 1) * x1 – a(3, 2) * x2) / a(3, 3)
c = Abs(x1 – x10) + Abs(x2 – x20) + Abs(x3 – x30)
Loop While c > e
With Worksheets(“Лист2”)
Range(“K1”).Value = x1
Range(“K2”).Value = x2
Range(“K3”).Value = x3
Range(“K5”).Value = k
Для запуска программ нажать на кнопку или на Run .
Полученный результат находится на Листе 2.
Результаты
Выводы
Системы линейных алгебраических уравнений можно решать как с помощью прямых, так и итерационных методов. Для систем уравнений средней размерности чаще используют прямые методы.
Итерационные методы применяют главным образом для решения задач большой размерности, когда использование прямых методов невозможно из-за ограничений в доступной оперативной памяти ЭВМ или из-за необходимости выполнения чрезмерно большого числа арифметических операций.
В данной работе мы рассмотрели 5 методов решения линейных алгебраических уравнений: метод обратной матрицы, Крамера, Гаусса, простой итерации и Гаусса-Зейделя. Первые 3 метода составляют группу прямых методов. Это аналитические методы, в них отсутствует погрешность метода, но погрешность вычислений неизбежна. Тем не менее, методы обратной матрицы и Крамера достаточно просты в алгоритме, тем более нами было найдено решение трехмерной матрицы (небольшая размерность), значения неизвестных сошлись. Что касается метода Гаусса, алгоритм данного метода достаточно громоздкий. Каждая следующая формула вычисления коэффициентов при преобразовании матрицы содержит результат предыдущей формулы, а значит и ее ошибку при вычислении. Наибольшее влияние на эту ошибку оказывает величина знаменателя (коэффициенты главной диагонали) – она не должна быть равна 0 и малой по абсолютной величине. В нашем случае таких предпосылок нет, метод Гаусса был осуществлен с выбором главного элемента, что дает малые невязки.
Онлайн калькуляторы для решения математики
Рубрики
Математика
Онлайн калькуляторы по высшей математике
Здесь представлены онлайн калькуляторы для решения различных задач по математике. Охватываются такие области математики, как интегралы, производные, пределы, операции с матрицами, задачи по аналитической геометрии, построение графиков онлайн и т. д..
В разделе «Онлайн сервисы» вам предоставлена возможность решать онлайн интегралы, брать производные, пределы, считать ряды практически для любых функций. Решение задач производится автоматически программой и является быстрым и абсолютно бесплатным.
Все калькуляторы выдают ответ с подробным решением. Считайте легко, быстро и надежно вместе с нами.
С помощью онлайн сервиса получите правильный ответ и проверьте своё решение!
- Правила ввода функций и констант Инженерный калькулятор Математический анализ
- Вычислить неопределенный интеграл Вычислить определенный интеграл Вычислить двойной интеграл Вычислить производную Вычислить предел функции Вычислить сумму ряда
- Найти определитель матрицы Найти обратную матрицу
- Решение дифференциальных уравнений Решение квадратных уравнений Решение системы линейных уравнений (метод подстановки) Решение системы линейных уравнений (метод Гаусса) Решение системы линейных уравнений (метод Крамера) Решение системы линейных уравнений (матричный метод)
- Уравнение прямой по двум точкам Уравнение плоскости по трем точкам Расстояние между точкой и прямой Расстояние между точкой и плоскостью
- Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Проверить, образуют ли вектора базис Разложить вектор по базису
- Построить график онлайн
Закажите работу
Компания Matematikam.
ru предлагает вам свои услуги по решению контрольных работ по математике, физике, теории вероятности!
Контрольные работы на заказ!
Только у нас вы найдете одновременно низкие цены, короткие сроки и высокое качество исполнения контрольных работ на заказ. Мы решаем контрольные работы любой сложности. Наши специалисты имеют большой опыт и сердняя оценка, выставляемая клиентами за выполненные работы, составляет 9.75 баллов.
Заказать работу по физике
Закажите контрольную по физике или математике на Matematikam. ru и вы получите отличный сервис, полное сопровождение заказа, бесплатные доработки и ответы по работе на любые ваши вопросы и уточнения. Закажите контрольную работу у нас и вы убедитесь — как просто и безопасно может быть получение решения сложной и трудоемкой работы!
Здесь представлены онлайн калькуляторы для решения различных задач по математике. Охватываются такие области математики, как интегралы, производные, пределы, операции с матрицами, задачи по аналитической геометрии, построение графиков онлайн и т.
д..
В разделе «Онлайн сервисы» вам предоставлена возможность решать онлайн интегралы, брать производные, пределы, считать ряды практически для любых функций. Решение задач производится автоматически программой и является быстрым и абсолютно бесплатным.
Все калькуляторы выдают ответ с подробным решением. Считайте легко, быстро и надежно вместе с нами.
С помощью онлайн сервиса получите правильный ответ и проверьте своё решение!
- Правила ввода функций и констант Инженерный калькулятор Математический анализ
- Вычислить неопределенный интеграл Вычислить определенный интеграл Вычислить двойной интеграл Вычислить производную Вычислить предел функции Вычислить сумму ряда
- Найти определитель матрицы Найти обратную матрицу
- Решение дифференциальных уравнений Решение квадратных уравнений Решение системы линейных уравнений (метод подстановки) Решение системы линейных уравнений (метод Гаусса) Решение системы линейных уравнений (метод Крамера) Решение системы линейных уравнений (матричный метод)
- Уравнение прямой по двум точкам Уравнение плоскости по трем точкам Расстояние между точкой и прямой Расстояние между точкой и плоскостью
- Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Проверить, образуют ли вектора базис Разложить вектор по базису
- Построить график онлайн
Решение системы линейных уравнений метод подстановки.
Matematikam. ru
02.01.2019 11:07:37
2019-01-02 11:07:37
Источники:
Https://matematikam. ru/calculate-online/
Онлайн-калькулятор. Примеры решений задач по математике » /> » /> .keyword { color: red; }
Онлайн калькуляторы по высшей математикеДля преобразования сложных математических вычислений и оформления их результатов можно использовать этот калькулятор.
Примеры решений
Теория вероятностей и математическая статистика
Информатика
Высшая математика
Линейная алгебра
Методы решения СЛАУ
Аналитическая геометрия
Математический сервис
Методы оптимизации
Линейное программирование
Методы решения задачи линейного программирования
Задачи линейного программирования
Транспортная задача
Целочисленное программирование
Динамическое программирование
Нелинейное программирование
Сетевое планирование
Исследование операций
Модели теории игр
Системы и модели массового обслуживания
Статистика
Эконометрика
Все права защищены и охраняются законом.
Copyright © ООО Новый семестр 2006-2021
Информация, размещенная на сервисе Калькуляторы, относится к информационной продукции, допускаемой к обороту для детей, достигших возраста двенадцати лет в соответствии со ст. 8 ФЗ №436 от 29.12.2010 г.
Методы оптимизации.
Math. semestr. ru
29.08.2018 17:07:45
2018-08-29 17:07:45
Источники:
Https://math. semestr. ru/example. php
Онлайн калькуляторы по математике » /> » /> .keyword { color: red; }
Онлайн калькуляторы по высшей математике«Онлайн калькулятор» — это инновационная разработка нашей команды, которая безустанно работает для облегчения вашего процесса обучения. Используя такой калькулятор, решение задач онлайн будет осуществляться быстро и легко, ведь он способен помочь значительно больше, чем вы ожидаете. Математика – это предмет, который легко дается к освоению далеко не каждому ребенку. Но теперь онлайн решение уравнений, неравенств и интегралов не будет вызывать у ученика панику и страх сложного задания, ведь ребенку будет необходимо запомнить суть решения, а сложные вычисления за него сделает наш онлайн калькулятор.
Пользуются – ли нашим нововведением учителя? Безусловно, ведь такой решатель задач значительно экономит время педагога на подготовку к урокам. И абсолютно верно, если учитель позволит себе уделить время личным делам, а калькулятор, поработает вместо него. Если вы все еще сомневаетесь – попробуйте на собственном опыте, и возможности превысят ваши ожидания: действия с матрицами, статистика, теория вероятностей, действия с дробями, комбинаторика и другое. Онлайн калькулятор по школьной и высшей математике — это незаменимая вещь для каждого учащегося, не зависимо от уровня учебного заведения!
Действия с дробями
Калькулятор дробей онлайн. Сложение, вычитание, умножение и деление дробей
Вычисления с обыкновенной и десятичной дробями
Сравнение дробей онлайн
Сокращение дробей онлайн
Преобразование смешанных чисел в неправильные дроби
Преобразование неправильных дробей в смешанные числа
Онлайн калькулятор. Преобразование десятичной дроби в обыкновенную дробь
Действия с матрицами
Онлайн калькулятор.
Сложение и вычитание матрицОнлайн калькулятор. Умножение матриц
Онлайн калькулятор. Транспонированная матрица
Онлайн калькулятор. Определитель матрицы. Детерминант матрицы
Онлайн калькулятор. Ранг матрицы
Онлайн калькулятор. Обратная матрица
Онлайн калькулятор. Обратная матрица методом алгебраических дополнений
Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса
Онлайн калькулятор. Решение систем линейных уравнений. Метод Крамера
Онлайн калькулятор. Решение систем линейных уравнений. Матричный метод
Теория вероятностей, комбинаторика, статистика
Онлайн калькулятор. Нахождение числа перестановок из n элементов
Онлайн калькулятор. Нахождение числа размещений из n по k
Онлайн калькулятор. Нахождение числа сочетаний из n по k
Онлайн калькулятор. Нахождение математического ожидания дискретного распределения
Онлайн калькулятор. Нахождение дисперсии дискретного распределения
Отзывы учениковОставить отзыв
К ЕГЭ по математике я готовилась сама, без репетитора.
Ничего сверхъестественного я не делала: зубрила формулы и решала задачи на сайте ШпаргалкаЕГЭ.
Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.
Большое спасибо! Сервис нереально помог. К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов.
Hello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.
Использовала сайт на контрольных. У нас училка брала задания из СтатГрада. В утро перед контрольной на сайте все задачи с подробными видео решениями. Лепота!
Если вы все еще сомневаетесь попробуйте на собственном опыте, и возможности превысят ваши ожидания действия с матрицами, статистика, теория вероятностей, действия с дробями, комбинаторика и другое.