вычисление матрицы онлайн методом гаусса онлайн
Вы искали вычисление матрицы онлайн методом гаусса онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить систему уравнений онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «вычисление матрицы онлайн методом гаусса онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает.
Где можно решить любую задачу по математике, а так же вычисление матрицы онлайн методом гаусса онлайн Онлайн?
Решить задачу вычисление матрицы онлайн методом гаусса онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Обратная матрица онлайн
Для любой невырожденной квадратной матрицы (т.
е. такой определитель которой отличен от нуля), существует
обратная матрица,
такая, что её произведение на исходную матрицу равно единичной:
A∙A−1 = A−1∙A = E
Наш калькулятор поддерживает два различных способа вычисления обратной матрицы: по методу Гаусса-Жордана и при помощи построения алгебраических дополнений к исходной матрице.
Для нахождения обратной матрицы по методу Гаусса-Жордана, к исходной матрице справа дописывают единичную матрицу:
( A | E )
Затем, с помощью элементарных преобразований приводят исходную матрицу к единичной, выполняя теже самые операции и над единичной матрицей, записанной справа. В результате таких действий исходная матрица приводится к единичной, а единичная к обратной:
( A | E) → ( E | A−1)
Метод довольно простой, удобный и не очень трудоемкий.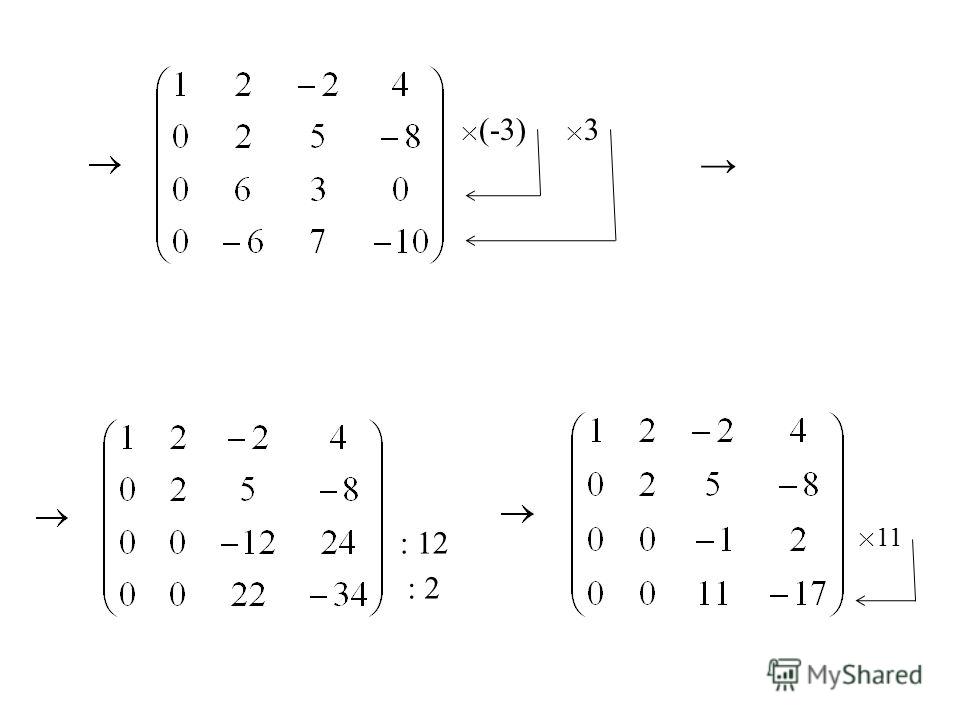
Для нахождения обратной матрицы при помощи метода алгебраических дополнений используют следующую формулу:
где
| A |
– определитель матрицы
A,
Ai j
– алгебраическое дополнение элемента
ai j
матрицы
A.
По определению:
Ai j = (-1) i+j Mi j
где Mi j – минор элемента ai j матрицы A.
По определению – минор элемента
ai j
матрицы
A
– это определитель, полученный путем вычеркивания
i
строки,
j
столбца матрицы
A.
Таким образом, метод алгебраических дополнений для вычисления обратной матрицы порядка n является достаточно трудоемким, поскольку помимо определителя исходной матрицы, нужно вычислить n2 определителей n-1 порядка.
Вычислить определитель матрицы системы методом гаусса онлайн. Вычисление определителя
Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.
О методе
При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.
- Записываем расширенную матрицу.
- Фактически решение разделяют на прямой и обратный ход метода Гаусса. Прямым ходом метода Гаусса называется приведение матрицы к ступенчатому виду. Обратным ходом метода Гаусса называется приведение матрицы к специальному ступенчатому виду. Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
- Важно отметить, что при решении методом Гаусса, наличие в матрице хотя бы одной нулевой строки с НЕнулевой правой частью (столбец свободных членов) говорит о несовместности системы. Решение линейной системы в таком случае не существует.
Чтобы лучше всего понять принцип работы алгоритма Гаусса онлайн введите любой пример, выберите “очень подробное решение” и посмотрите его решение онлайн.
В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы . Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики.
Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей , он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!
Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.
На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .
Определитель четвертого порядка тоже не антиквариат, и к нему мы подойдём в конце урока.
Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!
(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см.
следующий урок Свойства определителя и понижение его порядка)
Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!
Обозначения : Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .
1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса в вышерассмотренных примерах – это совершенно обыкновенные числа.
2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.
Начнем с определителя «два» на «два» :
ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.
Сразу рассмотрим пример:
Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.
Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 – нормальные.
Начнем с двух простых способов
Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:
Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:
Пример:
Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.
Теперь рассмотрим шесть нормальных способов для вычисления определителя
Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.
Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу .
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.
Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.
В следующем примере будем раскрывать определитель по первой строке .
Для этого нам понадобится матрица знаков: . Легко заметить, что знаки расположены в шахматном порядке.
Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.
Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:
И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?
Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ .
Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.
Коль скоро выбран способ разложения определителя по первой строке , очевидно, что всё вращается вокруг неё:
Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)
Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:
1) Из матрицы знаков выписываем соответствующий знак:
2) Затем записываем сам элемент:
3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:
Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).
Переходим ко второму элементу строки.
4) Из матрицы знаков выписываем соответствующий знак:
5) Затем записываем второй элемент:
6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:
Ну и третий элемент первой строки.
Никакой оригинальности:
7) Из матрицы знаков выписываем соответствующий знак:
8) Записываем третий элемент:
9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:
Оставшиеся четыре числа записываем в маленький определитель.
Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!
Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.
Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:
В следующем примере я раскрыл определитель по четвертому столбцу :
А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.
Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя .
БУДЬТЕ ВНИМАТЕЛЬНЫ!
Содержание
Введение…………………………………………………………………………………………….. 2
1. Постановка задачи………………………………………………………………………….. 3
2. Математические и алгоритмические основы решения задачи……………… 5
2.1 Определитель матрицы………………………………………………………………….. 5
2.2 Метод Гаусса для решения систем линейных уравнений…………………… 6
2.3 Метод Гаусса для вычисления определителя……………………………………. 8
3.
Функциональные модели и блок-схемы решения задачи…………………….. 9
4. Программная реализация решения задачи………………………………………. 11
5. Пример выполнения программы…………………………………………………….. 16
Заключение………………………………………………………………………………………. 18
Список использованных источников и литературы……………………………… 19
Введение
Многие проблемы, возникающие в экономических исследованиях, планировании и управлении, будучи сформулированными математически, представляют собой задачи, в которых необходимо решить систему алгебраических уравнений.
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной.
При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.
Помимо аналитического решения СЛАУ, метод Гаусса также применяется для нахождения матрицы, обратной к данной, определения ранга матрицы и нахождения определителя.
Целью данной курсовой работы является реализация вычисления определителя методом исключения Гаусса.
1. Постановка задачи
Вычисление определителя матрицы заключается в выполнении над матрицей алгоритма Гаусса для решения систем линейных алгебраических уравнений. В результате выполнения алгоритма получаем диагональную матрицу, её определитель равен произведению элементов, стоящих на диагонали.
Вычислить определитель матрицы методом A исключения Гаусса.
.Приведем матрицу к диагональному виду методом Гаусса.
~.Тогда определитель матрицы равен произведению ее элементов, стоящих на диагонали:
.Знак определяется количеством обменов строк, следовательно определитель матрицы
.2. Математические и алгоритмические основы решения задачи
2.1 Определитель матрицы
Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка n, нужно уже знать, что такое определитель матрицы порядка n-1. Отметим также, что определитель существует только у квадратных матриц.
Определитель квадратной матрицы A будем обозначать
или det A.Определение. Определителем квадратной матрицы
второго порядка называется число
.Определителем
квадратной матрицы порядка n,
, называется число – определитель матрицы порядка n-1, полученной из матрицы A вычеркиванием первой строки и столбца с номером k.
2.2 Метод Гаусса для решения систем линейных уравнений
Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель.
Воспользуемся идеями метода Гаусса решения систем линейных уравнений.
Дана система:
a11 x1 + a12 x2 + … + a1n xn = b1
a21 x1 + a22 x2 + … + a2n xn = b2
an1 x1 + an2 x2 + … + ann xn = bn
Выполним следующий алгоритм.
На первом шаге найдём в первом столбце наибольший по модулю элемент, поставим уравнение с этим элементом на первую строчку (обменяв две соответствующие строки матрицы A и два соответствующих элемента вектора B), а затем будем отнимать это уравнение от всех остальных, чтобы в первом столбце все элементы (кроме первого) обратились в ноль. Например, при прибавлении ко второй строке будем домножать первую строку на -a21/a11, при добавлении к третьей – на -a31/a11, и т.д.
На втором шаге найдём во втором столбце, начиная со второго элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на вторую строчку, и будем отнимать это уравнение от всех остальных (в том числе и от первого), чтобы во втором столбце все элементы (кроме второго) обратились в ноль.
Понятно, что эта операция никак не изменит первый столбец – ведь от каждой строки мы будем отнимать вторую строку, домноженную на некоторый коэффициент, а во второй строке в первом столбце стоит ноль.
Т.е. на i-ом шаге найдём в i-ом столбце, начиная с i-го элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на i-ю строчку, и будем отнимать это уравнение от всех остальных. Понятно, что это никак не повлияет на все предыдущие столбцы (с первого по (i-1)-ый).
В конце концов, мы приведём систему к так называемому диагональному виду:
Т.е. мы нашли решение системы.
Замечание 1. На каждой итерации найдётся хотя бы один ненулевой элемент, иначе система бы имела нулевой определитель, что противоречит условию.
Замечание 2. Требование, что на каждом шаге мы выбираем наибольший по модулю элемент, очень важно в смысле численной устойчивости метода. Если выбирать произвольный ненулевой элемент, то это может привести к гигантской погрешности, когда получившееся решение будет отличаться в разы от правильного.
2.3 Метод Гаусса для вычисления определителя
Будем выполнять те же самые действия, что и при решении системы линейных уравнений, исключив только деление текущей строки на a[i][i] (точнее, само деление можно выполнять, но подразумевая, что число выносится за знак определителя). Тогда все операции, которые мы будем производить с матрицей, не будут изменять величину определителя матрицы, за исключением, быть может, знака (мы только обмениваем местами две строки, что меняет знак на противоположный, или прибавляем одну строку к другой, что не меняет величину определителя).
Но матрица, к которой мы приходим после выполнения алгоритма Гаусса, является диагональной, и определитель её равен произведению элементов, стоящих на диагонали. Знак, как уже говорилось, будет определяться количеством обменов строк (если их нечётное, то знак определителя следует изменить на противоположный). Таким образом, мы можем с помощью алгоритма Гаусса вычислять определитель матрицы за O(N3).
Осталось только заметить, что если в какой-то момент мы не найдём в текущем столбце ненулевого элемента, то алгоритм следует остановить и вернуть 0.
3. Функциональные модели и блок-схемы решения задачи
Блок-схема решения задачи представлена на рисунке 1.
Рисунок 1 – Блок-схема решения задачи для функции DETERMINATE
4 Программная реализация решения задачи
;ФУНКЦИЯ, ВЫЧИСЛЯЮЩАЯ ОПРЕДЕЛИТЕЛЬ
(DEFUN DETERMINANT (MATRIX SIZE)
;ОБЪЯВЛЕНИЕ ПЕРЕМЕННЫХ
;ОПРЕДЕЛИТЕЛЬ
(DECLARE (SPECIAL DET))
;ВСПОМОГАТЕЛЬНЫЕ МАССИВЫ И ПЕРЕМЕННЫЕ
(DECLARE (SPECIAL PAR))
(DECLARE (SPECIAL R))
(DECLARE (SPECIAL T_))
(DECLARE (SPECIAL I))
(DECLARE (SPECIAL II))
;*********************
(SETQ R (MAKE-ARRAY SIZE:ELEMENT-TYPE “FLOAT:INITIAL-ELEMENT 0))
((>= J (- SIZE 1)))
;ИСКЛЮЧАЕМ ДЕЛЕНИЕ НА 0
(IF (= (AREF MATRIX J J) 0)
(SETQ II (+ J 1))
;ИЩЕМ СТРОКУ В КОТОРОЙ J-Й ЭЛЕМЕНТ НЕ 0
((OR (/= (AREF MATRIX II J) 0) (= II (- SIZE 1))))
(SETQ II (+ II 1))
;ЕСЛИ НЕТ ТАКОЙ СТРОКИ ОПРЕДЕЛИТЕЛЬ РАВЕН 0
(IF (AND (= (AREF MATRIX II J) 0) (= II (- SIZE 1))) (SETQ T_ 0))
Вычислим определитель методом Гаусса.
Суть метода состоит в следующем: определитель приводится к треугольному виду с помощью элементарных преобразований, и тогда он равен произведению элементов, стоящих на главной диагонали.
Идея метода состоит в следующем: пусть дан определитель третьего порядка
элементдолжен быть равен
,
для этого первую строку разделим на.
Получим определитель вида
(2)
Обнулим элементы, стоящие в первом
столбце, кроме первого. Для этого из
второй строки вычтем первую, умноженную
на
,
далее из третьей строки вычтем первую,
умноженную на.
Получим определитель вида
.
Обозначим его элементы буквой с, тогда
(3)
Теперь надо обнулить элемент
.
Элемент
должен быть равен
,
для этого вторую строку разделим на
.
Получим определитель вида
.
.
Обозначим его элементы буквой t, тогда
(4)
Вот мы привели определитель к треугольному
виду, теперь он равен
.
Разберем теперь это на конкретном примере.
Пример 4: Вычислить определительметодом Гаусса.
Решение: Поменяем местами первую и третью строки (при замене двух столбцов (строк) определитель меняет знак на противоположный).
Получили
Из второй строки вычтем первую, умноженную
на 2, далее из третьей строки вычтем
первую, умноженную на 3. Получили
Получили –
§2.Матрицы Виды матриц
Определение 7: Если в матрицеmстрок иnстолбцов, то она
называетсяразмерностью mnи пишут
.
Определение 8: Если
,
то матрица называется квадратной.
Определение 9: Матрица, состоящая лишь из одной строки (столбца) называется матрицей-строкой (столбцом).
Определение 10: Матрица, состоящая из нулей, называется нулевой матрицей.
Определение 11: Диагональной матрицей называется квадратная матрица, у которой все элементы, не принадлежащие главной диагонали равны нулю.
Определение 12: Единичной матрицей
называется диагональная матрица, у
которой все элементы, стоящие на главной
диагонали равны единице.
Определение 13: Треугольной называется квадратная матрица, у которой элементы, расположенные по одну сторону от главной диагонали равны нулю.
Действиянад матрицами.
Определение 14: Две матрицы считаются равными, если они имеют одинаковое число строк и столбцов и равные соответствующие элементы.
Пример 5:
Матрицы А и В равны, т.е.
Определение 15: Суммой (разностью)
матриц А и В называется такая матрица
С, у которой каждый элемент равен
.
Пример 6: Найти матрицу
,
если
Решение:
Cвойства сложения
А+В=В+А(переместительное)
2 0 А+О=А, где О-нулевая матрица
3 0 А+(В+С)=(А+В)+С (дистрибутивное)
4 0 А+(-А)=О, где – А противоположная матрица
(т.е. элементы имеют противоположные знаки)
Определение 16: Произведением матрицы
А на число
называется матрица, полученная из
данной умножением всех ее элементов на
число.
Пример 7:
Умножение матиц
Это действие распространяется на так
называемые согласованные матрицы.
Определение 17: Матрица А называетсясогласованной с матрицей В, если число столбцов у матрицы А равно числу строк у матрицы В.
Пример 8:
и
– согласованные
и
– несогласованные
и
несогласованные
Определение 18: Произведением двух матриц А и В называется такая матрица С, каждый элемент которой равен сумме произведений элементовiстроки матрицы А на соответствующие элементыj-го столбца матрицы В.
Если матрица А имеет размерность
,
а матрица В
,
то
.
Пример 9: Умножить матрицы
Решение системы линейных уравнений методом Гаусса онлайн
Для решения любой системы линейных уравнений метод Гаусса или метод последовательного исключения неизвестных является наиболее универсальным и достаточно простым при небольшом количестве переменных. Этот метод универсален, его применяют, когда система уравнений имеет:
- единственное решение;
- бесконечное множество решений;
- вовсе не имеет решений.
Суть метода состоит в переходе от заданной системы линейных уравнений к более простой с помощью таких эквивалентных преобразований в системе, как:
- перемена двух уравнений местами;
- умножение обеих частей уравнения на любое действительное число, не равное 0;
- прибавление к одному уравнению соответствующих частей другого, умноженных на произвольное число.
С помощью преобразований последовательно исключаем одну переменную за другой пока в одной из строк не будет определена переменная xi.
Метод Гаусса позволяет решать СЛАУ при небольшом числе вычислительных операций.
Алгоритм решения:
- записываем систему в виде расширенной матрицы;
- прямой ход — приводим матрицу к ступенчатому виду;
- обратный ход — приводим матрицу к специальному ступенчатому виду.
Пусть дана система из n уравнений с n неизвестными переменными:
Определитель основной матрицы не равен 0.
Исключим из всех уравнений системы переменную х1, начиная со 2-го, для чего:
- ко 2-му уравнению прибавим 1-е, умноженное на — а21/а11;
- к 3-му уравнению прибавим 1-е, умноженное на — а31/а11, и т. д.;
- к n-му уравнению прибавим 1-е, умноженное на — аn1/а11.
д.;В результате преобразований система приняла вид:
Далее таким же путем исключаем неизвестную переменную х2 из всех уравнений, начиная с 3-го.
Для этого к 3-му уравнению прибавляем 2-е, умноженное на — а32/а22 и т.д. К n-му уравнению прибавим 2-е, умноженное на — аn2/а22.
Таким же способом исключаем неизвестную х3 из всех уравнений системы, начиная с 4-го.
Прямой ход продолжается, пока в последнем уравнении не останется единственная неизвестная. Система будет иметь вид:
аnn(n-1) хn = bn(n-1)
После окончания прямого хода метода Гаусса — последовательного исключения неизвестных, вычисляем неизвестную в последнем уравнении:
- из последнего уравнения системы находим хn по формуле:
- из предпоследнего уравнения находим хn-1 и т. д.
- из первого уравнения находим х1.
д.Последовательное нахождение неизвестных, начиная с последнего уравнения к первому, называется обратным ходом.
Заметим, если в матрице есть хоть одна нулевая строка, у которой правая часть (свободный член) не равна 0, система несовместима, решения отсутствуют.
Для быстрого и правильного решения СЛАУ методом Гаусса можно воспользоваться калькулятором онлайн.Решение системы линейных уравнений методом Гаусса
| 123456 — количество неизвестных |
Решение системы линейных уравнений методом Гаусса-Жордана
метод Гаусса–Жордана – один из наиболее известных и широко применяемых методов решения систем линейных уравнений. Матричный метод и метод Крамера обладают тем недостатком,
что они не дают ответа в том случае, когда detA = 0, а определяют лишь единственное решение при detA неравном 0.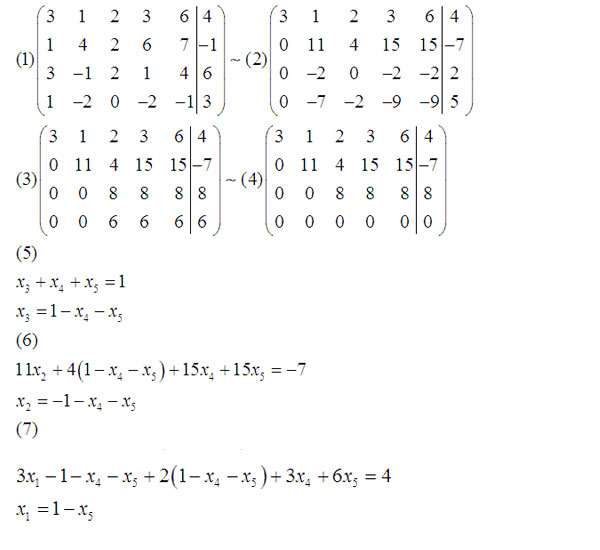
Еще одним недостатком является то, что объем математических вычислений
в рамках этих методов резко возрастает с ростом числа уравнений. Метод Гаусса практически свободен от этих недостатков.
Алгоритм метода Гаусса
- На основании системы линейных уравнений составляем расширенную матрицу системы;
- Приводим матрицу к “треугольному” виду;
- Определяем ранги основной и расширенной матриц, и на основании этого делаем вывод о совместности системы и количестве допустимых решений;
- В случае, если система имеет единственное решение производим обратную подстановку и находим его, если система имеет множество решений: выражаем базисные переменные через
переменные которые могут принимать произвольные значения;
Комментарий к шагу 2 Метода Гаусса. Треугольной называют матрицу, в которой все элементы расположенные ниже главной диагонали равны нулю.
Для приведения исходной расширенной матрицы к треугольному виду используем следующие два свойства определителей:
Свойство 1.
Определитель не изменит свое значение, если ко всем элементам какой-либо строки (столбца) матрицы прибавить соответствующие элементы параллельной строки (столбца), умноженные на произвольное одно и то же число.
Свойство 2. При перестановке двух любых столбцов или строк матрицы ее определитель меняет знак на противоположный, а абсолютная величина определителя остается неизменной.
На основании этих свойств определителей составим алгоритм преобразования матрицы к треугольному виду:
- Рассматриваем строку i(начиная с первой). Если, элемент aii равен нулю, меняем местами i-ю и i+1-ю строки матрицы. Знак определителя при этом изменится на противоположный. Если a11 отличен от нуля – переходим к следующему шагу;
- Для каждой строки j, ниже i-й находим значение коэффициента Kj=aji/aii;
- Пересчитываем элементы всех строк j, расположенных ниже текущей строки i, с использованием соответствующих коэффициентов по формуле: ajkнов.
После чего, возвращаемся к первому шагу алгоритма и рассматриваем следующую строку, пока не доберемся до строки i=n-1, где n – размерность матрицы A- В полученной треугольной матрице расчитываем произведение всех элементов главной диагонали Пaii, которое и будет являтся определителем;
=ajk-Kj*aik;Другими словами, суть метода можно сформулировать следующим образом. Нам необходимо сделать нулевыми все элементы матрицы ниже главной диагонали. Сначала мы получаем нули в первом столбце.
Для этого мы последовательно вычитаем первую строку, домноженную на нужное нам число (такое, чтоб при вычитании мы получили ноль в первом элементе строки), из всех ниже лежащих строк.
Затем проделываем то же самое для второй строки, чтобы получить нули во втором столбце ниже главной диагонали матрицы. И так далее пока не доберемся до предпоследней строки.
Комментарий к шагу 3 Метода Гаусса.
Рангом матрицы A размера m × n называется наивысший порядок отличного от нуля минора этой матрицы. Ранг матрицы A обозначается через r(A) = rangA = rankA.
Минором M (от латинского “minor” меньший) k-го порядка матрицы A называется определитель некоторой матрицы, составленной из элементов матрицы A, стоящих на пересечении произвольно выбранных k
строк и k столбцов с сохранением их порядка. Если номера столбцов, в которых расположен минор M, совпадают с номерами строк, то этот минор называется главным. Каждая матрица A порядка n имеет
(Ckn)2 миноров k-го порядка. Минорами 1-го порядка являются сами элементы матрицы A.
Основываясь на сравнении полученных значений рангов для основной и расширенной матрицы можно сделать следующие выводы о разрешимости системы:
- если ранг основной системы равен рангу расширенной и равен числу уравнений системы (rangA=rangA’=n), то система совместна и имеет единственное решение;
- если ранг основной системы равен рангу расширенной, но меньше числа уравнений в системе (rangA=rangA’
- если ранг основной системы меньше ранга расширенной (rangA
Матричный метод онлайн калькулятор с подробным решением.
Матричный метод онлайнДля решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, – так называемые системы крамеровского типа :
a 11 x 1 + a 12 x 2 +… + a 1n x n = b 1 ,
a 21 x 1 + a 22 x 2 +… + a 2n x n = b 2 , (5.3)
… … … … … …
a n1 x 1 + a n1 x 2 +… + a nn x n = b n .
Системы (5.3) решаются одним из следующих способов: 1) методом Гаусса, или методом исключения неизвестных; 2) по формулам Крамера; 3) матричным методом.
Пример 2.12 . Исследовать систему уравнений и решить ее, если она совместна:
5x 1 – x 2 + 2x 3 + x 4 = 7,
2x 1 + x 2 + 4x 3 – 2x 4 = 1,
x 1 – 3x 2 – 6x 3 + 5x 4 = 0.
Решение. Выписываем расширенную матрицу системы:
.
Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу = 7 0; содержащие его миноры третьего порядка равны нулю:
Следовательно,
ранг основной матрицы системы равен 2,
т.
е. r(A) = 2. Для вычисления ранга расширенной
матрицы A
рассмотрим окаймляющий минор
значит, ранг расширенной матрицы r(A) = 3. Поскольку r(A) r(A), то система несовместна.
Это понятие, которое обобщает все возможные операции, производимые с матрицами. Математическая матрица – таблица элементов. О такой таблице, где m строк и n столбцов, говорят, что это матрица имеет размерность m на n .
Общий вид матрицы:
Для решения матриц необходимо понимать, что такое матрица и знать основные ее параметры. Основные элементы матрицы:
- Главная диагональ, состоящая из элементов а 11 ,а 22 …..а mn .
- Побочная диагональ, состоящая из элементов а 1n ,а 2n-1 …..а m1 .
Основные виды матриц:
- Квадратная – такая матрица, где число строк = числу столбцов (m=n ).
- Нулевая – где все элементы матрицы = 0.
- Транспонированная матрица — матрица В , которая была получена из исходной матрицы A путем замены строк на столбцы.
- Единичная – все элементы главной диагонали = 1, все остальные = 0.
- Обратная матрица — матрица, при умножении на которую исходная матрица даёт в результате единичную матрицу.
Матрица может быть симметричной относительно главной и побочной диагонали. Т.е., если а 12 =а 21 , а 13 =а 31 ,….а 23 =а 32 …. а m-1n =а mn-1 , то матрица симметрична относительно главной диагонали. Симметричными могут быть лишь квадратные матрицы.
Методы решения матриц.
Почти все методы решения матрицы заключаются в нахождении ее определителя n -го порядка и большинство из них довольно громоздки. Чтобы найти определитель 2го и 3го порядка есть другие, более рациональные способы.
Нахождение определителей 2-го порядка.
Для вычисления определителя матрицы А 2го порядка, необходимо из произведения элементов главной диагонали вычесть произведение элементов побочной диагонали:
Методы нахождения определителей 3го порядка.
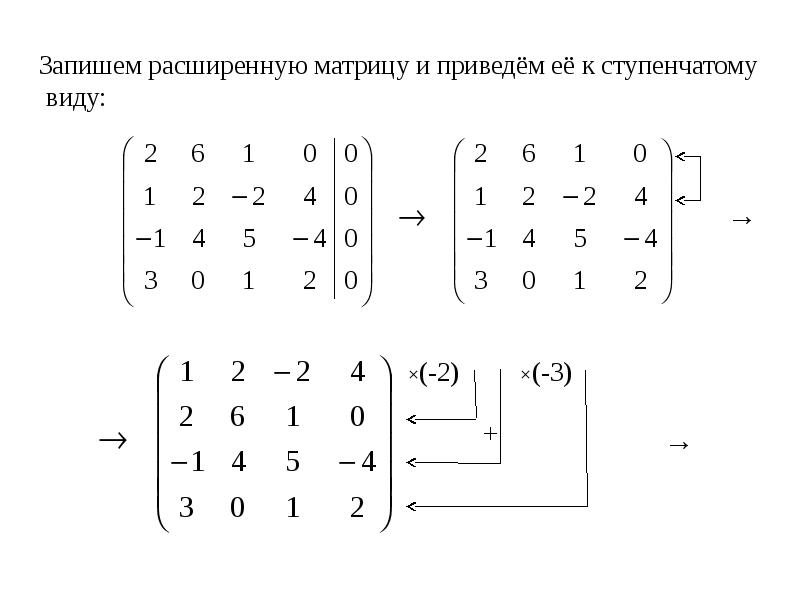
Ниже приведены правила для нахождения определителя 3го порядка.
Упрощенно правило треугольника, как одного из методов решения матриц , можно изобразить таким образом:
Другими словами, произведение элементов в первом определителе, которые соединены прямыми, берется со знаком “+”; так же, для 2го определителя – соответствующие произведения берутся со знаком “-“, то есть по такой схеме:
При решении матриц правилом Саррюса , справа от определителя дописывают первые 2 столбца и произведения соответствующих элементов на главной диагонали и на диагоналях, которые ей параллельны, берут со знаком “+”; а произведения соответствующих элементов побочной диагонали и диагоналей, которые ей параллельны, со знаком “-“:
Разложение определителя по строке или столбцу при решении матриц.
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули.
Строку либо столбец, по которой/ому ведется разложение, будут обозначать стрелкой.
Приведение определителя к треугольному виду при решении матриц.
При решении матриц методом приведения определителя к треугольному виду, работают так: с помощью простейших преобразований над строками либо столбцами, определитель становится треугольного вида и тогда его значение, в соответствии со свойствами определителя, будет равно произведению элементов, которые стоят на главной диагонали.
Теорема Лапласа при решении матриц.
Решая матрицы по теореме Лапласа, необходимо знать непосредственно саму теорему. Теорема Лапласа: Пусть Δ – это определитель n -го порядка. Выбираем в нем любые k строк (либо столбцов), при условии k ≤ n – 1 . В таком случае сумма произведений всех миноров k -го порядка, содержащихся в выбранных k строках (столбцах), на их алгебраические дополнения будет равна определителю.
Решение обратной матрицы.
Последовательность действий для решения обратной матрицы :
- Понять, квадратная ли данная матрица. В случае отрицательного ответа становится ясно, что обратной матрицы для нее не может быть.
- Вычисляем алгебраические дополнения.
- Составляем союзную (взаимную, присоединённую) матрицу C .
- Составляем обратную матрицу из алгебраических дополнений: все элементы присоединённой матрицы C делим на определитель начальной матрицы. Итоговая матрица будет искомой обратной матрицей относительно заданной.
- Проверяем выполненную работу: умножаем матрицу начальную и полученную матрицы, результатом должна стать единичная матрица.
Решение систем матриц.
Для решения систем матриц наиболее часто используют метод Гаусса.
Метод Гаусса — это стандартный способ решения систем линейных алгебраических уравнений (СЛАУ) и он заключается в том, что последовательно исключаются переменные, т.е., при помощи элементарных изменений систему уравнений доводят до эквивалентной системы треугольного вида и из нее, последовательно, начиная с последних (по номеру), находят каждый элемент системы.
Метод Гаусса является самым универсальным и лучшим инструментом для нахождения решения матриц. Если у системы бесконечное множество решений или система является несовместимой, то ее нельзя решать по правилу Крамера и матричным методом.
Метод Гаусса подразумевает также прямой (приведение расширенной матрицы к ступенчатому виду, т.е. получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и есть метод Гаусса, обратный – метод Гаусса-Жордана. Метод Гаусса-Жордана отличается от метода Гаусса лишь последовательностью исключения переменных.
Матричный метод решения СЛАУ применяют к решению систем уравнений, у которых количество уравнений соответствует количеству неизвестных. Метод лучше применять для решения систем низкого порядка. Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц.
Этот способ, другими словами метод обратной матрицы, называют так, так как решение сводится к обычному матричному уравнению, для решения которого нужно найти обратную матрицу.
Матричный метод решения СЛАУ с определителем, который больше или меньше нуля состоит в следующем:
Предположим, есть СЛУ (система линейных уравнений) с n неизвестными (над произвольным полем):
Значит, её легко перевести в матричную форму:
AX=B , где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на A −1 — обратную матрицу к матрице A: A −1 (AX)=A −1 B.
Т.к. A −1 A=E , значит, X=A −1 B . Правая часть уравнения дает столбец решений начальной системы. Условием применимости матричного метода есть невырожденность матрицы A . Необходимым и достаточным условием этого есть неравенство нулю определителя матрицы A :
detA≠0.
Для однородной системы линейных уравнений , т.е. если вектор B=0 , выполняется обратное правило: у системы AX=0 есть нетривиальное (т.е. не равное нулю) решение лишь когда detA=0 . Эта связь между решениями однородных и неоднородных систем линейных уравнений называется альтернатива Фредгольма.
Т.о., решение СЛАУ матричным методом производится по формуле . Либо, решение СЛАУ находят при помощи обратной матрицы A −1 .
Известно, что у квадратной матрицы А порядка n на n есть обратная матрица A −1 только в том случае, если ее определитель ненулевой. Таким образом, систему n линейных алгебраических уравнений с n неизвестными решаем матричным методом только в случае, если определитель основной матрицы системы не равен нулю.
Не взирая на то, что есть ограничения возможности применения такого метода и существуют сложности вычислений при больших значениях коэффициентов и систем высокого порядка, метод можно легко реализовать на ЭВМ.
Пример решения неоднородной СЛАУ.
Для начала проверим, не равен ли нулю определитель матрицы коэффициентов у неизвестных СЛАУ.
Теперь находим союзную матрицу , транспонируем её и подставляем в формулу для определения обратной матрицы.
Подставляем переменные в формулу:
Теперь находим неизвестные, перемножая обратную матрицу и столбик свободных членов.
Итак, x=2; y=1; z=4.
При переходе от обычного вида СЛАУ к матричной форме будьте внимательными с порядком неизвестных переменных в уравнениях системы. Например :
НЕЛЬЗЯ записать как:
Необходимо, для начала, упорядочить неизвестные переменные в кадом уравнении системы и только после этого переходить к матричной записи:
Кроме того, нужно быть внимательными с обозначением неизвестных переменных, вместо x 1 , x 2 , …, x n могут оказаться другие буквы. К примеру :
в матричной форме записываем так:
Матричным методом лучше решать системы линейных уравнений, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы не равен нулю. Когда в системе более 3-х уравнений, на нахождение обратной матрицы потребуется больше вычислительных усилий, поэтому, в этом случае целесообразно использовать для решения метод Гаусса.
Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку “Вычислить”.
×
Предупреждение
Очистить все ячейки?
Закрыть Очистить
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Матричный метод решения систем линейных уравнений
Рассмотрим следующую систему линейных уравнений:
Учитывая определение обратной матрицы, имеем A −1 A =E , где E – единичная матрица. Следовательно (4) можно записать так:
Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b .
Примеры решения системы линейных уравнений матричным методом
Пример 1. Решить следующую систему линейных уравнений матричным методом:
Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:
Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:
Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:
Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:
Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :
Матричный вид записи системы линейных уравнений: Ax=b , где
Вычислим все алгебраические дополнения матрицы A :
| , |
| , |
| , |
| , |
| , |
| , |
| , |
| , |
| . |
Обратная матрица вычисляется из следующего выражения.
Решение системы линейных уравнений методом гаусса-жордана
Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.
О методе
При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.
- Записываем расширенную матрицу.
- Фактически решение разделяют на прямой и обратный ход метода Гаусса. Прямым ходом метода Гаусса называется приведение матрицы к ступенчатому виду. Обратным ходом метода Гаусса называется приведение матрицы к специальному ступенчатому виду. Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
- Важно отметить, что при решении методом Гаусса, наличие в матрице хотя бы одной нулевой строки с НЕнулевой правой частью (столбец свободных членов) говорит о несовместности системы. Решение линейной системы в таком случае не существует.
Чтобы лучше всего понять принцип работы алгоритма Гаусса онлайн введите любой пример, выберите “очень подробное решение” и посмотрите его решение онлайн.
метод Гаусса–Жордана – один из наиболее известных и широко применяемых методов решения систем линейных уравнений. Матричный метод и метод Крамера обладают тем недостатком, что они не дают ответа в том случае, когда detA = 0, а определяют лишь единственное решение при detA неравном 0. Еще одним недостатком является то, что объем математических вычислений в рамках этих методов резко возрастает с ростом числа уравнений. Метод Гаусса практически свободен от этих недостатков.
Алгоритм метода Гаусса
Комментарий к шагу 2 Метода Гаусса. Треугольной называют матрицу, в которой все элементы расположенные ниже главной диагонали равны нулю.
- На основании системы линейных уравнений составляем расширенную матрицу системы;
- Приводим матрицу к “треугольному” виду;
- Определяем ранги основной и расширенной матриц, и на основании этого делаем вывод о совместности системы и количестве допустимых решений;
- В случае, если система имеет единственное решение производим обратную подстановку и находим его, если система имеет множество решений: выражаем базисные переменные через переменные которые могут принимать произвольные значения;
Для приведения исходной расширенной матрицы к треугольному виду используем следующие два свойства определителей:
Свойство 1. Определитель не изменит свое значение, если ко всем элементам какой-либо строки (столбца) матрицы прибавить соответствующие элементы параллельной строки (столбца), умноженные на произвольное одно и то же число.
Свойство 2. При перестановке двух любых столбцов или строк матрицы ее определитель меняет знак на противоположный, а абсолютная величина определителя остается неизменной.
На основании этих свойств определителей составим алгоритм преобразования матрицы к треугольному виду:
- Рассматриваем строку i(начиная с первой). Если, элемент a i i равен нулю, меняем местами i-ю и i+1-ю строки матрицы. Знак определителя при этом изменится на противоположный. Если a 1 1 отличен от нуля – переходим к следующему шагу;
- Для каждой строки j, ниже i-й находим значение коэффициента K j =a j i /a i i ;
- Пересчитываем элементы всех строк j, расположенных ниже текущей строки i, с использованием соответствующих коэффициентов по формуле: a j k нов.=a j k -K j *a i k ; После чего, возвращаемся к первому шагу алгоритма и рассматриваем следующую строку, пока не доберемся до строки i=n-1, где n – размерность матрицы A
- В полученной треугольной матрице расчитываем произведение всех элементов главной диагонали Пa i i , которое и будет являтся определителем;
Другими словами, суть метода можно сформулировать следующим образом. Нам необходимо сделать нулевыми все элементы матрицы ниже главной диагонали. Сначала мы получаем нули в первом столбце. Для этого мы последовательно вычитаем первую строку, домноженную на нужное нам число (такое, чтоб при вычитании мы получили ноль в первом элементе строки), из всех ниже лежащих строк. Затем проделываем то же самое для второй строки, чтобы получить нули во втором столбце ниже главной диагонали матрицы. И так далее пока не доберемся до предпоследней строки.
4. Метод Жордана – Гаусса.
Схема с выбором главного элемента состоит в том, что требование неравенства нулю диагональных элементов akk, на которые происходит деление в процессе исключения, заменятся более жестким: из всех элементов К-го столба выбрать наибольший по модулю и переставить уравнения так, чтобы этот элемент оказался на месте элемента акк. Выбор главного элемента и связанная с ним перестановка строк необходимы в тех случаях, когда на каком-либо i-ом шаге акк=0 либо же акк очень мало по остальными элементами i- го столбца: при делении на такое «малое» акк будут получаться большие числа с большими абсолютными погрешностями, в результате чего решение может сильно исказиться.
Ниже излагается алгоритм полного исключения неизвестных или метод Жордана – Гаусса. Суть метода состоит в том, что, рассмотрев первое уравнение, в нем неизвестное с коеффициэнтом, отличным от нуля (в дальнейшем разрешающий элемент), и разделив первое уравнение на этот коэффициент, с помощью первого уравнения исключают это неизвестное из всех уравнений, кроме первого. Выбрав во втором уравнении неизвестное с коэффициентом, отличным от нуля, и разделив на него второе уравнение, с помощью второго исключают другие неизвестные из всех уравнений, кроме второго и т.д., т.е. с помощью одного уравнения производят полное исключение одного неизвестного. Процесс продолжается до тех пор, пока не будут использованы все уравнения.
Как известно, системы линейных алгебраических уравнений могут имеет одно решение, множество решений или системы несовместны. При элементарных преобразованиях элементов матрицы системы эти случаи выявляются в следующем:
1. В процессе исключений левая часть I –го уравнения системы обращается в нуль, а правая часть равна некоторому числу, отличному от нуля. т.е. 02+=bc0.
Это означает, что система не имеет решений, так как I – му уравнению не могут удовлетворять никакие значения неизвестных;
2. Левая и правая части I – го уравнения обращаются в нуль. Это означает, что I – ое уравнение является линейной комбинацией остальных, ему удовлетворяет любое найденное решение системы, поэтому оно может быть отброшено. В системе количество неизвестных больше количества уравнений и, следовательно, такая система имеет множество решений;
3. После того как все уравнения использованы для исключения неизвестных получено решение системы.
Таким образом, конечной целью преобразований Жордана-Гаусса является получение из заданной линейной системы
| a11x1 + a12x2 + … + a1nxn = b1,n+1 |
a21x1 + a22x2 + … + a2nxn = b2,n+1 |
| am1x1 + am2x2 + … + amnxn = bm.n+1 |
Здесь x1, x2, …, xn – неизвестные, которые надо определить. a11, a12, …, amn – коэффициенты системы – и b1, b2, … bm – свободные члены – предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе – неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) – совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все ее уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).
Совместная система вида (1) называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.
Решим следующую систему уравнений:
Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:
Проведём следующие действия:
· К строке 2 добавим: -4 * Строку 1.
· К строке 3 добавим: -9 * Строку 1.
· К строке 3 добавим: -3 * Строку 2.
· Строку 2 делим на -2
· К строке 1 добавим: -1 * Строку 3.
· К строке 2 добавим: -3/2 * Строку 3.
· К строке 1 добавим: -1 * Строку 2.
В правом столбце получаем решение:
.
В методе Ньютона наблюдается ускорение сходимости процесса приближений. 5. Метод касательных (метод Ньютона) Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f ¢(x) (x-x0) (1.5) Графики…
Решения от численных методов расчёта. Для определения корней уравнения не требуется знания теорий групп Абеля, Галуа, Ли и пр. и применения специальной математической терминологии: колец, полей, идеалов, изоморфизмов и т.д. Для решения алгебраического уравнения n – ой степени нужно только умение решать квадратные уравнения и извлекать корни из комплексного числа. Корни могут быть определены с…
Математики тригонометрической подстановки и проверка эффективности разработанной методики преподавания. Этапы работы: 1. Разработка факультативного курса на тему: «Применение тригонометрической подстановки для решения алгебраических задач» с учащимися классов с углубленным изучением математики. 2. Проведение разработанного факультативного курса. 3. Проведение диагностирующей контрольной…
… «проявляется» лишь в процессе преобразований. Очевидность и «завуалированность» новой переменной мы рассмотрим на конкретных примерах во второй главе данной работы. 2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных…
Однажды немецкий математик Вильгельм Йордан (мы неверно транскрибируем с немецкого Jordan как Жордан) сел решать очередную систему уравнений. Он любил этим заниматься и в свободное время совершенствовал свои навыки. Но вот настал момент, когда ему наскучили все методы решения и метод Гаусса в том числе…
Предположим, дана система с тремя уравнениями, тремя неизвестными и записана её расширенная матрица . В наиболее распространенном случае получаются стандартные ступеньки , и так каждый день…. Одно и то же – как беспросветный ноябрьский дождь.
На некоторое время развевает тоску другой способ приведения матрицы к ступенчатому виду: , причём он совершенно равноценен и может быть неудобен только по причине субъективного восприятия. Но всё рано или поздно приедается…. И подумал тогда Жо рдан – а зачем вообще мучиться с обратным ходом гауссовского алгоритма? Не проще ли сразу получить ответ с помощью дополнительных элементарных преобразований?
…да, такое бывает только по любви =)
Для освоения данного урока «чайникам» придётся пойти путём Жо рдана и прокачать элементарные преобразования хотя бы среднего уровня, прорешав, минимум, 15-20 соответствующих заданий. Поэтому если вы смутно понимаете, о чём идёт разговор и/или у вас возникнет недопонимание чего-либо по ходу занятия, то рекомендую ознакомиться с темой в следующем порядке:
Ну, и совсем замечательно, если отработано понижение порядка определителя .
Как все поняли, метод Гаусса-Жордана представляет собой модификацию метода Гаусса и с реализацией основной, уже озвученной выше идеи, мы встретимся на ближайших экранах. Кроме того, в число немногочисленных примеров данной статьи вошло важнейшее приложение – нахождение обратной матрицы с помощью элементарных преобразований .
Не мудрствуя лукаво:
Пример 1
Решить систему методом Гаусса-Жордана
Решение : это первое задание урока Метод Гаусса для чайников , где мы 5 раз трансформировали расширенную матрицу системы и привели её к ступенчатому виду:
Теперь вместо обратного хода в игру вступают дополнительные элементарные преобразования. Сначала нам необходимо получить нули на этих местах: ,
а потом ещё один ноль вот здесь: .
Идеальный с точки зрения простоты случай:
(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.
(7) К первой строке прибавили вторую строку, умноженную на –2.
Не могу удержаться от иллюстрации итоговой системы:
Ответ :
Предостерегаю читателей от шапкозакидательского настроения – это был простейший демонстрационный пример. Для метода Гаусса-Жордана характерны свои специфические приёмы и не самые удобные вычисления, поэтому, пожалуйста, настройтесь на серьёзную работу.
Не хочу показаться категоричным или придирчивым, но в подавляющем большинстве источников информации, которые я видел, типовые задачи рассмотрены крайне плохо – нужно обладать семью пядями во лбу и потратить массу времени/нервов на тяжёлое неуклюжее решение с дробями. За годы практики мне удалось отшлифовать, не скажу, что самую лучшую, но рациональную и достаточно лёгкую методику, которая доступна всем, кто владеет арифметическими действиями:
Пример 2
Решить систему линейных уравнений методом Гаусса-Жордана.
Решение : первая часть задания хорошо знакома:
(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на 3. К четвертой строке прибавили первую строку, умноженную на –5.
(2) Вторую строку разделили на 2, третью строку разделили на 11, четвёртую строку разделили на 3.
(3) Вторая и третья строки пропорциональны, 3-ю строку удалили. К четвёртой строке прибавили вторую строку, умноженную на –7
(4) Третью строку разделили на 2.
Очевидно, что система имеет бесконечно много решений, и наша задача – привести её расширенную матрицу к виду .
Как действовать дальше? Прежде всего, следует отметить, что мы лишились вкусного элементарного преобразования – перестановки строк. Точнее говоря, переставить-то их можно, но в этом нет смысла (просто выполним лишние действия). И далее целесообразно придерживаться следующего шаблона:
Находим наименьшее общее кратное чисел третьего столбца (1, –1 и 3), т.е. – наименьшее число, которое бы делилось без остатка и на 1, и на –1 и на 3. В данном случае, это, конечно же, «тройка». Теперь в третьем столбце нам нужно получить одинаковые по модулю числа , и этими соображениями обусловлено 5-е преобразование матрицы:
(5) Первую строку умножаем на –3, вторую строку умножаем на 3. Вообще говоря, первую строку можно было умножить тоже на 3, но это было бы менее удобно для следующего действия. К хорошему привыкаешь быстро:
(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.
(7) Во втором столбце два ненулевых значения (24 и 6) и нам снова нужно получить одинаковые по модулю числа . В данном случае всё сложилось довольно удачно – наименьшее кратное 24, и эффективнее всего умножить вторую строку на –4.
(8) К первой строке прибавили вторую.
(9) Заключительный штрих: первую строку разделили на –3, вторую строку разделили на –24 и третью строку разделили на 3. Это действие выполняется В ПОСЛЕДНЮЮ ОЧЕРЕДЬ! Никаких преждевременных дробей!
В результате элементарных преобразований получена эквивалентная исходной система:
Элементарно выражаем базисные переменные через свободную:
и записываем:
Ответ : общее решение:
В подобных примерах применение рассмотренного алгоритма чаще всего оправдано, поскольку обратный ход метода Гаусса обычно требует трудоёмких и неприятных вычислений с дробями.
И, разумеется, крайне желательна проверка, которая выполняется по обычной схеме, рассмотренной на уроке Несовместные системы и системы с общим решением .
Для самостоятельного решения:
Пример 3
Найти базисное решение с помощью элементарных преобразований
Такая формулировка задачи предполагает использование метода Гаусса-Жордана, и в образце решения матрица приводится к стандартному виду с базисными переменными . Однако всегда держите на заметке, что в качестве базисных можно выбрать и другие переменные . Так, например, если в первом столбце громоздкие числа, то вполне допустимо привести матрицу к виду (базисные переменные ), или к виду (базисные переменные ), или даже к виду с базисными переменными . Существуют и другие варианты.
Но всё-таки это крайние случаи – не стОит лишний раз шокировать преподавателей своими знаниями, техникой решения и уж тем более не надо выдавать экзотических жордановсих результатов вроде . Впрочем, бывает трудно удержаться от нетипового базиса, когда в исходной матрице, скажем, в 4-м столбце есть два готовых нуля.
Примечание : термин «базис» имеет алгебраический смысл и понятие геометрического базиса здесь не при чём!
Если в расширенной матрице данных размеров вдруг обнаруживается пара линейно зависимых строк, то её следует попытаться привести к привычному виду с базисными переменными . Образец такого решения есть в Примере №7 статьи об однородных системах линейных уравнений , причём там выбран другой базис .
Продолжаем совершенствовать свои навыки на следующей прикладной задаче:
Как найти обратную матрицу методом Гаусса?Обычно условие формулируют сокращённо, но, по существу, здесь также работает алгоритм Гаусса-Жордана. Более простой метод нахождения обратной матрицы для квадратной матрицы мы давным-давно рассмотрели на соответствующем уроке, и суровой поздней осенью тёртые студенты осваивают мастерский способ решения.
Краткое содержание предстоящих действий таково: сначала следует записать квадратную матрицу в тандеме с единичной матрицей: . Затем с помощью элементарных преобразований необходимо получить единичную матрицу слева, при этом (не вдаваясь в теоретические подробности) справа нарисуется обратная матрица. Схематически решение выглядит следующим образом:
(Понятно, что обратная матрица должна существовать)
Демо-пример 4
Найдём обратную матрицу для матрицы с помощью элементарных преобразований. Для этого запишем её в одной упряжке с единичной матрицей, и понеслась «двойка скакунов»:
(1) Ко второй строке прибавили первую строку, умноженную на –3.
(2) К первой строке прибавили вторую строку.
(3) Вторую строку разделили на –2.
Ответ :
Сверьтесь с ответом первого примера урока Как найти обратную матрицу?
Но то была очередная заманивающая задачка – в действительности решение гораздо более длительно и кропотливо. Как правило, вам будет предложена матрица «три на три»:
Пример 5
Решение : присоединяем единичную матрицу и начинаем выполнять преобразования, придерживаясь алгоритма «обычного» метода Гаусса :
(1) Первую и третью строки поменяли местами. На первый взгляд, перестановка строк кажется нелегальной, но на самом деле переставлять их можно – ведь по итогу слева нам нужно получить единичную матрицу, а справа же «принудительно» получится именно матрица (вне зависимости от того будем ли мы переставлять строки в ходе решения или нет) . Обратите внимание, что здесь вместо перестановки можно организовать «шестёрки» в 1-м столбце (наименьшее общее кратное (НОК) чисел 3, 2 и 1) . Решение через НОК особенно удобно, когда в первом столбце отсутствуют «единицы».
(2) Ко 2-й и 3-й строкам прибавили 1-ю строку, умноженную на –2 и –3 соответственно.
(3) К 3-й строке прибавили 2-ю строку, умноженную на –1
Вторая часть решения проводится по уже известной из предыдущего параграфа схеме: перестановки строк становятся бессмысленными, и мы находим наименьшее общее кратное чисел третьего столбца (1, –5, 4): 20. Существует строгий алгоритм нахождения НОК, но здесь обычно хватает подбора. Ничего страшного, если взять бОльшее число, которое делится и на 1, и на –5, и на 4, например, число 40. Отличие будет в более громоздких вычислениях.
К слову о вычислениях. Для решения задачи совсем не зазорно вооружиться микрокалькулятором – числа здесь фигурируют немалые, и будет очень обидно допустить вычислительную ошибку.
(4) Третью строку умножаем на 5, вторую строку на 4, первую строку на «минус двадцать»:
(5) К 1-й и 2-й строкам прибавили третью строку.
(6) Первую и третью строки разделили на 5, вторую строку умножили на –1.
(7) Наименьшее общее кратное ненулевых чисел второго столбца (–20 и 44) равно 220. Первую строку умножаем на 11, вторую строку – на 5.
(8) К первой строке прибавили вторую строку.
(9) Первую строку умножили на –1, вторую строку разделили «обратно» на 5.
(10) Теперь на главной диагонали левой матрицы целесообразно получить наименьшее общее кратное чисел диагонали (44, 44 и 4). Совершенно понятно, что это число 44. Третью строку умножаем на 11.
(11) Каждую строку делим на 44. Данное действие выполняется в последнюю очередь!
Таким образом, обратная матрица:
Внесение и вынесение -й, в принципе, лишние действия, но того требует протокол оформления задачи.
Ответ :
Проверка выполняется по обычной схеме, рассмотренной на уроке об обратной матрице .
Продвинутые люди могут несколько сократить решение, но должен предупредить, спешка тут чревата ПОВЫШЕННЫМ риском допустить ошибку.
Аналогичное задание для самостоятельного решения:
Пример 6
Найти обратную матрицу методом Гаусса-Жордана.
Примерный образец оформления задачи внизу страницы. И ради того, чтобы вы «не проехали мимо с песнями» я оформил решение в уже упомянутом стиле – исключительно через НОК столбцов без единой перестановки строк и дополнительных искусственных преобразований. По моему мнению, эта схема – если и не самая, то одна из самых надёжных .
Иногда бывает удобно более короткое «модернистское» решение, которое заключается в следующем: на первом шаге всё как обычно: .
На втором шаге накатанным приёмом (через НОК чисел 2-го столбца) организуются сразу два нуля во втором столбце: . Перед данным действием особенно трудно устоять, если во 2-м столбце нарисовались одинаковые по модулю числа, например, те же банальные «единицы».
И, наконец, на третьем шаге точно так же получаем нужные нули в третьем столбце: .
Что касается размерности, то в большинстве случаев приходится разруливать матрицу «три на три». Однако время от времени встречается лайт-версия задачи с матрицей «два на два» и хард… – специально для всех читателей сайт:
Пример 7
Найти обратную матрицу с помощью элементарных преобразований
Это задание из моей собственной физматовской контрольной работы по алгебре, …эх, где мой первый курс =) Пятнадцать лет назад (листочек на удивление ещё не пожелтел) , я уложился в 8 шагов, а сейчас – всего лишь в 6! Матрица, кстати, весьма творческая – на первом же шаге просматривается несколько заманчивых путей решения. Моя поздняя версия внизу страницы.
И заключительный совет – после таких примеров очень полезна гимнастика для глаз и какая-нибудь хорошая музыка для релаксации =)
Желаю успехов!
Решения и ответы:
Пример 3: Решение : запишем расширенную матрицу системы и с помощью элементарных преобразований получим базисное решение:
(1) Первую и вторую строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на 5.
(3) Третью строку разделили на 3.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 7.
(6) Наименьшее кратное чисел 3-го столбца (–3, 5, 1) равно 15. Первую строку умножили на 5, вторую строку умножили на –3, третью строку умножили на 15.
(7) К первой строке прибавили 3-ю строку. Ко второй строке прибавили 3-ю строку.
(8) Первую строку разделили на 5, вторую строку разделили на –3, третью строку разделили на 15.
(9) Наименьшее кратное ненулевых чисел 2-го столбца (–2 и 1) равно: 2. Вторую строку умножили на 2
(10) К первой строке прибавили вторую строку.
(11) Вторую строку разделили на 2.
Выразим базисные переменные через свободные переменные :
Ответ : общее решение:
Пример 6: Решение : обратную матрицу найдём с помощью элементарных преобразований:
(1) Первую строку умножили на –15, вторую строку умножили на 3, третью строку умножили на 5.
(2) Ко 2-й и 3-й строкам прибавили первую строку.
(3) Первую строку разделили на –15, вторую строку разделили на –3, третью строку разделили на –5.
(4) Вторую строку умножили на 7, третью строку умножили на –9.
(5) К третьей строке прибавили вторую строку.
(6) Вторую строку разделили на 7.
(7) Первую строку умножили на 27, вторую строку умножили на 6, третью строку умножили на –4.
(8) К первой и второй строкам прибавили третью строку.
(9) Третью строку разделили на –4. К первой строке прибавили вторую строку, умноженную на –1.
(10) Вторую строку разделили на 2.
(11) Каждую строку разделили на 27.
В результате:
Ответ :
Пример 7: Решение : найдём обратную матрицу методом Гаусса-Жордана:
(1) К 1-й и 4-й строкам прибавили 3-ю строку.
(2) Первую и четвёртую строки поменяли местами.
(3) Ко 2-й строке прибавили 1-ю строку. К 3-й строке прибавили 1-ю строку, умноженную на 2:
(4) К 3-й строке прибавили 2-ю строку, умноженную на –2. К 4-й строке прибавили 2-ю строку.
(5) К 1-й и 3-й строкам прибавили 4-ю строку, умноженную на –1.
(6) Вторую строку умножили на –1, третью строку разделили на –2.
Ответ :
Записывается в виде расширенной матрицы, т.е. в столбец свободных членов помещается в одну матрицу с коэффициентами неизвестных. Аалгоритм заключается в приведении исходной матрицы, характеризующей систему линейных уравнений, к единичной путем эквивалентных преобразований (домножения строки матрицы на константу и сложения с другой строкой матрицы). В качестве константы используется 1/a[i][i] , т.е. число, обратное по отношению к элементу диагонали. Естественно, в ряде случаев возникают проблемы, связанные с делением на ноль, которые решаются перестановкой строк и столбцов:
Весь алгоритм можно представить 10 пунктами:
В качестве опорной выбираем первую строку матрицы.
Если элемент опорной строки, индекс которого равен номеру опорной строки, равен нулю, то меняем всю опорную строку на первую попавшуюся строку снизу, в столбце которого нет нуля.
Все элементы опорной строки делим на первый слева ненулевой элемент этой строки.
Из оставшихся снизу строк вычитают опорную строку, умноженную на элемент, индекс которого равен номеру опорной строки.
В качестве опорной строки выбираем следующую строку.
Повторяем действия 2 – 5 пока номер опорной строки не превысит число строк.
В качестве опорной выбираем последнюю строку.
Вычитаем из каждой строки выше опорную строку, умноженную на элемент этой строки с индексом равным номеру опорной строки.
В качестве опорной строки выбираем строку выше.
Повторяем 8 – 9 пока номер опорной строки не станет меньше номера первой строки.
Пусть имеется система уравнений:
Запишем расширенную матрицу системы:
и выполним элементарные преобразования ее строк.
Для этого умножим первую строку на 1 и вычитаем из второй строки; затем умножим первую строку на 2 и вычтем из третьей строки.
В результате мы исключим переменную x 1 из всех уравнений, кроме первого. Получим:
Теперь вычтем из строки 3 строку 2, умноженную на 3:
Теперь вычитаем из 1 строки сначала 3 строку, а затем 2 строку:
После преобразований получаем систему уравнений:
Из этого следует, что система уравнений имеет следующее решение:
x1 = 1, x2 = 3 , x3 = -1
В качестве примера решим систему уравнений, представленную в виде матрицы (Таблица 1), методом Гаусса – Жордана.
Делим первую строку на 3 (элемент первой строки, расположенный на главной диагонали), получим:
Умножаем первую строку на 1 и вычитаем из второй строки. Умножаем первую строку на 6 и вычитаем из третьей строки. Получим:
В первом столбце все элементы кроме диагонального равны нулю, займемся вторым столбцом, для этого выберем вторую строку в качестве опорной. Вторая Делим ее на 17/3:
Умножаем строку 2 на -6 и вычитаем из третьей строки:
Теперь третья строка – опорная, делим ее на -33/17:
Умножаем опорную строку на 3/17 и вычитаем ее из второй. Умножаем третью строку на 1 и вычитаем ее из первой
Получена треугольная матрица, начинается обратный ход алгоритма (во время которого получим единичную матрицу). Вторая строка становится опорной. Умножаем третью строку на 4/3 и вычитаем ее из первой:
Последний столбец матрицы – решение системы уравнений.
Онлайн калькулятор: Метод исключения Гаусса
Система линейных уравнений:
может быть решена методом исключения Гаусса с помощью калькулятора.
В методе исключения Гаусса система линейных уравнений представлена как расширенная матрица, то есть матрица, содержащая коэффициенты уравнения и постоянные члены с размерами [n: n + 1]:
Исключение по Гауссу
8 3 4 5 31 14 4 33 23 17 15 4 23 7 22 4 11 17 1 51Матрица системы линейных уравнений
Точность вычисленийЦифры после десятичной точки: 2
Файл очень большой.Во время загрузки и создания может произойти замедление работы браузера.
Скачать закрыть
content_copy Ссылка сохранить Сохранить расширение Виджет
Исключение по Гауссу
Метод назван в честь Карла Фридриха Гаусса, гениального немецкого математика 19 века. Сам Гаусс не изобрел этот метод. Метод сокращения строк был известен древним китайским математикам; он был описан в «Девяти главах математического искусства», китайской книге по математике, изданной во II веке.
Ликвидация вперед
Первым шагом исключения Гаусса является получение матрицы строковой формы. Левая нижняя часть этой матрицы содержит только нули, и все нулевые строки находятся ниже ненулевых строк:
Матрица приводится к этой форме с помощью элементарных операций со строками: поменять местами две строки, умножить строку на константу, добавить к одной строке скалярное число, кратное другой.
Наш калькулятор получает форму эшелона путем последовательного вычитания верхних строк, умножения на нижние строки, умножения на, где i – ведущая строка коэффициентов (ведущая строка).
Важно, чтобы старший коэффициент отличался от нуля. Если он становится равным нулю, строка заменяется на более низкую с ненулевым коэффициентом в той же позиции.
Обратная замена
На этом этапе операции с элементарными строками продолжаются до тех пор, пока не будет найдено решение. Наконец, он преобразует матрицу в сокращенную форму эшелона строк:
,
Калькулятор метода исключения по Гауссу – Онлайн-программа для сокращения строк
Поиск инструмента
Исключение по Гауссу
Инструмент для применения метода исключения Гаусса и получения формы сокращенного эшелона строки с шагами, деталями, обратной матрицей и векторным решением.
Результаты
Исключение Гаусса – dCode
Тег (и): Матрица, Символьное вычисление
Поделиться
dCode и другие
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор исключения по Гауссу
Преобразователь системы уравнений в матрицу
Ответы на вопросы (FAQ)
Что такое метод исключения Гаусса?
Алгоритм исключения Гаусса (также называемый методом Гаусса-Жордана или методом поворота) позволяет находить решения системы линейных уравнений и определять обратную матрицу.
Алгоритм работает со строками матрицы путем обмена или умножения строк между ними (с точностью до множителя).
На каждом шаге алгоритм стремится ввести в матрицу на элементах за пределами диагонали нулевые значения.
Как вычислить решения системы линейных уравнений с Гауссом?
Первым шагом из системы линейных уравнений является преобразование уравнений в матрицу.
Пример: $$ \ left \ {\ begin {array} {} x & – & y & + & 2z & = & 5 \\ 3x & + & 2y & + & z & = & 10 \\ 2x & – & 3y & – & 2z & = & – 10 \\\ end {массив} \ право.$$ можно записать в форме умножения “> матричного умножения: $$ \ left (\ begin {array} {ccc} 1 & -1 & 2 \\ 3 & 2 & 1 \\ 2 & -3 & 2 \ end { array} \ right). \ left (\ begin {array} {c} x \\ y \\ z \ end {array} \ right) = \ left (\ begin {array} {c} 5 \\ 10 \\ -10 \ end {array} \ right) $$, который соответствует (расширенной) матрице $$ \ left (\ begin {array} {ccc | c} 1 & -1 & 2 & 5 \\ 3 & 2 & 1 & 10 \\ 2 & -3 & 2 & -10 \ end {array} \ right) $$
Затем для каждого элемента за пределами ненулевой диагонали выполните соответствующие вычисления, добавив или вычтя другие строки, чтобы элемент стал 0.
Пример: Отнимите 3 раза (строка 1) до (строка 2), например, элемент в строке 2, столбец 1 станет 0: $$ \ left (\ begin {array} {ccc | c} 1 & -1 & 2 & 5 \\ 0 & 5 & -5 & -5 \\ 2 & -3 & -2 & -10 \ end {array} \ right) $$
Вычтите 2 раза (строка 1) до (строка 3) например, элемент в строке 3, столбец 1 становится 0: $$ \ left (\ begin {array} {ccc | c} 1 & -1 & 2 & 5 \\ 0 & 5 & -5 & -5 \\ 0 & -1 & -6 & -20 \ end {array} \ right) $$
Вычтите 1/5 раз (строка 2) из (строка 3), например, элемент в строке 3, столбец 2 станет 0: $$ \ слева (\ begin {array} {ccc | c} 1 & -1 & 2 & 5 \\ 0 & 5 & -5 & -5 \\ 0 & 0 & -7 & -21 \ end {array} \ right) $$
Вычтите 1/5 раз (строка 2) из (строка 1), например, элемент в строке 1, столбец 2 станет 0: $$ \ left (\ begin {array} {ccc | c} 1 & 0 & 1 & 4 \\ 0 & 5 & -5 & -5 \\ 0 & 0 & -7 & -21 \ end {array} \ right) $$
Отнимите 1/7 раз (строка 3) до (строка 1), например как элемент в строке 1, столбец 3 становится 0: $$ \ left (\ begin {array} {ccc | c} 1 & 0 & 0 & 1 \\ 0 & 5 & -5 & -5 \\ 0 & 0 & -7 & -21 \ end {array} \ right) $$
Вычтите 5/7 раз (строка 3) из (строка 2), например, элемент в строке 2, столбец 3 станет 0: $$ \ left (\ begin {array} {ccc | c} 1 & 0 & 0 & 1 \\ 0 & 5 & 0 & 10 \\ 0 & 0 & -7 & -21 \ end {array} \ right) $$
Упростите каждую линию, разделив значение по диагонали.
Пример: $$ \ left (\ begin {array} {ccc | c} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 2 \\ 0 & 0 & 1 & 3 \ end {array } \ right) $$
Вектор результата – последний столбец.
Пример: $ {1,2,3} $, что соответствует $ {x, y, z} $, поэтому $ x = 1, y = 2, z = 3 $
Задайте новый вопросИсходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Исключение Гаусса». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любой алгоритм, апплет или фрагмент алгоритма исключения Гаусса (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой алгоритм исключения Гаусса ‘функция (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанная на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для «Исключения Гаусса» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Нужна помощь?
Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!
Вопросы / комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
исключение, точка поворота, гаусс, иордан, матрица, система, уравнение
Ссылки
Источник: https: // www.dcode.fr/gaussian-elimination
© 2021 dCode – Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.Калькулятор исключения Гаусса
Как найти неизвестные переменные в уравнениях методом исключения Гаусса?
Исключение Гаусса или сокращение строки , это алгоритм для решения системы линейных уравнений. Этот метод также называется исключением Гаусса-Жордана. Он представлен последовательностью операций, выполняемых над матрицей.Метод назван в честь Карла Фридриха Гаусса (1777-1855), хотя был известен китайским математикам. Метод решения системы линейных уравнений методом исключения Гаусса аналогичен методу решения матриц. Например, существует связь между системой трех линейных уравнений и ее матрицей коэффициентов. $$ \ begin {align} & a_1x + b_1y + c_1z = {d_1} \\ & a_2x + b_2y + c_2z = {d_2} \\ & a_3x + b_3y + c_3z = {d_3} \\ \ end {align} \ quad \ longmapsto \ left ( \ begin {array} {ccc} {a_1} & b_1 & c_1 \\ {a_2} & b_2 & c_2 \\ {a_3} & b_3 & c_3 \\ \ end {массив} \ right) $$ Есть три типа операций с элементарными строками:
- Замена двух рядов;
- Умножение строки на ненулевое число;
- Добавление числа, кратного одной строке, к другой строке.
- Старший коэффициент каждой строки должен составлять 1 доллар;
- Все элементы в столбце ниже $ 1 $ должны быть $ 0 $;
- Все строки, содержащие нули, находятся внизу матрицы.
- Разделите строку $ 1 $ на $ 4 $ ($ R_1 = \ frac {R_1} 4) $, чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & \ frac 54 & \ frac 34 & \ frac {5} 2 \\ 3 и 6 и 7 и 8 \\ 2 и 3 и 0 и 8 \\ \ end {массив} \ right) $$
- Вычтите строку $ 1 $, умноженную на $ 3 $, из строки $ 2 $ ($ R_2 = R_2-3R_1 $), чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & \ frac 54 & \ frac 34 & \ frac {5} 2 \\ 0 & \ frac 94 & \ frac {19} 4 & \ frac 12 \\ 2 и 3 и 0 и 8 \\ \ end {массив} \ справа) $$
- Вычтите строку $ 1 $, умноженную на $ 2 $, из строки $ 3 $ ($ R_3 = R_3-2R_1 $), чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & \ frac 54 & \ frac 34 & \ frac {5} 2 \\ 0 & \ frac 94 & \ frac {19} 4 & \ frac 12 \\ 0 & \ frac12 & – \ frac 32 & 3 \\ \ end {массив} \ справа) $$
- Умножьте строку $ 2 $ на $ \ frac 49 $ ($ R_2 = \ frac49 R_2 $), чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & \ frac 54 & \ frac 34 & \ frac {5} 2 \\ 0 & 1 & \ frac {19} 9 & \ frac 29 \\\ 0 & \ frac12 & – \ frac 32 & 3 \\ \ end {массив} \ справа) $$
- Вычтите строку $ 2 $, умноженную на $ \ frac 54 $, из строки $ 1 $ ($ R_1 = R_1- \ frac54 R_2 $), чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & 0 & – \ frac {17} 9 & \ frac {20} 9 \\ 0 & 1 & \ frac {19} 9 & \ frac 29 \\ 0 & \ frac12 & – \ frac 32 & 3 \\ \ end {массив} \ справа) $$
- Вычтите строку $ 2 $, умноженную на $ \ frac 12 $, из строки $ 3 $ ($ R_3 = R_3- \ frac12R_2 $), чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & 0 & – \ frac {17} 9 & \ frac {20} 9 \\ 0 & 1 & \ frac {19} 9 & \ frac 29 \\ 0 & 0 & – \ frac {23} 9 & \ frac {26} 9 \\ \ end {массив} \ right) $$
- Умножьте строку $ 3 $ на $ – \ frac9 {23} $ ($ R_3 = – \ frac9 {23} R_3 $), чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & 0 & – \ frac {17} 9 & \ frac {20} 9 \\ 0 & 1 & \ frac {19} 9 & \ frac 29 \\ 0 & 0 & 1 & – \ frac {26} {23} \\ \ end {массив} \ справа) $$
- Добавьте строку $ 3 $, умноженную на $ \ frac {17} 9 $, в строку $ 1 $ ($ R_1 = R_1 + \ frac {17} 9R_3 $), чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & 0 & 0 & \ frac2 {23} \\ 0 & 1 & \ frac {19} 9 & \ frac 29 \\ 0 & 0 & 1 & – \ frac {26} {23} \\ \ end {массив} \ справа) $$
- Вычтите строку $ 3 $, умноженную на $ \ frac {19} 9 $, из строки $ 2 $ ($ R_2 = R_2- \ frac {19} 9R_3 $), чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & 0 & 0 & \ frac2 {23} \\ 0 & 1 & 0 & \ frac {60} {23} \\ 0 & 0 & 1 & – \ frac {26} {23} \\ \ end {массив} \ right) $$ Итак, решение системы: $ (x, y, z) = (\ frac {2} {23}, \ frac {60} {23}, – \ frac {26} {23}) $.
M.7 Устранение Гаусса-Джордана | STAT ONLINE
Исключение Гаусса-Жордана – это алгоритм, который можно использовать для решения систем линейных уравнений и поиска обратной матрицы для любой обратимой матрицы. Он основан на трех операциях с элементарной строкой , которые можно использовать с матрицей:
- Поменять местами две строки
- Умножьте одну из строк на ненулевой скаляр.
- Добавить или вычесть скалярное кратное одной строки из другой строки.
В качестве примера операции с первой элементарной строкой поменяйте местами 1-ю и 3-ю строки.
\ [\ begin {pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \ end {pmatrix} \ Rightarrow \ begin {pmatrix} 7 & 5 & 0 \\ 2 & -2 & 3 \\ 4 & 0 & -1 \ end {pmatrix} \]
Для примера операции со второй элементарной строкой умножьте вторую строку на 3.
\ [\ begin {pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \ end {pmatrix} \ Rightarrow \ begin {pmatrix} 4 & 0 & -1 \\ 6 & -6 & 9 \\ 7 & 5 & 0 \ end {pmatrix} \]
В качестве примера операции с третьей элементарной строкой добавьте дважды первую строку ко второй строке.
\ [\ begin {pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \ end {pmatrix} \ Rightarrow \ begin {pmatrix} 4 & 0 & -1 \\ 10 & -2 & 1 \\ 7 & 5 & 0 \ end {pmatrix} \]
Редукторный эшелон формы
Цель метода исключения Гаусса-Жордана состоит в том, чтобы использовать три операции с элементарными строками для преобразования матрицы в эшелонированную форму сокращенных строк.Матрица находится в форме сокращенного эшелона строки , также известной как каноническая форма строки , если выполняются следующие условия:
- Все строки с нулевыми записями находятся внизу матрицы
- Первая ненулевая запись в строке, называемая ведущей записью или поворотной точкой , каждой ненулевой строки находится справа от ведущей записи строки над ней.
- Начальная запись, также известная как точка поворота, в любой ненулевой строке равна 1.
- Все остальные записи в столбце, содержащие в начале 1, являются нулями.
Например,
\ [A = \ begin {pmatrix} 1 & 0 & 0 \\ 0 & 1 & 3 \\ 0 & 0 & 0 \ end {pmatrix}, B = \ begin {pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {pmatrix}, C = \ begin {pmatrix} 0 & 7 & 3 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \ end {pmatrix}, D = \ begin {pmatrix} 1 & 7 & 3 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {pmatrix} \]
Матрицы A, и B находятся в форме уменьшенного ряда, а матрицы C и D – нет. C не находится в форме пониженного ряда, поскольку нарушает условия два и три. D не находится в форме пониженного ряда, поскольку нарушает четвертое условие. Кроме того, операции с элементарными строками могут использоваться для уменьшения матрицы D в матрицу B .
Шаги для исключения Гаусса-Джордана
Для выполнения исключения Гаусса-Джордана:
- Поменяйте местами строки так, чтобы все строки со всеми нулевыми записями находились внизу
- Поменяйте местами строки так, чтобы строка с самой большой левой ненулевой записью была наверху.
- Умножьте верхнюю строку на скаляр так, чтобы ведущая запись верхней строки стала 1.
- Сложить / вычесть кратные числа верхней строки из других строк, чтобы все остальные записи в столбце, содержащем ведущую запись верхней строки, были равны нулю.
- Повторите шаги 2–4 для следующей самой левой ненулевой записи, пока все ведущие записи не станут 1.
- Поменяйте местами строки так, чтобы ведущая запись каждой ненулевой строки находилась справа от ведущей записи строки над ней.
Выбранные примеры видео показаны ниже:
Чтобы получить инверсию матрицы n × n A :
- Создайте разделенную матрицу \ ((A | I) \), где I – единичная матрица.{-1} = I \).
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследовать
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О Массачусетском технологическом институте
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О Массачусетском технологическом институте
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
Онлайн-регрессия и видение гауссовского процесса разреженной матрицы…
Онлайн Редкая Матрица Гаусса Процесс Регрессия < strong> и Vision Applications Ananth Ranganathan 1 и Ming-Hsuan Yang 2 1 Исследовательский институт Honda, Mountain View, CA 94041 [email protected] 2 Калифорнийский университет, Мерсед, Калифорния, 95344 mhyang @ ucmerced.edu Abstract. Мы представляем новый алгоритм вывода Гаусса Процесс , который называется Онлайн Разреженная Матрица <сильная > Gaussian Process es (OSMGP), и демонстрируют свои достоинства с помощью нескольких приложений машинного зрения. OSMGP основан на наблюдении, что для ядер с локальной поддержкой матрица Грама обычно разреженная.Поддержание и обновления разреженного фактора Холецкого матрицы Грама может быть эффективно выполнено с помощью вращений Гивенса. Это приводит к точному онлайн-алгоритму, время обновления которого линейно зависит от размера матрицы Грама. Кроме того, если приблизительные обновления допустимы, коэффициент Холецкого можно поддерживать на постоянном уровне, используя гиперболические вращения для удаления определенных строк и столбцов, соответствующих отброшенным обучающим примерам. Мы демонстрируем, что с помощью этих значений матрицы можно включить онлайн-оценку гиперпараметров, не влияя на линейную сложность выполнения алгоритма.Алгоритм OSMGP применяется для решения задач визуального отслеживания смещения головы. Экспериментальные результаты показывают, что предложенный метод точен, эффективен и хорошо обобщается при использовании онлайн-обучения. 1 Введение Изучение функций регрессии на основе данных было важной проблемой в машинном обучении и компьютерном зрении с многочисленными приложениями. В последние годы машины с ядром, такие как Support Vector Machines и Gaussian Process es, продемонстрировали большой успех в изучении нелинейных отображений между данными большой размерности и их низкоразмерные представления.Для многочисленных приложений машинного зрения, где у нас есть непрерывный поток данных, очень интересно изучать функции нелинейной регрессии в интерактивном режиме. В этой статье мы предлагаем новый алгоритм регрессии Gaussian Process (GP), который называется Online Sparse . Матричная Гауссовская процессная (OSMGP) регрессия, то есть точная и позволяет быстро обновлять онлайн за линейное время для функций ядра с локальной поддержкой .Эта комбинация точного вывода и быстрых онлайн-обновлений является новым вкладом. Мы показываем, что, когда матрица Грама является разреженной, как в случае использования ядер с локальной поддержкой, эффективным представлением является поддержание и обновления фактора Холецкого матрицы Грама вместо самой матрицы. Во время онлайн-обучения, когда к обучающей последовательности добавляется новая точка, в матрицу Грама вводятся новые строки и столбца.Вместо того, чтобы пересчитывать коэффициент Холецкого для матрицы, что было бы дорогостоящим, мы используем вращения Гивенса для его постепенного обновления. Повороты Гивенса гарантированно обновляют факторизацию за время O (n) для разреженной матрицы, где матрица Грама имеет размер n × n, но на практике может быть намного быстрее.
Обращение матрицы с использованием исключения Гаусса-Джордана
М. Борна
В этом разделе мы увидим, как работает метод исключения Гаусса-Жордана, на примерах.
Вы можете повторно загружать эту страницу сколько угодно раз и каждый раз получать новый набор чисел. Вы также можете выбрать матрицу другого размера (внизу страницы).
(Если вам сначала нужна дополнительная информация, вернитесь к «Введение в матрицы»).
Выберите размер матрицы, который вас интересует, и нажмите кнопку.
Матрица A:
Пример, сгенерированный случайным образом, показан ниже.
Телефонные пользователи
ПРИМЕЧАНИЕ. Если вы разговариваете по телефону, вы можете прокрутить любую матрицу шириной на этой странице вправо или влево, чтобы увидеть все выражение.
Пример (3 × 3)
Найдите матрицу, обратную матрице A , используя метод исключения Гаусса-Жордана.
| А = | 12 | 6 | 13 | ||
| 7 | 2 | 10 | |||
| 14 | 9 | 11 |
Наша процедура
Запишем матрицу A слева и матрицу идентичности I справа, разделенную пунктирной линией, как показано ниже.Результат называется расширенной матрицей .
Мы включили номера строк, чтобы было понятнее.
| 12 | 6 | 13 | |
| 7 | 2 | 10 | |
| 14 | 9 | 11 |
| 1 | 0 | 0 | Ряд [1] | |
| 0 | 1 | 0 | Ряд [2] | |
| 0 | 0 | 1 | Ряд [3] |
Затем мы выполняем несколько операций со строками над двумя матрицами, и наша цель – получить единичную матрицу на левом , например:
| ? | ? | ? | Ряд [1] | |
| ? | ? | ? | Ряд [2] | |
| ? | ? | ? | Ряд [3] |
(Технически мы сокращаем матрицу A до сокращенного эшелона строк с формы , также называемой канонической формой строк ).
Результирующая матрица справа будет обратной матрицей A .
Наша процедура операций со строками выглядит следующим образом:
- Получим “1” в верхнем левом углу, разделив первую строку
- Тогда мы получим «0» в оставшейся части первого столбца
- Затем нам нужно получить “1” во второй строке, втором столбце
- Затем мы делаем все остальные записи во втором столбце «0».
Продолжаем так до тех пор, пока слева не останется единичная матрица.
Давайте теперь продолжим и найдем обратное.
Решение
Начнем с:
| 12 | 6 | 13 | |
| 7 | 2 | 10 | |
| 14 | 9 | 11 |
| 1 | 0 | 0 | Ряд [1] | |
| 0 | 1 | 0 | Ряд [2] | |
| 0 | 0 | 1 | Ряд [3] |
Новая строка [1]
Разделите строку [1] на 12 (чтобы получить “1” в нужной позиции):
Это дает нам:
| 1 | 0.5 | 1,0833 | |
| 7 | 2 | 10 | |
| 14 | 9 | 11 |
| 0,0833 | 0 | 0 | Ряд [1] | |
| 0 | 1 | 0 | Ряд [2] | |
| 0 | 0 | 1 | Ряд [3] |
Новый ряд [2]
Ряд [2] – 7 × Ряд [1] (чтобы получить 0 в желаемой позиции):
7 – 7 × 1 = 0
2 – 7 × 0.5 = -1,5
10 – 7 × 1,0833 = 2,4167
0 – 7 × 0,0833 = -0,5833
1 – 7 × 0 = 1
0 – 7 × 0 = 0
Это дает нам новую строку [2]:
| 1 | 0,5 | 1,0833 | |
| 0 | -1,5 | 2,4167 | |
| 14 | 9 | 11 |
| 0,0833 | 0 | 0 | Ряд [1] | |
| -0.5833 | 1 | 0 | Ряд [2] | |
| 0 | 0 | 1 | Ряд [3] |
Новый ряд [3]
Ряд [3] – 14 × Ряд [1] (чтобы получить 0 в желаемой позиции):
14 – 14 × 1 = 0
9 – 14 × 0,5 = 2
11 – 14 × 1,0833 = -4,1667
0 – 14 × 0,0833 = -1,1667
0 – 14 × 0 = 0
1 – 14 × 0 = 1
Это дает нам новую строку [3]:
| 1 | 0.5 | 1,0833 | |
| 0 | -1,5 | 2,4167 | |
| 0 | 2 | -4,1667 |
| 0,0833 | 0 | 0 | Ряд [1] | |
| -0,5833 | 1 | 0 | Ряд [2] | |
| -1,1667 | 0 | 1 | Ряд [3] |
Новый ряд [2]
Разделите строку [2] на -1.5 (чтобы получить “1” в желаемой позиции):
Это дает нам:
| 1 | 0,5 | 1,0833 | |
| 0 | 1 | -1,6111 | |
| 0 | 2 | -4,1667 |
| 0,0833 | 0 | 0 | Ряд [1] | |
| 0,3889 | -0.6667 | 0 | Ряд [2] | |
| -1,1667 | 0 | 1 | Ряд [3] |
Новая строка [1]
Ряд [1] – 0,5 × Ряд [2] (чтобы получить 0 в желаемой позиции):
1 – 0,5 × 0 = 1
0,5 – 0,5 × 1 = 0
1,0833 – 0,5 × -1,6111 = 1,8889
0,0833 – 0,5 × 0,3889 = -0,1111
0 – 0,5 × -0,6667 = 0,3333
0 – 0,5 × 0 = 0
Это дает нам новую строку [1]:
| 1 | 0 | 1.8889 | |
| 0 | 1 | -1,6111 | |
| 0 | 2 | -4,1667 |
| -0,1111 | 0,3333 | 0 | Ряд [1] | |
| 0,3889 | -0,6667 | 0 | Ряд [2] | |
| -1,1667 | 0 | 1 | Ряд [3] |
Новый ряд [3]
Ряд [3] – 2 × Ряд [2] (чтобы получить 0 в желаемой позиции):
0 – 2 × 0 = 0
2 – 2 × 1 = 0
-4.1667 – 2 × -1,6111 = -0,9444
-1,1667 – 2 × 0,3889 = -1,9444
0 – 2 × -0,6667 = 1,3333
1-2 × 0 = 1
Это дает нам новую строку [3]:
| 1 | 0 | 1.8889 | |
| 0 | 1 | -1,6111 | |
| 0 | 0 | -0,9444 |
| -0,1111 | 0,3333 | 0 | Ряд [1] | |
| 0.3889 | -0,6667 | 0 | Ряд [2] | |
| -1,9444 | 1,3333 | 1 | Ряд [3] |
Новый ряд [3]
Разделите строку [3] на -0,9444 (чтобы получить “1” в нужной позиции):
Это дает нам:
| 1 | 0 | 1.8889 | |
| 0 | 1 | -1.6111 | |
| 0 | 0 | 1 |
| -0,1111 | 0,3333 | 0 | Ряд [1] | |
| 0,3889 | -0,6667 | 0 | Ряд [2] | |
| 2,0588 | -1,4118 | -1,0588 | Ряд [3] |
Новая строка [1]
Ряд [1] – 1.8889 × Ряд [3] (чтобы получить 0 в желаемой позиции):
1 – 1.8889 × 0 = 1
0 – 1.8889 × 0 = 0
1.8889 – 1.8889 × 1 = 0
-0,1111 – 1,8889 × 2,0588 = -4
0,3333 – 1,8889 × -1,4118 = 3
0 – 1,8889 × -1,0588 = 2
Это дает нам новую строку [1]:
| 1 | 0 | 0 | |
| 0 | 1 | -1,6111 | |
| 0 | 0 | 1 |
| -4 | 3 | 2 | Ряд [1] | |
| 0.3889 | -0,6667 | 0 | Ряд [2] | |
| 2,0588 | -1,4118 | -1,0588 | Ряд [3] |
Новый ряд [2]
Строка [2] – -1,6111 × Строка [3] (чтобы получить 0 в желаемой позиции):
0 – -1,6111 × 0 = 0
1 – -1,6111 × 0 = 1
-1,6111 – -1,6111 × 1 = 0
0,3889 – -1,6111 × 2,0588 = 3,7059
-0,6667 – -1,6111 × -1,4118 = -2,9412
0 – -1.6111 × -1,0588 = -1,7059
Это дает нам новую строку [2]:
| -4 | 3 | 2 | Ряд [1] | |
| 3.7059 | -2,9412 | -1,7059 | Ряд [2] | |
| 2,0588 | -1,4118 | -1,0588 | Ряд [3] |
Мы достигли нашей цели по созданию матрицы идентичности слева.Таким образом, мы можем заключить, что инверсия матрицы A является правой частью расширенной матрицы:
| А -1 = | -4 | 3 | 2 | ||
| 3.7059 | -2,9412 | -1,7059 | |||
| 2,0588 | -1,4118 | -1,0588 |
Примечания
- Приведенное выше объяснение показывает все шаги.Человек обычно может пойти несколькими путями. Кроме того, иногда в правильной позиции уже есть «1» или «0», и в этих случаях нам не нужно ничего делать для этого шага.
- Всегда записывайте, что вы делаете на каждом этапе – очень легко заблудиться!
- Я показал результаты с точностью до 4 знаков после запятой, но с максимальной точностью использовалась повсюду. Имейте в виду, что небольшие ошибки округления будут накапливаться во всей задаче. Всегда используйте полную точность калькулятора! (Полностью используйте память вашего калькулятора.)
- Очень иногда возникают странные результаты из-за внутреннего представления чисел компьютером. То есть он может хранить «1» как 0,999999999872.
Смотрите еще?
Вы можете вернуться к началу страницы и выбрать другой пример.
.