Решение высшей математики онлайн
‹– Назад
Для того чтобы дать определение предела функции нескольких переменных, нужно напомнить общее определение базы предела и предела функции по данной базе. Пусть функция имеет область определения .
Определение 7.8 Базой называется такой набор множеств , называемых окончаниями базы, что, во-первых, все не пусты и, во-вторых, если , то найдётся такое окончание , что .
Определение 7.9 Пусть функция такова, что её область определения содержит целиком некоторое окончание базы . Число называется пределом функции по базе , если для любого, сколь угодно малого, числа найдётся такое окончание базы , что при всех выполняется неравенство .
Число обозначается тогда
Дадим примеры баз, используемых при вычислении пределов функций нескольких переменных.
Пример 7.6 Пусть . Назовём -окрестностью точки открытый шар радиуса с центром в точке . Множество всех таких шаров образует, как нетрудно видеть, базу окрестностей точки .
Назовём проколотой -окрестностью открытый шар радиуса с центром в точке , из которого выброшена сама точка , то есть
База всех проколотых -окрестностей точки обозначается .
Пусть — некоторое фиксированное непустое множество в и . Рассмотрим в качестве окончаний все пересечения с проколотыми -окрестностями точки :
Тогда совокупность всех образуют базу. Эту базу мы будем обозначать .
Рис.7.8.
Если , то при достаточно малых окончания совпадают с проколотыми окрестностями точки .
Рис.7.9.
Пример 7.7 Множества
то есть внешности шаров радиуса с центром в начале координат, образуют базу окрестностей бесконечности. Эта база обозначается .
По любой из приведённых баз можно вычислять предел функции нескольких переменных, при условии, что функция определена на каком-нибудь окончании данной базы.
Например, число служит пределом функции при , где — внутренняя точка области , если для любого числа найдётся такое (достаточно малое) число , задающее проколотую окрестность , что при будет выполнено неравенство .
В этом случае будем писать
Если же — не внутренняя, а граничная точка области , то можно рассмотреть предел функции по базе . (Заметим, что если и , то предел по базе заведомо не имеет смысла, так как функция не определена во всех точках ни одного из окончаний этой базы). Вся разница с пределом по базе будет состоять в том, что требовать выполнения неравенства мы теперь будем лишь в тех точках проколотой -окрестности точки , которые одновременно принадлежат и . Предел
мы будем называть пределом функции при , стремящемся к изнутри области .
Общие свойства пределов были нами изучены в курсе математики в первом семестре. Эти свойства верны и для пределов функций нескольких переменных.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Применение эквивалентных функций при решении пределов
Метод решения
Применение эквивалентных функций позволяет упростить вычисление пределов.
Если нам нужно вычислить предел дроби, то мы можем заменить множители в числителе и знаменателе эквивалентными функциями и вычислять предел от более простого выражения. Подчеркнем, что речь идет именно о множителях в дробях и произведениях. Замена эквивалентными функциями в других выражениях, например в суммах, может привести к неправильному результату. Однако, ошибки не будет, если выразить любую функцию в виде суммы эквивалентной ей функции и о малого (см. пример ⇓).
Все связанные с этим определения и теоремы приводятся на странице «О большое и о малое. Сравнение функций». Напомним некоторые из них.
Применяемые определения и теоремы
Определение эквивалентных функций
Функции f и g называются эквивалентными (асимптотически равными) при :
при ,
если на некоторой проколотой окрестности точки ,
при , причем
.
Если при , то ;
если , то .
При этом функцию называют главной частью при . См. теорему о связи эквивалентных функций с о малым
Теорема о замене функций эквивалентными в пределе частного
Если, при , и и существует предел
, то существует и предел
.
Доказательство
Отметим часто применяемое следствие этой теоремы. Пусть мы имеем частное, составленное из конечного произведения функций: . Тогда, при вычислении предела, эти функции можно заменить на эквивалентные:
,
где . Знак равенства означает, что если существует один из этих пределов, то существует и равный ему второй. Если не существует один из пределов, то не существует и второй.
Таблица эквивалентных функций
Далее приводится таблица функций, эквивалентных при . Здесь t может быть как переменной, так и бесконечно малой функцией при : ; .
| Эквивалентность при | Равенство при |
Предостережение
Как указывалось в самом начале, производить замену функций эквивалентными можно только в множителях дробей и произведений, предел которых мы хотим найти.
В других выражениях, например в суммах, делать такую замену нельзя.
В качестве примера рассмотрим следующий предел:
.
При . Но если заменить в числителе на x, то получим ошибку:
.
Ошибки не будет, если выразить синус через эквивалентную функцию и о малое, :
.
Поскольку и , то мы снова получили неопределенность 0/0. Это указывает на то, что для вычисления этого предела применение эквивалентной функции не достаточно. Нужно применить другой метод.
Можно решить этот пример разложением в ряд Маклорена:
.
Также можно применить правило Лопиталя:
.
Примеры
Все примеры Далее мы приводим подробные решения следующих пределов, упрощая вычисления с помощью эквивалентных функций.
⇓, ⇓, ⇓, ⇓.
Пример 1
Все примеры ⇑ Найти предел:
.
Решение
Из таблицы эквивалентных функций ⇑ имеем:
. Поскольку исходная функция является дробью и каждая из этих функций входит в нее в виде множителя в числителе или знаменателе, то заменим их на эквивалентные.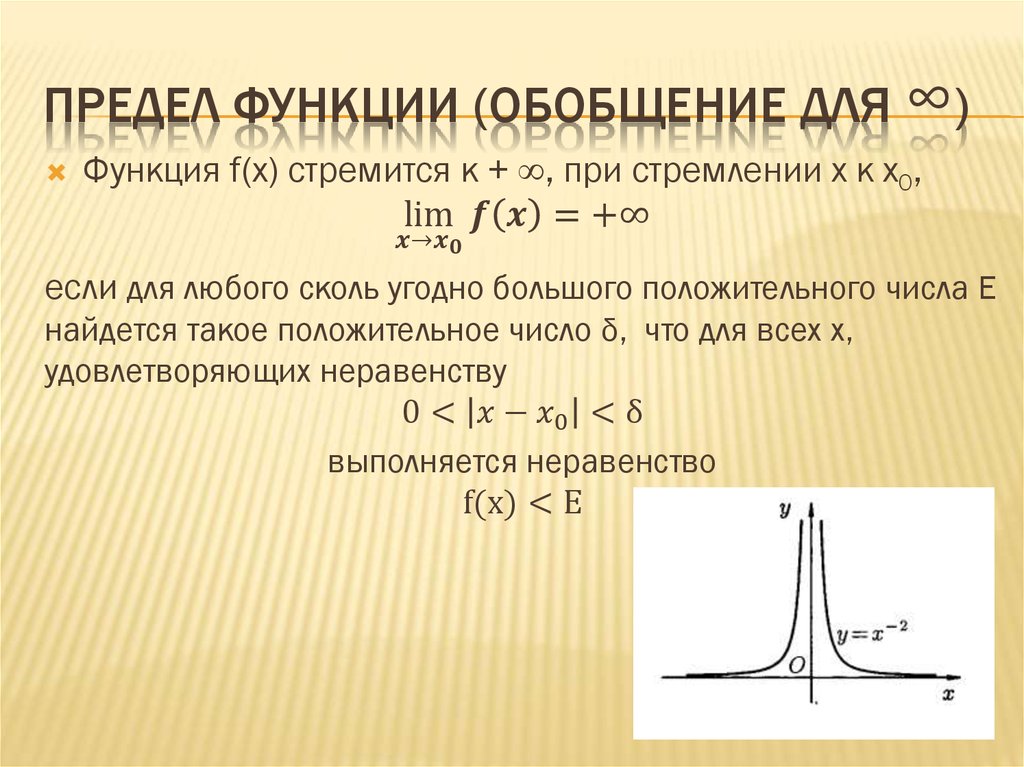
.
Ответ
Пример 2
Все примеры ⇑ Найти предел:
.
Решение
Из таблицы эквивалентных функций ⇑ находим:
.
Преобразуем квадрат логарифма:
.
Поскольку исходная функция является дробью и каждая из этих функций входит в нее в виде множителя в числителе или знаменателе, то заменим их на эквивалентные.
.
Ответ
Пример 3
Все примеры ⇑ Вычислить предел.
.
Решение
Здесь мы имеем неопределенность вида один в степени бесконечность. Приводим ее к неопределенности вида 0/0. Для этого воспользуемся тем, что экспонента и натуральный логарифм являются взаимно обратными функциями.
.
Теперь в показателе экспоненты у нас неопределенность вида 0/0.
Вычисляем предел:
.
Поскольку у нас дробь, то заменим некоторые множители в числителе и знаменателе эквивалентными функциями, пользуясь приведенной выше таблицей ⇑.
;
;
.
Поскольку экспонента непрерывна для всех значений аргумента, то по теореме о пределе непрерывной функции от функции имеем:
.
Ответ
Пример 4
Все примеры ⇑ Вычислить предел.
.
Решение
При . Выясним, к чему стремится . Поскольку здесь дробь, то заменим логарифм эквивалентной функцией: . Тогда
. Таким образом, мы имеем неопределенность вида ∞–∞.
Преобразуем ее к неопределенности вида 0/0. Для этого приводим дроби к общему знаменателю.
.
Здесь мы также воспользовались формулой . После преобразований, наш предел принимает следующий вид:
.
В знаменателе мы сразу можем заменить натуральный логарифм эквивалентной функцией, как это сделали выше:
.
В числителе имеется произведение двух множителей, каждый из которых тоже можно заменить эквивалентной функцией и, таким образом, упростить вычисления. В качестве эквивалентных, попробуем найти степенные функции:
.
Тогда . Считаем, что . Раскрываем неопределенность по правилу Лопиталя.
.
Если положить , то . Тогда
.
Тот же результат можно получить, применяя разложение в ряд Тейлора при :
.
Отсюда .
Найдем эквивалентную функцию для второго множителя, используя разложение в ряд Тейлора при :
.
Отсюда .
Теперь заменим множители эквивалентными функциями:
.
Примечание. Заметим, что делать замену функций на эквивалентные можно, только если функция, от которой ищется предел, является дробью или произведением. Тогда часть множителей в числителе или знаменателе можно заменить эквивалентными функциями. Так, если бы мы с самого начала заменили \ln (1+x) на x, то получили бы ошибку.
Ответ
Использованная литература:
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.
Исчисление I – Непрерывность
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.
е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2.9: Непрерывность
В последних нескольких разделах мы использовали термин «достаточно хороший» для определения тех функций, пределы которых мы могли бы оценить, просто оценивая функцию в рассматриваемой точке. Пришло время формально определить, что мы подразумеваем под «достаточно хорошим».
Определение
Функция \(f\left( x \right)\) называется непрерывной в точке \(x = a\), если
\[\ mathop {\lim }\limits_{x \to a} f\left( x \right) = f\left(a \right)\]
Функция называется непрерывной на отрезке \(\left[ {a,b} \right]\), если она непрерывна в каждой точке отрезка.
Обратите внимание, что это определение также неявно предполагает, что как \(f\left( a \right)\), так и \(\mathop {\lim }\limits_{x \to a} f\left( x \right)\ ) существует. Если любой из них не существует, функция не будет непрерывной в \(х = а\). 9+ }} f\left( x \right) = f\left( a \right)\]
Это точно такой же факт, который мы впервые записали, когда начали рассматривать пределы, за исключением того, что мы заменили фразу «достаточно приятно» на «непрерывно».
Приятно, наконец, узнать, что мы подразумеваем под «достаточно хорошим», однако это определение на самом деле не говорит нам, что именно означает, что функция должна быть непрерывной. Давайте рассмотрим пример, который поможет нам понять, что означает непрерывность функции.
Пример 1. Учитывая график \(f\left( x \right)\), показанный ниже, определите, является ли \(f\left( x \right)\) непрерывным в \(x = – 2\), \( х = 0\) и \(х = 3\).
Показать решение
Чтобы ответить на вопрос для каждой точки, нам нужно получить как предел в этой точке, так и значение функции в этой точке.
Если они равны, то функция в этой точке непрерывна, а если не равны, то функция в этой точке непрерывна.
Первый \(x = – 2\).
\[f\left( {- 2} \right) = 2\hspace{0.5in}\mathop {\lim }\limits_{x \to – 2} f\left(x \right)\,\,\, {\mbox{не существует}}\]
Значение функции и предел не совпадают, поэтому в этой точке функция не является непрерывной. Такой разрыв в графе называется разрывом
Теперь \(х = 0\).
\ [f \ влево ( 0 \ вправо) = 1 \ hspace {0,5 дюйма} \ mathop {\ lim } \ limit_ {x \ to 0} f \ влево ( x \ вправо) = 1 \]
В этой точке функция непрерывна, так как функция и предел имеют одно и то же значение.
Наконец \(x = 3\).
\ [f \ влево ( 3 \ вправо) = – 1 \ hspace {0,5 дюйма} \ mathop {\ lim } \ limit_ {x \ to 3} f \ влево ( x \ вправо) = 0 \]
В этот момент функция не является непрерывной. Этот вид разрыва называется устранимым разрывом . Устранимые разрывы — это те, где в графе есть дыра, как в этом случае.
Из этого примера мы можем быстро получить «рабочее» определение непрерывности. Функция непрерывна на отрезке, если мы можем нарисовать график от начала до конца, ни разу не взяв в руки карандаш. Граф в последнем примере имеет только два разрыва, так как есть только два места, где нам пришлось бы взяться за карандаш, рисуя его.
Другими словами, функция непрерывна, если на ее графике нет дыр или разрывов.
Для многих функций легко определить, где они не будут непрерывными. Функции не будут непрерывными там, где есть такие вещи, как деление на ноль или логарифмирование нуля. Давайте быстро рассмотрим пример определения того, где функция не является непрерывной.
2} – 2t – 15}}\]
92} – 2t – 15 = \left( {t – 5} \right)\left( {t + 3} \right) = 0\]
Значит, функция не будет непрерывной в точках \(t=-3\) и \(t=5\).
Приятным следствием преемственности является следующий факт.
Факт 2
Если \(f\left( x \right)\) непрерывно в \(x = b\) и \(\mathop {\lim }\limits_{x \to a} g\left( х \справа) = б\) тогда
\[\ mathop {\lim }\limits_{x \to a} f\left({g\left(x\right)} \right) = f\left( {\mathop {\lim }\limits_{x \ к } г\влево( х \вправо)} \вправо)\] 90} = 1\]
Другим очень хорошим следствием непрерывности является теорема о промежуточном значении.
Теорема о промежуточном значении
Предположим, что \(f\left( x \right)\) непрерывно на \(\left[ {a,b} \right]\) и пусть \(M\) будет любым числом между \(f\left( a \right)\) и \(f\left( b \right)\). Тогда существует число \(c\) такое, что
- \(a < c < b\)
- \(е\влево(с\вправо) = М\)
Теорема о промежуточном значении на самом деле говорит о том, что непрерывная функция будет принимать все значения между \(f\left( a \right)\) и \(f\left( b \right)\).
Как видно из этого изображения, если мы выберем любое значение \(M\), то есть между значением \(f\left( a \right)\) и значением \(f\left( b \right)\) и проведите из этой точки прямую линию, которая будет пересекаться с графиком хотя бы в одной точке. Другими словами, где-то между \(a\) и \(b\) функция примет значение \(M\). Кроме того, как показано на рисунке, функция может принимать значение более чем в одном месте.
Также важно отметить, что теорема о промежуточном значении говорит только о том, что функция будет принимать значение \(M\) где-то между \(a\) и \(b\). Не сказано, каким именно будет это значение. Это только говорит о том, что он существует.
Итак, теорема о промежуточном значении говорит нам, что функция будет принимать значение \(M\) где-то между \(a\) и \(b\), но она не говорит нам, где она примет значение или говорит ли он нам, сколько раз он будет принимать значение.
2} – 10x + 5\) имеет корень где-то в интервале \(\left[ { – 1, 2} \справа]\).
Показать решение
На самом деле мы спрашиваем здесь, примет ли функция значение
или нет. \[р\влево( х \вправо) = 0\]
где-то между -1 и 2. Другими словами, мы хотим показать, что существует число \(c\) такое, что \(- 1 < c < 2\) и \(p\left( c \right) = 0\). Однако если мы определим \(M = 0\) и признаем, что \(a = -1\) и \(b = 2\), мы увидим, что эти два условия на \(c\) являются в точности выводами промежуточного Теорема о ценности.
Итак, эта задача построена на использовании теоремы о промежуточном значении, и на самом деле все, что нам нужно сделать, это показать, что функция непрерывна и что \(M = 0\) находится между \(p\left( { – 1} \right)\) и \(p\left( 2 \right)\) ( 
Для этого все, что нам нужно сделать, это вычислить,
\[p\left( { – 1} \right) = 8\hspace{0.5in}\hspace{0.25in}p\left( 2 \right) = – 19\]
Итак, имеем
\[ – 19 = p\влево( 2 \вправо) < 0 < p\влево( { - 1} \вправо) = 8\]
Следовательно, \(M = 0\) находится между \(p\left( { – 1} \right)\) и \(p\left( 2 \right)\), а поскольку \(p\left( x \ right)\) — полином, он непрерывен везде и, в частности, непрерывен на отрезке \([-1,2]\). Таким образом, по теореме о промежуточном значении должно существовать число \(-1 \[р\влево( с \вправо) = 0\] Следовательно, у многочлена есть корень между -1 и 2. Для полноты картины вот график, показывающий корень, существование которого мы только что доказали. Обратите внимание, что мы использовали компьютерную программу, чтобы фактически найти корень, и что теорема о промежуточном значении не сказала нам, что это за значение.
Давайте рассмотрим еще один пример теоремы о промежуточном значении.
92}}}{2}} \right)\) принимает следующие значения в интервале \([0,5]\).- Соответствует ли \(f\left( x \right) = 10\)?
- Соответствует ли \(f\left( x \right) = – 10\)?
Показать все решения Скрыть все решения
Показать обсуждение
Итак, как и в предыдущем примере, нас просят определить, если возможно, принимает ли функция одно из двух значений выше в интервале [0,5]. Во-первых, давайте заметим, что это непрерывная функция, и поэтому мы знаем, что можем использовать теорему о промежуточном значении для решения этой проблемы.
Теперь для каждой части мы допустим, что \(M\) будет заданным значением для этой части, а затем нам нужно будет показать, что \(M\) находится между \(f\left( 0 \right)\) и \(f\left( 5 \right)\). Если это так, то мы можем использовать теорему о промежуточном значении, чтобы доказать, что функция будет принимать заданное значение.
Итак, поскольку нам понадобятся две оценки функций для каждой части, давайте приведем их здесь,
\[f\влево( 0 \вправо) = 2,8224\hspace{0,5 дюйма}\hspace{0,25 дюйма}f\влево( 5 \вправо) = 19.7436\]
Теперь давайте рассмотрим каждую часть.
a Соответствует ли \(f\left( x \right) = 10\)? Показать решение
Хорошо, в этом случае мы определим \(M = 10\) и увидим, что
\[f\влево( 0 \вправо) = 2,8224 < 10 < 19,7436 = f\влево( 5 \вправо)\]
Итак, по теореме о промежуточном значении должно быть число \(0 \le c \le 5\) такое, что
\[е\влево(с\вправо) = 10\]
b Соответствует ли \(f\left( x \right) = – 10\)? Показать решение
В этой части мы определим \(M = – 10\). Теперь у нас есть проблема. В этой части \(M\) не живет между \(f\left( 0 \right)\) и \(f\left( 5 \right)\).
2}) }}{2}} \right)\) в интервале [0,5].
Из этого графика видно, что не только \(f\left( x \right) = – 10\) в [0,5], но и всего 4 раза! Также обратите внимание, что, как мы проверили в первой части предыдущего примера, \(f\left( x \right) = 10\) в [0,5], и на самом деле это происходит всего 3 раза.
Итак, помните, что теорема о промежуточном значении проверяет только то, что функция принимает заданное значение. Он никогда не будет исключать получение значения функцией. Кроме того, если мы можем использовать теорему о промежуточном значении для проверки того, что функция будет принимать значение, она никогда не говорит нам, сколько раз функция будет принимать значение, она только говорит нам, что она действительно принимает значение.
15.3. Предел функции
Предел функции f(x) при приближении x к c является действительным числом L .
Для существования предела:
1) Правый предел существует.
2) Левый предел существует.
3) Правый предел равен левому пределу.
Когда предела не существует, может быть несколько вещей:
1) Правый предел не равен левому пределу.
2) Функция бесконечно возрастает как x приближается к c .
3) Функция колеблется между двумя фиксированными значениями, когда x приближается к c .
4) График функции имеет скачкообразный разрыв на x = c .
5) График функции имеет бесконечный разрыв на x = c .
Иллюстративный пример
Проверьте, существует ли ограничение. Если да, то найти предел.
Решение
1) Вычислить левый предел.
2) Вычислите правосторонний предел.
3) Если оба предела равны, то функция имеет предел при приближении x к c = 2.
Предел равен правому пределу, который равен левому пределу.
Поскольку правый и левый пределы равны 4, функция имеет предел 4, поскольку x приближается к 2.
Другие примеры
Проверьте, существует ли предел. Если да, то найти предел.
Калькулятор раствора 92-4)/(х-2))
Односторонние пределы равны, поэтому функция имеет предел 4, когда x приближается к 2.
Решение калькулятора
Правый предел: lim [ x = 2 + ] ( 2x – 1 )
Левый -hand limit: lim [ x = 2 – ] ( 2x – 1 )
Ограничение функции: lim [ x = 2 ] ( 2x – 1 )
Односторонние пределы равны, поэтому функция имеет предел 3, когда x приближается к 2.
Решение калькулятора 92 )
Односторонние пределы равны, поэтому предел функции равен 1/9 по мере того, как x приближается к 4. ( 2x – 1 ) )
Левый предел: lim [ x = 2 – ] ( 2 / ( 2x – 1 ))
Предел функции: lim [ x = 2 ] ( 2 / ( 2x – 1 ) )
Односторонние пределы не равны, так как правый предел равен ∞, а левый предел равен -∞.