Производные высших порядков для студентов
Аналогично, если производная существует и дифференцируема, то можно найти третью производную рассматриваемой функции:
Таким образом, понятие производной -го порядка вводится индуктивно путем последовательного вычисления производных, начиная с производной первого порядка. Переход к производной следующего, более высокого порядка производится с помощью рекуррентной формулы:
Замечание. Порядок производной, чтобы не путать с показателем степени, пишут в круглых скобках либо записывают римскими цифрами. Например, производная четвертого порядка
При нахождении производных высшего порядка используются следующие соотношения:
Примеры вычисления производных высших порядков
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Производные высших порядков
Дифференцируя производную первого порядка $f'(x)$, мы получим производную от производной — производную второго порядка. Производная от производной второго порядка называется производной третьего порядка, а производная $n$-го порядка называется производной от производной $n-1$-го порядка.
Производная второго порядка обозначается $y”$ или $f”(x)$. Таким образом, дифференцируя функцию $n$-раз, мы получим производную вида $f n(x)$.
Формула дифференцирования второго порядка имеет вид:
Производная n-го порядка равна нулю, если степень меньше порядка производной. Например, пятая производная функции $y = 5x^2$ равна нулю.
Пример 1
Найти вторую производную функции:
\[y=x\ln (2x+1)\]Решение.
- Найдем производную первого порядка сложной функции по формуле произведения: \[\left[f(x)\cdot g(x)\right]{{‘} } =f(x)’\cdot g(x)+f(x)\cdot g(x)’\] \[y’=\left[x\cdot \ln (2x+1)\right]{{‘} } =x’\cdot \ln (2x+1)+x\cdot \left(\ln (2x+1)\right){{‘} } =1\cdot \ln (2x+1)+x\cdot \left(\ln (2x+1)\right){{‘} } =\] \[y’=\ln (2x+1)+x\cdot \left(\ln (2x+1)\right){{‘} } =\ln (2x+1)+x\cdot \frac{1}{2x+1} \cdot (2x+1)’=\] \[=\ln (2x+1)+2x\cdot \frac{1}{2x+1} =\ln (2x+1)+\frac{2x}{2x+1} \]
- Найдем производную второго порядка для выражения \[y”=\left(\ln (2x+1)+\frac{2x}{2x+1} \right){{‘} } =\ln (2x+1)’+\left(\frac{2x}{2x+1} \right){{‘} } =\frac{1}{2x+1} \cdot (2x+1)’+\frac{2x’\cdot (2x+1)-2x\cdot (2x+1)’}{\left(2x+1\right)^{2} } =\] \[y”=\frac{2}{2x+1} +\frac{2(2x+1)-2x\cdot 2}{\left(2x+1\right)^{2} } =\frac{2}{2x+1} +\frac{2((2x+1)-2x)}{\left(2x+1\right)^{2} } =\frac{2}{2x+1} +\frac{2}{\left(2x+1\right)^{2} } =\]
- Упростим выражение \[y”=\frac{2\left(2x+1\right)}{\left(2x+1\right)^{2} } +\frac{2}{\left(2x+1\right)^{2} } =\frac{2\left(2x+1\right)+2}{\left(2x+1\right)^{2} } =\frac{4x+4}{\left(2x+1\right)^{2} } \]
Пример 2
Найти производную четвертого порядка
\[y=x^{5} -x^{4} +3x^{3} \]Решение.
- Найдем производную первого порядка \[y’=\left(x^{5} -x^{4} +3x^{3} \right){{‘} } =5x^{4} -4x^{3} +3\cdot 3x^{2} =5x^{4} -4x^{3} +9x^{2} \]
- Найдем производную второго порядка \[y”=\left(5x^{4} -4x^{3} +9x^{2} \right){{‘} } =20x^{3} -12x^{2} +18x\]
- Найдем производную третьего порядка \[y”’=\left(20x^{3} -12x^{2} +18x\right){{‘} } =60x^{2} -24x+18\]
- Найдем производную четвертого порядка \[y””=\left(60x^{2} -24x+18\right){{‘} } =120x-24\]
Пример 3
Найти производную четвертого порядка функции
\[y=\frac{x^{2} +5x^{3} }{18} \]Решение: Самая большая степень составного неизвестного равна 3, что меньше степени производной, а значит, производная четвертого порядка равна 0.
Пример 4
Найти производную 13-го порядка функции
\[y=\sin x\]Решение.
- Найдем производную первого порядка \[y’=sin’x=\cos x=\sin (x+\frac{\pi }{2} )\]
- Найдем производную второго порядка \[y”=cos’x=-\sin x=\sin (x+2\frac{\pi }{2} )\]
- Найдем производную третьего порядка \[y”’=-sin’x=-\cos x=\sin (x+3\frac{\pi }{2} )\]
- Найдем производную четвертого порядка \[y^{(4)} =-\cos x’=\sin x=\sin (x+4\frac{\pi }{2} )\]
- Найдем производную 13-го порядка: \[y^{(13)} =\sin (x+\frac{13\cdot \pi }{2} )=\cos x\]
Таким образом:
\[y^{(n)} =\sin (x+\frac{n\cdot \pi }{2} ),n\in N\]Пример 5
Найти производную n-порядка функции
\[y=\frac{x}{1-x} \]Решение.
- Найдем производную первого порядка \[y’=\left(\frac{x}{1-x} \right){{‘} } =\frac{x'(1-x)-x(1-x)’}{(1-x)^{2} } =\frac{1-x+x}{(1-x)^{2} } =\frac{1}{(1-x)^{2} } =\frac{1!}{(1-x)^{1+1} } \]
- Найдем производную второго порядка \[y”=\left(\frac{1}{(1-x)^{2} } \right){{‘} } =\left((1-x)^{-2} \right){{‘} } =-2(1-x)^{-3} (1-x)’=-2(1-x)^{-3} \cdot (-1)=\frac{2}{(1-x)^{3} } =\frac{2!}{(1-x)^{2+1} } \]
- Найдем производную 3 порядка \[y”’=\left(\frac{2}{(1-x)^{3} } \right){{‘} } =2\left((1-x)^{-3} \right){{‘} } =2\cdot \left(-3\right)(1-x)^{-4} (1-x)’=-6\cdot (1-x)^{-4} \cdot (-1)=\frac{1\cdot 2\cdot 3}{(1-x)^{4} } =\frac{3!}{(1-x)^{3+1} } \]
Выведем формулу производной $n$-порядка
\[y^{(n)} =\frac{n!}{(1-x)^{n+1} } \]Пример 6
Найти значение второй производной в точке 1
\[y=e^{2x-1} \]Решение.
- Найдем производную первого порядка \[y’=\left(e^{2x-1} \right){{‘} } =e^{2x-1} \cdot 2\]
- Найдем производную второго порядка \[y”=\left(2\cdot e^{2x-1} \right){{‘} } =2\cdot e^{2x-1} \cdot 2=4e^{2x-1} \]
- Найдем производную в точке 1 \[y”=4e^{2x-1} =4e^{2\cdot 1-1} =4e\]
spravochnick.ru
Вычисления производной любого порядка
Пусть $y = uv$, где $u$ и $v$ — некоторые функции от переменной $х$, имеющие производные любого порядка. Тогда
Правая часть данных выражений похожа на разложение степеней бинома $(u + v)n$ по формуле Ньютона, вместо показателей степени стоят числа, определяющие порядок производных, а $u$ и $v$ можно рассматривать как производные 0-го порядка. Таким образом, общий вид $n$-й производной произведения двух функций:
Формула получила название формулы Лейбница для нахождения производных любого порядка.
Пример 1
Найти производную третьего порядка
\[y(x)=5x^{2} \ln x\]Решение.
- Запишем производную по формуле Лейбница \[y^{(3)} (x)=\left(5x^{2} \right)^{(3)} \ln x+C_{3}^{1} \left(5x^{2} \right){{‘} } {{‘} } \ln x’+C_{3}^{2} \left(5x^{2} \right){{‘} } \ln x”+5x^{2} \ln x^{(3)} \]
- Посчитаем коэффициенты при слагаемых \[C_{3}^{1} =\frac{3!}{1!(3-1)!} =\frac{3!}{2!} =\frac{2!3}{2!} =3\] \[C_{3}^{2} =\frac{3!}{2!(3-2)!} =\frac{3!}{2!} =\frac{2!3}{2!} =3\]
- Найдем производные первого сомножителя \[\left(5x^{2} \right){{‘} } =10x\] \[\left(5x^{2} \right){{‘} } {{‘} } =\left(10x\right){{‘} } =10\] \[\left(5x^{2} \right){{‘} } {{‘} {‘} } =\left(10\right){{‘} } =1\]
- Найдем производные второго сомножителя \[\ln x’=\frac{1}{x} \] \[\ln x”=\left(\frac{1}{x} \right){{‘} } =-\frac{1}{x^{2} } \] \[\ln x”’=\left(-\frac{1}{x^{2} } \right){{‘} } =\frac{2}{x^{3} } \]
- Подставим найденные значения в формулу Лейбница \[y^{(3)} (x)=1\cdot \ln x+3\cdot 10\cdot \frac{1}{x} -3\cdot 10x\cdot \frac{1}{x^{2} } +5x^{2} \frac{2}{x^{3} } \]
- Упростим выражение \[y^{(3)} (x)=\ln x+\frac{30}{x} -\frac{30}{x} +\frac{10}{x} =\ln x+\frac{10}{x} \]
Пример 2
Найти производную четвертого порядка
\[y(x)=e^{4x} \sin 3x\]Решение.
- Запишем производную по формуле Лейбница \[y^{(4)} (x)=\left(e^{4x} \right)^{(4)} \sin 3x+C_{4}^{1} \left(e^{4x} \right)^{(3)} \sin 3x’+C_{4}^{2} \left(e^{4x} \right)^{(2)} \sin 3x”+C_{4}^{3} \left(e^{4x} \right){{‘} } \sin 3x”’+e^{4x} \sin 3x^{(4)} \]
- Посчитаем коэффициенты при слагаемых \[C_{4}^{1} =\frac{4!}{1!(4-1)!} =\frac{4!}{3!} =\frac{3!4}{3!} =4\] \[C_{4}^{2} =\frac{4!}{2!(4-2)!} =\frac{4!}{2!2!} =\frac{1\cdot 2\cdot 3\cdot 4}{1\cdot 2\cdot 1\cdot 2} =6\] \[C_{4}^{3} =\frac{4!}{3!(4-3)!} =\frac{4!}{3!1!} =\frac{3!4}{3!} =4\]
- Найдем производные первого сомножителя \[\left(e^{4x} \right){{‘} } =e^{4x} \cdot 4x’=4e^{4x} \] \[\left(e^{4x} \right){{‘} } {{‘} } =\left(4e^{4x} \right){{‘} } =16e^{4x} \] \[\left(e^{4x} \right){{‘} } {{‘} } {{‘} } =\left(16e^{4x} \right){{‘} } =64e^{4x} \] \[\left(e^{4x} \right)^{(4)} =\left(64e^{4x} \right){{‘} } {{‘} } {{‘} } =256e^{4x} \]
- Найдем производные второго сомножителя \[\sin 3x’=\cos 3x\cdot 3x’=3\cos 3x\] \[\sin 3x”=\left(3\cos 3x\right){{‘} } =3\left(-\sin 3x\right)\cdot \left(3x\right){{‘} } =-9\sin 3x\] \[\sin 3x”’=\left(-9\sin 3x\right){{‘} } ^{} =-27\cos 3x\] \[\sin 3x^{(4)} =\left(-27\cos 3x\right){{‘} } =81\sin 3x\]
- Подставим найденные значения в формулу Лейбница \[y^{(4)} (x)=256e^{4x} \sin 3x+4\cdot 64e^{4x} \cdot 3\cos 3x+6\cdot 16e^{4x} \cdot \left(-9\sin 3x\right)+4\cdot 4e^{4x} \cdot \left(-27\cos 3x\right)+e^{4x} \cdot 81\sin 3x\]
- Упростим \[y^{(4)} (x)=e^{4x} (336\cos 3x-527\sin 3x)\]
Пример 3
Найти производную пятого порядка
\[y(x)=x^{10} e^{x} \]Решение.
- Запишем производную по формуле Лейбница \[x^{10} {{‘} } =10x^{9} \]
- Посчитаем коэффициенты при слагаемых \[C_{5}^{1} =\frac{5!}{1!(5-1)!} =\frac{4!5}{4!} =5\] \[C_{5}^{2} =\frac{5!}{2!(5-2)!} =\frac{3!4\cdot 5}{2!3!} =10\] \[C_{5}^{3} =\frac{5!}{3!(4-2)!} =\frac{5!}{3!2!} =\frac{1\cdot 2\cdot 3\cdot 4\cdot 5}{1\cdot 2\cdot 3\cdot 1\cdot 2} =10\] \[C_{5}^{4} =\frac{5!}{4!(5-4)!} =\frac{5!}{4!} =\frac{4!5}{4!} =5\]
- Производная любого порядка $ех$ равна $ех$
- Найдем производные второго сомножителя \[x^{10}{{‘} } =10x^{9} \] \[x^{10}{{‘} }{{‘} } =\left(10x^{9} \right){{‘} } =90x^{8} \] \[x^{10}{{‘} }{{‘} }{{‘} } =\left(90x^{8} \right){{‘} } =720x^{7} \] \[x^{10}{(4)} =720x^{7} {{‘} } =5040x^{6} \] \[x^{10}{(5)} =5040x^{6} {{‘} } =30240x^{5} \]
- Подставим найденные значения в формулу Лейбница \[y^{(5)} (x)=30240x^{5} e^{x} +5\cdot 5040x^{6} e^{x} +10\cdot 720x^{7} e^{x} +10\cdot 90x^{8} e^{x} +5\cdot 10x^{9} e^{x} +x^{10} e^{x} \]
- Упростим \[y^{(5)} (x)=30240x^{5} e^{x} +25200x^{6} e^{x} +7200x^{7} e^{x} +900x^{8} e^{x} +50x^{9} e^{x} +x^{10} e^{x} =\] \[y^{(5)} (x)=x^{5} e^{x} \left(30240+25200x+7200x^{2} +900x^{3} +50x^{4} +x^{5} \right)\]
spravochnick.ru
1. Производные высших порядков Понятие производных высших порядков
Пусть
функция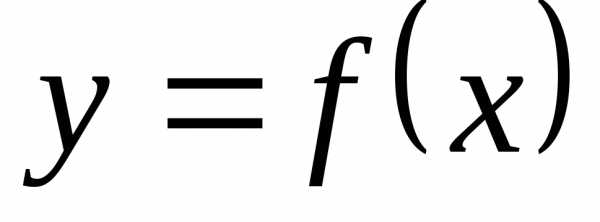
дифференцируема в некотором интервале.
Тогда её производная 
,
вообще говоря, зависит отх , то есть
является функцией от х.
Следовательно, по отношению к ней снова
можно ставить вопрос о существовании
производной.
Определение. Производная
от первой производной называется производной
второго порядка или второй производной
и обозначается символом 
или
,
то есть
.
Пример
1. Найти
вторую производную от функции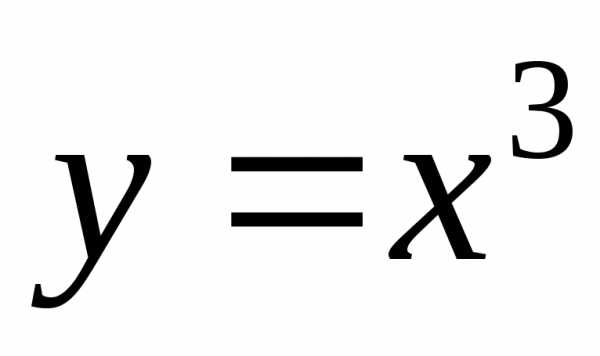 
.
Решение. Найдем первую производную функции:
.
Находим вторую производную как производную первой производной:
.
Определение. Производная
от второй производной называется
производной третьего порядка или третьей
производной и обозначается символом 
или
.
Определение. Производной n-ого
порядка функции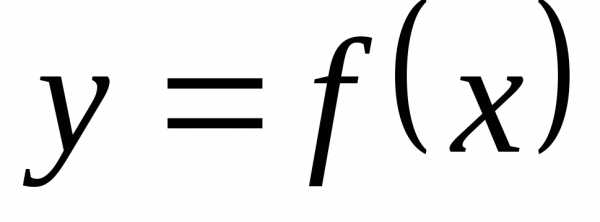 
называется
первая производная от производной
(n-1)-го
порядка данной функции и обозначается
символом 
или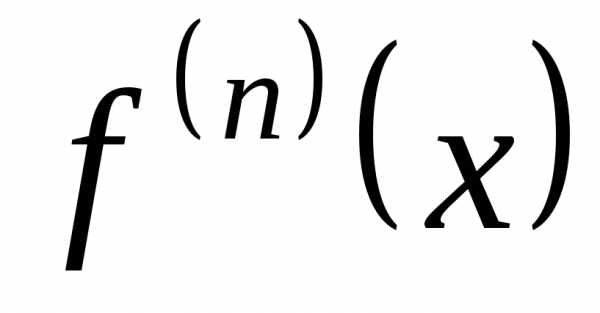
:
.
Определение. Производные порядка выше первого называются высшими производными.
Пример
2. Найти
производную четвертого порядка функции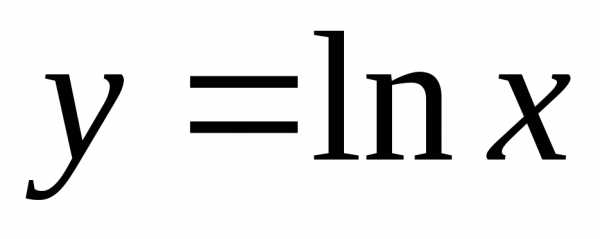 
.
Решение. Находим последовательно первую, вторую, третью и четвертую производные:
, 
,,
.
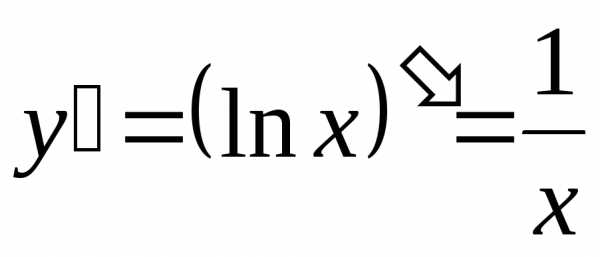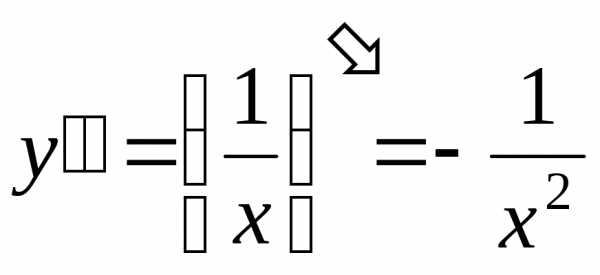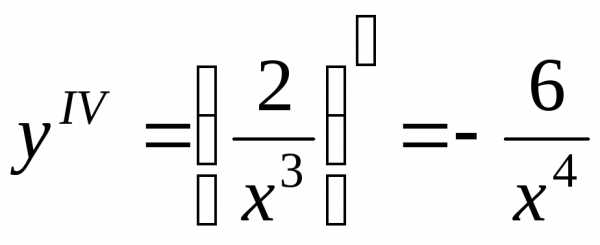Пример
3.Найти
производную n-ого
порядка для функции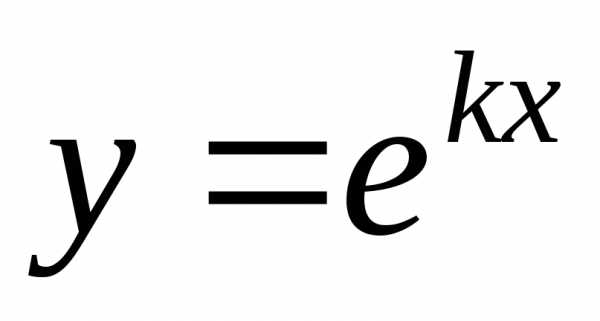 
Решение. Имеем:
,
,
,.
Пример
4. Найти
производную n-ого
порядка для функции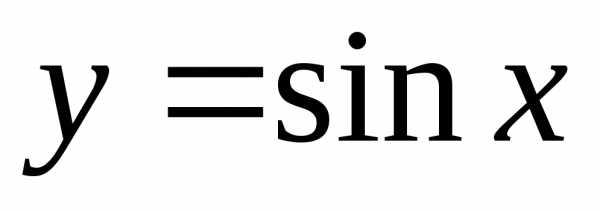 
.
Решение. Имеем:
,
,
,
.
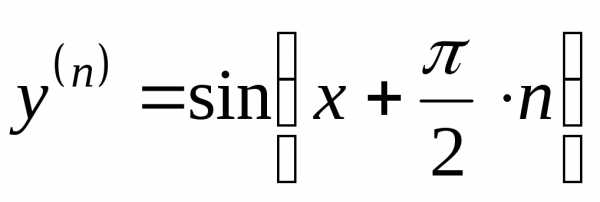Замечание.
Аналогично можно получить формулу n-ой
производной функции
:
.
, где
и
– любое вещественное число. 
Решение.
Дифференцируя последовательно, получим:
,
,
.
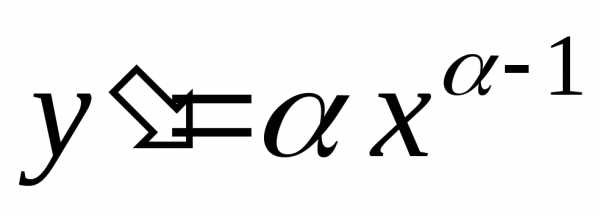В частном случае, когда , гдеm – натуральное число, получим:
, 
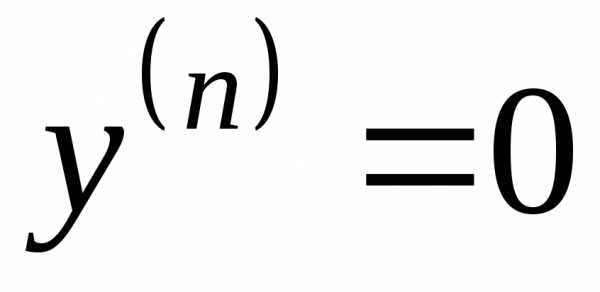при
.
Замечание. При строгом выводе формулы для производной n-ого
порядка следует применять метод
математической индукции.
Вторая
производная параметрически заданной
функции
Если функция задана параметрически уравнениями , то для нахождения производной второго порядка нужно продифференцировать выражение для её первой производной, как сложной функции независимой переменной.
Так
как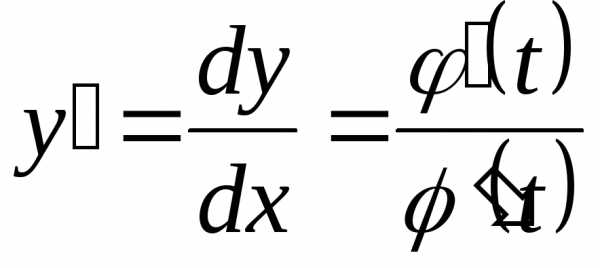 
,
то
,
и с учетом того, что
,
получим
.
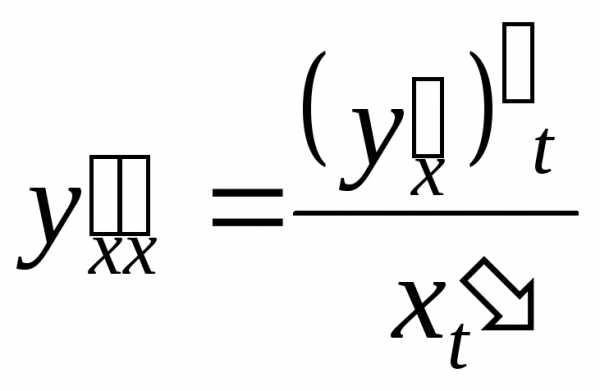Аналогично можно найти третью производную
.
Пример
7. Найти
вторую производную параметрически
заданной функции 
,
.
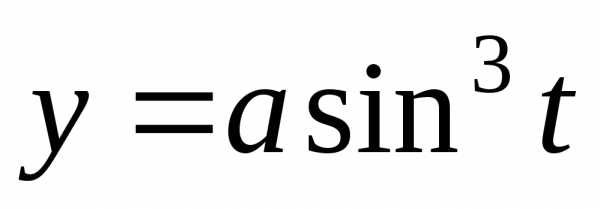Решение.,
.
Формула Лейбница
Для нахождения производной
Пусть u и v – некоторые функции от переменной х, имеющие производные любого порядка и y=uv. Выразим n-ую производную через производные функцийu и v.
Имеем последовательно
,
,
.
Легко подметить аналогию между выражениями для второй и третьей производных и разложением бинома Ньютона соответственно во второй и третьей степенях, но вместо показателей степени стоят числа, определяющие порядок производной, а сами функции можно рассматривать как «производные нулевого порядка». Учитывая это, получим формулу Лейбница:
. (2)
Эту формулу можно доказать методом математической индукции.
Пример. Найти пятую
производную функции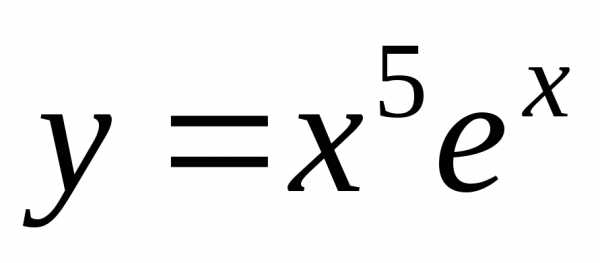 
.
Решение.
Положим 
и
.
Найдем
,,,,;.
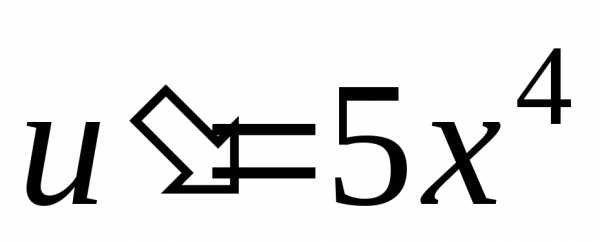Подставляя эти выражения в формулу
Лейбница при
.
studfiles.net
24. Производные высших порядков
Билет 24
Производные высших порядков явно заданной функции
Производная у’=ƒ'(х) функции у=ƒ(х) есть также функция от х и называется производной первого порядка.
Если функция ƒ'(х) дифференцируема, то ее производная называется производной второго порядка и обозначается у”
Итак, у”=(у’)’.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'” (или ƒ'”(х)). Итак, у'”=(y”)’
Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка:
y(n)=(y(n-1)) .
Производные порядка выше первого называются производными высших порядков.
Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (уν или у(5)— производная пятого порядка).
<< Пример 23.1
Найти производную 13-го порядка функции у=sinx.
Решение:
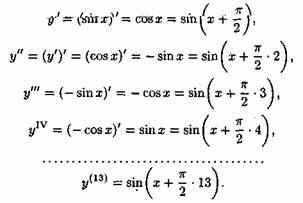
ФОРМУЛА ТЕЙЛОРА
В определении функции у=ƒ(х) не говорится о том, при помощи каких средств находятся значения у по значениям х. В тех случаях, когда функция является формулой вида у=х3/5-5х+7, значения функции найти легко с помощью четырех арифметических действий. Но как найти значения, например, функций у=sinx, у=ln(1+х) при любых (допустимых) значениях аргумента?
Для того, чтобы вычислить значения данной функции у=ƒ(х), ее заменяют многочленом Рn(х) степени n, значения которого всегда и легко вычисляемы. Обоснование возможности представлять функцию многочленом дает формула Тейлора.
26.1. Формула Тейлора для многочлена
Пусть функция ƒ(х) есть многочлен Рn(х) степени n:
ƒ(х)=Рn(х)=а0+а1х+а2х2+…+аnхn.
Преобразуем этот многочлен также в многочлен степени n относительно разности х-х0, где х0 — произвольное число, т. е. представим Рn(х) в виде
Рn(х)=А0+A1(x-х0)+А2(х-х0)2+…+Аn(х-х0)n (26.1)
Для нахождения коэффициентов А0, А1 ,…, Аn продифференцируем n раз равенство (26.1):
Р’n(х)=А1+2А2(х-x0)+3A3(x-x0)2+…+nAn(x-x0)n-1,
Рn”(х)=2А2+2•3А3(х-х0)+…+n(n-1)Аn(х-х0)n-2,
Рn“‘(х)=2•3А3+2•3•4А4(х-х0)+…+n(n-1)(n-2)Аn(х-х0)n-3,
– – – – – – – – – – – – – – – – – –
Рn(n)(х)=n(n-1)( n-2)…2•1Аn
Подставляя х=х0 в полученные равенства и равенство (26.1), имеем:
Подставляя найденные значения A0,A1,…,An в равенство (26.1), получим разложение многочлена n-й степени Рn(х) по степеням (х-х0):
Формула (26.2) называется формулой Тейлора для многочлена Рn(х) степени n.
<< Пример 26.1
Разложить многочлен Р(х)=-4х3+3х2-2х+1 по степеням х+1.
Решение: Здесь х0=-1, Р'(х)=-12х2+6х-2, Р”(х)=-24х+6, Р'”(х)=-24. Поэтому Р(-1)=10, Р'(-1)=-20, Р”(-1)=30, Р'”(-1)=-24. Следовательно,
т. е. -4х3+3х2-2х+1=10-20(х+1)+15(х+1)2-4(х+1)3.
Ряд Тейлора. Разложение функции в ряд Тейлора.
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1:
При использовании рядов, называемых рядами Тейлора, смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.
Ряд Тейлора в окрестности точки a имеет виды:
1), где f(x) – функция, имеющая при х=а производные всех порядков. Rn – остаточный член в ряде Тейлора определяется выражением
2)
k-тый коэффициент (при хk) ряда определяется формулой
3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)
при a=0
члены ряда определяются по формуле
Условия применения рядов Тейлора.
1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).
2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.
Свойства рядов Тейлора.
Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:
Ряды Тейлора применяются при аппроксимации ( приближение – научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от linearis — линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.
studfiles.net