Онлайн расчет lc контура: Расчёт частоты резонанса колебательного контура

Расчёт частоты резонанса колебательного контура

Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.

Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.

– Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
– Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.

Рассмотрим, как возникают и поддерживаются свободные электрические колебания в параллельном контуре LC.

Основные свойства индуктивности

– Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией .
– Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.

Природа электромагнитных колебаний в контуре

Период свободных колебаний контура

LC можно описать следующим образом:

Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток разряда конденсатора, создавая магнитное поле в катушке.

Внешний магнитный поток создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в каждом витке, поэтому конденсатор разрядится не мгновенно, а через время t₁, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t₁ = .
По истечении времени t

₁, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, E_C будет равна E_L. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Далее изменение (уменьшение от максимума) магнитного потока накопленной энергии катушки будет создавать в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени

t₂ = t₁, он перезарядит конденсатор от нулевого до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.

Описанные интервалы t₁ и t₂ составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени t

₃, сменив полярность полюсов.

В течении заключительного этапа колебания (t₄), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U (в случае отсутствия потерь) и процесс колебания повторится.

В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t₁ + t₂ + t₃ + t₄ составит период колебаний .

Частота свободных колебаний контура ƒ = 1 / T

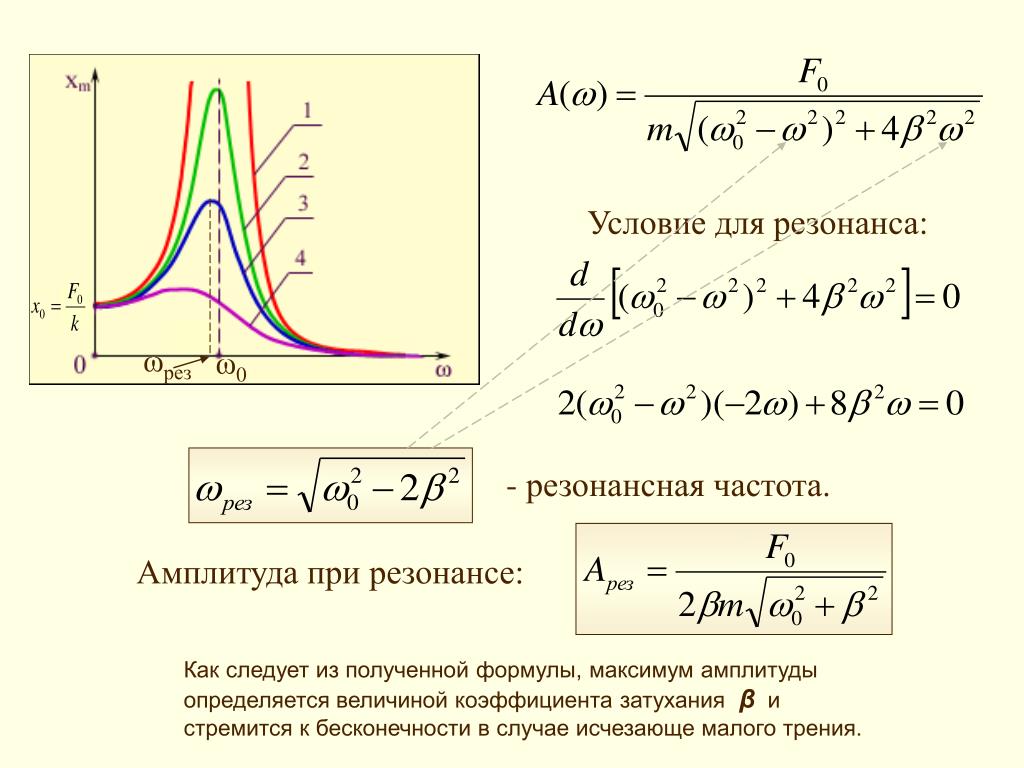
Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности X_L=2πfL равно реактивному сопротивлению ёмкости X_C=1/(2πfC).

---

Расчёт частоты резонанса

LC-контура:

Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Наверх

Расчёт частоты:

Частота резонанса колебательного контура LC. ƒ = 1/(2π√(LC))

Расчёт ёмкости:

Ёмкость для колебательного контура LC C = 1/(4𲃲L)

Расчёт индуктивности:

Индуктивность для колебательного контура LC L = 1/(4𲃲C) Частота: MHzkHzHz Ёмкость: pFnFµF Индуктивность: µHnHmH

---

Похожие страницы с расчётами:

Рассчитать импеданс.

Рассчитать реактивное сопротивление.

Рассчитать реактивную мощность и компенсацию.

---

Замечания и предложения принимаются и приветствуются!

Калькулятор параллельного колебательного LC-контура

Электрическая цепь, состоящая из соединеных в контур конденсатора емкостью С и катушки индуктивностью L, обладающая сопротивлением R(сопротивление активных потерь в катушке), называется электрическим колебательным контуром. В контуре возникает колебательный процесс ввиду перехода энергии электрического поля в энергию магнитного и наоборот. Реактивные сопротивления индуктивности и емкости зависят от частоты переменного тока. При увеличении частоты реактивное сопротивление индуктивности растет, а емкости падает. При уменьшении частоты, наоборот, индуктивное сопротивление падает, а емкостное – растет. При некоторой частоте ƒ

0, емкостное сопротивление конденсатора и индуктивное сопротивление катушки становятся численно равными: Xc = XL. При этом токи индуктивной и емкостной ветвей также равны, что приводит к возрастанию амплитуды вынужденных колебаний. Режим, возникающий в цепи, состоящей из генератора и параллельно включенных катушки и конденсатора, при равенстве емкостного и индуктивного сопротивлений, называют режимом резонанса токов. Явление резонанса токов используется в полосовых фильтрах для выделения определенной частоты. Такая схема необходима для работы телевизора, радиоприемника, ёмкостного генератора и т.п.

Расчет частоты резонанса параллельного LC-контура описывается формулами:

X_L =

2πƒL

X_C =

1

 

2πƒC

ƒ₀ =

1

 

2π√LC

X_L — индуктивное реактивное сопротивление, Ом;

X_С — ёмкостное реактивное сопротивление, Ом;

ƒ₀ — резонансная частота, Гц;

Расчет частоты резонанса LC-контура

Введите значения индуктивности и ёмкости конденсатора, чтобы узнать резонансную частоту контура, или введите резонансную частоту генератора, чтобы рассчитать необходимые значения индуктивности и емкости.

IC

IL

Iƒ

мкФнФпФ

ГнмГнмкГн

МГцкГцГц

X_L = X_C = ƒ₀ = φ = °

X_L > X_C Цепь имеет емкостной характер,ее емкостное реактивное сопротивление меньше индуктивного. Угол фазового сдвига между напряжением генератора и током в контуре приближается к 90°

Чем больше частота генератора отличается от собственной (резонансной) частоты контура, тем больше различаются токи IL и Іс, тем больше реактивный ток в общей части цепи и меньше реактивное сопротивление контура.

Внимание! Производители объединяют элементы в серии или ряды: E6, E12, E24…
Для подбора компонентов будет использована серия E12.

Подбор конденсатора на сайте

Подбор катушки индуктивности на сайте

Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!

Калькулятор резонансной частоты для LC-контура

Если вы хотите рассчитать резонансную частоту LC-контура, не смотрите дальше — этот калькулятор резонансной частоты — это инструмент для вас. Введите индуктивность и емкость, и в кратчайшие сроки вы найдете резонансную и угловую частоту. Мы также предоставим немного теории, поскольку это может быть удобно – ниже вы узнаете, как рассчитать резонансную частоту, а также краткое определение того, что такое резонансная частота на самом деле.

Если вы интересуетесь электронными схемами, вы, вероятно, хотели бы знать, как получить некоторую долю входного напряжения – наш калькулятор делителя напряжения необходим для этой задачи.

Что такое LC-цепь (резервуарная цепь)?

LC-цепь (также называемая резонансной схемой, колебательной схемой или настроенной схемой) представляет собой идеализированную RLC-цепь с нулевым сопротивлением. Если вы ищете «неидеальную» схему, воспользуйтесь нашим калькулятором схемы RLC!

LC-цепь содержит только катушку индуктивности и конденсатор, соединенные параллельно или последовательно:

Parallel LC CircuitSeries LC Circuit

Резервуарные цепи обычно используются в качестве генераторов сигналов и полосовых фильтров — это означает, что они выбирают сигнал на определенной частоте из более сложного сигнала. Они широко применяются в электронике — LC-схемы можно найти в усилителях, генераторах, тюнерах, радиопередатчиках и приемниках. Цепи LC и RC можно использовать для фильтрации сигнала путем блокировки определенных частот.

🙋 У Omni есть и другие замечательные инструменты, которые помогут вам в изучении электроники: попробуйте наш калькулятор RC-цепей или нашу коллекцию инструментов для простых схем:

• Калькулятор последовательного резистора;
• Вычислитель параллельных резисторов;
• Калькулятор последовательно включенных конденсаторов; и
• Калькулятор параллельных конденсаторов.

Что такое резонансная частота?

Резонансная частота — это собственная незатухающая частота системы. Если применить резонансную частоту, то колебания приобретают максимальную амплитуду, и даже относительно небольшие силы могут производить большие амплитуды. Однако, если выбрана любая другая частота, этот сигнал затухает. Существует множество различных типов резонансов, например.

• механические и акустические,
• электрический,
• оптический,
• орбитальная,
• молекулярный.

Для LC-цепей резонансная частота определяется емкостью C и импедансом L.

Как рассчитать резонансную частоту?

Следующая формула описывает соотношение в LC-цепи:

f=12πL⋅Cf = \frac{1}{2\pi\sqrt{L\cdot C}}f=2πL⋅C

​1​

Где:

• fff — Резонансная частота;
• LLL — Индуктивность цепи; и
• ССС — Цепь емкостная.

Откуда взялась эта формула? Резонанс в LC-цепи возникает, когда индуктивное сопротивление катушки индуктивности становится равным емкостному сопротивлению конденсатора. Итак:

xL=2π⋅f⋅LxL = 2\pi\cdot f\cdot LxL=2π⋅f⋅L

xC=12π⋅f⋅CxC = \frac{1}{2\pi\cdot f\ cdot C}xC=2π⋅f⋅C1​

Тогда после преобразования уравнения находим: 92\cdot L \cdot C}f2=4π2⋅L⋅C1​

И наконец:

f=12πL⋅Cf = \frac{1}{2\pi\sqrt{L\cdot C}}f=2πL ⋅C

​1​

Также угловую частоту можно рассчитать по следующей известной формуле:

ω=2⋅π⋅f\omega = 2\cdot \pi \cdot fω=2⋅π ⋅f

Как использовать калькулятор резонансной частоты

Использование нашего инструмента – это прогулка в парке:

1. Введите значение конденсатора . Например, наша емкость равна 1 мкФ1\ \mathrm{мкФ}1 мкФ.
2. Введите индуктивность . Наш дроссель в нашей LC-цепи равен 0,18 мГн0,18\ \mathrm{мГн}0,18 мГн.
3. Калькулятор резонансной частоты сделал свое дело! Мы быстро выяснили, что такое резонансная частота: 11,863 кГц. Если вы хотите также проверить угловую частоту, просто нажмите кнопку Расширенный режим , и результат появится внизу.

Калькулятор резонансной частоты является гибким инструментом, поэтому, как обычно, вы можете ввести любые две переменные, и недостающая будет рассчитана мгновенно.

Coil32 – О LC-схеме для начинающих

Детали

Опубликовано: 17 декабря 2014 г.

Просмотров: 7092

Для начинающих радиолюбителей хотелось бы дать немного информации о параметрах схемы LC-генератора. Ведь индуктивность катушки является ее основой. Цепь генератора, как известно, состоит из 9Катушка 0009 индуктивность и конденсатор.

Основные характеристики схемы LC-генератора:

• Резонансная частота
• Добротность
• Эквивалентное сопротивление Z _E
• Диапазон полосы пропускания

 

Резонансная частота LC-контура рассчитывается по формуле:

Где L и C в Генри и Фарадах соответственно

Однако, необходимо помнить об одном очень важном моменте. «С» не является номинальной емкостью конденсатора LC-цепи. Он состоит из множества емкостей – это конденсатор, паразитная емкость катушки, емкость внешних цепей, подключенных к LC-контуру (например, выходная и входная емкости транзистора), монтажная паразитная емкость. Эти вносимые емкости существенны, особенно на высоких частотах, где они соизмеримы с емкостью конденсатора LC-контура. Их необходимо учитывать! Иногда на форумах можно прочитать всякие сообщения: “Рассчитал катушку вот такой программой, сделал самодельную катушку, а потом оказалось, что катушку надо делать методом “ручного подбора витков”, значит эта программа плохая “. Программа считает правильно. Действительно, рассчитывает катушку в ненагруженном LC-контуре, но надо с учетом конструктивных особенностей.

Теоретически все вышеперечисленное относится к индуктивности “L” , однако в реальности введенные в цепь индуктивности в 10 раз меньше и их в большинстве случаев можно не учитывать.

Добротность ненагруженного LC-контура Q определяется добротностью катушки Q _L и конденсатора Q _C . Q _L зависит от сопротивления r _L (см. схему1.), эквивалентного потерям электрической энергии в проводе, в изоляции провода, витке-образователе, листе, сердечнике витка. Вопрос _л = 2πƒ л / об _л . Обычно в зависимости от качества конструкции катушки индуктивности и качества применяемых материалов – Q _L ≈50÷250 .

Добротность конденсатора Q _C зависит от сопротивления R _C , эквивалентного потерям электрической энергии в конденсаторе. Q _C = 2πƒR _C . Обычно Q _C ≈400÷1000 .

Различные сопротивления потерь (r _L ,R _C ) можно для удобства расчетов заменить одним сопротивлением R _e , подключенный параллельно к идеальной LC-цепи без потерь, который называется эквивалентным сопротивлением цепи. Он характеризует все потери реальной цепи и равен сопротивлению цепи на резонансной частоте. Заметим, что на резонансной частоте реактивные сопротивления катушки индуктивности и конденсатора равны и противоположны по знаку и компенсируют друг друга, в результате чего общее сопротивление цепи чисто активно.

Значение R _и связано с другими параметрами цепи следующими соотношениями: R _e = 2πƒLQ = 2πƒCQ

Здесь снова есть важный момент. Дополнительные сопротивления, поступающие из внешних цепей, подключаются к LC-цепи параллельно R _и . Таким образом, R _e и, следовательно, Q уменьшаются. А для высокодобротных LC-цепей это снижение может оказаться существенным. Для минимизации влияния внешних цепей на контур применяют частичное включение через делитель мощности, отвод катушки или применяют катушку связи.

Полоса пропускания равна полосе частот, где величина контурных передач равна 70,7% от эффективности передачи на резонансной частоте.

Справедливо соотношение: Q = f/Δf , которое можно использовать для измерения добротности реальной цепи.