Аналитическое вычисление производной функции на языке Scala / Хабр
Введение
Данный алгоритм реализован на языке Scala, характерной особенностью которого является использование case-классов, так удачно подходящих для написания алгоритма дифференцирования. В этой статье планируется описать лишь часть программы, содержащей алгоритм нахождения производной, поскольку разработка парсера для математических выражений это другая большая тема,
заслуживающая отдельной статьи
Подготовка
Сначала опишем структуру данных, в которой будет храниться исходная математическая функция. Опишем трейт MathAST:
sealed trait MathAST
И его наследников:
sealed trait SingleToken extends MathAST{
val a: MathAST
}
sealed trait DoubleToken extends MathAST{
val a: MathAST
val b: MathAST
}
sealed trait LeafToken extends MathAST
SingleToken
будет реализовывать case-классы унарных операторов, таких как sin(a), -a, ln(a) и т.
LeafToken
— «листья» дерева, т.е. константы, переменные и зарезервированные имена констант (число Пи и экспонента).
Опишем классы/объекты операторов и токенов:
case object Pi extends LeafToken case object Exponenta extends LeafToken case class Sin(override val a: MathAST) extends SingleToken case class Cos(override val a: MathAST) extends SingleToken … case class Mul(override val a: MathAST, override val b: MathAST) extends DoubleToken case class Add(override val a: MathAST, override val b: MathAST) extends DoubleToken … case class Differentiate(f: MathAST, dx: Variable) extends MathAST case class Variable(name: String) extends LeafToken case class Constant(value: BigDecimal) extends LeafToken
Обратите внимание на класс
Differentiate, он имеет особую сигнатуру:
f– исходная функция,
dx– переменная, по которой происходит дифференцирование.
Теперь есть все, чтобы представить математическую функцию в виде дерева вычислений, для примера возьмем функцию: , которая примет вид:
Mul(Constant(BigDecimal(2)), Pow(x, Constant(BigDecimal(2)))
Конечно, чтобы получить дерево-выражение из обычной строки, введенной пользователем, нужно написать парсер, но, как было упомянуто выше, это уже другая тема.
Алгоритм нахождения производной
В основе которого лежат правила дифференцирования и таблица производных.
Опишем рекурсивную функцию, которая и будет преобразовывать исходную математическую функцию в результирующую функцию-производную:
def differentiate(f: MathAST)(implicit dx: String): MathASTАргумент dx, содержащий имя переменной (по которой происходит дифференцирование) помечен как неявный (
implicit), это позволит не передавать ее в рекурсивные вызовы, пусть этим занимается компилятор.
На вход рекурсивной функции подается выражение — исходная функция f(x) (в формате MathAST), возвращаемое значение — функция-производная в том же формате.
Примечание 1: Выражение может быть бинарным, унарным или токеном.
Примечание 2: Оператором может быть один из: «+», «-», «^», «*», «/», «abs», «sin», «cos», «tg», «ctg», «ln», «arcsin», «arccos», «arctg», «arcctg», «(», «)».
Примечание 3: Входные и выходные данные представлены в формате MathAST — дерево-выражение.
Общий алгоритм
В общем виде алгоритм слишком абстрактный, поэтому дальше разберем его подробнее.
- Рекурсивная функция получает на вход данные и используя сопоставление с образцом (pattern-matching) выполняет необходимые действия, в зависимости от типа данных.
- Функция высчитывает производную для входного выражения и возвращает выражение-результат. Может получиться, что аргументы a и/или b оказались не константой и не переменной, а сложной функцией u(x),
тогда понадобится рекурсивно посчитать еще и производную u’(x), т.е. вернуть [ differentiate(u(x)) ] — перейти к шагу 1 с новыми данными — u(x). - Если данные не корректны вернуть сообщение об ошибке.
Детали принципа работы и связь с математическими абстракциями
Функция приняла на вход данные — выражение-функцию, которую следует обработать в соответствии с правилами дифференцирования
Если бинарное выражение
Бинарные выражения помечены трейтом DoubleToken. »):
»):
case Add(a, b) => Add(differentiate(a), differentiate(b))
case Sub(a, b) => Sub(differentiate(a), differentiate(b))
…
- Если оператор «+»: вернуть [ differentiate(a) + differentiate(b) ].
- Если оператор «-»: вернуть [ differentiate(a) — differentiate(b) ].
- Если оператор «*»: Умножение представляет из себя более сложный случай, операнды a и b могут быть константами или переменными (всего 4 комбинации: u(x)*c, u(x)*v(x), c*c, c*u(x)).
Функция анализирует какой из 4 вариантов попался и возвращает выражение используя правило дифференцирования № 1, № 3, и №5,
если один из операндов – сложная функция. Например: если a = u(x), а b = v(x), то вернуть [ differentiate(a) * b + a * differentiate(b)) ].
Приватный метод isDependsOnVar проверяет, зависит ли подвыражение от переменной, по которой производится дифференцирование. c, c=const
Constant(BigDecimal(0))
}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
}
c, c=const
Constant(BigDecimal(0))
}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
}Если унарное выражение
Классы SingleToken обрабатываются следующим образом:
case e: SingleToken => val d = e match { case Sin(x) => Cos(x) case Cos(x) => Usub(Sin(x)) case Tg(x) => Div(Constant(BigDecimal(1)), Pow(Cos(x), Constant(BigDecimal(2)))) … } if (isLeaf(e.a)) d else Mul(d, differentiate(e.a))Оператор проверяется на соответствие одному из доступных операторов («sin», «-», «cos», …)
Для примера, оператор «sin»: вернуть
[ cos(a) ], если
a = x, если же
a— сложная функция
u(x), то вернуть
[ cos(a) * differentiate(a) ].
С остальными операторами происходят аналогичные действия, используя правило дифференцирования сложной функции и табличные правила взятия производной.
Отдельно следует рассмотреть оператор abs — модуль, поскольку его нет в таблице.

Приватный метод
isLeafвыясняет сложная функция или нет, в первом случае нужно вернуть текущий результат умноженный на производную вложенной функции, а во втором просто вернуть текущий результат.
Если один токен
Речь идет о переменной или константе
case Variable(a) => if (a == dx) Constant(BigDecimal(1)) else Constant(BigDecimal(0)) case Constant(a) => Constant(BigDecimal(0)) case Pi | Exponenta => Constant(BigDecimal(0)) case _ => throw new AbstractEvaluateException("Differentiate: Wrong input data")- Введены некорректные данные, вывести сообщение об ошибке и завершить работу.
- Если переменная (по которой осуществляется дифференцирование, например x), вернуть [ 1 ].
- Если константа, вернуть [ 0 ].
Напоследок добавим строку:
case Differentiate(_f, _dx) => differentiate(_f)(_dx.name)Это на случай, если внутри функции есть вложенная производная, т.
 c, c=const
Constant(BigDecimal(0))
}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
} case e: SingleToken =>
val d = e match {
case Sin(x) => Cos(x)
case Cos(x) => Usub(Sin(x))
case Tg(x) => Div(Constant(BigDecimal(1)), Pow(Cos(x), Constant(BigDecimal(2))))
case Ctg(x) => Usub(Div(Constant(BigDecimal(1)), Pow(Sin(x), Constant(BigDecimal(2)))))
case Abs(x) => Div(x, Abs(x))
case Ln(x) => Div(Constant(BigDecimal(1)), x)
case Sqrt(x) => Div(Constant(BigDecimal(1)), Mul(Constant(BigDecimal(2)), Sqrt(x)))
case Usub(x) => Usub(differentiate(x))
case Arcsin(x) => Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
case Arccos(x) => Usub(Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))))
case Arctg(x) => Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))
case Arcctg(x) => Usub(Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
case _ => throw new AbstractEvaluateException(“Differentiate: Unknown unary operator”)
}
if (isLeaf(e.
c, c=const
Constant(BigDecimal(0))
}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
} case e: SingleToken =>
val d = e match {
case Sin(x) => Cos(x)
case Cos(x) => Usub(Sin(x))
case Tg(x) => Div(Constant(BigDecimal(1)), Pow(Cos(x), Constant(BigDecimal(2))))
case Ctg(x) => Usub(Div(Constant(BigDecimal(1)), Pow(Sin(x), Constant(BigDecimal(2)))))
case Abs(x) => Div(x, Abs(x))
case Ln(x) => Div(Constant(BigDecimal(1)), x)
case Sqrt(x) => Div(Constant(BigDecimal(1)), Mul(Constant(BigDecimal(2)), Sqrt(x)))
case Usub(x) => Usub(differentiate(x))
case Arcsin(x) => Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
case Arccos(x) => Usub(Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))))
case Arctg(x) => Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))
case Arcctg(x) => Usub(Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
case _ => throw new AbstractEvaluateException(“Differentiate: Unknown unary operator”)
}
if (isLeaf(e.
Заключение
Весь код исходников можно скачать на github’е, протестировать программу онлайн можно на сайте Калькулятор производных онлайн, приложение выполнено в виде REST сервиса и дополнено модулями упрощения выражений.

Список литературы
Конвертер электрического заряда • Электротехника • Компактный калькулятор • Онлайн-конвертеры единиц измерения
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления.Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др.
 единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. МенделееваОбщие сведения
Как ни удивительно, но мы сталкиваемся со статическим электричеством ежедневно — когда гладим любимую кошку, расчесываем волосы или натягиваем свитер из синтетики. Так мы сами поневоле становимся генераторами статического электричества. Мы буквально купаемся в нём, ведь мы живем в сильном электростатическом поле Земли. Это поле возникает из-за того, что её окружает ионосфера, верхний слой атмосферы — электропроводящий слой.
 Ионосфера образовалась под действием космического излучения и имеет свой заряд. Занимаясь обыденными делами вроде разогрева пищи, мы совершенно не задумываемся о том, что пользуемся статическим электричеством, повернув кран подачи газа на горелке с автоподжигом или поднеся к ней электрозажигалку.
Ионосфера образовалась под действием космического излучения и имеет свой заряд. Занимаясь обыденными делами вроде разогрева пищи, мы совершенно не задумываемся о том, что пользуемся статическим электричеством, повернув кран подачи газа на горелке с автоподжигом или поднеся к ней электрозажигалку.Примеры статического электричества
Грозы на Земле. Вид с Международной космической станции. Фотографии НАСА.
Мы с детства инстинктивно боимся грома, хотя сам по себе он абсолютно безопасен — просто акустическое следствие грозного удара молнии, которая и вызвана атмосферным статическим электричеством. Моряки времён парусного флота впадали в священный трепет, наблюдая огоньки святого Эльма на своих мачтах, которые тоже являются проявлением атмосферного статического электричества. Люди наделяли верховных богов древних религий неотъемлемым атрибутом в виде молний, будь то греческий Зевс, римский Юпитер, скандинавский Тор или Перун русичей.
Самолет Air Canada на земле во время заправки
С тех пор, как люди впервые начали интересоваться электричеством, прошли века, и мы даже порой не подозреваем, что учёные, сделав из изучения статического электричества глубокомысленные выводы, спасают нас от ужасов пожаров и взрывов.
 Мы укротили электростатику, нацелив в небо пики громоотводов и снабдив бензовозы заземляющими устройствами, позволяющими электростатическим зарядам безопасно уходить в землю. И, тем не менее, статическое электричество продолжает хулиганить, создавая помехи приёму радиосигналов — ведь на Земле одновременно бушует до 2000 гроз, которые ежесекундно генерируют до 50 разрядов молний.
Мы укротили электростатику, нацелив в небо пики громоотводов и снабдив бензовозы заземляющими устройствами, позволяющими электростатическим зарядам безопасно уходить в землю. И, тем не менее, статическое электричество продолжает хулиганить, создавая помехи приёму радиосигналов — ведь на Земле одновременно бушует до 2000 гроз, которые ежесекундно генерируют до 50 разрядов молний.Исследованием статического электричества люди занимались с незапамятных времён; даже термину «электрон» мы обязаны древним грекам, хотя они подразумевали под этим несколько иное — так они называли янтарь, который прекрасно электризовался при трении (др. – греч. ἤλεκτρον — янтарь). К сожалению, наука о статическом электричестве не обошлась без жертв — российский учёный Георг Вильгельм Рихман во время проведения эксперимента был убит разрядом молнии, которая является наиболее грозным проявлением атмосферного статического электричества.
Статическое электричество и погода
В первом приближении, механизм образования зарядов грозового облака во многом сходен с механизмом электризации расчёски — в нём точно так же происходит электризация трением.
 Льдинки, образуясь из мелких капелек воды, охлаждённой из-за переноса восходящими потоками воздуха в верхнюю, более холодную, часть облака, сталкиваются между собой. Более крупные льдинки заряжаются при этом отрицательно, а меньшие — положительно. Из-за разницы в весе происходит перераспределение льдинок в облаке: крупные, более тяжёлые, опускаются в нижнюю часть облака, а более лёгкие льдинки меньшего размера собираются в верхней части грозового облака. Хотя всё облако в целом остаётся нейтральным, нижняя часть облака получает отрицательный заряд, а верхняя — положительный.
Льдинки, образуясь из мелких капелек воды, охлаждённой из-за переноса восходящими потоками воздуха в верхнюю, более холодную, часть облака, сталкиваются между собой. Более крупные льдинки заряжаются при этом отрицательно, а меньшие — положительно. Из-за разницы в весе происходит перераспределение льдинок в облаке: крупные, более тяжёлые, опускаются в нижнюю часть облака, а более лёгкие льдинки меньшего размера собираются в верхней части грозового облака. Хотя всё облако в целом остаётся нейтральным, нижняя часть облака получает отрицательный заряд, а верхняя — положительный.Франклин на стодолларовой купюре
Подобно наэлектризованной расческе, притягивающей воздушный шарик из-за индуцирования на его ближней к расческе стороне противоположного заряда, грозовое облако индуцирует на поверхности Земли положительный заряд. По мере развития грозового облака, заряды увеличиваются, при этом растёт напряжённость поля между ними, и, когда напряжённость поля превысит критическое значение для данных погодных условий, происходит электрический пробой воздуха — разряд молнии.

На бога надейся, а про молниеотвод не забывай!
Человечество обязано Бенджамину Франклину — впоследствии президенту Высшего исполнительного совета Пенсильвании и первому Генеральному почтмейстеру США — за изобретение громоотвода (точнее было бы назвать его молниеотводом), навсегда избавившего население Земли от пожаров, вызываемых попаданием молний в здания. Кстати, Франклин не стал патентовать своё изобретение, сделав его доступным для всего человечества.
Не всегда молнии несли только разрушения — уральские рудознатцы определяли расположение железных и медных руд именно по частоте ударов молний в определённые точки местности.
Лейденские банки в экспозиции Канадского музея науки и техники
В числе учёных, посвятивших своё время исследованию явлений электростатики, необходимо упомянуть англичанина Майкла Фарадея, впоследствии одного из основателей электродинамики, и голландца Питера ван Мушенбрука, изобретателя прототипа электрического конденсатора — знаменитой лейденской банки.

Наблюдая за гонками DTM, IndyCar или Formula 1, мы даже не подозреваем, что механики зазывают пилотов для смены резины на дождевую, опираясь на данные метеорологических РЛС. А эти данные, в свою очередь, основаны именно на электрических характеристиках подступающих грозовых облаков.
Метеорологическая РЛС в аэропорту им. Пирсона, Торонто
Статическое электричество — наш друг и враг одновременно: его недолюбливают радиоинженеры, натягивая заземляющие браслеты при ремонте сгоревших плат в результате удара поблизости молнии — при этом, как правило, выходят из строя входные каскады оборудования. При неисправном заземляющем оборудовании оно может стать причиной тяжёлых техногенных катастроф с трагическими последствиями — пожаров и взрывов целых заводов.
Статическое электричество в медицине
Тем не менее, оно приходит на помощь людям при нарушениях сердечного ритма, вызванных хаотическими судорожными сокращениями сердца больного. Его нормальная работа восстанавливается пропусканием небольшого электростатического разряда при помощи прибора, называемого дефибриллятором.
 Сцена возвращения пациента с того света с помощью дефибриллятора является своего рода классикой для кино определённого жанра. При этом следует отметить, что в кино традиционно показывают монитор с отсутствующим сигналом сердцебиения и зловещей прямой линией, хотя на самом деле применение дефибриллятора не помогает, если сердце пациента остановилось.
Сцена возвращения пациента с того света с помощью дефибриллятора является своего рода классикой для кино определённого жанра. При этом следует отметить, что в кино традиционно показывают монитор с отсутствующим сигналом сердцебиения и зловещей прямой линией, хотя на самом деле применение дефибриллятора не помогает, если сердце пациента остановилось.Разрядники на крыле самолета Boeing 738-800 предназначены для снятия статического электричества для обеспечения надежной работы бортового электронного оборудования.
Другие примеры
Нелишне будет вспомнить о необходимости металлизации самолетов для защиты от статического электричества, то есть, соединения всех металлических частей самолета, включая двигатель, в одну электрически целостную конструкцию. На законцовках всего оперения самолета устанавливают статические разрядники для стекания статического электричества, накапливающегося во время полета вследствие трения воздуха о корпус самолета. Эти меры необходимы для защиты от помех, возникающих при разряде статического электричества, и обеспечения надежной работы бортового электронного оборудования.

Электростатика играет определённую роль в знакомстве учеников с разделом «Электричество» — более эффектных опытов, пожалуй, не знает ни один из разделов физики — тут тебе и волосы, вставшие дыбом, и погоня воздушного шарика за расческой, и таинственное свечение люминесцентных ламп безо всякого подключения проводов! А ведь этот эффект свечения газонаполненных приборов спасает жизни электромонтёрам, имеющих дело с высоким напряжением в современных линиях электропередач и распределительных сетях.
И самое главное, учёные пришли к выводу, что статическому электричеству, точнее его разрядам в виде молний, мы, вероятно, обязаны появлению жизни на Земле. В ходе экспериментов в середине прошлого века, с пропусканием электрических разрядов через смесь газов, близкую по составу к первичному составу атмосферы Земли, была получена одна из аминокислот, которая является «кирпичиком» нашей жизни.
Источники бесперебойного питания (ИБП) используются для защиты оборудования от провалов напряжения, пропадания электропитания и импульсов высокого напряжения в промышленной электросети, которые могут возникать во время непрямых ударов молний
Для укрощения электростатики очень важно знать разность потенциалов или электрическое напряжение, для измерения которого придуманы приборы, называемые вольтметрами.
 Ввел понятие электрического напряжения итальянский учёный 19-го века Алессандро Вольта, по имени которого и названа эта единица. В своё время для измерения электростатического напряжения использовались гальванометры, названные по имени соотечественника Вольта Луиджи Гальвани. К сожалению, эти приборы электродинамического типа вносили искажения в измерения.
Ввел понятие электрического напряжения итальянский учёный 19-го века Алессандро Вольта, по имени которого и названа эта единица. В своё время для измерения электростатического напряжения использовались гальванометры, названные по имени соотечественника Вольта Луиджи Гальвани. К сожалению, эти приборы электродинамического типа вносили искажения в измерения.Изучение статического электричества
К систематическому изучению природы электростатики учёные приступили со времён работ французского учёного 18-го века Шарля Огюстена де Кулона. В частности, он ввёл понятие электрического заряда и открыл закон взаимодействия зарядов. По его имени названа единица измерения количества электричества — кулон (Кл). Правда, ради исторической справедливости, надо заметить, что годами ранее этим занимался английский учёный лорд Генри Кавендиш; к сожалению, он писал в стол и его работы были опубликованы наследниками лишь спустя 100 лет.
Работы предшественников, посвященные законам электрических взаимодействий, дали возможность физикам Джорджу Грину, Карлу Фридриху Гауссу и Симеону Дени Пуассону создать изящную в математическом отношении теорию, которой мы пользуемся до сих пор.
 Главным принципом в электростатике является постулат об электроне — элементарной частице, входящей в состав любого атома и легко отделяющейся от него под воздействием внешних сил. Помимо этого, действуют постулаты об отталкивании одноимённых зарядов и притягивании разноимённых.
Главным принципом в электростатике является постулат об электроне — элементарной частице, входящей в состав любого атома и легко отделяющейся от него под воздействием внешних сил. Помимо этого, действуют постулаты об отталкивании одноимённых зарядов и притягивании разноимённых.Измерение электричества
Цифровой мультиметр, позволяющий измерять ток, напряжение, сопротивление и проверять транзисторы.
Одним из первых измерительных приборов явился простейший электроскоп, изобретённый английским священником и физиком Абрахамом Беннетом — два листочка золотой электропроводной фольги, помещённые в стеклянную ёмкость. С тех пор измерительные приборы значительно эволюционировали — и теперь они могут измерять разницу в единицы нанокулон. С помощью особо точных физических инструментов, российский учёный Абрам Иоффе и американский физик Роберт Эндрюс Милликен сумели измерить электрический заряд электрона
Ныне, с развитием цифровых технологий, появились сверхчувствительные и высокоточные приборы с уникальными характеристиками, которые, благодаря высокому входному сопротивлению, почти не вносят искажений в измерения.
 Помимо измерения напряжения такие приборы позволяют измерять и другие важные характеристики электрический цепей, таких, как омическое сопротивление и протекающий ток в широком диапазоне измерений. Самые продвинутые приборы, называемые из-за их многофункциональности мультиметрами, или, на профессиональном жаргоне, тестерами, позволяют измерять также и частоту переменного тока, емкость конденсаторов и осуществлять проверку транзисторов и даже измерять температуру.
Помимо измерения напряжения такие приборы позволяют измерять и другие важные характеристики электрический цепей, таких, как омическое сопротивление и протекающий ток в широком диапазоне измерений. Самые продвинутые приборы, называемые из-за их многофункциональности мультиметрами, или, на профессиональном жаргоне, тестерами, позволяют измерять также и частоту переменного тока, емкость конденсаторов и осуществлять проверку транзисторов и даже измерять температуру.Как правило, современные приборы имеют встроенную защиту, не позволяющую вывести прибор из строя при неправильном применении. Они компактны, просты в обращении и абсолютно безопасны в работе — каждый из них проходит через ряд испытаний на точность, проверяется в тяжёлых режимах работы и заслужено получает сертификат безопасности.
Литература
Автор статьи: Сергей Акишкин
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.

Расчеты для перевода единиц в конвертере «Конвертер электрического заряда» выполняются с помощью функций unitconversion.org.
Расчет транспортных тарифов
Раздел 1. Термины и определения
В настоящем Пользовательском соглашении (далее – Соглашение) используются следующие термины и определения:
Общество Акционерное общество «Санкт-Петербургская Международная Товарно-сырьевая Биржа», являющееся организатором торговли и клиринговой организацией. Сайт Официальный сайт Общества в сети Интернет, доступ к которому осуществляется по адресу https://spimex.com, включая все страницы указанного сайта, содержащие в своем доменном имени обозначения s-pimex.ru, spimex.ru или spimex.com. Биржевая информация Информация о ходе и итогах организованных торгов, проводимых в товарных секциях и Секции срочного рынка Общества, обязанность по раскрытию которой предусмотрена законами, нормативными актами Банка России, иными нормативными правовыми актами Российской Федерации, или которую Общество раскрывает по своему усмотрению путем размещения на Сайте. 
Индексы Ценовые показатели, рассчитываемые Обществом на основе информации о ходе и итогах организованных торгов, проводимых в товарных секциях и Секции срочного рынка Общества, информации о зарегистрированных в Обществе внебиржевых договорах, а также иной информации, предоставляемой Обществу третьими лицами. Производная информация Индексы, а также иные показатели, рассчитанные Обществом на основе Биржевой информации, данных, полученных по результатам клиринга обязательств из договоров, заключенных на организованных торгах, проводимых в товарных секциях и Секции срочного рынка Общества, Индексов и информации, предоставляемой Обществу третьими лицами. Материалы Тексты, аудиоматериалы, любые изображения, в том числе любое фото, графическое и/или видео изображение, фотографии, размещенные на Сайте, правообладателем которых является Общество. 
Информация Материалы, Биржевая информация, Индексы и иная Производная информация, размещенная на Сайте или предоставляемая на основании договора. Информационные услуги Оказываемые Обществом услуги по предоставлению заинтересованным лицам Информации на возмездной основе. Пользователь Лицо, осуществляющее использование Сайта. Распространение Действия, направленные на получение информации неопределенным кругом лиц или передачу информации неопределенному кругу лиц. Раздел 2. Общие положения
2.1. Соглашение определяет условия использования Информации, права и обязанности Пользователя, возникающие при получении доступа к Информации и Информационным услугам посредством Сайта.
Состав доступной на Сайте Информации определяется Обществом по собственному усмотрению с учетом требований законов, нормативных актов Банка России и иных нормативных правовых актов Российской Федерации.

Порядок и условия получения бесплатного доступа к Информации посредством Сайта определяются Соглашением. Порядок и условия доступа к Информационным услугам, использования Информации определяются Соглашением, а также договорами, заключаемыми между Обществом и Пользователями.
2.2. Соглашение является публичной офертой в соответствии со ст. 437 Гражданского кодекса Российской Федерации (далее – ГК РФ). Соглашение публикуется на Сайте и вступает в силу с момента опубликования.
Пользователь, приступивший к использованию Сайта, считается подтвердившим свое согласие с условиями Соглашения в порядке, предусмотренном п. 3 ст. 434 ГК РФ.
2.3 В соответствии с законодательством Российской Федерации и заключенными договорами Общество является правообладателем Информации, включая, но не ограничиваясь, размещенную на Сайте Биржевую информацию, Индексы и иную Производную информацию.
Раздел 3. Порядок и условия доступа к Информации.
3.
 1 В соответствии с п. 1 ч. 3 ст. 6 Федерального закона от 27.07.2006 №149‐ФЗ «Об информации, информационных технологиях и о защите информации» Общество определяет порядок и условия доступа Пользователя к размещаемой на Сайте Информации.
1 В соответствии с п. 1 ч. 3 ст. 6 Федерального закона от 27.07.2006 №149‐ФЗ «Об информации, информационных технологиях и о защите информации» Общество определяет порядок и условия доступа Пользователя к размещаемой на Сайте Информации.3.2 Общество безвозмездно обеспечивает предоставление доступа к Биржевой информации, Индексам и иной Производной информации, подлежащей размещению на Сайте в соответствии с требованиями законов, нормативных актов Банка России, иных нормативных правовых актов Российской Федерации. Биржевая информация, Индексы и иная Производная информация могут использоваться на условиях, установленных разделом 4 настоящего Соглашения.
3.3 Все Индексы рассчитываются Обществом с использованием методик, опубликованных на Сайте. Значения дополнительных параметров, используемых при расчете Индексов (коэффициенты, тарифы), раскрываются на Сайте в открытом доступе.
3.4 Биржевая информация, а также любые Материалы, размещаемые на Сайте, не являются рекламой и не могут расцениваться в качестве рекомендаций или предложений, направленных на стимулирование Пользователя к заключению договоров с какими‐либо биржевыми товарами (инструментами), допущенными к организованным торгам, проводимым в товарных секциях и Секции срочного рынка Общества.

3.5 Информация, размещаемая на Сайте, может содержать ссылки на сайты третьих лиц. При переходе по гиперссылкам, размещенным на Сайте, на внешние по отношению к Сайту информационные ресурсы, Пользователь покидает Сайт.
Общество не несет ответственность за недостоверность сведений, размещаемых на внешних по отношению к Сайту информационных ресурсах, а также за несвоевременную актуализацию и обновление соответствующей информации в их составе.3.6 Общество не выступает в качестве представителя третьих лиц, указанных в пункте 3.5 настоящего раздела Соглашения. Размещение указанных ссылок преследует исключительно информационные цели и не должно рассматриваться в качестве советов, рекламы продуктов, рекомендаций, предложений, реализуемых какими‐либо третьими лицами.
3.7 Предоставление Информационных услуг Пользователю осуществляется на основании договора на оказание Информационных услуг, заключаемого между Пользователем и Обществом.
 Порядок и условия предоставления доступа к Информации, предоставляемой в соответствии с договором на оказание Информационных услуг, определяются указанным договором.
Порядок и условия предоставления доступа к Информации, предоставляемой в соответствии с договором на оказание Информационных услуг, определяются указанным договором.Раздел 4. Условия использования Информации
4.1 Пользователь вправе использовать Информацию, размещенную на Сайте, на условиях и с учетом ограничений, предусмотренных настоящим Соглашением.
4.2 Информация может использоваться Пользователем при условии соблюдения следующих условий и ограничений:
4.2.1 Допускаются любые действия с Информацией, за исключением Распространения, совершаемые Пользователем в личных/служебных целях, не связанных с извлечением прибыли.
4.2.2 Распространение Биржевой информации Пользователем допускается только при условии заключения договора, предусмотренного пунктом 3.7 настоящего Соглашения.
4.2.3 Распространение Пользователем Производной информации, в том числе Индексов допускается при условии получения предварительного письменного разрешения от Общества и указания ссылки на источник такой информации, в частности на Сайт.

4.2.4 Распространение Пользователем Материалов допускается при условии указания ссылки на источник такой информации, в частности на Сайт.
4.2.5 При Распространении Информации не допускается переработка ее оригинального текста. Сокращение или изменение расположения составных частей Информации, снабжение иллюстрациями, комментариями или какими бы то ни было пояснениями, допускается только в той мере, в какой это не приводит к искажению Информации.
4.2.6 Пользователь не вправе совершать какие‐либо действия, направленные на технологическое извлечение или копирование информации с Сайта в обход средств доступа, непосредственно предоставляемых Пользователю на Сайте.
4.2.7 Запрещается использование Пользователем Информации с целью извлечения прибыли, за исключением случая, когда получение Информации осуществляется на основании договора, предусмотренного пунктом 3.7 настоящего Соглашения.
4.3 Условия использования Информации, предоставляемой в соответствии с договором на оказание Информационных услуг, определяются таким договором.

Раздел 5. Права интеллектуальной собственности
5.1 Вся Информация является объектом интеллектуальной собственности Общества. Исключительные права на Информацию, предоставляемую Обществом в связи с оказанием Информационных услуг, сохраняются за Обществом.
5.2 Материалы, их подборка и взаимное расположение подлежат защите в соответствии с положениями законов, нормативных актов Банка России и иных нормативных правовых актов Российской Федерации. Использование Материалов допускается только с учетом соблюдения условий, предусмотренных разделом 4 настоящего Соглашения.
5.3 Исключительные права на использование товарных знаков, коммерческих обозначений и иных объектов интеллектуальной собственности, размещенных на Сайте, принадлежат Обществу или его партнерам.
5.4 Общество, как правообладатель объектов интеллектуальной собственности, вправе по своему усмотрению разрешать или запрещать третьим лицам использование объектов интеллектуальной собственности.
 При этом отсутствие запрета не считается согласием или разрешением на использование.
При этом отсутствие запрета не считается согласием или разрешением на использование.5.5 Условия Соглашения не могут и не должны рассматриваться в качестве оснований для передачи или предоставления Пользователю Сайта каких‐либо исключительных (лицензионных) прав на использование Материалов.
Раздел 6. Обработка персональных данных
6.1 Пользователь дает Обществу свое согласие на обработку его персональных данных, указываемых Пользователем в соответствующей веб-форме Сайта.
6.2 Порядок и условия обработки персональных данных Пользователя определяются Политикой Акционерного общества «Санкт-Петербургская Международная Товарно-сырьевая Биржа» в отношении обработки персональных данных, опубликованной на Сайте.
Раздел 7. Ответственность
7.1 Любое неправомерное использование Информации, размещенной на Сайте, является нарушением прав Общества как правообладателя и/или третьих лиц и может повлечь за собой ответственность, предусмотренную законодательством Российской Федерации.

7.2 Общество не гарантирует непрерывность функционирования и круглосуточную доступность Сайта, сервисов и услуг, оказываемых посредством предоставления доступа к Сайту.
7.3 Общество не несет ответственности за:
7.3.1 убытки, причиненные сбоями и иными нарушениями в функционировании Сайта, в том числе связанные с нарушениями в работе оборудования, систем связи или сетей, которые эксплуатируются и/или обслуживаются третьими лицами;
7.3.2 убытки, понесенные Пользователем в результате наличия вредоносных программ в оборудовании и программном обеспечении, используемом Пользователем для доступа к Сайту;
7.3.3 нарушение Пользователем условий настоящего Соглашения;
7.3.4 неправомерные действия третьих лиц, в том числе связанные с использованием данных Пользователя, а также с использованием сведений о Пользователе, если такие сведения стали доступны третьим лицам не по вине Общества;
7.3.5 косвенные, случайные, непреднамеренные убытки Пользователя (включая вред, вызванный потерей данных или ущерб, причиненный чести, достоинству или деловой репутации), возникшие в связи с использованием Сайта, в том числе при переходе по размещенной на Сайте внешней ссылке, обеспечивающей переход на сайт третьего лица;
7.
 3.6 косвенные, случайные, непреднамеренные убытки Пользователя (включая вред, вызванный потерей данных или ущерб, причиненный чести, достоинству или деловой репутации), которые вызваны недостоверностью информации, указанной или размещенной Пользователем в процессе регистрации на Сайте;
3.6 косвенные, случайные, непреднамеренные убытки Пользователя (включая вред, вызванный потерей данных или ущерб, причиненный чести, достоинству или деловой репутации), которые вызваны недостоверностью информации, указанной или размещенной Пользователем в процессе регистрации на Сайте;7.3.7 несоответствие требованиям законодательства Российской Федерации информации и материалов, размещенных на Сайте Пользователем, нарушение вещных, неимущественных и иных прав третьих лиц, связанных с использованием Сайта Пользователем.
7.4 Ответственность Сторон договора на оказание Информационных услуг, определяется указанным договором, заключенным между Обществом и Пользователем.
Размер ответственности Сторон ограничивается суммой причиненного другой Стороне реального ущерба.Раздел 8. Направление жалоб
8.1 Пользователь, который полагает, что какие‐либо информационные материалы, размещенные на Сайте, нарушают его права и законные интересы, должен направить соответствующую жалобу на электронный адрес Общества info@spimex.
 com.
com.8.2 Обществом рассматриваются жалобы, соответствующие указанным требованиям:
8.2.1 Жалоба содержит имя, фамилию и отчество заявителя/наименование, место нахождения и фактический адрес, контактную информацию.
8.2.2 Жалоба содержит подробное описание предполагаемого нарушения прав Пользователя.
8.2.3 Жалоба содержит контактную информацию для направления ответа: адрес электронной почты и телефон.
8.2.4 Жалоба содержит согласие на обработку персональных данных (для заявителя – физического лица).
Жалобы, не соответствующие указанным требованиям, не рассматриваются Обществом.
8.3 Жалобы рассматриваются Обществом в срок не позднее 30 календарных дней с даты поступления жалобы на электронный адрес Общества, указанный в пункте 8.1 настоящего раздела Соглашения.
Раздел 9. Заключительные положения
9.1 Любые споры, связанные с заключением, изменением, исполнением или прекращением настоящего Соглашения, подлежат разрешению в соответствии с законодательством Российской Федерации.

9.2 Общество вправе вносить изменения в условия Соглашения путем публикации на Сайте Соглашения в новой редакции. Соответствующие изменения вступают в силу с момента публикации на Сайте Соглашения в новой редакции.
9.3 Пользователь обязан периодически знакомиться с текстом Соглашения с целью изучения последних внесенных в него изменений. Продолжая использование Сайта после вступления в силу соответствующих изменений, Пользователь выражает свое согласие с условиями Соглашения в новой редакции.
Онлайн-калькулятор производных с шагами
Онлайн-калькулятор вычислит производную любой функции, используя общие правила дифференцирования (правило произведения, правило частного, правило цепочки и т. д.), с показанными шагами. Он может обрабатывать полиномиальные, рациональные, иррациональные, экспоненциальные, логарифмические, тригонометрические, обратные тригонометрические, гиперболические и обратные гиперболические функции. Кроме того, при необходимости он оценит производную в данной точке.
 Он также поддерживает вычисление первой, второй и третьей производных до 10.
Он также поддерживает вычисление первой, второй и третьей производных до 10.Связанный калькулятор: Калькулятор неявной дифференциации с шагами
Ваш ввод
Найдите $$$\frac{d}{dx} \left(x \sin{\left(x \right)}\right)$$$.
Решение
Применить правило произведения $$$\frac{d}{dx} \left(f{\left(x \right)} g{\left(x \right)}\right) = \ frac {d} {dx} \ left (f {\ left (x \ right)} \ right) g {\ left (x \ right)} + f {\ left (x \ right)} \ frac {d} { dx} \left(g{\left(x \right)}\right)$$$ с $$$f{\left(x \right)} = x$$$ и $$$g{\left(x \right)} = \sin{\left(x \right)}$$$:
$$\color{red}{\left(\frac{d}{dx} \left(x \sin{\left (x \right)}\right)\right)} = \color{red}{\left(\frac{d}{dx} \left(x\right) \sin{\left(x \right)} + x \frac{d}{dx} \left(\sin{\left(x \right)}\right)\right)}$$Применить степенное правило $$$\frac{d}{dx} \ left(x^{n}\right) = nx^{n – 1}$$$ с $$$n = 1$$$, другими словами, $$$\frac{d}{dx} \left( x\right) = 1$$$:
$$x \frac{d}{dx} \left(\sin{\left(x \right)}\right) + \sin{\left(x \right) )} \color{red}{\left(\frac{d}{dx} \left(x\right)\right)} = x \frac{d}{dx} \left(\sin{\left(x \right)}\right) + \sin{\left(x \right)} \color{red}{\left(1\right)}$$Производная синуса равна $$$\frac{d}{dx} \left(\sin{\left(x \right)}\right) = \cos{\left(x \right)}$$$ :
$$x \color{red}{\left(\frac{d}{dx} \left(\sin{\left(x \right)}\right)\right)} + \sin{\left (x \right)} = x \color{red}{\left(\cos{\left(x \right)}\right)} + \sin{\left(x \right)}$$Таким образом, $ $$\frac{d}{dx} \left(x\sin{\left(x\right)}\right) = x \cos{\left(x\right)} + \sin{\left(x \ правильно)}$$$.

Ответить
$$$\frac{d}{dx} \left(x \sin{\left(x\right)}\right) = x \cos{\left(x \right)} + \sin{\left (х \справа)}$$$A
Калькулятор производных: шаги, результаты, часто задаваемые вопросы
Калькулятор производных — это инструмент для вычисления производной определенного порядка заданной функции. Онлайн-калькулятор производных Protonstalk Инструмент поможет вам найти производные функций от первого до десятого порядка за считанные секунды и сделает вашу работу проще и быстрее.
О калькуляторе производных
Входы
Ниже приведены входные данные калькулятора.
- Порядок вычисления производной.
- Функция, для которой нам нужно вычислить производную.
Шаги
Использование калькулятора производных с шагами выглядит следующим образом
- Введите функцию в поле ввода и выберите порядок производных.

- Теперь нажмите кнопку «Рассчитать», чтобы получить производную.
- В новом окне будет отображена производная данной функции.
Выходы
Ниже приведены выходные данные калькулятора.
- Представление производной и производная функции
Что такое производная функции?
Производная является фундаментальным понятием в исчислении. Нахождение производной называется дифференцированием. Производная функции описывает скорость изменения этой функции в данной точке.
Представим производную функцию как:
dx обозначает бесконечно малое изменение переменной «x». Таким образом, dy/dx представляет собой производную от «y» по переменной «x».
Часто задаваемые вопросы
Что такое производные первого и второго порядка?
Однократное дифференцирование функции дает ее производную первого порядка, тогда как двукратное дифференцирование дает ее производную второго порядка.
На графике наклон заданной функции в точке представлен графически производной первого порядка.Производная второго порядка объясняет, как наклон данной функции изменяется в зависимости от независимой переменной.
Что такое производная от нуля?При дифференцировании мы знаем основное правило, что производная любой константы равна нулю, поэтому, очевидно, производная нуля сама по себе равна нулю.
Больше калькуляторов :
Калькулятор второй производной– StudyFAQ.com
Что такое калькулятор второй производной?
Калькулятор второй производной – это инструмент, который помогает найти производную от производной функции f.Этот онлайн-калькулятор делает расчеты простыми и приятными. Также проблемы могут быть решены мгновенно. Он используется для вычисления второй производной функции (f). Дифференциация — это метод расчета скорости изменения (или наклона в точке на графике).
Примеры:
- Найдите вторую производную функции: 3x 2 ?
Шаг 1: Заданная функция: 3x 2
F′ (x) = ddx (3x 2 ) => 3 ddx (x 2 )
F′3 (2) => 6x
Шаг 2: F′′(x) = ddx (6x)
F′′(x) = 6 ddx(x)
F′′(x) = 6(1)
F′′( x) = 6
Ответ: Вторая производная = 6 - Найдите вторую производную функции: 12 x 4 ?
Шаг 1: Заданная функция: 12x 4
F′ (x) = ddx (12x 4 ) => 12 ddx (x 4 ) x 2 9091 F′0(1×9091) 3 ) => 48x 3
Шаг 2:
F′′ (x) = ddx (48x 3 )
F′′ (x) = 48 ddx (x 3 )(x) = 48(3x 2 )
F′′ (x) = 144 x 2
Ответ: Вторая производная = 144 x 2
Использование калькулятора второй производной:
- Калькулятор второй производной показывает пошаговое дифференцирование.
 Кроме того, это помогает в вычислении первых, вторых, третьих … шестых производных
Кроме того, это помогает в вычислении первых, вторых, третьих … шестых производных - Это также помогает дифференцировать функции со многими переменными или частными производными
- Вычисляет также корни/нули
- Используя вторую производную функции, также можно найти относительные максимумы и минимумы. Для этого вычислите первую производную функции и найдите ее критические точки. После первой производной вычислить вторую производную функции.Затем подставьте критические точки, найденные во второй производной. Результаты показывают, является ли это относительным максимумом или минимумом .
- Если результат положительный = относительный минимум (график в этой точке вогнутый вверх)
- Если результат отрицательный = относительный максимум (график в этой точке вогнут вниз)
- Если вторая производная равна 0 в критической точке, то тест не пройден, и вы должны использовать тест первой производной, чтобы узнать, является ли эта точка максимальной или минимальной
Примечание:
- Максимум или максимумы (множественное число) — это высшая точка
- Минимум или минимумы (во множественном числе) являются нижней точкой
Как правило, слово экстремум (множественное число экстремум) используется для обозначения максимума или минимума, а также местный максимум или минимум используется, когда, возможно, есть более высокие или более низкие точки вдали, но не близко.

Схематические диаграммы, графики и графики помогают понять функции в интерактивном режиме.
Вогнутость графика f измеряется второй производной функции f. Вогнутость означает, что вторая производная положительна, что иногда также называют выпуклой. Это означает, что касательная будет лежать ниже графика функции. Вогнутость вниз означает, что вторая производная отрицательна, также называемая просто вогнутой, и касательная будет лежать над графиком функции.
Некоторые полезные ссылки:
https://www.symbolab.com/solver/second-derivative-calculator
http://www.derivative-calculator.net/
http://calculator.tutorvista.com/math/580/second-derivative-calculator.html
http://www.emathhelp.net/calculators/calculus-1/derivative-calculator/
http://community.wolfram.com/groups/-/m/t/283665
http://www.analyzemath.com/calculus/Differentiation/find_derivative_function.html
http://www.
 rasmus.is/uk/t/F/Su41k05.htm
rasmus.is/uk/t/F/Su41k05.htmhttps://en.wikipedia.org/wiki/Second_derivative
Калькулятор деривативов. Производный плоттер
В математике производная — это способ показать скорость изменения или величину изменения функции в любой заданной точке. Если у вас есть функция f x, есть несколько способов отметить производную от f, когда дело доходит до x. Этот член также будет считаться производной более высокого порядка. Для производных второго порядка принято использовать обозначение f”x.
Калькулятор производных с пошаговыми пояснениями
Предел для этой производной может отсутствовать. Когда дело доходит до использования деривативов, они служат мощным инструментом с множеством применений. Например, их можно использовать для поиска точек перегиба, описания движения объектов и решения задач оптимизации.
Производная Производная Калькулятор Частная Производная. Английский английский. Калькулятор производных Этот простой и удобный калькулятор производных поможет вам решить любую задачу, достаточно ввести значение функции и вы сразу получите решение с подробным пошаговым описанием.
 Удобный интерфейс калькулятора позволяет быстро рассчитать любые функции.
Удобный интерфейс калькулятора позволяет быстро рассчитать любые функции.Попробуйте этот удобный расчет производных прямо сейчас! Расчет производных Другие калькуляторы. Поделиться DerivativeCalc. Как использовать производный калькулятор Введите функцию для решения Чтобы начать, введите значение функции и нажмите кнопку отправки.
Через мгновение вы получите результат расчета. Посмотреть пошаговое решение После получения результата вы можете ознакомиться с подробным пошаговым описанием решения.
Это поможет вам понять решение проблемы. Сохраните результаты вашего расчета. После завершения вы можете скопировать результат расчета в буфер обмена или ввести новую задачу для решения.
Что такое производные? О DerivativeCalc.Summary: Калькулятор производных позволяет пошагово вычислять производную функции по переменной. Описание: Калькулятор производных позволяет выполнять символьное дифференцирование, используя свойство вывода, с одной стороны, и производные других обычных функций.
 Полученный расчет производной возвращается после упрощения с этапами расчета.
Полученный расчет производной возвращается после упрощения с этапами расчета.Калькулятор производной может вычислить онлайн производную любого многочлена. Калькулятор производных может вычислять онлайн все распространенные производные: sin, cos, tan, ln, exp, sh, th, sqrt квадратный корень и многие другие. Производная суммы представляет собой сумму производных, калькулятор использует это свойство для дифференцирования функций . Чтобы вычислить производную суммы онлайн, просто введите математическое выражение, содержащее сумму, укажите переменную и примените функцию производной.
Эгба демонОбратите внимание, что шаги вычислений для получения вычисления производной также отображаются функцией. Чтобы вычислить производную разности онлайн, просто введите математическое выражение, содержащее разность, укажите переменную и примените функцию производной. Отмечено, что описание и этапы вычисления производной также отображаются функцией. Чтобы рассчитать производную продукта онлайн, просто введите математическое выражение, содержащее продукт, укажите переменную и примените функцию производной.

Обратите внимание, что производная также вычисляется онлайн с описанием и шагами вычислений. Чтобы вычислить цепное правило производных, просто введите математическое выражение, содержащее цепное правило, укажите переменную и примените функцию производной.
Онлайн-калькулятор производных с шагами
Для дифференцирования функции необходимо знать следующие правила расчета и формулы:. Также необходимо знать дифференцированные обычные функции, которые находятся в следующей таблице:.
Применяя формулы вывода и пользуясь обычной таблицей вывода, можно вычислить производную любой функции. Это методы расчета, используемые калькулятором для нахождения производных. Фактор Факторизация Факторизация Онлайн-калькулятор факторинга Расширить Упростить Уменьшить Факторизация онлайн Факторизировать выражение онлайн Факторизировать выражение Факторизировать выражение Упростить выражение онлайн Калькулятор упрощения выражений Калькулятор упрощения выражений Уменьшить выражение онлайн Расширить выражение онлайн Расширить и упростить выражение Расширить и упростить Расширить и сократить математический Расширить математический Расширить продукт.

Дробь Дроби Расчет дроби Вычислить дробь Упростить дробь Упростить калькулятор дробей Упрощенный калькулятор дробей Вычислить дробь онлайн Вычислить дроби Вычислить дроби Калькулятор простой факторизации CAS Исчисление онлайн.
Дифференцировать Калькулятор производной Калькулятор дифференцирования Калькулятор дифференциации Функция дифференциации онлайн Вычислить производную онлайн Расчет производных Дифференциальное исчисление Производная функции Символьное дифференцирование Антидифференцировать Калькулятор первообразной Интегрировать функцию онлайн Функция интеграции онлайн Символическое интегрирование Антидифференцирование Вычислить первообразную онлайн Вычислить интеграл онлайн Интегральное исчисление Вычислить разложение Тейлора онлайн Калькулятор рядов Калькулятор полиномов Тейлора Калькулятор рядов Маклорена.
Графический калькулятор Онлайн-плоттер Функция плоттера Графика Онлайн-графика Построитель кривых Функции рисования Онлайн-графический калькулятор Уравнение тангенса.
 Математические онлайн игры для детей: игра Обратный отсчет игра Таблицы умножения игра Умножение игра Таблицы сложения игра Таблицы вычитания Легкая арифметическая игра Разделение игры. Переключить навигацию Солуматы. Выберите функцию или введите выражение для расчета. Производная онлайн Описание: Калькулятор производной позволяет выполнять символьное дифференцирование, используя свойство деривации, с одной стороны, и производные других обычных функций.
Математические онлайн игры для детей: игра Обратный отсчет игра Таблицы умножения игра Умножение игра Таблицы сложения игра Таблицы вычитания Легкая арифметическая игра Разделение игры. Переключить навигацию Солуматы. Выберите функцию или введите выражение для расчета. Производная онлайн Описание: Калькулятор производной позволяет выполнять символьное дифференцирование, используя свойство деривации, с одной стороны, и производные других обычных функций.Расчет производных полиномов онлайн Калькулятор производных может вычислять онлайн производную любого полинома. Вычислить онлайн общую производную Калькулятор производной может рассчитать онлайн все распространенные производные: sin, cos, tan, ln, exp, sh, th, sqrt квадратный корень и многие другие Вычислить онлайн производные суммы Производная суммы представляет собой сумму производные, калькулятор использует это свойство для дифференцирования функций.
Дифференциация разностей Чтобы вычислить онлайн производную разности, просто введите математическое выражение, содержащее разность, укажите переменную и примените функцию производной.
 Расчет производной продукта онлайн Чтобы рассчитать производную продукта онлайн, просто введите математическое выражение, содержащее продукт, укажите переменную и примените функцию производной.
Расчет производной продукта онлайн Чтобы рассчитать производную продукта онлайн, просто введите математическое выражение, содержащее продукт, укажите переменную и примените функцию производной.Расчет цепного правила производных Для расчета цепного правила производных просто введите математическое выражение, содержащее цепное правило, укажите переменную и примените функцию производной. Как рассчитать производную? Калькулятор производных позволяет пошагово вычислять производную функции по переменной.
Рассчитайте онлайн с помощью калькулятора производных производных. Калькулятор первообразных позволяет рассчитать примитив онлайн с подробностями и шагами расчета. Калькулятор производных: производная. Интегральный калькулятор : интеграл. Интегральная функция вычисляет в режиме онлайн интеграл функции между двумя значениями.
Калькулятор для определения, является ли функция четной и нечетной функцией. Калькулятор производных позволяет вычислять производные функций онлайн — бесплатно! Наш калькулятор позволяет вам проверить свои решения математических упражнений.
CASIO FX 991ES PLUS – Навыки работы с калькулятором – дифференциация
Это поможет вам попрактиковаться, показывая вам полную пошаговую дифференциацию работы. Вы также можете проверить свои ответы! Чтобы узнать больше о том, как использовать Калькулятор производных, перейдите в раздел «Справка» или посмотрите примеры. Введите функцию, которую вы хотите дифференцировать, в калькулятор производных. Калькулятор производных покажет вам графическую версию вашего ввода, пока вы печатаете.
Убедитесь, что он показывает именно то, что вы хотите.Используйте круглые скобки, если необходимо, e. В разделе «Примеры» вы можете увидеть, какие функции поддерживает Калькулятор производных и как их использовать.
Когда вы закончите вводить свою функцию, нажмите «Перейти! В «Параметры» вы можете установить переменную дифференцирования и порядок первой, второй, … производной.
 Вы также можете выбрать, показывать ли шаги и включать упрощение выражения. Пример вводит его в Калькулятор производных. При наведении на него указателя мыши отображается текст.
Вы также можете выбрать, показывать ли шаги и включать упрощение выражения. Пример вводит его в Калькулятор производных. При наведении на него указателя мыши отображается текст.Генератор практических задач позволяет создавать любое количество случайных упражнений.Ниже вы найдете некоторые параметры конфигурации и предлагаемую проблему. Вы можете принять его, а затем ввести в калькулятор или сгенерировать новый. Не то, что вы имеете в виду? Используйте скобки! Установите переменную дифференциации и порядок в «Опциях».
Чрезвычайно хорошо написанная книга для студентов, впервые изучающих математический анализ, а также для тех, кто нуждается в освежении знаний. Эта книга заставляет вас понять, что математический анализ не так уж и сложен. Платная ссылка. Как партнер Amazon я зарабатываю на соответствующих покупках.
Для тех, кто имеет техническое образование, в следующем разделе объясняется, как работает калькулятор производных. Сначала синтаксический анализатор анализирует математическую функцию.
 Он преобразует его в форму, более понятную компьютеру, а именно в дерево, см. рисунок ниже.
Он преобразует его в форму, более понятную компьютеру, а именно в дерево, см. рисунок ниже.При этом производный калькулятор должен соблюдать порядок операций. Калькулятор производных должен обнаруживать эти случаи и вставлять знак умножения. Парсер реализован на JavaScript на основе алгоритма Shunting-yard и может работать прямо в браузере.Это позволяет быстро получать обратную связь при наборе текста путем преобразования дерева в код LaTeX.
Онлайн-калькулятор производных
MathJax позаботится об их отображении в браузере. Когда “Go! С точки зрения математики, частная производная функции или переменной является противоположностью ее производной, если константа противоположна полной производной. Частные производные обычно используются в математической геометрии и векторном исчислении. Мы предоставляем нашу FAM с множеством инструментов калькулятора, которые могут помочь вам найти решение различных математических уравнений.
Калькулятор частных производных – это инструмент, который позволяет легко и весело решать уравнения в частных производных.
 Он используется для получения уравнений производной или двух переменных и даже принимает многомерные.
Он используется для получения уравнений производной или двух переменных и даже принимает многомерные.Это может быть причиной того, что люди называют это множественной производной, а не частной производной. Помня об этом, вы должны ввести уравнение, которое хотите решить, а затем нажать на кнопку результата, чтобы проверить результат.Что действительно хорошо в визуальных эффектах и графике, так это то, что они помогают вам понять результат так хорошо и быстро.
Давайте покажем вам пример частной производной, которая включает более одной переменной. Ну вот. Позвольте вам понять это на другом примере, который наверняка зацепит вас, и вам все станет ясно. Теперь я почти уверен, что приведенные выше примеры могут помочь вам понять концепцию частичной переменной.
Наши разработчики проделали замечательную работу по настройке всех требований, необходимых для создания этого инструмента.Все, что вам нужно сделать, это просто указать функцию, которую вы хотите, чтобы этот инструмент решил для вас, и он покажет вам пошаговый ответ на ваш вопрос.
 Калькулятор направленной производной имеет возможность пошагового ответа или средства прямого ответа, если вы хотите подтвердить ответ на свой вопрос, установите флажок «Прямой ответ» или, если вы хотите, чтобы все шаги данной функции, затем установите другой флажок .
Калькулятор направленной производной имеет возможность пошагового ответа или средства прямого ответа, если вы хотите подтвердить ответ на свой вопрос, установите флажок «Прямой ответ» или, если вы хотите, чтобы все шаги данной функции, затем установите другой флажок .Наш калькулятор производных позволяет вычислить все производные функции, просто составив уравнение и нажав кнопку результата.Он предоставит вам пошаговую интеграцию, чтобы вы могли практиковать ее где угодно и произвести впечатление на вас, учитель.
Наш инструмент «Калькулятор производных» поддерживает все новейшие функции, вычисления и многие другие переменные, которые необходимы в одном инструменте. Вы можете проверить свой ответ на графиках и визуализациях, потому что это помогает любому человеку быстро понять вещи.
Наш калькулятор первообразных позволяет вычислить все функции первообразных, просто составив уравнение и нажав кнопку результата.Он предоставит вам пошаговую интеграцию, чтобы вы могли практиковать ее где угодно и произвести впечатление на своего учителя.
Проекты по биологии для 9 класса Наш инструмент «Калькулятор антипроизводных» поддерживает все новейшие функции, вычисления и многие другие переменные, которые необходимы в одном инструменте. Если в ваших числах есть все следующие точки, то должны быть и производные числа.
Наш инструмент «Калькулятор антипроизводных» поддерживает все новейшие функции, вычисления и многие другие переменные, которые необходимы в одном инструменте. Если в ваших числах есть все следующие точки, то должны быть и производные числа.Эти правила также известны как правила частных производных. Partial Derivative Solver — это еще один инструмент, который мы предоставляем нашим уважаемым клиентам для решения их проблем, чтобы они могли получить свои результаты.Получайте удовольствие от производных! Введите функцию и посмотрите ее наклон ниже, рассчитанный программой. Затем посмотрите, сможете ли вы вычислить производную самостоятельно. Он отображает вашу функцию синим цветом, а наклон функции на графике ниже красным цветом, вычисляя разницу между каждой точкой в исходной функции, поэтому он не знает формулы для производной.
У вас также есть возможность отобразить другую функцию зеленым цветом под рассчитанным уклоном. Введите функцию вверху, а затем посмотрите, сможете ли вы найти производную, попробовав разные функции внизу.
 Это просто числовая оценка, она не знает формулы для производной. Кроме того, поскольку она просто выполняет простые вычисления, она не будет обрабатывать специальные условия, такие как дыры, скачки и т. д.
Это просто числовая оценка, она не знает формулы для производной. Кроме того, поскольку она просто выполняет простые вычисления, она не будет обрабатывать специальные условия, такие как дыры, скачки и т. д.См. Преемственность. Скрыть рекламу о рекламе. Производный плоттер Получайте удовольствие от производных! Что попробовать! Посмотрите, сможете ли вы обнаружить закономерность! Экспоненциальные функции: функция: e x ln x производная:? Предостережения: это просто числовая оценка, она не знает формулы для производной Но это забавный и образовательный инструмент, так что наслаждайтесь!
Расчетный индекс.Онлайн-калькулятор логарифмического дифференцирования для дифференцирования функции путем получения логарифмической производной.
Revel психология, глава 3 викторинаПравила указания функции ввода 1. Используйте скобки при выполнении арифметических операций. Запишите sin -1 x как asin x 5. Пример ввода для практики. Убедитесь, что входная строка соответствует указанным выше правилам.
 Используйте наш бесплатный калькулятор логарифмического дифференцирования, чтобы найти дифференцирование заданной функции на основе логарифмов. Логарифмическое дифференцирование — это метод, используемый для дифференцирования функций путем использования логарифмической производной функции.
Используйте наш бесплатный калькулятор логарифмического дифференцирования, чтобы найти дифференцирование заданной функции на основе логарифмов. Логарифмическое дифференцирование — это метод, используемый для дифференцирования функций путем использования логарифмической производной функции.Это особенно полезно для функций, в которых переменная возводится в переменную степень, и для дифференцирования логарифма функции, а не самой функции. В калькуляторе логарифмического дифференцирования введите функцию дифференцирования. Логарифмическое дифференцирование — это дифференцирование алгебраически сложных функций или функций, для которых не применяются обычные правила дифференцирования. Калькулятор логарифмических производных. Код для добавления этого калькулятора на ваш веб-сайт Просто скопируйте и вставьте приведенный ниже код на свою веб-страницу, где вы хотите отобразить этот калькулятор.
Калькуляторы и преобразователи. Задайте вопрос. Wolfram Alpha — отличный калькулятор для первых, вторых и третьих производных; производные в точке; и частные производные.
Как использовать сканер тегов
Узнайте, что такое производные и как Wolfram Alpha их вычисляет. Введите ваши запросы, используя простой английский язык. Чтобы избежать двусмысленных запросов, обязательно используйте круглые скобки там, где это необходимо. Вот несколько примеров, иллюстрирующих, как запрашивать производную. Получите немедленную обратную связь и рекомендации с помощью пошаговых решений и Генератора проблем Wolfram.Для данной функции есть много способов обозначить производную по отношению к. Наиболее распространены способы и .
Когда производная берется раз, используется обозначение или. Они называются производными высшего порядка. Обратите внимание, что для производных второго порядка часто используется обозначение. В точке производная определена как. Существование этого предела не гарантируется, но если он существует, то говорят, что он дифференцируем при . Геометрически говоря, это наклон касательной к .
Например, если то и тогда мы можем вычислить :.
 Производная является мощным инструментом со многими приложениями. Wolfram Alpha вызывает D-функцию Wolfram Languages, которая использует таблицу тождеств, намного большую, чем можно найти в стандартном учебнике по математическому анализу. Он использует известные правила, такие как линейность производной, правило произведения, правило степени, правило цепи и так далее. Кроме того, D использует менее известные правила для вычисления производной широкого спектра специальных функций.
Производная является мощным инструментом со многими приложениями. Wolfram Alpha вызывает D-функцию Wolfram Languages, которая использует таблицу тождеств, намного большую, чем можно найти в стандартном учебнике по математическому анализу. Он использует известные правила, такие как линейность производной, правило произведения, правило степени, правило цепи и так далее. Кроме того, D использует менее известные правила для вычисления производной широкого спектра специальных функций.Для производных более высокого порядка определенные правила, такие как общее правило произведения Лейбница, могут ускорить вычисления.О, о! Wolfram Alpha не работает без JavaScript. Пожалуйста, включите JavaScript. Если вы не знаете, как, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram Alpha. Вычисляйте ответы экспертного уровня, используя революционные алгоритмы, базу знаний и технологию искусственного интеллекта Wolfram. производные в точке; и частные производные.

Производная — важный инструмент исчисления, представляющий бесконечно малое изменение функции по отношению к одной из ее переменных.Как Wolfram Alpha вычисляет производные Wolfram Alpha называет D-функцией Wolfram Languages, которая использует таблицу тождеств, намного большую, чем можно найти в стандартном учебнике по математическому анализу.
Супер-пупер онлайн калькулятор производной матрицы в сравнении с нормальной матрицей (для Стэна)
Я реализую матричное нормальное распределение для Стэна, которое обеспечивает многомерную плотность для матрицы с ковариацией, разложенной на ковариации строк и столбцов.
Мотивация
Джейми Мортон, мой новый коллега из Flatiron’s Center for Comp Bio, использует нормаль матрицы для моделирования биома океана.Несколько лет назад людям из группы Ричарда Бонно в Flatiron удалось расширить современное состояние искусства с нескольких измерений до нескольких десятков измерений, используя Stan, как описано здесь
. {{Р} / {2}}}.$
{{Р} / {2}}}.$Он относится к многомерной нормали через векторизацию (суммирование столбцов матрицы) и произведения Кронекера как
$latex \textrm{matrix\_normal}(Y \mid M, U, V) = \textrm{multi\_normal}(\textrm{vec}(Y) \mid \textrm{vec}(M), V \ otimes U).$
После мучений с тензорными дифференциалами для производных матрицы, нормальной относительно ее параметров ковариационной матрицы, достаточно долго, чтобы понять, как это сделать, но недостаточно долго, чтобы добиться в этом успеха или доверять своим результатам, я подумал, что лучше попробуй Вольфрам Альфа.Я не мог сделать это.
matrixcalculus.org на помощь
Немного постаравшись, я ввел в Google запрос
[матричная производная программа], и первое попадание было победным:Это красивое онлайн-программное обеспечение имеет интерфейс 1990-х годов и функциональность 2020-х годов. Я помог, выполнив преобразование в логарифмическую шкалу и убрав постоянные члены,
. {-1} \cdot (Y – M)\right] – N \cdot \log \textrm{det}(V) – P \cdot \log \textrm{det}(U) \right) + \textrm{const}.{-1}$. Тем не менее, когда вы проталкиваете дифференциал, вы получаете тензорные производные внутри этой трассы, которыми трудно манипулировать без догадок на моем уровне навыков матричной алгебры.
{-1} \cdot (Y – M)\right] – N \cdot \log \textrm{det}(V) – P \cdot \log \textrm{det}(U) \right) + \textrm{const}.{-1}$. Тем не менее, когда вы проталкиваете дифференциал, вы получаете тензорные производные внутри этой трассы, которыми трудно манипулировать без догадок на моем уровне навыков матричной алгебры.
В отличие от меня, сайт матричного исчисления прожевал это и выплюнул в аккуратно отформатированном LaTeX за долю секунды:
Несмотря на простоту, это действительно красивый интерфейс. Вы вводите формулу, и она анализирует переменные и запрашивает их форму (скаляр, вектор, вектор-строку или матрицу).Еще одно преимущество делегирования типов данных в том, что оно позволяет интерфейсу разрешать все символы. Возможно, в Wolfram Alpha есть способ сделать это, но он не встроен в их интерфейс.
Бумага
За этим стоит очень хороший документ, в котором объясняется, что они сделали и как это связано с автодиффом.
Я еще не все переварил, но как вы подозреваете, они реализуют тензорную алгебру для производных.
 Вот содержательная часть аннотации.
Вот содержательная часть аннотации.Эта структура может использоваться как для символического, так и для автоматического дифференцирования в прямом и обратном режимах.Эксперименты показывают ускорение до двух порядков по сравнению с современными платформами при оценке производных более высокого порядка на процессорах и ускорение примерно на три порядка на графических процессорах.
Насколько я могу судить, инструмент только первого порядка. Но это все, что нам нужно для специализированных реализаций прямого и обратного режимов в Stan. Производные более высокого порядка начинаются с обратного узла, а затем вкладываются в еще один экземпляр прямого режима. Мне интересно, даст ли это нам лучший способ специализации fvar в Stan (тип, используемый для вторых производных).
Некоторые предложения по инструменту
Блог Эндрю не был бы без предложений по улучшению интерфейсов. Мои предложения на
- установите флажок «Общие подвыражения» по умолчанию (альтернатива удобна для преобразования в код),
- придерживаться простого интерфейса флажков, указывающего с помощью проверки, что совместное использование общего подвыражения включено (как есть, текст говорит «Вкл.
 » с пустым флажком, когда он выключен, и «Выкл.» с пустым флажком, когда он включен),
» с пустым флажком, когда он выключен, и «Выкл.» с пустым флажком, когда он включен), - избавиться от лишних вертикальных пробелов в нижней части поля возврата и
- предоставляют способ сделать поле ввода текста больше и состоять из нескольких строк (как есть, я написал в emacs и вырезал и вставил в интерфейс), и
- позволяют использовать стандартные многосимвольные идентификаторы (похоже, разрешены только односимвольные имена переменных).
Я не пробовал вывод Python, но это отличная идея, если он создает код для эффективного вычисления как функции, так и партиалов.
Перевод в математическую библиотеку Stan
Имея в руках градиент, несложно определить эффективный автодифф в прямом и обратном режимах в Stan, используя нашу общую структуру построителя операндов и частей. Но теперь, когда я смотрю на наш код, я вижу, что наша базовая многовариантная норма даже не использует этот эффективный код.Так что мне придется исправить это тоже, что должно быть победой для всех.

На самом деле я собираюсь определить норму матрицы с точки зрения факторов Холецкого. Это имеет огромное преимущество, заключающееся в том, что не нужно собирать вместе всю ковариационную матрицу только для ее факторизации (нам нужен логарифмический определитель). Использование коэффициентов Холецкого на всем пути гораздо более арифметически устойчиво и требует только квадратичного времени для факторизации, а не кубического.
Что касается использования сайта производной матрицы, просто замените U и V на (L_U * L_U’) и (L_V & L_V’) в формулах, и все должно быть хорошо.На самом деле этого не произойдет, потому что синтаксический анализатор, по-видимому, требует однобуквенных переменных. Поэтому я просто использовал (U * U’), что действительно работает.
Вот формула, которую я использовал для плотности бревен с точностью до константы:
-1/2 * (N * log(det(V * V')) + P * log(det(U * U')) + tr([inv(V * V') * (Y - M)' ] * [инв(U * U') * (Y - M)]))
Поскольку невозможно сказать, что U и V являются факторами Холецкого и, следовательно, что U * U’ симметрично и положительно определено, мне пришлось выполнить некоторое сокращение вручную, например,
инв(U * U') * U = инв(U')
Это дает множество общих подвыражений между функцией и ее градиентом, и я думаю, что могу пойти немного дальше, отметив (U * U’) = (U * U’)’.

matrix_normal_lpdf(Y | M, U, V) = -1/2 * (N * log (det (V * V')) + P * лог(дет (U * U')) + tr([inv(V * V') * (Y - M)'] * [inv(U * U') * (Y - M)])) + константа d/d.Y: -[инв(U * U') * (Y - M)] * инв(V * V') d/d.M: -[инв(U * U') * (Y - M)] * инв(V * V') д/д.У: -P * инв(U') - инв(U * U') * (Y - M)] * [инв(V * V') * (Y - M)'] * инв(U') д/д.В: -N * инв(V') -[inv(V * V') * (Y - M)'] * [inv(U * U') * (Y - M)] * inv(V')Это полностью входит в книгу
Далее я хотел бы добавить все многомерные плотности к следующей незавершенной работе.
На GitHub есть черновик со всеми вводными материалами, справочной реализацией на C++, множеством производных матриц и даже алгебраическими решателями и HMM. Однако многое еще предстоит сделать.
Мы еще не выполнили основные плотности, поэтому мы можем начать с многомерной нормали и T со всеми четырьмя параметризациями (ковариация, точность и одинаковые факторы Холецкого), а также с (обратными) Wisharts и LKJ, которые нам нужны для априорных значений.


 c, c=const
Constant(BigDecimal(0))
}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
}
c, c=const
Constant(BigDecimal(0))
}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
}
 c, c=const
Constant(BigDecimal(0))
}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
} case e: SingleToken =>
val d = e match {
case Sin(x) => Cos(x)
case Cos(x) => Usub(Sin(x))
case Tg(x) => Div(Constant(BigDecimal(1)), Pow(Cos(x), Constant(BigDecimal(2))))
case Ctg(x) => Usub(Div(Constant(BigDecimal(1)), Pow(Sin(x), Constant(BigDecimal(2)))))
case Abs(x) => Div(x, Abs(x))
case Ln(x) => Div(Constant(BigDecimal(1)), x)
case Sqrt(x) => Div(Constant(BigDecimal(1)), Mul(Constant(BigDecimal(2)), Sqrt(x)))
case Usub(x) => Usub(differentiate(x))
case Arcsin(x) => Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
case Arccos(x) => Usub(Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))))
case Arctg(x) => Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))
case Arcctg(x) => Usub(Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
case _ => throw new AbstractEvaluateException(“Differentiate: Unknown unary operator”)
}
if (isLeaf(e.
c, c=const
Constant(BigDecimal(0))
}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
} case e: SingleToken =>
val d = e match {
case Sin(x) => Cos(x)
case Cos(x) => Usub(Sin(x))
case Tg(x) => Div(Constant(BigDecimal(1)), Pow(Cos(x), Constant(BigDecimal(2))))
case Ctg(x) => Usub(Div(Constant(BigDecimal(1)), Pow(Sin(x), Constant(BigDecimal(2)))))
case Abs(x) => Div(x, Abs(x))
case Ln(x) => Div(Constant(BigDecimal(1)), x)
case Sqrt(x) => Div(Constant(BigDecimal(1)), Mul(Constant(BigDecimal(2)), Sqrt(x)))
case Usub(x) => Usub(differentiate(x))
case Arcsin(x) => Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
case Arccos(x) => Usub(Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))))
case Arctg(x) => Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))
case Arcctg(x) => Usub(Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
case _ => throw new AbstractEvaluateException(“Differentiate: Unknown unary operator”)
}
if (isLeaf(e.

 единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева Ионосфера образовалась под действием космического излучения и имеет свой заряд. Занимаясь обыденными делами вроде разогрева пищи, мы совершенно не задумываемся о том, что пользуемся статическим электричеством, повернув кран подачи газа на горелке с автоподжигом или поднеся к ней электрозажигалку.
Ионосфера образовалась под действием космического излучения и имеет свой заряд. Занимаясь обыденными делами вроде разогрева пищи, мы совершенно не задумываемся о том, что пользуемся статическим электричеством, повернув кран подачи газа на горелке с автоподжигом или поднеся к ней электрозажигалку. Мы укротили электростатику, нацелив в небо пики громоотводов и снабдив бензовозы заземляющими устройствами, позволяющими электростатическим зарядам безопасно уходить в землю. И, тем не менее, статическое электричество продолжает хулиганить, создавая помехи приёму радиосигналов — ведь на Земле одновременно бушует до 2000 гроз, которые ежесекундно генерируют до 50 разрядов молний.
Мы укротили электростатику, нацелив в небо пики громоотводов и снабдив бензовозы заземляющими устройствами, позволяющими электростатическим зарядам безопасно уходить в землю. И, тем не менее, статическое электричество продолжает хулиганить, создавая помехи приёму радиосигналов — ведь на Земле одновременно бушует до 2000 гроз, которые ежесекундно генерируют до 50 разрядов молний.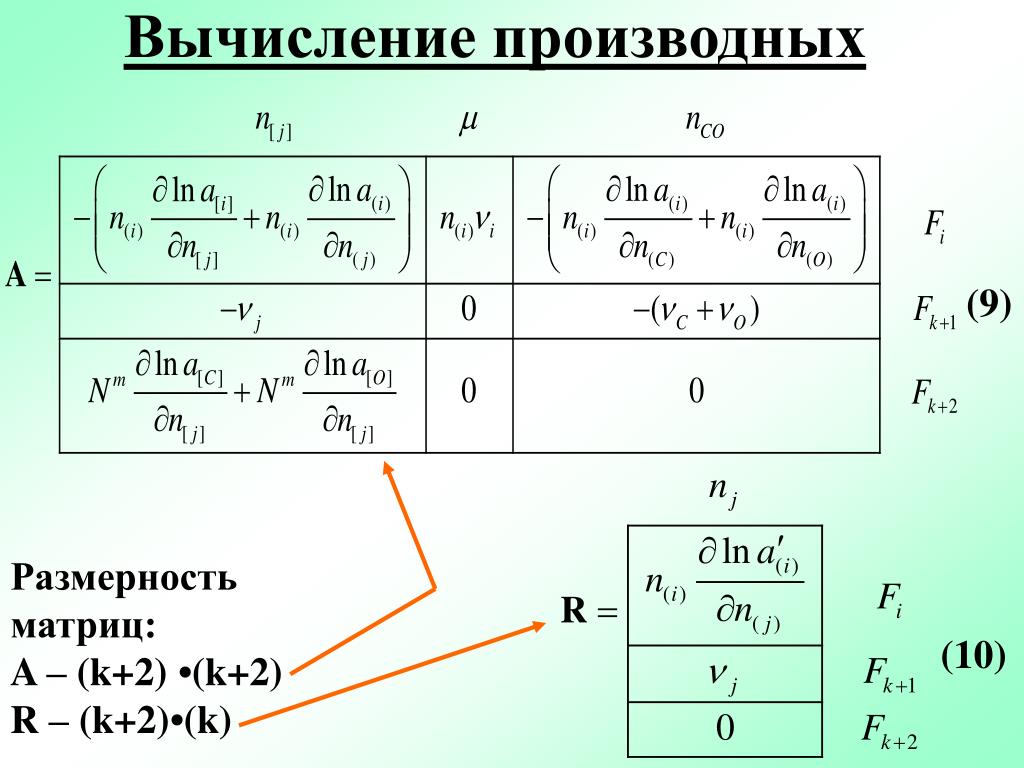 Льдинки, образуясь из мелких капелек воды, охлаждённой из-за переноса восходящими потоками воздуха в верхнюю, более холодную, часть облака, сталкиваются между собой. Более крупные льдинки заряжаются при этом отрицательно, а меньшие — положительно. Из-за разницы в весе происходит перераспределение льдинок в облаке: крупные, более тяжёлые, опускаются в нижнюю часть облака, а более лёгкие льдинки меньшего размера собираются в верхней части грозового облака. Хотя всё облако в целом остаётся нейтральным, нижняя часть облака получает отрицательный заряд, а верхняя — положительный.
Льдинки, образуясь из мелких капелек воды, охлаждённой из-за переноса восходящими потоками воздуха в верхнюю, более холодную, часть облака, сталкиваются между собой. Более крупные льдинки заряжаются при этом отрицательно, а меньшие — положительно. Из-за разницы в весе происходит перераспределение льдинок в облаке: крупные, более тяжёлые, опускаются в нижнюю часть облака, а более лёгкие льдинки меньшего размера собираются в верхней части грозового облака. Хотя всё облако в целом остаётся нейтральным, нижняя часть облака получает отрицательный заряд, а верхняя — положительный.

 Сцена возвращения пациента с того света с помощью дефибриллятора является своего рода классикой для кино определённого жанра. При этом следует отметить, что в кино традиционно показывают монитор с отсутствующим сигналом сердцебиения и зловещей прямой линией, хотя на самом деле применение дефибриллятора не помогает, если сердце пациента остановилось.
Сцена возвращения пациента с того света с помощью дефибриллятора является своего рода классикой для кино определённого жанра. При этом следует отметить, что в кино традиционно показывают монитор с отсутствующим сигналом сердцебиения и зловещей прямой линией, хотя на самом деле применение дефибриллятора не помогает, если сердце пациента остановилось.
 Ввел понятие электрического напряжения итальянский учёный 19-го века Алессандро Вольта, по имени которого и названа эта единица. В своё время для измерения электростатического напряжения использовались гальванометры, названные по имени соотечественника Вольта Луиджи Гальвани. К сожалению, эти приборы электродинамического типа вносили искажения в измерения.
Ввел понятие электрического напряжения итальянский учёный 19-го века Алессандро Вольта, по имени которого и названа эта единица. В своё время для измерения электростатического напряжения использовались гальванометры, названные по имени соотечественника Вольта Луиджи Гальвани. К сожалению, эти приборы электродинамического типа вносили искажения в измерения. Главным принципом в электростатике является постулат об электроне — элементарной частице, входящей в состав любого атома и легко отделяющейся от него под воздействием внешних сил. Помимо этого, действуют постулаты об отталкивании одноимённых зарядов и притягивании разноимённых.
Главным принципом в электростатике является постулат об электроне — элементарной частице, входящей в состав любого атома и легко отделяющейся от него под воздействием внешних сил. Помимо этого, действуют постулаты об отталкивании одноимённых зарядов и притягивании разноимённых. Помимо измерения напряжения такие приборы позволяют измерять и другие важные характеристики электрический цепей, таких, как омическое сопротивление и протекающий ток в широком диапазоне измерений. Самые продвинутые приборы, называемые из-за их многофункциональности мультиметрами, или, на профессиональном жаргоне, тестерами, позволяют измерять также и частоту переменного тока, емкость конденсаторов и осуществлять проверку транзисторов и даже измерять температуру.
Помимо измерения напряжения такие приборы позволяют измерять и другие важные характеристики электрический цепей, таких, как омическое сопротивление и протекающий ток в широком диапазоне измерений. Самые продвинутые приборы, называемые из-за их многофункциональности мультиметрами, или, на профессиональном жаргоне, тестерами, позволяют измерять также и частоту переменного тока, емкость конденсаторов и осуществлять проверку транзисторов и даже измерять температуру.



 1 В соответствии с п. 1 ч. 3 ст. 6 Федерального закона от 27.07.2006 №149‐ФЗ «Об информации, информационных технологиях и о защите информации» Общество определяет порядок и условия доступа Пользователя к размещаемой на Сайте Информации.
1 В соответствии с п. 1 ч. 3 ст. 6 Федерального закона от 27.07.2006 №149‐ФЗ «Об информации, информационных технологиях и о защите информации» Общество определяет порядок и условия доступа Пользователя к размещаемой на Сайте Информации.
 Порядок и условия предоставления доступа к Информации, предоставляемой в соответствии с договором на оказание Информационных услуг, определяются указанным договором.
Порядок и условия предоставления доступа к Информации, предоставляемой в соответствии с договором на оказание Информационных услуг, определяются указанным договором.

 При этом отсутствие запрета не считается согласием или разрешением на использование.
При этом отсутствие запрета не считается согласием или разрешением на использование.
 3.6 косвенные, случайные, непреднамеренные убытки Пользователя (включая вред, вызванный потерей данных или ущерб, причиненный чести, достоинству или деловой репутации), которые вызваны недостоверностью информации, указанной или размещенной Пользователем в процессе регистрации на Сайте;
3.6 косвенные, случайные, непреднамеренные убытки Пользователя (включая вред, вызванный потерей данных или ущерб, причиненный чести, достоинству или деловой репутации), которые вызваны недостоверностью информации, указанной или размещенной Пользователем в процессе регистрации на Сайте; com.
com.
 Он также поддерживает вычисление первой, второй и третьей производных до 10.
Он также поддерживает вычисление первой, второй и третьей производных до 10.


 Кроме того, это помогает в вычислении первых, вторых, третьих … шестых производных
Кроме того, это помогает в вычислении первых, вторых, третьих … шестых производных
 rasmus.is/uk/t/F/Su41k05.htm
rasmus.is/uk/t/F/Su41k05.htm Удобный интерфейс калькулятора позволяет быстро рассчитать любые функции.
Удобный интерфейс калькулятора позволяет быстро рассчитать любые функции. Полученный расчет производной возвращается после упрощения с этапами расчета.
Полученный расчет производной возвращается после упрощения с этапами расчета.

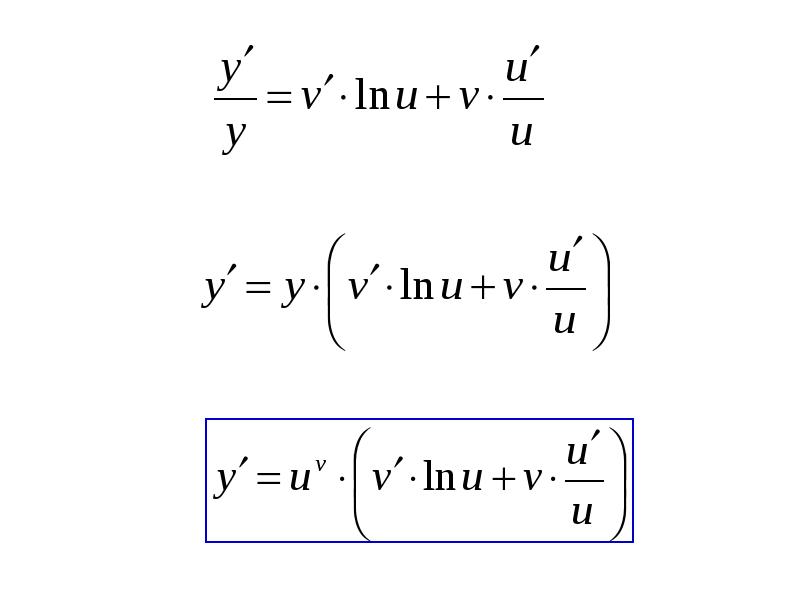 Математические онлайн игры для детей: игра Обратный отсчет игра Таблицы умножения игра Умножение игра Таблицы сложения игра Таблицы вычитания Легкая арифметическая игра Разделение игры. Переключить навигацию Солуматы. Выберите функцию или введите выражение для расчета. Производная онлайн Описание: Калькулятор производной позволяет выполнять символьное дифференцирование, используя свойство деривации, с одной стороны, и производные других обычных функций.
Математические онлайн игры для детей: игра Обратный отсчет игра Таблицы умножения игра Умножение игра Таблицы сложения игра Таблицы вычитания Легкая арифметическая игра Разделение игры. Переключить навигацию Солуматы. Выберите функцию или введите выражение для расчета. Производная онлайн Описание: Калькулятор производной позволяет выполнять символьное дифференцирование, используя свойство деривации, с одной стороны, и производные других обычных функций. Расчет производной продукта онлайн Чтобы рассчитать производную продукта онлайн, просто введите математическое выражение, содержащее продукт, укажите переменную и примените функцию производной.
Расчет производной продукта онлайн Чтобы рассчитать производную продукта онлайн, просто введите математическое выражение, содержащее продукт, укажите переменную и примените функцию производной.
 Вы также можете выбрать, показывать ли шаги и включать упрощение выражения. Пример вводит его в Калькулятор производных. При наведении на него указателя мыши отображается текст.
Вы также можете выбрать, показывать ли шаги и включать упрощение выражения. Пример вводит его в Калькулятор производных. При наведении на него указателя мыши отображается текст. Он преобразует его в форму, более понятную компьютеру, а именно в дерево, см. рисунок ниже.
Он преобразует его в форму, более понятную компьютеру, а именно в дерево, см. рисунок ниже. Он используется для получения уравнений производной или двух переменных и даже принимает многомерные.
Он используется для получения уравнений производной или двух переменных и даже принимает многомерные. Калькулятор направленной производной имеет возможность пошагового ответа или средства прямого ответа, если вы хотите подтвердить ответ на свой вопрос, установите флажок «Прямой ответ» или, если вы хотите, чтобы все шаги данной функции, затем установите другой флажок .
Калькулятор направленной производной имеет возможность пошагового ответа или средства прямого ответа, если вы хотите подтвердить ответ на свой вопрос, установите флажок «Прямой ответ» или, если вы хотите, чтобы все шаги данной функции, затем установите другой флажок . Наш инструмент «Калькулятор антипроизводных» поддерживает все новейшие функции, вычисления и многие другие переменные, которые необходимы в одном инструменте. Если в ваших числах есть все следующие точки, то должны быть и производные числа.
Наш инструмент «Калькулятор антипроизводных» поддерживает все новейшие функции, вычисления и многие другие переменные, которые необходимы в одном инструменте. Если в ваших числах есть все следующие точки, то должны быть и производные числа. Это просто числовая оценка, она не знает формулы для производной. Кроме того, поскольку она просто выполняет простые вычисления, она не будет обрабатывать специальные условия, такие как дыры, скачки и т. д.
Это просто числовая оценка, она не знает формулы для производной. Кроме того, поскольку она просто выполняет простые вычисления, она не будет обрабатывать специальные условия, такие как дыры, скачки и т. д. Используйте наш бесплатный калькулятор логарифмического дифференцирования, чтобы найти дифференцирование заданной функции на основе логарифмов. Логарифмическое дифференцирование — это метод, используемый для дифференцирования функций путем использования логарифмической производной функции.
Используйте наш бесплатный калькулятор логарифмического дифференцирования, чтобы найти дифференцирование заданной функции на основе логарифмов. Логарифмическое дифференцирование — это метод, используемый для дифференцирования функций путем использования логарифмической производной функции.
 Производная является мощным инструментом со многими приложениями. Wolfram Alpha вызывает D-функцию Wolfram Languages, которая использует таблицу тождеств, намного большую, чем можно найти в стандартном учебнике по математическому анализу. Он использует известные правила, такие как линейность производной, правило произведения, правило степени, правило цепи и так далее. Кроме того, D использует менее известные правила для вычисления производной широкого спектра специальных функций.
Производная является мощным инструментом со многими приложениями. Wolfram Alpha вызывает D-функцию Wolfram Languages, которая использует таблицу тождеств, намного большую, чем можно найти в стандартном учебнике по математическому анализу. Он использует известные правила, такие как линейность производной, правило произведения, правило степени, правило цепи и так далее. Кроме того, D использует менее известные правила для вычисления производной широкого спектра специальных функций.
 {{Р} / {2}}}.$
{{Р} / {2}}}.$ {-1} \cdot (Y – M)\right] – N \cdot \log \textrm{det}(V) – P \cdot \log \textrm{det}(U) \right) + \textrm{const}.{-1}$. Тем не менее, когда вы проталкиваете дифференциал, вы получаете тензорные производные внутри этой трассы, которыми трудно манипулировать без догадок на моем уровне навыков матричной алгебры.
{-1} \cdot (Y – M)\right] – N \cdot \log \textrm{det}(V) – P \cdot \log \textrm{det}(U) \right) + \textrm{const}.{-1}$. Тем не менее, когда вы проталкиваете дифференциал, вы получаете тензорные производные внутри этой трассы, которыми трудно манипулировать без догадок на моем уровне навыков матричной алгебры.  Вот содержательная часть аннотации.
Вот содержательная часть аннотации. » с пустым флажком, когда он выключен, и «Выкл.» с пустым флажком, когда он включен),
» с пустым флажком, когда он выключен, и «Выкл.» с пустым флажком, когда он включен),

