Онлайн решение крамера метод: Онлайн калькулятор. Решение систем линейных уравнений. Метод Крамера - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

решаем системы линейных алгебраических уравнений (слау)

В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.

А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера.

Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие

. Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы.

По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:

Сделаем аналогичное действие, заменив в первом определителе второй столбец:

Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.

Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Решение систем методом подстановки.

Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.

и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Применять формулы Крамера нельзя. Решим эту систему методом подстановки

Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет

Рассмотрим систему 3-х уравнений с тремя неизвестными

Используя определители 3-го порядка, решение такой системы можно записать в таком же виде, как и для системы двух уравнений, т.е.

(2.4)

если 0. Здесь

Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .

Пример 2. 3. Решить систему линейных уравнений при помощи правила Крамера:

Решение . Находим определитель основной матрицы системы

Поскольку 0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще три определителя:

Проверка:

Следовательно, решение найдено правильно. 

Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, наводят на мысль, что такие же правила можно сформулировать и для линейных систем любого порядка. Действительно имеет место

Теорема Крамера. Квадратная система линейных уравнений с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение и это решение вычисляется по формулам

(2.5)

где  – определитель основной матрицы ,  i – определитель матрицы , полученной из основной, заменой i -го столбца столбцом свободных членов .

Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо не имеет вообще решений, либо имеет бесконечно много решений.

Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.

2.4. Определители n-го порядка

Дополнительным минором M ij элемента a ij называется определитель, получаемый из данного путем вычеркивания i -й строки и j -го столбца. Алгебраическим дополнением A ij элемента a ij называется минор этого элемента, взятого со знаком (–1) i + j , т.е. A ij = (–1) i + j M ij .

Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя

Получаем



Используя понятие алгебраического дополнения можно сформулировать теорему о разложении определителя n -го порядка по строке или столбцу .

Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:

(2.6)

Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка . В результате разложения определителя n -го порядка по какой-либо строке или столбцу, получается n определителей (n –1)-го порядка. Чтобы таких определителей было меньше, целесообразно выбирать ту строку или столбец, в которой больше всего нулей. На практике формулу разложения определителя обычно записывают в виде:

т.е. алгебраические дополнения записывают в явном виде через миноры.

Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.



2.

5. Основные свойства определителей

Разлагая определитель по какой-либо строке или столбцу, мы получим n определителей (n –1)-го порядка. Затем каждый из этих определителей (n –1)-го порядка также можно разложить в сумму определителей (n –2)-го порядка. Продолжая этот процесс, можно дойти до определителей 1-го порядка, т.е. до элементов матрицы, определитель которой вычисляется. Так, для вычисления определителей 2-го порядка придется вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых. Число слагаемых будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, непосильной даже для ЭВМ. Однако вычислять определители можно и по-другому, используя свойства определителей.

Свойство 1 . Определитель не изменится, если в нем поменять местами строки и столбцы, т. е. при транспонировании матрицы :

Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.

Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).

Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.

Свойство 3 . Общий множитель всех элементов в какой-либо строке (столбце) можно вынести за знак определителя .

Например,

Следствие . Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю .

Свойство 4 . Определитель не изменится, если к элементам одной строки (столбца), прибавить элементы другой строки (столбца), умноженной на какое-либо число .

Например,

Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко ходить не надо.

Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).

Теорема Крамера.

Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :

где Δ – определитель матрицы системы ,

Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.

Когда определитель системы нулевой, значит, система может стать совместной или несовместной.

Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.

Описание метода Крамера.

Есть система уравнений:

Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.

Составляем определитель из коэффициентов у неизвестных:

Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:

Решаем систему по формулам Крамера :

Примеры решения систем уравнений методом Крамера.

Пример 1 .

Дана система:

Решим ее методом Крамера.

Сначала нужно вычислить определитель матрицы системы:

Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:

Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:

решаем системы линейных алгебраических уравнений (слау)

2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Теорема Крамера.

где Δ – определитель матрицы системы ,

Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.

Когда определитель системы нулевой, значит, система может стать совместной или несовместной.

Описание метода Крамера.

Есть система уравнений:

Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.

Составляем определитель из коэффициентов у неизвестных:

Решаем систему по формулам Крамера :

Примеры решения систем уравнений методом Крамера.

Пример 1 .

Дана система:

Решим ее методом Крамера.

Сначала нужно вычислить определитель матрицы системы:

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера – весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .

А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!

Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т.е. имеет вид

Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,

. (1.6)

Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:

(j = 1, 2, …, n ). (1.7)

Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:

(1. 8)

Пример 1.5. Методом Крамера решить систему уравнений

Вычислим главный определитель системы:

Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):

Таким образом,

Действия над матрицами

1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.

2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть

. (1.9)

Пример 1.6. .

Сложение матриц.

Данная операция вводится только для матриц одного и того же порядка.

Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:

(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.

Пример 1.7. .

Умножение матриц.

Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:

Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:

Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :

Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :

2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .

Обратная матрица. Решение систем линейных уравнений матричным способом

Матрица A – 1 называется обратной к квадратной матрице А , если выполнено равенство:

где через I обозначается единичная матрица того же порядка, что и матрица А :

Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:

, (1.13)

где A ij – алгебраические дополнения к элементам a ij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).

Пример 1.9. Найти обратную матрицу A – 1 к матрице

Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:

Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 – 3 × 3 × 3 – 1 × 5 × 4 – 2 × 2 × 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.

1) Найдем алгебраические дополнения A ij :

Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.

Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:

Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:

где

Умножая обе части равенства (1. 14) слева на A – 1 , мы получим решение системы:

, откуда

Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.

Задача 1.10. Решить систему линейных уравнений

с помощью обратной матрицы.

Решение. Запишем систему в матричном виде: ,

где – основная матрица системы, – столбец неизвестных и – столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :

Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:

Решение системы находим по формуле (1. 15):

Таким образом,

Решение систем линейных уравнений методом обыкновенных жордановых исключений

Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:

(1.16)

Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.

При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.

Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.

Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.

В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.

Пример 1.11.

После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:

Выразим y из второго уравнения и подставим его в первое уравнение:

Запомним второе уравнение, а из первого найдем z :

Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :

Затем подставим и в первое запомненное уравнение , откуда найдем x :

Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:

. (1.17)

Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

Запомним первое уравнение

В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.

Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.

Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.

Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:

. (1.18)

Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:

Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.

В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда

Подставим y и z в первое запомненное равенство и найдем x :

Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :

(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1. 18).

В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.

Пусть дана система линейных форм (уравнений):

, (1.20)
где x j – независимые (искомые) переменные, a ij – постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.

Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.

Мы получим следующую систему:

. (1.21)

Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.

Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:

Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:

(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):

После приведения подобных членов, получим:

(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):

(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».

Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:

Таблица 1.1

	x 1	x 2	…	x j	…	x s	…	x n
y 1 =	a 11	a 12		a 1j		a 1s		a 1n
…………………………………………………………………. .
y i =	a i 1	a i 2		a ij		a is		a in
…………………………………………………………………..
y r =	a r 1	a r 2		a rj		a rs		a rn
………………………………………………………………….
y n =	a m 1	a m 2		a mj		a ms		a mn

Жорданова таблица 1.1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.

Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:

Таблица 1.2

	x 1	x 2	…	x j	…	y r	…	x n
y 1 =	b 11	b 12		b 1 j		b 1 s		b 1 n
…………………………………………………………………..
y i =	b i 1	b i 2		b ij		b is		b in
…………………………………………………………………..
x s =	b r 1	b r 2		b rj		b rs		b rn
………………………………………………………………….
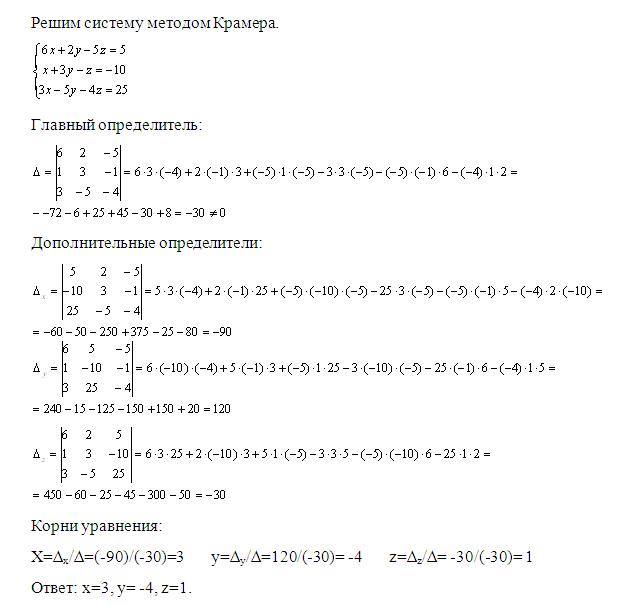y n =	b m 1	b m 2		b mj		b ms		b mn

Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.

Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).

1. Разрешающий элемент заменяется обратным числом:

2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:

3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:

4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:

Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:

-21-26-13-37

Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т. к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.

Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1.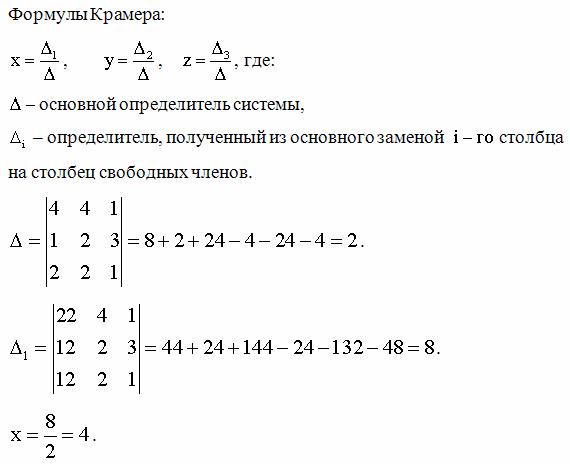 4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: x 1 = – 3 + 2x 5 .

Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:

Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:

x 1 = – 3 + 2t

x 2 = – 1 – 3t

x 3 = – 2 + 4t . (1.27)
x 4 = 4 + 5t

x 5 = t

Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; – 1; – 2; 4; 0).

Решение систем с помощью формул крамера. Метод крамера решения систем линейных уравнений. К началу страницы

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Решение СЛАУ методом Крамера

Согласно методу Крамера, решение находится по формулам:

Теорема Крамера.

где Δ – определитель матрицы системы ,

Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.

Когда определитель системы нулевой, значит, система может стать совместной или несовместной.

Описание метода Крамера.

Есть система уравнений:

Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.

Составляем определитель из коэффициентов у неизвестных:

Решаем систему по формулам Крамера :

Примеры решения систем уравнений методом Крамера.

Пример 1 .

Дана система:

Решим ее методом Крамера.

Сначала нужно вычислить определитель матрицы системы:

Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.

Теорема 1

Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений: $x_i = \frac{D_i}{D}$

В чем заключается метод Крамера

Суть метода Крамера в следующем:

Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ – номер крайнего справа столбца.
После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.

Приёмы для вычисления определителя матрицы

Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:

Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей – со знаком минус.

Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера

С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.

Решение систем уравнений методом Крамера

Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:

$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$

Отобразим её в расширенной форме для удобства:

$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$

Найдём определитель основной матрицы, также называемый главным определителем системы:

$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$

Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:

$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$

$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$

Теперь найдём неизвестные $x_1$ и $x_2$:

$x_1 = \frac {D_1}{D}$

$x_2 = \frac {D_2}{D}$

Пример 1

Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.

Решите систему уравнений:

$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 – x_3 = 10 \\ \end{cases}$

Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:

$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 3 = – 12 – 8 -12 -32 – 6 + 6 = – 64$

А теперь три других детерминанта:

$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 21 = – 84 – 40 – 36 – 160 – 18 + 42 = – 296$

$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = – 27 + 120 + 84 – 72 + 63 – 60 = 108$

$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 – (-2) \cdot 3 \cdot 10 – (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = – 60$

Найдём искомые величины:

$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$

$x_2 = \frac{D_1} {D} = \frac{108} {-64} = – 1 \frac {11} {16}$

$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$

решаем системы линейных алгебраических уравнений (слау)

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Решение СЛАУ методом Крамера

Согласно методу Крамера, решение находится по формулам:

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т. е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Теорема 1

В чем заключается метод Крамера

Суть метода Крамера в следующем:

Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ – номер крайнего справа столбца.
После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.

Приёмы для вычисления определителя матрицы

Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:

Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей – со знаком минус.

Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера

С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.

Решение систем уравнений методом Крамера

Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:

$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$

Отобразим её в расширенной форме для удобства:

$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$

Найдём определитель основной матрицы, также называемый главным определителем системы:

$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$

$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$

$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$

Теперь найдём неизвестные $x_1$ и $x_2$:

$x_1 = \frac {D_1}{D}$

$x_2 = \frac {D_2}{D}$

Пример 1

Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.

Решите систему уравнений:

$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 – x_3 = 10 \\ \end{cases}$

Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:

А теперь три других детерминанта:

Найдём искомые величины:

$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$

$x_2 = \frac{D_1} {D} = \frac{108} {-64} = – 1 \frac {11} {16}$

$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$

Рассмотрим систему 3-х уравнений с тремя неизвестными

(2.4)

если 0. Здесь

Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .

Пример 2.3. Решить систему линейных уравнений при помощи правила Крамера:

Решение . Находим определитель основной матрицы системы

Проверка:

Следовательно, решение найдено правильно. 

(2.5)

Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.

2.4. Определители n-го порядка

Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя

Получаем



(2.6)

т.е. алгебраические дополнения записывают в явном виде через миноры.



2.

5. Основные свойства определителей

Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).

Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.

Например,

Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:

Решите методом Крамера онлайн с подробным решением. Линейные уравнения. Решение систем линейных уравнений. Метод Крамера. Системы линейных алгебраических уравнений

Для освоения этого параграфа необходимо уметь открывать классификаторы «два на два» и «три на три». Если определители плохие, изучите урок Как вычислить определитель?

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? «Ведь простейшую систему можно решить школьным методом, почленным сложением!

Дело в том, что пусть иногда, но есть такая задача – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет вам понять, как использовать правило Крамера для более сложного случая — системы из трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые желательно решать точно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычисляем определитель , он называется главный определитель системы .

Метод Гаусса.

Если , то система имеет единственное решение, и для нахождения корней необходимо вычислить еще два определителя:
и

На практике вышеуказанные определители можно обозначать и латинской буквой.

Корни уравнения находятся по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Видим, что коэффициенты уравнения достаточно большие, в правой части стоят десятичные дроби через запятую. Запятая — довольно редкий гость в практических задачах по математике; Я взял эту систему из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся ужасные навороченные дроби, с которыми крайне неудобно работать, а оформление решения будет выглядеть просто ужасно. Вы можете умножить второе уравнение на 6 и вычесть член за членом, но здесь появятся те же самые дроби.

Что делать? В таких случаях на помощь приходят формулы Крамера.

;

Ответ : ,

Оба корня имеют бесконечные хвосты и находятся приближенно, что вполне приемлемо (и даже обычно) для задач эконометрики.

Комментарии здесь не нужны, так как задача решается по готовым формулам, однако есть один нюанс. При использовании этого метода обязательно Фрагментом задания является следующий фрагмент: “значит система имеет единственное решение” . В противном случае рецензент может наказать вас за неуважение к теореме Крамера.

Не лишней будет проверка, которую удобно проводить на калькуляторе: подставляем приблизительные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, находящиеся в правой части.

Пример 8

Выразите ответ в обыкновенных неправильных дробях. Сделайте чек.

Это пример для самостоятельного решения (пример изящного оформления и ответ в конце урока).

Перейдем к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Найдем главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решения). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.

Если , то система имеет единственное решение, и для нахождения корней надо вычислить еще три определителя:
, ,

И, наконец, ответ вычисляется по формулам:

Как видим, « Случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «гуляет» слева направо по столбцам главного определителя.

Пример 9

Решите систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, поэтому система имеет единственное решение.

Ответ : .

Собственно, тут опять комментировать особо нечего, ввиду того, что решение принимается по готовым формулам. Но есть пара замечаний.

Бывает, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Рекомендую следующий алгоритм “лечения”. Если под рукой нет компьютера, делаем так:

1) Возможна ошибка в расчетах. Как только вы столкнулись с «плохим» кадром, нужно сразу же проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители с помощью разложения в другой строке (столбце).

2) Если в результате проверки ошибок не обнаружено, то, скорее всего, в условии задания допущена опечатка. В этом случае спокойно и ВНИМАТЕЛЬНО решите задачу до конца, а затем обязательно проверить и оформить на чистом экземпляре после принятия решения. Конечно, проверка дробного ответа — занятие неприятное, но это будет обезоруживающим аргументом для преподавателя, который ну очень любит ставить минус за всякую гадость вроде. Как обращаться с дробями, подробно описано в ответе к Примеру 8.

Если у вас есть под рукой компьютер, то используйте для его проверки автоматизированную программу, которую можно скачать бесплатно в самом начале урока. Кстати, пользоваться программой выгоднее всего сразу (еще до запуска решения), вы сразу увидите промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически вычисляет решение системы матричным методом.

Второе замечание. Время от времени встречаются системы, в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении нет переменной, во втором нет переменной. В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать основной определитель:
– вместо пропущенных переменных ставятся нули.
Кстати, определители с нулями рационально открывать в той строке (столбце), в которой стоит ноль, так как вычислений заметно меньше.

Пример 10

Решите систему, используя формулы Крамера.

Это пример для самостоятельного решения (завершающий образец и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Вы можете увидеть живой пример в уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне разрешимы. Хотя задание уже очень напоминает профессорский ботинок на груди счастливчика-студента.

Решение системы с помощью обратной матрицы

Метод обратной матрицы является по существу частным случаем матричного уравнения (см. Пример №3 указанного урока).

Для изучения этого раздела необходимо уметь разлагать определители, находить обратную матрицу и производить умножение матриц. Соответствующие ссылки будут даны по мере продвижения объяснения.

Пример 11

Решить систему матричным методом

Решение : Запишем систему в матричной форме:
, где

Посмотрите пожалуйста на систему уравнений и матрицы. По какому принципу мы записываем элементы в матрицы, думаю всем понятно. Единственное замечание: если бы в уравнениях отсутствовали какие-то переменные, то в матрице на соответствующие места пришлось бы ставить нули.

Находим обратную матрицу по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разберемся с определителем:

Здесь определитель расширяется первой строкой.

Внимание! Если , то обратной матрицы не существует и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (метод Гаусса).

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Ссылка: Полезно знать значение двойных нижних индексов в линейной алгебре. Первая цифра — это номер строки, в которой находится элемент. Вторая цифра – это номер столбца, в котором находится элемент:

То есть двойной нижний индекс указывает на то, что элемент находится в первой строке, третьем столбце, тогда как, например, элемент находится в 3-й строке, 2-м столбце

В ходе решения лучше описать подсчёт несовершеннолетних подробно, хотя при определённом опыте их можно приспособить к счёту с ошибками устно.

В первой части мы рассмотрели теоретический материал, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу, рекомендую прочитать первую часть. Возможно, некоторым посетителям материал покажется слишком простым, но в ходе решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.

А теперь разберем правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными методами.

Рассмотрим систему уравнений

На первом шаге вычисляем определитель , он называется главный определитель системы .

Метод Гаусса.

На практике вышеуказанные определители можно обозначать и латинской буквой.

Корни уравнения находятся по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В таких случаях на помощь приходят формулы Крамера.

;

Ответ : ,

Пример 8

Выразите ответ в обыкновенных неправильных дробях. Сделайте чек.

Это пример для самостоятельного решения (пример изящного оформления и ответ в конце урока).

Перейдем к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Найдем главный определитель системы:

Если , то система имеет единственное решение, и для нахождения корней надо вычислить еще три определителя:
, ,

И, наконец, ответ вычисляется по формулам:

Пример 9

Решите систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, поэтому система имеет единственное решение.

Ответ : .

Пример 10

Решите систему, используя формулы Крамера.

Это пример для самостоятельного решения (завершающий образец и ответ в конце урока).

Решение системы с помощью обратной матрицы

Метод обратной матрицы по существу является частным случаем матричного уравнения (см. Пример №3 указанного занятия).

Пример 11

Решить систему матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разберемся с определителем:

Здесь определитель расширяется первой строкой.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Габриэль Крамер – швейцарский математик, ученик и друг Иоганна Бернулли , один из основоположников линейной алгебры. Крамер рассмотрел систему произвольного числа линейных уравнений с квадратной матрицей. Он представил решение системы в виде столбца дробей с общим знаменателем – определителем матрицы. Метод Крамера основан на использовании определителей при решении систем линейных уравнений, что позволяет значительно ускорить процесс решения. Этот метод можно применять при решении системы линейных уравнений, количество которых равно количеству неизвестных в каждом уравнении. Главное, чтобы определитель системы не был равен “0”, тогда в решении можно использовать метод Крамера, если “0” – этот метод использовать нельзя. Также этот метод можно применять для решения систем линейных уравнений с единственным решением.

Теорема Крамера. Если определитель системы отличен от нуля, то система линейных уравнений имеет единственное решение, а неизвестное равно отношению определителей. В знаменателе стоит определитель системы, а в числителе – определитель, полученный из определителя системы заменой коэффициентов с неизвестными свободными членами. Эта теорема верна для системы линейных уравнений любого порядка.

Допустим, нам дали такую СЛАУ:

\[\left\(\begin(matrix) 3x_1 + 2x_2 =1\\ x_1 + 4x_2 = -3 \end(matrix)\right.\]

По теореме Крамера получаем:

Ответ: \

Где можно решить уравнение по методу Крамера онлайн-решателем?

Решить уравнение можно на нашем сайте https://сайт.Бесплатный онлайн-решатель позволит решить онлайн-уравнение любой сложности за считанные секунды. Все, что вам нужно сделать, это просто ввести свои данные в решатель.Также вы можете посмотреть видеоинструкцию и научиться решать уравнение на нашем сайте.А если у вас есть какие-либо вопросы, вы можете задать их в нашей группе Вконтакте http:/ /vk.com/pocketteacher Вступайте в нашу группу, мы всегда рады вам помочь

Пусть система линейных уравнений содержит столько уравнений, сколько независимых переменных, т.е. имеет вид

Такие системы линейных уравнений называются квадратичными. Определитель, составленный из коэффициентов независимых переменных системы (1. 5), называется главным определителем системы. Обозначим его греческой буквой Д. Таким образом,

. (1.6)

Если в главном определителе произвольный ( j -й) столбец заменить его столбцом свободных членов системы (1.5), то можно получить еще n вспомогательные определители:

( j = 1, 2, …, n ). (1.7)

Правило Крамера решения квадратных систем линейных уравнений выглядит следующим образом. Если главный определитель D системы (1.5) отличен от нуля, то система имеет единственное решение, которое находится по формулам:

(1.8)

Пример 1.5. Решите систему уравнений методом Крамера

Вычислим главный определитель системы:

Поскольку D¹0, система имеет единственное решение, которое можно найти по формулам (1.8):

Таким образом,

Действия с матрицами

1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.

2. Чтобы умножить матрицу на число, нужно умножить все ее элементы на это число. То есть

. (1.9)

Пример 1.6. .

Добавление матрицы.

Эта операция вводится только для матриц одного порядка.

Для сложения двух матриц необходимо сложить соответствующие элементы другой матрицы с элементами одной матрицы:

(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.

Пример 1.7. .

Умножение матриц.

Если количество столбцов матрицы А совпадает с количеством строк матрицы AT , then for such matrices the operation of multiplication is introduced:

Thus, when multiplying the matrix BUT dimensions m ´ n to matrix AT dimensions n ´ k получаем матрицу С размерами m ´ k . В этом случае элементы матрицы С рассчитываются по следующим формулам:

Задача 1. 8. Найдите, если возможно, произведение матриц AB и BA :

Решение. 1) Чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :

2) Произведения BA не существует, так как количество столбцов матрицы B не соответствует количеству строк матрицы A .

Обратная матрица. Решение систем линейных уравнений матричным способом

Матрица А- 1 называется обратной квадратной матрице А , если выполняется равенство:

где через I обозначает единичную матрицу того же порядка, что и матрица А :

Чтобы квадратная матрица имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратная матрица находится по формуле:

, (1.13)

где A ij – алгебраические дополнения к элементам aij матрицы А (обратите внимание, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).

Пример 1.9. Найти обратную матрицу A- 1 к матрице

Находим обратную матрицу по формуле (1.13), которая для случая n = 3 имеет вид:

Найдем det A = | А | = 1 х 3 х 8 + 2 х 5 х 3 + 2 х 4 х 3 – 3 х 3 х 3 – 1 х 5 х 4 – 2 х 2 х 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.

1) Найти алгебраические дополнения A ij :

Для удобства нахождения обратной матрицы мы разместили алгебраические дополнения к строкам исходной матрицы в соответствующих столбцах.

Квадратные системы линейных уравнений с ненулевым главным определителем можно решать с помощью обратной матрицы. Для этого система (1.5) записывается в матричной форме:

где

Умножая обе части равенства (1. 14) слева на А- 1 , получаем решение системы:

, где

Таким образом, для того, чтобы найти решение квадратной системы , нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.

Задача 1.10. Решить систему линейных уравнений

с помощью обратной матрицы.

Решение. Запишем систему в матричной форме: ,

где – основная матрица системы, – столбец неизвестных, – столбец свободных членов. Так как главный определитель системы, то главная матрица системы А имеет обратную матрицу А -1. Чтобы найти обратную матрицу А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :

Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим на определитель D. Таким образом, мы нашли обратную матрицу:

Находим решение системы по формуле (1. 15):

Таким образом,

Решение систем линейных уравнений обыкновенными жордановыми исключениями

Пусть задана произвольная (не обязательно квадратная) система линейных уравнений:

(1.16)

Требуется найти решение системы, т.е. такой набор переменных удовлетворяющее всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесконечное число решений. Она также может вообще не иметь решений.

При решении подобных задач используется известный из школьного курса метод исключения неизвестных, который также называют методом обыкновенных жордановых исключений. Суть этого метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого была выражена переменная, запоминается.

Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. Например, в процессе исключения неизвестных некоторые уравнения могут превратиться в истинные тождества. Такие уравнения исключаются из системы, так как они справедливы при любых значениях переменных и, следовательно, не влияют на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например, ), то делаем вывод, что система не имеет решения.

Если в ходе решения несовместных уравнений не возникло, то одна из оставшихся в ней переменных находится из последнего уравнения. Если в последнем уравнении остается только одна переменная, то она выражается числом. Если в последнем уравнении останутся другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем делается так называемый «обратный ход». Найденная переменная подставляется в последнее запомненное уравнение и находится вторая переменная. Затем две найденные переменные подставляются в предпоследнее запоминаемое уравнение и находится третья переменная, и так до первого запоминаемого уравнения.

В результате получаем решение системы. Это решение будет единственным, если найденные переменные являются числами. Если первая найденная переменная, а затем и все остальные зависят от параметров, то система будет иметь бесконечное число решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от определенного набора параметров, называются общим решением системы.

Пример 1.11.

Запомнив первое уравнение и приведя во втором и третьем уравнениях аналогичные члены, придем к системе:

Выразим из второго уравнения

6 y 9000 первое уравнение:

Вспоминаем второе уравнение, и из первого находим z :

Делая обратный ход, последовательно находим y и з . Для этого сначала подставляем в последнее запомненное уравнение, из которого находим y :

Затем подставляем и в первое запомненное уравнение откуда находим х :

Задача 1.12. Решите систему линейных уравнений, исключив неизвестные:

. (1.17)

Решение. Выразим из первого уравнения переменную х и подставим во второе и третье уравнения:

Запомните первое уравнение

В этой системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получаем, что 14 = 17. Это равенство не выполняется при любых значениях переменных х , y и z . Следовательно, система (1.17) несовместна, т. е. не имеет решения.

Читателям предлагается самостоятельно проверить равенство нулю главного определителя исходной системы (1.17).

Рассмотрим систему, отличающуюся от системы (1.17) только одним свободным членом.

Задача 1. 13. Решите систему линейных уравнений, исключив неизвестные:

. (1.18)

Решение. Как и прежде, выразим из первого уравнения переменную x и подставим во второе и третье уравнения:

Вспомним первое уравнение и представим аналогичные члены во втором и третьем уравнениях. Приходим к системе:

выразив y из первого уравнения и подставив его во второе уравнение, получим тождество 14 = 14, которое не влияет на решение системы, а, следовательно, его можно исключить из системы.

В последнем запомненном равенстве в качестве параметра будет рассматриваться переменная z . Мы верим. Затем

Подставляем y и z в первое запомненное равенство и находим x :

Таким образом, система (1.18) имеет бесконечное множество решений, и любое решение можно найти по формулам (1.19) при выборе произвольного значения параметра t :

(1.19)
Таким образом, решения системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1.18).

В случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обычных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы за один шаг в общем виде и формализовать решение задачи в виде специальных таблиц Жордана.

Пусть задана система линейных форм (уравнений):

, (1.20)
где x j – независимые (искомые) переменные, aij – постоянные коэффициенты
( i = 1,2016 1,2016 …, m ; j = 1, 2,…, n ). Правые части системы y i ( i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решения этой системы путем исключения неизвестных.

Рассмотрим следующую операцию, именуемую в дальнейшем «один шаг обычных жордановых исключений». Из произвольного ( r th) равенства выразим произвольную переменную ( x s ) и подставим во все остальные равенства. Конечно, это возможно только в том случае, если а rs ¹ 0. Коэффициент а rs называется разрешающим (иногда ведущим или основным) элементом.

Получим следующую систему:

. (1.21)

Из s -го равенства системы (1.21) впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S Строка th запоминается и впоследствии исключается из системы. Оставшаяся система будет содержать одно уравнение и на одну независимую переменную меньше, чем исходная система.

Вычислим коэффициенты получившейся системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет иметь вид:

Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:

( 1.23)
Теперь вычислим новые коэффициенты b ij ( i ¹ r ) произвольного уравнения. Для этого подставим переменную, выраженную в (1.22), x s в i -е уравнение системы (1.20):

После приведения подобных членов получаем:

(1.24)
Из равенства (1.24) получаем формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -е уравнение):

(1.25)
Преобразование систем линейных уравнений методом обычных жордановых исключений представлено в виде таблиц (матриц). Эти таблицы называются «таблицами Иордании».

Таким образом, задаче (1.20) соответствует следующая таблица Жордана:

Таблица 1.1

	х 1	х 2	…	х	…	х с	…	х
у 1 =	и 11	и 12		и 1 и		а 1 с		а 1 n
…………………………………………………………………. .
у я =	и 1	и 2		ай		а есть		а в
……………………………………………………………………..
г р =	1	2		рдж		а рс		а р-н
………………………………………………………………….
д н =	а м 1	а м 2		а мдж		мс		утра

Таблица Жордана 1.1 содержит левый головной столбец, в котором записаны правые части системы (1.20), и верхнюю головную строку, в которой записаны независимые переменные.

Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1. 20). Если умножить матрицу А на матрицу, состоящую из элементов верхней заголовочной строки, то получим матрицу, состоящую из элементов левого заголовочного столбца. То есть, по сути, таблица Жордана представляет собой матричную форму записи системы линейных уравнений: . В этом случае системе (1.21) соответствует следующая таблица Жордана:

Таблица 1.2

	х 1	х 2	…	х	…	г р	…	х
у 1 =	б 11	б 12		б 1 к		б 1 с		б 1 н
…………………………………………………………………..
у я =	б и 1	б и 2		б идж		б это		б в
…………………………………………………………………. .
х с =	бр 1	бр 2		б рдж		брс		б р-н
………………………………………………………………….
д н =	б м 1	б м 2		бмж		б мс		бмн

Разрешающий элемент a rs выделим жирным шрифтом. Напомним, что для реализации одного шага жордановых исключений разрешающий элемент должен быть ненулевым. Строка таблицы, содержащая разрешающий элемент, называется разрешающей строкой. Столбец, содержащий элемент включения, называется столбцом включения. При переходе от данной таблицы к следующей таблице одна переменная ( x s ) из верхней строки заголовка таблицы перемещается в левый столбец заголовка и, наоборот, один из свободных членов системы ( г. р. ) перемещается из левого столбца заголовка таблицы в верхнюю строку заголовка.

Опишем алгоритм пересчета коэффициентов при переходе от таблицы Жордана (1.1) к таблице (1.2), который следует из формул (1.23) и (1.25).

1. Разрешающий элемент заменяется обратным номером:

2. Остальные элементы разрешающей строки делятся на разрешающий элемент и меняют знак на противоположный:

3. Остальные элементы разрешающего столбца равны разделен на активирующий элемент:

4. Элементы, не входящие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:

Последнюю формулу легко запомнить, если заметить, что элементы, составляющие дробь, находятся на пересечении i -ой и r -й строк и j й и s -го столбцов (разрешающая строка, разрешающий столбец и строка и столбец, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно пользоваться следующей схемой:

-21 -26 -13 -37

Выполняя первый шаг жордановых исключений, любой элемент таблицы 1. 3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Вы должны не только выбрать разрешающий элемент в последнем столбце, так как нужно найти независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 с переменной х 3 в третьей строке таблицы 1.3 (активирующий элемент выделен жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней строки заголовка заменяется константой 0 из левого столбца заголовка (третья строка). При этом переменная х 3 выражается через остальные переменные.

string x 3 (таблица 1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Таблица 1.4 также исключает третий столбец с нулем в верхней строке заголовка. Дело в том, что вне зависимости от коэффициентов этого столбца b i 3 все соответствующие ему члены каждого уравнения 0 b i 3 системы будут равны нулю. Следовательно, эти коэффициенты не могут быть рассчитаны. Исключив одну переменную х 3 и вспомнив одно из уравнений, мы придем к системе, соответствующей табл. 1.4 (с перечеркнутой линией х 3). Выбрав в таблице 1.4 в качестве разрешающего элемента b 14 = -5, перейти к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем вверху).

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: х 1 = – 3 + 2 х 5 .

Последовательно подставляя уже найденные переменные в запомненные строки, находим оставшиеся переменные:

Таким образом, система имеет бесконечное число решений. переменная x 5 , вы можете присвоить произвольные значения. Эта переменная действует как параметр x 5 = t. Мы доказали совместность системы и нашли ее общее решение:

x 1 = – 3 + 2 t

x 2 = – 1 – 3 t

x 1 = – 9 0 2 (1.27)
х 4 = 4 + 5 t

х 5 = t

Придавая параметру t различные значения, мы получаем исходную систему из бесконечного числа решений. Так, например, решением системы является следующий набор переменных (- 3; – 1; – 2; 4; 0).

Метод Крамера основан на использовании определителей при решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера можно использовать для решения системы линейных уравнений, количество которых равно количеству неизвестных в каждом уравнении. Если определитель системы не равен нулю, то при решении можно использовать метод Крамера; если он равен нулю, то не может. Кроме того, метод Крамера можно использовать для решения систем линейных уравнений, имеющих единственное решение.

Определители

получаются заменой коэффициентов при соответствующих неизвестных свободными членами:

;

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет единственное решение, а неизвестное равно отношению определителей. В знаменателе стоит определитель системы, а в числителе – определитель, полученный из определителя системы заменой коэффициентов с неизвестными свободными членами. Эта теорема верна для системы линейных уравнений любого порядка.

Пример 1 Решить систему линейных уравнений:

Согласно Теореме Крамера имеем:

Итак, решение системы (2), решение Крамера онлайн

1 9 .

Три случая при решении систем линейных уравнений

Как следует из теорем Крамера , при решении системы линейных уравнений могут иметь место три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система непротиворечивая и определенная)

Второй случай: система линейных уравнений имеет бесконечное число решений

(система непротиворечивая и неопределенная)

** ,

т.е. коэффициенты при неизвестных и свободных членах пропорциональны.

Третий случай: система линейных уравнений не имеет решений

(система несовместная)

Итак, система m линейных уравнений с n переменных называется несовместимой , если не имеет решений, и совместной , если имеет хотя бы одно решение. Совместная система уравнений, которая имеет только одно решение, называется определенным , а более одного неопределенным .

Примеры решения систем линейных уравнений методом Крамера

Пусть система

На основе теоремы Крамера

………….
,

где
–

системный идентификатор. Остальные определители получаются заменой в столбце коэффициентов соответствующей переменной (неизвестной) со свободными членами:

Пример 2

Следовательно, система определена. Чтобы найти ее решение, вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) — единственное решение системы.

Для проверки решений систем уравнений 3 X 3 и 4 X 4 можно воспользоваться онлайн-калькулятором, методом решения Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях нет переменных, то в определителе соответствующие им элементы равны нулю! Это следующий пример.

Пример 3 Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система определена. Чтобы найти ее решение, вычисляем определители для неизвестных

По формулам Крамера находим:

Итак, решение системы (2;-1;1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже было сказано, если определитель системы равен нулю, а определители при неизвестных не равны нулю, то система несовместна, то есть не имеет решений. Проиллюстрируем на следующем примере.

Пример 6 Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определена, либо несовместна, то есть не имеет решений. Для уточнения вычислим определители для неизвестных

Определители для неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

В задачах на системы линейных уравнений есть и такие, где кроме букв, обозначающих переменные, есть еще и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное число. На практике такие уравнения и системы уравнений приводят к задачам нахождения общих свойств каких-либо явлений и объектов. То есть вы изобрели какой-то новый материал или устройство, и для описания его свойств, общих вне зависимости от размера или количества экземпляров, вам нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных стоят буквы. За примерами далеко ходить не надо.

Следующий пример для аналогичной задачи, только увеличивается количество уравнений, переменных и букв, обозначающих некоторое действительное число.

Пример 8 Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Нахождение определителей неизвестных

Использование правила Крамера для решения системы трех уравнений с тремя переменными | Колледж Алгебра |

Вычисление определителя матрицы 3 × 3

Найти определитель матрицы 2×2 несложно, но найти определитель матрицы 3×3 сложнее. Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем мы вычисляем сумму произведений записей 91 566 вниз по 91 567 по каждой из трех диагоналей (слева вверху справа внизу) и вычитаем произведения записей 91 566 вверх по 91 567 по каждой из трех диагоналей (слева внизу справа вверху). Это легче понять с визуальным и пример.

Найдите определитель матрицы 3×3.

A=[a1b1c1a2b2c2a3b3c3]A=\left[\begin{array}{ccc}{a}_{1}& {b}_{1}& {c}_{1}\\ {a}_{ 2}& {b}_{2}& {c}_{2}\\ {a}_{3}& {b}_{3}& {c}_{3}\end{массив}\right ]A=⎣

⎡a1a2a3b1b2b3c1c2c3⎦

⎤

Дополните
AAA
первыми двумя столбцами.
det(A)=∣a1b1c1a2b2c2a3b3c3∣a1a2a3b1b2b3∣\mathrm{det}\left(A\right)=|\begin{array}{ccc}{a}_{1}& {b}_{1}& { c}_{1}\\ {a}_{2}& {b}_{2}& {c}_{2}\\ {a}_{3}& {b}_{3}& { c}_{3}\end{массив}|\begin{массив}{c}{a}_{1}\\ {a}_{2}\\ {a}_{3}\end{массив} \begin{массив}{c}{b}_{1}\\ {b}_{2}\\ {b}_{3}\end{массив}|det(A)=∣a1a2a3 b1b2b3c1c2c3∣a1a2a3b1b2b3∣
С левого верхнего угла в правый нижний: умножьте числа по первой диагонали. Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали.
Из нижнего левого угла в верхний правый: вычтите произведение записей вверх по первой диагонали. Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали.

9Рисунок 2 }_{3}+{b}_{1}{c}_{2}{a}_{3}+{c}_{1}{a}_{2}{b}_{3}- {a}_{3}{b}_{2}{c}_{1}-{b}_{3}{c}_{2}{a}_{1}-{c}_{3 }{a}_{2}{b}_{1}∣A∣=a1b2c3+b1c2a3+c1a2b3−a3b2c1−b3c2 a1−c3a2b1

Пример 3. Нахождение определителя матрицы 3 × 3

Найдите определитель матрицы 3 × 3 по данным

A=[0213−11401]A=\left[\begin{array}{ccc}0& 2& 1\\ 3& -1& 1\\ 4& 0& 1\end{array }\right]A=⎣

⎡0342−10111⎦

⎤

Решение

Дополните матрицу первыми двумя столбцами, а затем следуйте формуле. Таким образом,

∣A∣=∣0213−11401∣0342−10∣=0(−1)(1)+2(1)(4)+1(3)(0)−4(−1)(1 )−0(1)(0)−1(3)(2)=0+8+0+4−0−6=6\begin{массив}{l}|A|=|\begin{массив}{ ccc}0& 2& 1\\ 3& -1& 1\\ 4& 0& 1\end{массив}|\begin{массив}{c}0\\ 3\\ 4\end{массив}\begin{массив}{c} 2\\ -1\\ 0\end{массив}|\qquad \\ =0\влево(-1\вправо)\влево(1\вправо)+2\влево(1\вправо)\влево(4\вправо) )+1\влево(3\вправо)\влево(0\вправо)-4\влево(-1\вправо)\влево(1\вправо)-0\влево(1\вправо)\влево(0\вправо) -1\влево(3\вправо)\влево(2\вправо)\qquad \\ =0+8+0+4 – 0-6\qquad \\ =6\qquad \end{массив}∣A∣=∣ 0342−10111∣0342−10∣=0(−1)(1)+2(1)(4)+1(3)(0)−4(−1)(1) −0(1)(0)−1(3)(2)=0+8+0+4−0−6=6

Попробуйте 2

Найдите определитель матрицы 3 × 3.

det(A)=∣1−371111−23∣\mathrm{det}\left(A\right)=|\begin{array}{ccc}1& -3& 7\\ 1& 1& 1\\ 1& -2& 3\end{array}|det(A)=∣111−31−2713∣

Решение

Вопросы и ответы

Можно ли использовать тот же метод для нахождения определителя большей матрицы?

Нет, этот метод работает только для

2 × 22\text{ }\times \text{ }22 × 2

и
3 × 3\text{3}\text{ }\times \text{ }33 × 3
матрицы. Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.

Использование правила Крамера для решения системы трех уравнений с тремя переменными

Теперь, когда мы можем найти определитель матрицы 3 × 3, мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными . Правило Крамера является простым и следует шаблону, согласующемуся с правилом Крамера для матриц 2 × 2. Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.

Когда мы вычисляем, что определитель равен нулю, правило Крамера не указывает, имеет ли система решение или бесконечное число решений. Чтобы выяснить это, мы должны выполнить исключение в системе.

Рассмотрим систему уравнений 3 × 3.

Рисунок 3

x=DxD,y=DyD,z=DzD,D≠0x=\frac{{D}_{x}}{D},y=\frac{{D}_{y }}{D},z=\frac{{D}_{z}}{D},D\ne 0x=DDx,y=DDy,z=DDz,D=0

где

Рисунок 4

Если мы записываем определитель

Dx{D}_{x}Dx

, мы заменяем столбец

xxx

постоянным столбцом. Если мы записываем определитель

Dy{D}_{y}Dy

, мы заменяем столбец

yyy

постоянным столбцом. Если мы записываем определитель

Dz{D}_{z}Dz

, мы заменяем столбец

zzz

постоянным столбцом. Всегда проверяйте ответ.

Пример 4. Решение системы 3 × 3 с использованием правила Крамера

Найдите решение данной системы 3 × 3, используя правило Крамера.

x+y-z=63x-2y+z=-5x+3y-2z=14\begin{array}{c}x+y-z=6\\ 3x – 2y+z=-5\\ x+3y – 2z=14\end{массив}x+y−z=63x−2y+z=−5x+3y−2z=14

Решение

Используйте правило Крамера.

D=∣11−13−2113−2∣,Dx=∣61−1−5−21143−2∣,Dy=∣16−13−51114−2∣,Dz=∣1163−2−51314∣D =|\begin{массив}{ccc}1& 1& -1\\ 3& -2& 1\\ 1& 3& -2\end{массив}|,{D}_{x}=|\begin{массив}{ccc} 6& 1& -1\\ -5& -2& 1\\ 14& 3& -2\end{массив}|,{D}_{y}=|\begin{массив}{ccc}1& 6& -1\\ 3& -5& 1\\ 1& 14& -2\end{массив}|,{D}_{z}=|\begin{массив}{ccc}1& 1& 6\\ 3& -2& -5\\ 1& 3& 14\end{массив }|D=∣1311−23−11−2∣,Dx=∣6−5141−23−11−2∣,Dy=∣1316−514−11− 2∣,Dz=∣1311−236−514∣

Тогда

x=DxD=−3−3=1y=DyD=−9−3=3z=DzD=6−3=−2\begin{array}{l}x=\frac{{D}_{ x}}{D}=\frac{-3}{-3}=1\qquad \\ y=\frac{{D}_{y}}{D}=\frac{-9}{-3} =3\qquad \\ z=\frac{{D}_{z}}{D}=\frac{6}{-3}=-2\qquad \end{array}x=DDx=−3 −3=1y=DDy=−3−9=3z=DDz=−36=−2

Решение:

(1,3,−2)\left(1,3,-2\right)(1,3,−2)

Попробуйте 3

Используйте правило Крамера, чтобы решить матрицу 3 × 3.

x−3y+7z=13x+y+z=1x−2y+3z=4\begin{array}{r}\qquad x – 3y+7z=13\\ \qquad x+y+z=1\ \ \qquad x – 2y+3z=4\end{массив}x−3y+7z=13x+y+z=1x−2y+3z=4

Решение

Пример 5. Использование правила Крамера для решения несогласованной системы

Решить систему уравнений по правилу Крамера.

3x−2y=4 (1)6x−4y=0 (2)\begin{array}{l}3x – 2y=4\text{ }\left(1\right)\\ 6x – 4y=0\ text{ }\left(2\right)\end{array}3x−2y=4 (1)6x−4y=0 (2)

Решение

Начнем с нахождения определителей

D,Dx и DyD,{D}_{x},\text{и {D}_{y}D,Dx, и Dy

D=∣3−26−4∣=3(−4)−6(−2)=0D=|\begin{массив}{cc}3& -2\\ 6& -4\end{массив}|= 3\влево(-4\вправо)-6\влево(-2\вправо)=0D=∣36−2−4∣=3(−4)−6(−2)=0

Мы знаем, что определитель, равный нулю, означает, что либо система не имеет решений, либо имеет бесконечное число решений. Чтобы увидеть, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных.

Умножить уравнение (1) на
−2-2−2
.
Добавьте результат к уравнению
(2)\влево(2\вправо)(2)
.

−6x+4y=−86x−4y=0————–0=8\begin{matrix} \qquad-6x+4y=-8 \\ \qquad6x-4y=0 \\ \qquad\text{ ————–} \\ \qquad 0=8\end{matrix}−6x+4y=−86x−4y=0————–0=8

Получаем уравнение

0=−80=-80=−8

, что неверно. Следовательно, система не имеет решения. График системы показывает две параллельные линии.

Рис. 5

Пример 6. Использование правила Крамера для решения зависимой системы

Решите систему с бесконечным числом решений.

x−2y+3z=0(1)3x+y−2z=0(2)2x−4y+6z=0(3)\begin{массив}{rr}\qquad x – 2y+3z=0& \ qquad \left(1\right)\\ \qquad 3x+y – 2z=0& \qquad \left(2\right)\\ \qquad 2x – 4y+6z=0& \qquad \left(3\right)\end {массив}x−2y+3z=03x+y−2z=02x−4y+6z=0(1)(2)(3)

Решение

Сначала найдем определитель. Настройте матрицу, дополненную первыми двумя столбцами.

∣1−2331−22−46 ∣1−2312−4∣|\begin{array}{rrr}\qquad 1& \qquad -2& \qquad 3\\ \qquad 3& \qquad 1& \qquad -2\\ \qquad 2& \qquad -4& \qquad 6\end{массив}\text{ }|\text{ }\begin{массив}{rr}\qquad 1& \qquad -2\\ \qquad 3& \qquad 1\\ \ qquad 2& \qquad -4\end{массив}|∣132−21−43−26 ∣ 132−21−4∣

Тогда

1(1)(6)+(−2)(−2)(2)+3(3)(−4)−2(1)(3)−(−4)(−2)( 1)−6(3)(−2)=01\влево(1\вправо)\влево(6\вправо)+\влево(-2\вправо)\влево(-2\вправо)\влево(2\вправо) )+3\влево(3\вправо)\влево(-4\вправо)-2\влево(1\вправо)\влево(3\вправо)-\влево(-4\вправо)\влево(-2\вправо) )\влево(1\вправо)-6\влево(3\вправо)\влево(-2\вправо)=01(1)(6)+(-2)(-2)(2)+3(3) (−4)−2(1)(3)−(−4)(−2)(1)−6(3)(−2)=0

Так как определитель равен нулю, то решений либо нет, либо их бесконечное множество. Мы должны выполнить исключение, чтобы узнать.

Умножьте уравнение (1) на
−2-2−2
и добавьте результат к уравнению (3):
−2x+4y−6x=02x−4y+6z=00=0\frac{\begin{ array}{r}\qquad -2x+4y – 6x=0\\ \qquad 2x – 4y+6z=0\end{массив}}{0=0}0=0-2x+4y-6x=02x-4y +6z=0
Получение ответа
0=00=00=0
, утверждение, которое всегда верно, означает, что система имеет бесконечное число решений. Изобразив систему, мы видим, что две плоскости одинаковы и обе пересекают третью плоскость по прямой.

Автор

Предоставлено

Расположен по адресу

Лицензия

CC BY: Attribution

Решающие системы с правилом Крамера · Precalculus

В этом разделе вы:

Оцените 2 × 2 определителей.
Используйте правило Крамера, чтобы решить систему уравнений с двумя переменными.
Вычислите 3 × 3 определителей.
Используйте правило Крамера, чтобы решить систему из трех уравнений с тремя переменными.
Знать свойства определителей.

Мы научились решать системы уравнений с двумя переменными и тремя переменными, а также несколькими методами: подстановкой, сложением, методом исключения Гаусса, использованием обратной матрицы и построением графика. Некоторые из этих методов легче применять, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.

Вычисление определителя матрицы 2×2

Определитель — это действительное число, которое может быть очень полезно в математике, поскольку имеет множество применений, например, для вычисления площади, объема и других величин. Здесь мы будем использовать определители, чтобы определить, является ли матрица обратимой, используя элементы квадратной матрицы 91 832 91 573, чтобы определить, существует ли решение системы уравнений. Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимая матрица и определитель. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.

Найти определитель матрицы 2 × 2

Определитель матрицы a 2 × 2

, заданной

A=[abcd]

определяется как

Обратите внимание на изменение обозначения. Есть несколько способов указать определитель, в том числе det(A)

и заменив скобки в матрице прямыми, \|A\|.

Нахождение определителя матрицы 2 × 2

Нахождение определителя заданной матрицы.

A=[52−63]

det(A)=\|52−63\| =5(3)−(−6)(2) =27

Использование правила Крамера для решения системы двух уравнений с двумя переменными

Теперь мы представим последний метод решения систем уравнений, использующий определители. Известен как Правило Крамера г., эта техника восходит к середине 18 века и названа в честь ее новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил ее в 1750 г. во Введении к анализу линий алгебры. Правило Крамера — жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, как и неизвестных.

Правило Крамера даст нам единственное решение системы уравнений, если она существует. Однако, если система не имеет решения или имеет бесконечное число решений, на это будет указывать нулевой определитель. Чтобы выяснить, является ли система противоречивой или зависимой, придется использовать другой метод, такой как исключение.

Чтобы понять правило Крамера, давайте внимательно посмотрим, как мы решаем системы линейных уравнений, используя основные операции со строками. Рассмотрим систему двух уравнений с двумя переменными.

a1x+b1y=c1 (1)a2x+b2y=c2 (2)

Мы исключаем одну переменную, используя операции со строками, и находим другую. Скажем, что мы хотим найти x.

Если уравнение (2) умножить на коэффициент, обратный y

в уравнении (1), уравнение (1) умножается на коэффициент y

в уравнении (2), и мы добавляем два уравнения, переменная y

будет устранен.

b2a1x+b2b1y=b2c1Умножить R1 на b2−b1a2x−b1b2y=−b1c2Умножить R2 на −b1\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ b2a1x−b1a2x=b2c1−b1c2

Теперь найдите x.

b2a1x−b1a2x=b2c1−b1c2 x(b2a1−b1a2)=b2c1−b1c2 x=b2c1−b1c2b2a1−b1a2=[c1b1c2b2][b21b1a2][a21b1a2]

Аналогично, чтобы решить для y,

мы удалим x.

a2a1x+a2b1y=a2c1Умножить R1 на a2−a1a2x−a1b2y=−a1c2Умножить R2 на −a1\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ a2b1y−a1b2y=a2c1−a1c2

Решение для y

дает

Обратите внимание, что знаменатель для обоих x

и y

— определитель матрицы коэффициентов.

Мы можем использовать эти формулы, чтобы найти x

и у,

, но правило Крамера также вводит новое обозначение:

D:
определитель матрицы коэффициентов
Dx:
определитель числителя в решении
х
х=DxD
Dy:
определитель числителя в решении
у
г=DyD

Ключом к правилу Крамера является замена интересующего столбца переменных столбцом констант и вычисление определителей. Тогда мы можем выразить x

и y

как частное двух определителей.

Правило Крамера для систем 2×2

Правило Крамера — это метод, использующий определители для решения систем уравнений, в которых число уравнений равно количеству переменных.

Рассмотрим систему двух линейных уравнений с двумя переменными.

a1x+b1y=c1a2x+b2y=c2

Решение по правилу Крамера дается как

Если мы вычисляем x,

, столбец x

заменяется столбцом констант. Если мы находим для y,

, столбец y

заменяется столбцом констант.

Использование правила Крамера для решения системы 2 × 2

Решите следующее 2 × 2

с использованием правила Крамера.

12x+3y=15 2x−3y=13

Решите для x.

x=DxD=\|15313−3\|\|1232−3\|=−45−39−36−6=−84−42=2

Решите для y.

y=DyD=\|1215213\|\|1232−3\|=156−30−36−6=−12642=−3

Решение (2,−3).

Используйте правило Крамера, чтобы решить систему уравнений 2 × 2.

x+2y=−11−2x+y=−13

(3,−7)

Вычисление определителя матрицы 3 × 3

Найти определитель матрицы 2×2 несложно, но найти определитель матрицы 3×3 сложнее. Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем вычисляем сумму произведений записей вниз по по каждой из трех диагоналей (слева вверху справа внизу) и вычесть произведения записей вверх по по каждой из трех диагоналей (слева внизу справа вверху). Это легче понять с визуальным и пример.

Найдите определитель матрицы 3×3.

А=[а1b1c1a2b2c2a3b3c3]

Дополнение A
с первыми двумя столбцами.
det(A)=\|a1b1c1a2b2c2a3b3c3 \| a1a2a3 b1b2b3\|
С левого верхнего угла в правый нижний: умножьте числа по первой диагонали. Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали.
Из нижнего левого угла в верхний правый: вычтите произведение записей вверх по первой диагонали. Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали.

Алгебра выглядит следующим образом:

\|A\|=a1b2c3+b1c2a3+c1a2b3−a3b2c1−b3c2a1−c3a2b1

Нахождение определителя матрицы 3 × 3

Найдите определитель матрицы 3 × 3 по данным

A=[0213−11401]

Дополните матрицу первыми двумя столбцами и следуйте формуле. Таким образом,

\|A\|=\|0213−11401 \|03 4 2−10\| =0(−1)(1)+2(1)(4)+1(3)(0)−4(−1)(1)−0(1)(0)−1(3)(2) =0+8+0+4−0−6 =6

Найдите определитель матрицы 3 × 3.

det(A)=\|1−371111−23\|

−10

Можно ли использовать тот же метод, чтобы найти определитель большей матрицы?

*Нет, этот метод работает только для матриц 2 × 2

и 3 × 3

. Для больших матриц лучше всего использовать графическую утилиту или компьютерную программу.*

Использование правила Крамера для решения системы трех уравнений с тремя переменными

Теперь, когда мы можем найти определитель матрицы 3 × 3, мы можем применить Правило Крамера решить систему из трех уравнений с тремя переменными . Правило Крамера является простым и следует шаблону, согласующемуся с правилом Крамера для матриц 2 × 2. Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.

Рассмотрим систему уравнений 3 × 3.

х=DxD,y=DyD,z=DzD,D≠0

где

Если мы пишем определитель Dx,

заменяем x

с постоянным столбцом. Если мы пишем определительDy,

заменяем y

с постоянным столбцом. Если мы записываем определитель Dz,

заменяем z

с постоянным столбцом. Всегда проверяйте ответ.

Решение системы 3 × 3 с помощью правила Крамера

Найдите решение данной системы 3 × 3 с помощью правила Крамера.

x+y-z=63x-2y+z=-5x+3y-2z=14

Используйте правило Крамера.

D=\|1 1−13−2 11 3−2\|,Dx=\|61−1−5−2 114 3−2\|,Dy=\|1 6−13−5 1114−2 \|,Dz=\|1 163−2−51 314\|

Тогда

x=DxD=−3−3=1y=DyD=−9−3=3z=DzD=6−3=−2

Решение (1,3,−2).

Используйте правило Крамера, чтобы решить матрицу 3 × 3.

x−3y+7z=13x+y+z=1 x−2y+3z=4

(−2,35,125)

Использование правила Крамера для решения несовместимой системы

Решите систему уравнений, используя правило Крамера.

3x−2y=4 (1)6x−4y=0 (2)

Начнем с нахождения определителей D,Dx и Dy.

D=\|3−26−4\|=3(−4)−6(−2)=0

Мы знаем, что нулевой определитель означает, что либо система не имеет решений, либо имеет бесконечное число решений. Чтобы увидеть, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных.

Умножить уравнение (1) на −2.
Добавить результат в уравнение (2).

−6x+4y = −8 6x –4y = 0 \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ 0 = −8

Получаем уравнение 0=−8,

, что неверно. Следовательно, система не имеет решения. График системы показывает две параллельные линии. См. [ссылка].

Используйте правило Крамера для решения зависимой системы

Решите систему с бесконечным числом решений.

x−2y+3z=0(1)3x+y−2z=0(2)2x−4y+6z=0(3)

Сначала найдем определитель. Настройте матрицу, дополненную первыми двумя столбцами.

\|1−2331−22−46 \| 1−2312−4\|

Тогда

1(1)(6)+(−2)(−2)(2)+3(3)(−4)−2(1)(3)−(−4)(−2 )(1)−6(3)(−2)=0

Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное число решений. Мы должны выполнить исключение, чтобы узнать.

Умножить уравнение (1) на −2
и добавить результат к уравнению (3):
−2x+4y−6x=02x−4y+6z=0 0=0 9000
Получение ответа 0=0,
утверждение, которое всегда верно, означает, что система имеет бесконечное число решений. Изобразив систему, мы видим, что две плоскости одинаковы и обе пересекают третью плоскость по прямой. См. [ссылка].

Понимание свойств определителей

Есть много свойств определителей . Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.

Свойства определителей

Если матрица имеет верхнетреугольную форму, определитель равен произведению элементов по главной диагонали.
При перестановке двух строк определитель меняет знак.
Если две строки или два столбца совпадают, определитель равен нулю.
Если матрица содержит строку нулей или столбец нулей, определитель равен нулю.
Определитель обратной матрицы A−1
является обратной величиной определителя матрицы
. А.
Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.

Иллюстрация свойств определителей

Проиллюстрируйте каждое из свойств определителей.

Свойство 1 гласит, что если матрица имеет форму верхнего треугольника, определитель равен произведению элементов, расположенных вниз по главной диагонали.

A=[1 230 210 0−1]

Дополните A

первыми двумя столбцами.

А=[12302100−1\| 100 220]

Тогда

det(A)=1(2)(−1)+2(1)(0)+3(0)(0)−0(2)(3)−0(1) (1)+1(0)(2) =−2

Свойство 2 утверждает, что перестановка строк меняет знак. Учитывая

A=[−154−3], det(A)=(−1)(−3)−(4)(5)=3−20=−17B=[4−3−15], det( Б)=(4)(5)−(−1)(−3)=20−3=17

Свойство 3 гласит, что если две строки или два столбца идентичны, определитель равен нулю.

A=[122222−122 \| 12−1 222]det(A)=1(2)(2)+2(2)(−1)+2(2)(2)+1(2)(2)−2(2)(1) −2(2)(2) =4−4+8+4−4−8=0

Свойство 4 утверждает, что если строка или столбец равны нулю, определитель равен нулю. Таким образом,

A=[1200], det(A)=1(0)−2(0)=0

Свойство 5 утверждает, что определитель обратной матрицы A−1

является обратной величиной определителя A .

Таким образом,

A=[1234],det(A)=1(4)−3(2)=−2A−1=[−2132−12],det(A−1)=−2(− 12)−(32)(1)=−12

Свойство 6 гласит, что если любая строка или столбец матрицы умножается на константу, определитель умножается на тот же коэффициент. Таким образом,

A=[1234],det(A)=1(4)−2(3)=−2B=[2(1)2(2)34],det(B)=2(4)− 3(4)=−4

Использование правила Крамера и свойств определителя для решения системы

Найдите решение данной системы 3 × 3.

2x+4y+4z=2(1)3x+7y+7z=−5(2) x+2y+2z=4(3)

Используя Правило Крамера , мы имеем

D=\|244377122\|

Обратите внимание, что второй и третий столбцы идентичны. Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо решений бесконечное множество. Мы должны выполнить исключение, чтобы узнать.

Умножьте уравнение (3) на –2 и добавьте результат к уравнению (1).
−2x – 4y – 4x = −8 2x+4y+4z = 2 0 = −6

Получение утверждения, являющегося противоречием, означает, что система не имеет решения.

Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с правилом Крамера.

Решение системы двух уравнений с помощью правила Крамера
Решение системы трех уравнений с помощью правила Крамера

Ключевые понятия

Раздел Упражнения

Устный

Объясните, почему мы всегда можем вычислить определитель квадратной матрицы.

Определитель — это сумма и произведение элементов матрицы, поэтому вы всегда можете оценить это произведение, даже если оно в конечном итоге равно 0.

Изучая правило Крамера, объясните, почему нет единственного решения системы, когда определитель вашей матрицы равен 0. Для простоты используйте матрицу a 2 × 2

Объясните, что означает в терминах обратной матрицы наличие нулевого определителя.

Обратное не существует.

Определитель 2 × 2

матрица A

равна 3. Если вы поменяете строки и умножите первую строку на 6, а вторую строку на 2, объясните, как найти определитель, и дайте ответ.

Алгебраический

Для следующих упражнений найдите определитель.

\|1234\|

−2

\|−123−4\|

\|2−5−16\|

\|−84−15\|

\|103−4\|

−4

\|10200−10\|

\|100.250.1\|

\|6−384\|

\|−2−33,14 000\|

−7 990,7

\|-1.10.67.2-0,5\|

\|−10001000−3\|

\|−14002300−3\|

\|101010100\|

−1

\|2−313−41−561\|

\|−214−42−82−8−3\|

224

\|6-12-4-3519-1\|

\|51−12313−6−3\|

\|1,12−1−4004,1−0,42,5\|

\|2−1. 63.11.13−8−9.302\|

−17,03

\|−12131415−16170018\|

Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.

2x−3y=−14x+5y=9

(1,1)

5x−4y=2−4x+7y=6

6x−3y=2 −8x+9y=−1

(12,13)

2x+6y=125x−2y=13

4x+3y=23 2x−y=−1

(2,5)

10x−6y=2 −5x+8y=−1

4x−3y=−32x+6y=−4

(−1,−13)

4x−5y=7−3x+9y=0

4x+10y=180 −3x−5y=−105

(15,12)

8x−2y=−3−4x+6y=4

Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.

x+2y−4z=−1 7x+3y+5z=26 −2x−6y+7z=−6

(1,3,2)

−5x+2y−4z=−47 4x−3y−z=−94 3x−3y+2z=94

4x+5y−z=−7−2x−9y+2z=8 5y+7z=21

(−1,0,3)

4x−3y+4z=105x−2z=−23x+2y−5z=−9

4x−2y+3z=6 −6x+y=−22x+7y+8z=24

(12,1,2)

5x+2y−z=1 −7x−8y+3z=1,56x−12y+z=7

13x−17y+16z=73 −11x+15y+17z=61 46x+10y−30z=−18

(2,1,4)

−4x−3y−8z=−7 2x−9y+5z=0,5 5x−6y−5z=−2

4x−6y+8z=10 −2x+3y−4z=−5 x+y+z=1

Бесконечные решения

4x−6y+8z=10 −2x+3y−4z=−5 12x+18y−24z=−30

Технология

В следующих упражнениях используйте функцию определителя в графической утилите.

\|10810300243\|

\|10210--2-1011-2\|

\|1217401210050022,0000002\|

\|1000230045607890\|

Реальные приложения

Для следующих упражнений создайте систему линейных уравнений для описания поведения. Затем вычислить определитель. Будет ли уникальное решение? Если да, то найти единственное решение.

Два числа в сумме дают 56. Одно число на 20 меньше другого.

Да; 18, 38

Два числа в сумме дают 104. Если вы дважды сложите первое число и два раза второе число, получится 208

.
Три числа в сумме дают 106. Первое число на 3 меньше второго числа. Третье число на 4 больше первого числа.
Да; 33, 36, 37
Три числа в сумме дают 216. Сумма первых двух чисел равна 112. Третье число на 8 меньше первых двух вместе взятых.
Для следующих упражнений создайте систему линейных уравнений для описания поведения. Затем решите систему для всех решений, используя правило Крамера.
Вы инвестируете 10 000 долларов на два счета, на которые начисляются 8% и 5% годовых. В конце года на ваших объединенных счетах было 10 710 долларов. Сколько было вложено в каждый счет?
7000 долларов на первый счет, 3000 долларов на второй счет.
Вы инвестируете 80 000 долларов США в два счета, 22 000 долларов США в один счет и 58 000 долларов США в другой счет. В конце года, при условии простых процентов, вы заработали 2470 долларов в виде процентов. Второй счет получает на полпроцента меньше, чем удвоенный процент по первому счету. Каковы процентные ставки для ваших счетов?
Кинотеатру необходимо знать, сколько билетов для взрослых и детей было продано из 1200 билетов. Если детские билеты стоят 5,95 долл. США, билеты для взрослых — 11,15 долл. США, а общая сумма выручки составила 12 756 долл. США, сколько было продано детских билетов и билетов для взрослых?
120 детей, 1080 взрослых
Концертный зал продает одиночные билеты по 40 долларов каждый и билеты для пар по 65 долларов. Если общий доход составил 18 090 долларов США и был продан 321 билет, то сколько было продано одиночных билетов и сколько билетов для пар?
Вы решили покрасить кухню в зеленый цвет. Вы создаете цвет краски, смешивая желтую и синюю краски. Вы не можете вспомнить, сколько галлонов каждого цвета вошло в вашу смесь, но вы знаете, что всего было 10 галлонов. Кроме того, вы сохранили квитанцию и знаете, что общая потраченная сумма составила 29,50 долларов США. Если каждый галлон желтого цвета стоит 2,59 доллара, а каждый галлон синего стоит 3,19 доллара, сколько галлонов каждого цвета входит в вашу зеленую смесь?
4 галлона желтого цвета, 6 галлона синего цвета
Вы продали два вида шарфов на фермерском рынке и хотели бы знать, какой из них более популярен. Всего было продано 56 шарфов, желтый шарф стоил 10 долларов, фиолетовый — 11 долларов. Если ваш общий доход составил 583 доллара, сколько желтых шарфов и сколько фиолетовых шарфов было продано?
В вашем саду выращивают два вида помидоров, зеленый и красный. Красный весит 10 унций, а зеленый весит 4 унции. У вас есть 30 помидоров общим весом 13 фунтов 14 унций. Сколько у вас помидоров каждого вида?
13 зеленых помидоров, 17 красных помидоров
На рынке три самых популярных овоща составляют 53% продаж овощей. Продажи кукурузы на 4% выше, чем у брокколи, продажи которой на 5% выше, чем у лука. Какую долю рынка занимает каждый овощ?
На том же рынке три самых популярных фрукта составляют 37% от общего количества продаваемых фруктов. Клубники продают вдвое больше, чем апельсинов, а киви продают на один процент больше, чем апельсинов. Для каждого фрукта найдите процент от общего количества проданных фруктов.
Клубника 18%, апельсины 9%, киви 10%
Три группы выступили на концертной площадке. Первая группа взимала 15 долларов за билет, вторая группа взимала 45 долларов за билет, а последняя группа взимала 22 доллара за билет. Было продано 510 билетов на общую сумму 12 700 долларов. Если у первой группы было на 40 зрителей больше, чем у второй группы, сколько билетов было продано на каждую группу?
Кинотеатр продал билеты на три фильма. Билеты на первый фильм стоили 5 долларов, билеты на второй фильм — 11 долларов, а на третий фильм — 12 долларов. На первый фильм было продано 100 билетов. Общее количество проданных билетов составило 642, а общий доход составил 6 774 доллара. Сколько билетов на каждый фильм было продано?
100 для фильма 1, 230 для фильма 2, 312 для фильма 3
В прошлом году мужчины в возрасте 20–29, 30–39 и 40–49 лет составляли 78% заключенных в тюрьме. В этом году те же возрастные группы составили 82,08% населения. 20–29возрастная группа увеличилась на 20%, возрастная группа 30–39 лет увеличилась на 2%, а возрастная группа 40–49 лет уменьшилась до 34
их предыдущего населения. Первоначально в возрастной группе 30–39 лет заключенных было на 2% больше, чем в возрастной группе 20–29 лет. Определите процент заключенных для каждой возрастной группы в прошлом году.
В женской тюрьме по дороге общее число заключенных в возрасте от 20 до 49 лет составило 5525 человек. В этом году возрастная группа 20-29 лет увеличилась на 10%, возрастная группа 30-39 лет уменьшилась на 20%, а возрастная группа 40-49 летвозрастная группа удвоилась. Сейчас там 6040 заключенных. Первоначально в возрастной группе 30–39 лет было на 500 человек больше, чем в возрастной группе 20–29 лет. Определите количество заключенных для каждой возрастной группы в прошлом году.
20–29: 2 100, 30–39: 2 600, 40–49: 825
Для следующих упражнений используйте этот сценарий: Компания, заботящаяся о своем здоровье, решает приготовить пищевую смесь из миндаля, сушеной клюквы и орехов кешью в шоколаде. Информация о пищевой ценности этих продуктов приведена в [ссылка].
Жир (г) Белок (г) Углеводы (г)
Миндаль (10) 6 2 3
Клюква (10) 0,02 0 8
Кешью (10) 7 3,5 5,5
Для специальной «низкоуглеводной» трейловой смеси имеется 1000 штук смеси. Общее количество углеводов 425 г, общее количество жиров 570,2 г. Если орехов кешью на 200 штук больше, чем клюквы, сколько штук каждого предмета будет в смеси?
Для смеси «походной» в смеси 1000 штук, содержащих 390,8 г жира, 165 г белка. Если миндаля столько же, сколько орехов кешью, то сколько каждого элемента содержится в смеси?
300 миндаля, 400 клюквы, 300 кешью
Для смеси «Энергия-бустер» в смеси 1000 штук, содержащих 145 г белка и 625 г углеводов. Если количество миндаля и кешью в сумме равно количеству клюквы, сколько каждого элемента содержится в смеси?
Обзор упражнений
Системы линейных уравнений: две переменные
В следующих упражнениях определите, является ли упорядоченная пара решением системы уравнений.
3x−y=4x+4y=−3
и (−1,1)
Нет
6x−2y=24−3x+3y=18
и (9,15)
В следующих упражнениях используйте замену для решения системы уравнений.
10x+5y=−5 3x−2y=−12
(−2,3)
47x+15y=437056x−13y=−23
5x+6y=144x+8y=8
(4,−1)
В следующих упражнениях используйте сложение для решения системы уравнений.
3x+2y=-72x+4y=6
3x+4y=29x+12y=3
Решений не существует.
8x+4y=26x−5y=0,7
Для следующих упражнений напишите систему уравнений для решения каждой задачи. Решите систему уравнений.
Завод имеет себестоимость C(x)=150x+15 000
и функцию дохода R(x)=200x.
Какова точка безубыточности?
(300,60,000)
Исполнитель взимает плату C(x)=50x+10 000,
, где x
— общее количество посетителей шоу. Заведение берет 75 долларов за билет. После того, как много людей купят билеты, место станет безубыточным, и какова общая стоимость билетов, проданных в этот момент?
(400,30,000)
Системы линейных уравнений: три переменные
Для следующих упражнений решите систему из трех уравнений, используя замену или сложение.
     0,5x−0,5y=10 −0,2y+0,2x=4      0,1x+0,1z=2
(10,−10,10)
5x+3y−z=5 3x−2y+4z=134x+3y+5z=22
x+y+z=12x+2y+2z=13x+3y=2
Решений не существует.
    2x−3y+z=−1         x+y+z=−4   4x+2y−3z=33
3x+2y−z=−10 x−y+2z=7−x+3y+z=−2
(-1,-2,3)
3x+4z=-11x-2y=5 4y-z=-10
2x−3y+z=02x+4y−3z=06x−2y−z=0
(x,8×5,14×5)
6x−4y−2z=23x+2y−5z=46y−7z=5
Для следующих упражнений напишите систему уравнений для решения каждой задачи. Решите систему уравнений.
Три нечетных числа в сумме дают 61. Меньшее число на одну треть больше, а среднее число на 16 меньше большего. Какие три числа?
11, 17, 33
Билеты на спектакль в местном театре распроданы. Они продают все 500 билетов на общую сумму 8 070 долларов. Билеты стоили 15 долларов для студентов, 12 долларов для детей и 18 долларов для взрослых. Если группа продала в три раза больше билетов для взрослых, чем билетов для детей, сколько билетов каждого типа было продано?
Системы нелинейных уравнений и неравенств: две переменные
Для следующих упражнений решите систему нелинейных уравнений.
y=x2−7y=5x−13
(2,−3),(3,2)
у=х2-4у=5х+10
x2+y2=16 y=x−8
Нет решения
x2+y2=25 y=x2+5
x2+y2=4y−x2=3
Нет решения
Для следующих упражнений постройте график неравенства.
у>x2−1
14×2+y2<4
![](../resources/CNX_Precalc_Figure_09_08_202.jpg)
Для следующих упражнений постройте график системы неравенств.
x2+y2+2x<3 y>−x2−3
x2-2x+y2-4x <4 y <−x+4
! [] (../ resources/cnx_precalc_figure_09_08_204.jpg)
x2+y2<1 y2
Частичные дроби
Для следующих упражнений разложите на частичные дроби.
−2x+6×2+3x+2
2x+2, −4x+1
10x+24×2+4x+1
7х+20х2+10х+25
7х+5,-15(х+5)2
х-18х2-12х+36
−x2+36x+70×3−125
3x−5,−4x+1×2+5x+25
−5×2+6x−2×3+27
x3-4×2+3x+11(x2-2)2
x-4(x2-2),5x+3(x2-2)2
4×4−2×3+22×2−6x+48x(x2+4)2
Матрицы и операции с матрицами
В следующих упражнениях выполните запрошенные операции над заданными матрицами.
A=[4−213],B=[67−311−24],C=[6711−2140],D=[1−49105−7285],E=[7−1432−13019]
−4A
[−168−4−12]
10D−6E
B+C
не определено; размеры не соответствуют
ВА
не определено; внутренние размеры не соответствуют
СВ
[11328104481−418498−42]
ЭД
[−127−74176−21140287738]
CE
не определено; внутренние размеры не соответствуют
Решающие системы с исключением Гаусса
г.
Для следующих упражнений напишите систему линейных уравнений из расширенной матрицы. Укажите, будет ли единственное решение.
[10−3012000  \| 7−50]
x−3z=7y+2z=−5
с бесконечными решениями
[10501−2000  \| −943]
Для следующих упражнений напишите расширенную матрицу из системы линейных уравнений.
−2x+2y+z=72x−8y+5z=019x−10y+22z=3
[−2212−8519−1022  \| 703]
4x+2y−3z=14−12x+3y+z=100 9х-6у+2г=31
x+3z=12 −x+4y=0 y+2z=−7
[103−140012  \| 120−7]
Для следующих упражнений решите систему линейных уравнений методом исключения Гаусса.
3x−4y=−7−6x+8y=14
3x−4y=1−6x+8y=6
Решений не существует.
−1,1x−2,3y=6,2−5,2x−4,1y=4,3
2x+3y+2z=1 −4x−6y−4z=−210x+15y+10z=0
Решений не существует.
−x+2y−4z=8 3y+8z=−4−7x+y+2z=1
Решающие системы с инверсиями
г.
Для следующих упражнений найдите обратную матрицу.
[−0,21.41,2−0,4]
18[2761]
[12−12−1434]
[129−6−132−4−32]
Обратное не существует.
[213123321]
Для следующих упражнений найдите решения, вычислив обратную матрицу.
0,3x−0,1y=−10−0,1x+0,3y=14
(−20,40)
0,4x−0,2y=−0,6−0,1x+0,05y=0,3
4x+3y-3z=-4,35x-4y-z=-6,1x+z=-0,7
(−1,0,2,0,3)
−2x−3y+2z=3−x+2y+4z=−5−2y+5z=−3
Для следующих упражнений напишите систему уравнений для решения каждой задачи. Решите систему уравнений.
Учеников попросили принести в класс свои любимые фрукты. 90% фруктов состояли из бананов, яблок и апельсинов. Если апельсины были вдвое менее популярны, чем бананы, а яблоки были на 5% популярнее бананов, каков процент каждого фрукта в отдельности?
17% апельсины, 34% бананы, 39% яблок
Женское общество устроило распродажу выпечки, чтобы собрать деньги, и продавало пирожные и печенье с шоколадной крошкой. Они оценили пирожные в 2 доллара, а печенье с шоколадной крошкой — в 1 доллар. Они собрали 250 долларов и продали 175 предметов. Сколько пирожных и сколько печенья было продано?
Решающие системы с правилом Крамера
Для следующих упражнений найдите определитель.
\|100000\|
0
\|0,2−0,60,7−1,1\|
\|−14302300−3\|
6
\|200020002\|
В следующих упражнениях используйте правило Крамера для решения линейных систем уравнений.
4x−2y=23 −5x−10y=−35
(6,12)
0,2x−0,1y=0−0,3x+0,3y=2,5
-0,5x+0,1y=0,3 -0,25x+0,05y=0,15
( x , 5 x + 3)
х+6у+3г=42х+у+2г=33х-2у+г=0
4x−3y+5z=−527x−9y−3z=32 x−5y−5z=52
(0,0,−12)
310x−15y−310z=−150110x−110y−12z=−95025x−12y−35z=−15
Практический тест
Является ли следующая упорядоченная пара решением системы уравнений?
−5x−y=12 x+4y=9
с (−3,3)
Да
Для следующих упражнений решите системы линейных и нелинейных уравнений с помощью замены или исключения. Укажите, если решения не существует.
12x−13y=432x−y=0
−12x−4y=42x+16y=2
Решений не существует.
5x−y=1 −10x+2y=−2
4x−6y−2z=110 x−7y+5z=−143x+6y−9z=65
120(10,5,4)
х+г=20х+у+г=20х+2у+г=10
5x−4y−3z=02x+y+2z=0x−6y−7z=0
(x,16×5−13×5)
у=х2+2х-3у=х-1
y2+x2=25y2−2×2=1
(−22,−17),(−22,17),(22,−17),(22,17)
Для следующих упражнений постройте график следующих неравенств.
y
x2+y2>4y
![](../resources/CNX_Precalc_Figure_09_08_207.jpg)
Для следующих упражнений запишите разложение на неполные дроби.
−8x−30×2+10x+25
13x+2(3x+1)2
53x+1−2x+3(3x+1)2
х4-х3+2х-1х(х2+1)2
Для следующих упражнений выполните заданные матричные операции.
5[49−23]+12[−6124−8]
[1751−811]
[14−7−295120−4]   [3−413510]
[12131415]−1
[12−20−1530]
дед\|004004,000\|
дет\|12−120−120120120\|
−18
Если det(A)=−6,
, какой будет определитель, если поменять местами строки 1 и 3, умножить вторую строку на 12 и взять обратное?
Перепишите систему линейных уравнений в виде расширенной матрицы.
14x−2y+13z=140−2x+3y−6z=−1x−5y+12z=11
[14−213−23−61−512  \| 140−111]
Перепишите расширенную матрицу в виде системы линейных уравнений.
[103−249−612\|12−58]
В следующих упражнениях используйте метод исключения Гаусса для решения систем уравнений.
x−6y=42x−12y=0
Решений не существует.
2x+y+z=−3x−2y+3z=6 x−y−z=6
В следующих упражнениях используйте обратную матрицу для решения системы уравнений.
4x−5y=−50−x+2y=80
(100,90)
1100x−3100y+120z=−4
x−7100y−1100z=13 9100x−9100y−9100z=99
В следующих упражнениях используйте правило Крамера для решения систем уравнений.
200x−300y=2400x+715y=4
(1100,0)
0,1x+0,1y−0,1z=−1,20,1x−0,2y+0,4z=−1,20,5x−0,3y+0,8z=−5,9
Для следующих упражнений решите систему линейных уравнений.
Завод по производству сотовых телефонов имеет следующие функции затрат и доходов: C(x)=x2+75x+2,688
и R(x)=x2+160x.
Какой ассортимент сотовых телефонов они должны производить каждый день, чтобы была прибыль? Округлите до ближайшего числа, приносящего прибыль.
32 и более сотовых телефона в день
Небольшая ярмарка стоит 1,50 доллара для студентов, 1 доллар для детей и 2 доллара для взрослых. За один день пришло в три раза больше детей, чем взрослых. Всего было продано 800 билетов на общую сумму 1050 долларов. Сколько билетов каждого типа было продано?
Глоссарий
Правило Крамера
метод решения систем уравнений, имеющих такое же количество уравнений, что и переменных, с использованием определителей
определитель
число, рассчитанное с использованием элементов квадратной матрицы, определяющее такую информацию, как наличие решения системы уравнений

Эта работа находится под лицензией Creative Commons Attribution 4.0 International License.
Вы также можете бесплатно скачать на http://cnx. org/contents/[email protected]
Атрибуция:
По вопросам, касающимся этой лицензии, обращайтесь по адресу [email protected].
Если вы используете данный учебник в качестве библиографической ссылки, то цитировать его следует следующим образом: Колледж OpenStax, Precalculus. OpenStax CNX. http://cnx.org/contents/[email protected].
Если вы распространяете этот учебник в печатном формате, вы должны указать на каждой физической странице следующее указание авторства: “Скачать бесплатно на http://cnx.org/contents/[email protected].”
Если вы повторно распространяете часть этого учебника, вы должны сохранять при каждом просмотре страницы в цифровом формате (включая, помимо прочего, EPUB, PDF и HTML) и на каждой физической печатной странице следующее указание авторства: «Загрузите бесплатно по адресу http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8. 1».
Введение в линейную алгебру, 5-е издание
Введение в линейную алгебру, 5-е издание
Гилберт Странг   ([email protected])     ISBN : 978-09802327-7-6
Wellesley-Cambridge Press
Заказ книги в Wellesley-Cambridge Press
Заказ книги для членов SIAM
Заказ книги Американского математического общества
Заказ книги в Cambridge University Press (за пределами Северной Америки)
Введение в линейную алгебру, индийское издание , доступен в издательстве Wellesley Publishers
Обзор 5-го издания профессора Фареника для Международного общества линейной алгебры
Обзор книги «Внутри BigData» (2016)
Связанные веб -сайты:
Линейная алгебра для всех (новый учебник, сентябрь 2020 г.) См. Примечание ниже
. Страница
Я надеюсь, что этот сайт станет ценным ресурсом для всех изучение и выполнение линейной алгебры. Вот основные ссылки:
Содержание
Предисловие
Раздел 1.3 книги: Матрицы
Раздел 2.5 книги: Обратные матрицы
Раздел 3.5 книги: Измерения четырех подпространств
Раздел 6.1 книги: Введение в собственные значения
Раздел 7.1 книги: Обработка изображений с помощью линейной алгебры
Раздел 12.1 книги: Среднее значение, дисперсия и вероятность
Матричные факторизации
Индекс
6 великих теорем
Транспонирование производной
Eigshow в MATLAB
18.06 Сайт OpenCourseWare с видеолекциями 18.06 по OCW
Сайт издателя учебника www.wellesleycambridge.com

Руководство по решению для учебника (обновлено в сентябре 2020 г. )
Глава 1
Глава 2
Глава 3
Глава 4
Глава 5
Глава 6
Глава 7
Глава 8
Глава 9
Глава 10
Глава 11
Глава 12

Мир матриц: картина всех матриц, Кендзи Хиранабэ
LU и CR Исключение (появится в разделе «Образование» SIAM Review)
** Каждый раздел в оглавлении содержит ссылки на наборы задач, решения,
** другие веб-сайты и все материалы, относящиеся к теме этого раздела.
** Читателям предлагается предлагать возможные ссылки.
Оглавление для введения в линейную алгебру (5-е издание, 2016 г.
)
1 Введение в векторы
1.1 Векторы и линейные комбинации
1.2 Длины и скалярные произведения
1.3 Матрицы
2 Решение линейных уравнений
2.1 Векторы и линейные уравнения
2.2 Идея ликвидации 91 587
2.3 Исключение с использованием матриц
2.4 Правила матричных операций
2.5 Обратные матрицы
2.6 Исключение = Факторизация: A = ЛЕ
2.7 Транспонирование и перестановки
3 векторных пространства и подпространства
3.1 Пространства векторов
3.2 Нуль-пространство A : Решение Ax = 0 и Rx = 0
3. 3 Полное решение для Ax = b
3.4 Независимость, основа и измерение
3.5 Измерения четырех подпространств
4 Ортогональность
4.1 Ортогональность четырех подпространств
4.2 Проекции
4.3 Метод наименьших квадратов
4.4 Ортонормированные базисы и Грам-Шмидт
5 Детерминанты
5.1 Свойства определителей
5.2 Перестановки и кофакторы
5.3 Правило Крамера, инверсии и объемы
6 Собственные значения и собственные векторы
6.1 Введение в собственные значения
6. 2 Диагонализация матрицы
6.3 Системы дифференциальных уравнений
6.4 Симметричные матрицы
6.5 Положительно определенные матрицы
7 Разложение по сингулярным числам (SVD)
7.1 Обработка изображений с помощью линейной алгебры
7.2 Базы и матрицы в СВД
7.3 Анализ главных компонентов (PCA по SVD)
7.4 Геометрия СВД
8 линейных преобразований
8.1 Идея линейного преобразования
8.2 Матрица линейного преобразования
8.3 Поиск хорошего основания
9 Комплексные векторы и матрицы
9. 1 Комплексные числа
9.2 Эрмитовы и унитарные матрицы
9.3 Быстрое преобразование Фурье
10 приложений
10.1 Графики и сети
10.2 Матрицы в технике
10.3 Марковские матрицы, население и экономика
10.4 Линейное программирование
10.5 Ряды Фурье: линейная алгебра функций
10.6 Компьютерная графика
10.7 Линейная алгебра для криптографии
11 Числовая линейная алгебра
11.1 Метод исключения Гаусса на практике
11.2 Нормы и номера условий
11.3 Итерационные методы и предварительные условия
12 Линейная алгебра в теории вероятностей и статистике
12. 1 Среднее значение, дисперсия и вероятность
12.2 Ковариационные матрицы и совместные вероятности
12.3 Многомерный метод Гаусса и взвешенный метод наименьших квадратов
Матричные факторизации
Индекс
Шесть великих теорем / Линейная алгебра в двух словах
[верх]
В каждом разделе книги есть набор задач.
В следующих видеороликах щелкните значок «Воспроизвести» ►
Во время воспроизведения щелкните слово «YouTube»
, чтобы просмотреть увеличенное видео на отдельной вкладке

Загрузить выбранные решения (небольшие отличия от приведенных выше решений)
Практические экзаменационные вопросы
Экзамен 1 (1997-2009)
Экзамен 1 (2010-2015)
Экзамен 2 (1997-2009)
экзамен 2 (2010-2015)
Экзамен 3 (1997-2009)
Экзамен 3 (2010-2015)
Финал (1998-2009)
Финал (2010-2015)
Задачи по лемме по линейной алгебре
Мой друг Павел Гринфельд из Drexel прислал мне подборку интересных задач — в основном элементарных, но каждая с небольшим поворотом. Они являются частью его более крупного обучающего сайта под названием LEM.MA, и он создал страницу http://lem.ma/LAProb/ специально для этого веб-сайта, связанного с 5-м изданием.
Видеостандарт H.264 (обещано в разделе 7.1 книги)
Этот видеостандарт описывает систему кодирования и декодирования (“Кодек”), которую инженеры определили для таких приложений, как ТВ высокой четкости. Не ожидается, что вы будете знать значение каждого слова — этого не знает и автор вашей книги. Суть в том, чтобы увидеть важный пример «стандарта», созданного отраслью после многих лет разработки, чтобы все компании знали, какой системе кодирования должна соответствовать их продукция.
Слова «компенсация движения» относятся к способу оценки каждого видеоизображения по сравнению с предыдущим. Проще всего было бы предположить, что последовательные видеоизображения одинаковы. Тогда нам понадобятся только изменения между кадрами — надеюсь, небольшие. Но если камера следит за действием, вся сцена немного сдвинется и потребует коррекции. Идея получше — увидеть, в каком направлении движется сцена, и встроить это изменение в следующую сцену. Это КОМПЕНСАЦИЯ ДВИЖЕНИЯ. На самом деле движение может быть разным в разных частях экрана.
Именно такие идеи — о которых легко говорить, но для их совершенствования требуются годы усилий — делают видеотехнологии и другие технологии возможными и успешными. Инженеры делают свою работу. Я надеюсь, что эти ссылки дают представление о необходимых деталях.
http://www.h364info.com/h364.html
http://en.wikipedia.org/wiki/H.264/MPEG-4_AVC
http://www.axis.com/files/whitepaper/wp_h364_31669_en_0803_lo.pdf
г.
Заметки по линейной алгебре
Доказательство теоремы Шура
Разложение действительных матриц по сингулярным числам (проф. Джугал Верма, ИИТ Бомбея, март 2020 г.)
Наш последний учебник «Линейная алгебра для всех» начинается с идеи независимых столбцов
.
    Это приводит к факторизации
A = CR , где C содержит те независимые столбцы из A
    Матрица
R указывает, как объединить эти столбцы из C для производства всех столбцов A
    Затем в Разделе 3.2 объясняется, как решить
Rx = 0 . Это дает нулевое пространство A !!
К этой странице обращались по крайней мере раз с января 2009 г.
Доступность
Правило Крамера требует больших вычислительных ресурсов
ВНИМАНИЕ: Правило Крамера требует больших вычислительных ресурсов.
ВНИМАНИЕ: правило Крамера требует больших вычислительных ресурсов

Специальные примечания для MCS 471
Рекурсивные вычислительные формулы:
Детерминанты: fl _n ^(det) = n*(fl _n-1 ^(det) +2)-1 флопс при вычислении определителей n -го порядка (каждый n-й порядок определитель можно разложить как сумму определителей (n-1)-го порядка, каждый умножается на элементы расширенной строки или столбца.
Правило Крамера: фл _п ^(кр) (n+1)*(fl _n ^(det) +1)-1 флопс для решения n
4-го порядка алгебраических систем уравнений (A*x=b) (есть n компонентов решения и каждый компонент по Крамерову правило представляет собой частное определителя n-го порядка матрицы кофакторов который находится путем замены i-го столбца матрицы коэффициентов на вектор правой стороны b, затем делящий определитель кофактора на определитель А).
Асимптотический анализ:
Основная идея состоит в том, что fl _n ^(det) ~ c _n *n! для некоторого ограниченного фактора c _n с с ₁ := 0 , используя это отношение в детерминантном рекурсивном отношении, решая результирующая рекурсия для c _n и обнаружение того, что это является первым (n-1) членом экспоненциального ряда e ¹ := e с остатком быстро ноль как n —> бесконечность по теореме Тейлора с остатком и экспоненциальное обобщение приближения Стирлинга, данное ниже.
Детерминантная вычислительная работа fl _n ^(det) ~ e*n! флопов as n —> бесконечность при вычислении n -й порядок детерминанты.
Вычисление по правилу Крамера fl _n ^(cr) ~ e*(n+1)! флопов as n —> бесконечность при решении n th алгебраические системы уравнений порядка.
Предположения:
MegaFlop Machine на 1 мкс/флоп или T _n ^(cr) = fl _n ^(cr) *10 ^(-6) .
Точность с отсечением до ближайшего десятичного знака.
Расчетная оценка как функция размера задачи
n :
Проблема
Заказ № fl _n ^(cr)
(flops) T _n ^(cr)
(единицы времени) Комментарии

1 1F 1 мкс F = флопс, микросекунды = мкс = 10 ^(-6) с
2 10F 10µs ”
3 60F 60µs ”
4 300F 300µs ”
5 2KF 2 мс KF = килофлопс = 10 ³ флопс, миллисекунды = мс = 10 ^(-3) с
6 10KF 10 мс ”
7 100KF 100 мс ”
8 1MF 1s MF = MegaFlops = 10 ⁶ flops, seconds = s
9 10MF 10s ”
10 100MF 2min ”
11 1GF 20 минут GF = гигафлопс = 10 ⁹ флопс
12 20GF 5hours ”
13 200GF 3days ”
14 4TF 6weeks TF = TeraFlops = 10 ¹² flops
15 60TF 2years ”
16 1PF 30decades PF = петафлопс = 10 ¹⁵ флопс
17 20PF 6веков ”
18 300PF 10Kyears 1Kyear = 10 ³ лет = 1 тысячелетие EF = ExaFlops = 10 ¹⁸ флопов
20 100EF 4Myears Myears = миллион лет
2
2 flops := Операции с плавающей запятой (т. е. +, -, *, / )
Расчетная оценка как функция производительности машины:
Машина для заказа
Производительность Задача
10×10 Задача
20×20 Комментарии

100 тыс. флопс 20 мин 40 млн лет старый ПК; M = Mega := 10 ⁶ , K = Kilo := 10 ³
Мегафлопс 2 мин 4 млн типичная рабочая станция 908; М = Мега := 10 ⁶
Гигафлопс 0,1 с 4 тысячи лет типичный суперкомпьютер; G = Giga := 10 ⁹
Терафлопс 0,1 мс 4 года ультракомпьютер для ок. 1995 год; Тера := 10 ¹²
Пробег будет варьироваться в зависимости от компьютеров, но даже не думайте о вычислениях с Правило Крамера для n>4 , скажем.
flops := операции с плавающей запятой (т. е. +, -, *, / )
FLOPS := Операций с плавающей запятой в секунду (т.е. +, -, *, / в секунду)
Исключение Гаусса с обратной заменой ~ (2/3)*n ³ FLOPS, n —> бесконечность , поэтому 20×20 можно решить за время ~ 5 мс, на рабочей станции MFLOPS.
100×100 данные случая: Дж. Дж. Донгарра, 9 лет1807 LINPACK Benchmark: Производительность различных компьютеров, использующих программное обеспечение стандартных линейных уравнений , Обзор суперкомпьютеров , том. 5, стр. 54-63, март 1992 г.
Сравните с экспоненциальной формулой Хэнсона-Стирлинга: н! ~ sqrt{2*Pi*n}e ^-n n ⁿ as n —> бесконечность .
FB Hanson
Координатор MCS 471
Веб-источник: http://www.math.
Оставить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Поиск:
Рубрики
2019 © Все права защищены. Карта сайта
Меню
Поиск:

	Жир (г)	Белок (г)	Углеводы (г)
Миндаль (10)	6	2	3
Клюква (10)	0,02	0	8
Кешью (10)	7	3,5	5,5