Динамика (физика) – это… Что такое Динамика (физика)?
У этого термина существуют и другие значения, см. Динамика.Дина́мика (греч. δύναμις — сила) — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия.
Также динамикой нередко называют, применительно к другим областям физики (например, к теории поля), ту часть рассматриваемой теории, которая более или менее прямо аналогична динамике в механике, противопоставляясь обычно кинематике (к кинематике в таких теориях обычно относят, например, соотношения, получающиеся из преобразований величин при смене системы отсчета).
Иногда слово динамика применяется в физике и не в описанном смысле, а в более общелитературном: для обозначения просто процессов, развивающихся во времени, зависимости от времени каких-то величин, не обязательно имея в виду конкретный механизм или причину этой зависимости.
Динамика, базирующаяся на законах Ньютона, называется классической
 Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду.
Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду.Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам.
С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов.
В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п.
Основная задача динамики
Исторически деление на прямую и обратную задачу динамики сложилось следующим образом.
- Прямая задача динамики: по заданному характеру движения определить равнодействующую сил, действующих на тело.
- Обратная задача динамики: по заданным силам определить характер движения тела.

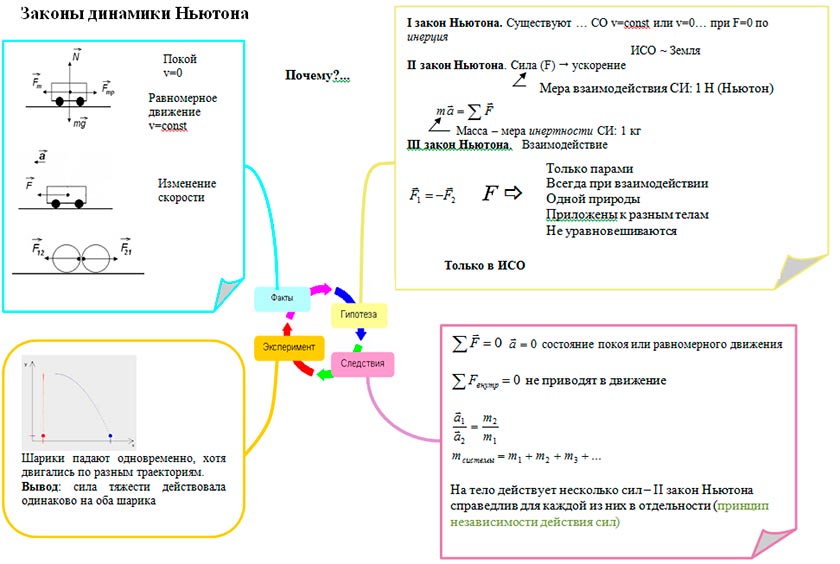
Классическая динамика основана на трёх основных законах Ньютона:
- 1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.
- 2-й: В инерциальной системе отсчета сумма всех сил, действующих на тело, равна произведению массы этого тела на векторное ускорение этого же тела (действие на тело силы, проявляется в сообщении ему ускорения).
В наиболее общем случае, который описывает также движение тела с изменяющейся массой (например, реактивное движение), 2-й закон Ньютона принято записывать следующим образом:
- ,
где — импульс тела. Таким образом, сила характеризует быстроту изменения импульса.
- 3-й: Тела действуют друг на друга силами равными по модулю и противоположными по направлению
Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса
Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса
Законы Ньютона в неинерциальных системах отсчета
Существование инерциальных систем отсчета лишь постулируется первым законом Ньютона. Реальные системы отсчета, связанные, например, с Землей или с Солнцем, не обладают в полной мере свойством инерциальности в силу их кругового движения. Вообще говоря, экспериментально доказать существование ИСО невозможно, поскольку для этого необходимо наличие свободного тела (тела на которое не действуют никакие силы), а то, что тело является свободным, может быть показано лишь в ИСО. Описание же движения в неинерциальных системах отсчета, движущихся с ускорением относительно инерциальных, требует введения т. н. фиктивных сил таких как сила инерции, центробежная сила или сила Кориолиса.
- ,
где — сумма всех фиктивных сил, возникающих в неинерциальной системе отсчета.
Многие законы динамики могут быть описаны исходя не из законов Исаака Ньютона, а из принципа наименьшего действия.
Формулы некоторых сил, действующих на тело
- Сила всемирного тяготения:
или в векторной форме:
вблизи земной поверхности:
- Сила Архимеда:
См. также
Литература
- Алешкевич В. А., Деденко Л. Г., Караваев В. А.
 html?mid=1186208&s=120000000
html?mid=1186208&s=120000000 - Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560с.
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие. М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
Ссылки
Динамика (физика) – это… Что такое Динамика (физика)?
У этого термина существуют и другие значения, см. Динамика.Дина́мика (греч. δύναμις — сила) — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия.
Также динамикой нередко называют, применительно к другим областям физики (например, к теории поля), ту часть рассматриваемой теории, которая более или менее прямо аналогична динамике в механике, противопоставляясь обычно кинематике (к кинематике в таких теориях обычно относят, например, соотношения, получающиеся из преобразований величин при смене системы отсчета).
Иногда слово динамика применяется в физике и не в описанном смысле, а в более общелитературном: для обозначения просто процессов, развивающихся во времени, зависимости от времени каких-то величин, не обязательно имея в виду конкретный механизм или причину этой зависимости.
Динамика, базирующаяся на законах Ньютона, называется классической динамикой. Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду.
Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам.
Такие движения подчиняются другим законам.
С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов.
В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п.
Основная задача динамики
Исторически деление на прямую и обратную задачу динамики сложилось следующим образом.
- Прямая задача динамики: по заданному характеру движения определить равнодействующую сил, действующих на тело.
- Обратная задача динамики: по заданным силам определить характер движения тела.
Классическая динамика основана на трёх основных законах Ньютона:
- 1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.
- 2-й: В инерциальной системе отсчета сумма всех сил, действующих на тело, равна произведению массы этого тела на векторное ускорение этого же тела (действие на тело силы, проявляется в сообщении ему ускорения).

В наиболее общем случае, который описывает также движение тела с изменяющейся массой (например, реактивное движение), 2-й закон Ньютона принято записывать следующим образом:
- ,
где — импульс тела. Таким образом, сила характеризует быстроту изменения импульса.
- 3-й: Тела действуют друг на друга силами равными по модулю и противоположными по направлению
Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса
Законы Ньютона в неинерциальных системах отсчета
Существование инерциальных систем отсчета лишь постулируется первым законом Ньютона. Реальные системы отсчета, связанные, например, с Землей или с Солнцем, не обладают в полной мере свойством инерциальности в силу их кругового движения. Вообще говоря, экспериментально доказать существование ИСО невозможно, поскольку для этого необходимо наличие свободного тела (тела на которое не действуют никакие силы), а то, что тело является свободным, может быть показано лишь в ИСО. Описание же движения в неинерциальных системах отсчета, движущихся с ускорением относительно инерциальных, требует введения т. н. фиктивных сил таких как сила инерции, центробежная сила или сила Кориолиса. Эти «силы» не обусловлены взаимодействием тел, то есть по своей природе не являются силами и вводятся лишь для сохранения формы второго закона Ньютона:
Реальные системы отсчета, связанные, например, с Землей или с Солнцем, не обладают в полной мере свойством инерциальности в силу их кругового движения. Вообще говоря, экспериментально доказать существование ИСО невозможно, поскольку для этого необходимо наличие свободного тела (тела на которое не действуют никакие силы), а то, что тело является свободным, может быть показано лишь в ИСО. Описание же движения в неинерциальных системах отсчета, движущихся с ускорением относительно инерциальных, требует введения т. н. фиктивных сил таких как сила инерции, центробежная сила или сила Кориолиса. Эти «силы» не обусловлены взаимодействием тел, то есть по своей природе не являются силами и вводятся лишь для сохранения формы второго закона Ньютона:
- ,
где — сумма всех фиктивных сил, возникающих в неинерциальной системе отсчета.
Многие законы динамики могут быть описаны исходя не из законов Исаака Ньютона, а из принципа наименьшего действия.
Формулы некоторых сил, действующих на тело
- Сила всемирного тяготения:
или в векторной форме:
вблизи земной поверхности:
- Сила Архимеда:
См.
 также
такжеЛитература
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560с.
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие. М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
Ссылки
Урок 7. законы динамики ньютона – Физика – 10 класс
Законы динамики Ньютона
Необходимо запомнить
ВАЖНО!
Масса – одна из основных характеристик материи. {n}Fi$.
{n}Fi$.
Первый закон Ньютона: если на тело не действуют другие тела, то тело движется прямолинейно и равномерно: $\overrightarrow{F} = 0$.
Важно! Если есть ИСО, то любая другая система, движущаяся относительно неё прямолинейно и равномерно, также является инерциальной.
Второй закон Ньютон: ускорение тела прямо пропорционально силе, действующей на него, и обратно пропорционально его массе: $\overrightarrow{a} = \frac{\overrightarrow{F}}{m}$.
Другая запись формулы второго закона Ньютона (основное уравнение динамики): $\overrightarrow{F} = m \overrightarrow{a}$ .
Третий закон Ньютона: тела действуют друг на друга с силами, равными по модулю и противоположными по направлению: $\overrightarrow{F}_{12} = -\overrightarrow{F}_{21}$.
Второй закон Ньютона для системы тел: приращение импульса $\Delta \overrightarrow{P}$ системы тел равно по величине и по направлению импульсу внешних сил, действующих на тело, за то же время: $\Delta \overrightarrow{p} = \overrightarrow{F} \Delta t$.
Границы применимости: справедливы для материальных точек или поступательно движущихся тел; для скоростей много меньше скорости света в вакууме; выполняются в ИСО.
Решение задачи на применение второго закона Ньютона
Динамика
Основным свойством материи является движение. Именно движение – в широком смысле этого слова – является предметом изучения науки физики.
Классическая механика изучает механическое движение с досветовыми скоростями. При этом составляющие её науки изучают разные аспекты механического движения. Так, кинематика изучает законы движения безотносительно к порождающим это движение причинам. Статика изучает силы, действующие на тело, их взаимодействие, и условия равновесия этих сил, при которых тело не будет двигаться.
Однако центральным разделом механики является динамика, исследующая причины изменений в движении тела. Причинами таких изменений являются силы, действующие на тело.
Сила $( \overrightarrow{F)}$ – векторная физическая величина, являющаяся количественной характеристикой действия одного тела на другое (или частей одного и того же тела).
Движение тел в данной системе отсчета начинаются и прекращаются, они становятся более быстрыми или более медленными, изменяются напрявления движений. Во всех этих случаях мы имеем дело с изменением скорости, то есть появлением ускорения. Понятно, насколько важно знать, при каких условиях возникают ускорения, а при каких условиях тела движутся без ускорений, как определять ускорения (их абсолютные значения и направления). Без этого нельзя решать задачи механики, без этого нельзя управлять движением. На все эти вопросы дает ответ динамика. Поэтому справедливо и такое определение предмета изучения динамики:
Вопрос о причинах механического движения имеет долгую историю. Аристотель в своём трактате, который назывался «Физика», утверждал, что всякому движению есть движущая сила, поэтому все учёные-физики до XVI века искали силу, которая движет. Например, в трактате XIII века причины движения пущенной стрелы со скоростью были описаны следующим образом: сдвинувшись, стрела разрезает воздух, который находится впереди, но за оперением остаётся пустое пространство, в него входит воздух из окружающей среды и подталкивает эту стрелу (Рис. 1). Из этого объяснения выходит, что воздух является движущей силой и в разряжённом воздухе стрела будет лететь меньшее расстояние, что совершенно неверно.
Например, в трактате XIII века причины движения пущенной стрелы со скоростью были описаны следующим образом: сдвинувшись, стрела разрезает воздух, который находится впереди, но за оперением остаётся пустое пространство, в него входит воздух из окружающей среды и подталкивает эту стрелу (Рис. 1). Из этого объяснения выходит, что воздух является движущей силой и в разряжённом воздухе стрела будет лететь меньшее расстояние, что совершенно неверно.
Рис. 1. Движение стрелы
Утверждения Аристотеля считались абсолютной истиной до трудов Галилея. Он сформулировал закон инерции: если на тело не действуют никакие силы или действие этих сил скомпенсировано, тело сохраняет состояние покоя или равномерного прямолинейного движения.
Следующим этапом развития динамики были труды И. Ньютона. Он сформулировал систему законов (3 закона Ньютона), которые являются основными законами классической механики. В механике Ньютона силы могут иметь различную физическую природу: сила трения, сила тяжести, упругая сила и др.
Динамика Галилея – Ньютона называется классической (нерелятивистской) динамикой. В ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света с в вакууме (с = 3$.$108 м/с). Макроскопическими называют тела, состоящие из множества молекул; макроскопические тела не всегда можно принимать за материальные точки.
С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов.
В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п.
Основные понятия классической механики:
Мамсса – скалярная физическая величина, являющаяся количественной мерой инертности тела, а также характеризующая количество вещества в теле;
Симла – векторная физическая величина, являющаяся мерой взаимодействия тел и приводящая к появлению у тела ускорения или к деформации тела. Сила характеризуется величиной, направлением и точкой приложения;
Сила характеризуется величиной, направлением и точкой приложения;
Линия действия силы – это линия, вдоль которой действует сила. Если тело является абсолютно твердым, то точку приложения силы можно перемещать вдоль линии действия силы в пределах тела;
Импульс – векторная физическая величина, равная произведению массы тела на его скорость: $\overrightarrow{р}=m\overrightarrow{v}$;
Энергия – количественная характеристика движения и взаимодействия тел, их способности совершать изменения во внешнем мире.
Кинематика, динамика и статика в физике. Что это такое?
Одним из основополагающих разделов физики является механика – дисциплина, изучающая законы, согласно которым происходит движение тел, а также изменение параметров движения в результате влияния тел друг на друга.
Основными направлениями механики является изучение динамики, кинематики и статики. Подробному изучению этих наук специалисты посвящают всю жизнь, так как их положения лежат в основе наиболее важных общеинженерных дисциплин – теории механизмов, сопромата, деталей машин и др.
Что изучает теоретическая механика?
Движение и взаимодействие физических тел подчиняются строгим законам, по которым существует наша Вселенная. Описанию и обоснованию этих законов посвящена механика – раздел физики, позволяющий рассчитывать и предсказывать движение физических тел, исходя из их основных параметров и действующих на эти тела сил. В механике рассматриваются идеальные объекты:
- материальная точка – объект, основной характеристикой которого является масса, но размеры не учитываются;
- абсолютно твёрдое тело – заполненный веществом определённый объём, форма которого не изменяется ни при каких воздействиях, а между любыми двумя точками внутри этого объёма всегда сохраняется одно и то же расстояние;
- сплошная деформируемая среда – состояние вещества в конечном объёме либо в неограниченном пространстве, в котором расстояния между произвольно взятыми точками могут изменяться в результате внешних воздействий.
Механика рассматривает законы движения, когда с течением времени изменяется либо положение одного тела относительно другого, либо взаимное расположение частей одного тела. Время, масса и расстояние для механики являются базовыми величинами.
Время, масса и расстояние для механики являются базовыми величинами.
Кинематика
Раздел механики, изучающий законы движения, его геометрические свойства, законы скоростей и ускорений, называется кинематикой. Название дисциплины образовано от греческого слова «κινειν», означающего движение. Кинематика изучает чистое движение с точки зрения пространства и времени, не учитывая массы физических тел и действующие на них силы.
Движение в кинематике описывается исключительно математическими средствами, для чего используются алгебраические и геометрические методы, матанализ и т.д. При этом в классической кинематике не рассматриваются причины, по которым происходит механическое движение тел, а характеристики, присущие движению, считаются абсолютными, т.е. на них не влияет выбор системы отсчёта. Помимо классической, существует релятивистская механика, которая рассматривает общее понятие пространства-времени с инвариантными интервалами.
Динамика
Ещё один раздел механики, который рассматривает причины, порождающие механическое движение тел, называется динамикой. Это наименование образовано от греческого слова «δύναμις», означающего силу. Основными понятиями динамики являются масса тела, сила, которая на него воздействует, энергия, импульс и момент импульса. Основными задачами – определение силы, действующей на физическое тело, по характеру его движения, и определение характера движения, исходя из заданных сил воздействия.
Это наименование образовано от греческого слова «δύναμις», означающего силу. Основными понятиями динамики являются масса тела, сила, которая на него воздействует, энергия, импульс и момент импульса. Основными задачами – определение силы, действующей на физическое тело, по характеру его движения, и определение характера движения, исходя из заданных сил воздействия.
Значительный вклад в развитие динамики внёс британский учёный Исаак Ньютон, сформулировавший три своих знаменитых закона, которые описывают взаимодействия сил, и фактически ставший родоначальником классической динамики. Эта дисциплина изучает закономерности движения при скоростях, ограниченных интервалом от долей одного миллиметра в секунду до десятков километров в секунду. Однако при рассмотрении движения сверхмалых объектов (элементарных частиц) и сверхвысоких скоростей, приближающихся к скорости света, законы классической динамики перестают действовать.
Статика
Законы пребывания тел и систем в равновесии при приложении к ним различных сил и моментов, изучает статика – ещё одно направление механики. Название дисциплины происходит от греческого слова «στατός», означающего неподвижность. Для статики сформулированы шесть аксиом, описывающих условия нахождения тела или системы физических тел в состоянии равновесия, а также два следствия из этих аксиом.
Основным объектом в статике является тело или материальная точка, находящаяся в состоянии равновесия, т.е. неподвижно либо движется в рассматриваемой инерциальной системе координат равномерно и по прямой линии. Ограничивающими факторами для тела, находящегося в равновесии, служат внешние силы, которые на него воздействуют, а также другие тела, называемые связями.
кому сегодня не прожить без физики и как ее изучают в ЛЭТИ
На вопросы о том, где сегодня востребованы знания по физике, как изучают физику в ЛЭТИ и где можно погрузиться в физику с головой, отвечает заведующий кафедрой физики СПбГЭТУ «ЛЭТИ», доктор технических наук, профессор Александр Сергеевич Чирцов.
12.05.2020 3008
Физику в ЛЭТИ преподают и изучают с первого дня существования Первого электротехнического: учебный план Технического училища почтово-телеграфного ведомства с момента его открытия в 1886 года уже включал предмет «физика». Кафедра физики является старейшей кафедрой университета. В 1901 году на должность ординарного профессора физики в ЭТИ был приглашен А.С. Попов – он преподавал в 1901-1906 годах и вел интенсивную научную деятельность. Сегодня физику изучают на всех факультетах университета, за исключением гуманитарного. Физика входит в число вступительных испытаний на 11 из 23 направлений подготовки бакалавриата и специальностей. На наши вопросы ответил заведующий кафедрой физики, доктор технических наук, профессор Александр Сергеевич Чирцов.
– Уважаемый Александр Сергеевич, разговор о физике мы начнем с… математики. «Математику уже затем учить надо, что она ум в порядок приводит», – утверждал в свое время Ломоносов. А зачем, по-Вашему, нужно учить физику? Насколько знание физики востребовано в наше время и кому без нее точно не прожить – сегодня и в будущем?
– Первое, что приходит голову в качестве ответа на этот вопрос, это утверждение о том, что физика является главной областью приложения математики, которую, как убедил всех Михаил Васильевич (Ломоносов), учить надо. Кроме физики, настоящая математика по-настоящему нужна еще самой математике (которая сама по себе прекрасна и самодостаточна), но на этом, пожалуй, область ее востребованности в полной мере и заканчивается. Остальные применения ближе к арифметике, чем к математике. Математика и физика очень близки и сильно переплетены друг с другом. Но между ними есть и принципиальное различие. Математика подобна игре: «Прими утверждения, которые я придумал, а я строго выведу из них такое, о чем ты даже не подозревал». Таким образом, математика опирается на выдумки человека, нередко весьма изощренные выдумки, но… всего лишь на выдумки всего лишь человека или человечества – не важно.
Физика занимается другой задачей – попытаться понять, а если не получается или не получится – хотя бы смоделировать наш окружающий мир, который настолько изощрен и нетривиален, что до сих пор человечеству удалось разобраться (и то далеко не до конца) в его лишь самых простых проявлениях.
Зачем нужны попытки разобраться в окружающем мире? Ну, первое (для меня это, пожалуй, самое главное) – это фантастически ИНТЕРЕСНО и ЭЛЕГАНТНО. Мне очень нравится это второе слово в качестве характеристики современной картины мира. Второе – это ПОЛЕЗНО, ибо физика и построенные на ее фундаменте другие естественные науки позволяют с хорошей достоверностью предсказывать будущее (правда, пока только для достаточно простых систем нашего мира, но прогресс науки уверенно движется в сторону усложнения поддающихся анализу систем и объектов). Сегодня в предсказаниях будущего точные науки вне конкуренции: попробуйте спросить у самой преуспевающей гадалки, на каком расстоянии от вас упадет камень, брошенный под заданным углом к горизонту со склона горы с заданным наклоном с учетом эффектов трения о воздух и вращения Земли. Боюсь, что ее прогноз не окажется конкурентоспособным по сравнению с физическим. Ну и, наконец, существование физики УДОБНО. Удобно, ибо она подарила человечеству (помимо атомной и водородной бомб) множество весьма полезных «мелочей», без которых выжить, конечно, можно, но на такое выживание согласится далеко не каждый…
Вы спрашиваете, кто точно не смог бы прожить без физики? Прежде всего, НЕФИЗИКИ. Физики – они живучи, изобретательны и имеют представление о том, как устроены «приятные мелочи», созданные на базе физики. И в случае чего, самые необходимые из этих «мелочей» физик-то сможет воспроизвести или хотя бы попытаться. А вот что будет в подобной ситуации с НЕФИЗИКАМИ? – Да пофантазируйте сами после того, как я кратко перечислю эти «мелочи»: электричество, транспорт (особенно воздушный и скоростной наземный), связь, энергетика, обогревание/охлаждение, электроника (особенно микроэлектроника), телекоммуникации, IT-технологии… Достаточно? Если бы те наши современники, кто пытается громко заявлять о том, что лично им физика абсолютно не нужна, были людьми честными и приличными, они бы отказались от использования всего того, что создано на базе физических знаний. Результат бы не заставил себя долго ждать – через 2-3 месяца подобные заявления полностью бы исчезли по причине исчезновения заявителей…
– На каких факультетах и каких направлениях подготовки в ЛЭТИ изучают физику? Как строится вузовский курс? Отличается ли он от того, что изучали в ЛЭТИ будущие инженеры в прошлом веке?
– Сегодня в ЛЭТИ физика изучается студентами факультетов ФРТ, ФЭЛ, ФЭА, ФКТИ, ФИБС, на ФЭМ физика читается в рамках курса «Концепции современного естествознания». Безусловным лидером по востребованности физики в ЛЭТИ является факультет электроники. Это является следствием и его специализации, и менталитета научно-педагогического коллектива факультета. Именно на его базе кафедра физики успешно осуществляет проект по предоставлению наиболее подготовленным и мотивированным студентам возможности изучения курса физико-математических дисциплин в объеме, приближенном к программам физико-математических факультетов ведущих классических университетов России.
К сожалению, число часов, отводимых на изучение физики и других дисциплин, соответствующих точным наукам, в последние годы сокращается в рамках общей образовательной политики постперестроечного периода. Частично это происходит за счет выделения большего количества часов на самостоятельные занятия обучаемых. Именно эти часы мы и предлагаем наиболее мотивированным и подготовленным студентам провести не в одиночку, а вместе с наиболее квалифицированными и успешными в науке преподавателями. КПД от такой «самоподготовки» оказывается весьма высоким. Право выбора формы «самостоятельных занятий», естественно остается за студентом: он может потратить освобожденное для него время на интенсивное изучение физики, может самостоятельно заняться собственным проектом создания очередного вечного двигателя, а может – просто хорошо провести время на футбольном поле или на волейбольной площадке. Слава Богу, теперь конкурентоспособность каждого выпускника на трудовом рынке – это прежде всего его личная проблема. Хотя нам, и преподавателям, и руководству университета, конечно же, далеко не безразлична дальнейшая судьба выпускников. Но для самих учащихся эта проблема, я уверен, должна быть определяюще-значимой в первую очередь.
Вы спрашиваете, отличается ли обучение в ЛЭТИ будущих инженеров сегодня от обучения в прошлом веке. За последние тридцать лет отличия безусловно возникли и связаны с серьезной компьютеризацией практически всех сторон нашей жизни, включая и естественнонаучное образование. Только, на мой взгляд, компьютеризация в обучении точным наукам пока идет не совсем в правильном направлении: все увлекаются созданием электронных журналов, ведомостей для оценок, виртуальными зачетными книжками. Это все, конечно, достаточно позитивно, но лишь в том случае, когда экономит время, а не отнимает его от основного дела – обучения. Меня вот что теперь настораживает: сегодняшние студенты почему-то по-прежнему при изучении физики испытывают заметные трудности в использовании математики – например, при вычислении интегралов. Несмотря на то, что теперь практически любой интеграл (даже принципиально «не берущийся») легко берется простым нажатием нескольких кнопок на персональном компьютере…
Что касается сопоставления современного обучения точным наукам с «прошлым в квадрате» XIX веком, то мне хочется упомянуть один документ того времени, принятый нашим вузом в те далекие времена. Речь идет о требованиях к выставлению оценки «отлично». Студент мог получить такую оценку лишь в случае представления им результатов самостоятельного оригинального исследования по теме соответствующего курса при дополнительном условии его полных и исчерпывающих ответов на все задаваемые ему вопросы, включая КАВЕРЗНЫЕ. Если такой документ когда-то реально существовал и, главное, исполнялся на практике, сегодняшнее возобновление его действия было бы весьма полезно – как минимум, для студентов, выбравших для своего обучения усиленный поток.
– В «гранит» вузовской физики «вгрызаются» первокурсники. Легко ли вчерашние школьники справляются с вузовской программой? Как Вы оцениваете уровень подготовки по физике в современной школе?
– Этот вопрос не имеет однозначного ответа. Все зависит от того, какие имеются в виду школьники и из каких они пришли школ. Выпускники ряда школ (прежде всего, физико-математических, но нередко и «обычных», если они попали в руки учителей, которые «чего-то хотят», и при этом не сильно сопротивлялись «хотениям» последних), приходят на первый курс с навыками вычисления интегралов, решения простых дифференциальных уравнений, начальными представлениями о теории относительности и квантовой механики. А среди их новых товарищей и коллег на первом курсе оказываются и те, кто испытывает трудности с решением квадратных уравнений и формулировками понятий классической механики Ньютона. Понятно, что перед этими группами студентов и их преподавателями стоят совершенно разные задачи. Кому-то (догадайтесь, кому) необходимо начать с восполнения пробелов образования на предшествующем уровне, догнать лидеров и стать к моменту завершения обучения полноправными обладателями дипломов, свидетельствующих об их высокой профессиональной квалификации. А другим надо… остаться недосягаемыми для их товарищей-конкурентов (рынок, господа, рынок!) и оказаться после окончания лидерами на российском, а еще лучше – международном уровне. Каждый должен иметь возможность получить от обучения столько, сколько он пожелает и сможет взять, но, разумеется, не ниже уровня, устанавливаемого государственным стандартом.
Именно по этой причине я ставлю сегодня перед кафедрой физики задачу реализации МАССОВОГО ИНДИВИДУАЛИЗИРОВАННОГО ОБРАЗОВАНИЯ, обеспечивающего каждому обучаемому возможность приобретения знаний и компетенций в том объеме, который он может и хочет получить. Отсюда вытекает необходимость создания учебных потоков с различной интенсивностью и глубиной обучения и использования дополнительных гибких электронных образовательных ресурсов, допускающих их самоадаптацию под запросы потенциальных потребителей таких ресурсов. Уверен, что такой подход открывает широкие возможности преподавателям для научно-педагогического творчества, а модным сегодня технологиям машинного самообучения и искусственного интеллекта – достойное поле для их приложений и развития.
Задан вопрос об оценке уровня подготовки по физике в современной школе. Тут я не решусь давать категорических ответов. В разных школах он разный, более того, среди выпускников одного учебного заведения этот уровень может различаться в разы (при его представлении в логарифмическом масштабе). Меня настораживает только одно. Несколько лет назад я записал триаду («Кинематика», «Классическая динамика материальной точки», «Основы небесной механики») удаленных курсов для школьников, желающих закрепить свои знания в изучаемой ими ньютоновской механике. В этих курсах я практически ничего от себя не выдумывал, а лишь повторил то, что знал вместе со своими одноклассниками к моменту окончания питерской физ-мат школы №38. Меня поразила оценка этого курса, данная ректором одного из далеко не последних наших университетов (по понятным причинам не буду уточнять какого): «Такой курс сможет освоить далеко не каждый наш профессор или доктор наук»). Не хочу ничего комментировать. Кому интересно – зайдите на образовательную видеотеку «Лекториум», посмотрите курсы и самостоятельно делайте свои выводы.
– Какие возможности предоставляет вуз для студентов «обычных» и одаренных? «Гибкая образовательная траектория» – это уже реальность или только перспектива? Какие инструменты и педагогические технологии используются?
– Я не верю ни в «гениев», ни в «посредственностей». Не бывает людей ни «обычных», ни «одаренных». Есть люди трудолюбивые и не очень. Есть студенты, мотивированные на получение качественного образования, а есть – с очень широким кругом мотиваций, таким широким, что на каждый сегмент мотивационного круга физически не хватает входящих в сутки 24 часов. Последних можно пытаться привести к сужению круга потребляющих время интересов, заинтересовав их физикой и/или математикой. НО не более того – человек должен сам выбирать, во что ему следует погружаться с головой или вообще никуда не погружаться, а продолжать барахтаться на поверхности.
Для не заинтересовавшихся любителей плавать на поверхности должно быть одно требование к глубине погружения – государственный стандарт. Он должен быть выполнен любым выпускником, получающим диплом. Для тех, у кого с этим возникают реальные проблемы, должен существовать «базовый поток», на котором ставится задача-минимум – обязательное достижение уровня государственного стандарта или… отчисление. А как иначе? Если кто-то оказался на базовом потоке вопреки наличию у него мотивации к серьезной учебе из-за пробелов на уровне довузовской подготовки – у него есть шанс, не подвергаясь «репрессиям», догнать слушателей традиционного потока и подняться на ступень выше.
Традиционный поток (наиболее многочисленный, в который студенты попадают «по умолчанию») соответствует сложившимся традициям университета, среднему уровню начальной подготовки, потребностям работодателей.
Двумя образовательными потоками можно было бы ограничиться, но… Но в каждом уважающем себя университете или просто вузе всегда имеются две не слишком многочисленные группы (студентов и преподавателей), которые все время хотят чего-то большего. Не ради красного диплома, не ради прибавки к зарплате. Просто ради интереса к жизни и, может быть, ради позиционирования себя в своих же глазах и по своим критериям. Таких не очень много с обеих сторон (и обучаемых, и обучающих). Такие бывают не совсем удобны для их «однокашников» и коллег по работе. Но иногда (совершенно неожиданно и не гарантированно) случается так, что кто-то из этих двух групп становится ЛИЦОМ университета на долгие годы. Именно по такому пути развивалась и развивается наука и наукоемкие технологии. Так вот третий (усиленный, углубленный – не важно, как его называть) поток, пока существующий не совсем официально на базе ФЭЛ, но уже сейчас посещаемый студентами и с других факультетов, обеспечивает возможность совместной учебной работы студентов и преподавателей, которые хотят и могут большего. Пусть они встретят друг друга и будут по возможности счастливы.
– Сегодня все обучающиеся и преподаватели оказались в непростой ситуации исключительно дистанционного обучения. Физика онлайн – это возможно? Каковы, на Ваш взгляд, преимущества и недостатки преподавания и изучения физики «по удаленке»?
– Я, как физик, не вижу больших различий между очной и on-line формами обучения. Ибо любая очная форма по сути – это on-line. Посудите сами: когда читается «ОЧНАЯ» лекция, что видят студенты? Лектора? – Не совсем! Они видят вторичные электромагнитные поля (или фотоны – не важно, как это называть), рассеянные его телом и одеждой. Что они слышат – акустические волны, генерируемые в атмосфере голосовой системой. И все! Вкусовые, обонятельные и осязательные канали передачи информации в обучении, слава Богу, широко не используются. Что изменится, если в качестве источника световых и акустических полей использовать не лектора, а какие-либо технические устройства? Н И Ч Е Г О. Ничего, но лишь при условии качественной работы устройств, генерирующих эти поля и при наличии устойчивого, легко доступного, достаточно широкого и высокоскоростного двустороннего канала обмена информацией между обучаемым и обучающим. Пока эти телекоммуникационные каналы сильно уступают тем, что бесплатно предоставляет нам Природа в случае «очного» обучения. Но я почти уверен: этот проигрыш используемых в «удаленке» каналов Природе носит чисто количественный, а не принципиальный характер и требует решения не безумно большого числа технических и финансовых проблем.
С другой стороны, правильно организованная «удаленка» может оказаться очень удобной «штукой». Когда-то давно студенты меня спрашивали о возможности прокладки волоконной линии связи в общежития, чтобы слушать лекции, не вставая с кровати. Моя мечта более амбициозна. В Альпах все лица после 75 лет (независимо от гражданства) могут неограниченно и бесплатно использовать все горнолыжные подъемники. Я почти уверен, что к тому времени, когда я получу это право, технологии генерации изображения и звука вместе с доступными для удаленного обучения каналами разовьются до такого уровня, что…
– Последний вопрос – конечно, про любовь. Почему студенты ЛЭТИ любят (или не любят) физику? И что в преподавательской деятельности больше всего любите Вы?
– Любовь – это дело очень субъективное, почти интимное. Легче говорить про себя: я люблю учить тех, кто хочет и может учиться.
Говорить же за других – дело абсолютно неблагодарное. Я лучше процитирую мнение одной из моих весьма успешных учеников – Марии Чернышевой, ставшей лауреатом конкурса на самую успешную в науке «мадемуазель Франции». На мой вопрос, почему она выбрала физику, несмотря на то, что ее родители были математиками и готовили ей карьеру в гуманитарной области, Мария, со свойственной ей скромностью, ответила примерно так: «Я не скажу, что физика – это то, что мне очень нравится, но я почти уверена, что это единственное занятие, которое меня достойно».
– «Что-то физики в почете. Что-то лирики в загоне. Дело не в сухом расчете, дело в мировом законе…», – писал поэт. Физика в ЛЭТИ отмечена особым «знаком качества» – Нобелевской премией в области физики выпускника ЛЭТИ 1952 года Жореса Ивановича Алферова. Желаем, чтобы кто-нибудь из сегодняшних и будущих лэтишников обязательно одержал победы, достойные этой. Благодарим Вас за интересную беседу.
Задачи ⚠️ по динамике с решениями: основы, как научиться, методы
Физика — серьезная наука, которая состоит из нескольких крупных разделов и множества менее объемных подразделов. Проще всего с каждым из них знакомиться отдельно, чтобы избежать путаницы в голове. В этой статье подробно поговорим о динамике.
Что такое динамика в физике
Динамика в физике — это раздел механики, который изучает взаимодействие тел и причины возникновения/изменения движения.
Источник: prezentacii.orgДинамика, которая опирается на законы Ньютона, называется классической. Этот раздел изучает движение объектов со скоростями в пределах от миллиметров в секунду до километров в секунду. В классической механике причинами движения всегда выступают силы. Законы динамики изучают также:
- движение упруго и пластически деформируемых тел;
- жидкостей;
- газов.
Не все виды движения можно описать законами динамики. Например, движение элементарных частиц при скоростях, близких к скорости света, подчиняется другим физическим законам.
В ходе изучения динамики конкретных объектов, возникли специальные дисциплины:
- баллистика;
- небесная механика;
- динамика корабля и самолёта и др.
Основные понятия и определение
Классическая механика изучает такие понятия, как:
- масса;
- энергия;
- импульс;
- момент импульса;
- сила;
- равнодействующая сила и др.
Масса — это скалярная физическая величина, которая является характеристикой такого свойства объекта, как инертность, и определяет количество вещества в теле.
Энергия — это количественная мера, характеризующая движение и взаимодействие объектов, а также их способность воздействовать на окружающий мир.
Импульс — это векторная физическая величина, измеряющая механическое движение тела, которая рассчитывается по формуле: \vec p=m\times\vec v
Момент импульса — это количественная характеристика вращательного движения.
Сила — это векторная величина, которая является причиной изменения скорости тела или его деформации, а также количественной мерой взаимодействия тел.
Любая сила в физике характеризуется 3 параметрами:
- точкой приложения;
- направлением;
- численным значением или модулем.
Линией действия силы называют прямую, вдоль которой эта сила действует.
Равнодействующая сила — это сила, которая оказывает на тело такое же действие, как все другие вместе взятые силы, воздействующие на него. Величина рассчитывается по формуле:
\(\vec F=\vec F_1+\vec F_2+\vec F_3 \)
В том случае, когда объект находится в состоянии покоя, равнодействующая всех сил, действующих на него, равна нулю.
В динамике встречаются следующие виды сил:
- Тяжести. Приложена к центру массы тела и направлена вертикально вниз (всегда перпендикулярно горизонту). Рассчитывается по формуле: \(F=m\times g\) где \(m\) — масса тела, \(g\) — ускорение свободного падения.
- Трения. Приложена к поверхности касания тела и опоры и направлена в противоположную сторону той, куда направлены другие силы, действующие на тело. Вычисляется по формуле: \(F=\mu\times N\), где \(\mu\) — коэффициент трения, \(N\) — сила реакции опоры.
- Сопротивления. Возникает при движении тела в газе или жидкости, всегда направлена против скорости движения.
- Реакции опоры. Действует на тело со стороны опоры, направлена перпендикулярно от нее.
- Натяжения нити. Направлена от тела вдоль нити.
- Упругости. Возникает при деформации тела, направлена против деформации. Вычисляется она согласно закону Гука по формуле: \(F=k\times\Delta l\), где \(k\) — коэффициент упругости, \(\Delta l\) — удлинение тела при деформации.
Основные законы динамики, формулы
Законы, на которых строится динамика, были впервые сформулированы Исааком Ньютоном в 1687 году. Именно поэтому их чаще всего и называют законами Ньютона.
Источник: infourok.ruЗаконы Ньютона верны только для описания движений, которые происходят в инерциальных системах отсчета (ИСО). Инерциальной называют такую систему отсчета, в которой тела двигаются равномерно и прямолинейно.
Первый закон Ньютона
Согласно первому закона Ньютона, тело остается в покое или равномерно прямолинейно движется, если на него не действуют никакие силы или равнодействующая всех сил равна нулю.
Инерцией называется способность тел сохранять скорость движения при отсутствии воздействия на него других объектов. Иногда первый закон Ньютона называют еще законом инерции.
Второй закон Ньютона
Второй закон Ньютона считается основным законом динамики и представляет собой формулу нахождения ускорения: ускорение, которое приобретает тело, прямо пропорционально равнодействующей сил (F), воздействующих на тело и обратно пропорционально массе (\(m\)) этого тела:
\(\vec a=\frac{\vec F}m\)
Когд на тело действуют сразу несколько сил, под силой в этом уравнении подразумевается равнодействующая всех сил.
Третий закон Ньютона
Третий закон Ньютона гласит: тела воздействуют друг на друга с силами, которые равны по модулю и противоположны по направлению, лежат на одной прямой и имеют одну физическую природу:
\(\vec F=-\vec F\)
Данные силы не могут уравновесить друг друга, так как приложены к разным телам. По этой же причине их нельзя складывать.
Методы решения задач, алгоритм
Как правило, все задачи из раздела динамики решаются с использованием законов Исаака Ньютона.
Для того, чтобы существенно упростить процесс решения задач по динамике, нужно:
- Внимательно прочитать условие задачи, разобраться, какие силы воздействуют на тела, указанные в задании.
- Нарисовать рисунок, на котором изобразить все векторные силы и указать их направление.
- Выбрать систему отсчета: одну координатную ось направить по направлению ускорения рассматриваемого тела, другую — перпендикулярно ускорению.
- Вспомнить второй закон Ньютона: \(\vec F_1+\vec F_2+\vec F_3=m\times \vec a\)
- Записать скалярную форму уравнения, учитывая, что силы, которые направлены против выбранных осей координат, будут иметь отрицательные значения. Получится такая система уравнений: \(\left\{\begin{array}{l}F_{1x}+F_{2x}+F_{3x}=m\times a_x\\F_{1y}+F_{2y}+F_{3y}=m\times a_y\end{array}\right.2, F=?\)
- Находим силу по формуле, иллюстрирующей второй закон Ньютона: \(F=m\times a.\)
- Подставляем числовые данные в формулу и получаем ответ: \(12 Н.\)
Задача №2:
Источник: infourok.ruЗадачи по динамике вращательного движения с решениями
Решение задач на вращательное движение производится при помощи законов Ньютона, также важно помнить основное уравнение динамики вращательного движения:
\(\vec M=J\times\vec\epsilon\)
где \(M\) — момент силы, которая действует на тело, \(J\) — инерция, \(\epsilon\) — угловое ускорение.
Задача:
Источник: zen.yandex.mdЗадачи по физике могут изрядно испортить настроение, если предмет не нравится, а суть его остается неясной. В таком случае за помощью можно обратиться к образовательному сервису Феникс.Хелп. Наши специалисты с легкостью разбираются в любых темах.
Dynamics – The Physics Hypertextbook
Обсуждение
Почему существует эта страница?
Это не страница о каком-то фундаментальном принципе физики. Это страница о решении конкретной (и распространенной) проблемы механики.
Неформально динамика – это исследование сил и движения. Говоря более формально, динамика – это раздел механики, изучающий влияние сил на движение объектов. Напротив, statics – это изучение сил без движения; или, более формально, раздел механики, который имеет дело с силами при отсутствии изменений в движении.Динамика предполагает изменение. Статика предполагает неизменность. Важное изменение – это ускорение.
Цель этого раздела этой книги – служить хранилищем проблем в динамике. Ускорение в каждой задаче будет отличным от нуля в одном направлении. Это верно только для этого раздела. Идея состоит в том, чтобы увидеть, каково решать такие проблемы, чтобы вы могли распознать их, когда они появятся позже.
Чистая сила
Возьмите первый закон движения Ньютона и разделите его на две части.«Покоящийся объект имеет тенденцию оставаться в покое, а объект в движении имеет тенденцию продолжать движение с постоянной скоростью…». В этом длинном главном предложении живет статика. «Если только на это не действует чистая внешняя сила». В этом коротком придаточном предложении мы находим динамику.
Слово чистая во фразе чистая сила означает общую, комбинированную или общую. Это то, что вы получаете, когда все обдумываете. Слово «сеть» связано со словом «аккуратный». Поиск чистой стоимости – это что-то вроде устранения математического беспорядка (или, по крайней мере, уменьшения беспорядка).Это может быть записано как ∑ F (с использованием греческой буквы сигма для обозначения суммы и жирным шрифтом, чтобы указать, что силы являются векторами) или как F net (с использованием нижнего индекса net, чтобы символ читался больше как произносимый язык и курсив, чтобы указать, что знание величины силы часто имеет значение) или другие подобные варианты.
Сила – это векторная величина, что означает, что направление имеет значение. Используйте положительные значения для сил, которые указывают в предпочтительном направлении, и отрицательные значения для сил, которые направлены в противоположном направлении.Если проблема двумерная, выберите два предпочтительных направления под прямым углом – что-то вроде вверх и вправо. Выбирайте предпочтительные направления, которые облегчат вашу жизнь. Законы физики не заботятся о том, называете ли вы правое положительное или левое положительным. Пространство в математическом смысле изотропно . Он измеряет одинаково во всех направлениях.
Второй закон движения Ньютона описывает, как связаны чистая сила, масса и ускорение. По сути, чистая сила вызывает ускорение, а масса ему сопротивляется.Лучше всего писать не словами, а символами. Примерно так…
| ∑ F = м a | или | F нетто = ма |
Теперь вы готовы начать следующий этап обучения.
Например,
Возьмем беспрецедентный пример обычного велосипеда, который безупречно крутили педалями по ничем не примечательной ровной и ровной дороге.Какие силы действуют на велосипед и гонщика (вместе в целом)?
Начните с очевидного. У всего вес и вес вниз. Велосипед стоит на твердой поверхности, поэтому нормальная сила и направлена перпендикулярно этой поверхности. Поверхность ровная, нормальное направление – вверх. Всадник крутит педали. Это означает, что есть какая-то сила, толкающая велосипед вперед. Я не хочу чрезмерно анализировать ситуацию, поэтому давайте просто назовем эту силу push .Даже должным образом накачанные шины сопротивляются качению, ось может нуждаться в смазке, а может и не нуждаться в смазке, и воздух определенно затягивает движущееся тело. Давайте упростим жизнь и назовем все эти силы вместе трением . Гонщик толкает велосипед вперед, а трение толкает назад.
Готовы сделать свободную схему тела. Нарисуйте рамку, изображающую велосипед и всадника. Нарисуйте четыре стрелки, выходящие из центра прямоугольника, чтобы обозначить четыре силы, действующие на велосипед и гонщика. Хотя это не всегда необходимо, следует попытаться нарисовать стрелки, длина которых соответствует относительным величинам сил.Длинные стрелки для сильных сил. Короткие для слабых.
Начните с легкой пары – весовой и нормальной. В этом сценарии ничего не происходит в вертикальном направлении. Дорога ровная, и гонщик не выполняет трюков. Вес и нормальный вес уравновешивают друг друга. Нарисуйте одну стрелку вниз, а другую вверх и придайте им одинаковую длину.
Завершите несколько менее легкой парой – толчок и трение. Что-то это происходит в горизонтальном направлении. Движение происходит в горизонтальном направлении.Велосипед куда-то едет. Это должно быть для чего-то полезно. Разве не должно?
Извините, но нет. Движение не имеет значения. Изменение движения – вот что важно. Велосипед ускоряется или движется с постоянной скоростью? Ускорение делает ситуацию динамичной. Отсутствие ускорения делает его статичным. Направление чистой силы определяет ускорение. Сила, направленная в направлении чистой силы, будет более сильной из двух.
Если велосипед ускоряется, значит, гонщик толкает велосипед вперед больше, чем трение толкает его назад.Если велосипед движется с постоянной скоростью, то толчок и трение равны. Если велосипед замедляется, сила трения побеждает силу, толкающую велосипед вперед.
Вот несколько рисунков, которые показывают то, что я только что сказал.
Вот набор уравнений, которые показывают то, что я только что сказал. Мне нравится использовать «вверх» и «вправо» в качестве положительных направлений, но это не закон физики. Это просто предпочтение.
| ||||||||||||||
| ||||||||||||||
| ↙ | ↓ | ↘ | ||||||||||||
|
|
|
Идите и решайте проблемы.
Перевернутые (деформированные) координаты
два тела, соединенные струной
Определение динамики по Merriam-Webster
dy · nam · ics | \ dī-na-miks \ 1 физика : раздел механики (см. Механический смысл 1), который имеет дело с силами и их отношением в первую очередь к движению, но иногда также и к равновесию (см. Смысл равновесия 2) тел.2 : модель или процесс изменения, роста или активности динамика населения
3 : вариация и контраст по силе или интенсивности (как в музыке)
множественное число от динамическая запись 2
Введение в динамику: законы движения Ньютона
Motion привлекает наше внимание.Само движение может быть прекрасным, заставляя нас восхищаться силами, необходимыми для достижения впечатляющего движения, такого как движение дельфина, выпрыгивающего из воды, или прыгающего с шестом, или полета птицы, или орбиты спутника. Изучение движения – это кинематика, но кинематика описывает только способ движения объектов – их скорость и ускорение. Dynamics учитывает силы, которые влияют на движение движущихся объектов и систем. Законы движения Ньютона – основа динамики.Эти законы служат примером широты и простоты принципов, в соответствии с которыми функционирует природа. Они также являются универсальными законами в том смысле, что они применимы к аналогичным ситуациям как на Земле, так и в космосе.
Законы движения Исаака Ньютона (1642–1727) были лишь частью монументальной работы, сделавшей его легендарным. Развитие законов Ньютона знаменует переход от эпохи Возрождения к современной эпохе. Этот переход характеризовался революционным изменением взглядов людей на физическую вселенную.На протяжении многих веков натурфилософы обсуждали природу Вселенной, основываясь в основном на определенных правилах логики, уделяя большое внимание мыслям более ранних классических философов, таких как Аристотель (384–322 до н. Среди многих великих мыслителей, внесших вклад в это изменение, были Ньютон и Галилей.
Галилей сыграл важную роль в установлении наблюдения как абсолютного детерминанта истины, а не «логического» аргумента. Использование Галилеем телескопа было его самым заметным достижением в демонстрации важности наблюдений.Он обнаружил спутники, вращающиеся вокруг Юпитера, и сделал другие наблюдения, несовместимые с некоторыми древними идеями и религиозными догмами. По этой причине, а также из-за того, как он обращался с властью, Галилей был осужден инквизицией и наказан. Последние годы своей жизни он провел под домашним арестом. Поскольку другие до Галилея также сделали открытия, обнаружив природу Вселенной, и поскольку повторные наблюдения подтвердили наблюдения Галилея, его работу нельзя было ни скрыть, ни опровергнуть.После его смерти его работа была подтверждена другими, и его идеи в конечном итоге были приняты церковью и научными сообществами.
Галилей также внес вклад в формирование того, что сейчас называют первым законом движения Ньютона. Ньютон использовал работы своих предшественников, которые позволили ему разработать законы движения, открыть закон гравитации, изобрести исчисление и внести большой вклад в теории света и цвета. Удивительно, что многие из этих разработок были сделаны с участием Ньютона, работающего в одиночку, без преимуществ обычных взаимодействий, которые имеют место среди ученых сегодня.
Лишь с появлением современной физики в начале 20 века было обнаружено, что законы движения Ньютона дают хорошее приближение к движению только тогда, когда объекты движутся со скоростями, намного, намного меньшими, чем скорость света, и когда те объекты больше, чем размер большинства молекул (примерно в диаметре). Эти ограничения определяют сферу классической механики, как обсуждалось во введении в природу науки и физики. В начале 20- -х годов века Альберт Эйнштейн (1879–1955) разработал теорию относительности и вместе со многими другими учеными разработал квантовую теорию.Эта теория не имеет ограничений, присущих классической физике. Все ситуации, которые мы рассматриваем в этой главе, и все ситуации, предшествующие введению теории относительности в специальную теорию относительности, относятся к сфере классической физики.
Установление связей: философия прошлого и настоящего
Важность наблюдения и концепция причины и следствия не всегда так укоренились в человеческом мышлении. Это осознание было частью эволюции современной физики от натурфилософии.Достижения Галилея, Ньютона, Эйнштейна и других явились ключевыми вехами в истории научной мысли. Большинство научных теорий, описанных в этой книге, возникли в результате работ этих ученых.
Dynamics | Физика для идиотов
Динамика – это название правил движения. Это то, что, как вы могли подумать, станет одним из первых, о чем нужно будет разобраться, но не было полностью заблокировано до недавнего времени. При этом правила не сильно изменились и довольно предсказуемы, по крайней мере, в больших масштабах.Кто-то однажды сказал мне, что все, что вам нужно знать для экзамена по динамике, это: а все остальное можно извлечь из этого. Так и не узнал, правы ли они, на всякий случай узнал и эти:
Если вы уже знакомы с уравнениями, возможно, вы захотите перейти к следующему разделу, иначе я объясню, откуда они взялись и как их использовать.
При работе с измерениями вы можете использовать скалярные или векторные величины.
Скалярные величины:
- Укажите только величину.
- Энергия, Длина, Масса, Скорость, Температура и Время – все это скалярные величины.
Векторные величины:
- Имеют и величину, и направление
- Смещение, Сила, Скорость, Ускорение и Импульс – все векторные величины.
Иногда может показаться, что скорость и скорость – одно и то же (часто они равны друг другу), но на самом деле они немного отличаются.Скорость – это то, насколько быстро что-то движется, не имеет значения, идет ли он вверх, вниз, влево или вправо, все, что имеет значение, – это то, как далеко он перемещается за установленное время. Вероятно, лучший способ рассматривать скорость – это если вы думаете или обычная ось x, y. Если тело движется горизонтально по прямой со скоростью 10, затем останавливается и движется в совершенно противоположном направлении, при скорости 10, очевидно, произошло изменение, однако скорость этого не отражает. Скорость до разворота такая же, как и после.Однако скорость не та. Если бы мы сказали, что скорость вначале была такой же, как и скорость: 10, тогда, когда тело движется точно в противоположном направлении с той же скоростью, скорость будет -10.
Исаак Ньютон был умным парнем. Мы должны благодарить его за гравитацию (я, вероятно, должен добавить, что он открыл, а не изобрел ее, иначе люди начнут обвинять его каждый раз, когда падают). Больше всего Ньютон известен (помимо случая с яблоком) своими законами движения:
- Частица останется в покое или продолжит движение, если на нее не будет действовать внешняя сила.
- Сила, действующая на объект, равна его массе, умноженной на его ускорение ().
- Каждое действие имеет равную и противоположную реакцию.
Все это нормально, но что на самом деле означают эти законы?
1. Частица останется в покое или продолжит свое движение, если на нее не будет действовать внешняя сила.
Это просто означает, что если на частицу не действует внешняя сила, она никоим образом не изменит ее движения. Если бы не было трения или сопротивления воздуха, то частица, движущаяся со скоростью 5, продолжалась бы бесконечно.Очевидно, что в реальной жизни этого не происходит из-за сопротивления воздуха и трения, поэтому практически невозможно иметь внешнюю силу на движущуюся частицу. Однако, если вы думаете о неподвижной частице, это имеет гораздо больший смысл. Если к неподвижной частице не приложить силу, она не начнет двигаться.
2. Сила, действующая на объект, равна его массе, умноженной на его ускорение.
Проще говоря, это, вероятно, одна из самых фундаментальных формул в динамике.Это один из тех, которые часто возникают в Dynamics, и его действительно стоит изучить. Понять это тоже не так уж и сложно. Имеет смысл, что если что-то имеет большую массу, потребуется большая сила, чтобы придать ему такое же ускорение, как и что-то с меньшей массой.
3. Каждое действие имеет равную и противоположную реакцию
Этот закон в основном означает, что если вы толкнетесь о стену, это оттолкнет вас назад, что на самом деле является хорошей работой, потому что в противном случае вы бы прошли прямо!
У них так много разных названий, что иногда трудно угнаться за ними.Возможно, вы слышали, что их называют кинематическими уравнениями, уравнениями движения, уравнениями SUVAT, а может быть, вы вообще о них не слышали. Прежде всего, давайте взглянем на них:
(1)
(2)
(3)
(4)
(5)
Может показаться, что там есть что вспомнить, но поверьте, это не так сложно, как кажется. Как будто эти уравнения невероятно важны в динамике.
SUVAT Equation 1
Как вы, наверное, уже знаете, скорость, разделенная на время, равна ускорению, а скорость, умноженная на время, равна смещению.Это означает, что на графике зависимости скорости от времени уклон линии равен ускорению, а площадь под линией равна смещению.
Если у вас есть начальная скорость и конечная скорость, график будет выглядеть примерно так:
График, показывающий u против tКак я уже сказал, уклон линии равен ускорению. Так . Переставив это так, чтобы получился объект, мы получаем нашу первую формулу постоянного ускорения:
SUVAT Equation 2
Ладно, один проиграл, осталось четыре!
Мы знаем, что площадь под графиком равна смещению.Итак, мы знаем, что умножение на дает нам нижний прямоугольник площади, а деление на 2 дает нам верхний треугольник. Это дает нам:
Теперь мы уже знаем это, поэтому можем переставить это, чтобы получить, а затем подставить это в наше уравнение для смещения. Из этого у нас есть. Если мы просто умножим скобку, которая дает нам нашу вторую формулу:
Для тех из вас, кто любит находить математику там, где это возможно, вам может быть интересно узнать, что это интеграл по отношению к.Если для вас это не имеет смысла, почему бы не заглянуть в замечательный раздел «Интеграция», где все станет ясно!
SUVAT Equation 3
Те из вас, кто увлечен поиском закономерностей, возможно, заметили, что это уравнение очень похоже на предыдущее. Это потому, что он очень похож на предыдущий. Те из вас, кто решил не переходить на страницу интеграции, могут пожалеть об этом сейчас.
Если переставить, чтобы сделать тему, то получится:
Теперь вам просто нужно интегрировать этот результат по времени, чтобы получить наше третье уравнение:
SUVAT Equation 4
Мы уже установили, что площадь под графиком (равная смещению) равна:
Если мы умножим скобку, получим:
, что совпадает с:
Наконец, мы просто разложим это на множители, чтобы получить:
SUVAT Equation 5
Можем переставить, сделать тему:
Затем мы просто подставляем это значение в наше предыдущее уравнение:, что дает нам:
, который можно упростить до,
, а затем
это в конечном итоге дает нам окончательную форму
Вот и все! Эти уравнения определенно стоит изучить, потому что они полезны снова и снова.Есть несколько правил, например, их можно использовать только в тех случаях, когда есть постоянное ускорение. Это означает, что если ускорение составляет примерно 12 мс –2 , они в порядке, но если ускорение составляет 12 мс –2 , тогда они не будут работать, поскольку ускорение зависит от.
Большая часть динамики достигается за счет игнорирования сопротивления воздуха, и хотя это значительно упрощает работу, всегда стоит знать, какое влияние это окажет.Для любого объекта, движущегося в жидкости, силу сопротивления можно рассчитать по формуле:
– плотность жидкости (998,2071 кг · м для воды при 30 градусах и 1,204 кг · м для воздуха), – скорость объекта, площадь поперечного сечения объекта и коэффициент сопротивления. Коэффициент аэродинамического сопротивления – это число, которое относится к аэродинамике объекта: куб имеет, а сфера имеет.
Объект, падающий на Землю, в конце концов (если он будет падать достаточно долго) достигнет скорости, при которой сила сопротивления равна силе тяжести, тянущей его вниз.Это называется Конечная скорость , и вы можете получить выражение для этого, приравняв силу сопротивления к, а затем переставив на:
Для человека, падающего в воздухе (сверху), у нас есть 70 кг, площадь 0,5 м и коэффициент сопротивления около 0,8 (приблизительное предположение где-то около углового куба или цилиндра), мы получаем конечную скорость около 53 мс (что оказывается быть довольно хорошей приблизительной оценкой).
Это самый простой экземпляр в динамике.Тело движется по плоской поверхности по прямой. Например:
1. Преподобный ведет свою машину, как вдруг двигатель перестает работать! Если он едет со скоростью 10 мс -1 , а его замедление составляет 2 мс -2 , сколько времени потребуется машине, чтобы остановиться?
Хорошо, с такого рода проблемами всегда полезно перечислить то, что вы знаете. Нам даны начальная скорость, и ускорение,. Мы также знаем, что если машина собирается финишировать в состоянии покоя, эта конечная скорость должна быть 0 мс -1 .Мы хотим узнать время,. Лично я считаю, что лучше всего изложить эту информацию так:
u = 10 мс -1
v = 0 мс -1
a = -2 мс -2
t =? с
Отсюда видно, какое уравнение нам нужно. В этом случае мы видим, что нам нужно уравнение. Мы переставляем это так, чтобы получился объект, давая нам
Наконец, мы помещаем числа в уравнение:
.
2. Майкл выходит на дорогу в 30 метрах от места, где двигатель не работает.Очки преподобного упали, и он не видит Майкла. Остановится ли машина вовремя, чтобы не сбить Майкла?
Еще раз, лучше всего выложить всю имеющуюся у нас информацию:
u = 10 мс -1
v = 0 мс -1
a = -2 мс -2
t = 5 с
с =? м
На этот раз мы хотим найти смещение s, поэтому нам нужно выбрать уравнение с этим in. Я собираюсь использовать. Я мог бы использовать или, однако, поскольку нам не дали времени, а вместо этого мы разработали это самостоятельно, любая ошибка, сделанная в предыдущих расчетах, будет перенесена в эту.
Я снова перегруппирую уравнение, на этот раз сделав его предметом обсуждения. Это хорошая привычка, теперь это может не иметь большого значения, переставляете ли вы уравнение до или после ввода чисел, но с более сложными формулами это может стать действительно беспорядочным, если вы не измените его сначала. Также в экзаменационных ситуациях, если вы допустили ошибку, вы все равно можете получить оценки по методу, если экзаменатор может видеть, что вы сделали.
В любом случае, это дает нам
Подставляя числа в уравнение, получаем:
, чтобы Майкла не ударили! (Уф!)
В приведенном выше примере трение полностью проигнорировано.В реальном мире мы не можем этого сделать (очень удачно, потому что мы все время падали, и люди думали, что мы пьяны). Итак, теперь нам лучше взглянуть на ситуацию с трением. Коэффициент трения обозначается символом μ. Результирующая (нормальная) сила веса уравновешивает вес автомобиля (чтобы он не проезжал по дороге). Сила трения равна μ (или μN).
3. Машина преподобного сломалась на трассе М1. Ему нужно подтолкнуть его к твердому плечу. Автомобиль весит 5000Н.Rev может выдвинуть около 1800N. Коэффициент трения между автомобилем и дорогой составляет 0,6. Сможет ли Rev подтолкнуть машину к твердой обочине?
Хорошо, в такой ситуации сначала хорошо нарисовать небольшой набросок того, что происходит.
Диаграмма сил, показывающая, что происходит в примере 3.Из этого мы знаем, что для того, чтобы машина двигалась, Rev должен толкать с силой не менее μR. Просто умножив коэффициент трения на результирующую силу, мы обнаружим, что сила трения равна 3000 Н, поэтому Rev не сможет толкнуть машину на обочину дороги.
4. Бодибилдер случайно проходит мимо и, пытаясь облегчить заторы на постоянно загруженном М1, он решает помочь. Он может толкать с силой 3200Н. Каким будет ускорение машины с учетом того, что бодибилдер и Rev.NB – Принять массу автомобиля 510 кг
Итак, на самом деле ситуация та же, что и раньше, только на этот раз силы не уравновешиваются и будет ускорение. Мы получили это от очень умного Исаака Ньютона.
Помните, что для определения общей силы вам нужно убрать силу трения. Итак, это (3200 + 1800) – 3000. Таким образом, общая сила составляет 2000Н. Опять же, нам нужно изменить формулу, чтобы на этот раз в качестве испытуемого использовалось и . Это дает нам. Подставляя числа, получаем:
a = 3.9 мс -2 (2 s.f.)
Это очень похоже на движение по плоской поверхности, только одна или две другие переменные … о, и мы больше не будем говорить об автомобиле Rev, так как я не уверен, что это поможет ему подняться в гору!
В любом случае, боюсь, я немного сбился с пути.Введение «наклонной плоскости» или «уклона», как ее называют большинство из нас, означает, что вам придется освежить свою тригонометрию. С другой стороны, вы узнаете, почему люди годами пытались вбить это в вас! Если вы знакомы со старым добрым порядком операций, все будет в порядке.
Итак, давайте начнем с простого простого примера.
Пример наклонной плоскостиНа картинке выше показан блок, стоящий на склоне. Хорошее место для начала (возможно, единственное место, с которого можно начать, если вы хотите получить хоть какой-то шанс получить хоть что-нибудь с вопросом), – это объединить силы.Предполагая, что блок находится в состоянии покоя, мы знаем, что он находится в равновесии, поэтому горизонтальные силы должны быть равны, как и вертикальные силы (если это не один из тех прекрасных левитирующих блоков).
Снарядыничем не отличаются от Движения по прямой, просто вместо того, чтобы тело двигалось слева направо, оно также движется вверх или вниз. Сначала рассмотрим типичный пример движения снаряда:
.Мяч брошен под углом 30 °. Имеет начальную скорость 20 мс -1 .Найдите максимальную высоту, которую может достичь мяч.
Ладно, как обычно, рисуем диаграмму:
Пример движения снарядаТеперь давайте перечислим то, что мы знаем:
- u = 20 sin30 мс -1
- v = 0 мс -1
- a = -9,81 мс -2
- с =? м
Теперь мы выбираем одну из кинематических формул, которая даст нам результат наиболее прямым путем, это:, и переставляем ее так, чтобы получился объект:
Затем, наконец, введите числа в уравнение:
и выскакивает ответ:
Смотри, не так ли сложно было? Вопросы о снарядах иногда могут показаться довольно сложными, но если вы не забудете просто использовать тригонометрию для нахождения компонентов x и y, вы не ошибетесь.
Иногда вы знаете максимальную высоту, но какой-то другой компонент будет отсутствовать. Например, время, когда мяч находится в воздухе … Опять же, это не проблема, вы просто посмотрите, что вы знаете, , , и воспользуйтесь формулами, чтобы вычислить остальное.
Терминология– В чем разница между «кинематикой» и «динамикой»?
Кинематика – это диапазон движения или изменения, которому может подвергаться система, или пространство состояний, в котором она действует. Динамика – это движение, которому она подвергается в соответствии с законами движения.
Например, кинематика твердого тела в пространстве описывает его возможные координатные положения и ориентации, а также диапазон скоростей и угловых скоростей и т. Д. Динамика описывает, как они будут меняться под действием данной системы сил.
Это означает, что сохранение энергии и других величин является динамическим, потому что оно выполняется только тогда, когда действуют уравнения движения.
Хотя кинематика и динамика чаще всего используются в классической механике, вы можете распространить эту идею на квантовую механику, где кинематика описывается фазовым пространством и операторами, а динамика – это эволюция под влиянием данного гамильтониана.
Принято считать, что различие между кинематикой и динамикой является абсолютно четким, но, возможно, самое важное, что нужно понимать, – это то, что это не всегда так. В качестве простого примера рассмотрим случай частицы, которая может двигаться по фиксированной траектории. Вы можете рассматривать ограничение, удерживающее его на траектории, как кинематическое, и только его фактическое движение по треку будет частью динамики, но мы знаем, что на более глубоком уровне частица удерживается на траке динамическими силами.
Другой пример – сохранение заряда. Если вы рассмотрите уравнение Дирака для заряженной частицы в присутствии электромагнитного поля, вы обнаружите, что заряд сохраняется только под влиянием уравнений движения. При квантовании системы заряд определяется суммой квантованных зарядов позитронов и электронов, которые могут быть созданы и уничтожены только парами. Это можно рассматривать как кинематическое ограничение, когда динмаика учитывает только движение частиц.
Возможно, лучший пример – электродинамика, где векторный потенциал описывает кинематику поля с электрическими и магнитными полями, задаваемыми подходящими производными. В этом случае уравнение Максвелла, которое говорит нам, что магнитное поле имеет нулевую дивергенцию, является кинематическим, потому что оно следует без использования уравнений движения, но дивергенция электрического поля равна электрическому току согласно уравнениям движения. Итак, некоторые уравнения Максвелла кинематические, а некоторые – динамические.В более глубокой теории эти поля могут быть получены из системы, которая демонстрирует электромагнитную дуальность, в которой магнитные монополи действуют как источники магнитного поля. В этом случае кинематическая и динамическая части уравнения Максвелла меняются местами из-за дуальности, поэтому мы вынуждены понимать, что первоначальное различие между кинематикой и динамикой было иллюзией.
В конечном счете, эволюция Вселенной не делает такого же различия между кинематикой и динамикой, как это делают физики, и важно понимать, что на более глубоком уровне кинематика может оказаться динамикой или наоборот.Так что любая попытка определить разницу в некоторой степени произвольна и может не выдержать испытания временем.
Законы динамики – Энциклопедия окружающей среды
Закон Ньютона, связывающий силу и ускорение, лежит в основе современной физики. Применяемый к каждому графику жидкости, он лежит в основе моделей прогнозирования погоды и климата. Интуитивное понятие силы использовалось с древних времен для понимания статического равновесия. Это позволяет спроектировать своды в архитектуре, использовать рычаг, чтобы описать баланс жидкости под действием тяги Архимеда.Именно принцип инерции, открытый Галилеем, проложил путь к законам ньютоновской динамики, чей большой успех заключался в объяснении движения планет и спутников, а также приливов и отливов. Это потребовало большого математического опыта, который имеет свои пределы для более сложных систем, таких как атмосфера или океан. Решение уравнений динамики стало возможным только с момента появления компьютерных вычислений. Однако законы сохранения, количества движения, энергии, кинетического момента накладывают глобальные ограничения, позволяющие более непосредственно понять определенные явления.
1. Уравновешивающие силы
Понятие силы выражает механическое воздействие на объект. Силы имеют четко определенное физическое происхождение, например, гравитационная сила (вес ), электрическая сила на заряженной частице , контакт или напряжение сила на кабеле, или сила упругости пружина. Как и многие фундаментальные понятия физики, силу сложно определить сама по себе, но к ней можно подойти с помощью экспериментальных примеров, а также с помощью математических соотношений, которые она имеет с другими величинами.
Рис. 1. Равновесие противоположных сил, а) в пружинном динамометре, б) в воздушном шаре. [Источник: Traité de Physique Elemententaire – DRION et FERNET – 1885] Сила, таким образом, характеризуется интенсивностью (или модуль упругости ) и направлением , а также точкой приложения, и математически представляется в виде вектор . Сумма сил, действующих на покоящийся объект, должна нейтрализовать друг друга. Сила может быть измерена по удлинению пружины из ее положения покоя (рис. 1).Экспериментально подтверждается, что это удлинение пропорционально силе путем последовательного добавления нескольких одинаковых грузов. После калибровки этот датчик силы пружины может использоваться для измерения различных сил. Для теплового шара, неподвижного в воздухе, общий вес уравновешивается тягой Архимеда , равной и противоположной массе вытесненного объема воздуха. Это не что иное, как результат сил атмосферного давления , действующих по всей оболочке: из-за уменьшения давления с высотой давление внизу оболочки выше, чем вверху, что переводится в чистую силу, направленную вверх. .Этот баланс между давлением и силой тяжести фактически применяется к любому объему жидкости в равновесии, известном как гидростатическое равновесие (см. «Давление, температура, тепло»). Именно благодаря этому балансу воздушные участки или водные участки в бассейне не падают на землю под действием силы тяжести. Когда воздух нагревается, его плотность и, следовательно, масса данного объема уменьшается, в то время как давление остается неизменным, поскольку оно контролируется весом окружающего воздуха.Затем равновесие нарушается, что приводит к вертикальному ускорению воздушного шара. В атмосфере воздушная масса, локально нагретая солнечным излучением, также имеет тенденцию подниматься: это принцип конвекции .
Рис. 2. Перевернутая модель Собора Святого Семейства Гауди. Форма равновесия такова, что на каждом пересечении проводов векторная сумма сил равна нулю. Каждый элемент балки представлен проволокой, а его масса моделируется грузом. Сила натяжения пряжи обязательно совпадает с пряжей.В реальной перевернутой конфигурации соответствующая сила будет тогда силой сжатия, направленной вдоль балки, что гарантирует ее механическую прочность. [Источник: http://olive-art.weebly.com/uploads/2/6/0/5/26053332/6555663_orig.jpg]. В общем, баланс сил должен быть выражен как векторов , что является Основу для расчета структур в архитектуре см. Рисунок 2. Для каждой материальной точки, например, узла пересечения проводов, векторная сумма сил должна уравновешивать друг друга в состоянии равновесия, как показано на рисунке 3a.Это позволяет, например, найти интенсивности сил F1 и F2 , зная силу F3 и углы θ1 и θ2 , либо геометрическим построением, либо численно. путем проецирования векторов по вертикальной и горизонтальной осям. Протяженный объект, например твердое тело , описывается в физике как набор из материальных точек , удерживаемых вместе внутренними силами .Эти силы следует отличать от внешних сил , таких как вес или силы контакта с другими объектами. Сумма внутренних сил компенсируется принципом действия и противодействия , так что равновесие требует отмены суммы внешних сил.
Рисунок 3. Баланс сил на материальной точке а) и баланс моментов на протяженном объекте – рычаге.Но состояние равновесия протяженного объекта также требует отмены полного момента сил, чтобы избежать его вращения.Момент силы относительно оси определяется как произведение силы, проецируемой перпендикулярно оси, на расстояние до оси. Классическим примером является рычаг, показанный на рисунке 3b. В состоянии равновесия или квазиравновесия для медленного движения для компенсации моментов требуется, чтобы F1d1 = F2d2 (силы здесь перпендикулярны оси), что позволяет усилить силу, действующую в обратном отношении расстояния до оси (согласно обычному соглашению мы отмечаем здесь F1 интенсивность силы, а F1 представляет вектор силы).Обычно моменты рассматривают относительно оси рычага, потому что момент силы реакции R земли компенсируется сам собой. Однако тот же результат можно получить, вычислив момент относительно любой математической оси, добавив момент реакции R , который является равным вектором и противоположен сумме двух сил F1 и F2 .
2. Силы и ускорение
Теперь, покидая область статики, ускорение объекта связано с общей силой F , которая действует на него по знаменитому закону Ньютоновская динамика , F = мг где м. – это масса объекта, а г, – его вектор ускорения.Это позволяет определить единицу силы, Ньютон (Н), как силу, создающую ускорение в 1 (м / с) / с над массой 1 кг, что записывается как 1 Н = 1 кг · м · с-2. .
В отсутствие силы объект движется с постоянной скоростью, это принцип инерции , впервые сформулированный Галилеем (1564-1642). В то время этот принцип был не очень интуитивно понятным, потому что в повседневной жизни любое движение имеет тенденцию останавливаться без усилия. Это замедление (отрицательное ускорение) теперь приписывается трению сил, которые противоположны скорости.Но трение становится незначительным в межпланетной пустоте, и большой успех Ньютона (1643-1727) заключался в математическом описании движения планет и спутников на основе простого закона всемирной гравитационной силы, уменьшающейся как величина, обратная квадрату расстояния r. .
Применение закона Ньютона потребовало изобретения математической концепции производной , определяющей понятия скорости и ускорения. Отметим скорость v = dz / dt, где dz – небольшое смещение во временном интервале dt.Фактически, мы считаем предел из очень коротким временным интервалом. Точно так же ускорение обозначается как g = dv / dt. Для постоянного ускорения g скорость пропорциональна времени, v = gt , и легко продемонстрировать, что расстояние падения (разница между начальной высотой z0 и высотой z ) будет тогда z0- z = (1/2) gt2 . Таким образом, на Земле под действием силы тяжести, г, = 9,8 м / с, объект достигает скорости 9.8 м / с (35 км / ч) за 1 секунду, падает с высоты 4,9 м.
Закон Ньютона в более общем случае применяется в векторной форме : объект может падать вертикально, как указано ранее, сохраняя при этом свою горизонтальную составляющую скорости за счет инерции. При достаточно высокой горизонтальной скорости необходимо принять во внимание кривизну Земли и получить круговое движение спутника , см. Рисунок 4. В этом случае скорость постоянна по модулю, но вектор скорости вращается на такая же угловая скорость [1], что и у спутника.Ускорение тогда перпендикулярно скорости и направлено к центру Земли, со значением g = v2 / r , как показано на рисунке 4. Таким образом, для спутника, близкого [2] к Земле, g = 9,8 мс-2, r = 6500 км, что приводит к: скорости v = (gr ) 1/2 = 8 км / с, времени обращения (длина 40 000 км) T = 5000 с (1 ч 23 мин).
Рисунок 4. a) Движение запущенного тела с увеличивающейся горизонтальной скоростью до спутника на круговой орбите (8000 м / с) и выброс Земли (11000 м / с) [Источник: иллюстрация теории Ньютона, опубликованная в «Popular Astronomy» ].(б) Закон динамики применительно к круговому движению спутника: за короткий промежуток времени dt спутник поворачивается на угол dq = (v / r) dt, а вектор скорости поворачивается на тот же угол dq = (g / v) dt, из которого выводится g = (v2 / r), что позволяет рассчитать скорость спутника v = 8000 м / с у поверхности Земли (r = 6500 км, g = 9,81 м / с-2). ). Если теперь сила тяжести g уменьшается на 1 / r2, скорость v = (gr ) 1/2 от кругового движения уменьшается на 1 / r1 / 2, а период вращения равен 2πr / v , увеличивается в r3 / 2 .Таким образом, Луна удалена от Земли r = 384 000 км, т.е. е. В 60 раз больше радиуса Земли, он должен вращаться за время в 465 раз дольше, чем ближайший спутник, т.е. е. 27 дн. Это согласуется с наблюдениями [3]. Закон роста времени обращения в r3 / 2 был открыт Kepler (1571-1630) для планет, вращающихся вокруг Солнца. Помимо частного случая круговой орбиты, Ньютон смог продемонстрировать, что общее движение следует за эллипсом (или гиперболой за пределами скорости истечения), и он смог найти три закона, ранее установленные Кеплером, на основе точных измерений положения планет.
Бывает, что сила тяжести сама по себе пропорциональна массе, поэтому возникающее ускорение не зависит от нее: все тела падают с одинаковым ускорением в одном и том же месте. Это равенство между тяжелой массой и инертной массой было заявлено Галилеем и проиллюстрировано его знаменитыми экспериментами (возможно, только воображаемыми) с падающими объектами с Пизанской башни. Это было сделано снова с большой точностью в вакууме, избегая трения воздуха. В качестве демонстрации для публики был снят фильм, сравнивающий падение молотка и пера на Луне во время полета Аполлона XV [4], и аналогичный эксперимент был снят на Земле в огромной вакуумной камере [5].Именно из-за этого принципа эквивалентности все объекты плавают в невесомости на спутнике, каждый движется по одной и той же орбите вокруг Земли. Эта эквивалентность сейчас проверяется с относительной точностью 10-13 (1/10 триллиона), а точность 10-15 ожидается от недавно запущенного спутника «Микроскоп». Эти сверхточные измерения предназначены для проверки отклонений от принципа эквивалентности, предсказываемого новыми теориями гравитации.
3. Кинетическая и потенциальная энергия
В приведенном выше примере свободного падения можно отметить, что мг (z0-z ) = м (1/2 ) g2t2 = (1/2 ) mv2 .Это соответствует более общему свойству сохранения полной энергии, состоящему из кинетической энергии (1/2 ) mv2 и потенциальной энергии mgz . Когда объект падает, его кинетическая энергия увеличивается, но его потенциальная энергия также уменьшается, так что полная механическая энергия сохраняется (при отсутствии трения). В общем случае кинетическая энергия (1/2 ) mv2 выражается как функция модуля скорости. Сохранение механической энергии становится все более распространенным в случае спутника, но выражение потенциальной энергии затем должно быть изменено, чтобы учесть уменьшение силы тяжести.Эта потенциальная энергия зависит только от положения объекта, так что он принимает то же значение после вращения, и кинетическая энергия также имеет такое же значение в соответствии с тем фактом, что движение планеты сохраняется бесконечно. Гравитационный потенциал определяется путем деления этой потенциальной энергии на массу объекта. Этот потенциал характеризует гравитационное поле независимо от объекта, вращающегося вокруг него (до тех пор, пока объект мал и не приводит планету в движение посредством реакции).
Сохранение механической энергии требует особой формы законов силы. Силы трения, в отличие от силы тяжести, уменьшают механическую энергию, так что спутник в конечном итоге входит в контакт с остаточной атмосферой. Однако потерянная механическая энергия преобразуется в тепло, так что общая энергия сохраняется (см. «Энергия»). Тепло по существу соответствует неупорядоченной кинетической энергии молекул газа. Для однородной сферической планеты потенциал изменяется в пределах -1 / r, так что эквипотенциалы представляют собой концентрические сферы.Однако эти сферы слегка деформированы из-за вращения Земли и неоднородностей. Равновесная форма поверхности океана является таким эквипотенциалом (см. «Морская среда»). В самом деле, объект, движущийся по эквипотенциалу, сохраняет ту же потенциальную энергию, и, поскольку его полная энергия сохраняется, он не может приобретать (или терять) скорость под действием только силы тяжести. И наоборот, если форма океана отклоняется от эквипотенциальной, поверхностная вода стремится течь в области с более низким потенциалом, пока не заполнит их и не достигнет состояния равновесия, при котором поверхность является эквипотенциальной.Поверхность твердой Земли также приближается к эквипотенциальности из-за эрозии и пластичности мантии Земли.
4. Количество движения
Количество движения, равное элементарной массе (рассматриваемой как точечная), определяется как произведение массы и скорости, определение, которое может быть распространено на любую физическую систему, добавляя (векторно) количества движения каждой из ее элементарные массы. Легко продемонстрировать, что величина движения равна величине движения центра инерции (центр тяжести ) системы, на которую воздействует ее общая масса.Затем закон динамики Ньютона указывает, что производная от количества движения по времени равна сумме сил, действующих на систему.
Согласно фундаментальному принципу физики, количество перемещений изолированной системы сохраняется. Другими словами, его центр инерции движется поступательно с постоянной скоростью, и только внешние силы могут изменить эту скорость. Другой эквивалентной формулировкой является принцип действия и противодействия , который предусматривает, что любое тело A, оказывающее силу на тело B, испытывает силу равной интенсивности, но в противоположном направлении, действующую со стороны тела B.Затем закон динамики указывает, что эти внутренние силы не изменяют величину движения глобальной системы A + B. Это обобщает рассмотренное выше условие статического равновесия.
Зная начальные массы m1 и m2 и начальные скорости u1 и u2 каждой массы, вычисляется величина движения до удара m1u1 + m2u2 , которая должна сохраниться после удара , таким образом, обеспечивая ограничение на конечные скорости.Если дополнительно предположить, что амортизатор упругий , т.е. е. что кинетическая энергия (1/2 ) m1u12 + (1/2 ) m2u22 сохраняется, мы можем вывести две конечные скорости. Для двух равных масс мы имеем обмен скоростями (рис. 5а). В случае полностью неупругого удара , массы остаются связанными после удара с конечной скоростью, равной средневзвешенному значению начальных скоростей m1u1 + m2u2 / (m1 + m2 ) при сохранении количества движение.Применительно к молекулам газа эти ударные свойства позволяют интерпретировать явление вязкости, которое уравнивает количество движений быстрой и медленной зон внутри жидкости, сохраняя при этом общее количество движений.
Привод ракет или самолетов – еще один классический пример: величина движения, передаваемого транспортному средству, прямо противоположна движению выбрасываемого газа, независимо от задействованных сложных механизмов. Это также относится к силам гравитации: Луна притягивает Землю с силой, равной силе тяжести Земли, действующей на Луну, и противоположной ей.Таким образом, Земля вращается вокруг центра инерции системы Земля-Луна так же, как и молотковая установка, которая должна вращаться, чтобы компенсировать реакцию вращающегося шара (см. «Приливы»). Именно этот центр инерции описывает эллиптическую орбиту вокруг Солнца, а не саму Землю.
Рисунок 5-а. Choc élastique entre deux masses égales [Источник: Саймон Штайнманн (собственная работа) [CC BY-SA 2.5 (http://creativecommons.org/licenses/by-sa/2.5)]] Рис. 5-b.Choc élastique entre deux masses inégales [Источник: Саймон Штайнманн (собственная работа) [CC BY-SA 2.5 (http://creativecommons.org/licenses/by-sa/2.5) через Wikimedia Commons] Рисунок 5-c. Отличное неэластичное блюдо из двух масс [Источник: Par Raul Roque (персонал Travail) [CC BY-SA 2.5 (http://creativecommons.org/licenses/by-sa/2.5)], через Wikimedia Commons]
5. Угловой момент
Угловой момент относительно оси определяется для точечной массы как произведение расстояния до оси на величину ее движения, проецируемого перпендикулярно этой оси.Это определение обобщается на протяженное тело, например твердое тело, путем деления его мыслью на элементарные массы и сложения их угловых моментов. Мы демонстрируем из закона динамики, что производная кинетического момента по времени равна суммарному моменту сил (также называемых «крутящий момент »), действующих на систему. Это обобщает закон статики, который требует, чтобы полный момент сил был равен нулю.
Закон сохранения кинетического момента гласит, что полный момент внутренних сил уравновешивается, и поэтому только момент внешних сил может изменить кинетический момент.Таким образом, в твердом состоянии внутренние силы сцепления не вмешиваются в баланс кинетического момента, так же как они не вмешиваются в величину движения. Это фундаментальный закон физики, отличный от принципа действия и противодействия и дополняющий его.
Другими словами, система не может начать самопроизвольное вращение или потерять свое начальное вращение без действия внешних сил. Однако его скорость вращения может измениться в случае сжатия или растяжения.Действительно, для точечной массы это произведение , скорости и на расстояние r до оси, которая сохраняется, поэтому скорость u увеличивается обратно пропорционально расстоянию r , и его угловая скорость u / r обратно пропорциональна квадрату этого расстояния.
Классический пример – фигурист, а в естественной среде – образование торнадо и циклонов (см. «Торнадо: мощные разрушительные водовороты»).Само вращение Земли является результатом увеличения угловой скорости при аккреции вещества, которое привело к ее образованию. Самый яркий пример – пульсары, чрезвычайно плотные звезды, вращающиеся с периодом от нескольких секунд до нескольких миллисекунд. Эти объекты возникают в результате коллапса массивной звезды, обычно в радиусе от 1 миллиона км до 10 км. Такое сжатие увеличивает угловую скорость вращения в 10 миллиардов раз (часть углового момента выбрасывается вместе с газом, испускаемым взрывом).
Момент импульса на самом деле является вектором, выровненным с осью вращения [6], и поэтому он сохраняется как по направлению, так и по модулю. Это принцип работы гироскопа . Точно так же ось вращения Земли остается выровненной по отношению к звездам, а Северный полюс по-прежнему указывает на область, близкую к Полярной звезде.
Рисунок 6. Прецессия фрезера: вес создает разрез, ориентированный перпендикулярно рисунку и горизонтальный. Таким образом, результирующее изменение вектора кинетического момента перпендикулярно этому вектору, что приводит к прецессионному движению, показанному на рисунке.Аналогичное явление происходит с вращением Земли под действием крутящего момента из-за лунного притяжения (однако, прецессия происходит в противоположном направлении, потому что крутящий момент имеет противоположный знак по отношению к вершине). Источник: http://hyperphysics.phy astr.gsu.edu/hbase/mechanics/imgmechs/imgmech/topp.gif]Это верно только для изолированной системы, а точнее при отсутствии крутящего момента (или момента) от внешние силы. Крутящий момент, перпендикулярный оси вращения, вызывает вращение оси вращения без какого-либо изменения угловой скорости: это явление прецессии , наблюдаемое на маршрутизаторе, см. Рисунок 6 (точно так же, как ускорение, перпендикулярное скорости, производит вращение скорости без изменения ее модуля).Аналогичный эффект происходит с Землей из-за ее уплощенной формы на полюсе: крутящий момент возникает из-за более сильного притяжения Луны на части около бусинки, чем на ее противоположной части. Это приводит к медленному прецессионному движению вращения Земли в течение 26000 лет (см. Рисунок 6). Таким образом, направление полюса медленно перемещается по небесной сфере на протяжении столетий. Это приводит к смещению орбиты Земли относительно положения равноденствий, когда ось вращения Земли ориентирована перпендикулярно направлению Солнца.Вот почему это явление называется «прецессия равноденствий ». Связанное с этим изменение солнечного света происходит при изменении климата между ледниковым и умеренным периодами.
Ссылки и примечания
Фотография на обложке. Автор http://creativecommons.org/licenses/by-sa/2.0 (загружен на Flickr как обычный jfpds) [CC BY-SA 2.0 (极 博 双 板 滑雪 俱乐部)] через Wikimedia Commons.
[1] Угловая скорость Ω – это угол, пройденный за единицу времени, обычно выражаемый в радианах / с, так что Ω = v / r.Радиан определяется как угол, пересекающий дугу окружности, равную радиусу, так что полный оборот (окружность 2πr ) представляет 2π радиан, а период вращения равен T = 2π / Ω = 2πr / v .
[2] Высота должна составлять несколько сотен километров, чтобы избежать атмосферного трения, но ускорение свободного падения остается близким к ускорению земной поверхности, а радиус орбиты мало отличается от радиуса Земли.
[3] Это сидеральная революция, i.е. относительно звезд, в то время как время между двумя полными лунами, равное 29,5 дня, является синодическим оборотом, i. е . по отношению к Солнцу.
[4] Молот и перо Аполлона 15 – Youtube
[5] Брайан Кокс посещает самую большую в мире вакуумную камеру – Вселенная человека: превью 4 серии – BBC Two – Youtube
[6] Угловой момент более точно определяется относительно исходной точки O. Для точки массой м в точке M это векторное произведение вектора на вектор OM на величину движения м u массы в точке М.Для осесимметричного твердого тела, такого как маршрутизатор или Земля, кинетический момент выровнен по оси вращения со значением, пропорциональным угловой скорости и моменту инерции .
Экологическая энциклопедия окружающей среды Ассоциации энциклопедий окружающей среды и энергии (www.a3e.fr), по контракту связана с Университетом Гренобль-Альп и ИЯФ Гренобля и спонсируется Французской академией наук .
Для цитирования: SOMMERIA Joël (2021), Законы динамики, Энциклопедия окружающей среды, [онлайн ISSN 2555-0950] URL: https://www.encyclopedie-environnement.org/en/physics/laws-of -динамика /.
Статьи в Энциклопедии окружающей среды доступны в соответствии с условиями лицензии Creative Commons BY-NC-SA, которая разрешает воспроизведение при следующих условиях: ссылка на источник, не коммерческое использование их, использование идентичных исходных условий, воспроизведение в при каждом повторном использовании или распространении эта лицензия Creative Commons BY-NC-SA упоминается.
Линейная динамика
Молекулярная динамика – это изучение того, как и почему молекулы движутся по пути что они делают. До Ньютона Аристотель говорил, что тела движутся только потому, что другие тела заставляют их делать это. Это совершенно разумное предложение было обращено против голову Ньютона, который сказал, что тела будут продолжать двигаться в униформе скорость, если на нее не действует сила, которая вызывает ускорение на тело.
2.1 Измерение движения – кинематика
Прежде чем мы сможем схватиться с идеями Ньютона и применить их к движениям такие вещи, как атомы, ионы и молекулы, нам нужно будет узнать, как мы можем измерить их движение.
2.1.1 Центр масс
Все атомы и ионы состоят из ядра, состоящего из протонов и нейтронов, окружен рядом электронов. Хотя сказать довольно сложно каков точный размер очень маленьких объектов, мы знаем, что ядро около 10 -15 м в диаметре, а атом имеет порядок 10 -10 м в поперечнике.Оценить размер электрона довольно сложно и весьма сомнительно, но его диаметр примерно такой же, как у ядра. Этот делает довольно очевидным, что атомы не являются математическими точками массы, они являются протяженными объектами. Действительно, по своему масштабу они чрезвычайно распространены. над космосом. Если это так для атомов, то, очевидно, еще более верно для молекул.
Следовательно, может показаться, что для описания движения или кинематики атомов и молекул мы будем вынуждены приступить к сложной задаче определения положение каждого компонента, когда он движется в пространстве.Фактически позже в этим курсом мы докажем, что есть одна особенная точка в молекула, движение которой очень легко описать. Эта точка называется центром массы, и это точка, в которой вся масса атома или молекулы может считаться проживающим.
Например, положение центра масс X двухатомной молекулы показано на рисунке 2.1.1, соответствует
(2.1.1).
Используя центр масс для описания движения молекулы, мы имеем потеряли способность описывать вращательные и колебательные движения, мы только может описать движение всей молекулы, как если бы это была точка частица.Это означает, что мы можем объяснить только движение молекул, вызванное силы, внешние по отношению к молекуле, используя эту картину частиц. Вибрационный и вращательные движения, которые являются внутренними по отношению к молекуле, не влияют на общая траектория молекулы в пространстве. На языке физики говорят, что внутренние движения отделены от внешних. Этот окажется очень мощной идеей, которую мы будем использовать неоднократно.
Рисунок 2.1.1. В центр масс двухатомной молекулы (код см. в разделе “Физические Химия: молекулярные взаимодействия: двухатомный центр масс »).
2.1.2 Определение положения, скорости и ускорения – в одном измерении
Чтобы изучить движение частицы, мы должны иметь возможность отслеживать ее положение с помощью уважение ко времени. Мы сделаем это, установив измерительную линию параллельно траектории частицы, пусть это будет ось x, и запустите часы, идущие до записать время t.Начало оси x и нулевая точка для нашего времени совершенно произвольны.
Теперь мы можем создать график положения по оси x как функцию время, рисунок 2.1.2.
Рисунок 2.1.2. График положения частицы как функции времени.
Средняя скорость перемещения из положения x1 в положение x2 в истекшее время t2 – t1 определяется как
(2.1.2)
Скорость имеет как величину, так и направление, e.г. на рисунке 2.1.2 частица движется в отрицательном направлении x в течение первых 2,5 с перед впоследствии движется в положительном направлении оси x. На языке математики это означает, что скорость является векторной величиной, она имеет как величину, так и направление. Скорость, которая является лишь величиной скорости, называется скаляром. количество.
Обычно построение графика x как функции времени не дает прямого линия, т.е. равномерная скорость. В этих более общих случаях мы определяем мгновенная скорость в некотором заданном положении, которая должна быть задана уменьшением интервал Δt до бесконечно малого значения dt.
Рисунок 2.1.3. Определение мгновенной скорости.
Таким образом, мы измеряем наклон или касательную в точке (x1, t1), рисунок 2.1.3. Математически это обозначено как
.(единицы СИ мс -1 ) (2.1.3)
где dx / dt – мгновенная скорость изменения расстояния относительно время. Измеряя наклон нашего графика при всех x как функцию от t, мы можем построить график зависимости v от t, рисунок 2.1.4. Во многих случаях может быть математическая связь между x и t, обозначенная символом x = x (t), и мы можем затем найти выражение для скорости путем дифференцирования x по к т.
Если скорость менялась со временем, как в нашем примере, то мы также можем измерить мгновенную скорость изменения скорости или ускорения,
(единицы СИ мс -2 ) (2.1.4).
Рисунок 2.1.4. В график скорость – время.
Опять же, это векторная величина, и, как мы увидим, она играет первичную кинематическая роль в описании динамики частиц Ньютоном. Если, как в случае в нашем примере скорость линейно пропорциональна времени, тогда ускорение постоянное, рисунок 2.1.5.
Рисунок 2.1.5. В график ускорения от времени. Ускорение постоянное, 2 мс -2 в этом примере.
2.1.3 Линейное движение при постоянном ускорении
Частица при постоянном ускорении, показанная выше, является простой, но полезный случай кинематики частиц с аналитическим выражением.
Если a константа, то по определению также dv / dt и v = v (t) будет прямая линия. Общий прямолинейный граф имеет простую форму y = mx + c. В в этом случае y – скорость, x – время, а градиент m равен a, в то время как постоянная c равна v0, скорость при t = 0. Следовательно,
(2.1.5).
Мы можем получить это более формально путем интеграции. По определению, после малый интервал времени dt будет дано сопутствующее изменение скорости dv пользователем dv = a dt.Если мы хотим узнать полное изменение скорости от t = 0 до t = t, мы должны сложить каждое небольшое изменение скорости между 0 и t (и, следовательно, между v = v0 и v = v). Формально это выражается следующим образом:
(2.1.6)
, а для постоянного ускорения результат этого простого интеграла равен
по
(2.1.7)
, что идентично (2.1.5). Однако следует отметить, что интегральное выражение чрезвычайно мощный, поскольку он может решить наше уравнение движения, даже когда не постоянный.Эта ситуация является общим правилом для атомных и молекулярных систем. взаимодействия.
Теперь перепишем выражение для скорости, заменив v на dx / dt
(2.1.8).
Мы можем найти x как функцию времени, решив интеграл
(2.1.9)
, где x = x0 при t = 0. Решение интеграла дает нам
(2.1.10).
Уравнения (2.1.7) и (2.1.10) выражают зависимость скорости от времени и положение. Зависимость скорости от положения также можно найти по формуле подставив t в уравнение (2.1.10) с помощью (2.1.7). Это дает
(2.1.11).
2.1.4 Трехмерное движение
До сих пор мы ограничивались движением в одном измерении. Мы будем сейчас расширите наше описание до трех измерений пространства. Делая это, вы должен понимать, что все, что мы сделали до сих пор, на самом деле выражен таким образом, что его использование в трех измерениях не потребует изменений к форме основных уравнений, нам просто нужно знать, как выразить положение, скорость и ускорение как трехмерные векторы.
Вектор положения r , определяющий положение частицы, может можно рассматривать как стрелку, указывающую от начала координат к частице
Рисунок 2.1.6. Вектор положения.
Чтобы добраться от начала координат до частицы, мы должны пройти x шагов по x оси y шагает в направлении y, а z – в направлении z. Мы можем выразить это в компактном виде как
(2.1.12)
где – векторы длина 1, называемая единичными векторами, направлена по осям x, y и z соответственно а x, y и z – это просто множители, которые говорят нам, как далеко нужно продвинуться. каждая ось (величина) и в каком направлении (знак).В одном размерный случай, описанный в [[section]] 2.1.2 и 2.1.3, мы эффективно полагаем y = г = 0,
Если мы теперь хотим определить скорость частицы, мы должны измерить положение частицы в момент времени t, r (t) и малое время Δt позже, r (t + Δt). Вектор Δ r = r (t + Δt) – r (t), следовательно, движение, совершаемое частицей в Δt.
В пределе, когда Δt становится бесконечно малым, можно определить мгновенная скорость v = d r / dt
(2.1.13).
Рисунок 2.1.7. Вектор смещения.
Раскладывая вектор на составляющие, получаем
(2.1.14)
, что приводит к простому выражению
(2.1.15).
Не вдаваясь в подробности, понятно, что мы получим именно ту такое же выражение для ускорения.
(2.1.16)
Самый важный аспект этих выражений для скорости и ускорения состоит в том, что вектор состоит из трех взаимно независимых компонентов. Этот означает, что если сила приложена к атому или молекуле вдоль оси z, только скорость в этом направлении будет изменена. Поскольку никакая сила не действует вдоль другие направления. Законы движения Ньютона говорят нам, что эти компоненты скорость останется неизменной.
Это дает понять, что выбор ориентации системы координат поскольку данная проблема может сделать ее решение намного проще, чем это могло бы быть в противном случае быть.Во многих атомных и молекулярных системах естественная система координат не работает. Декартова как здесь, но сферическая или цилиндрическая. Тем не менее такой система координат и связанное с ней векторное описание всегда будут состоять трех взаимно независимых компонентов (радиальное расстояние и два угла для сферические координаты).
2.2 Сила и импульс
2.2.1 Законы Ньютона
Ньютон выдвинул гипотезу о существовании трех основных законов движения.
Закон 1
“Частица, на которую не действуют другие тела, движется с равномерным скорость. “
Это утверждение крайне противоречит интуиции. Наш общий опыт что мы должны толкать или тянуть вещи, чтобы заставить их двигаться, но когда мы прекращаем прилагая такие силы, он перестает двигаться. Ньютон предположил, что каждый день опыт показал, что на частицу действуют дополнительные силы, замедли это. Это конечно силы трения!
Закон 2
«Приложение силы к телу вызывает ускорение в обратно пропорциональна его массе.«
Это означает, что если мы приложим силу к объекту, мы заставим его скорость изменить. Согласно первому закону мы можем только изменить скорость при приложении силы. Как только мы перестанем применять силу, объект продолжит его путь с постоянной скоростью. Второй закон далее гласит, что если мы применим приложив силу к объекту, мы заставим его ускоряться тем меньше, чем больше его масса. Другими словами, чем массивнее объект, тем труднее его достать. изменить скорость.Имея в виду эту картину, массу часто называют инертная масса. Это также подчеркивает разницу между массой объект, который относится к количеству материи, из которой он состоит, и его вес, который относится к гравитационной силе, действующей на объект. В химии гравитационная сила не играет существенной роли в молекулярных и поведение атома, поэтому нас всегда будет интересовать инертная масса, а не вес.
Ясно, что сила – это векторная величина.Толкать объект в позитиве Направление x имеет кинематический результат, отличный от того, что он толкает его в отрицательном направлении z. направление. Это приводит нас к следующей компактной математической форме
F = m a (единицы СИ Ньютон (Н) = кгмс -2 ) (2.2.1)
Второй закон кажется очень простым, на самом деле именно эта простота что дает ему универсальную применимость. Это, конечно, означает, что он находится в факт чрезвычайно глубокое выражение!
Закон 3
«На каждое действие есть равная и противоположная реакция.«
Это довольно непонятное утверждение означает, что если тело A воздействует на тело B с сила F AB, затем B действует на A с силой F BA = – F AB. Опять же, это очень нелогично. Мы привыкли что-то толкать и наблюдая, как он удаляется от нас, в то время как на самом деле оба объекта отталкиваются друг друга и, следовательно, расходятся. Мы остаемся неподвижными относительно земли как мы толкаем стул только из-за трения между нами и полом.
2.2.2 Электростатическая сила
Использование силы – это повседневный опыт, о котором мы редко задумываемся. Мы толкать или тянуть объект, и мы можем заставить его ускоряться в соответствии со вторым законом Ньютона. предсказывает. Мы чувствуем прямой контакт между нами и ускоряемым объектом, но полезна ли эта картина в молекулярном масштабе? Ответ: строго говоря, нет.
Как мы уже видели, атомы и их родственники по большей части пусты. пространство.Силы такого масштаба действуют не путем прямого контакта, а посредством некоторых, скорее, загадочное действие на расстоянии. Фактически, когда вы толкаете объект, контакт вы чувствуете, действуют ли эти силы в областях пустого пространства между молекулы на поверхности вашей руки и молекулы на поверхности объект.
Преобладающим источником сил, действующих между атомами и молекулами, являются электростатический. В 1785 году Шарль Огюстен де Кулон провел экспериментальную определение силы между двумя заряженными частицами.Он обнаружил, что сила была пропорциональна произведению заряда и была привлекательной, если частицы имели противоположный знак и были отталкивающими, если имели один и тот же знак, и что сила уменьшалась по величине пропорционально обратному квадрату их разделение. Кроме того, сила, действующая между заряженными частицами всегда был направлен по прямой, соединяющей две частицы.
Таким образом, электростатическая сила между двумя ионами равна
.(2.2.2)
, где F 12 – сила, прилагаемая частицей 1 к частице 2, q1 – заряд частицы 1, а q2 – заряд частицы 2, r – расстояние разделяющие частицы, а 12 – единичный радиальный вектор, указывающий от 1 до 2. Константа пропорциональности также является универсальной константой, ε0 – диэлектрическая проницаемость вакуума. Множитель 1 / 4πε0 равен до 8,99×10 9 Нм 2 C -2 . Кулон (C) – это СИ единица заряда и электрон имеет заряд -1.6×10 -19 C. заряд на протоне, заряженном компоненте ядра, имеет такой же величина, но положительная.
Если q1 и q2 имеют одинаковый знак, их произведение всегда будет положительным. С 12 баллов от 1 до 2 сила и отталкивающая, и действующая вдоль линии, соединяющей ионы, как того требуют кулоновские наблюдения, изобразите 2.2.1.
Мы выразили закон Кулона с помощью сферической системы координат и следовательно, радиальный единичный вектор, потому что это наиболее компактная форма, которую мы можем записать.Однако можно записать закон Кулона, используя декартову координату система. Если частица 1 находится в позиции r 1, а частица 2 находится в позиции позиция r 2, тогда вектор, указывающий от 1 до 2, будет r 12 = r 2 – r 1. Квадрат ионного разделения равен затем r 12. r 12 (векторное скалярное произведение) и единица измерения вектор, указывающий от 1 до 2, равен r 12 / [[радикал]] ( r 12. r 12). Следовательно,
(2.2.3).
Рисунок 2.2.1. Кулоновское взаимодействие.
2.2.3 Столкновение двух ионов
Теперь мы, по-видимому, в состоянии предсказать динамическое поведение между взаимодействующими заряженными частицами. В качестве примера того, что мы можем сделать, давайте посмотрите, что произойдет при очень простом столкновении двух ионов. В столкновение, которое мы рассмотрим, – это такое столкновение, при котором два ионизированных атома водорода приближаются друг к другу лицом к лицу.Мы настраиваем нашу ось x так, чтобы она лежала в одном и том же направление как траектория полета протонов.
Рисунок 2.2.2. Встречающиеся протоны.
Протоны имеют одинаковую скорость v0 при t = 0, но в противоположных направлениях, и в это время разделены расстоянием 2×0. Поскольку обе частицы имеют одинаковая масса m и заряд e, ясно, что они будут вести себя как зеркальные отражения друг друга, поэтому мы просто исследуем динамику протона на справа.
Мы определим поведение x (t) и v (t). Для этого мы будем должны решить закон Ньютона для этой системы. В этом случае настройка начального уравнение довольно тривиально, сила, заданная законом Кулона, равна масса протона, умноженная на ускорение протона, и находится в положительном значении x направление.
(2.2.4)
На этом мы застряли! Это дифференциальное уравнение второго порядка который не имеет аналитического решения.Однако мы можем решить уравнение, используя численный метод и результаты представлены ниже.
Рисунок 2.2.3. x (t) для сталкивающегося протона, используя m = 1,7 x 10 -27 кг, x0 = 0,5 м и v0 = -20 мс -1 (код см. «Физическая химия: молекулярные взаимодействия: сталкивающиеся ионы»).
Рисунок 2.2.4. v (t) для сталкивающегося протона с использованием тех же значений, что и выше.
Первое, на что следует обратить внимание, это то, что простое динамическое уравнение (2.2.4) рождает довольно сложную кинематику; это не случай постоянного ускорение. На самом деле ионы никогда не соприкасаются; кулон отталкивание чрезвычайно сильное.
Это все хорошо, но мы всегда должны делать эти сложные вычисления если мы хотим изучить эффекты молекулярных столкновений? К счастью, ответ – нет, если мы не слишком озабочены деталями того, что происходит когда молекулы находятся близко друг к другу и сильно взаимодействуют.Мы можем увидеть это, если мы посмотрим на предыдущий эксперимент со столкновениями, но за более длительный период Весы.
В этих масштабах мы можем наблюдать простое поведение. Величина скорость (20 мс -1 ) до и после столкновения одинакова и положение как функция времени является функцией прямой линии по обе стороны от столкновение. Теперь мы посмотрим, как мы можем формализовать эти экспериментальные наблюдения.
Рисунок 2.2.5. x (t) в более длительных временных масштабах.
Рисунок 2.2.6. v (t) в более длительных временных масштабах.
2.2.4 Сохранение линейного импульса при столкновениях
Во время столкновения на частицу 2 действует сила частицы 1. Эта сила должен меняться со временем, поэтому мы будем называть его F 12 (t) (вы можете определить его форму при столкновении ионов в [[раздел]] 2.2.3). Согласно второму закону движения эта сила вызовет ускорение пропорционально массе m1
(2.2.5).
Если мы проинтегрируем эту силу по времени взаимодействия t, мы получить
(2.2.6)
, где u 1 – скорость первой частицы при t = 0, а v 1 – его скорость при t = t. Конечно, частица 2 оказывает равное и противоположное сила на частицу 1 дает нам второе соотношение
(2.2.7)
, но поскольку F 12 = – F 21, получаем
(2.2,8)
и, следовательно,
(2.2.9)
, который перестроен, чтобы дать нам
(2.2.10).
Произведение массы частицы на скорость называется линейным импульсом, и сохраняется полный импульс системы частиц. до и после столкновения. Возвращаясь к нашему ионному столкновению, тот факт, что начальная и конечная скорости были равны, а противоположное предсказано правильно. Он смог сделать это предсказание, вообще ничего не зная. о взаимодействии между ионами.Интересно и важно отметить что сохранение импульса сохраняется даже при взаимодействии квантовая механика. На самом деле никогда не было обнаружено, что закон противоречит любой эксперимент.
Мы можем обобщить закон сохранения количества движения, отметив, что масса могут быть обменены во время столкновений, то есть химической реакции. Поэтому мы даем импульса обозначьте символом p и примите это, чтобы обозначить, что обе массы и скорость могла измениться во время столкновения.Уравнение (2.2.10), тогда становится
(2.2.11)
, где верхний индекс i означает начальное состояние, а f означает конечное состояние.
Мы можем расширить закон сохранения, включив в него более двух тел. довольно просто
(2.2.12).
Обратите внимание, что суммирование по обе стороны от равенства не обязательно распространяются на то же количество частиц. При этом учитывается возможность того, что новые виды были уничтожены или созданы во время столкновение.Более того, вы обнаружите, что в квантовомеханическом мире даже безмассовые частицы, такие как фотон (корпускула света), имеют импульс, и это должны быть включены для выполнения равенства.
Мы можем перефразировать это словами.
«Полный импульс системы сталкивающихся частиц остается не изменилось при столкновении. Полный импульс сохраняется “.
Удивительно, но Ньютон не обсуждал концепцию импульса в «Началах». Импульс и его использование для понимания столкновений стало результатом встречи. состоялась в 1668 году (через год после публикации «Принципов») в Королевском обществе в г. который Джон Уоллис (математик), Кристофер Рен и Кристиан Гюйгенс представил доклады по явлениям столкновения.Эта работа привела к переформулировке Второй закон Ньютона в более общем виде
(2.2.13).
2.3 Электростатика
Мы уже рассмотрели силу между двумя точечными зарядами в нашем обсуждение теории столкновений. Теперь перейдем к более общему обсуждению теория электростатики.
2.3.1 Принцип суперпозиции и электростатический диполь
Если мы хотим определить чистую силу, оказываемую совокупностью заряженных частицы друг на друга, которые мы будем называть пробной частицами, мы делаем это просто путем определения векторной суммы электростатических сил.Важный пример эта идея в химии – это сила, действующая электростатическим диполем на заряженная частица. (В химии изобилуют диполярные молекулы, например, HCl или NaCl в газовая фаза.)
Рисунок 2.3.1. Принцип суперпозиции с использованием диполя в качестве пример. Диполь состоит из зарядов + Q и -Q.
Рисунок 2.3.1 наглядно иллюстрирует принцип наложения. А довольно простой пример того, как на самом деле рассчитывается чистая сила: определить силу, действующую на положительный заряд, помещенный вдоль оси диполя, как показано ниже.
Рисунок 2.3.2. Диполярная сила, действующая вдоль оси молекулы.
Мы установим начало оси x в середине диполя. Тест Таким образом, charge + q находится в позиции -r . Измерение другого расстояния аналогично, результирующая сила, действующая на заряд + q, равна
(2.3.1).
Используя 2 l = 1,5 и q = Q = 1,6 x 10 -19 C, мы можем построить график сила, прилагаемая диполем к + q вдоль оси диполя, рисунок 2.3.3. В большинстве физические ситуации r намного больше, чем l , и тогда можно упростить (2.3.1), используя биномиальную теорему для разложения знаменателей, а затем отбрасывая все термины выше первого порядка в l / r.
(2.3.2)
Точки данных, рассчитанные с использованием (2.3.2), были нанесены кружками поверх сила, рассчитанная по (2.3.1), изображена сплошной линией. Вертикальные линии около r = 0 из-за проблем с вычислением силы, близкой к диполю. обвинения.
Условно мы определяем вектор дипольного момента. Вектор направлен от отрицательного к отрицательному. положительный заряд и имеет величину, определяемую произведением заряда диполя и расстояние между зарядами. Отсюда осевая сила на больших расстояниях от диполь задается
(2.3.3).
Итак, здесь мы имеем межмолекулярное взаимодействие, которое, по крайней мере, оси молекулы и на больших расстояниях имеет скорее зависимость 1 / r 3 чем 1 / r 2 .Это сокращает радиус действия диполей и в целом слабее, чем из-за одиночных ионов.
Рисунок 2.3.3. Осевая сила из-за электростатического диполя.
2.3.2 Электростатическое поле
Вы могли заметить, что заряд + q нашей “тестовой” частицы исключено из определения силы на нем. Это генерал явления при проведении расчетов с использованием суперпозиции и предполагает, что один может определить новую векторную величину, электростатическое поле E , определенное по
(единицы СИ NC -1 ) (2.3.4)
Другими словами, электрическое поле в позиции r представляет силу, которая единичный положительный заряд будет испытывать в этом положении. Это конечно чрезвычайно удобно, так как мы в принципе можем определять поле по любому сбор заряженных частиц, что в дальнейшем позволит нам определить силы, которые испытывала бы частица, движущаяся в этом поле. Это Однако следует понимать, что это предполагает, что частица, движущаяся в поле практически не влияет на положение зарядов, создающих поле.В некоторых ситуациях это хорошее приближение к истине, поскольку Например, электроны проводимости в твердом теле не сильно нарушают решетку, в других случаях это серьезное искажение, например, при сольватации ионов.
Для примера диполя и силы, которую он проявляет на относительно больших расстояниях. вдоль оси молекулы можно разумно вычислить поле
(2.3.5)
2.3.3 Представление поля – линии поля
Визуальное представление полей очень информативно.Они разрешают один, чтобы создать качественную картину как величины, так и направления силы, которую может испытать другая заряженная частица в присутствии поле. Сначала смотрим на поле от точечного положительного заряда. В все векторы электростатического поля должны быть направлены от положительного заряда, поскольку поле определено для положительного тестового заряда. Если мы нарисуем поле векторы хвоста к голове, происходящие от точечного заряда, мы также знаем, что они следовать по прямой и уменьшать величину обратно пропорционально величине квадрат расстояния.Если мы посмотрим на такое представление поля на плоскости который делит положительный заряд пополам, он должен выглядеть примерно так, как показано на рисунке 2.3.4.
Рисунок 2.3.4. Линии поля вокруг точечного положительного заряда. Первый стиль.
Это предлагает более простое и стандартное представление, где конец векторы конечного поля изображены в виде непрерывных линий поля. Плотность поля линии затем представляют величину поля.
Рисунок 2.3.5. Линии поля вокруг точечного положительного заряда. Второй стиль.
Правила рисования линий поля для произвольного набора начисленных участников можно резюмировать следующим образом.
* Линии начинаются при положительном заряде и заканчиваются отрицательным зарядом и
должен быть непрерывным и гладким.
* Линии не пересекаются. Поле однозначно во всех точках пространства.
* Плотность линий пропорциональна напряженности поля.
* Вблизи любого точечного заряда поле всегда радиально.
Таким образом, мы можем набросать внешний вид поля вокруг диполя в самолет проходит через каждую зарядку, используя эти правила.
Рисунок 2.3.6. Эскиз дипольного поля.
Трехмерные представления векторного поля могут быть созданы на Mathematica (код см. В разделе «Физическая химия: молекулярные взаимодействия: E Поля »).
2.3.4 Силы Ван-дер-Ваальса
Силы Ван-дер-Ваальса даже слабее, чем силы, действующие на диполи. ионы.Они присутствуют во всех атомных и молекулярных взаимодействиях, но поскольку они слабы, они часто замаскированы другими силами, которые также играют роль. Однако они играют важную роль во многих химически интересных системах, так как пример в стабилизации двухслойных мембранных пакетов и связывания анестетики. Силы Ван-дер-Ваальса фактически охватывают три различных типа взаимных атомные и межмолекулярные взаимодействия: дисперсионные силы, диполь-дипольные силы и дипольные дипольные силы.Мы разберемся с первым из них, оставив читать о других.
Если мы рассмотрим электрически нейтральный и химически инертный атом, такой как Ксенон, мы могли бы представить, что электронное облако будет полностью утилизировано симметрично относительно положительно заряженного ядра, и поэтому не будет сетевого поля от такого атома. Однако это не так. В распределение электронов колеблется во времени из-за квантово-механических последствия.Другими словами, хотя распределение электронов в среднем сферически симметричный, большую часть времени распределение будет асимметричным или диполярный и создаст соответствующее дипольное поле.
(2.3.6).
Давайте теперь рассмотрим второй атом ксенона на расстоянии r от нашего мгновенный диполь. Влияние поля флуктуационного диполя будет притягивать к себе отрицательно заряженное электронное облако и отталкивать положительно заряженное ядро прочь.По очевидной причине этот второй диполь называется индуцированным диполем и имеет дипольный момент P , который не обязательно должен быть таким же, как у флуктуационного диполя.
Рисунок 2.3.7. Флуктуационный диполь в левой части рисунок индуцирует дипольный момент в молекуле справа.
Поле, действующее на -q ‘: E (r – l ‘), что означает E на расстоянии r – l ‘, аналогично поле, действующее на + q’, равно E (r + л ‘).Таким образом, результирующая сила на индуцированный диполь составляет
(2.3.7)
, где происхождение члена Δ E / Δr показано в рисунок 2.3.8 и для r >> l ‘, Δ E / Δr становится d E / dr.
Помня, что индуцированный диполь, P ‘, указывает на против направления поля от флуктуационного диполя получаем
(2.3.8)
, где я удалил векторные обозначения, чтобы упростить задачу.Делая дифференциация получаем
(2.3.9.
Знак минус означает, что сила направлена противоположно полю, т.е. к флуктуационному диполю.
Рисунок 2.3.8. Приближение наклона.
Последний шаг в вычислении дисперсионной силы Ван-дер-Ваальса состоит в том, чтобы сказать, что пытаясь развести электроны и протоны в атоме, он ведет себя как весна. Это означает, что расширение l ‘и, следовательно, P’ будет пропорционально приложенной силе, т.е.е. пропорционально 1 / r 3 . Подставляя эту зависимость вместо P ‘, находим
(2.3.10).
Такая же зависимость от расстояния обнаружена для диполь-дипольных взаимодействий. и для диполь-индуцированных дипольных взаимодействий.
2.3.5 Другие межатомные и межмолекулярные силы
До сих пор мы могли использовать классическую электростатику и теорию суперпозиция для объяснения ион-ион, диполь-ион, диполь-диполь, диполь – индуцированные дипольные и дисперсионные взаимодействия.Ряд важных, повсеместных остаются взаимодействия, не поддающиеся объяснению в терминах классической физики.
Первым, наиболее известным и наиболее распространенным из них является ковалентная связь. Это промежуточное звено между ионной связью и связкой Ван-дер-Ваальса. В бывшем заряд передается между атомами и в последних нет такого передача. Вместо этого электроны, которые образуют связь, никогда полностью не получают переносятся между атомами, но проводят большую часть своего времени между двумя ядра.Положительно заряженные ядра притягиваются к электронам, которые находятся между ними, но ощущают некоторое чистое отталкивание друг от друга, когда хорошо. Среднее атомное разделение, конечно, устанавливается балансом между этими силы.
Вы могли подумать, что сила ковалентной связи где-то была степенным законом между пропорциональным 1 / r 2 и 1 / r 7 . Фактически частичный перенос заряда можно объяснить только квантово-механически и когда расчеты выполнены, простая степенная зависимость силы никогда не бывает найденный.
Другая распространенная сила сцепления, которую можно объяснить только с точки зрения квантовая механика – это водородная связь, в которую вставляется атом водорода. между двумя атомами или ионами, например HF2.
Наконец, следует упомянуть так называемые стерические силы отталкивания между атомы. Вы должны заметить, что наше описание силы Ван-дер-Ваальса будет предсказывать притяжение между всеми атомами. Но мы знаем, что хотя бы небольшой разделение там очень сильное отталкивание.Мы думаем об этом как о описании стерический размер атома или молекулы. Это сильное стерическое отталкивание возникает потому, что принципа исключения Паули, квантово-механического закона, который гласит, что два электрона не могут находиться в одном и том же квантовом состоянии.
2.3.6 Модели межатомных и межмолекулярных сил
Мы часто хотим предсказать поведение атомных и молекулярных систем, где взаимодействия слишком сложны, чтобы их можно было рассчитать непосредственно на основе фундаментальных принципов.В таких случаях мы прибегаем к эвристическим моделям атомных и молекулярных взаимодействия.
Самая известная из этих моделей принадлежит Леннарду и Джонсу, что почти всегда используется для описания систем с силой притяжения, которая задается взаимодействие Ван-дер-Ваальса. В этом случае чистая сила равна
.(2.3.11)
где r0 – равновесное расстояние (F (r0) = 0), а ε связано с сила взаимодействия. Первый член в скобках – это притягивающий компонент к чистой силе, т.е.е. притяжение Ван-дер-Ваальса и второй – отталкивание жесткого ядра. Вектор r является радиальным единичный вектор, указывающий от молекулы, прилагающей силу к молекуле на рассмотрении.
2.3.7 Электростатический потенциал, энергия и потенциал
Мы начинаем обсуждение потенциальной энергии в электростатических полях с дать общее определение работы. Мы определяем, dW, работу, проделанную при перемещении частица на малом расстоянии ds под действием силы F на
(единицы СИ Джоули (J) = Nm) (2.3.12)
, где угол θ указан на рисунке 2.3.9. Это определение делает интуитивно понятным смысл, так как работа явно пропорциональна силе и расстоянию перемещается, но также, если сила не действует в направлении движения, никакой работы было сделано. Более аккуратный способ выразить это, сохраняя векторную характер силы и смещения, заключается в использовании векторного скалярного произведения
(2.3.13).
Рисунок 2.3.9. Определение работы, выполняемой при перемещении частицы.
Давайте теперь посмотрим на работу, совершаемую при перемещении частицы заряда q в электростатическое поле точечного заряда, Q.
(2.3.14).
Теперь с r – это радиальный вектор, только составляющая движения что тоже
радиальный приведет к любой работе, рисунок 2.3.10. Это означает, что проделанная работа зависит только от радиальных смещений dr в этом электростатическом поле.
(2.3.15).
Чтобы определить общую работу, проделанную для перехода от радиального расстояния r1 к r2, мы просто просуммируйте все приращения dr, i.е. мы интегрируем выражение выше.
(2.3.16).
Рисунок 2.3.10. Следуя по пути, обозначенному жирной линией, только на участке от радиуса r1 до r2 производятся какие-либо работы, так как по На окружности r1 сила и смещение всегда перпендикулярны.
Как и следовало ожидать, этот интеграл зависит только от конечных точек пути мы идем, любой маршрут, который мы выберем, потребует эквивалентного объема работы.Маршрут показанный на рисунке 2.3.10, является только одним из бесконечного множества, которое начинается и заканчивается в показаны точки, и все они требуют равного объема работы. Кроме того, если мы выбираем любой маршрут, который начинается и заканчивается в одной и той же позиции, общая работа сделано – ноль. Это свойство характеризует консервативное поле. показать, что, поскольку силовые линии электростатического поля не пересекаются, все электростатические поля консервативны. Поэтому имеет смысл определить новый скаляр величина, электростатическая потенциальная энергия, U, которая имеет хорошо определенные значения во всех регионах космоса.По условию это минус работы. Для точечный сбор
(2.3.17)
Все измерения потенциальной энергии должны производиться относительно другого (U2 – U1) и мы обычно выбираем нулевую потенциальную энергию на бесконечном разделение, следовательно,
(2.3.18).
По аналогии с полем определим также потенциал V (r) для точки заряд Q
(единицы СИ вольт (V) = JC -1 ) (2.3.19).
Теперь мы можем построить график зависимости потенциала от радиального расстояния, рис. 2.3.11. Здесь мы определили потенциал для Q = -1,6×10 -19 C. Поскольку тестовый заряд, который мы используем при определении V, определен как положительный, мы видим что привлекательное взаимодействие представлено потенциальной «ямой».
Рисунок 2.3.11. Потенциал точечного заряда Q = -1,6х10 -19 кл.
Конечно, потенциал является сферически-симметричной функцией (потенциал имеет такое же значение на поверхности сферы, начало координат которой лежит в позиции точечного заряда Q), поэтому мы построили контурную карту из линий равной потенциал в плоскости, пересекающей точечный заряд, рисунок 2.3.12. Этот контур сюжет следует читать как обычную карту, каждый контур нанесен на равных с шагом в V и чем темнее штриховка, тем отрицательнее значение V.
Рисунок 2.3.12. График эквипотенциальных контуров точечного заряда Q = -1,6×10 -19 C в плоскости y-z, с зарядом в точке x = y = z = 0.
Если мы хотим определить потенциал диполя, все, что нам нужно сделать, это добавить потенциал от положительного и отрицательного заряда, размещенных на расстоянии 2 l друг от друга, все вместе.Если мы воспользуемся декартовыми координатами и поместим положительный заряд + q, при и отрицательный charge, -q, затем потенциал задается
(2.3.20).
Мы построили это как контурный график на рисунке 2.3.13. Трехмерный представление дипольного потенциального ландшафта в плоскости y-z было изображено на рисунке 2.3.14.
Мы можем сделать ряд наблюдений относительно графика эквипотенциального контура. для диполя. Ясно, что линия, разделяющая вектор дипольного импульса пополам, также является линией эквипотенциальности, и что по симметрии это наиболее эквипотенциальная линия, где V = 0.Из нашего определения V получаем следующее взаимосвязь между полем и потенциалом,
(2.3.21)
, что указывает на то, что векторное поле можно восстановить, найдя отрицательный градиент потенциала. Градиент потенциала равен просто самый крутой склон в интересующей точке на потенциальной поверхности. Это дает градиенту V как величину, так и направление, которое имеет курс – E . Направление силовых линий диполя может довольно легко определяется для плоскости, показанной на рисунке 2.3.13, когда это осознали, что самый крутой градиент всегда должен быть перпендикулярен эквипотенциальные контуры (представьте контуры на карте ордонансной съемки).
Рисунок 2.3.13. График эквипотенциального контура для диполя с 2l = 1.4, q = 1.6×10 -19 C, построено в плоскости y-z с x = 0 (для кода см. «Физическая химия: молекулярные взаимодействия: дипольный потенциал»).
Это восстановление поля из потенциальной карты (что обычно довольно легко вычислить) является общим свойством и приводит к следующему вывод.
Потенциал (или потенциальная энергия) также позволяет визуализировать пейзаж. которое напрямую связано с полем (или силой). Положительный заряд (который обычное определение состояний поля – это тестовый заряд), тогда может быть представлял собой шарик, движущийся по потенциальной поверхности. Ясно мрамор попадут в «дыры», созданные отрицательными точечными зарядами, тогда как положительный точечный заряд будет выглядеть как холм и оттолкнет положительный тест заряжать.
Рисунок 2.3.14. Потенциальная поверхность для диполя с 2l = 1,4, q = 1,6×10 -19 C, нанесенный в плоскости y-z с x = 0 (код см. «Физическая химия: молекулярные взаимодействия: дипольный потенциал»).
2.4 Сохранение энергии
Энергия – это то, что нужно платить за работу. Энергия бывает разных валюты и физические процессы представляют собой преобразование одной валюты в Другой.Это не определение, но оно дает представление о том, что мы представить себе энергию быть. Это странно безвкусная концепция, но, как Физик Крамерс сказал
«Самыми важными и плодотворными концепциями являются те, для которых невозможно придать четко определенный смысл “.
Ценность энергии как идеи – это гипотеза о том, что она всегда законсервировано. Он преображается, но никогда не теряется. Это самый важный идея в термодинамике и, вероятно, самый мощный инструмент в количественном науки.Любопытно, что Ньютон никогда об этом не упоминал!
2.4.1 Кинетическая энергия
Из того, что мы уже сделали, подразумевается, что энергия сохраняется в электростатическое поле, так как общая работа, выполненная, если мы выберем путь, начинающийся и окончание в той же точке равно нулю. Если бы энергия рассеивалась, это не так.
Однако мы хотели бы знать, какая энергия продается, если путь, по которому мы взять не петлю. Мы делаем это, определяя «интеграл от движение »в поле.Здесь мы рассматриваем частицу заряда q, движущуюся в поле частицы с зарядом Q вдоль радиального направления между радиальными расстояние r1 и r2.
(2.4.1)
, где 1/2 мв 2 называется кинетической энергией частицы, а v1 – скорость в точке r1, а v2 – скорость в точке r2. Теперь, если не было энергии рассеивается, мы можем приравнять это к разнице в потенциальной энергии между эти точки
(2.4.1)
и обнаруживаем, что сумма кинетической энергии K и потенциальной энергии U должно быть константой.
(2.4.2).
Значит, это означает, что полная энергия частицы постоянна, кинетическая энергия и потенциальная энергия торгуются, и мы можем начать делать прогнозы о динамическом поведении заряженных частиц в полях.
2.4.2 Молекулярная диссоциация
Простейшая реакция, которую мы можем изучить, используя закон сохранения энергии, – это реакция диссоциация двухатомной молекулы. В нашем случае моделируем диссоциацию диполярной двухатомной молекулы NaCl.В NaCl связь почти полностью ионный, поэтому у нас уже есть выражение (2.3.18) для притягивающего член взаимодействия между ионами. Однако у нас нет выражения для стабилизирующее отталкивание. Причина этого в том, что отталкивание в значительной степени из-за квантово-механических эффектов, когда ионы перекрываются. Теория предложила бы экспоненциальная сила отталкивания exp (-kr), где k – постоянная, а r – радиальная расстояние. К сожалению, это выражение математически неудобно и расчеты фактов довольно нечувствительны к термину отталкивания, пока он довольно крутой.Поэтому в традициях физической химии мы моделируем отталкивающее взаимодействие как функция межатомного расстояния r, как V [[пропорционально]] 1 / r 9 (см. [[раздел]] 2.3.5 и 2.3.6). Общая потенциальная энергия тогда имеет вид
(2.4.3)
где A и B – константы. А, конечно, известно, а В – нет. Чтобы найти B определяем равновесное расстояние r0, используя тот факт, что dU / dr = 0 при эта позиция.
(2.4.4).
Следовательно, мы находим B равным
(2.4.5).
Таким образом, мы можем переформулировать (2.4.3) через r0 и электростатические термины
(2.4.6)
и при r0 = 2,5 для молекулы NaCl находим потенциальную энергию как функция расстояния, рисунок 2.4.1.
Рисунок 2.4.1. Функция потенциальной энергии молекулы NaCl.
Энергия, необходимая для разделения ионов Na + и Cl –. – разность потенциальной энергии при бесконечном разделении и при равновесие.Поскольку U на бесконечности по определению равна нулю, энергия диссоциации просто -U (r0) = 8,2 x 10 -19 Дж (5,1 эВ), что находится в пределах четырех процент от экспериментально измеренного значения.
В этом расчете мы предположили, что при бесконечном разделении потенциальная энергия равна нулю, как и кинетическая энергия. То есть мы просто положили достаточно начальной кинетической энергии в системе, чтобы разорвать связь. Поскольку полная энергия сохраняется до и после реакции, и мы не предполагаем никаких других потери или выигрыш энергии, начальная полная энергия также должна быть равна нулю, т.е.е. Ki = -U (r0).
Итак, полная начальная кинетическая энергия составляет 8,2 x 10 -19 Дж, но это разделяется между двумя ионами. Чтобы узнать, в какой пропорции мы используем сохранение импульса. Чтобы разорвать связь, ионы должны разойтись в противоположном направлении. направления (любое движение не в этом направлении не способствует связыванию нарушение). Поскольку мы предполагаем, что молекула находится в состоянии равновесия, начальное импульс равен нулю, а значит, и конечный импульс. Поэтому сохранение импульса дает нам
(2.4.7)
, а сохранение энергии дает нам
(2.4.8).
Подставляя в (2.4.8) из (2.4.7), находим
(2.4.9).
Следовательно, vCl = 2,7 км -1 и vNa = 8,2 км -1 , и это из (2.4.9) видно, что начальные кинетические энергии не равны (KCl = 2,0 x 10 -19 Дж и KNa = 6,2 x 10 -19 Дж).
2.4.3 Могут ли произойти реакции?
Представим себе большой контейнер, содержащий одну диссоциированную молекулу NaCl, я.е. U = 0 и K> = 0. Теперь посмотрим, что произойдет с течением времени. Один может возникнуть соблазн сказать, что ион Na + и Cl – будет в конечном итоге встречаются, когда они подпрыгивают внутри коробки, и когда они это делают, они реагируют с образованием NaCl.
В свете обсуждения в [[section]] 2.4.2 мы видим, что это на самом деле совершенно ошибочны. Полная энергия системы из двух частиц равна больше или равна энергии связи, поэтому невозможно ни при каких условиях реакция должна произойти.Проблема в том, что нам нужно унести лишнее. энергия от двух частиц, когда они реагируют. Для этого нам понадобится третье тело. А Простой пример: если бы у нас была одна молекула KCl и один Na + ion в нашей коробке. Теперь, когда ион сталкивается с молекулой, он может реагировать: потому что избыточная кинетическая энергия может быть передана высвободившемуся K + ион. Даже здесь мы видим, что если мы будем ждать достаточно долго, произойдет еще одно столкновение.
