Определение эдс источника тока: Электродвижущая сила – Умскул Учебник

Измерение ЭДС и внутреннего сопротивления источника тока | Учебно-методический материал по физике (10 класс) по теме:

Урок физики в 11 классе

Урок: виртуальная лабораторная работа

А. Г. Некрасов

Тема: Измерение ЭДС и внутреннего сопротивления источника тока

Статья отнесена к разделу: Преподавание физики.

---

Цели урока: На основе виртуального эксперимента по измерениям тока и напряжения определить ЭДС и внутреннее сопротивление источника.

Задачи урока:

Образовательная: На виртуальном опыте показать использование закона Ома для полной цепи.

Развивающая: Развивать внимание, умение творчески и логически анализировать экспериментальные данные, собирать электрические цепи на моделях, измерять электрические величины. Повышать интерес к физике путем выполнения лабораторной работы расчета требуемых величин.

Воспитательная: Развивать самостоятельность, аккуратность и внимание при проведении компьютерного эксперимента, чувство ответственности за полученные результаты. Воспитание мировоззренческих понятий: познаваемость окружающего мира, явлений.

Форма урока:  виртуальная исследовательская лабораторная работа.

Программный продукт «Начала электроники» (“Beginnings of ELECTRONICS”) , который используется в данной виртуальной лабораторной работе, можно скачать в Интернете. Статус программы – бесплатный. Данный программный продукт предназначен в помощь преподавателям и учащимся школ для изучения раздела физики «Электрический ток». Он удачно дополняет классическую схему обучения, состоящую из усвоения теоретического материала и выработки практических навыков экспериментирования в физической лаборатории. Наглядность продукта предоставляет учителю возможность проведения урока более интересно и насыщенно. При использовании этого продукта формы урока могут быть различными: лабораторный практикум, демонстрация, возможность работать ученику в домашних условиях. Данный продукт нагляден, что важно, т.к. 90% информации поступает в мозг через зрительный нерв. И, наконец, занятие может носить игровую форму, уходя от «обязаловки». Ученику будет интересно и весело разглядывать изучаемые физические явления, что не только упростит, но и ускорит процесс обучения.

Оборудование: Источник постоянного напряжения 1 В, мультиметр в режиме вольтметра, мультиметр в режиме амперметра, ключ, соединительные провода, переменное сопротивление (реостат).

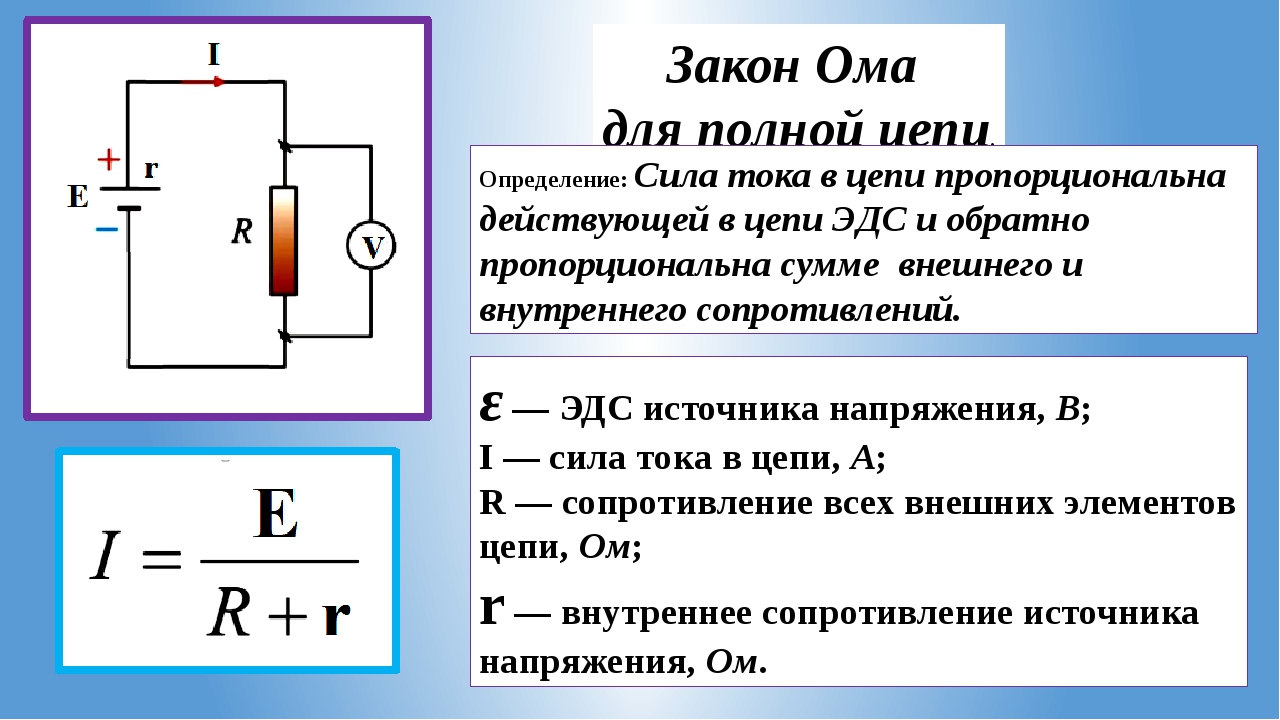
Для определения ЭДС источника питания и его внутреннего сопротивления применим закон Ома для замкнутой цепи:

I = E / (R + r),                     (1)

Отсюда

Е = I (R + r).                        (2)

Здесь Е – ЭДС источника, I – сила тока, R – сопротивление внешней цепи (в нашем случае реостата), r – внутреннее сопротивление источника. Так как ЭДС источника постоянная, то, как следует из (2), для двух измеренных значений тока при двух заданных произвольных R1 и R2 получим:

E=I1 (R1 + r),

E=I2 (R2 + r).

Приравнивая правые части, получим

I1 (R1 + r) = I2 (R2 + r).

Учитывая, что U1=I1 R1 и U2=I2 R2 для определения внутреннего сопротивления получим выражение:

r = (U2 – U1) / (I1 – I2).                   (3)

Где I1 и I2 – измеренные на опыте силы тока, U1 и U2 соответствующие напряжения при двух значениях сопротивлений реостата R1 и R2. Зная r по формуле (1) найдем ЭДС Е.

Схема цепи представлена на рис.3.

На монтажном столе цепь может выглядеть так: Рис.4

Замкнуть ключ, снять показания тока и напряжения. Это первое измерение. Затем передвинуть движок реостата, снять вторые показания. Измеренные данные занести в таблицу. По формулам (3) и (1) рассчитать ЭДС и внутреннее сопротивление.

I1, A	U1, B	I2, A	U2, B

ЛИТЕРАТУРА

1. Перышкин А. А. Физика. 8 кл.: учебн. для общеобразоват. учреждений. – 13-е изд., стер. – М.: Дрофа. 2010. – 192 с.

2. Касьянов В. А. Физика. 11 кл.: учебн. для общеобразоват. учреждений. – 3-е изд., дораб. – М.: Дрофа, 2003. – 416 с.

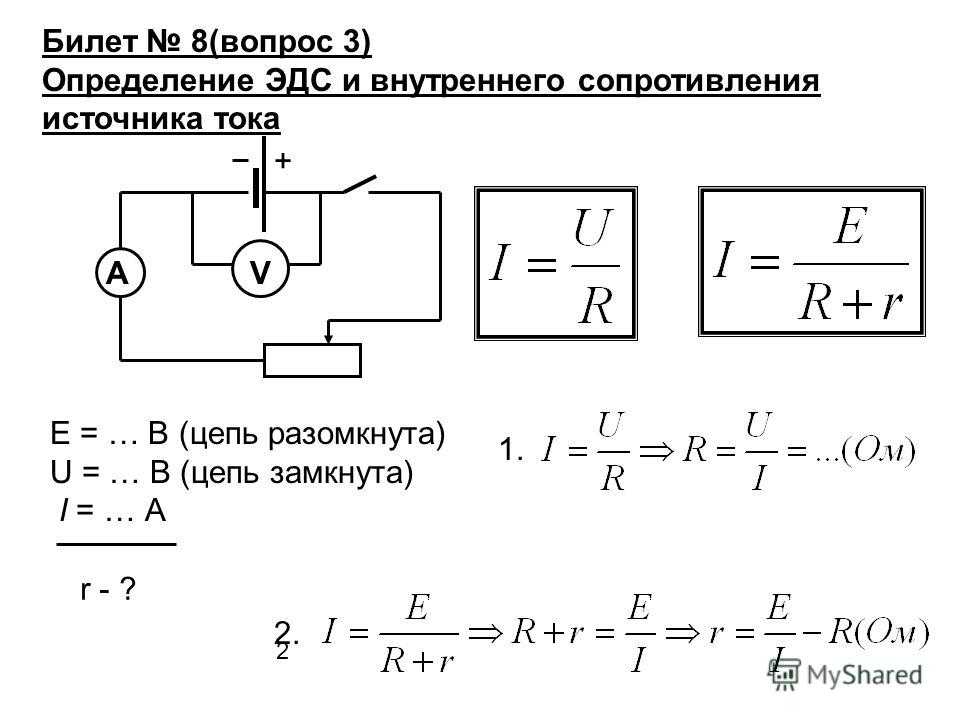
Измерение эдс и внутреннего сопротивления источника тока

Цель работы: изучить метод измерения ЭДС и внутреннего сопротивления источника тока с помощью амперметра и вольтметра.

Оборудование: металлический планшет, источник тока, амперметр, вольтметр, резистор, ключ, зажимы, соединительные провода.

Для измерения ЭДС и внутреннего сопротивления источника тока собирают электрическую цепь, схема которой показана на рисунке 1.

К источнику тока подключают амперметр, сопротивление и ключ, соединенные последовательно. Кроме того, непосредствен­но к выходным гнездам источника подключают еще и вольтметр.

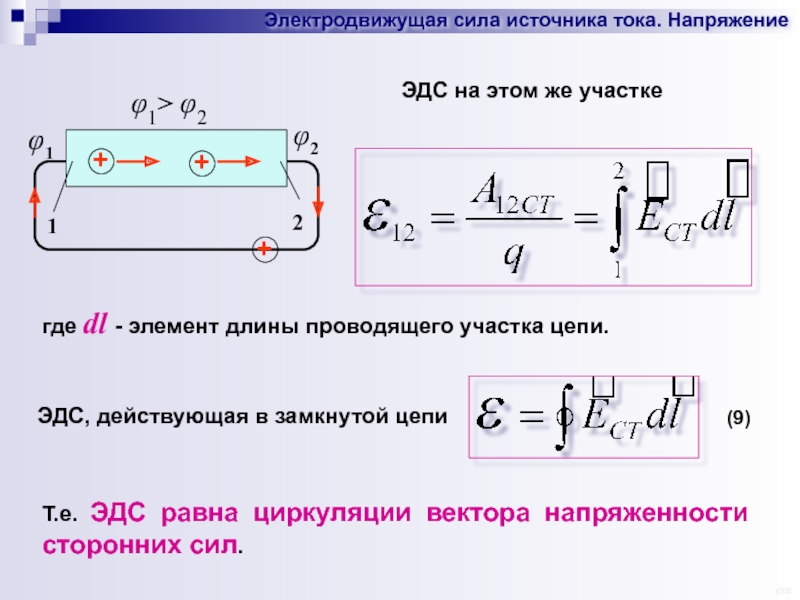
ЭДС измеряют по показанию вольтметра при разомкнутом ключе. Этот прием определения ЭДС основан на следствии из за­кона Ома для полной цепи, согласно которому при бесконечно большом сопротивлении внешней цепи напряжение на зажимах источника равно его ЭДС.

(См. параграф “Закон Ома для полной цепи” учебника “Физика 10”).

Для определения внутреннего сопротивления источника за­мыкают ключ К. При этом в цепи можно условно выделить два участка: внешний (тот, который подключен к источнику) и внутренний (тот, который находится внутри источника тока). Поскольку ЭДС источника равна сумме падения напряжений на внутрен­нем и внешнем участках цепи:

ε= U_r+U_R, то U_r = ε -U_R (1)

По закону Ома для участка цепи U_r = I

·r (2). Подставив равенство (2) в (1) получают:

I·r = ε – U_r , откуда r = (ε –U_R)/J

Следовательно, чтобы узнать внутреннее сопротивление источника тока, необходимо пред­варительно определить его ЭДС, затем замкнуть ключ и измерить падение напряжения на внеш­нем сопротивлении, а также силу тока в нем.

Ход работы

1. Подготовьте таблицу для записи результатов измерений и вычислений:

ε ,в	Ur,B	i,a	r, Ом

2. Начертите в тетради схему для измерения ЭДС и внутреннего сопротивления источника.

2. После проверки схемы соберите электрическую цепь. Ключ разомкните.

3. Измерьте величину ЭДС источника.

4. Замкните ключ и определите показания амперметра и вольтметра.

5. Вычислите внутреннее сопротивление источника.

2. Определение эдс и внутреннего сопротивления источника тока графическим методом

Цель работы: изучить измерения ЭДС, внутреннего сопротивления и тока короткого замы­кания источника тока, основанный на анализе графика зависимости напряже­ния на выходе источника от силы тока в цепи.

Оборудование: гальванический элемент, амперметр, вольтметр, резистор R

₁ , переменный резистор, ключ, зажимы, металлический планшет, соединительные провода.

Из закона Ома для полной цепи следует, что напряжение на выходе источника тока зависит прямо пропорционально от силы тока в цепи:

так как I =E/(R+r), то IR + Ir = Е, но IR = U, откуда U + Ir = Е или U = Е – Ir (1).

Если построить график зависимости U от I, то по его точкам пересечения с осями координат можно определить Е, I _К.З. – силу тока короткого замыкания (ток, который потечет в цепи источни­ка, когда внешнее сопротивление R станет равным нулю).

ЭДС определяют по точке пересечения графика с осью напряжений. Эта точка графика со­ответствует состоянию цепи, при котором ток в ней отсутствует и, следовательно, U = Е.

Силу тока короткого замыкания определяют по точке пересечения графика с осью токов. В этом случае внешнее сопротивление R = 0 и, следовательно, напряжение на выходе источника U = 0.

Внутреннее сопротивление источника находят по тангенсу угла наклона графика относи­тельно оси токов. (Сравните формулу (1) с математической функцией вида У = АХ +В и вспомни­те смысл коэффициента при X).

Ход работы

1. Исходя из перечня оборудования, рекомендованного для выполнения работы, составьте схему установки для исследования зависимости напряжения на выходе источника тока от силы тока в цепи.

2. Для записи результатов измерений подготовьте таблицу:

3. U, (В)
   I, (А)

   После проверки схемы преподавателем соберите электрическую цепь. Ползунок переменного резистора установите в положение, при котором сопротивление цепи, подключенной к источ­нику тока, будет максимальным.

4. Определите значение силы тока в цепи и напряжение на зажимах источника при максимальной величине сопротивления переменного резистора. Данные измерений занесите в таблицу.

5. Повторите несколько раз измерения силы тока и напряжения, уменьшая всякий раз величину переменного сопротивления так, чтобы напряжение на зажимах источника уменьшалось на 0,1В. Измерения прекратите, когда сила тока в цепи достигнет значения в 1А.

6. Нанесите полученные в эксперименте точки на график. Напряжение откладывайте по верти­кальной оси, а силу тока – по горизонтальной. Проведите по точкам прямую линию.

7. Продолжите график до пересечения с осями координат и определите величины Е и , I _К.З.

8. Измерьте ЭДС источника, подключив вольтметр к его выводам при разомкнутой внешней це­пи. Сопоставьте значения ЭДС, полученные двумя способами, и укажите причину возможного расхождения результатов.

9. Определите внутреннее сопротивление источника тока. Для этого вычислите тангенс угла на­клона построенного графика к оси токов. Так как тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то практически это можно сделать, найдя отношение Е / I _К.З

Определение внутреннего сопротивления (4.4.3) | OCR AS Physics Revision Notes 2018

Определение внутреннего сопротивления

Цели эксперимента

Общая цель эксперимента — исследовать взаимосвязь между ЭДС и внутренним сопротивлением путем измерения изменения тока и напряжения с помощью переменного резистора

Переменные

• Независимая переменная = сопротивление, Ом (Ом)
• Зависимая переменная = напряжение, В (В) и ток, I (А)
• Переменные управления:
  • ЭДС ячейки
  • Внутреннее сопротивление ячейки

Перечень оборудования

• Разрешение измерительного оборудования:
  • Вольтметр = 1 мВ
  • Амперметр = 0,1 мА

Метод

1. Ячейка и резистор с маркировкой r должны быть соединены последовательно и считаются одной ячейкой
2. При разомкнутом выключателе запишите показание В на вольтметре
3. Установите переменный резистор на максимальное значение, замкните переключатель и запишите В и показание I на амперметре – обязательно разомкните переключаться между показаниями
4. Варьировать сопротивление переменного резистора до минимум 8-10 показаний и записывать значения для В и I для каждого сопротивления. Обеспечить снятие показаний для всего диапазона переменного резистора

• Пример подходящей таблицы может выглядеть следующим образом:

Анализ результатов а внутреннее сопротивление определяется как

ε = I ( R + r )

• Где:
  • ε = электродвижущая сила (В)
  • I = ток (A)
  • R = сопротивление нагрузки в цепи (Ом)
  • r = внутреннее сопротивление элемента (Ом) ε = IR + Ir = В + Ir
    • Преобразование этого уравнения для В :

    В = – rI + ε

    • Сравнивая это с уравнением прямой линии: y = mx + c
      • y = В (В)
      • x = I (A)
      • Градиент = – r (Ом)
      • Y-отрезок = ε 90 015 (В)

     

    1. Постройте график зависимости V от I и нарисуйте линию наилучшего соответствия
    2. Измерьте градиент графика и сравните его со значением резистора, установленным производителем
    3. Точка пересечения с осью Y будет ЭДС, а градиент будет отрицательным внутреннее сопротивление:
    Ом0071

    Оценка эксперимента

    Систематические ошибки:

    • Замкните переключатель только на время, необходимое для снятия каждой пары показаний
      • Это предотвратит изменение внутреннего сопротивления батареи или элемента во время эксперимента

    Случайные ошибки:

    • Используйте только достаточно новые ячейки, иначе Э. Д.С. внутреннее сопротивление разряженных аккумуляторов может меняться в ходе эксперимента
    • Подождите, пока показания вольтметра и амперметра стабилизируются (перестанут колебаться), прежде чем записывать значения
    • Сделайте несколько повторных измерений (не менее 3) для каждого напряжения и тока и рассчитайте среднее значение для уменьшения случайных ошибок

    Соображения безопасности

    • длительный период
    • Немедленно отключите питание при появлении запаха гари
    • Убедитесь, что рядом с оборудованием нет жидкостей, так как это может привести к повреждению электрооборудования

    Пример работы

    В эксперименте учащийся использует переменный резистор в качестве внешней нагрузки. Ток, протекающий через цепь, измеряется подходящим миллиамперметром, а разность потенциалов на переменном резисторе измеряется вольтметром для диапазона значений сопротивления. Собранные данные были следующими: Постройте график этих результатов и определите ЭДС. и внутреннее сопротивление прямо из графика.

    Шаг 1: Нанесите данные на график В против I и нарисуйте линию наилучшего соответствия

    Шаг 2: Нарисуйте максимально возможный треугольник для расчета градиента

          Шаг 3: Определите e. .ф. и внутреннее сопротивление из графика

    В = – rI + E

    • Из этого уравнения:
      • Градиент = – r (Ом)
      • Y-точка = E ( В)
    • Следовательно:
      • Внутреннее сопротивление, r = 22,7 Ом
      • Э.д.с. E = 1,60 В

    Автор:

    Ашика

    Руководитель проекта по физике создание увлекательный контент, чтобы помочь студентам на всех уровнях. Ашика, опытный репетитор по физике и математике на уровне GCSE и A Level, помогает расширять и улучшать наши ресурсы по физике.

    Еще от AshikaПроверь себяПредыдущая:4.4.2 Расчет ЭДССледующая заметка:4.4.4 ЭДС и разность потенциалов

    Компания

    Быстрые ссылки

    Калькулятор внутреннего сопротивления

    Калькулятор внутреннего сопротивления Omni позволяет вычислить сопротивление источника напряжения протекающему через него току .

    Знаете ли вы, что и в грузовиках, и в мотоциклах используются батареи с одинаковой электродвижущей силой (ЭДС = 12 В)? Однако аккумулятор грузовика может дать гораздо больший заряд, чем аккумулятор мотоцикла, из-за меньшего внутреннего сопротивления.

    Чтобы узнать больше о внутреннем сопротивлении, продолжайте читать эту статью. Вы узнаете:

    • Что такое внутреннее сопротивление?
    • Как найти внутреннее сопротивление аккумулятора.
    • Каково внутреннее сопротивление идеального источника напряжения/тока?

    Если вы хотите рассчитать сопротивление проводника, воспользуйтесь нашим калькулятором сопротивления проводов.

    Что такое внутреннее сопротивление – определение внутреннего сопротивления

    Внутреннее сопротивление источника напряжения (например, батареи) представляет собой сопротивление электролитов и электродов батареи протеканию тока через источник .

    Внутреннее сопротивление новой батареи обычно низкое; однако по мере того, как батарея используется все чаще и чаще, ее внутреннее сопротивление увеличивается.

    В следующем разделе мы узнаем, как найти внутреннее сопротивление батареи.

    Как найти внутреннее сопротивление батареи – формула внутреннего сопротивления

    Рассмотрим ячейку с электродвижущей силой (ЭДС) ε\varepsilonε и внутренним сопротивлением rrr.

    Рис. 1. Источник напряжения с ЭДС ε и внутренним сопротивлением r, подключенный к внешнему резистору R.

    Если мы подключим эту ячейку к внешнему нагрузочному резистору RRR (см. рисунок 1), общее сопротивление (RTR_TRT​) цепи станет:

    RT=r+R\footnotesize R_T = r + RRT​=r+R

    И по формуле закона Ома ток III через цепь будет:

    I=εR+r\footnotesize I = \frac{\varepsilon}{R+r}I=R+rε​

    Преобразовав приведенное выше уравнение, мы получим уравнение для внутреннего сопротивления:

    r=εI−R\footnotesize \начать{выравнивать*} г = \ гидроразрыва {\ varepsilon} {I} – R \\ \конец{выравнивание*} r=Iε−R​

    Если мы знаем ток в цепи, мы также можем рассчитать напряжение на выводах батареи VVV.

    V=ε−Ir\размер сноски V = \varepsilon – IrV=ε−Ir

    Напряжение на клемме батареи представляет собой выходное напряжение, измеренное на ее клемме . Приведенное выше уравнение показывает, что чем больше ток, тем ниже напряжение на клеммах. Точно так же, чем меньше внутреннее сопротивление, тем больше напряжение на клеммах.

    Расчет внутреннего сопротивления – пример

    В качестве примера рассчитаем внутреннее сопротивление элемента ЭДС 3 В3~\rm В3 В. Пусть ток в цепи равен 3 мА3\ \rm {мА}3 мА при сопротивлении нагрузки 995 Ом995\ \Omega995 Ом подключен через него.

    1. Дано сопротивление нагрузки R=995 Ом R = 995\ \OmegaR=995 Ом, ЭДС ячейки ε=3 В\varepsilon = 3~\rm Vε=3 В, ток в цепи I=3 mAI = 3\ \rm {мА}I=3 мА.

    2. Подставив эти значения в формулу внутреннего сопротивления, получим: 9{-3}\ \rm {A} \times 5 \\Omega) \\[.5em] & = 2,985 ~ \rm В \end{align*}V​=ε−ir=3 V−(3×10−3 A×5 Ω)=2,985 В​

       Как использовать калькулятор внутреннего сопротивления

       Теперь давайте посмотрим, как мы можем решить та же проблема с использованием нашего калькулятора внутреннего сопротивления:

       1. Введите значение сопротивления нагрузки R=995 ΩR = 995\ \OmegaR=995 Ω.

       2. Введите ЭДС ячейки (ε=3 В\varepsilon = 3~\rm Vε=3 В) и ток по цепи (I=3 мАв = 3\ \rm {мА}I=3 мА) в соответствующих полях. Вы можете выбрать раскрывающееся меню, чтобы выбрать соответствующую единицу измерения тока.

       3. Калькулятор отобразит внутреннее сопротивление элемента (r=5 Ωr = 5 \\Omegar=5 Ω) и напряжение на клеммах (V=2,985 VV = 2,985 ~ \rm VV=2,985 V).

       Если вас интересует расчет срока службы батареи на основе ее емкости и энергопотребления устройства, рекомендуем воспользоваться нашим калькулятором срока службы батареи.

       Часто задаваемые вопросы

       Как рассчитать внутреннее сопротивление батареи?

       Чтобы рассчитать внутреннее сопротивление батареи, следуйте приведенным инструкциям:

       1. Узнать ток по схеме.

       2. Разделите ЭДС батареи на ток через цепь.

       3. Вычесть сопротивление нагрузки из значения, полученного из шаг 2 .

       4. Вы получите внутреннее сопротивление батареи.

       Как рассчитать напряжение на клеммах аккумулятора?

       Для расчета напряжения на клеммах выполните следующие действия:

       1. Умножьте ток через цепь на внутреннее сопротивление батареи .

       2. Вычесть значение из шаг 1 из ЭДС батареи.

       3. Поздравляем! Вы рассчитали напряжение на клеммах.

       Каково внутреннее сопротивление идеального источника напряжения?

       Ноль . Согласно закону Ома сопротивление определяется как r = V / I. Напряжение на идеальном источнике напряжения постоянно и не зависит от протекающего тока. Это означает, что кривая V-I будет прямой линией с нулевым наклоном .