Движение — что это, определение и ответ
Движением тела называется изменение его положения в пространстве относительно других.
Координата — величина, служащая для определения положения какой-либо точки на плоскости или в пространстве.
Перемещением тела называется вектор, соединяющий начальное положение тела с его последующим положением.
Траектория — это линия, вдоль которой движется тело.
Путь — это длина траектории, вдоль которой движется тело.
Прямолинейным равномерным движением называется движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.
Скоростью равномерного прямолинейного движения называется величина, равная отношению перемещения тела \(\overrightarrow{S}\) к времени t, за которое это перемещение произошло:
\(\overrightarrow{v} = \frac{\overrightarrow{S}}{t}\)
Скорость ― это векторная величина!
В заданиях, где дана зависимость скорости тела от времени. {2}}{2}\)
{2}}{2}\)
Где x0 ― начальная координата тела;
v0 ― проекция начальная скорость на ось x;
a ― проекция ускорения на ось x;
t ― время движения.
Если существует зависимость координаты от времени x(t), то зависимость скорости от времени можно получив взяв производную по времени от этой зависимости.
Скорость ― это производная координаты тела по времени vx(t) = x‘(t). Например, если зависимость координаты тела при равноускоренном движении имеет вид x(t) = 6 – 2t + 12t2, то, взяв первую производную от координаты мы получим зависимость скорости тела от времени vx(t) = –2 + 12 ∙ 2t = –2 + 24t.
Точно так же, ускорение ― это производная от скорости тела. ax(t) = vx‘(t).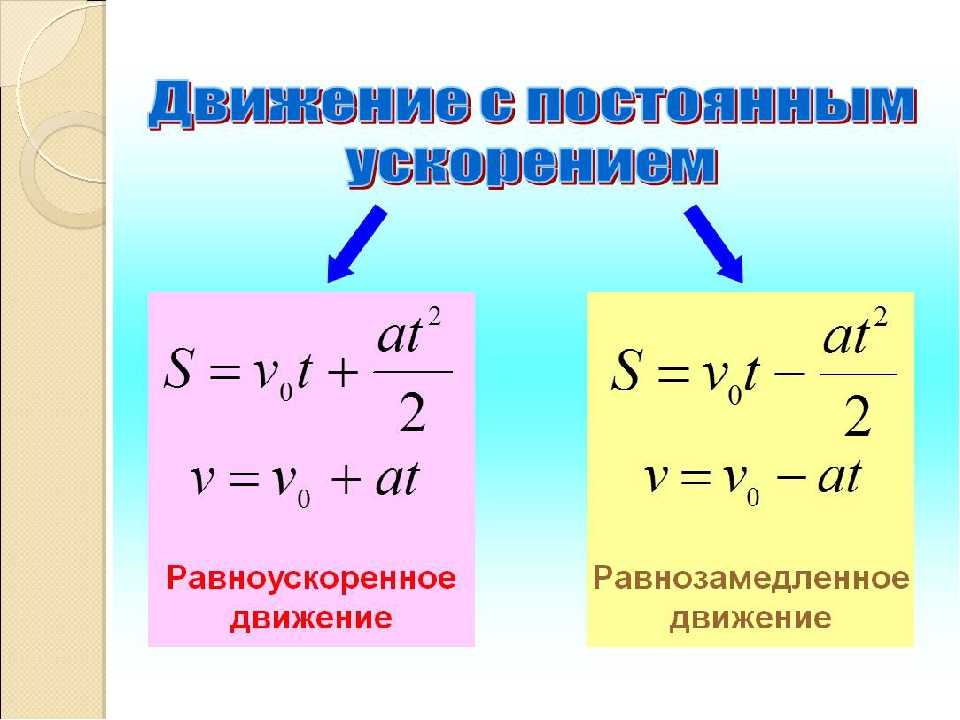 {2}}{2}\),
{2}}{2}\),
Где:
H(t) — высота тела над нулевым уровнем в момент времени t [м],
h — начальная высота тела над нулевым уровнем [м],
v0 — начальная скорость тела [м/с]
α — угол, под которым бросили тело [°],
t — время движения тела [c],
g — ускорении свободного падения [м/с2].
Зависимость горизонтальной координаты от времени при движении под углом к горизонту:
S(t) = v0 ‧ cos a ‧ t, где:
S(t) — путь, пройденный телом за время t [м]
Угол между вектором скорости тела и горизонтом в любой момент времени может быть выражен из геометрических соображений как:
\(\alpha\left( t \right) = arctg(\frac{v_{y}}{v_{x}})\),
Где:
α(t) — угол между скоростью и горизонтом в момент времени t [°],
vy = v0 ∙ sin α – gt — вертикальная проекция скорости тела в момент времени t [м/с],
vх = v0 ∙ cos α — горизонтальная проекция скорости тела [м/с].
Работа силы тяжести при падении тела на тот же уровень, с которого тело взлетело (с Земли на Землю, с балкона на балкон и т.д.) равна нулю.
В этом случае выполняется симметрия полета:
угол, под которым тело упадет, равен углу, под которым тело бросили;
скорость, с которой тело упадет, равна скорости, с которой тело бросили;
время взлета тела до максимальной высоты равно времени падания с неё обратно.
Если работа силы тяжести не равна нулю (бросок с Земли на балкон, с балкона на Землю и так далее), симметрия полета не выполняется.
Время взлета на максимальную высоту:
\(t_{взлета} = \frac{v_{0}\sin\alpha}{g}\).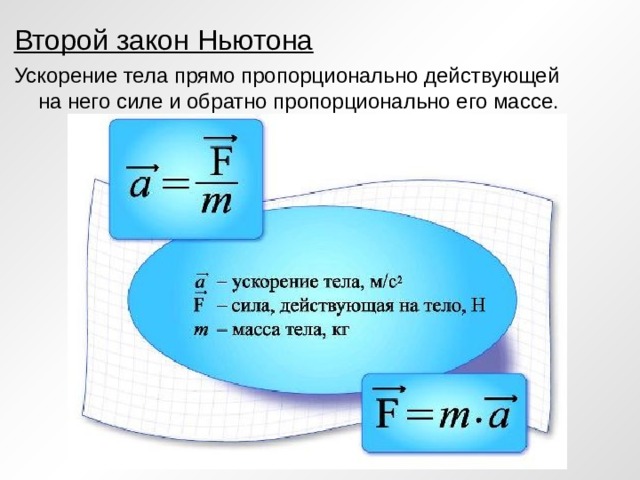 {2}\sin{2\alpha}}{g}\).
{2}\sin{2\alpha}}{g}\).
Выводится с помощью подставления прошлой формулы в уравнения равномерного движения вдоль горизонтальной оси:
S = v0 ‧ cos a ‧ t полета
Здесь используются формула синуса двойного угла и свойство симметрии полета: время взлета равно времени падения, или полное время движения равно удвоенному времени взлета: tполета = 2tвзлета
Очевидно, что формула применима только при падении тела на тот же уровень, с которого оно взлетело.
Время падения тела с балкона (без начальной скорости) или при броске горизонтально:
\(t_{падения} = \sqrt{\frac{2H}{g}}\)
Формула выводится при проецировании уравнения координаты при равноускоренном движении на ось OY:
\(H\left( t \right) = h + v_{0}\sin a \cdot t – \frac{gt^{2}}{2}\)
с учетом, что проекция начальной скорости на эту ось равна нулю, а конечная координата — тоже ноль:
\(0 = h – \frac{gt_{падения}^{2}}{2}\)
Максимальная высота подъема тела над Землей:
\(\ h = \frac{v_{0}^{2}\sin^{2}\alpha}{2g}\)
Формулу легко получить объединением уравнения координаты при равноускоренном движении на ось OY с поверхности Земли:
\(\left( t \right) = h + v_{0} \cdot \sin a \cdot t – \frac{gt^{2}}{2}\)
с формулой времени подъема тела на максимальную высоту:
\(t_{взлета} = \frac{v_{0}\sin\alpha}{g}\)
Все представленные выше формулы могут быть использованы без вывода в задачах первой части, но в задачах второй части за это будут снимать баллы.
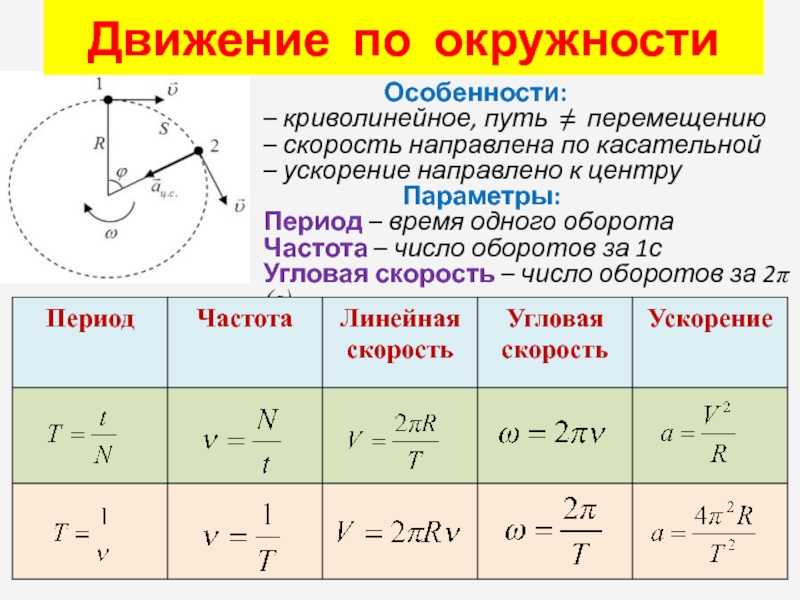
При движении по окружности часто удобно использовать не обычную скорость, а угловую скорость.
Угловая скорость численно равна углу поворота радиуса за единицу времени.
Угловая скорость для тела, двигающегося из точки 1 в точку 2, будет равна:
\(\omega = \frac{\mathrm{\Delta}\varphi}{\mathrm{\Delta}t}\), где
∆φ ― угол поворота [рад],
∆t ― промежуток времени [с],
ω ― угловая скорость \(\lbrack\frac{рад}{с}\rbrack\).
Линейную скорость точки на определенном расстоянии (радиусе) R от оси вращения можно считать как: v = ωR.
Соответственно, чем больше будет радиус окружности, тем больше будет линейная скорость, при постоянной угловой скорости.
Период — время, за которое тело делает полный оборот по окружности.
\(T = \frac{2\pi R}{v}\), где
T ― период [с],
R ― радиус окружности [м],
v ― скорость [м/с]. {2}R\), где
{2}R\), где
R ― радиус окружности [м],
an ― нормальное ускорение [м/с2],
v ― скорость [м/с],
ω ― угловая скорость \(\lbrack\frac{рад}{с}\rbrack\).
исчерпывающие подходы и факты –
Как найти ускорение с помощью коэффициента трения – еще одна важная и общепринятая тема, которую необходимо решить. Это фактор, который определенным образом увеличивает ускорение.
Когда тело находится в движении, оно будет продолжать движение до тех пор, пока на него не подействует сила, изменяющая размеры объекта. Таким образом, этот процесс будет продолжаться до тех пор, пока скорость не будет увеличена или уменьшена.
Как только объект изменяет скорость, он либо ускоряется (положительно), либо замедляется (отрицательно), обычно в направлении, противоположном движению. Изменение скорости также известно как скорость с точки зрения физики.
Изменение скорости происходит в другое время, и, следовательно, это будет влиять на ускорение движущегося тела либо положительно, либо отрицательно. Внезапный рывок в системе также влияет на ускорение.
Внезапный рывок в системе также влияет на ускорение.
Когда тело находится в движении, на него влияет несколько факторов, и одним из них является ускорение, на которое будет влиять термин, называемый трением. Постепенно мы будем иметь дело с нахождением ускорения с помощью коэффициент трения.
Мы можем продолжать говорить об ускорении по-разному, но когда на ускорение влияет другой фактор, нам нужно сосредоточиться на этом. Трение – это, по сути, фактор, присутствующий между телом и активной поверхностью.
Понимание трения и коэффициента фиксацииПрежде чем мы углубимся в это подробно, необходимы первые знания о трении и коэффициенте трения. Трение по сути, это сила, которая сопротивляется движению при ходьбе, беге и т. д.
Между объектом и поверхностью присутствует небольшой фактор, который называется трением. Эта конкретная сила называется силой трения. Эта сила помогает любому случайному телу в действии двигаться.
Когда поверхность шероховатая, трение больше, а когда поверхность гладкая, трение меньше. Таким образом, когда трение увеличивается, ускорение уменьшается, а когда трение уменьшается, ускорение уменьшается. Это также базовое понимание в знакомых терминах.
Таким образом, когда трение увеличивается, ускорение уменьшается, а когда трение уменьшается, ускорение уменьшается. Это также базовое понимание в знакомых терминах.
Теперь давайте посмотрим, что именно означает коэффициент трения. Этот коэффициент трения представляет собой безразмерный коэффициент, представляющий собой соотношение между нормальной силой и силой трения движущегося тела.
Итак, все мы знаем, что движению тела способствуют несколько различных аспектов. Так или иначе, он будет ускоряться. Во-первых, это изменение скорости, называемое скоростью, которое помогает в подвижности тела.
В некоторых случаях это тоже кажется существенным. Это будет внешняя сила или любая другая сила и чистая сила в целом. Фактор, называемый трением, вносит большой вклад в движение любого объекта или тела. Коэффициент трения будет определять, сколько силы потребуется для такого движения тела.
Поскольку это мера отношения, она будет иметь нулевые размеры, а значение будет варьироваться от минимального 0 до максимального значения 0. 5. Также может быть коэффициент трения, который может быть больше единицы.
5. Также может быть коэффициент трения, который может быть больше единицы.
Требуется знание формулы для определения ускорения. Согласно второму закону Ньютона, ускорение пропорционально силе и косвенно пропорционально массе объекта.
Следовательно, мы получаем его как а = Ф / м. это формула базового ускорения без каких-либо атрибутов. Когда трение действует на тело и его движение, не менее важен тип поверхности.
Таким образом, формула изменяется в соответствии с коэффициентом трения, a = (fn-μ) / m. μ известен как коэффициент трения, и он указывает количество силы, необходимой для дальнейшего движения тела.
Давайте посмотрим, как это сделать, на лучшем примере. Трение весом 10 кг прикладывается к правому трению 7 Н. Допускается ускорение на неровной поверхности. Сила трения имеет значение 0.3 Н. Теперь вычислите ускорение объекта.
а = (20 – 0.3) / 7
а = 19.7 / 7
a = 2. 81 мс-2
81 мс-2
Вот как найти ускорение с коэффициентом трения. Но где использовать коэффициент трения – это вопрос. Мы тоже с этим разберемся. В вопросе прямо дана постоянная силы трения.
Сила трения и сила нормали не будут указаны явно, но значения могут быть нарисованы с использованием коэффициента трения. По приведенным данным мы должны рассчитать коэффициент трения, чтобы применить его к формуле и найти ускорение.
Задача о том, как найти ускорение по коэффициенту тренияПроблема:
Автомобиль весом 1100 кг с коэффициентом трения μ = 0.95 относительно шин. Теперь определим ускорение. Он движется с силой 880 Н.
Решение:
Нам нужно понять эту проблему, используя диаграмму свободного тела. Теперь давайте погрузимся в движение автомобиля и силы, действующие на него. Поскольку автомобиль находится в движении, на него будет воздействовать как можно больше сил.
Мы знаем, что по умолчанию на тело действует нормальная сила; теперь, когда он находится в движении, действует также сила трения.
Значение, данное для коэффициента трения: μ = 0.95. Здесь нам нужно найти фрикционную и нормальные силы, так как коэффициент значение трения уже задано.
Отметим, что нормальная сила равна силе гравитации. Известно, что сила тяжести составляет 9.8 мс-1. А теперь это значение, умноженное на массу, дает нормальную силу. Fn = 1100 × 9.8 = 10780.
Сила трения – это коэффициент трения, умноженный на нормальную силу. Следовательно ff = 10241. Теперь, когда сила трения найдена, следующим шагом будет определение ускорения. Сила трения также считается чистой силой.
а = ф / м
а = 10241/1100
а = 9.31 мс-2
Часто задаваемые вопросыКак найти скорость с трением?Поскольку ускорение можно найти с помощью трения, можно найти и скорость, поскольку это не что иное, как изменение скорости.
Во-первых, нам нужно известна начальная скорость и сила тяжести. Таким образом, скорость с учетом трения находится по формуле: начальная скорость минус коэффициент трения, умноженный на силу тяжести и заданное время. v(t) = v0 – µ g t.
Таким образом, скорость с учетом трения находится по формуле: начальная скорость минус коэффициент трения, умноженный на силу тяжести и заданное время. v(t) = v0 – µ g t.
Коэффициент трения – это фактор, который присутствует между движущимся телом и поверхностью, с которой оно движется.
Формула для коэффициента трения: μ = (сила трения) / (сила в норме). Еще один момент, который следует отметить, заключается в том, что сила трения иногда равна чистой силе, действующей на тело, что упрощает вычисление ускорения. Нормальная сила рассчитывается путем умножения силы тяжести и массу тела.
Какие бывают типы трения?Статическое и кинетическое трение – это два разных типа, которые подпадают под одну тему трения.
Статическое трение называется трением, когда тело не движется. Из самого слова «статика» очевидно, что ничего не движется. В таких случаях найденное трение называется трением покоя. Когда тело выходит из равновесия, это также происходит из-за трения, которое называется кинетическим трением. Статическое и кинетическое трение различается в зависимости от случая и условий.
Когда тело выходит из равновесия, это также происходит из-за трения, которое называется кинетическим трением. Статическое и кинетическое трение различается в зависимости от случая и условий.
Статическое трение называется так, потому что это сила, противодействующая неподвижному телу.
Когда тело не движется и остается в положении равновесия, трение, действующее на тело, называется трением покоя. Это трение всегда действует в направлении, противоположном силе, действующей вместе с движением тела, даже когда оно не действует.
Что такое ускорение? – Формула, единица измерения, типы, примеры и часто задаваемые вопросы
Ускорение — одно из важных понятий, подобных скорости и скорости, в физике, которое используется для определения движения и решения связанных с ним проблем. Ускорение в механике определяется как скорость изменения скорости. Это означает, что если скорость объекта увеличивается или уменьшается, то объект ускоряется. Ускорение имеет как величину, так и направление, поэтому оно является векторной величиной. Согласно второму закону движения Ньютона, величина ускорения объекта представляет собой комбинацию двух факторов, то есть чистой результирующей силы и массы объекта. Следовательно, единица ускорения м/с 2 . Давайте узнаем больше об ускорении и связанных с ним понятиях, таких как формула ускорения, ее единица измерения, типы, графики, решенные примеры и часто задаваемые вопросы по ней, в этой статье!
Ускорение имеет как величину, так и направление, поэтому оно является векторной величиной. Согласно второму закону движения Ньютона, величина ускорения объекта представляет собой комбинацию двух факторов, то есть чистой результирующей силы и массы объекта. Следовательно, единица ускорения м/с 2 . Давайте узнаем больше об ускорении и связанных с ним понятиях, таких как формула ускорения, ее единица измерения, типы, графики, решенные примеры и часто задаваемые вопросы по ней, в этой статье!
Ускорение определяется как скорость изменения скорости объекта во времени. Говорят, что объект ускоряется или имеет ускорение, когда его скорость изменяется.
Ускорение можно также назвать скоростью изменения скорости и изменением во времени. Величина вектора ускорения говорит нам, насколько изменится скорость, а направление говорит нам, как изменится скорость: увеличивается скорость или уменьшается, вектор скорости меняет направление или какая-то комбинация этих трех факторов.
Ускорение может быть положительным, нулевым или отрицательным. В случае, если скорость объекта увеличивается со временем, его можно назвать Положительное ускорение . В случае, если скорость равна нулю, это называется Нулевым Ускорением , в то время как отрицательное ускорение, также известное как Замедление , указывает на уменьшение скорости со временем.
Формула ускорения
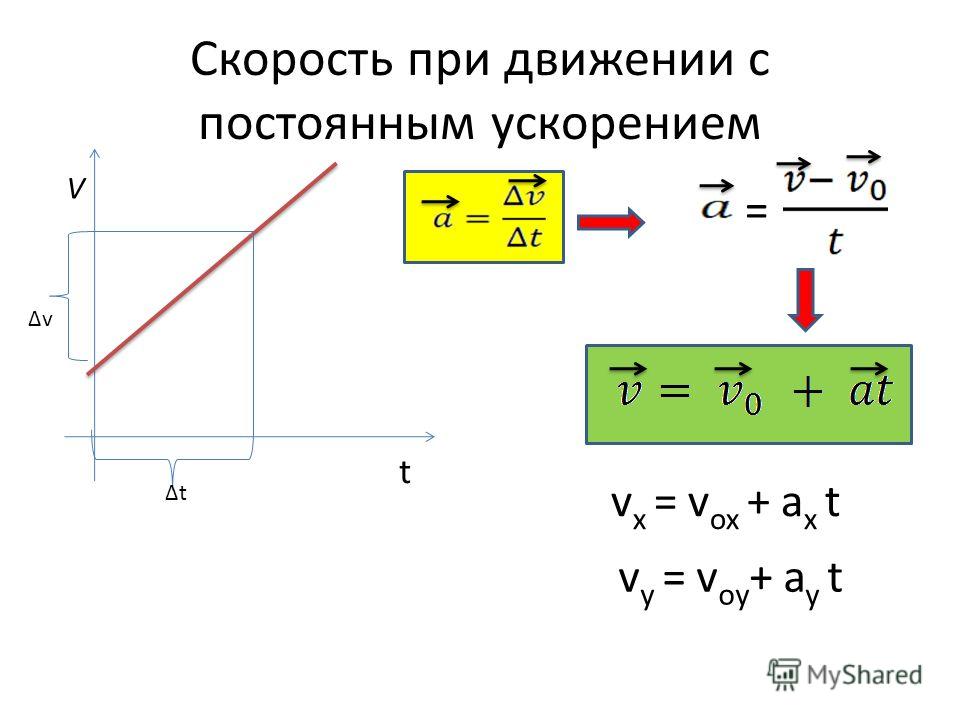
Математически изменение скорости движущегося объекта определяется как (v – u) , где v и u – конечная и начальная скорости.
Следовательно, ускорение объекта определяется,
Ускорение = изменение скорости / времени, взятого
или
A = (V – U) / T
, где
- A ускорение,
- v — конечная скорость,
- u — начальная скорость,
- t — время, затрачиваемое объектом.
Единица ускорения
- Это векторная величина , которая связана как с величиной, так и с направлением.
 Он обозначается как « a ».
Он обозначается как « a ». - Единицей ускорения является метр в секунду в квадрате или метр в секунду (скорость или скорость объекта) в секунду или м/с 2 .
- Размерная формула ускорения: [M 0 L 1 T -2 ] .
Типы ускорения
Ниже приведены различные типы ускорения, связанные с объектом:
Равномерное ускорение
Если скорость объекта изменяется одинаково в течение одного и того же интервала времени, говорят, что тело движется с равномерным ускорением. В этом случае ни направление, ни величина не меняются со временем.
Например:
- Мяч катится по склону.
- Когда велосипедист едет на велосипеде по склону, когда задействованы обе педали.
- Ребенок сползает с ползунка.
- Движение автомобиля с постоянной скоростью и т. д.
Неравномерное ускорение
Переменное ускорение — это скорость тела, изменяющаяся на различную величину за один и тот же интервал времени. Переменное ускорение проявляется, когда направление или величина объекта или и то, и другое изменяется во времени.
Переменное ускорение проявляется, когда направление или величина объекта или и то, и другое изменяется во времени.
Например:
- Изменение скорости автомобиля
- Равномерное круговое движение
- Движение маятника с изменением скорости
Среднее ускорение определяется как изменение скорости за определенный заданный интервал времени. Среднее ускорение можно рассчитать для временного интервала следующим образом: ) / (т ф – т и )
, где
- V F – это окончательная скорость,
- V I – начальная скорость,
- T I – это начальное время, а
- T F – это последнее время
- T .
Чтобы рассчитать мгновенное ускорение, можно вычислить среднюю скорость между двумя моментами времени, разделенными Δt, и пусть Δt приближается к нулю. Полученный результат представляет собой производную функции скорости v(t), которая представляет собой мгновенное ускорение. Математически
Полученный результат представляет собой производную функции скорости v(t), которая представляет собой мгновенное ускорение. Математически
Таким образом, подобно тому, как скорость является производной функции положения, мгновенное ускорение является производной функции скорости. Мы можем показать это графически так же, как мгновенную скорость. На (Рисунке) мгновенное ускорение в момент времени t 0 представляет собой наклон касательной к графику зависимости скорости от времени в момент времени t 0 . Мы видим, что среднее ускорение определяется как
График зависимости скорости от времени
Кривые показывают, что график зависимости скорости от времени отложен по оси x, а скорость отложена по оси y. При нахождении смещения по графику v – t учитывайте знак.
- Когда скорость частицы постоянна или ускорение равно нулю.
- Когда частица движется с постоянным ускорением и ее начальная скорость равна нулю.

- Когда частица движется с постоянным замедлением.
- Когда частица движется с неравномерным ускорением и ее начальная скорость равна нулю.
- При уменьшении и увеличении ускорения.
- Общая площадь, ограниченная кривой зависимости скорости от времени, представляет собой расстояние, пройденное телом.
Разница между ускорением и скоростью
Вот несколько важных различий между ускорением и скоростью:
Ускорение | Скорость |
|---|---|
| Ускорение определяется как скорость изменения скорости во времени. | Однако скорость – это скорость изменения смещения во времени. |
| Ускорение может быть положительным или отрицательным, но не нулевым. | Пока скорость может быть нулевой, положительной или отрицательной. |
Единицей ускорения в системе СИ является м/с 2 . | Единицей скорости в системе СИ является м/с. |
The formula for acceleration is, Acceleration = Velocity/Time | The formula for velocity is, Velocity = Acceleration/Time |
Solved Examples on Acceleration
Пример 1: Если грузовик разгоняется с 6 м/с до 10 м/с за 10 с. Вычислите его ускорение.
Решение:
Учитывая, что
Начальная скорость, u = 6 м/с,
Конечная скорость, v = 10 м/с,
Затраченное время, t = 10 с.
Нужно найти Ускорение a
Ускорение a = (v – u) / t
= (10 м/с – 6 м/с) / 10 с
= 0,4 м/с 2
Таким образом, ускорение грузовика равно 0,4 м/с 2 .
Пример 2. Если мяч падает с террасы здания на землю. Если мячу потребовалось 6 с, чтобы коснуться земли. Найдите высоту террасы от земли.
Найдите высоту террасы от земли.
Решение:
Учитывая, что
Начальная скорость u = 0 {поскольку мяч находился в покое},
Время, за которое мяч коснулся земли t = 6 секунд
Ускорение свободного падения a = g = 9,8 м/с 2 ,
Расстояние, пройденное камнем = высота моста = s
Расстояние, пройденное мячом от террасы до земли
Следовательно,
терраса от земли 29,4 м .
Пример 3: Если человек едет на машине со скоростью 108 км/ч, он должен замедлить скорость и разогнать ее до 72 км/ч за 5 с. Рассчитать замедление автомобиля?
Решение:
Учитывая, что
Начальная скорость, u = 108 км/ч или
Конечная скорость, v = 72 км/ч или
Следовательно, 52
Время, t0 = 05 секунд ускорение равно,
Знак минус показывает замедление.
Пример 4: Если автомобиль движется из состояния покоя, а затем равномерно ускоряется со скоростью 7,5 м/с 2 в течение 10 с. Найдите скорость поезда через 10 с.
Решение:
Учитывая, что,
Начальная скорость U = 0 {По мере того, как автомобиль был в состоянии. = u + at
= 0 + 7,5 × 10
= 75 м/с
Пример 5: Если объект движется вдоль оси x согласно соотношению x = 1 – 2t + 3t 2 , где x в метрах и t в секундах. Определить ускорение тела в момент времени t = 3 с.
Решение:
Указано, что,
x = 1 – 2t + 3t 2
Velocity, V = DX/DT
= D/DT {1 – 2T + 3T 2 }
= -2 + 6t
Следовательно, Ускорение a = dv/dt
= d/dt {-2 + 6t}
= 6 м/с 2
Часто задаваемые вопросы об ускорении
Вопрос 1. Дайте определение радиальному ускорению.
Дайте определение радиальному ускорению.
Ответ:
Ускорение объекта по радиусу к центру радиальной траектории называется радиальным ускорением.
Вопрос 2: Что такое ускорение под действием силы тяжести?
Ответ:
Ускорение свободного падения определяется как ускорение, испытываемое гравитационным притяжением Земли.
Вопрос 3: Что вы подразумеваете под тангенциальным ускорением?
Ответ:
Тангенциальное ускорение — это скорость изменения тангенциальной скорости при вращательном движении любого объекта. Он действует в направлении касательной в точке движения объекта.
Вопрос 4: Что вы понимаете под центростремительным ускорением?
Ответ:
Центростремительное ускорение определяется как ускорение, направленное к центру кривизны, поскольку скорость постоянно меняется, а ускорение присутствует.
Вопрос 5: Как ускорение зависит от Силы?
Ответ:
Ускорение прямо пропорционально силе, приложенной к объекту с постоянной массой.
Связанные статьи
- Угловое ускорение
- График времени ускорения
- Однократно ускоренное движение
Ука0005
Ускорение
Ускорение является важным понятием в физике и используется для определения движения. Ускорение определяется как скорость изменения скорости, которая подразумевает, что объект ускоряется, когда скорость объекта увеличивается или уменьшается. Ускорение имеет как величину, так и направление, что делает его векторной величиной. Величина ускорения объекта представляет собой комбинацию двух факторов, чистой результирующей силы и массы объекта в соответствии со вторым законом движения Ньютона. Давайте разберемся подробнее об ускорении, его единицах, типах и графиках.
Что такое ускорение?
Ускорение определяется как скорость изменения скорости объекта относительно времени. Когда скорость объекта изменяется, говорят, что он ускоряется.
Ускорение можно также определить как скорость изменения скорости и изменение во времени. Ускорение может быть положительным, отрицательным или нулевым.
- Положительное ускорение возникает, когда скорость объекта увеличивается со временем.
- Нулевое ускорение происходит, когда скорость не уменьшается и не увеличивается, она равна нулю.
- Отрицательное ускорение возникает, когда скорость уменьшается со временем. Это также известно как задержка.
Формула ускорения
Изменение скорости движущегося объекта определяется как «v-u», где v — конечная скорость, а u — начальная скорость. Следовательно, ускорение объекта с начальной скоростью «u», конечной скоростью «v» и временем, затраченным на «t», составляет
Ускорение = изменение скорости / затраченное время
Что дает формулу
a = (
S.
 I Единица ускорения
I Единица ускоренияУскорение является векторной величиной, поскольку оно имеет как величину, так и направление. Оно обозначается буквой a. Единицей ускорения является метр на секунду в квадрате, что равно м/с 2 . Размерная формула ускорения: [M 0 L 1 T -2 ]. ускорение
Равномерное ускорение
Когда скорость объекта изменяется одинаково в течение одних и тех же интервалов времени, говорят, что объект находится в равномерном ускорении. При равномерном ускорении направление и величина со временем не меняются.
Пример: движение автомобиля с постоянной скоростью или мяч, катящийся по склону.
Неравномерное ускорение
Неравномерное ускорение также известно как переменное ускорение. При переменном ускорении скорость объекта изменяется на различную величину в течение одного и того же интервала времени. При неравномерном ускорении величина и направление изменяются со временем.
Пример: Автомобиль меняет скорость после каждого пройденного километра.
Среднее ускорение
Когда объект меняет свою скорость в течение определенного заданного интервала времени, говорят, что он имеет среднее ускорение. Формула для расчета среднего ускорения приведена ниже.
A v =∆v/∆t или a v = (v f -v i ) / (t f -t i )
Here, v f is the final velocity
v i is the initial velocity
t i is the initial time
t f is the final time
Мгновенное ускорение
Мгновенное ускорение определяется как отношение изменения скорости в течение заданного интервала времени, при котором этот интервал времени стремится к нулю. Чтобы рассчитать мгновенное ускорение, можно рассчитать среднюю скорость между двумя моментами времени, разделенными ∆t, и ∆t приближается к нулю. Полученный результат представляет собой вывод функции скорости v (t), которая представляет собой мгновенное ускорение, которое при математическом выражении дает
Полученный результат представляет собой вывод функции скорости v (t), которая представляет собой мгновенное ускорение, которое при математическом выражении дает
a(t) = v(t)
График ускорения, скорости и времени
Кривые представляют собой график зависимости скорости от времени, где время отложено по оси x, а скорость отложена по оси y.
- Когда скорость объекта постоянна или имеет нулевое ускорение.
- Когда объект движется с постоянным ускорением и начальная скорость равна нулю.
- Когда объект движется с постоянным замедлением
- Когда объект движется с неравномерным ускорением и начальная скорость равна нулю.
- Когда ускорение уменьшается и увеличивается.
Разница между ускорением и скоростью
| Критерии | Определение | Формула | Блок |
| Ускорение | Ускорение определяется как изменение скорости объекта относительно времени. | Скорость/Время | м.с -2 |
| Скорость | Скорость определяется как скорость объекта в определенном направлении. | Перемещение/Время | мс -1 |
Решенные примеры ускорения
1. Если автомобиль разгоняется с 5 м/с до 10 м/с за 20 с. Вычислите его ускорение.
Ответ. Дано,
Начальная скорость, u = 5 м/с
Конечная скорость, v = 10 м/с
Затраченное время, t = 20 с
Ускорение, a= (v-u)/t
= (10 м/с – 5 м/с) / 20
= 0,25 м/ s 2
- Если грузовик едет со скоростью 100 км/ч, его тормозят и доводят до 70 км/ч за 5 с. Рассчитать замедление грузовика?
Ответ. Дано,
Начальная скорость, u = 90 м/с или 90 x = 25 м/с
Конечная скорость, v = 72 м/с или 72 x = 20 м/с
Затраченное время, t = 20 с
Ускорение, a= (v-u)/t
= (20 м/с – 25 м/с) / 20
= -0,25 м/с 2
- Если автомобиль движется из состояния покоя, а затем равномерно ускоряется при 8,2 м/с 2 на 10 с.

Дано,
Начальная скорость, u = 0 м/с (вагон покоится)
Время, t = 10 с
Ускорение, a = 8,2 м/с 2
v = u + at
= 0 + 8,2 х 10
= 82 м/с
Ускорение – Часто задаваемые вопросы
- Каково среднее ускорение с течением времени?
Ответ. Среднее ускорение за время ka определяется как общее изменение скорости за заданные интервалы времени, деленное на общее время, затраченное на изменение.
- Что такое ускорение под действием силы тяжести?
Ответ. Ускорение свободного падения определяется как ускорение, испытываемое гравитационным притяжением Земли.
- Что вы понимаете под центростремительным ускорением?
Ответ. Центростремительное ускорение определяется как ускорение, направленное к центру кривизны, поскольку скорость постоянно меняется и ускорение присутствует.
- Как ускорение связано с силой?
Ответ.

 Он обозначается как « a ».
Он обозначается как « a ».