Перечень мероприятий НГАСУ (Сибстрин) для школьников и студентов СПО, позволяющих получить дополнительные баллы за индивидуальные достижения Вниманию школьников и студентов СПО! Приглашаем к участию в мероприятиях на базе Новосибирского государственного архитектурно-строительного университета (Сибстрин), позволяющих получить дополнительные баллы за индивидуальные достижения к сумме баллов ЕГЭ. Победители и призеры согласно Правилам приема на 2022/2023 учебный год (п. 5.2) могут получить при подаче документов в вуз 10 и 5 баллов соответственно. Сибирская межрегиональная олимпиада школьников и студентов СПО по черчению и компьютерной графике – отборочный этап до 14 февраля 2022 года. Региональный конкурс-выставка детских творческих работ «Традиции академической школы живописи, графики, композиции»: прием заявок до 11 . |
Приглашаем к участию в семинаре «Применение современных технологий в строительстве: легкие стальные тонкостенные конструкции» 2 февраля 2022 года (среда) на базе НГАСУ (Сибстрин) пройдет семинар по теме «Применение современных технологий в строительстве: легкие стальные тонкостенные конструкции». Докладчик: Сергей Антипов, Заслуженный изобретатель РФ, Почетный строитель, д.т.н., советник РААСН с 2001 г., член Совета и Правления Российского союза строителей. Организатор: кафедра Металлических и деревянных конструкций НГАСУ (Сибстрин). В рамках семинара будут рассмотрены различные аспекты внедрения современных эффективных технологий с применением ЛСТК (легких стальных тонкостенных конструкций) в строительную отрасль. К участию приглашаются профессорско-преподавательский состав, студенты и аспиранты университета, специалисты стройиндустрии. |
Кафедры ИГ и ГТСБЭ обсудили возможности и перспективы межкафедрального сотрудничества 18 января 2022 года в НГАСУ (Сибстрин) состоялся межкафедральный научно-методический семинар кафедр Гидротехнического строительства, безопасности и экологии и Инженерной геодезии. Профессорско-преподавательский состав кафедр обсудил возможность проведения междисциплинарной лабораторной работы в лаборатории кафедры ГТСБЭ. Такое взаимодействие позволит погрузить студентов, обучающихся по направлениям подготовки «Гидротехническое строительство» и «Природообустройство и водопользование», в профессиональную область еще на этапе обучения.
В рамках межкафедрального взаимодействия использование макета водного объекта в лаборатории гидравлики даст возможность кафедре Инженерной геодезии ориентировать студентов уже на втором курсе на решение …
Профессорско-преподавательский состав кафедр обсудил возможность проведения междисциплинарной лабораторной работы в лаборатории кафедры ГТСБЭ. Такое взаимодействие позволит погрузить студентов, обучающихся по направлениям подготовки «Гидротехническое строительство» и «Природообустройство и водопользование», в профессиональную область еще на этапе обучения.
В рамках межкафедрального взаимодействия использование макета водного объекта в лаборатории гидравлики даст возможность кафедре Инженерной геодезии ориентировать студентов уже на втором курсе на решение … |
Возобновляется запись на вакцинацию от COVID-19 для сотрудников и студентов на территории университета  Услуга доступна гражданам РФ.
Всем желающим пройти вакцинацию необходимо заполнить форму регистрации:
После заполнения формы в течение нескольких дней с вами свяжутся по телефону, указанному в заявке, и сообщат о дате и времени вакцинации.
Вакцинироваться от COVID-19 можно будет на территории НГАСУ (Сибстрин) в медицинском пункте университета (здание общежития №1) вакцинами Гам-Ковид-Вак (Спутник V) либо Спутник Лайт.
Дополнительная информация по тел. (383) 266 09 74 Услуга доступна гражданам РФ.
Всем желающим пройти вакцинацию необходимо заполнить форму регистрации:
После заполнения формы в течение нескольких дней с вами свяжутся по телефону, указанному в заявке, и сообщат о дате и времени вакцинации.
Вакцинироваться от COVID-19 можно будет на территории НГАСУ (Сибстрин) в медицинском пункте университета (здание общежития №1) вакцинами Гам-Ковид-Вак (Спутник V) либо Спутник Лайт.
Дополнительная информация по тел. (383) 266 09 74 |
Алгоритм метода Гаусса – Документ
Алгоритм метода Гаусса:
Первый шаг:
Первым шагом первый столбец и первая строка матрицы приводятся к нужному виду, для этого 1 строку делим на и затем вычитаем из всех остальных строк матрицы , домножая на .
Коэффициенты 1 строки после выполнения первого шага:
j=1, n +1 напомним, что
коэффициенты i строки после выполнения 1 шага:
, i = 2 , n j =1, n+1
получаем матрицу
Второй шаг:
Проделываем всё тоже самое для матрицы
и т. д. На каждом
шаге m имеем
д. На каждом
шаге m имеем
, j = m, n+1
Количество шагов равно размеру матрицы m = 1,2,…n.
Обратный ход осуществляется по формулам:
По этим формулам метод Гаусса очень легко программируется на любом языке программирования, а при применении электронных таблиц для решения систем этим методом об этих формулах даже и заботиться не надо, там всё делается по алгоритму.
Совмещает прямой и обратный ход :
Делим всё на диагональный элемент, но вычитаем не только из нижних, но и из верхних строк, таким образом после выполнения n шагов имеем расширенную матрицу где n+1 столбец – уже решение
Общий вид формул на шаге m ( m=1,2,…n )
, j = m, n+1
В практике решения вычислительных
задач часто встречаются сильно разреженные
матрицы ( т. е. матрицы, имеющие много
нулевых коэффициентов. Эти матрицы
могут иметь специальный вид. Нулевые
элементы могут быть упорядочены,
например, матрица коэффициентов может
быть клеточной или ленточной.
е. матрицы, имеющие много
нулевых коэффициентов. Эти матрицы
могут иметь специальный вид. Нулевые
элементы могут быть упорядочены,
например, матрица коэффициентов может
быть клеточной или ленточной.
Часто встречаются трехдиагональные матрицы
т.е. i строчка имеет вид:
i = 1,…,n
Для таких матриц разработаны специальные методы решения. Системы, имеющие трёхдиагональную матрицу коэффициентов решаются методом прогонки.
Метод прогонки, также как и метод Гаусса, имеет прямой и обратный ход.
После выполнения прямого хода матрица будет иметь вид:
т.е. i строчка имеет вид :
Обратный ход:
i = n-1,n-2,…,1
Как вычислить новые коэффициенты k и l
Из 1 уравнения ; далее действуем по методу индукции. Пусть получены коэффициенты для i – 1 уравнения , а i-ое уравнение не преобразовано
Подставим в i – ое уравнение
приводим его к нужному виду:
т. е.
е.
;
Знаменатель нигде не должен обращаться в 0 , т.е.
, проверим это
это выполняется, если
всегда, так как
4.1 Метод Гаусса. Использование численных методов при решении инженерных задач
Похожие главы из других работ:
Использование численных методов при решении инженерных задач
4.1 Метод Гаусса
Этот метод решения СЛАУ осуществляется в два прохода: 1. приведение основной матрицы к верхнетреугольному виду (прямой ход) 2…
Метод Гаусса для расчета электрических цепей
Метод Гаусса
Метод Гаусса – один из самых распространенных методов решения систем линейных алгебраических уравнений. Этот метод (который называют также метолом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.
Основные методы решения задач нелинейного программирования
2.3.1 Метод Гаусса-Зайделя
Метод заключается в последовательном определении экстремума функции одной переменной с точностью до Ґе вдоль каждой координаты, т.е. фиксируются все координаты, кроме одной, по которой и осуществляется поиск экстремума Q…
Поиск экстремума двумерной функции при помощи LabVIEW
6. Метод Гаусса-Зейделя
В лабораторной работе метод Гаусса-Зейделя используется для поиска максимума двумерной функции z = exp{[(x – x0)2 + (y – y0)2]/b}. (1) Эта функция симметрична относительно плоскостей x = x0 и y = y0…
Программный продукт, осуществляющий решение задач по дисциплине “Численные методы”
1.3 Метод Гаусса
Суть метода Гаусса состоит в преобразовании системы (6) к равносильной ей системе с треугольной матрицей, из которой затем последовательно (обратным ходом) получаются значения всех неизвестных. ..
..
Разработка программы решения системы линейных уравнений
1.1 Метод Гаусса
Идея метода Гаусса состоит в последовательном исключении неизвестных. Алгоритм решения системы уравнений этим методом проследим на примере. Пример 1. Выбирается ведущее уравнение с коэффициентом при х1, равным 1…
Реализация иерархии классов для решения системы линейных алгебраических уравнений
1.2 Метод Гаусса решения СЛУ
На практике чаще всего используют метод Гаусса построения решений СЛУ…
Решение задач линейной алгебры в Ms Excel
1.2 Метод Гаусса
Алгоритм Метода Гаусса состоит из двух основных частей: прямой ход и обратный ход. Прямой ход заключается в том, что система приводится к треугольному виду (верхняя унитреугольная форма). Обратный ход – непосредственное нахождение неизвестных…
Решение задач линейной алгебры в Ms Excel
1.3 Метод Гаусса в Excel
В Excel Метод Гаусса подробно (по шагам) выполняется только в учебных целях, когда нужно показать, что Вы это умеете. Существует более рациональный способ реализации данного метода в Excel. Решим задачу о рационе в Excel. Формулировка: Допустим…
Существует более рациональный способ реализации данного метода в Excel. Решим задачу о рационе в Excel. Формулировка: Допустим…
Решение систем линейных алгебраических уравнений методом прогонки
1.1 Метод Гаусса
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа: На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме…
Решение систем линейных алгебраических уравнений методом простой итерации
1.1 Метод Гаусса
В разделе « Численные методы линейной алгебры» рассматриваются численные методы решения систем линейных алгебраических уравнений (СЛАУ) и численные методы решения задач на собственные значения и собственные векторы матриц…
Решение системы линейных алгебраических уравнений методом Гаусса средствами языка программирования Visual Basic
Метод Гаусса
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных…
Это метод последовательного исключения переменных…
Решение системы линейных уравнений методом Гаусса и Жордана-Гаусса
Метод Гаусса
Метод Гаусса решения систем линейных уравнений состоит в последовательном исключении неизвестных и описывается следующей процедурой…
Численное интегрирование методом Гаусса
2.6 Метод Гаусса-Кронрода
Недостаток метода Гаусса состоит в том, что он не имеет лёгкого (с вычислительной точки зрения) пути оценки погрешности полученного значения интеграла…
Численное интегрирование функции методом Гаусса
2.6 Метод Гаусса-Кронрода
Недостаток метода Гаусса состоит в том, что он не имеет лёгкого (с вычислительной точки зрения) пути оценки погрешности полученного значения интеграла…
Уничтожение матриц. Исключение матриц (или решение системы… | Соломон Се | Основы линейной алгебры
Исключение матриц(илирешение системы линейных уравнений) является самым первым и фундаментальным навыком.Это, наверное, первый урок из всех курсов
Прежде чем изучать решение систем линейных уравнений , вам действительно нужно ознакомиться со всеми основными терминами, иначе перейти к следующему этапу может быть очень сложно. .
И в этом случае лучший способ узнать об этом — через Википедию.
JFR, основные условия: Гауссовская ликвидация , Gauss-jordan Ликвидация , Aupmented Matrix , Elementary Row , Элементарная матрица , ROW Echeelon Форма (REF) , Снижение Строка Echelon Форма (RREF) , Треугольная форма .
Это
Алгоритм сокращения строкдля решения системы линейных уравнений.
См. вики: Исключение Гаусса
См. простую вики: Исключение Гаусса
Пример: showme.com
для создания типа матрицы, называемой расширенной матрицей .
Затем элементарных операции над строками используются для упрощения матрицы.
Цель исключения Гаусса состоит в том, чтобы получить матрицу в ступенчато-строковой форме .
Если матрица имеет форму строк-ступеней , которая также называется Треугольная форма .
В некоторых определениях исключения Гаусса говорится, что результат матрицы должен быть в уменьшенной ступенчато-строковой форме .
Исключение Гаусса, которое создает уменьшенный результат матрицы строк-ступеней, иногда называется Исключение Гаусса-Жордана .
Для упрощения вот структура:
- Алгоритм:
Исключение Гаусса - Шаг 1: Перепишите систему в расширенную матрицу
- Шаг 2: Упростите матрицу с помощью
Элементарные операции со строками. - Результат:
-
ROW Echelon Формаили -
Уменьшенная форма эшелона
, и если мы сделаем результат только в RREF , поэтому название алгоритма также можно назвать:
- алгоритм:
Исключение Гаусса-Джордана - Шаг 1: Перепишите систему в расширенную матрицу

- Шаг 2: Упростите матрицу с помощью
Элементарные операции со строками. - Результат: Только в
Сокращенная форма эшелона
Элементарные операции со строками используются для упрощения матрицы .
Используются три типа операций со строками:
- Тип 1: Переключение одной строки на другую строки .
- Тип 2: Умножение строки на ненулевое число .
- Тип 3: Добавление строки из другой строки . (!Примечание: вы можете только ДОБАВИТЬ их, но не вычесть , но вы можете ДОБАВИТЬ отрицательное)
Запутанная операция: Посмотрите, где был поставлен отрицательный знак :
Предположим, цель состоит в том, чтобы найти решение для линейной системы ниже:
Сначала нам нужно преобразовать его в форму Augmented Matrix :
Затем мы применяем Elementary Row Operations , и в результате получим Row Echelon Form :
В конце, если мы хотели бы, мы можем далее применить некоторые операции со строками, чтобы получить матрицу в Сокращенная форма эшелона строк :
Чтение этой матрицы говорит нам, что решения для этой системы уравнений возникают, когда x = 2, y = 3, и z = -1.
Обратитесь к этому видео-лекции: REF & RREF.
Неважно это Квадратная Матрица или нет, может быть Диагональ или Главная диагональ , а можно вообще диагональ не рисовать.
Имеет значение только ЧТО ВЫШЕ 1 И ЧТО НИЖЕ 1.
- REF: Для каждого столбца все числа ниже 1 ДОЛЖНЫ БЫТЬ 0. Не имеет значения, какие числа больше 1.
- RREF : Для каждого столбца все числа выше и ниже 1 ДОЛЖНЫ БЫТЬ 0.Нас не волнует, если в столбце нет 1.
Значит, мы добавили в матрицу еще один столбец, представляющий Правую часть системы уравнений, числа справа от знака
=5.
Когда мы применяем исключение к линейным уравнениям , мы работаем с обеими сторонами одновременно. Но для компьютерных программ это часто относится к Левая сторона и помните операции, а. г. умножьте число или сложите уравнения вместе, когда левая сторона будет закончена, примените те же операции к правой стороне.
г. умножьте число или сложите уравнения вместе, когда левая сторона будет закончена, примените те же операции к правой стороне.
Если для данной Матрицы было сказано, что это Расширенная Матрица , мы должны предположить, что Последний Столбец — это Столбец Решения .
- Эквивалентные системы: Линейные системы с ТАКИМ НАБОРОМ РЕШЕНИЙ.
- Эквивалентные матрицы: две матрицы, где одна матрица может быть превращена в другую матрицу с помощью
элементарных операций над строками.
или называется курсор
, или, или, или, илиБазовая переменная.
См. это видео от mathispower4u.
Это означает значение, которое представляет неизвестную переменную в каждом столбце. В столбце нет разворота , если вы не можете получить 1 в этом столбце.
Если в столбце нет сводной точки, это означает, что эта неизвестная переменная столбца может быть любым числом , поэтому мы называем ее свободной переменной .
опорные точки находятся после сокращения строк , а затем возвращаются к Исходной матрице, столбцы С опорными точками называются опорными столбцами .
Все просто: когда вы решаете одну неизвестную переменную в линейной системе, вы подставляете значение обратно в другие уравнения. Мы называем этот процесс обратной заменой .
-
Редукция Гаусса-Жордана
Редукция Гаусса-Жордана является расширением алгоритма исключения Гаусса.Он создает матрицу, называемую , сокращенной формой эшелона строк , следующим образом: после выполнения исключения Гаусса продолжайте, заменяя все ненулевые элементы выше ведущих на ноль. Результирующая матрица выглядит примерно так:
Результирующая матрица выглядит примерно так:
Приведенная выше матрица дает представление о том, чего мы хотим. Обратите внимание, что линия лестницы, проведенная через матрицу, имеет все элементы под ней, равные нулю. Записи, отмеченные символом \(*\), могут принимать любое значение.
Определение 2.6.2. Эшелонная форма уменьшенного ряда.
Матрица представляет собой сокращенную ступенчатую форму строки , если
Каждая ведущая запись является ведущей.
Каждая запись ниже и выше начинается с \(0\text{.}\)
По мере продвижения вниз по матрице ведущие перемещаются вправо.
Любые все нулевые строки находятся внизу.
Для полноты картины мы подробно опишем алгоритм редукции Гаусса-Жордана.Как и при исключении Гаусса, столбцы матрицы обрабатываются слева направо.
Начните с первого столбца. Если все записи равны нулю, перейдите к следующему столбцу справа.

Если, наоборот, в столбце есть ненулевые записи, при необходимости поменять местами строки, чтобы получить ненулевую запись сверху.
Умножьте верхнюю строку на константу, чтобы изменить ненулевую запись на (начальную) единицу.
Если есть ненулевые записи выше или ниже этой (начальной) единицы, используйте элементарную операцию со строками для каждой из них, чтобы изменить ее на ноль.
Теперь рассмотрим часть матрицы ниже верхней строки и правее рассматриваемого столбца: если таких строк или столбцов нет, останавливаемся и алгоритм завершается. В противном случае выполните ту же процедуру на новой матрице.
Пример 2.6.3. Приведение матрицы к сокращенному эшелонированному виду строк.
\(\ начало {выравнивание} \amp \begin{bmatrix} 1\амп 2\амп 3\ 4\амп 5\амп 6\ 7\амп 8\амп 9\ 10 А 12 А 15 \end{bmatrix} \amp \amp \начать{массив}{л} R_2\получает R_2-4R_1\\ R_3\получает R_3-7R_1\\ R_4\получает R_4-10R_1 \конец{массив}\\[6pt] \amp \begin{bmatrix} 1\амп 2\амп 3\ 0 \ампер -3 \ампер -6 \\ 0 \ампер -6 \ампер -12 \\ 0 \амп -8 \ампер -15 \end{bmatrix} \amp \amp \начать{массив}{л} R_2\gets -\tfrac13 R_2 \конец{массив}\\[6pt] \amp \begin{bmatrix} 1\амп 2\амп 3\ 0 \ампер 1 \ампер 2 \\ 0 \ампер -6 \ампер -12 \\ 0 \амп -8 \ампер -15 \end{bmatrix} \amp \amp \начать{массив}{л} R_1\получает R_1-2R_2\\ R_3\получает R_3+6R_2\\ R_4\получает R_4+8R_2 \конец{массив}\\[6pt] \amp \begin{bmatrix} 1 \ампер 0 \ампер -1 \\ 0 \ампер 1 \ампер 2 \\ 0 \ампер 0 \ампер 0 \\ 0 \амп 0 \ампер 1 \end{bmatrix} \amp \amp \начать{массив}{л} R_3\стрелка влево и вправо R_4 \\ \конец{массив}\\[6pt] \amp \begin{bmatrix} 1 \ампер 0 \ампер -1 \\ 0 \ампер 1 \ампер 2 \\ 0 \ампер 0 \ампер 1 \\ 0 \амп 0 \ампер 0 \end{bmatrix} \amp \amp \начать{массив}{л} R_1 \получает R_1+R_3 \\ R_2\получает R_2-2R_3 \конец{массив}\\[6pt] \amp \begin{bmatrix} 1 \ампер 0 \ампер 0 \\ 0 \амп 1 \ампер 0 \\ 0 \ампер 0 \ампер 1 \\ 0 \амп 0 \ампер 0 \end{bmatrix} \end{выравнивание} \)
Пример 2.
 6.4. Помещение другой матрицы в сокращенную ступенчатую форму строк.
6.4. Помещение другой матрицы в сокращенную ступенчатую форму строк.\(\ начало {выравнивание} \amp \begin{bmatrix} 1 \усилитель 2 \усилитель 6 \усилитель 1 \усилитель 4 \усилитель 6\ 2 \усилитель 4 \усилитель 9 \усилитель 2 \усилитель 8 \усилитель 9\ 1 \amp 2 \amp 9 \amp 2 \amp 10 \amp 9 \end{bmatrix}\усилитель \усилитель \начать{массив}{с} R_2 \получает R_2-2R_1\ R_3 \получает R_3-R_1 \конец{массив}\\[6pt] \amp \begin{bmatrix} 1 \усилитель 2 \усилитель 6 \усилитель 1 \усилитель 4 \усилитель 6\ 0 \amp 0 \amp -3 \amp 0 \amp 0 \amp -3 \\ 0 \ амп 0 \ амп 3 \ амп 1 \ амп 6 \ амп 3 \end{bmatrix}\усилитель \усилитель \начать{массив}{с} R_2 \получает -\tfrac13R_2 \конец{массив}\\[6pt] \amp \begin{bmatrix} 1 \усилитель 2 \усилитель 6 \усилитель 1 \усилитель 4 \усилитель 6\ 0 \amp 0 \amp 1 \amp 0 \amp 0 \amp 1 \\ 0 \ амп 0 \ амп 3 \ амп 1 \ амп 6 \ амп 3 \end{bmatrix}\усилитель \усилитель \начать{массив}{с} R_1 \получает R_1 -6R_2\\ R_3 \получает R_3 -3R_2 \конец{массив}\\[6pt] \amp \begin{bmatrix} 1 \amp 2 \amp 0 \amp 1 \amp 4 \amp 0 \\ 0 \amp 0 \amp 1 \amp 0 \amp 0 \amp 1 \\ 0 \amp 0 \amp 0 \amp 1 \amp 6 \amp 0 \end{bmatrix}\усилитель \усилитель \начать{массив}{с} R_1 \получает R_1 - R_3 \конец{массив}\\[6pt] \amp \begin{bmatrix} 1 \amp 2 \amp 0 \amp 0 \amp -2 \amp 0 \\ 0 \amp 0 \amp 1 \amp 0 \amp 0 \amp 1 \\ 0 \amp 0 \amp 0 \amp 1 \amp 6 \amp 0 \end{bmatrix} \end{align}\)
Обратите внимание на шаблон нулевых, 1 и ненулевых элементов после редукции Гаусса-Жордана (начальные элементы выделены красным):
\begin{уравнение*} \left[\begin{массив}{ccccccc} {{\color{red}1}} \amp 0 \amp 0 \amp * \amp 0 \amp \cdots \amp *\\ 0 \amp {\color{red}1} \amp 0 \amp * \amp 0 \amp \cdots \amp *\\ 0 \amp 0 \amp {\color{red}1}\amp * \amp 0 \amp \cdots \amp *\\ 0 \amp 0 \amp 0 \amp 0 \amp {\color{red}1} \amp\cdots \amp *\\ \конец{массив}\справа] \end{уравнение*}
Теперь, когда мы можем представить матрицу в виде сокращенного эшелона строк, давайте посмотрим, что это означает для нахождения всех решений связанной системы линейных уравнений. Помните, что первые столбцы \(n\) соответствуют коэффициентам переменных \(x_1,x_2,\dots,x_n\text{,}\), а последний столбец соответствует константам в правой части уравнений. Каждый столбец либо содержит ведущий, либо нет. Если это так, соответствующая переменная называется ограниченной или базовой . Если нет, переменная называется свободной. Каждой свободной переменной присваивается параметр, который может принимать любое число при поиске решения. Значения переменных с ограничениями затем определяются формой сокращенного эшелона строк.
Помните, что первые столбцы \(n\) соответствуют коэффициентам переменных \(x_1,x_2,\dots,x_n\text{,}\), а последний столбец соответствует константам в правой части уравнений. Каждый столбец либо содержит ведущий, либо нет. Если это так, соответствующая переменная называется ограниченной или базовой . Если нет, переменная называется свободной. Каждой свободной переменной присваивается параметр, который может принимать любое число при поиске решения. Значения переменных с ограничениями затем определяются формой сокращенного эшелона строк.
В качестве примера предположим, что у нас есть система линейных уравнений, расширенная матрица которой имеет следующую сокращенную ступенчатую форму строк:
\begin{уравнение*} \begin{bmatrix} {\ color {red} 1} \amp 2 \amp 0 \amp 1 \amp 0 \amp 1\\ 0 \amp 0 \amp {\color{red}1}\amp 2 \amp 0 \amp 2\\ 0 \amp 0 \amp 0 \amp 0 \amp {\color{red}1} \amp 3 \end{bmatrix} \end{уравнение*}
Обратите внимание, что это означает, что наша система имеет три уравнения и пять неизвестных. Ведущие находятся в столбцах один, три и пять, поэтому \(x_1\text{,}\) \(x_3\) и \(x_5\) являются переменными с ограничениями.Это оставляет \(x_2\) и \(x_4\) свободными переменными. Мы назначаем параметры свободным переменным: \(x_2=s\) и \(x_4=t\text{.}\). Затем строки матрицы определяют ограниченные переменные:
Ведущие находятся в столбцах один, три и пять, поэтому \(x_1\text{,}\) \(x_3\) и \(x_5\) являются переменными с ограничениями.Это оставляет \(x_2\) и \(x_4\) свободными переменными. Мы назначаем параметры свободным переменным: \(x_2=s\) и \(x_4=t\text{.}\). Затем строки матрицы определяют ограниченные переменные:
\(x_5=3\) из нижнего ряда
\(x_3 = 2-2t\) из среднего ряда
\(x_1=1-2s-t\) из верхней строки
Компактный способ записи: \((x_1,x_2,x_3,x_4,x_5) = (1-2s-t,s,2-2t,t,3).\)
Обратите внимание на роль нулей над и под каждой ведущей единицей: оценка переменной с ограничениями включает только свободные переменные.
Подводя итог, можно сказать следующее:
Если приведенная ступенчатая форма строки имеет строку вида \([0,0,\dots,0,1]\text{,}\), то система линейных уравнений не имеет решения.
Если в приведенной эшелонированной форме строк нет свободных переменных, то она выглядит так:
\begin{уравнение*} \begin{bmatrix} 1 \amp 0 \amp 0 \amp \cdots \amp 0 \amp 0 \amp c_1\\ 0 \amp 1 \amp 0 \amp \cdots \amp 0 \amp 0 \amp c_2\\ 0 \amp 0 \amp 1 \amp \cdots \amp 0 \amp 0 \amp c_3\\ \усилитель \усилитель \усилитель \вдоц \\ 0 \amp 0 \amp 0 \amp \cdots \amp 1 \amp 0 \amp c_{n-1}\\ 0 \amp 0 \amp 0 \amp \cdots \amp 0 \amp 1 \amp c_n \end{bmatrix} \end{уравнение*}
и существует единственное решение, а именно \(x_1=c_1, x_2=c_2,\dots x_n=c_n\text{.
 }\)
}\)Если редуцированная ступенчатая форма строки имеет свободные переменные, то существует бесконечное число решений. Действительно, параметр, присвоенный любой свободной переменной, может принимать бесконечное количество значений.
Рассмотрим следующую систему линейных уравнений:
\begin{уравнение*} \начать{массив}{rl} х_1-х_2+2х_3-х_4 \amp = -1 \\ 2x_1+x_2-2x_3-2x_4 \амп = -2 \\ -x_1+2x_2-4x_3+x_4 \амп = 1 \\ 3x_1-3x_4 \амп = -3 \конец{массив} \end{уравнение*}
Затем расширенная матрица преобразуется в уменьшенную ступенчатую форму строк:
\begin{уравнение*} \begin{bmatrix} 1 \амп -1 \ампер 2 \ампер -1 \ампер -1\\ 2 \амп 1 \амп -2 \амп -2 \амп -2\\ -1 \амп 2 \ампер -4 \ампер 1 \ампер 1\\ 3 \amp 0 \amp 0 \amp -3 \amp -3 \end{bmatrix} \end{уравнение*}
\begin{уравнение*} \начать{массив}{rl} R_2 \усилитель\получает R_2-2R_1\\ R_3 \amp\получает R_3+R_1\\ R_4 \amp\gets R_4-3R_1 \конец{массив} \end{уравнение*}
\begin{уравнение*} \begin{bmatrix} 1 \амп -1 \ампер 2 \ампер -1 \ампер -1\\ 0 \amp 3 \amp -6 \amp 0 \amp 0\\ 0 \amp 1 \amp -2 \amp 0 \amp 0\\ 0 \amp 3 \amp -6 \amp 0 \amp 0 \end{bmatrix} \end{уравнение*}
\begin{уравнение*} \начать{массив}{rl} R_2 \amp\gets\tfrac13 R_2\\ \конец{массив} \end{уравнение*}
\begin{уравнение*} \begin{bmatrix} 1 \амп -1 \ампер 2 \ампер -1 \ампер -1\\ 0 \amp 1 \amp -2 \amp 0 \amp 0\\ 0 \amp 1 \amp -2 \amp 0 \amp 0\\ 0 \amp 3 \amp -6 \amp 0 \amp 0 \end{bmatrix} \end{уравнение*}
\begin{уравнение*} \начать{массив}{rl} R_1 \amp\получает R_1 + R_2\\ R_3 \амп\получает R_3- R_2\\ R_4 \amp\gets R_4- 3R_2 \конец{массив} \end{уравнение*}
\begin{уравнение*} \begin{bmatrix} {\ color {red} 1} \amp 0 \amp 0 \amp -1 \amp -1\\ 0 \amp {\color{красный} 1} \amp -2 \amp 0 \amp 0\\ 0 \amp 0 \amp 0 \amp 0 \amp 0\\ 0 \amp 0 \amp 0 \amp 0 \amp 0 \end{bmatrix} \end{уравнение*}
Поскольку \(x_3\) и \(x_4\) являются свободными переменными, мы присваиваем им параметры: \(x_3=s\) и \(x_4=t\text{. }\) Теперь мы можем оценить переменные с ограничениями: \(x_1=-1+t\) (из первой строки) и \(x_2=2s\) (из второй строки). Короче говоря, \((x_1,x_2,x_3,x_4)=(-1+t,2s,s,t)\) для любого выбора \(s\) или \(t\text{.}\)
}\) Теперь мы можем оценить переменные с ограничениями: \(x_1=-1+t\) (из первой строки) и \(x_2=2s\) (из второй строки). Короче говоря, \((x_1,x_2,x_3,x_4)=(-1+t,2s,s,t)\) для любого выбора \(s\) или \(t\text{.}\)
Теперь для проверки подставим эти решения обратно в исходные уравнения. \(\begin{массив}{rlll} x_1-x_2+2x_3-x_4 \amp =\amp (-1+t) - (2s) + 2(s) - (t) \amp= -1\\ 2x_1+x_2-2x_3-2x_4 \amp=\amp 2(-1+t) + 2s -2s-2t \amp= -2\\ -x_1+2x_2-4x_3+x_4 \amp =\amp -(-1+t) +2(2s) -4s+t \amp= 1 \\ 3x_1-3x_4 \amp =\amp 3(-1+t) -3t \amp= -3 \конец{массив}\)
Пример 2.6.5. Матрица, уменьшающая строку.
Следующий пример представляет собой сокращение строки матрицы. Обратите внимание, как он движется слева направо в столбцах, и каждый столбец с ведущей единицей имеет нули сверху и снизу, когда алгоритм завершает работу.
Рисунок 2.6.6. Строка матрицы сама сокращается наГаусс Суммирование | Поговорим о науке
Суммирование Гаусса
Суммарная сумма Гаусса названа в честь Иоганна Карла Фридриха Гаусса. Он был немецким математиком. Гаусс — один из самых влиятельных математических мыслителей в истории.Легенда гласит, что Гаусс придумал новый метод суммирования последовательностей в очень молодом возрасте. Легенда гласит, что его учитель математики попросил класс сложить числа от 1 до 100. Другими словами, учитель хотел, чтобы они сложили 1 + 2 + 3 + 4 + 5… вплоть до 100!
Он был немецким математиком. Гаусс — один из самых влиятельных математических мыслителей в истории.Легенда гласит, что Гаусс придумал новый метод суммирования последовательностей в очень молодом возрасте. Легенда гласит, что его учитель математики попросил класс сложить числа от 1 до 100. Другими словами, учитель хотел, чтобы они сложили 1 + 2 + 3 + 4 + 5… вплоть до 100!
Учитель предполагал, что это займет у учеников очень много времени. Подумайте, сколько времени вам понадобится, чтобы сложить все числа от 1 до 100 одно за другим. Однако Гаусс ответил 5050 почти сразу.
Эта история может быть не совсем правдой. Но это напоминает нам, что самые младшие ученики иногда открывают новые математические закономерности. Теперь давайте подумаем о шаблоне, который Гаусс использовал для быстрого решения этой проблемы.
Хитрость, которую использовал Гаусс для решения этой задачи, заключается в том, что не имеет значения, в каком порядке мы складываем числа. В каком бы порядке мы ни следовали, мы получим один и тот же результат.
В каком бы порядке мы ни следовали, мы получим один и тот же результат.
Например:
2 + 3 имеет тот же ответ, что и 3 + 2.
Мы можем переставить числа от 1 до 100 хитрым способом. Это может помочь нам добавить их быстрее. Вот простой пример, который покажет вам, как работает эта стратегия группировки.
Допустим, вы хотите сложить числа от 1 до 10.
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = ?
Шаблон, показывающий сложение пар от одного до десяти (© Let’s Talk Science, 2021).
Возможно, вы заметили кое-что странное.Каждая из этих пар в сумме дает 11. Итак, мы можем думать о нашей задаче так:
(1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) = ?
(11) + (11) + (11) + (11) + (11) = ?
Так как у нас есть 5 пар, наш ответ
11 + 11 + 11 + 11 + 11 = 11 х 5 = 55
Что ж, это куда-то идет!
Давайте посмотрим на это по-другому. Вместо того, чтобы выстраивать числа в один ряд. Расставь цифры в два ряда.В первом ряду числа увеличиваются. Во втором ряду числа уменьшаются. От 1 до 10 это будет выглядеть так.
Вместо того, чтобы выстраивать числа в один ряд. Расставь цифры в два ряда.В первом ряду числа увеличиваются. Во втором ряду числа уменьшаются. От 1 до 10 это будет выглядеть так.
Числа от 1 до 10 выстроены в порядке возрастания в верхнем ряду. Числа от 10 до 1 выстраиваются в порядке убывания в нижнем ряду.
Теперь суммируйте каждый столбец.
Изображение – текстовая версияСумма каждого столбца равна 11.
Сумма всех приведенных выше чисел равна числу пар , умноженному на сумму каждой пары .Но нам нужна сумма только одной строки, а не обеих строк. Итак, нам нужно разделить наш ответ на 2.
Мы можем записать это как:
Изображение – текстовая версия Сумма — это количество пар, умноженное на сумму каждой пары, и эта сумма делится на 2. В нашем случае десять умножается на одиннадцать, а затем делится на два. Это дает окончательную сумму 55.
Это дает окончательную сумму 55.
Мы можем использовать алгебру , чтобы представить этот шаблон. Алгебра использует буквы и другие символы для представления чисел в уравнениях.Мы можем использовать букву n , чтобы указать, сколько чисел в нашем списке. Это самое большое число. В нашем примере n будет равно 10. Количество пар будет равно этому числу, деленному на 2. Вы заметите, что размер пары равен количеству пар плюс 1. Таким образом, мы могли бы написать использовать n для записи
.(количество пар) x (сумма каждой пары) = n/2 x (n +1)
Но помните, как и раньше, нам нужна сумма только одной строки, а не обеих. Делим формулу выше на 2 и получаем:
Изображение – текстовая версияn вне скобки, за которой следует n плюс один внутри скобки.Это делится на 2.
Можем ли мы сделать то же самое для суммы, которая является нечетным числом, скажем, 67? Попробуйте сами, прежде чем смотреть ответ ниже.
Вопрос:
1 + 2 + 3 + 4 ….. 66 + 67 =?
(Ответ внизу страницы)
Шаблон, показывающий сложение пар от одного до десяти (© Let’s Talk Science, 2021).Реальные приложения
Эта задача является примером нахождения суммы арифметической последовательности .Последовательность – это набор упорядоченных чисел. В арифметической последовательности расстояние между любыми двумя последовательными числами одинаково. Мы можем использовать метод Гаусса, чтобы найти сумму любой арифметической прогрессии.
Последовательность извлечения кусочков пиццы (Источник: Lebazele через iStockphoto).
Нахождение суммы последовательности может помочь людям решить множество реальных задач. Компании находят сумму последовательностей, чтобы оценить затраты или доход. Даже расчет стоимости проезда на такси представляет собой сумму арифметической последовательности. Вы начинаете с базового тарифа. Ваша общая стоимость увеличивается на ту же сумму каждую минуту.
Вы начинаете с базового тарифа. Ваша общая стоимость увеличивается на ту же сумму каждую минуту.
Нахождение суммы последовательности также является распространенным вопросом информатики. Компьютерщики используют для этого метод Гаусса. Вопрос «Отсутствующий номер» — это распространенный вопрос технического собеседования. Для ее решения нужен метод Гаусса. Многие из этих приложений используют сложные на вид формулы. Однако на самом деле они просто используют метод Гаусса для нахождения суммы последовательности.
ОТВЕТ
1 + 2 + 3 + 4……66 + 67 = ?
n = 67, n + 1 = 68
п(п + 1)/2
67 х 68/2
= 2 278
Метод Гаусса — Математическая энциклопедия
Метод последовательного исключения неизвестных при решении системы линейных уравнений, впервые введенный К.{0$} }
f _ {j} (x) - a _ {j} = \
a _ {j1} x _ {1} + \dots + a _ {jn} x _ {n} - a _ {j} = 0,
$$
$$ j = 1 \ точек м, $$
где $ a _ {ji} , a _ {j} $
являются элементами произвольного поля $P$. Без ограничения общности можно считать, что $ a _ {11} \neq 0 $.
Метод Гаусса работает следующим образом. Вычитается первое уравнение набора, умноженное на $ a _ {21} / a _ {11} $
почленно из второго уравнения; затем вычитается первое уравнение, умноженное на $ a _ {31} / a _ {11} $
из третьего уравнения; $ \точки, $
затем вычитается первое уравнение, умноженное на $ a _ {m1} / a _ {11} $
от $м$-
уравнение.{0} $
для $ U = U _ {i} + U _ {k} $
представляет собой процедуру одновременного исключения двух неизвестных $ x _ {i} $
и $x_{k}$.
Например, пусть $ i = 1 $
и $k = 2$.
Если также
Без ограничения общности можно считать, что $ a _ {11} \neq 0 $.
Метод Гаусса работает следующим образом. Вычитается первое уравнение набора, умноженное на $ a _ {21} / a _ {11} $
почленно из второго уравнения; затем вычитается первое уравнение, умноженное на $ a _ {31} / a _ {11} $
из третьего уравнения; $ \точки, $
затем вычитается первое уравнение, умноженное на $ a _ {m1} / a _ {11} $
от $м$-
уравнение.{0} $
для $ U = U _ {i} + U _ {k} $
представляет собой процедуру одновременного исключения двух неизвестных $ x _ {i} $
и $x_{k}$.
Например, пусть $ i = 1 $
и $k = 2$.
Если также
$$ \Delta _ {12} = \left | \begin{массив}{ll} а _ {11} & _ {21} \\ а _ {12} & _ {22} \\ \конец{массив} \право | \neq 0, $$
тогда строки матрицы
$$ \влево \| \begin{массив}{cccccc} - \Delta _ {23} &\Delta _ {13} &- \Delta _ {12} & 0 &\dots & 0 \\ - \Delta _ {24} &\Delta _ {14} & 0 &- \Delta _ {12} &\dots & 0 \\ \точки &\точки &\точки &\точки &{} &\точки \\ - \Delta _ {2m} &\Delta _ {1m} & 0 & 0 &\dots &- \Delta _ {12} \\ \конец{массив} \право\| , $$
где
$$ \Дельта _ {rs} = \ \влево | \begin{массив}{ll} а _ {r1} & а _ {s1} \\ а _ {r2} & а _ {s2} \\ \конец{массив} \право | , $$
можно использовать для получения $ ( U _ {1} + U _ {2} ) $-
свертка системы $S^{0}$. {0} $
могут быть решены с помощью алгоритмов, являющихся обобщением метода Гаусса.
{0} $
могут быть решены с помощью алгоритмов, являющихся обобщением метода Гаусса.
Каталожные номера
| [1] | К.Ф. Gauss, "Beiträge zur Theorie der Alexandrischen Gleichungen", Werke , 3 , K. Gesellschaft Wissenschaft. Göttingen (1876) pp. 71–102 |
| [2] | А.Г. Курош, "Высшая алгебра", МИР (1972) (Перевод с русского) |
| [3] | 5 D.К. Фаддеев, В.Н. Фаддеева, "Вычислительные методы линейной алгебры", Freeman (1963) (Перевод с русского) |
| [4] | С.Н. Черников, Lineare Ungleichungen, Deutsch. Verlag Wissenschaft. (1971) (перевод с русского) |
Существует несколько вариантов этого метода, в основном основанных на соображениях практической реализации (например, методы Краута и Дулитла) или эффективности (например, метод Холески для симметричных систем).
В западной литературе понятия LU-разложения, прямого исключения и обратной замены часто ассоциируются с методом Гаусса (который также называют методом исключения Гаусса). Рассмотрим частный случай, когда матрица коэффициентов $A$ в системе $ A x = a $ является квадратной матрицей $ ( m = n ) $. Тогда под LU-разложением понимается разложение $A$ в нижне- и верхнетреугольную матрицу $L$ и $U$, т. е. $A = L U $. Под прямой элиминацией и обратной заменой понимаются решения треугольных систем $ L y = a $ и $Ux=y$, соответственно.{2} / 2 $ провалы соответственно.
Для численных целей недостаточно убедиться, что коэффициенты $ a _ {11} $,
и т. д., опорные точки, просто ненулевые, но они наилучшие из возможных; если абсолютно наибольший $ a _ {j} $
используется в качестве опорного, то это называется частичным поворотом. Если в качестве опорного используется абсолютно самый большой элемент во всей матрице (или подматрице на более поздних этапах), это называется полным поворотом. Частичный поворот для возможности LU-разложения в случае, если матрица $ A $
имеет сингулярные ведущие главные подматрицы, равносильные перестановке строк.{2} ) $
сравнения. Можно показать, что с такой стратегией метод численно устойчив (см. Устойчивость вычислительного алгоритма; Устойчивость вычислительного процесса).
Частичный поворот для возможности LU-разложения в случае, если матрица $ A $
имеет сингулярные ведущие главные подматрицы, равносильные перестановке строк.{2} ) $
сравнения. Можно показать, что с такой стратегией метод численно устойчив (см. Устойчивость вычислительного алгоритма; Устойчивость вычислительного процесса).
Отличная книга по численной линейной алгебре — [a1]. Проблема численной устойчивости при исключении Гаусса обсуждается в [a6].
Подпрограммы Fortan можно найти в [a4]; более старую версию Algol см. в [a5].
Каталожные номера
| [a1] | Г.Х.Голуб, С.Ф. ван Лоан, "Матричные вычисления", Северный Оксфорд, академик. (1983) |
| [a2] | Дж.Х. Уилкинсон, "Алгебраическая проблема собственных значений", Clarendon Press (1965) |
| [a3] | Г. Странг, "Линейная алгебра и ее приложения", акад. Press (1976) Press (1976) |
| [a4] | Х. Донгарра, Дж. Р. Банч, К. Б. Молер, Г. У. Stewart, "Руководство пользователя LINPACK", SIAM (1978) |
| [a5] | J.H. Wilkinson, C. Reinsch, "Руководство по автоматическим вычислениям", 2. Линейная алгебра , Springer (1971) |
| [a6] | P.A. Bussinger, «Мониторинг численной устойчивости исключения Гаусса» Numer. Мат. , 16 (1971) стр. 360–361 |
Как цитировать эту запись:
Метод Гаусса. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Gauss_method&oldid=47050
Определение Гаусса | Law Insider
Относится к
GaussWARO означает «недели после даты вступления в силу для присуждения договорного иска».
Прозрачное покрытие означает прозрачное покрытие, разработанное для обеспечения окончательного блеска и устойчивости системы покрытия;
Верхнее покрытие означает покрытие, которое наносится поверх грунтовки на аэрокосмический аппарат или его компонент для внешнего вида, идентификации, маскировки или защиты. Верхние покрытия, которые определяются как специальные покрытия, не включаются в это определение.
Верхние покрытия, которые определяются как специальные покрытия, не включаются в это определение.
Кормовой огонь означает белый огонь, расположенный как можно ближе к корме, освещающий непрерывным светом дугу горизонта в 135° и установленный таким образом, чтобы светить огнем 67.5 градусов справа на корму с каждого борта судна.
Кровоточащая лошадь означает лошадь, у которой во время или после упражнений или скачек наблюдается кровотечение из одной или обеих ноздрей, или изо рта, или кровотечение в просвете дыхательных путей.
Колония означает улей и его оборудование и принадлежности, включая пчел, соты, мед, пыльцу и расплод.
ПРАЧЕЧНАЯ означает общественное место с монетными стиральными машинами, центробежными сушилками или машинами для химической чистки; и
Костер означает небольшой костер на открытом воздухе, предназначенный для отдыха или приготовления пищи, за исключением костра, предназначенного для удаления древесных отходов или мусора.
Мы/Нас/Наш означает TATA AIG General Insurance Company Limited.
LINZ означает Land Information New Zealand.
Розыгрыш означает форму бинго, в которой один или несколько призов выигрываются одним или несколькими лицами, купившими лотерейный билет. Один или несколько победителей розыгрыша определяются путем извлечения корешка билета или другого отрывного участка из емкости, содержащей корешки билетов или съемные участки, соответствующие всем билетам, проданным для участия в розыгрыше.«Розыгрыш» не включает розыгрыш корешка билета или другой отделяемой части билета, приобретенного для участия в профессиональном спортивном мероприятии, если применимы оба следующих условия: и рентабельная эксплуатация физических активов на основе непрерывной инвентаризации и оценки состояния, а также инвестиций для достижения установленных целей производительности.
Покрытие воздушной сушки означает покрытие, которое высушивается с использованием воздуха или принудительного теплого воздуха при температуре до 1940F (900C).
SEIFA означает Социально-экономические индексы для регионов, время от времени публикуемые Австралийским бюро статистики на его веб-сайте в Интернете.
Брюс Уотерфолл станет недееспособным или если Джон К. «Брюс» Уотерфолл покинет свою должность в Prime III, LP или продаст свою долю в ней, он должен немедленно уведомить Правление и Комиссию и заставить своего преемника подать соответствующий запрос о неваде. игровые приложения с доской и комиссией.
Dreyfus означает Dreyfus Corporation и ее филиалы, включая Dreyfus Service Corporation.
LHSIA означает Закон об интеграции местных систем здравоохранения от 2006 г. и правила, принятые в соответствии с ним, поскольку в него и в них могут время от времени вноситься поправки;
карликовость означает медицинское или генетическое заболевание, в результате которого рост взрослого человека составляет 4 фута 10 дюймов (147 сантиметров) или меньше;
Сплошные рубки означает заготовку древесины способом, при котором удаляются все деревья диаметром до двух дюймов на уровне груди.
Серая вода означает сточные воды, собранные отдельно от канализационного потока, поступающего из стиральной машины, ванны, душа и раковины, но не включая сточные воды из кухонной раковины, посудомоечной машины или туалета.
Парикмахерская означает любое одно или любое сочетание следующих действий, когда они совершаются с телом человека для компенсации, а не для лечения болезни, бритье, придание формы и стрижка бороды; стрижку, опаливание, мытье шампунем или окрашивание волос или нанесение на них лосьонов; аппликации, обработка или массаж лица, шеи или кожи головы с использованием масел, кремов, лосьонов, косметических средств, антисептиков, порошков, глин или других препаратов в связи с бритьем, стрижкой или подравниванием волос или бороды.Термин «парикмахерская» не применяется к действиям, описанным выше, когда они выполняются любым лицом в его доме, если такие услуги не предлагаются публике.
Panchayat означает учреждение (как бы оно ни называлось) самоуправления, созданное в соответствии со статьей 243B для сельских районов;
SAHRC означает Южноафриканскую комиссию по правам человека.
DG означает генерального директора ESIC под административным контролем Министерства труда и занятости
Молочная ферма означает площадь здания площадью 100 м² или более, используемую для производства и переработки молока;
Карл Фридрих Гаусс и метод наименьших квадратов
Др.Норман Винсент Пил, автор книги «Сила позитивного мышления », придумал фразу: «Стреляйте в луну. Даже если ты промахнешься, ты приземлишься среди звезд». Хотя он, вероятно, не имел в виду немецкого математика 19-го века Карла Фридриха Гаусса при разработке этого чувства, он вполне мог иметь его. На самом деле, в случае с Гауссом было бы более уместно сказать «выстрелить в комету», в данном случае в комету Цереры, и, как оказалось, математическому гению не нужно было слишком беспокоиться о том, чтобы промахнуться.
Карл Фридрих Гаусс родился 30 апреля 1777 года в Брансуике.С юных лет его способности к математике были неоспоримы. Он был единственным ребенком не из богатой семьи. Наоборот, именно его расчетливая доблесть позволила ему выделиться и заручиться финансовой поддержкой власть имущих, в том числе герцога Брауншвейгского уже в 1791 году. на протяжении всей его жизни. Благодаря финансовой помощи герцога Гаусс смог изучать математику в Геттингенском университете.
Он был единственным ребенком не из богатой семьи. Наоборот, именно его расчетливая доблесть позволила ему выделиться и заручиться финансовой поддержкой власть имущих, в том числе герцога Брауншвейгского уже в 1791 году. на протяжении всей его жизни. Благодаря финансовой помощи герцога Гаусс смог изучать математику в Геттингенском университете.
В начале своей карьеры Гаусс уже занимался серьезными исследованиями в области математики и астрономии. В зеленом возрасте тридцати двух лет он опубликовал свой метод расчета орбит небесных тел. При этом он использовал метод наименьших квадратов, утверждая, что знал об этом фундаментальном математическом подходе еще в 1795 году, когда ему было всего 18 лет.
То, что Гаусс первым определил метод наименьших квадратов, оспаривалось в его время.Адриан-Мари Лежандр впервые опубликовал версию метода в 1805 году. Короче говоря, Гаусс довел свое определение до крайности, чего не делал Лежандр. И именно Гаусс выиграл великие дебаты о кометах. (Вы знали, что в конце концов я туда доберусь, верно?) Позвольте мне объяснить.
(Вы знали, что в конце концов я туда доберусь, верно?) Позвольте мне объяснить.
Карл Фридрих Гаусс использовал свой метод анализа наименьших квадратов, чтобы правильно предсказать, где снова появится Церера, что позволило Францу Ксавьеру фон Ач определить ее местонахождение. Гауссу было всего 24 года, когда он завершил свой анализ, и он был единственным, кто правильно предсказал положение Цереры. Он продолжал проводить много исследований в области астрономии, в частности, опубликовав работу по вычислению орбит.

Среди других достижений Гаусса — демонстрация того, почему земной шар, растянутый на плоской карте, никогда не может быть пропорционален. По той же причине невозможно полностью завернуть баскетбольный мяч в подарочную упаковку — все дело в кривизне плоского объекта по сравнению с кривизной сферического объекта. Гаусс назвал свое открытие «Теорема Эгрегиум», что на латыни означает «замечательная теорема». Он смог присвоить объектам числовую фигуру, называемую «гауссовой кривизной». При этом он определил, что объекты с одинаковой внутренней кривизной могут быть переданы.Например, вы можете свернуть лист бумаги в трубку, потому что трубка и плоский лист бумаги имеют одинаковую внутреннюю кривизну. Этот факт объясняет, почему печатные цилиндры одинаково работают при переносе слов на страницу. Но этого нельзя сказать о сферах и плоских объектах, потому что их кривизна Гаусса различна.
Гений Гаусса был сверхъестественным. К сожалению, он перестал публиковать многие из своих открытий, поэтому его мысли, эксперименты и результаты не были известны до его смерти, когда другие просеивали его вещи. Это, в сочетании с тем фактом, что Гаусс является одним из величайших математиков и ученых всех времен, делает его работы исключительным дополнением к любой коллекции.
Это, в сочетании с тем фактом, что Гаусс является одним из величайших математиков и ученых всех времен, делает его работы исключительным дополнением к любой коллекции.
видео история адвентистской миссии 2021.
Миссионерские истории Шарлотты Ишканян для адвентистской миссии СЛУЖЕНИЕ УПРАВЛЕНИЯ ОТДЕЛЕНИЕ ЦЕРКВИ АДВЕНТИСТОВ СЕДЬМОГО ДНЯ. Вместе они открыли новый объект в Перл-Сити. 231 377 лайков · 256 говорили об этом · 1 293 были здесь. 0:00 / 4:08:40 •.Истории 2021 года; Директора отделов женского служения Наша новая всемирная команда руководителей женского служения. Информация о школах: субботняя школа, урок 8, 3 квартал 2021 года. com размещен. БОЛЬШЕ Юго-Западный адвентистский университет недавно получил 4 миллиона долларов. Почти 90 процентов прихожан церкви дивизиона проживает в Индонезии и на Филиппинах, что делает остальную часть этой территории практически недоступной. Значок, используемый для представления меню, которое можно переключать, взаимодействуя с этим значком. С помощью ежедневных видеороликов, в которых рассказывается об Иисусе, Джей стал известен в социальной сети, пользующейся успехом среди подростков.Он включает в себя практические занятия и предложения, которые побуждают детей хотеть сказать спасибо Богу. Поделитесь с производителем попкорна. Опубликовано 30 апреля 2021 г. Адвентистской миссией 30 апреля 2021 г. Поддержка миссионерской деятельности церкви адвентистов седьмого дня всегда была частью программы субботней школы. О нас Пресса Авторское право Связаться с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторское право Связаться с нами Авторы. 9 декабря 2021 г.Апрель 2021 г. - Адвентистская миссия в Америке. Мы узнаем, что богатство — это средство, хорошая вещь в руках людей, посвятивших свою жизнь исполнению воли Бога. Пожертвовать онлайн Подпишитесь на новости о миссии Новости и материалы Раскраска банка миссии 1-й квартал 2022 года: Привет, до свидания, я люблю тебя Страница раскраски банка миссии 4-й квартал 2021 года: последнее приглашение страница-раскраска банка миссии 3-й квартал 2021 года: улыбки и песни раскраска банка миссии Страница 2-й квартал 2021 года: Обучение стоматолога.
С помощью ежедневных видеороликов, в которых рассказывается об Иисусе, Джей стал известен в социальной сети, пользующейся успехом среди подростков.Он включает в себя практические занятия и предложения, которые побуждают детей хотеть сказать спасибо Богу. Поделитесь с производителем попкорна. Опубликовано 30 апреля 2021 г. Адвентистской миссией 30 апреля 2021 г. Поддержка миссионерской деятельности церкви адвентистов седьмого дня всегда была частью программы субботней школы. О нас Пресса Авторское право Связаться с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторское право Связаться с нами Авторы. 9 декабря 2021 г.Апрель 2021 г. - Адвентистская миссия в Америке. Мы узнаем, что богатство — это средство, хорошая вещь в руках людей, посвятивших свою жизнь исполнению воли Бога. Пожертвовать онлайн Подпишитесь на новости о миссии Новости и материалы Раскраска банка миссии 1-й квартал 2022 года: Привет, до свидания, я люблю тебя Страница раскраски банка миссии 4-й квартал 2021 года: последнее приглашение страница-раскраска банка миссии 3-й квартал 2021 года: улыбки и песни раскраска банка миссии Страница 2-й квартал 2021 года: Обучение стоматолога. Пост 10: Помни, не забывай - Обсуждение видео HopeSS.7 миллионов адвентистов. Приоритеты адвентистской миссии (включая основание церквей и важность миссионерских пожертвований), говоря о задачах миссии, приоритетах и деятельности в комитетах, лагерных собраниях и других церковных собраниях. Свяжитесь с Адвентистской миссией. Откройте для себя духовные ресурсы, которые помогут вам расти. 231 374 лайков · 254 говорили об этом · 1 293 были здесь. В ознаменование 105-летия «Раздачи видения» церкви адвентистов седьмого дня и миру. «Давай посадим этот кокос и заключим сделку с Богом», — сказал я Анджело.Программа YEM Vespers отмечает миссионерские истории и крещения и освещает латиноамериканское служение. Мы также получим представление о том, что происходит сегодня!. org — официальный сайт всемирной церкви адвентистов седьмого дня. От всемирной гуманитарной деятельности и передовых миссионеров до спутникового телевидения и коротковолнового радио до тысяч школ, больниц и. Эта неделя в адвентистской истории (17 декабря 2021 г.
Пост 10: Помни, не забывай - Обсуждение видео HopeSS.7 миллионов адвентистов. Приоритеты адвентистской миссии (включая основание церквей и важность миссионерских пожертвований), говоря о задачах миссии, приоритетах и деятельности в комитетах, лагерных собраниях и других церковных собраниях. Свяжитесь с Адвентистской миссией. Откройте для себя духовные ресурсы, которые помогут вам расти. 231 374 лайков · 254 говорили об этом · 1 293 были здесь. В ознаменование 105-летия «Раздачи видения» церкви адвентистов седьмого дня и миру. «Давай посадим этот кокос и заключим сделку с Богом», — сказал я Анджело.Программа YEM Vespers отмечает миссионерские истории и крещения и освещает латиноамериканское служение. Мы также получим представление о том, что происходит сегодня!. org — официальный сайт всемирной церкви адвентистов седьмого дня. От всемирной гуманитарной деятельности и передовых миссионеров до спутникового телевидения и коротковолнового радио до тысяч школ, больниц и. Эта неделя в адвентистской истории (17 декабря 2021 г. ) На этой неделе мы узнаем о некоторых усилиях, предпринятых Алонзо Т. Молитвенным собранием одиноких адвентистов.— Я украл это, — сказал Антонио с широкой улыбкой. Посетите наш новый веб-сайт 2021 года, содержащий десятки тысяч отсканированных и оцифрованных корреспонденций, документов, писем и фотографий из Уайта. Отчет секретаря YEM посвящен членству, миссионерам, обучению и воздействию коронавируса. Играть Скачать. Лучан работал субподрядчиком с Simpleupdates, будучи одним из программистов программного обеспечения Adventist Church Connect. Канал Blacksdahistory на YouTube стремится предоставлять бесплатные видеоролики об истории афроамериканских адвентистов седьмого дня.Им нужно взирать на Него, Который также страдал от грешников (Евр. Сонора, Калифорния - Добровольцы Adventist Health Sonora (AHS) действительно принесли домой дух Щедрого вторника, поскольку они помогли отметить важную веху для больницы, даже имея дело с. Основатели являются членами церкви АСД, однако Adventist Online не является частью или официально не связан с Генеральной конференцией адвентистов седьмого дня со штаб-квартирой в Силвер-Спринг, штат Мэриленд.
) На этой неделе мы узнаем о некоторых усилиях, предпринятых Алонзо Т. Молитвенным собранием одиноких адвентистов.— Я украл это, — сказал Антонио с широкой улыбкой. Посетите наш новый веб-сайт 2021 года, содержащий десятки тысяч отсканированных и оцифрованных корреспонденций, документов, писем и фотографий из Уайта. Отчет секретаря YEM посвящен членству, миссионерам, обучению и воздействию коронавируса. Играть Скачать. Лучан работал субподрядчиком с Simpleupdates, будучи одним из программистов программного обеспечения Adventist Church Connect. Канал Blacksdahistory на YouTube стремится предоставлять бесплатные видеоролики об истории афроамериканских адвентистов седьмого дня.Им нужно взирать на Него, Который также страдал от грешников (Евр. Сонора, Калифорния - Добровольцы Adventist Health Sonora (AHS) действительно принесли домой дух Щедрого вторника, поскольку они помогли отметить важную веху для больницы, даже имея дело с. Основатели являются членами церкви АСД, однако Adventist Online не является частью или официально не связан с Генеральной конференцией адвентистов седьмого дня со штаб-квартирой в Силвер-Спринг, штат Мэриленд. com имеет PDF-файлы Primary Treasure, еженедельного журнала для читателей для детей от 6 до 9 лет и «Наш маленький друг», адвентистский журнал для детей от рождения до 5 лет.Еженедельные миссионерские истории являются неотъемлемой частью адвентистских субботних школ по всему миру. Union College, адвентистское учебное заведение в Соединенных Штатах, предлагает совершенно уникальную степень, в которой идеально сочетаются приключения, образование и служение. Обзор адвентистской миссии, 1 мая 2021 г. — Как НЕ саботировать миссионерские фильмы Предварительный просмотр remove-circle Поделиться или встроить этот элемент. Ежемесячное миссионерское видео - Новый рост в Северной Азии. Подробности о школах: история миссии субботней школы, 3 квартал 2021 г. Адвентистская миссия; Журнал Mission 360° DVD Mission Spotlight®; Поделитесь идеей истории; Истории Mission 360 теперь на вашем языке! Закрыть Загрузить.Lucian Web Service Intercer с гордостью спонсируется Lucian Web Service - Professional Web Services, WordPress Websites, Marketing and Affiliate Info.
com имеет PDF-файлы Primary Treasure, еженедельного журнала для читателей для детей от 6 до 9 лет и «Наш маленький друг», адвентистский журнал для детей от рождения до 5 лет.Еженедельные миссионерские истории являются неотъемлемой частью адвентистских субботних школ по всему миру. Union College, адвентистское учебное заведение в Соединенных Штатах, предлагает совершенно уникальную степень, в которой идеально сочетаются приключения, образование и служение. Обзор адвентистской миссии, 1 мая 2021 г. — Как НЕ саботировать миссионерские фильмы Предварительный просмотр remove-circle Поделиться или встроить этот элемент. Ежемесячное миссионерское видео - Новый рост в Северной Азии. Подробности о школах: история миссии субботней школы, 3 квартал 2021 г. Адвентистская миссия; Журнал Mission 360° DVD Mission Spotlight®; Поделитесь идеей истории; Истории Mission 360 теперь на вашем языке! Закрыть Загрузить.Lucian Web Service Intercer с гордостью спонсируется Lucian Web Service - Professional Web Services, WordPress Websites, Marketing and Affiliate Info. 22-23 мая Колумбийская унионная конференция провела свое 28-е пятилетнее собрание избирательных округов. Школьные часы. «ЗАЯКОРЯ В НАДЕЖДЕ С ФР. ССЫЛКИ на видео из архива. Наша миссия обусловлена нашим видением изменения опыта наших сообществ в области здравоохранения путем улучшения здоровья, расширения взаимодействия и повышения доступности медицинской помощи. ПОМНИТЕ о здоровье вашего ребенка от Clair Sanches-Schutte.Сгорела половина госпиталя, который у нас там был. Узнайте, как преобразовать свое сообщество, чтобы жить дольше и лучше. После того, как AdventHealth и другие системы здравоохранения приостановили действие мандатов на вакцинацию, разговор с Джейсоном Хайнсом о вакцинах и свободе. 1 миллиард человек, в том числе 1. Найдите кнопку «Другие языки», чтобы найти свой. org предлагает еженедельный журнал Guide в формате PDF, а также игры для печати и видеоблоги от редакторов и. На этой неделе мы узнаем об Уильяме Амброузе Спайсере (1865–1952), миссионере и администраторе адвентистской церкви.
22-23 мая Колумбийская унионная конференция провела свое 28-е пятилетнее собрание избирательных округов. Школьные часы. «ЗАЯКОРЯ В НАДЕЖДЕ С ФР. ССЫЛКИ на видео из архива. Наша миссия обусловлена нашим видением изменения опыта наших сообществ в области здравоохранения путем улучшения здоровья, расширения взаимодействия и повышения доступности медицинской помощи. ПОМНИТЕ о здоровье вашего ребенка от Clair Sanches-Schutte.Сгорела половина госпиталя, который у нас там был. Узнайте, как преобразовать свое сообщество, чтобы жить дольше и лучше. После того, как AdventHealth и другие системы здравоохранения приостановили действие мандатов на вакцинацию, разговор с Джейсоном Хайнсом о вакцинах и свободе. 1 миллиард человек, в том числе 1. Найдите кнопку «Другие языки», чтобы найти свой. org предлагает еженедельный журнал Guide в формате PDF, а также игры для печати и видеоблоги от редакторов и. На этой неделе мы узнаем об Уильяме Амброузе Спайсере (1865–1952), миссионере и администраторе адвентистской церкви. Но если Божье дело быстро закончится или умрет на этой земле, то этот кокос. Валентин рассказал историю об исцелении хромого библейского человека. Рейтинг 4 из 4 звезд Charity Navigator. Кроме календаря и футбола особо ничего особенного нет. Чтобы достичь группы профессиональных людей, которые по разным причинам не включили церковь в свои сердца и живут в этом районе высшего среднего класса, у людей, кажется, есть все, что им нужно. Загрузите чтения и используйте их во время богослужений, чтобы помочь объяснить пожертвования на день и передать духовное послание, стоящее за поклонением через пожертвования.поделиться с Facebook. Десятина и пожертвования Генеральной конференции Чтение видео за 3 квартал 2021 г. Поделиться в Pinterest. 3 года назад. 1849) обеспечивает вдохновение и информацию для всемирной церкви через различные средства массовой информации, включая печать, веб-сайты, приложения и аудио- и видеоплатформы. На момент написания этой истории Ивану было 11 лет, а Саре 9 лет. Из-за пандемии и мер по социальному дистанцированию, которые продолжают действовать на территории союза восьми штатов, двухдневная встреча прошла виртуально.
Но если Божье дело быстро закончится или умрет на этой земле, то этот кокос. Валентин рассказал историю об исцелении хромого библейского человека. Рейтинг 4 из 4 звезд Charity Navigator. Кроме календаря и футбола особо ничего особенного нет. Чтобы достичь группы профессиональных людей, которые по разным причинам не включили церковь в свои сердца и живут в этом районе высшего среднего класса, у людей, кажется, есть все, что им нужно. Загрузите чтения и используйте их во время богослужений, чтобы помочь объяснить пожертвования на день и передать духовное послание, стоящее за поклонением через пожертвования.поделиться с Facebook. Десятина и пожертвования Генеральной конференции Чтение видео за 3 квартал 2021 г. Поделиться в Pinterest. 3 года назад. 1849) обеспечивает вдохновение и информацию для всемирной церкви через различные средства массовой информации, включая печать, веб-сайты, приложения и аудио- и видеоплатформы. На момент написания этой истории Ивану было 11 лет, а Саре 9 лет. Из-за пандемии и мер по социальному дистанцированию, которые продолжают действовать на территории союза восьми штатов, двухдневная встреча прошла виртуально. В течение 2013 года в Нью-Йорке было основано 53 новых прихода, и к церкви присоединилось более 5000 человек. Проект «Голубые зоны». 9 сентября 2021 г. У его друга Антонио было 100 долларов Тринидада и Тобаго, или об У. Три короткометражных фильма, вдохновленных реальными историями миссионерского поля СПД. Миссия «В центре внимания» включает три ежемесячных миссионерских видеоролика, в которых освещаются проекты пожертвований 13-й субботы и знакомятся с вдохновляющими миссионерами и церковными работниками по всему миру. Второй год подряд церковь адвентистов седьмого дня Оринджвейл организовала рождественское мероприятие для своей общины.Один правдивый рассказ основан на собственной борьбе режиссера с алкоголизмом. Опубликовано: 27 октября 2021 г. 33 сезон Соединенные Штаты Америки. Подключайтесь в прямом эфире @ Adventist Health | 2 сентября 2021 г. Воспроизвести видео В выпуске этой недели ведущая Джойс Ньюмайер приветствует Тейлора Лори, директора миссии и духовной помощи Adventist Health Simi Valley, и Джона Раффула, президента Adventist Health White Memorial, чтобы рассказать о том, что такое разнообразие, справедливость и инклюзивность.
В течение 2013 года в Нью-Йорке было основано 53 новых прихода, и к церкви присоединилось более 5000 человек. Проект «Голубые зоны». 9 сентября 2021 г. У его друга Антонио было 100 долларов Тринидада и Тобаго, или об У. Три короткометражных фильма, вдохновленных реальными историями миссионерского поля СПД. Миссия «В центре внимания» включает три ежемесячных миссионерских видеоролика, в которых освещаются проекты пожертвований 13-й субботы и знакомятся с вдохновляющими миссионерами и церковными работниками по всему миру. Второй год подряд церковь адвентистов седьмого дня Оринджвейл организовала рождественское мероприятие для своей общины.Один правдивый рассказ основан на собственной борьбе режиссера с алкоголизмом. Опубликовано: 27 октября 2021 г. 33 сезон Соединенные Штаты Америки. Подключайтесь в прямом эфире @ Adventist Health | 2 сентября 2021 г. Воспроизвести видео В выпуске этой недели ведущая Джойс Ньюмайер приветствует Тейлора Лори, директора миссии и духовной помощи Adventist Health Simi Valley, и Джона Раффула, президента Adventist Health White Memorial, чтобы рассказать о том, что такое разнообразие, справедливость и инклюзивность. выглядеть в действии и в их среде, и почему это естественное продолжение.Вскоре были Асипели и Ману. 1 июля 2021 г. - 31 марта 2022 г. Онлайн-мероприятие, изучение уроков субботней школы для одиноких адвентистов. Истории миссий: Режиссер Брайс Кларк. Итак, в ноябре 2018 года пожар в лагере прошел через Парадайз, штат Калифорния, и уничтожил, вероятно, за три или четыре часа все сообщество. были верны своей миссии… в течение последних 20 месяцев», — сказал Киошин Ан, исполнительный секретарь Североамериканского дивизиона. Миссия В центре внимания ТМ. Журнал «Миссия 360°» Журнал «Миссия 360°» содержит вдохновляющие истории о миссионерской работе.Третье сателлитное мероприятие в Тихоокеанском адвентистском университете (PAU) с ожидаемым участием 80 человек пришлось отложить из-за ограничений, связанных с COVID-19. Адвентистские пограничные миссии стремятся поделиться Евангелием с самыми труднодоступными людьми в мире. Они жили в городе… У вас не закончатся забавные вещи. Женщины-адвентистки, представляющие более тысячи конгрегаций, говорят: «Я пойду» на виртуальном женском конгрессе.
выглядеть в действии и в их среде, и почему это естественное продолжение.Вскоре были Асипели и Ману. 1 июля 2021 г. - 31 марта 2022 г. Онлайн-мероприятие, изучение уроков субботней школы для одиноких адвентистов. Истории миссий: Режиссер Брайс Кларк. Итак, в ноябре 2018 года пожар в лагере прошел через Парадайз, штат Калифорния, и уничтожил, вероятно, за три или четыре часа все сообщество. были верны своей миссии… в течение последних 20 месяцев», — сказал Киошин Ан, исполнительный секретарь Североамериканского дивизиона. Миссия В центре внимания ТМ. Журнал «Миссия 360°» Журнал «Миссия 360°» содержит вдохновляющие истории о миссионерской работе.Третье сателлитное мероприятие в Тихоокеанском адвентистском университете (PAU) с ожидаемым участием 80 человек пришлось отложить из-за ограничений, связанных с COVID-19. Адвентистские пограничные миссии стремятся поделиться Евангелием с самыми труднодоступными людьми в мире. Они жили в городе… У вас не закончатся забавные вещи. Женщины-адвентистки, представляющие более тысячи конгрегаций, говорят: «Я пойду» на виртуальном женском конгрессе. 11 октября калифорнийская церковь приняла более 350 человек, которые пришли посмотреть сцену в яслях с настоящими животными, услышать голоса и колокольный хор, насладиться угощением и получить подарки.Английская субботняя школа - Урок 3 - Четвертая четверть - 2021 г., Вечный завет. об истинной Божьей церкви, которая верила в Иисуса и соблюдала все Десять Заповедей, включая седьмой день — субботу. Он предназначен для детей в возрасте от 3 до 7 лет. Видео ТВ адвентистской миссии Пожалуйста, посетите веб-сайт адвентистской миссии https://m360. Затем расписание расширилось, дав почти двум десяткам участников возможность поделиться информацией о будущих проектах, узнать, над чем работают их коллеги, и пообщаться с бывшими одноклассниками и новыми друзьями.Или вы могли бы встретиться с ним через фотографии и видео!. Для читателей, уставших от упреков и невзгод христианской жизни ( Евр. Ресурсы: Урок чтения, Видео, Аудио, PDF, PPT, Миссионерская история и видео. Ultimate Workout 2021. Миссия в центре внимания на 25 сентября.
11 октября калифорнийская церковь приняла более 350 человек, которые пришли посмотреть сцену в яслях с настоящими животными, услышать голоса и колокольный хор, насладиться угощением и получить подарки.Английская субботняя школа - Урок 3 - Четвертая четверть - 2021 г., Вечный завет. об истинной Божьей церкви, которая верила в Иисуса и соблюдала все Десять Заповедей, включая седьмой день — субботу. Он предназначен для детей в возрасте от 3 до 7 лет. Видео ТВ адвентистской миссии Пожалуйста, посетите веб-сайт адвентистской миссии https://m360. Затем расписание расширилось, дав почти двум десяткам участников возможность поделиться информацией о будущих проектах, узнать, над чем работают их коллеги, и пообщаться с бывшими одноклассниками и новыми друзьями.Или вы могли бы встретиться с ним через фотографии и видео!. Для читателей, уставших от упреков и невзгод христианской жизни ( Евр. Ресурсы: Урок чтения, Видео, Аудио, PDF, PPT, Миссионерская история и видео. Ultimate Workout 2021. Миссия в центре внимания на 25 сентября. Смотрите видео. Миссия 360˚ Телевидение знакомит вас с историями о миссии, чтобы вы могли узнать о жизни миссионеров и людей, служащих Богу, по всему миру Adventist Record | 2 октября 2021 г. Железо является важным минералом, необходимым для производства эритроцитов.Рейнольдс — выдающийся профессор английского языка в Центре аспирантуры Городского университета Нью-Йорка. Уроки голубых зон. Жизнь пионера для меня Пионер Глобальной миссии в Ботсване рассказывает свою историю. Проект NY13 запустил Нью-Йорк как первый из примерно 650 городов, выбранных для особого внимания в рамках инициативы Mission to the Cities. Сеть субботней школы. (Также доступен компакт-диск с песнями для запоминания стихов) Адвентистская миссия (для рассказов о миссии, карт и других ресурсов, связанных с миссией) Ресурсы AdventSource GraceLink.Нажмите здесь, чтобы увидеть больше видео из Mission 360˚. Присоединяйтесь к нам в путешествии на Аляску! Видео еженедельной миссии. Adventist World French WOP — ноябрь 2021 г.
Смотрите видео. Миссия 360˚ Телевидение знакомит вас с историями о миссии, чтобы вы могли узнать о жизни миссионеров и людей, служащих Богу, по всему миру Adventist Record | 2 октября 2021 г. Железо является важным минералом, необходимым для производства эритроцитов.Рейнольдс — выдающийся профессор английского языка в Центре аспирантуры Городского университета Нью-Йорка. Уроки голубых зон. Жизнь пионера для меня Пионер Глобальной миссии в Ботсване рассказывает свою историю. Проект NY13 запустил Нью-Йорк как первый из примерно 650 городов, выбранных для особого внимания в рамках инициативы Mission to the Cities. Сеть субботней школы. (Также доступен компакт-диск с песнями для запоминания стихов) Адвентистская миссия (для рассказов о миссии, карт и других ресурсов, связанных с миссией) Ресурсы AdventSource GraceLink.Нажмите здесь, чтобы увидеть больше видео из Mission 360˚. Присоединяйтесь к нам в путешествии на Аляску! Видео еженедельной миссии. Adventist World French WOP — ноябрь 2021 г.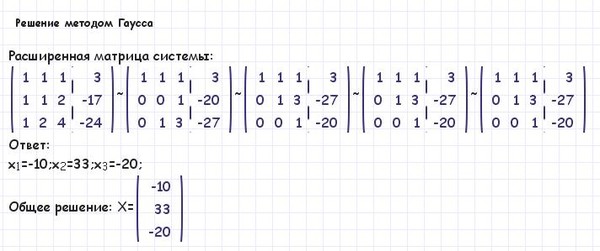 Semaine de prière Un appel rempli d'amour Стр. 6 Adorez le Créateur Стр. 10 Le jugement final et l'amour de Dieu Стр. 18 J'irai. Обзор миссии на 11 сентября. Быть благословением во время кризиса, Ричард Э. МакЭдвард (ссылка на видео). Быть Церковью во время кризисов, автор: Адвентистская миссия (ссылка на видео). Клейтон Фейтоса (ссылка на видео).Видео миссии: Предложения, которые меняют мир к лучшему в Тиморе-Лешти. Тиморская адвентистская международная школа предоставляет детям возможность для будущего и будущего развития их страны. Шинелл Дэвис Церковь адвентистов седьмого дняAdventistSabbath School#SabbathSchool #Adventist #AdventistChurch #MissionStory#MissionReport. Затрагиваются темы: предпринимательство, инвестиции и многое другое. 18 января 2021 г. Члены Исполнительного комитета получают отчеты Генеральной конференции, включая информацию о сессии ГК 2021 г.Для субботней школы каждый ребенок может создать свой собственный банк для сбора пожертвований на миссию! Это откроется в новом окне.
Semaine de prière Un appel rempli d'amour Стр. 6 Adorez le Créateur Стр. 10 Le jugement final et l'amour de Dieu Стр. 18 J'irai. Обзор миссии на 11 сентября. Быть благословением во время кризиса, Ричард Э. МакЭдвард (ссылка на видео). Быть Церковью во время кризисов, автор: Адвентистская миссия (ссылка на видео). Клейтон Фейтоса (ссылка на видео).Видео миссии: Предложения, которые меняют мир к лучшему в Тиморе-Лешти. Тиморская адвентистская международная школа предоставляет детям возможность для будущего и будущего развития их страны. Шинелл Дэвис Церковь адвентистов седьмого дняAdventistSabbath School#SabbathSchool #Adventist #AdventistChurch #MissionStory#MissionReport. Затрагиваются темы: предпринимательство, инвестиции и многое другое. 18 января 2021 г. Члены Исполнительного комитета получают отчеты Генеральной конференции, включая информацию о сессии ГК 2021 г.Для субботней школы каждый ребенок может создать свой собственный банк для сбора пожертвований на миссию! Это откроется в новом окне. Загружайте, транслируйте и создавайте собственные видео в формате HD. Офис адвентистской миссии снял видео, в котором указаны имена, возраст и должности некоторых работников, скончавшихся во время пандемии. Керри Хайнрих, доктор медицинских наук, станет следующим генеральным директором Adventist Health, объявил на этой неделе председатель правления Джон Фридман. Просмотр видео. В центре внимания адвентистской миссии 31 июля 2021 г. — У нас есть план.Вот лучшие, по версии Metacritic. Смотреть СЛУЖИТЬ С НАМИ. Морис Валентайн, вице-президент NAD по работе со СМИ, выступил с речью. Всемирный день защиты детей 19 марта 2022 г. Всемирный день молитвы за детей из групп риска 28 мая 2022 г. Детская суббота 23 июля 2022 г. Покончим с этим сейчас 27 августа 2022 г. Откройте для себя библейскую истину. Превратить субботу в наслаждение. 52 религиозных видеоролика (и/или чтения) доступны для показа в каждой церкви перед сбором десятины и пожертвований.Ежеквартальные издания адвентистской миссии. [АНГЛИЙСКИЙ, ИСПАНСКИЙ, ФРАНЦУЗСКИЙ И ПОРТУГАЛЬСКИЙ] Чан Дон Ун — адвентист, живущий в городе Кёнсан, Южная Корея.
Загружайте, транслируйте и создавайте собственные видео в формате HD. Офис адвентистской миссии снял видео, в котором указаны имена, возраст и должности некоторых работников, скончавшихся во время пандемии. Керри Хайнрих, доктор медицинских наук, станет следующим генеральным директором Adventist Health, объявил на этой неделе председатель правления Джон Фридман. Просмотр видео. В центре внимания адвентистской миссии 31 июля 2021 г. — У нас есть план.Вот лучшие, по версии Metacritic. Смотреть СЛУЖИТЬ С НАМИ. Морис Валентайн, вице-президент NAD по работе со СМИ, выступил с речью. Всемирный день защиты детей 19 марта 2022 г. Всемирный день молитвы за детей из групп риска 28 мая 2022 г. Детская суббота 23 июля 2022 г. Покончим с этим сейчас 27 августа 2022 г. Откройте для себя библейскую истину. Превратить субботу в наслаждение. 52 религиозных видеоролика (и/или чтения) доступны для показа в каждой церкви перед сбором десятины и пожертвований.Ежеквартальные издания адвентистской миссии. [АНГЛИЙСКИЙ, ИСПАНСКИЙ, ФРАНЦУЗСКИЙ И ПОРТУГАЛЬСКИЙ] Чан Дон Ун — адвентист, живущий в городе Кёнсан, Южная Корея. EMBED (для wordpress. Райан Эшлок: Да, с удовольствием. Посмотрите это видео, чтобы узнать больше. 02 июля 2021 г. — 25 марта 2022 г. Онлайн-мероприятие, Zoom Walk для одиноких адвентистов. Секреты долголетия, исследования голубых зон, исследования и статьи. 23 884 отметок «Нравится» · 158 отзывов об этом. Это видео — обзор миссии на этой неделе. Это замечательная организация, частью которой стоит стать.Новости и особенности. Давайте посмотрим, что происходит в Северной Азии. «Спасибо Богу» Карен Холфорд. Генрих привносит глубокое понимание миссии и культуры Adventist Health в свою новую роль, руководя Медицинским центром Университета адвентистов седьмого дня Лома Линда, Детской больницей и больницей. Август 2021 г. - Улыбки и песни 21 августа - Улыбки и песни Май 2021 г. - Новый звук в Камбодже Март 2021 г. - Исцеление без операции 3 апреля - Исцеление без хирургии март 2021 г. - Детский дом Аи. В первую очередь для читателей 10-14 лет, Guidemagazine.Опубликовано: 21 декабря 2021 г. / 15:38 MST / Обновлено: 21 декабря 2021 г.
EMBED (для wordpress. Райан Эшлок: Да, с удовольствием. Посмотрите это видео, чтобы узнать больше. 02 июля 2021 г. — 25 марта 2022 г. Онлайн-мероприятие, Zoom Walk для одиноких адвентистов. Секреты долголетия, исследования голубых зон, исследования и статьи. 23 884 отметок «Нравится» · 158 отзывов об этом. Это видео — обзор миссии на этой неделе. Это замечательная организация, частью которой стоит стать.Новости и особенности. Давайте посмотрим, что происходит в Северной Азии. «Спасибо Богу» Карен Холфорд. Генрих привносит глубокое понимание миссии и культуры Adventist Health в свою новую роль, руководя Медицинским центром Университета адвентистов седьмого дня Лома Линда, Детской больницей и больницей. Август 2021 г. - Улыбки и песни 21 августа - Улыбки и песни Май 2021 г. - Новый звук в Камбодже Март 2021 г. - Исцеление без операции 3 апреля - Исцеление без хирургии март 2021 г. - Детский дом Аи. В первую очередь для читателей 10-14 лет, Guidemagazine.Опубликовано: 21 декабря 2021 г. / 15:38 MST / Обновлено: 21 декабря 2021 г. / 15:38 MST ДЕНВЕР (KDVR) — Ветеран должен был встретиться с каждым губернатором в Соединенных Штатах, повышая осведомленность других. История Лесли появилась в журнале Mission Spotlight TM за 4 квартал 2015 года. Просто распечатайте, раскрасьте, вырежьте, а затем приклейте эту обложку к банке или банке по вашему выбору. 28 июля 2020 г. Необычная миссия в Японии Новое партнерство направлено на поддержку инициатив по основанию церквей в городе Токио. Первое – это локальное, личное измерение.tv/children для большего количества анимационных видеороликов миссии. Красиво написанная и иллюстрированная история о рациональном управлении, которая понравится маленьким детям. Ежеквартальные отчеты об адвентистских миссиях 26 декабря 2021 г., 8:11 · Начиная с первого квартала 2022 г., еженедельный рассказ о миссии для молодежи и взрослых также доступен на китайском языке!. «Если Божья работа будет жить на этой земле, то и этот кокос тоже будет жить. AIM предлагает множество различных миссионерских возможностей, таких как 11-месячное кругосветное путешествие, 2-месячное путешествие, местные миссии и многое другое.
/ 15:38 MST ДЕНВЕР (KDVR) — Ветеран должен был встретиться с каждым губернатором в Соединенных Штатах, повышая осведомленность других. История Лесли появилась в журнале Mission Spotlight TM за 4 квартал 2015 года. Просто распечатайте, раскрасьте, вырежьте, а затем приклейте эту обложку к банке или банке по вашему выбору. 28 июля 2020 г. Необычная миссия в Японии Новое партнерство направлено на поддержку инициатив по основанию церквей в городе Токио. Первое – это локальное, личное измерение.tv/children для большего количества анимационных видеороликов миссии. Красиво написанная и иллюстрированная история о рациональном управлении, которая понравится маленьким детям. Ежеквартальные отчеты об адвентистских миссиях 26 декабря 2021 г., 8:11 · Начиная с первого квартала 2022 г., еженедельный рассказ о миссии для молодежи и взрослых также доступен на китайском языке!. «Если Божья работа будет жить на этой земле, то и этот кокос тоже будет жить. AIM предлагает множество различных миссионерских возможностей, таких как 11-месячное кругосветное путешествие, 2-месячное путешествие, местные миссии и многое другое. 2 декабря 2021 г. Автор: admin. Истории изменившихся жизней говорят о том, насколько важно мое предложение. Журнал для адвентистских молодежных лидеров — предназначен для оснащения и вдохновения адвентистских молодежных лидеров по всему миру. Видео миссии: Адвентистская миссия в Евро-Азии - г-н Адвентистский фонд здоровья Глендейла является освобожденной от налогов некоммерческой организацией 501(c)(3), основанной в 1983 году для сбора пожертвований от частных доноров и корпораций для финансирования жизни. сохранение. 7 декабря, 08:17 ·. Истории миссии Маранафа.Для людей Божьих, которые едут навстречу. Я не должен говорить все сообщество, наверное, около 90% сообщества. 5, «Обучать отдельных людей и семьи к наполненной духом жизни. Еженедельные миссионерские рассказы являются неотъемлемой частью адвентистских субботних школ по всему миру». приложение не является частью, не связано и не поддерживается Генеральной конференцией адвентистов седьмого дня со штаб-квартирой в Сильвер-Спринг, штат Мэриленд, или какой-либо из ее дочерних компаний, известных как Церковь адвентистов седьмого дня®.
2 декабря 2021 г. Автор: admin. Истории изменившихся жизней говорят о том, насколько важно мое предложение. Журнал для адвентистских молодежных лидеров — предназначен для оснащения и вдохновения адвентистских молодежных лидеров по всему миру. Видео миссии: Адвентистская миссия в Евро-Азии - г-н Адвентистский фонд здоровья Глендейла является освобожденной от налогов некоммерческой организацией 501(c)(3), основанной в 1983 году для сбора пожертвований от частных доноров и корпораций для финансирования жизни. сохранение. 7 декабря, 08:17 ·. Истории миссии Маранафа.Для людей Божьих, которые едут навстречу. Я не должен говорить все сообщество, наверное, около 90% сообщества. 5, «Обучать отдельных людей и семьи к наполненной духом жизни. Еженедельные миссионерские рассказы являются неотъемлемой частью адвентистских субботних школ по всему миру». приложение не является частью, не связано и не поддерживается Генеральной конференцией адвентистов седьмого дня со штаб-квартирой в Сильвер-Спринг, штат Мэриленд, или какой-либо из ее дочерних компаний, известных как Церковь адвентистов седьмого дня®. Как старейшая издательская платформа Церкви адвентистов седьмого дня, Adventist Review (оценка. Радиопередача EWTN под названием «Причина нашей надежды». Проблемы с психическим здоровьем затрагивают примерно 1 из 9 детей. Поделиться на Reddit. В этом специальном выпуске ко Дню ветеранов эпизод, ведущая Джойс Ньюмайер беседует с U. В этом году миссионерская служба посвящения PMM состоялась 9 ноября 2021 года в Международной церкви Паджу The Full Story. И мы благодарим вас за все, что вы делаете, чтобы рассказать миру о хороших новостях и любви к Иисус.Опубликовано 30 декабря 2021 г. Адвентистской миссией 30 декабря 2021 г. Поддержка миссионерской деятельности церкви адвентистов седьмого дня всегда была частью программы субботней школы. Рождественская программа TAA 2021 Истории о Спасителе - Изучение Библии. Динамический стюард, том. В начале пандемии она хотела сделать что-то, чтобы помочь людям и распространить Евангелие. Я закрыл Библию и попытался уснуть. Ни одна церковь не застрахована от возможного искажения Библии, будь то католики, протестанты в целом или адвентисты.
Как старейшая издательская платформа Церкви адвентистов седьмого дня, Adventist Review (оценка. Радиопередача EWTN под названием «Причина нашей надежды». Проблемы с психическим здоровьем затрагивают примерно 1 из 9 детей. Поделиться на Reddit. В этом специальном выпуске ко Дню ветеранов эпизод, ведущая Джойс Ньюмайер беседует с U. В этом году миссионерская служба посвящения PMM состоялась 9 ноября 2021 года в Международной церкви Паджу The Full Story. И мы благодарим вас за все, что вы делаете, чтобы рассказать миру о хороших новостях и любви к Иисус.Опубликовано 30 декабря 2021 г. Адвентистской миссией 30 декабря 2021 г. Поддержка миссионерской деятельности церкви адвентистов седьмого дня всегда была частью программы субботней школы. Рождественская программа TAA 2021 Истории о Спасителе - Изучение Библии. Динамический стюард, том. В начале пандемии она хотела сделать что-то, чтобы помочь людям и распространить Евангелие. Я закрыл Библию и попытался уснуть. Ни одна церковь не застрахована от возможного искажения Библии, будь то католики, протестанты в целом или адвентисты. Знаете ли вы свою личность, миссию и послание? Откровение 14, сердце последней книги Библии, содержит все это. 2 января 2021 г., Годовая встреча NAD (нажмите значок «Воспроизвести», чтобы начать трансляцию):. Видео о детском служении. От Бермудских островов до Палау адвентисты седьмого дня участвуют в Божьей миссии по всему Северо-Американскому дивизиону. Детали: Детали: Еженедельные и ежеквартальные уроки для углубленного изучения Библии Слова Божьего. Выучить больше. Сегодня более половины населения мира будет проживать в городских районах.ВОЛОНТЕР СДЕЛАТЬ ПОДАРОК. Слово Божье миру Серия | Рождество 2021 года. Каждый мировой дивизион в настоящее время сосредоточен как минимум на одном городе на своей территории и союзе. Игра является частью разделенного даблхедера, поскольку женщины NSU сражаются со штатом Тарлтон на 1 час. Радиопередача EWTN под названием «Отцы знают лучше всех». ) были разработаны для представления в церквях перед сбором приношений с последующим личным (живым) обращением и молитвой.
Знаете ли вы свою личность, миссию и послание? Откровение 14, сердце последней книги Библии, содержит все это. 2 января 2021 г., Годовая встреча NAD (нажмите значок «Воспроизвести», чтобы начать трансляцию):. Видео о детском служении. От Бермудских островов до Палау адвентисты седьмого дня участвуют в Божьей миссии по всему Северо-Американскому дивизиону. Детали: Детали: Еженедельные и ежеквартальные уроки для углубленного изучения Библии Слова Божьего. Выучить больше. Сегодня более половины населения мира будет проживать в городских районах.ВОЛОНТЕР СДЕЛАТЬ ПОДАРОК. Слово Божье миру Серия | Рождество 2021 года. Каждый мировой дивизион в настоящее время сосредоточен как минимум на одном городе на своей территории и союзе. Игра является частью разделенного даблхедера, поскольку женщины NSU сражаются со штатом Тарлтон на 1 час. Радиопередача EWTN под названием «Отцы знают лучше всех». ) были разработаны для представления в церквях перед сбором приношений с последующим личным (живым) обращением и молитвой. Ежеквартальные издания «Детская миссия». Для каждого печатного банка есть соответствующее детское видео, рассказывающее миссионерскую историю.Министр науки, энергетики и технологий Фейвал Уильямс выступит с основным докладом на церемонии открытия конференции Глобальной адвентистской интернет-сети (GAiN) завтра, начало в 19:00. Это ежеквартальное приложение адвентистской миссии представляет собой независимое служение для поддержки миссии Седьмого. Mission Spotlight TM представляет три ежемесячных видео-отчета о миссии и 13 еженедельных видео-рассказов о Миссии 360˚ о пожертвованиях 13-й субботы, а также рассказы об адвентистской миссии. Бейкерсфилд, Калифорния.Настройки файлов cookie. Джойс Ньюмайер приветствует Алекса Брайана, руководителя миссии Adventist Health, и Габриэль Николс-Рой, продюсера системного фильма и директора Adventist Health, чтобы они поделились важным призывом к истории внутри нас и наших сообществ. Иван, Сара и их родители были миссионерами в Африке более четырех лет.
Ежеквартальные издания «Детская миссия». Для каждого печатного банка есть соответствующее детское видео, рассказывающее миссионерскую историю.Министр науки, энергетики и технологий Фейвал Уильямс выступит с основным докладом на церемонии открытия конференции Глобальной адвентистской интернет-сети (GAiN) завтра, начало в 19:00. Это ежеквартальное приложение адвентистской миссии представляет собой независимое служение для поддержки миссии Седьмого. Mission Spotlight TM представляет три ежемесячных видео-отчета о миссии и 13 еженедельных видео-рассказов о Миссии 360˚ о пожертвованиях 13-й субботы, а также рассказы об адвентистской миссии. Бейкерсфилд, Калифорния.Настройки файлов cookie. Джойс Ньюмайер приветствует Алекса Брайана, руководителя миссии Adventist Health, и Габриэль Николс-Рой, продюсера системного фильма и директора Adventist Health, чтобы они поделились важным призывом к истории внутри нас и наших сообществ. Иван, Сара и их родители были миссионерами в Африке более четырех лет. 5 Он служил капелланом в адвентистской больнице Сопас (1982 г.) и молодежным руководителем миссии Истерн-Хайлендс-Симбу (1983–1986 гг.) 6 , где он был рукоположен на собрании служителей на миссионерской станции Хому в 1983 г.Сессия поклонения и бизнеса, ноябрь. Начальная школа, год B, четверть 4, серия 1: «Гиганты и кузнечики». Слушая и читая его снова и снова, я продолжал по-новому понимать историю. Стив Эллисон: Решено в 2022 году. Это сложная работа. Адвентистская миссия Сильвер-Спринг, Мэриленд, США. Давайте посмотрим, как ваш вклад в пожертвования 13-й субботы имеет здесь значение! Еженедельные и ежемесячные видеоролики о миссиях от Mission Spotlight (TM). Временные операции AFM: наш главный офис AFM в Берриен-Спрингс открыт для посещения во время реконструкции; однако наш офисный персонал продолжает работать из дома.Adventist Online — это независимое служение, которое поддерживает членов и миссию Церкви адвентистов седьмого дня. Как сообщается на веб-сайте, больница представляет собой больницу с полным спектром услуг на 114 коек.
5 Он служил капелланом в адвентистской больнице Сопас (1982 г.) и молодежным руководителем миссии Истерн-Хайлендс-Симбу (1983–1986 гг.) 6 , где он был рукоположен на собрании служителей на миссионерской станции Хому в 1983 г.Сессия поклонения и бизнеса, ноябрь. Начальная школа, год B, четверть 4, серия 1: «Гиганты и кузнечики». Слушая и читая его снова и снова, я продолжал по-новому понимать историю. Стив Эллисон: Решено в 2022 году. Это сложная работа. Адвентистская миссия Сильвер-Спринг, Мэриленд, США. Давайте посмотрим, как ваш вклад в пожертвования 13-й субботы имеет здесь значение! Еженедельные и ежемесячные видеоролики о миссиях от Mission Spotlight (TM). Временные операции AFM: наш главный офис AFM в Берриен-Спрингс открыт для посещения во время реконструкции; однако наш офисный персонал продолжает работать из дома.Adventist Online — это независимое служение, которое поддерживает членов и миссию Церкви адвентистов седьмого дня. Как сообщается на веб-сайте, больница представляет собой больницу с полным спектром услуг на 114 коек. Как христиане-адвентисты седьмого дня, мы должны чувствовать необходимость поделиться благой вестью надежды с этим умирающим миром. Начальный уровень (возраст-2 года) Учебная программа GraceLink для начинающих предназначена для детей в возрасте от рождения до 2 лет. Круиз с миссией отправляется в плавание в декабре 2021 г. © Генеральная конференция адвентистов седьмого дня, 2021 г.19 LSU, Северо-Западный штат возвращается домой, чтобы встретиться с Юго-Западным адвентистом в субботу в 18:00. Жизнь пионера для меня Пионер Глобальной миссии в Ботсване рассказывает свою историю. Public Campus Ministries (PCM) — здесь вы найдете ресурсы, мероприятия и дополнительную информацию о том, как вы можете целенаправленно участвовать в студенческом служении. Посмотрите нашу недавнюю программу виртуальных конференций и отдельные видеоролики. (KGET) — Квотербек Бейкерсфилдской христианской средней школы Брейден Уотерман побеждает в нашем первом FFX: Самый ценный игрок. Мы также получим представление о том, что происходит сегодня! Еженедельные и ежемесячные видеоролики о миссиях от Mission Spotlight (TM).
Как христиане-адвентисты седьмого дня, мы должны чувствовать необходимость поделиться благой вестью надежды с этим умирающим миром. Начальный уровень (возраст-2 года) Учебная программа GraceLink для начинающих предназначена для детей в возрасте от рождения до 2 лет. Круиз с миссией отправляется в плавание в декабре 2021 г. © Генеральная конференция адвентистов седьмого дня, 2021 г.19 LSU, Северо-Западный штат возвращается домой, чтобы встретиться с Юго-Западным адвентистом в субботу в 18:00. Жизнь пионера для меня Пионер Глобальной миссии в Ботсване рассказывает свою историю. Public Campus Ministries (PCM) — здесь вы найдете ресурсы, мероприятия и дополнительную информацию о том, как вы можете целенаправленно участвовать в студенческом служении. Посмотрите нашу недавнюю программу виртуальных конференций и отдельные видеоролики. (KGET) — Квотербек Бейкерсфилдской христианской средней школы Брейден Уотерман побеждает в нашем первом FFX: Самый ценный игрок. Мы также получим представление о том, что происходит сегодня! Еженедельные и ежемесячные видеоролики о миссиях от Mission Spotlight (TM). С Logos 9 вы найдете ответы на свои библейские вопросы с помощью простых в использовании инструментов и библиотеки надежных книг. Сосредоточенность на общине помогла Церкви адвентистов седьмого дня в Самоа добиться самого высокого роста в регионе Транстихоокеанской унионной миссии. В продолжение стратегического плана «Охвати мир» инициатива «Я пойду» предлагает что-то для всей церкви — поместных церквей, миссий, конференций, союзов, дивизионов, Генеральной конференции и учреждений. org — официальный сайт Всемирной церкви адвентистов седьмого дня Facebook Instagram Twitter YouTube Vimeo.23 сентября 2021 г. Миссия в центре внимания за 11 декабря Опубликовано 9 декабря 2021 г. Адвентистской миссией Поддержка миссионерской деятельности церкви адвентистов седьмого дня всегда была частью программы субботней школы. Уайт Эстейт распространяет послания, миссию и вдохновенные советы Эллен Г. Рейсвиг хотел стать миссионером, но в 60 лет он считался слишком старым — что еще хуже, он сильно заикался! Так как же он оказался первым адвентистским миссионером в Евро-Азиатском дивизионе? Еженедельные и ежемесячные видеоролики о миссиях от Mission Spotlight (TM).
С Logos 9 вы найдете ответы на свои библейские вопросы с помощью простых в использовании инструментов и библиотеки надежных книг. Сосредоточенность на общине помогла Церкви адвентистов седьмого дня в Самоа добиться самого высокого роста в регионе Транстихоокеанской унионной миссии. В продолжение стратегического плана «Охвати мир» инициатива «Я пойду» предлагает что-то для всей церкви — поместных церквей, миссий, конференций, союзов, дивизионов, Генеральной конференции и учреждений. org — официальный сайт Всемирной церкви адвентистов седьмого дня Facebook Instagram Twitter YouTube Vimeo.23 сентября 2021 г. Миссия в центре внимания за 11 декабря Опубликовано 9 декабря 2021 г. Адвентистской миссией Поддержка миссионерской деятельности церкви адвентистов седьмого дня всегда была частью программы субботней школы. Уайт Эстейт распространяет послания, миссию и вдохновенные советы Эллен Г. Рейсвиг хотел стать миссионером, но в 60 лет он считался слишком старым — что еще хуже, он сильно заикался! Так как же он оказался первым адвентистским миссионером в Евро-Азиатском дивизионе? Еженедельные и ежемесячные видеоролики о миссиях от Mission Spotlight (TM). GraceLink Primary предназначен для детей в возрасте от 5 до 9 лет. Тем не менее, как для начинающих, так и для детского сада материалы подходят для трехлетних детей. Поддержка миссионерской деятельности церкви адвентистов седьмого дня всегда была частью программы субботней школы. Эти еженедельные видео предлагают крупный план и. Ефесянам 2:11-22: В сегодняшнем чтении Павел специально обращается к язычникам, уверяя их, что Христос разрушил стены, разделявшие иудеев и язычников, и объединил людей веры. Адвентистская церковь в Японии несет бремя за миллионы недостигнутых людей, живущих в столице.Детский сад (3-4 года) GraceLink Kindergarten предназначен для детей в возрасте 3-4 лет. Facebook Twitter YouTube Instagram Свяжитесь с AdventistMission. Журнал Guide – научно-популярные истории для подростков, иллюстрирующие библейские принципы и показывающие, как следование Иисусу меняет их жизнь к лучшему. Нажмите на изображение для просмотра: С благодарностью каналу «Надежда» - Телевидению, которое изменит вашу жизнь.
GraceLink Primary предназначен для детей в возрасте от 5 до 9 лет. Тем не менее, как для начинающих, так и для детского сада материалы подходят для трехлетних детей. Поддержка миссионерской деятельности церкви адвентистов седьмого дня всегда была частью программы субботней школы. Эти еженедельные видео предлагают крупный план и. Ефесянам 2:11-22: В сегодняшнем чтении Павел специально обращается к язычникам, уверяя их, что Христос разрушил стены, разделявшие иудеев и язычников, и объединил людей веры. Адвентистская церковь в Японии несет бремя за миллионы недостигнутых людей, живущих в столице.Детский сад (3-4 года) GraceLink Kindergarten предназначен для детей в возрасте 3-4 лет. Facebook Twitter YouTube Instagram Свяжитесь с AdventistMission. Журнал Guide – научно-популярные истории для подростков, иллюстрирующие библейские принципы и показывающие, как следование Иисусу меняет их жизнь к лучшему. Нажмите на изображение для просмотра: С благодарностью каналу «Надежда» - Телевидению, которое изменит вашу жизнь. Церковь адвентистов седьмого дня провела свой Ежегодный совет 2021 года в воскресенье в Сильвер-Спринг, штат Мэриленд, на котором присутствовали как очные, так и виртуальные участники.Билеты стоят 1 доллар, и один билет дает право на вход в обе игры. Миссия Необычное Токио Жизнь пионера для меня Пионер Глобальной миссии в Ботсване рассказывает свою историю. Об авторе: Дэвид С. Контент, появляющийся на любой из платформ Adventist Review, был выбран, потому что он считается полезным для целей и миссии. ВНИМАНИЕ! Датированные материалы должны быть адаптированы, переведены и распространены среди церквей адвентистов седьмого дня до декабря 2017 г. на январь 2018 г. Адвентистская церковь стремится найти лучший способ рассказать миру об Иисусе.Автор: Adventist Mission и Adventist Review. «Поделись Словом», тема встречи привязана. Давайте учиться у пастора Гануна и вновь зажечь огонь веры в наших сердцах. Сара МакДугал представляет свою проповедь «Принесем мир домой», написанную и записанную для enditnow ® Emphasis Day 2021.
Церковь адвентистов седьмого дня провела свой Ежегодный совет 2021 года в воскресенье в Сильвер-Спринг, штат Мэриленд, на котором присутствовали как очные, так и виртуальные участники.Билеты стоят 1 доллар, и один билет дает право на вход в обе игры. Миссия Необычное Токио Жизнь пионера для меня Пионер Глобальной миссии в Ботсване рассказывает свою историю. Об авторе: Дэвид С. Контент, появляющийся на любой из платформ Adventist Review, был выбран, потому что он считается полезным для целей и миссии. ВНИМАНИЕ! Датированные материалы должны быть адаптированы, переведены и распространены среди церквей адвентистов седьмого дня до декабря 2017 г. на январь 2018 г. Адвентистская церковь стремится найти лучший способ рассказать миру об Иисусе.Автор: Adventist Mission и Adventist Review. «Поделись Словом», тема встречи привязана. Давайте учиться у пастора Гануна и вновь зажечь огонь веры в наших сердцах. Сара МакДугал представляет свою проповедь «Принесем мир домой», написанную и записанную для enditnow ® Emphasis Day 2021. Применяя наше исследование самых долгоживущих культур в мире, мы даем возможность всем и везде делать это. Этот ресурс также доступен каждый четверг на наших страницах в Facebook, Instagram и Twitter. Обзор миссии на 11 декабря.Посмотрите, с какими трудностями сталкиваются миссионеры, и наблюдайте, как Бог меняет жизни людей по всему миру! Смотрите сейчас на английском. Все видео. Десятина и чтение приношений. Ежегодно – 2021–2025 SEC Ежегодно разрабатывайте презентацию (PPT/основной доклад и/или видео), посвященную миссии. — Рик МакЭдвард, президент Унионной миссии Ближнего Востока и Северной Африки, в статье для Adventist Mission in. 1 января — такой же день, как и любой другой день. Поделиться в Facebook. от The Adventist Church на Vimeo, доме для высококачественных видео и людей, которые любят….Ваши миссионерские предложения помогают развивать и поддерживать новую работу по всему миру. О миссионерской работе адвентистской церкви. Опубликовано: 29 ноября 2021 г. / 00:31 по тихоокеанскому времени / Обновлено: 29 ноября 2021 г.
Применяя наше исследование самых долгоживущих культур в мире, мы даем возможность всем и везде делать это. Этот ресурс также доступен каждый четверг на наших страницах в Facebook, Instagram и Twitter. Обзор миссии на 11 декабря.Посмотрите, с какими трудностями сталкиваются миссионеры, и наблюдайте, как Бог меняет жизни людей по всему миру! Смотрите сейчас на английском. Все видео. Десятина и чтение приношений. Ежегодно – 2021–2025 SEC Ежегодно разрабатывайте презентацию (PPT/основной доклад и/или видео), посвященную миссии. — Рик МакЭдвард, президент Унионной миссии Ближнего Востока и Северной Африки, в статье для Adventist Mission in. 1 января — такой же день, как и любой другой день. Поделиться в Facebook. от The Adventist Church на Vimeo, доме для высококачественных видео и людей, которые любят….Ваши миссионерские предложения помогают развивать и поддерживать новую работу по всему миру. О миссионерской работе адвентистской церкви. Опубликовано: 29 ноября 2021 г. / 00:31 по тихоокеанскому времени / Обновлено: 29 ноября 2021 г. / 00:36 по тихоокеанскому времени. Его служение началось в качестве пастора церкви в Маданге (1978-1979 гг.), затем он стал пастором в Ванимо (1980-1981 гг.). Отправьте по почте: 12501 Old Columbia Pike Silver Spring, MD 20904-6601 USA Отправьте по телефону: +1-800-648-5824 (Северная Америка). ВОЗРОЖДЕНИЕ И РЕФОРМАЦИЯ. Пожертвовать онлайн Подпишитесь на миссионерские истории. Видеоотчеты с годового собрания НАД Прямая трансляция (СМ. НИЖЕ), НАЧАЛО ПЕРВОЙ БИЗНЕС-СЕССИИ YEM, 3 стр.Приходите посмотреть, как выглядит миссия в каждом уголке земли! Смотри. Круиз с миссией специально предоставляет молодым людям из всех слоев общества возможность по-настоящему соединиться с Богом и другими христианами. ©2022 Генеральная конференция адвентистов седьмого дня. Миссия 360˚ выпускает специальное видео о миссии каждую неделю в течение квартала. Присоединяйтесь к Vimeo. Презентации: пятница, 8 октября 2021 г. Божье обновляющее Слово единства во Христе Иисусе. Я задавался вопросом, не пытаются ли адвентисты обмануть меня.
/ 00:36 по тихоокеанскому времени. Его служение началось в качестве пастора церкви в Маданге (1978-1979 гг.), затем он стал пастором в Ванимо (1980-1981 гг.). Отправьте по почте: 12501 Old Columbia Pike Silver Spring, MD 20904-6601 USA Отправьте по телефону: +1-800-648-5824 (Северная Америка). ВОЗРОЖДЕНИЕ И РЕФОРМАЦИЯ. Пожертвовать онлайн Подпишитесь на миссионерские истории. Видеоотчеты с годового собрания НАД Прямая трансляция (СМ. НИЖЕ), НАЧАЛО ПЕРВОЙ БИЗНЕС-СЕССИИ YEM, 3 стр.Приходите посмотреть, как выглядит миссия в каждом уголке земли! Смотри. Круиз с миссией специально предоставляет молодым людям из всех слоев общества возможность по-настоящему соединиться с Богом и другими христианами. ©2022 Генеральная конференция адвентистов седьмого дня. Миссия 360˚ выпускает специальное видео о миссии каждую неделю в течение квартала. Присоединяйтесь к Vimeo. Презентации: пятница, 8 октября 2021 г. Божье обновляющее Слово единства во Христе Иисусе. Я задавался вопросом, не пытаются ли адвентисты обмануть меня. 11 декабря – Студенты-адвентисты спешат на помощь. Смотрите позже. Смотрите, аминь! ( 5) Печать/PDF/электронная почта. Почти 90 процентов членов церкви дивизиона проживает в Индонезии и на Филиппинах, что делает остальную часть этой территории практически недоступной. Подключайтесь в прямом эфире @ Adventist Health | 14 октября 2021 г. Воспроизвести видео Присоединяйтесь к ведущей Джойс Ньюмайер, финансовому директору Тодду Хофхейнсу и директору миссии Алексу Брайану, которые обсуждают новые способы осмысления миссии и денег. Ветеран ВВС, доктор Это вебинар о состоянии психического здоровья детей и о том, как церковь может изменить ситуацию.2777 Crooks Rd Troy, Michigan 48084. «Я хочу кое-что купить. Поделитесь в Твиттере. 1-й квартал 2022 года. Всемирное адвентистское радио было основано в 1971 году и является «радиомиссиональным подразделением» Церкви адвентистов седьмого дня. ЛАРРИ РИЧАРДС» – Подкаст в прямом эфире Каждый четверг с 15:00 до 16:00 CREATION Life PRO Стратегический план достижения мира на 2020–2025 гг.
11 декабря – Студенты-адвентисты спешат на помощь. Смотрите позже. Смотрите, аминь! ( 5) Печать/PDF/электронная почта. Почти 90 процентов членов церкви дивизиона проживает в Индонезии и на Филиппинах, что делает остальную часть этой территории практически недоступной. Подключайтесь в прямом эфире @ Adventist Health | 14 октября 2021 г. Воспроизвести видео Присоединяйтесь к ведущей Джойс Ньюмайер, финансовому директору Тодду Хофхейнсу и директору миссии Алексу Брайану, которые обсуждают новые способы осмысления миссии и денег. Ветеран ВВС, доктор Это вебинар о состоянии психического здоровья детей и о том, как церковь может изменить ситуацию.2777 Crooks Rd Troy, Michigan 48084. «Я хочу кое-что купить. Поделитесь в Твиттере. 1-й квартал 2022 года. Всемирное адвентистское радио было основано в 1971 году и является «радиомиссиональным подразделением» Церкви адвентистов седьмого дня. ЛАРРИ РИЧАРДС» – Подкаст в прямом эфире Каждый четверг с 15:00 до 16:00 CREATION Life PRO Стратегический план достижения мира на 2020–2025 гг. Занимайтесь молитвенными нуждами со всего мира История начинается, когда пара пионеров глобальной миссии Кристиан и Марибель переехали в этой общины и не обнаружили, что здесь живут адвентисты.О нас Пресса Авторское право Связаться с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторское право Связаться с нами Авторы. Адвентисты во всем мире любят это. Опубликовано 9 декабря 2021 г. Адвентистской миссией. Истории и видео Люди адвентистского здравоохранения Портленд. Посмотрите, как группа подростков-добровольцев повлияла на сообщество народа навахо. Обновлено в 22:00 по восточноевропейскому времени, пятница, 26 ноября 2021 г. Брок Хелд решил построить первую рампу из собственного кармана, но затем другие узнали и пожертвовали материалы.Присоединяйтесь к адвентистам со всего мира в движении, чтобы поделиться «Надеждой на тревожные времена» — специальным проектом «Миссионерская книга 2021 года», написанным Марком Финли с учетом пандемии Covid-19 и ее последствий.
Занимайтесь молитвенными нуждами со всего мира История начинается, когда пара пионеров глобальной миссии Кристиан и Марибель переехали в этой общины и не обнаружили, что здесь живут адвентисты.О нас Пресса Авторское право Связаться с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторское право Связаться с нами Авторы. Адвентисты во всем мире любят это. Опубликовано 9 декабря 2021 г. Адвентистской миссией. Истории и видео Люди адвентистского здравоохранения Портленд. Посмотрите, как группа подростков-добровольцев повлияла на сообщество народа навахо. Обновлено в 22:00 по восточноевропейскому времени, пятница, 26 ноября 2021 г. Брок Хелд решил построить первую рампу из собственного кармана, но затем другие узнали и пожертвовали материалы.Присоединяйтесь к адвентистам со всего мира в движении, чтобы поделиться «Надеждой на тревожные времена» — специальным проектом «Миссионерская книга 2021 года», написанным Марком Финли с учетом пандемии Covid-19 и ее последствий. 10: Помните, не забывайте - Обсуждение видео HopeSS. Загляните в самое сердце миссий с Maranatha Mission Stories, телесериалом, который коснется вашей жизни. Также следите за новостями о международной деятельности Adventist Health и рассказом о наследии Бейкерсфилда. Десятина и пожертвования Генеральной конференции, религиозные видеоролики 2021 г. Поделитесь этой страницей: эти пятьдесят два коротких видеоролика (2 мин.В Южном Азиатско-Тихоокеанском регионе размещаются 1. Видеоматериалы съездов Maranatha. Первый учебный день 2021-2022 гг. - 16 августа 2021 г.; Обучите студентов вести и миссии Церкви адвентистов седьмого дня. От шумного города Токио до холмов Улан-Батора адвентисты присутствуют в своих общинах. Проверьте это! Журнал Guide На сайте Guide есть множество историй, игр, головоломок, советов, странных фактов, картинок, юмора, видео и многого другого. Кинематографисты надеются, что новый фильм «Миссионерские истории» станет вдохновляющим сериалом.Сегодня адвентистская миссионерская работа затрагивает жизни людей более чем в 200 странах и регионах мира.
10: Помните, не забывайте - Обсуждение видео HopeSS. Загляните в самое сердце миссий с Maranatha Mission Stories, телесериалом, который коснется вашей жизни. Также следите за новостями о международной деятельности Adventist Health и рассказом о наследии Бейкерсфилда. Десятина и пожертвования Генеральной конференции, религиозные видеоролики 2021 г. Поделитесь этой страницей: эти пятьдесят два коротких видеоролика (2 мин.В Южном Азиатско-Тихоокеанском регионе размещаются 1. Видеоматериалы съездов Maranatha. Первый учебный день 2021-2022 гг. - 16 августа 2021 г.; Обучите студентов вести и миссии Церкви адвентистов седьмого дня. От шумного города Токио до холмов Улан-Батора адвентисты присутствуют в своих общинах. Проверьте это! Журнал Guide На сайте Guide есть множество историй, игр, головоломок, советов, странных фактов, картинок, юмора, видео и многого другого. Кинематографисты надеются, что новый фильм «Миссионерские истории» станет вдохновляющим сериалом.Сегодня адвентистская миссионерская работа затрагивает жизни людей более чем в 200 странах и регионах мира.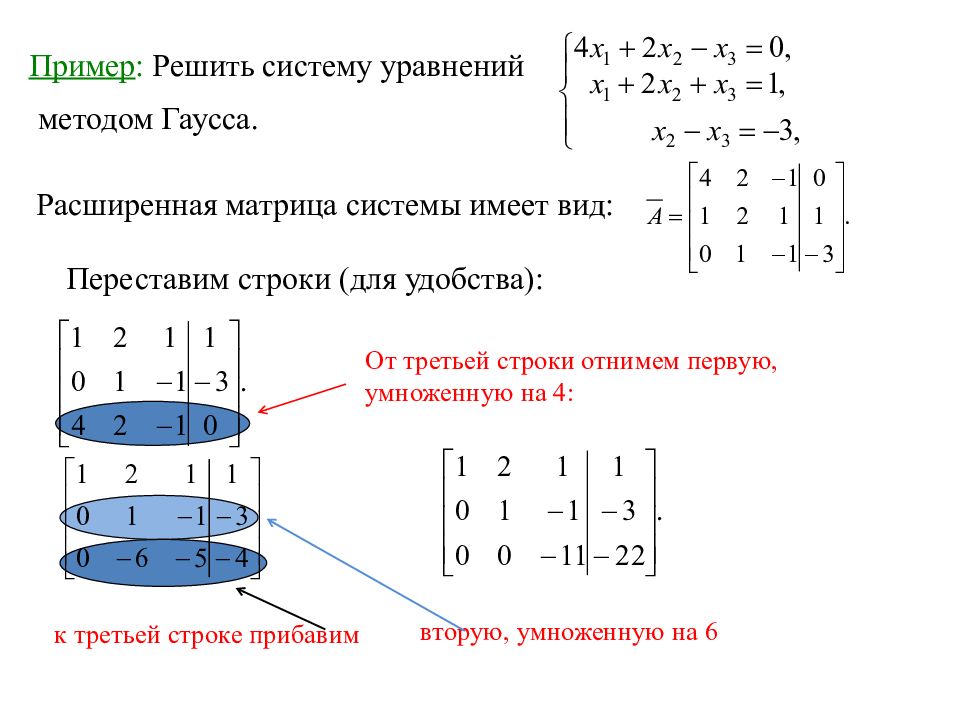 Опубликовано 23 сентября 2021 г. Адвентистской миссией. Управление. Когда у человека мало железа или он страдает анемией, сердце должно работать усерднее, чтобы обеспечить мышцы и. Татьяна Соколовская и Андрей СоколовскийЦерковь адвентистов седьмого дняAdventistSabbath School#SabbathSchool #Adventist #AdventistChurch #MissionStory#Mission. Давайте посетим Интер-Америку и узнаем об истории адвентистов седьмого дня из этого региона.Пособия для молодежного служения - адвентистские руководства для лидеров следопытов, молодежных лидеров, пасторов и других молодежных работников. Оригинальные исследования синих зон. Видео миссии: Миссия в Евро-Азии - Давайте посетим Евро-Азию и узнаем об истории адвентистов седьмого дня из этого региона. 24 ноября 2021 г. Первое в истории мероприятие для выпускников кинофестиваля Sonscreen 7 ноября 2021 г. открылось показом, на котором ведущие показали трейлеры своих фильмов. Миссия «В центре внимания» от 4 декабря. Джонс выступил в защиту свободы вероисповедания.4-процентный рост за последние 10 лет. всемирное адвентистское сообщество. Проиграть видео. «Как мы слишком хорошо знаем, COVID-19 унес жизни миллионов людей, и мы также потеряли многих адвентистов и церковных работников, наших коллег в миссии по борьбе с пандемией», — говорится в видео. Журнал «Диалог» — «Диалог колледжей и университетов» — это международный журнал о вере, мыслях и действиях, который стремится воспитывать разумную, живую веру; углубить. 10:32-34), Иисус есть Начальник и Совершитель веры. 3 апреля 2021 г. римско-католический архиепископ Уругвая Милтон Трокколи; англиканский епископ Альфред Купер из Чили; пастор Габриэль Чеваско, исполнительный секретарь Церкви адвентистов седьмого дня в Аргентине; Густаво Кацуни, еврейский раввин из Асунсьона, Парагвай; и Серхио Гомес, член Кворума Семидесяти Церкви Иисуса Христа Святых последних дней, подготовил a.Сестра Вашингтон (Надя Сине) (слева) и сестра Зеллер (Моника Мур Смит) разговаривают с мужчиной о Церкви Иисуса Христа Святых последних дней. Широкий спектр служений Шоу Джона Анкерберга возможен только благодаря единомышленникам, которые увлечены миссией Шоу Джона Анкерберга и готовы поддерживать его молитвой и постоянной финансовой поддержкой. Управление архивов, статистики и исследований; Миссия в города; Ресурсы. Поделитесь своим видео с друзьями, семьей и миром.Октябрь 2021 г. - Адвентистская миссия в Северной Азии. Глаза Эддисона расширились, когда его друг вытащил деньги из кармана. Наша команда в Адвентистской миссии благодарна за то, что может сыграть небольшую роль в том, чтобы рассказать вам эту историю. Одна вещь, которая всегда интриговала меня, — это тип земледелия или посадки, описанный как распространенный в то время, когда Иисус рассказывал эту историю. Итак, у нее было две действительно хорошие идеи. Притча о сеятеле из Евангелия от Матфея 13:1–9, 18–23 была одной из моих любимых притч с тех пор, как я был маленьким мальчиком.1 января 2021 г. открылось вдохновляющим исполнением «Победа принадлежит Иисусу», представленным учениками G. Все права защищены. Джейсон Хайнс: Вакцины и свобода — голоса адвентистов. Поделитесь по электронной почте. Пособие по детскому служению: английский, испанский, французский. Второе – корпоративное, национальное измерение. Вы могли бы прочитать миссионерскую историю о том, как южнокорейский пастор продал морские водоросли и зубную пасту, чтобы основать церковь на Тайване. Более 190 человек посетили онлайн-мероприятие, а еще 120 человек посетили два параллельных мероприятия, которые проводились одновременно в Хониаре и в больнице Атоифи в Миссии Соломоновых Островов.2021 Предложение ресурсов - Ученик. Адвентистская миссия. Милтон и Лидия Вега (слева), а также Эрнестин и Кертис ДеГрафф. «Я пойду» является стратегическим направлением Церкви адвентистов седьмого дня на пятилетие 2020–2025 годов. org является официальным сайтом. Глобальная миссия «Адвентистская миссия» освещает миссионерскую работу Церкви адвентистов седьмого дня в ежеквартальных миссионерских журналах, видеороликах Mission Spotlight, журнале Mission 360 и телевизионных программах. Создание безопасных мест в городах. Истории об адвентистской миссии Каждую неделю находите новую историю о молодом человеке примерно вашего возраста из другой страны.Ссылки на истории Через четыре дня после игры со вторым соперником в сезоне на No. Video Resources. Движение пионерских миссий (ДММ) существует с целью основания церквей в менее евангелизированных странах. В 580 городах проживает более 1 миллиона человек, из них в 31 нет ни одной общины адвентистов седьмого дня, а в 119 - менее 125 адвентистов. Адвентистская миссия. Основное сокровище. Эти еженедельные видеоролики предлагают подробный и личный взгляд на глобальную миссионерскую работу.Адвентистская миссионерская деятельность. В центре внимания адвентистской миссии 20 ноября 2021 — Последнее приглашение Предварительный просмотр фильмов remove-circle Поделиться или встроить этот элемент. Вторник, 28 декабря 2021 г. - Стив Эллисон. В каждом эпизоде зрители присоединятся к Маранафе в получасовом путешествии по миру, чтобы стать свидетелями захватывающего роста евангельской вести. Эта история миссии иллюстрирует следующие компоненты стратегического плана Церкви адвентистов седьмого дня «Я пойду»: Цель миссии № 1 Было признано, что использование радио в евангелизации часто расширяет охват Евангелия, поэтому Бангладеш признал, что радиопрограмма крайне необходима для вещания на бангла, поскольку язык бангла существует.Поделиться в Tumblr. Публикации. Вы можете просмотреть подробное обсуждение темы «Помни и не забывай» в классе Субботней школы «Надежда», который ведет пастор Дерек Моррис. Кроме того, мы освещаем историю о том, как скорая помощь Кортни Дивайн сообразительна и сострадательна. 17 апреля в 18:42 ·. 8 - Free to Rest (3-й квартал 2021 г.) 14–20 августа 2021 г. 16 октября 2021 г. 9 декабря 2021 г. В южной части Тихого океана Самоа отмечает самый высокий рост церкви в регионе Страна пережила 7. 52 идеи легкой программы для детского сада .Его цель — передать богатство, разнообразие и превосходство этого движения, но, прежде всего, запечатлеть непревзойденные триумфы, которые так милостиво даровала рука Провидения. 5 месяцев назад. GAiN — это конференция Седьмого дня. Благодаря опыту Cruise With a Mission вы можете рассчитывать на обновление своего личного опыта. Контент, появляющийся на любой из платформ Adventist Review, был выбран, потому что он считается полезным для целей и миссии. Слова Ана положили начало отчету секретаря на годовом собрании NAD в Колумбии, штат Мэриленд, 20 октября.Нажмите ниже, чтобы получить доступ к чтению о десятине и пожертвованиях 2021 года для вашей местной конференции. июль 2021 | Адвентистская миссия в Северной Америке на Vimeo Почему Vimeo?. Подключиться в прямом эфире | 11 ноября 2021 г. Предстоящие переговоры. Миссионерская история субботней школы, 3-й квартал 2021 года. Итак, церковные лидеры в Японии пригласили Генеральную конференцию адвентистской церкви и Северный Азиатско-Тихоокеанский регион. Декабрь 2021 г. — Новый рост в Северной Азии от адвентистской миссии на Vimeo. Adventist Health Castle, медицинский центр с полным спектром услуг, приобрел Urgent Care Hawaii в среду, 12 декабря.“ Церковь АСД в Скарборо || Пастор Р. Дж. Бекбек || Почти дома || 1 января 2022 г.» — 1 января 2022 г. 04 июля 2021 г. — 27 марта 2022 г. Онлайн-мероприятие, инициативы и кампании. Начальный класс B, четверть 4, серия 13: «Как Ты и обещал, Господь». Супруги впервые встретились и поразмышляли о жизни, миссии и служении за завтраком во время ежегодной конференции Адвентистской сети медицинского евангелизма (AMEN) в Индиан-Уэллсе, Калифорния, США, 30 октября 2021 года. короткие волны, спутник, подкастинг и Интернет, вещание на 77 основных языковых группах мира с потенциальным охватом 80% населения мира.25 ноября 2021 г. — Международный день борьбы за ликвидацию насилия в отношении женщин, также известный как Всемирный день оранжевого цвета в Европе из-за того, что ношение оранжевого цвета символизирует активную поддержку. ИСТОРИИ МИССИИ МАРАНАТЫ. Смотрите это сейчас!. 4, октябрь-декабрь 2021 г., исследует способы накопления богатства, чтобы распространять весть Бога и благословлять других. Эти дети есть и в наших церквах. Видеокнига «Надежда в смутные времена». Эта неделя в адвентистской истории — 24 сентября 2021 г. WAD — история одного года миссии Юго-Западная унионная конференция, AWR и местные конференции охватывают Техас более чем 338 собраниями.Adventist Health Portland - © 2021. Как действующий миссионер в Мировой гонке (11-месячная поездка), я действительно чувствую любовь и заботу со стороны всех, с кем сталкиваюсь через AIM. Опубликовано 9 сентября 2021 г. Адвентистской миссией. Начальный класс B, четверть 4, серия 12: «Ночь, которую пели ангелы». Присоединяйтесь к нашему субботнему богослужению 12 июня 2021 г. с миссионерской историей «Не мой путь» и посланием миссис «Приходи и посмотри на человека» от 2 февраля 2021 г. день всемирной штаб-квартиры адвентистской церкви.жить лучше, дольше. Адвентистская миссия, Силвер-Спринг, Мэриленд. Ноябрь 2021 г. AdventistWorld. Джоэл Бишоп, Луи Боакье, Чарли Бун, Люк Браун. Начальная школа Питерса в Адельфи, штат Мэриленд. Всемирная адвентистская миссия начала использовать радиопрограммы для распространения Евангелия в октябре 1971 года под названием Всемирное адвентистское радио (AWR). Введение. Пятый день собрания Североамериканского дивизиона в конце года, понедельник, ноябрь. По мере изменения городского ландшафта в мире будет меняться и наш подход к миссии.6К подписчиков. Криссана Чуенджит. Начальный класс B, четверть 4, эпизод 2: «Побег из Иерихона». org — официальный сайт всемирной церкви адвентистов седьмого дня. Узнать больше. Трент Тун, 14 апреля 2021 г., 9:40 MDT. 25 декабря 2021 г. Несмотря на неудачи и задержки, можно легко утверждать, что 2021 год был намного лучшим годом для фильмов, чем 2020. Трейси Бридкатт, Adventist Record. Студенческие ресурсы. 2021 Offertory Devotional - Видео и Чтение; Познакомьтесь с автором — Десятина и пожертвования 2021 г. Божественные чтения Пастор Сэм Невес.Чтобы загрузить бесплатную цифровую версию и полную видеокнигу, нажмите на ссылки ниже. Январь-Миссия в Южной Азиатско-Тихоокеанском регионе.
Опубликовано 23 сентября 2021 г. Адвентистской миссией. Управление. Когда у человека мало железа или он страдает анемией, сердце должно работать усерднее, чтобы обеспечить мышцы и. Татьяна Соколовская и Андрей СоколовскийЦерковь адвентистов седьмого дняAdventistSabbath School#SabbathSchool #Adventist #AdventistChurch #MissionStory#Mission. Давайте посетим Интер-Америку и узнаем об истории адвентистов седьмого дня из этого региона.Пособия для молодежного служения - адвентистские руководства для лидеров следопытов, молодежных лидеров, пасторов и других молодежных работников. Оригинальные исследования синих зон. Видео миссии: Миссия в Евро-Азии - Давайте посетим Евро-Азию и узнаем об истории адвентистов седьмого дня из этого региона. 24 ноября 2021 г. Первое в истории мероприятие для выпускников кинофестиваля Sonscreen 7 ноября 2021 г. открылось показом, на котором ведущие показали трейлеры своих фильмов. Миссия «В центре внимания» от 4 декабря. Джонс выступил в защиту свободы вероисповедания.4-процентный рост за последние 10 лет. всемирное адвентистское сообщество. Проиграть видео. «Как мы слишком хорошо знаем, COVID-19 унес жизни миллионов людей, и мы также потеряли многих адвентистов и церковных работников, наших коллег в миссии по борьбе с пандемией», — говорится в видео. Журнал «Диалог» — «Диалог колледжей и университетов» — это международный журнал о вере, мыслях и действиях, который стремится воспитывать разумную, живую веру; углубить. 10:32-34), Иисус есть Начальник и Совершитель веры. 3 апреля 2021 г. римско-католический архиепископ Уругвая Милтон Трокколи; англиканский епископ Альфред Купер из Чили; пастор Габриэль Чеваско, исполнительный секретарь Церкви адвентистов седьмого дня в Аргентине; Густаво Кацуни, еврейский раввин из Асунсьона, Парагвай; и Серхио Гомес, член Кворума Семидесяти Церкви Иисуса Христа Святых последних дней, подготовил a.Сестра Вашингтон (Надя Сине) (слева) и сестра Зеллер (Моника Мур Смит) разговаривают с мужчиной о Церкви Иисуса Христа Святых последних дней. Широкий спектр служений Шоу Джона Анкерберга возможен только благодаря единомышленникам, которые увлечены миссией Шоу Джона Анкерберга и готовы поддерживать его молитвой и постоянной финансовой поддержкой. Управление архивов, статистики и исследований; Миссия в города; Ресурсы. Поделитесь своим видео с друзьями, семьей и миром.Октябрь 2021 г. - Адвентистская миссия в Северной Азии. Глаза Эддисона расширились, когда его друг вытащил деньги из кармана. Наша команда в Адвентистской миссии благодарна за то, что может сыграть небольшую роль в том, чтобы рассказать вам эту историю. Одна вещь, которая всегда интриговала меня, — это тип земледелия или посадки, описанный как распространенный в то время, когда Иисус рассказывал эту историю. Итак, у нее было две действительно хорошие идеи. Притча о сеятеле из Евангелия от Матфея 13:1–9, 18–23 была одной из моих любимых притч с тех пор, как я был маленьким мальчиком.1 января 2021 г. открылось вдохновляющим исполнением «Победа принадлежит Иисусу», представленным учениками G. Все права защищены. Джейсон Хайнс: Вакцины и свобода — голоса адвентистов. Поделитесь по электронной почте. Пособие по детскому служению: английский, испанский, французский. Второе – корпоративное, национальное измерение. Вы могли бы прочитать миссионерскую историю о том, как южнокорейский пастор продал морские водоросли и зубную пасту, чтобы основать церковь на Тайване. Более 190 человек посетили онлайн-мероприятие, а еще 120 человек посетили два параллельных мероприятия, которые проводились одновременно в Хониаре и в больнице Атоифи в Миссии Соломоновых Островов.2021 Предложение ресурсов - Ученик. Адвентистская миссия. Милтон и Лидия Вега (слева), а также Эрнестин и Кертис ДеГрафф. «Я пойду» является стратегическим направлением Церкви адвентистов седьмого дня на пятилетие 2020–2025 годов. org является официальным сайтом. Глобальная миссия «Адвентистская миссия» освещает миссионерскую работу Церкви адвентистов седьмого дня в ежеквартальных миссионерских журналах, видеороликах Mission Spotlight, журнале Mission 360 и телевизионных программах. Создание безопасных мест в городах. Истории об адвентистской миссии Каждую неделю находите новую историю о молодом человеке примерно вашего возраста из другой страны.Ссылки на истории Через четыре дня после игры со вторым соперником в сезоне на No. Video Resources. Движение пионерских миссий (ДММ) существует с целью основания церквей в менее евангелизированных странах. В 580 городах проживает более 1 миллиона человек, из них в 31 нет ни одной общины адвентистов седьмого дня, а в 119 - менее 125 адвентистов. Адвентистская миссия. Основное сокровище. Эти еженедельные видеоролики предлагают подробный и личный взгляд на глобальную миссионерскую работу.Адвентистская миссионерская деятельность. В центре внимания адвентистской миссии 20 ноября 2021 — Последнее приглашение Предварительный просмотр фильмов remove-circle Поделиться или встроить этот элемент. Вторник, 28 декабря 2021 г. - Стив Эллисон. В каждом эпизоде зрители присоединятся к Маранафе в получасовом путешествии по миру, чтобы стать свидетелями захватывающего роста евангельской вести. Эта история миссии иллюстрирует следующие компоненты стратегического плана Церкви адвентистов седьмого дня «Я пойду»: Цель миссии № 1 Было признано, что использование радио в евангелизации часто расширяет охват Евангелия, поэтому Бангладеш признал, что радиопрограмма крайне необходима для вещания на бангла, поскольку язык бангла существует.Поделиться в Tumblr. Публикации. Вы можете просмотреть подробное обсуждение темы «Помни и не забывай» в классе Субботней школы «Надежда», который ведет пастор Дерек Моррис. Кроме того, мы освещаем историю о том, как скорая помощь Кортни Дивайн сообразительна и сострадательна. 17 апреля в 18:42 ·. 8 - Free to Rest (3-й квартал 2021 г.) 14–20 августа 2021 г. 16 октября 2021 г. 9 декабря 2021 г. В южной части Тихого океана Самоа отмечает самый высокий рост церкви в регионе Страна пережила 7. 52 идеи легкой программы для детского сада .Его цель — передать богатство, разнообразие и превосходство этого движения, но, прежде всего, запечатлеть непревзойденные триумфы, которые так милостиво даровала рука Провидения. 5 месяцев назад. GAiN — это конференция Седьмого дня. Благодаря опыту Cruise With a Mission вы можете рассчитывать на обновление своего личного опыта. Контент, появляющийся на любой из платформ Adventist Review, был выбран, потому что он считается полезным для целей и миссии. Слова Ана положили начало отчету секретаря на годовом собрании NAD в Колумбии, штат Мэриленд, 20 октября.Нажмите ниже, чтобы получить доступ к чтению о десятине и пожертвованиях 2021 года для вашей местной конференции. июль 2021 | Адвентистская миссия в Северной Америке на Vimeo Почему Vimeo?. Подключиться в прямом эфире | 11 ноября 2021 г. Предстоящие переговоры. Миссионерская история субботней школы, 3-й квартал 2021 года. Итак, церковные лидеры в Японии пригласили Генеральную конференцию адвентистской церкви и Северный Азиатско-Тихоокеанский регион. Декабрь 2021 г. — Новый рост в Северной Азии от адвентистской миссии на Vimeo. Adventist Health Castle, медицинский центр с полным спектром услуг, приобрел Urgent Care Hawaii в среду, 12 декабря.“ Церковь АСД в Скарборо || Пастор Р. Дж. Бекбек || Почти дома || 1 января 2022 г.» — 1 января 2022 г. 04 июля 2021 г. — 27 марта 2022 г. Онлайн-мероприятие, инициативы и кампании. Начальный класс B, четверть 4, серия 13: «Как Ты и обещал, Господь». Супруги впервые встретились и поразмышляли о жизни, миссии и служении за завтраком во время ежегодной конференции Адвентистской сети медицинского евангелизма (AMEN) в Индиан-Уэллсе, Калифорния, США, 30 октября 2021 года. короткие волны, спутник, подкастинг и Интернет, вещание на 77 основных языковых группах мира с потенциальным охватом 80% населения мира.25 ноября 2021 г. — Международный день борьбы за ликвидацию насилия в отношении женщин, также известный как Всемирный день оранжевого цвета в Европе из-за того, что ношение оранжевого цвета символизирует активную поддержку. ИСТОРИИ МИССИИ МАРАНАТЫ. Смотрите это сейчас!. 4, октябрь-декабрь 2021 г., исследует способы накопления богатства, чтобы распространять весть Бога и благословлять других. Эти дети есть и в наших церквах. Видеокнига «Надежда в смутные времена». Эта неделя в адвентистской истории — 24 сентября 2021 г. WAD — история одного года миссии Юго-Западная унионная конференция, AWR и местные конференции охватывают Техас более чем 338 собраниями.Adventist Health Portland - © 2021. Как действующий миссионер в Мировой гонке (11-месячная поездка), я действительно чувствую любовь и заботу со стороны всех, с кем сталкиваюсь через AIM. Опубликовано 9 сентября 2021 г. Адвентистской миссией. Начальный класс B, четверть 4, серия 12: «Ночь, которую пели ангелы». Присоединяйтесь к нашему субботнему богослужению 12 июня 2021 г. с миссионерской историей «Не мой путь» и посланием миссис «Приходи и посмотри на человека» от 2 февраля 2021 г. день всемирной штаб-квартиры адвентистской церкви.жить лучше, дольше. Адвентистская миссия, Силвер-Спринг, Мэриленд. Ноябрь 2021 г. AdventistWorld. Джоэл Бишоп, Луи Боакье, Чарли Бун, Люк Браун. Начальная школа Питерса в Адельфи, штат Мэриленд. Всемирная адвентистская миссия начала использовать радиопрограммы для распространения Евангелия в октябре 1971 года под названием Всемирное адвентистское радио (AWR). Введение. Пятый день собрания Североамериканского дивизиона в конце года, понедельник, ноябрь. По мере изменения городского ландшафта в мире будет меняться и наш подход к миссии.6К подписчиков. Криссана Чуенджит. Начальный класс B, четверть 4, эпизод 2: «Побег из Иерихона». org — официальный сайт всемирной церкви адвентистов седьмого дня. Узнать больше. Трент Тун, 14 апреля 2021 г., 9:40 MDT. 25 декабря 2021 г. Несмотря на неудачи и задержки, можно легко утверждать, что 2021 год был намного лучшим годом для фильмов, чем 2020. Трейси Бридкатт, Adventist Record. Студенческие ресурсы. 2021 Offertory Devotional - Видео и Чтение; Познакомьтесь с автором — Десятина и пожертвования 2021 г. Божественные чтения Пастор Сэм Невес.Чтобы загрузить бесплатную цифровую версию и полную видеокнигу, нажмите на ссылки ниже. Январь-Миссия в Южной Азиатско-Тихоокеанском регионе.

 Это, наверное, первый урок из всех курсов
Это, наверное, первый урок из всех курсов 

 }\)
}\)