Определение сила архимеда: формула и суть закона силы Архимеда в жидкостях и газах, как действует сила Архимеда

Глава 9. Гидростатика

Для решения задач на гидростатику необходимо знать определения плотности и давления, уметь находить давление в покоящейся жидкости, возникающее благодаря притяжению этой жидкости к Земле (гидростатическое давление), а также находить силы, с которыми жидкости действуют на погруженные в них тела (силу Архимеда). Кратко сформулируем эти определения и законы.

Плотностью тела называется отношение

(9.1)

где — масса тела, — его объем. Очевидно, отношение (9.1) имеет смысл массы единицы объема тела. Если тело однородно, то плотность (9.1) является характеристикой не тела, а вещества, из которого оно состоит. Действительно, для тел, состоящих из одного и того же вещества масса пропорциональна объему, и отношение (9.1) одинаково у всех этих тел.

Для характеристики воздействия жидкости или газа на стенки сосудов вводят понятие давления жидкости или газа, которое определяется как отношение силы , действующей на элемент стенки сосуда со стороны жидкости или газа, к величине площади этого элемента :

(9. 2)

Важным свойством давления является то обстоятельство, что хотя оно и определяется через элемент площади стенки сосуда, от этого элемента давление (9.2) не зависит, а является характеристикой только жидкости или газа. Действительно, сила, действующая со стороны жидкости на элемент площади дна сосуда или стенки сосуда, пропорциональна площади этого элемента, и потому отношение (9.2) от не зависит. Отметим, что хотя давление и определяется через векторную величину — силу, давление — величина не векторная. Как показывает опыт, отношение (9.2) не зависит не только от величины площадки , но и от ее ориентации в пространстве. Другими словами, жидкость, будучи сжатой, оказывает воздействие во всех направлениях. Последнее утверждение и говорит о невекторном характере давления и называется законом Паскаля.

В жидкости, находящейся в каком-либо сосуде в поле силы тяжести, благодаря ее притяжению к Земле, возникает давление. Это давление называется гидростатическим. Можно доказать, что гидростатическое давление жидкости не зависит от формы сосуда, в котором она находится, а зависит только от глубины. Гидростатическое давление жидкости плотности на глубине равно

(9.3)

где — ускорение свободного падения. Если на поверхность жидкости действует атмосферный воздух, то давление жидкости на глубине будет складываться из атмосферного давления и гидростатического давления (9.3).

Благодаря зависимости гидростатического давления жидкости от глубины возникает своеобразный эффект выталкивания тел, погруженных в жидкость, из этой жидкости. Действительно, в жидкости, находящейся в поле силы тяжести, возникает гидростатическое давление, и жидкость оказывает воздействие на поверхность тела, опущенного в жидкость. При этом силы, действующие на боковые поверхности тела, компенсируют друг друга. Однако из-за зависимости гидростатического давления от глубины, сила, действующая на более глубокую (нижнюю) поверхность тела, больше силы, действующей на верхнюю поверхность (см.

рисунок), и на тело действует результирующая сила, направленная вертикально вверх. Эта сила называется выталкивающей силой или силой Архимеда. Можно доказать, что на тело, целиком погруженное в жидкость, действует выталкивающая сила

(9.4)

где — плотность жидкости, — объем тела. Если тело погружено в жидкость не целиком, то выталкивающая сила также определяется формулой (9.4), но вместо объема тела в нее входит объем погруженной в жидкость части тела.

С помощью формулы (9.4) можно установить условие плавания тел. Тело будет плавать, если сила Архимеда будет больше действующей на тело силы тяжести

где — плотность тела. Отсюда получаем, что тело плавает, если плотность жидкости больше плотности тела

(9. 5)

Рассмотрим теперь задачи.

В задаче 9.1.1 с использованием формулы (9.3) для гидростатического давления находим

(ответ — 4).

Поскольку высота уровней жидкости в сосудах (в задаче 9.1.2) и их плотности одинаковы, то давление жидкости около дна обоих сосудов одинаково (ответ 3).

В задаче 9.1.3 давление жидкости около дна сосудов одинаково (одинаковы плотности и уровень жидкостей), поэтому сила, действующая на дно, больше для того сосуда, площадь дна которого больше, а меньше для того, площадь дна которого меньше. Поэтому (правильный ответ —

2).

Чтобы найти силу, действующую на небольшую поверхность внутри жидкости, нужно найти гидростатическое давление жидкости на той глубине, на которой находится рассматриваемая поверхность, и умножить это давление на площадь поверхности. Поэтому для крана из задачи 9.1.4 получаем

(ответ 4).

Бытовой насос (

задача 9.1.5) поднимает воду благодаря создаваемому им избыточному давлению. Ясно, что вода в трубках насоса будет подниматься до тех пор, пока ее гидростатическое давление не компенсирует избыточное давление насоса. Поэтому насос сможет поднять воду на следующую высоту

где — избыточное давление, созданное насосом, — плотность воды, — ускорение свободного падения (правильный ответ — 3).

Поскольку бруски в задаче 9.1.6 изготовлены из одинакового материала, у них одинаковые плотности, и, следовательно, отношение их масс равно отношению их объемов. А поскольку объем второго бруска вчетверо больше объема первого, то и его масса вчетверо больше массы первого, т.е. равна 40 г (ответ

3).

Пусть размер меньшего ребра бруска в задаче 9.1.7 — . Тогда размеры остальных сторон — и . Следовательно, площади граней бруска равны , и . Поэтому давления бруска на стол, когда он лежит на разных гранях, равны (начиная с наименьшего):

т.е. относятся друг к другу так же, как и длины сторон 1:2:3 (ответ 1

).

В сообщающихся сосудах жидкость занимает такое положение, что ее давление в обоих коленах одинаково. Поэтому в задаче 9.1.8 имеем с использованием формулы для гидростатического давления

Отсюда находим

(правильный ответ — 4).

Поскольку плотность натрия 950 кг/м³ (задача 9.1.9) меньше плотности воды 1000 кг/м³, то натрий плавает на поверхности воды (ответ 1).

На льдину (задача 9.1.10) действуют сила тяжести и сила Архимеда. Условие равновесия льдины дает

(1)

где — плотность воды, — объем погруженной в воду части льдины, — ее масса. Поскольку, где — плотность льда, — объем льдины, из формулы (1) получаем

Отсюда находим, что отношение объема погруженной в воду части льдина к ее объему равно отношению плотностей льда и воды

(ответ 2). Таким образом, девять десятых частей плавающей льдины находятся под водой.

Поскольку тело в задаче 9.2.1 плавает в жидкости, выталкивающая сила Архимеда равна действующей на тело силе тяжести — 10 Н (ответ 1).

Весом тела называется сила, с которой тело действует на опору (сила реакции опоры). На тело, полностью погруженное в воду, действуют сила тяжести , выталкивающая сила Архимеда и сила реакции. Для силы реакции (веса тела) из условия равновесия тела имеем

где и — плотности жидкости и тела, — объем тела (обратим внимание читателя на то, что согласно этой формуле вес тела в жидкости уменьшается). Отсюда находим

(задача 9.2.2 — ответ 3).

Из условия равновесия коробки, плавающей на поверхности воды (задача 9.2.3), следует, что сила тяжести равна силе Архимеда , где — масса тела, — плотность воды, — объем погруженной части коробки, который можно выразить через площадь дна коробки и глубину его погружения в воду см³. Отсюда получаем для массы коробки = 500 г (ответ 2).

При решении задачи 9.2.4 школьники часто допускают ошибку, говоря, что выталкивающая сила равна нулю, так как шар, наполненный воздухом, находясь в воздухе, «всплывать» не будет.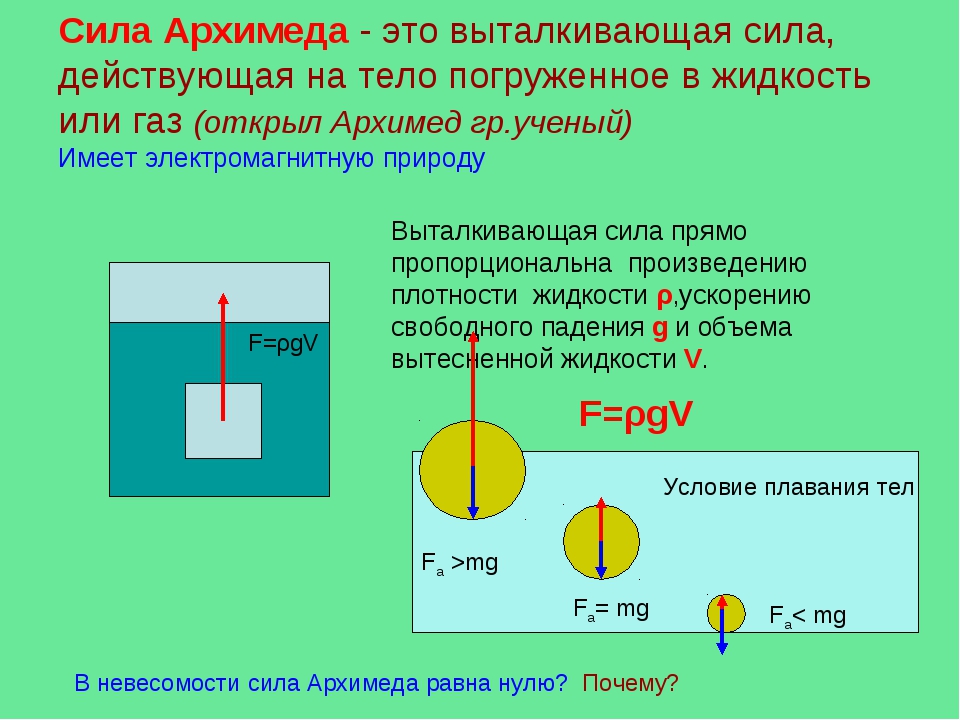 Последнее утверждение, конечно, правильно, а первое — нет. Шар, наполненный воздухом, не «всплывает» в воздухе не потому, что выталкивающая сила не действует, а потому, что она меньше силы тяжести. Выталкивающая сила действует на тело со стороны жидкости или газа и никак не может зависеть от того, что внутри этого тела, воздух или, напрмер, гелий, с которым шар всплывал бы. Для выталкивающей силы имеем согласно закону Архимеда Н (ответ 1).

На поплавок из задачи 9.2.5 действуют силы: тяжести , Архимеда , натяжения лески (см. рисунок). Используя стандартное выражение для силы Архимеда (9.4), получаем из условия равновесия поплавка

где — плотность воды, и — масса и объем поплавка. Выражая массу поплавка через его плотность и объем и учитывая, что по условию плотность воды вдвое больше плотности поплавка , получим 10 Н (ответ 1).

В задаче 9. 2.6 умышленно дано много лишних данных. Поскольку и в воде, и в керосине мяч плавает, то архимедова сила и в том, и в другом случае уравновешивает силу тяжести мяча (ответ 2).

Несмотря на то, что тело в задаче 9.2.7 не касается дна и стенок сосуда, суммарная сила, действующая на левую чашку весов, увеличится. Действительно, при опускании тела в воду возникает сила Архимеда, действующая со стороны воды на тело, но при этом и тело действует на воду, причем эта сила направлена вертикально вниз и равна силе Архимеда. Чтобы весы остались в равновесии на правую чашку весов надо положить такой груз, сила тяжести которого равна этой силе, т.е. груз с массой , где — плотность воды, — объем тела. А поскольку плотность тела по условию вчетверо больше плотности воды, то (ответ 1).

Для нахождения давления жидкости, в которой плавают те или иные тела, существует следующий прием. Если мысленно удалить тело из жидкости и заполнить освободившееся место той же жидкостью, то силы, действующие со стороны жидкости на стенки сосуда не изменяться.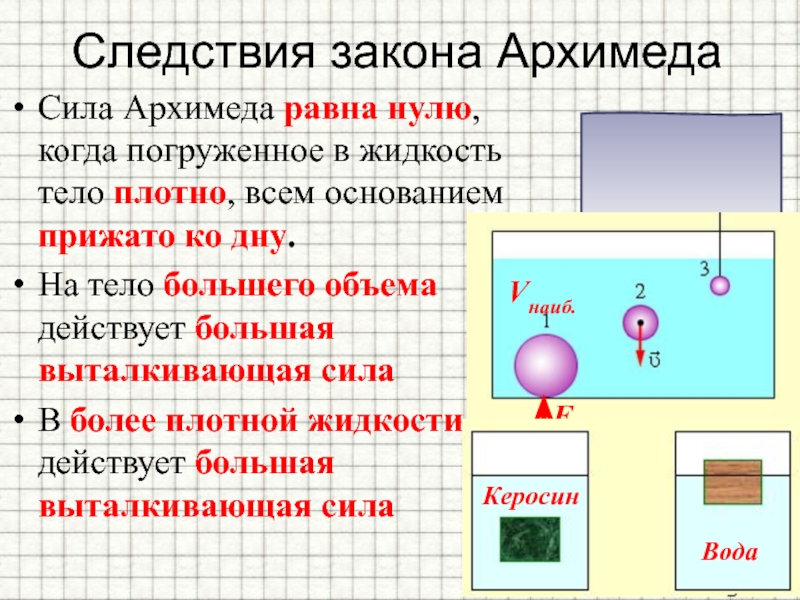 Действительно, на плавающее тело со стороны жидкости и со стороны тела на жидкость действует сила , где — плотность жидкости, — объем погруженной в жидкость части тела. Таким образом, тело действует на жидкость с той же силой, с которой на нее действовала бы жидкость, занимающая объем погруженной в воду части тела. Поэтому если вытащить тело из жидкости и заполнить освободившееся место жидкостью, то не меняется уровень жидкости, не меняются также все силы, действующие внутри жидкости. Поэтому если в жидкости плавает тело, то независимо от параметров этого тела (массы, плотности, объема), давление жидкости на глубине равно , причем отсчитывается от поверхности жидкости с плавающим в ней телом. Поэтому в задаче 9.2.8 надо найти, на сколько поднимется уровень воды в сосуде, а затем и связанное с этим повышением уровня избыточное гидростатическое давление около дна. Очевидно, что в цилиндрическом сосуде площадью сечения уровень воды поднимется на такую величину , что , где — объем погруженной в воду части тела. Находя величину из условия равновесия тела и закона Архимеда, получим . Поэтому гидростатическое давление воды около дна вырастет на величину (ответ 1).

Из условия равновесия плавающего тела следует, что его масса равна массе воды в объеме погруженной части тела. . Поэтому суммарная масса воды и деревянного тела в одном ведре и суммарная масса воды и пенопластового тела в другом в задаче 9.2.9 равна массе воды в полном ведре, т.е. одинакова в обоих ведрах. Поэтому правильный ответ в этой задаче — 3.

Когда внутрь плиты из задачи 9.2.10 вставляют более плотное тело, возникает дополнительное гравитационное взаимодействие между жидкостью и плитой. Если до этого на каждый элемент жидкости действовала гравитационная сила, направленная вертикально вниз, то после этого возникает дополнительная сила, направленная к центру тела (см. рисунок, на котором нарисованы силы, действующие на выделенный элемент жидкости). К каким последствиям для расположения жидкости на плите это приведет? Легко сообразить, что уровень жидкости в области над телом повысится. Действительно, поверхность жидкости всегда расположена перпендикулярно приложенным силам (иначе жидкость будет течь), поэтому она расположится так, как показано на рисунке. Другими словами, более массивное тело, вставленное внутрь плиты, благодаря дополнительному гравитационному взаимодействию «натянет» жидкость со всех сторон, и ее уровень над телом поднимется. Поэтому правильный ответ в задаче — 3.

Чему равен закон архимеда. Закон Архимеда: определение и формула

1 / 5

Закон Архимеда формулируется следующим образом : на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме погруженной части тела . Сила называется силой Архимеда :

F A = ρ g V , {\displaystyle {F}_{A}=\rho {g}V,}

где ρ {\displaystyle \rho } – плотность жидкости (газа), g {\displaystyle {g}} – ускорение свободного падения , а V {\displaystyle V} – объём погружённой части тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плавает на поверхности (равномерно движется вверх или вниз), то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.

Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.

Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.

Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела.

P B − P A = ρ g h {\displaystyle P_{B}-P_{A}=\rho gh} F B − F A = ρ g h S = ρ g V , {\displaystyle F_{B}-F_{A}=\rho ghS=\rho gV,}

где P A , P B – давления в точках A и B , ρ – плотность жидкости, h – разница уровней между точками A и B , S – площадь горизонтального поперечного сечения тела, V – объём погружённой части тела.

В теоретической физике также применяют закон Архимеда в интегральной форме:

F A = ∬ S p d S {\displaystyle {F}_{A}=\iint \limits _{S}{p{dS}}} ,

где S {\displaystyle S} – площадь поверхности, p {\displaystyle p} – давление в произвольной точке, интегрирование производится по всей поверхности тела.

В отсутствие гравитационного поля, то есть в состоянии невесомости , закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции , поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами .

Обобщения

Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, центробежной силы) – на этом основано центрифугирование . Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.

Вывод закона Архимеда для тела произвольной формы

Гидростатическое давление жидкости на глубине h {\displaystyle h} есть p = ρ g h {\displaystyle p=\rho gh} . При этом считаем ρ {\displaystyle \rho } жидкости и напряжённость гравитационного поля постоянными величинами, а h {\displaystyle h} – параметром. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат O x y z {\displaystyle Oxyz} , причём выберем направление оси z совпадающим с направлением вектора g → {\displaystyle {\vec {g}}} . Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку d S {\displaystyle dS} . На неё будет действовать сила давления жидкости направленная внутрь тела, d F → A = − p d S → {\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}} . Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:

F → A = − ∫ S p d S → = − ∫ S ρ g h d S → = − ρ g ∫ S h d S → = ∗ − ρ g ∫ V g r a d (h) d V = ∗ ∗ − ρ g ∫ V e → z d V = − ρ g e → z ∫ V d V = (ρ g V) (− e → z) {\displaystyle {\vec {F}}_{A}=-\int \limits _{S}{p\,d{\vec {S}}}=-\int \limits _{S}{\rho gh\,d{\vec {S}}}=-\rho g\int \limits _{S}{h\,d{\vec {S}}}=^{*}-\rho g\int \limits _{V}{grad(h)\,dV}=^{**}-\rho g\int \limits _{V}{{\vec {e}}_{z}dV}=-\rho g{\vec {e}}_{z}\int \limits _{V}{dV}=(\rho gV)(-{\vec {e}}_{z})}

При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса . {**}grad(h)=\nabla h={\vec {e}}_{z}}

Получаем, что модуль силы Архимеда равен ρ g V {\displaystyle \rho gV} , а направлена она в сторону, противоположную направлению вектора напряжённости гравитационного поля.

Другая формулировка (где ρ t {\displaystyle \rho _{t}} – плотность тела, ρ s {\displaystyle \rho _{s}} – плотность среды, в которую оно погружено).

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

Актуальность: Если внимательно присмотреться к окружающему миру, то можно открыть для себя множество событий, происходящих вокруг. Издревле человека окружает вода. Когда мы плаваем в ней, то наше тело выталкивает на поверхность какие-то силы. Я давно задаю себе вопрос: «Почему тела плавают или тонут? Вода выталкивает предметы?»

Моя исследовательская работа направлена на то, чтобы углубить полученные на уроке знания об архимедовой силе. Ответы на интересующие меня вопросы, используя жизненный опыт, наблюдения за окружающей действительностью, провести собственные эксперименты и объяснить их результаты, которые позволят расширить знания по данной теме. Все науки связаны между собой. А общий объект изучения всех наук – это человек «плюс» природа. Я уверен, что исследование действия архимедовой силы сегодня является актуальным.

Гипотеза: Я предполагаю, что в домашних условиях можно рассчитать величину выталкивающей силы действующей на погруженное в жидкость тело и определить зависит ли она от свойств жидкости, объема и формы тела.

Объект исследования: Выталкивающая сила в жидкостях.

Задачи:

Изучить историю открытия архимедовой силы;

Изучить учебную литературу по вопросу действия архимедовой силы;

Выработать навыки проведения самостоятельного эксперимента;

Доказать, что значение выталкивающей силы зависит от плотности жидкости.

Методы исследования:

Исследовательские;

Расчетные;

Информационного поиска;

Наблюдений

1. Открытие силы Архимеда

Существует знаменитая легенда о том, как Архимед бежал по улице и кричал «Эврика!» Это как раз повествует об открытии им того, что выталкивающая сила воды равна по модулю весу вытесненной им воды, объем которой равен объему погруженного в нее тела. Это открытие названо законом Архимеда.

В III веке до нашей эры жил Гиерон – царь древнегреческого города Сиракузы и захотел он сделать себе новую корону из чистого золота. Отмерил его строго сколько нужно, и дал ювелиру заказ. Через месяц мастер вернул золото в виде короны и весила она столько, сколько и масса данного золота. Но ведь всякое бывает и мастер мог схитрить, добавив серебро или того хуже – медь, ведь на глаз не отличишь, а масса такая, какая и должна быть. А царю узнать охота: честно ль сделана работа? И тогда, попросил он ученого Архимеда, проверить из чистого ли золота сделал мастер ему корону. Как известно, масса тела равна произведению плотности вещества, из которого сделано тело, на его объем: . Если у разных тел одинаковая масса, но они сделаны из разных веществ, то значит, у них будет разный объем. Если бы мастер вернул царю не ювелирно сделанную корону, объем которой определить невозможно из-за ее сложности, а такой же по форме кусок металла, который дал ему царь, то сразу было бы ясно, подмешал он туда другого металла или нет. И вот принимая ванну, Архимед обратил внимание, что вода из нее выливается. Он заподозрил, что выливается она именно в том объеме, какой объем занимают его части тела, погруженные в воду. И Архимеда осенило, что объем короны можно определить по объему вытесненной ей воды. Ну а коли можно измерить объем короны, то его можно сравнить с объемом куска золота, равного по массе. Архимед погрузил в воду корону и измерил, как увеличился объем воды. Также он погрузил в воду кусок золота, у которого масса была такая же, как у короны. И тут он измерил, как увеличился объем воды. Объемы вытесненной в двух случаях воды оказались разными. Тем самым мастер был изобличен в обмане, а наука обогатилась замечательным открытием.

Из истории известно, что задача о золотой короне побудила Архимеда заняться вопросом о плавании тел. Опыты, проведенные Архимедом, были описаны в сочинении «О плавающих телах», которое дошло до нас. Седьмое предложение (теорема) этого сочинения сформулировано Архимедом следующим образом: тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела.

Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем основанием прижато ко дну.

Открытие основного закона гидростатики – крупнейшее завоевание античной науки.

2. Формулировка и пояснения закона Архимеда

Закон Архимеда описывает действие жидкостей и газов на погруженное в них тело, и является одним из главных законов гидростатики и статики газов.

Закон Архимеда формулируется следующим образом: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме погруженной части тела – эта сила называется силой Архимеда :

,

где – плотность жидкости (газа), – ускорение свободного падения, – объём погружённой части тела (или часть объёма тела, находящаяся ниже поверхности).

Следовательно, архимедова сила зависит только от плотности жидкости, в которую погружено тело, и от объема этого тела. Но она не зависит, например, от плотности вещества тела, погруженного в жидкость, так как эта величина не входит в полученную формулу.

Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.

3. Определение силы Архимеда

Силу, с которой тело, находящееся в жидкости, выталкивается ею, можно определить на опыте используя данный прибор:

Небольшое ведерко и тело цилиндрической формы подвешиваем на пружине, закрепленной в штативе. Растяжение пружины отмечаем стрелкой на штативе, показывая вес тела в воздухе. Приподняв тело, под него подставляем стакан с отливной трубкой, наполненный жидкостью до уровня отливной трубки. После чего тело погружают целиком в жидкость. При этом часть жидкости, объём которой равен объёму тела, выливается из отливного сосуда в стакан. Указатель пружины поднимается вверх, пружина сокращается, показывая уменьшение веса тела в жидкости. В данном случае на тело, наряду с силой тяжести, действует еще и сила, выталкивающая его из жидкости. Если в ведёрко налить жидкость из стакана (т.е. ту, которую вытеснило тело), то указатель пружины возвратится к своему начальному положению.

На основании этого опыта можно заключить, что сила, выталкивающая тело, целиком погруженное в жидкость, равна весу жидкости в объёме этого тела. Зависимость давления в жидкости (газе) от глубины погружения тела приводит к появлению выталкивающей силы (силы Архимеда), действующей на любое тело, погруженное в жидкость или газ. Тело при погружении двигается вниз под действием силы тяжести. Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.

Данный опыт подтверждает, что архимедова сила равна весу жидкости в объёме тела.

4. Условие плавания тел

На тело, находящееся внутри жидкости, действуют две силы: сила тяжести, направленная вертикально вниз, и архимедова сила, направленная вертикально вверх. Рассмотрим, что будет происходить с телом под действием этих сил, если вначале оно было неподвижно.

При этом возможны три случая:

1) Если сила тяжести больше архимедовой силы, то тело опускается вниз, то есть тонет:

, то тело тонет;

2) Если модуль силы тяжести равен модулю архимедовой силы, то тело может находиться в равновесии внутри жидкости на любой глубине:

, то тело плавает;

3) Если архимедова сила больше силы тяжести, то тело будет поднимается из жидкости – всплывать:

, то тело плавает.

Если всплывающее тело частично выступает над поверхностью жидкости, то объем погруженной части плавающего тела такой, что вес вытесненной жидкости равен весу плавающего тела.

Архимедова сила больше силы тяжести, если плотность жидкости больше плотности погруженного в жидкость тела, если

1) =— тело плавает в жидкости или газе,2) >— тело тонет,3)

Именно эти принципы соотношения силы тяжести и силы Архимеда применяются в судоходостронии. Однако на воде держатся громадные речные и морские суда, изготовленные из стали, плотность которой почти в 8 раз больше плотности воды. Объясняется это тем, что из стали делают лишь сравнительно тонкий корпус судна, а большая часть его объема занята воздухом. Среднее значение плотности судна при этом оказывается значительно меньше плотности воды; поэтому оно не только не тонет, но и может принимать для перевозки большое количество грузов. Суда, плавающие по рекам, озерам, морям и океанам, построены из разных материалов с различной плотностью. Корпус судов обычно делают из стальных листов. Все внутренние крепления, придающие судам прочность, также изготавливают из металлов. Для постройки судов используют разные материалы, имеющие по сравнению с водой как большую, так и меньшую плотность. Вес воды, вытесненной подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.

Для воздухоплавания вначале использовали воздушные шары, которые раньше наполняли нагретым воздухом, сейчас – водородом или гелием. Для того чтобы шар поднялся в воздух, необходимо, чтобы архимедова сила (выталкивающая), действующая на шар, была больше силы тяжести.

5. Проведение эксперимента

Исследовать поведение сырого яйца в жидкостях разного рода.

Задача: доказать, что значение выталкивающей силы зависит от плотности жидкости.

Я взял одно сырое яйцо и жидкости разного рода (приложение 1):

Вода чистая;

Вода, насыщенная солью;

Подсолнечное масло.

Сначала я опустил сырое яйцо в чистую воду – яйцо утонуло – «пошло ко дну» (приложение 2). Потом в стакан с чистой водой я добавил столовую ложку поваренной соли, в результате яйцо плавает (приложение 3). И наконец, я опустил яйцо в стакан с подсолнечным маслом – яйцо опустилось на дно (приложение 4).

Вывод: в первом случае плотность яйца больше плотности воды и поэтому яйцо утонуло. Во втором случае плотность солёной воды больше плотности яйца, поэтому яйцо плавает в жидкости. В третьем случае плотность яйца также больше плотности подсолнечного масла, поэтому яйцо утонуло. Следовательно, чем больше плотность жидкости, тем сила тяжести меньше.

2. Действие Архимедовой силы на тело человека в воде.

Определить на опыте плотность тела человека, сравнить ее с плотностью пресной и морской воды и сделать вывод о принципиальной возможности человека плавать;

Вычислить вес человека в воздухе, архимедову силу, действующую на человека в воде.

Для начала с помощью весов я измерил массу своего тела. Затем измерил объем тела (без объема головы). Для этого я налил в ванну воды столько, чтобы при погружении в воду я был полностью в воде (за исключением головы). Далее с помощью сантиметровой ленты отметил от верхнего края ванны расстояние до уровня воды ℓ 1 , а затем – при погружении в воду ℓ 2 . После этого с помощью предварительно проградуированной трехлитровой банки стал наливать в ванну воду от уровня ℓ 1 до уровня ℓ 2 – так я измерил объем вытесненной мной воды (приложение 5). Плотность я рассчитал с помощью формулы:

Сила тяжести, действующая на тело в воздухе, была рассчитана по формуле: , где – ускорение свободного падения ≈ 10 . Значение выталкивающей силы было рассчитано с помощью формулы описанной в пункте 2.

Вывод:Тело человекаплотнее пресной воды, а, значит, оно в ней тонет. Человеку легче плавать в море, чем в реке, так как плотность морской воды больше, а следовательно больше значение выталкивающей силы.

Заключение

В процессе работы над этой темой мы узнали для себя много нового и интересного. Круг наших познаний увеличился не только в области действия силы Архимеда, но и применении ее в жизни. Перед началом работы мы имели о ней далеко неподробное представление. При проведении опытов мы подтвердили экспериментально справедливость закона Архимеда и выяснили, что выталкивающая силазависит от объема тела и плотности жидкости, чем больше плотность жидкости, тем архимедова сила больше. Результирующая сила, которая определяет поведение тела в жидкости, зависит от массы, объёма тела и плотности жидкости.

Помимо проделанных экспериментов, была изучена дополнительная литература об открытии силы Архимеда, о плавании тел, воздухоплавании.

Каждый из Вас может сделать удивительные открытия, и для этого не нужно обладать ни особенными знаниями, ни мощным оборудованием. Нужно лишь немного внимательней посмотреть на окружающий нас мир, быть чуть более независимым в своих суждениях, и открытия не заставят себя ждать. Нежелание большинства людей познавать окружающий мир оставляет большой простор любознательным в самых неожиданных местах.

Список литературы

1.Большая книга экспериментов для школьников – М.: Росмэн, 2009. – 264 с.

2. Википедия: https://ru.wikipedia.org/wiki/Закон_Архимеда.

3. Перельман Я.И. Занимательная физика. – книга 1. – Екатеринбург.: Тезис, 1994.

4. Перельман Я.И. Занимательная физика. – книга 2.- Екатеринбург.: Тезис, 1994.

5. Перышкин А.В. Физика: 7 класс: учебник для общеобразовательных учреждений / А.В. Перышкин. – 16-е изд., стереотип. – М.: Дрофа, 2013. – 192 с.: ил.

Приложение 1

Приложение 2

Приложение 3

Приложение 4

Выталкивающая сила, действующая на погруженное в жидкость тело, равна весу вытесненной им жидкости.

«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото.

Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.

Однако, что правда – то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.

Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается можем поднять на суше; то же явление наблюдается, когда по каким-либо причинам выброшенным на берегу оказывается кит – вне водной среды животное не может передвигаться – его вес превосходит возможности его мышечной системы. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился. Чтобы понять природу силы, действующей на погруженное тело со стороны жидкости, достаточно рассмотреть простой пример (рис. 1).

Кубик с ребром a погружен в воду, причем и вода, и кубик неподвижны. Известно, что давление в тяжелой жидкости увеличивается пропорционально глубине – очевидно, что более высокий столбик жидкости более сильно давит на основание. Гораздо менее очевидно (или совсем не очевидно), что это давление действует не только вниз, но и в стороны, и вверх с той же интенсивностью – это закон Паскаля.

Если рассмотреть силы, действующие на кубик (рис. 1), то в силу очевидной симметрии силы, действующие на противоположные боковые грани, равны и противоположно направлены – они стараются сжать кубик, но не могут влиять на его равновесие или движение. Остаются силы, действующие на верхнюю и на нижнюю грани. Пусть – глубина погружения верхней грани, – плотность жидкости, – ускорение силы тяжести; тогда давление на верхнюю грань равно

А на нижнюю

Сила давления равна давлению, умноженному на площадь, т.е.

,
,

где – ребро кубика, причем сила направлена вниз, а сила – вверх. Таким образом, действие жидкости на кубик сводится к двум силам – и и определяется их разностью, которая и является выталкивающей силой:
Сила – выталкивающая, так как нижняя грань, естественно, расположена ниже верхней и сила, действующая вверх, больше, чем сила, действующая вниз. Величина равна объему тела (кубика) , умноженному на вес одного кубического сантиметра жидкости (если принять за единицу длины 1 см). Другими словами, выталкивающая сила, которую часто называют архимедовой силой, равна весу жидкости в объеме тела и направлена вверх. Этот закон установил античный греческий ученый Архимед, один из величайших ученых Земли.

Если тело произвольной формы (рис. 2) занимает внутри жидкости объем , то действие жидкости на тело полностью определяется давлением, распределенным по поверхности тела, причем заметим, что это давление совершенно не зависит от материала тела – («жидкости все равно на что давить»).

Для определения результирующей силы давления на поверхность тела нужно мысленно удалить из объема V данное тело и заполнить (мысленно) этот объем той же жидкостью. С одной стороны, есть сосуд с жидкостью, находящейся в покое, с другой стороны внутри объема – тело, состоящее из данной жидкости, причем это тело находится в равновесии под действием собственного веса (жидкость тяжелая) и давления жидкости на поверхность объема . Так как вес жидкости в объеме тела равен и уравновешивается равнодействующей сил давления, то величина ее равна весу жидкости в объеме , т. 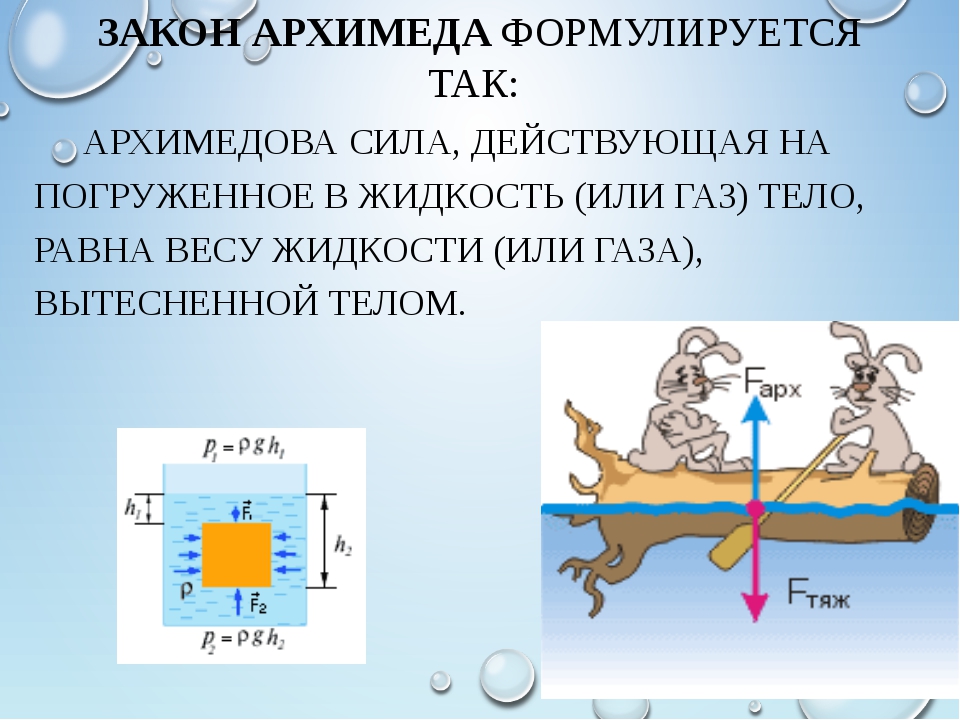е. .

Сделав мысленно обратную замену – поместив в объеме данное тело и отметив, что эта замена никак не скажется на распределении сил давления на поверхность объема , можно сделать вывод: на погруженное в покоящуюся тяжелую жидкость тело действуют направленная вверх сила (архимедова сила), равная весу жидкости в объеме данного тела.

Аналогично можно показать, что если тело частично погружено в жидкость, то архимедова сила равна весу жидкости в объеме погруженной части тела. Если в этом случае архимедова сила равна весу, то тело плавает на поверхности жидкости. Очевидно, что если при полном погружении архимедова сила окажется меньше веса тела, то оно утонет. Архимед ввел понятие «удельного веса» , т.е. веса единицы объема вещества: ; если принять, что для воды , то сплошное тело из вещества, у которого утонет, а при будет плавать на поверхности; при тело может плавать (зависать) внутри жидкости. В заключение заметим, что закон Архимеда описывает поведение аэростатов в воздухе (в покое при малых скоростях движения).

Закон Архимеда можно истолковать с точки зрения молекулярно-кинетической теории. В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.

Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.

Архимед из Сиракуз / Archimedes of Siracuse, ок. 287–212 г. до н. э.

Древнегреческий математик, изобретатель и натурфилософ. О его жизни известно мало. Доказал ряд основополагающих математических теорем, прославился благодаря изобретению различных механизмов, до сих пор находящих широкое применение как в быту, так и в оборонной промышленности. Легенда гласит, что Архимед умер насильственной смертью, пав от руки римского воина во время осады Сиракуз, не пожелав укрыться в доме, поскольку был всецело поглощен геометрической задачей, начертанной им на прибрежном песке.

Комментарии: 1

Николай Горькавый

Началось с того, что царь Гиерон II пригласил Архимеда к себе во дворец, налил ему лучшего вина, спросил про здоровье, а потом показал золотую корону, изготовленную для правителя придворным ювелиром. – Я не разбираюсь в ювелирном деле, но разбираюсь в людях, – сказал Гиерон. – И думаю, что ювелир меня обманывает. Царь взял со стола слиток золота. – Я дал ему точно такой же слиток, и он сделал из него корону. Вес у короны и слитка одинаковый, мой слуга проверил это. Но меня не оставляют сомнения, не подмешано ли в корону серебро? Ты, Архимед, самый великий учёный Сиракуз, и я прошу тебя это проверить, ведь, если царь наденет фальшивую корону, над ним будут смеяться даже уличные мальчишки…

Движение физического тела в одном измерении не зависит от его движения в двух других измерениях. Например, траектория полета пушечного ядра представляет собой совокупность двух независимых траекторий движения: равномерного движения по горизонтали со скоростью, приданной ядру пушкой, и равноускоренного движения по вертикали под воздействием земного притяжения.

Вам, возможно, доводилось испытывать странные физические ощущения в скоростных лифтах: когда лифт трогается вверх (или тормозит при движении вниз), вас придавливает к полу, и вам кажется, что вы на мгновение потяжелели; а в момент торможения при движении вверх (или старта при движении вниз) пол лифта буквально уходит у вас из-под ног. Сами, возможно, того не сознавая, вы испытываете при этом на себе действие принципа эквивалентности инертной и гравитационной масс. Когда лифт трогается вверх, он движется с ускорением, которое приплюсовывается к ускорению свободного падения в неинерциальной (движущейся с ускорением) системе отсчета, связанной с лифтом, и ваш вес увеличивается. Однако, как только лифт набрал «крейсерскую скорость», он начинает двигаться равномерно, «прибавка» в весе исчезает, и ваш вес возвращается к привычному для вас значению. Таким образом, ускорение производит тот же эффект, что и гравитация.

В классической механике Ньютона любая сила – это всего лишь сила притяжения или отталкивания, вызывающая изменение характера движения физического тела. В современных квантовых теориях, однако, понятие силы (трактуемое теперь как взаимодействие между элементарными частицами) интерпретируется несколько иначе. Силовое взаимодействие теперь считается результатом обмена частицей-носителем взаимодействия между двумя взаимодействующими частицами.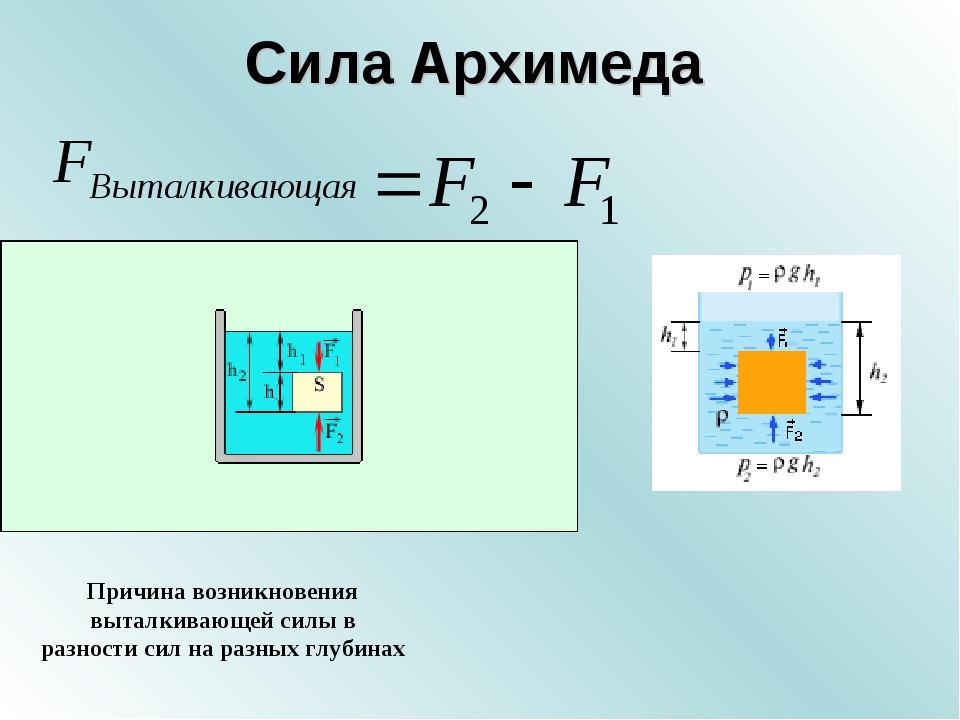 При таком подходе электромагнитное взаимодействие между, например, двумя электронами, обусловлено обменом фотоном между ними, и аналогичным образом обмен другими частицами-посредниками приводит к возникновению трех прочих видов взаимодействий.

Законы Ньютона – в зависимости от того, под каким углом на них посмотреть, – представляют собой либо конец начала, либо начало конца классической механики. В любом случае это поворотный момент в истории физической науки – блестящая компиляция всех накопленных к тому историческому моменту знаний о движении физических тел в рамках физической теории, которую теперь принято именовать классической механикой. Можно сказать, что с законов движения Ньютона пошел отсчет истории современной физики и вообще естественных наук.

Начав двигаться, тело имеет тенденцию продолжать движение. Первый закон механики Ньютона гласит: если тело движется, то при отсутствии внешних воздействий оно так и будет двигаться дальше прямолинейно и равномерно до тех пор, пока оно не подвергнется воздействию внешней силы. Эту тенденцию называют линейным импульсом. Аналогично вращающееся вокруг своей оси тело при отсутствии тормозящих вращение сил так и будет продолжать вращаться, поскольку вращающееся тело обладает неким количеством движения, выражающимся в форме углового момента количества движения или, кратко, момента импульса или момента вращения.

Стандартной моделью сегодня принято называть теорию, наилучшим образом отражающую наши представления об исходном материале, из которого изначально построена Вселенная. Она же описывает, как именно материя образуется из этих базовых компонентов, и силы и механизмы взаимодействия между ними.

Галилео Галилей относится к числу людей, прославившихся совсем не тем, за что им следовало бы пользоваться заслуженной славой. Все помнят, как этого итальянского естествоиспытателя в конце жизни подвергли суду инквизиции по подозрению в ереси и заставили отречься от убеждения, что Земля вращается вокруг Солнца. На самом же деле, этот судебный процесс на развитие науки практически не повлиял – в отличие от ранее проделанных Галилеем опытов и сделанных им на основании этих опытов выводов, которые фактически предопределили дальнейшее развитие механики как раздела физической науки

Магнитное поле в точке пространства, создаваемое малым отрезком проводника, по которому течет электрический ток, пропорционально силе тока, обратно пропорционально квадрату расстояния от этой точки до проводника и направлено перпендикулярно по отношению и к току, и к направлению на проводник.

Во вращающейся системе отсчета наблюдатель испытывает на себе действие силы, уводящей его от оси вращения. Вам, наверное, доводилось испытывать неприятные ощущения, когда машина, в которой вы едете, входила в крутой вираж. Казалось, что сейчас вас так и выбросит на обочину. И если вспомнить законы механики Ньютона, то получается, что раз вас буквально вдавливало в дверцу, значит на вас действовала некая сила. Ее обычно называют «центробежная сила». Именно из-за центробежной силы так захватывает дух на крутых поворотах, когда эта сила прижимает вас к бортику автомобиля. (Между прочим, этот термин, происходящий от латинских слов centrum («центр») и fugus («бег»), ввел в научный обиход в 1689 году Исаак Ньютон.)

Казалось бы, нет ничего проще, чем закон Архимеда. Но когда-то сам Архимед здорово поломал голову над его открытием. Как это было?

С открытием основного закона гидростатики связана интересная история.

Интересные факты и легенды из жизни и смерти Архимеда

Помимо такого гигантского прорыва, как открытие собственно закона Архимеда, ученый имеет еще целый список заслуг и достижений. Вообще, он был гением, трудившимся в областях механики, астрономии, математики. Им написаны такие труды, как трактат «о плавающих телах», «о шаре и цилиндре», «о спиралях», «о коноидах и сфероидах» и даже «о песчинках». В последнем труде была предпринята попытка измерить количество песчинок, необходимых для того, чтобы заполнить Вселенную.

Роль Архимеда в осаде Сиракуз

В 212 году до нашей эры Сиракузы были осаждены римлянами. 75-летний Архимед сконструировал мощные катапульты и легкие метательные машины ближнего действия, а также так называемые “когти Архимеда”. С их помощью можно было буквально переворачивать вражеские корабли. Столкнувшись со столь мощным и технологичным сопротивлением, римляне не смогли взять город штурмом и вынуждены были начать осаду. По другой легенде Архимед при помощи зеркал сумел поджечь римский флот, фокусируя солнечные лучи на кораблях. Правдивость данной легенды представляется сомнительной, т.к. ни у одного из историков того времени упоминаний об этом нет.

Смерть Архимеда

Согласно многим свидетельствам, Архимед был убит римлянами, когда те все-таки взяли Сиракузы. Вот одна из возможных версий гибели великого инженера.

На крыльце своего дома ученый размышлял над схемами, которые чертил рукой прямо на песке. Проходящий мимо солдат наступил на рисунок, а Архимед, погруженный в раздумья, закричал: «Прочь от моих чертежей». В ответ на это спешивший куда-то солдат просто пронзил старика мечом.

Ну а теперь о наболевшем: о законе и силе Архимеда…

Как был открыт закон Архимеда и происхождение знаменитой “Эврика!”

Античность. Третий век до нашей эры. Сицилия, на которой еще и подавно нет мафии, но есть древние греки.

Изобретатель, инженер и ученый-теоретик из Сиракуз (греческая колония на Сицилии) Архимед служил у царя Гиерона второго. Однажды ювелиры изготовили для царя золотую корону. Царь, как человек подозрительный, вызвал ученого к себе и поручил узнать, не содержит ли корона примесей серебра. Тут нужно сказать, что в то далекое время никто не решал подобных вопросов и случай был беспрецедентным.

Архимед долго размышлял, ничего не придумал и однажды решил сходить в баню. Там, садясь в тазик с водой, ученый и нашел решение вопроса. Архимед обратил внимание на совершенно очевидную вещь: тело, погружаясь в воду, вытесняет объем воды, равный собственному объему тела. Именно тогда, даже не потрудившийся одеться, Архимед выскочил из бани и кричал свое знаменитое «эврика», что означает «нашел». Явившись к царю, Архимед попросил выдать ему слитки серебра и золота, равные по массе короне. Измеряя и сравнивая объем воды, вытясняемой короной и слитками, Архимед обнаружил, что корона изготовлена не из чистого золота, а имеет примеси серебра. Это и есть история открытия закона Архимеда.

Суть закона Архимеда

Если Вы спрашиваете себя, как понять закон Архимеда, мы ответим. Просто сесть, подумать, и понимание придет. Собственно, этот закон гласит:

На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.

Как видим, сила Архимеда действует не только на тела, погруженные в воду, но и на тела в атмосфере. Сила, которая заставляет воздушный шар подниматься вверх – та же сила Архимеда. Высчитывается Архимедова сила по формуле:

Здесь первый член – плотность жидкости (газа), второй – ускорение свободного падения, третий – объем тела. Если сила тяжести равна силе Архимеда, тело плавает, если больше – тонет, а если меньше – всплывает до тех пор, пока не начнет плавать.

В данной статье мы рассмотрели закон Архимеда для чайников. Если Вы хотите узнать, как как решать задачи, где есть закон Архимеда, обращайтесь к . Лучшие авторы с удовольствием поделятся знаниями и разложат решение самой сложной задачи «по полочкам».

Зависимость давления в жидкости или газе от глубины погружения тела приводит к появлению выталкивающей силы / или иначе силы Архимеда /, действующей на любое тело, погруженное в жидкость или газ.

Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.

Величина Архимедовой силы определяется по закону Архимеда.

Закон назван в честь древнегреческого ученого Архимеда, жившего в 3 веке до нашей эры.

Открытие основного закона гидростатики – крупнейшее завоевание античной науки. Скорее всего вы уже знаете легенду о том, как Архимед открыл свой закон: “Вызвал его однажды сиракузский царь Гиерон и говорит…. А что было дальше? …

Закон Архимеда, впервые был упомянут им в трактате ” О плавающих телах”. Архимед писал: ” тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.

Еще одна формула для определения Архимедовой силы:

Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем основанием прижато ко дну.

ВЕС ТЕЛА, ПОГРУЖЕННОГО В ЖИДКОСТЬ (ИЛИ ГАЗ)

Вес тела в вакууме Pо=mg .
Если тело погружено в жидкость или газ,
то P = Pо – Fа = Ро – Pж

Вес тела, погруженного в жидкость или газ, уменьшается на величину выталкивающей силы, действующей на тело.

Или иначе:

Тело, погруженное в жидкость или газ, теряет в своем весе столько, сколько весит вытесненная им жидкость.

КНИЖНАЯ ПОЛКА

ОКАЗЫВАЕТСЯ

Плотность оганизмов, живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны!

Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.

У берегов Египта, водится удивительная рыба фагак. Приближение опасности заставляет фагака быстро заглатывать воду. При этом в пищеводе рыбы происходит бурное разложение продуктов питания с выделением значительного количества газов. Газы заполняют не только действующую полость пищевода, но и имеющийся при ней слепой вырост. В результате тело фагака сильно раздувается, и, в соответствии с законом Архимеда, он быстро всплывает на поверхность водоема. Здесь он плавает, повиснув вверх брюхом, пока выделившиеся в его организме газы не улетучатся. После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.

Чилим (водяной орех) после цветения дает под водой тяжелые плоды. Эти плоды настолько тяжелы, что вполне могут увлечь на дно все растение. Однако в это время у чилима, растущего в глубокой воде, на черешках листьев возникают вздутия, придающие ему необходимую подъемную силу, и он не тонет.

Сила Архимеда – Методика физики Б2503

Здравствуй, дорогой друг!

В данной статье, ты можешь ознакомиться с теорией по теме “Архимедова сила”, а так же подготовится к лабораторной работе “Определение выталкивающей силы, действующей на тело, погруженное в жидкость”.

Опыт: выталкивающая сила и вес тела

Проделаем опыт (рис. 133). Подвесим к пружине 1 небольшое ведерко 2 и тело цилиндрической формы 3. Отметив положение стрелки-указателя на штативе (рис. 133, а), поместим тело в сосуд, наполненный жидкостью до уровня отливной трубки. При этом часть жидкости, объем которой равен объему тела, выльется из сосуда в находящийся рядом стакан (рис. 133, б). Одновременно с этим вес тела в жидкости уменьшится и указатель пружины переместится вверх.

 

Вес тела в жидкости уменьшается на величину, равную архимедовой (выталкивающей) силе. Связана ли эта величина с количеством вытесненной телом жидкости? Чтобы выяснить это, перельем эту жидкость из стакана в ведерко 2. Мы увидим, как стрелка-указатель снова возвратится к своему прежнему положению (рис. 133, в). Это означает, что вытесненная телом жидкость весит столько же, сколько теряет в своем весе погруженное в жидкость тело. Но вес тела в жидкости меньше веса того же тела в воздухе на величину, равную выталкивающей силе. Поэтому окончательный вывод, к которому мы приходим, можно сформулировать следующим образом:

Выталкивающая сила, действующая на погруженное в жидкость тело, равна весу жидкости, вытесненной этим телом.

Этот закон был открыт Архимедом и потому носит его имя — закон Архимеда.

А как же это сделал Архимед?

Предлагаю посмотреть небольшой видеоролик, в котором говорится о том, как же эту силу открыл ученный Архимед.

Видео YouTube

Немного теории

Рассмотрим простейший случай, когда погруженное в жидкость тело состоит из той же жидкости, в которую оно погружено. Это (жидкое) тело, как и любая другая часть окружающей жидкости, будет, очевидно, находиться в равновесии. Поэтому приложенная к нему архимедова сила FА будет уравновешена действующей вниз силой тяжести mжg (где mж —масса жидкости в объеме данного тела):

    FA = mжg .     (47.1)

Но сила тяжести mжg равна весу вытесненной жидкости Рж. Таким образом, FA = Рж, что и требовалось доказать.

Формулу (47.1) можно переписать в другом виде. Учитывая, что масса жидкости mж равна произведению ее плотности ρж на объем Vж, получаем

     FA = ρж Vж g .      (47.2)

Реклама admitadЧерез Vж здесь обозначен объем вытесненной жидкости. Этот объем равен объему той части тела, которая погружена в жидкость. Если тело погружено в жидкость целиком, то он совпадает с объемом V всего тела; если же тело погружено в жидкость частично, то он меньше объема V тела (рис. 134).

Формула (47.2) остается справедливой и для архимедовой силы, действующей в газе; только в этом случае в нее следует подставлять плотность газа и объем вытесненного газа, а не жидкости.

С учетом вышеизложенного закон Архимеда в настоящее время формулируют следующим образом:

На всякое тело, погруженное в покоящуюся жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная произведению плотности жидкости (или газа), ускорения свободного падения и объема той части тела, которая погружена в жидкость (или газ).

Лабораторная

Ну вот мы и подошли к самой лабораторной работе.

В данном видеоролике ты можешь ознакомится с темой лабораторной работы.

Длительность

Видео YouTube

Здесь я представлю материалы:

• которые описывают ход данной лабораторной работы, для этого посмотри документ “описание и ход работы”;
• если тебе нужен  готовый шаблон с таблицей, для оформления лабораторной работы, ты можешь распечатать его с документа “шаблон”;
• также в презентации “обработка результатов” ты можешь найти пример расчетов силы Архимеда по конкретным значениям.

И так, начнем!)

Какие приборы нам понадобятся?

Посмотри видеоролик, это займет немного времени(длительность )

Здесь ты увидишь какие приборы необходимы для выполнения данной работы.

Видео YouTube

Как же проводить сам эксперимент?

В видеоролике, представленном ниже ты можешь посмотреть порядок выполнения эксперимента, что поможет тебе в лабораторной работе! (Длительность)

Видео YouTube

Как рассчитать?

Пример расчетов представлен в презентации “обработка результатов”.

Игра-тест

Прежде чем приступить к выполнению лабораторной работы, давай проверим на сколько ты к этому готов?

Желаю удачи!
Литература:Учебник “Физика 7 класс” Пёрышкин.

https://multiurok.ru/files/zakon-arkhimieda-i-laboratornaia-rabota-2-uroka.html

тест: https://www.branchtrack.com/projects/6k0vghfn 

http://files.school-collection.edu.ru/dlrstore/ad5923b4-b323-f783-2644-ec25a29dfc2e/00144676385676630.htm

задачи по механике: https://videouroki.net/projects/2/index.php?id=zfmehanika&utm_source=multiurok&utm_medium=banner&utm_campaign=mpopupopen&utm_content=fizika&utm_term=zfmehanika

Решение задач на определение силы Архимеда

Технологическая карта урока.

Учебная дисциплина: физика.

Сформировать понятие об Архимедовой силе; продолжить формирование умений находить равнодействующую двух сил, применять закон Паскаля для объяснения давления внутри жидкостей и газов на находящиеся в них тела обеспечить усвоение и закрепление нового материала.

Развивающая Активизировать познавательную деятельность учащихся. Находить ответы на поставленные нестандартные вопросы. Приобретать навыки исследовательской деятельности. Развивать умение применять формулу для расчета архимедовой силы; показать роль физического эксперимента; развивать умение сравнивать, систематизировать знания.

Воспитательная: Формировать умение отстаивать свое мнение. Актуализировать точку зрения, оперировать фактами. Аргументировать свое утверждение. Познакомить учащихся с примерами практического применения закона в технике, для повышения интереса к изучаемому материалу осветить роль Архимеда в физике.

2. воспитывать ответственное отношение к учебному труду, продолжить формирование представлений о связи природы и духовности мира человека.

Тип и форма учебного занятия

урок повторения и закрепления знаний

Формы работы

Ф – фронтальная, И – индивидуальная,

Планируемые образовательные результаты

Метапредметные

Личностные

предметные

Строить логичное рассуждение, включающее установление причинно-следственных связей.

Отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами

Представлять информацию в виде конспектов, таблиц

Определение общей цели и путей её достижения.

Формирование умения планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями её реализации.

Умение осуществлять информационный поиск для выполнения учебных заданий.

Овладение логическими действиями анализа, синтеза, сравнения, обобщения, установление причинно-следственных связей.

1. Развитие мотивов учебной деятельности и формирование личностного смысла обучения.

2. Развитие навыков сотрудничества.

Повторение физических величин (ρ), определений, формул (Р, F_T), прибор для измерения силы

– измерять силу тяжести, силу упругости, силу Архимеда;

Умение обобщать, слушать и вступать в диалог, делать поясняющие рисунки. Умение высказывать предположение.

Прогнозируемый результат: 

знать в полном объёме теоретический материал по данной теме, уметь классифицировать полученные знания в единую систему, осознанно применять полученные знания на практике.

Технологии обучения или элементы технологий

технологии коллективной мыслительной деятельности; активные методы обучения; проблемное обучение;

Средства обучения, дидактическое обеспечение урока

1. Физика. 7 кл.: учеб. для общеобразоват. учреждений/А. В. Пёрышкин. – 14-е изд., стереотип. – М. Дрофа, 2010. – 192 с.:ил.

2. Методические рекомендации к тематическому и поурочному планированию. Авт. Е.М. Гутник, Е.В. Рыбакова, Е.В. Шаронина Журнал «Физика» («Первое сентября») № 25-26/02.

3. Сборник задач по физике для 7-9 классов общеобразовательных учреждений/В.И. Лукашик, Е.В. Иванова. -17-е изд.- М.: Просвещение, 2004. – 224.

. Интернет – ресурсы.

4. Организационная структура урока

Этапы урока

5. Деятельность преподавателя

6. Деятельность учащихся

7. 1.Организационный момент (2мин)

8. мотивация учащихся

    -метод самодиагностики 
   (обучение анализу своих индивидуальных возможностей) 
    – метод самопрогнозирования 
   (построение перспектив своего дальнейшего обучения)

9. Подготовка класса для проведения урока. Приветствие учащихся.

Здравствуйте, ребята! .

10. -И я рада приветствовать вас на уроке, на котором мы продолжим открывать новые страницы физики. Проверьте все ли у Вас готово к уроку.  Ребята пусть вас это не удивляет, но урок я хочу начать с отрывка из повести Антона Павловича Чехова “Степь”. Слушая внимательно, постарайтесь понять, какая сила подействовала на Егорушку. “Егорушка разбежался и полетел с полутарасаженной вышки. Описав в воздухе дугу, он упал в воду, глубоко погрузился, но дна не достал, какая-то сила холодная и приятная на ощупь, подхватила и понесла его обратно наверх”.

11. Проблема: Какая сила подняла Егорушку наверх?

Да, Архимедова сила, но то, что она существует, мы познакомились на том уроке. А сегодня мы научимся её находить теоретически, Рассмотрим различные виды задач, Откроем тетради и запишем тему урока. Решение задач на нахождение Архимедовой силы.

12. Приветствие преподавателя.

13. Учащиеся, уже имеющие на тот момент представление о структуре работы, обращают внимание еще раз на части работы, число заданий, тип заданий, уровень сложности, максимальный первичный балл, что способствует повышению стрессоустойчивости учащихся при подготовке к экзамену.
    
    

14. 2. Актуализация знаний

15. 10 мин.

 метод проблемного обучения
 наглядный метод

  метод взаимоконтроля

16. Проверка задания предыдущих уроков.

Значение выталкивающей силы древнегреческий ученый Архимед установил примерно за 250 лет до н.э. По преданию сиракузский царь Гиерон поручил ювелиру изготовить золотую корону. Когда корона была изготовлена, то возникло подозрение, что ювелир часть золота заменил равной по массе частью серебра. Как же Архимеду удалось разоблачить ювелира?

Начнём мы наш урок, как обычно, с повторения изученного материала.

Фронтальный опрос по теории.

Что мы называем Архимедовой силой?

Какими способами можно определить F_A? (по формуле F_A = ρ_ЖgV_пчт ; опытным путём F_А = Р – Р₁)

От каких величин зависит F_A? От каких величин она не зависит? (Зависит от ρ_ж Чем больше плотность жидкости, в которую погружено тело, тем больше выталкивающая сила, действующая на тело со стороны данной жидкости.и от V_пчт ; не зависит от массы тела, глубины погружения, формы тела, плотности тела, расположения тела в жидкости,)

Опишите поведение твёрдых тел в жидкости. (Твёрдые тела в жидкости могут тонуть, плавать в жидкости и на её поверхности, всплывать)

Изменится ли архимедова сила, действующая на тело, если тело не полностью погружено в жидкость, а лишь наполовину?

– Архимедова сила будет меньше, так как объем тела в жидкости будет меньше.

17. Ребята, перед тем как приступить к решению задач , вам предстоит ответить на несколько вопросов. На ваших столах лежат чистые небольшие листы. Я вам предлагаю их взять, подписать свою фамилию и имя и всё внимание на экран.

18. По окончании работы, листки передаются учителю для дальнейшей проверке и выставлению оценок за работу в журнал (дневник).

19. Итак, мы вспомнили теоретический материал, а теперь будем теорию применять на практике.

20. Отвечают на вопросы

21. 3.Решение задач. комплексное применение знаний
    -метод практического занятия
    -метод дифференцированного подхода

Решение расчетных задач.

Чему равна сила Архимеда, действующая на камень объемом 1дм³, который полностью погружен в воду и удерживается канатом? Найти силу, действующую на канат.

(ρ_в = 1000 кг/м³, ρ _к = 4000 кг/м³.)

Дано: СИ Решение

V = 1 дм³ 10^-3 м³ FА = ρ_в g V

ρ_в = 1000 кг/м³ FА =1000 кг/м³_* 10Н/кг _*10^-3 м³= 10Н

ρ_к = 4000 кг/м³ P = m _* g – FА

P = ρ_{к *} g _* V_к – FА

FА = ? P = ? P = 4000 кг/м³_* 10Н/кг _*10^-3 м³– 10Н= 30 Н.

Ответ: FА = 10Н, P = 30 Н.

1)Объём куска железа 0,1 дм³. Какая выталкивающая сила будет действовать на него в керосине?

2)Стальная балка массой 1,56 т удерживается на канате в пресной воде. Вычислить архимедову силу, действующую на балку.

3)Цепь выдерживает нагрузку 70000 Н. Можно ли на этой цепи удерживать под водой гранитную плиту объемом 4 м³?

4)Сила Архимеда,которая действует на полностью погружонное в керосин тело,равна 1,6 Н.Найдите объем тела?

5)При полном погружении в жидкость на тело объемом 4 дм³действует архимедова сила 40Н. Какая это жидкость?

Решают задачи у доски .

Физкультминутка

  – метод самореабилитации  (смена видов деятельности) 

– метод самоконтроля

 -метод педагогической поддержки здоровья 

В зависимости от эмоционального климата в классе он  предлагает учащимся выбрать их действия при ответах «да» или «нет» ( встать ,поднять руку,  и т.д.)

Изменится ли архимедова сила, если:

1.      изменить глубину погружения (нет)

2.      изменить плотность тела (нет)

3.      уменьшить  объем тела (да)

4.      вращать тело на определенной глубине (нет)

5.      перенести тело в жидкость с большей плотностью  (да)

Учащиеся выбирают свои действия при ответах «да» или «нет»:

вставать – садиться;

поднимать правую руку – поднимать левую руку и т.д.

23. Рефлексия

24. – метод коллективного анализа деятельности

    -метод рефлексии

    –  интерактивный метод

Молодцы! Вы хорошо умеете решать задачи на применение закона Архимеда. Действительно, с каждым годом мы с вами будем знать все больше и больше, знания нам пригодятся везде, и, надеюсь, каждый из вас жизнь проживет мудро.

Если не было бы Архимедовой силы…

Учитель: Мы сегодня на уроке разобрали различные задачи по теме “Архимедова сила”. Вспомните девиз нашего урока и подумайте какое было ваше участие в уроке и на сколько вы закрепили свои знания плывете вы на

Составьте задачу по рисунку

Примерное условие задачи: на поверхности воды плавают бруски из дерева пробки и льда. Укажите, где какой брусок?

26. Учащиеся дают оценку успешности достижения целей урока, называют основные трудности в работе и в ходе совместного обсуждения  способы для их преодоления, затем анализируя свою деятельность,

Итоги урока

Учитель: Вернемся к нашей проблеме и составим задачи к отрывку, предложенному в начале урока.

Примерные задачи:

1. Чему равна подъемная сила Егорушки, если его масса 50 кг?Предложите свой алгоритм решения задач по теме: Архимедова сила?

28. Учитель: Оценки вы получите за тест, за ответы, а также за решенные задачи. Спасибо за урок

Домашнее задание

Решение задачи.

F_А= ρ_ж ∙g V_к → V_к= F_А / ρ_ж ∙g = ρ_ж / ρ_ж ∙g

F_А= ρ_ж; ρ_ж= ρ₁– ρ₂=20Н-18,75Н=1,25Н

V_к=1,25Н / 1000кг/м³∙10Н/кг=0,000125 м³

ρ_к=m_к / V_к=2 кг/0,000125 м³=16000кг/м³

ρ₁= m_к∙g → m_к= ρ₁/ g=20Н/10Н/кг=2 кг

m_к= m_з+ m_с; V_с= V- V_з

m_к= ρ_з V_з+ ρ_сV_с= ρ_з V_з+ρ_с(V- V_з)

m_к= ρ_з V_з+ ρ_сV- ρ_с V_з

m_к– ρ_с V_к= ρ_з V_з– ρ_с V_з

m_к– ρ_с V_к= V_з(ρ_з– ρ_с) → V_з= (m_к– ρ_с V_к) / (ρ_з– ρ_с)

V_з=(2 кг – 10000∙0,000125)/(20000-10000)=0,000075 м³

m_з=20000∙0,000075=1,5 кг

m_с=2-1,5=0,5кг

Ответ: ρ=16000 m_з=1,5 кг m_с=0,5кг

Сообщается тема проекта, как домашнее задание: «Как заставить тело плавать?»

Архимедова сила и её значение в жизни человека

В процессе работы над индивидуальным проектом по физике “Архимедова сила и её значение в жизни человека” ученица 10 класса школы провела исследование истории Архимедовой силы, изучила биографию Архимеда, а также рассмотрела легенды, создаваемые вокруг имени ученого.

Подробнее о проекте:

В ученической исследовательской работе по физике “Архимедова сила и её значение в жизни человека” автор выясняет интересные факты об Архимеде и дает развернутое определение его закона, объясняет, в чем заключается значимость этого закона в жизни человека. Практическая часть проекта сконцентрирована на изучении основного закона гидростатики – закона Архимеда. Автор рассматривает действие этой силы на поведение тела, погруженного в жидкость.

В готовом творческом и исследовательском проекте по физике “Архимедова сила и её значение в жизни человека” автор определяет роль силы Архимеда в жизни организмов, рассказывает про мертвое море и выталкивающую силу и проводит анкетирования по теме исследования среди учащихся, по результатом которого можно сделать вывод о том, насколько школьники осведомлены о законе Архимеда и применяют свои знания в жизни.

Оглавление

Введение
1.  История Архимедовой силы и биография Архимеда.
1.1. Биография Архимеда.
1.2. Легенды, создаваемые вокруг имени ученого.
1.3. Теоретическая часть.
1.4. Интересные факты про Архимеда и его закон.
2.  Значимость закона Архимеда в жизни.
2.1. Роль силы Архимеда в жизни организмов.
2.2. Про мертвое море и выталкивающую силу.
3. Проведение анкетирования среди учащихся.
3.1. Результаты анкетирования среди одноклассников.
3.2. Результаты проведенного теста на тему «Выталкивающая сила».
3.3. Обобщение результатов.
Заключение
Список литературы

Введение

Актуальность работы. Если внимательно присмотреться к окружающему миру, то можно открыть для себя множество событий, происходящих вокруг. С этими явлениями мы встречаемся ежедневно, и с каждым из явлений связан определенный закон, которому оно будет подчиняться и действовать, но чаще всего мы не задумываемся об этом.

Об одном из таких законов и пойдет речь в моей исследовательской работе. Это закон Архимеда.

Проблема. У большинства людей не возникает интереса к Архимедовой силе и пониманию о ее пользе для нас, так же многие ученики сталкиваются с проблемой понимания и усвоения материала по закону Архимеда.

Цель работы: Сконцентрировать внимание на основном законе гидростатики – законе Архимеда. Рассмотреть действие этой силы на поведение тела, погруженного в жидкость.

Задачи работы:

1. Изучить литературу по теме исследования.
2. Рассмотреть историю архимедовой силы и биографию Архимеда.
3. Провести анкетирование и опрос одноклассников с целью выявления их отношения к Архимедовой силе для нашей жизни.  

           

Методы изучения

1. Научно-поисковый – сбор информации об Архимедовой силе
2. Анкетирование (с целью выявления отношения респондентов к цели исследования)
3. Изучение литературных источников

Практическая значимость. Вызвать интерес к закону Архимеда, к его значимости в нашей жизни; заинтересовать в изучении данного закона.

История Архимедовой силы и биография Архимеда

Архимед — древнегреческий математик, физик инженер из Сиракуз, греческой колонии на острове Сицилия. Сведения о жизни Архимеда оставили нам многие древнегреческие писатели и историки (Полибий, Тит Ливий, Цицерон, Плутарх, Витрувий и другие).

Отцом Архимеда был математик и астроном Фидий, состоявший, как утверждает Плутарх, в близком родстве с Гиероном II. Отец привил сыну любовь к математике, механике и астрономии. Для обучения Архимед отправился в Александрию – научный и культурный центр Египта. Большую часть своей жизни провёл в родном городе Сиракузы. Где и был убит при захвате города воинами Марцелла во время Второй Пунической войны.

Легенды, создаваемые вокруг имени ученого

Уже при жизни Архимеда вокруг его имени создавались легенды, поводом для которых служили его поразительные изобретения. Известна легенда об Архимеде и золотой короне. Царь Гиерон поручил ему проверить честность мастера, изготовившего золотую корону. Хотя корона весила столько, сколько было отпущено на неё золота, царь заподозрил, что она изготовлена из сплава золота с более дешёвыми металлами. Архимеду было поручено узнать есть ли в короне примесь. Много дней мучила Архимеда эта задача. И вот однажды, находясь в бане, он погрузился в наполненную водой ванну, и его внезапно осенила мысль, давшая решение задачи.

Архимед заказал два слитка — один из золота, другой из серебра, равные весу короны. Каждый слиток он погружал поочерёдно в сосуд, доверху наполненный водой. Архимед заметил, что при погружении слитка из серебра воды вытекает больше. Затем он погрузил в воду корону и обнаружил, что воды вылито больше, чем при погружении золотого слитка, а ведь он был равен весу короны. По объёму вытесненной жидкости Архимед определил, что корона была изготовлена не из чистого золота, а с примесью серебра. Тем самым мастер был изобличён в обмане.

Задача о золотой короне побудила Архимеда заняться вопросом о плавании тел.

Закон Архимеда, впервые были им упомянут в трактате «О плавающих телах».  Архимед написал: “Тела, которые тяжелее жидкости, будучи опущены в неё, погружаются всё глубже, пока не достигают дна, и, пребывая в жидкости, теряют в своём весе столько, сколько весит жидкость, взятая в объёме тел”.

В науку гидростатику это открытие вошло как закон Архимеда.

Интересные факты про Архимеда и его закон

Архимедова сила направлена всегда противоположно силе тяжести. Она равна нулю, если погруженное в жидкость тело плотно, всем основанием прижато ко дну.

На тело, находящееся в жидкости или газе, в обычных земных условиях действуют две противоположно направленные силы: сила тяжести и архимедова сила: Fт — сила тяжести, FА— сила Архимеда.

Если сила тяжести по модулю больше архимедовой силы (Fт > FА), то тело опускается вниз – тонет. Если модуль силы тяжести равен модулю архимедовой силы (Fт = FА), то тело может находиться в равновесии на любой глубине ( тело плавает в жидкости или газе). Если архимедова сила больше силы тяжести (Fт < FА), то тело поднимается вверх – всплывает до тех пор, пока не начнет плавать .

Архимедова сила больше силы тяжести, если плотность жидкости больше плотности погруженного в жидкость тела: ρ1 — плотность тела, ρ2 — плотность среды, в которую погрузили тело. ρ1 = ρ2 — тело плавает в жидкости или газе, ρ1 > ρ2 — тело тонет, ρ1 < ρ2 — тело всплывает до тех пор, пока не начнет плавать.

Примечание

• Закон Архимеда не работает в состоянии невесомости
• Роль силы Архимеда в жизни организмов
• Именно Архимед изготовил первый в мире планетарий.

Знаменитое устройство «архимедов винт» было изобретено им ещё в юности, и оно нашло своё применение в ирригации полей. Архимедов винт и по сей день применяется с этой целью в некоторых странах.

Архимед первым выдвинул идеи касательно измерения расстояния до других небесных тел. И это за много сотен лет до Коперника и Галилея, отстаивавших гелиоцентрическую систему мира

Архимед изобрёл способ решения кубических уравнений.

Понятие «центр тяжести» было введено в науку именно Архимедом.

Роль силы Архимеда в жизни организмов

Плотность живых организмов, обитающих в водной среде, очень мало отличается от плотности воды, поэтому их вес полностью уравновешивается архимедовой силой. Благодаря этому водные животные не нуждаются в столь массивных скелетах, как наземные. Например: кит дышит лёгкими, и регулирует глубину своего погружения за счёт уменьшения и увеличения объёма лёгких, но, попадая случайно на сушу, не проживает и часу. Масса кита достигает 90-100 т. В воде эта масса частично уравновешивается силой Архимеда. На суше у кита под действием столь огромной массы сжимаются кровеносные сосуды, из-за чего он погибает.

Интересна роль плавательного пузыря у рыб. Это единственная часть тела рыбы, обладающая заметной сжимаемостью; сжимая пузырь усилиями грудных и брюшных мышц, рыба меняет объем своего тела и тем самым среднюю плотность, благодаря чему она может в определенных пределах регулировать глубину своего погружения.

У берегов Египта, водится удивительная рыба фагак. При опасности фагак быстро заглатывать воду. При этом в пищеводе рыбы происходит бурное разложение продуктов питания с выделением значительного количества газов. Газы заполняют не только действующую полость пищевода, но и имеющийся при ней слепой вырост. В результате тело фагака сильно раздувается, и, в соответствии с законом Архимеда, он быстро всплывает на поверхность водоема. После этого сила тяжести опускает его на дно водоема.

Многие водные растения сохраняют вер­тикальное положение, несмотря на чрезвычайную гибкость их стеблей, потому, что на концах их разветвлений заключены крупные пузыри воздуха, играющие роль поплавков.

Про мертвое море и выталкивающую силу

«Мертвое море»- Бессточное соленое озеро на Ближнем Востоке, является одним из самых соленых на Земле.

Из Мертвого моря не вытекает ни единой реки, зато оно само вбирает в себя воды реки Иордан, впадающей в него с севера, и множество маленьких ручьев, стекающих со склонов окружающих холмов. В результате этого в его водах создалась необычайно высокая концентрация минеральных солей.

В мертвом море очень сложно утонуть ил хотя бы нырнуть, а все потому что в нем содержится такое количество солей, что ρ1 < ρ2 ( плотность воды выше, чем плотность тела, погруженного в жидкость).

Результаты анкетирования среди одноклассников

Проведение анкетирование на тему: «Выталкивающая сила. Закон архимеда.» в соц. Сети ВК.

Анкета содержала 3 вопроса: Первый вопрос: «Знаете ли вы, что такое закон Архимеда и можете ли вы его сформулировать?» Ответ: На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу тому количеству жидкости или газа, которое вытеснено погруженной частью тела Второй вопрос: «Запишите 3 формулы, которые будут подходить к плавающему телу на поверхности, внутри жидкости или утонувшего тела

Ответ: . ρ1 = ρ2 — тело плавает в жидкости или газе, ρ1 > ρ2 — тело тонет, ρ1 < ρ2 — тело всплывает до тех пор, пока не начнет плавать. Третий вопрос: «Какие изобретения изобрел ученый Архимед?» Ответ: Архимед изобрел кохлею (Архимедов винт), катапульту, планетарий, Коготь Архимеда, Поджигающие зеркала, Одометр, Произвел улучшение рычага. (если анкетируемый напишет хотя бы одно из изобретений, то задание будет считаться выполненным).

Результаты анкетирования: Было проанкетировано 19 учащихся 10 класса, среди которых: На все вопросы смогли верно ответить 75% учащихся класса. Только на два вопроса верно ответили 20% учащихся класса. Только на один вопрос верно смогли ответить 5% учащихся класса.  

Результаты проведенного теста на тему «Выталкивающая сила»

Так же в моем классе был проведен тест на тему «Выталкивающая сила. Закон Архимеда.»

Тест содержал 4 заданий с 3 вариантами ответа:

1) Архимедову силу рассчитывают по формуле:
а) р = gρh
б) F = pS
в) F = gρжVт

Ответ: в)

2) Действует ли архимедова сила на тела, находящиеся в воздухе?
а) Нет, она действует только в воде
б) Да, так как воздух — газ
в) Среди ответов нет верного

Ответ: б)

3) По какой формуле можно рассчитать архимедову силу, дей­ствующую в газе?
а) F = gρгVт
б) F = gρhS
в) F = gρжVт

Ответ: а)

4) Архимедова сила зависит от:

а) глубины погружения тела в жидкость
б) веса тела в) объёма тела

Ответ: в)

Результаты Тестирования:

Было протестировано 19 учащихся 10 класса, среди которых:

На все вопросы смогли ответить 60% учащихся. На три вопроса смогли ответить 20% учащихся. На два вопроса смогли ответить 10% учащихся. На один вопрос смогли ответить 10% учащихся.  

Обобщение результатов

В ходе обобщения результатов было выявлено, что 67% учащихся хорошо ознакомлены с данной темой, смогли ответить на большинство заданных вопросов и пройти тестирование с удовлетворительным результатом.

Другие 23% знакомы с данной темой, но им следует до конца  ознакомиться с ней Оставшиеся 5% не знакомы с основным законом гидростатики

Заключение

Данная работа может помочь лучше понять основной закон гидростатики, научиться определять архимедову силу на физических опытах, проверить свои знания и узнать что-нибудь новое в данной теме.

Данный проект помогает понять, что многие задачи на закон Архимеда можно решать как теоретически, так и практически.

Я считаю, что исследовательская работа может быть использована для более подробного изучения Архимедовой силы, углубления и более масштабного изучения школьной программы, которые связаны с этим законом. Так же данная работа может быть полезна учащимся для сдачи ОГЭ, ЕГЭ, школьных контрольных и проверочных работ.

Список литературы

1. Физика: Справ. материалы: Учебное пособие для учащихся.
2. А.П. Перышкин. Физика. 7 класс. Москва «Дрофа», 2006 г.
3. Каган В.Ф., Архимед. Краткий очерк о жизни и творчестве, М.-Л., 1951.
4. Лурье С.Я., Архимед, М.-Л., 1945.
5. Сергей Викторович Житомирский. Архимед: Пособие для учащихся. – М.: Просвещение, 1981.
6. Смышляев В.К. О математике и математиках. – Йошкар-Ола: Наука, 1977.

Если страница Вам понравилась, поделитесь в социальных сетях:

Формула вытеснения воды. Выталкивающая сила

Выталкивающая сила, действующая на погруженное в жидкость тело, равна весу вытесненной им жидкости.

«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото.

Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.

Однако, что правда – то правда: именно Архимед открыл принцип плавучести . Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.

Закон Архимеда можно истолковать с точки зрения молекулярно-кинетической теории . В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.

Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.

Один из первых физических законов, изучаемых учениками средней школы. Хотя бы примерно этот закон помнит любой взрослый человек, как бы далек он ни был от физики. Но иногда полезно вернуться к точным определениям и формулировкам – и разобраться в деталях этого закона, которые могли позабыться.

О чем говорит закон Архимеда?

Существует легенда, что свой знаменитый закон древнегреческий ученый открыл, принимая ванну. Погрузившись в емкость, наполненную водой до краев, Архимед обратил внимание, что вода при этом выплеснулась наружу – и испытал озарение, мгновенно сформулировав суть открытия.

Скорее всего, в реальности дело обстояло иначе, и открытию предшествовали долгие наблюдения. Но это не столь важно, потому что в любом случае Архимеду удалось открыть следующую закономерность:

• погружаясь в любую жидкость, тела и объекты испытывают на себе сразу несколько разнонаправленных, но направленных перпендикулярно по отношению к их поверхности сил;
• итоговый вектор этих сил направлен вверх, поэтому любой объект или тело, оказавшись в жидкости в состоянии покоя, испытывает на себе выталкивание;
• при этом сила выталкивания в точности равна коэффициенту, который получится, если умножить на ускорение свободного падения произведение объема предмета и плотности жидкости.

Итак, Архимед установил, что тело, погружённое в жидкость, вытесняет такой объём жидкости, который равен объёму самого тела. Если в жидкость погружается только часть тела, то оно вытеснит жидкость, объём которой будет равен объёму только той части, которая погружается.

Та же самая закономерность действует и для газов – только здесь объем тела необходимо соотносить с плотностью газа.

Можно сформулировать физический закон и немного проще – сила, которая выталкивает из жидкости или газа некий предмет, в точности равна весу жидкости или газа, вытесненных этим предметом при погружении.

Закон записывается в виде следующей формулы:

Какое значение имеет закон Архимеда?

Закономерность, открытая древнегреческим ученым, проста и совершенно очевидна. Но при этом ее значение для повседневной жизни невозможно переоценить.

Именно благодаря познаниям о выталкивании тел жидкостями и газами мы можем строить речные и морские суда, а также дирижабли и воздушные шары для воздухоплавания. Тяжелые металлические корабли не тонут благодаря тому, что их конструкция учитывает закон Архимеда и многочисленные следствия из него – они построены так, что могут удерживаться на поверхности воды, а не идут ко дну. По аналогичному принципу действуют воздухоплавательные средства – они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.

Цели урока: убедиться в существовании выталкивающей силы, осознать причины её возникновения и вывести правила для её вычисления, содействовать формированию мировоззренческой идеи познаваемости явлений и свойств окружающего мира.

Задачи урока: Работать над формированием умений анализировать свойства и явления на основе знаний, выделять главную причину, влияющую на результат. Развивать коммуникативные умения. На этапе выдвижения гипотез развивать устную речь. Проверить уровень самостоятельности мышления школьника по применению учащимися знаний в различных ситуациях.

Архимед – выдающийся ученый Древней Греции, родился в 287 году до н.э. в портовом и судостроительном г. Сиракузы на острове Сицилия. Архимед получил блестящее образование у своего отца, астронома и математика Фидия, родственника сиракузского тирана Гиерона, покровительствовавшего Архимеду. В юности провёл несколько лет в крупнейшем культурном центре в Александрии, где у него сложились дружеские отношения с астрономом Кононом и географом-математиком Эратосфеном. Это послужило толчком к развитию его выдающихся способностей. В Сицилию вернулся уже зрелым ученым. Он прославился многочисленными научными трудами главным образом в области физики и геометрии.

Последние годы жизни Архимед был в Сиракузах, осажденных римским флотом и войском. Шла 2-я Пуническая война. И великий ученый, не жалея сил, организовывает инженерную оборону родного города. Он построил множество удивительных боевых машин, топивших вражеские корабли, разносивших их в щепы, уничтожавших солдат. Однако слишком маленьким было войско защитников города по сравнению с огромным римским войском. И в 212 г. до н.э. Сиракузы были взяты.

Гений Архимеда вызывал восхищение у римлян и римский полководец Марцелл приказал сохранить ему жизнь. Но солдат, не знавший в лицо Архимеда, убил его.

Одним из важнейших его открытий стал закон, впоследствии названный законом Архимеда. Существует предание, что идея этого закона посетила Архимеда, когда он принимал ванну, с возгласом “Эврика!” он выскочил из ванны и нагим побежал записывать пришедшую к нему научную истину. Суть этой истины и предстоит выяснить, нужно убедиться в существовании выталкивающей силы, осознать причины её возникновения и вывести правила для её вычисления.

Давление в жидкости или газе зависит от глубины погружения тела и приводит к появлению выталкивающей силы, действующей на тело и направленной вертикально вверх.

Если тело опустить в жидкость или газ, то под действием выталкивающей силы оно будет всплывать из более глубоких слоев в менее глубокие. Выведем формулу для определения силы Архимеда для прямоугольного параллелепипеда.

Давление жидкости на верхнюю грань равно

где: h2 – высота столба жидкости над верхней гранью.

Сила давления на верхнюю грань равна

F1= р1*S = ж*g*h2*S,

Где: S – площадь верхней грани.

Давление жидкости на нижнюю грань равно

где: h3 – высота столба жидкости над нижней гранью.

Сила давления на нижнюю грань равна

F2= p2*S = ж*g*h3*S,

Где: S – площадь нижней грани куба.

Поскольку h3 > h2, то р2 > р1 и F2 > F1.

Разность между силами F2 и F1 равна:

F2 – F1 = ж*g*h3*S – ж*g*h2*S = ж*g*S* (h3 – h2).

Так как h3 – h2 = V – объему тела или части тела, погруженной в жидкость или газ, то F2 – F1 = ж*g*S*H = g* ж*V

Произведение плотности на объем есть масса жидкости или газа. Следовательно, разность сил равна весу вытесненной телом жидкости:

F2 – F1= mж*g = Pж = Fвыт.

Выталкивающая сила есть сила Архимеда, определяющая закон Архимеда

Равнодействующая сил, действующих на боковые грани равна нулю, поэтому в расчетах не участвует.

Таким образом, на тело, погруженное в жидкость или газ, действует выталкивающая сила равная весу вытесненной им жидкости или газа.

Закон Архимеда, впервые был упомянут Архимедом в трактате “О плавающих телах”. Архимед писал: “тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.

Рассмотрим, как зависит сила Архимеда и зависит ли от веса тела, объема тела, плотности тела и плотности жидкости.

Исходя из формулы силы Архимеда, она зависит от плотности жидкости, в которую погружено тело, и от объёма этого тела. Но она не зависит, например, от плотности вещества тела, погружаемого в жидкость, так как эта величина не входит в полученную формулу.
Определим теперь вес тела, погружённого в жидкость (или газ). Так как две силы, действующие на тело в этом случае, направлены в противоположные стороны (сила тяжести вниз, а архимедова сила вверх), то вес тела в жидкости будет меньше веса тела в вакууме на архимедову силу:

P А = m т g – m ж g = g (m т – m ж)

Таким образам, если тело погружено в жидкость (или газ), то оно теряет в своём весе столько, сколько весит вытесненная им жидкость (или газ).

Следовательно:

Сила Архимеда зависит от плотности жидкости и объема тела или его погруженной части и не зависит от плотности тела, его веса и объема жидкости.

Определение силы Архимеда лабораторным методом.

Оборудование: стакан с чистой водой, стакан с соленой водой, цилиндр, динамометр.

Ход работы:

• определяем вес тела в воздухе;
• определяем вес тела в жидкости;
• находим разницу между весом тела в воздухе и весом тела в жидкости.

4. Результаты измерений:

Сделать вывод как зависит сила Архимеда от плотности жидкости.

Выталкивающая сила действует на тела любых геометрических форм. В технике наиболее распространены тела цилиндрической и сферической форм, тела с развитой поверхностью, полые тела в форме шара, прямоугольного параллелепипеда, цилиндра.

Гравитационная сила приложена к центру масс погруженного в жидкость тела и направлена перпендикулярно к поверхности жидкости.

Подъемная сила действует на тело со стороны жидкости, направлена по вертикали вверх, приложена к центру тяжести вытесненного объема жидкости. Тело движется в направлении, перпендикулярном к поверхности жидкости.

Выясним условия плавания тел, которые основываются на законе Архимеда.

Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести F т и силы Архимеда F A , которые действуют на это тело. Возможны следующие три случая:

• F т > F A – тело тонет;
• F т = F A – тело плавает в жидкости или газе;
• F т

Другая формулировка (где P t – плотность тела, P s – плотность среды, в которую оно погружено):

• P t > P s – тело тонет;
• P t = P s – тело плавает в жидкости или газе;
• P t

Плотность организмов живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны! Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.

Если тело лежит на дне в жидкости или газе, то сила Архимеда равна нулю.

Закон Архимеда используется в судостроении и воздухоплавании.

Схема плавающего тела:

Линия действия силы тяжести тела G проходит через центр тяжести K (центр водоизмещения) вытесненного объема жидкости. В нормальном положении плавающего тела центр тяжести тела Т и центр водоизмещения K размещены по одной вертикали, называемой осью плаванья.

При качке центр водоизмещения К перемещается в точку К1, и сила тяжести тела и Архимедова сила FА образуют пару сил, которая стремится либо вернуть тело в исходное положение, либо увеличить крен.

В первом случае плавающее тело обладает статической устойчивостью, во втором случае устойчивость отсутствует. Устойчивость тела зависит от взаимного расположения центра тяжести тела Т и метацентра М (точки пересечения линии действия архимедовой силы при крене с осью плавания).

В 1783 году братья МОНГОЛЬФЬЕ изготовили огромный бумажный шар, под которым поместили чашку с горящим спиртом. Шар наполнился горячим воздухом и начал подниматься, достигнув высоты 2000 метров.

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам – очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите

На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной этим телом жидкости или газа.

В интегральной форме

Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.

Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой ) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.

Что касается тел, которые находятся в газе, например в воздухе, то для нахождения подъёмной силы (Силы Архимеда) нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.

В отсутствие гравитационного поля (Сила тяготения), то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление конвекции (естественное перемещение воздуха в пространстве), поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами

В формуле мы использовали.

Жидкостей и газов, согласно которому на всякое тело, пог-руженное в жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная весу вытесненной телом жидкости (газа) и направленная по вертикали вверх.

Этот закон был открыт древнегреческим ученым Архимедом в III в. до н. э. Свои исследования Архимед описал в трактате «О плавающих телах», который считается одним из последних его научных трудов.

Ниже приведены выводы, следующие из закона Архимеда .

Действие жидкости и газа на погруженное в них тело.

Если погрузить в воду мячик, наполненный воздухом, и отпустить его, то он всплывет. То же самое произойдет со щепкой, с пробкой и многими другими телами. Какая же сила заставляет их всплывать?

На тело, погруженное в воду, со всех сторон действуют силы давления воды (рис. а ). В каж-дой точке тела эти силы направлены перпендикулярно его поверхности. Если бы все эти силы были одинаковы, тело испытывало бы лишь всестороннее сжатие. Но на разных глубинах гидростати-ческое давление различно: оно возрастает с увеличением глубины. Поэтому силы давления, приложенные к нижним участкам тела, оказываются больше сил давления, действующих иа тело сверху.

Если заменить все силы давления , приложенные к погруженному в воду телу, одной (резуль-тирующей или равнодействующей) силой, оказывающей на тело то же самое действие, что и все эти отдельные силы вместе, то результирующая сила будет направлена вверх. Это и заставляет тело всплывать. Эта сила называется выталкивающей силой, или архимедовой силой (по имени Архимеда, который впервые указал на ее существование и установил, от чего она зависит). На рисунке б она обозначена как F A .

Архимедова (выталкивающая) сила действует на тело не только в воде, но и в любой другой жидкости, т. к. в любой жидкости существует гидростатическое давление, разное на разных глу-бинах. Эта сила действует и в газах, благодаря чему летают воздушные шары и дирижабли.

Благодаря выталкивающей силе вес любого тела, находящегося в воде (или в любой другой жидкости), оказывается меньше, чем в воздухе, а в воздухе меньше, чем в безвоздушном про-странстве. В этом легко убедиться, взвесив гирю с помощью учебного пружинного динамометра сначала в воздухе, а затем опустив ее в сосуд с водой.

Уменьшение веса происходит и при переносе тела из вакуума в воздух (или какой-либо другой газ).

Если вес тела в вакууме (например, в сосуде, из которого откачан воздух) равен P 0 , то его вес в воздухе равен:

,

где F´ A — архимедова сила, действующая на данное тело в воздухе. Для большинства тел эта сила ничтожно мала и ею можно пренебречь, т. е. можно считать, что P возд. =P 0 =mg .

Вес тела в жидкости уменьшается значительно сильнее, чем в воздухе. Если вес тела в воздухе P возд. =P 0 , то вес тела в жидкости равен P жидк = Р 0 — F A . Здесь F A — архимедова сила, действующая в жидкости. Отсюда следует, что

Поэтому чтобы найти архимедову силу, действующую на тело в какой-либо жидкости, нужно это тело взвесить в воздухе и в жидкости. Разность полученных значений и будет архимедовой (выталкивающей) силой.

Другими словами, учитывая формулу (1.32), можно сказать:

Выталкивающая сила, действующая на погруженное в жидкость тело, равна весу жидкости, вытесненной этим телом.

Определить архимедову силу можно также теоретически. Для этого предположим, что тело, погруженное в жидкость, состоит из той же жидкости, в которую оно погружено. Мы имеем пра-во это предположить, так как силы давления, действующие на тело, погруженное в жидкость, не зависят от вещества, из которого оно сделано. Тогда приложенная к такому телу архимедова сила F A будет уравновешена действующей вниз силой тяжести m ж g (где m ж — масса жидкости в объеме данного тела):

Но сила тяжести равна весу вытесненной жидкости Р ж . Таким образом.

Учитывая, что масса жидкости равна произведению ее плотности ρ ж на объем, формулу (1.33) можно записать в виде:

где V ж — объем вытесненной жидкости. Этот объем равен объему той части тела, которая погру-жена в жидкость. Если тело погружено в жидкость целиком, то он совпадает с объемом V всего тела; если же тело погружено в жидкость частично, то объем V ж вытесненной жидкости меньше объема V тела (рис. 1.39).

Формула (1.33) справедлива и для архимедовой силы, действующей в газе. Только в этом слу-чае в нее следует подставлять плотность газа и объем вытесненного газа, а не жидкости.

С учетом вышеизложенного закон Архимеда можно сформулировать так:

На всякое тело, погруженное в покоящуюся жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная произведению плотности жидкости (или га-за), ускорения свободного падения и объема той части тела, которая погружена в жидкость (или газ).

Лабораторная работа 7 определение выталкивающей силы. Лабораторная работа “определение величины выталкивающей силы, действующей на погруженное в жидкость тело”

Тема: Лабораторная работа «Определение выталкивающей силы, действующей на погруженное в жидкость тело» .

Цели:

научиться измерять выталкивающую силу, действующую на тело, погруженное в жидкость;

развивать навыки самостоятельной индивидуальной работы, умение сравнивать, наблюдать, делать выводы;

воспитывать познавательный интерес к предмету

Ход урока:

1. Оргмомент. Целеполагание

2. Актуализация опорных знаний

3. Выполнение лабораторной работы с компьютерной моделью.

4. Итоги урока.

5. Домашнее задание.

Учитель: Здравствуй, наш великий соотечественник М.В. Ломоносов говорил: “Один опыт я ставлю выше, чем тысяча мнений, рожденных только воображением”. Сегодня мы попробуем себя не просто в роли ученика, а в роли ученого исследователя. А с чего начинается любое исследование? Конечно же,с эксперимента.

Но, для начала вспомним пройденный материал.

Вопросы учителя:

Ответы учащегося:

– Какие силы действуют на погруженное в жидкость тело?

F Т , F А

– Какая сила называется выталкивающей силой?

Сила, возникающая при погружении тела в жидкость или газ

– Куда направлена F Т ?

Вниз

– Куда направлена F А ?

Вверх

– Назвать формулу F А , охарактеризовать входящие в нее величины

F А .= ж V Т g

Как определить вес тела, погруженного в жидкость?

Р = F Т – F А

Учитель:

Если тело в воду бросить

Или просто опустить,

Будет сила Архимеда

Снизу на него давить.

Если вес воды в объеме

Погруженной части знать,

Можно силу Архимеда

3. Этим мы и займемся на сегодняшнем уроке, выполнив лабораторную работу , используя интерактивн ую модель .

Оборудование: компьютер, интерактивная модель.

Для того чтобы приступить к работе необходимо определить цену деления приборов, с которыми сегодня ты будешь работать используя интерактивную модель. Вспомним правило.

Ученик:

найти два ближайших штриха шкалы, возле которых написаны значения величины;

вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

С = – цена деления шкалы прибора

Опыт 1 .

(Описание в работе) Заполнить таблицу 1

Таблица 1.

№ опыта

P, вес тела в воздухе (H)

Р 1 , вес тела в воде (H)

F Арх

F Арх = P – P 1

1.цилиндр алюминиевый

2. цилиндр медный

2 часть

Опыт 2 .

1.Измерить объем воды, налитой в мензурку(Vо).

2.Измерить его же после погружения туда цилиндров(V б , V м ).

3.Вычислить V тела =V- Vо. (Перевести V в м 3 , зная, что 1мл= 1см 3 =0,000001м 3)

4.Рассчитать F Арх =Pжидкости=Мж*g= ρ ж gV (ρ ж= 1000 кг\ м 3)

Заполнить таблицу 2

Таблица 2.

№ опыта

Vо, объем налитой воды,

(см 3 )

V, объем воды

3 )

V т , объем тела, см 3

V т , объем

тела, м 3

F Арх

1.цилиндрбольшой

2.цилиндр малый

На основе выполненных опытов сделать вывод

Вывод:

1. Архимедова сила, не зависит от плотности вещества, из которого изготовлено тело

2. Сила, действующая на тело, погруженная в жидкость, прямо пропорциональна объему тела

Рефлексия

Закончи фразу:

Сегодня на уроке я научился…………..

Было интересно узнать…………..

Было трудно……………

5.Д/з

§ 48, 49 упр. 24 (1, 2)

Опыт1. Исследование зависимости выталкивающей силы от плотности тела

Таблица 1.

№ опыта

P, вес тела в воздухе (H)

Р 1 , вес тела в воде (H)

F Арх

F Арх = P – P 1

1.цилиндр алюминиевый

2. цилиндр медный

100

Опыт 2. Исследование зависимости выталкивающей силы от объема погруженного тела.

Таблица 2.

№ опыта

Vо, объем налитой воды,

(см 3 )

V, объем воды

после погружения в нее тела, (см 3 )

V т , объем тела, см 3

V т , объем

тела, м 3

F Арх

1.цилиндрбольшой

100

137

0,000037

2.цилиндр малый

100

113

0,000013

Тема: Определение выталкивающей силы, действующей на погруженное в жидкость тело.

Тип урока: Лабораторная работа: определение выталкивающей силы, действующей на погруженное в жидкость тело.

Класс: 7, Перышкин: Учеб. Для 7 класса общеобразоват. учреждений. М.: Просвещение, 2007.

Цели:

Образовательные:

Организовать деятельность учащихся по определению выталкивающей силы, действующей на тело погруженное в воду;

В ходе выполнения лабораторного эксперимента формировать у учащихся знание о зависимости выталкивающей силы от объема тела;

Сформировать знание о методе определения вычисления выталкивающей силы;

Научить определять выталкивающую силу при помощи измеренного веса тела в воздухе и в жидкости;

Сформировать умение собирать установку по определению выталкивающей силы, действующей на погруженное в жидкость тело;

Воспитательные:

Обратить внимание учащихся на правильное оформлении лабораторной работы и поддержании порядка на рабочем столе.

Развивающие:

Развивать логическое мышление путем предложения ученикам самостоятельно делать вывод о проделанной работе.

Ход урока:

1.Организационный этап.(1 мин) Здравствуйте! Садитесь. 2.Актуализация знаний.(2 мин) Давайте вспомним, что вы изучали на прошлом занятии. 3. Постановки целей и задач урока. (2 мин) Ребята сейчас я Вам расскажу интересную историю. День выдался очень жаркий и Настя с Таней отправились купаться. Они долго плавали, а потом занялись изучением речного дна. Сколько разных камушков можно было найти! Один из них особенно заинтересовал сестер. Это был огромный булыжник, гладкий со всех сторон. Девочки решили вытащить его на берег. Девочки легко в воде перенесли камень ближе к берегу. Но вытащить его на сушу оказалось делом не простым. Камень был слишком тяжелым. Пришлось просить помощь у мальчишек. Общими усилиями добились своего и долго не могли нарадоваться своему успеху. Почему перенести камень ближе к берегу девочки смогли, а поднять его, чтобы вытащить на сушу не смогли? А давайте проверим действительно ли вес тела в воде меньше чем в воздухе и определим величину силы действующей в воде. 4.Выполнение работы.(25 мин) Откройте тетради и запишите тему урока Лабораторная работа №7 Тема: Определение выталкивающей силы, действующей на погруженное в жидкость тело Цель работы: обнаружить на опыте выталкивающее действие жидкости на погруженное в неё тело и определить выталкивающую силу. Оборудование: динамометр, штатив с муфтой и лапкой, два тела разного объема, стаканы с водой и насыщенным раствором соли в воде. Пользуясь инструкцией к выполнению, определите выталкивающую силу, действующую на погруженное в жидкость тело и результаты занесите в таблицу Жидкость Вес тела в воздухе Р, Н Вес тела в жидкости Выталкивающая сила F, Н Нас. рас. соли в воде

Здравствуйте! Дети садятся. Выталкивающая сила равна весу вытесненной жидкости Fa=mжg В воде камень легче, так как на него действует направленная вертикально вверх выталкивающая сила. На берегу она действует со стороны воздуха, но меньше чем со стороны воды. Ученики внимательно слушают инструктаж по выполнению работы и выполняют требования к работе. Проделывают работу.

Тема: Определение выталкивающей силы, действующей на погруженное в жидкость тело

Цель работы : обнаружить на опыте выталкивающее действие жидкости на погруженное в неё тело и определить выталкивающую силу.

Оборудование : динамометр, штатив с муфтой и лапкой, два тела разного объема, стаканы с водой и насыщенным раствором соли в воде.

Ход работы:

1.Укрепите динамометр на штативе и подвести к нему на нити тело. Отметьте и запишите в таблице показание динамометра. Это будет вес тела в воздухе.

2.Подставьте стакан с водой и опускайте муфту с лапкой и динамометром, пока все тело не окажется под водой. Отметьте и запишите в таблицу показание динамометра. Это будет вес тела в воде.

3.По полученным данным вычислите выталкивающую силу, действующую на тело.

4.Вместо чистой воды возьмите насыщенный раствор соли и снова определите выталкивающую силу, действующую на тоже тело.

5.Подвесте к динамометру тело другого объема и определите указанным способом(см. пункты 2 и 3) выталкивающую силу, действующую на него в воде.

6.Результаты запишите в таблицу.

Жидкость	Вес тела в воздухе Р, Н	Вес тела в жидкости	Выталкивающая сила F, Н
Насыщенный раствор соли в воде

7.На основе выполненных опытов сделайте выводы. От каких величин зависит значение выталкивающей силы?

Обоснование

Я считаю, что за работу можно поставить оценку «5».Потому что ученик написал цель и ход измерений, перечислил приборы с которыми выполняется измерение, собрал простую установку для выполнения измерений, пользовался измерительными приборами: определял цену деления шкалы, снимал показания, определил относительные и абсолютные погрешности, устранял действие побочных факторов, влияющих на результаты измерений, объяснил наблюдаемые физические явления, составил отчет о работе в виде таблицы. Знал устройство и принцип действия приборов, с которыми выполняются измерения, правило обращения с приборами, способы измерения данной физической величины. Самостоятельно анализировал полученные результаты и сделал вывод.

То есть ученик применил знания и умения I, II, III уровня.

ЛАБОРАТОРНАЯ РАБОТА.

ОПРЕДЕЛЕНИЕ ВЫТАЛКИВАЮЩЕЙ СИЛЫ.

Цели : обнаружить на опыте выталкивающее действие жидкости на погруженное в нее тело и определить выталкивающую силу.

Приборы и материалы : динамометр, штатив с муфтой и лапкой, два тела разного объема, стаканы с водой и насыщенным раствором соли в воде.

Указание к работе:

1. Согласно закону Архимеда на погруженное в жидкость тело действует выталкивающая сила F A , равная весу mg вытесненной жидкости:

F A = mg . (1)

Для сравнения архимедовой силы с весом тела нужно измерить вес тела P с помощью динамометра и вычислить архимедову силу F A . архимедова сила F A определяется по формуле:

F A = mg =  Vg (2),

где  – плотность воды ( = 1000 кг/м 3 ), V – объем вытесненной телом воды, g – ускорение свободного падения (g = 9,81 м/с 2 ).

Объем V вытесненной воды можно измерить с помощью измерительного цилиндра как разность уровня воды при погружении в него исследуемого тела и без тела.

Архимедову силу FA , действующего на тело, тонущее в воде, можно найти, измерив с помощью динамометра вес тела P в воздухе и силу P 1 , удерживающую тело в равновесии при погружении его в воду:

P = F A + P 1 , F A = P – P 1 .

2. Измерьте вес Р первого тела с помощью динамометра.

3. Измерьте силу P 1 , действующую на крючок динамометра при полном погружении тела в воду. Для этого укрепите динамометр на штативе и подвесьте к нему груз. Поставьте стакан с водой и опускайте муфту с лапкой и динамометром, пока все тело не окажется под водой. Это будет вес тела в воде.

4. Вычислите выталкивающую силу, действующую на тело.

5
. Вместо чистой воды возьмите насыщенный раствор соли и вычислите выталкивающую силу.

6. Подвесьте к динамометру другое тело и проделайте п.2 – п.5

7. Результаты измерений и вычислений запишите в отчетную таблицу.

Жидкость

Вес тела в воздухе

Вес тела в жидкости

Выталкивающая сила

F , Н F =P -P 1

Р ’

P’’

P 1 ’

P 1 ’’

F’

F’’

Вода

Насыщенный раствор соли в воде

На основе выполненных опытов сделайте выводы.

Контрольные вопросы.

1. В какой воде и почему легче плавать: в морской или речной?

2. Подвешенный на нити стальной брусок погружен в воду. Назовите взаимодействующие тела и силы, действующие на брусок. Изобразите эти силы графически.

3. Объем куска железа 0,1 м 3 . Какая выталкивающая сила будет на него действовать при полном погружении в керосин?

Цели:

• измерить выталкивающую силу, действующую на тело, погруженное в жидкость;
• развивать навыки самостоятельной индивидуальной работы и работы в группе, умение сравнивать, наблюдать;
• воспитывать самостоятельность делать выводы, подходить творчески к выполнению эксперимента, повысить познавательный интерес к науке.

Задачи:

• проверять теоретические предположения экспериментально, рассчитывать F А – силу Архимеда;
• развивать умение логически мыслить, сопоставлять, сравнивать, самостоятельно делать выводы;
• проявлять инициативу, активность, самостоятельность, творческий интерес.

Оборудование: компьютер, установочный диск «Лабораторные работы по физике»; мензурка, весы, разновески, тела – алюминиевый и латунный одинакового объема, динамометр.

План урока:

№ п		Методы и приемы
1.	Повторение вопросов о выталкивающей силе, действующей на погруженное в жидкость или газ тело	Беседа, фронтальный опрос.
2.	Изложение и закрепление материала.	Беседа, демонстрация опытов, лабораторная работа.
3.	Выталкивающая сила.. Сила Архимеда. Измерение F А	Применение учащимися научных методов: наблюдение, сравнение, сопоставление, выдвижение гипотез, теоретические выводы, экспериментальная проверка теоретического предвидения.
4.	Вопросы заданий.	Запись на карточках и в тетрадях.
5.	Задание на дом.	Запись на доске и в дневниках.

ХОД УРОКА

1. Организационный момент.

Мотивация. (Приветствие, отметка отсутствующих, сообщение темы, целей урока, прочтение эпиграфа)

– Тема сегодняшнего урока чрезвычайна важна и интересна. С выталкивающей силой, действующей на погруженное в жидкость или газ тело мы встречаемся очень часто – поэтому мы должны учитывать этот фактор при выполнении различных работ, определять величину выталкивающей силы и определять условия, влияющие на величину этой силы. Этому и посвящено сегодняшнее исследование.
Схема исследования: исходные факты – гипотеза – исследование научной литературы – проведение эксперимента – анализ результатов – выводы.

2. Актуализация знаний

3. Исходные факты: итак тело помещенное в жидкость становится «легче»

4. Выдвижение гипотезы: поскольку изменение действия силы на тело можно осуществить только действием другой силы, следовательно против силы тяжести действует противоположно направленная выталкивающая сила – наша цель определить величину этой силы и проверить формулу: F А .= ж V Т g
Из-за разности давлений в жидкости на разных уровнях возникает выталкивающая или архимедова сила

Рис. 1.15.3 поясняет появление архимедовой силы. В жидкость погружено тело в виде прямоугольного параллелепипеда высотой h и площадью основания S . Разность давлений на нижнюю и верхнюю грани есть:

Поэтому выталкивающая сила будет направлена вверх, и ее модуль равен

где V – объем вытесненной телом жидкости, а V – ее масса.

Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом.

Это утверждение, называемое законом Архимеда , справедливо для тел любой формы.

Из закона Архимеда вытекает, что если средняя плотность тела т больше плотности жидкости (или газа) , тело будет опускаться на дно. Если же т

5. Выдвижение гипотез и следствия

На доске записано:

6. Эксперимент (лабораторная работа)

Наш великий соотечественник М.В. Ломоносов говорил: “Один опыт я ставлю выше, чем тысяча мнений, рожденных только воображением”. Поэтому подвергнем экспериментальной проверке все наши гипотезы.
(На столах лежат приборы и все необходимое для проверки и проведения лабораторной работы).
Образцы карточек – памяток № 1-4, в которых дети будут записывать результаты, прилагается. По ходу работы по карточкам учитель записывает результаты на доске с комментариями (Приложение 1 ).

Таким образом, мы подтверждаем наши гипотезы и опыты ученых.
Проверим закон Архимеда, выполнив виртуальную лабораторную работу (Приложение 2 )

6. Итоги: проведенные работы подтвердили справедливость закона Архимеда.

Рефлексия:

1. Как можно на опыте определить, с какой силой тело, погруженное целиком в жидкость, выталкивается из жидкости?
2. Чему равна эта сила?
3. Как называют силу, которая выталкивает тела, погруженные в жидкости и газы?
4. Как подсчитать архимедову силу?
5. От каких величин зависит архимедова сила? От каких величин она не зависит?

7. Домашнее задание: §48, 49, упр. 24, стр. 119.

Литература : учебник «Физика 7» А.В. Перышкин, «Поурочные разработки по физике» В.А. Волков, С.Е. Полянский.

МБОУ СОШ № 117 Учитель физики Дмитракова Л.Н.

г.Снежинск Челябинской области

7 класс

Урок по теме: «Лабораторная работа № 7».

«Определение выталкивающей силы,

действующей на погруженное в жидкость тело»

Цели урока: Обнаружить на опыте выталкивающее действие жидкости на погруженное в нее тело и определить выталкивающую силу.

Оборудование урока: по описанию в учебнике стр. 167.

Тип урока: урок–исследование – лабораторная работа.

Образовательная цель: формировать теоретические и практические навыки и умения учащихся на опыте определять выталкивающую силу; умение сравнивать и делать выводы; умение измерять вес тела в воздухе и в жидкости.

Развивающая цель: развивать познавательный интерес учащихся к физике, развивать умение выполнять лабораторную работу по образцу; развивать умение находить закономерности; развивать умение заполнять таблицу; развивать исследовательские умения; развивать умение работать в парах.

Воспитательная цель: воспитывать чувство ответственности и уважения к своим товарищам; прививать культуру взаимоотношений, воспитывать организованность, воспитывать культуру работы с лабораторным оборудованием.

ДЗ: Л. № 605, 606, 623, 626.

Ход урока:

I . Организационный момент.

Мобилизующее начало урока. Проверка отсутствующих. Организация внимания.

Цель : психологический настрой учащихся на урок. Запись домашнего задания с пояснением № 626 (объем тела = abc ).

II . Сообщение темы и цели урока.

Цель : обнаружить на опыте выталкивающую силу; выяснить от чего зависит сила Архимеда (от плотности и от объема тела) и как?

III . Проверка усвоения изученного материала (фронтальный опрос учащихся).

Цель : проверка и оценка ЗУН

Вопросы для контроля:

1. Написать (на доске) формулу для расчета выталкивающей силы, действующей на погруженное в жидкость тело.

2. От чего зависит выталкивающая сила? От чего не зависит?

3. Как направлена эта сила?

4. Кто впервые указал на существование выталкивающей силы и рассчитал ее значение?

5. Что гласит закон Архимеда?

IV . Выполнение лабораторной работы № 7

«Определение выталкивающей силы, действующей на погруженное в жидкость тело»

(проводится по описанию в учебнике страница 167.).

Цель : исследование, заполнение таблицы, рассуждение учащихся (работа в парах под руководством учителя).

V . Анализ и выводы из опытов .

Цель : сформировать умение сравнивать и делать выводы из опытов (коллективное обсуждение; самостоятельные записи в тетрадях).

Задания сравнить:

1. силу Архимеда, действующую на тела разного объема.

2. силу Архимеда, действующую на тело в чистой и соленой воде.

Выводы:

1. сила Архимеда зависит от объема погруженной части тела.

2.Сила Архимеда зависит от плотности жидкости.

3. При погружении тела в жидкость тело теряет в своем весе.

VI . Легенда об Архимеде (если останется время) .

Цель : формирование интереса учащихся к предмету; усвоение фактов и основных идей (беседы с учащимися о прочитанном).

VII . Решение задач (если останется время).

Цель : применение знаний о зависимости силы Архимеда от объема тела и плотности жидкости при решении качественных и вычислительных задач.

РЕШЕНИЕ ЗАДАЧ.

На какой из опущенных в воду стальных шаров действует наибольшая выталкивающая сила?

Подвешенные к коромыслу весов одинаковые шары погрузили один — в масло, а другой – в воду. На какой шар будет действовать большая сила Архимеда?

3) Металлическая деталь весит в воздухе 44,5 Н., а при погружении в керосин – 40,5 Н. Чему равна Архимедова сила, действующая на деталь? Каков объем этой детали?

Дано:

P в в воздухе = 44,5 Н

P в в керосине = 40,5 Н

F а — ? V т — ?

Решение: F а = P в воздухе – P в керосине F а = 44,5 – 40,5 = 4Н F а = ρ к g V т V т = F а_ ρ к g ρ r = 800 кг/м 3 V т = 4Н__________ = 0,0005 м 3 800 кг/м 3 , 10 н/кг Ответ : 0,0005 м 3 4 Н

VIII . Итоги урока.

(Что нового узнали? Чему научились? Трудно ли вам было? Интересно ли вам было на уроке?). Сдать тетради на проверку.

Для самоанализа урока (для учителя):

Методы творческой деятельности:

1. Мотивационные рисунки.

2. Самостоятельная практическая деятельность учащихся.

3. Наблюдение, анализ, сравнение, выводы, заполнение таблицы.

4. Поисковое задание.

5. Работа в парах.

Форма организации:

1. Фронтальная.

2. Парная.

3. Коллективная деятельность учащихся на уроке.

Принцип Архимеда: определение, теория и применение

Определение: что такое принцип Архимеда?

Принцип Архимеда – это физический закон, фундаментальный для гидродинамики. В нем говорится, что восходящая выталкивающая сила, прилагаемая к телу, погруженному в жидкость, полностью или частично погруженному в воду, равна весу жидкости, которую тело вытесняет. Если вес вытесненной жидкости меньше веса объекта, объект утонет. Объект будет плавать, если вес вытесненной жидкости равен весу объекта.Эта восходящая сила известна как тяга или подъемная сила. Это следствие разницы в давлении жидкости на разной высоте. Давление жидкости распространяется во всех направлениях (принцип Паскаля) и увеличивается с глубиной. На дно погруженного объекта действует несбалансированная направленная вверх сила.

Принцип Архимеда

История принципа Архимеда

История этого принципа восходит к 3 9000 9 веку до нашей эры, когда он был открыт Архимедом Сиракузским, греческим математиком, физиком, инженером, изобретателем и астрономом.Это открытие часто ассоциируется с термином «момент эврики».

Согласно популярной легенде, Архимеду было поручено выяснить, была ли корона, сделанная для короля, из чистого золота или поддельного золота. Однажды он принимал ванну и заметил, как поднимался уровень воды, когда он погружал свое тело. Понимая, что если золотую корону уронить в ванну, она вытеснит весь объем воды за борт. Эта идея, по сути, дала ему простой способ измерить объем короны.Взвесив корону, он мог эффективно вычислить ее плотность (массу, деленную на объем) и сравнить ее с плотностью золота. Если плотность была ниже, чем у золота, корона была подделкой.

Вот простое видео, объясняющее принцип Архимеда:

Примеры принципа Архимеда

Принцип Архимеда – обычное явление в реальной жизни. Вот некоторые известные примеры.

Пример принципа Архимеда

Изображение предоставлено: Сатьям Бхуян

• Корабль или лодка могут плавать по воде, потому что вес вытесненной воды равен весу корабля или лодки.
• Подводная лодка может нырять в воду или плавать на ней. Подводная лодка состоит из балластных цистерн, наполненных воздухом или водой. Резервуары весят меньше, чем равный объем воды, и заставляют субмарину плавать на поверхности. Если резервуары частично заполнены воздухом, можно заставить подводную лодку плавать на некоторой глубине воды, не поднимаясь и не опускаясь.
• Воздушные шары поднимаются в воздух, потому что более теплый воздух внутри воздушного шара менее плотный, чем более холодный воздух снаружи.Основной принцип работы воздушного шара – использование горячего воздуха для создания плавучести, которая создает подъемную силу.
• Водомер может плавать по воде, так как его ноги выталкивают воду, а вес выталкиваемой воды равен силе плавания.

Теория принципа Архимеда

Тяга, создаваемая жидкостью, противодействует весу под действием силы тяжести. Объект внутри жидкости ощущает только общую силу, действующую на него, которая называется кажущейся массой.Поскольку тяга жидкости уменьшает действительную гравитационную силу, объект чувствует, как будто его вес уменьшился. Кажущийся вес определяется по формуле:

.

Кажущийся вес = Вес объекта в воздухе – Тяга или выталкивающая сила

Главное уравнение Архимеда

Принцип Архимеда говорит нам, что эта потеря веса равна массе жидкости, полностью или частично вытесненной объектом. Соответствующее уравнение имеет вид,

F _b = ρ X g X V

Где,

F _b – подъемная сила (или тяга)

ρ – плотность жидкости, в которую погружен объект

V – объем объекта, погруженного в жидкость

g – ускорение свободного падения

Вывод формулы принципа Архимеда: закон плавучести

Масса вытесненной жидкости

Масса = Плотность X Объем

M = ρ X V

Масса вытесняемой жидкости

Вес = Масса X Гравитация

W = M X g

Или, W = ρ X V X g

Согласно принципу Архимеда,

Кажущаяся потеря веса = Вес вытесненной жидкости

Эта кажущаяся потеря веса представляет собой тягу или выталкивающую силу ( F _b ).Следовательно,

F _b = ρ X g X V

Именно эта сила отвечает за плавание объектов. Таким образом, это уравнение еще называют законом плавучести.

Главное уравнение Архимеда

Использование и применение принципа Архимеда

Принцип Архимеда применим к следующей ситуации.

• Существенным применением принципа Архимеда является измерение объема и плотности объектов неправильной формы.
• В ареометре твердое тело подвешено в жидкости и поддерживается силой, равной весу жидкости, вытесняемой погруженной частью.
• Он используется в большом количестве научных исследований, включая медицину, инженерию, энтомологию, инженерию и геологию. Например, его используют для определения плотности костей и зубов.

Последнее обновление статьи: среда, 8 сентября 2021 г.

Принцип Архимеда

Принцип Архимеда

---

Фоновое чтение

Историки науки в целом согласны с тем, что идея его принципа пришла в голову. Архимед вошел в бассейн для ванны.Когда он вошел в более глубокую воду, силы на ногах стало меньше.

Принцип Архимеда заключается в том, что объект полностью или частично погружен в воду. в жидкости (жидкости или газе) поднимается (поднимается) вверх силой, равной вес вытесняемой жидкости.

Он имеет множество приложений, одним из которых является определение плотности. и удельный вес. В следующем обсуждении индексы S , W и A представляют собой модель S , W после, и A ir соответственно.

Плотность – масса единицы объема вещества. = M / V

Удельный вес – это отношение плотности вещества к плотность воды. SG = _S / _Вт .

Метрическая системная единица ГРАМ определяется как масса одного кубического сантиметр (один миллилитр) чистой воды при 3,98 ^o С. Таким образом, для воды _Вт = 1 грамм / см ³ и, если ошибки из-за примесей и / или температуры терпимые, это большое удобство.Определения Приведенные выше предлагают различные методы определения удельного веса.

SG = _S / _Вт = (M _S / V _S ) / (M _W / V _W ) = (M _S г / В _S ) / (M _W г / В _W ) = (W _S / V _S ) / (W _W / V _W )

Определение SG применялось к первому равенству; определение плотность была применена для второго равенства.Для третьего равенства числитель и знаменатель умножались на “g”. W _S – это вес вещества, измеренный в воздухе; W _W – это вес вода вытесняется веществом при его погружении.

В некоторых случаях объем вещества равен объему вода. В частности, когда твердый объект на полностью погружен на в воде объем вытесненной воды должен быть равен объему объект.Кроме того, согласно принципу Архимеда, при погружении в воду объект получит подъемную силу, равную весу воды смещен. Таким образом, объект взвешивался в воздухе, а затем взвешивался при погружении. в воде имел бы эффективный вес , который был уменьшен за счет веса вытесненной воды, если подъемная сила воздуха незначительна. При взвешивании в воздухе объект получает подъемную силу, равную весу воздуха, вытесняемого объектом. Однако плотность воздуха невелика. достаточно (по сравнению с плотностью большинства твердых тел), чтобы эта выталкивающая сила которым следует пренебречь при взвешивании большинства твердых частиц в воздухе.( _воздух = 1,3 x 10 ^-3 г / см ³ )

Для объекта плотнее воды

SG = (W _S / V) / (W _W / V) = W _S / W _W = W _S / (выталкивающая сила) = W _S / (потеря веса в воде)
= W _S / (W _S – масса вещества в воде)

Это предлагает метод определения удельной плотности объекта плотнее, чем воды; а именно, взвесить объект в воздухе и взвесить его, полностью погружен в воду.Тогда удельный вес будет равен весу в воздухе, разделенному на кажущаяся потеря веса при взвешивании в воде.

Устройство под названием Jolly Balance предназначен для измерения веса объекты в воздухе и в воде, считывая удлинение пружины. Это использует шкалу Вернье для определения удлинения пружины до ближайшего 0,05 мм, и это очень точно. Закон Гука

F = – k x

должна применяться к пружине, где F – сила (вес), растягивающая пружина на величину x, а k – жесткость пружины.Подставляя в уравнение выше, мы находим

SG = W _S / (W _S – масса вещества в воде) = (k x _A ) / (k x _A – k x _W )

Когда неизвестная жесткость пружины отменена, SG можно найти, используя только два пружинных удлинения

• x _A : объект в воздухе
• x _W : объект полностью погружен в воду

SG = x _A / (x _A – x _Вт )

Для объекта с меньшей плотностью, чем вода

Вышеприведенное уравнение верно только в том случае, если объект более плотный, чем вода.Если объект менее плотный, чем вода, необходимо прикрепить свинцовый груз и три Для определения удельного веса пружины необходимо измерить удлинение пружины. Три удлинения

• x _A : один объект в воздухе
• x _B : объект в воздухе с погруженным свинцовым грузилом завершен в воде
• x _C : и объект, и грузило полностью погружены в воду

Последние два удлинения используются для определения потери веса в воде, то есть знаменатель определения SG.Вы должны вывести это формула в виде x _A , x _B и x _C .

SG = W _S / (потеря веса в воде) =?

Определив СГ для тонущих и плавучих объектов по Архимеду. Принцип и Веселый Баланс, желательно использовать независимый метод для сравнения. С SG = _S / _Вт , а с _W = 1 грамм / см ³ ), плотность объекта можно определить по непосредственно измеряя его массу и объем.

Для жидкости

Мерная колба (или пикнометр ) имеет пробку с полым штоком. Это позволяет с высокой воспроизводимостью готовить равные объемы жидкостей. Если измеряется масса колбы: (1) когда она пуста, (2) когда заполнена жидкостью, и (3) при заполнении водой можно определить удельную плотность жидкости. С объем такой же, он будет компенсироваться из фракции ПГ.

---

Процедура

Мы проведем три отдельных эксперимента, в которых мы определим плотность и удельный вес

1. твердое вещество плотнее воды
2. твердое вещество менее плотное, чем вода
3. жидкость

Настройка баланса Jolly

• Выровняйте весы Jolly с помощью винтов на ножках так, чтобы разметочный стержень не касается прозрачной пластмассовой втулки.
• Установите шкалу Нониуса на ноль (0,00 см) с помощью ручки рядом с основанием.
• Переместите прозрачную пластиковую втулку до совмещения линии разметки на ней. с линией разметки на подвесном металлическом стержне.
• Весы Jolly теперь откалиброваны так, чтобы показывать ноль при отсутствии нагрузки. на пружине, поэтому прозрачная пластиковая втулка НЕ ДОЛЖНА ПЕРЕМЕЩАТЬСЯ на время эксперимента.

Часть 1 – объект плотнее воды

• Измерьте массу плотного (темного) шара на трехлучевой баланс.
• Измерьте диаметр шара с помощью Штангенциркуль несколько раз. Вы сами решаете, сколько. Выбирайте разные ориентации, не все в тот же самолет. (Почему?)
• Поместите шарик на пружину весов Jolly.
• Поверните ручку у основания до тех пор, пока линия разметки на металлическом стержне не станет выровняйте по линии разметки на пластиковом рукаве.
• Запишите удлинение пружины x _A .
• Заполните большую металлическую мензурку водой примерно на 3/4 емкости и поместите это на столе поддержки.
• Затем мяч должен быть полностью погружен в воду и линия разметки на металлический стержень должен быть совмещен с линией разметки на пластиковой втулке. Для этого отрегулируйте удлинение пружины с помощью ручки на основании. весов Jolly и отрегулируйте высоту опорного стола, или отрегулируйте уровень воды в большом стакане, наполнив его из маленький стакан.
• Запишите удлинение пружины x _Вт .

Часть 2 – объект менее плотный, чем вода

• Измерьте массу плавающего (светлого) шара на трехлучевой баланс.
• Измерьте диаметр шара с помощью Штангенциркуль несколько раз. Вы сами решаете, сколько. Выбирайте разные ориентации, не все в тот же самолет. (Почему?)
• Поместите шарик на пружину весов Jolly.
• Поверните ручку у основания до тех пор, пока линия разметки на металлическом стержне не станет выровняйте по линии разметки на пластиковом рукаве.
• Запишите удлинение пружины x _A .
• Прикрепите свинцовое грузило ко дну плавающего шара.
• Погрузить все свинцовое грузило, но не плавающий шар.
• Запишите удлинение пружины x _B .
• Погрузите свинцовое грузило и плавающий шар.
• Запишите удлинение пружины x _C .

Часть 3 – жидкость

• Измерьте массу чистого, сухого пикнометра.
• Заполнить пикнометр доверху спиртом из «чистой» бутылки. с помощью пипетки с грушей. Обязательно используйте пипетку с надписью «АЛКОГОЛЬ», чтобы избежать перекрестного загрязнение.
• Вставьте стопор полого штока. Обратите внимание, что некоторое количество жидкости будет принудительно через полый стержень. Объем жидкости в пикнометре составляет теперь очень воспроизводимый; пикнометр можно заполнить до такого же уровня (а именно верхнюю часть полого стержня) с большой точностью.
• Высушите спирт, который мог пролиться на внешнюю поверхность пикнометра.
• Измерьте массу пикнометра, наполненного спиртом.
• Вылейте отработанный спирт в «мусорную» бутыль.
• Промойте пикнометр несколько раз водой и заполните его до верха. с помощью пипетки с пометкой «ВОДА».
• Вставьте стопор полого штока. Обратите внимание, что некоторое количество жидкости будет принудительно через полый стержень.
• Высушите всю воду, которая могла пролиться на внешнюю поверхность пикнометра.
• Измерьте массу пикнометра, заполненного водой.
• Вылейте воду в раковину и переверните пикнометр, чтобы он высох.
• Для чистого изопропилового спирта SG = 0.810, но если разрезать 30% воды тогда SG = 0,867. Последнее следует использовать как теоретическое значение для сравнение.

Анализ ошибок

• Определите удельную плотность плотного шара с помощью весов Jolly. с оценкой погрешности.
• Определите удельную плотность плотного шара, используя измерения массы и объема. с оценкой погрешности.
• Сравните SG, полученные двумя методами. Совместимы ли они?
• Определите удельную плотность плавающего шара с помощью весов Jolly. с оценкой погрешности.
• Определить удельную плотность плавающего шара по массе и объему. измерения с оценкой погрешности.
• Сравните SG, полученные двумя методами. Совместимы ли они?
• Определите удельную плотность 70% изопропилового спирта с оценкой погрешности и сравните с теоретическим значением. Находится ли теоретическое значение в пределах ваши планки погрешностей?
• Укажите как минимум два источника статистической ошибки.
• Определите как минимум два источника систематической ошибки.
• Воздух – это жидкость, в которую погружены вы и эксперимент. Какова относительная погрешность при пренебрежении выталкивающей силой? воздуха на каждой из деревянных сфер? То есть какова масса вытесненного воздуха, деленного на массу, которую вы измерили на трехлучевой баланс? Обоснуйте пренебрежение этой плавучей силой.

---

Назад к руководству по механике

Принцип Архимеда | Infoplease

Принцип Архимеда, принцип , согласно которому тело, погруженное в жидкость, подпитывается силой, равной весу вытесненной жидкости.Принцип применим как к плавающим, так и к погруженным телам, а также ко всем жидкостям, то есть жидкостям и газам. Это объясняет не только плавучесть кораблей и других судов в воде, но также подъем воздушного шара в воздухе и очевидную потерю веса объектов под водой. При определении того, будет ли данное тело плавать в данной жидкости, необходимо учитывать как вес, так и объем; то есть относительная плотность или вес на единицу объема тела по сравнению с жидкостью определяет выталкивающую силу.Если тело менее плотное, чем жидкость, оно будет плавать или, в случае воздушного шара, подниматься. Если тело плотнее жидкости, оно утонет. Относительная плотность также определяет долю плавающего тела, которое будет погружено в жидкость. Если тело на две трети плотнее жидкости, то две трети его объема будут погружены, вытесняя при этом объем жидкости, вес которой равен всему весу тела. В случае погруженного тела кажущийся вес тела равен его весу в воздухе за вычетом веса равного объема жидкости.Жидкость, наиболее часто встречающаяся при применении принципа Архимеда, – это вода, и удельный вес вещества является удобной мерой его относительной плотности по сравнению с водой. Однако при вычислении выталкивающей силы, действующей на тело, необходимо также принимать во внимание форму и положение тела. Стальная гребная лодка, поставленная боком в воду, утонет, потому что плотность стали намного выше плотности воды. Однако в нормальном положении, когда киль опущен вниз, эффективный объем лодки включает весь воздух внутри нее, так что ее средняя плотность меньше плотности воды, и в результате она будет плавать.

Колумбийская электронная энциклопедия, 6-е изд. Авторское право © 2012, Columbia University Press. Все права защищены.

Дополнительные статьи в энциклопедии: Physics

Buoyancy Archimedes Principle – Fluids

Выталкивающая сила, действующая на объект, может быть рассчитана по принципу Архимеда.

Когда объект погружен в жидкость, восходящая сила на нижнюю часть объекта больше, чем направленная вниз сила на верхнюю часть объекта.Результатом является чистая направленная вверх сила (выталкивающая сила ) на любой объект в любой жидкости. Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и будет плавать. Если подъемная сила меньше веса объекта, объект утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует в жидкости, независимо от того, плавает ли объект, тонет или остается в подвешенном состоянии.

Простой метод расчета плавучести основан на принципе Архимеда , который гласит, что подъемная сила, действующая на тело, погруженное в жидкость, равна весу жидкости, которую тело вытесняет.Другими словами, чтобы вычислить выталкивающую силу, действующую на объект, мы предполагаем, что погруженная часть объекта состоит из воды, а затем вычисляем вес этой воды. Принцип можно сформулировать в виде формулы:

F _объект = w _{жидкость}

Обоснование принципа Архимеда состоит в том, что выталкивающая сила, действующая на объект, зависит от давления, оказываемого жидкостью на его погруженную поверхность. Представьте, что мы заменяем погруженную часть объекта жидкостью, в которой он содержится.Сила плавучести на этом количестве жидкости должна быть такой же, как на исходном объекте. Однако мы также знаем, что сила плавучести, действующая на жидкость, должна быть равна ее весу, поскольку жидкость не тонет сама по себе. Следовательно, выталкивающая сила, действующая на исходный объект, равна весу «вытесненной жидкости». Принцип Архимеда применим для любой жидкости – не только для жидкостей (например, воды), но и для газов (например, воздуха).

Принцип Архимеда легче всего понять и применить в случае полностью погруженных в воду объектов.В общем, сила плавучести для полностью погруженного объекта рассчитывается по формуле:

F _B = V _ρg

где V – объем объекта,

ρ

– плотность жидкости, а

g

– ускорение свободного падения. Это непосредственно следует из принципа Архимеда и того факта, что объект полностью погружен (и поэтому объем вытесненной жидкости – это просто объем объекта).

Объект плавает, если выталкивающая сила, оказываемая на него жидкостью, уравновешивает его вес.Но принцип Архимеда гласит, что подъемная сила – это вес вытесняемой жидкости. Итак, для плавающего объекта на жидкости вес вытесненной жидкости равен весу объекта. Когда любая лодка вытесняет воду, равную ее собственному весу, она плывет. Это часто называют «принципом плавучести», когда плавающий объект вытесняет жидкость, равную его собственному весу. Каждый корабль, подводная лодка и дирижабль должны быть спроектированы так, чтобы перемещать жидкость, равную ее собственному весу.

Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, оставляя:

погруженная фракция = ρ _объект / ρ _{жидкость}

В связи с этим выражением следует отметить несколько моментов:

1) Обратите внимание, что здесь упоминается средняя плотность объекта. Это может быть намного меньше плотности материала, из которого сделан объект. Например, стальной корабль на самом деле в основном заполнен воздухом (подумайте о коридорах, грузовых трюмах и т. Д.), поэтому его средняя плотность находится между плотностью воздуха и стали. Чтобы быть более точным, средняя плотность определяется как общая масса объекта, деленная на его общий объем: ρ = m / V.

2) Эта формула имеет смысл, только если плотность объекта меньше плотности жидкости. В противном случае доля погруженного в воду становится больше единицы – признак того, что объект вообще не плавает, а тонет!

Практические вопросы

Академия Хана

Весы под водой

Гидротерапия и полное погружение в тело

Официальная подготовка MCAT (AAMC)

Карточки онлайн по физике Вопрос 15

Пакет вопросов по физике Вопрос 19

Physics Question Pack Отрывок 12, вопрос 72

Пакет вопросов по физике, вопрос 91

Образец теста C / P Раздел Вопрос 46

Ключевые точки

• Сила плавучести вызвана давлением жидкости, в которую погружен объект.

• Сила плавучести всегда направлена ​​вверх, потому что давление жидкости увеличивается с глубиной.

• Вы можете рассчитать выталкивающую силу либо напрямую, вычислив силу, действующую на каждую из поверхностей объекта, либо косвенно, определив вес вытесненной жидкости.

• Если объект полностью погружен в воду, объем вытесненной жидкости равен объему объекта.

• Сила плавучести воздушных шаров, дирижаблей и других объектов может быть рассчитана, если предположить, что они полностью погружены в воздух.

• Сила плавучести не зависит от формы объекта, только от его объема.

• Сила плавучести, испытываемая объектом, зависит от его формы.

• Доля объема погруженного объекта определяется отношением его средней плотности к плотности жидкости: объект ρ / _{жидкость} ρ.

• Объект плавает, если выталкивающая сила, прикладываемая к нему жидкостью, уравновешивает его вес.

Ключевые термины

Выталкивающая сила : восходящая сила, создаваемая жидкостью, которая противодействует весу погруженного объекта.

Принцип Архимеда : Выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, которую тело вытесняет.

Что такое принцип Архимеда

Принцип Архимеда

Пункты упоминания вы узнаете из этого видео

Что такое формула принципа Архимеда и что такое принцип Архимеда?

Определение принципа Архимеда простыми словами?

Концепция принципа Архимеда для класса 9

Что такое эксперимент с принципом Архимеда?

Что такое принцип Архимеда?

Как лучше всего применять принцип Архимеда?

Принцип Архимеда, названный в физическом законе плавучести, открытый и сформулированный древнегреческим математиком и изобретателем Архимедом Сиракузским, он заявляет, что любое тело, полностью или частично погруженное в жидкость (газ или жидкость) в состоянии покоя, подвергается действию восходящего или плавучая, сила, величина которой равна весу жидкости, вытесняемой телом.Он сказал, что объем вытесненной жидкости эквивалентен объему объекта, полностью погруженного в жидкость, или той части объема под поверхностью для объекта, частично погруженного в жидкость. Вес вытесненной части жидкости эквивалентен величине выталкивающей силы. Выталкивающая сила, действующая на тело, плавающее в жидкости или газе, также эквивалентна по величине весу плавающего объекта и противоположна по направлению; объект не поднимается и не опускается.

Определение: Принцип Архимеда гласит, что восходящая выталкивающая сила, действующая на тело, погруженное в жидкость, полностью или частично, равна весу жидкости, которую тело вытесняет. Принцип Архимеда является фундаментальным законом физики к механике жидкости. Это было .

Применение принципа Архимеда – Воздушный шар:
Воздушные шары поднимаются и плавают в воздухе потому, что подъемная сила воздушного шара меньше, чем у окружающего воздуха.Когда подъемная сила воздушного шара больше, он начинает снижаться. Это делается и контролируется изменением количества горячего воздуха в воздушном шаре.

Ссылка на YouTube – https://youtu.be/W4lLmWDV33M

Что такое принцип Архимеда?

Принцип Архимеда – это научный закон, объясняющий, почему некоторые объекты тонут, а некоторые плавают. Архимед был одним из величайших ученых мира. Он был математиком, изобретателем, инженером и астрономом, но, возможно, наиболее известен своим моментом Эврика , который привел к развитию принципа Архимеда .

Плавучесть и Архимед

Объекты плавают или тонут в зависимости от их плавучести .

Что такое плавучесть?

Плавучесть – это то, насколько хорошо объект плавает в воде или воздухе. Вы можете увидеть плавучесть в действии с нашим заданием « Спасите супергероя ».Или когда мы делаем раковину из лимона!

Кем был Архимед?

Архимед был греческим математиком и изобретателем. Однажды, забираясь в ванну, он заметил, как вода поднимается, когда его тело входит в воду.

Это наблюдение привело к принципу Архимеда .

Что такое принцип Архимеда?

Принцип Архимеда гласит, что на любой объект , погруженный в жидкость, действует восходящая или плавучая сила, равная весу жидкости, вытесняемой объектом .

Когда объект падает в воду (или человек залезает в ванну или бассейн), часть воды вытесняется. Это означает, что вода поднимается вверх, когда объект или человек отталкивают воду со своего пути.

В то же время плавучесть толкает вверх объект, изменяя его вес. Если вес объекта в воде больше, чем количество вытесненной воды, объект утонет!

Если вес объекта и количество вытесненной воды одинаковы или вес меньше, объект будет плавать.

В супергеройской активности выше плавучести фигуры увеличивается с лапшой в бассейне, которая увеличивает количество вытесняемой воды, но не увеличивает общий вес.

На диаграмме ниже выталкивающая сила (восходящая сила), действующая на плавающий объект, равна весу (направленной вниз силе) вытесняемой жидкости.

Почему важен принцип Архимеда?

Этот принцип используется, вероятно, чаще, чем вы думаете.Одно очевидное использование – убедиться, что корабли плавают в море. Обычно корабли изготавливаются из металла с полым корпусом, позволяющим равномерно перемещать воду. Корабли тонут в воде, поскольку вес вытесненной воды равен весу корабля!

Что такое плавучесть? Вычислительная гидродинамика

Плавучесть – это восходящая сила, оказываемая жидкостью на погруженный объект в поле силы тяжести. В жидкостях давление увеличивается с глубиной; следовательно, когда объект погружен в жидкость, давление, оказываемое на его нижнюю поверхность, выше, чем давление, оказываемое на его верхнюю поверхность.Эта разница в давлении приводит к чистой восходящей силе (силе плавучести), которая противостоит силе тяжести и эквивалентна весу жидкости, которая в противном случае занимала бы объем объекта, то есть вытесненной жидкости. Таким образом, если объект менее плотный, чем жидкость, сила плавучести будет выше, чем его вес, и объект будет плавать; наоборот, если объект плотнее жидкости, он утонет. Статический баланс возникает, когда вес погруженной части объекта равен весу вытесненной жидкости, т.е.е. плотности совпадают. Обратите внимание, что под плотностью объекта понимается усредненное значение, как простое соотношение между массой и объемом погруженной части. Наиболее распространенный случай – погружение твердого тела в жидкость (например, корабли в море), но это еще не все: поднимающийся пузырь (газ в жидкости), падающая капля (жидкость в газе) и аэростаты (теплый воздух в холодный). воздух) также являются примерами явлений, управляемых силами плавучести.

История

Физический принцип, выходящий за рамки плавучести, был впервые провозглашен Архимедом Сиракузским (рис. 1) в его работе «О плавучих телах», написанной в 3 веке до нашей эры.C. Его книга представляет собой собрание физических наблюдений и предположений о физике жидкостей, которые привели к апостериорному определению так называемого «принципа Архимеда», который гласит: «Любой объект, полностью или частично погруженный в жидкость, поддерживается силой, равной весу жидкости, вытесняемой объектом ».

Рисунок 1: Архимед

Следовательно, за столетия до разработки последовательного научного метода, Архимед указал на два основных фактора, влияющих на силы плавучести:

• плотность жидкости
• объем погруженного объекта

, произведение которого представляет собой «вес жидкости, вытесненной объектом».

Баланс сил и равновесие

Силы плавучести могут быть обнаружены в статическом равновесии любой области, погруженной в жидкость, но становятся очевидными, когда эта область имеет другие характеристики (например, другую фазу или ту же фазу, но другую плотность), чем окружающая жидкость. Таким образом, физическая основа плавучести может быть получена из статического равновесия погруженного объема следующим образом:

Дидактическое дело

Рассмотрим прямоугольный объем, погруженный в жидкость, как показано на рисунке 2, размеры которого составляют \ (L_x \) в горизонтальном направлении и \ (L_y \) в вертикальном направлении.Все силы, действующие на объект, можно вычислить как интегрирование по граничной поверхности гидростатического давления, как показано:

$$ p = \ rho g h \ tag {1} $$

где \ (ρ \) – плотность жидкости, \ (g \) – ускорение свободного падения, а \ (h \) – глубина относительно свободной поверхности.

Рисунок 2: Статический баланс погруженного объема в жидкость со сбалансированными силами в горизонтальном направлении и несбалансированными в вертикальном направлении.

Горизонтальное равновесие вычисляется как сумма сил, действующих на левую грань прямоугольника, и сил, действующих на правую грань:

$$ F_x = \ int_ {h_b} ^ {h_t} p \, dh- \ int_ {h_b} ^ {h_t} p \, dh = \ int_ {h_b} ^ {h_t} \ rho gh \, dh- \ int_ {h_b} ^ {h_t} \ rho gh \, dh \ tag {2} $$

, где все переменные считаются независимыми от координаты \ (x \).Следовательно, мы получаем, что горизонтальное равновесие достигается естественным образом (т.е. \ (F_x≡ 0 \)), поэтому мы не видим сил плавучести. Ту же процедуру можно проделать и в вертикальном направлении:

$$ F_h = F_ {плавучесть} – W = – \ int_ {L_x} p_t \, dx + \ int_ {L_x} p_b \, dx – W \ tag {3} $$

где \ (L_x \) – горизонтальный размер прямоугольника, \ (W \) – вес объекта, а \ (p_t \) и \ (p_b \) – давление вверху и внизу прямоугольник соответственно. Уравнение (3) можно представить в виде:

$$ F_h = – \ int_ {L_x} \ rho g h_t \, dx + \ int_ {L_x} \ rho g h_b \, dx – g \ rho_ {объект} V_ {объект} $$

$$ = – \ rho g h_t L_x + \ rho h_b L_x – g \ rho_ {объект} L_x L_y = \ rho L_x (h_b-h_t) -L_x L_y g \ rho_ {объект} $$

$$ = \ rho g L_x L_y – L_x L_y g \ rho_ {object} = gL_x L_y (\ rho – \ rho_ {object}) \ tag {4} $$

Из уравнения (4) мы можем вывести все основные характеристики явлений, определяемых плавучестью:

• Сила плавучести зависит от веса движущейся жидкости, то есть от плотности самой жидкости (\ (ρ \)) и объема погруженной части объекта (\ (L_xL_y \) в нашем случае).
• Сила плавучести противоположна весу.
• Объект будет плавать (\ (F_h> 0 \)), если он менее плотен, чем окружающая жидкость, утонет (\ (F_h <0 \)), если он более плотный, и останется в идеальном равновесии (\ (F_h = 0 \)), когда он имеет ту же плотность, что и окружающая жидкость.

Общий случай

Процедура для конечного 2D-квадратного объекта может быть расширена до общего бесконечно малого объема и может использоваться для любой формы интерфейса и задачи механики жидкости.Равновесие для бесконечно малой части континуума задается дифференциальным уравнением:

$$ f + div (\ sigma) = 0 \ tag {5} $$

где \ (f \) – плотность внешней телесной силы, а \ (σ \) – тензор напряжений Коши. В нашем случае единственной внешней объемной силой является сила тяжести (вес), таким образом:

$$ f = \ rho g \ tag {6} $$

Чтобы вычислить полную силу плавучести, нам нужно суммировать все поверхностные силы, оказываемые жидкостью на границе раздела с погруженным объемом.{n} \, dS = \ int_S n \ cdot \ sigma \, dS \ tag {8} $$

Применяя теорему Гаусса, поверхностный интеграл можно преобразовать в объемный интеграл:

$$ F_ {плавучесть} = \ int_V div (\ sigma) \, dV \ tag {9} $$

Таким образом, подставляя уравнения (5) и (6) в уравнение (9), мы получаем общее значение выталкивающих сил:

$$ F_ {плавучесть} = – \ int_V f \, dV = – \ rho g \ int_V \, dV \ tag {10} $$

где \ (V \) – объем погруженной области, а знак «\ (- \)» означает, что она противостоит силе тяжести.Заметим, что \ (ρ \) и \ (g \) для простоты считаются однородными в жидкости и поэтому исключены из интеграла.

Уравнение (10) снова устанавливает те же принципы, которые предложил Архимед и которые были получены в дидактическом случае в уравнении (4).

Важно отметить, что плавучести не всегда достаточно для анализа статического или динамического баланса объема, погруженного в жидкость, и другие переменные могут рассматриваться для точного прогнозирования потока.Например, поверхностное натяжение – это дополнительная сила, приложенная к границе раздела жидкость – объект, которая влияет как на динамику (например, тонущий объект), так и на статику (например, затонувший объект) проблемы. На динамику плавучести также сильно влияют вязкость жидкости и турбулентность потока. Наконец, основные величины могут быть непостоянными во времени и однородными в пространстве: поверхность раздела жидкость – объект может изменяться (например, пузырьки деформируются при подъеме в воде), а также плотность (например, из-за изменения температуры) и глубина погружения. объем (е.грамм. плавающий объект, который движется вне жидкости, уменьшая погруженный объем). По всем этим причинам силы плавучести обычно рассматриваются как только часть задачи гидродинамики, описываемой уравнениями Навье-Стокса. В уравнениях Навье-Стокса плавучесть естественным образом рассматривается через неоднородность плотности в жидкой области. Однако реализация этого случая обычно не является простой. Следовательно, во многих случаях сила плавучести моделируется как внешняя объемная сила, в то время как плотность считается постоянной для инерционных расчетов.Это приближение называется «приближением Буссинеска» и обычно используется для моделирования явлений естественной конвекции, в которых изменение плотности происходит из-за изменения температуры.

Применения плавучести

Как указывалось ранее, плавучесть не должна относиться только к случаям твердого тела в жидкости (например, судов в воде). По крайней мере, две большие категории приложений могут быть напрямую связаны с эффектами плавучести: естественная конвекция и многофазные потоки. Естественная конвекция основана на том факте, что материалы обычно становятся менее плотными с повышением температуры (например, см. Рисунок 3).

Рисунок 3: Пример изменения плотности воздуха в зависимости от температуры. Более теплые жидкости, как правило, имеют относительно меньшую плотность и, следовательно, имеют тенденцию всплывать.

Это означает, что теплая жидкость будет «плавать» при погружении в область той же жидкости, но более холодной. В этом случае мы будем говорить не о «плавании» или «опускании», а о восходящих потоках горячей жидкости и нисходящих потоках холодной жидкости. Это явление обычно сочетается с термическим анализом и является основой многих приложений, таких как метеорология, стальное литье и отопление / охлаждение.Естественная конвекция часто усиливается принудительным наложением потока для достижения определенных условий. В этом случае мы говорим о «принудительной конвекции», при которой силы плавучести все еще присутствуют, но менее доминирующие. На рис. 4 показана естественная конвекция, вызванная кондиционированием воздуха в помещении кинотеатра. AC вдувает холодный воздух в верхнюю часть помещения, который течет вниз из-за восходящей выталкивающей силы теплого воздуха внизу помещения. Таким образом, холодный воздух образует нисходящие потоки, а схема рециркуляции показана на рисунке ниже.

Рис. 4. Принудительная конвекция в кинотеатре с рециркуляцией воздушного потока.

В многофазных потоках изменение плотности происходит не из-за разницы температур (как при естественной конвекции), а из-за состояния вещества. Если мы ограничимся механикой жидкости, две наиболее распространенные возможности – это жидкость в газе и газ в жидкости. В обоих случаях фаза с более высокой плотностью будет двигаться вниз; На рис. 5 показан случай поднимающегося пузыря. Поскольку пузырек газа легче окружающей жидкости, силы плавучести превышают его вес; эти неуравновешенные силы превращаются в силы инерции, что приводит к динамической реакции пузыря.Также интересно отметить, что пузырь не только перемещается, но и деформируется. Это связано с тем, что плавучесть – не единственная сила, действующая на пузырь – силы поверхностного натяжения и вязкости также влияют на поток.

Рисунок 5: Поднимающийся пузырь в жидкой области деформируется под действием других сил, таких как вязкость и поверхностное натяжение.

Плавучесть с SimScale

С SimScale вы можете моделировать и визуализировать эффекты, на которые влияет плавучесть. Пример – это имитация ниже, где вы можете увидеть тепло, излучаемое радиатором в комнате.Теплый воздух поднимается вверх по стене до потолка и распределяется по квартире.

Анимация 1: Теплый воздух из радиатора поднимается до потолка. Эти динамические температурные контуры помогают определить размеры квартиры с учетом распределения тепла и эффективности радиатора.

Последнее обновление: 2 сентября 2021 г.

Эта статья решила вашу проблему?

Как мы можем сделать лучше?

Мы ценим и ценим ваши отзывы.

Отправьте свой отзыв

Что дальше

Что такое аэродинамика? .