Определение узла электрической цепи: Узел электрической цепи

Законы Кирхгофа и их применение

Для расчета разветвленной сложной электрической цепи существенное значение имеет число ветвей и узлов.
Ветвью электрической цепи и ее схемы называется участок, состоящий только из последовательно включенных источников ЭДС и приемников с одним и тем же током. Узлом цепи и схемы называется место или точка соединения трех и более ветвей (узлом иногда называют и точку соединения двух ветвей).
При обходе по соединенным в узлах ветвям можно получить замкнутый контур электрической цепи; каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза.

На рис. 1.13 в качестве примера показана схема электрической цепи с пятью узлами и девятью ветвями. В частных случаях встречаются ветви только с резистивными элементами без источников ЭДС (ветвь 1 — у) и с сопротивлениями, практически равными нулю (ветвь 2 — р). Так как напряжение между выводами ветви 2 — р равно нулю (сопротивление равно нулю), то потенциалы точек 2 и р одинаковы и оба узла можно объединить в один.
Режим электрической цепи произвольной конфигурации полностью определяется первым и вторым законами Кирхгофа.
Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна пулю:

В этом уравнении одинаковые знаки должны быть взяты для токов, имеющих одинаковые положительные направления относительно узловой точки. В дальнейшем будем в уравнениях, составленных по первому закону Кирхгофа, записывать токи, направленные к узлу, с отрицательными знаками, а направленные от узла, — с положительными.
Если к данному узлу присоединен источник тока, то ток этого источника также должен быть учтен. В дальнейшем будет показано, что в ряде случаев целесообразно писать в одной части равенства (1.19а) алгебраическую сумму токов в ветвях, а в другой части алгебраическую сумму токов, обусловленных источниками токов:

где I — ток одной из ветвей, присоединенной к рассматриваемому узлу, a J — ток одного из источников тока, присоединенного к тому же самому узлу; этот ток входит в (1. 196) с положительным знаком, если направлен к узлу, и с отрицательным, если направлен от узла.
Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом контуре алгебраическая сумма напряжений на всех элементах и участках цепи, входящих в этот контур, равна нулю:

при этом положительные направления для напряжений на элементах и участках выбираются произвольно; в уравнении (1.20а) положительные знаки принимаются для тех напряжений, положительные направления которых совпадают с произвольно выбранным направлением обхода контура.

Часто применяется другая формулировка второго закона Кирхгофа: в любом замкнутом контуре алгебраическая сумма напряжений на всех участках с сопротивлениями, входящими в этот контур, равна алгебраической сумме ЭДС:

В этом уравнении положительные знаки принимаются для токов и ЭДС, положительные направления которых совпадают с произвольно выбранным направлением обхода рассматриваемого контура.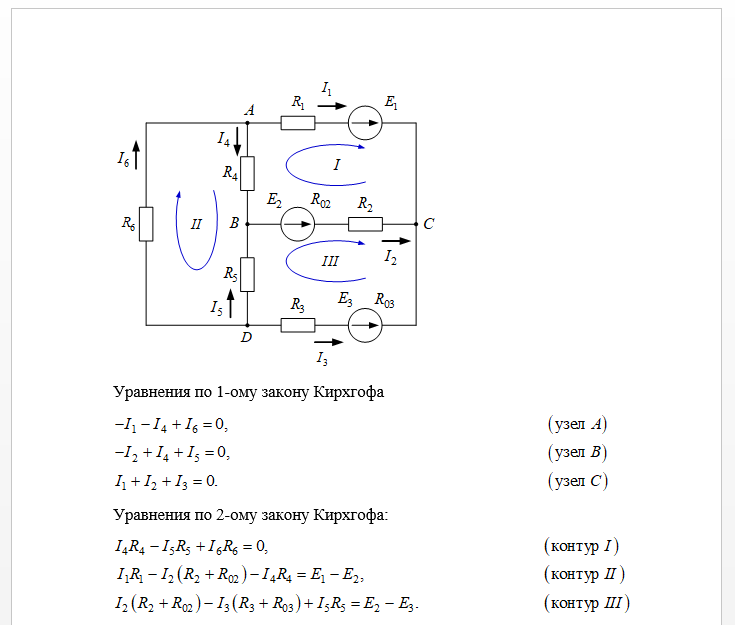
В теории электрических цепей решаются задачи двух типов. К первому типу относятся задачи анализа электрических цепей, когда, например, известны конфигурация и элементы цепи, а требуется определить токи, напряжения и мощности тех или иных участков. Ко второму типу относятся обратные задачи, в которых, например, заданы токи и напряжения на некоторых участках, а требуется найти конфигурацию цепи и выбрать ее элементы. Такие задачи называются задачами синтеза электрических цепей. Отметим, что решение задач анализа намного проще решения задач синтеза.
В практической электротехнике довольно часто встречаются задачи анализа. Кроме того, для овладения приемами синтеза цепей необходимо предварительно изучить методы их анализа, которые преимущественно и будут в дальнейшем рассматриваться.
Задачи анализа могут быть решены при помощи законов Кирхгофа. Если известны параметры всех элементов цепи и ее конфигурация, а требуется определить токи, то при составлении уравнений по законам Кирхгофа рекомендуется придерживаться такой последовательности: сначала выбрать произвольные положительные направления токов во всех ветвях электрической цепи, затем составить уравнения для узлов на основании первого закона Кирхгофа и, наконец, составить уравнения для контуров на основании второго закона Кирхгофа.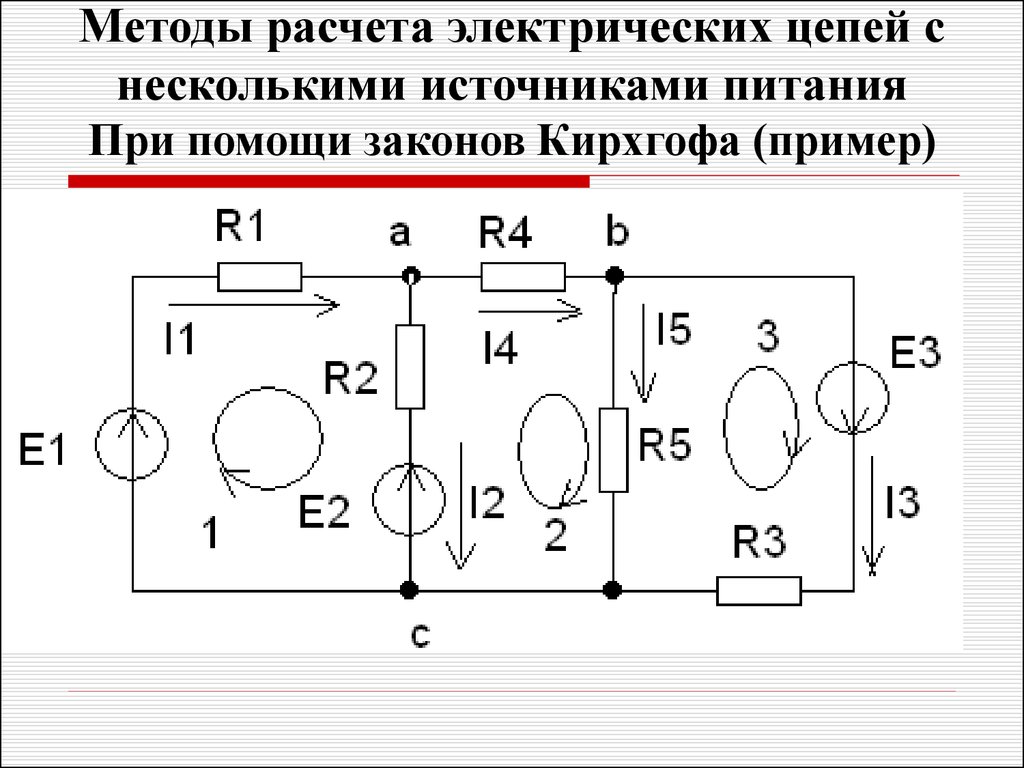
Пусть электрическая цепь содержит В ветвей и У узлов. Покажем, что на основании первого и второго законов Кирхгофа можно составить соответственно У — 1 и В — У + 1 взаимно независимых уравнений, что в сумме дает необходимое и достаточное число уравнений для определения В токов (во всех ветвях).
На основании первого закона Кирхгофа для У узлов (рис. 1.13) можно написать У уравнений:

Так как любая ветвь связывает между собой только два узла, то ток каждой ветви должен обязательно войти в эти уравнения 2 раза, причем I₁₂=-I₂₁; I₁₃=-I₃₁ и т.д.
Следовательно, сумма левых частей всех У уравнений дает тождественно нуль. Иначе говоря, одно из У уравнений может быть получено как следствие остальных У — 1 уравнений или число взаимно независимых уравнений, составленных на основании первого закона Кирхгофа, равно У — 1, т. е. на единицу меньше числа узлов. Например, в случае цепи по рис. 1.14,о с четырьмя узлами

Добавим к этим У — 1 = 3 уравнениям уравнение

Суммируя четыре уравнения, получаем тождество 0 = 0; следовательно, из этих четырех уравнений любые три независимые, например первые три (1. 21а).
Так как беспредельное накопление электрических зарядов не может происходить как в отдельных узлах электрической цепи, так и в любых ее частях, ограниченных замкнутыми поверхностями, то первый закон Кирхгофа можно применить не только к какому-либо узлу, но и к любой замкнутой поверхности — сечению.

Например, для поверхности S (рис. 1.14,а), как бы рассекающей электрическую схему на две части, справедливо уравнение , что можно также получить из уравнений (1.21) для узлов 3 и 4.
Чтобы установить число взаимно независимых уравнений, вытекающих из второго закона Кирхгофа, напишем для всех В ветвей схемы (рис. 1.13) В уравнений на основании закона Ома (1.11а):

где

— сопротивление ветви, соединяющей узлы р и у; Е_ру — суммарная ЭДС, действующая в ветви р — у в направлении от р к у; — потенциалы узлов р и у.
В этих уравнениях суммарное число неизвестных токов В ветвей и потенциалов У узлов равняется В + У.
Не изменяя условий задачи, можно принять потенциал одного из узлов равным любому значению, в частности нулю. Если теперь из системы В уравнений (1.22) исключить оставшиеся неизвестными У — 1 потенциалов, то число уравнений уменьшится до В — (У — 1). Но исключение потенциалов из уравнений (1.22) приводит к уравнениям, связывающим ЭДС источников с напряжениями на резистивных элементах, т. е. к уравнениям, составленным на основании второго закона Кирхгофа.
Таким образом, число независимых уравнений, которые можно составить на основании второго закона Кирхгофа, равно В — (У- 1).
В качестве примера напишем уравнения, связывающие потенциалы узлов с токами и ЭДС для схемы рис. 1.14, а по ( 1.126):

Сложив третье и четвертое уравнения и вычтя полученную сумму из первого, получим

Если применим второй закон Кирхгофа (1.206) к контуру 1-4-2-1 (при обходе вдоль контура по направлению движения часовой стрелки), то получим это же уравнение.
Аналогичным путем можно получить уравнения для других контуров:
для контура 1-3-2-1

для котуpa 2-4-3-2

Совместное решение любых пяти уравнений (1. 21), (1.23) и (1.24) дает значения токов во всех ветвях электрической цепи, показанной на рис. 1.14, а. Если и результате решения этих уравнений получится отрицательное значение для какого-либо тока, то это значит, что действительное направление противоположно принятому за положительное.
При записи уравнений по второму закону Кирхгофа следует обращать особое внимание на то, чтобы составленные уравнения были взаимно независимыми. Контуры необходимо выбрать гак. чтобы в них вошли все ветви схемы, а в каждый из контуров — возможно меньшее число ветвей. Контуры взаимно независимы, если каждый последующий контур, для которого составляется уравнение, имеет не меньше одной новой ветви и не получается из контуров, для которых уже написаны уравнения, путем удаления из этих контуров общих ветвей. Например, контур 1-3-4-2-1 (рис. 1.14, а) можно получить из контуров 1-3-4-1 и 1-4-2-1 путем удаления ветви 1-4. Поэтому уравнение для контура 1-3-4-2-1 является следствием уравнений (1.23), (1.24а) и получается путем их суммирования. Далее будет дано наиболее общее правило выбора контуров, обеспечивающих получение независимых уравнений.
Вторым законом Кирхгофа можно пользоваться для определения напряжения между двумя произвольными точками схемы. В этом случае необходимо ввести в левую часть уравнений (1.20) искомое напряжение вдоль пути, как бы дополняющего незамкнутый контур до замкнутого. Например, для определения напряжения U₅₂ (рис. 1.14, а) можно написать уравнение для контура 2-1-5-2

или для контура 5-4-2-5

откуда легко найти искомое напряжение.
Пример 1.2.
Пользуясь законами Кирхгофа, написать два выражения для тока I0 в ветви с гальванометром (рис. 1.15), приняв известным в одном случае ток I, а в другом напряжение U.
Решение.
На основании законов Кирхгофа напишем для заданной схемы с шестью неизвестными токами уравнения:

Решив совместно эти уравнения, получим выражения для тока I0 при заданном напряжении U

и при заданном токе I

Для полной характеристики электрического состояния цепи надо знать не только токи и напряжения, но также мощности источников и приемников энергии.
В соответствии с законом сохранения энергии развиваемая всеми источниками мощность равна суммарной мощности приемников и мощности потерь в источниках (из-за внутренних сопротивлений)

В левой части (1.25) суммы алгебраические. Это значит, что если при заданных направлениях действия источника ЭДС (см. рис. 1.7) или тока (см. рис. 1.8) для тока I в источнике ЭДС или напряжения U₁₂ на выводах источника тока получится отрицательное численное значение, то этот источник в действительности не разовьет мощность, а получит ее от других источников. Соответствующее слагаемое в левой части (1.25) получится со знаком минус. Если требуется найти необходимую мощность источников питания цепи, то такие слагаемые следует записать с обратным знаком в правой части (1.25).

Первый и второй законы Кирхгофа

В сложных электрических цепях, то есть где имеется несколько разнообразных ответвлений и несколько источников ЭДС имеет место и сложное распределение токов. Однако при известных величинах всех ЭДС и сопротивлений резистивных элементов в цепи мы можем вычистить значения этих токов и их направление в любом контуре цепи с помощью первого и второго закона Кирхгофа. Суть законов Кирхгофа я довольно кратко изложил в своем учебнике по электронике, на страницах сайта http://www.sxemotehnika.ru.

 

Пример сложной электрической цепи вы можете посмотреть на рисунке 1.

Рисунок 1. Сложная электрическая цепь.

Иногда законы Кирхгофа называют правилами Кирхгофа, особенно в старой литературе.

Итак, для начала напомню все-таки суть первого и второго закона Кирхгофа, а далее рассмотрим примеры расчета токов, напряжений в электрических цепях, с практическими примерами и ответами на вопросы, которые задавались мне в комментариях на сайте.

Первый закон Кирхгофа

Формулировка №1: Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.

Формулировка №2: Алгебраическая сумма всех токов в узле равна нулю.

Поясню первый закон Кирхгофа на примере рисунка 2.

Рисунок 2. Узел электрической цепи.

Здесь ток I₁– ток, втекающий в узел , а токи I₂ и I₃ — токи, вытекающие из узла.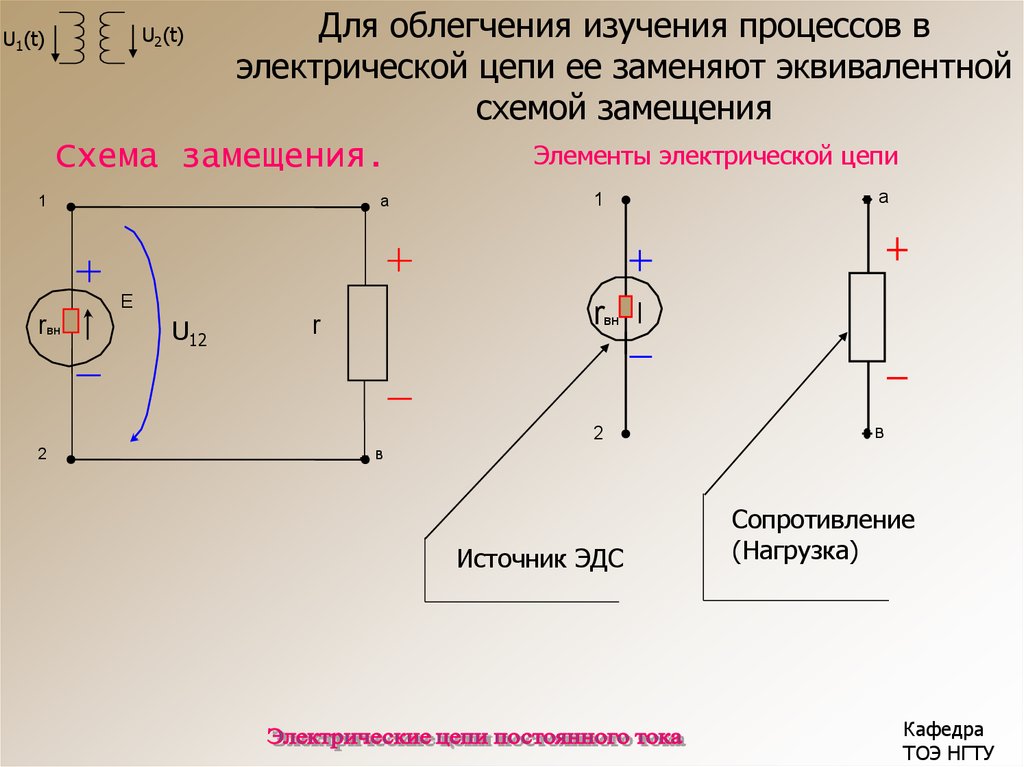 Тогда применяя формулировку №1, можно записать:

I₁ = I₂ + I₃  (1)

Что бы подтвердить справедливость формулировки №2, перенесем токи I₂ и I₃ в левую часть выражения (1), тем самым получим:

I₁ – I₂ – I₃ = 0   (2)

Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.

Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «-» (например как получилось в выражении (2)).

Можно посмотреть отдельный видеоурок по первому закону Кирхофа в разделе ВИДЕОУРОКИ.

Второй закон Кирхгофа.

Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.

Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму:

1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).

2. Произвольно выбираем направление токов через элементы цепи.

3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:

– ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-».

– напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».

Например, рассмотрим цепь, представленную на рисунке 3, и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке, и выбрав направление токов через резисторы, как показано на рисунке.

Рисунок 3. Электрическая цепь, для пояснения второго закона Кирхгофа.

E₁– Е₂ = -UR₁ – UR₂ или E₁ = Е₂ – UR₁ – UR₂   (3)

Предлагаю посмотреть отдельный видеоурок по второму закону Кирхогфа (теория).

Расчеты электрических цепей с помощью законов Кирхгофа.

Теперь давайте рассмотрим вариант сложной цепи, и я вам расскажу, как на практике применять законы Кирхгофа.

Итак, на рисунке 4 имеется сложная цепь с двумя источниками ЭДС величиной E₁=12 в и E₂=5 в , с внутренним сопротивлением источников r₁=r₂=0,1 Ом, работающих на общую нагрузку R = 2 Ома. Как же будут распределены токи в этой цепи, и какие они имеют значения, нам предстоит выяснить.

Рисунок 4. Пример расчета сложной электрической цепи.

Теперь согласно первому закону Кирхгофа для узла А составляем такое выражение:

I = I₁ + I₂,

так как I₁ и I₂ втекают в узел А, а ток I вытекает из него.

Используя второй закон Кирхгофа, запишем еще два выражения для внешнего контура и внутреннего левого контура, выбрав направление обхода по часовой стрелке.

Для внешнего контура:

E₁-E₂ = Ur₁ – Ur₂ или E₁-E₂ = I₁*r₁ – I₂*r₂

Для внутреннего левого контура:

E₁ = Ur₁ + UR или E₁ = I₁*r₁ + I*R

Итак, у нас получилась система их трех уравнений с тремя неизвестными:

I = I₁ + I₂;

E₁-E₂ = I₁*r₁ – I₂*r₂;

E₁ = I₁*r₁ + I*R.

Теперь подставим в эту систему известные нам величины напряжений и сопротивлений:

I = I₁ + I₂;

7 = 0,1I₁ – 0,1I₂;

12 = 0,1I₁ +2I.

Далее из первого и второго уравнения выразим ток I₂

I₂=I – I₁;

I₂ = I₁ – 70;

12 = 0,1I₁ + 2I.

Следующим шагом приравняем первое и второе уравнение и получим систему из двух уравнений:

I – I₁= I₁ – 70;

12 = 0,1I₁ + 2I.

Выражаем из первого уравнения значение I

I = 2I₁– 70;

И подставляем его значение во второе уравнение

12 = 0,1I₁ + 2(2I₁ – 70).

Решаем полученное уравнение

12 = 0,1I₁ + 4I₁ – 140.

12 + 140= 4,1I₁

I₁=152/4,1

I₁=37,073 (А)

Теперь в выражение I = 2I₁– 70 подставим значение

I₁=37,073 (А) и получим:

I = 2*37,073 – 70 = 4,146 А

Ну, а согласно первому закона Кирхгофа ток I₂=I – I₁

I₂=4,146 – 37,073 = -32,927

Знак «минус» для тока I₂ означает, то что мы не правильно выбрали направление тока, то есть в нашем случае ток I₂ вытекает из узла А.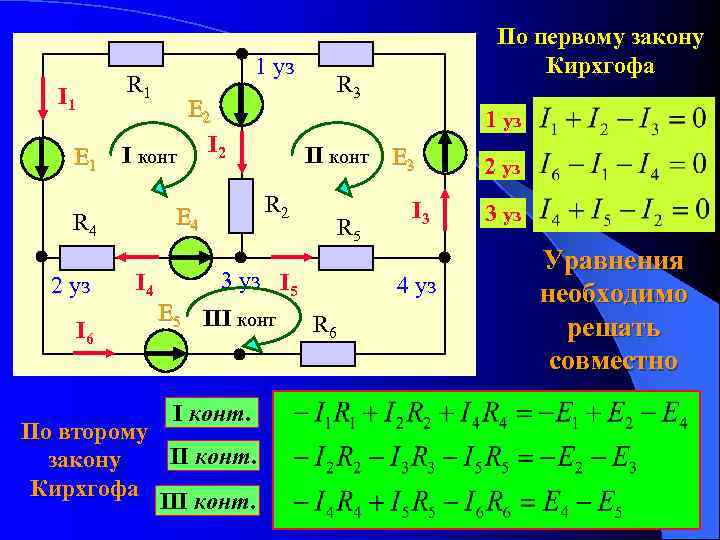

Теперь полученные данные можно проверить на практике или смоделировать данную схему например в программе Multisim.

Скриншот моделирования схемы для проверки законов Кирхгофа вы можете посмотреть на рисунке 5.

 Рисунок 5. Сравнение результатов расчета и моделирования работы цепи.

Для закрепления результатата предлагаю посмотреть подготовленное мной видео:

7.2: Узловой анализ — Инженерные тексты LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

25134

• Джеймс М. Фиоре
• Муниципальный колледж Mohawk Valley

Узловой анализ — это метод, который можно применять практически к любой цепи. В общем случае его можно считать универсальным методом решения, поскольку нет практических схемных конфигураций, с которыми он не может справиться. Узловой анализ основан на применении закона тока Кирхгофа для создания ряда узловых уравнений, которые можно решить для узловых напряжений. Эти уравнения основаны на законе Ома и будут иметь вид \(I = V/R\) или, в более общем случае, \(I = (1/RX) \cdot VA + (1/RY) \cdot VB \dots \) Как только напряжения в узлах получены, нахождение любых токов ветвей или мощностей компонентов становится почти тривиальной задачей. Мы рассмотрим два варианта; общая версия, которую можно использовать как с источниками напряжения, так и с источниками тока, и вторая, несколько более быстрая версия, которую можно использовать со схемами, управляемыми только источниками тока.

Общий метод

Рассмотрим схему, показанную на рис. 7.2.1. . Начнем с маркировки узлов соединения и назначения текущих направлений. Нас особенно интересуют токовые соединения, то есть места, где токи могут объединяться или разделяться.

Они также известны как узлы суммирования и обведены на рисунке зеленым цветом. Текущие направления выбираются произвольно и могут противоречить действительности. Это не проблема. Если мы назначим неправильные направления, результирующие направления в конечном итоге будут отображаться в обратном порядке, но вычисленные напряжения узлов будут в порядке.

Рисунок 7.2.1 : Базовая схема источника двойного напряжения с заданными токами и узлами.

В качестве эталона выбран один узел. Это точка, относительно которой будут измеряться напряжения всех других узлов. Обычно эталонный узел заземляется, хотя это и не обязательно.

Теперь запишем текущее уравнение суммирования для каждого узла суммирования, кроме опорного узла. В этой цепи есть только один узел, где объединяются токи (кроме земли), и это узел \(b\). Точки \(a\) и \(c\) — это места, где компоненты соединяются, но они не являются узлами суммирования, поэтому их пока можно игнорировать. Используя KCL на узле \(b\), мы можем сказать:

\[I_1 + I_2 = I_3 \номер \]

Далее мы описываем эти токи в терминах узловых напряжений и связанных с ними компонентов по закону Ома. Например, \(I_3\) – это напряжение в узле \(b\), деленное на \(R_3\), а \(I_1\) – напряжение на \(R_1\), деленное на \(R_1\). Это напряжение равно \(V_a − V_b\). Следовательно,

\[\frac{V_a −V_b}{R_1} + \frac{V_c −V_b}{R_2} = \frac{V_b}{R_3} \nonumber \]

Заметим, что \(\frac{V_a = E_1}\) и \(\frac{V_c = E_2}\), с помощью небольшой алгебры это можно свести к ряду произведений проводимостей и напряжений:

\[\left( \frac{1}{R_1} \right) E_1 + \left( \frac{1}{R_2} \right) E_2 = \left( \frac{1}{R_1} + \frac {1}{R_2} + \frac{1}{R_3} \right) V_b \nonumber \]

Все величины известны, кроме \(V_b\), поэтому ее легко найти, приложив немного больше алгебры. Как мы увидим, такой формат произведения проводимости на напряжение оказывается удобным способом записи этих уравнений. Также обратите внимание, что первые два члена слева сводятся к фиксированным текущим значениям. Если бы узлов было больше, то и уравнений было бы больше, по одному на каждый узел.

Рисунок 7. 2.2 : Базовая схема двойного источника тока.

Для источников тока возможен более прямой подход. Рассмотрим схему на рис. 7.2.2. . Мы начинаем, как и раньше, определяя узлы и маркируя токи. Это показано на рисунке 7.2.3. . Затем мы записываем текущие уравнения суммирования в каждом узле (кроме земли). Токи, входящие в узел, считаем положительными, а выходящие — отрицательными.

Рисунок 7.2.3 : Базовая схема двойного источника тока с заданными токами и узлами.

\[\text{Узел } a: I_1 = I_3 + I_4 \nonumber \]

\[\text{Узел } b: I_3 = I_2 + I_5, \text{ и перестановка в терминах фиксированного источника,} \nonumber \]

\[\text{Узел } b: −I_2 = −I_3 + I_5 \nonumber \]

Затем токи описываются их эквивалентами закона Ома:

\[\text{Узел } a: I_1 = \frac{V_a −V_b}{R_3} + \frac{V_a}{R_1} \nonumber \]

\[\text{Узел} b: −I_2 = − \frac{V_a −V_b}{R_3} +\frac{V_b}{R_2} \номер\]

Расширение и сбор терминов дает:

\[\text{Узел} a: I_1 = \left( \frac{1}{R_1} + \frac{1}{R_3} \right) V_a − \left( \frac {1}{R_3} \right) V_b \nonumber \]

\[\text{Узел } b: −I_2 =− \left( \frac{1}{R_3} \right) V_a + \left( \frac {1}{R_3} + \frac{1}{R_2} \right) V_b \nonumber \]

Поскольку номиналы резисторов и токи известны, для определения напряжений в узлах можно использовать методы совместного решения уравнений. Опять же, будет столько уравнений, сколько узловых напряжений. Очень важно, чтобы члены «выстроились» при выписывании итоговой системы уравнений. То есть должен быть столбец для терминов \(V_a\), столбец для терминов \(V_b\) и так далее. Их не следует выписывать в случайном порядке. Этот формат значительно облегчит ввод коэффициентов в калькулятор или решение вручную.

Пример 7.2.1

Определить \(V_b\) по схеме рис. 7.2.4 .

Рисунок 7.2.4 : Схема для примера 7.2.1 .

Эта цепь имеет два узла суммирования тока, землю и узел \(b\). Предположим, что токи от двух источников текут в узел \(b\), а выходящий ток течет вниз через резистор 5 кОм\(\Омега\). Будет удобно, если мы найдем эквиваленты проводимости резисторов, прежде чем продолжить. Взяв обратные величины, находим: 1к\(\Омега\) = 1 мСм, 4к\(\Омега\) = 0,250 мСм и 5к\(\Омега\) = 0,2 мСм. Через KCL мы можем сказать:

\[I_{1k} + I_{4k} = I_{5k} ​​\номер \]

Замена этих токов их эквивалентами по закону Ома дает,

\[\frac{15 V −V_b}{1k \Omega } + \frac{6V −V_b}{4 k \Omega } = \frac{V_b}{5 k \Omega } \nonumber \]

условия сбора,

\[15 мА+1,5 мА = \left( \frac{1}{1k \Omega } + \frac{1}{4k \Omega } + \frac{1}{5k \Omega } \right) V_b \nonumber \ ]

и решение для \(V_b\),

\[V_b = \frac{16,5 мА}{1 мСм +0,25 мСм +0,2 мСм} \номер\]

\[V_b = 11,379 \text{ вольт} \номер\]

Поскольку \(V_b\) выше, чем у источника 6 вольт, наше предполагаемое направление тока для резистора 4 кОм\( \Omega \) было неправильным; мы предположили, что это справа налево, но на самом деле это слева направо, течет от 11,379 вольт до 6 вольт.

Как видите, это не вызвало затруднений.

Для сравнения, эта схема была решена в главе 6 с использованием преобразования источника, а также с использованием суперпозиции.

Метод проверки

Систему уравнений можно получить непосредственно путем проверки, если в цепи нет источников напряжения. Для проверяемого узла суммируйте все источники тока, подключенные к нему, чтобы получить постоянную тока. Термин проводимости для этого узла будет суммой всех проводимостей, связанных с этим узлом. Для проводимостей других узлов определите проводимости между проверяемым узлом и этими другими узлами. Все эти термины будут отрицательными. В качестве перекрестной проверки полученная система уравнений должна обладать диагональной симметрией, то есть, если провести диагональ из левого верхнего угла в правый нижний через пары проводимость-напряжение, то коэффициенты, найденные выше диагонали, должны совпадать с найденными ниже диагонали, когда мы движемся перпендикулярно диагонали.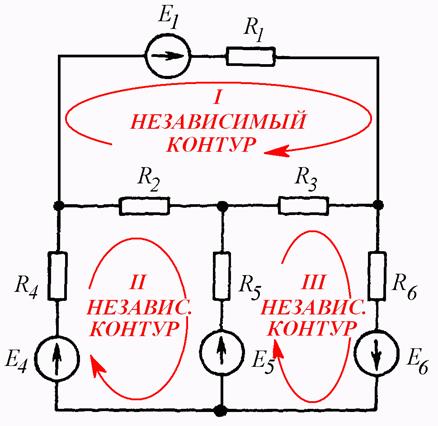

Это показано на рисунке 7.2.5. . Диагональную симметрию можно увидеть в примере 7.2.1. отметив совпадающие коэффициенты «\(−1/R_3\)» в последней паре уравнений. В качестве примера метода проверки сосредоточьтесь на узле \(a\) на рисунке 7.2.2. , находим фиксированный источник тока \(I_1\), питающий его (входящий, следовательно, положительный). Проводимости, непосредственно связанные с узлом \(a\), равны \(1/R_1\) и \(1/R_3\), что дает коэффициент для \(V_a\). Единственная общая проводимость между узлами \(a\) и \(b\) – это \(1/R_3\), что дает коэффициент \(V_b\).

Рисунок 7.2.5 : диагональная симметрия.

Кратко описан метод проверки:

1. Убедитесь, что в цепи используются только источники тока с резисторами, а не источники напряжения. Если существуют источники напряжения, перед продолжением их необходимо преобразовать в источники тока.

2. Найдите все текущие узлы суммирования и пронумеруйте их. Также определитесь с эталонным узлом (обычно земля).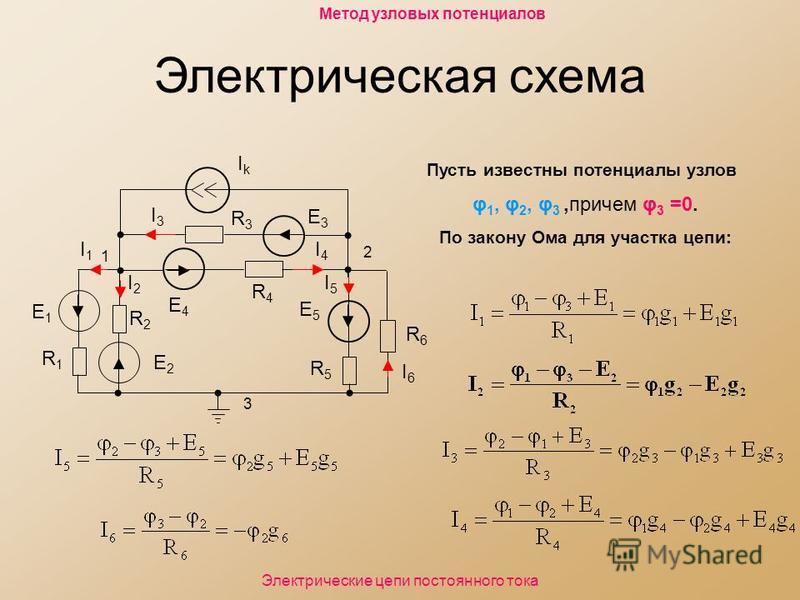

3. Чтобы сгенерировать уравнение, найдите первый узел. Это интересующий узел, и следующие несколько шагов будут связаны с ним.

4. Суммируйте источники тока, питающие интересующий узел. Вход считается положительным, а выход считается отрицательным. Сумма ставится по одну сторону от знака равенства.

5. Затем найдите все резисторы, подключенные к интересующему узлу, и запишите их как сумму проводимостей по другую сторону знака равенства, группу умножив на напряжение этого узла (например, \(V_1\) ).

6. Теперь найдите все резисторы, подключенные к интересующему узлу и к другим узлам (кроме опорного заземления). Для каждого из этих других узлов умножьте сумму проводимостей между интересующим узлом и этим другим узлом на напряжение этого другого узла, а затем вычтите это произведение из уравнения, построенного до сих пор. Как только все остальные узлы учтены, это уравнение завершается.

7. Найдите следующий узел и обработайте его как новый интересующий узел.

8. Повторяйте шаги с 4 по 7, пока все узлы не будут рассматриваться как интересующие узлы. Каждая итерация создает новое уравнение. Уравнений будет столько, сколько узлов, за вычетом опорного узла. Проверьте диагональную симметрию и решите.

Метод проверки лучше всего наблюдать в действии; как в следующем примере.

Пример 7.2.2

Определить \(V_a\) и \(V_b\) в схеме рис. 7.2.6 . Также определите ток, протекающий через резистор 100 \(\Омега\).

Рисунок 7.2.6 : Схема для примера 7.2.2 .

Эта схема имеет три узла суммирования тока; земля, узел \(a\) и узел \(b\). Кроме того, он использует только источники тока и не использует источники напряжения. Следовательно, мы можем использовать метод проверки для получения системы уравнений (в данном случае двух уравнений).

Начнем с того, что сосредоточимся на узле \(a\), первом интересующем нас узле. Мы будем строить первое выражение по частям. Сначала находим источники тока, питающие этот узел:

\[800 мА – 2А = \точки \нечисло \]

Затем мы находим все резисторы, подключенные к узлу \(a\), и записываем их как проводимости, группу умножая на напряжение узла \(a\):

\[800 мА – 2А = \left( \frac{1}{10 \Omega } + \frac{1}{50 \Omega } + \frac{1}{100 \Omega } \right) V_a \dots \nonumber \]

Теперь найдите все резисторы, подключенные к этому узлу и к другим узлам.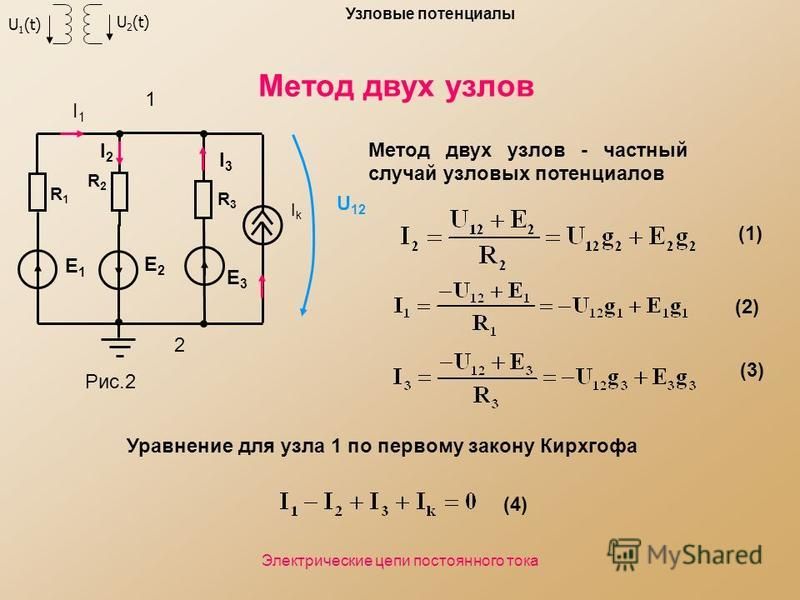 Умножьте эти резисторы (выраженные как проводимости) на напряжения других связанных узлов и вычтите произведения из выражения, построенного до сих пор. Повторите для всех оставшихся узлов, кроме привязки к земле. В этом примере есть только один другой узел, узел \(b\), и, следовательно, только одна итерация.

\[800 мА −2 A = \left( \frac{1}{10 \Omega } + \frac{1}{50 \Omega } + \frac{1}{100 \Omega } \right) V_a − \left ( \frac{1}{50 \Omega } + \frac{1}{100 \Omega } \right) V_b \nonumber \]

Наконец, упростите константы и коэффициенты, и первое выражение готово:

\[−1,2 A = 130 мСм V_a − 30 мСм V_b \номер \]

Теперь мы повторяем весь процесс для следующего уравнения. Узел \(b\) — это новый интересующий нас узел. Фиксированные источники тока:

\[−800 мА −300 мА = \dots \nonnumber \]

Затем мы находим все резисторы, подключенные к узлу \(b\), и записываем их как проводимости, группу умножая на напряжение узла \(b\):

\[−800 мА −300 мА = \left( \frac{1}{25 \Omega } + \frac{1}{50 \Omega } + \frac{1}{100 \Omega } \right) V_b \dots \номер\]

Теперь мы находим все резисторы, которые подключены к этому узлу и к другим узлам.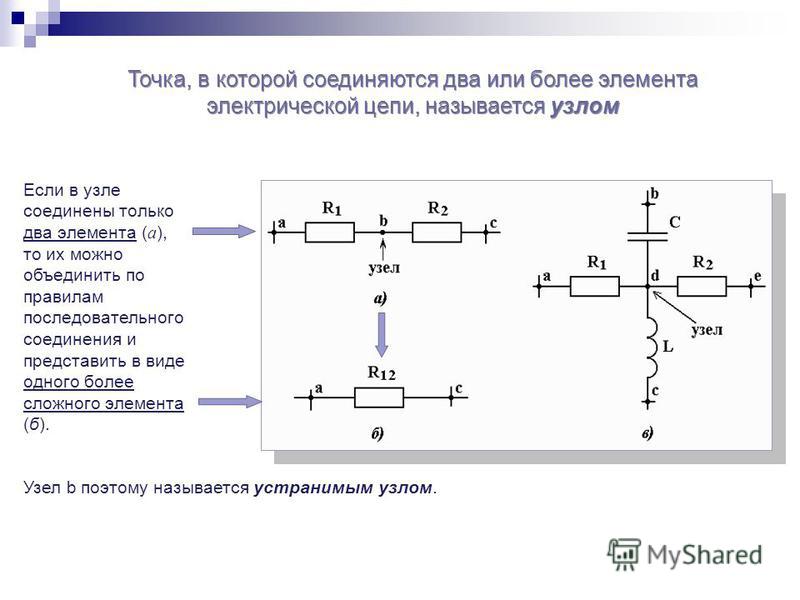 Умножьте эти резисторы (выраженные в виде проводимости) на напряжения этих других узлов и вычтите эти произведения из выражения, построенного до сих пор. Убедитесь, что термины выровнены по вертикали в зависимости от узловых напряжений.

\[−800 мА −300 мА = − \left( \frac{1}{50 \Omega } + \frac{1}{100 \Omega } \right) V_a+ \left( \frac{1}{25 \Omega } + \frac{1}{50 \Omega } + \frac{1}{100 \Omega } \right) V_b \nonumber \]

Наконец, упростите константы и коэффициенты, и это выражение будет полным:

\[−1,1 A =−30 мСм V_a +70 мСм V_b \номер \]

Теперь у нас есть два уравнения с двумя неизвестными. Проверим диагональную симметрию:

\[−1,2 A = 130 мСм V_a − 30 мСм V_b \номер \]

\[−1,1 A = −30 мСм V_a + 70 мСм V_b \номер \]

Перпендикулярный коэффициент составляет −30 мСм с каждой стороны. Теперь мы можем решить систему. Результаты: \(V_a\) = -14,27 вольт и \(V_b\) = -21,83 вольт. Ток, протекающий через резистор 100, составляет (-14,27 В – (-21,83 В))/100 \(\Омега\), или приблизительно 75,6 мА, текущий слева направо.

Давайте проверим правильность этих значений. Мы можем выполнить суммирование KCL в узле \(a\) и посмотреть, уравновешивается ли оно. Мы уже знаем, что на выходе 2 ампера и 75,6 мА, а на входе 800 мА. Нам нужно только найти токи через резисторы 10\(\Омега\) и 50\(\Омега\). Во-первых, обратите внимание, что 50 \(\Омега\) видит то же напряжение, что и 100\(\Омега\) резистор. Поскольку это половина сопротивления, он должен производить вдвое больший ток или 151,2 миллиампер на выходе. Ток через 10 \(\Омега\) находится по закону Ома, или -14,27 В/10 \(\Омега\), что составляет 1,427 ампер на входе.

\[\text{Ввод: } 0,8 А + 1,427 А = 2,227 А \номер\]

\[\text{Выход: } 2 A + 0,0756 A + 0,1512 A \ приблизительно 2,227 A \nonumber \]

KCL удовлетворен. Для завершения проверки выполняем такое же суммирование по узлу \(b\). Это оставлено в качестве упражнения.

Пример 7.2.3

Напишите уравнения узлов для схемы на рис. 7.2.7. .

Рисунок 7.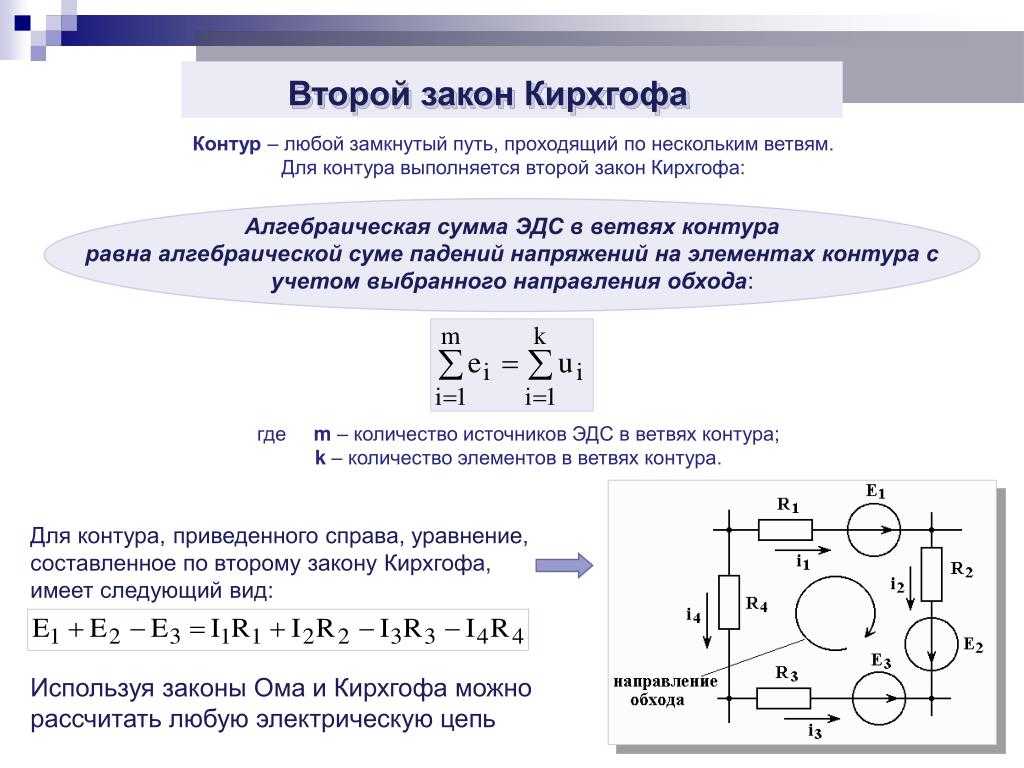 2.7 : Схема для примера 7.2.3 .

Эта схема имеет четыре узла суммирования тока; земля и узлы \(a\), \(b\) и \(c\). Кроме того, он использует только источники тока и не использует источники напряжения. Следовательно, мы можем использовать метод проверки для получения системы уравнений (три уравнения).

Как мы уже видели, в окончательных уравнениях мы получим значения проводимости. Мы можем сэкономить часть работы позже, найдя значение проводимости каждого резистора прямо сейчас. Результат показан на рисунке 7.2.8. .

Рисунок 7.2.8 : Схема рисунка 7.2.7 показан с проводимостями вместо сопротивлений.

Начнем с того, что сосредоточимся на узле \(a\), первом интересующем нас узле. Мы будем строить первое выражение по частям. Сначала находим источники тока, питающие этот узел. Вот только источник 1,5 А, вход положительный.

\[1.5A = \точки\номер\]

Затем мы находим все проводимости, связанные с узлом a, и умножаем на напряжение узла a:

\[1. 5A = (0.2S +0.25S) V_a \dots \nonnumber \]

Найдите все проводимости, которые связаны с этим узлом и с другими узлами. Умножьте эти проводимости на напряжения других связанных узлов и вычтите эти произведения из выражения, построенного до сих пор. Повторите для всех оставшихся узлов, кроме привязки к земле.

\[1,5A = (0,2S +0,25S) V_a −(0,25S) V_b − (0) V_c \номер\]

Наконец, упростите константы и коэффициенты, и первое выражение готово:

\[1,5 A = 0,45 S V_a − 0,25 S V_b − 0 V_c \номер \]

Мы оставляем нулевой член только для выравнивания. Теперь мы повторяем весь процесс для следующего уравнения. Интересующий узел теперь является узлом \(b\). Вот результат:

\[0 = −0,25 S V_a +0,8 S V_b − 0,5 V_c \номер \]

И, наконец, для узла \(c\) имеем:

\[1A = 0 V_a − 0,5S V_b +0,6 V_c \номер \]

Наши три уравнения (с некоторыми дополнениями, чтобы лучше видеть столбцы):

\[1,5A = 0,45S V_a −0,25S V_b −0 V_c \номер \]

\[0 = −0,25 SV_a +0,8SV_b −0,5V_c \номер \]

\[1A = −0V_a −0,5SV_b +0,6V_c \номер \]

Проверьте диагональную симметрию: у нас есть пары значений −0,25, 0 и −0,5, расположенных по обеим сторонам диагонали.

Теперь можно решить систему уравнений для трех узловых напряжений и проверить ее с помощью суммирования KCL в каждом узле. Это оставлено в качестве упражнения.

Преобразование источников и другие упрощения

Имея цепи с источниками напряжения, может быть проще преобразовать их в источники тока, а затем применить метод проверки, а не использовать общий подход, описанный изначально. Есть одна ловушка, которую следует остерегаться при использовании преобразования источника: напряжение или ток через преобразованный компонент, скорее всего, не будет таким же, как напряжение или ток в исходной цепи. Это связано с тем, что расположение преобразованного компонента изменится. Например, схема на рис. 7.2.9.можно решить с помощью узлового анализа путем преобразования источника напряжения и соответствующего сопротивления в источник тока. То есть \(E/R_1\) будет преобразован в источник \(I_3\) с параллельным резистором \(R_1\). Это показано на рисунке 7.2.10. .

Рисунок 7. 2.9 : Цепь с источниками тока и напряжения.

Рисунок 7.2.10 : Цепь преобразуется только в источники тока.

Вот и ловушка: в переделанной схеме, хотя \(R_1\) по-прежнему соединяется с узлом \(a\), другой конец уже не соединяется с источником напряжения. Скорее правая сторона теперь соединяется с узлом \(c\). Следовательно, падение напряжения на \(R_1\) в преобразованной цепи вряд ли будет равно падению напряжения на \(R_1\) в исходной схеме (единственный способ, которым они были бы равны, – это если \(E\) был 0 вольт). В преобразованной схеме узлы \(a\) и \(c\) не изменились по сравнению с исходной, поэтому исходное напряжение на \(R_1\) можно определить через \(V_a\), \(V_c\) и \(E\) в исходной схеме.

Если в цепи используются исключительно источники напряжения или даже очень большая часть источников напряжения, альтернативный метод, называемый анализом сетки, может быть лучшим выбором, чем использование многочисленных преобразований. Анализ сетки будет подробно описан позже в этой главе.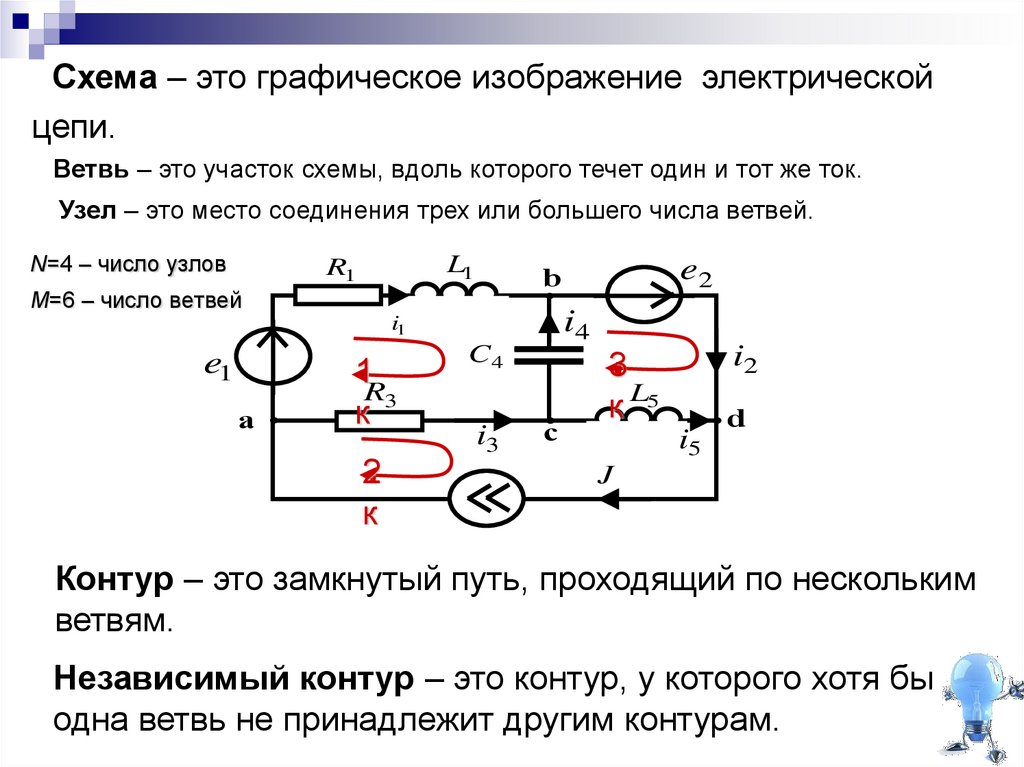

Последний пункт, который необходимо рассмотреть, — это упростить резисторные цепи, чтобы уменьшить количество узлов. Меньшее количество узлов означает меньшее количество уравнений и более быстрое решение. Например, часть сети может состоять из двух параллельных резисторов, включенных последовательно с третьим резистором. Обычно общее соединение этих трех резисторов представляет собой узел суммирования тока, и для него необходимо вывести уравнение. Может быть проще просто заменить тройку одним резистором, равным номиналу последовательно-параллельной комбинации. Это удалит узел и упростит создание системы уравнений, но не изменит оставшуюся часть схемы.

Суперузел

Иногда вы можете столкнуться с цепью, подобной показанной на рис. 7.2.11. который имеет источник напряжения без связанного с ним последовательного сопротивления. Без этого сопротивления становится невозможным создать выражение для тока, проходящего через источник, используя общий метод, и невозможно преобразовать источник напряжения в источник тока, чтобы использовать метод контроля.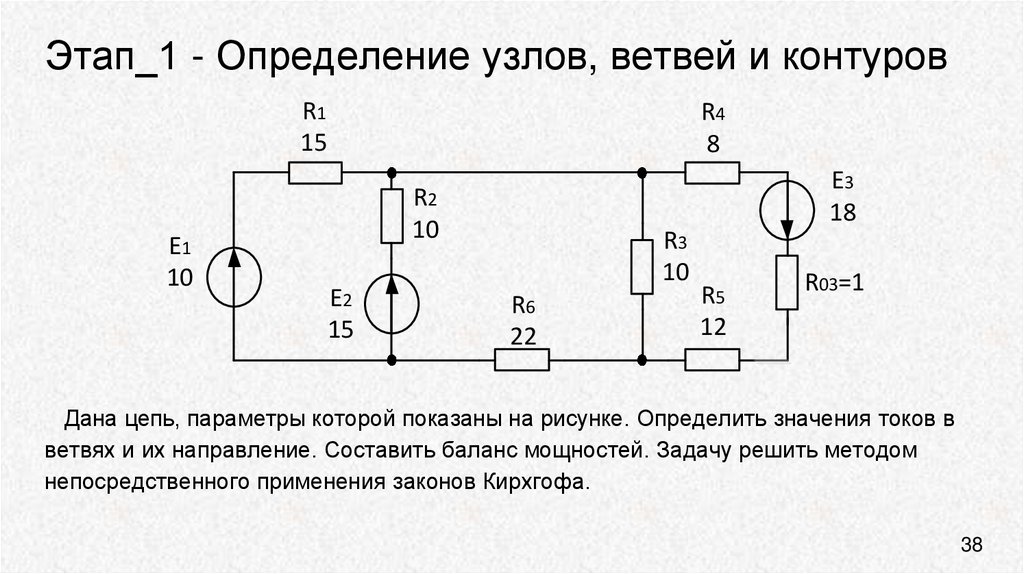 Один из возможных выходов из этого затруднения — просто добавить очень маленький резистор последовательно с ним, чтобы стало возможным преобразование источника. Рассматриваемый резистор должен быть намного меньше, чем любые окружающие резисторы, чтобы иметь минимальное влияние на результаты. Уменьшение на два порядка, как правило, дает меньшую вариацию, чем допуск резисторов во всех схемах, кроме высокоточных. Другой выход — использовать суперноду.

Рисунок 7.2.11 : Схема для анализа суперузла.

Суперузел фактически представляет собой комбинацию двух узлов. Он основан на простом наблюдении. Если мы рассмотрим схему рис. 7.2.11 , путь источника напряжения создает одинаковые токи, втекающие в узлы \(a\) и \(b\) и выходящие из них. Как следствие, если мы будем рассматривать два узла как один большой узел, то при записи суммирования KCL эти два члена сократятся. Чтобы увидеть, как это работает, обратитесь к рисунку 7.2.12. .

В этой версии мы заменили источник напряжения на его идеальное внутреннее сопротивление, короткое замыкание.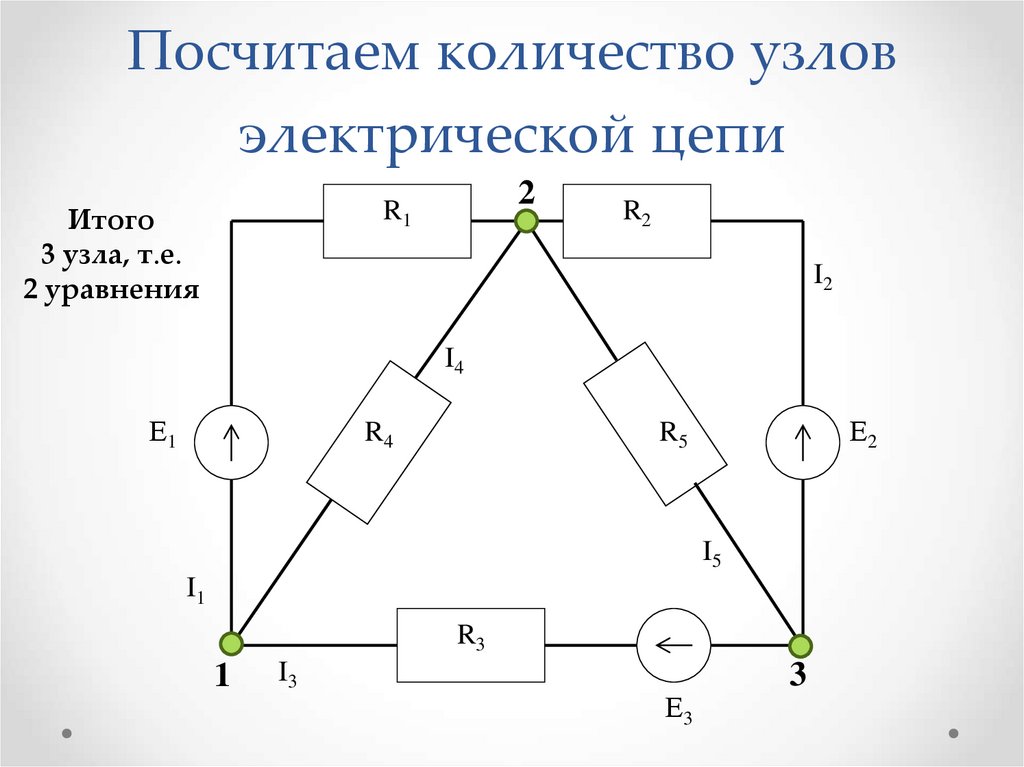 Мы также пометили два интересующих узла, \(a\) и \(b\), и пометили потоки, нарисованные с удобными направлениями.

Рисунок 7.2.12 : Схема изменена для анализа суперузла.

Из-за закороченного источника напряжения узлы \(a\) и \(b\) теперь являются одним и тем же узлом. Рассмотрим токи, входящие и выходящие из этого комбинированного или «супер» узла. С левой стороны (ранее узел \(a\)) мы видим постоянный ток \(I_x\), входящий, в то время как \(I_1\), \(I_2\) и \(I_3\) выходят. С правой стороны (ранее узел \(b\)) мы видим выход \(I_y\) вместе с \(I_4\), а вход мы видим \(I_1\) и \(I_2\). Теперь установим входящие токи слева от знака равенства с исходящими токами справа:

\[\sum I_{in} = \sum I_{out} \nonumber \]

\[I_x+I_1+I_2 = I_y+I_1+I_2+I_3+I_4 \nonumber \]

Это можно упростить to:

\[I_x − I_y = I_3 +I_4 \nonumber \]

Записав это в терминах закона Ома, мы получим:

\[I_x − I_y = \frac{1}{R_1} V_a + \frac{ 1}{R_3} V_b \nonumber \]

Мы также знаем, что \(V_a − V_b = E\) из исходной схемы. Предполагая, что все источники и резисторы известны, это делает два уравнения с двумя неизвестными, решаемыми с использованием методов одновременных уравнений. Это показано в следующем примере.

Пример 7.2.4

Найти \(V_a\) и \(V_b\) для схемы на рис. 7.2.13 .

Рисунок 7.2.13 : Схема для примера 7.2.4 .

Рисунок 7.2.14 : Схема изменена для анализа суперузла.

Как показано на рис. 7.2.14. , закорачиваем источник 60 вольт и записываем сумму тока в суперузле \(a\) \(b\):

\[\сумма I_{вход} = \сумма I_{выход} \номер\]

\[1A + I_1+I_2 = 2,5 A +I_1+I_2+I_3+I_4 \номер\]

Можно упростить до:

\[−1,5 А = I_3 +I_4 \номер \]

Записав это с точки зрения закона Ома, мы получим:

\[−1.5A = \frac{1}{4 \Omega } V_a + \frac{1}{10 \Omega } V_b \nonumber \]

\[−1,5 A = 0,25S V_a +0,1S V_b \номер \]

Мы также знаем, что \(V_a − V_b = 60\) вольт. Поэтому \(V_b = V_a − 60\) вольт.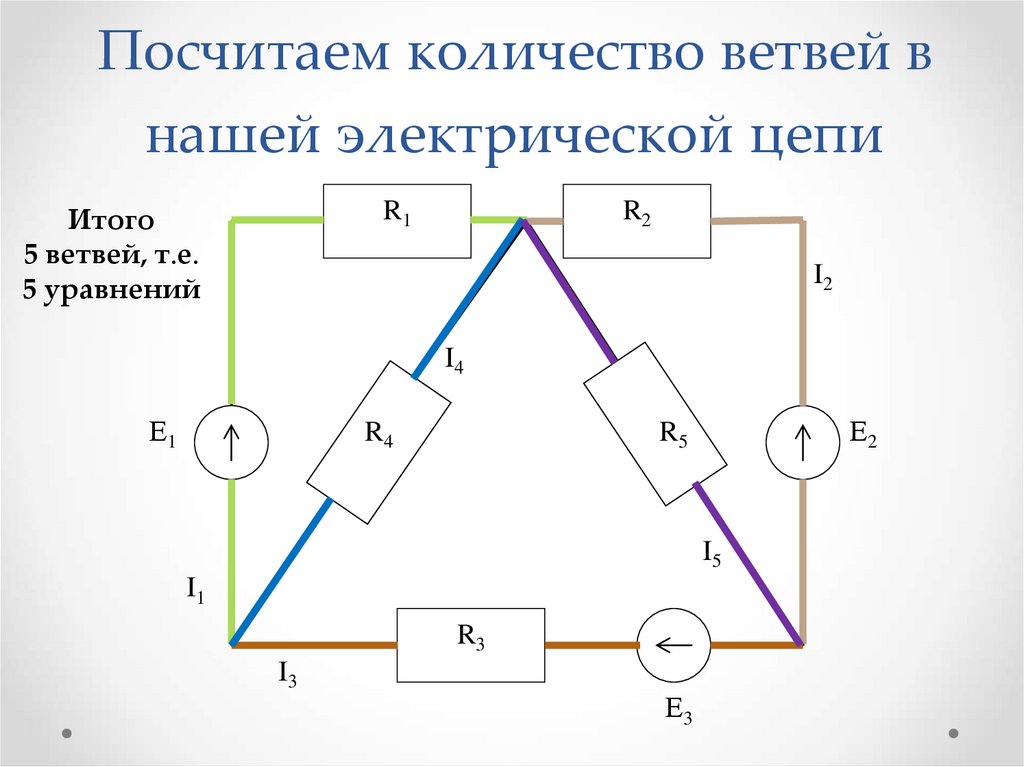 Подставляя это в предыдущее уравнение, получаем:

\[−1,5 A = 0,25S V_a +0,1S(V_a −60 V) \номер \]

\[−1,5 A = 0,25S V_a +0,1S V_a −6A \номер \]

\[4,5 A = 0,35S V_a \номер\]

\[V_a = 12,857 В \номер\]

Мы знаем, что \(V_b\) на 60 вольт ниже \(V_a\), поэтому \(V_b = −47,143\) вольт.

Для проверки выполним суммирование KCL на каждом узле. Для узла \(a\), предполагая, что \(I_1\) выходит как нарисовано:

\[I_1 = 1A – \frac{V_a}{4 \Omega } – \frac{V_a−V_b}{20 \Omega } \nonumber \]

\[I_1 = 1 А- \frac{12,857В}{4 \Omega } – \frac{12,857В-(-47,143 В)}{20 \Omega } \nonumber \]

\[I_1 =−5.2143A \text{ (отрицательный выход означает вход)} \nonumber \]

То же самое делаем для узла \(b\) и предполагаем, что \(I_1\) входит как нарисовано:

\[I_1 = 2,5 А+ \frac{V_b}{10 \Omega } − \frac{V_a−V_b}{20 \Omega } \nonumber \]

\[I_1 = 2,5 А+ \frac{−47,143 В}{10 \Omega } − \frac{12,857V−(-47,143V)}{20 \Omega } \nonumber \]

\[I_1 =−5. 2143A \text{ (отрицательный ввод означает выход)} \nonumber \]

Эти токи совпадают, что означает, что ток через источник напряжения проверен на то, чтобы быть одинаковым на обеих клеммах, как и должно быть.

Альтернативой базовому методу суперузла является простое описание напряжения одного узла в терминах другого с самого начала. Это показано в следующем примере.

Пример 7.2.5

Найти \(V_a\), \(V_b\) и \(V_c\) для схемы на рис. 7.2.15 .

Рисунок 7.2.15 : Схема для примера 7.2.5 .

Опять у нас ситуация с источником напряжения без последовательного сопротивления. Не закорачивая его и, таким образом, рассматривая узлы \(a\) и \(c\) как явный суперузел, мы можем вместо этого заметить путем наблюдения, что токи, входящие и выходящие из источника напряжения, должны быть идентичными.

Схема перерисована на рис. 7.2.16. с маркировкой токов и использованием эквивалентных проводимостей вместо сопротивлений. На этот раз источник напряжения остается.

Рисунок 7.2.16 : Схема примера 7.2.5 с помеченными токами и с использованием проводимостей.

Начнем с наблюдения, что \(V_c = V_a − 8\) V. Другими словами, \(V_c\) привязано к \(V_a\), и если мы найдем одно из них, мы сможем определить другое. Поэтому вместо того, чтобы писать уравнения с использованием трех узлов, мы будем ссылаться на узел \(c\) по отношению к узлу \(a\), то есть мы будем писать \(V_a\) − 8 В везде, где нам нужно \(V_c \). Таким образом, для этой трехузловой схемы потребуется всего два уравнения.

Мы начинаем с узла \(a\) и применяем KCL как обычно.

\[\сумма I_{вход} = \сумма I_{выход} \номер\]

\[I_1+I_3 = I_2 \номер\]

Это расширяется с помощью закона Ома, и мы находим \(I_1\):

\[I_1 = I_2 −I 3 \номер\]

\[I_1 = 0,2S V_a −0,5S (V_b −V_a ) \номер \]

\[I_1 = 0,7S V_a −0,5S V_b \номер \]

На узле \(b\):

\[1A = I_3+I_4 \номер\]

\[1A = 0,5S(V_b −V_a )+0,25S(V_b −V_c ) \номер\]

\[1A = 0,5S(V_b −V_a )+0,25S(V_b −(V_a −8V)) \номер \]

\[1A = 0,5S(V_b −V_a )+0,25S(V_b −V_a+8 V) \номер\]

\[−1 A =−0,75V_a+0,75V_b \номер \]

И, наконец, узел \(c\):

\[I_4 = I_1+I_5 \номер\]

\[I_1 = I_4 −I_5 \номер\]

\[I_1 = 0,25S(V_b −V_c )−0,1SV_c \номер\]

\[I_1 = 0,25S(V_b-(V_a-8V))-0,1S(V_a-8V) \номер \]

\[I_1 = 0,25S(V_b −V_a+8 В)−0,1S(V_a −8V) \номер\]

\[I_1 =−0,35V_a+0,25V_b+2,8A \номер\]

Окончательные уравнения для узлов \(a\) и \(c\) равны \(I_1\), то есть равны друг другу. Таким образом,

\[0,7SV_a −0,5SV_b = −0,35SV_a+0,25SV_b+2,8 A \номер \]

\[2,8 A = 1,05SV_a −0,75SV_b \номер \]

Итоговые уравнения:

\[2,8A = 1,05SV_a −0,75SV_b \номер\]

\[−1 A =−0,75SV_a +0,75SV_b \номер \]

Решение: \(V_a = 6\) вольт и \(Vb \примерно 4,6667\) вольт. Поскольку \(V_c\) на 8 вольт меньше, чем \(V_a\), то \(V_c = −2\) вольт.

Компьютерное моделирование

Для проверки результата Примера 7.2.5 , схема вводится в симулятор, как показано на рисунке 7.2.17. .

Рисунок 7.2.17 : Схема примера 7.2.5 в симуляторе.

Выполняется имитация рабочей точки постоянного тока. Результаты показаны на рисунке 7.2.18. и полностью соответствуют расчетным значениям. Узел 1 соответствует \(V_b\), узел 2 соответствует \(V_a\), а узел 3 соответствует \(V_c\).

Рисунок 7.2.18 : Результаты моделирования для схемы примера 7.2.5. .

---

Эта страница под названием 7. 2: Nodal Analysis распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джеймсом М. Фиоре с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Джеймс М. Фиоре

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. source@http://www. dissidents.com/resources/DCElectricalCircuitAnalysis.pdf

Как анализировать схемы. Основы схем

Прежде чем мы углубимся в обсуждение анализа схем, давайте сначала определим схему или электронную схему.

Электронная схема представляет собой систему, состоящую из электронных компонентов, таких как резисторы, транзисторы, конденсаторы, катушки индуктивности, диоды и многих других, соединенных проводами, по которым может протекать электрический ток. Создание схем — это использование электричества для создания полезных устройств для нашей повседневной жизни.

Итак, что такое анализ цепи? Это математический анализ электрической или электронной цепи. Это процесс изучения и анализа электрических величин посредством расчетов. С помощью этого анализа мы можем найти неизвестные элементы цепи, такие как напряжение, ток, сопротивление, импеданс, мощность и т. д., по ее компоненту. При анализе цепей нам необходимо понимать электрические величины, отношения, теоремы и некоторые основные законы.

Есть два основных закона, которые нам необходимо усвоить для анализа цепей. Это основные сетевые законы, а именно: (1) KCL или закон тока Кирхгофа и (2) KVL или закон напряжения Кирхгофа.

Что такое KCL?

Текущий закон Кирхгофа (KCL) также известен как первый закон Кирхгофа, правило точек Кирхгофа или правило соединения Кирхгофа (или узловое правило). Это один из фундаментальных законов, используемых для анализа цепей. В нем указано, что общий ток t , входящий в соединение или узел, равен току, выходящему из узла, поскольку в узле ток не теряется. Другими словами, KCL утверждает, что алгебраическая сумма всех токов, входящих в узел и выходящих из него, должна быть равна нулю . Густав Кирхгоф основывал свою идею на законе сохранения заряда.

Математически это может быть выражено как:

Поскольку KCL также называется узловым правилом, мы можем связать его с анализом узлового напряжения. Мы можем выполнить узловой анализ с помощью KCL. Узловой анализ или метод анализа узлового напряжения определяет напряжение (разность потенциалов) между «узлами» в электрической цепи с точки зрения токов ветвей. Метод анализа узловых напряжений решает неизвестные напряжения в узлах схемы с помощью системы уравнений KCL.

Как использовать анализ узлового напряжения

Для иллюстрации рассмотрим схему ниже.

Во-первых, давайте вспомним Текущий закон Кирхгофа, который может быть выражен как:

Из рисунка мы видим, что есть два узла, V1 и V2. Напомним, что узел — это место, где соединены две или более ветвей. Эти узлы представляют собой неизвестные напряжения узлов, которые нам нужно найти. Ниже схемы находится эталонный узел, где нулевое напряжение. Для каждого узла должно быть уравнение. Поскольку у нас есть два узла, нам понадобятся два уравнения.

Чтобы применить KCL к V ₁ и V ₂ , нам нужно знать направления каждого тока. Но сначала нам нужно обратиться к источникам.

Для источника питания 20 В обратите внимание, что ток выходит из положительной клеммы и идет к V ₁ . Для источника тока мы уже знаем его текущее направление на основе символа на схеме; ток идет к V ₂ .

Помните, что ток течет от высокого потенциала к низкому, а опорный узел имеет 0 В. Следовательно, мы можем сказать, что это низкий потенциал, что означает, что ток течет от V1 и V2 к эталонному узлу.

Теперь, для тока в ответвлении с резистором 4 Ом, мы можем просто предположить, что ток течет от V ₁ до V ₂ .

Чтобы получить уравнения тока для каждого элемента, нам нужно применить закон Ома, который гласит, что ток равен разнице между высоким и низким потенциалом, деленной на сопротивление. Это выражается как:

Чтобы упростить задачу, нам нужно назначить полярность резисторам в соответствии с направлением тока. Нам также нужно назначить токи, протекающие по каждой ветви:

i ₁ = ветвь резистора 2 Ом
i ₂  = ветвь резистора 4 Ом
i ₃ = ветвь резистора 10 Ом
i ₄ = ветвь резистора 20 Ом3 применит KCL к каждому узлу. Выразите каждый ток через V ₁ и V ₂ , используя закон Ома.

Затем мы можем написать узловые уравнения. А так как у нас два узла, то нужно написать два уравнения. Для простоты предположим, что токи, входящие в узел, положительны, а токи, выходящие из узла, отрицательны.

@node 1 or V ₁ : i ₁ – i ₃ – i ₂ = 0

@node 2 or V ₂ : i ₂ – i ₄ + 4 = 0

Выразив эти два уравнения через V ₁ и V ₂ , мы получим:

@узел 1,

@узел 2,

два неизвестных, мы можем начать решать.

Для первого уравнения упростите:

Для второго уравнения упростите:

Примените сокращение для двух уравнений.

Подставьте значение в любое из двух уравнений, чтобы получить V ₂ .

Для проверки:

Теперь, когда у нас есть значения V ₁ и V ₂ , мы можем найти ток, протекающий по каждой ветви.

Что такое КВЛ?

Вторым фундаментальным законом анализа цепей является закон Кирхгофа о напряжении или KVL. Это также называется вторым законом Кирхгофа или правилом петли (или сетки) Кирхгофа. КВЛ утверждает, что направленная сумма разностей потенциалов (напряжений) вокруг любого замкнутого контура равна нулю . Проще говоря, в нем говорится, что алгебраическая сумма всех напряжений в контуре должна быть равна нулю .

Математически это может быть выражено как:

Поскольку KVL также называется правилом сетки, мы можем связать его с текущим анализом сетки. Мы можем выполнить анализ сетки с помощью KVL.

Анализ сетки или анализ тока сетки используется для решения схемы с меньшим количеством неизвестных переменных и меньшим количеством одновременных уравнений. Это особенно полезно, если вам нужно решить ее без калькулятора. Это хорошо организованный метод решения схемы, но для анализа сети с помощью анализа сетки нам необходимо выполнить определенные условия. Анализ сетки применим только к схемам или сетям планировщика, которые проще и не имеют перекрестных проводов.

Как использовать анализ тока сетки

Сетка — это одиночный замкнутый контур, указанный в цепи. Чтобы проиллюстрировать анализ тока сетки, давайте рассмотрим схему ниже.

Вспоминая KVL, мы выражаем его в следующем уравнении:

Из рисунка видно, что две сетки назначены как сетка 1 и сетка 2.

Перед применением KVL к каждой сетке, давайте вспомним соглашение о полярности напряжения . Напряжение, возникающее от положительного (+) к отрицательному (-), является положительным, а напряжение, возникающее от отрицательного (-) к положительному (+), является отрицательным.

Теперь давайте назначим потоки сетки в каждой сетке. Для сетки 1 у нас есть i ₁ , а для сетки 2 у нас есть i ₂ .

Затем смотрим текущее направление в каждой ветке.

Затем примените KVL к каждому из мешей. А так как в КВЛ сумма напряжений в замкнутом контуре равна нулю, то нужно найти напряжение на каждом элементе. Мы будем использовать закон Ома: V=IR.

Итак, если у нас есть резистор сопротивлением 1 Ом, по закону Ома напряжение равно 2i ₁ . Для ветки с резистором 6 Ом напряжение находится между сеткой 1 и сеткой 2. Мы должны назначить ток i ₃ для отделения.

Глядя на узел, мы имеем:

Применяя KCL, мы можем получить i ₃ через i ₁ и i ₂ по:

Затем мы можем написать уравнения сетки.

@mesh 1 или I ₁ :

@mesh 2 или I ₂ :

, экспрессируя I ₃ , используя I ₁ и I ₂ . два уравнения для двух сеток, мы можем начать решать.

Подставив i ₂ в уравнение 1, мы получим:

Для проверки подставим полученные значения в любое из двух уравнений сетки.

Теперь, когда у нас есть значения i1 и i2, мы можем найти падение напряжения на каждом резисторе.

Используя закон Ома, мы можем просто найти падение напряжения путем подстановки.