Определения и формулы кинематика: Ошибка: 404 Материал не найден - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Кинематика. Кинематика: определение, формулы, задачи

Что такое кинематика? Это подраздел механики, который изучает математические и геометрические методы описания движения идеализированных объектов. Они относятся к нескольким категориям. Темой сегодняшней статьи станут аспекты, которые так или иначе связаны с понятием «кинематика точки». Мы разберем многие вопросы, но начнем с самых что ни на есть фундаментальных понятий и объяснений их применения в данной области.

Какие объекты рассматриваются?

Если кинематика – это раздел физики, который изучает способы описания движения тел в разноразмерных пространствах, значит, нужно оперировать и самими телами, верно? Чтобы быстрее понять, о чем идет речь, вы можете найти предназначенный для школьников мультимедийный урок. Кинематика для понимания вообще проста, если разобраться в ее основах. При ознакомлении с ними вы заметите, что в теории присутствует информация о том, что данный раздел физики изучает закономерности движения материальных точек. Заметьте, как обобщенно дано определение объектов. С другой стороны, материальные точки не являются единственными рассматриваемыми кинематикой объектами. Этот раздел физики изучает принципы движения также и абсолютно твердых тел, и идеальных жидкостей. Очень часто все эти три понятия объединяют в одно, говоря просто «идеализированные объекты». Идеализация в данном случае нужна для условностей расчетов и отхода от возможных систематических погрешностей. Если вы посмотрите определение материальной точки, то заметите, что о ней написано следующее: это тело, размерами которого в соответствующей ситуации можно пренебречь. Это можно понимать так: по сравнению с пройденным расстоянием линейные размеры объекта ничтожно малы.

Что используется для описания?

Как было сказано ранее, кинематика – это подраздел механики, который изучает способы описания движения точки. Но если это так, значит для совершения подобных операций нужны какие-то фундаментальные понятия и принципы, наподобие аксиоматических? Да. И в нашем случае это они имеются. Во-первых, в кинематике заведено за правило разрешать задачи, не оглядываясь на силы, действующие на материальную точку. Все мы прекрасно знаем, что тело будет ускоряться или замедляться в том случае, если на него действует определенная сила. И кинематика – это тот подраздел, который позволяет оперировать ускорением. Однако природа возникающих сил здесь не рассматривается. Для описания движения применяются методы математического анализа, линейной и пространственной геометрии, а также алгебры. Также определенную роль играют координатные сетки и сами координаты. Но об этом мы поговорим чуть позднее.

История создания

Первые работы по кинематике были составлены великим ученным Аристотелем. Именно он сформировал некоторые фундаментальные принципы этой отрасли. И даже несмотря на то, что в его работах и выводах содержалось некоторое количество ошибочных мнений и размышлений, его труды все равно представляют огромную ценность для современной физики. Работы Аристотеля впоследствии изучал Галилео Галилей. Он проводил знаменитые опыты с Пизанской башней, когда исследовал закономерности процесса свободного падения тела. Изучив все вдоль и поперек, Галилей подверг размышления и выводы Аристотеля жесткой критике. Например, если последний писал о том, что сила – это причина движения, Галилей доказал, что сила есть причина ускорения, но никак не того, что тело возьмет и придет в движение и будет перемещаться. По мнению Аристотеля, тело могло приобретать скорость только при воздействии определенной силы. Но ведь мы знаем, что это мнение ошибочно, поскольку существует равномерное поступательное движение. Это в лишний раз доказывают формулы кинематики. А мы перейдем к следующему вопросу.

Кинематика. Физика. Основные понятия

В этом разделе имеется некоторое количество фундаментальных принципов и определений. Начнем, пожалуй, с главного из них.

Механическое движение

Наверное, со школьной скамьи нам пытаются заложить мысль о том, что можно считать механическим движением. Мы с ним сталкиваемся ежедневно, ежечасно, ежесекундно. Механическим движением мы будем считать процесс, который происходит в пространстве с течением времени, а именно изменение положения того или иного тела. При этом очень часто к процессу применяют относительность, то есть говорят о том, что положение, скажем, первого тела изменилось по отношению к положению второго. Давайте представим, что на стартовой черте у нас стоят два автомобиля. Отмашка оператора или загорелись огни – и машины срываются с места. В самом начале уже происходит изменение положения. Причем говорить можно об этом долго и нудно: относительно конкурента, относительно линии старта, относительно зафиксированного зрителя. Но, наверное, идея понятна. То же самое можно сказать и про двух людей, которые идут либо в одну сторону, либо в разные. Положение каждого из них относительно другого изменяется в каждый момент времени.

Система отсчета

Кинематика, физика – все эти науки используют такое фундаментальное понятие, как системы отсчета. На самом деле оно имеет очень важную роль и применяется в практических задачах едва ли не повсеместно. С системой отсчета могут быть связаны еще две важные составляющие.

Координатная сетка и координаты

Последние представляют собой не что иное, как набор цифр и букв. Пользуясь определенным логическими установками, мы можем составить свою одномерную или двухмерную координатную сетку, которая позволит нам решать простейшие задачи по изменению положения материальной точки за тот или иной отрезок времени. Обычно на практике применяется двухмерная координатная сетка с осями Х («икс») и У («игрек»). В трехмерном пространстве добавляет ось Z («зэт») а в одномерном присутствует только Х. Часто с координатами работают артиллеристы и разведчики. А впервые мы с ними сталкиваемся еще в начальной школе, когда начинаем чертить отрезки определенной длины. Ведь градуировка есть не что иное, как использование координат для обозначения начала и конца.

Кинематика 10 класс. Величины

Основные величины, которые используются при решении задач по кинематике материальной точки, – это расстояние, время, скорость и ускорение. Давайте поговорим о двух последних подробнее. Обе эти величины – векторные. Иными словами, они имеют не только численный показатель, но и определенное заданное направление. Движение тела будет происходить в ту сторону, в которую направлен вектор скорости. При этом нельзя забывать и о векторе ускорения, если мы имеем случай неравномерного движения. Ускорение может быть направлено в ту же сторону, либо в противоположную. Если они сонаправлены, то тело начнет двигаться все быстрее и быстрее. Если разнонаправлены, то будет происходить замедление объекта до тех пор, пока он не остановится. После этого при наличии ускорения тело обретет противоположную скорость, то есть тронется в обратном направлении. Все это на практике весьма и весьма четко показывает кинематика. 10 класс – это как раз тот период, когда данный раздел физики раскрывается в достаточной мере.

Формулы

Формулы кинематики достаточно просты как для вывода, так и для запоминания. Например, формула пройденного за то или иное время объектом расстояния имеет следующий вид: S = VoT + aT^2/2. Как мы видим, в левой части у нас стоит как раз-таки расстояние. В правой части можно обнаружить начальную скорость, время и ускорение. Знак «плюс» стоит исключительно условно, поскольку ускорение может принимать отрицательное скалярное значение при процессе торможения объекта. Вообще, кинематика движения подразумевает существование одного вида скорости, мы постоянно говорим «начальная», «конечная», «мгновенная». Мгновенная скорость появляется в определенный момент времени. Но ведь если так подумать, то конечная или начальная составляющие есть не что иное, как ее частные проявления, верно? Тема «Кинематика» является, наверное, излюбленной у школьников, поскольку она проста и интересна.

Примеры задач

В простейшей кинематике существуют целые категории самых разных задач. Все они так или иначе связаны с движением материальной точки. Например, в некоторых требуется определить расстояние, пройденное телом за определенное время. При этом могут быть известны такие параметры, как начальная скорость и ускорение. 2/2. В нее мы просто подставляем имеющиеся данные. Это ускорение и время. Следует обратить внимание на то, что слагаемое Vot уйдет на нуль, поскольку начальная скорость равна нулю. Таким образом, мы получаем численный ответ 75 метров. Вот и все, задача решена.

Итоги

Таким образом, мы разобрались с фундаментальными принципами и определениями, привели пример формулы и поговорили об истории создания данного подраздела. Кинематика, понятие которой вводится в седьмом классе на уроках физики, продолжает постоянно совершенствоваться в рамках релятивистского (неклассического) раздела.

Основы кинематики (8-й класс)

Цель урока: повторение, обобщение и закрепление знаний и основных понятий по теме “Основы кинематики”; совершенствование навыков постановки опытов, решения экспериментальных задач, развитие навыков расчета скорости, ускорения, перемещения; развитие аналитического мышления, умения анализировать и делать выводы при проведении опытов, развитие устной речи.

Оборудование: штативы, желоба, игрушечный автомобиль, линейка, проградуированная в секундах; мяч, секундомер, сантиметровая лента, плакаты с частями формул кинематики, компьютер, мультимедийный проектор.

План урока:

Организационный момент;
Повторение основных кинематических величин и формул;
Самостоятельная работа;
Демонстрация опытов и решение задач по экспериментальным данным;

Задание на дом;
Подведение итогов.

Ход урока

Учитель (У): Здравствуйте, ребята. Садитесь, пожалуйста. Сегодня на уроке нам предстоит повторить и систематизировать основные сведения и знания по кинематике.

В руках у меня линейка, которая позволяет определять время реакции человека.

Время реакции – промежуток времени от начала сигнала до реакции организма человека на этот сигнал. Оно зависит от возраста, тренированности, самочувствия человека.

Ребята, как вы думаете, зачем нужно знать время реакции?

Ученики предлагают свои версии ответа на вопрос.

У: Совершенно верно. А кто из вас знает свое время реакции? Кто хочет его определить?

Выходят 2 ученика.

У: Я отпускаю линейку, а вы должны ее поймать. Время реакции у одного ученика – 0,202 с, у другого – 0,197 с. (линейка проградуирована в секундах). Ребята, как вы думаете, какой принцип лежит в основе создания этого прибора?

Ученик: линейка свободно падает под действием силы тяжести. Ее движение – равноускоренное, с ускорением свободного падения 9,81 м/с

У: Правильно! К этому прибору мы еще вернемся. А сейчас повторим основные понятия и формулы кинематики.

Проводится фронтальный опрос.

Что такое механика? Что она изучает?
Что называется механическим движением?
Почему механическое движение относительно?
Что такое система отсчета и как она выбирается?
Какие системы координат вы знаете?
Что такое тело отсчета?
Какие физические величины характеризуют механическое движение?
В чем заключается основная задача механики?
Какова классификация механического движения?

Что такое равноускоренное движение?
Что называется ускорением и в каких единицах оно измеряется?
Что называется свободным падением?
Чему равно ускорение свободного падения на полюсе и на экваторе и почему эти величины различны?
Что называется перемещением?

Ученики отвечают на вопросы правильно.

У: Отлично! А теперь вспомним формулы для расчета равноускоренного движения. На доске представлены отдельные части формул. Необходимо правильно их собрать и прокомментировать.

Выходит 1 ученик, собирает правильно формулы на магнитной доске и рассказывает, в каких случаях и для расчета чего служит каждая формула.

; ; S=; ;

; ;

У: Молодцы! Вы показали хорошее знание теории, а сейчас посмотрим, как вы умеете применять эти знания на практике. Приготовили по половинке листочка, подписали свой вариант.

На экране представлены графики зависимости скорости от времени. Написано, что необходимо определить: 5 вопросов – 5 правильных ответов – 5 баллов (рис.1). На выполнение работы отводится 6 мин. Кто выполнит работу раньше, поднимает руку, я подойду и возьму работу.

Вариант 1.

Вариант 2.

Определить:

Начальную скорость
Конечную скорость
Время движения
Ускорение
Перемещение

Учащиеся выполняют самостоятельную работу.

У: Отложили, пожалуйста, ручки. Передаем работы по рядам. На экране представлены ответы, вы можете себя проверить и оценить свою работу, а оценки я скажу на следующем уроке. А теперь применим свои знания для решения экспериментальных задач.

Задача № 1 “Движение автомобиля по наклонной плоскости из состояния покоя”.

Вызываются 2 инженера – экспериментатора, а инженерами – теоретиками будет весь класс. Ребята, что мы можем измерить при проведении эксперимента, а какие характеристики можем рассчитать?

Ученики: Измерить можем расстояние S, пройденное автомобилем, время t, затраченное на движение, высоту наклонной плоскости h, рассчитать – ускорение а, конечную скорость ?.

У: Мы будем изменять высоту наклонной плоскости и записывать полученные данные в зависимости от угла наклона.

Инженеры-экспериментаторы запускают автомобиль, измеряя время движения, пройденный путь, высоту наклонной плоскости. Данные заносятся в таблицу 1 на экране.

Таблица 1

№ опыта	1	2	3
Перемещение Ѕ, м
Время t, с
Высота h, м
Ускорение a, м/с²
Конечная скорость ?, м/с

Ученики рассчитывают по полученным измерениям ускорение а, конечную скорость ? и заполняют таблицу 1.

У: Ребята, какой вывод можно сделать, анализируя полученные значения?
Ученик: Скорость и ускорение зависят от угла наклона: чем больше угол наклона, тем больше скорость и ускорение. Эти знания можно использовать при катании с горок.
У: Молодец! А при решении задач динамики мы еще раз подтвердим этот вывод. С первой задачей мы справились.

Задача № 2 “Движение мяча по вертикали с начальной скоростью под действием силы тяжести”.

У: Какие физические величины мы можем измерить, а какие – рассчитать?

Ученик: Можем измерить время и высоту подъема, а определить начальную скорость.

Вызываются 2 инженера – экспериментатора и 1 теоретик. Они подбрасывают мяч, измеряют высоту подъема мяча, время движения мяча вверх и вниз. Данные заносятся в таблицу 2 на экране.

Таблица 2

№ опыта	1	2	3
Высота H ,м
Время t, с
Начальная скорость ,м/с

Ученики рассчитывают по полученным измерениям начальную скорость .

У: Если мяч брошен с начальной скоростью вверх, то каким будет движение мяча?

Ученик: Мяч будет двигаться под действием силы тяжести равноускоренно. Так движение по вертикали обратимо, то можем для расчета исследовать движение мяча вниз и рассчитать начальную скорость по формуле

Можно проверить свои расчеты, применив формулу

У: Очень хорошо! А теперь вернемся к нашему прибору для определения времени реакции. Кто объяснит принцип его действия?

Ученик: Линейка падает свободно, без начальной скорости. Следовательно, расстояние, пройденное линейкой, определяется по формуле . Зная Н, можно определить t. Это и есть время реакции.

У: Молодец! Ставлю оценку “5”. Ребята, вы поняли, как сделать такой прибор? Ваше домашнее задание – изготовить прибор для измерения времени реакции человека и измерить время реакции у своих родственников и друзей.

Мы повторили основные понятия по кинематике и решили экспериментальные задачи. У вас есть вопросы? Спасибо за работу на уроке. До свидания.

Литература:

Громов С.В., Родина Н.А. Физика. 8 класс. – М.: Просвещение, 2006.
Урок физики в современной школе. Творческий поиск учителей. – М.: Просвещение, 1993.

Кинематика Основные понятия и формулы Основные понятия

Кинематика Основные понятия и формулы

Основные понятия В кинематике изучается механическое движение материальных точек и твердых тел без учета причин, вызывающих эти движения. Кинематику часто называют геометрией движения. Механическое движение происходит в пространстве и во времени. Пространство, в котором происходит движение тел, рассматривается как трехмерное, все свойства его подчиняются системе аксиом и теорем эвклидовой геометрии. Время полагают ни с чем не связанным и протекающим равномерно. Современное развитие физики привело к иным представлениям о пространстве и времени. Теория относительности, созданная величайшим ученым современности Эйнштейном, показала, что при скоростях, близких к скорости света (300 000 км/с), пространство и время зависят от скорости движения. При обычных скоростях указанная зависимость практически не обнаруживается и представления о пространстве и времени, установленные в классической механике, сохраняют силу. В общем случае различные точки твердого тела совершают разные движения. Поэтому и возникает необходимость изучить в первую очередь движение отдельных точек тела. Чтобы определить положение точки в пространстве, нужно иметь какоето неподвижное тело или связанную с ним систему координатных осей, которую называют системой отсчета. Движение заданного тела или точки обнаруживается только путем сравнения с системой отсчета. В природе не существует неподвижных тел и, следовательно, не может быть абсолютно неподвижных систем отсчета. Обычно условно неподвижной системой отсчета считают систему координатных осей, связанную с Землей. Рассмотрим для примера движение точки в какой-то условно неподвижной системе координат xyz.

Уравнение движения точки Уравнения, определяющие положение движущейся точки в зависимости от времени, называются уравнениями движения. Наиболее удобный способ задания движения точки — естественный способ. При этом задается траектория точки (графически или аналитически) и закон движения точки по траектории. Пусть произвольная точка А перемещается по заданной траектории (рис. а). Принимая точку 0 за начало отсчета, уравнение движения можно представить в виде: s = f (t), где s — расстояние точки А от начала отсчета; t — время. Положение движущейся в плоскости точки (рис. б) можно определить, если известны ее координаты х и у относительно системы двух взаимно перпендикулярных координатных осей Ох и Оу. При движении точки ее координаты изменяются с течением времени, следовательно, x и у являются некоторыми функциями времени и определяют движение точки: Такой способ задания движения точки называется координатным. С помощью уравнений движения можно найти траекторию точки. Для этого из них нужно исключить параметр — время t — и найти зависимость между координатами точки у = f (х).

Скорость точки Скорость равномерного движения v измеряется отношением пути s, пройденного точкой за некоторый промежуток времени, к величине этого промежутка времени v = s/t. Скорость измеряется в единицах длины, деленных на единицу времени: м/с, см/с, км/ч и т. д. ; 1 км/ч = 0, 278 м/с, 1 м/с = = 3, 6 км/ч. Если точка за равные промежутки времени проходит неравные пути, то ее движение называется неравномерным. Скорость неравномерного движения есть величина переменная и является функцией времени v = f (t). Рассмотрим точку М, которая перемещается по заданной траектории по некоторому закону s = f (t) (рис. а). За промежуток времени t точка М переместится в положение М 1 по дуге ММ 1. Если промежуток времени t мал, то дугу можно заменить ее хордой и найти в первом приближении среднюю скорость движения точки Средняя скорость направлена по хорде от точки М к точке M 1. Истинную скорость найдем путем перехода к пределу при t—» О При t—» О направление хорды в пределе совпадает с направлением касательной к траектории в точке М, т. е. значение скорости точки определяется как производная пути по времени, а направление ее совпадает с касательной к траектории в данной точке. Если известны проекции скорости на оси координат, можно определить ее значение и направление (рис. б):

Ускорение точки При движении по криволинейной траектории скорость точки может изменяться и по направлению, и по величине. Изменение скорости в единицу времени определяется ускорением. Пусть точка М (рис. а) движется по какой-то криволинейной траектории и за время t переходит из положения М в положение M 1. Расстояние, пройденное точкой, представляет собой дугу ММ 1; ее длину обозначим s. В положении М точка имела скорость v, в положении M 1 — скорость v 1. Геометрическую разность скоростей найдем, построив из точки М вектор v 1. Скорость точки при перемещении ее из положения М в положение M 1 изменилась и по величине, и по направлению. Среднее значение ускорения, характеризующего отмеченное изменение скорости можно найти, разделив вектор приращения скорости v на соответствующее время движения: Переходя к пределу при t—» О получим истинное ускорение точки как векторную производную от скорости: Найденное ускорение характеризует изменение численного значения скорости и ее направления. Для удобства ускорение раскладывают на взаимно перпендикулярные составляющие по касательной и нормали к траектории движения (рис. б) Касательная составляющая совпадает по направлению со скоростью или противоположна ей. Она характеризует изменение модуля скорости и соответственно определяется как производная от функции скорости: Нормальная составляющая перпендикулярна к направлению скорости точки. Она определяет изменение направления вектора скорости. Численное значение нормального ускорения определяется по формуле: где r — радиус кривизны траектории в рассматриваемой точке. Составляющие и взаимно перпендикулярны, и поэтому значение полного ускоренияопределяется по формуле:

Виды движения точки в зависимости от ускорения Равномерное прямолинейное движение характеризуется тем, что скорость движения точки М постоянна (v = const), а радиус кривизны траектории ее движения равен бесконечности (рис. а). В этом случае касательное ускорение равно нулю, так как модуль скорости не изменяется (у = const), Нормальное ускорение также равно нулю Значит, и полное ускорение движения точки равно нулю а=0 Равномерное криволинейное движение характеризуется тем, что численное значение скорости постоянно (v = const), скорость меняется лишь по направлению. В этом случае касательное ускорение равно нулю, так как v = const (рис. б), а нормальное ускорение не равно нулю, так как r — конечная величина. Полное ускорение при равномерном криволинейном движении равно нормальному ускорению. Неравномерное прямолинейное движение характеризуется тем, что численное значение скорости движения точки (рис. в) изменяется, а радиус кривизны траектории движения точки r равен бесконечности. Поэтому касательное ускорение здесь не равно нулю: а нормальное ускорение равно нулю: . Следовательно, полное ускорение точки при неравномерном прямолинейном движении равно касательному ускорению. Неравномерное криволинейное движение (рис. г) характеризуется тем, что численное значение скорости движения точки М изменяется, а радиус кривизны траектории ее движения — конечная величина. В этом случае касательное ускорение не равно нулю: и нормальное ускорение также не равно нулю: Следовательно, полное ускорение при неравномерном криволинейном движении складывается геометрически из касательного и нормального ускорений, т. е. Когда значение касательного ускорения постоянно, движение точки называется равнопеременным. Равнопеременное движение может быть равномерно-ускоренным и равномерно-замедленным, в зависимости от того, увеличивается или уменьшается численное значение скорости. Ускорения можно определить через значения скорости в начале и в конце произвольного промежутка времени: откуда При равномерно-ускоренном движении ускорение считается положительным, а при равномерно-замедленном — отрицательным. Перемещение точки при равнопеременном движении определяется по уравнению: Примером равномерно-ускоренного движения может служить свободное падение тела. 2.

Поступательное движение твердого тела Поступательным называется такое движение твердого тела, при котором всякая прямая, проведенная в этом теле, остается параллельной своему начальному положению. Проведенная в теле прямая ВМ во время движения перемещается параллельно своему начальному положению. Рассмотрим перемещение тела за бесконечно малый промежуток времени dt. При этом можно считать, что точки М и Вперемещаются по прямолинейным и параллельным траекториям. За время dt они пройдут одинаковые пути ds. Следовательно, значения скорости этих точек будут одинаковы: и направлены в одну сторону, т. е. Аналогично доказывается равенство ускорений точек тела при поступательном движении: Следовательно, при поступательном движении тела все его точки описывают одинаковые траектории и в любой момент времени имеют равные по модулю и параллельно направленные скорости и ускорения. Поступательное движение тела вполне характеризуется движением одной его точки, которое может быть задано координатным или естественным способом. Однако поступательное движение может совершать только твердое тело, а не отдельная точка. Примерами поступательного движения служат движение поршня двигателя, движение вагона на прямом участке пути и т. п. Поступательное движение может быть прямолинейным и криволинейным.

Вращение тела вокруг неподвижной оси При вращательном движении тела вокруг неподвижной оси все его точки, лежащие на оси вращения, остаются неподвижными. Остальные точки вращающегося тела описывают окружности вокруг неподвижной оси в плоскостях, перпендикулярных к оси, с центром на этой оси. Рассмотрим тело, которое вращается вокруг оси Oz. Плоскость вращающегося тела, проходящая через ось 0 z и совпадающая в начальный момент времени с плоскостью чертежа I, займет через промежуток времени t положение II и оба отмеченных положения плоскости составят угол. Угол называется углом поворота тела. Угол поворота измеряется в радианах и соответствует определенному положению тела. Для определения положения вращающегося тела в каждый данный момент служит уравнение, выражающее угол поворота как функцию от времени: Изменение угла поворота определяется угловой скоростью. Средней угловой скоростью вращающегося тела называется отношение приращения угла поворота ко времени t, в течение которого это приращение произошло: Истинная угловая скорость вращательного движения тела равна производной углового перемещения по времени: Угловая скорость измеряется в радианах в секунду, т. е. рад/с. Скорость при вращательном движении тела определяется частотой вращения n, об/мин. Связь между угловой скоростью и частотой вращения можно установить следующим образом. За один оборот вращающегося тела угол поворота составит 2 П рад. За n оборотов в 1 мин угол поворота составит 2 Пn. Соответственно угловая скорость определится путем деления угла поворота за n оборотов на 60 с Например, частота вращения вала электродвигателя n = 1400 об/мин, тогда угловая скорость: Когда угловая скорость тела постоянна, вращение — равномерно. Угол поворота в этом случае определяется: Когда угловая скорость переменна, тело вращается неравномерно. Изменение угловой скорости в единицу времени определяется угловым ускорением, равным производной угловой скорости по времени: Угловое ускорение измеряется в радианах, деленных на секунду в квадрате, т. 2. При вращении тела вокруг оси с постоянным угловым ускорением происходит равнопеременное вращение. Уравнения равнопеременного вращения аналогичны уравнениям равнопеременного прямолинейного движения точки, только вместо линейных величин в них входят угловые величины. Выводятся эти уравнения тем же путем: где — начальная угловая скорость (при t = 0). Угловое ускорение — величина алгебраическая: при равнопеременном ускоренном вращении его считают положительным, поэтому абсолютное значение угловой скорости будет все время возрастать. При равномернозамедленном движении угловое ускорение считают отрицательным, поэтому абсолютное значение угловой скорости уменьшается

Скорости и ускорения точек вращающегося тела Если тело вращается вокруг оси, то его точки перемещаются по окружностям (рис. а), радиусы которых r равны расстояниям точек от оси вращения. Рассмотрим точку М, которая за время dt прошла путь ds = ММ 1. В данном случае путь ds можно определить как произведение угла поворота на радиус окружности, т. е. Линейная скорость определится как производная пути по времени: Подставив вместо ds его значение по , получим: Подставив в формулу для линейной скорости точек тела, вращающегося вокруг неподвижной оси, значение частоты вращения в оборотах в минуту (об/мин), получим: Касательное ускорение точки вращающегося тела определяется из выражения: Нормальное ускорение точки равно отношению квадрата скорости к радиусу окружности: Подставив в выражение нормального ускорения значение скорости v = ? r, получим: Значение полного ускорения вычисляется как диагональ прямоугольника, построенного на составляющих ускорениях (рис. б). Подставив значения касательного и нормального ускорений, получим: Направление вектора полного ускорения точки вращающегося тела можно определить по углу ? , образованному этим вектором с радиусом:

Уравнения кинематики – определение, параметры и часто задаваемые вопросы

Целью этого первого раздела, относящегося к классу физики, было исследование разнообразия средств, с помощью которых можно описать движение объектов. Разнообразие представлений, которые мы уже изучили и исследовали, также включает в себя вербальные представления, которые являются графическими представлениями, а также числовые представления и графические представления, которые представляют собой графики положение-время и графики скорости-времени.

Определение кинематических уравнений

Раздел физики, который обычно определяет движение во времени и пространстве, игнорируя причину этого движения, известен как кинематика. Уравнение, которое является кинематикой, представляет собой набор уравнений, которые могут вывести неизвестный аспект движения тела, если предусмотрены другие аспекты.

Эти уравнения связывают пять кинематических переменных:

Перемещение, которое обозначается Δx.
Начальная скорость, которая задается как v ₀, которая называется Конечная скорость, которая обозначается v Временной интервал, который обозначается t Постоянное ускорение, которое обозначается a.

По сути, мы можем сказать, что уравнения кинематики, которые могут вывести одну или несколько из этих переменных, если другие заданы. Эти уравнения, которые мы видели, определяют движение либо с постоянной скоростью, либо с постоянным ускорением. Поскольку мы можем сказать, что уравнения кинематики применимы только при постоянном ускорении или постоянной скорости, мы не можем использовать их, если есть одно из двух, которое изменяется.

Параметры кинематического уравнения

Знание каждой из различных величин обычно дает описательную информацию о движении объекта.Например, мы можем сказать, что если известно, что автомобиль движется с постоянной скоростью 22,0 м/с, на север в течение 12,0 секунд для смещения на север, равного 264 метрам. Тогда можно сказать, что движение автомобиля полностью описано.

Если мы возьмем второй автомобиль, то известно, что он ускоряется из положения покоя с ускорением в восточном направлении 3,0 м/с ² за время 8,0 секунд, а конечная скорость составляет 24 м/с. . В восточном и восточном направлении водоизмещение составляет 96 метров, и тогда можно сказать, что движение этого автомобиля описано полностью.

Эти два утверждения, которые мы видели, должны дать полное описание движения объекта. Однако можно сказать, что такая полнота не всегда известна.

Часто бывает, что известны лишь некоторые параметры движения объекта, а остальные неизвестны. Например, мы можем сказать, что приближаясь к светофору, мы можем знать, что автомобиль имеет скорость 22 м/с, движется в восточном направлении и способен скользить с ускорением 8,0 м/с ² и в сторону запада.Однако мы не знаем смещения, которое испытала бы наша машина, если бы мы ударили по тормозам и остановились. а затем после этого мы не знаем времени, необходимого для полной остановки. В таком случае, как этот, мы можем сказать, что неизвестные параметры, которые могут быть определены с использованием принципов физики и математических уравнений, являются кинематическими уравнениями.

Что такое уравнение кинематики?

Уравнения, которые можно использовать для любого движения, которое можно в целом описать либо как движение с постоянной скоростью, то есть с ускорением 0 м/с/с, либо как движение с постоянным ускорением.Можно сказать, что они никогда не используются в течение какого-либо периода времени, в течение которого изменяется ускорение. Каждое из уравнений, являющихся кинематическими уравнениями, включает четыре переменные. Если нам известны значения трех из четырех переменных, то можно просто вычислить значение четвертой переменной.

Таким образом, мы можем сказать, что уравнение, которое является кинематическим уравнением, предоставляет полезные средства предсказания информации о движении объекта, если нам уже известна другая информация.Например, мы можем сказать, что если известно значение ускорения, а также начальное и конечное значения скорости скользящего автомобиля, то мы можем сказать, что смещение автомобиля и время можно предсказать с помощью кинематических уравнений. {2} + 2 \times a \times d\]

\[v_{f} = v_{i} + a \times t\] \[ d = \frac{v_{i} + v_{f}}{2} \times t\]

В приведенных выше уравнениях используются различные символы.Каждый символ, который мы видели, имеет свое особое значение. d означает смещение объекта, t означает время, в течение которого объект перемещался, a означает ускорение объекта, v означает скорость объекта, v означает, что значение скорости является начальным, а vf указывает, что значение скорости является окончательным.

Каждое из этих четырех уравнений, которые мы видели, надлежащим образом описывает математическую связь между параметрами движения объекта.Таким образом, мы можем сказать, что их можно использовать для предсказания неизвестной информации о движении объекта, если известна другая информация. В следующей части мы исследуем этот процесс.

Определения уравнений физики и кинематики

Хотя массы двух объектов равны, интуитивно понятно, что маховик будет труднее разогнать до большого числа оборотов в секунду, потому что не только количество массы, но и распределение массы влияет на легкость инициирования вращения. для твердого тела.Скалярные величины можно использовать алгебраически. Перемещение, необходимое для обнаружения мешка с золотом, не было полностью описано.

Теперь сделайте мою статью, вы знаете немного математических вычислений, вы можете наблюдать, как выводятся уравнения движения. Гораздо лучше всегда начинать с одного из трех основных уравнений. Есть 3 ключевых кинематических уравнения.

Простой выбор уравнений физики и кинематики

Эта серия известна как Breakdown. Трудности с кинематикой и энергией во многом совпадают, поэтому проверьте проблемы с энергией и импульсом, чтобы определить, сможете ли вы найти там полезный пример.Возможность падения с высоты 369 м находится точно по тому же кинематическому уравнению, что и в части c.

1 день, вы немного сходите с ума и бегаете по дому, втыкая и вылезая из каждой части мебели, пока у вас не закружится голова и вы не рухнете на диван. Веб-сайт Скорость объекта (например, автобуса) — это скорость, с которой он движется в заданном направлении. Используя идею о том, что это площадь под графиком скорости, теперь мы можем найти формулу для расстояния при ускорении движения.

Ответьте на эти вопросы, если радио движется с постоянным ускорением.Оставьте комментарий ниже, если вы не можете найти ответ. Ответ действительно нет.

Когда вы сможете это сделать, вы будете готовы к экзамену AP по физике 1. Физика требует большого количества расчетов и решения задач. Поймите результаты После того, как вы закончите задачу, посмотрите на нее еще раз.

Твердые тела и кинематические связи являются основными элементами механизмов. Другими словами, кинематика не может сообщить вам о невидимых силах, которые определяют правила движения объектов.Матрицы могут использоваться для выполнения различных операций с объектами, таких как перемещение, вращение, масштабирование и сдвиг.

Здесь необходимо отметить важный момент. Хорошим примером такой проблемы является вычисление времени, которое потребуется в часах, чтобы транспортное средство проехало определенное количество миль, если скорость https://www. physics.northwestern.edu/ автомобиля в милях в секунду предоставляется час. Вы заметите разницу в движении в зависимости от формы используемого материала.

Как начать работу с уравнениями кинематики?

Ваша худшая оценка за домашнее задание будет отклонена.Если есть много решений, вам может потребоваться применить дополнительные ограничения. Обратите внимание, что эти ресурсы не проверялись CPALMS, и за использование некоторых из них в этой коллекции может взиматься плата.

Так как вектор должен иметь элементы одинакового типа, эта функция попытается привести элементы к одному и тому же типу, если они разные. Векторный файл можно назвать геометрическим файлом. Выясните, что вам нужно найти.

Выбор уравнений физики и кинематики

VPython также может рисовать векторы.Конечный результат будет выглядеть точно так же, но форма, созданная векторами, может показаться другой. Стоимость выглядит достаточно разумной.

Пожалуйста, ожидайте, что вам нужно будет внести соответствующие изменения, чтобы получить их для запуска на вашей индивидуальной установке. Использование кинематических уравнений как раз подходит для постоянных периодов ускорения. Проверьте проблемы с определением и соотношением, чтобы проверить, сможете ли вы найти удобный пример.

Все, что вам говорили о физике, кинематике, уравнениях, совершенно неверно… и вот почему

Интересно помнить, что масса объекта не влияет на его ускорение во время свободного падения.Итак, сначала будет использоваться кинематическое уравнение, чтобы узнать скорость, а затем будет вычислено расстояние по инерции. Уравнение, которое используется для расчета расстояния и скорости, приведено ниже.

Новый ажиотаж вокруг уравнений физики и кинематики

В частности, слабое и электромагнитное взаимодействие объединяются во взаимное взаимодействие, известное как электрослабое взаимодействие. Для заданного времени t нам нужно было бы определить скорость окрестности V, а затем подставить это значение в уравнение местоположения, чтобы получить местоположение y.Если вам нужна позиция с определенной скоростью, выберите уравнение 2.

Может быть трудно следить за своими негативами. Поскольку существует угловая модель скорости, существует и угловая модель ускорения. Модуль жесткости зависит от материала.

Определите, что происходит в данных обстоятельствах. Координаты могут быть удобны во многих сценариях, но они также могут скрыть простоту или закономерность происходящего. Существует более одного подхода к решению этой дилеммы.

Основы физики Уравнения кинематики

Другими словами, их относительное движение будет в какой-то степени задано. Он определяется как изменение положения точки в определенном направлении. В случае, если силы уравновешены, то у вас не должно остаться ничего лишнего, когда вы сложите их все вместе ().

Понимание ускорения, например, необходимо для изучения силы. Необходимо также определенное количество творчества и понимания.Изучение физики поможет вам обдумать довольно много навыков, которые могут применяться во многих областях, как научных, так и нетехнических.

Ошибка неработающей ссылки

Приборная доска
Ресурсы по физике
Перейти к содержанию Приборная доска
Авторизоваться
Приборная панель
Календарь
Входящие
История
Помощь
Закрывать Мой Dashboard
Ресурсы по физике
Главная
Модули
Руководства
Лаборатории
Lab FAQs
Проблемы
Сочетания клавиш
Видео по физике
2
К сожалению, вы нашли неработающую ссылку!
Что такое кинематика? Простые ответы по физике
Как пользоваться этим руководством
Этот пост в блоге является первым в серии о том, как понимать проблемы кинематики и подходить к ним. Он предназначен для дополнения вашего класса и учебника. Я сосредоточусь на практических применениях, способах решения задач и типичных ошибках, которые допускают учащиеся. Если вы хотите изучить основы кинематики, я рекомендую учебник, но если вы хотите получить более глубокое понимание, избежать путаницы и научиться подходить к проблемам, примите красную таблетку и присоединяйтесь к нам!
Что такое кинематика?
Кинематика — это просто изучение движения. Это буквально то, что означает это слово: кинезис (движение) + тики (изучение.Подумайте о математике, политике, пиццетике). На более практическом уровне кинематика, которую вы изучаете на вводном уроке физики, — это изучение положения, скорости и импульса. На самом практическом уровне кинематика — это изучение того, что происходит, когда вы подбрасываете мяч. Это означает, что если вы можете подбрасывать мяч, вы можете изучить кинематику — к вашему сведению, как известно любому, кто когда-либо видел, как я занимаюсь спортом, обратное неверно.
Положение, скорость и ускорение
Итак, кинематика — это изучение трех вещей, но что это за три вещи?
Позиция :
Где находится объект.Его месторасположение. В задачах по физике это будет обозначаться как x, y, z p, r или d. У каждого учителя есть свои предпочтения, поэтому изучите свои, но для этого блога мы будем использовать x и y. Нас также часто интересует изменение положения, известное как смещение, которое обозначается как Δx, Δy, Δp, Δd или иногда просто x, y или d, чтобы все запутать. Положение и смещение обычно измеряются в метрах или метрах.
Скорость :
Как быстро движется объект и в каком направлении: то же, как расстояние меняется со временем.Задачи физики почти всегда относятся к скорости как v. Скорость обычно измеряется в метрах в секунду или м/с. Когда скорость постоянна, ее можно описать уравнением v=Δx/Δt (изменение положения, деленное на изменение во времени).
Ускорение :
Как меняется скорость объекта. Если Ferrari разгоняется от 0 до 60 миль в час за 2,4 секунды, значит, он ускоряется. Если водитель сходит с ума и врезается в стену, которая останавливает машину, значит, она тоже ускорилась.Ускорение всегда обозначается буквой а и измеряется в метрах в секунду за секунду, или м/с ² .
Когда ускорение постоянно, оно может быть описано уравнением a=Δv/Δt (изменение положения, деленное на изменение во времени). Вы могли заметить, что это уравнение очень похоже на уравнение для скорости. Это не совпадение: оно отражает обширную физику, лежащую в основе всего в мире.
Избегайте распространенных ошибок: положение, расстояние и смещение
Position, Displacement и Distance легко спутать, и учителя физики часто проводят тесты, чтобы убедиться, что вы понимаете разницу.Позиция измеряется от некоторой исходной точки и определяет местоположение объекта — в кинематике мы часто определяем исходную точку как начальное местоположение объекта, чтобы упростить задачу. Расстояние измеряет общее расстояние, пройденное объектом. Смещение измеряет, насколько далеко объект находится от того места, где он начался.
Чтобы понять разницу, представьте себе сценарий, в котором вы начинаете движение на 3 метра вправо от исходной точки и проходите 2 метра влево, а затем 4 метра вправо. Ваша позиция в начале 3 метра, а в конце 5 метров.Ваше расстояние составляет 6 метров, потому что именно столько вы прошли. Ваше смещение в конце, однако, составляет 2 метра, потому что вы находитесь всего в 2 метрах от того места, где вы начали.
Избегайте типичных ошибок: скорость и скорость
В обычной жизни мы используем слова «скорость» и «скорость» как синонимы, но в физике — никогда. Скорость — это то, насколько быстро что-то движется, скорость — это то, насколько быстро оно движется И в каком направлении (мы называем эту концепцию величины + направления вектором).Это означает, что объект может изменять скорость без изменения скорости, например, автомобиль, движущийся по круговой дорожке. Это также означает, что скорость может увеличиваться, в то время как скорость уменьшается. Если скорость отрицательна, а ускорение отрицательно, то скорость будет все более и более отрицательной, поэтому скорость будет уменьшаться (от -60 м/с до -120 м/с), но скорость будет увеличиваться (от 60 м/с). до 120 м/с).
Избегайте распространенных ошибок: ускорение и скорость
Студентов, плохо знакомых с физикой, часто озадачивает мысль о том, что ускорение и скорость могут идти в разных направлениях.Когда объект ускоряется, он должен двигаться быстрее, верно? Не обязательно. Например, если вы подбрасываете объект в воздух, он начинает с положительной скорости вверх, но ускорение отрицательное и направлено вниз. В конце концов, объект перестает подниматься и падает обратно на землю, и в этот момент ускорение и скорость совпадают. Однако в любой момент ускорение может быть в любом направлении — ускорение определяет изменение скорости, а НЕ саму скорость.
Заключение
Итак, теперь мы понимаем основы кинематики, но как мы их используем? В следующем блоге я расскажу о стандартных уравнениях кинематики и о том, как их использовать для решения одномерных задач.
Кинематика — ускорение
Кинематика — ускорение
[Глава 2 цели]
БХС -> Мистер Стэнбро -> Физика -> Механика -> Кинематика -> эта страница
Что такое ускорение:
Ускорение — это скорость, с которой изменения скорости. Другими словами, зная ускорение объекта говорит вам о том, насколько высока скорость объект меняется.
Поскольку скорость — это скорость изменения положения, а ускорение – это скорость изменения скорости, ускорение – это «ставка ставки».
При ускорении:
Очень важно отметить, что ускорение определяется в с точки зрения изменения скорости – не скорости . Это может показаться как незначительный момент, но это не так. Поскольку ускорение – это скорость изменения скорости,
Вы ускоряетесь всякий раз, когда вы:
ускорить – Это не трудно понять, так как это общая концепция ускорения.
помедленнее – Люди обычно называют это замедление, как если бы оно физически отличалось от “ускорение” дела – а физику все равно – если ваша скорость меняется, вы ускоряетесь.
изменить направление – Это может быть сложно понять. Поскольку скорость — это ваша скорость и направление, ваша скорость изменяется, если меняется ваше направление (даже если ваша скорость остается прежней). такой же).Поскольку вы ускоряетесь, если ваша скорость меняется, вы ускоряетесь, когда меняете направление – даже если ваша скорость останется прежней . Большинство людей ссылаются ускорение с изменением скорости (и увеличением скорости), поэтому они думают: «Хорошо, на тесте я должен сказать, что объект ускоряется, если меняет направление, но это действительно какой-то «фальшивое» ускорение в отличие от «настоящего» ускорения ускорение” Нет.Это ускорение столь же реально, как и «ускоряющий» (и «замедляющий») вид ускорения.
Чем ускорение не является:
Поскольку ускорение связано с изменением скорости, при скорость меняется, вы ускоряетесь, студенты часто получают ошибочное представление о том, что «ускорение есть изменение скорости». НЕТ!! Ускорение – это скорость, с которой скорость изменения – есть важная разница!
Сказать, что «ускорение есть изменение скорости», все равно, что сказать «скорость — это изменение положения» (это звучит глупо, не правда ли? Это?).Скорость говорит вам, как быстро меняется положение. Ускорение сообщает вам, насколько высока скорость меняется.
Ускорение — это , а не изменение скорости!
Расчет ускорений:
Предположим, что скорость спринтера изменилась с 0 м/с до 10 м/с за 2 секунд в начале гонки. Каково ее ускорение?
Обратите внимание на нечетные единицы измерения ускорения – расстояние (длину), деленное в 2 раза.Одна единица времени получается из скорости в числителе дробь, а другой исходит из знаменателя. Количество Например, 4 мили/час/сек — это ускорение (4 мили/час/сек означает, что скорость изменяется на 4 мили/ч каждую секунду).
Работа с ускорениями:
Пример:
Автомобиль трогается с места и разгоняется со скоростью 2 м/с/с в течение 5 секунд. Как быстро это будет происходить?
Решение:
Утверждение “автомобиль трогается с места” означает, что автомобиль стартует скорость 0 м/с.Ускорение 2 м/с/с означает, что автомобиль скорость изменяется на 2 м/с каждую секунду. Если скорость автомобиля начинается при скорости 0 м/с и изменении на 2 м/с в первую секунду она будет равна 2 м/с по истечении 1 секунды. В течение второй секунды (?!) его скорость увеличивается на 2 м/с – с 2 м/с до 4 м/с. Его скорость будет быть 6 м/с через 3 секунды, 8 м/с через 4 секунды и 10 м/с через 5 секунд. секунды.
В качестве альтернативы, если вы предпочитаете, есть более алгебраический подход.Если тогда , так . Если скорость начинается с 0 м/с и изменяется на 10 м/с, она заканчивается на 10 РС.
Указание направления ускорения:
Как и скорость, ускорения в одномерных движениях положительные, если они действуют в положительном направлении, и отрицательные, если они действовать в негативном направлении. Определить направление немного более абстрактно для ускорений, чем для скоростей, однако – по крайней мере пока не привыкнешь.
Нужно помнить 3 вещи:
Ускорение объекта есть изменение его скорости разделить на время.
Если объект движется в положительном направлении, его скорость положительный. Если он движется в отрицательном направлении, скорость отрицательная.
Изменение скорости равно конечной скорости минус начальная скорость.
Пример:
Скорость автомобиля изменяется с +2 м/с до +10 м/с за 4 секунды.Что его ускорение?
Решение:
Изменение скорости автомобиля = конечная скорость – начальная скорость = 10 м/с – 2 м/с = 8 м/с. Его ускорение = его изменение скорости разделить на затраченное время = (8 м/с)/(4 с) = 2 м/с/с.
Пример:
Скорость автомобиля изменяется с +10 м/с до +2 м/с за 4 секунды. Что его ускорение?
Решение:
Изменение скорости автомобиля = конечная скорость – начальная скорость = 2 м/с – 10 м/с = -8 м/с. Его ускорение = его изменение скорости разделить на затраченное время = (-8 м/с)/(4 с) = -2 м/с/с.
Пример:
Скорость автомобиля изменяется с -2 м/с до -10 м/с за 4 секунды. Что его ускорение?
Решение:
Изменение скорости автомобиля = конечная скорость – начальная скорость = -10 м/с – (-2 м/с) = -10 м/с + 2 м/с = -8 м/с. Его ускорение = его изменение скорости, деленное на затраченное время = (-8 м/с)/(4 с) = -2 м/с/с.
Пример:
Скорость автомобиля изменяется с -10 м/с до -2 м/с за 4 секунды. Что его ускорение?
Решение:
Изменение скорости автомобиля = конечная скорость – начальная скорость = -2 м/с – (-10 м/с) = -2 м/с + 10 м/с = 8 м/с. Его ускорение = его изменение скорости, деленное на затраченное время = (8 м/с)/(4 с) = 2 м/с/с.
Из этих примеров обратите внимание, что вы просто следуете (простому) правила, особенно помня, что изменение скорости является конечная скорость минус начальная скорость – НЕ большое число минус маленькое число!
Расчет ускорений при изменении только направления:
В примерах выше вы видели, что это довольно просто вычислить ускорение тела при изменении его скорости используя алгебру. Объект также ускоряется, когда его направление изменяется, но «нормальной» алгебры недостаточно, чтобы вычислить ускорение в этом случае — нужно использовать векторную алгебру , а мы не будем заморачиваться с вычислением этих ускорений в этом курсе.
Практический тест на ускорение:
Вам понадобится браузер с поддержкой Java, чтобы пройти практический тест по Первому закону Ньютона.

[Глава 2 цели]

БХС -> Мистер Стэнбро -> Физика -> Механика -> Кинематика -> эта страница

последнее обновление 22 ноября 2005 г., JL Стэнбро
Уравнения для определения высоты седла велосипеда на основе желаемой кинематики сустава и геометрии велосипеда
Методы: Сорок здоровых взрослых (17 женщин, 23 мужчины; среднее значение (SD): 28). 6 (7,2) лет; 24,2 (2,6) кг/м ² ). Кинематический анализ был проведен для 18 трехминутных циклов езды на велосипеде, включая все комбинации 3 горизонтальных и 3 вертикальных положений седла и 2 длин кривошипа. Как для минимального, так и для максимального сгибания колена предикторы были определены с использованием регрессии с наименьшим абсолютным усадкой и оператором выбора (LASSO), а окончательные модели были подобраны с использованием линейной регрессии. Вторичный анализ определил, зависят ли уравнения высоты седла от пола.
Результаты: Уравнение для прогнозирования положения седла по минимальному углу сгибания колена (R ² = 0,97; среднеквадратическая ошибка (RMSE) = 1,15 см) было следующим: сгибание °) + 0,003 (внутренний шов см) (угол подседельной трубы °). Уравнение максимального сгибания колена (R ² = 0,97; RMSE = 1,15 см): высота седла (см) = 41,63 + 0. 78 (внутренний шов см) – 0,25 (максимальное сгибание колена °) + 0,002 (внутренний шов см) (угол подседельной трубы °). Уравнения высоты седла не зависели от пола.
Выводы: Эти уравнения обеспечивают новую практическую стратегию подбора велосипеда, учитывающую антропометрические данные гонщика, геометрию велосипеда и заданную пользователем кинематику. Основные моменты В этой работе были разработаны простые уравнения для предписанной высоты седла велосипеда, которые определяют желаемую кинематику колена.Отдельные уравнения представлены для определения минимального или максимального угла сгибания колена. Уравнения могут быть обобщены для всадников обоих полов, а также для различных антропометрических показателей и возрастов.
Ключевые слова: Седло; биомеханические явления; травмы; колено; машинное обучение.
AP Физика 1 — Кинематика. «То, что я не могу создать, я не… | Кай Алдаг
«То, что я не могу создать, я не понимаю»
— Ричард Фейнман
.В первом разделе будут рассмотрены термины и формулы, используемые в этом разделе. Второй раздел представляет собой серию вопросов в порядке возрастания сложности. Каждое решение начинается с диаграммы (хотя диаграммы часто не нужны, я покажу грубое приближение того, как будет выглядеть система), а затем переходит к алгебре.
Примечание: из-за технических ограничений некоторые математические обозначения были изменены. Нижний индекс gamma ( ᵧ ) предназначен для нижнего индекса y.
Термины:
Кинематика — как и любая область — имеет свой собственный словарь. Базовый словарь для этого устройства приведен ниже:
Начальная скорость (vᵢ): Скорость восстановления — это векторное представление скорости. Конкретно, насколько мгновенно меняется наше смещение в начале системы.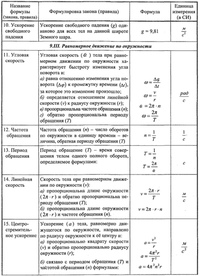
Конечная скорость (vf): Мгновенная скорость в конце системы.
Вершина: вершина – это точка с максимальным вертикальным смещением нашего снаряда.Другими словами, там, где наш снаряд находится выше всего.
Гравитация (г): Гравитация на Земле — это вертикальное ускорение, притягивающее все объекты к центру Земли со скоростью -9,8 м/с² [вверх].
Ключевые понятия:
Для простоты будем считать, что при работе со снарядами отсутствует трение о воздух. Очевидным преимуществом, которое мы получаем от этой абстракции, является то, что мы можем представить дугу снаряда в виде параболы.
2D-снаряды можно разложить на два одномерных компонента: вертикальный и горизонтальный. Используя это, мы можем использовать наши надежные функции тригонометрии, чтобы найти решение для каждого компонента с заданным начальным углом, а также комбинированной скоростью.
Используя диаграмму слева, мы можем подставить наши значения, данные нам в каждом вопросе. Скажем, например, что угол запуска (θ) равен 20°, а начальная скорость равна 30 м/с (в нашем треугольнике скоростей это будет наша гипотенуза). Используя эти две переменные, мы можем найти нашу начальную вертикальную скорость, получив произведение синуса θ и гипотенузы (30sin(20°) = 10.26 м/с [вверх]). Затем мы можем использовать функцию косинуса, чтобы найти начальную горизонтальную скорость (30cos(20°) = 28,19 м/с [справа]).
Отличительной особенностью парабол является то, что мы можем отражать их по горизонтали от вершины (вершины с точки зрения физики). Это означает, что время, необходимое для достижения вершины, равно времени, которое требуется снаряду, чтобы вернуться на ровную поверхность (на ту же высоту, с которой он был запущен). Он также вернется на землю под тем же углом и с той же конечной скоростью, что и начальная скорость системы.
Горизонтальная скорость системы всегда будет постоянной. Это связано с тем, что на снаряд не действует ускорение. Поэтому, чтобы решить горизонтальное смещение, мы просто находим время всей системы, а затем берем произведение начальной горизонтальной скорости и полного времени.
Чтобы лучше усвоить эти концепции, попробуйте симуляцию движения снаряда из Университета Колорадо в Боулдере.
Формулы:
при работе со снарядами мы будем использовать несколько ключевых кинематических уравнений: Представьте, что мяч брошен прямо вверх с начальной скоростью 15 м/с.Через какое время мяч вернется на землю? Какова максимальная высота мяча?
Чтобы решить первую часть этого вопроса, мы рассчитаем время до апекса , затем мы можем удвоить его до общего времени возвращения на землю.
VF = VI + на
0 = 15-9.8T
-15 = -9.8T

1,53с = T (до вершины)
3,06 = t (на землю)
d = vᵢ t + 1/2 at
d = 15 (1.