Главная
Определенного интеграла формулы: Определенный интеграл и методы его вычисления с примерами решения

Определенного интеграла формулы: Определенный интеграл и методы его вычисления с примерами решения

Формулы и уравнения определенных интегралов

  1. Формула Ньютона-Лейбница:
    , где
  2. Формула интегрирования по частям в определенном интеграле:
  3. Замена переменной в определенном интеграле:
    Если функция f(x) непрерывна на отрезке [a;b], а функция x=ϕ(t) непрерывно дифференцируема на отрезке [α;β], где a=ϕ(α), b=ϕ(β), то
  4. Интегралы с бесконечными пределами:
  5. Признаки сходимости интегралов с бесконечными пределами (признаки сравнения):
    1. Если a≤x≤+∞, 0≤f(x)≤g(x), то из сходимости
    сходимость
    ≤
    из расходимости расходимость
    2. Если при a≤x≤+∞, f(x)>0, g(x)>0 и существует конечный предел ≠0, то интегралы сходятся или расходятся одновременно.
    Эталоном сравнения служит интеграл:
    он сходится при p>1 и расходится при p≤1.
  6. Интегралы от неограниченных функций:
    Если функция f(x) непрерывна при a≤x<b и
    , то
    .
  7. Признаки сходимости несобственных интегралов от неограниченных функций:
    Аналогичны признакам сходимости интегралов с бесконечными пределами. Эталоном сравнения служит интеграл он сходится при 0<p<1 и расходится при p>1.
    Приложения определенного интеграла
  1. Площадь плоской фигуры
    1.1. Фигура ограничена графиком функции y=f(x)(f(x)≥0), прямыми x=a, x=b и осью Ox:
    .
    1.2. Фигура ограничена графиками функций y=f1(x) и y=f2(x), f1(x)≤2f2(x), и прямыми x=a, x=b:
    .
    1.3. Фигура ограничена кривой, имеющей параметрические уравнения
    x=x(t)    , y=y(t), прямыми x=a, x=b и осью Ox:
    , где f=x(t1), b=x(t2), y(t)≥0 на отрезке [t1; t2].
    1.4. Площадь криволинейного сектора, ограниченного графиком непрерывной функции ρ=ρ(ϕ), лучами ϕ=α, ϕ=β, где ϕ и ρ — полярные координаты:
    .
  2. Длина дуги кривой
    2.1. Гладкая кривая задана явно, y=f(x), a≤x≤b:
    .
    2.2. Кривая задана параметрически, x=x(t), y=y(t), z=z(t), t1≤t≤t2:
    (для плоской кривой z(t)≡0).
    2.3. Кривая задана в полярных координатах, ρ=ρ(ϕ), α≤ϕ≤β:
    .
  3. Площадь поверхности вращения, образованной вращением вокруг оси Ox дуги кривой
    3.1. Дуга задана явно, y=f(x), a≤x≤b:
    .
    3.2. Дуга задана параметрически, x=x(t), y=y(t), t1≤t≤t2:
    .
    3.3. Дуга задана в полярных координатах, ρ=ρ(ϕ), α≤ϕ≤β:
    .
  4. Объем тела
    4.1. Тело заключено между плоскостями x=a и x=b, площадь сечения тела плоскостью, перпендикулярной оси
    Ox     – известная функция S=f(x), непрерывная на отрезке [a; b], f(x)≥0:
    .
    4.2. Криволинейная трапеция, ограниченная кривой y=f(x), a≤x≤b вращается вокруг оси Ox:
    .
    4.3. Криволинейная трапеция, ограниченная кривой x=g(y), c≤y≤d вращается вокруг оси Oy:
    .

Приложения определенного интеграла – интернет энциклопедия для студентов

  1. Площадь плоской фигуры
  2. Длина дуги кривой
  3. Вычисление объема тела по площадям параллельных сечений
  4. Объем тела вращения
  5. Площадь поверхности тела вращения

Свое широкое применение определенный интеграл находит в многочисленных прикладных математических и физических задачах.

Например, применение определенного интеграла в геометрических задачах проявляет себя при решении задач на нахождение площадей плоских фигур и поверхностей, которые имеют сложные формы. Определенный интеграл применим для нахождения объема тела вращения, тела произвольной формы, а также для нахождения длины кривой, как на плоскости, так и в пространстве.

При помощи определенного интеграла вычисляются статистические моменты, массы и центры масс для произвольной кривой и поверхности в задачах физики и теоретической механики.

{b} y(x) \cdot d x} \)

6.5 Вычисление определенных интегралов – методы исчисления 1

Перейти к содержимому

Цели обучения

  • Применить основные формулы интегрирования.
  • Объясните значение теоремы о чистом изменении.
  • Используйте теорему о чистом изменении для решения прикладных задач.
  • Применить интегралы от нечетных и четных функций.

В этом разделе мы используем некоторые основные формулы интегрирования, изученные ранее, для решения некоторых ключевых прикладных задач. Важно отметить, что эти формулы представлены в терминах неопределенные интегралов. Хотя определенные и неопределенные интегралы тесно связаны между собой, следует помнить о некоторых ключевых различиях. Определенный интеграл — это либо число (когда пределы интегрирования — константы), либо отдельная функция (когда один или оба предела интегрирования — переменные). Неопределенный интеграл представляет собой семейство функций, каждая из которых отличается на константу.

По мере того, как вы будете лучше знакомиться с интегрированием, вы почувствуете, когда использовать определенные интегралы и когда использовать неопределенные интегралы. Вы, естественно, выберете правильный подход к данной проблеме, не слишком задумываясь об этом. Однако до тех пор, пока эти концепции не закрепятся в вашем уме, тщательно подумайте, нужен ли вам определенный интеграл или неопределенный интеграл, и убедитесь, что вы используете правильную запись, основанную на вашем выборе.

Напомним правило о свойствах определенных интегралов. Рассмотрим несколько примеров применения этих правил.

 

Теорема о чистом изменении

Теорема о чистом изменении рассматривает интеграл скорости изменения . В нем говорится, что при изменении количества новое значение равно первоначальному значению плюс интеграл скорости изменения этого количества. Формула может быть выражена двумя способами. Второй более знаком; это просто определенный интеграл. 9{b}F\text{‘}(x)dx=F(b)-F(a).\hfill \end{array}$$

Вычитание [латекс]F(a)[/латекс] с обеих сторон из первого уравнения дает второе уравнение. Поскольку это эквивалентные формулы, какую из них мы используем, зависит от приложения.

Значение теоремы о чистом изменении заключается в результатах. Чистое изменение может быть применено к площади, расстоянию и объему, и это лишь некоторые из приложений. Чистое изменение учитывает отрицательные величины автоматически, без необходимости писать более одного интеграла. Чтобы проиллюстрировать это, давайте применим теорему о чистом изменении к функции скорости, результатом которой является смещение.

Мы рассмотрели простой пример этого в разделе «Площадь и определенный интеграл». Предположим, что автомобиль движется прямо на север (в положительном направлении) со скоростью 40 миль в час между 14:00 и 14:00. и 16:00, затем машина движется на юг со скоростью 30 миль в час между 16:00 и 16:00. и 17:00 Мы можем изобразить это движение, как показано на этом рисунке.

Рисунок 6.17 На графике показана зависимость скорости от времени при заданном движении автомобиля.

Подробное описание: Линии y=40 и y=-30 проведены над [2,4] и [4,5] соответственно. Области между линиями и осью x заштрихованы. 9{5}30dt\hfill \\ & =80+30\hfill \\ & =110.\hfill \end{array}$$

Таким образом, между 14:00 и 17:00 машина проехала в общей сложности 110 миль.

Подводя итог, чистый водоизмещение может включать как положительные, так и отрицательные значения. Другими словами, функция скорости учитывает как расстояние вперед, так и расстояние назад. Чтобы найти чистое смещение, проинтегрируйте функцию скорости по интервалу. С другой стороны, общее пройденное расстояние всегда положительно. Чтобы найти общее расстояние, пройденное объектом независимо от направления, нам нужно проинтегрировать абсолютное значение функции скорости.

 

Применение теоремы о чистом изменении

Теорему о чистом изменении можно применить к потоку и потреблению жидкостей, как показано в следующем примере.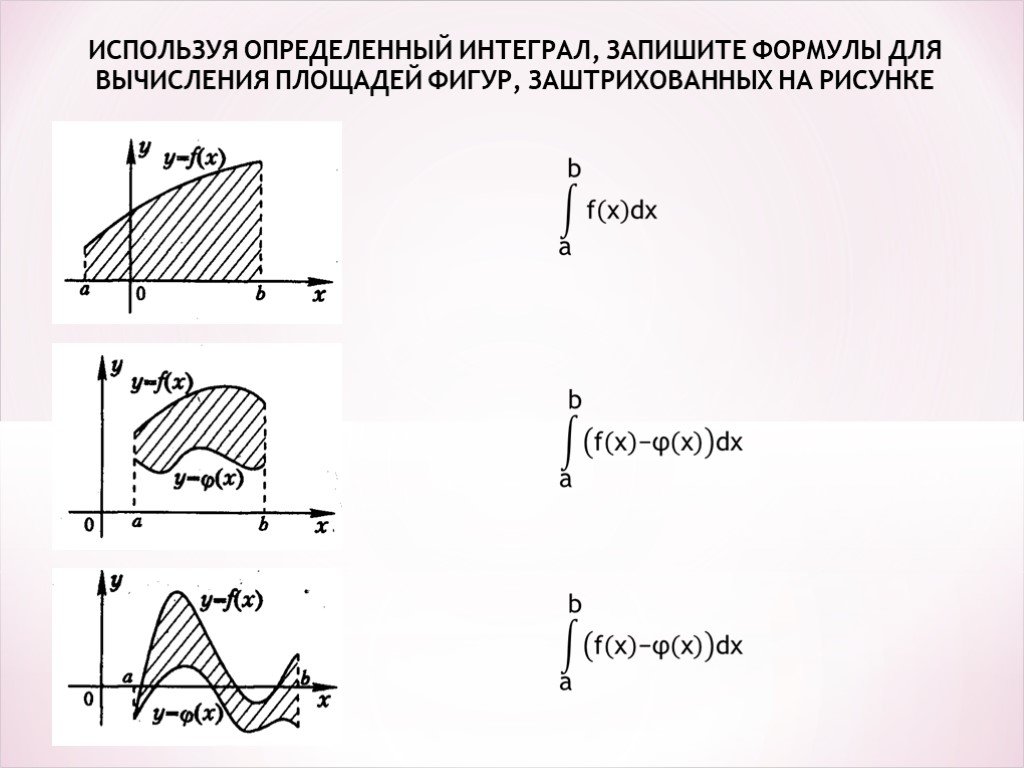

 

В разделе «Функции» мы видели, что четная функция — это функция, в которой [latex]f(\text{−}x)=f(x)[/latex] для всех [latex]x[/latex] в домен, то есть график кривой не изменится, если [latex]x[/latex] заменить на −[latex]x[/latex]. Графики четных функций симметричны относительно оси [latex]y[/latex]. Нечетная функция — это функция, в которой [latex]f(\text{−}x)=\text{−}f(x)[/latex] для всех [latex]x[/latex] в домене, а граф функция симметрична относительно начала координат.

Интегралы четных функций, когда пределы интегрирования от −[latex]a[/latex] до [latex]a[/latex], включают две равные площади, поскольку они симметричны относительно [latex]y[/ латекс]-ось. Интегралы нечетных функций, когда пределы интегрирования равны [латекс]\влево[\текст{−}а,а\вправо],[/латекс] равны нулю, поскольку площади выше и ниже [латекс]х[/ латекс]-оси равны.

 

Правило: интегралы от четных и нечетных функций

Для непрерывных четных функций, таких что [latex]f(\text{−}x)=f(x),[/latex] 9{а}f(x)dx=0. $$

 

License

Techniques of Calculus 1 Ларри Мусолино находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, если не указано иное.

Поделиться этой книгой

Поделиться в Твиттере

Интегрирование по частям для Определенные интегралы с пределами, правила, примеры

Главная > Определенный интеграл с использованием формулы интегрирования по частям

Интегрирование по частям для определенного интеграла с пределами, формулами UV и правилами

В этой статье вы узнаете, как вычислить определенный интеграл

с помощью интегрирования по частям по формуле UV . Как правило, большинство студентов не понимают, как использовать предел интегральной функции после применения формулы UV интегрирования по частям.

Формула интегрирования по частям для решения пределов определенного интеграла задач-

9{ b } v.

Оставить комментарий