Определить расстояние от точки D до плоскости треугольника АВС (пример выполнения) — АСФ.NOPS
Определить расстояние от точки D до плоскости треугольника АВС (пример выполнения) — АСФ.NOPS- Дисциплины
- Начертательная геометрия, инженерная и компьютерная графика
- Определить расстояние от точки D до плоскости треугольника АВС (пример выполнения)
РЕШЕНИЕ: Расстояние от точки до плоскости определяется длиной отрезка перпендикуляра, проведенного из заданной точки к заданной плоскости.
Далее приводится поэтапное графическое решение варианта №17 из данного списка вариантов.
Задачу решаем в следующей последовательности:
|
Рис. |
Строим плоскость треугольника АВС A (70, 45, 60), Построить свой треугольник онлайн можно перейдя по ссылке. |
|
Рис.2 |
Затем строим в плоскости треугольника АВС фронталь и горизонталь (см. рис.2).
Фронталь это линия, которая параллельна оси ОХ на горизонтальной плоскости проекции (нижняя часть).
Данные линии проводятся через вершины треугольника (через точки А, B, C).
В нашем случае через вершину А мы проводим фронталь AF,
а через вершину С проводим горизонталь CH. |
|
Рис.3 |
После того как мы построили фронталь и горизонталь, необходимо из точки При этом горизонтальная проекция перпендикуляра (от точки D1) должна быть перпендикулярна к горизонтальной проекции горизонтали C1H1. А фронтальная проекция (от точки D2) перпендикулярна к фронтальной проекции фронтали A2F2; |
|
Рис.4 |
Теперь необходимо определить точку пересечения перпендикуляра с данной плоскостью,
заключив перпендикуляр во вспомогательную плоскость частного положения (см. Перпендикуляр через точку D1 заключаем во вспомогательную плоскость частного положения ∑1 Примечание: необязательно это делать через точку D1, результат через точку D2 будет идентичным. Так же необязательно рисовать вспомогательную плоскость частного положения ∑1, ее можно просто представить, что мы ее там проводим. После того как мы провели вспомогательную плоскость ∑1 находим точки пересечения данной плоскости (M1P1) с треугольником АВС. Проецируем их на фронтальную плоскость проекции и получаем точки M2P2.
Потом находим точку пересечения линии M2P2 вспомогательной плоскости
с перпендикуляром от точки D2 и отмечаем точку К2. |
|
Рис.5 |
После того как мы провели перпендикуляр DK, осталось определить его действительную величину способом прямоугольного треугольника (см. рис.5). Определяем расстояние по вертикали от точки D до точки K на какой-либо плоскости проекций. Например на горизонтальной (нижней) плоскости проекции. Примечание:
Откладываем это расстояние перпендикулярно отрезку DK
на противоположной плоскости проекции (в нашем случа на фронтальной) от любой из вершин (например от точки D)
и получили нулевую точку D0.
Расстояние от точки D0 до точки K2
и является искомым расстоянием от точки |
|
Рис.6 |
Найдя расстояние от точки до плоскости треугольника АВС, можно начать строить точку симметричную точке D относительно данного треугольника (см. рис.6). Симметричная точка подразумевает собой точку, которая отстоит от плоскости треугольника АВС на таком же расстоянии, что и точка D, но с противоположной стороны.
Рассмотрим полученный нами отрезок D0K2.
В противоположную сторону от точки |
|
Рис.7 |
Затем проводим перпендикуляр к линии пенпендикуляра от точки D на рассматриваемой плоскости проекции (см. рис.7).
В нашем случае на фронтальной плоскости проекции к удлиненной линии D2K2.
На пересечении ставим точку Е2. |
|
Рис.8 |
Строим проекцию полученной точки на противоположную плоскость проекции так же на линию перепендикуляра (см. рис.8).
В нашем случае проецируем полученную точку Е2 на горизонтальную плоскость проекции
на линию перепендикуляра (удлинненную линию D1K1). |
Используя этот сайт, вы соглашаетесь с тем, что мы используем файлы cookie.
2.3. Определение расстояния от точки до плоскости
Расстояние от точки до плоскости можно определить одним из следующих способов:
1) прямым путем: опустить перпендикуляр из точки на плоскость, найти основание перпендикуляра и определить расстояние между точками – заданной и найденной;
2) вращением привести заданную систему в положение, когда плоскость перпендикулярна какой-либо плоскости проекций;
3) совмещением: провести через точку горизонтально или вертикальнопроецирующую плоскость, перпендикулярную к заданной плоскости, и совмещением вспомогательной плоскости с какой-либо плоскостью проекций найти положение заданной точки и линии пересечения плоскостей;
4)
заменой плоскостей проекций: заменить
одну из плоскостей проекций новой,
которая перпендикулярна заданной
плоскости.
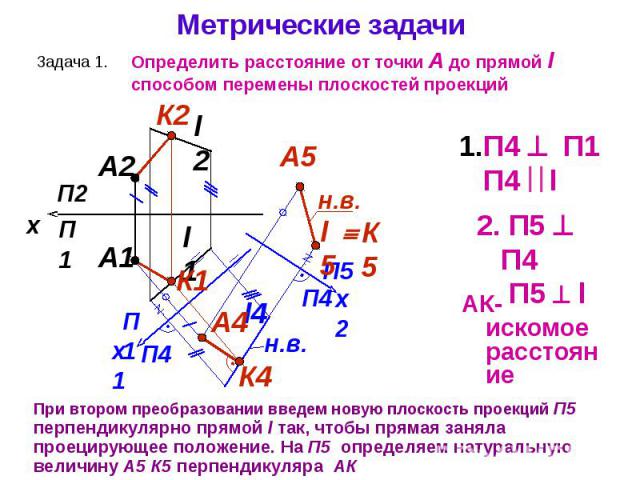
Задача 11. Определить расстояние от точки К до плоскости треугольника ABC (рис. 14) методом замены плоскостей проекций.
Рис. 14. Определение расстояния от точки до плоскости
Решение. Заменяем плоскость проекций П2 П4. Проводим горизонталь в плоскости треугольника. Новая ось проекций X1 h1. Находим проекции точки К4 и треугольника А4В4С4. Опускаем из точки К4 перпендикуляр на проекцию треугольника А4В4С4. Отрезок К4 К4‘ является искомым расстоянием.
2.4. Определение расстояния от точки до поверхности вращения
Расстояние
от точки до
поверхности вращения
измеряется величиной отрезка нормали,
проведенной из заданной точки. Основание
нормали лежит на ближайшей точке
меридиана, расположенного в одной
плоскости с заданной точкой и осью
вращения.
Задача 12. Найти расстояние от точки до поверхности вращения (рис. 15).
а б в
Рис. 15. Определение расстояния от точки до сферы
Решение. Если бы точка А находилась в одной плоскости с меридианом или экватором, тогда достаточно было бы соединить соответствующую проекцию с центром, чтобы определить искомое.
Решим
эту задачу вращением вокруг фронтально
проецирующей пря-
мой – оси i, проходящей
через центр сферы. Введем плоскость-посредник
– фронтально Σ2 проецирующую плоскость через заданную
точку А2 и ось i2.
Плоскость Σ пересекает сферу по
полуокружности, которая на плоскость
П1 проецируется в полуэллипс. Повернем
плоскость Σ2 вместе с точкой А2 вокруг оси до горизонта. Теперь сечение
плоскостью Σ’2 спроецируется на П1 без искажения и совпадет с проекцией
экватора, значит, новая проекция точки
А’2 лежит в одной плоскости с экватором. Соединим А’1 с О1 и там, где этот отрезок пересечет экватор,
обозначим точку М1.
Соединим А’1 с О1 и там, где этот отрезок пересечет экватор,
обозначим точку М1.
Отрезок А’1М’1 измеряет расстояние от точки А’ до преобразованного сечения сферы. Этот отрезок определяет расстояние от точки А до сферы, а точка М – ближайшая точка сферы к точке А.
2.5. Определение расстояния между параллельными прямыми
Расстояние между параллельными прямыми измеряется отрезком перпендикуляра между ними.
Задача 13. Найти расстояние между параллельными прямыми общего положения методом замены плоскостей проекций.
Рис. 16. Определение расстояния между параллельными прямыми
Решение.
Сначала построено изображение прямых
на плоскости П1 П4.
В этой системе плоскостей прямые занимают
положение линии уровня:
а1(b1)||
П4 (рис. 16).
16).
В системе плоскостей П4 П5 прямые занимают проецирующее по отношению к плоскости П5 положение: П5 а4(b4). Отрезок M5K5 между проекциями прямых определяет истинную величину расстояния между прямыми а и b.
Расстояние между точкой и плоскостью
Расстояние между точкой и плоскостью — это длина перпендикуляра к плоскости, проходящего через данную точку. Другими словами, мы можем сказать, что расстояние между точкой и плоскостью — это длина вектора нормали, опущенного из данной точки на данную плоскость. Если мы хотим определить расстояние между точкой P с координатами (x o , y o , z o ) и данной плоскостью уравнением Ax + By + Cz = D, то расстояние между точкой P и данная плоскость задается |Ax o + By o + Cz o + D|/√(A 2 + B 2 + C 2 ).
| 1. | Что такое расстояние между точкой и плоскостью? |
| 2. | Формула расстояния между точкой и плоскостью |
| 3. | Расстояние между точкой и плоскостью Доказательство |
| 4. | Как применить формулу расстояния между точкой и плоскостью? |
| 5. | Часто задаваемые вопросы о расстоянии между точкой и плоскостью |
Что такое расстояние между точкой и плоскостью?
Расстояние между точкой и плоскостью — это кратчайшее перпендикулярное расстояние от точки до данной плоскости. Проще говоря, кратчайшее расстояние от точки до плоскости — это длина перпендикуляра, параллельного вектору нормали, опущенного из данной точки на данную плоскость. Давайте теперь посмотрим формулу для расстояния между точкой и плоскостью.
Расстояние между точкой и плоскостью Формула
Кратчайшее расстояние между точкой и плоскостью равно длине вектора нормали, который начинается в данной точке и касается плоскости. Рассмотрим точку P с координатами (x o , y o , z o ) и данную плоскость π с уравнением Ax + By + Cz = D. Тогда расстояние между точкой P и плоскостью π равно определяется |Ax o + By o + Cz o + D|/√(A 2 + B 2 + C 2 ).
Рассмотрим точку P с координатами (x o , y o , z o ) и данную плоскость π с уравнением Ax + By + Cz = D. Тогда расстояние между точкой P и плоскостью π равно определяется |Ax o + By o + Cz o + D|/√(A 2 + B 2 + C 2 ).
Расстояние между точкой и плоскостью Доказательство
Теперь, когда мы знаем формулу расстояния между точкой и плоскостью, выведем ее формулу, используя различные формулы трехмерной геометрии. Рассмотрим точку P с координатами (x o , y o , z o ) в трехмерном пространстве и плоскость с вектором нормали, скажем, v = (A, B, C) и точку Q с координатами (x 1 , у 1 , з 1 ) на самолете. Тогда уравнение плоскости задается как A(x – x 1 ) + B(y – y 1 ) + C(z – z 1 ) = 0. Это уравнение можно переписать как Ax + By + Cz + (- Ax 1 – By 1 – Cz 1 ) = 0 ⇒ Ax + By + Cz + D = 0, где D = – (Ax 1 + By 1 + Cz 1 ). Отсюда имеем:
Отсюда имеем:
- Уравнение плоскости: Ax + By + Cz + D = 0
- Точка P: (x или , у или , я или )
- Нормальный вектор: Ai + Bj + Ck
Пусть w — вектор, соединяющий точки P(x o , y o , z o ) и Q(x 1 , y 1 , z 6 1 ). Тогда w = (x o – x 1 , y o – y 1 , z o – z 1 ). Теперь давайте вычислим единичный вектор нормали, т. Е. Вектор нормали с величиной, равной 1, который определяется делением вектора нормали v на его величину. Единичный вектор нормали определяется выражением
n = v/||v||
= (A, B, C)/√(A 2 + B 2 + C 2 )
Теперь расстояние между точкой P и данной плоскостью есть не что иное, как длина проекции вектор w на единичный вектор нормали n. Как мы знаем, длина вектора n равна единице, расстояние от точки P до плоскости есть модуль скалярного произведения векторов w и n, т.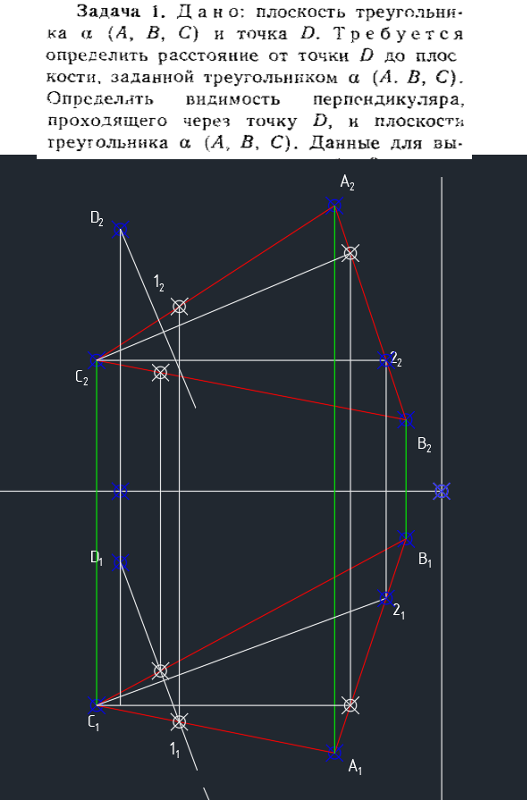 е.
е.
Расстояние, d = |w.n|
= | (х о – х 1 , у o – у 1 , z o – z 1 ). [(A, B, C)/√(A 2 + B 2 + C 2 )] |
= |A(x o – x 1 ) + B(y o – y 1 ) + C(z o – z 1 7 )|/0 + В 2 + С 2 )
= | Ax o + By o + Cz o – (Ax 1 + By 1 + Cz 1 ) |/√(A 2 + В 2 + С 2 )
= | Ax o + By o + Cz o + D |/√(A 2 + B 2 + C 2 ) [Поскольку D = – (Ax 90 6 90 0 60 1 90 + Cz 1 )]
Так как точка Q с координатами (x 1 , y 1 , z 1 ) является произвольной точкой на данной плоскости и D = – (Ax 1 + By 1 + Cz 1 ), поэтому формула остается той же для любой точки Q на плоскости и, следовательно, не зависит от точки Q, т. е. где бы точка Q ни лежала на плоскости, формула для расстояния между точкой и плоскостью остается прежним. Следовательно, расстояние между точкой P(x o , y o , z o ) и плоскость π: Ax + By + Cz + D = 0 определяется выражением, d = |Ax o + By o + Cz o + D |/√(А 2 + В 2 + С 2 )
е. где бы точка Q ни лежала на плоскости, формула для расстояния между точкой и плоскостью остается прежним. Следовательно, расстояние между точкой P(x o , y o , z o ) и плоскость π: Ax + By + Cz + D = 0 определяется выражением, d = |Ax o + By o + Cz o + D |/√(А 2 + В 2 + С 2 )
Как применить формулу расстояния от точки до плоскости?
Мы вывели формулу расстояния от точки до плоскости, решим пример с помощью формулы, чтобы понять ее применение и определить расстояние между точкой и плоскостью.
Пример: Определить расстояние между точкой P = (1, 2, 5) и плоскостью π: 3x + 4y + z + 7 = 0
Решение: Мы знаем, что формула для расстояния между точкой и плоскость: d = |Ax o + By o + Cz o + D |/√(A 2 + B 2 + C 2 )
,, Здесь B = 4, C = 1, D = 7, x o = 1, y o = 2, z o = 5
Подставляя значения в формулу, имеем
d = |Ax o + By o + Cz o + D |/√(A 2 + B 2 + C 2 + 3 × 3 ×
) | 2 + 1 × 5 + 7|/√(3 2 + 4 2 + 1 2 )= |3 + 8 + 5|/√(9 + 16 + 1)
= |16 |/√26
= 8√26/13 ед.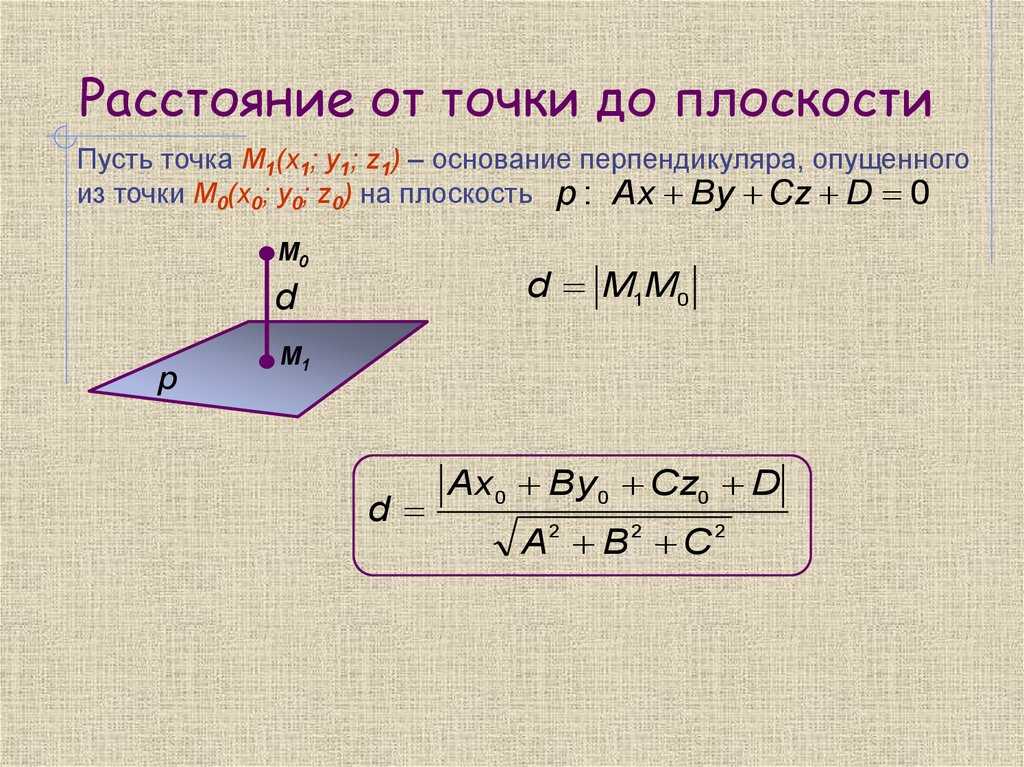 0006 + Cz o + D |/√(A 2 + B 2 + C 2 )
0006 + Cz o + D |/√(A 2 + B 2 + C 2 )
Темы, связанные с расстоянием между точкой и плоскостью
- Формула расстояния
- Расстояние между двумя точками
- Формула Евклидова расстояния
Часто задаваемые вопросы о расстоянии между точкой и плоскостью
Что такое расстояние между точкой и плоскостью в геометрии?
Расстояние между точкой и плоскостью — это длина перпендикуляра к плоскости, проходящего через данную точку. Другими словами, расстояние между точкой и плоскостью есть кратчайшее перпендикулярное расстояние от точки до данной плоскости.
Какая формула для расстояния между точкой и плоскостью?
Расстояние между точкой P(x o , y o , z o ) и плоскость π: Ax + By + Cz + D = 0 определяется выражением, d = |Ax o + By o + Cz o + D |/√(A 2 + B 2 + C 2 )
Как найти кратчайшее расстояние между точкой и плоскостью?
Чтобы найти кратчайшее расстояние между точкой и плоскостью, воспользуемся формулой 2 ), где (х o , у o , z o ) — заданная точка, а Ax + By + Cz + D = 0 — уравнение данной плоскости.
Какое расстояние между точкой и плоскостью x-z?
Расстояние между точкой (x o , y o , z o ) и плоскостью x-z определяется координатой y, т. е. y o
Как найти кратчайшее расстояние точка к плоскости?
Чтобы вычислить кратчайшее расстояние от точки до плоскости, мы рассматриваем длину вектора, параллельного вектору нормали к плоскости, которая опускается из данной точки на данную плоскость.
Каково расстояние между точкой и плоскостью, когда точка лежит на данной плоскости?
Расстояние между точкой и плоскостью равно нулю, если данная точка лежит на данной плоскости.
Расстояние от точки до плоскости
Вот краткий набросок того, как рассчитать расстояние от точки
$P=(x_1,y_1,z_1)$ в плоскость, определяемую вектором нормали
$\vc{N}=(A,B,C)$ и точка $Q=(x_0,y_0,z_0)$. Уравнение для
плоскость, определяемая $\vc{N}$, и $Q$ есть $A(x-x_0)+B(y-y_0) +C(z-z_0) =
0$, что можно записать как $Ax+By+Cz+D=0$, где
$D=-Ax_0-By_0-Cz_0$.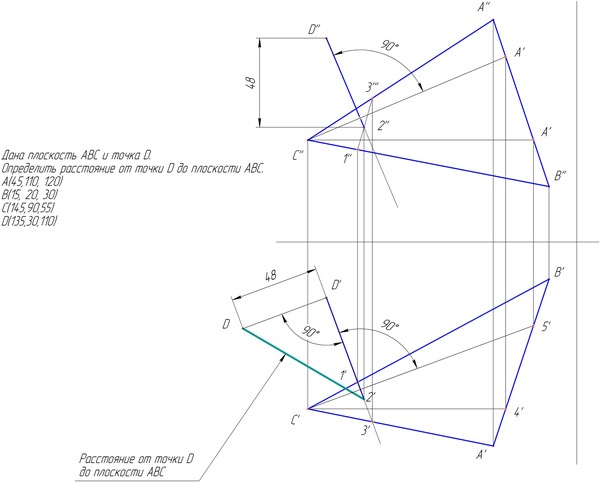
Этот апплет демонстрирует настройку задачи и метод, который мы будем использовать для вывода формулы расстояния от плоскости до точка $P$.
Загрузка апплета
Расстояние от точки до плоскости. Набросок способа расчета расстояния от точки $\color{red}{P}$ (выделена красным) до плоскости. Вектор $\color{green}{\vc{n}}$ (выделен зеленым цветом) является единичным вектором нормали к плоскости. Вы можете перетаскивать точку $\color{red}{P}$, а также вторую точку $\vc{Q}$ (желтого цвета), которая ограничена плоскостью. Хотя вектор $\color{green}{\vc{n}}$ не меняется (поскольку плоскость фиксирована), он перемещается вместе с $\color{red}{P}$, чтобы всегда находиться в конце серого цвета. отрезок прямой из $\color{red}{P}$, перпендикулярный плоскости. Это расстояние от $\color{red}{P}$ до плоскости равно длине этого сегмента серой линии. Это расстояние является длиной проекции вектора из $Q$ в $P$ (фиолетового цвета) на вектор нормали $\color{green}{\vc{n}}$.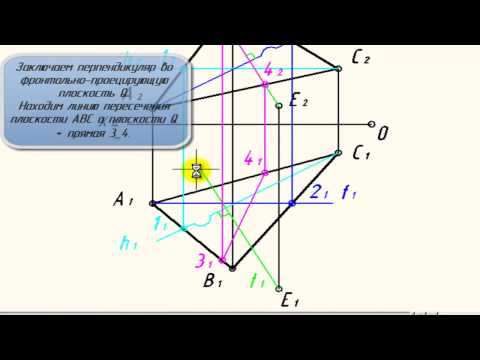

 1
1


 Проецируем точку
Проецируем точку 
 Ставим точку Е0.
Ставим точку Е0.
 Получаем точку Е1.
Линии
Получаем точку Е1.
Линии