Определить усилие в стержнях техническая механика: Определение усилий в стержнях скрепленных шарнирно

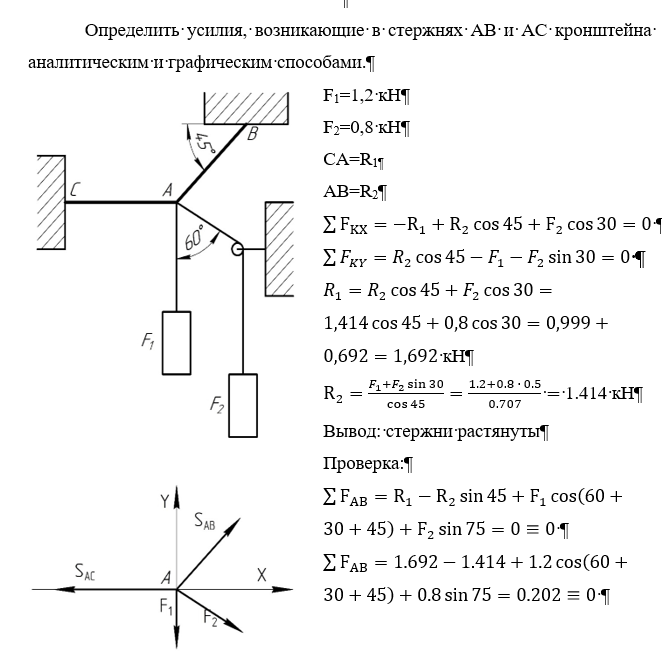
Определение усилий в стержнях скрепленных шарнирно

Пример решения задачи по определению усилий в двух стержнях, скрепленных шарнирно между собой и с вертикальной опорной стеной, в точке соединения которых подвешен груз.

Задача

Груз Q=1000Н удерживается с помощью двух невесомых стержней, шарнирно скрепленных между собой в точке A и в шарнирах B и C с вертикальной стеной (α=60°, β=30°).

Рисунок 2.1

Определить усилия в стержнях AB и BC (рисунок 2.1,а).

Другие примеры решений >
Помощь с решением задач >

Решение

Короткое видео про реакции в разных типах связей:

Другие видео

В данном случае следует рассмотреть равновесие точки A, т.к. все силы приложены в этой точке.

Нить с грузом натянута силой Q. В равновесии точку A удерживают два невесомых стержня. Их реакции всегда направлены вдоль стержней.

Реакции принято направлять от узла (точки A), т.

е. предполагается, что стержни работают на растяжение (рисунок 2.1, б). В случае отрицательного ответа при решении уравнений стержень работает на сжатие.

При равновесии системы сил выполняется равенство

Это векторное равенство можно построить. Откладываем в масштабе известную силу Q, к концу вектора прибавляем S_AB, т.к. его величина и направление неизвестны, проводим через конец вектора Q горизонтальную линию (параллельно S_AB, рисунок 2.1, б).

Замыкающий вектор S_AC должен пройти через начало вектора Q под углом β к вертикали. Результатом построения является замкнутый треугольник (рисунок 2.1, в). Величины усилий в стержнях можно получить, умножая замеренные значения векторов сил на масштаб или воспользовавшись теоремой синусов:

Направление силы S_AC в силовом треугольнике говорит о том, что этот стержень работает на сжатие.

Задача может быть решена и аналитически. Для этого выбираем систему координат xAy (рисунок 2. 1, б) и проецируем на ее оси векторное равенство (2.3):

При этом

После решения уравнений равновесия находим

То есть и в этом решении по знакам в ответах получаем, что стержень AC работает на сжатие, а стержень AB – на растяжение.

Другие примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Подробнее

ВЫБЕРИТЕ РАЗДЕЛ МЕХАНИКИ

• Техническая механика (техмех)
• Теоретическая механика (теормех)
• Сопротивление материалов (сопромат)
• Строительная механика (строймех)
• Теория механизмов и машин (ТММ)
• Детали машин и ОК (ДМ)
• Инженерная механика (инжмех)

---

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

– Рамки A4 для учебных работ
– Миллиметровки разного цвета
– Шрифты чертежные ГОСТ
– Листы в клетку и в линейку

Сохранить или поделиться с друзьями

---

Помощь с решением

Поиск формул и решений задач

Карта сайта || Филиал КузГТУ г.

Прокопьевск

Университет Университет Сведения об образовательной организации История филиала Новости Новости Медиацентр Оценка качества образовательной деятельности Внутренний контроль результатов обучения Открытые международные Интернет-олимпиады Федеральный интернет-экзамен в сфере профессионального образования (ФЭПО) Для сотрудников Стоп коронавирус Студенту Расписание Внеучебная работа СНС “СИСТЕМА” Автошкола КузГТУ Портфолио Шаблоны документов Практико-ориентированное обучение Социальная поддержка Личный кабинет студента Реквизиты Трудоустройство Вакансии для выпускников Трудоустройство иностранных студентов Трудоустройство лиц с ограниченными возможностями здоровья Полезные ссылки Поступающему Бакалавриат Специалитет Среднее профессиональное Политехнический лицей Дополнительное образование Подготовительные курсы Плата за обучение

Научная работа Отдел научно-технического развития Сборники и публикации Контакты Контакты

Глава 4.

5, Задача 4.31P | bartleby

Literature guidesConcept explainersWriting guidePopular textbooksPopular high school textbooksPopular Q&ABusinessAccountingEconomicsFinanceLeadershipManagementMarketingOperations ManagementEngineeringBioengineeringChemical EngineeringCivil EngineeringComputer EngineeringComputer ScienceElectrical EngineeringMechanical EngineeringLanguageSpanishMathAdvanced MathAlgebraCalculusGeometryProbabilityStatisticsTrigonometryScienceAdvanced PhysicsAnatomy and PhysiologyBiochemistryBiologyChemistryEarth ScienceHealth & NutritionNursingPhysicsSocial ScienceAnthropologyGeographyHistoryPolitical SciencePsychologySociology

Learn

Напишите

плюс

Log In

Механика материалов (10th Edition)

10th Edition

ISBN: 9780134319650

Автор: Russell C. Hibbeler

. См. аналогичные книги

Механика материалов (10-е издание)

Осевая нагрузка. 4.31P

Глава 4.5, Задача 4.31P

Колонна построена из высокопрочного бетона и восьмигранника А992 стальных арматурных стержня. Если на колонну действует осевая сила в 200 тысяч фунтов, определите среднее нормальное напряжение в бетоне и в каждом стержне. Каждый стержень имеет диаметр 1 дюйма

См. Solution Проверьте решение для образец учебника

См. Решение. Проверьте выбор из учебника

Расписание 03:20

Chevron_left

Предыдущий . Глава 4.2, Проблема 4.30P

chevron_right

Next chevron_right

Глава 4.5, Задача 4.32P

Trustpilot

Trustpilot

Три поперечных стержня изготовлены из стали 2-5 мм2 и имеют одинаковое сечение 94мм2 из стали А2-22. Определите среднее нормальное напряжение в каждом стержне, если на жесткую балку действует указанная нагрузка.

Болт имеет диаметр 20 (мм) и проходит через трубку с внутренним диаметром 50 (мм) и внешним диаметром 60 (мм). Если болт и трубка изготовлены из стали А-36, определите нормальное напряжение в трубке и болте при приложении к болту усилия 40 (кН). Предположим, что торцевые заглушки жесткие.

Стальная труба А-36 имеет сердечник из алюминия 6061-Т6. На него действует растягивающая сила 200 кН. Определить среднее нормальное напряжение в алюминии и стали, вызванное этой нагрузкой. Труба имеет внешний диаметр 80 мм и внутренний диаметр 70 мм.

Механика материалов (10-е издание)

10-е издание

ISBN: 9780134319650

Автор: Рассел С. Хиббелер

Издатель: PEARSON

Бесполезно? Посмотреть похожие книги

Механика материалов (10-е издание)

Осевая нагрузка. 4.31P

5.2: Двухкомпонентные элементы — инженерные тексты LibreText

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

50591

• Джейкоб Мур и участники
• Государственный университет Пенсильвании в Мон-Альто через Mechanics Map

Двухсиловой элемент представляет собой тело, на которое действуют силы (и только силы, а не моменты), действующие только в двух местах. Чтобы элемент с двумя силами находился в статическом равновесии, результирующая сила в каждом месте должна быть равной, противоположной и коллинеарной. Это приведет к тому, что все элементы с двумя силами будут либо растягиваться, либо сжиматься, как показано на диаграмме ниже.

Рисунок \(\PageIndex{1}\): Силы, действующие на стержни с двумя силами, должны быть равными, противоположными и коллинеарными, чтобы тело находилось в равновесии.

Почему силы должны быть равны, противоположны и коллинеарны:

Представьте себе балку, в которой силы действуют только на каждом конце балки (элемент с двумя силами). На тело действует некоторая ненулевая сила, действующая на один конец балки, которую мы можем изобразить в виде вектора силы. Если это тело находится в равновесии, то мы знаем две вещи:

1. сумма сил должна быть равна нулю, и
2. сумма моментов должна быть равна нулю.

Чтобы сумма сил была равна нулю, вектор силы на другой стороне балки должен быть равным по величине и противоположным по направлению. Это единственный способ гарантировать, что сумма сил равна нулю только с двумя силами.

Чтобы сумма моментов была равна нулю, силы должны быть коллинеарны. Если бы силы не были коллинеарны, то две равные и противоположные силы образовали бы пару. Эта пара будет воздействовать на балку моментом, когда нет других моментов, противодействующих паре. Поскольку момент, создаваемый двумя силами, должен быть равен нулю, перпендикулярное расстояние между силами \((d)\) должно быть равно нулю. Единственный способ добиться этого – заставить силы быть коллинеарными.

Рисунок \(\PageIndex{2}\): Чтобы сумма моментов была равна нулю, силы, действующие на стержни с двумя силами, всегда должны быть коллинеарны и действовать вдоль линии, соединяющей две точки, в которых действуют силы. применяемый.

Почему важны члены с двумя силами:

Идентифицируя члены с двумя силами, мы значительно уменьшаем количество неизвестных в нашей задаче. В двухсиловых элементах мы знаем, что силы должны действовать вдоль линии между двумя точками соединения на теле. Это означает, что направление векторов силы известно по обе стороны от тела. Кроме того, мы знаем, что силы равны и противоположны, поэтому, если мы определяем величину и направление силы, действующей на одну сторону тела, мы автоматически знаем величину и направление силы, действующей на другую сторону тела.

Рисунок \(\PageIndex{3}\): Силы в стержнях с двумя силами всегда будут действовать вдоль линии, соединяющей две точки приложения сил.

Элементы двух сил также важны для различения ферм, рам и машин. Когда мы анализируем фермы, используя либо метод соединений, либо метод сечений, мы будем предполагать, что все является элементом с двумя силами. Если это предположение неверно, это вызовет серьезные проблемы при анализе. Тем не менее, делая это предположение, мы можем использовать некоторые упрощения, которые сделают анализ ферм проще и быстрее, чем анализ рам и машин.

Видеолекция по этому разделу, прочитанная доктором Джейкобом Муром. Источник на YouTube: https://youtu.be/m3GhMaZwHJw.

---

Эта страница под названием 5.2: Two-Force Members доступна в соответствии с лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Jacob Moore & Contributors (Mechanics Map) посредством исходного контента, который был отредактирован в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.