лекции_1_курс_2_поток_осень_2019 | Кафедра высшей алгебры
1-я лекция 07.09. Решение систем линейных уравнений методом Гаусса. Теоретические следствия метода Гаусса.
2-я лекция 11.09. Операции над матрицами, их свойства. Правило умножения матриц в терминах линейных комбинаций строк (столобцов) второй (первой) матрицы. Умножение на диагональную матрицу. Единичная матрица. Элементарные преобразования строк (столбцов) матрицы как умножения слева (справа) на «элементарные» матрицы.
Обратная матрица, ее единственность. Обратимость элементарных матриц и произведения обратимых матриц.
3-я лекция 14.09. Критерий обратимрсти квадратной матрицы в терминах ее ступенчатого вида. Практический способ нахождения обратной матрицы.
Абелевы группы, кольца и поля. Подгруппы и подкольца.
4-я лекция 21.09. Понятие изоморфизма алгебраических структур. Аксиоматическое определение и построение поля комплексных чисел.
5-я лекция 25.09.
Алгебраическая форма комплексного числа.
Комплексное сопряжение.
Геометрическое изображение комплексного числа. Геометрический смысл сложения и вычитания комплексных чисел.
Тригонометрическая форма комплексного числа. Умножение, деление, возведение в степень и извлечение корня в тригонометрической форме.
Векторные пространства. Подпространства. Линейная зависимость. Порождающие системы векторов и базисы.
6-я лекция 02.10. Конечномерные векторные пространства, базис и размерность. Описание всех базисов конечномерного векторного пространства. Формула преобразования координат.
Линейная оболочка и ранг системы векторов. Ранг матрицы как ранг системы ее строк, его сохранение при элементарных преобразованиях строк. Ранг ступенчатой матрицы.
7-я лекция 05.10. Теорема о том, что линейные зависимости между столбцами матрицы не меняются при элементарных преобразованиях строк. Совпадение рангов систем строк и столбцов матрицы.
Критерии совместности и определенности системы линейных уравнений в терминах рангов матриц.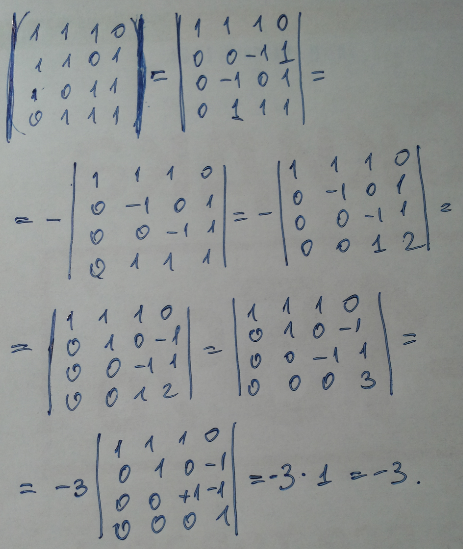
Размерность пространства решений системы однородных линейных уравнений. Связь между множествами решений совместной системы линейных уравнений и соответствующей системы однородных линейных уравнений.
Ранг произведения матриц. Критерий обратимости квадратной матрицы в терминах ее ранга.
8-я лекция 09.10. Перестановки. Четность и знак перестановки, их изменение при транспозиции.
Определение определителя квадратной матрицы (явной формулой). Теорема о том, что определитель является кососимметрической полилинейной функцией строк матрицы. Поведение определителя при элементарных преобразованиях строк матрицы. Определитель треугольной матрицы. Критерий обратимости матрицы в терминах ее определителя.
9-я лекция 12.10. Определитель транспонированной матрицы. Определитель матрицы с углом нулей. Разложение определителя по строке (столбцу). Определитель Вандермонда. Определитель произведения матриц.
10-я лекция 19.10.
Формулы Крамера. Явный вид обратной матрицы.
12-я лекция 26.10. Алгебры. Таблица умножения алгебры.
Формальное построение алгебры многочленов K[x} над произвольным полем K. Совпадение формального и функционального равенства многочленов над бесконечным полем.
Степень многочлена. Степень суммы и произведения многочленов. Отсутствие делителей нуля в алгебре K[x].
13-я лекция 30.10. Деление многочленов с остатком. Деление на x-c. Теорема Безу. Схема Горнера. Разложение многочлена по степеням x-c. Формула Тейлора (для многочленов над полем нулевой характеристики).
Кратность корня многочлена. Число корней многочлена с учетом их кратностей. Определение кратности корня по значениям производных (над полем нулевой характеристики).
14-я лекция 06.11. Основная теорема алгебры комплексных чисел. Число корней (с учетом кратностей) многочлена над полем комплексных чисел.
15-я лекция 09.11.
Многочлены с вещественными коэффициентами: свойство мнимых корней и разложение на линейные множители и квадратичные множители с отрицательным дискриминантом.
Теорема Декарта.
16-я лекция 16.11. Евклидовы кольца: наибольший общий делитель и разложение на простые множители.
17-я лекция 20.11. Многочлены с рациональными коэффициентами: рациональные корни, лемма Гаусса. Неприводимость многочлена деления круга на простое число частей.
Алгебра многочленов от нескольких переменных. Совпадение формального и функционального равенства многочленов в случае бесконечного поля. Отсутствие делителей нуля в алгебре многочленов. Степень многочлена по совокупности переменных. Однородные многочлены. Степень суммы и произведения многочленов.
18-я лекция 23.11. Лексикографическое упорядочение одночленов. Симметрические многочлены, их выражение через элементарные симметрические многочлены.
19-я декция 30.11. Дискриминант (неполного) кубического многочлена. Определение числа вещественных корней кубического многочлена с вещественными коэффициентами.
Поле отношений целостного кольца.
20-я лекция 04.12. Поле рациональных дробей.
Представление рациональной дроби в виде суммы многочлена и правильной дроби. Представление правильной рациональной дроби в виде суммы простейших дробей (без доказательства единственности). Явная формула для случая, когда знаменатель данной дроби разложен в произведение различных линейных множителей, ее связь с интерполяционной формулой Лагранжа.
Понятия группы и подгруппы. Простейшие следствия из аксиом группы. Группы преобразований.
21-я лекция 07.12. Разбиение группы на смежные классы по подгруппе. Теорема Лагранжа.
Гомоморфизмы и изоморфизмы групп. Ядро и образ гомоморфизма. Полный прообраз элемента при гомоморфизме.
Знак подстановки. Группа четных подстановок.
Гомоморфизм группы S_4 нв группу S_3, его ядро.
22-я лекция 14.12. Порядок элемента группы. Циклическая подгруппа, порожденнная элементом группы, ее строение. Порядок элемента конечной группы. Группы простого порядка.
Малая теорема Ферма и теорема Эйлера, их групповой смысл.
Подгруппы циклических групп.
23-я лекция 18.12. Квадратичные расширения полей.
Данное решение сделано калькулятором, представленным на сайте.Вычислим det A используя элементарные преобразования определителя.
К элементам строки 4 прибавляем соответствующие элементы строки 2, умноженные на -1. подробнее
Разложим определитель по элементам столбца 1.
К элементам строки 4 прибавляем соответствующие элементы строки 2, умноженные на 2. подробнее
Разложим определитель по элементам строки 4.
К элементам столбца 3 прибавляем соответствующие элементы столбца 2, умноженные на 2. подробнее
Разложим определитель по элементам строки 2.
= 24 * ( 12 * 2 – ( -12) * ( -8) ) = = 24 * ( 24 – 96 ) = = -1728 |
подробнеематриц – Ожидаемый определитель случайной матрицы NxN
спросил
Изменено 5 лет, 1 месяц назад
Просмотрено 14 тысяч раз
$\begingroup$
Каково математическое ожидание определителя при равномерном распределении всех возможных матриц 1-0 NxN? К чему стремится это ожидаемое значение, когда размер матрицы N приближается к бесконечности? 9п$$
$\endgroup$
10
$\begingroup$
Если $N \ge 2$, то ожидаемое значение равно $0$, поскольку перестановка двух строк сохраняет распределение, но инвертирует определитель.
2$ проще для (-1,+1)-матриц, чем для (0,1), просто n !. Также понятнее, почему определитель симметрично распределен вокруг начала координат.)
Известно, что журнал $\log |\det(A_n)|$ матрицы (-1,+1) асимптотически равен $\log \sqrt{n!} + O( \sqrt{n \log n} )$ с вероятностью $1-o(1)$; см. эту статью Ву и меня. Более точным результатом должно быть то, что логарифм имеет асимптотическое нормальное распределение со средним значением $\log \sqrt{(n-1)!}$ и дисперсией $2 \log n$. Этот результат был заявлен Гирко; доказательство, к сожалению, не совсем полное, но результат все же, вероятно, верен.
$\endgroup$
3
$\begingroup$
Некоторые другие результаты такого рода см. в Упражнении 5.64 из Enumerative Combinatorics , vol. 2. В этом упражнении рассматривается равномерное распределение на (0,1)-матрицах или $(-1,1)$-матрицах, но аргументы могут быть перенесены на другие распределения, где элементы матрицы являются i.
i.d. Доказательства аналогичны аргументу в комментарии Дэвида Шпейера.
9n$ зависит от знака, а количество четных и нечетных перестановок одинаково (при $n \ge 2$, как отмечалось выше).Вероятно, стоит упомянуть, что старый результат Комлоса показывает, что, несмотря на это, вероятность того, что определитель на самом деле равен 0, равна $o(1)$.
$\endgroup$
$\begingroup$
Не равен ли он нулю, если $n \geq 2$? Пусть $A$ — матрица перестановок размером $n \times n$ с определителем $-1$ (что требует $n \geq 2$). Тогда равномерное распределение случайной $n \times n$ $(0,1)$-матрицы $X$ совпадает с распределением $AX$. Определитель мультипликативен, поэтому Det$(AX)=$Det$(A)$Det$(X)=-$Det$(X)$. Следовательно, вероятность Det$(X)=x$ такая же, как вероятность Det$(X)=-x$.
$\endgroup$
2
$\begingroup$
Миодраг Живкович провел классификацию матриц малого порядка 0-1 по рангу и значению абсолютного определителя.
