Введение в матрицы для начинающих
Перевод Ссылка на автора
Матрицы являются строительными блоками науки о данных. Они появляются в различных аватарах на разных языках. От массива в Python до массивов данных в R и матриц в MATLAB.
Матрица в своей основной форме представляет собой набор чисел, расположенных в прямоугольной или массивной форме. Это может представлять изображение, или сеть, или даже абстрактную структуру.
Прямоугольный массив из 3 строк и 4 столбцов.Матрицы, множественное число для матрицы, на удивление встречаются чаще, чем вы думаете.
Все наши мемы, созданные с помощью Adobe Photoshop, используют матрицы для обработки линейных преобразований для визуализации изображений.квадратная матрицаможет представлять линейное преобразование геометрического объекта.
Например, в декартовой плоскости X-Y матрица
Интересная матрицаиспользуется для создания отражения объекта по вертикальной оси Y.
В прикладной физике матрицы используются для изучения электрических цепей, квантовой механики и оптики. Аэрокосмическая инженерия, химическая инженерия и т. Д. Требуют идеально откалиброванных вычислений, полученных в результате матричных преобразований. В больницах, медицинских изображениях, компьютерной томографии и МРТ для получения результатов используются матрицы.
фото JESHOOTS.COM на UnsplashВ программировании матрицы и обратные матрицы используются для кодирования и шифрования сообщений. В робототехнике и автоматизации матрицы являются основными компонентами движений робота. Входные данные для управления роботами получены на основе расчетов с использованием матриц.
Условно число строк в матрице обозначаетсями количество столбцов поN, Так как площадь прямоугольникаростИксширина,мы обозначаем размер матрицымИксп.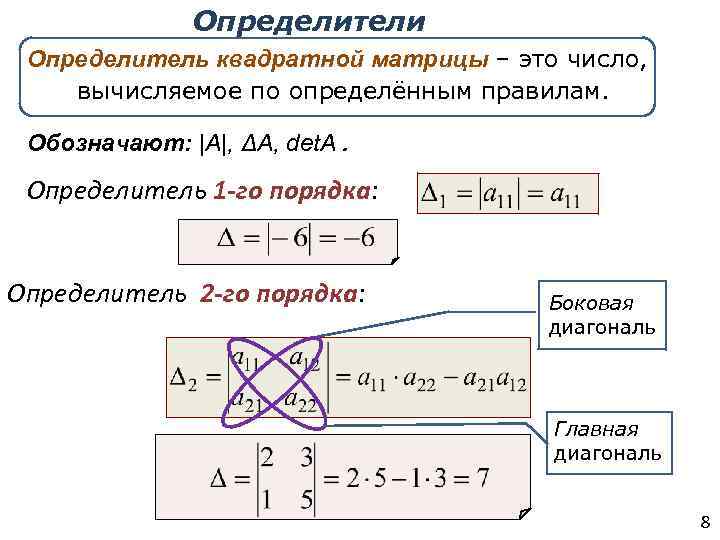 Таким образом, матрица должна была быть названаA,это будет записано в нотации как
Таким образом, матрица должна была быть названаA,это будет записано в нотации как
Здесь m = 3 и n = 4. Таким образом, в матрице А 12 элементов. Квадратная матрица имеетт = п,
Квадратная матрицаМатрица с одной строкой называетсяматрица строки матрица с одним столбцом называетсяматрица столбцов.
Матрицы так же, как числа могут быть добавлены, вычтены и умножены. Разделение немного нюанс. Не все матрицы могут быть разделены.
Существуют определенные правила даже для сложения, вычитания и умножения.
Дополнение матрицСложение двух матриц А (м * п)а такжеB (м * п)дает матрицу С (м * п). Элементы C являются суммой соответствующих элементов в A и B
Вычитание работает аналогично.
Здесь следует отметить, что вы можете только добавлять / вычитать матрицы с одинаковым количеством строк и столбцов, т. е.тот же порядок (порядок = строки х столбцы)
е.тот же порядок (порядок = строки х столбцы)
- Количество рядов A = Количество рядов B
- Количество столбцов A = Количество столбцов B
Указывает на заметку
- Добавление матрицкоммутативнойчто означает A + B = B + A
- Добавление матрицассоциативныйчто означает A + (B + C) = (A + B) + C
- Вычитание матрицнекоммутативноечто означает A-B ≠ B-A
- Вычитание матрицнеассоциативнымчто означает A- (B-C) ≠ (A-B) -C
- Порядок матриц A, B, A-B и A + B всегда одинаков
- Если порядок A и B различен, A + B, A-B не могут быть вычислены
- Сложность операции сложения / вычитания составляет O (m * n), где m * n – порядок матриц
Умножение хоть немного сложнее
Умножение матриц
Умножение двух матриц A (м * п)а такжеВ (п*п)дает матрицу С (м * р). Обратите внимание, что для умножения вам не нужно, чтобы строки / столбцы A и B были одинаковыми.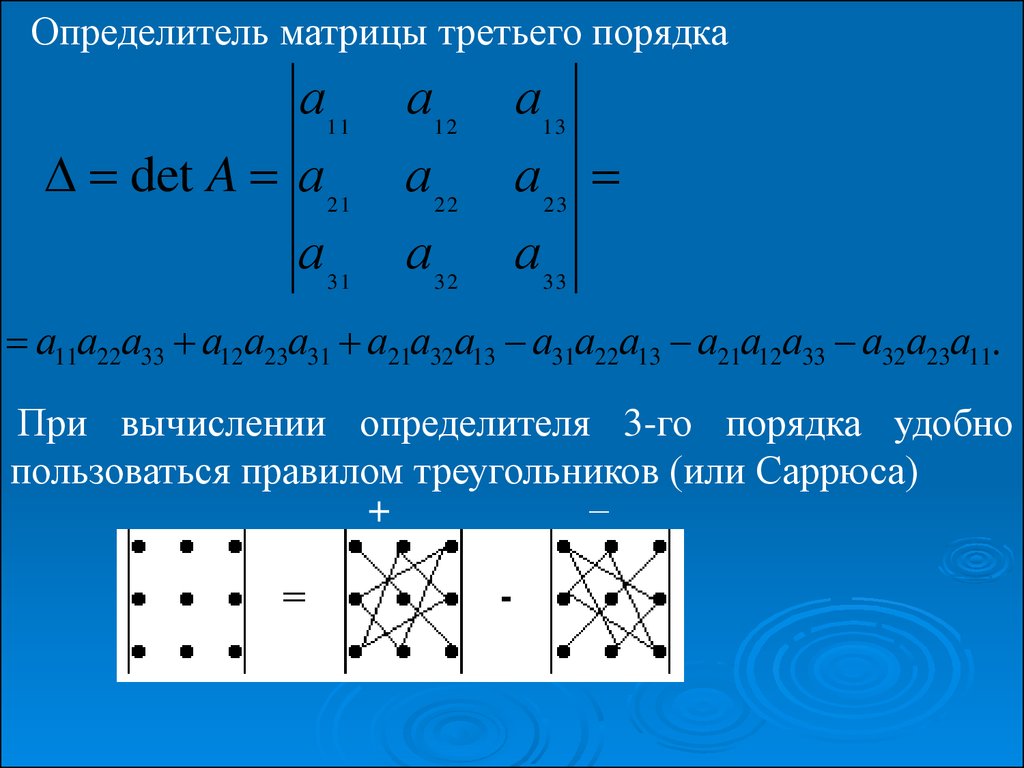 Вам нужно только
Вам нужно только
- Кол-во столбцов А = Кол-во строк Б
- Или, Кол-во Колонок B = Кол-во Строк А.
Чтобы вычислить верхний левый элемент полученной матрицы C, умножьте элементы 1-й строки A на 1-й столбец B и сложите их
умножениеУказывает на заметку
- Умножение матриц некоммутативно, что означает A * B ≠ B * A
- Умножение матриц является ассоциативным, что означает A * (B * C) = (A * B) * C
- Существование A * B не подразумевает существование B * A
- Сложность операции умножения (A * B) составляет O (m * n * p), где m * n и n * p – порядок A и B соответственно
- Порядок матрицы C, вычисляемой как A * B, равен m * p, где m * n и n * p – порядок A и B соответственно.
В следующем издании этой статьи мы увидим больше операций, которые могут быть выполнены над матрицами, например, Инверсия матрицы, определитель матрицы, сопряжение матрицы и т. Д.
Мы также увидим, как эти матрицы действительно помогают в области нейронные сети и обработка изображений.
Матрицы имеют огромное значение почти во всех алгоритмах машинного обучения из КНН (Алгоритм ближайшего соседа) вплоть до Случайные Леса,
Линейная алгебра на Python. [Урок 4]. Определитель матрицы
Четвертый урок из цикла “Линейная алгебра на Python“, посвящен понятию определителя матрицы и его свойствам.
Определитель матрицыОпределитель матрицы размера (n-го порядка) является одной из ее численных характеристик. Определитель матрицы A обозначается как |A| или det(A), его также называют детерминантом. Рассмотрим квадратную матрицу 2×2 в общем виде:
Определитель такой матрицы вычисляется следующим образом:
➣ Численный пример
Перед тем, как привести методику расчета определителя в общем виде, введем понятие минора элемента определителя. Минор элемента определителя
 Для матрицы 3×3 следующего вида:
Для матрицы 3×3 следующего вида:Минор M23 будет выглядеть так:
Введем еще одно понятие – алгебраическое дополнение элемента определителя – это минор этого элемента, взятый со знаком плюс или минус:
В общем виде вычислить определитель матрицы можно через разложение определителя по элементам строки или столбца. Суть в том, что определитель равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения. Для матрицы 3×3 это правило будет выполняться следующим образом:
Это правило распространяется на матрицы любой размерности.
➣ Численный пример
➤ Пример на Python
На Python определитель посчитать очень просто. Создадим матрицу A размера 3×3 из приведенного выше численного примера:
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
Для вычисления определителя этой матрицы воспользуемся функцией det() из пакета linalg.
>>> np.linalg.det(A) -14.000000000000009
Мы уже говорили про особенность работы Python с числами с плавающей точкой, поэтому можете полученное значение округлить до -14.
Свойства определителя матрицы.
Свойство 1. Определитель матрицы остается неизменным при ее транспонировании:
➤Пример на Python
Для округления чисел будем использовать функцию round().
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> print(A.T)
[[-4 10 8]
[-1 4 3]
[ 2 -1 1]]
>>> det_A = round(np.linalg.det(A), 3)
>>> det_A_t = round(np.linalg.det(A.T), 3)
>>> print(det_A)
-14.0
>>> print(det_A_t)
-14.0
Свойство 2. Если у матрицы есть строка или столбец, состоящие из нулей, то определитель такой матрицы равен нулю:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 0 0 0; 8 3 1') >>> print(A) [[-4 -1 2] [ 0 0 0] [ 8 3 1]] >>> np.linalg.det(A) 0.0
Свойство 3. При перестановке строк матрицы знак ее определителя меняется на противоположный:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> B = np.matrix('10 4 -1; -4 -1 2; 8 3 1')
>>> print(B)
[[10 4 -1]
[-4 -1 2]
[ 8 3 1]]
>>> round(np.linalg.det(A), 3)
-14.0
>>> round(np.linalg.det(B), 3)
14.0
Свойство 4
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; -4 -1 2; 8 3 1')
>>> print(A)
[[-4 -1 2]
[-4 -1 2]
[ 8 3 1]]
>>> np. linalg.det(A)
0.0
linalg.det(A)
0.0
Свойство 5. Если все элементы строки или столбца матрицы умножить на какое-то число, то и определитель будет умножен на это число:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> k = 2
>>> B = A.copy()
>>> B[2, :] = k * B[2, :]
>>> print(B)
[[-4 -1 2]
[10 4 -1]
[16 6 2]]
>>> det_A = round(np.linalg.det(A), 3)
>>> det_B = round(np.linalg.det(B), 3)
>>> det_A * k
-28.0
>>> det_B
-28.0
Свойство 6. Если все элементы строки или столбца можно представить как сумму двух слагаемых, то определитель такой матрицы равен сумме определителей двух соответствующих матриц:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; -4 -1 2; 8 3 1') >>> B = np.matrix('-4 -1 2; 8 3 2; 8 3 1') >>> C = A.copy() >>> C[1, :] += B[1, :] >>> print(C) [[-4 -1 2] [ 4 2 4] [ 8 3 1]] >>> print(A) [[-4 -1 2] [-4 -1 2] [ 8 3 1]] >>> print(B) [[-4 -1 2] [ 8 3 2] [ 8 3 1]] >>> round(np.linalg.det(C), 3) 4.0 >>> round(np.linalg.det(A), 3) + round(np.linalg.det(B), 3) 4.0
Свойство 7. Если к элементам одной строки прибавить элементы другой строки, умноженные на одно и тоже число, то определитель матрицы не изменится:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> k = 2
>>> B = A.copy()
>>> B[1, :] = B[1, :] + k * B[0, :]
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> print(B)
[[-4 -1 2]
[ 2 2 3]
[ 8 3 1]]
>>> round(np. linalg.det(A), 3)
-14.0
>>> round(np.linalg.det(B), 3)
-14.0
linalg.det(A), 3)
-14.0
>>> round(np.linalg.det(B), 3)
-14.0
Свойство 8. Если строка или столбец матрицы является линейной комбинацией других строк (столбцов), то определитель такой матрицы равен нулю:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> k = 2
>>> A[1, :] = A[0, :] + k * A[2, :]
>>> round(np.linalg.det(A), 3)
0.0
Свойство 9. Если матрица содержит пропорциональные строки, то ее определитель равен нулю:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> k = 2
>>> A[1, :] = k * A[0, :]
>>> print(A)
[[-4 -1 2]
[-8 -2 4]
[ 8 3 1]]
>>> round(np.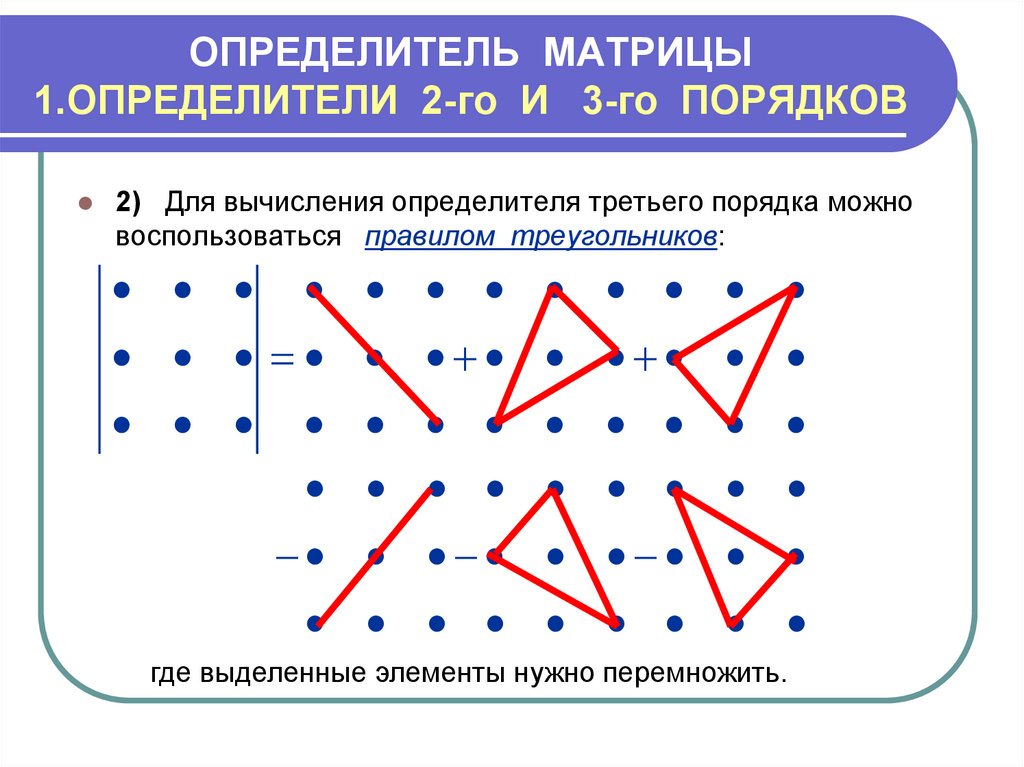 linalg.det(A), 3)
0.0
linalg.det(A), 3)
0.0P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Матрицы и определители – определение, различие, свойства, примеры, часто задаваемые вопросы
Матрицы и определители используются для выполнения различных арифметических операций с массивом элементов. Матрицы представляют собой прямоугольный массив элементов, представленных в виде строк и столбцов. И определители вычисляются для матрицы, и это единственное числовое значение, которое было вычислено из этого массива элементов. Матрица представлена буквой в верхнем регистре и записана как A, а определитель представлен как |A|.
Матрицы и определители имеют разные свойства. Умножение константы K на матрицу умножает каждый элемент матрицы, а умножение константы K на определитель умножает на элементы любой конкретной строки или столбца. Давайте узнаем больше о свойствах и различиях между матрицами и определителями с помощью примеров, часто задаваемых вопросов.
| 1. | Что такое матрицы и определители? |
| 2. | Разница между матрицами и определителями |
| 3. | Свойства матриц |
| 4. | Свойства определителей |
| 5. | Решение матриц и определителей |
| 6. | Примеры матриц и определителей |
| 7. | Практические вопросы |
| 8. | Часто задаваемые вопросы о матрицах и определителях |
Что такое матрицы и определители?
Матрицы и определители представляют массив элементов, и мы вычисляем значение одного элемента для всего определителя. Матрицы — это форма множественного числа матрицы, которая представляет собой прямоугольный массив или таблицу, в которой числа или элементы расположены в несколько строк и столбцов. Матрицы можно складывать или вычитать, только если они имеют одинаковое количество строк и столбцов, тогда как их можно умножать, если только столбцы в первом и строки во втором точно совпадают.
Матрицы — это форма множественного числа матрицы, которая представляет собой прямоугольный массив или таблицу, в которой числа или элементы расположены в несколько строк и столбцов. Матрицы можно складывать или вычитать, только если они имеют одинаковое количество строк и столбцов, тогда как их можно умножать, если только столбцы в первом и строки во втором точно совпадают.
Матрицы и определители тесно связаны в математике. Матрица — это массив элементов, который обозначается M, а определитель — это единственное числовое значение, представляющее эту матрицу и обозначаемое как |M|. Давайте посмотрим на определение матрицы и определителя.
Определение матрицы
Матрица представляет собой массив элементов, представленных в виде строк и столбцов. Детерминанты рассматриваются как скалярные множители матрицы. Матрица обычно обозначается заглавной буквой. Порядок матрицы представлен количеством строк и столбцов в матрице. Матрица порядка m x n имеет m строк и n столбцов.
\(A = \left[\begin{массив}{ccc}
а_{11} и а_{12} и а_{13} .. .& а_{1n} \\
а_{21} и а_{22} и а_{23} … и а_{2n} \\
a_{31} & a_{32} & a_{33} …& a_{3n} \\ : & : & : & : \\ a_{m1} & a_{m2} & a_{m3} … & a_{мн}
\end{array}\right] \)
Определение определителя
Для каждой квадратной матрицы C = [\(c_{ij}\)] порядка n×n определитель может быть определен как скалярное значение, которое действительное или комплексное число, где \(c_{ij}\) – (i,j) -й -й элемент матрицы C. Определитель можно обозначить как det(C) или |C|, здесь определитель записывается путем взятия сетки чисел и размещения их внутри столбцов абсолютного значения вместо использования квадратных скобок.
Рассмотрим матрицу C = \(\left[\begin{array}{ll}a & b \\c & d\end{array}\right]\)
Тогда ее определитель можно представить как:
|С| = \(\left|\begin{массив}{ll}a & b \\c & d\end{массив}\right|\)
Разница между матрицами и определителями
Разница между матрицами и определителями помогает лучше понять матрицы и определители.
- Матрица — это массив чисел, а определитель — это одно числовое значение, найденное после вычисления из матрицы.
- Значение определителя матрицы может быть вычислено, но матрица не может быть вычислена из определителя.
- Матрицы могут быть любого порядка. Но определитель можно найти только для квадратной матрицы, имеющей равное количество строк и столбцов.
- Умножение константы K на матрицу умножает ее на каждый элемент матрицы. Но умножение константы K на определитель умножает ее на каждый элемент конкретной строки или столбца определителя.
- Строки и столбцы определителя можно поменять местами, но многие строки и столбцы матрицы нельзя поменять местами.
- Значение определителя равно нулю, если любые две строки или столбца идентичны, но одинаковые строки или столбцы в матрице не делают ее нулевой матрицей.
- Элементы любой конкретной строки или столбца можно разделить на сумму или разность значений и записать в виде двух разных определителей.
 Но матричные элементы любой строки или столбца нельзя разбить на сумму или разность любых двух строк.
Но матричные элементы любой строки или столбца нельзя разбить на сумму или разность любых двух строк. - Если к любой строке или столбцу добавить равнократные числа другой строки или столбца, то значение определителя не изменится. Но подобную операцию нельзя выполнить над матрицей.
Свойства матриц
Следующие свойства матриц помогают легко выполнять многочисленные операции над матрицами.
Аддитивное свойство матриц
- Коммутативное право. Для данных двух матриц, матрицы A и матрицы B одного порядка, скажем, m x n, тогда A + B = B + A.
- Ассоциативный закон: для любых трех матриц A, B, C одного и того же порядка m x n имеем (A + B) + C = A + (B + C)
- Существование аддитивной идентичности. Пусть A — матрица порядка m × n, а O — нулевая матрица или нулевая матрица того же порядка m × n, тогда A + O = O + A = A. Другими словами, O является аддитивной идентичностью для сложения матриц.
- Существование аддитивной обратной Пусть A — матрица порядка m × n.
 и пусть -A — другая матрица порядка m × n такая, что A + (– A) = (– A) + A = O. Таким образом, матрица – A является аддитивной обратной матрицей A или отрицательной матрицей A.
и пусть -A — другая матрица порядка m × n такая, что A + (– A) = (– A) + A = O. Таким образом, матрица – A является аддитивной обратной матрицей A или отрицательной матрицей A.
Свойство скалярного умножения матриц
- Произведение константы на сумму матриц равно сумме отдельного произведения константы и матрицы. к(А + В) = кА + кВ
- Произведение суммы констант на матрицу равно сумме произведения каждой из констант на матрицу. (к + 1)А = кА + 1А
Свойство умножения матриц
- Ассоциативное свойство: Для любых трех матриц A, B, C, следующих условиям умножения матриц, мы имеем (AB)C = A(BC). Здесь определены обе части матричного умножения.
- Распределительное свойство: для любых трех матриц A, B, C, следующих условиям умножения матриц, мы имеем A(B + C) = AB + AC.
- Существование мультипликативной идентичности. Для квадратной матрицы A порядка m × n и единичной матрицы I того же порядка имеем AI = IA = A.
 Здесь произведение единичной матрицы на данную матрицу дает ту же матрицу.
Здесь произведение единичной матрицы на данную матрицу дает ту же матрицу.
Свойство транспонирования матриц
- Транспонирование матрицы при повторном транспонировании приводит к исходной матрице. (А’)’ = А
- Транспонирование произведения константы на матрицу равно произведению константы на транспонирование матрицы. (кА)’ = кА’
- Транспонирование суммы двух матриц равно сумме транспонирования отдельных матриц. (А + В)’ = А’ + В’
- Транспонирование произведения двух матриц равно произведению транспонирования второй матрицы и транспонирования первой матрицы. (АВ)’ = В’А’
Другие свойства матриц
- Для квадратной матрицы с вещественными элементами A + A’ является симметричной матрицей, а A – A’ является кососимметричной матрицей.
- Квадратная матрица может быть представлена как сумма симметричной и кососимметричной матриц. А = 1/2(А + А’) + 1/2(А – А’).
- Обратная матрица, если она существует, уникальна.
 АВ = ВА = I.
АВ = ВА = I. - Если матрица A обратна матрице B, то матрица B обратна матрице A.
- Если A и B — обратимые матрицы одного и того же порядка m × n, то (AB) -1 = B -1 A -1 .
Свойства определителей
Следующие семь свойств определителей помогают легко вычислить определители.
- Свойство обмена: Значение определителя остается неизменным, если строки или столбцы определителя изменены. A = \(\begin{vmatrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\end{vmatrix}\), A’ = \(\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}\) Det( А) = Дет(А’)
- Sign Свойство: Знак определителя меняется, если поменять местами любые две отдельные строки или два конкретных столбца определителя. A = \(\begin{vmatrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\end{vmatrix}\), B = \(\begin{vmatrix}a_1&a_2&a_3\\c_1&c_2&c_3\\b_1&b_2&b_3\end{vmatrix}\) Det(A ) = -Det(B)
- Нуль Свойство: Значение определителя равно нулю, если любые две строки или любые два столбца определителя содержат одни и те же элементы.
 A = \(\begin{vmatrix}a_1&a_2&a_3\\a_1&a_2&a_3\\b_1&b_2&b_3\end{vmatrix}\) Здесь элементы первой строки и второй строки идентичны. Отсюда значение определителя равно нулю Der(A) = 0
A = \(\begin{vmatrix}a_1&a_2&a_3\\a_1&a_2&a_3\\b_1&b_2&b_3\end{vmatrix}\) Здесь элементы первой строки и второй строки идентичны. Отсюда значение определителя равно нулю Der(A) = 0 - Свойство умножения: Значение определения становится в k раз больше предыдущего значения определителя, если каждый из элементов конкретной строки или столбца умножается на константу k.A = \(\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\ \a_3&b_3&c_3\end{vmatrix}\), B = \(\begin{vmatrix}ka_1&kb_1&kc_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}\) Det(B) = k× Det(B)
- Сумма Свойство: Если несколько элементов строки или столбца выражены в виде суммы термов, то определитель может быть выражен как сумма двух или более определителей. \(\begin{vmatrix}a_1+b_1&a_2 + b_2&a_3+b_3\\c_1&c_2&c_3\\d_1&d_2&d_3\end{vmatrix}\) = \(\begin{vmatrix}a_1&a_2 &a_3\\c_1&c_2&c_3\\d_1&d_2&d_3\end{vmatrix }\) + \(\begin{vmatrix}b_1& b_2&b_3\\c_1&c_2&c_3\\d_1&d_2&d_3\end{vmatrix}\)
- Свойство инвариантности: Если к каждому элементу строки и столбца определителя добавить равнократные элементы другой строки или столбца определителя, то значение определителя останется неизменным.
 Это можно выразить в виде формулы \(R_i \rightarrow R_i + kR_j\) или \(C_i \rightarrow C_i + kC_j\). A = \(\begin{vmatrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\end{vmatrix}\), B = \(\begin{vmatrix}a_1+kc_1&a_2+kc_2&a_3+kc_3\\b_1&b_2&b_3\\c_1&c_2&c_3 \end{vmatrix }\). Дет(А) = Дет(В)
Это можно выразить в виде формулы \(R_i \rightarrow R_i + kR_j\) или \(C_i \rightarrow C_i + kC_j\). A = \(\begin{vmatrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\end{vmatrix}\), B = \(\begin{vmatrix}a_1+kc_1&a_2+kc_2&a_3+kc_3\\b_1&b_2&b_3\\c_1&c_2&c_3 \end{vmatrix }\). Дет(А) = Дет(В) - Треугольность Свойство: Если элементы выше или ниже главной диагонали равны нулю, то значение определителя равно произведению элементов диагональной матрицы.
\(\begin{vmatrix}a_1&a_2&a_3\\0&b_2&b_3\\0&0&c_3\end{vmatrix}\) = \(\begin{vmatrix}a_1&0&0\\a_2&b_2&0\\a_3&b_3&c_3\end{vmatrix}\) = \(a_1. б_2.в_3\)
Решение матриц и определителей
Матрицы можно решать с помощью арифметических операций сложения, вычитания, умножения и нахождения их обратной. Кроме того, единственное числовое значение, которое можно вычислить для квадратной матрицы, называется определителем квадратной матрицы. Определители можно вычислить только для квадратных матриц.
Проверим различные операции сложения, вычитания, умножения матриц, а также найдем значение определителя порядка 2 х 2, 3 х 3.
Сложение матриц
Сложение матриц аналогично простому арифметическому сложению термов. Сложение двух матриц возможно, если две матрицы одного порядка. Добавление двух матриц возможно путем одновременного добавления их соответствующих элементов для получения новой матрицы.
Вычитание матриц
Поскольку мы знаем, что вычитание матриц возможно только в том случае, если матрицы имеют одинаковое количество строк и столбцов, следовательно, для вычитания матриц порядка 2 × 2 матрицы должны иметь 2 строки и 2 колонки. Теперь рассмотрим две матрицы A и B размерности 2 × 2. Чтобы вычесть B из A, мы вычтем элементы B из соответствующих элементов A. Общая форма вычитания B из A (порядок 2 × 2) такова :
Умножение матриц
Процесс одинаков для матриц любого порядка. Условие умножения двух матриц состоит в том, что количество столбцов в первой матрице должно быть равно количеству строк во второй матрице. Умножаем элементы каждой строки первой матрицы на элементы каждого столбца второй матрицы (поэлементно), как показано на рисунке. Наконец, мы добавляем продукты.
Умножаем элементы каждой строки первой матрицы на элементы каждого столбца второй матрицы (поэлементно), как показано на рисунке. Наконец, мы добавляем продукты.
Решение двумерного определителя
Для любой двумерной квадратной матрицы или квадратной матрицы порядка 2×2 мы можем использовать формулу определителя для вычисления ее определителя:
C = \(\left[\begin{array}{ll}a & b \\ c & d\end{массив}\right]\)
Его двумерный определитель можно вычислить как:
|C| = \(\left|\begin{array}{ll}a & b \\c & d\end{array}\right|\)
|C| = (a×d) – (b×c)
Например: C = \(\left[\begin{array}{ll}8 & 6 \\3 & 4\end{array}\right]\)
Его определитель можно вычислить как:
|С| = \(\left|\begin{array}{ll}8 & 6 \\3 & 4\end{array}\right|\)
|C| = (8×4) – (6×3) = 32 – 18 = 14
Решение трехмерных определителей
Для любой трехмерной квадратной матрицы или квадратной матрицы порядка 3×3 это процедура вычисления ее определителя.
\(C = \left[\begin{array}{ccc}a_{1} & b_{1} & c_{1} \\a_{2} & b_{2} & c_{2} \\a_ {3} & b_{3} & c_{3}\end{массив}\right] \)
Его определитель можно вычислить как:
|С| = \(\left|\begin{array}{ccc}a_{1} & b_{1} & c_{1} \\a_{2} & b_{2} & c_{2} \\a_{3} & b_{3} & c_{3}\end{array}\right| \)
- \(a_{1}\) фиксируется как номер привязки и двумерный определитель его подматрицы, которая представляет собой квадрат вычисляется матрица.
- Следующий номер привязки берется по порядку, теперь это \(b_{1}\) и вычисляется малый определитель, и, наконец, \(c_{1}\) берется в качестве номера привязки и его двумерного определителя рассчитывается.
- Попеременно продолжайте умножать меньший определитель на номер привязки и на его знак.
- |С| = \(\left|\begin{array}{ccc}+ &-& + \\- & + & – \\+ &-& + \end{array}\right| \)
- Наконец, суммируйте их.
|С| = \(a_{1} \cdot\left|\begin{array}{ll}b_{2} & c_{2} \\b_{3} & c_{3}\end{массив}\right|-b_ {1} \cdot\left|\begin{array}{cc}a_{2} & c_{2} \\a_{3} & c_{3}\end{array}\right|+c_{1} \ cdot\left|\begin{array}{ll}a_{2} & b_{2} \\a_{3} & b_{3}\end{array}\right|\)
|С| = \(a_{1}\left(b_{2} c_{3}-b_{3} c_{2}\right)-b_{1}\left(a_{2} c_{3}-a_{3 } c_{2}\right)+c_{1}\left(a_{2} b_{3}-a_{3} b_{2}\right)\)
☛ Связанные темы
- Свойства матриц
- Свойства определителей
- Типы матриц
- Детерминанты
- Умножение матриц
Часто задаваемые вопросы о матрицах и определителях
Что такое матрицы и определители?
Матрицы и определители имеют тесную связь в математике. Матрица — это массив элементов, который обозначается M, а определитель — это единственное числовое значение, представляющее эту матрицу и обозначаемое как |M|. Количество строк и столбцов в матрице называется порядком матрицы, а для определителя количество строк должно быть равно количеству столбцов.
Матрица — это массив элементов, который обозначается M, а определитель — это единственное числовое значение, представляющее эту матрицу и обозначаемое как |M|. Количество строк и столбцов в матрице называется порядком матрицы, а для определителя количество строк должно быть равно количеству столбцов.
Как решать матрицы и определители?
Над матрицами можно выполнять арифметические операции сложения, вычитания, умножения. И определитель можно вычислить для квадратной матрицы, и то же самое значение определителя можно использовать для вычисления обратной матрицы.
В чем разница между матрицами и детерминантами?
Ниже приведены три основных различия между матрицами и определителями.
- Матрица может быть представлена в виде A = \(\begin{pmatrix}a&b\\c&d\end{pmatrix}\), значение определителя равно |A| = |объявление – до н.э.|.
- Матрицы могут быть любого порядка. Но определитель можно найти только для квадратной матрицы, имеющей равное количество строк и столбцов.

- Умножение константы K на матрицу умножает ее на каждый элемент матрицы. Но умножение константы K на определитель умножает ее на каждый элемент конкретной строки или столбца определителя.
Каков порядок матриц и определителей?
Порядок матрицы равен m x n, так как она состоит из m строк и n столбцов, а порядок определителя равен n x n, так как он состоит из n строк и n столбцов. Определители можно вычислить только для квадратной матрицы, поэтому она имеет одинаковое количество строк и столбцов.
Что такое формулы матриц и определителей?
Формула матрицы заключается в нахождении транспонированной, присоединенной и обратной матрицы. И мы можем найти единственное числовое значение для определителя. Транспонированная матрица — это матрица, полученная после преобразования и записи элементов строки как элементов столбца, а элементов столбца — как элементов строки. Сопряженная матрица представляет собой транспонирование сомножителей элементов матрицы, а деление сопряженной матрицы на определитель матрицы дает обратную матрицу.
Матрицы и определители — одно и то же?
Матрицы и определители разные. Матрицы представляют собой массив элементов, представленных в виде строк и столбцов, а определитель представляет собой одно числовое значение, вычисленное из элементов матрицы. Для матрицы A = \(\begin{pmatrix}a&b\\c&d\end{pmatrix}\) значение определителя равно |A| = |объявление – до н.э.|.
Каковы применения матриц и определителей?
Матрица имеет большое применение в области науки о данных и искусственного интеллекта. Многочисленные алгебраические уравнения могут быть решены методом обращения матриц. Мы также можем найти транспонированную, сопряженную и обратную матрицы.
Что такое определитель матрицы? | Марсель Моосбруггер
Геометрическая интуиция, стоящая за детерминантами, может изменить ваше представление о них.
Изображение автора (marcelmoos.com) Вспоминая школьные годы, линейная алгебра была темой, которой я был особенно увлечен. Это дало мне умение решать большие системы линейных уравнений и геометрическую перспективу проблемы, что сделало весь процесс интуитивно понятным.
Однако, что касается определителей матриц, меня учили, что это числа для матриц, как их вычислять, и не более того. Только на курсах в университете я узнал красоту детерминантов.
Как только я узнал о геометрическом значении определителей, мне стало интересно, почему этому еще не учили в старшей школе, ведь это очень просто для понимания и познавательно.
В математике вопрос о том, как что-то вычислить, никогда не должен стоять на первом месте. Первый вопрос всегда: “Что это ТАКОЕ на самом деле?”. Только тогда мы должны спросить: «Хорошо, теперь, когда мы знаем, что это такое, как мы можем это вычислить». Возьмем, к примеру, деривативы, поскольку большинство из нас знает, что такое деривативы:
Для данной функции ее производной является наклон или скорость изменения.
Это такое простое описание. Тем не менее, определение производных таким образом очень мощно и освобождающе. Мы понимаем, что такое производная, независимо от конкретной функции или размерности функции и независимо от того, как ее вычислить. Фактическое вычисление производных сильно отличается для разных функций. Однако фундаментальный смысл производных связывает все воедино и вносит порядок в хаос.
Мы понимаем, что такое производная, независимо от конкретной функции или размерности функции и независимо от того, как ее вычислить. Фактическое вычисление производных сильно отличается для разных функций. Однако фундаментальный смысл производных связывает все воедино и вносит порядок в хаос.
Ни один учитель не стал бы знакомить учащихся с производными, например: «Для заданной функции производная — это просто еще одна функция, и вот как вы ее вычисляете…». Тем не менее, для определителей матриц такие объяснения, по-видимому, широко распространены. Определять детерминанты по их геометрическому смыслу, а не просто по некоторым числам, так же эффективно, как думать о производных как о наклонах, а не только как о функциях.
Прежде чем углубляться в детерминанты, давайте быстро вспомним, для чего они предназначены: Матрицы.
Матрица — это таблица чисел, представляющая линейную функцию , принимающая вектор в качестве входных данных и производящая другой вектор в качестве выходного:
Вместо матрицы, преобразующей один единственный вектор, мы также можем думать о матрице, все) векторов одновременно:
Видишь? Похоже, что выбранная нами матрица растягивает пространство на расстояние . Какую бы область во входном пространстве мы ни выбрали, кажется, что после преобразования площадь становится больше. Это именно то, что является определителем!
Какую бы область во входном пространстве мы ни выбрали, кажется, что после преобразования площадь становится больше. Это именно то, что является определителем!
Определитель матрицы — это коэффициент, на который площади масштабируются этой матрицей.
Поскольку матрицы являются линейными преобразованиями, достаточно знать коэффициент масштабирования для одной одной области, чтобы знать коэффициент масштабирования для всех областей. Вернемся к нашему примеру:
Прямоугольник, вписанный розовым и синим единичными векторами и имеющий площадь 1. После применения нашего матричного преобразования этот прямоугольник превратился в параллелограмм с основанием 9.0403 2 и высота 2. Таким образом, площадь равна 4. . Это означает, что наша матрица масштабирует площади в 4 раз. Следовательно, определитель нашей матрицы равен 4 . Аккуратно, не так ли?
В этой истории есть одно предостережение: определители могут быть отрицательными! Если мы начнем с площади 1 и масштабируем ее с отрицательным коэффициентом, мы получим отрицательную площадь. А отрицательные области – ерунда. Итак, как мы можем понять наше красивое геометрическое определение при наличии отрицательных определителей? К счастью, исправление простое: если матрица имеет отрицательный определитель, скажем -2, площади масштабируются на 2. Минус просто означает, что пространство изменило свою ориентацию. «Что теперь это вообще значит?», — справедливо спросите вы. Давайте посмотрим:
А отрицательные области – ерунда. Итак, как мы можем понять наше красивое геометрическое определение при наличии отрицательных определителей? К счастью, исправление простое: если матрица имеет отрицательный определитель, скажем -2, площади масштабируются на 2. Минус просто означает, что пространство изменило свою ориентацию. «Что теперь это вообще значит?», — справедливо спросите вы. Давайте посмотрим:
Мы видим, что данная матрица масштабирует площади в 2 раз. Если мы посмотрим внимательно, то заметим, что синий вектор был справа от розового вектора, но оказался слева. Вот что значит «пространство изменило свою ориентацию». Поэтому определитель матрицы не равен 2 но -2 . Включая отрицательные определители, мы получаем полную картину:
Определитель матрицы – это знаковый коэффициент, на который площади масштабируются этой матрицей. Если знак отрицательный, матрица меняет ориентацию.
Все наши примеры были двухмерными. Трудно рисовать многомерные графики. Геометрическое определение определителей применимо к высшим измерениям точно так же, как и к двум. В трехмерном пространстве определителем является масштабный коэффициент со знаком для объемов и даже в более высоких измерениях для гиперобъемов.
Трудно рисовать многомерные графики. Геометрическое определение определителей применимо к высшим измерениям точно так же, как и к двум. В трехмерном пространстве определителем является масштабный коэффициент со знаком для объемов и даже в более высоких измерениях для гиперобъемов.
Имея это новое геометрическое определение определителей , мы можем с легкостью решать задачи , с которыми без него было бы гораздо труднее справиться . Например, вы могли слышать или не слышать следующий факт:
Если определитель матрицы равен 0, она необратима.
Необратимость матрицы означает, что преобразование, которое представляет матрица, не может быть отменено или отменено. Если бы мы знали только, как вычисляются определители, и ничего не знали об их геометрическом значении, обосновать этот факт было бы сложно. Напротив, объяснить, почему это верно, используя нашу недавно установленную интуицию относительно детерминантов, становится не так сложно:
Допустим, у нас есть матрица с определителем 0 .

