Основные формулы: Основные формулы | Олимпиадный Центр МатРИЦА

Основные формулы | Олимпиадный Центр МатРИЦА

Математика: Все главные формулы

 

Оглавление:

• Таблица умножения

• Таблица квадратов двухзначных чисел

• Формулы сокращенного умножения

• Квадратное уравнение и формула разложения квадратного трехчлена на множители

• Свойства степеней и корней

• Арифметическая прогрессия

• Геометрическая прогрессия

• Геометрия на плоскости (планиметрия)

• Формулы с логарифмами

• Тригонометрия

• Тригонометрические уравнения

• Геометрия в пространстве (стереометрия)

• Координаты

• Скачать расширенную версию «Все главные формулы по школьной математике»

Весь курс алгебры для ОГЭ в схемах и таблицах >>>

Весь курс геометрии для ОГЭ в схемах и таблицах >>>

Весь курс по реальной математике для ОГЭ >>>

Все графики функций >>>

Таблица умножения

К оглавлению…

Таблица квадратов двухзначных чисел

К оглавлению…

Формулы сокращенного умножения

К оглавлению…

Квадрат суммы:

Квадрат разности:

Разность квадратов:

Разность кубов:

Сумма кубов:

Куб суммы:

Куб разности:

Последние две формулы также часто удобно использовать в виде:

#Квадратное уравнение и формула разложения квадратного трехчлена на множители

К оглавлению…

Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D < 0, то квадратное уравнение не имеет корней.

В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения может быть вычислено по формуле:

#Свойства степеней и корней

К оглавлению…

Основные свойства степеней:

Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.

Основные свойства математических корней:

Для арифметических корней:

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:

Для корня четной степени имеется следующее свойство:

Арифметическая прогрессия

К оглавлению…

Формулы n-го члена арифметической прогрессии:

Соотношение между тремя соседними членами арифметической прогрессии:

Формула суммы арифметической прогрессии:

Свойство арифметической прогрессии:

Геометрическая прогрессия

К оглавлению…

Формулы n-го члена геометрической прогрессии:

bn = b1 · q n-1

bn+1 =bn · q, где bn ≠ 0, q ≠ 0

q – знаменатель прогрессии

Соотношение между тремя соседними членами геометрической прогрессии:

Формула суммы геометрической прогрессии:

Формула суммы бесконечно убывающей геометрической прогрессии:

Свойство геометрической прогрессии:

Геометрия на плоскости (планиметрия)

К оглавлению…

Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника: 

Площадь треугольника через две стороны и угол между ними:  

Площадь треугольника через сторону и высоту опущенную на неё: 

Полупериметр треугольника находится по следующей формуле: 

Формула Герона для площади треугольника: 

Площадь треугольника через радиус описанной окружности: 

Формула медианы: 

Свойство биссектрисы: 

Формулы биссектрисы: 

Основное свойство высот треугольника: 

Формула высоты: 

Еще одно полезное свойство высот треугольника: 

Теорема косинусов: 

Теорема синусов: 

Радиус окружности, вписанной в правильный треугольник: 

Радиус окружности, описанной около правильного треугольника: 

Площадь правильного треугольника: 

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты): 

Радиус окружности, вписанной в прямоугольный треугольник: 

Радиус окружности, описанной вокруг прямоугольного треугольника: 

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу): 

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника: 

Длина средней линии трапеции: 

Площадь трапеции: 

Площадь параллелограмма через сторону и высоту опущенную на неё: 

Площадь параллелограмма через две стороны и угол между ними: 

Площадь квадрата через длину его стороны: 

Площадь квадрата через длину его диагонали: 

Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами): 

Площадь прямоугольника через две смежные стороны: 

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними: 

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т. е. в том числе для любых треугольников):  

Свойство касательных: 

Свойство хорды: 

Теорема о пропорциональных отрезках хорд: 

Теорема о касательной и секущей: 

Теорема о двух секущих: 

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу): 

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой): 

Свойство центральных углов и хорд: 

Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

Сумма углов n-угольника:

Центральный угол правильного n-угольника:

Площадь правильного n-угольника:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

 

Формулы с логарифмами

К оглавлению…

Определение логарифма:

Определение логарифма можно записать и другим способом: 

Свойства логарифмов:

Логарифм произведения: 

Логарифм дроби: 

Вынесение степени за знак логарифма: 

Другие полезные свойства логарифмов:

Тригонометрия

К оглавлению…

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса: 

Определение косинуса: 

Определение тангенса: 

Определение котангенса: 

Основное тригонометрическое тождество: 

Простейшие следствия из основного тригонометрического тождества: 

Формулы двойного угла

Синус двойного угла: 

Косинус двойного угла: 

Тангенс двойного угла: 

Котангенс двойного угла: 

Тригонометрические формулы сложения

Синус суммы: 

Синус разности: 

Косинус суммы: 

Косинус разности: 

Тангенс суммы: 

Тангенс разности: 

Котангенс суммы: 

Котангенс разности: 

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов: 

Разность синусов: 

Сумма косинусов: 

Разность косинусов: 

Сумма тангенсов: 

Разность тангенсов: 

Сумма котангенсов: 

Разность котангенсов: 

Тригонометрические формулы преобразования произведения в сумму

Произведение синусов: 

Произведение синуса и косинуса: 

Произведение косинусов: 

Формулы понижения степени

Формула понижения степени для синуса: 

Формула понижения степени для косинуса: 

Формула понижения степени для тангенса: 

Формула понижения степени для котангенса: 

Формулы половинного угла

Формула половинного угла для тангенса: 

Формула половинного угла для котангенса: 

Тригонометрические формулы приведения

Формулы приведения задаются в виде таблицы:

Тригонометрическая окружность

По тригонометрической окружности легко определять табличные значения тригонометрических функций:

Тригонометрические уравнения

К оглавлению…

Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:

Для остальных тригонометрических функций запись однозначна. Для косинуса:

Для тангенса:

Для котангенса:

Решение тригонометрических уравнений в некоторых частных случаях:

Геометрия в пространстве (стереометрия)

К оглавлению…

Главная диагональ куба:

Объем куба:

Объём прямоугольного параллелепипеда:

Главная диагональ прямоугольного параллелепипеда (трёхмерная Теорема Пифагора):

Объём призмы:

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Объём пирамиды:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т. е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара: 

Площадь поверхности шара (площадь сферы): 

Координаты

К оглавлению…

Длина отрезка на координатной оси: 

Длина отрезка на координатной плоскости: 

Длина отрезка в трёхмерной системе координат: 

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы): 

Как успешно подготовиться к экзамену по математике?

Для того чтобы успешно подготовиться к ОГЭ или ЕГЭ по математике,  необходимо выполнить три важнейших условия:

1. Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к экзамену по математике, изучению теории и решению задач хотя бы по часу, но каждый день. Дело в том, что ОГЭ или ЕГЭ — это экзамены, где мало просто знать математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно, но только, решив тысячи задач.
2. Выучить все формулы и методы в математике! На самом деле, выполнить это тоже очень просто, необходимых формул по математике меньше 200. В алгебре и геометрии есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить. И, таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ОГЭ или ЕГЭ. После этого Вам останется подумать только над самыми сложными задачами.
3. Посетить все три этапа репетиционного тестирования (РТ) по математике в нашем Центре (ЦР). Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на РТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на реальном экзамене может показаться неподготовленному человеку очень непривычным.

Успешное и ответственное выполнение этих трех пунктов позволит Вам показать на экзамене отличный результат, максимальный из того на что Вы способны!

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно через контактную форму на данном сайте. В письме укажите предмет (математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

<<< Структура сайта подготовки к ОГЭ по математике

План подготовки к ОГЭ по математике >>>

Полные сведения о формулах в Excel

Начните создавать формулы и использовать встроенные функции, чтобы выполнять расчеты и решать задачи.

Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.

Важно: В этой статье мы обсудим похожие проблемы с просмотром и просмотром. Попробуйте использовать новую функцию ПРОСМОТРX , улучшенную версию функции ВЛОП, которая работает в любом направлении и по умолчанию возвращает точные совпадения, что упрощает и удобнее в использовании, чем предшественницу.

Создание формулы, ссылающейся на значения в других ячейках

1. Выделите ячейку.

2. org/ListItem”>

   Введите знак равенства “=”.

   Примечание: Формулы в Excel начинаются со знака равенства.

3. Выберите ячейку или введите ее адрес в выделенной.

4. Введите оператор. Например, для вычитания введите знак “минус”.

5. Выберите следующую ячейку или введите ее адрес в выделенной.

6. Нажмите клавишу ВВОД. В ячейке с формулой отобразится результат вычисления.

Просмотр формулы

1. При вводе в ячейку формула также отображается в строке формул

   .

2. Чтобы просмотреть формулу, выделите ячейку, и она отобразится в строке формул.

Ввод формулы, содержащей встроенную функцию

1. Выделите пустую ячейку.

2. org/ListItem”>

   Введите знак равенства “=”, а затем — функцию. Например, чтобы получить общий объем продаж, нужно ввести “=СУММ”.

3. Введите открывающую круглую скобку “(“.

4. Выделите диапазон ячеек, а затем введите закрывающую круглую скобку “)”.

5. Нажмите клавишу ВВОД, чтобы получить результат.

Скачивание книги “Учебник по формулам”

Мы подготовили для вас книгу Начало работы с формулами, которая доступна для скачивания. Если вы впервые пользуетесь Excel или даже имеете некоторый опыт работы с этой программой, данный учебник поможет вам ознакомиться с самыми распространенными формулами. (крышка) применяется для возведения числа в степень, а * (звездочка) — для умножения.

Константа представляет собой готовое (не вычисляемое) значение, которое всегда остается неизменным. Например, дата 09.10.2008, число 210 и текст «Прибыль за квартал» являются константами. выражение или его значение константами не являются. Если формула в ячейке содержит константы, а не ссылки на другие ячейки (например, имеет вид =30+70+110), значение в такой ячейке изменяется только после редактирования формулы. Обычно лучше помещать такие константы в отдельные ячейки, где их можно будет легко изменить при необходимости, а в формулах использовать ссылки на эти ячейки.

Ссылка указывает на ячейку или диапазон ячеек листа и сообщает Microsoft Excel, где находятся необходимые формуле значения или данные. С помощью ссылок можно использовать в одной формуле данные, находящиеся в разных частях листа, а также использовать значение одной ячейки в нескольких формулах.

Вы также можете задавать ссылки на ячейки разных листов одной книги либо на ячейки из других книг. Ссылки на ячейки других книг называются связями или внешними ссылками.

• Стиль ссылок A1

  По умолчанию Excel использует стиль ссылок A1, в котором столбцы обозначаются буквами (от A до XFD, не более 16 384 столбцов), а строки — номерами (от 1 до 1 048 576). Эти буквы и номера называются заголовками строк и столбцов. Для ссылки на ячейку введите букву столбца, и затем — номер строки. Например, ссылка B2 указывает на ячейку, расположенную на пересечении столбца B и строки 2.

  Ячейка или диапазон	Использование
  Ячейка на пересечении столбца A и строки 10	A10
  Диапазон ячеек: столбец А, строки 10-20.	A10:A20
  Диапазон ячеек: строка 15, столбцы B-E	B15:E15
  Все ячейки в строке 5	5:5
  Все ячейки в строках с 5 по 10	5:10
  Все ячейки в столбце H	H:H
  Все ячейки в столбцах с H по J	H:J
  Диапазон ячеек: столбцы А-E, строки 10-20	A10:E20

• org/ListItem”>
  Создание ссылки на ячейку или диапазон ячеек с другого листа в той же книге

  В приведенном ниже примере функция СРЗНАЧ вычисляет среднее значение в диапазоне B1:B10 на листе “Маркетинг” в той же книге.

  1. Ссылка на лист “Маркетинг”.

  2. Ссылка на диапазон ячеек от B1 до B10

  3. Восклицательный знак (!) отделяет ссылку на лист от ссылки на диапазон ячеек.

  Примечание: Если название упоминаемого листа содержит пробелы или цифры, его нужно заключить в апострофы (‘), например так: ‘123’!A1 или =’Прибыль за январь’!A1.

• Различия между абсолютными, относительными и смешанными ссылками

  org/ItemList”>

  1. Относительные ссылки   . Относительная ссылка в формуле, например A1, основана на относительной позиции ячейки, содержащей формулу, и ячейки, на которую указывает ссылка. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка. При копировании или заполнении формулы вдоль строк и вдоль столбцов ссылка автоматически корректируется. По умолчанию в новых формулах используются относительные ссылки. Например, при копировании или заполнении относительной ссылки из ячейки B2 в ячейку B3 она автоматически изменяется с =A1 на =A2.

     Скопированная формула с относительной ссылкой   

  2. Абсолютные ссылки   .  Абсолютная ссылка на ячейку в формуле, например $A$1, всегда ссылается на ячейку, расположенную в определенном месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется. При копировании или заполнении формулы по строкам и столбцам абсолютная ссылка не корректируется. По умолчанию в новых формулах используются относительные ссылки, а для использования абсолютных ссылок надо активировать соответствующий параметр. Например, при копировании или заполнении абсолютной ссылки из ячейки B2 в ячейку B3 она остается прежней в обеих ячейках: =$A$1.

     Скопированная формула с абсолютной ссылкой   

  3. Смешанные ссылки   . Смешанная ссылка содержит либо абсолютный столбец и относительную строку, либо абсолютную строку и относительный столбец. Абсолютная ссылка на столбец имеет вид $A1, $B1 и т. д. Абсолютная ссылка на строку имеет вид A$1, B$1 и т. д. Если положение ячейки с формулой изменяется, относительная ссылка меняется, а абсолютная — нет. При копировании или заполнении формулы по строкам и столбцам относительная ссылка автоматически изменяется, а абсолютная ссылка не корректируется. Например, при копировании или заполнении смешанной ссылки из ячейки A2 в ячейку B3 она автоматически изменяется с =A$1 на =B$1.

     Скопированная формула со смешанной ссылкой   

• Стиль трехмерных ссылок

  Удобный способ для ссылки на несколько листов   . Трехмерные ссылки используются для анализа данных из одной и той же ячейки или диапазона ячеек на нескольких листах одной книги. Трехмерная ссылка содержит ссылку на ячейку или диапазон, перед которой указываются имена листов. В Microsoft Excel используются все листы, указанные между начальным и конечным именами в ссылке. Например, формула =СУММ(Лист2:Лист13!B5) суммирует все значения, содержащиеся в ячейке B5 на всех листах в диапазоне от Лист2 до Лист13 включительно.

  • При помощи трехмерных ссылок можно создавать ссылки на ячейки на других листах, определять имена и создавать формулы с использованием следующих функций: СУММ, СРЗНАЧ, СРЗНАЧА, СЧЁТ, СЧЁТЗ, МАКС, МАКСА, МИН, МИНА, ПРОИЗВЕД, СТАНДОТКЛОН.Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА.

  • Трехмерные ссылки нельзя использовать в формулах массива.

  • Трехмерные ссылки нельзя использовать вместе с оператор пересечения (один пробел), а также в формулах с неявное пересечение.

  Что происходит при перемещении, копировании, вставке или удалении листов   . Нижеследующие примеры поясняют, какие изменения происходят в трехмерных ссылках при перемещении, копировании, вставке и удалении листов, на которые такие ссылки указывают. В примерах используется формула =СУММ(Лист2:Лист6!A2:A5) для суммирования значений в ячейках с A2 по A5 на листах со второго по шестой.

  • Вставка или копирование   . Если вставить листы между листами 2 и 6, Microsoft Excel прибавит к сумме содержимое ячеек с A2 по A5 на новых листах.

  • Удаление   .  Если удалить листы между листами 2 и 6, Microsoft Excel не будет использовать их значения в вычислениях.

  • Перемещение   . Если листы, находящиеся между листом 2 и листом 6, переместить таким образом, чтобы они оказались перед листом 2 или после листа 6, Microsoft Excel вычтет из суммы содержимое ячеек с перемещенных листов.

  • Перемещение конечного листа   . Если переместить лист 2 или 6 в другое место книги, Microsoft Excel скорректирует сумму с учетом изменения диапазона листов.

  • Удаление конечного листа   . Если удалить лист 2 или 6, Microsoft Excel скорректирует сумму с учетом изменения диапазона листов.

• Стиль ссылок R1C1

  Можно использовать такой стиль ссылок, при котором нумеруются и строки, и столбцы. Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. При использовании стиля R1C1 в Microsoft Excel положение ячейки обозначается буквой R, за которой следует номер строки, и буквой C, за которой следует номер столбца.

  Ссылка	Значение
  R[-2]C	относительная ссылка на ячейку, расположенную на две строки выше в том же столбце
  R[2]C[2]	Относительная ссылка на ячейку, расположенную на две строки ниже и на два столбца правее
  R2C2	Абсолютная ссылка на ячейку, расположенную во второй строке второго столбца
  R[-1]	Относительная ссылка на строку, расположенную выше текущей ячейки
  R	Абсолютная ссылка на текущую строку

  При записи макроса в Microsoft Excel для некоторых команд используется стиль ссылок R1C1. Например, если записывается команда щелчка элемента Автосумма для вставки формулы, суммирующей диапазон ячеек, в Microsoft Excel при записи формулы будет использован стиль ссылок R1C1, а не A1.

  Чтобы включить или отключить использование стиля ссылок R1C1, установите или снимите флажок Стиль ссылок R1C1 в разделе Работа с формулами категории Формулы в диалоговом окне Параметры. Чтобы открыть это окно, перейдите на вкладку Файл.

  К началу страницы

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

См. также

Переключение между относительными, абсолютными и смешанными ссылками для функций

Использование операторов в формулах Excel

Порядок выполнения действий в формулах Excel

Использование функций и вложенных функций в формулах Excel

Определение и использование имен в формулах

Использование формул массива: рекомендации и примеры

Удаление формул

Рекомендации, позволяющие избежать появления неработающих формул

Поиск ошибок в формулах

Сочетания клавиш и горячие клавиши в Excel

Функции Excel (по категориям)

Основные математические формулы – GeeksforGeeks

Математика включает в себя бесконечный спектр исследований и исследований в области чисел и их операций.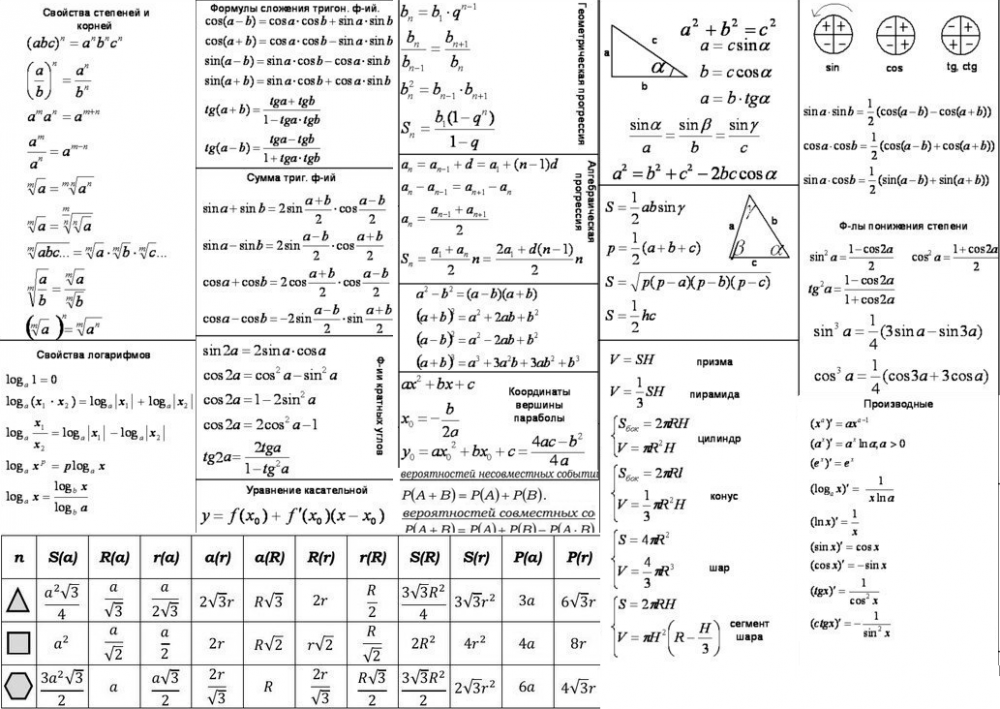 Каждая область математики имеет дело с чем-то другим. Филиалы исследуют новые методы и стандарты расчета, чтобы сделать ежедневную торговлю еще более удобной.

Математика делится на различные разделы в соответствии с используемыми способами вычислений и темами, которые они охватывают. Ветви включают геометрию, алгебру, арифметику, проценты, экспоненты и т. Д. Математика также предоставляет стандартные производные формулы, чтобы сделать операции или расчеты точными. В данной статье представлены все основные формулы, имеющиеся в математике по разным ее разделам или областям.

Основные математические формулы

Формула – это математическое выражение или определенное правило, которое выводится из отношения между двумя или более величинами, а полученный конечный продукт выражается в символах. Формулы математики включали числа, известные как константы, буквы, которые представляют неизвестные значения и известны как переменные, математические символы, известные как знаки, и в некоторых случаях экспоненциальные степени.

Арифметика

Арифметика – древнейший метод вычислений, известный до сих пор. Слово арифметика происходит от греческих слов «арифмос», что буквально означает числа. Брахмагупта индийский математик известен как «отец арифметики ». И Фундаментальная теория теории чисел была предложена Карлом Фридрихом Гауссом в 1801 году.

Основными арифметическими операциями являются сложение, вычитание, умножение и деление.

Арифметическая формула

Среднее арифметическое (среднее) = Сумма значений/Количество значений.

Алгебра

Алгебра — это элементарный предмет математики, который занимается изучением оценки чисел и символов. Алгебраические операции выполняются для определения неизвестных значений, которые выражаются буквами. Алгебраические уравнения представляют собой выражения, образованные комбинацией переменных, констант, факторов и коэффициентов переменных.

Базовая алгебраическая формула

• a ² – b ² = (a – b)(a + b)
• (a + b) 3 2 b + 4 = a ²
• A ² + B ² = (A + B) ² – 2AB
• (A – B) ² = A ² – 2AB + B ²
• (A ² – 2AB + B ² 9
• (A ² – 2AB + B ²
(A ² – 2AB + B ² (A ² – 2AB + B ^{2 2} – 2AB + B ² = A ² – 2AB + B ² = A a + b + c) ² = a ² + b ² + c ² + 2ab + 2bc + 2ca
• (a – b – c) ² = A ² + B ² + C ² – 2AB + 2BC – 2CA
• (A + B) ³ = A ³ + 3A ² B + 3AB ^{2 2} + 3A ² 444 3AB ² 4 + 3A ² 44. + b ²
• (a – b) ³ = a ³ – 3a ² b + 3ab ² – b ³
• a ³ – b ³ = (a – б)(а ² + аб + б ² )
• а ³ + б ³ = (а + б)(а ² – аб + б ² )
• (A + B) ⁴ = A ⁴ + 4A ³ B + 6A ² B ² + 4AB ³ + B ⁴ 797
• (A A AT ) ⁴ = A ⁴ – 4A ³ B + 6A ² B ² – 4AB ³ + B ⁴
• A ⁴ – B ⁴
• A ⁴ – B ⁴
. )(a + b)(a ² + b ² )
• (a ^m )(a ⁿ ) = a ^{m + n}
• (ab) ^m = a ^m b ^m
• (a ^m ) ⁿ = a ^mn

Geometry

Geometry is a part of mathematics that is concerned with the изучение форм, размеров, параметров, измерений, свойств и размеров. Обычно существует три типа геометрии. Это евклидова геометрия, сферическая геометрия и гиперболическая геометрия.

Формула базовой геометрии

• Прямоугольник

1. Периметр прямоугольника = 2 (L + B)
2. Площадь прямоугольника = L × B

, где ‘L’ длина, а ‘B’ – Beart

• – квадрат.

1. The area of ​​Square = a ²
2. The perimeter of Square = 4a

Where ‘a’ is the length of the sides of a Square

• Triangle

Area треугольника = 1/2 × b × h

Где «b» — основание треугольника, а «h» — высота треугольника

• Трапеция

Площадь трапеции = 1/2 × (b ₁ + b ) × h

, где B ₁ и B ₂ являются основаниями трапеции

и, H = высота трапеции

• Circle

• СРЕГО

8

8

• . r ²
• Длина окружности = 2πr

, где ‘r’ – это радиус круга

• Куб

Площадь поверхности куба = 6A ²

, где ‘a’ – это длина на сестрах.

• Цилиндр

1. Площадь изогнутой поверхности цилиндра = 2πrh
2. Общая площадь поверхности цилиндра = 2πr (r + h)
3. Объем цилиндра = V = πr ²
4. Объем цилиндра = V = πr ²
924794797 9247979797
11. .

    Где «r» — радиус основания цилиндра

    А, «h» — высота цилиндра

    • Конус

    1. Общая площадь криволинейной поверхности конуса = πrl
    поверхности площадь конуса = πr(r + l) = πr[r + √(h ² + r ² )]
    2. Объем конуса = V = 1/3× πr ² h

    Здесь ‘r’ — радиус основания конуса, а h = высота конуса

    • Сфера

    1. Площадь поверхности сферы = S = 4πr ²
    2. Объем сферы = v = 4/3 × πr ³

    , где r = radius of the Sphere

, где r = radius of the Sphere

, где r = radius of the Sphere

6 3

3

6 3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

.

Вероятность — это математический термин, используемый для определения вероятности наступления определенного события. Вероятность можно просто определить как возможность возникновения события. Она выражается по линейной шкале от 0 до 1. Существует три типа теоретической вероятности, экспериментальной вероятности и субъективной вероятности.

Базовая формула вероятности

P(A) = n(A)/n(S)

Где

P(A) — вероятность события.

n(A) — количество благоприятных исходов

n(S) — общее количество событий

Дробь

Дробь — это число, выраженное целыми числами, в котором числитель делится на знаменатель. Дробь – это в основном частное от деления.

Формула основных фракций

• (а + b/c) = (a × c) + b/c
• (a/b + d/b) = (a + d)/b
• (a/b + c/d ) = (a × d + b × c/b × d)
• a/b × c/d = ac/bd
• (a/b)/(c/d) = a/b × d/c

Процент

Процент — это числовое значение или отношение, выраженное в виде доли от 100. Обычно оно обозначается знаком %.

Базовая формула процентов

Процент = (Сумма в категории/Общая стоимость) × 100

Примеры задач

Вопрос 1: Определите вероятность получения туза из карты, взятой из колоды.

Решение:

Дано:

Общее количество благоприятных исходов n(S) = 52

Количество лицевых карт в колоде = 12 Теперь

P(A) = n(A)/n(S)

=> 12/52

=> 3/13

Следовательно, вероятность получить лицевую карту из колоды карт равна 3/ 13.

Вопрос 2: Упростить 3/(x – 1) + 1/(x(x – 1) = 2/x

Решение:

=> 3x + 1/x(x – 1) ) = 2(x – 1)/x(x – 1)

=> 3x + 1 = 2(x – 1)

=> x = -3

Вопрос 3: Если x + 1/x = 3. Найдите значение x ² + 1/x ² .

. => х ² + 2 × x × 1/x + (1/x) ² = 9

=> x ² + 1/x ² + 2 = 9

=> x ² + 1/ x ² = 7

Вопрос 4: Если радиус окружности равен 21 см. Найдите площадь данного круга.

Решение:

Дано:

Радиус окружности равен 21см.

Имеем,

Площадь круга (A) = πr ²

=> 22/7 × 21 × 21

=> 1386см ²

Следовательно, площадь данного круга равна 1386см ²

Вопрос 5: Найдите площадь треугольника с основанием 100см и высотой 20см.

Решение:

Дано:

Основание треугольника равно 100см.

Высота треугольника 20см.

У нас есть,

Площадь(A) = 1/2 × b × h

=> 1/2 × 10 × 20

=> 1000см ²

Вопрос 6: У Пунам есть 4/5 части поля, 2/5 из которых она использует для ведения сельского хозяйства. Какая часть фермы остается для других целей?

Решение:

Дано:

Общая доля земли 4/5.

Общая фракция, используемая для фарма 2/5.

Сейчас,

=> 4/5 – 2/5

=> 4 – 2/5

=> 2/5

Следовательно, осталось 2/5 часть поля.

Вопрос 7: Сколько будет 20% от 240 кг?

Решение:

=> 20/100 × 240

=> 48 кг

Следовательно, 20% от 240 кг будет 48 кг.




Базовые математические формулы — геометрия, вероятности, арифметика и часто задаваемые вопросы

Основная математическая формула обычно используется в базовой математике и используется не только в академических книгах, но и в нашей повседневной жизни. В начальных классах мы все узнали об общем правиле BODMAS. По мере того, как человек продолжает приближаться к более высоким классам от шести до десяти, он столкнется с различными формулами математики, основанными на различных концепциях, таких как алгебра.

Практикуя вопросы и ответы, основанные на различных формулах, можно выучить наизусть каждую формулу, прежде чем явиться на экзамены.

Некоторые другие понятия, имеющие формулы, приведены ниже:

Основная математическая формула

Основы математики показывают, как можно решить математическую задачу с помощью некоторых уравнений, таких как уравнение сил, ускорений или работы Выполнено. Что еще более важно, они используются для предоставления математических решений реальных проблем в нашей повседневной жизни.

Существует много типов уравнений, и они встречаются во многих областях математики. Но методы, используемые для их изучения, различаются в зависимости от их типа. Это может быть простая формула сложения или сложная, например интегрирование дифференцирования.

Формулы базовой геометрии

Где «a» — длина сторон квадрата

Где «l» — длина, а «b» — ширина

Где «a» — длина сторон квадрата

здесь «l» — длина, а «b» — ширина

Где «b» — основание треугольника, а «h» — высота треугольника

Где b1 и b2 — основания трапеции; h = высота трапеции

Где r — радиус окружности

Где а — длина сторон куба

• Площадь криволинейной поверхности цилиндра = 2πrh

• общая площадь поверхности цилиндра = 2πr(r + h)

• Объем цилиндра = V = πr ² h

Где «r» — радиус основания цилиндра, а «h» — высота цилиндра.

• Площадь криволинейной поверхности конуса = πrl (r + l) = πr[r + √(h ² + r ² )]

• Объем конуса = V = ⅓ × πr2h

Здесь ‘r’ — радиус основание конуса и h = высота конуса

Где r = радиус сферы

Базовая формула вероятности

P(A) = n(A)/n(S) Где P(A) — вероятность события. n(A) — количество благоприятных исходов. n(S) — общее количество событий в пространстве выборки.

Основные арифметические формулы

Математические формулы простыми словами могут быть выражены как выражение, которое было получено после того, как исследователи годами изучали конкретную задачу.