Раздел 1. Физические основы механики Основные формулы Кинематика поступательного движения
1. Скорость при прямолинейном движении в общем случае
= Vx + Vy + Vz ,
V 2 = Vx2+ Vy2+ Vz2.
2. Ускорение
= ax + ay + az ,
a 2 = ax2+ ay2+ az2
3. Уравнения кинематики равноускоренного поступательного движения:
V=V0+at,
S=V0 t+at2/2,
где V – скорость тела в момент времени t; V0 – начальная
скорость; a – ускорение движения тела; S – путь, пройденный за время t; t – время
движения тела.
4. Полное ускорение при криволинейном движении
a2=a2+an2,
где aτ = dV/dt– тангенциальное ускорение;an = V2/R– нормальное ускорение.
Кинематика вращательного движения
5. Угловая скорость при вращательном движении в общем случае
.
6. Угловое ускорение
.
7. Уравнения кинематики равноускоренного вращательного движения:
ω = ω0+t,
= ω0t+t2/2,
где ω –угловая скорость в момент времени
8. Угловая скорость при равномерном вращательном движении
ω = /t = 2π/T = 2π ν,
где T– период
обращения;ν– частота обращения,
т.
е. число оборотов в единицу времени.
9. Формулы, связывающие угловые и линейные величины при рассмотрении движения вращающегося тела:
S = R, V = ω R,
а = R, an = ω 2 R = V2/R,
где R– радиус траектории, по которой движется тело;a– тангенциальное ускорение;an– нормальное или центростремительное ускорение.
Динамика поступательного движения
10. Основной закон динамики поступательного движения
dt=d(m).
11. Второй закон Ньютона
= /m,
где – ускорение тела;– сила, действующая на тело; m– масса тела.
12. Закон Гука
= – kx,
где k– коэффициент упругости;х– величина деформации.
13. Сила трения
= ,
где – коэффициент трения;N– сила
нормального давления, прижимающая тело
к плоскости при скольжении.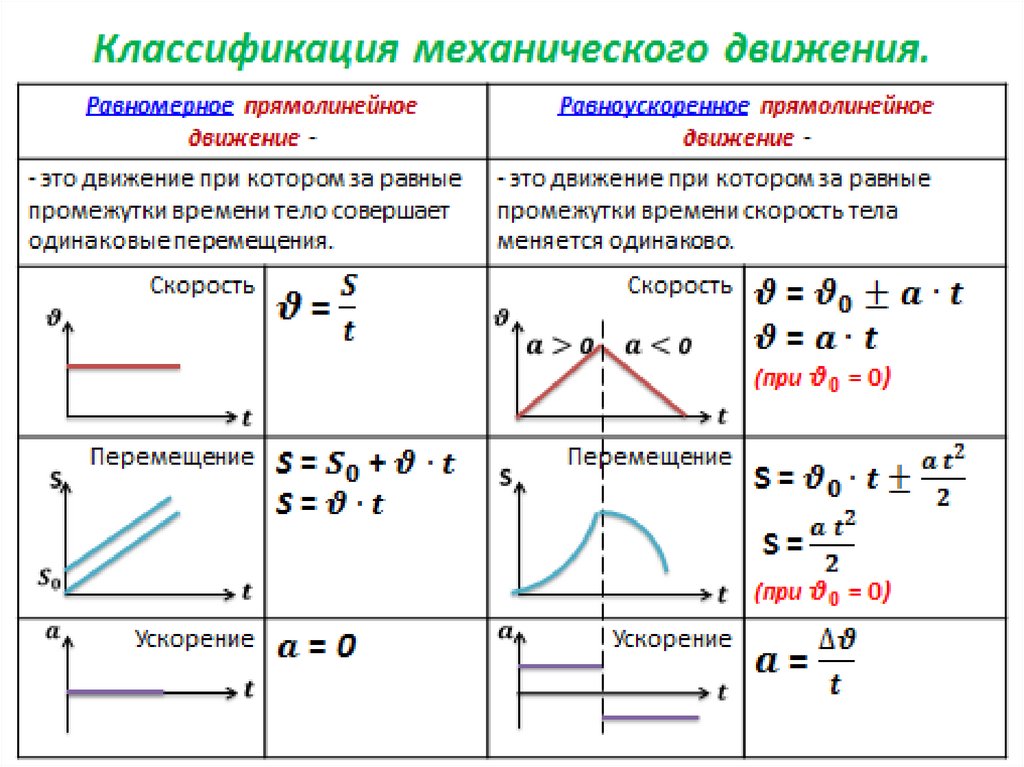
14. Гравитационная сила
F=Gm1m2/r2,
где F– сила гравитационного притяжения между двумя точечными массамиm1иm2;r– расстояние между ними;G– гравитационная постоянная.
15. Закон сохранения импульса
= m1
16. Скорость движения тел после неупругого, центрального удара
= (m11+m22)/(m1+m2),
где m1– масса первого тела;m2– масса второго тела;1– скорость первого тела до удара;2– скорость второго тела до удара.
17. Скорости первого и второго тел после упругого соударения:
1=[(m1–m2) 1 + 2m22] /(m1+m2
2=[(m2–m1) 2 + 2m11] /(m1+m2),
18.
Механическая
работа
A=,
где FS– проекция силы на направление пути;S– величина участка пути.
В частном случае постоянной силы, действующей под неизменным углом к перемещению, имеем
A=FScos ,
где F– модуль вектора силы;S– модуль вектора перемещения;– угол между векторами силы и перемещения.
19. Мощность
N=dA/dt.
При постоянной мощности
N = A/t = F V cos α,
где А– работа, произведенная какой-либо силой;t– время, за которое произведена эта работа.
20. Кинетическая энергия
Wк= mV2/2,
где m– масса движущегося тела;V– скорость, с которой это тело движется.
21. Потенциальная энергия тела в поле силы тяжести (вблизи поверхности Земли)
Wп = mgh,
где m– масса тела;g– ускорение свободного падения;h– высота тела над поверхностью
Земли.
22. Закон сохранения механической энергии
Wк+Wп=const.
23. Давление в жидкости и газе
P = Fдав/S,
где Fдав– cила давления;S– площадь поверхности.
24. Закон Архимеда
Fa = жgVпогр,
где ж– плотность жидкости;g– уcкорение свободного падения;Vпогр– объем жидкости, вытесненной погруженной частью тела.
Что такое кинематические уравнения?
Похожие материалы
сообщите об этом объявлении
Содержание урока
Четыре кинематических уравнения
Уравнение 1: V = V 0 + AT
Уравнение 2: V 2 = V 0 2927 + 2 + 2A 2A) 2 (2 = V 0 26 2 + 2 ).
Уравнение 3: x = x 0 + v 0 T
Уравнение 4: x = x 0 + V 0 T + 1 / 2 AT 2
KINEM 2
KINEMBLEAT v – Скорость
a – Ускорение
t – Время
Это четыре переменные, играющие роль в кинематических уравнениях. Уравнения описывают движение объекта с постоянным ускорением. Используя уравнения, мы можем найти начальное и конечное значения этих переменных.
Важно: Направленность переменных
Перемещение, скорость и ускорение являются направленными, тогда как время не направлено. Направленные переменные будут иметь положительное значение, если их вектор указывает в положительном направлении, и отрицательное значение, если их вектор указывает в отрицательном направлении. Поскольку время не имеет направления, оно всегда будет иметь положительное значение.
При использовании кинематических уравнений для решения задач полезно выбрать направление для положительных x , v и a . Иногда это направление дается в условии задачи. Противоположным положительному направлению будет отрицательное направление.
Когда использовать кинематические уравнения
Кинематика — это изучение движения объекта без учета сил, вызывающих движение. Кинематические уравнения представляют собой упрощение движения объекта. Три уравнения предполагают постоянное ускорение (уравнения 1, 2 и 4), а другое уравнение предполагает нулевое ускорение и постоянную скорость (уравнение 3).
Когда задача движения объекта попадает в эти категории, мы можем использовать кинематические уравнения для ее решения. Например, мы можем использовать их, чтобы выяснить, как далеко летит снаряд, пока снаряд испытывает постоянное ускорение во время полета. Еще одним примером простого и эффективного использования кинематических уравнений является движение автомобиля с постоянной скоростью.
Поскольку он имеет нулевое ускорение, мы можем использовать уравнение, в котором нет условий ускорения (уравнение 3).
Как выбрать кинематическое уравнение
Мы должны решить, какое кинематическое уравнение лучше всего подходит для того, что мы решаем. Как правило, задачи кинематики включают решение для некоторых неизвестных. Неизвестным может быть начальное перемещение, конечное перемещение, изменение смещения, начальная скорость, конечная скорость, ускорение или время.
Мы выбираем уравнение, исходя из того, что известно и что неизвестно. В некоторых случаях мы должны использовать несколько уравнений последовательно, чтобы найти значение нашего неизвестного. Приведенные ниже примеры задач дают больше понимания процесса выбора уравнения.
Примеры задач
Кинематическое уравнение 1 Пример
Снаряд вылетает из патронника пушки и разгоняется до скорости 1500 м/с 2 за 0,75 секунды до вылета из ствола.
Какова скорость снаряда в момент вылета из ствола пушки?
Решение:
1. Поскольку снаряд не движется до момента выстрела, наша начальная скорость будет равна нулю. Нам даны значения ускорения (1500 м/с 2 ) и время (0,75 секунды), поэтому мы будем использовать уравнение v = v 0 + at .
2. Поскольку мы знаем значения всех переменных, кроме конечной скорости, мы можем подставить наши известные значения, чтобы найти v, что дает нам v = (0 м/с) + (1500 м/с 2 )(0,75 секунд) = 1125 м/с .
3. Скорость снаряда составляет 1125 м/с при выходе из ствола.
Кинематическое уравнение 2 Пример
Спринтер движется со скоростью 5 м/с, когда он достигает 20 метров в своем забеге. Они сохраняют постоянное ускорение 2 м/с 2 через 40 метров в гонку. Какова скорость спринтера на 40-метровой дистанции?
Решение:
1. Нам известны значения начальной скорости (5 м/с), ускорения (2 м/с 2 ) и изменения смещения (40 – 20 = 20 метров).
Уравнение, которое мы будем использовать: v 2 = v 0 2 + 2a(Δx) .
2. Поскольку мы знаем значения всех переменных, кроме конечной скорости, мы можем подставить наши известные значения и найти v.
v 2 = (5 м/с) 2 + 2(2 м/с 2 )(20 метров)
v 2 = 105
2
Кинематическое уравнение 3 Пример
Автомобиль находится в 200 метрах от здания и начинает отъезжать от здания со скоростью 20 м/с. На каком расстоянии от здания находится автомобиль после движения в течение 6 секунд?
Решение:
1. Известны значения начального перемещения (200 метров), начальной скорости (20 м/с) и времени в движении (6 секунд). Мы должны найти конечное перемещение. Кинематическое уравнение, которое мы будем использовать: x = x 0 + v 0 t .
2. Поскольку мы знаем значения всех переменных, кроме одной, мы можем подставить известные значения, чтобы найти неизвестное значение x.
x = (200 метров) + (20 м/с)(6 секунд) = 320 метров
3. Через 6 секунд автомобиль проедет 320 метров подальше от здания.
Кинематическое уравнение 4 Пример
Человек стоит в 6 метрах позади вас. Они бросают мяч над головой с горизонтальной скоростью 20 м/с. Мяч испытывает постоянное горизонтальное замедление со скоростью 4 м/с 2 во время полета, и ему требуется 2 секунды, чтобы приземлиться. На каком расстоянии перед вами приземлится мяч?
Решение:
1. Нам известны значения начального перемещения (-6 метров), начальной скорости (20 м/с), ускорения (-4 м/с 2 ) и время (2 секунды). Уравнение, которое мы будем использовать: x = x 0 + v 0 t + 1 / 2 at 2 .
2.
Поскольку нам известны значения всех переменных, кроме конечного смещения, мы можем подставить известные значения и найти x.
x = (-6 метров) + (20 м/с)(2 секунды) + 1 / 2 (-4 м/с 2 )(2 секунды) 2
x = -6 + 40 – 8
х = 26 метров
3. Мяч приземляется 26 метров перед вами.
Бонусный урок кинематики
Что такое движение снаряда?
Ранее мы упоминали, что задачи движения снаряда можно решить с помощью кинематических уравнений. Хотя движение снаряда — это лишь одна из многих проблем, с которыми мы сталкиваемся в кинематике, очень полезно точно понять, что это такое.
Движение снаряда по определению — это движение объекта или частицы, на которое действует только сила тяжести. Снаряд движется по параболической траектории, аналогичной траектории броска мяча. Эта параболическая траектория также называется баллистической траекторией.
Как решить движение снаряда
Поскольку мы пренебрегаем силой сопротивления воздуха при движении снаряда, мы можем вычислить, как далеко улетит снаряд, разложив его скорость на вертикальную и горизонтальную составляющие. Горизонтальная составляющая скорости во время полета будет постоянной. Вертикальная составляющая скорости будет влиять на время полета снаряда или время зависания.
Вот уравнения для горизонтального и вертикального движения снаряда. Они выводятся из кинематических уравнений.
A x = 0
V x = V 0 COS (α)
X = V 0 COS (α) T + X 0
AS (α) T + X 0
A A 19. A 12 = -g
V y = V 0 SIN (α)
T = 2V Y / G
ПРИМЕРИ ДЛЯ ПРИМЕРЫ ДЛЯ ПРИМЕРИ
061 Мяч брошен с поверхности Земли со скоростью 25 м/с под углом 30° над горизонтом.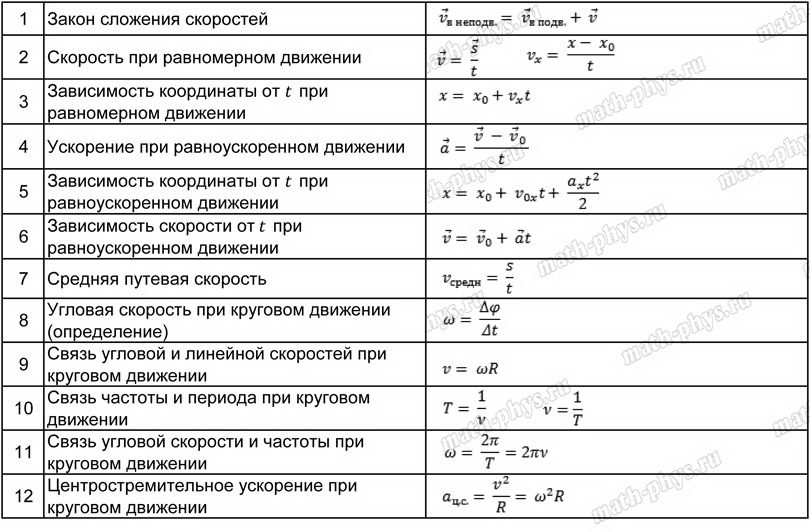
Пренебрегая сопротивлением воздуха, какое расстояние пролетит мяч по горизонтали, прежде чем упадет на землю?
Решение:
1. Сначала установим известные нам переменные.
v 0 = 25 м/с
α = 30°
g = 9,81 м/с 2 .
2. Найдем компоненты скорости.
v x = v 0 cos(α) = 25cos(30°) = 21,65 м/с
v y = v 0 sin(α) = 25sin(30°) = 12,5 м/с
3. Теперь мы можем найти время зависания и использовать его для расчета пройденного горизонтального расстояния.
T = 2V Y / G = 2 (12,5) / 9,81 = 2,55
x = V 0 COS (α) T + X 0 2020 2020 = 25COS = 25CS = 25COS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS = 25CS.
