| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Основные законы Динамики. Законы Ньютона – первый, второй, третий. Принцип относительности Галилея. Закон всемирного тяготения. Сила тяжести. Силы упругости. Вес. Силы трения – покоя, скольжения, качения + трение в жидкостях и газах. Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||
Основы динамики – Физика – Презентации
Просмотр содержимого документа
«Основы динамики»
Обобщение знаний по теме «Основы динамики»
Основные формулы
- Второй закон Ньютона F=ma
- Сила упругости F=kx
- Сила трения F=μN
Переведите в СИ:
400 г = … 252 км/ч = …
50 г = … 5 кН= …
20 см = … 40 мН = …
35 мм = … 0,3 т = …
36 км/ч= …
Равноускоренное движение тела
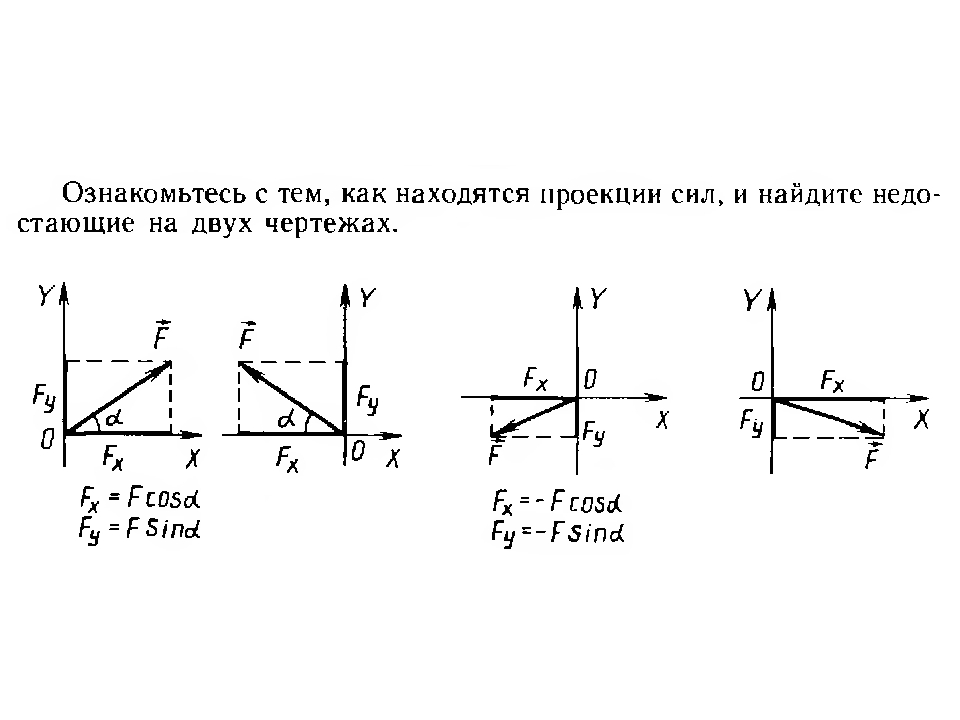
Y
X
Запишем второй закон ньютона в векторном виде
Найдём проекции векторов на координатные оси:
ОX: Fт-Fтр =ma
ОY: N-mg = 0
Fтр = μN
Движение тела по вертикали
Решение
Второй закон Ньютона:
В проекциях на ось Oy:
Равномерное движение по окружности
OX: F тр = ma ,
OY: N – mg = 0
N = mg .
Так как F тр = μ N ,
F тр = μmg.
Значит , μmg= =ma n
Y
X
Движение по окружности
Второй закон Ньютона:
N+mg=ma
OY: N+mg=ma
v 2
a ц
a=
R
Y
5
Два связанных тела с равными массами движутся равноускоренно. Пренебрегая силой трения, найдите модуль ускорения, с которым они движутся.
Дано:
=30
0
1. Движение первого тела по наклонной плоскости:
2. Движение второго тела по вертикали.
3. Подставляем второе уравнение в первое:
Повторительно-обобщающий урок в 10 классе «Основы динамики. Силы в природе»
Урок по физике
по теме:
«Повторительно-обобщающий урок «Основы динамики. Силы в природе»
Силы в природе»
10 класс
Тип урока: Обобщение изученного материала.
Тема урока: «Основы динамики. Силы в природе. Решение задач».
Цель урока:
1. Совершенствование умений решения задач по теме «Основы динамики», применять знания о сложении и вычитании векторов к решению физических задач.
2. Развитие элементов творческой деятельности учащихся.
3. Воспитание в учениках средствами урока уверенность в своих силах.
Задачи урока:
Образовательные:
– формировать практические навыки решения задач;
– учить обучающихся использовать теоретические знания для решения задач;
Развивающие:
– развивать умения применять математические знания в измененной ситуации при решении физических задач;
– развивать коммуникативные умения обучающихся;
– развивать умение обучающихся формулировать и выражать собственные мысли;
Воспитательные:
– способствовать формированию научного мировоззрения;
– учить детей видеть практическую пользу знаний.

Оборудование:
• Бруски
• Динамометры
• Лента измерительная
Наглядные пособия и раздаточный материал:
• Обобщающая таблица
• Тестовые задания
• Карточки с текстами задач
Ход урока
I. Обобщение материала по теме: «Законы динамики. Силы в природе».
Весь мир игра, а люди в нем актеры. Представьте, что вы пришли устраиваться на престижную работу. Здесь находится комиссия, которая проводит с вами собеседование. Сегодня мы распределим роли таким образом:
Вы презентуете себя, свои знания для поступления на престижную работу, требующую знаний законов динамики. ( У каждого на столе флажок с именем и фамилией)
Наши гости – независимые эксперты, выставляющие вам оценку.
Ну а я работодатель, оцениваю вашу профпригодность по средней оценке независимых экспертов.
Итак начнем.
Я хотела бы знать не сколько хорошо вы знаете теоретический материал – формулы, законы, определения. Предлагаю отгадать загадки и назвать силы.
Предлагаю отгадать загадки и назвать силы.
ЗАГАДКИ
С утра сегодня тарарам,
Пляшут вещи тут и там,
А мы кричим от радости:
“Исчезла сила … (…)!”
Вызвали меня к доске,
Я стою в большой тоске.
Мел держать не в силах я,
Ох, и где ж ты сила (…)!
Вот дощечка через речку
По ней как речку перейти?
Шагом иль бегом без трудности
Поможет мне сила (…).
Силу надо мне измерить
Какой прибор беру я смело?
Не амперметр, не вольтметр,
А прибор (…)!
Измеряем массу в килограммах,
Время точно уж в секундах,
Ну а силу круто так
Измеряем в (…).
На доске нарисована обобщающая таблица по силам. Заполнить эту таблицу. Задание
выполняет 1 учащийся.
Теперь меня интересует, насколько хорошо вы можете применять свои знания в объяснении различных жизненных ситуациий. Предлагаю вам выбрать одну из задач и дать ответ. Ответ прошу остальных учащихся прокоментировать ответ на вопрос. Это тоже будет учитываться экспертами.
Это тоже будет учитываться экспертами.
Качественные задачи
1. Два вагона разных масс движутся с одинаковой скоростью. Как изменится скорость вагонов, если приложить к ним одну и ту же силу, препятствующую движению. Какой из вагонов раньше остановится?
2. Почему автомобилю трудно тронуться с места на обледенелой улице?
4. Человек прыгает со стула, держа в руке гирю в 10 кг. С какой силой давит гиря на руку человека в то время, когда он находится в воздухе?
5. Почему медицинские иглы полируют до зеркального блеска?
6. Однажды семикласник Вася, только что изучивший на уроке физики взаимодействие тел, был сбит с ног нечаянно выскочившим из школы третьекласником Димочкой. С какой целью Вася после этого случая гнался за Димочкой полтора часа?
Ответ: чтобы привести в исполнение закон природы, по которому действие тела на другое тело не может быть односторонним. Всякое действие рождает противодействие.
Теперь я хочу проверить вашу коммуникабельность. Коммуника́бельность (новолат. соединимый, сообщающийся) — способность к общению, к установке связей, контактов, общительность.
Коммуника́бельность (новолат. соединимый, сообщающийся) — способность к общению, к установке связей, контактов, общительность.
Для этого предлагаю вам объединиться в группы и выполнить экспериментальное задание. (Приборы на столе, задание написано на листке бумаги)
Положите брусок на стол и отметьте его начальное положение. Толкните брусок рукой и заметьте его новое положение на столе. Измерив, тормозной путь, модуль силы трения скольжения, вес тела и определив массу тела, вычислите модуль начальной скорости и время торможения бруска.
Fтр =S =
v =
Проанализировать работу
Задания наши усложняются, поэтому необходимо сделать небольшой перерыв, то есть физкультминутку.
На каждой работе цениться человек эрудированный. Эруди́ция (от лат. eruditia — ученость, познания) — широкие (но не глубокие) познания.
Поэтому я предлагаю вам решить задачу, объединяющую знания по физике, истории, литературе и математике
– Какое произведение иллюстрирует этот рисунок?
-Кто автор этого произведения?
-Прочтите строки из басни.
«Однажды Лебедь, Рак да Щука
Везти с поклажей воз взялись
И вместе, трое, все в него впряглись;
Из кожи лезут вон,
А возу все нет ходу!
Поклажа бы для них казалась и легка:
Да Лебедь рвется в облака,
Рак пятится назад,
А Щука тянет в воду!
Кто виноват из них, кто прав –
Судить не нам;
Да только воз и ныне там!»
(И.А.Крылов)
– Каков смысл этой басни?
В басне выражено скептическое отношение к Александру I, она высмеивает неурядицы в Государственном Совете 1816 г. реформы и комитеты, затеваемые Александром I, не в силах были стронуть с места глубоко увязший воз самодержавия. В этом-то, с политической точки зрения, Иван Андреевич был прав.
– Каков физический аспект басни? Прав ли Крылов в том, что воз и ныне там?
– Как вы считаете, какие знания необходимы для решения этой задачи?
(Ответ: определить силы, действующие на тело и равнодействующую сил, правила нахождения равнодействующей сил)
-Какая сила называется равнодействующей сил?
сила, равная геометрической сумме всех приложенных к телу (точке) сил, называется равнодействующей или результирующей силой.
-Чему равна равнодействующая сил на этом рисунке?
Рисунок 1
R=0, т.к. |F1 | = |F2|
-Как ведет себя данное тело? (Ответ: либо покоится, либо движется прямолинейно и равномерно)
-Какой закон Ньютона это подтверждает?
(Ответ: I закона Ньютона: существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или действие этих тел скомпенсировано)
-Какое правило векторов необходимо применить для нахождения равнодействующей сил?
(Ответ: сложение и вычитание векторов)
-Как можно, опираясь на определение равнодействующей силы, сформулировать I закон Ньютона?
«Если равнодействующая сил, приложенных к телу, равна…, то тело сохраняет свое состояние … или … прямолинейного движения»
-Как поступить при нахождении равнодействующей, если силы, приложенные к телу, направлены в одну сторону по одной прямой?
Задача №1 (решение задачи №108 Григория Остера из задачника «Физика»)
Дед, взявшись за репку, развивает силу тяги до 600 Н, бабка – до 100 Н, внучка – до 50 Н, Жучка – до 30 Н, кошка – до 10 Н и мышка – до 2 Н. Чему равна равнодействующая всех этих сил, направленных по одной прямой в одну и ту же сторону? Справилась бы с репкой эта компания без мышки, если силы, удерживающие репку в земле, равны 791 Н?
Чему равна равнодействующая всех этих сил, направленных по одной прямой в одну и ту же сторону? Справилась бы с репкой эта компания без мышки, если силы, удерживающие репку в земле, равны 791 Н?
Вычислить алгебраически:
(Ответ. Модуль равнодействующей силы, равный сумме модулей сил, с которыми дед тянет за репку, бабка за дедку, внучка за бабку, Жучка за внучку, кошка за Жучку, а мышка за кошку, будет равен 792 Н. Вклад мускульной силы мышки в этот могучий порыв равен 2 Н. Без Мышкиных ньютонов дело не пойдет.
А если действующие на тело силы направлены под прямым углом друг к другу?
Вычислить геометрически.
Мы все повторили для того, чтобы ответить на вопрос, прав ли в басне И.А. Крылов?
Решение:
допустим, что силы действующие на воз, равны
найдите построением равнодействующую всех приложенных к возу сил.
(Ответ: после построения равнодействующей, что И.А. Крылов, безусловно, прав)
Подойдем к решению задачи с другой стороны.
Из таблицы видно, что все животные очень разные.
Мощность, развиваемая телами при равномерном прямолинейном движении, которое возможно при равенстве силы тяги и силы сопротивления, может быть рассчитана по следующей формуле:
N=F×ʋ (формула 7 класса)
При нахождении (построении) равнодействующей
-Какой вывод можно сделать?
(Ответ: при данных условиях воз будет смещаться в сторону движения Лебедя. Следовательно, с точки зрения физики, неправ был дедушка Крылов!)
Вы хорошо показали себя, и сейчас я предлагаю вам отдохнуть и решить пару устных задач
1. Чему равна сила, действующая на скворца на взлете, если его движение описывается уравнением x = x0+ 13t + 5t2, а его масса 80г?
Перед отлетом скворец решил подкрепиться . Нашёл червяка и стал тянуть его из земли силой 2Н. С какой силой должен сопротивляться червяк, чтобы остаться в живых?
и так ваши предварительные испытания подошли к концу.
5.Подведение итогов урока
Вот мы и раскрыли еще одну тайну… Ибо, как сказал А.Эйнштейн: «Самое прекрасное и глубокое из доступных нам чувств – это ощущение тайны, ибо в нем – источник истинной науки»
Методическая литература:
1. В. А. Буров, А. И. Иванов «Фронтальные экспериментальные задания по физике».
2. М. Е. Тульчинский «Качественные задачи по физике».
3. Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский «Физика 10».
4. Г. А. Рассказова «Основы механики 9 класс».
5. О. Ф. Кабардин «Задания для контроля знаний учащихся по физике в средней школе».
6. В. Н. Блинов «Тесты по физике для 9-10 класса».
Положите брусок на стол и отметьте его начальное положение. Толкните брусок рукой и заметьте его новое положение на столе. Измерив, тормозной путь, модуль силы трения скольжения, вес тела и определив массу тела, вычислите модуль начальной скорости и время торможения бруска.
Fтр =S =
v =
Положите брусок на стол и отметьте его начальное положение. Толкните брусок рукой и заметьте его новое положение на столе. Измерив, тормозной путь, модуль силы трения скольжения, вес тела и определив массу тела, вычислите модуль начальной скорости и время торможения бруска.
Толкните брусок рукой и заметьте его новое положение на столе. Измерив, тормозной путь, модуль силы трения скольжения, вес тела и определив массу тела, вычислите модуль начальной скорости и время торможения бруска.
S =
v =
Положите брусок на стол и отметьте его начальное положение. Толкните брусок рукой и заметьте его новое положение на столе. Измерив, тормозной путь, модуль силы трения скольжения, вес тела и определив массу тела, вычислите модуль начальной скорости и время торможения бруска.
Fтр =S =
v =
Силатяжести
Вес тела
Сила упругости
Сила трения
В басне выражено скептическое отношение к Александру I, она высмеивает неурядицы в Государственном Совете 1816 г. реформы и комитеты, затеваемые Александром I не в силах были стронуть с места глубоко увязший воз самодержавия. В этом-то, с политической точки зрения, Иван Андреевич был прав.
реформы и комитеты, затеваемые Александром I не в силах были стронуть с места глубоко увязший воз самодержавия. В этом-то, с политической точки зрения, Иван Андреевич был прав.
Алимпеева Таня
Кикот Таня
Шарова Лина
Извольский Саша
Коржос Артём
Воронин Дима
Шумарин Саша
Раздел долгосрочного плана Тематическое повторение | Школа: ФИО учителя: | |||||||
Дата: |
| |||||||
Класс: 10 | Количество присутствующих: |
отсутствующих: – | ||||||
Тема урока | Основы динамики | |||||||
Цели обучения, которые достигаются на данном уроке | 10. 10.1.2.2 – понимать закон Всемирного тяготения и описывать движение спутников: 10.1.2.3 – описывать изменение физических величин при движении тела вертивально вверх и под углом к горизонту; | |||||||
Цели урока | Научить учащихся решать задачи на -законы Ньютона -закон Всемирного тяготения -движение тела под углом к горизонтом | |||||||
Критерии оценки | Ученик достиг цели, если выполняет следующие критерии оценивания: умеет решать задачи на законы Ньютона умеет решать задачи на закон Всемирного тяготения и движение спутников умеет решать задачи на движение тела под углом к горизонтом умеет определять величины характеризующие криволинейное движение | |||||||
Языковые цели | Учащиеся могут …решать задачи на динамику Словарь специфических терминов и терминология: – ускорение; – скорость; – перемещение; –
пройденный путь. Набор полезных фраз для общения/письма: – Первый закон Ньютона утверждает, что…..; – По второму закону Ньютона… – Всякому действию есть …..; – Любая сила имеет…… | |||||||
Привитие ценностей
| Развивать
мышление учащихся, интерес к изучению физики. Обучение на протяжении всей жизни | |||||||
Межпредметные связи | Навыки использования калькулятора получены учениками на уроках математики. | |||||||
Первоначальные знания | Понятия: траектория, путь, перемещение, скорость, ускорение и т.д. | |||||||
План | ||||||||
Этапы урока | Запланированная деятельность на уроке | Ресурсы | ||||||
Начало 1 мин.
12 мин
|
Деятельность учителя: Определяет тему, цель, задачи урока и мотивирует учебную деятельность через осознание учащимися практической значимости применяемых знаний и умений. Задание 1 « Формулы и законы динамики » Цель: –Повторить формулы и законы динамики Описание: вопрос – ответ, пишем формулы -законы Ньютона -сила Всемирного тяготения -сила тяжести -вес -сила упругости -сила трения, нормального давления -сила Архимеда -сила центростремительная и центробежная Деятельность учителя: задает вопросы, пишет на доске Деятельность ученика: отвечают на вопросы, пишут в
тетради Оценивание: Взаимооценка, проверка знаний по теме. |
Приложение 1
| ||||||
Середина
15 мин
12мин
|
Задание 2 « Решение задач на формулы и законы динамики » Цель: вспомнить методику решения задач на динамику Описание: Письменные задания по динамике Деятельность учителя: задает задание, контролирует выполнение Деятельность ученика: решают письменное задание Оценивание: самооценивание Задание 3 «Простые механизмы» Цель: Повторить формулы , решить задачи Описание: Письменное задание на простые механизмыДеятельность учителя: С помощью учеников и наводящих вопросов записывает формулы для простых механизмов Деятельность ученика: Отвечают на вопросы и записывают в тетради, решают письменное задание Оценивание: Ученик-ученик и учитель-ученик |
Приложение 2
Приложение 3
| ||||||
Конец 2 мин
|
3. Цель: проверить усвоение материала Описание: беседа – что узнали нового? – где используется изученное? – что вам дает знание ? Оценивание: обратная связь
|
| ||||||
Дополнительная информация | ||||||||
Дифференциация – как Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание – как Вы планируете проверить уровень усвоения материала учащихся? | Межпредметные связи | ||||||
При
объяснении нового материала трудно дифференцировать подачу материала. | Взаимооценка учеников по готовым ответам при выполнении первого задания. Во время изучения нового материала – обратная связь и поддержка со стороны учителя. | При выполнении расчетов ученики используют знания, полученные на уроках математики. | ||||||
Общая оценка
Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1: Коллективная работа при осмыслении нового материала. 2:Использование слайдов при проверке глубины знаний ученика. Какие две вещи могли бы улучшить урок (подумайте как о преподавании, так и об обучении)? 1: 2:. Что я узнал(а) за время урока о классе или отдельных учениках такого, что поможет мне подготовиться к следующему уроку? Следующий урок
следует начать с проверки домашнего задания. | ||||||||
Решение задач по теме «Основы динамики»
Динамика. Законы Ньютона
Динамика. Сила – векторная физическая величина, являющаяся мерой физического воздействия на тело со стороны других тел. 1) Только действие не скомпенсированной силы (когда сил больше одной, то равнодействующей
ПодробнееОбучающие задания на тему «ДИНАМИКА»
Обучающие задания на тему «ДИНАМИКА» 1(А) Автобус движется прямолинейно с постоянной скоростью. Выберете правильное утверждение. 1) На автобус действует только сила тяжести. ) Равнодействующая всех приложенных
1) На автобус действует только сила тяжести. ) Равнодействующая всех приложенных
Инерция. Законы Ньютона. Силы в механике
Физика. 9 класс. Тренинг «Инерция. Законы Ньютона. Силы в механике» 1 Инерция. Законы Ньютона. Силы в механике Вариант 1 1 Металлический брусок подвешен к пружине и целиком погружён в сосуд с водой, находясь
ПодробнееПервый закон Ньютона
Динамика 1 A 2 Первый закон Ньютона Существуют такие системы отсчета (инерциальные), в которых всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, если на него не действуют
ПодробнееЛЕТНЯЯ ШКОЛА ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА
УРАЛЬСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ имени первого Президента России Б.Н.Ельцина СПЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР ЛЕТНЯЯ ШКОЛА ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ФИЗИКА 30 июня 0 года РАЗБОР. Лицеист ставил
Лицеист ставил
д) F1=5H 60 o F3=5H F2=5H F1=4H a) F2=6H F1=2H F2=3H
Урок 1. Лекция: «Основы теории относительносит». Урок 2. Работа с текстом: Г.Гамов «Приключение мистера Томпкинса». Урок 4. Лекция: Принцип относительности Галилея. Инерция. Неотличимость покоя и равномерного
ПодробнееДинамика. Лекция 1.2.
Динамика Лекция 1.2. Динамика – раздел механики, изучает причины движения тел и какими причинами вызвано взаимодействие между телами. Классическая механика Ньютон Область применимости классической механики
ПодробнееИТТ Вариант 2 ОСНОВЫ ДИНАМИКИ
ИТТ- 10.2.2 Вариант 2 ОСНОВЫ ДИНАМИКИ 1. Единицей измерения какой физической величины является килограмм? А. Силы Б. Массы В. Работы Г. Энергии Д. Мощности 2. Кто открыл закон инерции? А. Аристотель Б.
Аристотель Б.
Блок – 2 Блок 2 ВЗАИМОДЕЙСТВИЕ ТЕЛ
Н.А.Кормаков -1-7 класс Блок – 2 Блок 2 ВЗАИМОДЕЙСТВИЕ ТЕЛ Содержание Содержание опорного конспекта Стр. Параграф учебника Лист-2 вопросов ОК 7.2.5 9 14,15,16,17 1-8 1.Механическое движение 2.Траектория
Подробнее3 ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Тема 3 ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ Динамика изучает законы движения тел и причины, которые вызывают или изменяют это движение. Как говорилось, динамика изучает причины, которые вызывают именно такой характер
ПодробнееДинамика поступательного движения
Динамика поступательного движения 1 План: 1. Первый закон Ньютона 2. Второй закон Ньютона 3. Третий закон Ньютона 4. Законы сил в механике 5. Задачи динамики 6. Система частиц 7. Центр масс 2 Первый закон
ПодробнееДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ ЛЕКЦИЯ, (раздел ) (лек. 4 «КЛФ, ч.») Законы Ньютона. Силы в природе. Почему в кинематике вводят только первую и вторую производные от радиус-вектора: первую скорость и вторую
4 «КЛФ, ч.») Законы Ньютона. Силы в природе. Почему в кинематике вводят только первую и вторую производные от радиус-вектора: первую скорость и вторую
Закон сохранения импульса
Закон сохранения импульса Закон сохранения импульса Замкнутая (или изолированная) система – механическая система тел, на которую не действуют внешние силы. d v ‘ ‘ d d v d… ‘ v ‘ v v ‘… ‘ v… v v
ПодробнееДинамика А) mg F ; В) mg-f; С) F F mg. ; Д) ; Е) F-mg.
Динамика 008.Сила, возникающая между приводным ремнем и шкивом при его движении, является силой А) натяжения. В) трения скольжения. С) трения качения. D) упругости. Е) трения покоя.. Равнодействующая трех
ПодробнееЗадания к контрольной работе
Задания к контрольной работе Контрольная работа проводится по двум главам: «Законы движения» и «Силы в механике». Если ученик выполнил все тестовые задания и ответил на теоретический вопрос, то за выполненную
Если ученик выполнил все тестовые задания и ответил на теоретический вопрос, то за выполненную
Банк заданий по физике 10 класс
Банк заданий по физике 1 класс МЕХАНИКА Равномерное и равноускоренное прямолинейное движение 1 На рисунке приведён график зависимости координаты тела от времени при его прямолинейном движении по оси x.
Подробнееγ гравитационная постоянная, γ = 6,67 10.
006-007 уч. год., 9 кл. Физика. Динамика. 5. Силы Запись второго закона Ньютона в виде формулы () нельзя трактовать, как равенство двух сил F и ma. Эта запись представляет собой лишь выражение равнодействующей
ПодробнееИТТ Вариант 1 ОСНОВЫ ДИНАМИКИ
ИТТ- 10.2.1 Вариант 1 ОСНОВЫ ДИНАМИКИ 1. Единицей измерения какой физической величины является ньютон? А. Силы Б. Массы В. Работы Г. Энергии Д. Мощности 2. Кто открыл закон инерции? А. Гераклит Б. Аристотель
Силы Б. Массы В. Работы Г. Энергии Д. Мощности 2. Кто открыл закон инерции? А. Гераклит Б. Аристотель
Лекция 3 ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Лекция 3 ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ Термины и понятия Первый закон Ньютона Второй закон Ньютона Третий закон Ньютона Всемирное тяготение Гелиоцентрическая система отсчета Гравитационные силы Дифференциал
ПодробнееДинамика. Три закона Ньютона
Динамика Три закона Ньютона Обучающие вопросы и задания 140. Как направлена равнодействующая сил, приложенных к свободно падающему телу? 141. Тело равномерно движется по окружности. Как направлена равнодействующая
ПодробнееСилы в природе. 1. Сила. 2. Виды сил
Силы в природе 1. Сила Сила физическая величина, количественно характеризующая действие одного тела на другое. Признаки действия силы: изменение скорости или направления движения, изменение формы или размеров
Признаки действия силы: изменение скорости или направления движения, изменение формы или размеров
Тема «Основы механики»
муниципальное бюджетное вечернее (сменное) общеобразовательное учреждение «Центр образования» Тема «Основы механики» (учебное пособие по физике для обучающихся 10 класса очно заочной формы обучения вечерних
ПодробнееКузьмичев Сергей Дмитриевич
Кузьмичев Сергей Дмитриевич СОДЕРЖАНИЕ ЛЕКЦИИ 3 1. Динамика. 2. Инерциальные и неинерциальные системы отсчета. Первый закон Ньютона. 3. Фундаментальные взаимодействия. 4. Масса. Импульс частицы и системы
ПодробнееБАНК ЗАДАНИЙ 9 КЛАСС. ДИНАМИКА
БАНК ЗАДАНИЙ 9 КЛАСС. ДИНАМИКА 1.1 Первый закон Ньютона 1. Свойство тела сохранять свою скорость при отсутствии воздействий называется 1) инертностью)инерцией3) энергией4)мощностью. Из предложенных формулировок
Из предложенных формулировок
УРОК ФИЗИКИ В 10 КЛАССЕ. Законы Ньютона
УРОК ФИЗИКИ В 10 КЛАССЕ Законы Ньютона КАКИЕ МЫ ЗНАЕМ ВИДЫ ДВИЖЕНИЯ 1. Равномерное прямолинейное ( скорость постоянна по величине и направлению) 2. Равноускоренное прямолинейное ( скорость меняется, ускорение
Подробнее2) 8 м/с 3) 12 м/с 4) 16 м/с
Физика. 9 класс. Демонстрационный вариант 4 (90 минут) Физика. 9 класс. Демонстрационный вариант 4 (90 минут) Диагностическая тематическая работа по подготовке к ГИА-9 по ФИЗИКЕ по теме «Механические явления,
ПодробнееОбразовательный минимум
триместр предмет физика класс 9т Образовательный минимум Основные понятия Движения тела по вертикали, брошенного под углом к горизонту, горизонтально. Движение по с постоянной по модулю скоростью. Центростремительное
Центростремительное
), движется равномерно
РАВНОВЕСИЕ ТЕЛ Раздел механики, в котором изучается равновесие тел, называется статикой Равновесным называется состояние тела, неизменное во времени, т е равновесие это такое состояние тела, при котором
ПодробнееКонтрольная работа по теме «Основы динамики и законы сохранения в механике»
Контрольная работа № 2. «Основы динамики и законы сохранения в механике».
Вариант 1.
1. Навстречу друг другу летят шарики из пластилина. Модули их импульсов равны соответственно 5*10 -2 кг*м/с и 3*10-2 кг*м/с. Столкнувшись, шарики слипаются. Определите импульс слипшихся шариков.
2. Камень свободно падает с высоты 150 м. Какова скорость камня в момент падения на землю? Сколько времени продолжалось свободное падение?
3. Велосипедист движется по закруглению дороги радиусом 10 м со скоростью 50 км/ч. С каким ускорением он проходит закругление? Какова действующая на его колеса сила трения, выполняющая роль центростремительной силы, если масса велосипедиста 45 кг?
Велосипедист движется по закруглению дороги радиусом 10 м со скоростью 50 км/ч. С каким ускорением он проходит закругление? Какова действующая на его колеса сила трения, выполняющая роль центростремительной силы, если масса велосипедиста 45 кг?
4. Установите соответствие между физическими законами и их формулами.
ФИЗИЧЕСКИЕ ЗАКОНЫ | ФОРМУЛЫ |
А) Закон всемирного тяготения Б) Второй закон Ньютона В) Третий закон Ньютона | 1) 2) F=k*x 3) 4) 5) |
Вариант 2.
1. Электровоз массой 180 т, движущийся со скоростью 1 м/с, сталкивается с неподвижным вагоном массой 60 т, после чего они движутся вместе. Определите скорость их совместного движения.
Определите скорость их совместного движения.
2. Автомобиль на повороте движется по окружности радиуса 16 м с постоянной скоростью 36 км/ч. Каково центростремительное ускорение?
3. Легкоподвижную тележку массой 3 кг толкают силой 6 Н. Определите ускорение тележки.
4. Установите соответствие между видами движения и их основными свойствами.
ВИДЫ ДВИЖЕНИЯ | ОСНОВНЫЕ СВОЙСТВА |
А) Свободное падение Б) Движение по окружности с постоянным по модулю скоростью В) Реактивное движение | 1) Происходит за счет отделения от тела с некоторой скоростью какой-либо его части. 2) движение под действием только силы тяжести. 3) Движение, при котором ускорение в любой момент времени направлено к центру окружности. 4) Движение происходит в двух взаимно противоположных направлениях. 5) движение с постоянной скоростью |
Вариант 3.
1. Пластилиновый шарик массой 2 кг, движущийся со скоростью 6 м/с, налетает на покоящийся шарик массой 4 кг. Определите скорость их совместного движения.?
2. Поезд движется со скоростью 72 км/ч по закруглению дороги. Определите радиус дуги, если центростремительное ускорение поезда равно 0,5 м/с2.
3. С какой силой притягиваются Луна и Земля, если МЛ= 7,35*1022 кг, М3=6 *1024кг , а расстояние между ними R=3,844 *108 м.
4. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
А) Центростремительное ускорение Б) Первая космическая скорость В) Импульс тела | 1) 2) m* 3) 4) 5) |
Вариант 4.
1. Мальчик массой 30 кг, бегущий со скоростью 3 м/с, вскакивает сзади на платформу массой 15 кг. Чему равна скорость платформы с мальчиком?
2. Спустившись с горки, санки с мальчиком тормозят с ускорением 2 м/с2. Определите величину тормозящей силы, если общая масса мальчика и санок равна 45 кг.
3. Рассчитать ускорение свободного падения на высоте, равной 5 радиусу Земли.(М3=6 *1024кг. R=6400км.)
4. Установите соответствие между физическими величинами и их измерительными приборами.
ФИЗИЧЕСКИЕ ЗАКОНЫ | ФОРМУЛЫ |
А) вес Б) масса В) скорость | 1)мензурка 2) весы 3) динамометр 4)спидометр 5) секундомер |
формул для динамического анализа | Прил.
 Мех. Ред.
Мех. Ред.1R6. Формулы для динамического анализа. – RL Huston (Dept of Mech, Indust, and Nucl Eng, Univ of Cincinnati, 598 Rhodes Hall, Cincinnati OH 45221-0072) и CQ Liu (DiamlerChrysler, Auburn Hills MI). Марсель Деккер, Нью-Йорк. 2001. 624 с. ISBN 0-8247-9564-4. 175,00 долларов США.
Проверено Дж. Анджелесом (Департамент механотехники и Центр интеллектуальных машин, McGill Univ, 817 Sherbrooke St W, Монреаль, PQ, h4A 2K6, Канада).
Набор формул динамики твердого тела без контекста был бы, мягко говоря, бессмысленным. К счастью, рецензируемая книга выходит за рамки составления такого сборника. Эта книга, по сути, дает исчерпывающий взгляд на предмет, начиная с самых основ. Хотя такая книга обычно предназначена для специализированной аудитории с инженерным или научным образованием, авторы включают такие фундаментальные определения, как время, расстояние, частица и т. Д., Которые, как можно было бы предположить, хорошо известны этой аудитории.Таким образом, материал главы 1 кажется неуместным для такой книги; Более того, несказанный читатель может быть озадачен некоторыми ошибочными определениями, такими как определение частицы , которое авторы основывают на концепции тела , не определенной в этой главе, но не ранее, чем через две главы, и относящейся только к жесткий корпус . Частица , которую авторы намерены определить, как ее понимают в инженерных кругах, является механической единицей, не обязательно малой , поскольку здесь на карту поставлена неспособность этой сущности изменить свое отношение, и, следовательно, частица может быть вагоном поезда, если аналитик заинтересован в изучении только его вертикальных колебаний при чистом переводе.Фактически, авторы признают это понятие в главе 3 – читателю нужно пройти на две главы вперед, чтобы получить объяснение определения, которое впервые дается в главе 1.
Д., Которые, как можно было бы предположить, хорошо известны этой аудитории.Таким образом, материал главы 1 кажется неуместным для такой книги; Более того, несказанный читатель может быть озадачен некоторыми ошибочными определениями, такими как определение частицы , которое авторы основывают на концепции тела , не определенной в этой главе, но не ранее, чем через две главы, и относящейся только к жесткий корпус . Частица , которую авторы намерены определить, как ее понимают в инженерных кругах, является механической единицей, не обязательно малой , поскольку здесь на карту поставлена неспособность этой сущности изменить свое отношение, и, следовательно, частица может быть вагоном поезда, если аналитик заинтересован в изучении только его вертикальных колебаний при чистом переводе.Фактически, авторы признают это понятие в главе 3 – читателю нужно пройти на две главы вперед, чтобы получить объяснение определения, которое впервые дается в главе 1.
Глава 2 посвящена элементарной векторной алгебре и векторному исчислению, а глава 3 знакомит с кинематикой частиц. Здесь авторы вводят понятие твердого тела, хотя изучение этого объекта отнесено к главе 6. Рецензенту непонятно, почему основное понятие угловой скорости, собственно твердого тела, вводится в главе 3, хотя авторы возвращаются к этой концепции в главе 6, не связывая эти два обсуждения.Главы 4 и 5 посвящены кинетике и динамике частиц соответственно. Кинетика, как здесь упоминается, относится к независимому изучению активных сил и сил инерции, а динамика – к изучению взаимодействия этих двух видов сил. Обратной стороной посвящения каждой из этих двух частей по одной главе является то, что читателю приходится ждать до главы 6, которую авторы назвали Кинематика тел , чтобы натолкнуться на предмет, который действительно важен для инженеров, а именно на твердые тела. .Кроме того, авторы утверждают в первом абзаце главы 6, что глава «фокусируется» на твердых телах. Дело в том, что в этой главе и на балансе книги авторы не рассматривают ничего, кроме твердых тел.
Дело в том, что в этой главе и на балансе книги авторы не рассматривают ничего, кроме твердых тел.
Твердые тела, с другой стороны, можно рассматривать либо как совокупность материальных точек (частиц), либо как континуумы материи; в любом случае эта материальная сущность вынуждена двигаться таким образом, что сохраняется расстояние между любой парой ее точек (континуум занимает область пространства и, следовательно, он также включает точки).Авторы выбрали традиционный первый подход, который не безупречен. При таком подходе читатель должен поверить в то, что суммирование дискретных членов может привести к интегралу по континууму. С другой стороны, при втором подходе формулировка динамики проста, поскольку доступен весь объем знаний, а именно, относящийся к механике сплошных сред. В этом контексте второй закон Ньютона и уравнение баланса моментов Эйлера становятся естественными выводами законов Эйлера сохранения количества движения и углового момента, соответственно, которые действительны для любого континуума, будь то жидкость или твердое тело, а если последнее, то ли деформируемый или жесткий.
Особенностью книги является обширное обсуждение того, как получить матрицы вращения для различных триплетов элементарных поворотов вокруг осей координат. Здесь авторы включают то, что они называют графами конфигурации , мнемоническое средство создания этих матриц с использованием простых правил. Этот рецензент не совсем убежден в полезности этого обширного обсуждения. Авторы пошли еще дальше и включили подраздел с заголовком «Вычислительные алгоритмы.Проблема в том, что в этом подразделе на полстраницы не обнаружено ни одного единственного алгоритма. Затем обсуждение классификации движения имеет некоторые проблемы: обсуждаются смещение и прямолинейное смещение , а также плоское движение и общее плоское движение . Однако авторы упустили из виду рациональный анализ смещений с точки зрения теории групп, доступный в архивной литературе [1] и на английском языке в монографии этого рецензента [2]. В той же главе терминология винтового движения содержит ошибки. В самом деле, в наиболее общем случае движения твердого тела ни одна точка тела не остается неподвижной относительно наблюдателя (по сути, системы координат), каким бы наблюдатель ни был. Однако всегда можно найти набор точек тела, точки которых имеют скорость относительно этого наблюдателя минимальной евклидовой нормы, все точки лежат на прямой, которая называется мгновенной винтовой осью движения, все точки на этой линии с одинаковыми скоростями.В пользу этого общего движения авторы ошибочно говорят о существовании центра вращения .
В той же главе терминология винтового движения содержит ошибки. В самом деле, в наиболее общем случае движения твердого тела ни одна точка тела не остается неподвижной относительно наблюдателя (по сути, системы координат), каким бы наблюдатель ни был. Однако всегда можно найти набор точек тела, точки которых имеют скорость относительно этого наблюдателя минимальной евклидовой нормы, все точки лежат на прямой, которая называется мгновенной винтовой осью движения, все точки на этой линии с одинаковыми скоростями.В пользу этого общего движения авторы ошибочно говорят о существовании центра вращения .
Одним из плюсов книги является отход авторов от обычной практики обращения к так называемым квазикоординатам для учета предполагаемых переменных, из которых, как считается, получаются непроизводные величины, такие как угловая скорость, при дифференцировании по времени. . Здесь, как и во всей книге, авторы неукоснительно следуют подходу Кейна, который является пионером в этом отношении и не зависит от квази-координат и других эзотерических величин, таких как псевдопроизводных , печально известных тем, что преследует литературу по этой теме.Подход Кейна, по сути, чрезвычайно полезен при рассмотрении неголономных систем. В главе 10, посвященной этому вопросу, авторы буквально следуют более ранней работе (Пассерелло и Хьюстон) [3], в которой авторы ввели неголономные связи в уравнения Лагранжа анализируемой системы с целью сокращения числа управляющих уравнений к набору независимых обыкновенных дифференциальных уравнений второго порядка (ОДУ), свободных от сил связи. При этом авторы столкнулись с проблемой решения ряда неизвестных обобщенных скоростей из меньшего числа линейных алгебраических уравнений.Авторы обошли это затруднительное положение , добавив тождества в один и тот же набор обобщенных скоростей, тем самым сделав их линейную систему детерминированной, то есть с таким же количеством уравнений, как и неизвестных, и невырожденными. В процессе авторы сделали свои выводы излишне громоздкими. Действительно, как показали в 1998 г. Островская и Анхелес [4], в этом анализе фактически нет необходимости решать какую-либо систему уравнений. Жалко, что авторы не провели литературный обзор – количество библиографических указаний, появившихся за последние 10 лет в этой книге, составляет всего 11.Фактически, восемь из них представляют собой либо учебники для студентов, либо монографии; только три являются архивными публикациями, и два из них являются собственными работами первого автора. В главе 7 содержатся дополнительные формулы кинематики твердого тела, а в главе 8 подробно обсуждаются инерционные свойства твердого тела. Главы 9 и 10 посвящены кинетике и динамике твердого тела соответственно. Глава 11, в свою очередь, включает различные типы механических систем, математические модели которых получены с использованием различных формулировок, обсуждаемых в книге: принцип Д’Аламбера; Уравнения Кейна; и уравнения Лагранжа.Последние три главы посвящены механическим системам, состоящим из множества твердых тел. Кстати, набор мог быть намного лучше. Обычная практика требует выделения курсивом букв, встречающихся в математических отношениях; авторы использовали те же римские шрифты текста. В результате чтение становится довольно тяжелым. Не помогает то, что авторы использовали текстовый процессор с довольно ограниченными возможностями набора, а издатель печатал свой документ без набора.
Эта книга не содержит сборника задач в конце главы, по этой причине ее использование в качестве учебника весьма ограничено, но, возможно, авторы никогда не собирались выпускать учебник.В качестве справочного документа Формулы для динамического анализа рекомендуется практикующим инженерам и зрелым аспирантам.
ДИНАМИКА АВТОМОБИЛЯ
ДИНАМИКА АВТОМОБИЛЯ
Динамика автомобиля – сложный аналитический и экспериментальная технология, которая используется для изучения и понимания откликов автомобиль в различных ситуациях движения. В области обучения водителей нет необходимости иметь дело с особенности этой технологии, а скорее с некоторыми из основных физических принципы, вовлеченные в это.В следующие принципы будут обсуждаться в этом разделе.
И. Кинетическая энергия
II. Центробежная сила
III. Инерция
IV. Трение
В. Тяга
Есть не имеет намерения дать полное техническое определение каждого принципа, но представить их таким образом, чтобы было полезно понять, почему автомобиль действует так, как это делает.
Кинетическая энергия – это термин, описывающий энергию a автомобиль имеет благодаря своей массе и скорости. Его формула проста, но говорит о многом.
Кинетическая энергия = (масса) x (скорость) 2
Это показывает, что кинетическая энергия транспортного средства увеличивается как квадрат скорости. Это означает, что при удвоении скорости энергия увеличивается в четыре раза. раз.Это увеличение энергии не вызывает проблема, если ее не нужно быстро рассеять или перенаправить.
Один способ, которым кинетическая энергия может рассеиваться очень быстро, – это когда автомобиль сталкивается с твердый объект. В этом случае, когда скорость увеличивается вдвое, в четыре раза больше энергии, доступной для повреждения транспортного средства и травмировать пассажиров. Кинетический Энергия автомобиля весом 4000 фунтов, движущегося со скоростью 100 миль в час, равна 1,36 миллиона фут-фунтов достаточно, чтобы поднять мужчину весом 175 фунтов 1.5 миль. Чтобы остановить этот автомобиль, необходима огромная энергия. быть рассеянным. Это можно сделать ударом или тормозами. Остановка расстояние связано с квадратом скорости; следовательно, для скорости 30 миль в час требуется четыре умноженное на расстояние до остановки, превышающее 15 миль в час. Многие водители никогда не задумываются о последствиях увеличения скорости, но они должны осознавать связанные с этим риски.
ЦЕНТРОБЕЖНАЯ СИЛА
Когда автомобиль поворачивается, центробежная сила действует на автомобиль и пытается толкнуть его вне кривой.Формула это:
Центробежная сила = (масса) X (скорость) 2 / радиус поворота
Это показывает, что центробежная сила увеличивается как квадрат скорости. Также при заданной скорости малый (узкий) радиус повороты производят больше силы, чем повороты с большим радиусом. Большое количество центробежной силы требует одинаково больших количеств противодействующей силы от шин, если автомобиль должен оставаться на Дорога.Шины можно рассматривать как струны от каждого конца транспортного средства к центру поворота. Если центробежная сила выше, чем шины могут противодействовать, одна или обе струны порвутся. После этого автомобиль покинет поворот.
ИНЕРЦИЯ
Инерция сопротивление изменению направления или скорости тела в состоянии покоя. или в движении. В данном случае это связанные с изменением курса или направления транспортного средства; то есть изменение от движения прямо до поворота.
важность инерции и распределения веса, поскольку они связаны с вождением, заключается в том, что они влияют на количество времени, необходимое для перехода от прямого к поворот или наоборот. Хотя эти изменения при обычной загрузке транспортного средства невелики, водителю следует распознавать необычную загрузку транспортного средства, например, размещение большого груза на задней двери универсала (или добавление тяжелого груза на крыша транспортного средства) вызовет изменения в способе движения транспортного средства и регулировки должно производиться в управлении автомобилем соответственно.
С инерция диктует, что движущееся тело будет продолжать движение по прямой линии, необходимо приложить силу, чтобы заставить автомобиль повернуть. Эта сила называется Центростремительная сила , и возникает в результате растяжения шин при движении автомобиля с прямой дороги. Центробежная сила должна превышать центробежных усилие для поворота автомобиля.
МОМЕНТЫ ИНЕРЦИИ:
А. Шаг силы, ощущаемой при ускорении или торможении, вокруг (Горизонтальная ось) автомобиля
Б. Сила, ощущаемая при повороте, движение из стороны в сторону (Боковое ось) автомобиля
С. Рыскание сила, ощущаемая при вращении вокруг (вертикальной оси) автомобиль
ПОЛЯРНЫЙ МОМЕНТ ИНЕРЦИИ
Очень важная концепция обращения, которая диктует готовность автомобиля изменить направление движения, если это называется полярным моментом. инерции.Полюса инерции просто другой способ сказать центр концентрации веса. Момент в этой концепции определяется расположением центра тяжести спереди назад. Автомобиль поворачивает (меняет направление) вокруг своего центр тяжести в углу, поэтому чем дальше центры тяжести концентрации расположены от центра тяжести (что является их общим центр), тем больше момент.
Высокий полярный момент инерции присутствует, когда весовые концентрации велики и далеко друг от друга.Низкий полярный момент инерции обнаруживается, когда вес концентрации невелики и близки друг к другу. Другими словами, легче управлять транспортным средством с низкой полярностью. момент инерции.
Автомобиль с низким полярным моментом инерции дает быстрое реагирование на команды рулевого управления. А автомобиль с высоким полярным моментом имеет высокую курсовую устойчивость (т.е. сопротивляется изменению своего направления).
Трение определяется как сопротивление движению между двумя поверхностями.Есть четыре основных типа трения.
А. Статическая удерживающая сила между двумя неподвижными поверхностями
Б. Скольжение сопротивления движению между двумя поверхностями, которые перемещаются друг через друга
С. Rolling Сопротивление движению катящегося объекта, как мяча, цилиндр или колесо
Д. Внутреннее сопротивление движению в упругих объектах (шины получают нагреваются от внутреннего трения при изгибе)
величина трения между двумя поверхностями зависит от:
1) вещество материала
2) Шероховатость поверхностей
3) величина силы, прижимающей поверхности друг к другу
4) наличие смазочных материалов
величина трения между двумя поверхностями называется коэффициентом трения .
КОЭФФИЦИЕНТ ТРЕНИЯ
Термин «коэффициент трения» определяется как максимальная сила, которую может создать шина на заданном дорожном покрытии состояние, разделенное на вес шины. Его формула:
Максимально возможное усилие
Коэффициент трения = вес шины
ИЛИ
Максимальное доступное усилие = коэффициент трения X Вес нагрузки на колесо
Таким образом, маневренность автомобиля на сухой Дорога зависит в первую очередь от дорожного покрытия и веса транспортного средства.На мокрой дороге другие факторы, например, шина состояние также необходимо учитывать.
По мере ускорения или замедления автомобиля больше быстро, или когда автомобиль поворачивает на более высоких скоростях, он требует большего тяговые силы от автопоезда. Комбинация шины и дороги будет создавать эти силы вплоть до предел трения.
Тяга определяется как сцепление шины с поверхностью дороги.Тяговых сил три:
1) Привод тяги Для ускорения автомобиля
2) Тормозная тяга Для замедления или остановки автомобиля
3) Тяга на повороте Для поворота автомобиля
при каждый раз, когда сила тяги становится больше, чем коэффициент трения, автомобиль выйдет из-под контроля.
А водитель может задействовать три силы. Для любой ситуации существует определенный уровень трения. (коэффициент) для приложения этих сил и, следовательно, для маневрирования автомобиль. Когда водитель напрягает либо тормозная сила, либо сила ускорения, одновременно прилагая сила поворота, вы должны добавить силы, учитывая доступные трение. Другими словами, сумма тяга при вождении или торможении и тяга на поворотах не должны на , но на превышать предел трения, иначе автомобиль выйдет из-под контроля.По возможности избегайте торможения или ускоряется при прохождении поворотов. Этот позволяет использовать все имеющееся трение при прохождении поворотов.
А вращающаяся шина не может обеспечить полное сцепление с дорогой при ускорении. Если водитель вызывает пробуксовку ведущего колеса при при прохождении поворотов автомобиль может выйти из-под контроля.
А заблокированная шина обеспечивает no сцепление на поворотах и пониженное торможение тяга. Когда водитель блокирует колеса в углу не будет реагировать на рулевое управление .Во время торможения максимальный коэффициент трение; следовательно, максимальная тормозная способность – это когда водитель применяет тормоза на уровне 15% пробуксовки.
% PDF-1.4 % 1016 0 obj> эндобдж xref 1016 75 0000000016 00000 н. 0000005304 00000 н. 0000001837 00000 н. 0000005620 00000 н. 0000005766 00000 н. 0000006697 00000 н. 0000006775 00000 н. 0000007024 00000 н. 0000007073 00000 н. 0000007122 00000 н. 0000007171 00000 н. 0000007220 00000 н. 0000007269 00000 н. 0000007318 00000 н. 0000007367 00000 н. 0000007924 00000 н. 0000007972 00000 н. 0000008010 00000 н. 0000008058 00000 н. 0000008107 00000 н. 0000008155 00000 н. 0000008204 00000 н. 0000008253 00000 н. 0000008302 00000 н. 0000009538 00000 п. 0000010310 00000 п. 0000010565 00000 п. 0000010822 00000 п. 0000011078 00000 п. 0000011263 00000 п. 0000011521 00000 п. 0000011761 00000 п. 0000012046 00000 п. 0000012299 00000 п. 0000012556 00000 п. 0000012813 00000 п. 0000013075 00000 п. 0000013338 00000 п. 0000013596 00000 п. 0000013848 00000 п. 0000014069 00000 п. 0000014307 00000 п. 0000014547 00000 п. 0000014790 00000 п. 0000015036 00000 п. 0000015277 00000 п. 0000015513 00000 п. 0000015746 00000 п. 0000015944 00000 п. 0000021193 00000 п. 0000021467 00000 п. 0000021721 00000 п. 0000021981 00000 п. 0000022241 00000 п. 0000022431 00000 п. 0000022612 00000 п. 0000022788 00000 п. 0000022960 00000 п. 0000023021 00000 п. 0000023075 00000 п. 0000023178 00000 п. 0000023278 00000 п. 0000023375 00000 п. 0000023439 00000 п. 0000023533 00000 п. 0000023627 00000 п. 0000023727 00000 п. 0000023821 00000 п. 0000023918 00000 п. 0000024015 00000 п. 0000024109 00000 п. 0000024206 00000 п. 0000057088 00000 п. 0000059759 00000 п. 0000005103 00000 п. трейлер ] >> startxref 0 %% EOF 1018 0 obj> поток xY TS! `B @ $ 1A4 @” + PDc2 DynamicsДвижение – скорость и ускорение, силы и крутящие моментыAccelerationИзменение используемой скорости и времени Уравнения ускорения и скоростиПолезные уравнения, связанные с ускорением , средняя скорость, конечная скорость и пройденное расстояние Ускорение свободного падения и второй закон НьютонаУскорение свободного падения и второй закон Ньютона – единицы СИ и имперские единицы Конвертер единиц ускоренияПреобразование единиц ускорения Угловое движение – мощность и крутящий моментУгловая скорость и ускорение – мощность и крутящий момент Средняя скоростьЗависимость пройденного расстоянияиспользованное время Поворот с наклономПоворот с наклоном – это поворот или изменение направления, в котором транспортное средство кренится или наклоняется, обычно в сторону внутренней части поворота. Сила на боллардеТрение каната вокруг шеста – нагрузка и усилие в канате вокруг болларда Автомобиль – требуемая мощность и крутящий моментМощность, крутящий момент, эффективность и усилие на колесах Автомобиль – сила тягиСцепление и тяговое усилие усилие Ускорение автомобиляРассчитать ускорение автомобиля Центростремительная и центробежная сила – ускорениеЦентростремительное и центробежное ускорение – силы, обусловленные круговым движением Пройденное расстояние vs.Таблица калькулятора скорости и времениГрафик скорости на временной диаграмме Высота подъемного моста – силы и моментыРасчет момента подъема подъемного моста или балки Лифт – сила и мощностьТребуемая сила и мощность для подъема лифта Кинетическая энергия маховикаКинетическая энергия, запасенная в маховике – момент инерции СилаТретий закон Ньютона – масса и ускорение Силы, действующие на тело, движущееся по наклонной плоскостиСила, необходимая для перемещения тела по наклонной плоскости Формулы движения – линейное и круговоеЛинейное и угловое (вращательное) ускорение, скорость, скорость и расстояние Ударная силаУдарная сила действует на падающие объекты, ударяющиеся о землю, разбивающиеся автомобили и т.п. Импульсная и импульсная силаСилы, действующие очень короткое время называется импульсными силами Кинетическая энергияКинетическая энергия твердого тела – это энергия, которой обладает его движение Подъемные колесаПодъемные колеса – сила нагрузки и усилия Массовый момент инерцииМассовый момент Инерция (момент инерции) зависит от массы объекта, его формы и относительной точки вращения – Radius of Gyration Movement RatioМашины и отношение движения (отношение скоростей) PendulumПростой маятник колеблется в вертикальная плоскость из-за силы тяжести Потенциальная энергияГидроэнергетика – высота и потенциальная энергия Дальность полета снарядаДвижение в двух измерениях – расчет дальности полета снаряда ШкивыШкивы, блоки и приспособления Тяга самолетаСил, необходимых для о.у. ll air plane Сопротивление качениюТрение качения и сопротивление качению Вращающиеся тела – напряжениеНапряжение во вращающемся диске и кольцевых телах Универсальный закон гравитацииГравитационное притяжение между двумя объектами зависит от массы объектов и расстояние между ними Сложение векторовОнлайн-калькулятор векторов – добавление векторов с разной величиной и направлением, например силы, скорости и т. д. Транспортное средство – пройденное расстояние vs.Скорость и время (км / ч)Скорость (км в час), время (часы) и пройденное расстояние (км) ЛебедкиУсилие для подъема груза Работа, выполненная силамиРабота, выполненная сила, действующая на объект Законы динамики – Энциклопедия окружающей средыЗакон Ньютона, связывающий силу и ускорение, лежит в основе современной физики. Применяемый к каждому графику жидкости, он лежит в основе моделей прогнозирования погоды и климата.Интуитивное понятие силы использовалось с древних времен для понимания статического равновесия. Это позволяет спроектировать своды в архитектуре, использовать рычаг, чтобы описать баланс жидкости под действием тяги Архимеда. Именно принцип инерции, открытый Галилеем, проложил путь к законам ньютоновской динамики, чей большой успех заключался в объяснении движения планет и спутников, а также приливов и отливов. Это потребовало большого математического опыта, который имеет свои пределы для более сложных систем, таких как атмосфера или океан.Решение уравнений динамики стало возможным только с момента появления компьютерных вычислений. Однако законы сохранения, количества движения, энергии, кинетического момента накладывают глобальные ограничения, позволяющие более непосредственно понять определенные явления. 1. Уравновешивающие силыПонятие силы выражает механическое воздействие на объект. Силы имеют четко определенное физическое происхождение, например, гравитационная сила ( вес ), электрическая сила на заряженной частице , контакт или натяжение сила на кабеле, или сила упругости и пружина .Как и многие фундаментальные понятия физики, силу трудно определить сама по себе, но к ней можно подойти с помощью экспериментальных примеров, а также с помощью математических соотношений, которые она имеет с другими величинами. Рис. 1. Равновесие противоположных сил: а) в пружинном динамометре, б) в воздушном шаре. [Источник: Traité de Physique Elemententaire – DRION et FERNET – 1885] Сила, таким образом, характеризуется силой , интенсивностью (или модуля ) и направлением , а также точкой приложения, и математически представляется в виде вектор .Сумма сил, действующих на покоящийся объект, должна нейтрализовать друг друга. Сила может быть измерена по удлинению пружины из ее положения покоя (рис. 1). Экспериментально подтверждается, что это удлинение пропорционально силе путем последовательного добавления нескольких одинаковых грузов. После калибровки этот датчик силы пружины можно использовать для измерения различных сил. Для неподвижного воздушного шара в воздухе общий вес уравновешивается тягой Архимеда , равной и противоположной массе вытесненного объема воздуха.Это не что иное, как результат сил атмосферного давления , действующих по всей оболочке: из-за уменьшения давления с высотой давление внизу оболочки выше, чем вверху, что переводится в чистую силу, направленную вверх. . Этот баланс между давлением и силой тяжести фактически применяется к любому объему жидкости в равновесии, известном как гидростатическое равновесие (см. «Давление, температура, тепло»). Именно благодаря этому балансу воздушные участки или водные участки в бассейне не падают на землю под действием силы тяжести.Когда воздух нагревается, его плотность и, следовательно, масса данного объема уменьшается, в то время как давление остается неизменным, поскольку оно контролируется весом окружающего воздуха. Затем равновесие нарушается, что приводит к вертикальному ускорению воздушного шара. В атмосфере воздушная масса, локально нагретая солнечным излучением, также будет иметь тенденцию подниматься: это принцип конвекции . Рис. 2. Перевернутая модель Собора Святого Семейства Гауди. Форма равновесия такова, что на каждом пересечении проводов векторная сумма сил равна нулю.Каждый элемент балки представлен проволокой, а его масса моделируется грузом. Сила натяжения пряжи обязательно совпадает с пряжей. В реальной перевернутой конфигурации соответствующая сила будет тогда силой сжатия, направленной вдоль балки, что гарантирует ее механическую прочность. [Источник: http://olive-art.weebly.com/uploads/2/6/0/5/26053332/6555663_orig.jpg]. В общем, баланс сил должен быть выражен как векторов , что является Основа для расчета конструкций в архитектуре, см. рисунок 2.Для каждой материальной точки, например, узла пересечения проводов, векторная сумма сил должна уравновешивать друг друга в состоянии равновесия, как показано на рисунке 3a. Это позволяет, например, найти интенсивности сил F1 и F2 , зная силу F3 и углы θ1 и θ2 , либо геометрическим построением, либо численно. путем проецирования векторов по вертикальной и горизонтальной осям.Расширенный объект, например твердое тело , описывается в физике как набор из материальных точек , удерживаемых вместе внутренних сил. Эти силы следует отличать от внешних сил , таких как вес или силы контакта с другими объектами. Сумма внутренних сил компенсируется принципом действия и противодействия , так что равновесие требует отмены суммы внешних сил. Рис. 3. Баланс сил на материальной точке а) и баланс моментов на протяженном объекте – рычаге.Но состояние равновесия протяженного объекта также требует отмены полного момента сил, чтобы избежать его вращения. Момент силы относительно оси определяется как произведение силы, проецируемой перпендикулярно оси, на расстояние до оси. Классическим примером является рычаг, показанный на рисунке 3b. В состоянии равновесия или квазиравновесия для медленного движения для компенсации моментов требуется, чтобы F1d1 = F2d2 (силы здесь перпендикулярны оси), что позволяет увеличить силу, действующую в обратном отношении расстояния до оси (согласно обычному соглашению мы отмечаем здесь F1 интенсивность силы, а F1 представляет вектор силы).Обычно моменты рассматриваются относительно оси рычага, потому что момент силы реакции R земли компенсируется сам собой. Однако тот же результат можно получить, вычислив момент относительно любой математической оси, добавив момент реакции R , который является равным вектором и противоположен сумме двух сил F1 и F2 . . 2. Силы и ускорениеТеперь, покидая область статики, ускорение объекта связано с общей силой F , которая действует на него по знаменитому закону Ньютоновской динамики , F = мг , где м – масса объекта, г, – его вектор ускорения.Это позволяет определить единицу силы, Ньютон (Н), как силу, создающую ускорение в 1 (м / с) / с над массой 1 кг, что записывается как 1 Н = 1 кг · м · с-2. . В отсутствие силы объект движется с постоянной скоростью, это принцип инерции , впервые сформулированный Галилеем (1564–1642). В то время этот принцип был не очень интуитивно понятным, потому что в повседневной жизни любое движение имеет тенденцию останавливаться без усилия. Это замедление (отрицательное ускорение) теперь приписывается трению сил, которые противоположны скорости.Но трение становится незначительным в межпланетной пустоте, и большой успех Ньютона (1643-1727) заключался в математическом описании движения планет и спутников на основе простого закона универсальной гравитационной силы , убывающей как величина, обратная квадрату расстояния r. . Применение закона Ньютона потребовало изобретения математической концепции производной , определяющей понятия скорости и ускорения. Отметим скорость v = dz / dt, где dz – небольшое смещение во временном интервале dt.Фактически, мы считаем предел из очень коротким интервалом времени. Точно так же ускорение обозначается как g = dv / dt. Для постоянного ускорения g скорость пропорциональна времени, v = gt , и легко продемонстрировать, что расстояние падения (разница между начальной высотой z0 и высотой z ) будет тогда z0- z = (1/2) gt2 . Таким образом, на Земле под действием силы тяжести г = 9,8 м / с объект достигает скорости 9.8 м / с (35 км / ч) за 1 секунду, падает с высоты 4,9 м. Закон Ньютона в более общем смысле применяется в векторной форме : объект может падать вертикально, как было сказано ранее, сохраняя при этом свою горизонтальную составляющую скорости по инерции. При достаточно высокой горизонтальной скорости необходимо принять во внимание кривизну Земли и получить круговое движение спутника , см. Рисунок 4. В этом случае скорость постоянна по модулю, но вектор скорости вращается на такая же угловая скорость [1], что и у спутника.Тогда ускорение перпендикулярно скорости и направлено к центру Земли со значением g = v2 / r , как показано на рисунке 4. Таким образом, для спутника, близкого [2] к Земле, g. = 9,8 мс-2, r = 6500 км, что приводит к: скорости v = (gr ) 1/2 = 8 км / с, время обращения (длина 40 000 км) T = 5000 с (1 ч 23 мин). Рис. 4. a) Движение запущенного тела с увеличивающейся горизонтальной скоростью до спутника на круговой орбите (8000 м / с) и выброс Земли (11000 м / с) [Источник: иллюстрация теории Ньютона, опубликованная в «Popular Astronomy» ].(б) Закон динамики применительно к круговому движению спутника: за короткий промежуток времени dt спутник поворачивается на угол dq = (v / r) dt, а вектор скорости поворачивается на тот же угол dq = (g / v) dt, из которого выводится g = (v2 / r), что позволяет рассчитать скорость спутника v = 8000 м / с у поверхности Земли (r = 6500 км, g = 9,81 м / с-2). ). Если теперь сила тяжести g уменьшается на 1 / r2, скорость v = (gr ) 1/2 от круговое движение уменьшается на 1 / r1 / 2, а период вращения равен 2πr / v , увеличивается на r3 / 2 .Таким образом Луна удалена от Земли r = 384 000 км, т.е. е. В 60 раз больше радиуса Земли, он должен вращаться за время в 465 раз дольше, чем ближайший спутник, т.е. е. 27 дн. Это согласуется с наблюдениями [3]. Закон роста времени обращения в r3 / 2 был открыт Кеплером (1571-1630) для планет, вращающихся вокруг Солнца. Помимо частного случая круговой орбиты, Ньютон смог продемонстрировать, что общее движение следует за эллипсом (или гиперболой за пределами скорости истечения), и он смог найти три закона, ранее установленные Кеплером, на основе точных измерений положения планет. Бывает, что сила тяжести сама по себе пропорциональна массе, так что возникающее ускорение не зависит от нее: все тела падают с одинаковым ускорением в одном и том же месте. Это равенство между тяжелой массой и инертной массой было заявлено Галилеем и проиллюстрировано его знаменитыми экспериментами (возможно, только воображаемыми) с падающими объектами с Пизанской башни. Это было сделано снова с большой точностью в вакууме, избегая трения воздуха. В качестве демонстрации для публики был снят фильм, сравнивающий падение молотка и пера на Луне во время полета Аполлона XV [4], и аналогичный эксперимент был снят на Земле в огромной вакуумной камере [5].Именно из-за этого принципа эквивалентности все объекты плавают в невесомости на спутнике, каждый движется по одной и той же орбите вокруг Земли. Эта эквивалентность сейчас проверяется с относительной точностью 10-13 (1/10 триллиона), а точность 10-15 ожидается от недавно запущенного спутника «Микроскоп». Эти сверхточные измерения предназначены для проверки отклонений от принципа эквивалентности, предсказываемого новыми теориями гравитации. 3. Кинетическая и потенциальная энергияВ приведенном выше примере свободного падения можно отметить, что мг (z0-z ) = м (1/2 ) g2t2 = (1/2 ) mv2 .Это соответствует более общему свойству сохранения полной энергии, состоящему из кинетической энергии (1/2 ) mv2 и потенциальной энергии mgz . Когда объект падает, его кинетическая энергия увеличивается, но его потенциальная энергия также уменьшается, так что полная механическая энергия сохраняется (при отсутствии трения). В общем случае кинетическая энергия (1/2 ) mv2 выражается как функция модуля скорости. Сохранение механической энергии становится все более распространенным в случае спутника, но тогда выражение потенциальной энергии должно быть изменено, чтобы учесть уменьшение силы тяжести.Эта потенциальная энергия зависит только от положения объекта, так что он принимает то же значение после вращения, и кинетическая энергия также имеет такое же значение в соответствии с тем фактом, что движение планеты сохраняется бесконечно. Гравитационный потенциал определяется путем деления этой потенциальной энергии на массу объекта. Этот потенциал характеризует гравитационное поле независимо от объекта, вращающегося вокруг него (до тех пор, пока объект мал и не приводит планету в движение посредством реакции). Сохранение механической энергии требует особой формы законов силы. Силы трения, в отличие от силы тяжести, уменьшают механическую энергию, так что спутник в конечном итоге входит в контакт с остаточной атмосферой. Однако потерянная механическая энергия преобразуется в тепло, так что общая энергия сохраняется (см. «Энергия»). Тепло по существу соответствует неупорядоченной кинетической энергии молекул газа. Для однородной сферической планеты потенциал изменяется в пределах -1 / r, так что эквипотенциалы представляют собой концентрические сферы.Однако эти сферы слегка деформированы из-за вращения Земли и неоднородностей. Равновесная форма поверхности океана является таким эквипотенциалом (см. «Морская среда»). Действительно, объект, движущийся по эквипотенциалу, сохраняет ту же потенциальную энергию, и, поскольку его полная энергия сохраняется, он не может приобретать (или терять) скорость под действием только силы тяжести. И наоборот, если форма океана отклоняется от эквипотенциальной, поверхностная вода имеет тенденцию течь в области с более низким потенциалом, пока она не заполнит их и не достигнет состояния равновесия, при котором поверхность является эквипотенциальной.Поверхность твердой Земли также приближается к эквипотенциальности из-за эрозии и пластичности мантии Земли. 4. Количество движенияКоличество движения, равное элементарной массы (рассматриваемой как точечная), определяется как произведение массы и скорости, определение, которое может быть распространено на любую физическую систему, добавляя (векторно) количества движения каждой из ее элементарные массы. Легко продемонстрировать, что величина движения равна величине движения центра инерции (центр тяжести ) системы, на которую воздействует ее общая масса.Затем закон динамики Ньютона указывает, что производная от количества движения по времени равна сумме сил, действующих на систему. Согласно фундаментальному принципу физики, количество движения изолированной системы сохраняется. Другими словами, его центр инерции движется поступательно с постоянной скоростью, и только внешние силы могут изменить эту скорость. Другой эквивалентной формулировкой является принцип действие и противодействие , который предусматривает, что любое тело A, оказывающее силу на тело B, испытывает силу равной интенсивности, но в противоположном направлении, действующую со стороны тела B.Затем закон динамики указывает, что эти внутренние силы не изменяют величину движения глобальной системы A + B. Это обобщает рассмотренное выше условие статического равновесия. Зная начальные массы m1 и m2 и начальные скорости u1 и u2 каждой массы, вычисляется величина движения до удара m1u1 + m2u2 , которая должна сохраняться после удара , таким образом, обеспечивая ограничение на конечные скорости.Если дополнительно предположить, что ударная волна , упругая , т.е. е. что кинетическая энергия (1/2 ) m1u12 + (1/2 ) m2u22 сохраняется, мы можем вывести две конечные скорости. Для двух равных масс мы имеем обмен скоростями (рис. 5а). В случае полностью неупругого удара массы остаются связанными после удара с конечной скоростью, равной средневзвешенному значению начальных скоростей m1u1 + m2u2 / (m1 + m2 ) при сохранении количества движение.Применительно к молекулам газа эти ударные свойства позволяют интерпретировать явление вязкости, которое уравнивает количество движений быстрой и медленной зон внутри жидкости, сохраняя при этом общее количество движений. Привод ракет или самолетов – еще один классический пример: величина движения, передаваемого транспортному средству, прямо противоположна движению выбрасываемого газа, независимо от задействованных сложных механизмов. Это также относится к силам гравитации: Луна притягивает Землю с силой, равной силе тяжести Земли, действующей на Луну, и противоположной ей.Таким образом, Земля вращается вокруг центра инерции системы Земля-Луна так же, как и молотковая установка, которая должна вращаться, чтобы компенсировать реакцию вращающегося шара (см. «Приливы»). Именно этот центр инерции описывает эллиптическую орбиту вокруг Солнца, а не саму Землю. Рисунок 5-а. Choc élastique entre deux masses égales [Источник: Саймон Штейнманн (собственная работа) [CC BY-SA 2.5 (http://creativecommons.org/licenses/by-sa/2.5)]] Рис. 5-b.Choc élastique entre deux masses inégales [Источник: Саймон Штайнманн (собственная работа) [CC BY-SA 2.5 (http://creativecommons.org/licenses/by-sa/2.5) через Wikimedia Commons] Рисунок 5-c. Отличное неэластичное блюдо из двух масс [Источник: Par Raul Roque (персонал Travail) [CC BY-SA 2.5 (http://creativecommons.org/licenses/by-sa/2.5)], через Wikimedia Commons] 5. Угловой моментУгловой момент относительно оси определяется для точечной массы как произведение расстояния до оси на величину ее движения, проецируемого перпендикулярно этой оси.Это определение обобщается на протяженное тело, например твердое тело, путем деления его мыслью на элементарные массы и сложения их угловых моментов. Мы демонстрируем из закона динамики, что производная кинетического момента по времени равна суммарному моменту сил (также называемых « крутящий момент »), действующих на систему. Это обобщает закон статики, который требует, чтобы полный момент сил был равен нулю. Закон сохранения кинетического момента гласит, что полный момент внутренних сил уравновешивается, и поэтому только момент внешних сил может изменить кинетический момент.Таким образом, в твердом состоянии внутренние силы сцепления не вмешиваются в баланс кинетического момента, так же как они не вмешиваются в величину движения. Это фундаментальный закон физики, отличный от принципа действия и противодействия и дополняющий его. Другими словами, система не может начать самопроизвольное вращение или потерять свое начальное вращение без действия внешних сил. Однако скорость его вращения может измениться в случае сжатия или растяжения.Действительно, для точечной массы это произведение , скорости u на расстояние r до оси, которая сохраняется, поэтому скорость u увеличивается обратно пропорционально расстоянию r , и его угловая скорость u / r обратно пропорциональна квадрату этого расстояния. Классический пример – фигурист, а в естественной среде – образование торнадо и циклонов (см. «Торнадо: мощные разрушительные водовороты»).Само вращение Земли является результатом увеличения угловой скорости при аккреции вещества, которое привело к ее образованию. Самый яркий пример – пульсары, чрезвычайно плотные звезды, вращающиеся с периодом от нескольких секунд до нескольких миллисекунд. Эти объекты возникают в результате коллапса массивной звезды, обычно в радиусе от 1 миллиона км до 10 км. Такое сжатие увеличивает угловую скорость вращения в 10 миллиардов раз (часть углового момента выбрасывается вместе с газом, испускаемым взрывом). Момент импульса на самом деле является вектором, выровненным с осью вращения [6], и поэтому он сохраняется как по направлению, так и по модулю. Это принцип работы гироскопа . Точно так же ось вращения Земли остается выровненной по отношению к звездам, а Северный полюс по-прежнему указывает на область, близкую к Полярной звезде. Рисунок 6. Прецессия фрезера: вес создает разрез, ориентированный перпендикулярно рисунку и горизонтальный. Таким образом, результирующее изменение вектора кинетического момента перпендикулярно этому вектору, что приводит к прецессионному движению, показанному на рисунке.Аналогичное явление происходит при вращении Земли под действием крутящего момента из-за лунного притяжения (однако, прецессия происходит в противоположном направлении, потому что крутящий момент имеет противоположный знак, чем у вершины). Источник: http://hyperphysics.phy astr.gsu.edu/hbase/mechanics/imgmechs/imgmech/topp.gif]Это верно только для изолированной системы, а точнее при отсутствии крутящего момента (или момента) от внешние силы. Крутящий момент, перпендикулярный оси вращения, вызывает вращение оси вращения без какого-либо изменения угловой скорости: это явление прецессии , наблюдаемое на маршрутизаторе, см. Рисунок 6 (точно так же, как ускорение, перпендикулярное скорости, производит вращение скорости без изменения ее модуля).Аналогичный эффект происходит с Землей из-за ее уплощенной формы на полюсе: крутящий момент возникает из-за более сильного притяжения Луны на части около бусинки, чем на ее противоположной части. Это приводит к медленному прецессионному движению вращения Земли в течение 26 000 лет (см. Рисунок 6). Таким образом, направление полюса медленно перемещается по небесной сфере на протяжении веков. Это приводит к смещению орбиты Земли относительно положения равноденствий, когда ось вращения Земли ориентирована перпендикулярно направлению Солнца.Вот почему явление называется « прецессия равноденствий ». Связанные с этим изменения солнечного света происходят при изменении климата между ледниковым и умеренным периодами. Ссылки и примечанияФотография на обложке. Автор http://creativecommons.org/licenses/by-sa/2.0 (загружен на Flickr как обычный jfpds) [CC BY-SA 2.0 (极 博 双 板 滑雪 俱乐部)] через Wikimedia Commons. [1] Угловая скорость Ω – это угол, пройденный за единицу времени, обычно выражаемый в радианах / с, так что Ω = v / r.Радиан определяется как угол, пересекающий дугу окружности, равную радиусу, так что полный оборот (окружность 2πr ) представляет 2π радиан, а период вращения равен T = 2π / Ω = 2πr / v . [2] Высота должна составлять несколько сотен километров, чтобы избежать атмосферного трения, но ускорение свободного падения остается близким к ускорению земной поверхности, а радиус орбиты мало отличается от радиуса Земли. [3] Это сидеральная революция, i.е. относительно звезд, в то время как время между двумя полными лунами, равное 29,5 дня, является синодическим оборотом, i. е . по отношению к Солнцу. [4] Молот и перо Аполлона 15 – Youtube [5] Брайан Кокс посещает самую большую в мире вакуумную камеру – Вселенная человека: превью 4 серии – BBC Two – Youtube [6] Момент импульса более точно определяется относительно исходной точки O. Для точки массой м в точке M это векторное произведение на вектор OM на величину движения м и массы в точке М.Для осесимметричного твердого тела, такого как маршрутизатор или Земля, кинетический момент выровнен по оси вращения со значением, пропорциональным угловой скорости и моменту инерции . Экологическая энциклопедия окружающей среды Ассоциации энциклопедий окружающей среды и энергии (www.a3e.fr), по контракту связана с Университетом Гренобль-Альп и ИЯФ Гренобля и спонсируется Французской академией наук . Для цитирования: SOMMERIA Joël (2021), Законы динамики, Энциклопедия окружающей среды, [онлайн ISSN 2555-0950] URL: https://www.encyclopedie-environnement.org/en/physics/laws-of -динамика /. Статьи в Энциклопедии окружающей среды доступны в соответствии с условиями лицензии Creative Commons BY-NC-SA, которая разрешает воспроизведение при условии: цитирования источника, не коммерческого использования их, использования идентичных исходных условий, воспроизведения в при каждом повторном использовании или распространении эта лицензия Creative Commons BY-NC-SA упоминается. Инженерные системы в движении: динамика частиц и тел в двухмерном движенииЭтот курс представляет собой введение в изучение движущихся тел применительно к инженерным системам и конструкциям. Мы будем изучать динамику движения частиц и тел в твердом плоском (2D) движении. Это будет состоять как из кинематики, так и из кинетики движения. Кинематика имеет дело с геометрическими аспектами движения, описывающими положение, скорость и ускорение как функцию времени.Кинетика – это изучение сил, действующих на эти тела, и их влияния на их движение. | ||||||||||||||||||||||

 Законы Ньютона – первый, второй, третий. Принцип относительности
Законы Ньютона – первый, второй, третий. Принцип относительности
 Определяется законом всемирного тяготения.
Определяется законом всемирного тяготения. Трение покоя = силе, приложенной к телу
Трение покоя = силе, приложенной к телу 1.2.1
– понимать законы Ньютона и определять
равнодействующую силу:
1.2.1
– понимать законы Ньютона и определять
равнодействующую силу:

 . В случае
спорных вопросов, ведется обсуждение всем классом
. В случае
спорных вопросов, ведется обсуждение всем классом «Рефлексия»
«Рефлексия» Для
учеников самостоятельно изучающих физику и опережающих программу следует
подготовить дополнительные задания с критериями оценивания.
Для
учеников самостоятельно изучающих физику и опережающих программу следует
подготовить дополнительные задания с критериями оценивания.