[PDF] Тема: «III закон Ньютона»
Download Тема: «III закон Ньютона»…
Тема: «III закон Ньютона» ЦЕЛИ УРОКА: 1. Образовательная: Изучить III закон Ньютона, его особенности и значение, сформировать умение у учащихся применять III закон Ньютона для решения практических, логических, качественных задач. 2. Развивающая: развивать умение наблюдать, анализировать. Делать выводы, формировать учебнокоммуникативные навыки и умения учащихся: – отвечать на вопросы в соответствии с их характером; – уметь вести диалог с целью уточнения, получения, систематизации информации, с целью закрепления данной темы; – строить рассказ о физическом законе на основе плана; – умение пользоваться физическими приборами. 3. Воспитательная: воспитывать культуру учебного труда, уверенность, самостоятельность, умение слушать своих товарищей. 4. Здоровьесберегающая: Обеспечить школьникам возможность сохранения здоровья во время обучения физике. Домашнее задание: Параграф 12, упражнение 12 (1,2) письменно.
 6. Мультимедиапроектор, компьютер, презентация. 7. Дополнительно: Карточки в двух вариантах (по 4 задания в каждом) с выбором ответа.
6. Мультимедиапроектор, компьютер, презентация. 7. Дополнительно: Карточки в двух вариантах (по 4 задания в каждом) с выбором ответа.ХОД УРОКА I. Мобилизующее начало урока. Взаимное приветствие учителя и учащихся. Организация класса. Цель: Психологический настрой учащихся на предстоящее занятие; обеспечение нормальной обстановки. – проверка отсутствующих; – проверка рабочих мест, внешнего вида учащихся; -организация внимания (использование здоровьесберегающих технологий: упражнения с «восьмеркой». Учащиеся стоя делают «восьмерку» правой рукой в воздухе, затем то же левой рукой). II. Актуализация знаний учащихся. Цель: проверка итогов предыдущей работы, воспроизводство знаний полученных на уроках, создание мотивации на освоение нового материала. 1) К доске вызвать 2-х учащихся: выполнить задачи № 1 и № 2 из домашнего упражнения 11. Учитель: Есть вопросы по домашнему заданию? 2) Работа с классом. (пока два ученика работают у доски) Учитель: На предыдущих уроках мы изучим I и II законы Ньютона.
9. По приведенным рисункам ответьте на вопросы: «Как движется тело?», «Куда направлено ускорение?» (слайд). Дайте краткий ответ. 10. Проверка задач из Упражнения 11 (1,2) (устные ответы детей). III. Изучение нового материала. Итак, ребята, мы изучили I и II закон Ньютона. Мы узнали, при каком условии тело сохраняет свою скорость постоянной в ИСО, о том, что в результате взаимодействия тело приобретает ускорение, которое прямо пропорционально силе и обратно пропорционально его массе. Но ни I, ни II закон Ньютона не говорит нам о том, что же будет происходить со вторым взаимодействующим телом.

– Можно ли эти силы складывать? Просмотр кинофильма. Ответы на вопросы к фильму. 3) Откроем учебник на странице 49, прочитаем формулировку, кратко запишем III закон Ньютона на доске и в тетрадях «Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению. Учитель: Ньютон сформулировал третий закон так: «Действию всегда есть равное и противоположное противодействие, иначе – действие двух тел друг на друга между собой равны и направлены в противоположные стороны». 4) Сделаем паузу (Упражнения для глаз). 5) А теперь исследуем на опытах III закон Ньютона. Вопросы: Как вы думаете, что произойдет, если… – Опыт с динамометрами. – Опыт с пробиркой. – Опыт с лезвием. 6) Рассмотрим особенности III закона Ньютона. У вас на партах лежат конспекты (слайд). Обсудим рисунки. IV. Закрепление. 1) А теперь попробуем объяснить. – почему линейка прогнулась под мальчиком? (стрелки прикрепить!). – почему руке больно, когда мы ударяем ею по парте? 2) Прослушаем подготовленное сообщение о том, как Ньютон проводил опыты (приложение № 1). 3) Работа по рисункам (слайд). – Мяч ударился о стенку и подействовал на стенку силой F1 . На каком из рисунков правильно показана сила, с которой стенка действует на мяч? Какова природа этих сил? (рис. 3, упругости). – На рисунке показана сила с которой Луна действует на Землю.
Учитель: Ньютон сформулировал третий закон так: «Действию всегда есть равное и противоположное противодействие, иначе – действие двух тел друг на друга между собой равны и направлены в противоположные стороны». 4) Сделаем паузу (Упражнения для глаз). 5) А теперь исследуем на опытах III закон Ньютона. Вопросы: Как вы думаете, что произойдет, если… – Опыт с динамометрами. – Опыт с пробиркой. – Опыт с лезвием. 6) Рассмотрим особенности III закона Ньютона. У вас на партах лежат конспекты (слайд). Обсудим рисунки. IV. Закрепление. 1) А теперь попробуем объяснить. – почему линейка прогнулась под мальчиком? (стрелки прикрепить!). – почему руке больно, когда мы ударяем ею по парте? 2) Прослушаем подготовленное сообщение о том, как Ньютон проводил опыты (приложение № 1). 3) Работа по рисункам (слайд). – Мяч ударился о стенку и подействовал на стенку силой F1 . На каком из рисунков правильно показана сила, с которой стенка действует на мяч? Какова природа этих сил? (рис. 3, упругости). – На рисунке показана сила с которой Луна действует на Землю.
*Если останется время, раздать карточки и листочки для ответов взаимопроверка).
(работа в парах,
Приложение № 1 Рассказ ученика «Опыты И.Ньютона». «Из сухой дощечки он вырезал две совершенно одинаковые лодочки. Потом налил в таз воды и пустил туда свои лодочки. В одну лодочку Ньютон положил маленький намагниченный брусок (стальной), а в другую точно такой же брусок, сделанный из железа. Обе лодочки Ньютон развел в стороны. Лодочку с железным бруском он отпустил, а нагруженную магнитом придержал рукой на месте. Повинуясь движению магнита, железный брусок потянул свою лодочку, поплыл и вскоре пристал к магниту. Ньютон продолжал опыт. Он снова развел лодочки в стороны, но на этот раз держал на месте лодочку с железным бруском, а лодочку с магнитом пустил в свободное плавание.
Приложение № 2 Упражнения.
[PDF] Законы Ньютона – Free Download PDF
Download Законы Ньютона…
УРОК ФИЗИКИ В 10 КЛАССЕ• Законы Ньютона
КАКИЕ МЫ ЗНАЕМ ВИДЫ ДВИЖЕНИЯ • 1. Равномерное прямолинейное ( скорость постоянна по величине и направлению) • 2. Равноускоренное прямолинейное ( скорость меняется, ускорение постоянно) • 3. Криволинейное движение ( меняется направление движения)
Зачем нужна динамика
• Кинематика позволяет определить вид движения, но не объясняет почему тело движется так, а не иначе?
3
В ЧЕМ ПРИЧИНА ДВИЖЕНИЯ ? • Аристотель – движение возможно только под действием силы; при отсутствии сил тело будет покоится. • Галилей – тело может сохранять движение и в отсутствии сил. Сила необходима для того чтобы уравновесить другие силы, например, силу трения • Ньютон – сформулировал законы движения
• Галилей – тело может сохранять движение и в отсутствии сил. Сила необходима для того чтобы уравновесить другие силы, например, силу трения • Ньютон – сформулировал законы движения
УПРОЩЕНАЯ ФОРМУЛИРОВКА ЗАКОНОВ НЬЮТОНА • Тело находится в покое или движется равномерно и прямолинейно, если действие других тел скомпенсированы (уравновешены)
• Ускорение движущегося тела пропорционально сумме приложенных к нему сил и обратно пропорционально его массе. • При взаимодействии двух тел, силы равны по величине и противоположны по направлению.
СИСТЕМЫ ОТСЧЕТА • Инерциальные – системы отсчета, в которых выполняется закон инерции (тело отсчета покоится или движется равномерно и прямолинейно) • Неинерциальные – закон не выполняется ( система движется неравномерно или криволинейно)
Примеры выполнения первого закона Ньютона • 1.
2.
• 3.
4.
• 5.
1.Земля – опора 2.Земля – нить
3. Земля – воздух 4. Земля – двигатель 5. Действия нет
тело в покое v=0
движение равномерное прямолинейное v = const
Ньютон
Первый закон
Физическая система Модель
Макроскопическое тело
Описываемое явление
Суть закона
Второй закон
Материальная точка
Состояние покоя или РПД Если F = 0, то V – const
Примеры Движение метепроявления орита вдали от притягивающих тел
Движение с ускорением
F a m
Движение планет, падение тел на Землю, разгон машины
Третий закон Система двух тел Система двух материальных точек Взаимодействие тел
F12 = – F21 Взаимодействие Солнца и Земли, Земли и Луны, машины и дороги
МАССА • Масса – это свойство тела, характеризующее его инертность. При одинаковом воздействии со стороны окружающих тел одно тело может быстро изменять свою скорость, а другое в тех же условиях – значительно медленнее. Принято говорить, что второе из этих двух тел обладает большей инертностью, или, другими словами, второе тело обладает большей массой.
При одинаковом воздействии со стороны окружающих тел одно тело может быстро изменять свою скорость, а другое в тех же условиях – значительно медленнее. Принято говорить, что второе из этих двух тел обладает большей инертностью, или, другими словами, второе тело обладает большей массой.
ОБЪЯСНИМ ОПЫТЫ
С И Л А • Сила – это количественная мера взаимодействия тел. Сила является причиной изменения скорости тела. В механике Ньютона силы могут иметь различную физическую причину: сила трения, сила тяжести, упругая сила и т. д. Сила является векторной величиной. Векторная сумма всех сил, действующих на тело, называется равнодействующей силой.
ХАРАКТЕРИСТИКИ
СИЛЫ
1. Модуль 2. Направление 3. Точка приложения Обозначается буквой F Измеряется в ньютонах (Н) Прибор для измерения силы – динамометр
РАВНОДЕЙСТВУЮЩАЯ ДВУХ СИЛ
ТРЕТИЙ ЗАКОН НЬЮТОНА
Особенности закона: 1. Силы возникают парами 2. Возникающие силы одной природы 3. Силы приложены к различным телам, поэтому не уравновешивают друг друга
ВЫВОД • 1. F = 0 РПД (a = 0, v = const) если равнодействующая сила равна нулю то тело покоится или движется равномерно и прямолинейно • 2. F ≠ 0 РУД ( a = F/m ) если силы нескомпенсированы, то тело движется равноускоренно
F = 0 РПД (a = 0, v = const) если равнодействующая сила равна нулю то тело покоится или движется равномерно и прямолинейно • 2. F ≠ 0 РУД ( a = F/m ) если силы нескомпенсированы, то тело движется равноускоренно
ЗАДАЧА 1 • Тело массой 4кг движется в соответствии с приведенным графиком. Вычислить V,м/с действующую силу и 5 определить вид 1 движения. 0
4
7 9
t,c
РЕШЕНИЕ v v 5 1 a ;a 1м / с • 1. F1 = ma1 t 4 F1 = 4кг·1м/с²=4Н движение равноускоренное • 2. v1 = v2 = 5м/с – не меняется, а2 = 0 F2 = 0 движение равномерное v3 v2 05 2 a ; a 2 , 5 м / с • 3. F3 = ma3 3 3 t3 2 F3 = 4кг·(- 2,5м/с²) = -10Н движение равнозамедленное 1
0
1
2
ЗАДАЧА 2 • Сила тяги ракетного двигателя первой ракеты на жидком топливе равнялась 660 Н, масса ракеты 30 кг. Какое ускорение приобрела ракета во время старта?
АНАЛИЗ ЗАДАЧИ • 1. Сколько сил действуют на ракету? • 2. Как они направлены? • 3. Какая сила совпадает по направлению с ускорением? • 4. Чему равна равнодействующая всех сил? • 5. Как записать уравнение второго закона Ньютона?
Чему равна равнодействующая всех сил? • 5. Как записать уравнение второго закона Ньютона?
ЗАДАЧА 2 • Дано: Решение m = 30кг ma = FТЯГ – FT Fтяг = 660Н FT = mg а-?
FТЯГ а FТ
Fтяг m g 660H 10м / с 2 30кг a ;a 12м / с 2 m 30кг Ответ: 12м/с²
ЗАДАЧА 3 • Мальчик массой 40кг качается на качелях, длина которых 2м. Найдите силу давления на качели при прохождении нижней точки, если скорость в этот момент равна 3м/с.
ЗАДАЧА 3 • Дано: Решение N a m = 40кг N – сила реакции опоры R = 2м ma = N – FT ( II з. Ньютона) F v = 3м/с N = ma + FT Р = – N ( III з. Ньютона) P -? a = v²/R – центростремительное ускорение Р = 40·10+40·3²/2 =400+180=580H Ответ: 580Н T
ДОМАШНЕЕ ЗАДАНИЕ • §24 – 28 • Конспект • Упр.6 (любые две задачи)
Основные законы механики – описание, специфические особенности и формулы
Движение разных тел в пространстве в физике изучает специальный раздел – механика. Последняя, в свою очередь, делится на кинематику и динамику. В данной статье рассмотрим законы механики в физике, концентрируя свое внимание на динамике поступательного и вращательного перемещения тел.
Историческая справка
Как и почему движутся тела, интересовало философов и ученых с давних времен. Так Аристотель полагал, что объекты перемещаются в пространстве только потому, что существует некоторое внешнее воздействие на них. Если это воздействие прекратить, то тело сразу же остановится. Многие древнегреческие философы полагали, что естественным состоянием всех тел является покой.
С приходом Нового времени многие ученые занялись изучением законов движения в механике. Следует отметить такие фамилии, как Гюйгенс, Гук и Галилей. Последний разработал научный подход к изучению явлений природы и, по сути, открыл первый закон механики, который, однако, носит не его фамилию.
В 1687 году в свет вышла научная публикация, автором которой был англичанин Исаак Ньютон. В своем научном труде он четко сформулировал основные законы движения тел в пространстве, который вместе с законом Всемирного тяготения, сформировали основу не только механики, но и всей современной классической физики.
О законах Ньютона
Их также называют законами классической механики в отличии от релятивистской, постулаты которой были изложены в начале XX века Альбертом Эйнштейном. В первой существуют всего три главных закона, на основе которых держится весь раздел физики. Они называются так:
- Закон инерции.
- Закон взаимоотношения между силой и ускорением.
- Закон действия и противодействия.
Почему именно эти три закона являются главными? Все просто, любая формула механики может быть получена на их основе, однако, ни один теоретический принцип не приводит ни к одному из них. Названные законы следуют исключительно из многочисленных наблюдений и экспериментов. Их справедливость подтверждается надежностью предсказаний, полученных с помощью них, при решении разных задач на практике.
Инерции закон
Первый закон Ньютона в механике гласит, что всякое тело при отсутствии внешнего воздействия на него будет сохранять состояние покоя или прямолинейного движения в любой инерционной системе отчета.
Чтобы понять этот закон, следует разобраться с системой отчета. Инерционной она называется только в том случае, если удовлетворяет изложенному закону. Иными словами, в инерционной системе не существует фиктивных сил, которые бы ощущали наблюдатели. Например, движущаяся равномерно и по прямой линии система может считаться инерционной. С другой стороны, система, которая равномерно вращается вокруг оси, является неинерционной из-за наличия в ней фиктивной центробежной силы.
Закон инерции устанавливает причину, по которой изменяется характер движения. Этой причиной является наличие внешней силы. Заметим, что на тело могут действовать несколько сил. В таком случае они должны быть сложены по правилу векторов, если результирующая сила окажется равной нулю, то тело продолжит свое равномерное движение. Важно также понимать, что в классической механике нет различия между равномерным движением тела и его состоянием покоя.
Второй ньютоновский закон
Он говорит о том, что причиной изменения характера перемещения тела в пространстве является наличие внешней ненулевой силы, приложенной к нему. По сути, этот закон является продолжением предыдущего. Математическая его запись выглядит следующим образом:
По сути, этот закон является продолжением предыдущего. Математическая его запись выглядит следующим образом:
F¯ = m*a¯.
Здесь величина a¯ – это ускорение, описывающее быстроту изменения вектора скорости, m – инерционная масса тела. Поскольку m всегда больше нуля, то вектора силы и ускорения направлены в одном и том же направлении.
Рассматриваемый закон применим к огромному числу явлений в механике, например, к описанию процесса свободного падения, движению с ускорением автомобиля, соскальзыванию бруска по наклонной плоскости, колебанию маятника, растяжению пружинных весов и так далее. Можно с уверенностью сказать, что он является главным законом динамики.
Количество движения и импульс
Если обратится непосредственно к научному труду Ньютона, то можно увидеть, что сам ученый второй закон механики сформулировал несколько иначе:
F*dt = dp, где p = m*v.
Величина p называется количеством движения. Многие ошибочно ее называют импульсом тела. Количество движения – это инерционно-энергетическая характеристика, равная произведению массы тела на его скорость.
Многие ошибочно ее называют импульсом тела. Количество движения – это инерционно-энергетическая характеристика, равная произведению массы тела на его скорость.
Изменить количество движения на некоторую величину dp может только внешняя сила F, действующая на тело в течение промежутка времени dt. Произведение силы на время ее действия называется импульсом силы или просто импульсом.
Когда два тела сталкиваются, то между ними действует сила столкновения, которая изменяет количества движения каждого тела, однако, поскольку эта сила является внутренней по отношению к изучаемой системе двух тел, то она не приводит к изменению общего количества движения системы. Этот факт носит название закона сохранения импульса.
Вращение с ускорением
Если сформулированный Ньютоном закон механики применить к движению вращения, то получится следующее выражение:
M = I*α.
Здесь M – момент импульса – это величина, которая показывает возможность силы совершить поворот в системе. Момент силы вычисляется, как произведение векторное силы на радиус-вектор, направленный от оси к точке приложения. Величина I – это момент инерции. Как и момент силы, он зависит от параметров вращающейся системы, в частности, от геометрического распределения массы тела относительно оси. Наконец, величина α – это угловое ускорение, позволяющее определить, на сколько радиан в секунду меняется угловая скорость.
Момент силы вычисляется, как произведение векторное силы на радиус-вектор, направленный от оси к точке приложения. Величина I – это момент инерции. Как и момент силы, он зависит от параметров вращающейся системы, в частности, от геометрического распределения массы тела относительно оси. Наконец, величина α – это угловое ускорение, позволяющее определить, на сколько радиан в секунду меняется угловая скорость.
Если внимательно посмотреть на записанное уравнение и провести аналогию между его величинами и показателями из второго ньютоновского закона, то мы получим полное их тождество.
Закон действия и противодействия
Нам осталось рассмотреть третий закон механики. Если первые два, так или иначе, были сформулированы предшественниками Ньютона, а сам ученый лишь придал им стройный математический вид, то третий закон является оригинальным детищем великого англичанина. Итак, он гласит: если два тела вступают в силовой контакт, то действующие между ними силы равны по модулю и противоположны по направлению.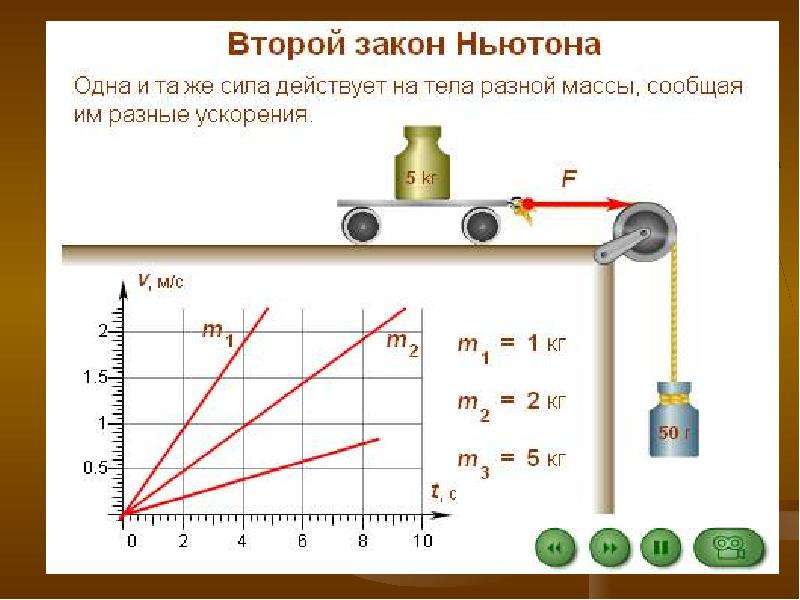 Более кратко можно сказать, что любое действие вызывает противодействие.
Более кратко можно сказать, что любое действие вызывает противодействие.
F12¯ = -F21¯.
Здесь F12¯ и F21¯ – действующие со стороны 1-го тела на 2-е и со стороны 2-го на 1-е силы, соответственно.
Примеров, подтверждающих этот закон, можно привести множество. Например, во время прыжка человек отталкивается от поверхности земли, последняя толкает его вверх. То же самое касается ходьбы пешехода и отталкивания от стенки бассейна пловца. Другой пример, если надавить рукой на стол, то ощущается обратное воздействие стола на руку, которое называется силой реакции опоры.
При решении задач на применение третьего ньютоновского закона следует не забывать, что сила действия и сила противодействия приложена к разным телам, поэтому сообщают им разные ускорения.
Третий закон Ньютона (о действии и противодействии)
Третий закон Ньютона (о действии и противодействии). [c.136]
[c.136]Третий закон Ньютона (о действии и противодействии). Действие всегда равно и противоположно противодействию, или взаимные действия двух тел друг на друга равны по величине и направлены в противоположные стороны. [c.82]
В современном понимании механика — это наука о механическом движении и взаимодействии материальных тел (см., например, [62]). Из всех взаимодействий в механике, основанной на аксиоматике Ньютона, выделено механическое взаимодействие посредством только сил, подчинённых третьему закону Ньютона (равенства действия и противодействия). Более того, дополнительно полагается, что силы действия и противодействия всегда возникают одновременно и представляют собой силы совершенно одинаковой природы [125]. Такие ограничения на способы передачи движения не позволяют с достаточной ясностью и общностью изучать механическое движение, если для взаимодействия не представлен (или вообще отсутствует) перевод на язык силовой механики.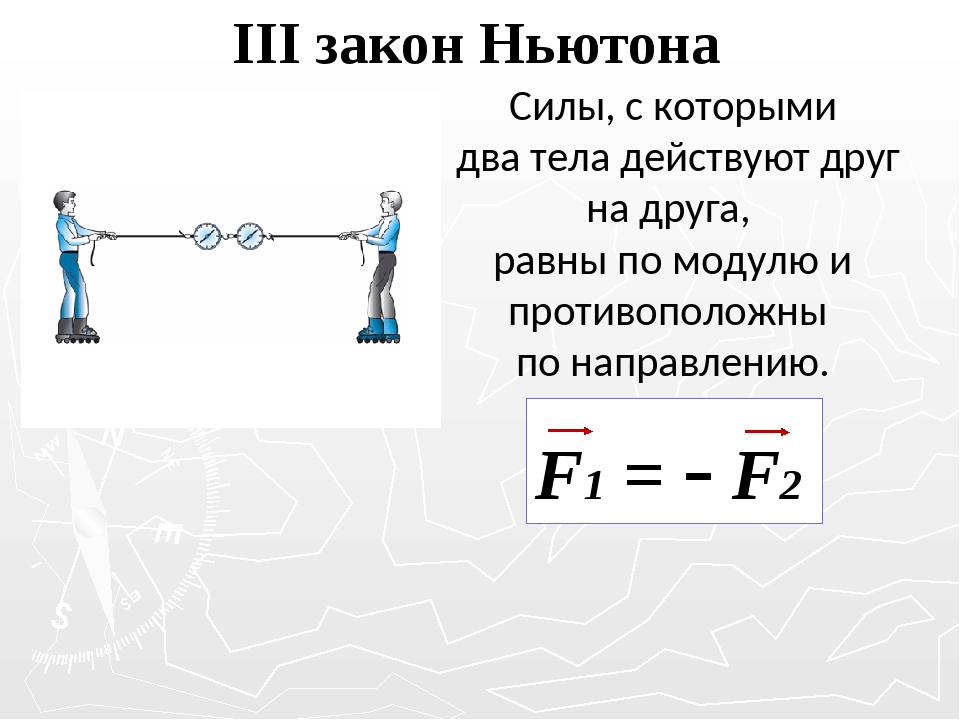 Этот перевод требует, чтобы в описании взаимодействия всегда имелись две силы с указанием реальных материальных источников силового действия и противодействия (обычно это тела, обладающие конечной, бесконечно большой или пренебрежимо малой массой).
[c.34]
Этот перевод требует, чтобы в описании взаимодействия всегда имелись две силы с указанием реальных материальных источников силового действия и противодействия (обычно это тела, обладающие конечной, бесконечно большой или пренебрежимо малой массой).
[c.34]
Закон сил является следствием третьего закона Ньютона о равенстве действия и противодействия. [c.52]
Отметим, что равенство действия и противодействия двух материальных точек (третий закон Ньютона), о котором уже говорилось в начале курса статики, является общим законом всей механики и справедливо не только в задачах статики, но и в задачах динамики. [c.12]
Основными понятиями классической механики являются понятия о пространстве и времени, о силе и массе, об инерциальной системе отсчета. Основными законами являются закон инерции Галилея — Ньютона (первый закон Ньютона), уравнение движения относительно инерциальной системы отсчета (второй закон Ньютона), закон равенства действия и противодействия (третий закон Ньютона). Эти понятия и законы были сформулированы И. Ньютоном в его гениальном трактате Математические начала натуральной философии (1687).
[c.7]
Эти понятия и законы были сформулированы И. Ньютоном в его гениальном трактате Математические начала натуральной философии (1687).
[c.7]
На рассматриваемый объем жидкости, кроме того, будет действовать сила со стороны тела, ибо если поток будет на тело оказывать давление, выражаемое результирующей силой F, проекции которой суть X, Y, то, по третьему закону Ньютона о равенстве действия и противодействия, тело будет действовать на рассматриваемую жидкость с силой —X, —У. Эти силы дадут импульсы (в единицу времени) [c.120]
Иногда считают, что сила тяжести, по третьему закону Ньютона, уравновешивается силой реакции опоры. Это неверно, так как в третьем законе Ньютона идет речь о силах, приложенных к различным телам, и их нельзя поэтому рассматривать как уравновешивающие друг друга. Сила тяжести и сила реакции опоры приложены к данному телу и только поэтому могут уравновешивать друг друга. Но они не находятся в отношении действия и противодействия . [c.95]
[c.95]
Следует обратить внимание на то, что закон сохранения импульса системы явился прямым следствием третьего закона Ньютона. Так как действие равно противодействию в любой момент времени в процессе взаимодействия частей системы (в этом состоит особенность ньютоновских сил ), то сумма импульсов частей системы также будет иметь одно и то же значение во все моменты времени. Однако допущение о ньютоновском характере сил взаимодействия не всегда выполняется на практике, так как не всегда можно считать, что действия тел друг на друга передаются мгновенно. В действительности воздействия передаются не мгновенно, но с конечной скоростью, не превышающей скорость света. Так, что в некоторый момент времени силы взаимодействия fi2 и fa, могут быть и не равны друг другу. Но тогда не будет постоянной сумма импульсов системы. Однако можно показать, что сумма импульсов до взаимодействия тел будет в точности равна сумме импульсов тел после взаимодействия даже в том случае, когда в процессе самого взаимодействия суммарный импульс не сохраняется. Таким образом, закон сохранения импульса для начальных и конечных стадий взаимодействия является самостоятельным законом природы, а не следствием законов Ньютона.
[c.116]
Таким образом, закон сохранения импульса для начальных и конечных стадий взаимодействия является самостоятельным законом природы, а не следствием законов Ньютона.
[c.116]
Рассмотрим возникновение реактивной силы, исходя из законов механики. Если пар между лопатками движется без изменения давления, то его скорость относительно лопаток, т. е. относительная скорость, остается постоянной, и в этом случае, как было объяснено ранее, лопатки находятся только под действием центробежной силы, возникающей вследствие изменения направления движения пара. Если же при движении между лопатками происходит, кроме того, и падение давления, то это вызывает увеличение скорости пара относительно лопаток, т. е. увеличение относительной скорости движения пара. Наличие увеличения скорости, т. е. наличие ускорения, говорит о том, что на движущуюся струю пара действует (согласно второму закону Ньютона) с и л а, направленная в сторону движения. Согласно же третьему закону Ньютона этой силе противодействует равная ей и противоположно направленная сила, приложенная к лопаткам. Эта последняя сила и называется реактивной силой. Таким образом, в этом случае на лопатки действуют в одну и ту же сторону две силы центробежная и реактивная.
[c.203]
Эта последняя сила и называется реактивной силой. Таким образом, в этом случае на лопатки действуют в одну и ту же сторону две силы центробежная и реактивная.
[c.203]
В первом и втором законах говорится о теле, считающемся материальной точкой в первом законе оно изолировано от всех остальных тел, а во втором — рассматривается действие на него другого тела без анализа последствий этого действия для другого тела. В третьем законе Ньютона рассматриваются два тела, моделируемые материальными точками. Точки на расстоянии взаимодействуют между собой, т. е. действуют друг на друга с некоторыми силами. Третий закон Ньютона, или закон равенства действия и противодействия, устанавливает характер взаимодействия материальных точек. Удобна и следующая формулировка третьего закона, в которой использованы введенные ранее понятия материальной точки и силы силы, с которыми две материальные точки действуют друг на друга, расположены по прямой, соединяющей точки, равны по модулю и противоположны по направлению.
 [c.74]
[c.74]Вывод теоремы об изменении количества движения системы, или, как се кратко называют, теоремы количества движения, основан на идее исключения внутренних сил из днф([)ереициаль-ных уравнений движения системы материальных точек (1). Пользуясь третьим законом Ньютона о равенстве действия и противодействия, можно утверждать, что главный вектор внутренних сил V равен нулю [c.107]
Поверхностная сила Т есть та сила, с которой среда, расположенная со стороны положительной нормали +п от элемента поверхности с единичной нормалью п, действует в сторону отрицательной нормали —п. По аналогии с третьим законом Ньютона о равеестве действия и противодействия имеем [c.24]
Ньютон (1642—1727). На основе более ранних исследований Леонардо да Винчи и Галилея Ньютоном были сформулированы основные уравнения движения. Были введены такие фундаментальные понятия, как импульс и действующая сила. Ньютонов закон движения решил задачу о движении изолированной частицы. Он мог также рассматриваться как общее решение задачи о движении, если только согласиться разбивать любую совокупность масс на изолированные частицы. Возникла, однако, трудность, связанная с тем, что не всегда были известны действующие силы. Эта трудность была частично преодолена с помощью третьего закона Ньютона, провозгласившего принцип равенства действия и противодействия. Это исключило неизвестные силы в случае движения твердого тела, однако движение механических систем с более сложными кинематическими условиями не всегда поддавалось ньютонову анализу. Последователи Ньютона считали законы Ньютона абсолютными и универсальными законами природы, интерпретируя их с таким догматизмом, к которому их создатель никогда бы не присоединился. Это догматическое почитание ньютоновой механики частиц помешало физикам отнестись без предубеждения к аналитическим принципам, появившимся в течение XVHI века благодаря работам ведущих французских математиков этого периода. Даже великий вклад Гамильтона в механику не был оценен современниками из-за преобладающего влияния ньютоновой формы механики.
Он мог также рассматриваться как общее решение задачи о движении, если только согласиться разбивать любую совокупность масс на изолированные частицы. Возникла, однако, трудность, связанная с тем, что не всегда были известны действующие силы. Эта трудность была частично преодолена с помощью третьего закона Ньютона, провозгласившего принцип равенства действия и противодействия. Это исключило неизвестные силы в случае движения твердого тела, однако движение механических систем с более сложными кинематическими условиями не всегда поддавалось ньютонову анализу. Последователи Ньютона считали законы Ньютона абсолютными и универсальными законами природы, интерпретируя их с таким догматизмом, к которому их создатель никогда бы не присоединился. Это догматическое почитание ньютоновой механики частиц помешало физикам отнестись без предубеждения к аналитическим принципам, появившимся в течение XVHI века благодаря работам ведущих французских математиков этого периода. Даже великий вклад Гамильтона в механику не был оценен современниками из-за преобладающего влияния ньютоновой формы механики. [c.387]
[c.387]
Соотпоп1епие (1.2) можно трактовать как непосредственное выражение третьего закона Ньютона (принцип равенства действия и противодействия). Но опо может быть также пепосред-ственно выведено из теоремы о количестве движения и из принципа папряжепий Коп1и. Совокупность векторов напряжений сгу(А) для всех направлений I/ определяет напряженное состояние в точке А. [c.17]
Какие неизвестные исключаются при составлении уравнений количеств движения и живых сил. Легко видеть, что при С0С1авлении уравнения количеств движения исключаются все внутренние силы. Это есть следствие третьего закона Ньютона, т. е. равенства между действием и противодействием. Внутренние силы в системе будуг всегда встречаться по две равные и противоположные. Когда же составляем импульс силы, то берем проокгщю силы на координатную ось и умножаем се на элемент времени эги вырал[c.180]
В самом деле, — говорит Ньютон в пояснение к этому за- кону, — если что-либо давит на что-нибудь другое или тянет его, то оно само этим последним давится или тянется. Если кто на- жимает пальцем на камень, то и палец его также нажимается камнем . Если какое-нибудь тело, ударившись о другое тело, изменяет его количество движения на сколько-нибудь, то и оно претерпит от второго тела в своем собственном количестве движения то же самое изменение, но обратно направленное, ибо давления этих тел друг на друга во время контакта равны. Первый и второй законы Ньютона были формулированы по отношению к материальной точке. Третий закон Ньютона является основным для механической системы точек. Нужно только отметить, что действие и противодействие не образуют системы сил, эквивалентной нулю (т. е. уравновешенной), так как дей ствие приложено к одному телу, а противодействие — к другому. По этой причине как действие, так и противодействие могут вызвать движение тел, к которым они приложены. Рассмотрим, например, камень, находящийся под действием силы притяже ния Земли сила противодействия в данном случае будет при ложена к Земле. Действие вызывает движение камня, противодействие-движение Земли.
Если кто на- жимает пальцем на камень, то и палец его также нажимается камнем . Если какое-нибудь тело, ударившись о другое тело, изменяет его количество движения на сколько-нибудь, то и оно претерпит от второго тела в своем собственном количестве движения то же самое изменение, но обратно направленное, ибо давления этих тел друг на друга во время контакта равны. Первый и второй законы Ньютона были формулированы по отношению к материальной точке. Третий закон Ньютона является основным для механической системы точек. Нужно только отметить, что действие и противодействие не образуют системы сил, эквивалентной нулю (т. е. уравновешенной), так как дей ствие приложено к одному телу, а противодействие — к другому. По этой причине как действие, так и противодействие могут вызвать движение тел, к которым они приложены. Рассмотрим, например, камень, находящийся под действием силы притяже ния Земли сила противодействия в данном случае будет при ложена к Земле. Действие вызывает движение камня, противодействие-движение Земли. Так как масса камня иичтожнн по сравнению с массой Земли, то смещения Земли не могут быть измерены современными приборами перемещения же камня обнаруживаются без специальных инструментов, простым глазом.
[c.163]
Так как масса камня иичтожнн по сравнению с массой Земли, то смещения Земли не могут быть измерены современными приборами перемещения же камня обнаруживаются без специальных инструментов, простым глазом.
[c.163]
Возможность расширения пара в лопаточном пространстве рабочего колеса реактивной ступени достигается тем, что профиль лопаточных каналов аналогичен профилю сопла, т. е. ишрина лопаточного канала по его протяженности не остается постоянной, как в активной ступени, и лопатка рабочего колеса реактивной ступени уже не имеет симметричного профиля (рис. 11.19). Естественно, что падение давления пара от Р1 до р2 при движении между лопатками обусловливает увеличение его относительной скорости и Шз > ьг, – Увеличение скорости, т. е. наличие ускорения в соответствии со вторым законом Ньютона, свидетельствует о том, что на движущуюся струю пара действует сила, направленная в сторону перемещения лопаток, а по третьему закону Ньютона этой силе противодействует равная ей и противоположно направленная сила, приложенная непосредственно к лопаткам.
 Эта последняя сила и называется реактивной. Таким образом, на лопатки действуют в одну и ту же сторону две силы — реактивная и центробежная, возникающая вследствие изменения направления двил[c.173]
Эта последняя сила и называется реактивной. Таким образом, на лопатки действуют в одну и ту же сторону две силы — реактивная и центробежная, возникающая вследствие изменения направления двил[c.173]Аналитическая форма механики, развитая Эйлером и Ла-гранжем, существенно отличается по своим методам и принципам от механики векторной. Основной закон механики, сформулированный Ньютоном произведение массы на ускорение равно движущей силе ,— непосредственно применим лишь к одной частице. Он был выведен при изучении движения частиц в поле тяготения Земли, а затем применен к движению планет под воздействием Солнца. В обоих случаях движущееся тело могло рассматриваться как материальная точка или частица , т. е. можно было считать массу сосредоточенной в одной точке. Таким образом, задача динамики формулировалась в следующем виде Частица, которая может свободно перемещаться в пространстве, находится под действием заданной силы. Описать движение в любой момент времени . Из закона Ньютона получалось дифференциальное уравнение движения, и решение задачи динамики сводилось к интегрированию этого уравнения Если частица не является свободной, а связана с други ми частицами, как, например, в твердом теле или в жидкости то уравнение Ньютона следует применять осторожно. Не обходимо сначала выделить одну частицу и определить силы которые на нее действуют со стороны остальных, окружа ющих ее частиц. Каждая частица является независимым объектом и подчиняется закону движения свободной частицы Этот анализ сил зачастую является затруднительным Так как природа сил взаимодействия заранее неизвестна приходится вводить дополнительные постулаты. Ньютон полагал, что принцип действие равно противодействию известный как его третий закон движения, будет достаточен для всех проблем динамики. Это, однако, не так. Даже в динамике твердого тела пришлось ввести дополнительное предположение о том, что внутренние силы являются цен-
[c.25]
Не обходимо сначала выделить одну частицу и определить силы которые на нее действуют со стороны остальных, окружа ющих ее частиц. Каждая частица является независимым объектом и подчиняется закону движения свободной частицы Этот анализ сил зачастую является затруднительным Так как природа сил взаимодействия заранее неизвестна приходится вводить дополнительные постулаты. Ньютон полагал, что принцип действие равно противодействию известный как его третий закон движения, будет достаточен для всех проблем динамики. Это, однако, не так. Даже в динамике твердого тела пришлось ввести дополнительное предположение о том, что внутренние силы являются цен-
[c.25]
PHYS 200 – Лекция 3 – Законы движения Ньютона
PHYS 200 – Лекция 3 – Законы движения Ньютона
Глава 1. Обзор векторов [00:00:00]
Профессор Рамамурти Шанкар: Позвольте мне начать с напоминания вам, что было сделано в прошлый раз. Если вы скажете: «Не могли бы вы в двух словах обрисовать для меня основные идеи?» Я бы хотел это сделать. В прошлый раз я показал вам, как управлять движением в нескольких измерениях. Я выбрал для него два измерения в качестве стандартного способа объяснения.Кстати, я хотел бы дать одну рекомендацию. Если вы, ребята, приходите немного позже, не беспокойтесь о домашних заданиях. Просто зайдите и успокойтесь, потому что читать лекцию с таким объемом трафика очень сложно. Я стараюсь начать на несколько минут позже, но я также должен закончить на несколько минут раньше, чтобы вы могли пойти на следующий урок. Кроме того, людям, которые приходят рано, возможно, стоит попытаться сесть в средней части класса, чтобы опоздавшие могли войти без особых неудобств.
В прошлый раз я показал вам, как управлять движением в нескольких измерениях. Я выбрал для него два измерения в качестве стандартного способа объяснения.Кстати, я хотел бы дать одну рекомендацию. Если вы, ребята, приходите немного позже, не беспокойтесь о домашних заданиях. Просто зайдите и успокойтесь, потому что читать лекцию с таким объемом трафика очень сложно. Я стараюсь начать на несколько минут позже, но я также должен закончить на несколько минут раньше, чтобы вы могли пойти на следующий урок. Кроме того, людям, которые приходят рано, возможно, стоит попытаться сесть в средней части класса, чтобы опоздавшие могли войти без особых неудобств.
Итак, подведение итогов последнего времени.Если вы живете в двух или более измерениях, вам придется использовать векторы для описания большинства вещей. Типичный вектор называется V или A или B со стрелкой на нем. Самый важный вектор – это вектор положения, который сообщает вам, где находится объект. В нем есть компоненты размером x и x , которые могут изменяться со временем. I и J – это единичные векторы в направлениях x и y . Вы можете работать с вектором одним из двух способов.Вы можете думать об этом как о стрелке и представить себе стрелу, или вы можете уменьшить ее до пары чисел: x и y . Если вы хотите сложить два вектора, вы можете добавить стрелки по правилу, которое я вам дал, или просто добавить компоненты двух парней, чтобы получить компонент суммы, и то же самое для y .
В нем есть компоненты размером x и x , которые могут изменяться со временем. I и J – это единичные векторы в направлениях x и y . Вы можете работать с вектором одним из двух способов.Вы можете думать об этом как о стрелке и представить себе стрелу, или вы можете уменьшить ее до пары чисел: x и y . Если вы хотите сложить два вектора, вы можете добавить стрелки по правилу, которое я вам дал, или просто добавить компоненты двух парней, чтобы получить компонент суммы, и то же самое для y .
Я упомянул кое-что, имеющее все большее значение, а именно то, что вы можете выбрать другой набор осей, но не в традиционном направлении x и y , а в наклонном направлении.Если вы это сделаете, единичные векторы называются I ′ и J ′, компоненты вектора изменяются. Вы можете представить, что если вектор смотреть под углом, его компоненты будут меняться в зависимости от перспективы. Таким образом, компоненты вектора не являются инвариантными характеристиками вектора. То есть у самого вектора есть своя жизнь. Компоненты приходят в тот момент, когда вы выбираете свою ось. Недостаточно сказать, что это компоненты вектора; вы должны сказать мне: «Я работаю с I и J , которые я определяю следующим образом.”
Таким образом, компоненты вектора не являются инвариантными характеристиками вектора. То есть у самого вектора есть своя жизнь. Компоненты приходят в тот момент, когда вы выбираете свою ось. Недостаточно сказать, что это компоненты вектора; вы должны сказать мне: «Я работаю с I и J , которые я определяю следующим образом.”
Я дал вам закон преобразования компонентов; а именно, если вектор имеет компоненты ax и ay в одной системе отсчета и ax ‘и ay ‘ в другой системе отсчета, как они связаны? Они исходят из записи I ‘и J ‘ в терминах I и J , затем вставляют это в выражение и идентифицируют новое представление. Каким-то образом, когда я сказал вам обратить преобразование, у некоторых из вас возникли трудности.Может быть, вы не понимали, что это просто одновременные уравнения, которые вы решаете. Обычно, если я говорю вам 3 x + 4 y = 6 и 9 x + 6 y = 14, вы знаете, как решить эту проблему. Это как действительно та же проблема, за исключением того, что все 3 и 4 будут размещены с помощью sin φ и cos φ , но это просто числа. Вы устраняете их так же, как устраняете их. Я дал вам домашнее задание, где вы можете попробовать свои силы.Когда вы пойдете сегодня и посмотрите домашнее задание, вы найдете задачу из учебника, еще одну дополнительную задачу, которая касается всего этого.
Это как действительно та же проблема, за исключением того, что все 3 и 4 будут размещены с помощью sin φ и cos φ , но это просто числа. Вы устраняете их так же, как устраняете их. Я дал вам домашнее задание, где вы можете попробовать свои силы.Когда вы пойдете сегодня и посмотрите домашнее задание, вы найдете задачу из учебника, еще одну дополнительную задачу, которая касается всего этого.
Затем я привел еще один очень важный пример движения частицы в плоскости xy . x и y могут быть какими угодно, но я выбрал очень особенный пример, где x выглядело так: r умножить на cos ωt . На этот раз I + r раз sin ωt .Вы должны вернуться и вспомнить, что мы сделали. Если вам потребовалось время, чтобы переварить это, я прошу вас подумать больше. Это описывает частицу, движущуюся по кругу. Мы знаем, что он движется по кругу, потому что, если я найду длину этого вектора, который представляет собой квадрат x плюс квадрат y , я всегда всегда получаю r 2 , потому что квадрат синуса плюс квадрат косинуса равен единице. Итак, мы знаем, что он движется по окружности радиуса r . Кроме того, с увеличением времени угол ωt увеличивается таким образом.Омега называется углом скорости. Я связал это с периодом времени, который представляет собой время, необходимое для обхода полного круга, сказав, что после того, как вы сделаете полный круг, ωt лучше будет 2 π .
Итак, мы знаем, что он движется по окружности радиуса r . Кроме того, с увеличением времени угол ωt увеличивается таким образом.Омега называется углом скорости. Я связал это с периодом времени, который представляет собой время, необходимое для обхода полного круга, сказав, что после того, как вы сделаете полный круг, ωt лучше будет 2 π .
Итак, эта новая величина ω , которая может быть для вас новой, связана с периодом времени. Сколько времени нужно, чтобы пройти один раунд таким образом? Вы также можете указать частоту. Период времени и частота являются обратными. Если на один обход у вас уходит 1/60 секунды, то вы делаете это 60 раз в секунду.Омега – действительно очень простое количество. Это связано с частотой, с которой вы движетесь по кругу, но умножается на 2 π . Это почему? Частоты, сколько раз вы оборачиваетесь, и 2 π – это скорость, с которой изменяется угол. Но если каждый оборот стоит 2 π радиан, то 2 πf – это количество радиан в секунду. f – обороты в секунду, а 2 πf – радианы в секунду. Это называется углом скорости.
f – обороты в секунду, а 2 πf – радианы в секунду. Это называется углом скорости.
Самым важным результатом прошлого раза было то, что если вы взяли этот r , и вы взяли две производные от него, чтобы найти ускорение, d 2 r более dt 2 , попробуйте сделать это в твоя голова. Если взять две производные этого парня, в первый раз это будет – ω , sin ωt ; второй раз станет – ω 2 cos ωt . Другими словами, она сама станет – ω 2 раз.Там то же самое. Конечный результат – ускорение – ω 2 раз больше положения. Это означает, что ускорение направлено к центру круга и имеет величину a . Когда я рисую что-то без стрелки, я говорю о величине. Это всего лишь ω 2 r . Вчера я показал вам, что скорость частицы, когда она движется по кругу, равна ( ωr ).
Опять же, вы должны убедиться, что знаете, как это получить. Вы можете делать это как хотите. Вы можете сделать один полный круг и понять, что пройденное расстояние составляет 2 πr , разделите на время, и вы получите это. Другой способ: возьмите производную от этого, получите вектор скорости, и вы заметите, что его величина постоянна, а константа будет равна ωr . Каким бы способом вы это ни сделали, вы можете переписать это как v 2 на r . Это называется центростремительным ускорением. Это ускорение, направленное к центру.Я сказал вам, что это очень важные результаты. Вы должны получить это в своей голове. Когда вы видите частицу, движущуюся по кругу, даже если она с постоянной скоростью, она имеет ускорение, направленное к центру: v 2 по сравнению с r .
Вы можете делать это как хотите. Вы можете сделать один полный круг и понять, что пройденное расстояние составляет 2 πr , разделите на время, и вы получите это. Другой способ: возьмите производную от этого, получите вектор скорости, и вы заметите, что его величина постоянна, а константа будет равна ωr . Каким бы способом вы это ни сделали, вы можете переписать это как v 2 на r . Это называется центростремительным ускорением. Это ускорение, направленное к центру.Я сказал вам, что это очень важные результаты. Вы должны получить это в своей голове. Когда вы видите частицу, движущуюся по кругу, даже если она с постоянной скоростью, она имеет ускорение, направленное к центру: v 2 по сравнению с r .
Эта формула не сообщает вам, в какую сторону она указывает, потому что это средство масштабирования; это не векторное уравнение. Если вы хотите записать это как векторное уравнение, вы хотите записать его как v 2 над r минус – я хочу сказать, что он указывает в направлении к центру. Иногда мы вводим здесь небольшой вектор под названием e r . Я расскажу вам об этом позже. e r – вектор в каждой точке длиной один, направленный радиально от центра. Это как единичный вектор I . Единичный вектор I указывает от начала координат в направлении x . J указывает от начала координат в направлении y . e r не является фиксированным вектором.В каждой точке e r – это другой вектор, указывающий в радиальном направлении длиной один. Преимущество представления этого парня в том, что теперь, если хотите, я могу написать уравнение для ускорения в виде вектора. Величина v 2 больше r . Направление – -e r . Итак, e r – это новая сущность, которую я ввел для удобства. Он играет большую роль в гравитации, в кулоновском взаимодействии.Хорошо иметь вектор, указывающий в радиальном направлении длины, равной единице.
Иногда мы вводим здесь небольшой вектор под названием e r . Я расскажу вам об этом позже. e r – вектор в каждой точке длиной один, направленный радиально от центра. Это как единичный вектор I . Единичный вектор I указывает от начала координат в направлении x . J указывает от начала координат в направлении y . e r не является фиксированным вектором.В каждой точке e r – это другой вектор, указывающий в радиальном направлении длиной один. Преимущество представления этого парня в том, что теперь, если хотите, я могу написать уравнение для ускорения в виде вектора. Величина v 2 больше r . Направление – -e r . Итак, e r – это новая сущность, которую я ввел для удобства. Он играет большую роль в гравитации, в кулоновском взаимодействии.Хорошо иметь вектор, указывающий в радиальном направлении длины, равной единице. Это и есть. Это действительно суть того, что я сделал в прошлый раз. Потом мы сделали несколько проблем с снарядами. Вы стреляете во что-то, вы должны знать, когда оно приземлится, где приземлится, с какой скоростью приземлится, как высоко пойдет. Я полагаю, что эти проблемы не такие уж и сложные, и я дал вам много практики.
Это и есть. Это действительно суть того, что я сделал в прошлый раз. Потом мы сделали несколько проблем с снарядами. Вы стреляете во что-то, вы должны знать, когда оно приземлится, где приземлится, с какой скоростью приземлится, как высоко пойдет. Я полагаю, что эти проблемы не такие уж и сложные, и я дал вам много практики.
Глава 2. Введение в законы движения Ньютона, первый закон и инерционные системы отсчета [00:09:29]
Теперь я перейду к действительно важной и центральной теме.Думаю, вы можете догадаться, что это такое. Поговорим о законах Ньютона. Это важный день в твоей жизни. Это когда вы изучаете законы, с помощью которых вы можете понимать и объяснять большое количество явлений. Фактически, пока мы не займемся электричеством и магнетизмом в следующем семестре, все будет основываться только на законах Ньютона. Это действительно удивительно, что кто-то может сжать столько информации в несколько, а именно в три разных закона. Вот о чем мы и поговорим.
Приступим. Ваша реакция может быть такой, что вы видели законы Ньютона, вы применяли их в школе. Должен сказать, что довольно поздно я понял, что они более тонкие, чем я представлял в первый раз. Одно дело подставить все числа и сказать: «Я знаю законы Ньютона и знаю, как они работают». Но по мере того, как вы становитесь старше и у вас появляется много свободного времени, вы думаете о том, что делаете, а это то, чем я могу себе позволить прямо сейчас, и я понял, что это сложнее. Я хочу поделиться с вами кое-чем из этого, чтобы вы могли быстро перемотать вперед и понять, что мне потребовалось гораздо больше времени.Это то, что я хочу подчеркнуть, больше, чем просто вводить цифры. Конечно, мы также должны знать, как подставлять числа, чтобы пройти все тесты, но хорошо понимать природу здания, построенного Ньютоном.
Ваша реакция может быть такой, что вы видели законы Ньютона, вы применяли их в школе. Должен сказать, что довольно поздно я понял, что они более тонкие, чем я представлял в первый раз. Одно дело подставить все числа и сказать: «Я знаю законы Ньютона и знаю, как они работают». Но по мере того, как вы становитесь старше и у вас появляется много свободного времени, вы думаете о том, что делаете, а это то, чем я могу себе позволить прямо сейчас, и я понял, что это сложнее. Я хочу поделиться с вами кое-чем из этого, чтобы вы могли быстро перемотать вперед и понять, что мне потребовалось гораздо больше времени.Это то, что я хочу подчеркнуть, больше, чем просто вводить цифры. Конечно, мы также должны знать, как подставлять числа, чтобы пройти все тесты, но хорошо понимать природу здания, построенного Ньютоном.
Первое высказывание Ньютона – мне не хочется его записывать. Это слишком долго, и все знают, каков закон. Это называется законом инерции. Позвольте мне просто сказать это и поговорить об этом. Закон инерции гласит: «Если на тело не действуют силы, оно будет оставаться в покое, если оно было в состоянии покоя с самого начала, или если оно изначально имело скорость, оно будет поддерживать эту скорость.Можно сказать, что каждое тело будет продолжать оставаться в состоянии покоя или равномерного движения по прямой линии. Это еще один способ сказать «поддержание скорости», если на нее не действует сила. Что делает закон удивительным, так это то, что если бы я дал вам только половину закона, а именно: все тела останутся в покое, если на них не будет действовать сила, вы скажете: «Ничего страшного. Я принимаю это, потому что здесь кое-что есть. Вы оставите его там, он не двигается. Это не большой сюрприз ». К этому привыкли со времен Аристотеля.Но Аристотель раньше думал, что если вы хотите, чтобы что-то двигалось, должна быть какая-то сила, заставляющая это двигаться. Это агентство можно назвать силой.
Закон инерции гласит: «Если на тело не действуют силы, оно будет оставаться в покое, если оно было в состоянии покоя с самого начала, или если оно изначально имело скорость, оно будет поддерживать эту скорость.Можно сказать, что каждое тело будет продолжать оставаться в состоянии покоя или равномерного движения по прямой линии. Это еще один способ сказать «поддержание скорости», если на нее не действует сила. Что делает закон удивительным, так это то, что если бы я дал вам только половину закона, а именно: все тела останутся в покое, если на них не будет действовать сила, вы скажете: «Ничего страшного. Я принимаю это, потому что здесь кое-что есть. Вы оставите его там, он не двигается. Это не большой сюрприз ». К этому привыкли со времен Аристотеля.Но Аристотель раньше думал, что если вы хотите, чтобы что-то двигалось, должна быть какая-то сила, заставляющая это двигаться. Это агентство можно назвать силой.
Великое открытие, сделанное Галилеем и Ньютоном, состоит в том, что для того, чтобы тело двигалось с постоянной скоростью, не нужна сила. Совершенно ясно, что вам не нужна сила, если что-то бездействует, просто сидит там. Тот факт, что вам не нужна сила, чтобы он мог вечно двигаться с заданной скоростью в заданном направлении, это не очевидно, потому что в повседневной жизни вы этого не видите.В повседневной жизни кажется, что все приходит в состояние покоя, если только вы не толкаете, не тянете или не прикладываете какую-то силу. Но все мы знаем, что причина того, что вещи останавливаются, когда вы их толкаете, заключается в том, что в конечном итоге возникает какое-то трение, сопротивление или что-то еще, что их останавливает. Каким-то образом, если бы вы могли изготовить действительно гладкую поверхность без трения, что, если вы возьмете хоккейную шайбу или что-то в этом роде и воздушную подушку и толкнете ее в каком-то идеализированном мире, она будет путешествовать вечно. Так что в земной ситуации это трудно понять.Но Галилею уже удалось найти примеры, когда все будет продолжаться очень и очень долго. В наши дни, если вы отправитесь в космос, вы можете сами убедиться, что если вы что-то выбросите, это будет продолжаться вечно без вашего вмешательства.
Совершенно ясно, что вам не нужна сила, если что-то бездействует, просто сидит там. Тот факт, что вам не нужна сила, чтобы он мог вечно двигаться с заданной скоростью в заданном направлении, это не очевидно, потому что в повседневной жизни вы этого не видите.В повседневной жизни кажется, что все приходит в состояние покоя, если только вы не толкаете, не тянете или не прикладываете какую-то силу. Но все мы знаем, что причина того, что вещи останавливаются, когда вы их толкаете, заключается в том, что в конечном итоге возникает какое-то трение, сопротивление или что-то еще, что их останавливает. Каким-то образом, если бы вы могли изготовить действительно гладкую поверхность без трения, что, если вы возьмете хоккейную шайбу или что-то в этом роде и воздушную подушку и толкнете ее в каком-то идеализированном мире, она будет путешествовать вечно. Так что в земной ситуации это трудно понять.Но Галилею уже удалось найти примеры, когда все будет продолжаться очень и очень долго. В наши дни, если вы отправитесь в космос, вы можете сами убедиться, что если вы что-то выбросите, это будет продолжаться вечно без вашего вмешательства. В природе вещей идти с постоянной скоростью. Для этого им не нужна ваша помощь.
В природе вещей идти с постоянной скоростью. Для этого им не нужна ваша помощь.
Вы должны быть осторожны, чтобы этот первый закон Ньютона не действовал для всех. На самом деле, я приведу пример из вашей собственной жизни, когда вы обнаружите, что этот закон не работает.Вот такая ситуация. Вы садитесь в самолет, а затем после обычных задержек самолет начинает ускоряться по взлетно-посадочной полосе. В этот момент, если вы оставите что-нибудь на полу, вы поймете, что это больше не ваше. Он будет скользить вниз, и парень в последнем ряду все соберет. Это почему? Поскольку мы обнаруживаем, что в этом плане, когда объекты остаются в том состоянии, которое, как вы думаете, находится в состоянии покоя, и на них не действует никакая внешняя сила, все они скользят назад к заднему концу плоскости. Это происходит во время взлета.Этого не происходит в полете, но это происходит во время взлета. Это пример человека, для которого Закон инерции не работает. Возможно, вы этого не осознали.
Законы Ньютона не для всех. Вы должны быть так называемым «инерционным наблюдателем». Если вы инерционный наблюдатель, то в вашей системе отсчета объекты, оставленные в покое, останутся неподвижными. Самолет, который готов к взлету или взлетает, не является такой системой. Земля кажется довольно хорошей инерциальной системой, потому что на земле вы что-то оставляете, а она остается там.Это зависит от того, что вы оставите. Если вы оставите свой iPod, он не останется там надолго. Но тогда вы можете отследить это до каких-то внешних сил, которые несут в себе ваш iPod. Но если ничего не делать, все остается.
Вы должны быть так называемым «инерционным наблюдателем». Если вы инерционный наблюдатель, то в вашей системе отсчета объекты, оставленные в покое, останутся неподвижными. Самолет, который готов к взлету или взлетает, не является такой системой. Земля кажется довольно хорошей инерциальной системой, потому что на земле вы что-то оставляете, а она остается там.Это зависит от того, что вы оставите. Если вы оставите свой iPod, он не останется там надолго. Но тогда вы можете отследить это до каких-то внешних сил, которые несут в себе ваш iPod. Но если ничего не делать, все остается.
Вот главное. Суть Ньютона состоит в двух вещах в Законе инерции, которые можно подумать тривиальными. Во-первых, свободную скорость, постоянную скорость можно получить бесплатно, ничего не делая. Есть люди, для которых это правда. Например, в космосе у вас есть космонавт.Вы что-то отправляете, и вы обнаружите, что это продолжается вечно. Вот еще кое-что. Если вы найдете одного инерционного наблюдателя, а именно одного человека, для которого действует этот Закон инерции, я могу создать для вас бесконечное количество других людей, для которых это верно. Кто эти другие люди? Вы понимаете, о чем я говорю? Если я дам вам одного наблюдателя, для которого закон инерции верен, я скажу, что другие, для которых также верен. Да?
Кто эти другие люди? Вы понимаете, о чем я говорю? Если я дам вам одного наблюдателя, для которого закон инерции верен, я скажу, что другие, для которых также верен. Да?
Студент : [неразборчиво]
Профессор Рамамурти Шанкар: Вы это слышали? Позвольте мне повторить это.Во-первых, если для меня действует закон инерции, то он действителен и для других людей, находящихся в той же комнате в состоянии покоя по отношению ко мне. Потому что, если я думаю, что он не движется, вы думаете, что он не движется. Это нормально. Но представьте, что вы в поезде, проезжаете мимо меня и смотрите на этот кусок мела. Конечно, для тебя все в моей комнате идет вспять. Но вещи, которые были в покое, будут двигаться с постоянной скоростью, противоположной той, что у вас по отношению ко мне. Вы обнаружите, что объекты, которые имеют постоянную начальную скорость, сохраняют эту скорость.Если я инерционный наблюдатель, другой человек, движущийся относительно меня с постоянной скоростью, также будет инерционным наблюдателем. Почему? Поскольку любую скорость я приписываю частице или объекту, вы добавите к ней некоторую константу по закону сложения скорости. Я вижу, что ко всем скоростям вы добавите определенное число, чтобы получить скорости в соответствии с вашими предпочтениями. Но добавление постоянной скорости к объектам не меняет того факта, что те, которые поддерживали постоянную скорость, по-прежнему сохраняют постоянную скорость.Это другая постоянная скорость.
Почему? Поскольку любую скорость я приписываю частице или объекту, вы добавите к ней некоторую константу по закону сложения скорости. Я вижу, что ко всем скоростям вы добавите определенное число, чтобы получить скорости в соответствии с вашими предпочтениями. Но добавление постоянной скорости к объектам не меняет того факта, что те, которые поддерживали постоянную скорость, по-прежнему сохраняют постоянную скорость.Это другая постоянная скорость.
В частности, вещи, о которых я говорю, находятся в состоянии покоя, вы скажете, что они движутся назад со скоростью, которую вы имеете относительно меня. То, о чем я говорю, идет со скоростью 50 миль в час, вы можете сказать, что со скоростью 80. Но 50 – это постоянная величина, а 80 – постоянная величина. Следовательно, дело не в том, что существует только одна счастливая семья инерционных наблюдателей. Их бесконечное количество, но все они движутся относительно друг друга с постоянной скоростью. Если Земля является инерциальной системой отсчета, если вы едете в поезде относительно Земли с постоянной скоростью, вы также инерциальны. Но если вы летите в самолете, который ускоряется, вы больше не являетесь инерционным. Это главное. Дело в том, что существуют инерциальные системы отсчета. Вы должны знать, что Земля не совсем инерциальна. У Земли есть ускорение. Вы можете сказать мне, почему я уверен, что у Земли есть ускорение? Да?
Но если вы летите в самолете, который ускоряется, вы больше не являетесь инерционным. Это главное. Дело в том, что существуют инерциальные системы отсчета. Вы должны знать, что Земля не совсем инерциальна. У Земли есть ускорение. Вы можете сказать мне, почему я уверен, что у Земли есть ускорение? Да?
Студент : Потому что он движется по кругу.
Профессор Рамамурти Шанкар: Он обращается вокруг Солнца. Представим, что это круговая орбита. Тогда мы только что показали здесь, это ускоренная система отсчета.Оказывается, если вы поместите v 2 и r , а r составляет 93 миллиона миль, вы обнаружите, что ускорение достаточно мало, чтобы мы могли его игнорировать. Но есть эффекты ускорения Земли, которые мы продемонстрируем. Маятник Focault – один из примеров, когда вы можете видеть, что Земля вращается вокруг своей оси. Затем факт, что Земля вращается вокруг Солнца. Все они означают, что он действительно не инерционный, но примерно инерционный. Но если вы сегодня отправитесь в космос, вы можете найти поистине инерциальные системы отсчета.
Но если вы сегодня отправитесь в космос, вы можете найти поистине инерциальные системы отсчета.
Это первый закон. Первый закон, если вы хотите, если вы хотите сказать: «Хорошо, каков итог всего этого?» Суть в том, что для постоянной скорости ничего не требуется. Причина, по которой это выглядит тавтологией, потому что вы смотрите вокруг, кажется, ничто не имеет своей скорости вечно. Затем вы говорите: «О, это потому, что на него действует сила». Это похоже на тавтологию, потому что вы никогда не сможете показать мне что-то, что вечно движется с постоянной скоростью, потому что каждый раз, когда вы не находите ничего подобного, я извиняюсь, а именно: действует сила.Но это не большой недостаток, потому что вы можете ставить эксперименты в свободном космосе далеко от всего, где объекты, по сути, будут сохранять свою скорость вечно. Это возможность. Это полезная концепция для Земли, потому что Земля приблизительно инерциальна.
Глава 3. Второй закон и измерения как условные обозначения [00:19:51]
Итак, мы подошли ко второму закону, который является «законом». Это закон, который мы все запоминаем и изучаем. В нем говорится: «Если у тела есть ускорение, тогда вам нужна сила, и отношение силы к ускорению таково: F = ma ». Теперь я должен сказать несколько слов о единицах измерения.Ускорение измеряется в метрах на секунду в квадрате. Масса измеряется в килограммах. Таким образом, сила измеряется в килограммах-метрах на секунду в квадрате. Но мы устали произносить это длинное выражение, поэтому назовем его Ньютоном, верно? Если бы вы его изобрели, мы бы назвали его, как ваше имя, но это тот парень, который его изобрел, поэтому его называют Ньютоном, обычно обозначаемым с большой буквы. Типичная проблема, которую вы, возможно, решили при первом проходе в Закон Ньютона, кто-то говорит вам, что сила в 36 Ньютонов действует на массу чего угодно, 4 килограмма; какое ускорение? Вы делите и обнаруживаете, что это 9, и говорите: «Хорошо, я знаю, что делать с законами Ньютона.”
Это закон, который мы все запоминаем и изучаем. В нем говорится: «Если у тела есть ускорение, тогда вам нужна сила, и отношение силы к ускорению таково: F = ma ». Теперь я должен сказать несколько слов о единицах измерения.Ускорение измеряется в метрах на секунду в квадрате. Масса измеряется в килограммах. Таким образом, сила измеряется в килограммах-метрах на секунду в квадрате. Но мы устали произносить это длинное выражение, поэтому назовем его Ньютоном, верно? Если бы вы его изобрели, мы бы назвали его, как ваше имя, но это тот парень, который его изобрел, поэтому его называют Ньютоном, обычно обозначаемым с большой буквы. Типичная проблема, которую вы, возможно, решили при первом проходе в Закон Ньютона, кто-то говорит вам, что сила в 36 Ньютонов действует на массу чего угодно, 4 килограмма; какое ускорение? Вы делите и обнаруживаете, что это 9, и говорите: «Хорошо, я знаю, что делать с законами Ньютона.”
Здесь я хочу сказать вам, что на самом деле все намного сложнее. Давайте действительно посмотрим на это уравнение. Вернитесь в 1600-й год – что бы там ни было, когда бы Ньютон придумывал эти законы. Вы не знаете ни одного из этих законов. У вас есть интуитивное определение силы. Вы вроде как знаете, что такое сила. Кто-то толкает или тянет вас. Это сила. Вдруг вам говорят, что есть закон. Тебе хоть как-то лучше? «Можете ли вы что-нибудь сделать с этим законом?» это то, о чем я вас спрашиваю. Что можно сделать с этим законом? Я даю вам закон Ньютона и говорю: «Удачи.” Что ты будешь делать? Что это помогает вам предсказывать? Можете ли вы даже сказать, правда ли это? Вот тело, которое движется, верно? Я хочу, чтобы вы сказали мне, прав ли Ньютон? Как мы собираемся это проверить? Итак, вы хотите измерить левую часть и вы хотите измерить правую часть. Если они равны, может быть, вы скажете, что закон работает. Что вы можете измерить в этом уравнении?
Давайте действительно посмотрим на это уравнение. Вернитесь в 1600-й год – что бы там ни было, когда бы Ньютон придумывал эти законы. Вы не знаете ни одного из этих законов. У вас есть интуитивное определение силы. Вы вроде как знаете, что такое сила. Кто-то толкает или тянет вас. Это сила. Вдруг вам говорят, что есть закон. Тебе хоть как-то лучше? «Можете ли вы что-нибудь сделать с этим законом?» это то, о чем я вас спрашиваю. Что можно сделать с этим законом? Я даю вам закон Ньютона и говорю: «Удачи.” Что ты будешь делать? Что это помогает вам предсказывать? Можете ли вы даже сказать, правда ли это? Вот тело, которое движется, верно? Я хочу, чтобы вы сказали мне, прав ли Ньютон? Как мы собираемся это проверить? Итак, вы хотите измерить левую часть и вы хотите измерить правую часть. Если они равны, может быть, вы скажете, что закон работает. Что вы можете измерить в этом уравнении?
Студент : [неразборчиво]
Профессор Рамамурти Шанкар: Простите меня?
Студент : Сила и ускорение.
Профессор Рамамурти Шанкар: Хорошо. Начнем с разгона. Как вы планируете измерить ускорение, если какая-то мелочь движется? Что нужно для его измерения?
Студент : изменение скорости по сравнению с изменением [неразборчиво]
Профессор Рамамурти Шанкар: Верно, но какие инструменты вам понадобятся для измерения? Вы должны действительно это измерить. О чем вы меня попросите?
Студент : Часы.
Профессор Рамамурти Шанкар: Часы? да.
Студент : [неразборчиво]
Профессор Рамамурти Шанкар: А что еще?
Студент : [неразборчиво]
Профессор Рамамурти Шанкар: Правитель? Хорошо. Верно. Вы ведь не имеете в виду королеву Елизавету? Вы имеете в виду … Очень хорошо. Чего вы действительно хотите – линейки может быть недостаточно, но, может быть, этого достаточно. Итак, вот длинная линейка и вот эта штука движется, верно? Вы просите Rolex, и вот ваши часы.Время показательное. Скажите, что именно вы хотите сделать, чтобы измерить ускорение. Что ты должен сделать? Я хочу ускорение сейчас. Что вы будете измерять? Хорошо, продолжай. Ты можешь попробовать.
Итак, вот длинная линейка и вот эта штука движется, верно? Вы просите Rolex, и вот ваши часы.Время показательное. Скажите, что именно вы хотите сделать, чтобы измерить ускорение. Что ты должен сделать? Я хочу ускорение сейчас. Что вы будете измерять? Хорошо, продолжай. Ты можешь попробовать.
Студент : [неразборчиво]
Студент : [неразборчиво] Я бы начал с неподвижного объекта, а затем [неразборчиво]
Профессор Рамамурти Шанкар: Возможно, с самого начала он не находится в состоянии покоя. Он делает свое дело. Идет с некоторой скоростью. Да?
Студент : Измерьте расстояние, которое он проходит за постоянный интервал времени?
Профессор Рамамурти Шанкар: Это даст вам скорость.
Студент : Что ж, если вы сделаете расстояние через одну секунду по сравнению с расстоянием в следующую секунду по сравнению с расстоянием в течение третьей секунды, вы увидите, как оно увеличивается.
Профессор Рамамурти Шанкар: В принципе хорошо. Позвольте мне повторить то, что он сказал. Он сказал, во-первых, позвольте ему пройти небольшое расстояние, увеличьте расстояние со временем. Теперь это дает вам скорость. Отпустите еще немного, это даст вам скорость позже. Возьмите разницу двух скоростей и разделите на разницу двух значений, и вы получите ускорение.Конечно, вы позволили ему переместиться на конечное расстояние за конечное время. Вы должны представить, что делаете эти три измерения все быстрее и быстрее. Вам нужно три позиционных измерения. Теперь, немного позже и немного позже, потому что между первым и вторым вы получаете скорость, а между вторым и третьим вы получаете другую скорость. Их разница, разделенная на разницу во времени, и будет ускорением. Но если вы вообразите, как делать эти измерения все чаще и быстрее, в конце концов, вы можете измерить то, что вы можете сказать сейчас, как ускорение.
В этом смысл предела в исчислении. Возьмем Δx и Δt . Что означают переходы Δx и Δt в 0? Это означает, что измеряйте их как можно быстрее. В реальном мире никто не собирается измерять это мгновенно, но мы можем сделать разницу настолько маленькой, насколько захотим. Математически мы можем сделать это равным нулю. В этом пределе мы можем измерить скорость прямо сейчас. Это означает, что мы также можем измерить скорость немного позже и приблизить немного позже к текущему моменту, насколько захотим.Тогда это соотношение даст вам ускорение. Из этих трех величин проще всего измерить ускорение. У всех нас есть хорошее интуитивное представление о том, что такое ускорение. Вы хотите проверить, верно ли то, что сказал вам Ньютон. Вы видите движущийся объект, вы находите a и даете a определенное числовое значение, 10 метров в секунду в квадрате. Но это еще не проверка уравнения, потому что вам нужно найти обе стороны. А что с массой? Какая масса у этого объекта? Кто-нибудь хочет попробовать из этого раздела здесь? Да?
Возьмем Δx и Δt . Что означают переходы Δx и Δt в 0? Это означает, что измеряйте их как можно быстрее. В реальном мире никто не собирается измерять это мгновенно, но мы можем сделать разницу настолько маленькой, насколько захотим. Математически мы можем сделать это равным нулю. В этом пределе мы можем измерить скорость прямо сейчас. Это означает, что мы также можем измерить скорость немного позже и приблизить немного позже к текущему моменту, насколько захотим.Тогда это соотношение даст вам ускорение. Из этих трех величин проще всего измерить ускорение. У всех нас есть хорошее интуитивное представление о том, что такое ускорение. Вы хотите проверить, верно ли то, что сказал вам Ньютон. Вы видите движущийся объект, вы находите a и даете a определенное числовое значение, 10 метров в секунду в квадрате. Но это еще не проверка уравнения, потому что вам нужно найти обе стороны. А что с массой? Какая масса у этого объекта? Кто-нибудь хочет попробовать из этого раздела здесь? Да?
Студент : Вы можете использовать какую-то стандартную единицу массы, а затем весы, чтобы измерить массу чего-то еще, например, поместите ее на определенном расстоянии от точки опоры на шкале и вычислите относительную массу.
Профессор Рамамурти Шанкар: Хорошо. Его идея заключалась в следующем. Вы берете стандартную массу и, возможно, идете на качели. Вы кладете стандартную массу сюда, а кого-то другого помещаете в ту массу, на которую вы смотрите. Вы складываете только длину, и когда она уравновешивается, вы можете сказать, что это за масса, верно? Но предположим, что вы были в открытом космосе. Нет гравитации. Тогда качели уравновесят, даже если вы положите картошку с одной стороны, а слона – с другой. Вы не можете определить массу, потому что то, что вы делаете сейчас, апеллирует к понятию массы как к чему-то, что связано с притяжением Земли к объекту.Но закон Ньютона таков: вы должны вернуться и стереть все, что вы знаете. Если это то, что у вас есть, в этих уравнениях нет упоминания о Земле. Тем не менее, понятие массы определено. Речь не идет о гравитационном притяжении Земли на объект. Да?
Студент : Если у вас есть объект, который, как вы говорите, имеет определенную массу, о которой вы не знаете, а затем вы выбрали объект такой же плотности, но, скажем, в два раза больше, и вы можете увидеть, замедляет ли он силу.
Профессор Рамамурти Шанкар: Но знаете ли вы, какая сила действует на тело? Мы тоже не знаем, как это измерить; ты согласен? Мы не знаем, что это за сила, потому что надеемся сказать, что сила будет м умножить на a .Мы только приступаем к измерению м . Сейчас это похоже на круговое определение. Да?
Студент : Вы имеете в виду, из какого материала сделан этот объект и его плотность [неразборчиво]
Профессор Рамамурти Шанкар: А, но плотность – это масса над объемом. Но мы ведь не знаем массы?
Студент : Но если использовать плотность [неразборчиво]
Профессор Рамамурти Шанкар: Как кто-нибудь может дать вам плотность чего-либо? Мы просто спрашиваем, какова масса любого объекта? Мы еще не нашли удовлетворительного ответа на вопрос, какова масса объекта? Да?
Студент : Мы все еще работаем в космосе?
Профессор Рамамурти Шанкар: Да. Это не может зависеть от планеты Земля.
Это не может зависеть от планеты Земля.
Студент : Может быть, у нас случайно будет пружина?
Профессор Рамамурти Шанкар: Да.
Студент : Чья жесткость пружины и определение [неразборчиво]
Профессор Рамамурти Шанкар: Мне очень жаль. Что вы только что сказали? Вы можете получить весну.
Студент : Да, у вас могла бы быть пружина, и вы могли бы сравнить, как быстро эти объекты будут перемещаться, когда пружина сжимается, когда они помещаются напротив нее и отпускаются, но тогда у вас будет только сравнение.
Профессор Рамамурти Шанкар: Хорошо. Позвольте мне повторить то, что он сказал. Он сказал, возьмите пружину в открытый космос, и мы подключим к ним некоторые объекты, посмотрим, с какой скоростью они движутся, и проведем сравнение. Это довольно близко к тому, что я имел в виду. Но это не идеальный ответ. Я просто хочу немного подумать об этом. Да?
Да?
Студент : [неразборчиво]
Профессор Рамамурти Шанкар: Чему я научился из этого периода?
Студент : [неразборчиво]
Профессор Рамамурти Шанкар: Как?
Студент : [неразборчиво]
Профессор Рамамурти Шанкар: Помните, вы не можете заглянуть в главы 6 и 7, потому что вы видели это раньше.Я спрашиваю вас, писал ли кто-нибудь, по-видимому, для него пьесы Шекспира; это один из слухов, верно? Предположим, Ньютон приходит к вам и говорит: «У меня есть этот великий закон, но я не хочу публиковать его под своим именем. Я отдам его тебе. У вас есть этот новый закон, но как вы собираетесь его продавать? Вы должны рассказывать людям, как им пользоваться. Вы понимаете, что это очень тонко, потому что самое первое в этом уравнении, а именно м , еще не определено. Он дал довольно близкий ответ.Он не полагается на гравитацию. Он не полагается на планету. Вы не можете сказать мне: «Возьмите силу, создаваемую пружиной, и посмотрите, какую силу она прилагает, разделите на ускорение и получите массу», потому что мы также не определили силу. Вы должны это понять. Позволь спросить у тебя кое-что. Как мы определяем длину метра? Вы можете мне сказать, как узнать длину метра?
Вы не можете сказать мне: «Возьмите силу, создаваемую пружиной, и посмотрите, какую силу она прилагает, разделите на ускорение и получите массу», потому что мы также не определили силу. Вы должны это понять. Позволь спросить у тебя кое-что. Как мы определяем длину метра? Вы можете мне сказать, как узнать длину метра?
Студент : Это произвольно.
Профессор Рамамурти Шанкар: Справа.
Студент : Вы также можете просто выбрать произвольную массу, например, один объект, который имеет произвольную массу.
Профессор Рамамурти Шанкар: И мы назовем это. Первое, что вам нужно сделать, это осознать, что некоторые из этих вещей не даны Богом. Счетчик, например, ни из чего не выводится. Наполеон или кто-то другой сказал: «Размер моего эго – один метр». Это новая единица длины. Вы берете такой материал, как серебро, и кладете его в стеклянный ящик, и это определение метра.Это не правильно или неправильно. Затем я спрашиваю вас: «Что такое два метра, а что три метра?» У нас есть способы сделать это. Я беру счетчик и кладу рядом со счетчиком, то есть два метра. Я разрезаю его пополам, воспользуюсь транспортиром, делителями и циркулем, вы можете разделить метр на любую дробь, какую захотите. Точно так же для массы мы возьмем кусок материала и назовем его килограммом. Я должен тебе кое-что подсказать. Этот килограмм, я не думаю, что вы догадаетесь. Это вопрос условности.Точно так же, как одна секунда – это какое-то соглашение, которое мы используем, а один метр – это какое-то соглашение, которое мы используем. Я вам немного помогу. Я дам вам стеклянную витрину, а в стеклянной витрине – объект с килограммом, по определению. Затем я даю вам еще один предмет – слона. Вот слон. Я говорю вам: “Какая масса у слона?” Как вам эта масса? Вы должны понять намек, который он дал. Даю вам пружину и слона. Что нам делать? Да?
Затем я спрашиваю вас: «Что такое два метра, а что три метра?» У нас есть способы сделать это. Я беру счетчик и кладу рядом со счетчиком, то есть два метра. Я разрезаю его пополам, воспользуюсь транспортиром, делителями и циркулем, вы можете разделить метр на любую дробь, какую захотите. Точно так же для массы мы возьмем кусок материала и назовем его килограммом. Я должен тебе кое-что подсказать. Этот килограмм, я не думаю, что вы догадаетесь. Это вопрос условности.Точно так же, как одна секунда – это какое-то соглашение, которое мы используем, а один метр – это какое-то соглашение, которое мы используем. Я вам немного помогу. Я дам вам стеклянную витрину, а в стеклянной витрине – объект с килограммом, по определению. Затем я даю вам еще один предмет – слона. Вот слон. Я говорю вам: “Какая масса у слона?” Как вам эта масса? Вы должны понять намек, который он дал. Даю вам пружину и слона. Что нам делать? Да?
Студент : Измерьте расстояние, если вы подвесите слона на пружине [неразборчиво]
Профессор Рамамурти Шанкар: No. Помните, когда мы вешаем слона в космос, ничего не произойдет.
Помните, когда мы вешаем слона в космос, ничего не произойдет.
Студент : Хорошо. Вы толкаете слона и измеряете, как далеко – на каком расстоянии от нерастянутой пружины слон движется в любом направлении.
Профессор Рамамурти Шанкар: Хорошо.
Студент : Тогда вы тоже сделаете это с одним килограммом. Оно должно быть пропорционально тому, насколько далеко пружина находится в состоянии покоя. Это должно быть соотношение одного килограммового объекта к другому.
Профессор Рамамурти Шанкар: Когда вы говорите «толкни слона», вы хотите толкнуть его определенным образом? Что ты хочешь делать?
Студент : В сторону [неразборчиво], чтобы сжать пружину, или [неразборчиво]
Профессор Рамамурти Шанкар: Это верно, но вы не хотите придавать этому решительный толчок. Да?
Студент : Вы толкаете его радиально вдоль оси пружины, потому что вы знаете, что центростремительная сила равна mv 2 больше t.
Профессор Рамамурти Шанкар: Ага. Может это интересно. Это правильно. Вы тоже можете это сделать. Позвольте мне вывести вас из вашего ожидания. Думаю, я повсюду слышал обрывки ответа, поэтому я не хочу ждать, пока мы получим его безупречно. Дело в том, что один килограмм – это условность. Мы хотим знать, какова масса слона. Вы предложили, что мы можем провести эксперимент с качелями, но эксперимент с качелями требует гравитации, поэтому мы не хотим этого делать.С другой стороны, пружина будет создавать силу. Мы не знаем, какова сила пружины. Если вы так думаете, вы не играете по правилу, потому что мы не знаем, какую силу оно оказывает. Мы знаем, что это оказывает влияние, поэтому вот что вы делаете. Вы цепляете один конец пружины за стену, вытаскиваете ее из состояния покоя на некоторое расстояние и прикрепляете к ней груз весом в один килограмм. Да?
Студент : Однако у нас возникнет одна проблема: если мы будем в открытом космосе, где мы найдем стену, которая не сдвинется с места?
Профессор Рамамурти Шанкар: Стена, которая не сдвинется?
Студент : На самом деле, если вы прикрепите его к любой стене в открытом космосе [неразборчиво]
Профессор Рамамурти Шанкар: Вы правы. На самом деле может случиться так, что если вы находитесь в огромной лаборатории, состоящей из огромного объекта, вы обнаружите, что можете прикрепить его к стене. Вы можете отправиться в космос –
На самом деле может случиться так, что если вы находитесь в огромной лаборатории, состоящей из огромного объекта, вы обнаружите, что можете прикрепить его к стене. Вы можете отправиться в космос –
Студент : Не будет сильно двигаться?
Профессор Рамамурти Шанкар: Нет, он не будет сильно двигаться. Как только мы узнаем достаточно динамики, мы сможем ответить на ваш вопрос. Неужели космическое пространство лишает вас чего-нибудь, к чему вы можете привязать пружину? Ответ – нет.«Вы можете привязать вещи к объектам в космосе. Они просто не будут действовать так, как сила тяжести. Но можно прибить его к стене и выдернуть за один конец. Итак, вы тянете за один конец. Мы не знаем, какую силу это оказывает. Но это оказывает некоторую силу. Теперь я привязываю к нему этот килограммовый груз и отпускаю его. Я нахожу ускорение. Это сила, величины которой я не знаю. Но это ускорение массы в один килограмм. Затем я беру слона, натягиваю пружину на ту же величину и нахожу ускорение слона, а знаменатель, очевидно, равен массе слона. Сила неизвестна, но это та же сила. Итак, когда я разделю эти два числа, я найду , , 1, , , , , E , , равный м, , E , , м, , что соответствует массе в один килограмм. Нам был нужен какой-то механизм приложения некоторой фиксированной силы. Нам не нужно было знать его масштабы. Но ускорение, которое он производит на слона и на массу, обратно пропорционально их массам. Если бы вы знали, что это один килограмм, тогда ускорение слона, которое будет небольшим числом, может быть, 100 th того, что сделал этот парень; тогда масса слона составляет 100 килограммов.
Сила неизвестна, но это та же сила. Итак, когда я разделю эти два числа, я найду , , 1, , , , , E , , равный м, , E , , м, , что соответствует массе в один килограмм. Нам был нужен какой-то механизм приложения некоторой фиксированной силы. Нам не нужно было знать его масштабы. Но ускорение, которое он производит на слона и на массу, обратно пропорционально их массам. Если бы вы знали, что это один килограмм, тогда ускорение слона, которое будет небольшим числом, может быть, 100 th того, что сделал этот парень; тогда масса слона составляет 100 килограммов.
Заметьте, здесь тоже есть свои тонкости. Если вы думаете больше, вы можете беспокоиться о других вещах. Например, как я узнаю, что когда я тяну пружину в первый раз для груза, она оказывала ту же силу, когда я тянул пружину во второй раз для слона? Ведь пружины изнашиваются. Вот почему вы меняете амортизаторы в машине. Через некоторое время они перестают делать то же самое.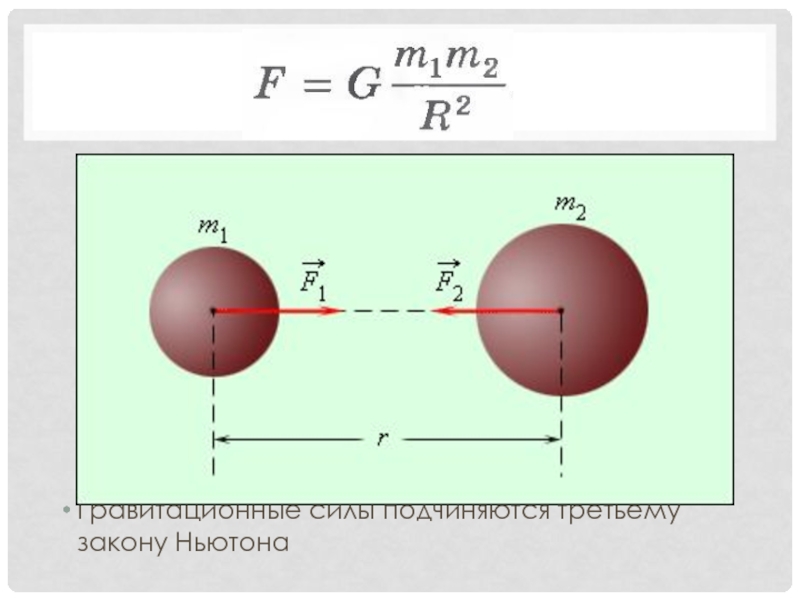 Во-первых, мы должны убедиться, что пружина каждый раз прилагает фиксированное усилие. Вы можете сказать: «Как мне это проверить? У меня еще нет определения силы.Но мы знаем следующее. Если я тяну один килограмм и отпускаю его, он что-то делает, ускоряется. Затем я снова тяну его на ту же величину и отпускаю; Я делаю это 10 раз. Если каждый раз я получаю одно и то же ускорение, я убеждаюсь, что это надежная пружина, которая каким-то образом создает одинаковую силу в одних и тех же условиях. В одиннадцатый раз тяну гирю. Я вставлю слона. С некоторой долей уверенности я работаю с надежной пружиной, и тогда я получу массу слона.
Во-первых, мы должны убедиться, что пружина каждый раз прилагает фиксированное усилие. Вы можете сказать: «Как мне это проверить? У меня еще нет определения силы.Но мы знаем следующее. Если я тяну один килограмм и отпускаю его, он что-то делает, ускоряется. Затем я снова тяну его на ту же величину и отпускаю; Я делаю это 10 раз. Если каждый раз я получаю одно и то же ускорение, я убеждаюсь, что это надежная пружина, которая каким-то образом создает одинаковую силу в одних и тех же условиях. В одиннадцатый раз тяну гирю. Я вставлю слона. С некоторой долей уверенности я работаю с надежной пружиной, и тогда я получу массу слона.
Почему это так важно? Вам, ребята, важно знать, что все, что вы записываете в блокноте или на доске в виде символов, на самом деле является измеряемой величиной. Вы всегда должны знать, как вы что-то измеряете. Если вы не умеете ничего измерять, вы занимаетесь алгеброй и тригонометрией. Вы не занимаетесь физикой. Это также говорит вам, что масса объекта не имеет ничего общего с гравитацией. Масса объекта – это то, насколько он ненавидит ускоряться в ответ на силу.Ньютон говорит вам, что силы вызывают ускорение. Но на разных объектах ускорение неодинаково. Некоторые объекты сопротивляются этому больше, чем другие. Говорят, что у них большая масса. Мы можем точно сказать, насколько больше, если скажем: «Если ускорение тела до заданной силы в десять раз превышает ускорение массы в один килограмм, то эта масса составляет одну десятую одного килограмма». Вот как можно табулировать массы с помощью пружины.
Масса объекта – это то, насколько он ненавидит ускоряться в ответ на силу.Ньютон говорит вам, что силы вызывают ускорение. Но на разных объектах ускорение неодинаково. Некоторые объекты сопротивляются этому больше, чем другие. Говорят, что у них большая масса. Мы можем точно сказать, насколько больше, если скажем: «Если ускорение тела до заданной силы в десять раз превышает ускорение массы в один килограмм, то эта масса составляет одну десятую одного килограмма». Вот как можно табулировать массы с помощью пружины.
Глава 4. Природа сил и их связь со вторым законом [00:37:13]
Представьте себе, что теперь мы можем найти массу любого объекта, верно? Теперь мы знаем, с той же самой пружиной, с помощью этого сравнения мы найдем.Всем объектам теперь можно приписать массу. Затем, исходя из этого уравнения, мы можем сказать, что в данной ситуации действует определенная сила, умножив m на a . Тогда вот что мы на самом деле делаем. Теперь вернемся к весне. Мы возвращаемся к весне и хотим узнать кое-что о весне. Мы хотим знать, какую силу он проявляет, когда я тяну его на определенную величину. Теперь я могу это измерить, потому что я тяну его на один сантиметр и нахожу ускорение, которое он оказывает на известную массу.То, что м, умножить на , – это сила, которую оказывает пружина. Потом тяну на 1,1 см, и нахожу ma . Нахожу 1.2, нахожу ma . Я рисую здесь график зависимости силы натяжения пружины от усилия, которое она прилагает. Обычно это будет выглядеть так, а формула, которую мы говорим: F = -kx , где k называется «силовой постоянной».
Мы возвращаемся к весне и хотим узнать кое-что о весне. Мы хотим знать, какую силу он проявляет, когда я тяну его на определенную величину. Теперь я могу это измерить, потому что я тяну его на один сантиметр и нахожу ускорение, которое он оказывает на известную массу.То, что м, умножить на , – это сила, которую оказывает пружина. Потом тяну на 1,1 см, и нахожу ma . Нахожу 1.2, нахожу ma . Я рисую здесь график зависимости силы натяжения пружины от усилия, которое она прилагает. Обычно это будет выглядеть так, а формула, которую мы говорим: F = -kx , где k называется «силовой постоянной».
Вы должны понимать, что здесь делает знак минус. Это сила, прилагаемая пружиной к массе.В нем говорится, что если вы потянете его вправо, так что x будет положительным, пружина будет оказывать силу в отрицательном направлении; вот почему у вас стоит знак минус. Тогда все пружины будут делать что-то подобное. Далее они могут делать разные вещи. Сила может сужаться, сила не может быть задана прямой линией, но для умеренных деформаций каждая пружина будет иметь линейный режим, в котором сила линейно пропорциональна растяжению. Это также говорит вам, что если вы сжимаете пружину, это означает, что x теперь составляет x отсчитывается от этого положения, в котором пружина не сжимается и не расширяется.Итак, x на самом деле не координата конечной точки. Вы должны это понять. Пружины имеют естественную длину; x отсчитывается от этой длины. Если он положительный, значит, вы растянули его, если отрицательный, значит сжатый. Это уравнение говорит вам, если вы сжимаете его, а именно, если x отрицательно, F будет положительным, потому что оно выталкивает вас наружу. Поэтому сейчас мы можем использовать все виды пружин и откалибровать силу, которую они будут оказывать в различных условиях.А именно, если вы потянете его так сильно, это будет сила, которую он проявит.
Сила может сужаться, сила не может быть задана прямой линией, но для умеренных деформаций каждая пружина будет иметь линейный режим, в котором сила линейно пропорциональна растяжению. Это также говорит вам, что если вы сжимаете пружину, это означает, что x теперь составляет x отсчитывается от этого положения, в котором пружина не сжимается и не расширяется.Итак, x на самом деле не координата конечной точки. Вы должны это понять. Пружины имеют естественную длину; x отсчитывается от этой длины. Если он положительный, значит, вы растянули его, если отрицательный, значит сжатый. Это уравнение говорит вам, если вы сжимаете его, а именно, если x отрицательно, F будет положительным, потому что оно выталкивает вас наружу. Поэтому сейчас мы можем использовать все виды пружин и откалибровать силу, которую они будут оказывать в различных условиях.А именно, если вы потянете его так сильно, это будет сила, которую он проявит.
Я хочу, чтобы вы на секунду задумались о двух уравнениях. Одно уравнение говорит, что F = ma . Другое уравнение говорит: F = -kx . В чем дело? Один из них закон Ньютона? Тогда что еще? Может быть, F = -kx следует назвать законом Ньютона? Почему F = ma называется законом Ньютона? Тогда что означает это выражение? В чем разница между словами F = -kx и F = ma ? Они говорят очень разные вещи.Да?
Одно уравнение говорит, что F = ma . Другое уравнение говорит: F = -kx . В чем дело? Один из них закон Ньютона? Тогда что еще? Может быть, F = -kx следует назвать законом Ньютона? Почему F = ma называется законом Ньютона? Тогда что означает это выражение? В чем разница между словами F = -kx и F = ma ? Они говорят очень разные вещи.Да?
Студент : F = ma – универсальный закон.
Профессор Рамамурти Шанкар: Справа. Позвольте мне повторить. F = ma истинно универсально, независимо от природы силы, действующей на тело. Потом?
Студент : F = -kx описывает только пружину.
Профессор Рамамурти Шанкар: Очень хорошо. В этом весь смысл. Цикл ньютоновской динамики состоит из двух частей.Первый гласит: если вы знали силу, действующую на любое тело, не вдаваясь в причину этой силы, то вы можете установить эту силу равной массе, умноженной на ускорение тела. Мы думаем о силе как о причине, а о , о – как о результате или следствии. Сила вызывает ускорение, и это точное утверждение. Здесь Ньютон не говорит вам, какие силы будут действовать на тело в данной ситуации. Если вы оставите тело в покое, возможно, на него не действует никакая сила. Если вы соедините тело с пружиной, которая не сжимается и не растягивается, на нее не действует сила.Если вы потянете за пружину, на нее будет действовать сила. Ньютон не собирается подойти и сказать вам, какую силу приложит пружина, если ее потянуть на определенную величину. Это еще одна часть вашего задания. Физику необходимо постоянно выяснять, какие силы действуют на тела. Это отдельное упражнение.
Мы думаем о силе как о причине, а о , о – как о результате или следствии. Сила вызывает ускорение, и это точное утверждение. Здесь Ньютон не говорит вам, какие силы будут действовать на тело в данной ситуации. Если вы оставите тело в покое, возможно, на него не действует никакая сила. Если вы соедините тело с пружиной, которая не сжимается и не растягивается, на нее не действует сила.Если вы потянете за пружину, на нее будет действовать сила. Ньютон не собирается подойти и сказать вам, какую силу приложит пружина, если ее потянуть на определенную величину. Это еще одна часть вашего задания. Физику необходимо постоянно выяснять, какие силы действуют на тела. Это отдельное упражнение.
В каждом контексте, в котором я помещаю тело, я должен знать, какие силы действуют на него. Мне нужно найти их, экспериментируя, помещая другие тела и наблюдая, как они реагируют, а затем выясняю, какая сила действует на тело, когда оно находится в той или иной ситуации.Как только вы его получите, вы вернетесь.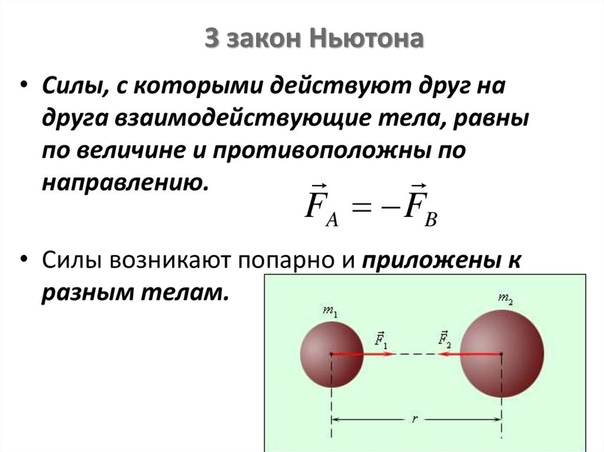 В случае пружины это закон, который вы должны вывести. Если это что-то еще, вам придется вывести другой закон. Например, мы знаем, что если тело находится около поверхности Земли, сила тяжести и этот объект кажутся равными м умножить на г , где г равно 9,8. Это вы узнаете экспериментально. Каждый раз вы обнаруживаете новую силу, действующую на тело разного происхождения. Говорят, оставьте любое тело около Земли, это дает силу.Я знаю, что это правильный ответ, потому что, если я сейчас найду ускорение, я нахожу, что это мг , разделенное на м , и я получу -g в качестве ответа для всех тел.
В случае пружины это закон, который вы должны вывести. Если это что-то еще, вам придется вывести другой закон. Например, мы знаем, что если тело находится около поверхности Земли, сила тяжести и этот объект кажутся равными м умножить на г , где г равно 9,8. Это вы узнаете экспериментально. Каждый раз вы обнаруживаете новую силу, действующую на тело разного происхождения. Говорят, оставьте любое тело около Земли, это дает силу.Я знаю, что это правильный ответ, потому что, если я сейчас найду ускорение, я нахожу, что это мг , разделенное на м , и я получу -g в качестве ответа для всех тел.
Между прочим, это очень примечательное свойство гравитационной силы – сокращение двух м с. Если вы посмотрите на электрическую силу, силу электричества, действующую на протон и электрон или что-то еще, она не пропорциональна массе любого объекта. Он пропорционален электрическому заряду любого объекта.Следовательно, когда вы делите на массу, чтобы получить ускорение, реакция различных тел обратна массе. Но у гравитации есть замечательное свойство: притяжение Земли само пропорционально инерции объекта. Итак, когда вы делите на м , м отменяется, и все падает с одинаковой скоростью на поверхность Земли. Фактически, свойство гравитационных полей есть где угодно, даже в космическом пространстве, но есть некоторое остаточное поле между всеми планетами и всеми звездами во Вселенной, что сила, действующая на тело, пропорциональна массе тела.Итак, когда вы разделите на массу, чтобы получить ускорение, вы получите тот же ответ. Все – золото, серебро, алмазы, частицы – все одинаково ускоряется в гравитационном поле из-за этого замечательного факта.
Но у гравитации есть замечательное свойство: притяжение Земли само пропорционально инерции объекта. Итак, когда вы делите на м , м отменяется, и все падает с одинаковой скоростью на поверхность Земли. Фактически, свойство гравитационных полей есть где угодно, даже в космическом пространстве, но есть некоторое остаточное поле между всеми планетами и всеми звездами во Вселенной, что сила, действующая на тело, пропорциональна массе тела.Итак, когда вы разделите на массу, чтобы получить ускорение, вы получите тот же ответ. Все – золото, серебро, алмазы, частицы – все одинаково ускоряется в гравитационном поле из-за этого замечательного факта.
Это было известно давно, но мистеру Эйнштейну понадобилось выяснить, почему природа ведет себя таким образом. Если будет время, расскажу позже. Но есть два одинаковых качества. Один из них – инерционная масса, то есть насколько вы ненавидите изменение скорости, насколько сильно вы сопротивляетесь ускорению.Это существует далеко от планет, далеко не все. Другой – гравитационная масса, которая является мерой того, насколько вас притягивает Земля. Нет причин, по которым эти два атрибута должны быть пропорциональными, но они пропорциональны и равны по выбору единиц, и вы можете спросить: «Это просто случайность или это часть большой картины?» Оказывается, это часть большой картины, и вся общая теория относительности основана на этой великой эквивалентности двух величин, которые являются очень разными атрибутами.Почему степень вашего притяжения к Земле должна быть также мерой того, насколько вы ненавидите ускорение? Две разные функции, верно? Но они совпадают.
Другой – гравитационная масса, которая является мерой того, насколько вас притягивает Земля. Нет причин, по которым эти два атрибута должны быть пропорциональными, но они пропорциональны и равны по выбору единиц, и вы можете спросить: «Это просто случайность или это часть большой картины?» Оказывается, это часть большой картины, и вся общая теория относительности основана на этой великой эквивалентности двух величин, которые являются очень разными атрибутами.Почему степень вашего притяжения к Земле должна быть также мерой того, насколько вы ненавидите ускорение? Две разные функции, верно? Но они совпадают.
Как бы то ни было, физики помещают тела в различные условия и выводят различные силы. Это сила тяжести. Это сила пружины. Вот еще одна сила, которую вы можете найти. Вы кладете кусок дерева на стол и пытаетесь перемещать его с постоянной скоростью. Тогда вы обнаружите, что вам нужно приложить минимальное усилие.Мы движемся с постоянной скоростью. Это означает, что сила, которую вы прикладываете, отменяется другой силой, которая должна быть силой трения. Итак, сила трения – это еще одна сила. Затем есть другие силы. Вы, ребята, знаете, что существует электрическая сила. Если вы поднесете положительный заряд к положительному заряду, если мое тело m имеет положительный заряд, а другой положительный заряд есть, он почувствует силу из-за этого. Ньютон этого не даст. Итак, Ньютон никогда не говорил вам, каково выражение силы в данном контексте.Это постоянное исследование. Кулон открыл закон Кулона – отталкивания зарядов. В настоящее время мы знаем, переходя к нейтрону или протону, есть кварки. Между кварками существуют силы. Вы можете спросить, какую силу будет проявлять этот кварк и этот кварк при определенном разделении. Очевидно, Ньютон не знал об этом.
Итак, сила трения – это еще одна сила. Затем есть другие силы. Вы, ребята, знаете, что существует электрическая сила. Если вы поднесете положительный заряд к положительному заряду, если мое тело m имеет положительный заряд, а другой положительный заряд есть, он почувствует силу из-за этого. Ньютон этого не даст. Итак, Ньютон никогда не говорил вам, каково выражение силы в данном контексте.Это постоянное исследование. Кулон открыл закон Кулона – отталкивания зарядов. В настоящее время мы знаем, переходя к нейтрону или протону, есть кварки. Между кварками существуют силы. Вы можете спросить, какую силу будет проявлять этот кварк и этот кварк при определенном разделении. Очевидно, Ньютон не знал об этом.
Помните, Ньютон сказал, что F = ma , но не сказал вам, какое значение имеет значение F в данном контексте. Он просто сказал, что всякий раз, когда есть ускорение, оно будет происходить из-за каких-то сил, и ваша работа – найти эти силы.Чтобы найти силу, вы должны предположить, что кто-то говорит: «Эй, у меня появилась новая сила. Каждый раз, когда я подхожу к трибуне, меня это тянет ». Хорошо, это новая сила. Слухи ходят, и мы хотим измерить силу. Что мне делать? Я стою возле этой трибуны. Меня это тянет. Я не могу остановиться. Я привязываю пружину к своей спине, прикрепляю ее к стене и смотрю, насколько пружина растягивается, прежде чем две силы уравновесятся. Тогда я знаю, что kx равно силе, возникающей при этом разделении.Я подхожу немного ближе и обнаруживаю, что растяжение – другое число. Может, сила становится сильнее. Вот так, уравновешивая неизвестную силу известной силой или просто измеряя ускорение, когда я падаю к этому подиуму, и умножая его на массу, вы можете найти силу, которая действует на меня. Это не цикличное и бесполезное определение. Это очень интересное взаимодействие, и это основа всей механики. Мы постоянно ищем значения F и постоянно ищем реакции или тела на известную силу.
Каждый раз, когда я подхожу к трибуне, меня это тянет ». Хорошо, это новая сила. Слухи ходят, и мы хотим измерить силу. Что мне делать? Я стою возле этой трибуны. Меня это тянет. Я не могу остановиться. Я привязываю пружину к своей спине, прикрепляю ее к стене и смотрю, насколько пружина растягивается, прежде чем две силы уравновесятся. Тогда я знаю, что kx равно силе, возникающей при этом разделении.Я подхожу немного ближе и обнаруживаю, что растяжение – другое число. Может, сила становится сильнее. Вот так, уравновешивая неизвестную силу известной силой или просто измеряя ускорение, когда я падаю к этому подиуму, и умножая его на массу, вы можете найти силу, которая действует на меня. Это не цикличное и бесполезное определение. Это очень интересное взаимодействие, и это основа всей механики. Мы постоянно ищем значения F и постоянно ищем реакции или тела на известную силу.
Вот простой пример полной ньютоновской проблемы. К пружине прикрепляется масса. Его тянут на некую величину х , и отпускают. Что он будет делать? Идем к Ньютону. Ньютон говорит, что F = ma , поэтому, чтобы сделать это полезным результатом этой задачи, мы знаем массу этого парня. Мы сравнивали со слоном или чем-то в этом роде; a – вторая производная от x , и для этой проблемы, когда F возникает из-за пружины, мы знаем, что это сила, изучая пружину.Внезапно перед вами возникает математически полная задача. Математически полная проблема состоит в том, что вы можете найти функцию x (t) , сказав, что вторая производная функции равна -k на m, в раз больше функции. Затем вы идете на математический факультет и говорите: «Пожалуйста, скажите мне, каков ответ на это уравнение?» Нам не нужно беспокоиться о том, как вы ее решите, но это проблема математики, и ответ будет – сюрприз, он будет колебаться взад и вперед, и это выйдет из стирки.Вот как вы формулируете проблемы.
Что он будет делать? Идем к Ньютону. Ньютон говорит, что F = ma , поэтому, чтобы сделать это полезным результатом этой задачи, мы знаем массу этого парня. Мы сравнивали со слоном или чем-то в этом роде; a – вторая производная от x , и для этой проблемы, когда F возникает из-за пружины, мы знаем, что это сила, изучая пружину.Внезапно перед вами возникает математически полная задача. Математически полная проблема состоит в том, что вы можете найти функцию x (t) , сказав, что вторая производная функции равна -k на m, в раз больше функции. Затем вы идете на математический факультет и говорите: «Пожалуйста, скажите мне, каков ответ на это уравнение?» Нам не нужно беспокоиться о том, как вы ее решите, но это проблема математики, и ответ будет – сюрприз, он будет колебаться взад и вперед, и это выйдет из стирки.Вот как вы формулируете проблемы.
Можно сформулировать еще одну задачу. Позже мы узнаем о гравитации. Ньютон обнаруживает, что на все действует сила тяжести. Вот солнце. Вот твоя планета. В этот момент планета может двигаться с такой скоростью. Тогда ускорение планеты – это сила тяжести между планетой и Солнцем, которая, как вам скажет Ньютон, направлена к Солнцу и зависит от того, как далеко вы находитесь. В зависимости от того, как далеко планета находится от Солнца и где она расположена, вы получите левую часть.Это еще один закон. Это Закон всемирного тяготения. Опять же, вы обнаружите эволюцию движения планеты, потому что скорость изменения положения связана с положением. Опять же, подойдите к математикам и спросите: “Что на это ответить?” и они говорят вам ответ, который будет некоторым эллиптическим движением. Хорошо.
Между прочим, у мистера Ньютона не было математиков, к которым он мог бы пойти. Он не только сформулировал законы гравитации, он также изобрел исчисление, и он также научился решать дифференциальные уравнения для исчисления.Он, вероятно, чувствовал, что вокруг никто не работает, потому что все это было отдано одному человеку. Поистине удивительно, что то, что сделал Ньютон в случае гравитации, – это найти для этого выражение. Несколькими годами ранее он тоже получил этот закон. Если сложить их вместе, мы получим эллиптическое движение планет. Мы еще вернемся к этому, но вы должны понять структуру ньютоновской механики. Как правило, любая механика требует знания силы.
Теперь я собираюсь добавить еще одну поправку.Вам не нужно писать в блокноте, но вы должны помнить. Может быть, вы просто наберете T и обведете его. Позвольте мне написать это здесь. F T означает общую силу, действующую на тело. На тело действует множество сил. Ускорение контролируется суммой. Если я сейчас работаю в одном измерении, это очевидно, потому что я не использую никаких векторов. Тогда у вас могут быть силы вправо, силы влево, толкающие, тянущие. Вы складываете их все алгебраически, отслеживая их знак, и это общая сила.Это связано с ускорением, умноженным на массу.
Глава 5. Третий закон Ньютона [00:50:50]
Теперь я дам вам третий закон. Третий закон гласит, что если есть два тела, называемые одним и двумя, сила одного на два минус сила второго на первом. В этом суть действия и противодействия. Все законы, которые кто-либо знает, обладают этим свойством. Что нужно, чтобы быть успешным механиком, чтобы решать все механические задачи? Вы должны уметь записывать силы, действующие на тело.Вот к чему все это сводится. Вот мой вам совет. Не забывайте о существующих силах и не составляйте свои собственные. Я видел и то, и другое. Прямо сейчас, на этом этапе нашего курса, всякий раз, когда у вас есть проблема, когда есть какое-то тело и кто-то говорит: «Приложите к нему все силы», то, что вам нужно сделать, очень просто.
Любую силу, за одним исключением, можно рассматривать как силу, возникающую при прямом контакте с телом. Либо веревка тянет, веревка ее толкает, вы ее толкаете, вы ее тянете.Это контакт с телом. Если ничто не касается тела, на него нет сил, за одним исключением, конечно, гравитацией. Гравитация – это сила, которая действует на тело, но источник силы не касается его. Вот и все. Не тяните больше сил. Люди привлекают другие силы. Когда тело движется по кругу, говорят, что действует некая центробежная сила. Нет такого. Будь осторожен. Всякий раз, когда есть сила, ее можно проследить до материальной материальной причины, которая всегда является силой контакта, за исключением силы тяжести.Ладно, с этим, если вы напишете правильные силы, у вас все будет хорошо. Вы сможете решить все проблемы, которые есть у нас в механике.
Теперь я приступлю к простым задачам по механике. Они начнутся с простых и, как обычно, будут становиться все сложнее. Начнем с нашего первого триумфа – движения в 1D. Вот какой-то объект, это 5 килограммов, я приложил 10 ньютонов. Кто-то говорит: “Какое ускорение?” Все знают, что 10 на 5 равно 2. Теперь мы знаем, как мы получили все числа, которые входят в сам вопрос.Как мы узнаем, что действует 10 ньютонов? Я думаю, вы знаете, как мы можем сказать это с уверенностью. Как мы узнаем, что это 5 килограммов? Мы знаем, как вы получили это из более раннего эксперимента. Теперь мы знаем, как появляются числа. Алгебра, конечно, здесь очень тривиальна.
Тогда следующая задача немного интереснее. Здесь у меня 3 кг, у меня 2 кг, я толкаю с 10 ньютонами и хочу знать, что происходит. Один из способов – просто руководствоваться здравым смыслом и понимать, что если вы будете настаивать на этом, эти два парня будут двигаться вместе.И интуитивно знайте, что если они будут двигаться вместе, они будут вести себя как объект с массой 5, и ускорение снова будет 2. Но есть другой способ сделать это, и я собираюсь привести вам простейший пример другого пути. который должен рисовать диаграммы свободного тела. Между прочим, когда я говорю, что 10 Ньютонов действуют таким образом, вы можете сказать: «А как насчет гравитации? А что насчет стола? ” Представьте, что это в открытом космосе, где пока нет гравитации. Движение происходит только по оси x .
На диаграмме свободного тела говорится, что вы можете выбрать любое тело, которое вам нравится, и применить к нему F = ma , при условии, что вы определите все силы, действующие на это тело. Сначала мы выберем тело с массой 3. Вот тело с массой 3. Какие силы действуют на него? Это, безусловно, действует на него. Затем вы должны спросить: «Какая еще сила действует?» Вот где нужно думать. Кто-нибудь хочет угадать из последнего ряда, какая сила? Да?
Студент : Реактивная сила 2 на 3?
Профессор Рамамурти Шанкар: Справа.Так что давайте дадим ему имя. Давайте укажем это на это и назовем F2 на 3. Это конец этого парня. Посмотрим на другого парня. Может, тебе стоит дополнить силу, действующую на этого. Вы можете мне сказать, что это? Тот же человек в последнем ряду.
Студент : [неразборчиво]
Профессор Рамамурти Шанкар: И насколько это велико?
Студент : То же, что и F2 , 3.
Профессор Рамамурти Шанкар: Справа.Я не хочу давать ему слишком много разных имен, потому что F2 , 3 и F3 , 2 равны и противоположны. Я уже показываю F2 , 3 действует слева. Позвольте мне дать ему другое имя, например f . Согласитесь, это будет тот же f , но в ту сторону. Вот ошибка, которую делают некоторые люди. Они добавляют к этому 10 ньютонов. На него действуют 10 Ньютонов, потому что я знаю, что 10 Ньютонов толкают меня, и я буду чувствовать это, даже если буду здесь.Это будет ошибкой. Это пример добавления силы, которую вам действительно не следует добавлять. Единственная сила, действующая на этого парня, – это маленький f . Это, в свою очередь, потому, что этого парня подталкивают 10 ньютонов, но это не ваша проблема. Ваша проблема в том, чтобы смотреть только на силы соприкосновения с вами, и это как раз этот f . Затем мы делаем F = ma для этих двух парней. Для этого парня F = ma будет 10 минус f будет в 3 раза больше a .Другой – f = 2 a .
Обратите внимание, что я использую одинаковое ускорение для обоих. Я знаю, что если вторая масса двигалась быстрее первой, то картина совершенно неверная. Если он двигался медленнее, чем первый, значит, он врезался в этот. Этого тоже не может быть, поэтому они движутся с одинаковым ускорением. Есть только один неизвестный a . Как только вы это получите, вы поймете, что вам нужно делать. Это уравнение просит вас добавить его к этому уравнению.У вас есть плюс f и минус f , так что вы должны делать то, что должны. Вы добавляете два, вы получаете 10 = 5, a , и вы получаете a = 2. Как только вы получили a = 2, вы можете вернуться и понять здесь, что f = 4, так что у вас действительно 4 Ньютоны. Теперь мы знаем всю историю. 4 Ньютона, действующие на 2 кг, дают вам ускорение 2. На этом парне у меня 10 слева, и у меня 4–10 действуют таким образом, 4 действуют таким образом. То есть 6 Ньютонов, разделенных на 3 кг, также ускорение 2.Это более простой пример. Простой пример схем свободного тела. Очень простой. Если вы можете это сделать, вы сможете решить большинство проблем, с которыми столкнетесь. Только не добавляйте то, чего там нет. Это все, о чем вам нужно быть осторожным. Иногда люди склонны добавлять то, что они продолжают рисовать 10 ньютонов, которые воздействуют на это.
А теперь еще один вариант. Вариант выглядит так. У меня 3 кг, и у меня есть веревка. У меня 2 кг, и я тяну этого парня с 10 ньютонами. Что произойдет? Опять же, здравый смысл подсказывает вам: «Послушайте, вы тянете что-то, эффективная масса которого равна 5, ответ – 2.Давайте рассмотрим это систематически, используя диаграммы свободного тела. Итак, здесь действительно три тела. Заблокируйте один, второй и веревку, соединяющую их. Во всех этих примерах предполагается, что эта веревка не имеет массы. Мы знаем, что нет ничего, что называется безмассовой веревкой, но большинство веревок имеют массу, но, возможно, незначительную по сравнению с двумя тянутыми вами блоками, поэтому мы возьмем идеализированный предел, при котором масса веревки равна 0. Вот иметь дело. 3 кг тянут веревку справа с силой, которую я назову T , что означает натяжение.Этот парень, T , тянет веревку назад. Какая сила на другой стороне? Что это должно быть? Кто сказал T ? Почему именно T , а не что-то другое? Что было бы, если бы это было что-то еще?
Студент : Если бы он был больше, то веревка порвалась бы. Хорошо, если бы оно было больше [неразборчиво]
Профессор Рамамурти Шанкар: Это не сломается, но кое-что еще будет проблемой. Да?
Студент : [неразборчиво]
Профессор Рамамурти Шанкар: Не только быстрее, но и каково будет его ускорение? Если две силы не отменяются, у вас есть чистая сила.На что вы собираетесь разделить, чтобы получить ускорение?
Студент : [неразборчиво]
Профессор Рамамурти Шанкар: Ноль, верно? Таким образом, на безмассовое тело не может быть действующей силы, потому что ускорение веревки не может быть бесконечным. Фактически, это должно быть какое-то конечное число, которое является ускорением любого из этих двух парней. Итак, безмассовые тела, как безмассовая веревка, всегда будут иметь равные и противоположные силы на обоих концах. Это называется натяжением веревки.Когда вы говорите, что веревка находится под натяжением, которую тянут с обеих сторон определенной силой, натяжение не равно 0 только потому, что это T и T отменяются. Это правда, что чистая сила равна 0, но это не значит, что вы можете ее игнорировать. Предположим, вас тянут мои любимые животные – слоны – с обеих сторон с одинаковой силой. Вы не находите утешения в том, что эти силы в сумме равны нулю. Вы чувствуете боль. Эта боль – вот что… Этот джентльмен не согласен. Один из вас кивает головой.Вы чувствуете боль? Ты согласен? Хорошо. Эта сила называется напряжением. Каждый раз, когда вас спрашивают: «Какое натяжение веревки?» вы ищете равные и противоположные силы, действующие на двух концах веревки. Мы не знаем, что это такое. Мы дадим ему имя, но, связав этот T с этим T , мы также сможем выяснить, что тот же самый T должен быть применен к этому по третьему закону Ньютона, потому что, если этот блок является единственным который мог бы тянуть этот трос с T .Следовательно, веревки будут тянуть блок с T в другую сторону, тогда у меня здесь 10 Ньютонов.
Теперь вы можете выполнить F = ma для трех разных объектов. Здесь делать нечего, потому что силы равны 0, а масса равна 0. Это вам ни о чем не говорит. Первый говорит вам T = 3 a . Другой говорит вам 10 – T = 2 a . Опять же, мы знаем, что делать. Складываем эти числа и получаем 10 = 5 a .Следовательно, мы находим a = 2. Как только вы найдете a = 2, вы найдете T = 6. Итак, натяжение веревки составляет 6 ньютонов. Это очень важно, потому что, когда вы покупаете веревку, вам скажут, какое натяжение она может выдержать, прежде чем она сломается. Если ваш план состоит в том, чтобы разогнать 3-килограммовую массу с ускорением 2 метра в секунду, вам лучше иметь веревку, которая может обеспечить эту силу, и она может выдержать натяжение в 6 ньютонов.
Глава 6. Невесомость [01:03:15]
А теперь – эй! Я собираюсь дать последнему классу довольно интересную задачу, которая происходит с вами, когда у вас есть лифт.Вот весы, а вы стоите на лифте. Мы собираемся спросить: «Что показывает стрелка в разное время?» Во-первых, возьмем корпус в лифте, который находится на первом этаже какого-то здания и полностью адресован. Затем давайте посмотрим на весну. Пружина сжимается, потому что вы давите вниз, а пол поднимается вверх. Вы толкаете вниз с помощью веса mg , а пол должен толкаться вверх с помощью md , потому что пружина никуда не движется.Итак, пружина подталкивается мг здесь и мг здесь. Следовательно, он сжимается на неизвестное значение x , равное мг , деленному на постоянную силы пружины.
Между прочим, люди, возможно, не осознали этого. Даже в случае с этой пружиной, когда тянешь, если тянешь вправо с какой-то силой. Помните, стена тянется влево с той же силой. Таким образом, пружины всегда толкаются или растягиваются с одной и той же стороны с одной и той же стороны.Мы сосредотачиваемся на одном, потому что платим за него, но стена делает наоборот. Мы не обращаем на это внимания. Вы не можете тянуть пружину только с одной стороны, потому что тогда она будет ускоряться с бесконечным ускорением в этом направлении. Эта пружина сжимается с обеих сторон, и она раздавится на определенную величину x , которая зависит от вашей массы, и это x будет превращено в движение иглы, которое будет считывать вашу массу.
Теперь, что произойдет, если лифт ускоряется вверх с ускорением a ? Это вопрос.Я говорю о том, как я это анализирую: если я смотрю на себя и записываю силы, действующие на меня, то есть mg , действующие вниз, тогда мы используем w как символ, представляющий силу, прилагаемую пружиной; w – мг = мА . То есть F = ma . Когда я не ускорялся и все было в состоянии покоя, мА было 0, Вт было мг и Вт было показанием на стрелке. Но если я ускоряюсь, сила пружины и, следовательно, стрелки, показываемой устройством для взвешивания, равна м умножить на г плюс a .Это означает, что когда вы ускоряетесь вверх, когда лифт набирает скорость, показания пружины будут больше, и вы почувствуете тяжесть. Вы чувствуете себя тяжелыми, и это больше, потому что плохая пружина не только должна поддерживать вас от падения через пол, но и ускорять вас вопреки тому, что хочет сделать сила тяжести. Вот почему это г плюс a . Итак, вы набрали некоторую скорость, а затем едете по инерции с постоянной скоростью. Затем выпадает a , и вы взвешиваетесь как обычно.Когда вы подойдете к вершине здания, лифт должен замедлиться, чтобы он потерял положительную скорость и остановился. Таким образом, a будет отрицательным, а w фактически будет меньше mg . Таким образом, вы почувствуете себя невесомым на короткое время или почувствуете, что ваш вес невелик. Затем вы отдыхаете, и по пути вниз происходит обратное.
Позвольте мне вкратце взглянуть на поездку по дороге вниз. Когда вы начинаете с вершины и спускаетесь, ваше ускорение отрицательное.Помните, что вы должны отслеживать знак ускорения, поэтому, если вы набираете скорость по направлению к земле, a отрицательны, поэтому это будет g плюс a , но a будет отрицательным. отрицательное число. Позвольте мне записать это как g минус абсолютное значение a . Вы можете видеть, что если a было равно g , ваше нисходящее ускорение является ускорением силы тяжести, а именно, трос оборвался в лифте, тогда вы не чувствуете никакого веса.Вы не чувствуете никакого веса, потому что ваш вес – это сопротивление, которое вы получаете при падении через пол; но если пол прогибается, и вы просто свободно падаете, вы чувствуете себя невесомым. Ошибочно думать, что вы чувствуете себя невесомым из-за того, что вы избежали притяжения силы тяжести. Все мы знаем, что в падающем лифте вы точно не избежите притяжения силы тяжести. Он догонит вас через несколько секунд. Точно так же, когда вы находитесь в космическом пространстве, когда вы вращаетесь вокруг Земли, люди всегда плавают на этих космических станциях.Они также не избежали притяжения силы тяжести. Они просто перестали с этим бороться. Если вы избежите притяжения гравитации, ваш космический корабль отключится, не будет вращаться вокруг Земли. В любом случае, я вернусь к этому в следующий раз. Решай свои проблемы. Есть довольно много проблем. Вы должны запустить их прямо сейчас.
[конец стенограммы]
НаверхSTEM Challenge Bottle Car с 3-м законом Ньютона от учителей потрясающе
Пришло время испытать STEM-вызов с законами движения Ньютона! Студентам понравится этот автомобильный «гоночный» вызов, и обучение вас поразит! Вашим ученикам понравится смотреть, как автомобили-воздушные шары мчатся друг с другом или просто крутятся по кругу!
Эта задача доступна в наборах для экономии денег!
В чем проблема? В этом задании учащиеся будут использовать материалы для проектирования и сборки автомобиля на воздушном шаре.Автомобиль должен катиться по прямой и проехать как можно большее расстояние, прежде чем воздушный шар иссякнет. Это задание продемонстрирует третий закон движения, а также позволит учащимся вместе разработать колеса, оси и продувочный механизм своих автомобилей. Хитрое крепление осей и колес заставит их испытать терпение и создать возможности для улучшения своих транспортных средств. Могут ли автомобили мчаться по прямой трассе? Колеса будут катиться правильно? Будет ли воздушный шар двигаться с достаточной силой, чтобы вызвать движение вперед?
Какая у вас подготовка?
Вам понадобятся припасы в дополнение к этому ресурсу.Сюда входят: пустые бутылки для воды, воздушные шары диаметром 8–9 дюймов, соломинки 2 размера, дюбели или деревянные шпажки, малярная лента, средства для чистки труб, резинки, круглые предметы для колес, кусочки картона и дорожки для гонок. (Дорожка не обязательна.)
В пакет специально входят:
- Обложка
- История учителя
- Страница материалов и подготовки
- 6 страниц инструкций учителя
- Список ограничений
- Специальная страница информации о законах Ньютона of Motion
- 4 страницы с фотографиями
- Студенческий лабораторный лист
- Подсчет очков
- Условия использования.
- Все формы доступны для редактирования !
- Листы с ответами учащихся не включены, но образцы работ учащихся включены в страницы с указаниями учителя.
- Количество страниц, указанное для этого пакета, включает все.
Для выполнения этого задания потребуется 2 занятия.
Эта задача отлично сочетается с другими о законах движения Ньютона!
Все три испытания Newton доступны в экономичном наборе!
STEM Challenge Bundle с законами движения Ньютона
ТРЕТИЙ ЗАКОН НЬЮТОНА
Упрощенная версия третьего закона: на каждое действие есть равная и противоположная реакция.Это версия, с которой, возможно, знакомо большинство студентов. Самый простой способ продемонстрировать этот закон – использовать устройство под названием «Колыбель Ньютона».
Итак, как это применимо к бутылочным вагонам?
Учащиеся поняли третий закон движения, увидев устройство «Колыбель Ньютона». Мы связали это с автомобилем из бутылок с простым объяснением. Что это за действие? Воздушный шар вытесняет воздух. Какая реакция? Автомобиль движется.
*********************************************** ****************************
Вам также могут понравиться эти события STEM о Force and Motion:
*** ************************************************ ************************
Будьте первым, кто узнает о моих новых скидках, бесплатных подарках и запуске продуктов:
Нажмите здесь, чтобы следите за моим магазином. Получать по электронной почте обновления о учителях – это просто потрясающе!
Оставайтесь на связи!
Блог
Большое спасибо,
Учителя действительно потрясающие!
Основы биомеханики: законы движения Ньютона
Сэр Исаак Ньютон сформулировал 3 физических «закона», которые легли в основу классической механики. Посредством этих законов он описывает взаимосвязь сил, объектов и движения.На протяжении трех столетий это было основой для понимания систем движения и физических сил.
Имейте в виду, что, хотя эти 3 закона изменили взгляд ученых на мир, он ни в коем случае не полон. Дальнейшие открытия, касающиеся квантовой физики и теории относительности, показали, что эти законы являются только основой механики, а не всеобъемлющими. Тем не менее, понимание этих трех законов является предпосылкой для изучения движения и их физических систем.
Первое правило законов Ньютона – вы не говорите о законах Ньютона.
Второе правило законов Ньютона – вы не говорите о законах Ньютона!
А если серьезно, вот они…
Объект в состоянии постоянной скорости имеет тенденцию оставаться в этом состоянии движения, если к нему не приложена неуравновешенная сила. Другими словами, это сопротивление изменениям движения. При концептуализации инерции следует учитывать важные моменты. Одно из этих соображений заключается в том, что покой – это постоянная скорость, и ее можно рассматривать как имеющую инерцию. Еще одно соображение заключается в том, что гравитация – это неуравновешенная сила, действующая на все объекты.
Прискорбное прозрение инерции
1) Как инерция применима к биомеханике
Рассмотрим позднюю фазу качания походки и силы, действующие на нижнюю конечность. Непосредственно перед ударом пятки почти не задействованы мышцы, которые продвигают конечность вперед, но она все еще продолжает двигаться вперед в пространстве. Это инерция. Чтобы справиться с этой инерцией, тело использует эксцентрическое сокращение подколенных сухожилий, чтобы замедлить конечность, подготовиться к удару пяткой и уменьшить резкие силы реакции.
Эксцентрическое замедление инерции на поздней фазе походки
Чистая сила, приложенная к телу (массе), вызывает пропорциональное ускорение. Этот закон описывает взаимосвязь между массой объекта, ускорением и приложенной силой. И ускорение, и сила должны иметь одинаковое направление вектора.
Это также можно рассматривать в других терминах:
Импульс = масса x скорость. Изменение количества движения тела пропорционально импульсу, приложенному к телу, и происходит вдоль прямой линии, на которой этот импульс воздействует.Импульс не может быть изменен, если на него не действует внешняя сила; его можно только сохранить.
Ускорение пропорционально неуравновешенным силам, действующим на него, и обратно пропорционально массе объекта (a = F / m)
У Кена Гриффи-младшего был один плавный второй закон движения
Как F = ma применимо к биомеханике
Практически каждое статическое и динамическое движение имеет силу. Мышцы – это ткани, которые сокращаются и создают силу на рычагах тела (соединительной ткани, костях).При любом движении человека F = ma можно использовать для упрощенного расчета силы. Это уравнение можно использовать даже со статическими позициями. Рассмотрим статичное положение головы вперед. Гравитация и масса головы накладывают передне-нижнюю силу. Чтобы противостоять этой силе и не дать вашей шее оторваться от стола, вы должны постоянно сокращать поднимающие лопатки, верхние трапециевидные и задние шейные мышцы, чтобы противостоять этой силе. Рассчитав ускорение свободного падения и массу головы, вы можете начать вычислять мышечные силы, необходимые для предотвращения движения.
Масса головы и сила тяжести вместе создают направленную вниз силу
На каждое действие есть равная и противоположная реакция. Этот закон описывает, как силы всегда приходят парами, а это означает, что каждый раз, когда объекты контактируют друг с другом, они проявляют силу. Важным моментом здесь является концепция, согласно которой гравитация ВСЕГДА касается каждого объекта.
Том Круз демонстрирует свой уверенный контроль над третьим законом движения Ньютона в классическом фильме «Цвет денег»
Как действие-реакция применяется к биомеханике
Перенос веса голеностопного сустава на ногу пациента приведет к увеличению силы массы и нисходящему натяжению под действием силы тяжести, реакция заключается в том, что противоположная мышца должна будет создать силу, чтобы преодолеть эту массу.Другой пример этого закона – силы реакции земли. Бег по мягкому грунту приведет к гораздо меньшим ударным нагрузкам, чем по твердому бетону.
Наземные силы реагирования на походке
3 закона движения Ньютона являются основой для понимания движения и систем корреляционных сил. Каждый закон можно применить к биомеханике по-своему.
- Инерция = объект с постоянной скоростью имеет тенденцию оставаться в этом состоянии движения, если к нему не приложена неуравновешенная сила
- F = MA = Чистая сила, приложенная к телу (массе), вызывает пропорциональное ускорение
- Действие-Реакция = Для каждого действия существует равная и противоположная реакция
Темы
Сила
Законы Ньютона
Рычаги
Момент
Гравитация
Давление
Биомеханические отношения
Копать глубже
http: // www.Physicsclassroom.com/class/newtlaws/
http://zonalandeducation.com/mstm/physics/mechanics/forces/newton/newton.html
http://www.youtube.com/watch?v=ih58Lc7wq0U&feature=related
–
Основная причина, по которой я веду этот блог, – поделиться знаниями и помочь людям стать лучшими клиницистами / тренерами. Я хочу, чтобы наша профессия росла и чтобы у наших пациентов были лучшие результаты. Независимо от вашей конкретной должности (PT, Chiro, Trainer, Coach и т. Д.), все мы преследуем одну и ту же цель – дать людям возможность решать свои проблемы с помощью движения. Я надеюсь, что содержание этого сайта поможет вам в этом.
Если вам понравилось и вы нашли это полезным, поделитесь им со своими коллегами. И если вы чувствуете себя щедрым, сделайте пожертвование, чтобы помочь мне запустить этот сайт. Мы очень ценим любую сумму, которую вы можете себе позволить.
Что происходит, когда нарушается третий закон Ньютона?
В новых экспериментах два слоя микрочастиц, парящих на двух разных высотах над электродом, позволили исследователям исследовать статистическую механику невзаимных взаимодействий, которые нарушают третий закон Ньютона.Авторы и права: А. В. Ивлев и др. CC-BY-3.0Даже если вы не знаете его по имени, каждый знаком с третьим законом Ньютона, который гласит, что для каждого действия существует равное и противоположное противодействие. Эту идею можно увидеть во многих повседневных ситуациях, например, при ходьбе, когда ступня человека упирается в землю, а земля толкается назад с равной и противоположной силой. Третий закон Ньютона также важен для понимания и разработки автомобилей, самолетов, ракет, лодок и многих других технологий.
Несмотря на то, что это один из фундаментальных законов физики, третий закон Ньютона может быть нарушен в определенных неравновесных (неуравновешенных) ситуациях. Когда два объекта или частицы нарушают третий закон, говорят, что они взаимодействуют невзаимно. Нарушения могут происходить, когда окружающая среда каким-то образом участвует во взаимодействии между двумя частицами, например, когда среда движется по отношению к двум частицам.(Конечно, закон Ньютона все еще сохраняется для полной системы «частицы плюс окружающая среда».)
Хотя было проведено множество экспериментов с частицами с невзаимным взаимодействием, не так много известно о том, что происходит на микроскопическом уровне – статистической механике – этих систем.
В новой статье, опубликованной в Physical Review X , Алексей Ивлев и др. Исследовали статистическую механику различных типов невзаимных взаимодействий и обнаружили некоторые удивительные результаты, такие как то, что экстремальные градиенты температуры могут возникать в масштабе частиц. .
«Я думаю, что наибольшее значение нашей работы состоит в том, что мы строго показали, что определенные классы существенно неравновесных систем могут быть точно описаны в терминах статистической механики равновесия (т. Е. Можно вывести псевдогамильтониан, который описывает такие системы)», Ивлев из Института внеземной физики Макса Планка в Гархинге, Германия, сообщил Phys.org . «Одно из самых удивительных выводов состоит в том, что, например, можно наблюдать смесь двух жидкостей в детальном равновесии, но каждая жидкость имеет свою собственную температуру.«
Один из примеров системы с невзаимным взаимодействием, который исследователи экспериментально продемонстрировали в своем исследовании, включает заряженные микрочастицы, парящие над электродом в плазменной камере. Нарушение третьего закона Ньютона возникает из-за того, что система включает два типа микрочастиц, которые левитируют на разной высоте из-за их разных размеров и плотности. Электрическое поле в камере приводит в движение вертикальный плазменный поток, подобный течению в реке, и каждая заряженная микрочастица фокусирует текущие ионы плазмы вниз по потоку, создавая за собой вертикальный плазменный след.
Хотя силы отталкивания, возникающие из-за прямого взаимодействия между двумя слоями частиц, являются взаимными, силы притяжения между частицами и следами между двумя слоями – нет. Это связано с тем, что следовые силы уменьшаются по мере удаления от электрода, а слои левитируют на разной высоте.В результате нижний слой оказывает большую общую силу на верхний слой частиц, чем верхний слой на нижний слой частиц. Следовательно, верхний слой имеет более высокую среднюю кинетическую энергию (и, следовательно, более высокую температуру), чем нижний слой. Настраивая электрическое поле, исследователи также могут увеличить разницу в высоте между двумя слоями, что еще больше увеличивает разницу температур.
«Обычно я довольно консервативен, когда думаю о том, какое« непосредственное »потенциальное применение может иметь конкретное открытие (по крайней мере, в физике)», – сказал Ивлев.«Однако я вполне уверен в том, что наши результаты представляют собой важный шаг к лучшему пониманию определенных видов неравновесных систем. Есть множество примеров очень разных неравновесных систем, в которых симметрия действие-реакция нарушена для межчастичных взаимодействий, но мы показывают, что, тем не менее, можно найти основную симметрию, которая позволяет нам описывать такие системы в терминах учебной (равновесной) статистической механики ».
Хотя плазменный эксперимент является примером нарушения симметрии действие-реакция в 2D-системе, такое же нарушение симметрии может происходить и в 3D-системах.Ученые ожидают, что оба типа систем демонстрируют необычное и замечательное поведение, и надеются продолжить изучение этих систем в будущем.
«Наши текущие исследования сосредоточены на нескольких темах в этом направлении», – сказал Ивлев. «Один из них – это эффект нарушения симметрии действие-реакция в сверхдемпфированных коллоидных суспензиях, где невзаимные взаимодействия приводят к удивительно богатому разнообразию явлений самоорганизации (динамическая кластеризация, формирование структуры, разделение фаз и т. Д.). Результаты этого исследования могут привести к нескольким интересным приложениям. Другая тема является чисто фундаментальной: как можно описать гораздо более широкий класс «почти гамильтоновых» невзаимных систем, чьи взаимодействия почти совпадают с взаимодействиями, описываемыми псевдогамильтонианом? Надеюсь, мы сможем сообщить об этих результатах очень скоро ».
Модельная система, используемая для иллюстрации фазового перехода смеси активных и пассивных частиц.
Дополнительная информация: А.В. Ивлев и др. «Статистическая механика, в которой нарушается третий закон Ньютона». Физический обзор X . DOI: 10.1103 / PhysRevX.5.011035
© 2015 Phys.org
Ссылка : Что происходит, когда нарушается третий закон Ньютона? (2015, 15 мая) получено 26 октября 2021 г. с https: // физ.org / news / 2015-05-newton-law-broken.html
Этот документ защищен авторским правом. За исключением честных сделок с целью частного изучения или исследования, никакие часть может быть воспроизведена без письменного разрешения. Контент предоставляется только в информационных целях.
Сил и движение – Три закона движения Ньютона
Три закона движения Ньютона
Теперь, когда мы освоили движение и векторы, по крайней мере, в умеренной степени, мы готовы изучать силы, еще одну векторную величину, связанную с движением.И как мы могли изучать силы, не представляя сэра Исаака Ньютона?
Законы движения Ньютона Ньютон, иначе известный как «Парень в причудливом парике». Источник. Рассматривая работы Коперника, Галилея и Кеплера, Исаак Ньютон соединил их точки и придумал три закона движения, впервые опубликованные в 1687 году, для которых мы навсегда в его долгу. Мы меньше благодарим его за то, что он попутно развивал математику.
Первый закон движения
Первый закон движения Ньютона гласит, что покоящийся объект имеет тенденцию оставаться в состоянии покоя, в то время как объект в движении имеет тенденцию оставаться в движении.А под «движением» мы подразумеваем постоянное движение: неизменную скорость. Мы заметили это в горизонтальном движении снаряда. Без посторонних воздействий (сил) движение не меняется по самой своей природе.
Этот закон часто называют законом инерции , где инерция – это свойство массы, которое, в свою очередь, является свойством количества вещества. Инерционная масса – это мера сопротивления объекта ускорению, сопротивление изменению движения.
Мы могли или не могли столкнуться с этой идеей в других жизнях. В литературе, на предыдущих уроках естествознания или на личном опыте.
Чем больше у чего-то массы, тем сложнее заставить его двигаться или остановить, когда оно проносится по вселенной. В этом вся философия того, что делают атакующие полузащитники. Или стационарные, если на то пошло.
Мы могли бы также думать о Первом Законе как о Законе о картофеле на подносе. Если мы вегетируем на диване, например, едим картофельные чипсы, мы вообще не будем двигаться.За исключением того, что это верно и для кушетки, движущейся с постоянной скоростью, эта аналогия прекрасна.
Время практики. Твити в конечном итоге теряет 0,1 г жира, много раз пролетая своей квадратной петлей. Теперь он менее склонен или более склонен сопротивляться изменению движения? Обратим внимание на формулировку здесь. Вопрос касается склонности Твити сопротивляться переменам. Теперь мы знаем, что что-то более тяжелое сопротивление изменяется сильнее. Твити (немного) легче после прохождения кругов, поэтому он (незначительно) будет менее склонен сопротивляться переменам.Его инерция (незначительно) меньше.
Подводя итог Первому Закону Движения: если бы объект был свободен просто существовать вне гравитации, электрических или магнитных полей, трения или сопротивления воздуха, он либо продолжал бы оставаться в покое, либо вечно двигаться по прямой линии на постоянная скорость.
Не пытаясь забегать слишком далеко вперед, давайте просто проверим, действительно ли мы наблюдаем объекты в состоянии покоя или в постоянном движении в нашем мире, но тогда и только тогда, когда силы, действующие на них, уравновешены.
Второй закон движения
Обращение Первого закона говорит о том, что все, что вызывает изменение движения объекта или его отсутствие, должно оказывать на этот объект силу, потому что в противном случае оно продолжалось бы, как было. Другими словами, внешняя сила изменит скорость объекта, вызывая ускорение инерционного, устойчивого к изменениям объекта.
Очевидно, мы видим это все время на Земле. Мы не взлетаем с поверхности планеты, когда начинаем бежать, и не бросаем шары в космос.Мы живем на поверхности планеты с постоянным ускорением силы тяжести, которое постоянно тянет нас к ее центру с силой тяжести , которая проистекает из ее огромной массы по сравнению с нашей собственной.
Неудивительно, что сэр Исаак Ньютон открыл свои знаменитые законы движения, мирно вздремнув под яблоней. История гласит, что яблоко упало ему на голову, что побудило Ньютона вскочить на ноги и крикнуть Eurêka! , когда он бежал по улице голым.
Хм. Подождите, это мог быть другой парень. Да еще кто-то. Ньютон изящно остался на земле, вероятно, съел яблоко и в конце концов пришел к выводу, что заставило яблоко упасть на землю. Он мог даже вызвать в воображении изображение, подобное приведенному ниже.
Яблоко, начиная с состояния покоя, разгонялось без видимых помех. Яблоко, объект с массой, ускоряется под действием силы тяжести.
Это приводит нас к Второму закону движения Ньютона :.
Да, второй закон – это математика. Так?
Сразу же мы замечаем, что сила – это вектор, мало чем отличающийся от ускорения, и поскольку математика есть математика и есть один вектор на каждой стороне уравнения, сила должна указывать в том же направлении, что и соответствующее ускорение. Наоборот.
Сила имеет единицы измерения массы, умноженной на ускорение. Так как это неудобно, их правильно переименовали в Newton (N). За мужчиной, а не за печеньем. Если мы используем граммы или дюймы или что-то еще, кроме единиц СИ в пределах массы и ускорения, мы не получим Ньютоны, но Ньютон – это единица СИ, так что давайте придерживаться ее, не так ли?
Математическое время: объект имеет массу 1 кг и движется со скоростью.Сколько силы нужно, чтобы удвоить его скорость за 1 секунду? Эээ… что? Начнем с определения того, что мы знаем.
Мы знаем, что F = ma , и что ускорение a определяется изменением скорости во времени, Δ t = 1 с, при v f = 2 v i , или. Следовательно, что означает для объекта весом 1 кг.
Поскольку практика ведет к совершенству, и сейчас нет времени, как настоящее, давайте попробуем другой пример.
Если скользящая книга весом 2 кг преодолевает расстояние d = 1 м за время t = 2 секунды с постоянной скоростью, затем замедляется перед полной остановкой через 1 секунду, какое количество силы действовало на нее чтобы замедлить это?
Ох, многоступенчатый вопрос; нам это нравится. Чтобы найти скорость (или скорость, но нам не указали направление, которое нужно учитывать), мы должны вытащить, что означает. Это его начальная скорость с точки зрения ускорения. Его конечная скорость – это математическое определение «остановки».
Чтобы найти ускорение, нам нужны обе скорости, а также время между двумя скоростями, которое составляет 1 секунду. Обратите внимание, что это , а не через 2 секунды с момента постоянной скорости. Потом . Наконец, F = ma , поэтому. Отрицательный знак указывает на то, что и ускорение, и сила противоположны направлению скорости, что имеет смысл, потому что объект замедлился.
Мы могли бы даже использовать Второй закон Ньютона, чтобы найти величины сил, которые уравновешивают друг друга, такую как сумму сил.В случае уравновешенных сил нет чистой силы или ускорения, и.
Скорее всего, мы все сейчас где-то сидим. Силы, действующие на каждого из нас в этом состоянии, – это сила тяжести, неизбежная (если мы на Земле) и сила поверхности того, на чем мы сидим, удерживая нас. Если бы нас не удерживала сила, мы бы ускорились к центру Земли.
Поверхностная или контактная сила называется нормальной силой . «Нормальный» на математическом языке означает «перпендикулярный».Нормальная сила толкает перпендикулярно поверхности. Если предположить, что наши стулья, кушетки, полы или все, на чем мы сидим, выровнены по горизонтали, нормальная сила направлена вверх, в точном противодействии силе тяжести.
Если сила тяжести составляет 700 Н каждая, то мы бы сказали, что F g = 700 Н, и, следовательно, нормальная сила F Н = 700 Н, потому что силы уравновешены .
Выше приведена диаграмма сил для нашего сидящего «я», также известная как диаграмма свободного тела .Он показывает силы как векторы, действующие на объект. Для уравновешенных сил стрелки должны быть одинаковой длины и указывать в противоположном направлении. Стрелки условно проводят от центра объекта наружу.
В следующий раз, когда мама захочет, чтобы мы встали и помогли на кухне, мы можем честно сказать ей, что не можем, потому что сейчас мы изучаем сбалансированные силы. Между прочим, уравновешенные силы приводят к тому, что объект находится в равновесии , без ускорения. Обратите внимание, что объект может находиться в равновесии с постоянной скоростью из-за Первого закона движения Ньютона.Черт возьми, мы можем «изучать» уравновешенные силы, постоянно идя на кухню … не говори маме.
Третий закон движения Ньютона
Грубо говоря, Третий закон движения Ньютона гласит, что каждое действие имеет равную и противоположную реакцию, и под «действием» мы подразумеваем «силу». Просто быть чистым. Чтобы быть еще более ясным, F AB = – F BA , что означает, что сила на A от B равна и противоположна силе на B от A .
Эта идея действия-противодействия также популярна в философии. Ньютон действительно что-то понимал в этом третьем законе.
Предупреждение: сила, с которой стул толкает вверх наши «сиденья», равна , а не силе реакции на силу тяжести. Сила реакции на силу тяжести, которую Земля накладывает на нас, – это сила тяжести, которую мы прикладываем к Земле. Сила реакции на нормальную силу стула, толкающую нас вверх, – это сила, с которой мы толкаем стул.
Ясно как грязь? Третий закон Ньютона так сбивает с толку.Давайте снова посмотрим на силовую диаграмму, э-э, диаграмму свободного тела. Хотя, безусловно, верно, что если мы поместим силы реакции на диаграмму сил, тогда все силы будут казаться сбалансированными, но сила реакции не имеет отношения к диаграмме сил.
Единственными силами, действующими на объект, которые относятся к его диаграмме свободного тела, являются внешние силы , вызывающие ускорение объекта. Если мы нажимаем на стол, мы не включаем этот толчок в нашу собственную FBD (диаграмма свободного тела). Скорее, мы включаем силу, отталкивающую нас от стола, которая, если она не уравновешивается какой-либо другой силой, заставляет наше ускорение отодвигаться от стола, что мы и планировали в первую очередь.
В случае нашего сидения на диаграмме сил присутствуют только гравитация и нормальная сила. В диаграмму сил стула следует включить силу нашего отталкивания и собственный вес стула, а также нормальную силу пола, действующую на стул.
Надеюсь, наше время с диаграммами свободного тела разделит для всех нас пары действие-противодействие на соответствующие диаграммы: какая бы диаграмма ни могла, сила, внешняя по отношению к себе, получает это.
Стул на приведенной выше диаграмме толкает вверх с силой 588 Н гигантского Tickle-me Elmo. Какую силу он прилагает к стулу? Поскольку Третий закон Ньютона гласит, что силы должны быть равными по величине, но противоположными по направлению, поэтому Эльмо прилагает к стулу силу -588 Н.
Что происходит, когда мы сталкиваемся со стеной? Или ударить по одному? Стена ударяет нас в ответ, вот почему это больно, и почему вообще не рекомендуется врезаться в стены.
Силы действия и реакции не нейтрализуют друг друга, и каждый объект может по-прежнему ускоряться от взаимодействия действия-противодействия, в зависимости от суммы сил, действующих на каждый объект.Например, два астронавта рядом друг с другом в космосе могут ускоряться в противоположных направлениях, толкая друг друга.
Общие ошибки
Пары действие-реакция – это , никогда не сила тяжести, которой противодействует нормальная сила. Величины могут быть одинаковыми, но это не делает их парой действие-реакция.
Обозначьте только силы, действующие на объект на его диаграмме свободного тела, а не те, которые он проявляет, например, его гравитационное притяжение к Земле или его толчок к любой поверхности, на которой он находится.
Если кажется, что для решения проблемы недостаточно информации, начните маркировать все данные и перечислять все уравнения, относящиеся к доступной информации. Например, мы можем найти ускорение по скорости и времени или по расстоянию и пару раз. Пока ускорение постоянное, мы можем использовать любое из уравнений снаряда.
Brain Snack
Галилей и Исаак Ньютон имели общие научные интересы: они оба были людьми эпохи Возрождения.Они искали новые знания, опираясь на работы Древних.
Три закона маркетинга (основанные на законах движения Ньютона)
Несколько лет назад я имел удовольствие смотреть выступление Дэна Кобли на TED Talk «Что научила меня физика в маркетинге». В этом выступлении Кобли показывает, как физику и научный метод можно применить к принципам маркетинга.
Как маркетолог и поклонник великого сэра Исаака Ньютона выступление Кобли вдохновило меня на то, чтобы исследовать, как три закона движения Ньютона могут помочь объяснить рост бренда и успех в маркетинге.Я адаптировал эти три закона специально к своему опыту, и в моем агентстве мы называем их «тремя законами маркетинга».
Первый закон маркетинга: применяйте силу
Согласно формуле Ньютона (сила равна массе, умноженной на ускорение), первый закон маркетинга – это применение силы. Как мы применяем силу? Мы наносим удары рано и часто, что мы называем «быстро начать – быстро потерпеть неудачу». Агентства часто имеют тенденцию придумывать тщательно продуманные кампании, на планирование которых требуются месяцы, только для того, чтобы обнаружить, что стратегия изначально была неправильной.Однако, решительно выйдя из ворот, мы можем нырнуть и начать быстро двигать иглу для наших клиентов.
На заре существования нашей компании Магнети работал со стартапом, у которого была отличная концепция: онлайн-площадка для студентов университетов, где они могут обмениваться учебниками друг с другом. Вместо того, чтобы заставлять покупать дорогие книги в книжном магазине, этот продукт давал студентам быструю, легкую и дешевую альтернативу. Учитывая небольшой первоначальный бюджет компании, нам нужно было быстро развернуть наши маркетинговые усилия.Мы пропустили типичную длительную, затяжную фазу стратегии в пользу более экономичного подхода. Мы взялись за дело и обнаружили серьезный недостаток в первоначальной стратегии работы с социальными сетями. Большинство студентов не обращались к социальным каналам, потому что эти каналы использовались в основном как бегство от учебы; все, что связано со школой, не было приветствием.
Наше открытие было связано с размещением сообщения и временем. Поскольку мы рано начали с сильного применения силы, мы смогли быстро развернуться и сэкономить клиенту тысячи долларов.Смена стратегии привела к минимальной цене за канал привлечения клиентов и по сей день является одной из наших величайших побед.
Мы поддерживаем фокус нашей команды на принципе «быстро начать – быстро потерпеть неудачу», который дает нам возможность быстро менять направление.
Второй закон маркетинга: однажды в движении, не останавливайся
Ньютон утверждал, что объект остается либо в движении, либо в состоянии покоя, если на него не действует внешняя сила. В своей классической книге « От хорошего к великому » Джим Коллинз описывает импульс со своей аналогией с маховиком: благодаря своей инерции и определенному весу маховик может сохранять импульс без остановки.Думайте о маркетинговых операциях как о маховике. Движение – ключ к устойчивому росту; на создание этого нужно время, но когда у вас есть импульс, его легко поддерживать.
FoodMaven, клиент, стремящийся к сокращению пищевых отходов, приложил значительные усилия для создания хорошей бизнес-модели и отличного бренда. За последние два года они выросли из комнаты в общежитии до 22 сотрудников. При таком быстром первоначальном успехе бренду было бы легко успокоиться. Независимо от усилий, которые потребовались, чтобы добраться до этой точки, сообразительные лидеры FoodMaven понимают, что сейчас самое время извлечь выгоду из ее динамики.Они ищут дополнительное финансирование и удваивают свои усилия по маркетингу и продажам.
Многие бренды добиваются успеха и потом останавливаются на достигнутом, но одна из самых больших ошибок, которую может сделать любой бренд, – это отдых. Рост требует постоянного движения и последовательности. В деловом мире я слышал, как импульс описывают как «серию успехов». Успех рождает успех. Поддерживать импульс непросто; это требует согласия, последовательности и терпения. Совет здесь прост: двигайтесь и оставайтесь в движении.
Третий закон маркетинга: противодействие оппозиции
Ньютон говорит нам, что каждое действие имеет равную и противоположную реакцию. Если вы действуете, применяете силу и сохраняете импульс, противодействие будет оказывать силы, находящиеся вне вашего контроля. Эти силы могут варьироваться от неожиданной конкуренции до кошмаров PR и бюрократических проблем. В любом случае решимость – залог успеха.
Меня часто спрашивают, в чем ключ к успеху бренда. Мне не нравится этот вопрос, но если мне приходится отвечать, я всегда говорю: «Будь последним, кто выживет.«Создать успешный бренд сложно – это требует решимости противодействовать множеству противоборствующих сил.
Всем великим брендам приходилось выдерживать сопротивление. Помните Reebok Pump конца 80-х? Выпуск этих кроссовок поставил Nike в штопор, что потребовало немедленной контратаки на рынке. Это противостояние привело к изобретению серии Nike Air, за которой последовало партнерство с легендарным игроком НБА Майклом Джорданом. Nike мастерски справился с противодействием оппозиции и, в свою очередь, привел организацию к невообразимому успеху.
Когда вы готовитесь создать неудержимую маркетинговую машину, помните об этих законах. Применяйте силу, продолжайте движение и будьте готовы противодействовать противодействию.
Маловероятная правильность законов Ньютона
В школах мы все изучали законы Ньютона как очевидный факт о нашей Вселенной. Я тоже снял видео, в котором их прославляют и преподносят как очевидную истину.
Тем не менее, вы когда-нибудь действительно медитировали до такой степени, что они чувствовали себя глупо неправыми? В конце концов, они были обнаружены всего около 350 лет назад, а это означает, что они полностью ускользнули от человеческих мыслей на протяжении тысячелетий.На самом деле, я готов поспорить, что большинство древних ученых жестоко дискредитировали бы их на основании их очевидной абсурдности. Предлагаю вам хорошенько поразмышлять над ними несколько минут…
Опять же, какие законы?
Хммм… Знаешь что? Давайте вместо этого послушаем Дерека Мюллера на Veritasium. Его фантастическое видео ниже указывает на неправильные представления о нашей интуиции.
Хммм … Это напортачило. Действительно ли законы Дерека неверны?
Они есть.Законы Дерека интуитивно понятны и в корне неверны. И наоборот, законы Ньютона и очень противоречивы, и гораздо более правильны.
Но подождите, разве Эйнштейн не доказал, что Ньютон неправ?
Он сделал. Но законы Ньютона по-прежнему прекрасно подходят для описания практически всех известных нам механических движений, от падения яблока до орбит планет Солнечной системы. От нашей повседневной жизни до ракетостроения, в нашем макроскопическом масштабе и в нашем масштабе времени, законы Ньютона настолько точны, что было бы бессмысленно заменять их теорией относительности Эйнштейна.Действительно, предсказания двух теорий почти полностью совпали бы.
Итак, если я последую за вами, законы Ньютона – это более простые приближения к более точным законам Эйнштейна?
Да. И все же, как только что показал вам Дерек, они уже невероятно нелогичны. Давайте рассмотрим их подробнее!
Видео Дерека великолепны, потому что они помогают нам понять, какие ошибки допускает наша интуиция. Это важный шаг в обучении, которого часто не хватает! В самом деле, поскольку наша интуиция часто ошибочна, очень важно знать, когда и почему, если мы когда-либо хотим иметь прочную основу, чтобы по-настоящему постигать окружающий нас мир.Вот сообщение в блоге, в котором я подробно рассказываю, почему я так думаю. Следуя открытиям Дерека, я не буду пытаться дать ясное, хорошо объясненное и легко читаемое введение в законы Ньютона. Вместо этого в этой статье мы подробно рассмотрим все, что идет не так с нашей интуицией, когда мы впервые узнаем законы Ньютона. Это более трудный путь, но я гарантирую, что он будет полезным, даже если вы уже знаете законы Ньютона!Первый закон – инерция
Интуитивно понятно, что все движущиеся объекты истощаются и замедляются.В конце концов, чтобы прийти в движение, нужна энергия, будь то сжигание калорий или сжигание топлива. И когда эта энергия иссякает, очевидно, объект больше не может двигаться. Так много тому примеров! Ударьте по мячу, ведите машину или посмотрите на Усейна Болта. Кажется, что каждый невозмущенный движущийся объект обречен на то, чтобы остановиться. . Звучит ясно, правда?
Как может быть не так?
Ответ буквально в небе.
В самом деле?
На Земле всегда найдется что-то, что помешает движению объекта.Мяч может быть остановлен сеткой, машина может врезаться в стену, а Усэйн Болт может использовать трение с воздухом и землей для замедления. Однако там, наверху, в пустоте космоса, мало что может нарушить движение астрономических объектов. И поэтому, если мы действительно хотим понять природу невозмущенных движений, только взглянув туда, мы можем найти ответ. Это то, что сделал Галилей и, что более важно, то, что сделал Ньютон. Они обнаружили, что там движущиеся объекты, кажется, не замедляются.
Итак, невозмущенные объекты никогда не замедляются…
Верно! Это как раз первый закон Ньютона, который иногда называют законом инерции. В нем говорится, что , если его не трогать, объекты будут продолжать движение вечно . Они не ускоряются и, что еще противоречит интуиции, не замедляются. Прекрасным примером этого является наша вращающаяся Земля. Раньше он вращался. Таким образом, согласно первому закону Ньютона, он будет вечно вращаться, как продемонстрировал Дерек в другом видео:
Что очень беспокоит первого закона Ньютона, так это то, что он никогда не применяется! Важно отметить, что в реальной жизни ни один объект не остается невозмутимым.Даже астрономические объекты там находятся под гравитационным воздействием. Вот почему этот первый закон так противоречит интуиции. Это абстрактный принцип, который делает всю теорию непротиворечивой. Тем не менее, это никогда не относится к реальности. Если задуматься над этим, даже трудно представить, что закон инерции считается первым и самым основным законом всей физики! В конце концов, это трудно проверить!
Так действительно ли это необходимо?
Технически первый закон Ньютона бесполезен, поскольку его можно рассматривать как частный случай второго закона! Тем не менее, это интересный первый шаг к погружению в картину мира Ньютона.И это совершенно очевидным образом показывает, насколько противоречивы законы. На самом деле попытка разобраться в этом довольно поучительна.
Как мне понять этот первый закон?
Представьте, что вам подали кофе в самолете. Кофе падает вниз, а самолет летит на большой скорости по горизонтали. Как вы думаете, стюардесса прицелилась перед чашкой, чтобы налить кофе? Будет ли она наливать его, как слева на рисунке ниже, или как справа?
Интуитивно я бы сказал, что она должна налить как справа…
Галилей сам провел этот мысленный эксперимент (с кораблем вместо самолета).Удивительно, но он пришел к выводу, что если движение самолета было постоянным, то левое решение было правильным. В более общем смысле, законы физики не должны изменяться в системе, находящейся в постоянном движении. Физика на плоскости должна быть точно такой же, как на Земле. Эта идея известна как принцип относительности . И этого простого принципа относительности достаточно, чтобы вывести первый закон Ньютона.
Как так?
Ключ – отметить, что движение относительное.Чашка кофе по-прежнему с уважением к стюардессе. И все же он движется с очень большой скоростью по сравнению с крестьянином, смотрящим на самолет со своих полей. Удивительно, но тот очевидный факт, что, если его не трогать, кофейная чашка на неопределенное время остается неподвижной по отношению к стюардессе, также подразумевает, что она будет сохранять свою очень высокую скорость по отношению к крестьянину. Вот почему, с крестьянской точки зрения, невозмущенные объекты будут сохранять свое движение неопределенно долго.
Второй Закон – Динамика
Второй закон – это самый фундаментальный закон Ньютона.Это, безусловно, самое странное из всех. Это отчасти потому, что в нем задействованы три концепции, которые сложнее, чем кажется.
Что это за концепции?
Во-первых, это концепция force . Как вы думаете, что это такое?
Разве не сила, которую мы даем объекту, который мы хотим переместить?
Хммм… Проблема в том, что слово power в физике означает нечто иное. Мощность соответствует количеству энергии, которое мы передаем объекту или которое объект передает нам.Возьмем пример, когда вратарь ловит мяч. Применяя силу к мячу, вратарь фактически получает кинетическую энергию от мяча. Итак, как ни странно, во многих случаях приложение силы может соответствовать противоположности приложения силы к объекту ! Точно так же, когда вы держите в руках тяжелый камень, вы прилагаете к нему большую силу, чтобы он не упал. Но вы не передаете ему никакой энергии! Итак, как ни странно, сильная сила может не иметь силы .
Так что же такое сила?
В определении Википедии говорится, что это то, что влияет на движение объектов … но это сводится к утверждению, что сила определяется вторым законом Ньютона! Это не то, что мы хотим, поскольку это должно использоваться для определения второго закона Ньютона. Другими словами, определения из Википедии дают тревожное круговое определение сил и вторых законов Ньютона. Вот как странно и нелогично само понятие силы!
Я вообще не критикую Википедию.Проще и полезнее представить силы и законы Ньютона через это круговое определение. Однако он определенно ошибочен, и глубокое понимание законов Ньютона требует от нас более глубокого понимания.
Можете дать определение, что такое силы?
Хорошее определение дает Дерек в следующем видео:
Вот ссылка на дополнительное видео обо всех силах, действующих на вас.
Итак, согласно Дереку, сила – это толчок или тяга. Этот толчок или притяжение характеризуется направлением и значением.Например, сила тяжести планеты притягивает объект к центру планеты со значением, пропорциональным массе планеты, пропорциональным массе объекта и обратно пропорциональным квадрату расстояния между планетой и планетой. центры масс объекта.
Свойства сил описывать довольно долго…
Это то, что, должно быть, подумал Ньютон. Поэтому он повторно использовал алгебраическую геометрию Рене Декарта, чтобы суммировать всю информацию о силе в один математический объект под названием вектор .Этот вектор имеет два представления. Один из них геометрический: сила – это стрелка, определяемая направлением и длиной. Другой – алгебраический: сила – это совокупность трех значений силы. Каждое значение обозначает силу силы в одном из 3 пространственных направлений. Согласно словарю Декарта, между этими двумя представлениями векторов существует естественный перевод. А именно, три алгебраических значения силы являются координатами геометрической стрелки. Вот пример для измерения 2.
Чтобы вычислить силу силы по ее координатам, вам нужно только применить теорему Пифагора! Подробнее о векторах читайте в моей статье о линейной алгебре.Ладно… Я понял, какие силы есть. О какой второй концепции вы говорили?
Вторая концепция называется инерционной массой , также известной как инерция или масса . Опять же, наша интуиция обычно очень ошибается в отношении того, что это за инерция. И снова это заблуждение прекрасно раскрывает Дерек:
По словам Дерека, инерцию не следует путать с весом.В то время как вес – это сила, направленная вниз, вызванная гравитацией, инерция, говоря словами Википедии, – это сопротивление объекта изменению своего движения. Однако, опять же, это определение ошибочно, поскольку оно ведет к круговому определению между инерцией и вторым законом Ньютона …
А что насчет массы? Это четко определенная концепция, не так ли?
Проблема с идеей массы в том, что она связана как с инерцией, так и с весом. И все же априори нет причин, по которым тяжелые предметы должны иметь большую инерцию! Вот почему физики давно различают инертную массу и гравитационную массу .Первое – это то, что нас сейчас интересует, а второе – вмешательство в закон всемирного тяготения.
Однако в законах Ньютона инерционная и гравитационная массы подозрительно одинаковы. Это очень загадочно. Спустя столетия эта странная загадка привела к тому, что Эйнштейн сформулировал принцип эквивалентности между ускорением и гравитацией, когда он изобрел общую теорию относительности.Так как бы вы определили инертную массу?
Еще раз, я украду слова Дерека. Инертная масса – это всего лишь мера количества вещества в объекте.
Если вы хотите узнать больше, у Дерека есть отличное видео о том, что такое единица инерционной массы (килограмм). Интересно, что раньше ее определяли в соответствии с гравитационной массой, но вскоре это может измениться! Используя исследования Лавуазье, он может превратиться во что-то более близкое к определению Дерека, то есть во что-то, что измеряет «количество вещества».Хорошо … Какая третья концепция?
Этот, безусловно, худший. Это ускорение , и я сильно подозреваю, что это источник ошибок большинства студентов.Вот еще одна классика Дерека, чтобы помнить об этом:
Нажмите здесь, чтобы увидеть ответы Дерека: a, b, c, d, e.
Как оказалось, правильный ответ – d , где, по словам Дерека, ускорение вдвое больше, чем у a . Это очень нелогично, потому что мы часто путаем ускорение и скорость. Важно отметить, что ускорение составляет , а не скорости или скорости. Объект может иметь сильное ускорение, при этом совсем не двигаясь.
Итак, что такое ускорение?
Это направление и значение изменения движения .В конце прыжка движение прыгуна полностью меняется. Он быстро спускался, и следующее, что он знает, он тоже быстро поднимается. При противодействии на максимальной скорости движения прыгуна не меняются. Он просто продолжает спускаться с той же максимальной скоростью.
Правильное определение ускорения требует языка вычислений, который для этой цели изобрел сам Ньютон. Вы можете узнать больше из моей статьи о дифференциальном исчислении.Означает ли это, что ускорение связано с изменением скорости?
№Ускорение – это не изменение скорости. Это изменение в движении. Возьмем, к примеру, Луну. Луна постоянно приближается к Земле. И все же его скорость остается постоянной. Но, что особенно важно, его движение – нет. В любой момент его движение искривляется по направлению к Земле, потому что оно ускоряется по направлению к Земле.
Значит, направление ускорения так же важно, как и его величина, верно?
Совершенно верно. Поэтому, как и силы, ускорения составляют векторов .Таким образом, ускорение геометрически представлено стрелкой, а аналитически – тремя координатами.
Хмм… Итак, ускорение имеет много общего с силой…
Лучше, чем это. Второй закон Ньютона утверждает, что силы, действующие на объект, определяют его ускорение. Другими словами, ускорение объекта – это стрелка, имеющая то же направление, что и сумма действующих на нее сил. Так, например, Луна ускоряется по направлению к Земле, потому что сила тяжести тянет ее к Земле.
А как насчет силы силы? Связано ли это со значением ускорения?
Да. Точнее, величина ускорения пропорциональна силе. Чем большую силу вы прикладываете к объекту, тем больше вы изменяете его движение. Величина ускорения также обратно пропорциональна инерционной массе объекта. Это означает, что чем больше материала, тем сложнее повлиять на его движение. Мы можем подытожить этот второй закон элегантной и простой математической формулой из четырех символов:
Разделив обе части на инертную массу $ m $, мы получим более интуитивную формулу $ \ vec a = \ vec F / m $, которая гласит, что ускорение имеет то же направление, что и силы, и его величина пропорциональна сила силы, деленная на инерционную массу.
На первый взгляд эта формула должна выглядеть как русалка, уводящая нас от Истины из-за ее вводящей в заблуждение элегантности. Как можно было свести физику к такому простому уравнению? Кроме того, зачем нужно ускорение? Разве мы не влияем на движение, а не на изменение движения? Наша интуиция подсказывает, что если мы хотим встать, мы можем встать. Если мы хотим двигаться дальше, то вперед. Другими словами, наша интуиция говорит, что мы контролируем свое движение и движения окружающих нас предметов.И мы делаем это в большинстве видеоигр. Мы контролируем движения наших героев.
Разве это не так в реальной жизни?
Что особенно важно, согласно второму закону Ньютона, ответ нет . Наша интуиция в корне ошибочна. Мы не можем контролировать движения напрямую. В лучшем случае мы контролируем изменения движений ! Чтобы полностью понять, усвоить и почувствовать второй закон Ньютона, я предлагаю вам хорошенько обдумать это предложение.
Так как же это может быть? Почему выполняется второй закон Ньютона?
Не знаю! Но она проверялась снова и снова и давала так много верных прогнозов.Этот закон до сих пор используется для вывода ракет на орбиту или для создания мощных механических машин. Все это принимают, потому что тщательные эксперименты показали, что это заслуживает доверия. Как бы маловероятно это ни звучало.
В конце концов, удивительно удивляться, как Ньютону удалось убедить других в точности своего второго закона. Чтобы ответить на этот вопрос, я должен рассказать вам о гравитационных и конических сечениях, которые я сделал здесь!Третий закон – действие / реакция
Третий закон известен всем.В конце концов, у него очень красивая формулировка: На каждое действие есть равная и противоположная реакция . Я подозреваю, что многие повторно использовали эту фразу с совершенно другим значением, чем у Ньютона. Почему-то на философском уровне это очень похоже на карма . И я думаю, поэтому нас это устраивает, когда мы впервые слышим это. И все же…
Но что?
Но это так же глупо, как и другие законы Ньютона! Почему на Земле была бы такая равная и противоположная реакция? Мой отец ругал меня много раз, но мне почти никогда не приходилось ругать его.На более физическом уровне Земля тянет меня с огромной силой. И все же было бы совершенно глупо сказать, что я тяну Землю с равной силой…
Это действительно глупо звучит…
Проверьте собеседников Дерека на аналогичном физическом примере:
Итак, оказывается, вы тянете Землю точно так же, как Земля тянет вас.
Но ведь я ведь не влияю на движение Земли?
Вы делаете немного. Но у Земли такая огромная инерционная масса, что для ее ускорения требуется гораздо большая сила, чем сила, которую она оказывает на вас.Запомни. Большие силы, приложенные к огромным инерционным массам, вызывают небольшие ускорения , как утверждается вторым законом.
Итак, как мы можем понять этот третий закон?
Давайте посмотрим на одно важное применение этого третьего закона, которое поможет нам понять его: ракетостроение. Ну, вообще-то, давайте посмотрим, как Дерек объяснит нам ракетостроение!
Так как же нам управлять движением ракеты?
Дерек объясняет ракетостроение в третьем законе.В то время как ракета отталкивает свое топливо, по третьему закону, топливо толкает ракету назад с равной и противоположной силой.
Но ведь это не интуитивно понятно, что две силы будут равны, не так ли?
Это не так. Интуитивно я полагаю, что большинство людей сказали бы, что сила, действующая на ракетное топливо, намного больше, чем сила, действующая на ракету.
Итак, как мы должны интуитивно думать об этом третьем законе?
Как я уже сказал, третий закон можно вывести из аддитивности второго закона.Рассмотрим ракету и ее топливо как единую систему. Предположим, что на них не действует никакая внешняя сила, поскольку они путешествуют в космическом пространстве. Тогда по первому закону система в целом должна продолжать движение бесконечно.
Пока все хорошо…
Теперь, если мы посмотрим на детали всех сил, то общая сила, действующая на систему, должна также включать внутренние силы. А именно, мы должны включить силу ракеты на топливо и силу топлива на ракету.Но поскольку система в целом поддерживает свое движение неопределенно долго, это также означает, что сумма всех сил равна нулю. Следовательно, сила ракетного топлива на ракетном топливе и сила ракетного топлива на ракете должны в сумме равняться нулю. Другими словами, каждый обязательно равен и противоположен другому!
Ключевой концепцией для полного понимания этого третьего закона является рассуждение в терминах импульсов . По-французски импульс переводится как «количество движения», и я думаю, что это очень хороший способ выразиться.Импульс представляет собой величину и скорость движения. Таким образом, массивный объект, движущийся медленно, может иметь такой же импульс, как и объект меньшего размера, движущийся очень быстро. Второй закон Ньютона гласит, что изменение количества движения определяется силами. Сочетание этого с третьим законом Ньютона означает, что системы без внешней силы, применяемой для сохранения их импульса. Это полезно иметь в виду, чтобы разобраться в эксперименте Дерека.Подведем итог
В заключение я должен сказать, что на самом деле существует только один закон: второй закон.В общем, этот второй закон утверждает, что для любого скопления материи сумма всех внешних сил, действующих на него, деленная на его полную инертную массу, должна равняться ускорению его центра масс. Из этого закона можно вывести все остальные законы! Когда вы думаете об этом, совершенно удивительно, что этот единственный закон почти идеально управляет большей частью известной нам физики. В этом мощном, предсказуемом и элегантном законе заключается красота и убедительность законов Ньютона. Хотя это очень нелогично.
Неужели нужно было так настаивать на том, насколько нелогичны эти законы?
Я так думаю. Посмотрите это последнее видео Дерека о его докторской степени, чтобы понять, почему:
Очень важно понимать наши заблуждения. Лично я даже в своих математических исследованиях имею дело с концепциями, относительно которых я сделал различные неправильные интуитивные предположения. Дело не всегда в том, чтобы стереть эти интуиции, а, скорее, в том, чтобы знать их пределы, чтобы я мог знать, в какой момент я могу им доверять.Обнаружение этих ограничений также может помочь мне развить новую лучшую интуицию в отношении концепций, с которыми я имею дело. Интересно, что то же самое и с теориями физики. Теперь мы довольно точно знаем пределы законов движения Ньютона, и это помогло нам (под нами я имею в виду Эйнштейна!) Придумать новые лучшие теории!
Вот вам последнее упражнение. Ниже приведено замечательное видео Джошуа Мэнли на TedEd о законах Ньютона. Он прекрасно иллюстрирован, очень хорошо объяснен и определенно точен.Тем не менее, я хочу, чтобы вы представили, какие заблуждения могли сохранить (или получить!) Полуослушающая и неподготовленная аудитория после просмотра:
