P маленькая в физике: Используемые обозначения в учебнике по физике, 8 класс

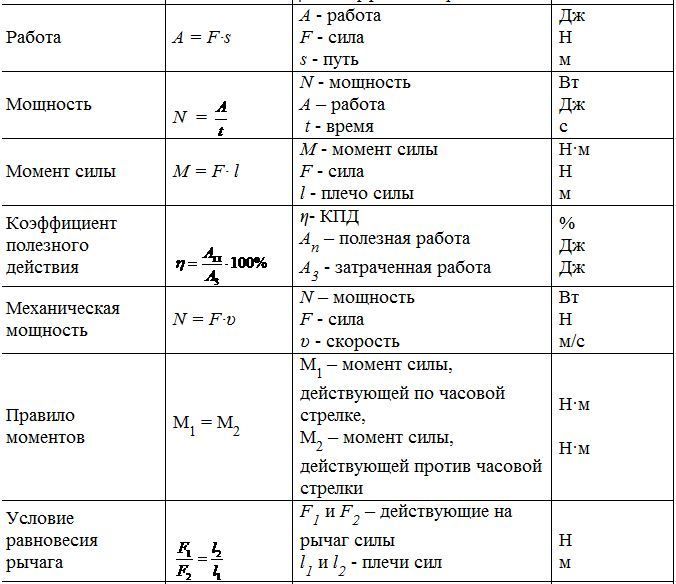
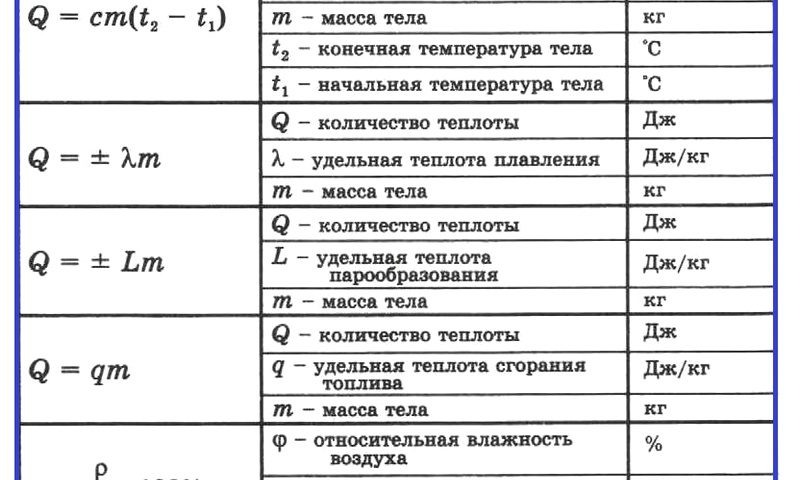
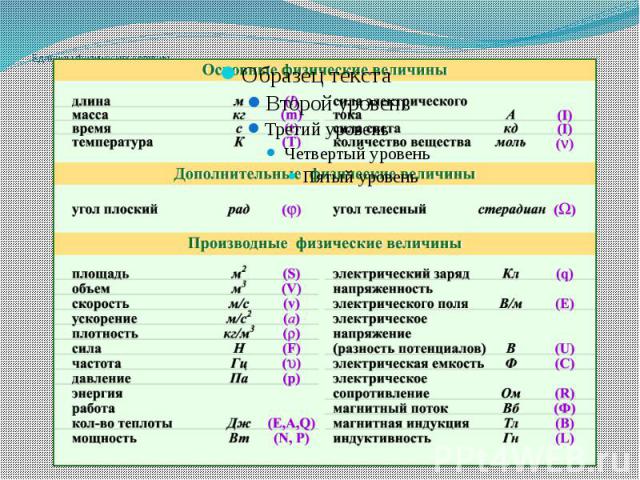
Что такое маленькая p в физике — Знания.site

Последние вопросы

• Физика

  1 час назад

  Два проводника соединены так как изображено на рисунке амперметр показывает силу тока 1 А какое напряжение показывает вольтметр если сопротивление второго проводника 2 Ом

  вырянты ответов а) 2В б) 1В в) 0,5В

• Физика

  1 час назад

  ПОМОГИТЕ СРОЧНО С ФИЗИКОЙ

• Физика

  1 час назад

  Помогите решить задачу по физике. Срочно.

• Физика

  1 час назад

  Визначте масу спирту, що піднявся по капілярній трубці діаметром 0,5 мм.

• Физика

  2 часа назад

  Длина тени дерева равна 15 м, а длина тени человека, рост которого 170 см, равна 2,5 м. найдите высоту дерева.

• Физика

  2 часа назад

  Физика Помогите пожалуйста

• Физика

  2 часа назад

  Магнитное поле физика, помогите решить

• Физика

  2 часа назад

  2. Коли батискаф занурили на деяку глибину в океан, прилади показали тиск 41,2 МПа. На яку саме глибину занурили батискаф?​

• Физика

  2 часа назад

  Магнитное поле помогите

• Физика

  3 часа назад

  Помогите с Физикой

• Физика

  3 часа назад

  Плавление вещества Физика

• Физика

  3 часа назад

  Физика 8 класс

• Физика

  3 часа назад

  Как изменяется общее напряжение 2х 12вольтовых батарей при параллельном соединении

• Физика

  3 часа назад

  Дифракційна ґратка має 100 штрихів на 1 мм. Одну з ліній спектра стронцію третього порядку видно під кутом 7 градусів. Визначити довжину хвилі, що відповідає цій лінії.

• Физика

  4 часа назад

  Срочно. Задание по Физике

Все предметы

English

United States

Polski

Polska

Bahasa Indonesia

Indonesia

English

India

Türkçe

Türkiye

English

Philippines

Español

España

Português

Brasil

Русский

Россия

How much to ban the user?

1 hour 1 day

Российские физики выяснили, как отличить чёрную дыру от очень маленькой звезды

• Профиль

• Избранное

Обнаружение и изучение чёрных дыр Вселенной 1 июля 2016, 08:52 1 июля 2016, 09:52 1 июля 2016, 10:52 1 июля 2016, 11:52 1 июля 2016, 12:52 1 июля 2016, 13:52 1 июля 2016, 14:52 1 июля 2016, 15:52 1 июля 2016, 16:52 1 июля 2016, 17:52 1 июля 2016, 18:52

• Иллюстрация NASA, ESA, C. -P. Ma and J.Thomas.

• Художественное изображение на тему “Чёрная дыра”.

  Иллюстрация предоставлена пресс-службой МФТИ.

• Иллюстрация NASA, ESA, C.-P. Ma and J.Thomas.

• Художественное изображение на тему “Чёрная дыра”.

  Иллюстрация предоставлена пресс-службой МФТИ.

Учёные из России выяснили, как отличить чёрные дыры от сверхкомпактных звёзд по энергетическому спектру частиц, располагающихся в непосредственной близости от этих удивительных объектов.

Способ отличить чёрные дыры от компактных массивных объектов, которые внешне неотличимы друг от друга, придумали учёные из МФТИ, ИТЭФ и НИУ ВШЭ. Для этого нужно изучить энергетический спектр частиц, которые пролетают по соседству, в одном случае он будет непрерывным, а в другом — дискретным. Об этом сообщает пресс-служба МФТИ.

Чёрные дыры имеют горизонт событий — границу, из-за которой ничто, даже свет, не может вернуться во внешний мир. Радиус этой границы называют радиусом Шварцшильда, в физическом смысле это радиус объекта, для которого вторая космическая скорость становится больше скорости света, а значит, ничто не может преодолеть его тяготение.

Чёрные дыры звёздной массы возникают в результате гравитационного коллапса, происходящего в тот момент, когда звезда “выжигает” все термоядерное горючее и сила газового давления уже не может противостоять гравитации.

Если звезда достаточно массивна, она “схлопывается” до размера меньше радиуса Шварцшильда, превращаясь в чёрную дыру. Однако время у горизонта событий замедляется настолько, что для внешнего наблюдателя процесс коллапса почти останавливается (точно так же корабль, падающий в чёрную дыру, с точки зрения удалённого наблюдателя будет вечно падать к горизонту). По это причине все чёрные дыры, которые наблюдают учёные, – это вечно коллапсирующие объекты.

Астрофизики пока не смогли “увидеть” чёрные дыры непосредственно, однако есть множество объектов, “подозреваемых” в том, что они являются чёрными дырами. Большинство учёных уверено, что в центре нашей Галактики находится сверхмассивная чёрная дыра, известны двойные системы, где один из компонентов, скорее всего, чёрная дыра.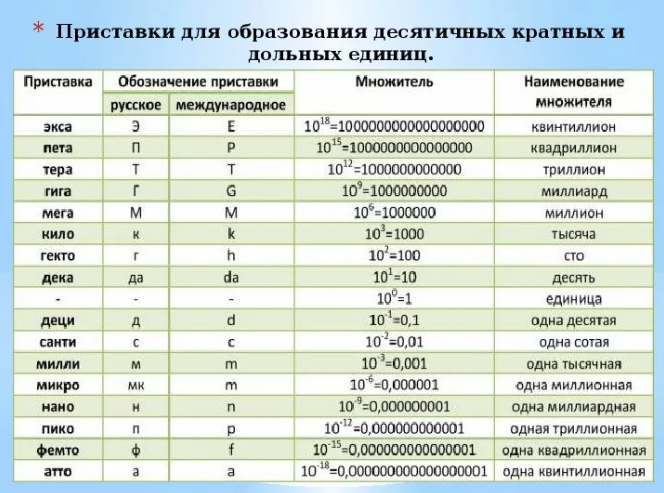

Однако некоторые исследователи считают, что могут существовать компактные массивные объекты, которые чуть-чуть не дотягивают до статуса чёрной дыры, их радиус лишь немного превышает радиус Шварцшильда. Не исключено, что некоторые из “подозреваемых” на самом деле как раз такие объекты. Но внешне их не отличить от чёрных дыр.

Российские физики придумали способ увидеть разницу между компактными массивными объектами и коллапсирующими объектами.

“Мы рассмотрели скалярное квантовое после на фоне чёрной дыры и компактного объекта и получили, что на фоне коллапсирующего объекта — чёрной дыры, нет связанных состояний, а на фоне компактного — есть”, — объясняет Федор Попов, сотрудник лаборатории физики высоких энергий МФТИ.

Он и его коллеги рассмотрели поведение скалярных частиц (спин таких частиц равен нулю, примером такой частицы может быть, например, бозон Хиггса в окрестностях чёрных дыр и массивных компактных объектов.

Учёные получили аналитические выражения для энергетического спектра частиц. Оказалось, что вблизи поверхности сверхкомпактной звезды, радиус которой чуть больше радиуса Шварцшильда, есть “потенциальная яма” — область пространства, где частицы попадают в гравитационную “ловушку”.

Задача в этом случае становится аналогичной простой задаче по квантовой механике, где нужно найти спектр частиц в потенциальной яме. Этот спектр оказывается дискретным, то есть в нем есть значения энергий, где частиц нет. Иначе говоря, потенциальная яма не выпускает частицы определенных энергий, и в спектре возникает “пустое место”.

В случае чёрной дыры вблизи сферы Шварцшильда не возникает стационарных потенциальных, поскольку идет постоянный процесс коллапса, граница “ямы” убегает, и энергетический спектр оказывается сплошным.

“Мы берём, рассеиваем пучок частиц на этом объекте, и смотрим на спектр. И видим, что если в этом спектре нет дискретных уровней, то это чёрная дыра, а если есть — то это компактный объект. Хотя мы сделали свою работу для бесспиновых частиц, можно предположить, что так же будет вести себя и спектр других типов частиц”, — говорит Попов.

Он отмечает, что это пока лишь теоретическая работа, у учёных пока нет средств наблюдать спектры частиц в окрестностях возможных черных дыр, однако шаг к этому сделан.

Результаты исследования опубликованы в научном издании Physical Review D.

• новости

Весь эфир

Вероятность: принцип неопределенности Гейзенберга

Цели обучения

К концу этого раздела вы сможете:

• Использовать обе версии принципа неопределенности Гейзенберга в расчетах.
• Объясните значение принципа неопределенности Гейзенберга для измерений.

Вероятностное распределение

Материя и фотоны — это волны, что означает, что они распространяются на некоторое расстояние. Каково положение частицы, например электрона? Это в центре волны? Ответ заключается в том, как вы измеряете положение электрона.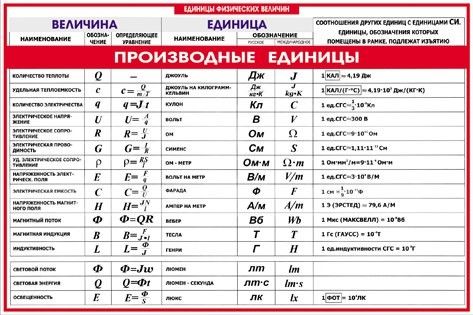 Эксперименты показывают, что вы найдете электрон в каком-то определенном месте, в отличие от волны. Но если вы создадите точно такую ​​же ситуацию и измерите ее снова, вы обнаружите, что электрон находится в другом месте, часто далеко за пределами любой экспериментальной неопределенности вашего измерения. Повторные измерения отобразят статистическое распределение местоположений, которое выглядит волнообразно. (См. рис. 1.)

Рис. 1. Построение дифракционной картины электронов, рассеянных от поверхности кристалла. Каждый электрон прибывает в определенное место, которое невозможно точно предсказать. Общее распределение, показанное внизу, можно предсказать как дифракцию волн, имеющих длину волны де Бройля электронов.

После того, как де Бройль предположил волновую природу материи, многие физики, в том числе Шредингер и Гейзенберг, исследовали последствия. Вскоре возникла идея, что из-за его волнового характера траектория и место назначения частицы не могут быть точно предсказаны для каждой частицы в отдельности . Однако каждая частица попадает в определенное место (как показано на рисунке 1). Собрав достаточно данных, вы получите распределение, связанное с длиной волны частицы и дифракционной картиной. Существует определенная вероятность обнаружения частицы в заданном месте, и общая закономерность называется распределением вероятностей . Те, кто разработал квантовую механику, разработали уравнения, которые предсказывали распределение вероятностей в различных обстоятельствах.

Несколько тревожно думать, что вы не можете точно предсказать, куда пойдет отдельная частица, или даже проследить за ней до места назначения. Давайте посмотрим, что произойдет, если мы попытаемся проследить за частицей. Рассмотрим двухщелевые картины, полученные для электронов и фотонов на рис. 2. Прежде всего отметим, что эти картины идентичны, следуя d sin θ = mλ , уравнение для двухщелевой конструктивной интерференции, разработанное в книге «Энергии фотонов и электромагнитный спектр», где d — расстояние между щелями, а λ — длина волны электрона или фотона.

Рис. 2. Двухщелевая интерференция электронов (а) и фотонов (б) идентична для одинаковых длин волн и одинакового расстояния между щелями. Оба паттерна являются вероятностными распределениями в том смысле, что они создаются отдельными частицами, пересекающими аппарат, траектории которых индивидуально предсказать невозможно.

Оба паттерна статистически складываются по мере того, как отдельные частицы падают на детектор. Это можно наблюдать для фотонов или электронов — пока давайте сосредоточимся на электронах. Вы можете себе представить, что электроны мешают друг другу, как это делают любые волны. Чтобы проверить это, вы можете уменьшить интенсивность до тех пор, пока между щелями и экраном не останется больше одного электрона. Выстраивается та же самая интерференционная картина! Это означает, что распределение вероятностей частиц охватывает обе щели, и частицы фактически интерферируют друг с другом. Означает ли это также, что электрон проходит через обе щели? Электрон — элементарная единица материи, которая не делится. Но это справедливый вопрос, и поэтому мы должны посмотреть, пересекает ли электрон одну щель, другую или обе. Одна из возможностей состоит в том, чтобы вокруг щелей располагались катушки, которые обнаруживают заряды, проходящие через них. Наблюдается, что электрон всегда проходит через одну или другую щель; он не разделяется, чтобы пройти через оба. Но есть одна загвоздка. Если вы определите, что электрон прошел через одну из щелей, вы больше не получите картину с двумя щелями — вместо этого вы получите интерференцию с одной щелью. Нет выхода, если использовать другой метод определения, через какую щель прошел электрон. Знание того, что частица прошла через одну щель, приводит к модели с одной щелью. Если вы не будете следить за тем, через какую щель проходит электрон, вы получите картину с двумя щелями.

Неопределенность Гейзенберга

Как знание того, через какую щель прошел электрон, меняет картину? Ответ принципиально важен — измерение влияет на наблюдаемую систему . Информация может быть потеряна, а в некоторых случаях невозможно измерить две физические величины одновременно с точной точностью. Например, вы можете измерить положение движущегося электрона, рассеивая от него свет или другие электроны. Эти зонды сами имеют импульс, и, рассеиваясь от электрона, они изменяют его импульс таким образом, что теряется информация . Есть предел абсолютному знанию, даже в принципе.

Рис. 3. Вернер Гейзенберг был одним из лучших физиков, разработавших раннюю квантовую механику. Его работа не только позволила описать природу в очень мелком масштабе, но и изменила наш взгляд на доступность знаний. Хотя он общепризнан за его гениальность и важность своей работы (например, он получил Нобелевскую премию в 1932 году), Гейзенберг оставался в Германии во время Второй мировой войны и возглавлял немецкие усилия по созданию ядерной бомбы, навсегда отчуждая себя от большую часть научного сообщества. (кредит: автор неизвестен, через Wikimedia Commons)

Вернер Гейзенберг первым сформулировал этот предел знания в 1929 году в результате своей работы по квантовой механике и волновым характеристикам всех частиц. (См. рис. 3). В частности, рассмотрим одновременное измерение положения и импульса электрона (это может быть любая частица). Существует неопределенность в положении Δ x , что примерно равно длине волны частицы. То есть Δ x ≈ λ .

Как обсуждалось выше, волна не находится в одной точке пространства. Если положение электрона измеряется неоднократно, будет наблюдаться разброс местоположений, что подразумевает неопределенность положения Δ х . Чтобы определить положение частицы, мы должны взаимодействовать с ней, например столкнуться с детектором. При столкновении частица теряет импульс. Это изменение импульса может быть где угодно, от близкого к нулю до полного импульса частицы, [латекс]p=\frac{h}{\lambda}\\[/latex]. Невозможно сказать, какое количество импульса будет передано детектору, поэтому также существует неопределенность в импульсе Δ p . На самом деле неопределенность импульса может быть такой же большой, как и сам импульс, что в форме уравнения означает, что [латекс]\Delta{p}\приблизительно\frac{h}{\lambda}\\[/latex].

Неопределенность положения можно уменьшить, используя более коротковолновый электрон, поскольку Δ x ≈ λ . Но укорочение длины волны увеличивает неопределенность импульса, поскольку [латекс]р=\фрак{ч}{\лямбда}\\[/латекс]. И наоборот, неопределенность импульса можно уменьшить, используя более длинноволновый электрон, но это увеличивает неопределенность положения. Математически вы можете выразить этот компромисс, умножив неопределенности. Длина волны отменяется, оставляя Δ x Δ p ≈ h .

Таким образом, если одна неопределенность уменьшается, другая должна увеличиваться, так что их произведение составляет ≈ ч .

Используя передовую математику, Гейзенберг показал, что лучшее, что можно сделать при одновременном измерении положения и импульса , это [латекс]\Delta{x}\Delta{p}\ge\frac{h }{4\пи}\\[/латекс].

Это известно как принцип неопределенности Гейзенберга . Невозможно измерить положение x и импульс p одновременно с неопределенностями Δ x и Δ p , которые умножаются, чтобы быть меньше [латекс]\фрак{ч}{4\пи}\\[/латекс]. Ни одна неопределенность не может быть равна нулю. Ни одна из неопределенностей не может стать малой без того, чтобы другая не стала большой. Небольшая длина волны позволяет точно измерять положение, но увеличивает импульс зонда до такой степени, что он еще больше нарушает импульс измеряемой системы. Например, если электрон рассеян атомом и его длина волны достаточно мала, чтобы определить положение электронов в атоме, его импульс может сбить электроны с их орбит таким образом, что будет потеряна информация об их первоначальном движении. Следовательно, невозможно проследить движение электрона по его орбите вокруг атома. Если вы измерите положение электрона, вы найдете его в определенном месте, но атом будет разрушен. Повторные измерения на идентичных атомах дадут интересные распределения вероятностей для электронов вокруг атома, но они не дадут информации о движении. Распределения вероятностей называются электронными облаками или орбиталями. Формы этих орбиталей часто показаны в учебниках по общей химии и обсуждаются в книге «Волновая природа материи вызывает квантование».

Пример 1. Принцип неопределенности Гейзенберга в определении положения и импульса атома

1. Если положение электрона в атоме измеряется с точностью до 0,0100 нм, какова неопределенность скорости электрона?
2. Если электрон имеет такую ​​скорость, какова его кинетическая энергия в эВ?

Стратегия

Неопределенность положения – это точность измерения, или Δ x = 0,0100 нм. Таким образом, наименьшая неопределенность импульса ∆ p можно рассчитать, используя [латекс]\Delta{x}\Delta{p}\ge\frac{h}{4\pi}\\[/latex]. Как только неопределенность импульса Δ p найдена, неопределенность скорости может быть найдена из Δ p = м Δ v .

Решение для части 1

Используя знак равенства в принципе неопределенности для выражения минимальной неопределенности, мы имеем

[латекс]\displaystyle\Delta{x}\Delta{p}=\frac{h}{4\ pi}\\[/latex]

Решение для Δ p 9{-19}\text{ J}}\right)=95,5\text{ эВ}\end{array}\\[/latex]

Обсуждение

Поскольку атомы имеют размер примерно 0,1 нм, зная положение электрон до 0,0100 нм достаточно хорошо локализует его внутри атома. Это было бы похоже на способность видеть детали размером в одну десятую размера атома. Но вытекающая из этого неопределенность скорости велика. Вы, конечно, не могли бы очень хорошо следить за ним, если его скорость настолько неопределенна. Чтобы получить дальнейшее представление о том, насколько велика неопределенность скорости, мы предположили, что скорость электрона равна его неопределенности, и обнаружили, что это дает кинетическую энергию 95,5 эВ. Это значительно больше, чем типичная разница энергий между уровнями в атомах (см. Таблицу 1 в Энергии фотонов и электромагнитного спектра), поэтому невозможно получить значимую энергию для электрона, если мы знаем его положение даже умеренно хорошо.

Почему мы не замечаем принцип неопределенности Гейзенберга в повседневной жизни? Ответ заключается в том, что постоянная Планка очень мала. Таким образом, нижняя граница погрешности измерения положения и импульса крупных объектов пренебрежимо мала. Мы можем обнаружить солнечный свет, отраженный от Юпитера, и проследить за планетой на ее орбите вокруг Солнца. Отраженный солнечный свет изменяет импульс Юпитера и создает неопределенность в его импульсе, но это совершенно ничтожно мало по сравнению с огромным импульсом Юпитера. Принцип соответствия говорит нам, что предсказания квантовой механики становятся неотличимыми от предсказаний классической физики для больших объектов, что и имеет место здесь.

Неопределенность Гейзенберга для энергии и времени

Существует другая форма принципа неопределенности Гейзенберга для одновременных измерений энергии и времени . В форме уравнения [латекс]\Delta{E}\Delta{t}\ge\frac{h}{4\pi}\\[/latex], где Δ E — неопределенность в энергии , а Δ t неопределенность во времени . Это означает, что в интервале времени Δ t невозможно точно измерить энергию — будет неопределенность Δ E в измерении. Для более точного измерения энергии (чтобы уменьшить Δ E ) нужно увеличить Δ t . Этот временной интервал может быть количеством времени, которое мы тратим на измерение, или это может быть количество времени, в течение которого существует определенное состояние, как в следующем примере 2.

Пример 2. Принцип неопределенности Гейзенберга для энергии и времени для Атом

Атом в возбужденном состоянии временно запасает энергию. Если время жизни этого возбужденного состояния составляет 1,0 × 10 ⁻¹⁰ с, какова минимальная неопределенность энергии состояния в эВ?

Стратегия

Минимальная неопределенность в энергии Δ E находится с использованием знака равенства в [латекс]\Delta{E}\Delta{t}\ge\frac{h}{4\pi}\\[ /латекс] и соответствует разумному выбору неопределенности во времени. Наибольшая неопределенность во времени, которая может быть, – это полное время жизни возбужденного состояния, или Δ t = 1,0 × 10 ^-10 с.

Решение

Решение принципа неопределенности для Δ 9{-6}\text{ эВ}\\[/latex]

Обсуждение

Время жизни 10 ⁻¹⁰ с типично для возбужденных состояний атомов — в масштабах человеческого времени они быстро излучают накопленную энергию. В результате получается неопределенность в энергии всего в несколько миллионных долей эВ. Эта неопределенность мала по сравнению с типичными энергиями возбуждения в атомах, которые составляют порядка 1 эВ. Так что здесь принцип неопределенности ограничивает точность, с которой мы можем измерить время жизни и энергию таких состояний, но не очень существенно.

Принцип неопределенности для энергии и времени может иметь большое значение, если срок службы системы очень короток. Тогда Δ t очень мало, а Δ E , следовательно, очень велико. Некоторые ядра и экзотические частицы имеют чрезвычайно короткое время жизни (всего 10 90 151 -25 90 152 с), что приводит к неопределенности в энергии, достигающей многих ГэВ (10 90 151 9 90 152 эВ). Запасенная энергия проявляется в виде увеличения массы покоя, а это означает, что существует значительная неопределенность в отношении массы покоя короткоживущих частиц. При повторном измерении получается разброс масс или энергий распада. Разброс Δ Е . Вы можете спросить, можно ли избежать этой неопределенности в энергии, не измеряя время жизни. Ответ – нет. Природа знает время жизни, и поэтому его краткость влияет на энергию частицы. Это настолько хорошо установлено экспериментально, что неопределенность в энергии распада используется для расчета времени жизни короткоживущих состояний. Некоторые ядра и частицы настолько короткоживущие, что их время жизни трудно измерить. Но если их энергия распада может быть измерена, ее разброс составляет Δ E , и это используется в принципе неопределенности [latex]\left(\Delta{E}\Delta{t}\ge\frac{h}{4\pi}\right)\\[/latex] to рассчитать срок службы Δ t .

Существует еще одно следствие принципа неопределенности для энергии и времени. Если энергия неопределенна на Δ E , то сохранение энергии может быть нарушено на Δ E за время Δ t . Ни физик, ни природа не могут сказать, что закон сохранения энергии был нарушен, если нарушение временное и меньше неопределенности в энергии. Хотя это звучит достаточно безобидно, в последующих главах мы увидим, что это позволяет временно создавать материю из ничего и влияет на то, как природа передает силы на очень небольшие расстояния.

Наконец, обратите внимание на то, что при обсуждении частиц и волн мы заявили, что отдельные измерения дают точные или подобные частицам результаты. Определенное положение определяется каждый раз, когда мы наблюдаем, например, электрон. Но повторные измерения дают разброс значений, соответствующий характеристикам волны. Великий физик-теоретик Ричард Фейнман (1918–1988) заметил: «Что есть, так это частицы». Когда вы наблюдаете достаточное их количество, они распределяются, как и следовало ожидать от волнового явления. Однако мы не можем сказать, что происходит, когда они путешествуют, потому что, когда мы пытаемся измерить, мы влияем на путешествие.

Резюме раздела

• Материя обладает теми же интерференционными характеристиками, что и любая другая волна.
• Теперь существует распределение вероятностей местоположения частицы, а не определенное положение.
• Другим следствием волнового характера всех частиц является принцип неопределенности Гейзенберга, который ограничивает точность, с которой определенные физические величины могут быть известны одновременно. Для положения и импульса принцип неопределенности таков: [латекс]\Дельта{х}\Дельта{р}\ге\фрак{ч} {4\пи}\\[/латекс], где Δ x — неопределенность положения, а Δ p — неопределенность импульса.
• Для энергии и времени принцип неопределенности: [латекс]\Delta{E}\Delta{t}\ge\frac{h}{4\pi}\\[/latex], где Δ E — неопределенность энергии Δ t – неопределенность во времени.
• Эти малые пределы принципиально важны в квантово-механическом масштабе.

Концептуальные вопросы

1. Что такое принцип неопределенности Гейзенберга? Накладывает ли она ограничения на то, что может быть известно?

Задачи и упражнения

1. (a) Если положение электрона в мембране измеряется с точностью до 1,00 мкм, какова минимальная неопределенность скорости электрона? б) Если электрон имеет такую ​​скорость, какова его кинетическая энергия в эВ? (c) Каково значение этой энергии по сравнению с типичными энергиями молекулярной связи?
2. (a) Если положение иона хлора в мембране измеряется с точностью до 1,00 мкм, какова минимальная неопределенность его скорости, если его масса составляет 5,86 × 10 ⁻²⁶ кг? (b) Если ион имеет эту скорость, какова его кинетическая энергия в эВ и как она соотносится с типичными энергиями связи молекул?
3. Предположим, что скорость электрона в атоме известна с точностью 2,0 × 10 ³ м/с (достаточно точно по сравнению с орбитальными скоростями). Какова минимальная неопределенность положения электрона и как она соотносится с приблизительным размером атома 0,1 нм?
4. Скорость протона в ускорителе известна с точностью до 0,250% скорости света. (Это может быть мало по сравнению с его скоростью.) Какова наименьшая возможная неопределенность его положения?
5. Относительно долгоживущее возбужденное состояние атома имеет время жизни 3,00 мс. Какова минимальная неопределенность его энергии?
6. (a) Время жизни крайне нестабильного ядра составляет 10 ⁻²⁰ с. Какова наименьшая неопределенность в энергии его распада? б) Сравните это с энергией покоя электрона.
7. Энергия распада короткоживущей частицы имеет погрешность 1,0 МэВ из-за ее короткого времени жизни. Какой наименьший срок службы у него может быть?
8. Энергия распада короткоживущего возбужденного состояния ядра имеет погрешность 2,0 эВ из-за его короткого времени жизни. Какой наименьший срок службы у него может быть?
9. Какова приблизительная неопределенность массы мюона, определяемой по времени его распада?
10. Выведите приближенную форму принципа неопределенности Гейзенберга для энергии и времени, Δ E Δ t ≈ h , используя следующие аргументы: где λ — длина волны фотона, использованного для его исследования, существует неопределенность во времени, за которое фотон проходит Δ х . Кроме того, фотон обладает энергией, связанной с его длиной волны, и он может передавать часть или всю эту энергию исследуемому объекту. Таким образом, неопределенность энергии объекта также связана с λ . Найдите Δ t и Δ E ; затем умножьте их, чтобы получить приблизительный принцип неопределенности.

Глоссарий

Принцип неопределенности Гейзенберга: фундаментальный предел точности, с которой могут быть измерены пары величин (импульс и положение, энергия и время)

неопределенность в энергии:  недостаток точности или незнание точных результатов измерения энергии

неопределенность во времени:  недостаток точности или незнание точных результатов в измерениях времени

неопределенность в импульсе .0005

распределение вероятностей: общее пространственное распределение вероятностей найти частицу в заданном месте

Избранные решения задач и упражнений

1. (a) 57,9 м/с; (б) 9.55 × 10 ^–9 эВ; (c) Из таблицы 1 в разделе «Энергии фотонов и электромагнитный спектр» мы видим, что типичные энергии молекулярной связи находятся в диапазоне примерно от 1 эВ до 10 эВ, поэтому результат в части (b) примерно на 9 порядков меньше, чем типичные энергии молекулярной связи.

3. 29 нм; 290 раз больше

5. 1,10 × 10 ⁻¹³ EV

7. 3,3 × 10 ^-22 S

9. 2,66 × 10 ^-46 KG

00. Физики мелкой мегавейской карты Dosimetry

00.

Обзор

. 2018 Февраль; 126 (2): 205-213.

doi: 10.1016/j.radonc.2017.11.001. Epub 2017 30 ноября.

Педро Андрео ¹

принадлежность

• ¹ Отделение медицинской радиационной физики и ядерной медицины, больница Каролинского университета, Стокгольм, Швеция; Отделение онкологии-патологии, Каролинский институт, Стокгольм, Швеция. Электронный адрес: [email protected].

• PMID: 29191457
• DOI: 10.1016/j.radonc.2017.11.001

Обзор

Педро Андрео. Радиотер Онкол. 2018 фев.

. 2018 Февраль; 126 (2): 205-213.

doi: 10.1016/j.radonc.2017.11.001. Epub 2017 30 ноября.

Автор

Педро Андрео ¹

принадлежность

• ¹ Отделение медицинской радиационной физики и ядерной медицины, больница Каролинского университета, Стокгольм, Швеция; Отделение онкологии-патологии, Каролинский институт, Стокгольм, Швеция. Электронный адрес: [email protected].

• PMID: 29191457
• DOI: 10.1016/j.radonc.2017.11.001

Абстрактный

Возросший в последние годы интерес к использованию пучков фотонов малого мегавольтажа в передовых методах лучевой терапии привел к разработке рекомендаций по дозиметрии различными национальными и международными организациями. Их потребность в данных, подходящих для различных доступных клинических вариантов, касающихся лечебных учреждений и дозиметрического оборудования, вызвала значительный объем исследований в научном сообществе за последнее десятилетие. Многочисленные публикации в этой области привели не только к получению новых бесценных данных, но и в значительной степени способствовали лучшему пониманию физики их дозиметрии. Эта работа представляет собой обзор наиболее важных аспектов, определяющих физику фотонной дозиметрии малого мегавольтажа.

Ключевые слова: конструкция детектора; Материал детектора; Протоколы дозиметрии; Дозиметрия малых полей.

Copyright © 2017 Elsevier B.V. Все права защищены.

Похожие статьи

• Дозиметрия малых статических полей, используемых при дистанционной фотонной лучевой терапии: Краткое изложение TRS-483, международного свода правил МАГАТЭ-AAPM для справочных целей и определения относительной дозы.

  Палманс Х., Андрео П., Хук М.С., Сентьенс Дж., Кристаки К.Е., Мегзифене А. Палманс Х. и др. мед. физ. 2018 ноябрь;45(11):e1123-e1145. doi: 10.1002/mp.13208. Epub 2018 17 октября. мед. физ. 2018. PMID: 30247757 Обзор.

• Отчет рабочей группы AAPM 155: Дозиметрия фотонного пучка мегавольтажа в малых полях и неравновесных условиях.

  Das IJ, Francescon P, Moran JM, Ahnesjö A, Aspradakis MM, Cheng CW, Ding GX, Fenwick JD, Saiful Huq M, Oldham M, Reft CS, Sauer OA. Дас И.Дж. и др. мед. физ. 2021 окт;48(10):e886-e921. doi: 10.1002/mp.15030. Epub 2021 21 июля. мед. физ. 2021. PMID: 34101836

• Сравнение рекомендаций эталонных протоколов дозиметрии AAPM TG-51 и TG-51.

  Маккоу Т.Дж., Хван М.С., Джанг С.И., Хук М.С. Маккоу Т.Дж. и соавт. J Appl Clin Med Phys. 2017 июль; 18 (4): 140-143. doi: 10.1002/acm2.12110. Epub 2017 2 июня. J Appl Clin Med Phys. 2017. PMID: 28574211 Бесплатная статья ЧВК.

• Спектральное распределение плотности потока частиц в детекторах малого поля и его влияние на дозиметрию малого поля.

  Бенмахлуф Х., Андрео П. Бенмахлуф Х. и соавт. мед. физ. 2017 фев; 44 (2): 713-724. doi: 10.1002/mp.12042. Epub 2017 30 января. мед. физ. 2017. PMID: 28032369

• Дозиметрия клинических нейтронных и протонных пучков: обзор рекомендаций.

  Винкер С; Международное агентство по атомной энергии; Международная комиссия по радиационным единицам и измерениям. Винкир С. и соавт. Радиационная дозиметрия. 2004;110(1-4):565-72. doi: 10.1093/rpd/nch321. Радиационная дозиметрия. 2004. PMID: 15353710 Обзор.

Посмотреть все похожие статьи

Цитируется

• Оценка и сравнение дозиметрических характеристик Semiflex ^® 3D и микроалмаз в относительной дозиметрии под пучками фотонов 6 и 15 МВ в малых полях.

  Момени Харзанджи З., Ларизаде М.Х., Намиранян Н., Никфарджам А. Момени Харзанджи З. и др. J Biomed Phys Eng. 2022 1 октября; 12 (5): 477-488. doi: 10.31661/jbpe.v0i0.2008-1160. Электронная коллекция 2022 окт. J Biomed Phys Eng. 2022. PMID: 36313410 Бесплатная статья ЧВК.

• Межучрежденческая оценка определения коэффициента выхода малых месторождений в соответствии с рекомендациями IAEA/AAPM TRS-483.

  Лехнер В., Альфонсо Р., Ариб М., Хук М.С., Исмаил А., Кинхикар Р., Ларрага-Гутьеррес Х.М., Мани К.Р., Мапхумуло Н., Зауэр О.А., Шуир С., Сурияпи С., Кристаки К. Лехнер В. и соавт. мед. физ. 2022 авг; 49 (8): 5537-5550. doi: 10.1002/mp.15797. Epub 2022 8 июля. мед. физ. 2022. PMID: 35717637 Бесплатная статья ЧВК.

• Ввод в эксплуатацию системы планирования лечения первой радиотерапевтической установки, ориентированной на клиническую биологию.

  Simiele E, Capaldi D, Breitkreutz D, Han B, Yeung T, White J, Zaks D, Owens M, Maganti S, Xing L, Surucu M, Kovalchuk N. Симиеле Э. и др. J Appl Clin Med Phys. 2022 авг;23(8):e13638. doi: 10.1002/acm2.13638. Epub 2022 29 мая. J Appl Clin Med Phys. 2022. PMID: 35644039 Бесплатная статья ЧВК.

• Пучковый ввод в эксплуатацию первой системы лучевой терапии, управляемой клинической биологией.

  Хан Б., Капальди Д., Ковальчук Н., Симиеле Э., Уайт Дж., Закс Д., Син Л., Суручу М. Хан Б. и др. J Appl Clin Med Phys. 2022 июнь;23(6):e13607. doi: 10.1002/acm2.13607. Epub 2022 28 апр. J Appl Clin Med Phys. 2022. PMID: 35482018 Бесплатная статья ЧВК.

• Исследование точности алгоритма сплющенного конуса на малых полях и в неоднородных средах.