Путь и перемещение – чем отличается, формулы
4.2
Средняя оценка: 4.2
Всего получено оценок: 131.
4.2
Средняя оценка: 4.2
Всего получено оценок: 131.
Важнейшими понятиями кинематики являются понятия пути и перемещения. Рассмотрим их подробнее, а также узнаем, чем отличается путь от перемещения.
Траектория пути
Кинематика изучает движение тел безотносительно причин этого движения. Главной задачей кинематики является математическое описание положения тела в принятой системе отсчета и изменение этого положения со временем.
Положение тела в системе отсчета задается одной или несколькими координатами (в зависимости от числа измерений) и временем.
Рис. 1. Координаты тела в пространстве.Если тело движется, то в разные моменты времени координаты тела будут различны. Умножая скорость тела на время движения, можно найти длину пройденного пути:
$$s=vt$$
Однако, даже зная точку, где находилось тело в нулевой момент времени, мы далеко не всегда можем определить, в какой точке тело будет находиться в другой произвольный момент времени.
Дело в том, что с помощью приведенной формулы можно найти длину пройденного пути. А сам путь при этом может иметь любую, сколь угодно сложную форму. Линия, вдоль которой перемещается тело, вовсе необязательно будет прямой, она может быть и окружностью, и ломанной, и более сложной фигурой, состоящих из многих частей.
Линия, вдоль которой двигалось тело на рассматриваемом участке времени, называется траекторией пути или просто траекторией.
Перемещение
Чтобы всегда знать, в какой точке находится тело в заданный момент времени, необходимо знать не длину пройденного пути, а другую кинематическую характеристику – перемещение.
Перемещение – это вектор, соединяющий начальное положение тела с его конечным положением.
Зная начальную точку в нулевой момент времени и перемещение за некоторое время, можно всегда найти координату тела в конце пути.
Рис. 2. Путь и перемещение.Сходство и различие.
Путь и перемещение – это не одно и то же. Если движение происходит на плоскости или в пространстве и криволинейно, то длина траектории всегда будет больше модуля перемещения.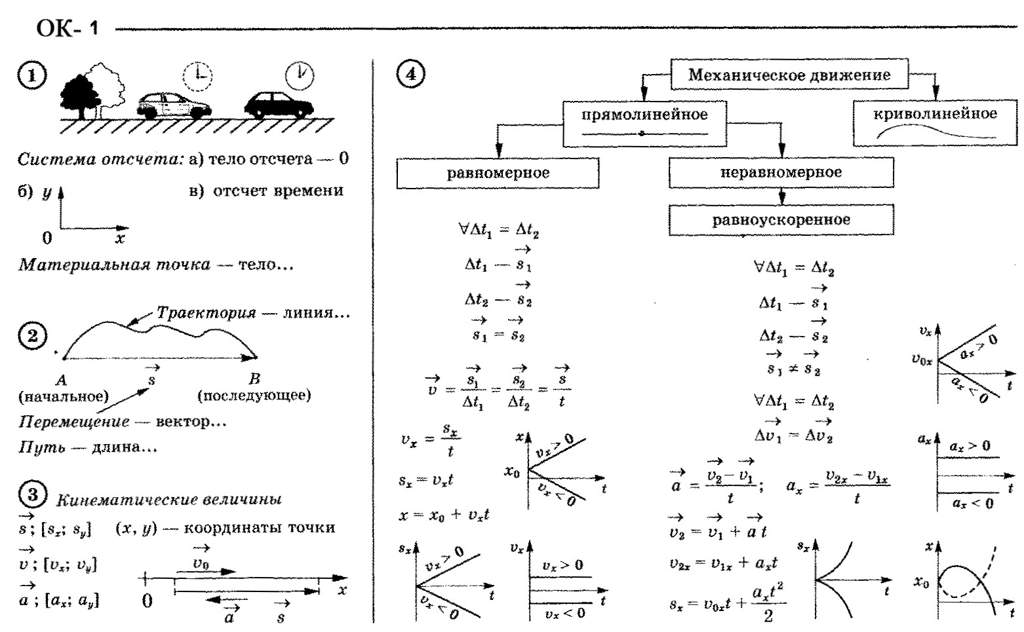
Происходит этот потому, что вектор является прямой, то есть, кратчайшим расстоянием между двумя точками. Криволинейная траектория же прямой не является.
Более того, перемещение может быть равно нулю, несмотря на то, что путь будет иметь большую длину. Например, планеты, двигаясь по окружностям, проходят за каждый оборот большой путь, однако, перемещение при этом никогда не превышает диаметра орбиты, и может быть равно нулю, если планета делает полный оборот.
Рис. 3. Орбиты планет.Однако, и перемещение и траектория пути служат одной и той же цели – описанию движения. Обе этих величины измеряются в единицах длины, к обоим могут быть применены формулы движения.
Но, если траектория описывает весь путь, пройденный телом, то перемещение акцентирует внимание на разнице положения тела между первым и последним моментами движения. Поэтому большинство формул в кинематике, в которые входит время, работают именно с перемещением.
Единственный случай, когда путь и перемещение равны – это случай прямолинейного движения, при условии, что скорость движения не меняла знак.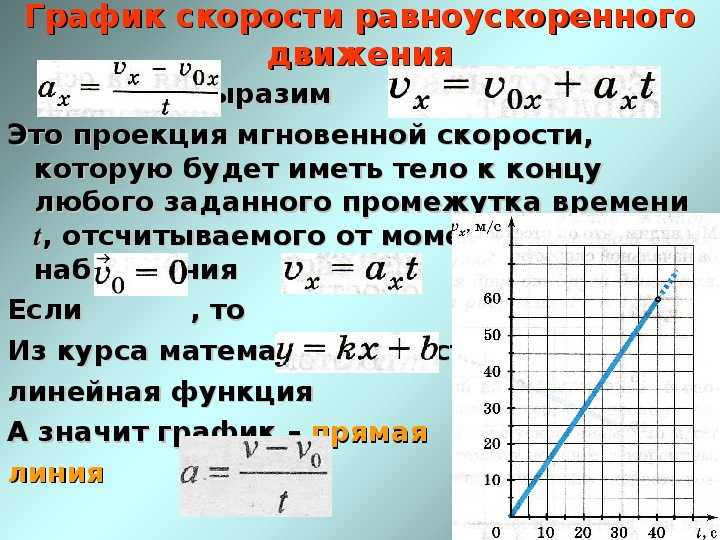
Что мы узнали?
Траектория пути – это линия, вдоль которой перемещалось тело во время своего движения. Перемещение – это вектор, направленный из точки начала движения в точку конца движения. Длина пути всегда равна или больше, чем длина перемещения.
Тест по теме
Доска почёта
Пока никого нет. Будьте первым!
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 131.
А какая ваша оценка?
Механические явления (коды ОГЭ 1.1 – 1.5)
Справочник по физики для ОГЭ. Версия для ознакомления перед покупкой.
Механические явления (коды ОГЭ 1.1 — 1.5).
Вы смотрели Справочник по физики «Механические явления (коды ОГЭ 1.1 — 1.5)». Выберите дальнейшее действие:
OSR-текст раздела (только текст)
Механические явления (коды ОГЭ 1.
1 — 1.5) 1.1. Механическое движение. Относительность движения. Траектория. Путь. Перемещение. Скорость. Ускорение. Равномерное и неравномерное движение. Средняя скорость. Формула для вычисления средней скорости Механическим движением называется изменение положения тела в пространстве относительно других тел с течением времени. Материальной точкой считается тело, размеры которого малы по сравнению с другими характерными размерами, встречающимися при решении поставленной задачи. Траектория – воображаемая линия, вдоль которой движется тело. Относительность механического движения: 1. Механическое движение можно наблюдать только относительно других тел. Тело, относительно которого рассматривается механическое движение, называется телом отсчёта. 2. В различных системах отсчёта скорость и перемещение, характеризующие движение одного и того же тела, могут иметь разные модули и направления. 3. Координаты тела, траектория движения, путь зависят от выбора системы отсчёта, то есть для одного и того же тела могут быть разными.
Основные физические величины, характеризующие механическое движение 1. Путь – длина траектории. Внимание! Путь не может быть отрицательным! 2. Перемещение – направленный отрезок прямой (вектор), соединяющий начальное положение тела с его последующим положением. Проекция вектора перемещения на координатную ось sХ = x – x0 , где х0 – начальная координата тела, х – конечная координата тела. Модуль вектора перемещения может не совпадать по числовому значению с длиной пути. Его можно рассчитать с помощью проекций вектора перемещения на координатные оси 3. Средняя путевая скорость равна отношению всего пути, пройденного телом, к промежутку времени, в течение которого этот путь пройден: ʋср = l/t. Внимание! Не является векторной величиной! 4. Вектор средней скорости равен отношению вектора перемещения к промежутку времени, в течение которого это перемещение произошло: . В проекциях на координатную ось 0х . Внимание! Вектор средней скорости сонаправлен с вектором перемещения. 5. Мгновенная скорость – скорость тела в данной точке пространства в данный момент времени.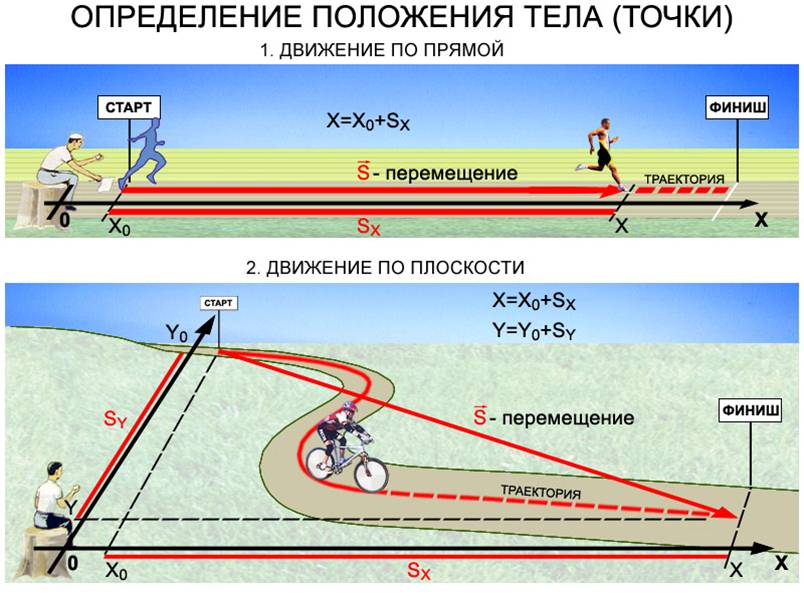
Внимание! 1). Вектор мгновенной скорости направлен по касательной к траектории движения в каждой её точке. 2). Проекция перемещения на соответствующую координатную ось численно равна площади под графиком зависимости проекции скорости на эту ось от времени. 6. Ускорение – векторная физическая величина, характеризующая изменение скорости с течением времени. Для равноускоренного движения вектор ускорения равен отношению вектора изменения скорости к тому промежутку времени, в течение которого это изменение произошло: . В проекциях на координатную ось . Физический смысл: численно равно изменению скорости за 1 с. 1.2. Равномерное прямолинейное движение. Зависимость координаты тела от времени в случае равномерного прямолинейного движения. Графики зависимости от времени для проекции скорости, проекции перемещения, пути, координаты при равномерном прямолинейном движении Равномерное прямолинейное движение – прямолинейное движение, при котором скорость тела не меняется. Внимание! Для описания любого прямолинейного движения достаточно одной координатной оси.
Уравнение движения – уравнение, выражающее зависимость координат от времени, например: x = x(t). Характер изменения основных величин, характеризующих движение 1. Ускорение. Равно нулю: а̅ = 0 . 2. Скорость. Не равна нулю, постоянна по величине и направлению: ʋ̅ = const. Для равномерного движения проекция вектора скорости равна отношению изменения координаты (проекции вектора перемещения) к тому промежутку времени, в течение которого это изменение произошло Физический смысл: численно равна изменению координаты (проекции вектора перемещения) за 1 с. 3. Перемещение. Вектор перемещения при равномерном прямолинейном движении прямо пропорционален времени: s = ʋt. В проекциях на координатную ось: sx = ʋxt. Внимание! Здесь и применительно к описанию зависимости других величин от времени под t понимается промежуток времени от начала движения (t0 = 0) ! В первом и во втором случае тело движется в направлении координатной оси Ох. Во втором случае тело движется в направлении, противоположном направлению оси Ох.
По модулю ʋ1 > ʋ2 > ʋ3 (сравниваем модули перемещения за одинаковые промежутки времени). Для расчёта проекции вектора перемещения удобно пользоваться графиком зависимости проекции скорости от времени: величина проекции вектора перемещения численно равна площади под графиком зависимости проекции скорости от времени. 4. Координата. Поскольку х = x0 + sx , зависимость координаты от времени описывается линейной функцией: х = x0 +vxt. На графике изображены следующие случаи движения. 1. Движение в направлении оси Ох, начальная координата отрицательна. 2. Движение в направлении оси Ох, начальная координата положительна. 3. Движение в направлении, противоположном направлению оси Ох, начальная координата равна нулю. 4. Движение в направлении оси Ох, начальная координата отрицательна. 5. Движение в направлении, противоположном направлению оси Ох, начальная координата положительна. 5. Путь. При равномерном прямолинейном движении в одном направлении равен модулю вектора перемещения: l = s. Внимание! Путь не может быть отрицательным! График зависимости проекции ускорения от времени График зависимости проекции вектора скорости на координатную ось от времени График зависимости проекции вектора перемещения на координатную ось от времени График зависимости координаты от времени 1.
3. Прямолинейное равноускоренное движение. Зависимость координаты тела от времени в случае равноускоренного прямолинейного движения. Формулы для проекции перемещения, проекции скорости и проекции ускорения при равноускоренном прямолинейном движении. Графики зависимости от времени для проекции ускорения, проекции скорости, проекции перемещения, координаты при равноускоренном прямолинейном движении Прямолинейное равноускоренное движение – прямолинейное движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени. Основные величины, характеризующие движение. 1. Ускорение. Не меняется, то есть постоянно по величине и направлению: . Физический смысл: ускорение численно равно изменению скорости за 1 с. Например, ускорение равно 5 м/с2 – это значит, что скорость тела изменяется на 5 м/с за каждую секунду своего движения. 2. Мгновенная скорость. Меняется равномерно, увеличиваясь или уменьшаясь одинаково за равные промежутки времени. Уравнение, описывающее изменение скорости с течением времени: , в проекциях ʋx = ʋ0x + axt.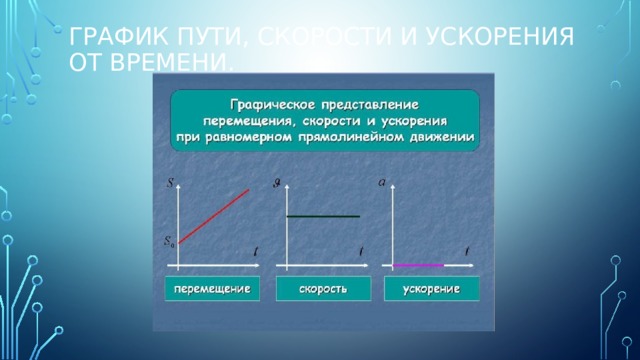
На графике изображены следующие случаи движения. 1. Проекция начальной скорости больше нуля. то есть тело движется в направлении координатной оси с увеличивающейся по модулю скоростью. 2. Проекция начальной скорости равна нулю. то есть тело движется в направлении координатной оси с увеличивающейся по модулю скоростью. 3. Проекция начальной скорости больше нуля, то есть тело движется в направлении координатной оси с уменьшающейся по модулю скоростью. 4. Проекция начальной скорости меньше нуля. то есть тело движется в направлении, противоположном направлению координатной оси, с уменьшающейся по модулю скоростью. 5. Проекция начальной скорости равна нулю. График зависимости проекции скорости на координатную ось от времени то есть тело движется в направлении, противоположном направлению координатной оси, с увеличивающейся по модулю скоростью. 6. Проекция начальной скорости отрицательна. то есть тело движется в направлении, противоположном направлению координатной оси, с увеличивающейся по модулю скоростью.
3. Перемещение. Зависимость перемещения от времени описывается квадратичной функцией: . В проекциях на координатную ось: . Иногда удобно пользоваться другими формулами для расчёта перемещения, которые получаются из исходной и уравнения зависимости проекции скорости от времени: Для расчёта проекции вектора перемещения удобно пользоваться графиком зависимости проекции скорости от времени. В случае, изображённом на рисунке: sx =S1 – S2, где S1, и S2 – числовые значения площадей треугольников. 4. Координата. Поскольку х = х0 + sx, зависимость координаты от времени тоже описывается квадратичной функцией: Если использовать другие варианты расчёта ускорения при равноускоренном движении, получаем: . 5. Путь. Если направление движения не меняется, то l = s. Если направление движения меняется, то l = s1 +s2, где s1 – модуль вектора перемещения до остановки, s2 – модуль вектора перемещения при движении в обратном направлении. Внимание! Путь не может быть отрицательным! 1.4. Свободное падение. Формулы, описывающие свободное падение тела по вертикали (движение тела вниз или вверх относительно поверхности Земли).
Графики зависимости от времени для проекции ускорения, проекции скорости и координаты при свободном падении тела по вертикали Свободное падение – движение под действием одной силы тяжести, частный случай равноускоренного движения. Ускорение свободного падения обозначается особой буквой: . Оно одинаково для всех тел в данной точке планеты, направлено к центру планеты и равно g ~ 10 м/с2 (см. раздел 1.13). В зависимости от направления начальной скорости тела может реализовываться один из представленных ниже вариантов движения. Независимо от направления движения тела (вверх или вниз) для свободного падения справедливы формулы для расчёта основных кинематических величин при равноускоренном движении с учётом того, что ускорение заранее известно и равно g = const. Проекция вектора перемещения: Координата в любой момент времени: или 1.5. Скорость равномерного движения тела по окружности. Направление скорости. Формула для вычисления скорости через радиус окружности и период обращения. Центростремительное ускорение.
Направление центростремительного ускорения. Формула для вычисления центростремительного ускорения. Формула, связывающая период и частоту обращения Равномерное вращение – движение точки с постоянной по модулю скоростью (ʋ = const) по траектории, представляющей собой окружность. Равномерное движение точки по окружности – это движение, при котором точка за любые равные промежутки времени проходит равные пути. Но так как скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Значит, равномерное движение по окружности – это ускоренное движение! Величины, характеризующие равномерное вращение 1. Линейная скорость равномерного вращения . По величине ʋ = l / t, где l – путь, пройденный по дуге окружности за промежуток времени t. Вектор линейной скорости в каждой точке направлен по касательной к дуге окружности в данной точке. 2. Период обращения . Время одного полного оборота: Т = t / N, где N – число полных оборотов за промежуток времени t. 3. Частота обращения .
Число оборотов в единицу времени: v = N / t. Связана с периодом обращения соотношением v = 1 / T. Внимание! Полезно установить связь между линейной скоростью с другими параметрами обращения! За один полный оборот . 4. Центростремительное ускорение : где ʋ – модуль линейной скорости в данной точке окружности. Вектор центростремительного ускорения перпендикулярен вектору скорости и направлен по радиусу к центру окружности. Центростремительное ускорение меняет скорость по направлению, но не меняет по величине. При равномерном вращении центростремительное ускорение постоянно по величине и связано с периодом и частотой вращения соотношениями:1.1. Механическое движение. Относительность движения. Траектория. Путь. Перемещение. Скорость. Ускорение. Равномерное и неравномерное движение. Средняя скорость. Формула для вычисления средней скорости.
1.2. Равномерное прямолинейное движение. Зависимость координаты тела от времени в случае равномерного прямолинейного движения. Графики зависимости от времени для проекции скорости, проекции перемещения, пути, координаты при равномерном прямолинейном движении.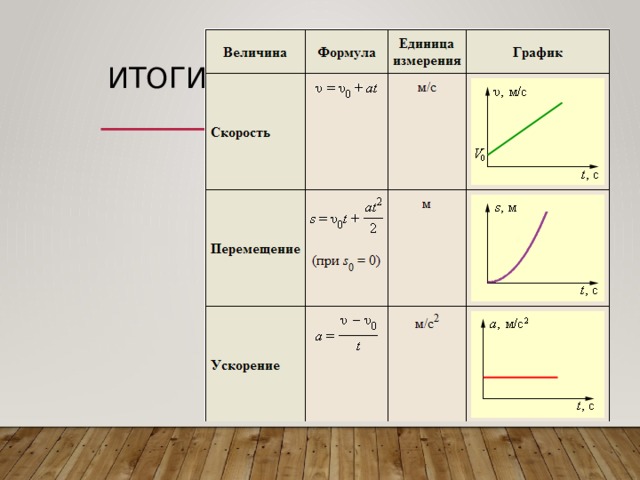
1.3. Прямолинейное равноускоренное движение. Зависимость координаты тела от времени в случае равноускоренного прямолинейного движения. Формулы для проекции перемещения, проекции скорости и проекции ускорения при равноускоренном прямолинейном движении. Графики зависимости от времени для проекции ускорения, проекции скорости, проекции перемещения, координаты при равноускоренном прямолинейном движении.
1.4. Свободное падение. Формулы, описывающие свободное падение тела по вертикали (движение тела вниз или вверх относительно поверхности Земли). Графики зависимости от времени для проекции ускорения, проекции скорости и координаты при свободном падении тела по вертикали.
1.5. Скорость равномерного движения тела по окружности. Направление скорости. Формула для вычисления скорости через радиус окружности и период обращения. Центростремительное ускорение. Направление центростремительного ускорения. Формула для вычисления центростремительного ускорения. Формула, связывающая период и частоту обращения.
Как быстро вы двигаетесь, когда сидите на месте? — Journal of Young Investigators
Автор: Сендес Иветт
Дата: ноябрь 2007 г.
В конце дня нет ничего лучше, чем рухнуть в большое удобное кресло, чтобы немного отдохнуть и расслабиться. Но прежде чем вы устроитесь поудобнее, задумывались ли вы когда-нибудь, сколько вы двигаетесь, даже когда изо всех сил стараетесь оставаться инертным комком? Ответ на этот вопрос на удивление сложен и может вас удивить!
Daily Motion
Практически каждый сегодня знает, что Земля круглая и делает один оборот за 24 часа. Именно это вращение вызывает ежедневное движение на нашей планете. Если бы вы стояли на экваторе Земли, вы бы двигались со скоростью почти 1000 миль/час (1600 км/час), но если бы вы начали идти к Северному или Южному полюсу, ваша скорость уменьшилась бы. Если вам трудно понять, почему представьте себе вращение мяча на палке: когда вы вращаете палку, «полюса» на палке остаются неподвижными, а точка в середине шара должна быстро двигаться, чтобы он прошел весь круг.
. Вам не нужно преодолевать такое большое расстояние ближе к полюсу, чтобы сделать один круг, поэтому ваша общая скорость будет ниже.
Хотя большинство людей на Земле двигаются со скоростью несколько сотен миль в час, в повседневной жизни мы почти не ощущаем это вращение. Тем не менее это ежедневное движение очень часто наблюдается учеными в форме того, что известно как эффект Кориолиса. Именно здесь объекты, которые выглядят так, как будто они движутся по прямой линии, кажутся искривленными, когда ваша система отсчета вращается. Военные артиллерийские подразделения впервые наблюдали эффект Кориолиса в шестнадцатом веке, когда они заметили, что их пушечные ядра отклоняются от цели при стрельбе на большие расстояния. Это связано с тем, что Земля будет вращаться под пушечным ядром в полете, поэтому с земли будет казаться, что пушечное ядро дрейфует в сторону. Именно это ежедневное вращение приводит к тому, что на Земле наблюдается эффект Кориолиса.
Эффект Кориолиса также очень важен в области метеорологии, поскольку вращение Земли определяет, как вращаются градиенты давления, подобные ураганам.
Он отличается для северного и южного полушарий: система в северном полушарии вращается против часовой стрелки, а система в южном полушарии вращается по часовой стрелке. Существует также городская легенда о том, что эффект Кориолиса определяет, каким образом вода будет стекать в ванну или унитаз, но в таком маленьком масштабе эффект Кориолиса незначителен.
Годовое движение
Следующим элементом движения, который необходимо рассмотреть, является годовое движение Земли вокруг Солнца. Земля находится на расстоянии 93 миллионов миль (150 миллионов километров) от Солнца и совершает оборот вокруг Солнца один раз в год, поэтому легко подсчитать, что мы путешествуем вокруг Солнца со скоростью 66 000 миль в час (107 миллионов километров в час). Для сравнения, если бы вы летели на этой скорости на самолете из Нью-Йорка в Лос-Анджелес, то путешествие заняло бы у вас чуть более 2 минут!
Однако, несмотря на эту головокружительную скорость, ни одна из сил, перечисленных здесь и далее, вообще не наблюдается в повседневной жизни на Земле.
Движение Солнца
Солнце может показаться стабильным приспособлением для жизни здесь, на Земле, но когда вы смотрите на масштабы размером с галактику, очевидно, что видимость может быть обманчивой. Наше Солнце — всего лишь одна из миллиардов звезд нашей Галактики Млечный Путь, которая имеет форму сплющенного диска с выпуклостью посередине. Наше Солнце находится примерно в 40 000 световых лет (расстояние, которое свет проходит за один год) от галактического центра Млечного Пути.
Все звезды в Галактике имеют индивидуальное движение относительно других звезд в своей части Галактики. Вычисляя среднее движение звезд в нашем звездном окружении, астрономы подсчитали, что Солнце (и Земля!) движутся со скоростью 43 000 миль/ч (70 000 км/ч), что является типичной случайной скоростью движения звезд в этой части нашей планеты. галактика. Стоит отметить, что эта скорость на самом деле меньше, чем скорость, с которой Земля движется по орбите вокруг Солнца — при такой скорости наше путешествие из Нью-Йорка в Лос-Анджелес заняло бы три с половиной минуты.
Когда дело доходит до скорости, случайное движение Солнца относительно других звезд вокруг нас меркнет по сравнению со скоростью его вращения внутри галактики. Наша галактика вращается, как гигантская вертушка, и, как и большинство других звезд, наше Солнце вращается вокруг центра галактики. Солнцу требуется колоссальные 225 миллионов лет, чтобы совершить один оборот вокруг галактики, временной масштаб настолько велик, что Солнце сделало это всего 20 раз с момента своего образования. Для этого наше Солнце должно двигаться с невероятной скоростью 483 000 миль в час (792000 км/час)! На такой скорости путешествие по Соединенным Штатам заняло бы всего 18 секунд.
Так что же происходит с планетами, вращающимися вокруг своих родительских звезд, когда они путешествуют по галактике? Если Солнце движется так быстро, почему Земля не остается позади? Ответ заключается в том, что Земля гравитационно связана с Солнцем точно так же, как Луна гравитационно связана с Землей. В результате, когда Солнце движется, все его планеты вынуждены двигаться вместе с ним, точно так же, как Луна продолжает вращаться вокруг Земли, несмотря на то, что Земля вращается вокруг Солнца.
Движение по Вселенной
Как вы уже догадались, скорость нашей галактики тоже надо учитывать. Однако для того, чтобы узнать его скорость, ученые сталкиваются с проблемой. До сих пор мы старались описывать различные скорости с точки зрения того, насколько быстро объект движется относительно других объектов. Это верно для скорости Земли по сравнению с Солнцем или Солнца по сравнению с центром галактики. Но какой была бы правильная система отсчета для движения нашей галактики? Мы всегда можем сравнить скорость Млечного Пути со скоростью другой галактики, но это не очень хорошо работает, потому что эта другая галактика тоже будет двигаться.
«Это сложная задача, — признает Джон Рул, физик из Университета Кейс Вестерн Резерв. Рул изучает космический микроволновый фон (CMB), который представляет собой излучение, оставшееся от ранней Вселенной всего через несколько тысяч лет после Большого взрыва. Поскольку это излучение заполняет все пространство, сказал Рул, «оно обеспечивает отличную систему отсчета для расчета относительного движения».
Это означает, что если мы сравним движение Млечного Пути с реликтовым излучением и вычтем все другие движения, о которых мы уже знаем (например, движение Земли вокруг Солнца), то останется движение Галактики Млечный Путь во Вселенной.
Когда астрономы делают этот расчет, оказывается, что Млечный Путь движется в космосе с поразительной скоростью 1,3 миллиона миль в час (2,1 миллиона км в час). При такой скорости перелет из Нью-Йорка в Лос-Анджелес займет чуть менее 7 секунд, что придаст новый смысл фразе «молния по стране». Хотя это может показаться удивительно быстрым, это все же намного медленнее, чем конечный предел скорости Вселенной, то есть скорость света. Луч света, совершающий такое же путешествие, оставил бы всех остальных в пыли, так как проделал бы это путешествие примерно за сотые доли секунды.
Галактика Млечный Путь в настоящее время мчится к области неба в созвездиях Льва и Девы, которую астрономы называют Великим Аттрактором. Считается, что Великий Аттрактор состоит из нескольких больших групп галактик, и многие соседние галактики также притягиваются в этом направлении.
Что насчет расширения?
Галактическое движение — это последняя часть головоломки движения, но это часто сбивает с толку людей, которые думают, что чего-то не хватает. «В конце концов, — говорится в размышлении, — я слышал, что Вселенная расширяется, так что не приведет ли это расширение к еще большему разделению объектов в Солнечной системе и галактике и, как следствие, к изменению их скорости?»
Хороший вопрос, но на самом деле это не совсем так.
«Вселенная расширяется, но только в однородных и изотропных масштабах», — говорит Рул. В этом масштабе все выглядит одинаково во всех направлениях, и вам нужно работать в очень большом масштабе, чтобы вселенная везде выглядела одинаково!
Возьмем батон пресного хлеба с изюмом, где батон – вселенная, изюм – галактики, а тесто – пустое пространство между галактиками. Если поставить батон в духовку, он расширится, и изюм будет дальше друг от друга, но сам изюм останется прежнего размера.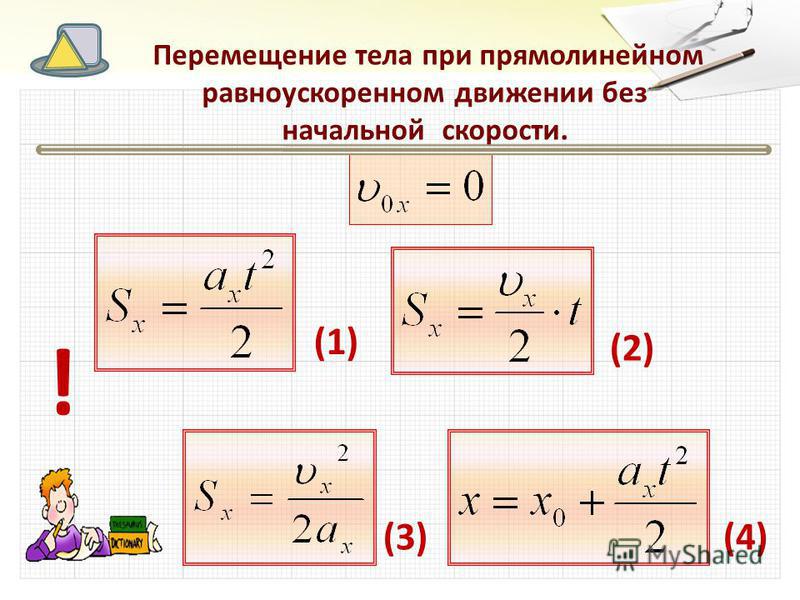
Расширение Вселенной работает аналогично этой модели: по мере расширения однородное тесто расширяется, но отдельные изюминки сохраняют свой размер и форму.
В дополнение к этому, если вы посмотрите на одну случайную часть нашей Солнечной системы или галактики, она будет сильно отличаться от другой случайной части. Это означает, к счастью, что вам не нужно беспокоиться о расширении Вселенной в нашей повседневной жизни.
Так во что же в сумме складываются все скорости? Если бы все было идеально выровнено в одном направлении, ваша конечная скорость составила бы 1,9 миллиона миль/ч (3 миллиона км/ч). Сидя в своем кресле, вы преодолеваете расстояние по стране всего за пять секунд, что определенно стоит обдумать в следующий раз, когда вы обнаружите, что удобно бездельничаете. Как жаль, что вы не можете накопить мили для часто летающих пассажиров за эту поездку!
Написано Иветт Сендес
Рецензировано Нирой Датта, Пуджа Гаталия
Опубликовано Пуджей Гаталией.
Возможно, лучший способ измерить скорость движения нашей собственной галактики в космосе
Вверху: изотропное распределение по всему небу выборки удаленных внегалактических объектов, смоделированной методом Монте-Карло. На левой панели двухмерные синие векторы показывают (вне масштаба) сигнал САПР, ожидаемый для LG, движущегося к вершине температурного диполя реликтового излучения, а на правой панели — случайный и доминирующий компонент ошибки, иллюстрирующий астрометрические неточности. добавлен. Внизу: мы моделируем сигнал САПР, восстановленный из выборки 2·10
Кредит: arXiv: 1802.04495 [астро-ф.CO]Большинство людей знают, что наша планета движется не только вокруг Солнца, но и в космосе как часть галактики Млечный Путь. Предыдущие исследования показали, что наша галактика движется в космосе со скоростью более 1 миллиона миль в час. Такие оценки основаны на измерении изменений положения Земли относительно очень удаленных объектов в ночном небе путем измерения величины красного смещения и последующего сравнения их друг с другом. Бел и Маринони утверждают, что можно получить более точные оценки скорости нашей галактики, изучая объекты, которые намного ближе к нам.
Исследователи предполагают, что ключом к измерению нашей собственной скорости является измерение нашего собственного ускорения относительно ускорения других объектов во Вселенной (они отмечают, что оба случая ускорения происходят из-за всеобщего расширения темной энергии и гравитационного притяжения между объектами).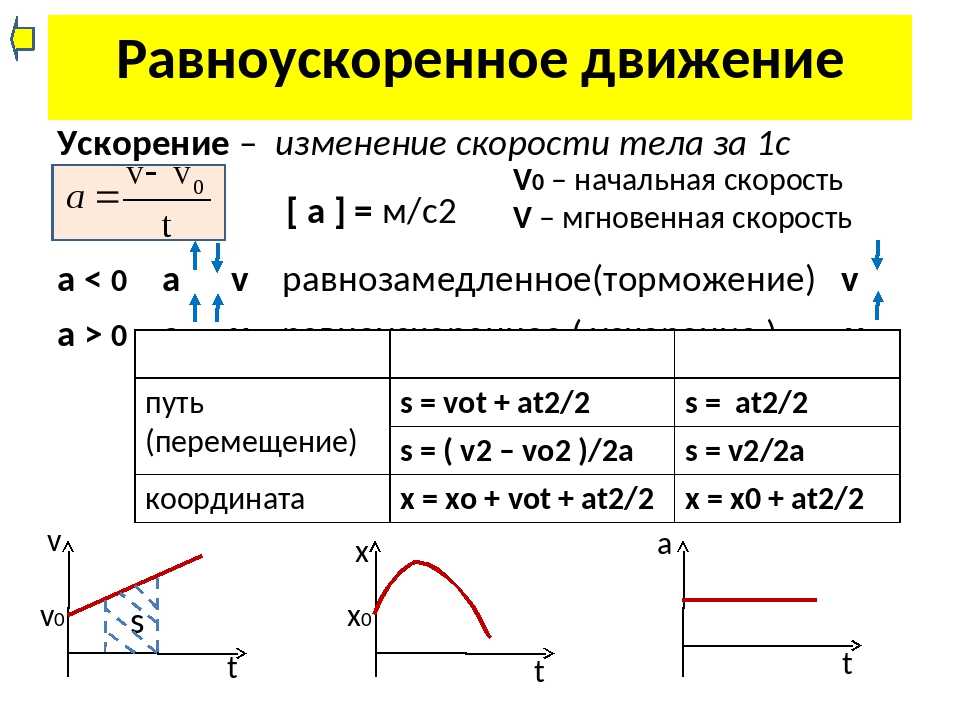
). Они предполагают, что это можно сделать, очень внимательно наблюдая и измеряя другие галактики и отслеживая, насколько сильно их положение относительно Земли меняется с течением времени. Они отмечают, что сделать это будет непросто — некоторые могут даже заявить, что с сегодняшними технологиями это невозможно. Но Бел и Маринони утверждают, что новая технология, подобная той, что используется в Большом синоптическом обзорном телескопе или даже в массиве квадратных километров, скорее всего, будет всем, что нужно. Потребовались бы согласованные усилия, чтобы использовать их для такой цели.
Исследователи отмечают, что их идея на данный момент является всего лишь предложением. Они все еще работают над более конкретными деталями, намекая на то, что вряд ли в ближайшее время будут предприняты попытки проверить их идеи с помощью новых телескопов. Они отмечают, что если их идеи когда-нибудь осуществятся, информация, полученная в результате таких усилий, может помочь доказать некоторые теории и, возможно, ограничить другие.
Дополнительная информация: Жюльен Бел и др. Предложение по обнаружению нашего ускорения в космосе в реальном времени, Письма о физическом обзоре (2018 г.). DOI: 10.1103/PhysRevLett.121.021101, Arxiv : arxiv.org/abs/1802.04495
РЕЗЮМЕ
Наше собственное ускорение по отношению к космическому микроволновому фону приводит к изменению углового положения далеких внегалактических источников в реальном времени. Космологическая составляющая этого сигнала аберрационного дрейфа, неинерционное движение, вызванное крупномасштабным распределением материи, в принципе может быть обнаружена будущими высокоточными астрометрическими экспериментами. Он предоставит интересные тесты на непротиворечивость стандартной модели космологии, установит независимые ограничения на амплитуду постоянной Хаббла и скорость линейного роста космических структур, а также поможет в поиске свидетельств новой физики за пределами стандартной модели. Мы представляем формализм этого нового космологического теста, обсуждаем физику, к которой он чувствителен, и показываем смоделированные прогнозы точности, с которой его можно реализовать.