Перемещение в физике единица измерения: Что такое перемещение? (статья) | Академия Хана - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

I Механика

1.1 Кинематика материальной точки

1.1.1 Понятие материальной точки. Система отсчета. Траектория, путь, перемещение Единицы измерения

Механика – часть физики, которая изучает закономерности механического движения. Для установления связей и отношений, которые имеют место в том или ином процессе, необходимо произвести измерения. Для этого нужно выбрать эталон данной физической величины и установить способ сравнения этих физических величин. Для построения системы единиц произвольно выбирают единицы для нескольких не зависящих друг от друга физических величин. Эти единицы называются основными. Основные единицы измерения имеют специальные эталоны измерения, которые, и хранятся в особых условиях. Остальные же величины и их единицы выводятся из законов, связывающих эти величины с основными единицами измерений. Они называются производными. Построенные по этому принципу системы единиц носят название абсолютных. Существует несколько систем единиц, отличающихся выбором тех величин, которые приняты за основные и для которых установлены специальные эталоны.

В настоящее время в физике согласно Государственному стандарту (ГОСТ 8.417—81), обязательна к применению Система Интернациональная (СИ), которая строится на семи основных единицах — метр, килограмм, секунда, ампер, кельвин, моль, кандела — и двух дополнительных — радиан и стерадиан.

Метр (м) —длина пути, проходимого светом в вакууме за 1/299 792 458 с.

Килограмм (кг) — масса, равная массе международного прототипа килограмма (платиноиридиевого цилиндра, хранящегося в Международном бюро мер и весов в Севре, близ Парижа).

Секунда (с) — время, равное 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.

Ампер (А) — сила постоянного тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, создает между этими проводниками силу, равную 2-10^-7Н на каждый метр длины.

Кельвин (К) — 1/273,16 часть термодинамической температуры тройной точки воды.

Моль (моль) — количество вещества системы, содержащей столько же структурных элементов, сколько атомов содержится в нуклиде

12С массой 0,012 кг.

Кандела (кд) — сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540•10¹² Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср.

Радиан (рад) — угол между двумя радиусами окружности, длина дуги между которыми равна радиусу.

Стерадиан (ср) — телесный угол с вершиной в центре сферы, вырезающий на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы.

С помощью основных величин можно получить другие величины либо используя выражения для законов природы, либо путем целесообразного определения через умножение или деление основных величин.

Например, Скорость = Путь/Время, Работа = Сила • Путь, Плотность = Масса/Объем, Заряд = Сила тока • Время, и т. д. При этом необходимо соблюдать правило размерности.

Размерность физической величины есть ее выражение в основных единицах. Размерности обеих частей физических равенств должны быть одинаковыми, так как физические законы не могут зависеть от выбора единиц физических величин. Поэтому можно проверять с помощью размерности правильность полученных физических формул.

Для представления физических величин, особенно в формулах, таблицах или на графиках, используются специальные символы — обозначения величин. В согласии с международными соглашениями. Единицы Международной системы (СИ) при практическом использовании часто оказываются слишком большими или слишком малыми, поэтому с помощью особых приставок могут быть образованы десятичные кратные и дольные единицы, если это не запрещено в отдельных случаях. Сводка этих приставок дана в специальных справочных таблицах. Существуют некоторые правила использования приставок. Приведем важнейшие из них:

а) единица измерения не может содержать более одной приставки.

б) комбинация сокращенного обозначения приставки и единицы измерения составляют единый символ.

Например, для измерения давления, допускается – исторически сложившееся единица измерения – мм.рт. столба, или, так как Фарад – очень крупная единица измерения, в повседневной жизни можно выражать емкость конденсатора долями Фарад: пФ, мФ и т.д. Но при расчетах необходимо придерживаться определенной системы, производить все расчеты в одной системе, предпочтительно в СИ.

Главной задачей механики является характеристика движения тела в пространстве с течением времени.

Механическое движение – это изменение с течением времени взаимного расположения тел или их частей в пространстве. Чтобы описать механическое движение применяют ряд научных абстракций, который позволяет отразить закономерности того или иного вида движения.

Движущееся тело обладает определенными размерами — протяженностью в пространстве. Иногда форма и размер тела не влияют на само движение и все процессы в ней. Тогда можно абстрагироваться от несущественного, незначительного, в условиях данной задачи, и рассматривать ее как геометрическую точку, приписав ей массу физического тела. Такая абстракция называется

материальной точкой. Следует указать, что вообще, вводя абстрактные понятия, в науке отвлекаются от всех свойств тел, несущественных для рассматриваемого явления, упрощая, таким образом, задачу и концентрируя внимание на тех свойствах тел, которые предопределяют характер изучаемого явления. Материальной точкой называется тело, размеры которого пренебрежимо малы по сравнению с масштабами движения.

Изучая более подробно внутренние свойства конкретных тел, мы можем прийти к понятию твердого тела как системы жестко связанных между собой материальных точек упругого тела, как системы точек, способных к небольшим относительным смещениям.

С помощью таких абстракций можно изучить, например, давление газа на стенки сосуда, в котором он заключен.

Определять положение точки «по отношению к пустому пространству» невозможно и физически бессмысленно. Можно определять положение любого тела, в том числе и материальной точки, лишь по отношению к другому, произвольно выбранному материальному телу, называемому телом отсчета. Выбранное таким образом тело условно считается неподвижным. Связывая с этим телом произвольную систему координат, мы получим

систему отсчета положений материальной точки. Для задания положения этого тела в пространстве система координат, которая будет каждый раз показывать ее местоположение в тот или иной момент времени общепринята трехмерная, простейшая декартовая прямоугольная система координат (рисунок – 1.1). Положение точки М в этой системе характеризуется тремя координатами: х — абсцисса, у — ордината и z — аппликата точки: М{х, у, z). Они являются проекциями радиуса-вектора ОМ=r, проведенного из начала координат в точку М(r).

Вместо координат х, у, z, радиус-вектор r может характеризовать положение точки в пространстве, задавая, например, его длину /r/ и два угла: θ, между радиусом-вектором r и осью 0Z и φ между проекцией r на плоскость XY и осью ОХ, как это показано на чертеже. Такая система описания движения называется сферической системой координат.

Во всех случаях, радиус-вектор r и положение точки в пространстве характеризуются количественно тремя числами, которые могут меняться независимо друг от друга. Это является математическим отражением того факта, что пространство

трехмерно. Поскольку три величины, характеризующие положение точки в пространстве, взаимно независимы, говорят, что материальная точка обладает тремя степенями свободы, которые описывают положение материальной точки или твердого тела в любой момент времени и называются законами движения. Такие уравнения называют кинематическими уравнениями движения. Для измерения хода времени, в течение которого происходило движение, необходим счетчик времени, который также входит, как обязательный для описания движения, элемент в систему отсчета.

Совокупность последовательных положений, занимаемых точкой М в процессе ее движения, образует в пространстве линию, называемую траекторией движущейся точки. На рисунке – 1.2 изображен отрезок траектории.


Рисунок – 1.1	Рисунок – 1.2

В какой-то момент времени t₁ точка М занимает на траектории положение М₁, характеризуемое радиус-вектором ОМ₁ = r₁. Если материальная точка движется, то ее положение в пространстве с течением времени меняется:

r = r(t)

(1.1)

либо

x = x(t), y = y(t), z = z(t)

(1.2)

M₁M₂ = S при этом представляет собой путь, пройденный точкой М за время ∆t. Вектор M₁M₂=∆r, проведенный из начального положения М₁ в конечное положение М₂, называется вектором перемещения точки М за время ∆t. При прямолинейном движении |∆r| = ∆s. В общем случае, как это видно из рисунка, |∆r| ≠∆s, но различие между ними тем меньше, чем меньше ∆r. Очевидно, что при произвольном криволинейном движении равенство |∆r|=∆s соблюдается лишь в пределе для бесконечно малого промежутка времени, т. е. когда ∆r →0:lim∆s/|∆r| = 1.Из рис. 1.2 видно, чтоr₂ = r₁ + |∆r|, или

∆r = r₂-r_l

(1.3)

т. е. вектор перемещения равен геометрической разности радиусов-векторов конечного и начального положения точки; этот вектор представляет собой приращение радиуса-вектора и характеризует изменение положения точки М в пространстве за время ∆t.

В чем разница между перемещением и путем. Перемещение

Траектория – это линия, которую тело описывает при движении.

Траектория пчелы

Путь – это длина траектории. То есть длина той, возможно, кривой линии, по которой двигалось тело. Путь скалярная величина ! Перемещение – векторная величина ! Это вектор, который проведен из начальной точки отправления тела в конечную точку. Имеет численное значение, равное длине вектора. Путь и перемещение – это существенно разные физические величины.

Обозначения пути и перемещения вы можете встретить разное:

Сумма перемещений

Пусть в течение промежутка времени t 1 тело совершило перемещение s 1 , а в течение следующего промежутка времени t 2 – перемещение s 2 . Тогда за все время движения перемещение s 3 – это векторная сумма

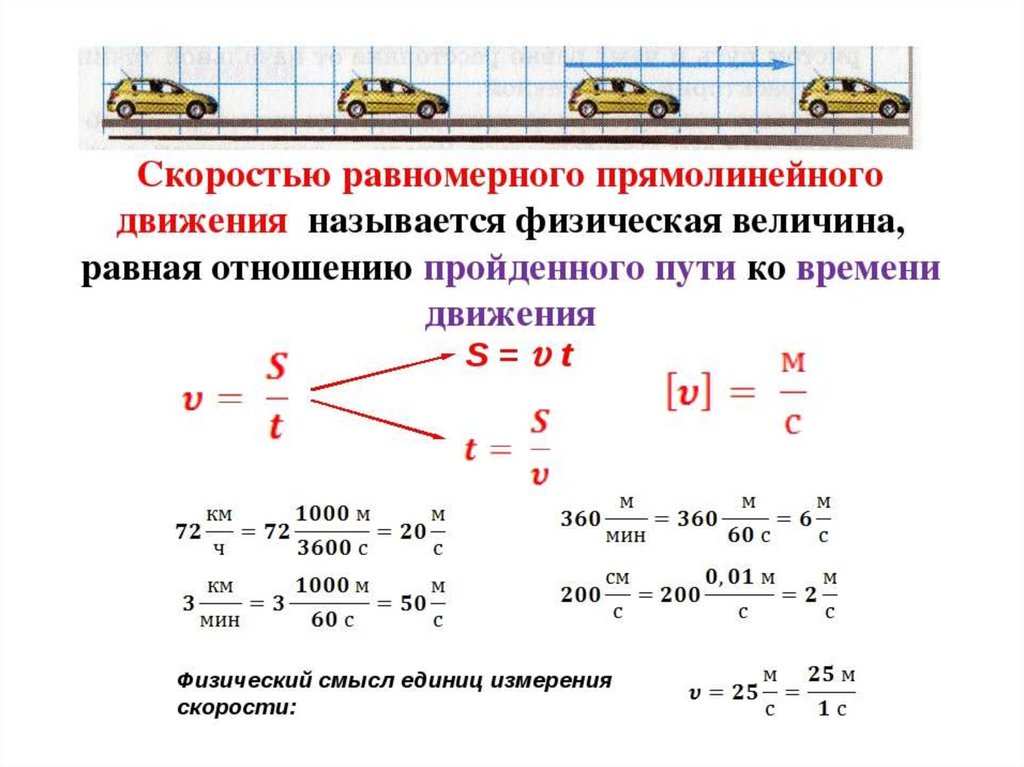
Равномерное движение

Движение с постоянной по модулю и по направлению скоростью. Что это значит? Рассмотрим движение машины. Если она едет по прямой линии, на спидометре одно и то же значение скорости (модуль скорости), то это движение равномерное. Стоит машине изменить направление (повернуть), это будет означать, что вектор скорости изменил свое направление. Вектор скорости направлен туда же, куда едет машина. Такое движение нельзя считать равномерным, несмотря на то, что спидометр показывает одно и то же число.

Направление вектора скорости всегда совпадает с направлением движения тела

Можно ли движение на карусели считать равномерным (если не происходит ускорение или торможение)? Нельзя, постоянно изменяется направление движения, а значит и вектор скорости. Из рассуждений можно сделать вывод, что равномерное движение – это всегда движение по прямой линии! А значит при равномерном движении путь и перемещение одинаковы (поясни почему).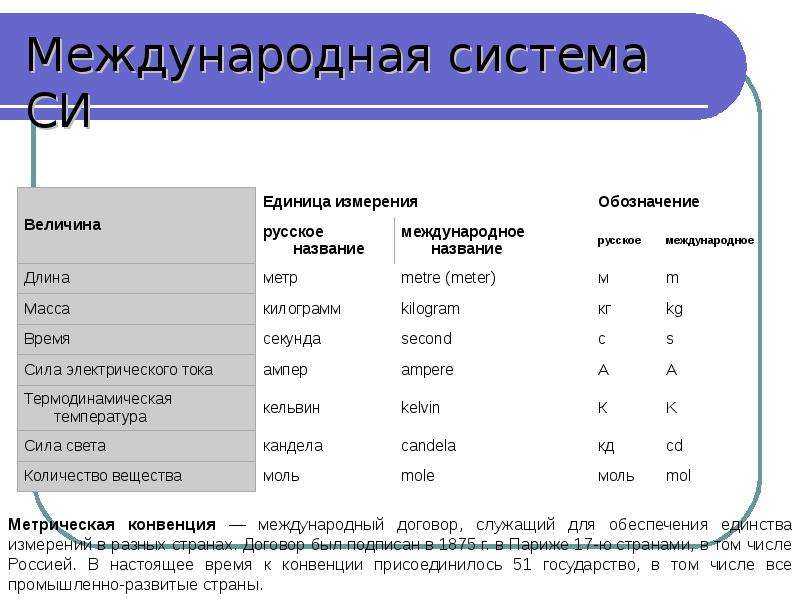

Нетрудно представить, что при равномерном движении за любые равные промежутки времени тело будет перемещаться на одинаковое расстояние.

Механика.

масса(кг)

Электрический заряд(Кл)

Траектория

Пройденный путь или просто путь(l ) –

Перемещение – это вектор S

Дайте определение и укажите единицу измерения скорости.

Скорость – векторная физическая величина, характеризующая быстроту перемещения точки и направление этого перемещения. [V]=м·с

Дайте определение и укажите единицу измерения ускорения.

Ускорение – векторная физическая величина характеризующая быстроту изменение модуля и направления скорости и равная приращению вектора скорости за единицу времени:

Дайте определение и укажите единицу измерения радиуса кривизны.

Радиус кривизны – скалярная физическая величина, обратная кривизне C в данной точке кривой и равная радиусу окружности, касательной к траектории в этой точке. Центр такой окружности называется центром кривизны для данной точки кривой. Радиус кривизны определяется: R = С -1 = , [R]=1м/рад.

Дайте определение и укажите единицу измерения кривизны

Траектории.

Кривизна траектории – физическая величина, равная , где – угол между касательными, проведенными в 2 точках траектории; – длина траектории между этими точками. Чем

Дайте определение и укажите единицу измерения угловой скорости.

Угловая скорость – векторная физическая величина, характеризующая быстроту изменения углового положения и равная углу поворота за ед. времени: . [w]= 1 рад/с=1с -1

Дайте определение и укажите единицу измерения периода.

Период (T) – скалярная физическая величина равная времени одного полного оборота тела вокруг своейоси или времени полного оборота точки по окружности. где N – число оборотов за время, равное t. [T]=1c.

Дайте определение и укажите единицу измерения частоты.

Частота обращения – скалярная физическая величина равная числу оборотов в единицу времени: . =1/с.

Дайте определение и укажите единицу измерения импульса тела (количества движения).

Импульс – векторная физическая величина, равная произведению массы на вектор скорости. . [p]=кг·м/с.

Дайте определение и укажите единицу измерения импульса силы.

Импульс силы – векторная физическая величина, равная произведению силы на время ее действия. [N]=Н·с.

Дайте определение и укажите единицу измерения работы.

Работа силы – скалярная физическая величина характеризующая действие силы и равная скалярному произведению вектора силы на вектор перемещения: где – проекция силы на направление перемещения, – угол между направлениями силы и перемещения (скорости). [А]= =1Н·м.

Дайте определение и укажите единицу измерения мощности.

Мощность – скалярная физическая величина характеризующая скорость совершения работы и равная работе произведённой за единицу времени: . [N]=1 Вт=1Дж/1с.

Дайте определение потенциальных сил.

Потенциальные или консервативныесилы – силы, работа которых при перемещении тела независит от траектории движения тела и определяется только начальным и конечным положениями тела.

Дайте определение диссипативных (непотенциальных) сил.

Непотенциальные силы – силы, при действии которых на механическую систему ее полная механическая энергия убывает, переходя в другие немеханические формы энергии.

Дайте определение плеча силы.

Плечом силы называется расстояние между осью и пря- мой, вдоль которой действует сила (расстояние x отсчитывается вдоль оси Ox перпендикулярной данной оси и силе).

Дайте определение момента силы относительно точки.

Момент силы относительно некоторой точки О – векторная физическая величина равная векторному произведению радиус- вектора проведённого из данной точки О в точку приложения силы и вектора силы. M= r * F= . [M] СИ =1Н·м=1кг·м 2 /с 2

Дайте определение абсолютно твёрдого тела.

Абсолютно твёрдое тело – тело, деформациями которого можно пренебречь.

Сохранения импульса.

Закон сохранения импульса: импульс замкнутой системы тел есть величина постоянная .

Механика.

1. Указать единицу измерения для понятий: сила (1 Н = 1 кг·м/с 2)

масса(кг)

Электрический заряд(Кл)

Дайте определение понятий: перемещение, путь, траектория.

Траектория – воображаемая линия, вдоль которой движется тело

Пройденный путь или просто путь(l ) –длина пути, по которому двигалось тело

Перемещение – это вектор S , направленный из начальной точки в конечную

Пусть из начального положения в точке А тело переместилось в конечное положение, которое находится в точке С, двигаясь по траектории в форме дуги АВС. Пройденный путь измеряется по дуге АВС. Длина этой дуги и есть путь.

Путь – это физическая величина, равная длине

траектории между начальным положением тела и

его конечным положением. Обозначается l.

Единицы пути – это единицы длины (м, см, км,…)

но основная единица длины в СИ метр. Записывается так

Расстояние между точками А и С не равно длине пути. Это другая физическая величина. Ее называют перемещением. Перемещение имеет не только численное значение, но и определенное направление, которое зависит от расположения начальной и конечной точек движения тела. Величины, имеющие не только модуль (численное значение), но и направление называются векторными величинами или просто векторами .

Перемещение – это векторная физическая величина, характеризующая изменение положения тела в пространстве, равная длине отрезка, соединяющего точку начального положения тела с точкой его конечного положения. Направлено перемещение от начального положения к конечному.

Обозначается . Единица .

Величины, не имеющие направления, как, например, путь, масса, температура, называются скалярными величинами или скалярами.

А могут быть равными путь и перемещение?

Если тело или материальная точка (МТ) движется вдоль прямой линии, и при этом всегда в одну и ту же сторону, то путь и перемещение совпадают, т.е. численно они равны . Так если в ущелье глубиной 100 м вертикально упадет камень, то его перемещение будет направлено вниз и s = 100 м . Путь l =100 м.

Если тело совершает несколько перемещений, то они складываются, но не так, как складываются числовые величины, а по другим правилам, по правилам сложения векторов. Вы их скоро пройдете в курсе математики. А пока рассмотрим пример.

Чтобы дойти до автобусной остановки, Петр Сергеевич идет сначала через двор 300 м на запад, а затем по проспекту 400 м на север. Найдите перемещение Петра Сергеевича и сравните его с величиной пройденного пути.

Дано: s 1 = 300 м; s 2 = 400 м.

______________________

s – ? l – ?

Решение:

Выполним чертеж. Чтобы найти весь путь, сложим два отрезка пути s 1 и s 2

l = s 1 + s 2 = 300 м +400 м = 700 м.

Чтобы найти перемещение, надо узнать длину отрезка, соединяющего начальное положение тела и конечное положение. Это длина вектора s.

Перед нами прямоугольный треугольник с известными катетами (300 и

400 м). Воспользуемся теоремой Пифагора, чтобы найти длину гипотенузы s:

Таким образом, путь, пройденный человеком, больше перемещения на 200 м.

Если бы, предположим, Петр Сергеевич, дойдя до остановки, вдруг решил вернуться назад и двинулся в обратном направлении, то длина его пути составила бы 1400 м, а перемещение – 0 м.

Система отсчета.

Решить основную задачу механики – значит указать, где будет находиться тело в любой заданный момент времени. Иными словами, рассчитать координаты тела. Да вот загвоздка: откуда отсчитывать будем координаты?

Можно, конечно, взять географические координаты – долготу и широту, но! Во-первых, тело (МТ) может перемещаться и вне планеты Земля. Во-вторых, система географических координат не учитывает трехмерность нашего пространства.

Для начала нужно выбрать тело отсчета . Это настолько важно, что иначе мы окажемся в ситуации, подобной той, что представлена в романе Р. Стивенсона «Остров сокровищ». Зарыв основную часть сокровища, капитан Флинт оставил карту и описание места.

Высокое дерево Подзорной горы. Направление – от дерева по тени в полдень. Пройти сто футов. Повернуть в направлении на запад. Пройти десять саженей. Копать на глубину десять вершков.

Недостаток описания места, где лежит клад, состоит в том, что дерево, которой в данной задаче является телом отсчета, невозможно найти по указанным признакам.

Этот пример говорит о важности выбора тела отсчета – любого тела, от которого ведется отсчет координат положения движущейся материальной точки.

Рассмотрите рисунок. В качестве движущегося объекта примите: 1) яхту; 2) чайку. За тело отсчета примите: а) скалу на берегу; б) капитана яхты; в) летящую чайку. Как зависит характер движения движущегося объекта, его координаты от выбора тела отсчета?

Описывая особенности движения того или иного тела, важно указывать относительно какого тела отсчета даются характеристики.

Попробуем ввести координаты тела или МТ. Воспользуемся прямоугольной декартовой системой координат ХУZ с началом в точке О. Помещаем начало системы отсчета там, где находится тело отсчета. От этой точки проводим три взаимно перпендикулярные координатные оси OX,OY,OZ. Теперь координаты материальной точки (x;y;z) можно будет указывать относительно тела отсчета.

Для изучения движения тела (МТ) нужны также часы или прибор для измерения времени. Начало отсчета времени свяжем с определенным событием. Чаще всего это начало движения тела (МТ).

Совокупность тела отсчета, системы координат, связанной с телом отсчета и прибора для измерения промежутков времени называется системой отсчета (СO) .

Если телом отсчета выбрано неподвижное тело, то и система отсчета будет неподвижной (НСО). Чаще всего за неподвижное тело отсчета выбирают поверхность Земли. Можно выбрать за тело отсчета движущееся тело и получить подвижную систему отсчета (ПСО).

Посмотрите на рисунок 1. Трехмерная система координат позволяет задать положение в пространстве любой точки. Например, координаты точки F, расположенной на столбике равны (6; 3; 1).

-2 – 1 0 1 2 3 4 5 6 7 8 9 10 X

Подумайте! Какую систему координат вы выберете при решении и задач, связанных с движением:

1) велосипедист участвует в соревнованиях на велотреке;

2) муха ползает по стеклу;

3) муха летает по кухне;

4) грузовик движется по прямому участку шоссе;

5) человек поднимается в лифте;

6) снаряд вылетает и летит от дула орудия.

Упражнение 1.

1. Выберите на рис.3 случаи, в которых совершается механическое движение.

3.В центре управления полетом находятся два оператора. Один контролирует параметры орбиты станции «Мир», а другой осуществляет стыковку корабля «Прогресс» с данной станцией. Какой из операторов может считать станцию «Мир материальной точкой?

4. Для исследования движения самолета-истребителя и воздушного шара (рис.4) выбрана прямоугольная система координат XOYZ. Охарактеризуйте систему отсчета, которая здесь использована. Можно ли было воспользоваться более простыми системами координат?

5.Спортсмен пробежал 400-метровую дистанцию (рис. 5). Найдите перемещение спортсмена и путь, пройденный им.

6. На рисунке 6 изображен лист растения, по которому ползет улитка. Рассчитайте, используя масштабную сетку, путь, пройденный улиткой от точки А до точки Б и от точки Б до точки В.

7. Машина, проехав по прямому участку шоссе от бензозаправочной станции до ближайшего населенного пункта, вернулась обратно. Рассчитайте модуль перемещения машины и пройденный ею путь. Что можно сказать о соотношении между модулем перемещения и пройденным ею расстоянием, если автомобиль проехал только от бензозаправки до населенного пункта?

| | 3 | | |

Класс: 9

Цели урока:

Образовательная:
– ввести понятия “перемещение”, “путь”, “траектория”.
Развивающая:
– развивать логическое мышление, правильную физическую речь, использовать соответствующую терминологию.
Воспитательная:
– достигать высокой активности класса, внимания, сосредоточенности учащихся.

Оборудование:

пластмассовая бутылка вместимостью 0,33 л с водой и со шкалой;
медицинский флакончик вместимостью 10 мл (или малая пробирка) со шкалой.

Демонстрации: Определение перемещения и пройденного пути.

Ход урока

1. Актуализация знаний.

– Здравствуйте, ребята! Садитесь! Сегодня мы с вами продолжим изучать тему “Законы взаимодействия и движения тел” и на уроке познакомимся с тремя новыми понятиями (терминами), касающихся этой темы. А пока проверим выполнение вами домашнего задания у данному уроку.

2. Проверка домашнего задания.

Перед уроком один учащийся выписывает на доске решение следующего домашнего задания:

Двум учащимся раздаются карточки с индивидуальными заданиями, которые выполняются во время устной проверки упр. 1 стр. 9 учебника.

1. Какую систему координат(одномерную, двухмерную, трехмерную) следует выбрать для определения положения тел:

а) трактор в поле;
б) вертолет в небе;
в) поезд
г) шахматная фигура на доске.

2. Дано выражение: S = υ 0 · t + (а · t 2) / 2, выразите: а, υ 0

1. Какую систему координат (одномерную, двухмерную, трехмерную) следует выбрать для определения положения таких тел:

а) люстра в комнате;
б) лифт;
в) подводная лодка;
г) самолет на взлетной полосе.

2. Дано выражение: S = (υ 2 – υ 0 2) / 2 · а, выразите: υ 2 , υ 0 2 .

3. Изучение нового теоретического материала.

С изменениями координат тела связана величина, вводимая для описания движения, – ПЕРЕМЕЩЕНИЕ.

Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.

Перемещение принято обозначать буквой . В СИ перемещение измеряется в метрах (м).

– [ м ] – метр.

Перемещение – величина векторная, т.е. кроме числового значения имеет еще и направление. Векторную величину изображают в виде отрезка , который начинается в некоторой точке и заканчивается острием, указывающим направление. Такой отрезок-стрелка называется вектором.

– вектор, проведенный из точки М в М 1

Знать вектор перемещения – значит, знать его направление и модуль. Модуль вектора – это скаляр, т.е. численное значение. Зная начальное положение и вектор перемещения тела, можно определить, где находится тело.

В процессе движения материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом движущаяся точка “описывает” в пространстве какую-то линию. Иногда эта линия видна, – например, высоко летящий самолет может оставлять за собой след в небе. Более знакомый пример – след куска мела на доске.

Воображаемая линия в пространстве, по которой движется тело называется ТРАЕКТОРИЕЙ движения тела.

Траектория движения тела – это непрерывная линия, которую описывает движущееся тело (рассматриваемое как материальная точка) по отношению к выбранной системе отсчета.

Движение, при котором все точки тела движутся по одинаковым траекториям , называется поступательным .

Очень часто траектория – невидимая линия. Траектория движущейся точки может быть прямой или кривой линией. Соответственно форме траектории движение бывает прямолинейным и криволинейным .

Длина траектории – это ПУТЬ . Путь является скалярной величиной и обозначается буквой l. Путь увеличивается, если тело движется. И остается неизменным, если тело покоится. Таким образом, путь не может уменьшаться с течением времени.

Модуль перемещения и путь могут совпадать по значению, только в том случае, если тело движется вдоль прямой в одном направлении.

Чем же отличается путь от перемещения? Эти два понятия часто смешивают, хотя на самом деле они очень сильно отличаются друг от друга. Рассмотрим эти отличия: (Приложение 3 ) (раздаются в виде карточек каждому ученику)

Путь – скалярная величина и характеризуется только числовым значением.
Перемещение – векторная величина и характеризуется как числовым значением (модулем), так и направлением.
При движении тела путь может только увеличиваться, а модуль перемещения может как увеличиваться, так и уменьшаться.
Если тело вернулось в начальную точку, его перемещение равно нулю, а путь нулю не равен.

	Путь	Перемещение
Определение	Длина траектории, описываемой телом за определенное время	Вектор, соединяющий начальное положение тела с его последующим положением
Обозначение	l [ м ]	S [м ]
Характер физических величин	Скалярная, т. е. определяется только числовым значением	Векторная, т.е. определяется числовым значением (модулем) и направлением
Необходимость введения	Зная начальное положение тела и путь l, пройденный за промежуток времени t, нельзя определить положение тела в заданный момент времени t	Зная начальное положение тела и S за промежуток времени t, однозначно определяется положение тела в заданный момент времени t
	l = S в случае прямолинейного движения без возвратов

4. Демонстрация опыта (учащиеся выполняют самостоятельно на своих местах за партами, учитель вместе с учащимися выполняет демонстрацию этого опыта)

Заполните водой до горловины пластмассовую бутылку со шкалой.
Флакончик со шкалой заполните водой на 1/5 его объема.
Наклоните бутылку так, чтобы вода подошла к горловине, но не вытекала из бутылки.
Быстро опустите флакончик с водой в бутылку (не закрывая его пробкой) так, чтобы горловина флакончика вошла в воду бутылки. Флакончик плавает на поверхности воды в бутылке. Часть воды при этом из бутылки выльется
Завинтите крышку бутылки.
Сжимая боковые стенки бутылки, опустите поплавок на дно бутылки.

Ослабляя давление на стенки бутылки, добейтесь всплытия поплавка. Определите путь и перемещение поплавка:________________________________________________________
Опустите поплавок на дно бутылки. Определите путь и перемещение поплавка:______________________________________________________________________________
Заставьте поплавок всплыть и утонуть. Каков путь и перемещение поплавка в этом случае?_______________________________________________________________________________________

5. Упражнения и вопросы для повторения.

Путь или перемещение мы оплачиваем при поездке в такси? (Путь)
Мяч упал с высоты 3 м, отскочил от пола и был пойман на высоте 1 м. 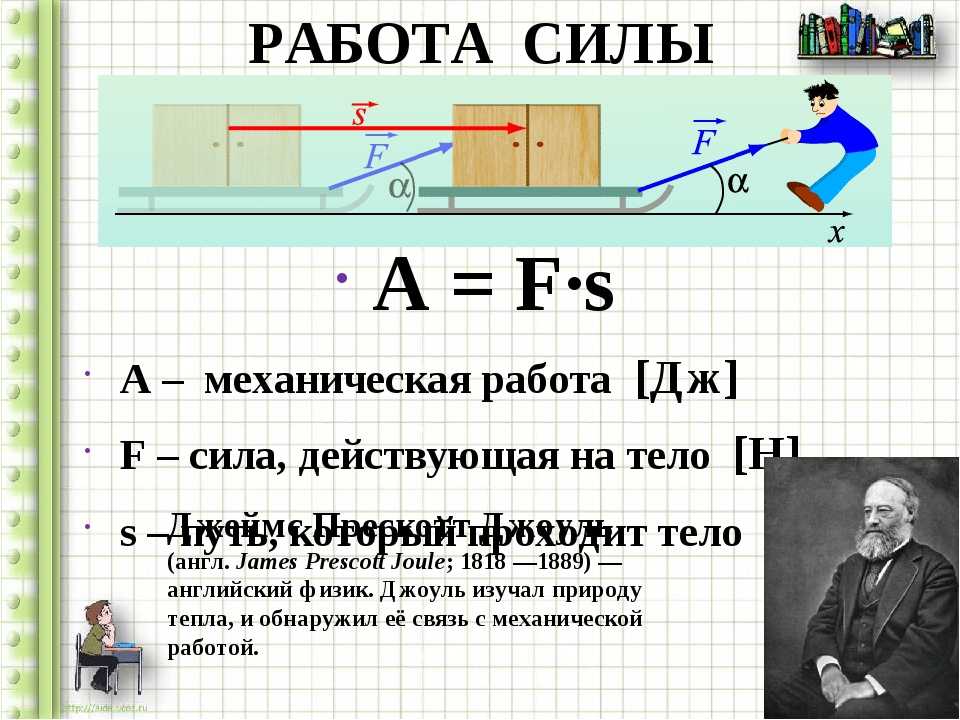найти путь и перемещение мяча. (Путь – 4 м, перемещение – 2 м.)

6. Итог урока.

Повторение понятий урока:

– перемещение;
– траектория;
– путь.

7. Домашнее задание.

§ 2 учебника , вопросы после параграфа, упражнение 2 (стр.12) учебника , повторить выполнение опыта урока дома.

Список литературы

1. Перышкин А.В., Гутник Е.М . Физика. 9 кл.: учеб.для общеобразоват.учреждений – 9-е изд., стереотип. – М.: Дрофа, 2005.

«Физика – 10 класс»

Чем отличаются векторные величины от скалярных?

Линия, по которой движется точка в пространстве, называется траекторией .

В зависимости от формы траектории все движения точки делятся на прямолинейные и криволинейные.

Если траекторией является прямая линия, движение точки называется прямолинейным , а если кривая – криволинейным .

Пусть в какой-то момент времени движущаяся точка занимает положение М 1 (рис. 1.7, а). Как найти её положение спустя некоторый промежуток времени после этого момента?

Допустим, известно что точка находится на расстоянии l относительно своего начального положения. Сможем ли мы в этом случае однозначно определить новое положение точки? Очевидно, нет, поскольку есть бесчисленное множество точек, которые удалены от точки М 1 на расстояние l. Чтобы однозначно определить новое положение точки, надо ещё знать, в каком направлении от точки М 1 следует отложить отрезок длиной l.

Таким образом, если известно положение точки в какой-то момент времени, то найти её новое положение можно с помощью определённого вектора (рис. 1.7, б).

Вектор, проведённый из начального положения точки в её конечное положение, называется вектором перемещения или просто перемещением точки

Поскольку перемещение – величина векторная, то перемещение, показанное на рисунке (1.7, б), можно обозначить

Покажем, что при векторном способе задания движения перемещение можно рассматривать как изменение радиус-вектора движущейся точки.

Пусть радиус-вектор 1 задаёт положение точки в момент времени t 1 , а радиус-вектор 2 – в момент времени t 2 (рис. 1.8). Чтобы найти изменение радиус-вектора за промежуток времени Δt = t 2 – t 1 , надо из конечного вектора 2 вычесть начальный вектор 1 . Из рисунка 1.8 видно, что перемещение, совершённое точкой за промежуток времени Δt, есть изменение её радиус-вектора за это время. Следовательно, обозначив изменение радиус-вектора через Δ , можно записать: Δ = 1 – 2 .

Путь s – длина траектории при перемещении точки из положения М 1 в положение М 2 .

Модуль перемещения может быть не равен пути, пройденному точкой.

Например, на рисунке 1.8 длина линии, соединяющей точки М 1 и М 2 , больше модуля перемещения: s > |Δ|. Путь равен перемещению только в случае прямолинейного однонаправленного движения.

Перемещение тела Δ – вектор, путь s – скаляр, |Δ| ≤ s.

Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Кинематика – Физика, учебник для 10 класса – Класс!ная физика

Физика и познание мира — Что такое механика —

Что такое скорость движения тела.

Скорость движения

Скорость – это количественная характеристика движения тела.

Средняя скорость – это физическая величина, равная отношению вектора перемещения точки к промежутку времени Δt, за который произошло это перемещение. Направление вектора средней скорости совпадает с направлением вектора перемещения Средняя скорость определяется по формуле:

Мгновенная скорость , то есть скорость в данный момент времени – это физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

Иными словами, мгновенная скорость в данный момент времени – это отношение очень малого перемещения к очень малому промежутку времени, за который это перемещение произошло.

Вектор мгновенной скорости направлен по касательной к траектории движения тела (рис. 1.6).

Рис. 1.6. Вектор мгновенной скорости.

В системе СИ скорость измеряется в метрах в секунду, то есть единицей скорости принято считать скорость такого равномерного прямолинейного движения, при котором за одну секунду тело проходит путь в один метр. Единица измерения скорости обозначается м/с . Часто скорость измеряют в других единицах. Например, при измерении скорости автомобиля, поезда и т.п. обычно используется единица измерения километр в час:

1 км/ч = 1000 м / 3600 с = 1 м / 3,6 с

1 м/с = 3600 км / 1000 ч = 3,6 км/ч

Сложение скоростей

Скорости движения тела в различных системах отсчёта связывает между собой классический закон сложения скоростей .

Скорость тела относительно неподвижной системы отсчёта равна сумме скоростей тела в подвижной системе отсчёта и самой подвижной системы отсчёта относительно неподвижной.

Например, пассажирский поезд движется по железной дороге со скоростью 60 км/ч. По вагону этого поезда идет человек со скоростью 5 км/ч. Если считать железную дорогу неподвижной и принять её за систему отсчёта, то скорость человека относительно системы отсчёта (то есть относительно железной дороги), будет равна сложению скоростей поезда и человека, то есть

60 + 5 = 65, если человек идёт в том же направлении, что и поезд

60 – 5 = 55, если человек и поезд движутся в разных направлениях

Однако это справедливо только в том случае, если человек и поезд движутся по одной линии. Если же человек будет двигаться под углом, то придётся учитывать этот угол, вспомнив о том, что скорость – это векторная величина .

А теперь рассмотрим описанный выше пример более подробно – с деталями и картинками.

Итак, в нашем случае железная дорога – это неподвижная система отсчёта . Поезд, который движется по этой дороге – это подвижная система отсчёта . Вагон, по которому идёт человек, является частью поезда.

Свяжем с неподвижной системой отсчёта (рис. 1.7) систему координат ХОY, а с подвижной системой отсчёта – систему координат X П О П Y П (см. также раздел Система отсчёта). А теперь попробуем найти скорость человека относительно неподвижной системы отсчёта, то есть относительно железной дороги.

Это закон сложения перемещений . В нашем примере перемещение человека относительно железной дороги равно сумме перемещений человека относительно вагона и вагона относительно железной дороги.

narod.ru/mechanics/img/01_007-speed-addition.swf” type=”application/x-shockwave-flash” align=”” name=”01_007-speed-addition” data-mce-fragment=”1″/>
Рис. 1.7. Закон сложения перемещений.

Это закон сложения скоростей :

Скорость тела относительно неподвижной системы отсчёта равна сумме скоростей тела в подвижной системе отсчёта и скорости самой подвижной системы отсчёта относительно неподвижной.

Которое потребовалось на этот путь:
v=s/t, где:
v – это скорость,

s – длина пройденного пути, а

t – время
Примечание.
Предварительно, все единицы измерения следует привести к одной системе (желательно СИ).
Пример 1
Разогнавшись до максимальной скорости, автомобиль проехал один километр за полминуты, после чего затормозил и .

Определите максимальную скорость автомобиля.
Решение.
Так как после разгона автомобиль двигался на максимальной скорости, то ее по условиям задачи можно считать равномерной. Следовательно:
s=1 км,

t=0,5 мин.
Приводим единицы измерения времени и пройденного пути к одной системе (СИ):
1 км=1000 м

0,5 мин= 30 сек
Значит, максимальная скорость автомобиля:
1000/30=100/3=33 1/3 м/с, или приблизительно: 33,33 м/с
Ответ: максимальная скорость автомобиля: 33,33 м/с.

Для определения скорости тела при равноускоренном движении необходимо знать начальную скорость и величину или другие связанные параметры. Ускорение может быть и отрицательным (в этом случае это, фактически, торможение).
Скорость равна начальной скорости плюс ускорение, умноженное на время. В виде это записывается следующим образом:
v(t)= v(0)+аt, где:
v(t) – скорость тела в момент времени t

Чему была равна скорость кирпича в момент приземления?
Решение.
Так как направление начальной скорости и ускорения свободного падения совпадают, то скорость кирпича у поверхности земли будет равной:
1+9,8*10=99 м/с.
Сопротивление в такого рода, как правило, не учитывается.

Скорость автомобиля постоянно меняется во время путешествия. Определением того, какая скорость у машины была в тот или иной момент пути, очень часто занимаются как сами автолюбители, так и компетентные органы. Тем более, что способов узнать скорость автомобиля огромное количество.

Инструкция

Самый простой способ определить скорость автомобиля знаком всем еще со школы. Для этого вам нужно зафиксировать количество километров, которое вы проехали, и время, за которое вы это расстояние преодолели. Рассчитывается скорость авто по : расстояние (км.) разделить на время (ч.). Так вы получите искомое число.

Вариант второй используется тогда, когда автомобиль резко остановился, но базовых замеров, как то время и расстояние, никто не проводил. В этом случае скорость автомобиля рассчитывают по его . Для подобных вычислений есть даже своя . Но использоваться она может только в том случае, если при торможении остался на дороге след.

Итак, формула следующим образом: начальная скорость автомобиля равна 0,5 х время нарастания торможения (м/с) х, установившееся замедление авто при торможении (м/с²) + корень из длины тормозного пути (м) х, установившееся замедление автомобиля при торможении (м/с²). Величина под названием «установившееся замедление авто при торможении» фиксированная и зависит только от того, какой асфальт имел место быть. В случае сухой дороги в формулу подставьте число 6,8 – оно прописано в ГОСТе, используемом для расчетов. Для мокрого асфальта данная величина будет равняться 5.

Скорость:

Скорость – векторная величина, характеризующая быстроту перемещения и направление движения.
Скорость (в технике) – степень изменения крутящего момента, скорости и направления движения, передаваемых от двигателя к колесу (рабочему органу), посредством изменения характеристик трансмиссии (например посредством изменения передаточного числа).
Скорость – вид скалолазания.
Скорость – русская калька с англ. speed – то же, что спид, спидуха – сленговое наименование вида психостимулирующих амфетаминов.
Скорость – наименование советского ракетного комплекса 15П666 с ракетой средней дальности.

Фильмы

Скорость – фильм (СССР), 1983.
Скорость – фильм (США), 1994.
Скорость 2: Контроль над круизом – фильм (США), 1997.

Сложение скоростей

При рассмотрении сложного движения (когда точка или тело движется в одной системе отсчёта, а эта система отсчёта в свою очередь движется относительно другой системы) возникает вопрос о связи скоростей в двух системах отсчёта.

Классическая механика

Основная статья: Теорема о сложении скоростей

В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:

V → a = v → r + v → e . {\displaystyle {\vec {v}}_{a}={\vec {v}}_{r}+{\vec {v}}_{e}.}

Данное равенство представляет собой содержание утверждения теоремы о сложении скоростей.

Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчёта, в которой в данный момент времени находится тело.

Примеры

Абсолютная скорость мухи, ползущей по радиусу вращающейся граммофонной пластинки, равна сумме скорости её движения относительно пластинки и той скорости, которую имеет точка пластинки под мухой относительно земли (то есть с которой её переносит пластинка за счёт своего вращения).
Если человек идёт по коридору вагона со скоростью 5 километров в час относительно вагона, а вагон движется со скоростью 50 километров в час относительно Земли, то человек движется относительно Земли со скоростью 50 + 5 = 55 километров в час, когда идёт по направлению движения поезда, и со скоростью 50 – 5 = 45 километров в час, когда он идёт в обратном направлении. Если человек в коридоре вагона движется относительно Земли со скоростью 55 километров в час, а поезд со скоростью 50 километров в час, то скорость человека относительно поезда 55 – 50 = 5 километров в час.
Если волны движутся относительно берега со скоростью 30 километров в час, и корабль также со скоростью 30 километров в час, то волны движутся относительно корабля со скоростью 30 – 30 = 0 километров в час, то есть относительно корабля они становятся неподвижными.

Релятивистская механика

В XIX веке физика столкнулась с проблемой распространения этого правила сложения скоростей на оптические (электромагнитные) процессы. По существу произошёл конфликт между двумя идеями классической механики (первая – Пространство-время теории Ньютона, вторая – принцип относительности), перенесёнными в новую область – теорию электромагнитных процессов.

Например, если рассмотреть пример с волнами на поверхности воды из предыдущего раздела и попробовать обобщить на электромагнитные волны, то получится противоречие с наблюдениями (см., например, опыт Майкельсона).

Классическое правило сложения скоростей соответствует преобразованию координат от одной системы осей к другой системе, движущиеся относительно первой без ускорения. Если при таком преобразовании мы сохраняем понятие одновременности, то есть сможем считать одновременными два события не только при их регистрации в одной системе координат, но и во всякой другой инерциальной системе, то преобразования называются галилеевыми . Кроме того, при галилеевых преобразованиях пространственное расстояние между двумя точками – разница между их координатами в одной инерциальной системе отсчёта – всегда равно их расстоянию в другой инерциальной системе.

Вторая идея – принцип относительности. Находясь на корабле, движущемся равномерно и прямолинейно, нельзя обнаружить его движение какими-то внутренними механическими эффектами. Распространяется ли этот принцип на оптические эффекты? Нельзя ли обнаружить абсолютное движение системы по вызванным этим движением оптическим или, что то же самое, электродинамическим эффектам? Интуиция (довольно явным образом связанная с классическим принципом относительности) говорит, что абсолютное движение нельзя обнаружить какими бы то ни было наблюдениями. Но если свет распространяется с определённой скоростью относительно каждой из движущихся инерциальных систем, то эта скорость изменится при переходе от одной системы к другой. Это вытекает из классического правила сложения скоростей. Говоря математическим языком, величина скорости света не будет инвариантна относительно галлилеевых преобразований. Это нарушает принцип относительности, вернее, не позволяет распространить принцип относительности на оптические процессы. Таким образом электродинамика разрушила связь двух, казалось бы, очевидных положений классической физики – правила сложения скоростей и принципа относительности. Более того, эти два положения применительно к электродинамике оказались несовместимыми.

Специальная теория относительности даёт ответ на этот вопрос. Она расширяет понятие принципа относительности, распространяя его и на оптические процессы. Одновременно специальная теория относительности кардинально изменяет представления о пространстве и времени. Правило сложения скоростей при этом не отменяется совсем, а лишь уточняется для больших скоростей с помощью преобразования Лоренца:

v r e l = v 1 + v 2 1 + v 1 v 2 c 2 . {\displaystyle v_{rel}={\frac {{v}_{1}+{v}_{2}}{1+{\dfrac {{v}_{1}{v}_{2}}{c^{2}}}}}. }

Можно заметить, что в случае, когда v / c → 0 {\displaystyle v/c\rightarrow 0} , преобразования Лоренца переходят в преобразования Галилея. Это говорит о том, что механика в специальной теории относительности сводится к механике Ньютона при скоростях, малых по сравнению со скоростью света. Это объясняет, каким образом соотносятся специальная теория относительности и классическая механика – первая является обобщением второй.

Имеется викиучебник по теме
«Сложение скоростей»

Физика. Дайте определение скорости тела и формула

Александра романова

Скорость тела – это векторная величина равная отношению пути, пройденного телом за некоторый период времени, к величине этого периода времени. v=s/t.
1.Пусть тело движется прямолинейно и равномерно. Тогда его скорость представлена постоянной величиной, не изменяется со временем: v = const. Формула скорости имеет вид v=v(const), где v(const) – конкретное значение.
2.Пусть тело движется равнопеременно (равноускоренно или равнозамедленно) . Как правило, говорят лишь о равноускоренном движении, просто в равнозамедленном ускорение отрицательно. Ускорение обозначается обычно буквой a. Тогда скорость выражается линейной зависимостью от времени: v=v0+a·t, где v0 – начальная скорость, a – ускорение, t – время.
3.Пусть тело движется по окружности с постоянной по модулю скоростью. В этом случае оно обладает центростремительным ускорением a(c), направленным к центру окружности. Его называют также нормальным ускорением a(n). Линейная скорость и центростремительное ускорение связаны соотношением a=v²/R, где R – радиус окружности, по которой движется тело.

Алексей

скорость – векторная физическая величина, характеризующая быстроту перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчёта.
а формула зависит от вида движения: если у тебя равноускоренное движение то v=v0+at. где a ускорение и t время. если у тебя равномерное движение то s=vt, где v=s/t.

Подскажите что такое скорость (определение) и прибор для определения скорости.

(ФИЗИКА)

Тамара

Скорость – это количественная характеристика движения тела. Скорость характеризует быстроту и направление движения тела в данный момент времени. Скорость измеряется в м/с (метр за секунду). Есть приборы, которые могут измерять скорость.
Спидометр (от англ. speed – скорость и греч. metreo – измеряю) – это прибор, показывающий мгновенную скорость автомобиля или локомотива.
Для измерения скорости корабля служит лаг, изобретённый в 1577 году. Единицей скорости является «узел», который равен одной морской миле в час (приблизительно 1,8 км/ч).
Первый прибор для измерения скорости ветра был изобретен в 1667 году англичанином Робертом Хуком. Прибор называется анемометр (греч. анемос – ветер, и метрео – измеряю.
Прибор для измерения скорости течения воды называется вертушка.

Пример 1

Например, автомобиль движется по дороге и в нем находятся люди. Они осуществляют движение вместе с транспортом по трассе. То есть люди передвигаются в пространстве относительно дороги, но относительно самой машины люди не движутся.

Из этого примера видно, что, изначально необходимо определить тело, рассматриваемое в движении, которое в наук называют точкой отсчета. Система координат тесно взаимосвязана с методикой измерения времени, что в результате создают концепцию отсчета.

В основном местоположение тела задается координатой. Проанализируем один пример: размеры станции, находящейся на орбите возле Земли, можно не принимать во внимание, а рассчитывать только траекторию перемещение космического корабля во время стыковки со станцией. Таким образом, размерами физических элементов возможно пренебречь, а иногда – тело считают материальной точкой. Линию, по которой перемещается данная величина, именуют траекторией, длину которой называют путем. Единица пути – метр (м). Механическое движение характеризуется тремя физиологическими величинами: скоростью, перемещением, и ускорением.

Понятие скорости механического движения

Определение 2

Скорость – физическая величина, которая равна перемещению тела к интервалу времени, в течение которого это взаимодействие произошло.

Механическое движение оценивается еще и тем, как быстро перемещается тело (точка). Это и есть скорость движения. Скорость представляет собой понятие векторной величины. Для того, чтобы в полном объеме задать ее, необходимо установить непосредственно направление и величину скорости, вдоль которых она была изначально замерена. Как правило скорость элементов рассматривают по траектории движения. В таком случае величина исследуемого объекта обусловливается как путь, пройденный за одну единицу времени. Другими словами, для нахождения правильного коэффициента траектории движения, путь тела надо разделить на время, в течение которого он был пройден.

Определение 3

Мгновенная скорость – это скорость точки в конкретный момент времени или в определенной точке траектории.

Это векторная физическая величина, численно равная пределу, к которому устремляется средняя скорость за очень малый промежуток времени. Указанная траектория является первой производной от вектора в соответствии с временем. Вектор моментальной скорости определяется по касательной к линии движения тела в сторону его дальнейшего перемещения.

Эта величина дает точное представление о движении объекта в данный момент времени.

Например, во время поездки в автомобиле в определенный момент времени водитель смотрит на спидометр и видит, что на табло 100 км/ч. Затем стрелка указывает на 90 км/ч, а спустя пару минут – 110 км/ч.

Замечание 1

Значением мгновенной скорости транспорта в определенные моменты времени являются полученные показания прибора.

Имеется ли физический смысл в понятии «мгновенной скорости»? Данный термин характеризуется изменением перемещения элементов в пространстве. Но, чтобы узнать, как изменилось его расположение, следует наблюдать за движением в течение определенного периода времени.

Даже самые современные приборы для замера скорости измеряют движение за конкретный отрезок времени – конечный временной интервал. Определение «скорость тела на данный момент» не считается корректным с точки зрения физики. Однако, именно этот тезис очень удобен в математических расчетах, поэтому им пользуются постоянно.

Закон сложения скоростей

Скорость любого физического тела относительно неподвижной концепции отсчета всегда равна векторной сумме перемещения элементов относительно подвижной системы. Эта теория помогает точно определить расположение объекта в конкретный период времени.

Для понимания указанного закона необходимо рассмотреть две системы отсчета, одна из которых связана с неподвижной точкой отсчёта $O$. Обозначим данную концепцию $K$, которая будет называться неподвижной.

Вторая система, обозначаемая $K’$ и перемещающаяся относительно тела $O$ со скоростью $ \bar{u}$ – будет считаться движущейся.

Необходимо понимать, что скорость является векторной величиной. По траектории движения возможно определить только направление скорости вектора. Вектор скорости направлен по касательной к траектории, по которой проходит тело, что движется на данный момент.

Отрицательная скорость

Замечание 2

Скорость тела может быть отрицательной в случае, когда тело движется в противоположном направлении от оси координат в выбранной системе отсчета.

Ученый из Великобритании, Роберта Бойд смог присвоить пучку света «отрицательную» скорость, при которой пик импульса продвигался к источнику, а не от него. Интересно, если менять среду специальным образом и пропускать через нее через свет, возможно легко управлять скоростью светового импульса – “замораживая” или замедлять его в десятки тысяч раз, а то и вовсе останавливать.

В этом аспекте речь идет о групповой скорости, которая определяет скорость распространения одного пучка импульса света. Из-за рассеивания этот элемент может передвигаться на несколько порядков медленнее, чем каждый фотон в отдельности, и наоборот -стремительнее скорости света в вакууме.

В данном случае речь не идет о нарушении законов природы, потому как самые первые фотоны в импульсе добегают до конца, не «быстрее света». В случае же остановки светового пучка необходимо говорить о поглощении импульса подготовленной средой с повторным излучением. При этом сохраняются все важные параметры исходного объекта, «до последнего фотона».

Как вы думаете, кто двигается быстрее агроном Васечкин, автомобиль Renault или самолет Боинг? Кто из них быстрее доберется от Москвы до Краснодара? Ответ очевиден Renault быстрее Васечкина, но медленнее Боинга.

То есть мы не только знаем, как двигаются разные объекты, но и можем сравнить их скорости. А что такое скорость в физике? Как найти скорость тела, и что такое единицы измерения скорости?

Скорость в физике: как найти скорость?

В 7 классе на уроках физики вводят понятие скорости. Без сомнения, все школьники к этому моменту уже знакомы с этим словом и представляют, что оно означает.

А также знают, что скорость измеряется в км/ч и обозначается буквой V.

Но объяснить, что же такое скорость в физике, каковы единицы скорости, связно вряд ли смогут. Именно потому это простое, казалось бы, понятие требует пояснений и разбора.

В физике быстроту движения Васечкина, Renault и Боинга называют скоростью их движения. И скорость эта характеризует, какой путь преодолевает каждый из участников этого путешествия за единицу времени. И если в полете расстояние в 1350 километров между Москвой и Краснодаром мы преодолеем за два часа, на машине нам потребуется никак не меньше 15 часов, то пешком бесшабашный Васечкин сможет в бодром темпе как раз прошагать весь свой отпуск и прибыть на место лишь для того, чтобы поцеловать тещу, отведать блинов и сесть на самолет до Москвы, дабы успеть на работу в понедельник.

Соответственно, за единицу времени за час самолет пролетит 670 километров, машина проедет 90 километров, а турист Васечкин отмахает аж целых пять километров дороги. И тогда говорят, что скорость самолета 670 километров в час, машины 90 км в час, а пешехода 5 км/ч. То есть, скорость определяется делением пройденного пути на единицу времени на час, на минуту или на секунду.

Единицы измерения скорости

На практике применяются такие единицы, как км/ч, м/с и некоторые другие. Обозначают скорость буквой v, расстояние буквой s, а время буквой t. Формула для нахождения скорости в физике выглядит так:

V = s / t,

Где s – пройденный путь
t – время, затраченное на преодоление этого пути

А если нам надо пересчитать скорость не в километрах в час, а в метрах за секунду, то пересчет происходит следующим образом. Так как 1 км=1000 м, а 1 ч = 60 мин = 3600 с, то можно записать: 1 км/ч=(1000 м)/(3600 с). И тогда скорость самолета будет равна: 670 км/ч=670×(1000 м)/(3600 с)=186м/с

Кроме своего числового значения, скорость имеет еще и направление, поэтому на рисунках скорость обозначают стрелкой и называют векторной величиной.

Средняя скорость в физике

Отметим еще один момент. В нашем примере водитель машины вел машину со скоростью 90 км/ч. По шоссе он мог ехать равномерно с такой скоростью долгое время. А вот проезжая по пути разные города, он то останавливался на светофорах, то полз в пробках, то короткими урывками набирал хорошую скорость.

Т.е. его скорость на разных участках пути была неравномерной. В таком случае вводят понятие средней скорости. Средняя скорость в физике обозначается V_ср и считается также как и скорость при равномерном движении. Только берут общее расстояние пути и делят на общее время.

Перемещение, скорость и ускорение

Home > High School > AP Physics > Notes > Перемещение, скорость и ускорение

Измерения и единицы измерения
Единицы, связанные с числами, важны в физике. Единицы связывают числа с реальными и измеримыми физическими величинами. Например, расстояние можно измерять во многих различных единицах, таких как дюймы, сантиметры, мили, километры или световые годы. В физике используется международная система единиц «СИ». SI использует метрические измерения, но SI также определяет «базовый» набор единиц, который используется для построения «составных» единиц, которым даются собственные имена. Базовым набором единиц СИ являются метр (м) для измерения расстояния, килограмм (кг) для измерения массы, секунда (с) для измерения времени, ампер (А) для измерения электрического тока, кельвин (К) для измерения. для измерения температуры, моль (моль) для измерения количества вещества и кандела (кд) для измерения интенсивности света.

Векторы в одном измерении
Многие измеримые величины имеют только число и единицу измерения. Эти величины, такие как масса или температура, называются «скалярными» величинами. Другие измеримые величины имеют значение (также известное как «величина») и направление. Примером могут служить значения, относящиеся к движению. Направление, в котором что-то движется, важно. Сказать кому-то «ехать одну милю на восток» очень отличается от того, чтобы сказать человеку «ехать одну милю на юг». Величины, имеющие величину и направление, являются «векторами».

В формулах буквы используются вместо определенного значения. Чтобы отличить векторы от скалярных величин, векторы обычно пишут со стрелкой над буквой,

Часто в уравнениях проще всего использовать только величину вектора. Величину вектора можно определить по вертикальным линиям по обе стороны от буквы или по букве с удаленной стрелкой. Величина вектора равна

Рабочий объем
Термин «расстояние» используется в физике для обозначения скалярного измерения, такого как «3 метра». Термин «смещение» используется для обозначения векторной величины. Следовательно, перемещение имеет как расстояние, так и направление. Когда объект движется по прямой линии, его начальное положение можно определить как начало координат O. Переменной x можно присвоить любое положение вдоль этой линии. Смещение — это вектор, который указывает от начала координат до положения x. Таким образом, перемещение является вектором .

Чтобы представить две или более позиции на прямой, переменным можно присвоить числа в нижнем индексе, например, x ₁ и x ₂ . Если объект перемещается из положения x ₁ в положение x ₂ , изменение положения объекта записывается как

Греческая заглавная буква ∆ («дельта») означает «изменение». Это изменение положения есть дистанция. Единицей измерения перемещения и расстояния в системе СИ является метр (м).

Скорость
Чтобы изучать движущиеся объекты, нам нужно понять, как движение связано со временем. Термин «скорость» используется в физике для обозначения скалярного измерения, тогда как термин «скорость» используется для обозначения векторной величины. Скорость — это скорость изменения смещения объекта при его перемещении из одного места в другое. Единицей скорости в СИ является метр в секунду, м/с. Величина скорости есть скорость. Представьте, что объект находится в позиции x ₁в определенное время t ₁ . Затем он движется по прямой так, чтобы достичь положения x ₂ в момент времени t ₂ . Используя ∆ для обозначения «изменения в», пройденное расстояние равно

Изменение во времени можно записать таким же образом:

Величина скорости v объекта равна пройденному расстоянию. деленная на изменение во времени,

Скорость изменения ∆x, деленная на ∆t, не обязательно должна быть постоянной. Если объект ускоряется или замедляется, в каждую единицу времени проходит большее или меньшее расстояние. Скорость объекта в любой конкретный момент времени t называется мгновенной скоростью. Однако между любыми двумя временами можно найти «среднюю» скорость. Для ∆x = x ₂ -x ₁ и ∆t = t ₂ -t ₁ , средняя скорость равна,

2 . Для частного случая, когда скорость постоянна, тогда в любое время между t ₁ и t ₂ величина скорости будет равна v _avg .

Ускорение
Изменение скорости во времени называется ускорением. Ускорение является векторной величиной, имеющей как величину, так и направление. Ускорение — это скорость изменения скорости объекта. Единицей ускорения в СИ является метр в секунду в квадрате (иногда пишется как «в секунду в секунду»), м/с ² . Представьте, что в момент времени t ₁ объект движется со скоростью v ₁ . Затем его скорость меняется, так что в момент времени t ₂ он движется с новой скоростью с величиной v ₂ . Используя ∆ для обозначения «изменения в», изменение величины скорости можно записать как

Изменение во времени можно записать таким же образом,

Величина ускорения, a , объекта есть изменение величины скорости объекта, деленное на изменение во времени,

Скорость изменения ∆v, деленная на ∆t, не обязательно должна быть постоянной. Ускорение тела в любой момент времени t называется мгновенным ускорением. Однако между любыми двумя временами можно найти «среднее» ускорение. Для ∆v = v ₂ – v ₁ и ∆t = t ₂ – t ₁ величина среднего ускорения равна

. раз т ₁ и т ₂ . В AP Physics ускорение почти всегда считается постоянным. В этом случае в любое время между t ₁ и t ₂ величина ускорения будет равна _avg .

5.1.2: Единицы – Физика LibreTexts

Последнее обновление
Сохранить как PDF

Код страницы: 33923

Безграничный
Безграничный

Длина

Длина — это физическая мера расстояния, которая в основном измеряется в единице СИ — метре.

цели обучения

Различать СИ и общепринятые единицы длины

Длина может быть определена как измерение физической величины расстояния. Многие качественные наблюдения, фундаментальные для физики, обычно описываются с помощью измерения длины. Расстояние между объектами, скорость, с которой объекты перемещаются, и сила, прикладываемая объектом, зависят от длины как от переменной. Чтобы описать длину стандартизированным и количественным образом, необходимо использовать общепринятую единицу измерения.

В мире используется множество различных единиц длины. В Соединенных Штатах обычные единицы измерения США оперативно описывают длину в терминах базовой единицы дюйма. Таким образом, различные длины описываются по отношению к дюйму, например, фут равен 12 дюймам, ярд равен трем футам, а миля равна 1760 ярдам.

Хотя региональное использование различных единиц измерения, как правило, не вызывает проблем, это может вызвать проблемы совместимости и понимания при работе за границей или при сотрудничестве с международными партнерами. Таким образом, необходима стандартная единица измерения, принятая на международном уровне. Основной единицей длины, определенной Международной системой единиц (СИ), является метр. Метр выражается более конкретно в терминах скорости света. 93\) метра).

Метр, определяемый скоростью света : Метр определяется как расстояние, которое свет проходит в $\frac{1}{299,792,458}$ секунды в вакууме. Пройденное расстояние равно скорости, умноженной на время.

Метрическая система – Длина : Краткое введение в метрическую систему и преобразования единиц измерения.

Масса

Масса — это количество вещества, которое содержит объект, измеряемое его сопротивлением ускорению.

цели обучения

Объясните разницу между массой и весом

Масса

Масса, особенно инерционная масса, является количественной мерой сопротивления объекта ускорению. Это внутреннее свойство объекта, и оно не меняется из-за окружающей среды. Единицей массы в системе СИ является килограмм (кг).

Килограмм определяется как масса международного прототипа килограмма (IPK), которая почти точно равна массе одного литра воды. Это также единственная единица СИ, которая напрямую определяется артефактом, а не фундаментальным физическим свойством, которое можно воспроизвести в разных лабораториях. Четыре из семи основных единиц в системе СИ определены относительно килограмма, поэтому стабильность этого измерения имеет решающее значение для точных и последовательных измерений.

В 2005 году Международный комитет мер и весов (МКМВ) рекомендовал переопределить килограмм с точки зрения фундаментальной константы природы из-за свидетельств того, что масса международного прототипа килограмма будет меняться с течением времени. На своем заседании в 2011 году Генеральная конференция по мерам и весам (CGPM) согласилась с тем, что килограмм следует переопределить с точки зрения постоянной Планка. Конференция отложила принятие окончательного решения до следующего заседания в 2014 году.

Массовый дрейф прототипов : График относительного изменения массы выбранных килограммовых прототипов.

Масса и вес

В повседневном использовании масса объекта в килограммах часто называется его весом. Это значение, хотя и дано в килограммах, на самом деле является единицей измерения, отличной от системы СИ, известной как килограмм-сила. С научной точки зрения, «вес» относится к силе гравитации, действующей на данное тело. Это измерение изменяется в зависимости от гравитационного притяжения противоположного тела. Например, вес человека на Земле отличается от веса человека на Луне из-за различий в гравитационном притяжении каждого тела. Напротив, масса объекта является внутренним свойством и остается неизменной независимо от гравитационных полей. Соответственно, космонавты в условиях микрогравитации должны приложить в 10 раз больше усилий, чтобы разогнать 10-килограммовый объект с той же скоростью, что и 1-килограммовый объект, даже если разница в весе незаметна.

Метрическая система – Масса : Краткое введение в метрическую систему и преобразование единиц измерения.

Время

Время является фундаментальной физической величиной длительности и измеряется единицей СИ, известной как секунда.

цели обучения

Связь времени с другими физическими величинами

Время — одна из семи основных физических величин Международной системы единиц (СИ). Время используется для определения других величин, таких как скорость или ускорение, и поэтому важно, чтобы оно было стандартизировано и точно определено количественно. Оперативное определение времени очень полезно при проведении как сложных экспериментов, так и повседневных жизненных дел.

Исторически измерение времени было основным мотивом в навигации и астрономии. Периодические события и движения долгое время служили эталоном единиц времени. Например, движение солнца по небу, фазы луны, колебания маятника и биение сердца использовались в качестве стандарта для измерения времени. Однако эти события и стандарты носят очень динамичный характер и не могут быть надежно использованы для точных количественных измерений. Между 1000 и 1960 секунда определялась как $\frac{1}{86 400}$ средних солнечных суток. Это определение изменилось между 1960 и 1967 годами и было определено с точки зрения периода обращения Земли вокруг Солнца в 1900 году. Сегодня единица СИ секунды определяется с точки зрения излучения, испускаемого атомами цезия.

Секунда теперь определяется как «длительность 9 192 631 770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133». Отсюда следует, что сверхтонкое расщепление в основном состоянии атома цезия-133 равно 9,192 631 770 герц. Другими словами, атомы цезия можно заставить колебаться очень устойчиво, и эти колебания можно легко наблюдать и сосчитать. Второе — это время, необходимое для возникновения 9 192 631 770 таких вибраций.

Цезиевые часы NIST-F1 : NIST-F1 называют фонтанными часами, потому что они используют фонтанообразное движение атомов для улучшения счета времени.

Метрическая система – Время : Краткое введение в метрическую систему и преобразование единиц измерения.

Префиксы и другие системы единиц

Префиксы SI предшествуют основной единице измерения для обозначения кратности или доли единицы измерения.

цели обучения

Применение префиксов к единицам и различие между СИ и обычными единицами

Префиксы

Метрический префикс или префикс СИ — это префикс единицы измерения, который предшествует основной единице измерения для обозначения кратности или доли единицы измерения. Каждый префикс имеет уникальный символ, который добавляется к символу единицы измерения. Префикс килограмм-, например, может быть добавлен к грамму для обозначения умножения на одну тысячу; один килограмм равен одной тысяче граммов (1 кг = 1000 г). Приставка санти- также может быть добавлена к метру для обозначения деления на сто; один сантиметр равен одной сотой метра (1 см = 0,01 м). Префиксы, кратные 10, характерны для всех форм метрической системы, причем многие из них восходят к введению системы в 179 г.0 с. Сегодня префиксы стандартизированы для использования в Международной системе единиц (СИ) Международным бюро мер и весов. СИ официально указывает двадцать префиксов.

Префиксы единиц СИ : Двадцать префиксов, официально указанных в Международной системе единиц

Важно отметить, что килограмм является единственной единицей СИ с префиксом в названии и условном обозначении. Поскольку нельзя использовать несколько префиксов, в случае килограмма названия префиксов используются с названием единицы измерения «грамм», а символы префикса используются с обозначением единицы измерения «г. За этим исключением любой префикс СИ может использоваться с любой единицей СИ, включая градус Цельсия и его символ °C.

Другие системы единиц

Система единиц СИ или метрическая система используется в большинстве стран мира и является стандартной системой, согласованной учеными и математиками. Однако в просторечии во многих странах используются другие системы единиц. Соединенные Штаты, например, преподают и используют 90 285 обычных единиц Соединенных Штатов 90 286. Эта система единиц была разработана на основе английских или имперских стандартов единиц Соединенного Королевства. Обычные единицы измерения в Соединенных Штатах определяют измерения с использованием стандартов, отличных от тех, которые используются в единицах СИ. Система измерения длины с использованием обычной системы США основана на дюймах, футах, ярдах и милях. Точно так же единицы площади измеряются в квадратных футах, а единицы мощности и объема измеряются в кубических дюймах, кубических футах или кубических ярдах. Единицы массы обычно определяются в унциях и фунтах, а не в килограммах в единицах СИ. Другие часто используемые единицы из обычной системы Соединенных Штатов включают единицы объема жидкости: чайную ложку, столовую ложку, жидкую унцию, чашку США, пинту, кварты и галлоны, а также градусы Фаренгейта, используемые для измерения температуры.

Некоторые широко используемые единицы не являются частью Международной системы единиц и считаются единицами, не входящими в систему СИ. Эти единицы, хотя и не являются официально частью единиц СИ, обычно принимаются для использования в сочетании с единицами СИ. Они могут включать минуты, часы и дни, используемые для временных измерений, литр для объемных измерений, а также градусы, минуты и секунды, используемые для измерения углов.

Метрическая система – Префиксы : Краткое введение в метрическую систему и преобразование единиц измерения.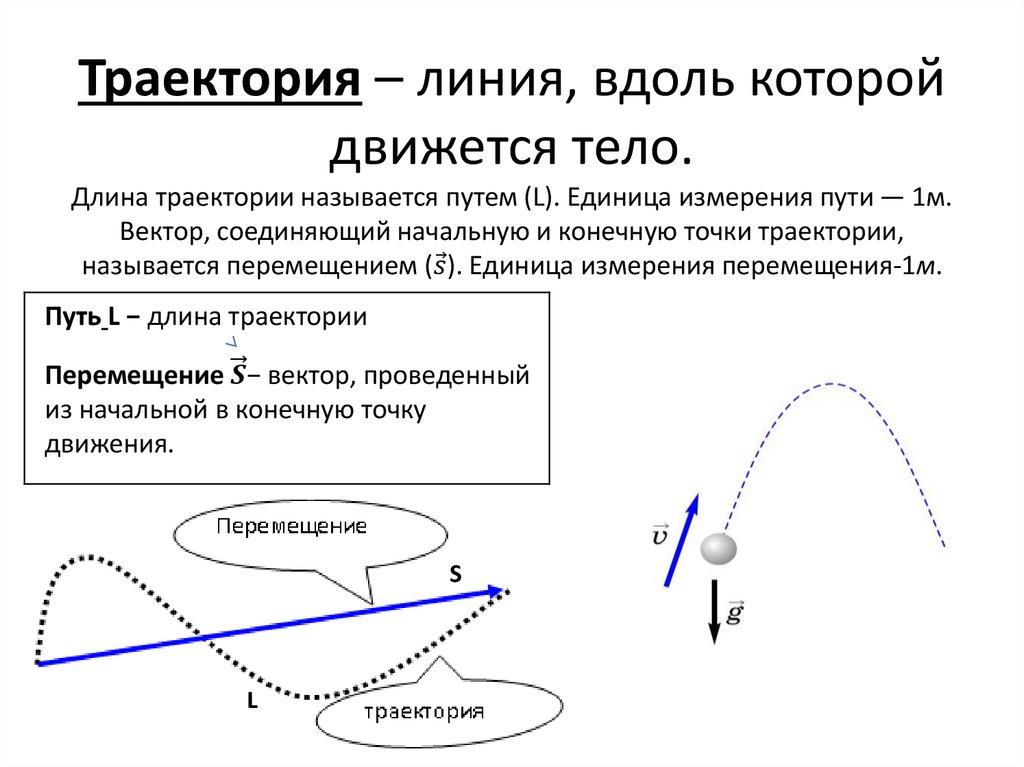

Преобразование единиц

Преобразование между единицами измерения можно выполнить с помощью коэффициентов пересчета или специальных формул пересчета.

цели обучения

Применить метод метки фактора для преобразования единиц

Перевод систем измерения

Часто необходимо преобразовать один тип единиц измерения в другой. Преобразование единиц — это преобразование различных единиц измерения для одного и того же количества, обычно с использованием коэффициентов преобразования. Например, если вы читаете европейскую кулинарную книгу, некоторые количества могут быть выражены в литрах; если вы готовите в США на стандартной кухне со стандартными инструментами, вам нужно будет преобразовать эти измерения в чашки. Или, возможно, вы читаете маршруты пеших прогулок из одного места в другое и интересуетесь, сколько миль вам предстоит пройти. В этом случае вам нужно будет преобразовать единицы измерения футов в мили. Это немного похоже на перевод кода подстановки с использованием формулы, которая помогает понять, что означает одна мера в терминах другой системы.

Преобразование единиц измерения в метрическую систему : ЛЕГКОЕ преобразование единиц измерения в метрическую систему – это простое дополнительное обучающее видео помогает объяснить метрическую систему и как сделать простые преобразования метрической системы.

Методы преобразования

Существует несколько подходов к выполнению преобразований. Один широко используемый метод известен как метод метки фактора для преобразования единиц или «железнодорожный метод».

Метод метки фактора представляет собой последовательное применение коэффициентов преобразования, выраженных в виде дробей и расположенных таким образом, что любая единица измерения, появляющаяся как в числителе, так и в знаменателе любой из дробей, может быть сокращена до тех пор, пока не будет получен только желаемый набор единиц измерения. полученный. Например, 10 миль в час можно преобразовать в метры в секунду, используя последовательность коэффициентов преобразования.

Каждый коэффициент преобразования эквивалентен единице. Например, начиная с 1 мили = 1609 метров и разделив обе части уравнения на 1 милю, мы получим $\mathrm{\frac{1 \; mile}{1 \; mile} = \frac{1609 \; метры}. 1 \; миля}}$, что при упрощении дает $\mathrm{1 = \frac{1609 \; метров}{1 \; миля}}$. Физическое вычеркивание единиц, которые компенсируют друг друга, также поможет визуализировать то, что осталось.

Преобразование 1 года в секунды с использованием метода метки фактора : Физическое вычеркивание единиц, которые сокращаются, помогает визуализировать «остаточные» единицы (единицы).

Итак, если вычесть милю и час и произвести арифметические действия, 10 миль в час преобразуются в 4,47 метра в секунду.

Ограничение метода метки фактора заключается в том, что он может преобразовывать только те единицы, которые имеют постоянное отношение, которое можно умножить, или коэффициент умножения. Этот метод нельзя использовать между единицами, имеющими смещение или разностный коэффициент. Примером может служить преобразование между градусами Цельсия и кельвинами или между градусами Цельсия и Фаренгейтами. Для них лучше всего использовать специальные формулы преобразования.

Например, если вы планируете поездку за границу в Испанию, а прогноз погоды предсказывает преимущественно облачную погоду и 16°C, вы можете преобразовать температуру в °F, единицу измерения, которую вам удобнее интерпретировать. Для этого нужно знать формулу перевода градусов Цельсия в градусы Фаренгейта. Эта формула: $\mathrm{[°F] = [°C] \times \frac{9}{5}+ 32}$.

\[\begin{align} \mathrm{[°F]} &= \mathrm{ [°C] \times \frac{9}{5}+ 32} \\ \mathrm{[°F]} & = \mathrm{ 28,8 + 32} \\ \mathrm{[°F]} &= \mathrm{ 60,8 + 32} \end{align}\]

Тогда вы будете знать, что 16°C эквивалентны 60,8°F, и сможете упаковать правильный тип одежды, чтобы чувствовать себя комфортно.

Ключевые моменты

Единицей длины в системе СИ является метр.
Один метр определяется как расстояние, которое свет проходит в вакууме за $\frac{1}{299,792,458}$ секунды.
Производные единицы измерения, связанные с метром, разработаны для удобства числа 10.
Килограмм — единственная единица СИ, непосредственно определяемая самим артефактом.
Масса — это свойство, не зависящее от гравитационных полей, в отличие от веса.
Один килограмм определяется как масса международного прототипа килограмма (IPK), цилиндра из платино-иридиевого сплава.
Один килограмм почти точно равен массе одного литра воды.
Время — это физическая величина длительности.
Единицей времени в системе СИ является секунда.
Второй определяется с точки зрения излучения, испускаемого атомами цезия.
Двадцать стандартных префиксов для использования в Международной системе единиц являются производными от числа, кратного 10.
Килограмм — единственная единица СИ с префиксом как частью названия и условного обозначения; как таковые, префиксы единиц СИ добавляются к единице грамма.
Обычные единицы США определяют измерения, основанные на английских или имперских стандартах единиц.
Преобразование единиц — это преобразование между различными единицами измерения для одной и той же величины, как правило, с помощью мультипликативных коэффициентов преобразования.
Метод метки фактора представляет собой последовательное применение коэффициентов пересчета, выраженных в виде дробей, в которых единицы, встречающиеся как в числителе, так и в знаменателе, могут быть исключены, оставляя только желаемый набор единиц.
Для преобразований с разностным коэффициентом следует использовать специальные формулы преобразования.

Ключевые термины

Длина : Расстояние между объектами физически.
ускорение : скорость изменения скорости тела со временем
инерция : тенденция объекта сопротивляться любому изменению его движения
Излучение : излучение энергии в виде электромагнитных волн или в виде движущихся или колеблющихся субатомных частиц.
префикс : То, что имеет префикс; особенно одна или несколько букв или слогов, добавленных к началу слова для изменения его значения; as, pre- в префиксе, con- в заклинании.
преобразование : переход между различными единицами измерения одной и той же величины.

ЛИЦЕНЗИИ И АВТОРСТВО

CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, ПРЕДОСТАВЛЕННОЕ РАНЕЕ

Курирование и пересмотр. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike

CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, КОНКРЕТНОЕ АВТОРСТВО

Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42091/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Единица длины. 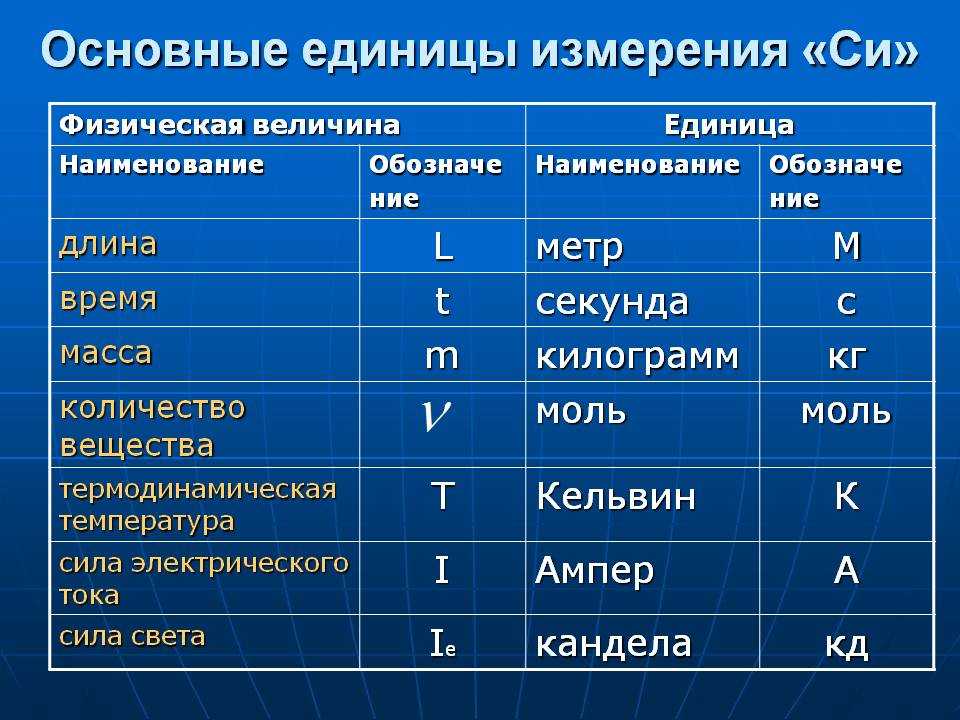Предоставлено : Википедия. Расположен по адресу : http://en.Wikipedia.org/wiki/Unit_of_length . Лицензия : CC BY-SA: Attribution-ShareAlike
Длина. Предоставлено : Википедия. Расположен по адресу : http://en.Wikipedia.org/wiki/Длина . Лицензия : CC BY-SA: Attribution-ShareAlike
Метрическая система — длина. Расположен по адресу : http://www.youtube.com/watch?v=W5xyF-mwitU . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Колледж OpenStax, Колледж физики. 10 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx. org/content/m42091/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
кг. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Килограмм . Лицензия : CC BY-SA: Attribution-ShareAlike
Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42091/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Массачусетс. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Mass . Лицензия : CC BY-SA: Attribution-ShareAlike
инерция. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/inertia . Лицензия : CC BY-SA: Attribution-ShareAlike
ускорение. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/acceleration . Лицензия : CC BY-SA: Attribution-ShareAlike
Метрическая система — длина. Расположен по адресу : http://www.youtube.com/watch?v=W5xyF-mwitU . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Колледж OpenStax, Колледж физики. 10 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx. org/content/m42091/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Массовый дрейф прототипа. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/File:Prototype_mass_drifts.jpg . Лицензия : Общественное достояние: Авторские права неизвестны
Метрическая система — Масса. Расположен по адресу : http://www.youtube.com/watch?v=W5xyF-mwitU . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx. org/content/m42091/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Секунда. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Second . Лицензия : CC BY-SA: Attribution-ShareAlike
Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/radiation . Лицензия : CC BY-SA: Attribution-ShareAlike
Метрическая система — длина. Расположен по адресу : http://www.youtube.com/watch?v=W5xyF-mwitU . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Колледж OpenStax, Колледж физики. 10 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42091/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Массовый дрейф прототипа. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/File:Prototype_mass_drifts.jpg . Лицензия : Общественное достояние: Нет данных Авторские права
Метрическая система – Масса Расположен по адресу : http://www.youtube.com/watch?v=W5xyF-mwitU . Лицензия : Общественное достояние: Нет данных Copyright . 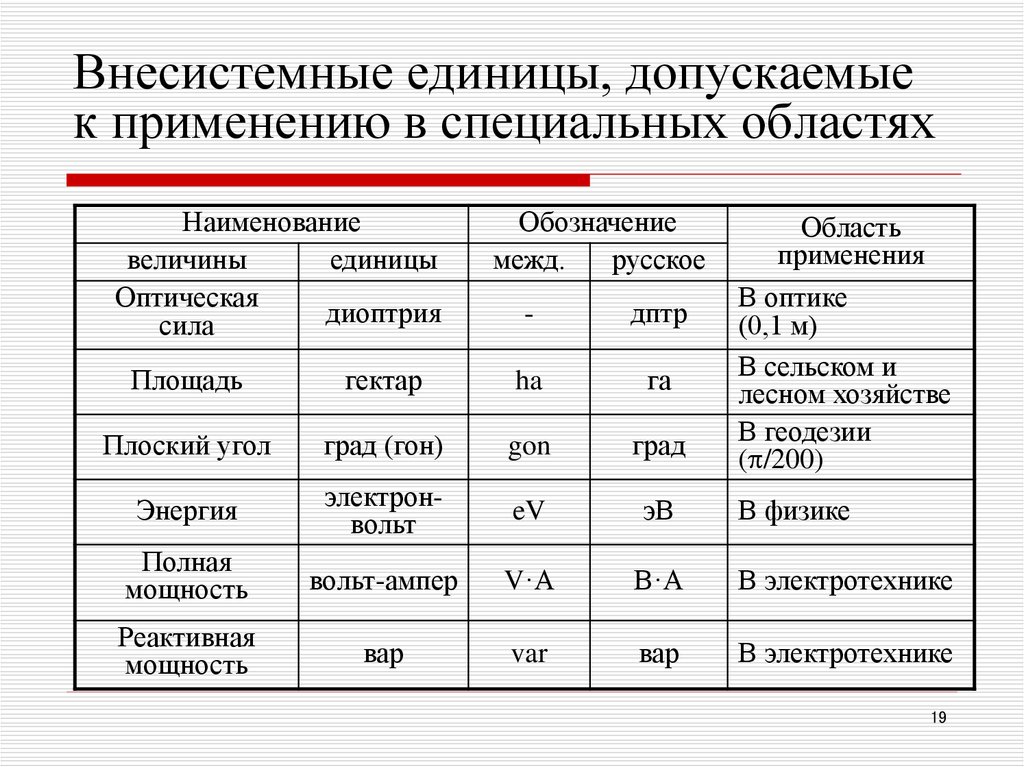Условия лицензии : Стандартная лицензия YouTube
Часы с цезиевым фонтаном NIST-F1. Предоставлено : http://www.nist.gov/public_affairs/r…ses/n99-22.cfm. Адрес: : http://www.nist.gov/public_affairs/releases/n99-22.cfm . Лицензия : CC BY: Attribution
Метрическая система – Время. Расположен по адресу : http://www.youtube.com/watch?v=W5xyF-mwitU . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
единиц измерения США. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/United_States_customary_units . Лицензия : CC BY-SA: Attribution-ShareAlike
Префиксы единиц СИ. 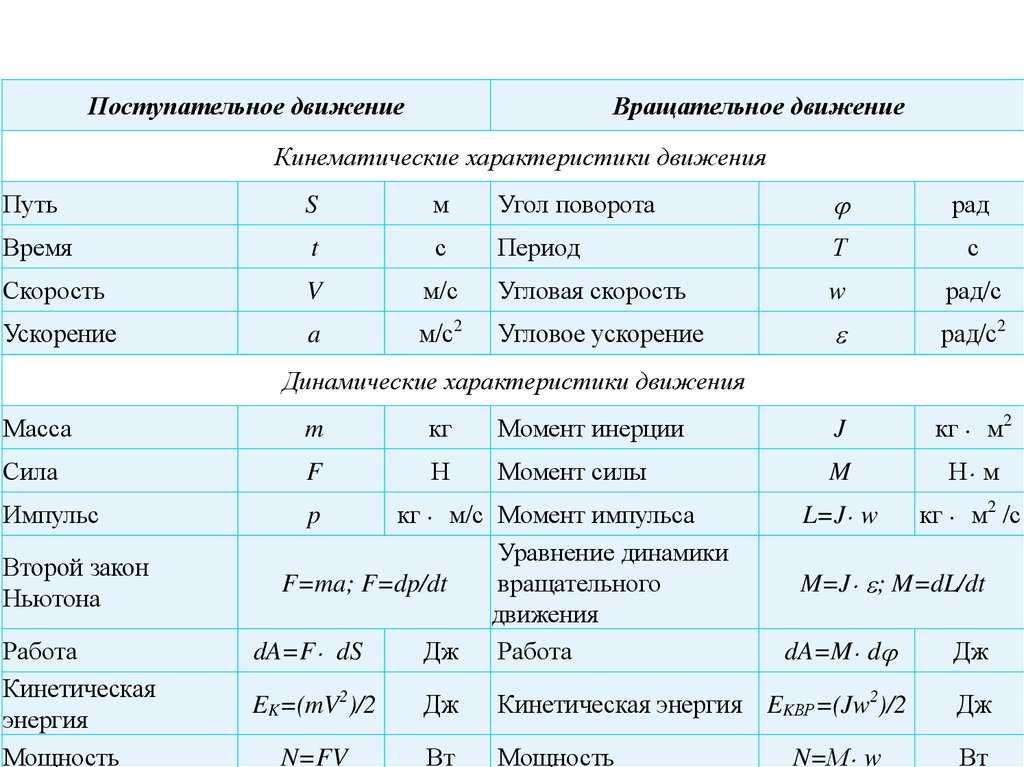Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/SI_Unit_Prefixes . Лицензия : CC BY-SA: Attribution-ShareAlike
Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42091/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/prefix . Лицензия : CC BY-SA: Attribution-ShareAlike
Метрическая система — длина. Расположен по адресу : http://www.youtube.com/watch?v=W5xyF-mwitU . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Колледж OpenStax, Колледж физики. 10 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42091/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Массовый дрейф прототипа. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/File:Prototype_mass_drifts.jpg . Лицензия : Общественное достояние: Нет данных Авторские права
Метрическая система — Масса. Расположен по адресу : http://www.youtube.com/watch?v=W5xyF-mwitU . Лицензия : Общественное достояние: Авторские права неизвестны . Условия лицензии : Стандартная лицензия YouTube
Часы с цезиевым фонтаном NIST-F1. Предоставлено : http://www.nist.gov/public_affairs/r…ses/n99-22.cfm. Адрес: : http://www.nist.gov/public_affairs/releases/n99-22.cfm . Лицензия : CC BY: Attribution
Метрическая система – Время. Расположен по адресу : http://www.youtube.com/watch?v=W5xyF-mwitU . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Метрический префикс. Предоставлено : Википедия. Расположен по адресу : http://en. 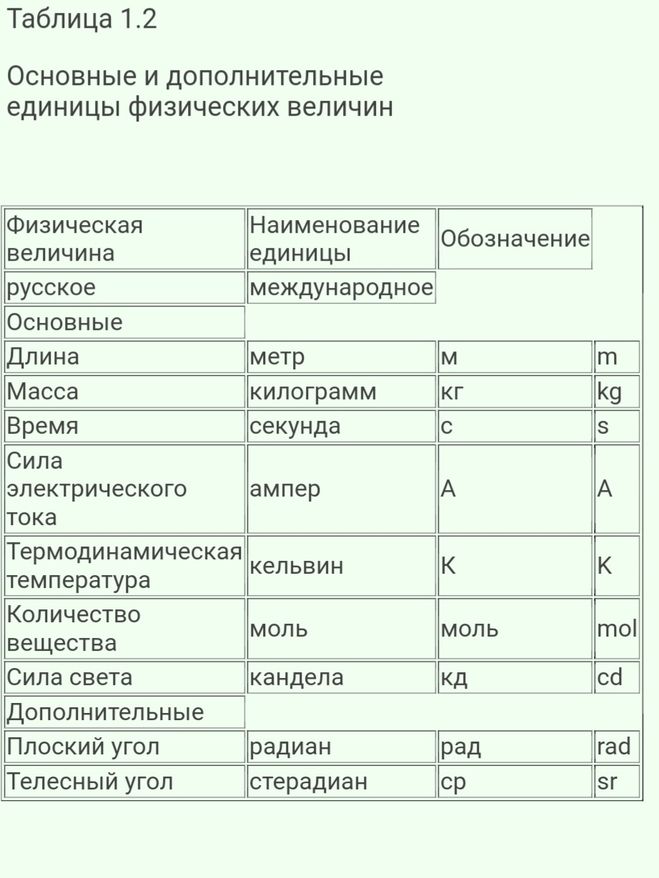Wikipedia.org/wiki/Metric_prefix . Лицензия : CC BY: Attribution
Метрическая система – Префиксы. Расположен по адресу : http://www.youtube.com/watch?v=W5xyF-mwitU . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Преобразование единиц по метке фактора. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Units_conversion_by_factor-label . Лицензия : CC BY-SA: Attribution-ShareAlike
Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42091/latest/?collection=col11406/1. 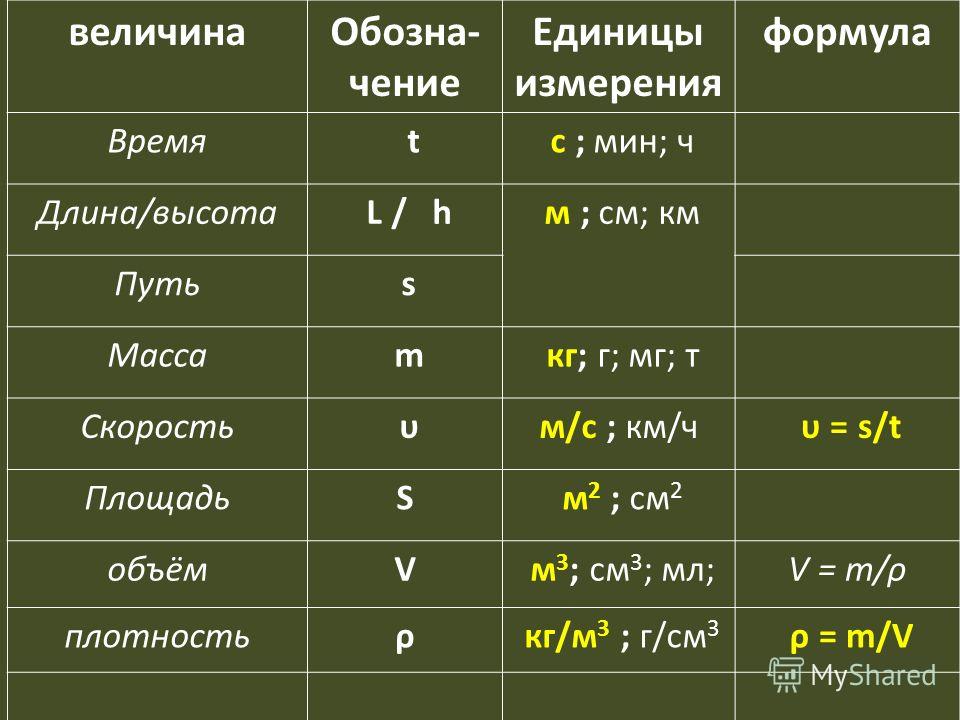7 . Лицензия : CC BY: Attribution
Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/conversion . Лицензия : CC BY-SA: Attribution-ShareAlike
Метрическая система — длина. Расположен по адресу : http://www.youtube.com/watch?v=W5xyF-mwitU . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Колледж OpenStax, Колледж физики. 10 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42091/latest/?collection=col11406/1.7 . 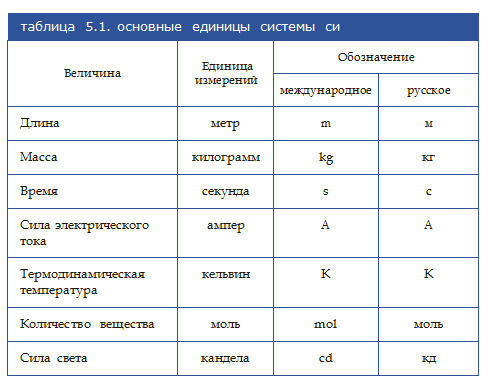Лицензия : CC BY: Attribution
Массовый дрейф прототипа. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/File:Prototype_mass_drifts.jpg . Лицензия : Общественное достояние: Нет данных Авторские права
Метрическая система – Масса Расположен по адресу : http://www.youtube.com/watch?v=W5xyF-mwitU . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Часы с цезиевым фонтаном NIST-F1. Предоставлено : http://www.nist.gov/public_affairs/r…ses/n99-22.cfm. Адрес: : http://www.nist.gov/public_affairs/releases/n99-22.cfm . Лицензия : CC BY: Attribution
Метрическая система – Время. Расположен по адресу : http://www.youtube.com/watch?v=W5xyF-mwitU . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Метрический префикс. Предоставлено : Википедия. Расположен по адресу : http://en.Wikipedia.org/wiki/Metric_prefix . Лицензия : CC BY: Attribution
Метрическая система – Префиксы. Расположен по адресу : http://www.youtube.com/watch?v=W5xyF-mwitU . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Перевод единиц измерения в метрическую систему. Расположен по адресу : http://www.youtube.com/watch?v=pEDVddQvimI . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Предоставлено : Свет и Материя. Расположен по адресу : http://lightandmatter.com/lma.pdf . Лицензия : CC BY: Attribution

Эта страница с заголовком 5.1.2: Units распространяется по незаявленной лицензии и была создана, изменена и/или курирована Boundless.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или страница
Автор
Безграничный
Показать оглавление
нет
Включено
да
Метки
1. ускорение
2. преобразование
3. инерция
4. длина
5. префикс
6. излучение
7. источник[1]-физ-14432

Примеры векторной и скалярной величины в физике

При изучении физики существует множество различных аспектов измерения и множество типов измерительных инструментов. Скалярные и векторные величины являются двумя из этих типов инструментов измерения. Продолжайте читать примеры скалярной величины и примеры векторной величины в физике.

инфографические скалярные и векторные примеры

Определение скалярных и векторных величин

Понимание разницы между скалярными и векторными величинами является важным первым шагом в физике. Основное различие в их определениях:

Скаляр — это единица измерения строго по величине .
Вектор — это измерение, которое относится как к величине единицы, так и к направлению движения, которое совершила единица.

Другими словами, скалярная величина имеет величину, такую как размер или длина, но не имеет определенного направления. Когда у него есть конкретное направление, это векторная величина.

Примеры скалярных величин

Скалярные величины, как указано выше, представляют собой измерения, строго относящиеся к величине среды.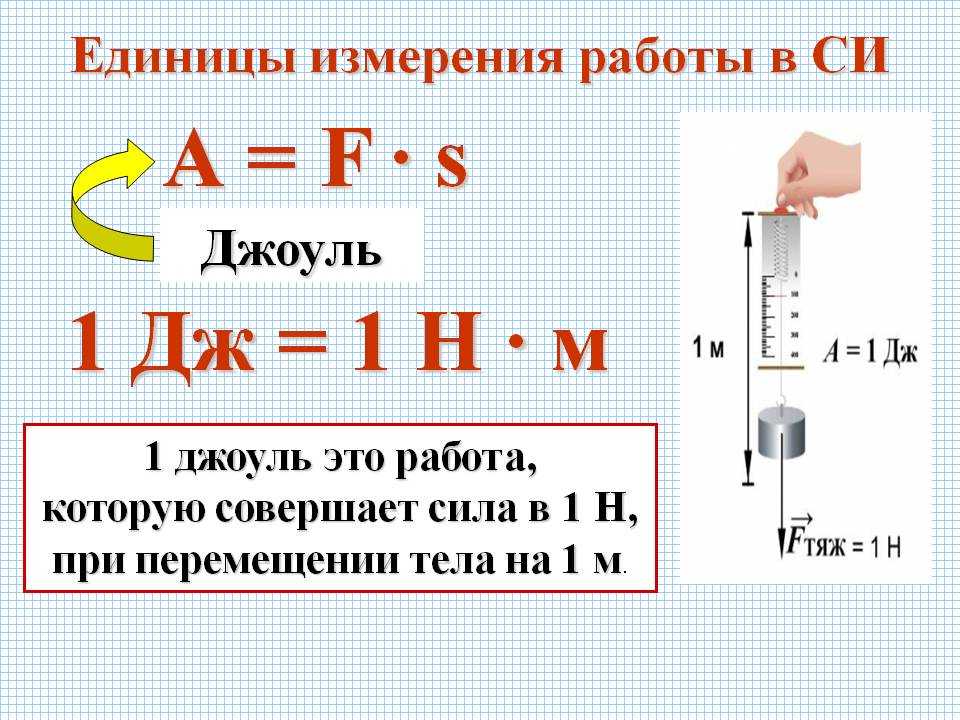 В скалярной величине совершенно нет направленных составляющих — только величина среды. Исследуйте 10 примеров скалярных величин.

Площадь

Если вы измеряете площадь поверхности участка земли или двумерного объекта, у него нет направления, только величина. Вы можете связать с ним направление, когда рассматриваемый объект является трехмерным, поскольку вы измеряете его в разных направлениях. Но площадь является скалярной, когда измерение простое и двумерное.

Плотность

Вы можете найти плотность объекта, разделив его массу на объем. Поскольку в этом расчете требуется только две точки, это скалярная величина. Направление не влияет на плотность объекта.

Расстояние

Сколько вы прошли? Измеряя расстояние, вы определяете величину пройденного вами пространства. Он не включает водоизмещение или скорость; скалярная величина расстояния обсуждает только то, сколько земли было пройдено.

Энергия

Как и другие скалярные величины, энергия является произведением двух факторов (в данном случае силы и смещения). Он описывает величину использования энергии без измерения направления.

Масса

Многие люди используют слова «вес» и «масса» как синонимы, но это не одно и то же. Масса – это количество материи, присутствующей в объекте. Это не зависит от направления; масса объекта одинакова независимо от того, в каком направлении движется объект.

Скорость

Может быть трудно понять разницу между скоростью и скоростью. Однако знание того, что скорость является скалярной величиной, может оказаться полезным, поскольку при измерении скорости направление не имеет значения.

Температура

Когда вы измеряете температуру термометром, вы измеряете среднюю тепловую энергию. Поскольку вы уже знаете, что энергия является скалярной величиной, вы, вероятно, можете понять, что температура также скалярна.

Время

Скалярные величины часто относятся ко времени, которое включает измерение лет, месяцев, недель, дней, часов, минут, секунд и даже миллисекунд. При измерении времени не учитывается или не измеряется направление, хотя кажется, что время всегда движется вперед.

Объем

Скалярное количество может относиться к объему среды, например, к тому, сколько среды присутствует. Все, от тонн и унций до граммов, миллилитров и микрограммов, — все это скалярные величины, если они применяются к измеряемой среде, а не к движению среды.

Работа

Работа — это энергия, переданная объекту силой. Это скалярная величина, поскольку она является произведением силы и перемещения. Работа — это не то же самое, что сила, которая является векторной величиной, потому что работа — это результат действия силы.

Примеры векторных величин

Векторные величины относятся как к направлению движения среды, так и к измерению скалярной величины. Вы можете заметить, что скалярные произведения часто являются произведениями двух векторных величин. Ознакомьтесь с этими 10 примерами векторных величин, встречающихся в вашей повседневной жизни.

Ускорение

Хотя скорость является скалярной величиной, ускорение отличается. Ускорение измеряет скорость изменения скорости объекта. Он учитывает период времени, а также направление, что делает его векторной величиной.

Смещение

Скалярная величина расстояния измеряет землю, пройденную движением, а смещение измеряет, насколько далеко она сместилась от своего первоначального местоположения. Вы можете видеть, что направление и величина очень важны при измерении смещения!

Сила

Сила имеет как величину, так и направление. В отличие от скалярного количества работы, сила заставляет объект изменять свою скорость. Думайте о таких силах, как гравитация, когда решаете, является ли это векторной величиной.

Повышение/снижение температуры

Измерение температуры среды является скалярной величиной. Однако измерение повышения или понижения температуры среды является векторной величиной. У него есть направление и величина.

Магнитная поляризация

Поляризация указывает на то, что два устройства отошли друг от друга. Направление (вдали друг от друга), а также величина (насколько далеко или насколько) являются важными факторами при измерении поляризации.

Импульс

Импульс показывает, что объект находится в движении. Это произведение массы и скорости, и его можно рассчитать только в том случае, если вы знаете, как быстро движется объект (величина) и в каком направлении.

Позиция

Может показаться, что фиксированное положение не имеет ни величины, ни направления. И это правильно — если вы определяете «позицию» таким образом. Вектор положения берется относительно начала системы координат; то есть он существует в конце прямой линии, которая соединяется с серединой оси. С этой точки зрения легко увидеть направление и величину.

Тяга

Тяга — это тип силы реакции, которая также имеет величину и направление. Подумайте о том, что вас толкают или толкают по воздуху — вы определенно движетесь в направлении, имеющем огромную величину! Чаще всего он используется в механике и аэронавтике.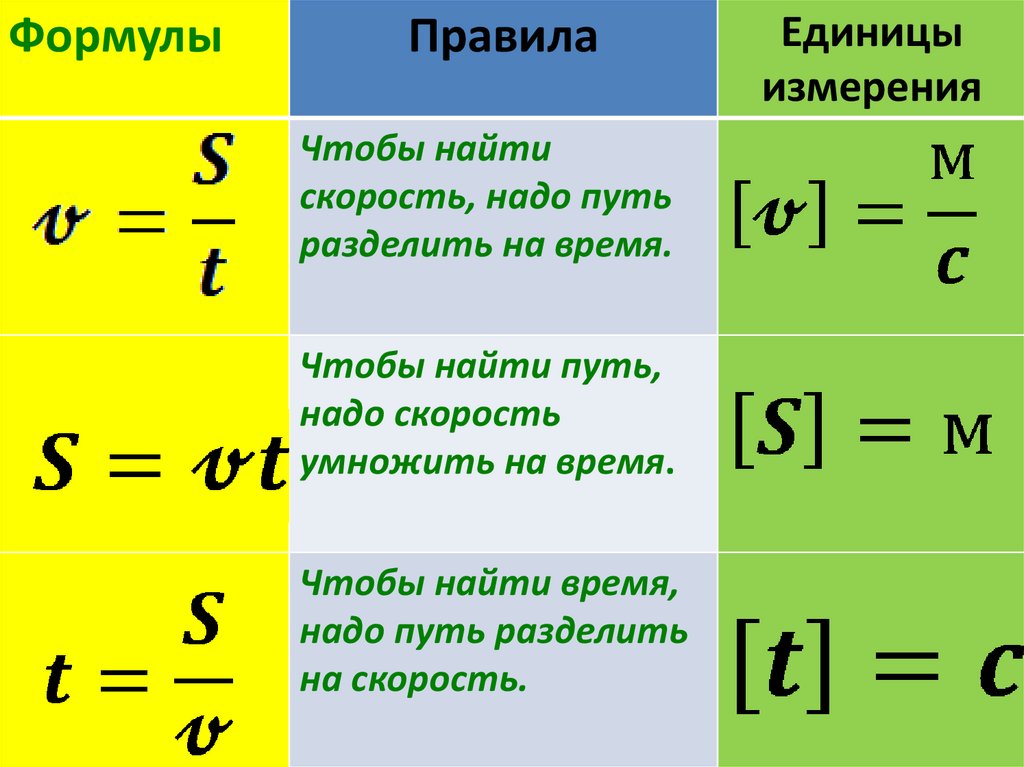

Скорость

Измерение скорости, с которой объект меняет положение, является векторной величиной. Чтобы измерить векторную величину среды, необходимо применить направленное измерение к скалярной величине. Другим элементом направления, который может быть применен к векторной величине, является разница между вертикальным и горизонтальным перемещениями.

Вес

Вес объекта является произведением его массы и действующего на него гравитационного ускорения. Поскольку это связано с силой тяжести, вес имеет направление (вниз), а также величину.

Источник дополнительной технической информации в Интернете

Высокотехнические примеры и пояснения, касающиеся скалярных и векторных величин, можно найти на веб-сайте National Aeronautics and Space. Он содержит полное описание скаляров и векторов, а также примеры и способы их использования.

Физика вокруг нас

Итак, теперь у вас есть несколько примеров скалярных и векторных величин, и вы понимаете некоторые различия между ними.

I Механика

1.1 Кинематика материальной точки

1.1.1 Понятие материальной точки. Система отсчета. Траектория, путь, перемещение Единицы измерения

В чем разница между перемещением и путем. Перемещение

Сумма перемещений

Равномерное движение

Что такое скорость движения тела.

Сложение скоростей

Фильмы

Сложение скоростей

Классическая механика

Примеры

Релятивистская механика

Физика. Дайте определение скорости тела и формула

Подскажите что такое скорость (определение) и прибор для определения скорости.

Понятие скорости механического движения

Закон сложения скоростей

Отрицательная скорость

Скорость в физике: как найти скорость?

Единицы измерения скорости

Средняя скорость в физике

Перемещение, скорость и ускорение

5.1.2: Единицы – Физика LibreTexts

Длина

Масса

Масса

Масса и вес

Время

Префиксы и другие системы единиц

Префиксы

Другие системы единиц

Преобразование единиц

Перевод систем измерения

Методы преобразования

Ключевые моменты

Ключевые термины

Примеры векторной и скалярной величины в физике

Определение скалярных и векторных величин

Примеры скалярных величин

Площадь

Плотность

Расстояние

Энергия

Масса

Скорость

Температура

Время

Объем

Работа

Примеры векторных величин

Ускорение

Смещение

Сила

Повышение/снижение температуры

Магнитная поляризация

Импульс

Позиция

Тяга

Скорость

Вес

Источник дополнительной технической информации в Интернете

Физика вокруг нас

Оставить комментарий Отменить ответ