4.4. Задача о перемножении матриц
Как известно из высшей математики, умножение матриц ассоциативно, то есть результат перемножения зависит только от порядка матриц и не зависит от расстановки скобок:
(А*В)*С = А*(В*С).
Результат перемножения от расстановки скобок не зависит, зато трудоемкость этого перемножения при разных расстановках скобок может отличаться существенно.
Оценим трудоемкость умножения двух матриц A(p×q) и B(q×r):
C(p×r) = A(p×q)* B(q×r),
каждый элемент матрицу C(p˟r) есть сумма q попарных произведений.
Трудоемкость перемножения двух матриц: T = p·q

Пример. Рассмотрим пример перемножения матриц разными способами:
Пусть имеется четыре матрицы разных размерностей:
М1[10×20], M2[20×50], M3[50×1], M4[1×100].
Решение.
Рассмотрим умножение матриц в следующей порядке:
М1 · (М2 · (М3 · М4) )
[50×1] · [1×100] = [50×100] трудоём. 50·1·100 = 5000
125 000 операций
[20×50]·[50×100] = [20×100] трудоём. 20·100·50 = 100 000
[10×20] · [20×100] = [10×100] трудоём. 10·20·100 = 20 000
Рассмотрим другой вариант умножения матриц:
(М1 · (М2 · М3 ) )· М)
[20×50]
· [50×1] = [20×1] трудоём. 20·50·1 = 1000
20·50·1 = 1000
2200 операций
[10×20]·[20×1] = [10×1] трудоём. 10·20·1 = 200
[10×1] · [1×100] = [10×100] трудоём. 10·1·100 = 1000
При умножении вторым способом действий потребовалось значительно меньше (2200 против 125 000). Придумаем формулу метода ДП применительно к данной задачу.
Допустим, нам необходимо оптимальным образом перемножить 5 матриц. i-тая матрица имеет размерность [ri-1× ri]. Смотрим, где стояла последняя пара скобок: существует 4 варианта:
(M1)·(M2·M3·M4·M5) [r0×r1] [r1×r5] | (1) |
(M1·M2) ·(M3·M4·M5) [r0 | (2) |
(M1·M2·M3) ·(M4·M5) [r0×r3] [r3×r5] | (3) |
(M1·M2·M3·M4) ·(M [r0×r4] [r4×r5] | (4) |
При первом варианте расстановок скобок нам потребуется
f(1,1)
+ f(2,5)
+ r0r1r5 операций.
Здесь f(k,l) – минимальное количество действий, за которое можно вычислить произведение матриц с k-той по
Для последующих трех вариантов:
f(1,2) + f(3,5) + r0r2r5
f(1,3) + f(4,5) + r0r3r5
f(1,4) + f(5,5) + r0r4r5
операций соответственно.
Здесь f(k,p) – минимальное количество действий, за которое можно вычислить произведение матриц с k-той по p-тую.
Выбираем минимум среди всех этих чисел и получаем общую формулу:
Замечание. В
отличии от задачи о рюкзаке, где была
динамика по одному параметру
(грузоподъемности), здесь динамика по
двум параметрам: начало и конец блока
перемножаемых матриц.
В
отличии от задачи о рюкзаке, где была
динамика по одному параметру
(грузоподъемности), здесь динамика по
двум параметрам: начало и конец блока
перемножаемых матриц.
Итак, в окончательном виде эта задача решается с помощью следующего алгоритма.
Заполняем трудоемкости матриц: Трудоемкости по главной диагонали равны 0:
for i:=0 to n do f(i,i):=0;
Средний цикл по k – местоположению блока;
Внутренний – поиски минимума по j.
for t:=1 to n-1 do
for k:=1 to n-1 do
Для матриц М1, М2, М3, М4 из рассмотренного выше примера расставим скобки оптимальным образом.
f(1,1) | f(1,2) | f(1,3) | f(1,4) |
f(2,2) | f(2,3) | f(2,4) | |
f(3,3) | f(3,4) | ||
f(4,4) |
Итак, заполняем такую матрицу в следующем порядке:
f(1,1) = f(2,2) = f(3,3) = f(4,4) = 0
f(1,2) = min (f(1,1) + f(2,2) + 10·20·50) = 10 000
f(2,3) = min (f(2,2) + f(3,3,) + 20·50·1) = 1000
f(3,4) = min (f(3,3) + f(4,4) + 50·1·100) = 5000
f(1,3) = min (f(1,1) + f(2,3) + 10·20·1; f(1,2) + f(3,3) + 10·50·1) = 1200
f(2,4) = min (f(2,2) + f (3,4) +20·50·100; f(2,3) + f (4,4) + 20·1·100) = 3000
f(1,4) = min (f(1,1) + f(2,4) + 10·20·100; f(1,2) + f(3,4) + 10·50·100; f(1,3) + f(4,4) + 10·1·100) = 2200
После
вычисления оптимальных трудоемкостей
восстанавливаем оптимальную расстановку
скобок.
Смотрим, где достигнут минимум в
Далее смотрим, где достигнут минимум в f(1,3). Он достигнут в f(1,1) + f(2,3) + 10·20·1. Т.е. следующими скобками будут (М1 (М2 М3) М4.
Т.к. у нас 3 вложенных цикла, длина каждого порядка n (n – количество перемножаемых матриц), то трудоемкость решаемой задачи методом ДП
При
решении этой задачи методом прямого
перебора получаем не полиноминальную
трудоемкость, а намного большую. То же
самое получаем и для задачи о рюкзаке:
её решение методом динамического
программирования имеет полиномиальную
трудоемкость (2 вложенных цикла), а
методом прямого перебора получаем
неполиномиальную трудоемкость.
Домашнее задание №6 (А, Б)
А) Задача грабителя (о рюкзаке). Имеет склад, на котором присутствует ассортимент товаров ( каждого товара неограниченный запас). У каждого товара своя стоимость Ci и масса mi. Выбрать набор товаров так, чтобы его суммарных вес не превышал заданную грузоподъемность М притом, что суммарная стоимость этого набора товаров была бы максимальной.
Номер товара, i | mi | Ci |
1 | 5 | 9 |
2 | 7 | 13 |
3 | 11 | 21 |
Максимальная
грузоподъемность: М = 23; 24.
Б) Расставить скобки при перемножении матриц оптимальным образом.
М1=[10×20], M2=[20×5], M3=[5×4], M4=[4×30], M5=[30×6].
при умножении 2 × 2 матриц
Ранд пограничного ранга по умножению двух на две матрицы составляет семь
- J. Landsberg
Математика
- 2004
I Показы менее семи умножений. Другими словами, я показываю, что оператор умножения матриц не находится в шестой секущей разновидности…
Об аддитивной сложности умножения матриц 2 x 2
- Бшуты Н.
Информатика, Математика
Инф. Процесс. лат.
- 1995
Нижняя граница для умножения матрикса
- N. Bshouty
Компьютерная наука, математика
[Распания 1988] что для вычисления произведения двух матриц n*n над двоичным полем требуется не менее 2,5n/sup 2/-O(n/sup 2/) умножений.
 <
<> О сложности умножения матриц малых форматов
- М. Блезер
Математика, информатика
Дж. Комплекс.
- 2003
A bilinear algorithm of length 22 for approximate multiplication of 2 × 7 and 7 × 2 matrices
- A. V. Smirnov
Computer Science, Mathematics
Computational Mathematics and Mathematical Physics
- 2015
Дана верхняя оценка билинейной сложности приближенного умножения матриц 2 × 2 и 2 × n (n ≥ 1).
Билинейный алгоритм длины 22 для приближенного умножения матриц 2 × 7 и 7 × 2
- Смирнов А.В. умножение матриц 2 × 2 и 2 × n (n ≥ 1).
Быстрое умножение матриц
- C. M. Fiduccia
Математика, информатика
STOC
- 1971
сложности нескольких наборов функций и нескольких матриц, представляющих общий интерес.

Сложность произведения кватернионов
- Т. Хауэлл, Дж. Лафон
Математика
- 1975
Пусть X и Y — два кватерниона над произвольным кольцом. Восемь умножений необходимы и достаточны для вычисления произведения XY. Если кольцо предполагается коммутативным, по крайней мере семь…
О геометрии граничных ранговых алгоритмов для умножения матриц n × 2 на 2 × 2
- Дж. Ландсберг, Николас Райдер
Информатика
Эксп. Мат.
- 2017
Проведено углубленное исследование известных алгоритмов граничного ранга для тензора умножения матриц, кодирующего умножение матрицы n × 2 на матрицу 2 × 2.
Введение в вычислительную сложность умножения матриц
- Y. Li, Shenglong Hu, Jie Wang, Zhenghai Huang
Математика
- 2019
рангами тензоров умножения матриц.
 Основные результаты и последние разработки в этой…
Основные результаты и последние разработки в этой…Калькулятор произведения матриц — онлайн-умножение матриц
Поиск инструмента
Найдите инструмент в dCode по ключевым словам:
Просмотрите полный список инструментов dCodeМатричный продукт
Инструмент для расчета матричных продуктов. Алгебра матричных произведений состоит из умножения матриц (квадратных или прямоугольных).
Результаты
Продукт Matrix – dCode
Тег(и) : Matrix
Поделиться
dCode и многое другое
dCode бесплатен, а его инструменты являются ценным помощником в играх, математике, геокэшинге, головоломках и задачах для решения любых задач. день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !Матричный продукт
Произведение двух матриц
Matrix M1Загрузка…
Matrix M2
(если это сообщение не исчезнет, попробуйте обновить эту страницу)Загрузка.
 ..
..
(если это сообщение не исчезнет, попробуйте обновить эту страницу)Произведение матрицы на скаляр (число)
Matrix MЗагрузка…
Скаляр A
(если это сообщение не исчезнет, попробуйте обновить эту страницу)См. также: Калькулятор матриц
Алфавит
Строка матрицыЗагрузка…
Столбец матрицы
(если это сообщение не исчезнет, попробуйте обновить эту страницу)Загрузка…
(если это сообщение не исчезнет, попробуйте обновить эту страницу)Ответы на вопросы (FAQ)
Что такое матричный продукт? (Определение)
Матричный продукт — это название, данное наиболее распространенному матричному умножению 9n a_{ik}b_{kj} $$
Умножение двух матриц $M_1$ и $M_2$ отмечается точкой $\cdot$ или . поэтому $M_1\cdot M_2$
Произведение матриц определяется только тогда, когда количество столбцов $M_1$ равно количеству строк $M_2$ (матрицы называются совместимыми)
Как умножить 2 матрицы? (Произведение матриц)
Умножение 2-х матриц $M_1$ и $M_2$ образует результирующую матрицу $M_3$.
 Матричный продукт заключается в выполнении сложений и умножений по позициям элементов в матрицах $M_1$ и $M_2$.
Матричный продукт заключается в выполнении сложений и умножений по позициям элементов в матрицах $M_1$ и $M_2$.$$ M_1 = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \ vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \\ M_2 = \begin{bmatrix} b_{11} & b_{ 12} & \cdots & b_{1p} \\ b_{21} & b_{22} & \cdots & b_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ b_{n1} & b_ {n2} & \cdots & b_{np} \end{bmatrix} \\ M_1 \cdot M_2 = \begin{bmatrix} a_{11}b_{11} +\cdots + a_{1n}b_{n1} & a_ {11}b_{12} +\cdots + a_{1n}b_{n2} & \cdots & a_{11}b_{1p} +\cdots + a_{1n}b_{np} \\ a_{21}b_ {11} +\cdots + a_{2n}b_{n1} и a_{21}b_{12} +\cdots + a_{2n}b_{n2} & \cdots & a_{21}b_{1p} +\ cdots + a_{2n}b_{np} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}b_{11} +\cdots + a_{mn}b_{n1} & a_{m1} b_{12} +\cdots + a_{mn}b_{n2} & \cdots & a_{m1}b_{1p} +\cdots + a_{mn}b_{np} \end{bmatrix} $$
Для вычисления значения элемента матрицы $M_3$ в позиции $i$ и столбце $j$ извлеките строку $i$ из матрицы $M_1$ и строку $j$ из матрицы $M_2$ и вычислить их скалярное произведение.
 То есть умножить первый элемент строки $i$ массива $M_1$ на первый элемент столбца $j$ массива $M_2$, затем второй элемент строки $i$ массива $M_1$ на второй элемент столбца $j$ из $M_2$ и так далее, обратите внимание на сумму полученных умножений, это значение скалярного произведения, следовательно, элемента в позиции $i$ и столбца $j$ в $M_3$.
То есть умножить первый элемент строки $i$ массива $M_1$ на первый элемент столбца $j$ массива $M_2$, затем второй элемент строки $i$ массива $M_1$ на второй элемент столбца $j$ из $M_2$ и так далее, обратите внимание на сумму полученных умножений, это значение скалярного произведения, следовательно, элемента в позиции $i$ и столбца $j$ в $M_3$.Пример: $$ \begin{bmatrix} 1 & 0 \\ -2 & 3 \end{bmatrix} \cdot \begin{bmatrix} 2 & -1 \\ 4 & -3 \end{bmatrix} = \begin{bmatrix} 1 \times 2 + 0 \times 4 & 1 \times -1 + 0 \times -3 \\ -2 \times 2 + 4 \times 3 & -2 \times -1 + 3 \times – 3 \end{bmatrix} = \begin{bmatrix} 2 & -1 \\ 8 & -7 \end{bmatrix} $$
Как умножить матрицу на скаляр?
Произведением матрицы $M=[a_{ij}]$ на скаляр (число) $\lambda$ является матрица того же размера, что и исходная матрица $M$, при этом каждый элемент матрицы умножается на $\лямбда$.
$$ \lambda M = [ \lambda a_{ij} ] $$
Что такое свойства умножения матриц?
Ассоциативность: $$ A \times (B \times C) = (A \times B) \times C $$
Дистрибутивность: $$ A \times (B + C) = A \times B + A \times C $$
$$ (A + B) \times C = A \times C + B \times C $$
$$ \lambda (A \times B) = (\lambda A) \times B = A \times (\lambda B) $$
Порядок операндов имеет значение при умножении матриц , поэтому $$ M_1.
 M_2 \neq M_2.M_1 $$
M_2 \neq M_2.M_1 $$Как перемножить две матрицы несовместимых форм?
Существует матричный продукт , совместимый с матрицами любых размеров: продукт Кронекера.
Исходный код
dCode сохраняет за собой право собственности на исходный код «Matrix Product». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Matrix Product», апплета или фрагмента (конвертер, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Matrix Product» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, скрипт, или доступ к API для «Матричного продукта» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложении для Android!
Напоминание: dCode можно использовать бесплатно.

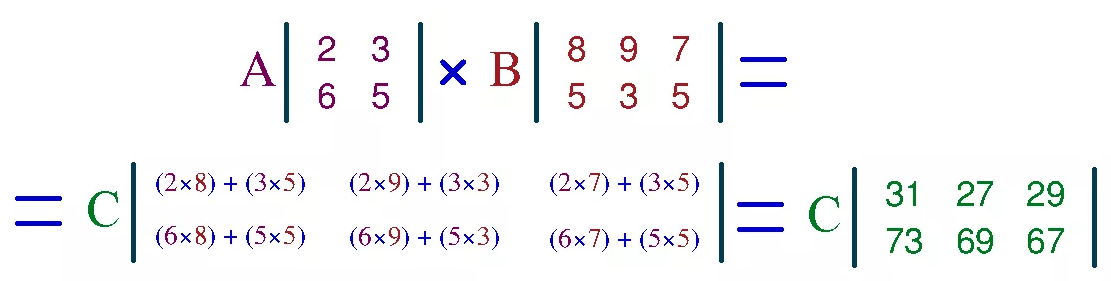 <
<
 Основные результаты и последние разработки в этой…
Основные результаты и последние разработки в этой… ..
..  Матричный продукт заключается в выполнении сложений и умножений по позициям элементов в матрицах $M_1$ и $M_2$.
Матричный продукт заключается в выполнении сложений и умножений по позициям элементов в матрицах $M_1$ и $M_2$. То есть умножить первый элемент строки $i$ массива $M_1$ на первый элемент столбца $j$ массива $M_2$, затем второй элемент строки $i$ массива $M_1$ на второй элемент столбца $j$ из $M_2$ и так далее, обратите внимание на сумму полученных умножений, это значение скалярного произведения, следовательно, элемента в позиции $i$ и столбца $j$ в $M_3$.
То есть умножить первый элемент строки $i$ массива $M_1$ на первый элемент столбца $j$ массива $M_2$, затем второй элемент строки $i$ массива $M_1$ на второй элемент столбца $j$ из $M_2$ и так далее, обратите внимание на сумму полученных умножений, это значение скалярного произведения, следовательно, элемента в позиции $i$ и столбца $j$ в $M_3$. M_2 \neq M_2.M_1 $$
M_2 \neq M_2.M_1 $$