Перемножение матриц с: C# .Net: Умножение матриц – programm.top

Блочное умножение матриц для программистов — Блог Евгения Жирнова

#include <stdio.h>
#include <string.h>
 
 
void Rec_Mult(int *C, const int *A, const int *B, int n, int rowsize)
{
    if (n == 2)
    {
        const int d11 = 0;
        const int d12 = 1;
        const int d21 = rowsize;
        const int d22 = rowsize + 1;
 
        C[d11] += A[d11] * B[d11] + A[d12] * B[d21];
        C[d12] += A[d11] * B[d12] + A[d12] * B[d22];
        C[d21] += A[d21] * B[d11] + A[d22] * B[d21];
        C[d22] += A[d21] * B[d12] + A[d22] * B[d22];
    }
    else
    {
        const int d11 = 0;
        const int d12 = n / 2;
        const int d21 = (n / 2) * rowsize;
        const int d22 = (n / 2) * (rowsize + 1);
 
        // C11 += A11 * B11
        Rec_Mult(C + d11, A + d11, B + d11, n / 2, rowsize);
        // C11 += A12 * B21
        Rec_Mult(C + d11, A + d12, B + d21, n / 2, rowsize);
 
        // C12 += A11 * B12
        Rec_Mult(C + d12, A + d11, B + d12, n / 2, rowsize);
        // C12 += A12 * B22
        Rec_Mult(C + d12, A + d12, B + d22, n / 2, rowsize);
 
        // C21 += A21 * B11
        Rec_Mult(C + d21, A + d21, B + d11, n / 2, rowsize);
        // C21 += A22 * B21
        Rec_Mult(C + d21, A + d22, B + d21, n / 2, rowsize);
 
        // C22 += A21 * B12
        Rec_Mult(C + d22, A + d21, B + d12, n / 2, rowsize);
        // C22 += A22 * B22
        Rec_Mult(C + d22, A + d22, B + d22, n / 2, rowsize);
    }
}
 
 
#define ROW_COUNT 8
 
 
void printMatrix(const char *name, const int *mat)
{
    printf("%s:\n", name);
 
    for (int i = 0; i < ROW_COUNT; ++i)
    {
        for (int j = 0; j < ROW_COUNT; ++j)
        {
            printf("%4d", mat[i * ROW_COUNT + j]);
        }
        printf("\n");
    }
    printf("\n");
}
 
 
int main()
{
    const int matA[ROW_COUNT * ROW_COUNT] =
    {
        1, 2, 3, 0, 0, 4, 5, 6,
        1, 2, 3, 0, 0, 4, 5, 6,
        1, 2, 3, 0, 0, 4, 5, 6,
        1, 2, 3, 0, 0, 4, 5, 6,
        1, 2, 3, 0, 0, 4, 5, 6,
        1, 2, 3, 0, 0, 4, 5, 6,
        1, 2, 3, 0, 0, 4, 5, 6,
        1, 2, 3, 1, 1, 4, 5, 6,
    };
 
    const int matB[ROW_COUNT * ROW_COUNT] =
    {
        2, 2, 2, 2, 2, 2, 2, 2,
        3, 3, 3, 3, 3, 3, 3, 3,
        0, 0, 0, 0, 0, 0, 0, 0,
        4, 0, 0, 0, 0, 0, 0, 2,
        4, 0, 0, 0, 0, 0, 0, 2,
        0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0,
        1, 1, 1, 1, 1, 1, 1, 1,
    };
 
    int matC[ROW_COUNT * ROW_COUNT];
    memset(matC, 0, sizeof(matC));
 
    Rec_Mult(matC, matA, matB, ROW_COUNT, ROW_COUNT);
 
    printMatrix("Matrix A", matA);
    printMatrix("Matrix B", matB);
    printMatrix("Multiply", matC);
 
    return 0;
}

Оптимальное умножение матриц – 2 – Задачи

Имея две матрицы A и B, мы можем вычислить C = AB используя стандартные правила умножения матриц:

Число колонок в матрице A должно совпадать с числом строк матрицы B. Пусть матрица A имеет размер m × n, матрица B имеет размер n × p. Тогда матрица С будет иметь размер m × p, а для ее вычисления следует совершить m * n * p умножений.

Например, если A имеет размер 10 × 20, B имеет размер 20 × 15, то необходимо совершить 10 × 20 × 15 = 3000 умножений для вычисления матрицы C.

Перемножать несколько матриц можно несколькими способами. Например, если у нас имеются матрицы X, Y и Z, то вычислить XYZ можно либо как (XY)Z, либо как X(YZ). Пусть X имеет размер 5 × 10, Y имеет размер 10 × 20, Z имеет размер 20 × 35.

Подсчитаем количество умножений, необходимых для перемножения трех матриц в каждом из этих двух случаях:

(XY)Z

• 5 × 20 × 10 = 1000 умножений для определения матрицы (XY), имеющей размер 5 × 20.
• Потом 5 × 35 × 20 = 3500 умножений для нахождения конечного результата.
• Общее количество умножений: 4500.

X(YZ)

• 10 × 35 × 20 = 7000 умножений для определения матрицы (YZ), имеющей размер 10 × 35.
• Потом 5 × 35 × 10 умножений для нахождения конечного результата.
• Общее количество умножений: 8750.

Очевидно, что при вычислении (XY)Z требуется меньшее количество умножений.

По заданной последовательности перемножаемых матриц следует найти оптимальный порядок их умножения. Оптимальным называется такой порядок умножения матриц, при котором количество элементарных умножений минимально.

Входные данные

Состоит из нескольких тестов. Первая строка каждого теста содержит количество n (n ≤ 10) перемножаемых матриц. Далее следуют n пар целых чисел, описывающих количество строк и столбцов в матрице, размеры матриц задаются в порядке их перемножения. Последний тест содержит n = 0 и не обрабатывается.

Выходные данные

Пусть матрицы пронумерованы A1, A2,. .., An. Для каждого теста в отдельной строке следует вывести его номер и скобочное выражение, содержащее оптимальный порядок умножения матриц. Тесты нумеруются начиная с 1. Вывод должен строго соответствовать формату, приведнному в примере. Если существует несколько оптимальных порядков перемножения матриц, выведите любой из них.

Перемножение матриц – это… Что такое Перемножение матриц?

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами.

Правила выполнения операций над матрицами сделаны такими, чтобы было удобно записывать системы линейных уравнений.

Обычно матрицу обозначают заглавной буквой латинского алфавита и выделяют круглыми скобками «(…)» (встречается также выделение квадратными скобками «[…]», двойными прямыми линиями «||…||»).

Числа, составляющие матрицу (элементы матрицы), часто обозначают той же буквой, что и саму матрицу, но строчной.

У каждого элемента матрицы есть 2 нижних индекса (a_ij) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Говорят «матрица размерности », подразумевая, что в матрице m строк и n столбцов.

История

Понятие матрицы впервые появилось в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу.

Матрица как запись коэффициентов системы линейных уравнений

Систему из m уравнений с n неизвестными

можно представить в матричном виде

и тогда всю систему можно записать так:

AX = B,

где A имеет смысл таблицы коэффициентов a_ij системы уравнений.

Если m = n и матрица A невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы A ^{– 1}, поскольку умножив обе части уравнения на эту матрицу слева

A ^{– 1}AX = A ^{– 1}B

A ^{− 1}A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений

X = A ^{– 1}B.

Все правила, по которым проводятся операции над матрицами выводятся из операций над системами уравнений.

Операции над матрицами

Пусть a_ij — элементы матрицы A, а b_ij — элементы матрицы B.

Линейные операции:

Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы

b_ij = λa_ij

Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен

c_ij = a_ij + b_ij

Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы

c_ij = a_ij – b_ij

Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть

A + Θ = A

Все элементы нулевой матрицы равны нулю.

Нелинейные операции:

Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция вычисления матрицы

В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность , B — , то размерность их произведения AB = C есть . Умножение матриц не коммутативно.

Умножение матриц ассоциативно. Возводить в степень можно только квадратные матрицы.

Транспонирование матрицы (обозначение: A^T) — операция, при которой матрица отражается относительно главной диагонали, то есть

Если A — матрица размера , то A^T — матрица размера

Квадратная матрица и смежные определения

Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.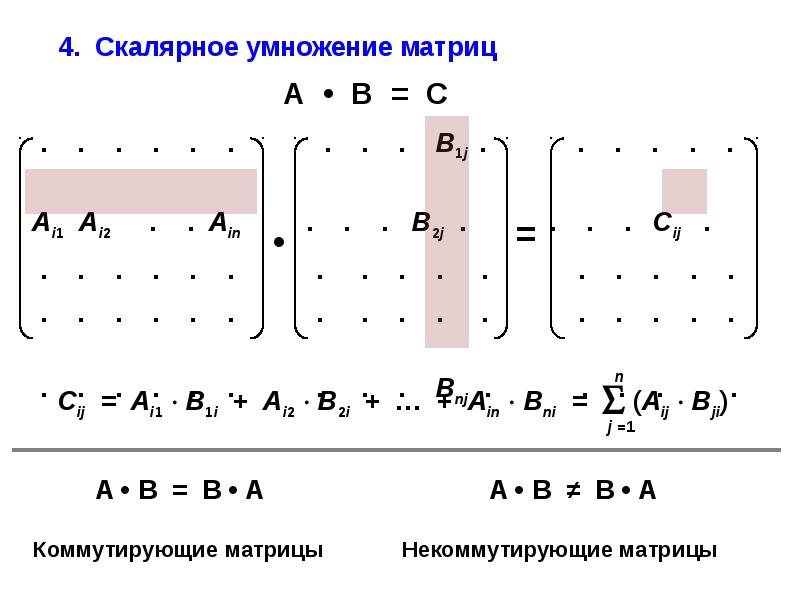

Для квадратных матриц существует единичная матрица E (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно

EA = AE = A

У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю

Для некоторых квадратных матриц можно найти так называемую

AA ^{− 1} = E

Обратная матрица существует не всегда. Матрицы, для которых обратная существует, называются невырожденными (или регулярными), а для которых нет — вырожденными (или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности на столбцах матрицы.

Свойства матриц

1. A + (B + C) = (A + B) + C
2. A + B = B + A
3. A(BC) = (AB)C
4. A(B + C) = AB + AC
5. (B + C)A = BA + CA
9. (A^T)^T = A
10. (A * B )^T = B^T * A^T

Элементарные преобразования матриц

Элементарными преобразованиями строк матрицы называются следующие преобразования:

1. Умножение строки на число отличное от нуля
2. Прибавление одной строки к другой строке

Элементарные преобразование столбцов матрицы определяются аналогично.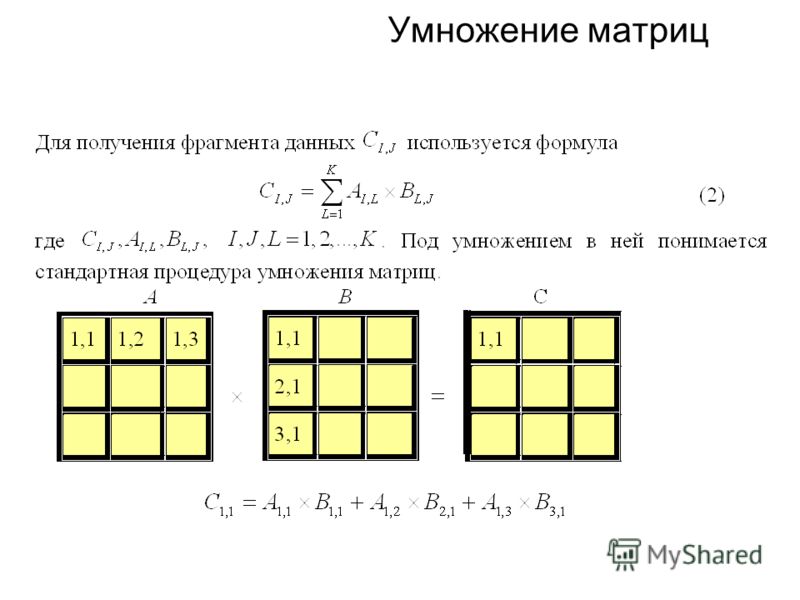

Типы матриц

Матрица линейного оператора

Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.

Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.

Выберем базис . Пусть  — произвольный вектор. Тогда его можно разложить по этому базису:

,

где x^k — координаты вектора в выбранном базисе.

Здесь и далее предполагается суммирование по немым индексам.

Пусть  — произвольный линейный оператор. Подействуем им на обе стороны предыдущего равенства, получим

.

Вектора также разложим в выбранном базисе, получим

,

где  — j-я координата k-го вектора из .

Подставим разложение в предыдущую формулу, получим

.

Выражение , заключённое в скобки, есть ни что иное, как формула умножения матрицы на столбец, и, таким образом, матрица при умножении на столбец x^k даёт в результате координаты вектора , возникшего от действия оператора на вектор , что и требовалось получить.

См. также

Литература

Ссылки

Wikimedia Foundation. 2010.

Матрицы – это способ группировки чисел, которые организованы в строки и столбцы. Матрицы часто используются как способ представления нескольких уравнений в более удобном для организации формате, однако для решения этих систем уравнений мы должны иметь возможность выполнять матричные операции, такие как умножение.

Строки и столбцы

Приведенная ниже матрица является примером матрицы [3×2]. Матрицы описываются в форме [RxC], где R представляет количество строк матрицы, а C представляет количество столбцов матрицы.

Вышеупомянутая матрица имеет размер [3×2], потому что у нее 3 строки и 2 столбца.

Умножение на скаляр

Любую матрицу можно умножить на так называемую скалярную величину. В этом случае скаляр представляет собой действительное число, умноженное на всю матрицу. Например:

Умножение матриц

Также возможно умножение двух матриц вместе, однако матрицы могут быть умножены только в том случае, если количество столбцов первой матрицы равно количеству строк второй матрицы.Если две матрицы соответствуют этому критерию, их можно умножить. Результатом будет третья матрица с таким же количеством строк, как в первой матрице, и с таким же количеством столбцов, как во второй матрице.

Пример

Можно ли перемножить следующие матрицы? Каковы будут размеры ответа?

1. [2×3] * [2×2]

2. [3×2] * [2×2]

3. [2 * 3] * [3 * 1]

Ответ

1. ср. невозможно умножить эти матрицы, потому что матрица 1 имеет три столбца, а матрица 2 – только две строки.

2. Мы можем умножать эти матрицы, потому что матрица 1 имеет два столбца, а матрица 2 – две строки. Результирующая матрица будет иметь столько же строк, сколько матрица 1 и столбцов, как матрица 2 – так что это будет [3×2].

3. Мы можем перемножить эти две матрицы, потому что матрица 1 имеет три столбца, а матрица 2 – три строки. Результатом будет [2×1].

Примечание: Это упражнение должно было прояснить, что порядок имеет значение при умножении двух матриц. Попробуйте изменить порядок любого из приведенных выше примеров и посмотрите, изменится ли результат.

Правила умножения матриц

Как только мы узнаем, можно ли умножить две матрицы, пора выполнить это умножение. Умножение двух матриц также известно как «скалярное произведение». Каждое число в матрице ответов является результатом умножения одной из строк матрицы 1 на один из столбцов матрицы 2.

Чтобы найти первую строку, первый столбец матрицы ответов, умножьте первую строку матрицы 1 на столбец один. матрицы 2. Чтобы найти строку 1, столбец 2 матрицы ответов, умножьте первую строку матрицы 1 на второй столбец матрицы 2.При умножении строки на столбец совпадающие термины умножаются и складываются.

Пример: Найдите скалярное произведение двух матриц

Матрица 1 имеет два столбца, а матрица 2 – две строки, поэтому эти две можно умножить. В ответе будет две строки, потому что в матрице 1 две строки и три столбца, потому что в матрице 2 три столбца. Таким образом, ответ будет [2×3].

Допустим, мы сначала хотим найти верхний левый угол матрицы ответов (отмечен X).Поскольку точка, которую мы хотим найти, находится в строке 1, столбце 1, мы должны умножить строку 1 первой матрицы на столбец 1 второй матрицы. Строка и столбец, которые необходимо умножить, отмечены стрелками.

При умножении строки и столбца мы умножаем первое число в строке на первое число в столбце, умножаем второе число в строке на второе число в столбце и складываем результат.

Чтобы найти нижний левый угол матрицы ответов, мы повторяем тот же процесс.Поскольку точка, которую мы ищем, находится во второй строке и первом столбце матрицы ответов, мы должны умножить вторую строку первой матрицы на первый столбец второй матрицы.

Процесс повторяется снова для строки 2, столбца 2:

После умножения всех строк и столбцов, как показано в предыдущих шагах, матрица ответов завершена.

Умножение матриц – Мэтью Н. Бернштейн

На первый взгляд определение произведения двух матриц может показаться неинтуитивным.В этом посте мы обсуждаем три перспективы просмотра умножения матриц. Это третья точка зрения, которая придает этому «неинтуитивному» определению силу: умножение матриц представляет собой композицию линейных преобразований.

Введение

Умножение матриц – это операция между двумя матрицами, которая создает новую матрицу. Студентам, знакомым с умножением матриц, может быть непонятно, что умножение матриц , а не просто влечет за собой вычисление произведения каждой пары соответствующих записей между двумя матрицами. То есть

Скорее, матричное умножение определяется гораздо более сложным способом:

Определение 1 (матричное умножение): Произведение $ m \ times n $ матрицы $ \ boldsymbol {A} $ Матрица , умноженная на на матрицу $ n \ times p $ $ \ boldsymbol {B} $, задается как

где $ \ boldsymbol {b} _ {*, i} $ – это $ i $ -й столбец $ \ boldsymbol {B} $.

То есть для двух матриц $ \ boldsymbol {A} $ и $ \ boldsymbol {B} $ каждый столбец матрицы произведения $ \ boldsymbol {AB} $ формируется путем умножения матрицы на вектор между $ \ boldsymbol { A} $ и каждый столбец $ \ boldsymbol {B} $. Обратите внимание, что это определение требует, чтобы количество столбцов первой матрицы было равно количеству строк второй матрицы. Если это не так, умножение матриц не определено.

Это сложное определение порождает вопрос: какова интуиция за умножением матриц? И почему это не определяется как просто попарные произведения между соответствующими элементами двух матриц, как описано выше? В этом посте мы рассмотрим три способа просмотра умножения матриц, и, надеюсь, станет очевидным, что это более сложное определение намного мощнее, чем наивное определение, вычисляющее попарные произведения.Его сила проистекает из третьей точки зрения, которую мы обсудим: умножение матриц представляет собой композицию линейных преобразований.

Три перспективы для понимания матричного умножения

Существует как минимум три перспективы, для каждой из которых можно рассматривать матричное умножение, в зависимости от точки зрения, взятой для каждого из матричных факторов. Напомним, мы можем рассматривать матрицу с нескольких точек зрения:

1. Как список векторов-столбцов
2. Как список векторов-строк
3. Как линейное преобразование

Учитывая эти различные способы возможного просмотра каждого матричного фактора, $ \ boldsymbol {A} $ и $ \ boldsymbol {B} $, мы можем просмотреть их продукт, $ \ boldsymbol {AB} $, следующим образом:

1. Умножение матриц вычисляет линейное преобразование на множестве векторов: Если мы рассматриваем $ \ boldsymbol {A} $ как линейное преобразование, а $ \ boldsymbol {B} $ как список векторов-столбцов, столбцы матрицы произведения $ \ boldsymbol {AB} $ являются результатами преобразования каждого столбца $ \ boldsymbol {B} $ под $ \ boldsymbol {A} $.
2. Умножение матриц вычисляет скалярные произведения для пар векторов: Эта перспектива следует из просмотра $ \ boldsymbol {A} $ как упорядоченного списка векторов-строк и просмотра $ \ boldsymbol {B} $ как упорядоченного списка столбцов -векторы. Матрица произведения $ \ boldsymbol {AB} $ затем сохраняет все попарные скалярные произведения между строками $ \ boldsymbol {A} $ и столбцами $ \ boldsymbol {B} $.
3. Умножение матриц вычисляет композицию двух линейных преобразований: Если мы рассматриваем оба $ \ boldsymbol {A} $ и $ \ boldsymbol {B} $ как линейные преобразования, то матрица произведения представляет собой линейное преобразование, образованное следующим образом: композиция линейных преобразований, определяемая $ \ boldsymbol {A} $ и $ \ boldsymbol {B} $.

Именно эта третья перспектива является наиболее абстрактной и, возможно, наиболее сильной. Давайте углубимся в каждую из этих точек зрения.

Умножение матриц вычисляет линейное преобразование для набора векторов

Эта перспектива наиболее прямо следует из нашего определения мультипликации матриц: если мы рассматриваем $ \ boldsymbol {A} $ как линейное преобразование, а мы рассматриваем матрицу $ \ boldsymbol {B} $ как упорядоченный список векторов-столбцов

то каждый столбец $ \ boldsymbol {AB} $ вычисляется путем взятия линейного преобразования, характеризуемого $ \ boldsymbol {A} $ каждого $ \ boldsymbol {b} _ {*, i} $:

Умножение матриц вычисляет точечные произведения для пар векторов

Если рассматривать матрицу $ \ boldsymbol {A} $ как список векторов-строк, а матрицу $ \ boldsymbol {B} $ как al ist векторов-столбцов, то произведение $ \ boldsymbol {AB} $ – это матрица, в которой хранятся все попарные скалярные произведения векторов в $ \ boldsymbol {A} $ и $ \ boldsymbol {B} $.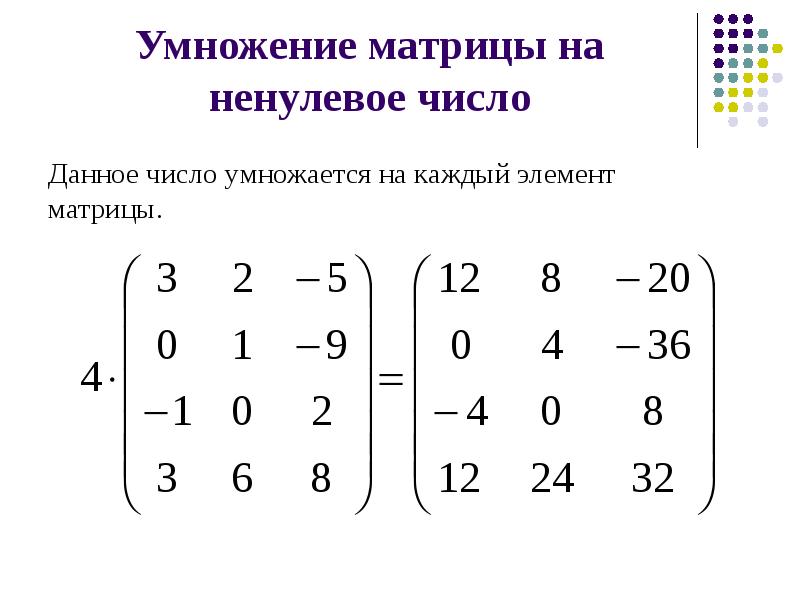 Более конкретно, $ i, j $ -й элемент $ \ boldsymbol {AB} $ – это скалярное произведение между $ i $ -й строкой $ \ boldsymbol {A} $ и $ j $ -м столбцом $ \ boldsymbol {B} $ (см. Теорему 1 в приложении к этому сообщению). Этот факт, часто называемый правилом строк и столбцов , можно использовать для вычисления каждого элемента $ \ boldsymbol {AB} $. Это проиллюстрировано ниже:

Умножение матриц вычисляет композицию двух линейных преобразований:

Третья и последняя перспектива для просмотра умножения матриц требует, чтобы мы просматривали как $ \ boldsymbol {A} $ , так и $ \ boldsymbol {B} $ как линейные преобразования.Тогда оказывается, что матрица $ \ boldsymbol {AB} $ – это матрица, которая характеризует линейное преобразование, образованное композицией линейных преобразований, характеризуемых $ \ boldsymbol {A} $ и $ \ boldsymbol {B} $ (см. Теорема 2 в Приложении к этому сообщению). То есть для двух линейных преобразований

матрица $ \ boldsymbol {AB} $ – это матрица, которая характеризует композицию $ f \ circ g $:

Это доказано в теореме 2 в Приложении к этой статье и проиллюстрировано ниже:

Напомним, что число матрицы rows определяет размеры векторов в своем диапазоне, а количество столбцов соответствует количеству измерений домена. Поскольку $ \ boldsymbol {AB} $ характеризует композицию $ f \ circ g $, отсюда следует, что матрица $ \ boldsymbol {AB} $ будет отображаться из области определения $ \ boldsymbol {B} $ в область значений $ \ boldsymbol {A} $.

Свойства умножения матриц

Вот несколько свойств умножения матриц, которые можно использовать в вычислениях и выводах с использованием матриц. Для краткости помещаем все доказательства в Приложение к записи блога:

1. Ассоциативное свойство матриц (теорема 3): $ \ boldsymbol {A} (\ boldsymbol {BC}) = (\ boldsymbol {AB}) \ boldsymbol {C} $
2. Коммутативность скаляров (теорема 4): $ r (\ boldsymbol {AB}) = (r \ boldsymbol {A}) \ boldsymbol {B} = \ boldsymbol {A} (r \ boldsymbol {B}) $, где $ r $ – скаляр.
3. Левое распределительное свойство (теорема 5): $ \ boldsymbol {A} (\ boldsymbol {B} + \ boldsymbol {C}) = \ boldsymbol {AB} + \ boldsymbol {AC} $
4. Правое распределительное свойство (теорема 6): $ (\ boldsymbol {B} + \ boldsymbol {C}) \ boldsymbol {A} = \ boldsymbol {BA} + \ boldsymbol {CA} $
5. Идентификация (теорема 7): $ \ boldsymbol {I} _m \ boldsymbol {A} = \ boldsymbol {A} = \ boldsymbol {AI} _n $

Приложение

Теорема 1 (правило строк и столбцов): Дана матрица размером $ m \ times n $ $ \ boldsymbol {A} $ и матрица $ n \ times p $ $ \ boldsymbol {B} $, $ i, j $ -й элемент $ \ boldsymbol {AB} $ вычисляется с помощью \ (\ boldsymbol {a} _ {i, *} \ cdot \ boldsymbol {b} _ {*, j} \), где \ (\ boldsymbol {a} _ {i, *} \) – $ i $ -й столбец $ \ boldsymbol { A} $ и \ (\ boldsymbol {b} _ {*, j} \) – это $ j $ -й столбец $ \ boldsymbol {B} $.

Проба:

$ \ square $

Теорема 2: Умножение матрицы на матрицу $ m \ times n $ $ \ boldsymbol {A} $ и $ n \ times p $ -матрица $ \ boldsymbol {B} $ приводит к матрице $ \ boldsymbol {AB} $ такой, что для вектора $ \ boldsymbol {x} \ in \ mathbb {R} ^ m $ выполняется следующее:

Доказательство: Во-первых, давайте расширим $ \ boldsymbol {Bx} $:

Теперь,

$ \ square $

Теорема 3 (ассоциативное свойство для матриц): Даны матрицы $ \ boldsymbol {A} \ in \ mathbb {R} ^ {m \ times l} $, $ \ boldsymbol {B} \ in \ mathbb {R} ^ {l * p} $ и $ \ boldsymbol {C} \ in \ mathbb {R} ^ {p \ times n} $ выполняется $ \ boldsymbol {A} (\ boldsymbol {BC}) = (\ boldsymbol {AB}) \ boldsymbol {C} $. {n \ times p} $ и скаляр $ r $, то $ r (\ boldsymbol {AB}) = (r \ boldsymbol {A}) \ boldsymbol {B} = \ boldsymbol {A} (r \ boldsymbol {B}) $

Доказательство: Сначала докажем $ r (\ boldsymbol {AB}) = (r \ boldsymbol {A}) \ boldsymbol {B} = \ boldsymbol {A} (r \ boldsymbol {B} ) $:

Затем мы докажите, что $ r (\ boldsymbol {AB}) = \ boldsymbol {A} (r \ boldsymbol {B}) $:

$ \ square $

Теорема 5 (Левое распределительное свойство умножения матриц): Данные матрицы $ \ boldsymbol {A} \ in \ mathbb {R} ^ {m \ times n} $, $ \ boldsymbol {B} \ in \ mathbb {R} ^ {n * p} $ и $ \ boldsymbol {C} \ in \ mathbb {R } ^ {n \ times p} $ имеет место следующее: $ \ boldsymbol {A} (\ boldsymbol {B} + \ boldsymbol {C}) = \ boldsymbol {AB} + \ boldsymbol {AC} $

Доказательство :

$ \ square $

Теорема 6 (Правое распределительное свойство умножения матриц): Данные матрицы $ \ boldsymbol {A} \ в \ mathbb {R} ^ {m \ times n} $, $ \ boldsymbol {B} \ in \ mathbb {R} ^ {n * p} $ и $ \ boldsymbol {C} \ in \ mathbb {R} ^ {n \ times p} $ выполняется следующее: $ (\ boldsymbol {B} + \ boldsymbol {C}) \ boldsymbol {A} = \ boldsymbol {BA} + \ boldsymbol {CA} $

Доказательство:

$ \ square $

Теорема 7 (Идентичность): Дана матрица $ m \ times n $ $ \ boldsymbol {A } $ выполняется следующее: $ \ boldsymbol {I} _m \ boldsymbol {A} = \ boldsymbol {A} = \ boldsymbol {AI} _n $

Доказательство: По тому факту, что тождественная функция просто отображает каждый элемент в своей области обратно к себе, он следует за при композиции функции $ f $, а тождественная функция – это просто функция $ f $. Единичная матрица определяет единичную функцию векторов. Кроме того, матричное умножение представляет собой композицию линейных преобразований. Таким образом, следует, что любая матрица, умноженная слева или справа на единичную матрицу, возвращает исходную матрицу (то есть саму функцию). Следовательно, $ \ boldsymbol {I} _m \ boldsymbol {A} = \ boldsymbol {A} = \ boldsymbol {AI} _n $. $ \ square $

– Бесплатная справка по математике

Вы, наверное, уже знаете, что такое матрица, если вас интересует умножение матриц.Однако быстрый пример не повредит. Матрица – это просто двумерная группа чисел. Вместо списка, называемого вектором, матрица представляет собой прямоугольник, как показано ниже:

Вы можете установить переменную как матрицу так же, как вы можете установить переменную как число. В этом случае x – это матрица, содержащая эти четыре числа (в определенном порядке). Теперь предположим, что у вас есть две матрицы, которые нужно умножить. Умножение чисел довольно просто, но как это сделать для матрицы?

Вот ключевой момент: Вы не можете просто умножить каждое число на соответствующее число в другой матрице .Умножение матриц не похоже на сложение или вычитание. Это сложнее, но общий процесс освоить несложно. Вот сначала пример, а потом я объясню, что я сделал :

Пример

Решение:

Вы, наверное, задаетесь вопросом, как вообще я получил этот ответ. Что ж, вы вправе так думать. Умножение матриц – непростая задача для изучения, и вам нужно быть внимательными, чтобы избежать одной или двух ошибок по неосторожности.Вот процесс:

• Шаг 1. Переместитесь через верхнюю строку первой матрицы и вниз по первому столбцу второй матрицы:

• Шаг 2: Умножьте каждое число из верхней строки первой матрицы на число в первом столбце второй матрицы. В данном случае это означает умножение 1 * 2 и 6 * 9. Затем возьмите сумму этих значений (2 + 54):

• Шаг 3. Вставьте полученное значение в матрицу ответов.Поскольку мы умножаем 1-ю строку и 1-й столбец, наш ответ помещается в этот слот в матрице ответов:

• Шаг 4: Повторите для других строк и столбцов. Это означает, что вам нужно пройти по первой строке первой матрицы и на этот раз по второму столбцу второй матрицы. Затем вторая строка первой матрицы и первый столбец второй, и, наконец, нижняя часть первой матрицы и правый столбец второй матрицы:

• Шаг 5: Вставьте все эти значения в матрицу ответов.Я только что показал вам, как делать верхний левый и нижний правый. Если вы работаете с двумя другими числами, вы получите 1 * 2 + 6 * 7 = 44 и 3 * 2 + 8 * 9 = 78. Вставьте их в матрицу ответов в соответствующие позиции, и вы получите:

Теперь я знаю, о чем вы думаете. Это было действительно сложно !!! Ну, так будет казаться, пока вы не привыкнете к процессу. Это может помочь вам записать всю свою работу и даже нарисовать стрелки, чтобы запомнить, в каком направлении вы двигаетесь в строках и столбцах. Просто не забудьте умножить каждую строку первой матрицы на каждый столбец второй матрицы .

Что делать, если матрицы не квадраты? Затем вам нужно добавить еще один шаг. Для умножения двух матриц матрица слева должна иметь столько столбцов, сколько строк в матрице справа. Таким образом, вы можете сопоставить каждую пару во время умножения. Размер окончательной матрицы определяется строками в левой матрице и столбцами в правой. Вот что я делаю:

Записываю размеры матриц. Левая матрица имеет 2 строки и 3 столбца, поэтому мы ее и пишем.Строки, столбцы в указанном порядке. Другая матрица представляет собой матрицу 3×1, потому что у нее 3 строки и только 1 столбец. Если числа в середине совпадают, вы можете умножать. Внешние числа дают вам размер ответа. Даже если вы все испортите, вы в конце концов разберетесь, потому что не сможете размножаться.

Важное напоминание: умножение матриц не коммутативно. Это означает, что вы не можете изменить порядок и ожидать того же результата ! Обычное умножение говорит нам, что 4 * 3 = 3 * 4, но это не умножение в обычном смысле.

Наконец, вот пример с неравномерными размерами матрицы, чтобы подвести итог:

Пример:

Если вам нужна дополнительная помощь в умножении матриц, посетите нашу доску справочных сообщений по математике, прочтите еще один урок по умножению матриц или поищите в Google больше уроков по умножению матриц.

2.2: Умножение матриц – математика LibreTexts

Следующая важная операция с матрицами, которую мы рассмотрим, – это умножение матриц.Операция матричного умножения – одна из самых важных и полезных из матричных операций. В этом разделе мы также продемонстрируем, как умножение матриц связано с линейными системами уравнений.

Во-первых, мы даем формальное определение векторов строк и столбцов. {th} \) матрицы-строки.

Матрица \ (n \ times 1 \) \ [X = \ left [\ begin {array} {c} x_ {1} \\ \ vdots \\ x_ {n} \ end {array} \ right] \] называется вектор-столбец . Вызывается матрица \ (1 \ times n \) \ [X = \ left [\ begin {array} {ccc} x_ {1} & \ cdots & x_ {n} \ end {array} \ right] \] вектор-строка .

Мы можем просто использовать термин вектор по всему тексту для обозначения вектора столбца или строки. Если мы это сделаем, контекст прояснит, о чем мы говорим.

В этой главе мы снова будем использовать понятие линейной комбинации векторов, как в определении [def: linearcombination]. В этом контексте линейная комбинация – это сумма, состоящая из векторов, умноженных на скаляры. Например, \ [\ left [\ begin {array} {r} 50 \\ 122 \ end {array} \ right] = 7 \ left [\ begin {array} {r} 1 \\ 4 \ end {array} \ right] +8 \ left [\ begin {array} {r} 2 \\ 5 \ end {array} \ right] +9 \ left [\ begin {array} {r} 3 \\ 6 \ end {array} \ right] \] представляет собой линейную комбинацию трех векторов.

Оказывается, любую систему линейных уравнений можно выразить как линейную комбинацию векторов. Фактически, векторы, которые мы будем использовать, – это просто столбцы соответствующей расширенной матрицы!

Определение \ (\ PageIndex {2} \): векторная форма системы линейных уравнений

Предположим, у нас есть система уравнений, заданная как \ [\ begin {array} {c} a_ {11} x_ {1} + \ cdots + a_ {1n} x_ {n} = b_ {1} \\ \ vdots \ \ a_ {m1} x_ {1} + \ cdots + a_ {mn} x_ {n} = b_ {m} \ end {array} \] Мы можем выразить эту систему в векторной форме , которая выглядит следующим образом: \ [ x_1 \ left [\ begin {array} {c} a_ {11} \\ a_ {21} \\ \ vdots \\ a_ {m1} \ end {array} \ right] + x_2 \ left [\ begin {array} {c} a_ {12} \\ a_ {22} \\ \ vdots \\ a_ {m2} \ end {array} \ right] + \ cdots + x_n \ left [\ begin {array} {c} a_ {1n } \\ a_ {2n} \\ \ vdots \\ a_ {mn} \ end {array} \ right] = \ left [\ begin {array} {c} b_1 \\ b_2 \\ \ vdots \\ b_m \ end {array} \ right] \]

Обратите внимание, что каждый используемый здесь вектор представляет собой один столбец из соответствующей расширенной матрицы. Для каждой переменной в системе есть один вектор вместе с постоянным вектором.

Первая важная форма умножения матриц – это умножение матрицы на вектор. Рассмотрим продукт, заданный как \ [\ left [\ begin {array} {rrr} 1 & 2 & 3 \\ 4 & 5 & 6 \ end {array} \ right] \ left [\ begin {array} {r} 7 \\ 8 \\ 9 \ end {array} \ right] \] Мы скоро увидим, что это равно \ [7 \ left [\ begin {array} {c} 1 \\ 4 \ end {array} \ right] + 8 \ left [\ begin {array} {c} 2 \\ 5 \ end {array} \ right] +9 \ left [\ begin {array} {c} 3 \\ 6 \ end {array} \ right] = \ left [\ begin {array} {c} 50 \\ 122 \ end {array} \ right] \]

В общих чертах, \ [\ begin {align} \ left [\ begin {array} {ccc} a_ {11} & a_ {12} & a_ {13} \\ a_ {21} & a_ {22} & a_ {23} \ end {array} \ right] \ left [\ begin {array} {c} x_ {1} \\ x_ {2} \\ x_ {3} \ end {array} \ right] & = & \ x_ {1} \ left [\ begin {array} {c} a_ {11} \\ a_ {21} \ end {array} \ right] + x_ {2} \ left [\ begin {array} {c} a_ {12} \\ a_ {22} \ end {array} \ right] + x_ {3} \ left [\ begin {array} {c} a_ {13} \\ a_ {23} \ end {array} \ right ] \\ & = & \ left [\ begin {array} {c} a_ {11} x_ {1} + a_ {12} x_ {2} + a_ {13} x_ {3} \\ a_ {21} x_ {1} + a_ {22} x_ {2} + a_ {23} x_ {3} \ end {array} \ right] \ end {align} \] Таким образом, вы берете \ (x_ {1} \) раз первый столбца, добавьте в \ (x_ {2} \) раз второй столбец и, наконец, умножьте на \ (x_ {3} \) третий столбец. {n} x_ {j} A_ {j} \]

Если мы запишем столбцы \ (A \) в терминах их записей, они будут иметь форму \ [A_ {j} = \ left [\ begin {array} {c} a_ {1j} \\ a_ {2j] } \\ \ vdots \\ a_ {mj} \ end {array} \ right] \] Затем мы можем записать продукт \ (AX \) как \ [AX = x_ {1} \ left [\ begin {array} {c} a_ {11} \\ a_ {21} \\ \ vdots \\ a_ {m1} \ end {array} \ right] + x_ {2} \ left [\ begin {array} {c} a_ {12 } \\ a_ {22} \\ \ vdots \\ a_ {m2} \ end {array} \ right] + \ cdots + x_ {n} \ left [\ begin {array} {c} a_ {1n} \\ a_ {2n} \\ \ vdots \\ a_ {mn} \ end {array} \ right] \]

Обратите внимание, что умножение матрицы \ (m \ times n \) и вектора \ (n \ times 1 \) дает вектор \ (m \ times 1 \).

Вот пример.

Пример \ (\ PageIndex {1} \): вектор, умноженный на матрицу

Вычислить произведение \ (AX \) для \ [A = \ left [\ begin {array} {rrrr} 1 & 2 & 1 & 3 \\ 0 & 2 & 1 & -2 \\ 2 & 1 & 4 & 1 \ end {array} \ right], X = \ left [\ begin {array} {r} 1 \\ 2 \\ 0 \\ 1 \ end {array} \ right] \]

Решение

Мы будем использовать Определение [def: multiplicationvectormatrix] для вычисления произведения. Следовательно, мы вычисляем произведение \ (AX \) следующим образом.\ [\ begin {align} & 1 \ left [\ begin {array} {r} 1 \\ 0 \\ 2 \ end {array} \ right] + 2 \ left [\ begin {array} {r} 2 \ \ 2 \\ 1 \ end {array} \ right] + 0 \ left [\ begin {array} {r} 1 \\ 1 \\ 4 \ end {array} \ right] + 1 \ left [\ begin {массив } {r} 3 \\ -2 \\ 1 \ end {array} \ right] \\ & = \ left [\ begin {array} {r} 1 \\ 0 \\ 2 \ end {array} \ right] + \ left [\ begin {array} {r} 4 \\ 4 \\ 2 \ end {array} \ right] + \ left [\ begin {array} {r} 0 \\ 0 \\ 0 \ end {массив } \ right] + \ left [\ begin {array} {r} 3 \\ -2 \\ 1 \ end {array} \ right] \\ & = \ left [\ begin {array} {r} 8 \\ 2 \\ 5 \ end {array} \ right] \ end {align} \]

Используя вышеуказанную операцию, мы также можем записать систему линейных уравнений в матричной форме .В этой форме мы выражаем систему как матрицу, умноженную на вектор. Рассмотрим следующее определение.

Определение \ (\ PageIndex {4} \): матричная форма системы линейных уравнений

Предположим, у нас есть система уравнений, заданная как \ [\ begin {array} {c} a_ {11} x_ {1} + \ cdots + a_ {1n} x_ {n} = b_ {1} \\ a_ {21 } x_ {1} + \ cdots + a_ {2n} x_ {n} = b_ {2} \\ \ vdots \\ a_ {m1} x_ {1} + \ cdots + a_ {mn} x_ {n} = b_ {m} \ end {array} \] Тогда мы можем выразить эту систему в матричной форме следующим образом. \ [\ left [\ begin {array} {cccc} a_ {11} & a_ {12} & \ cdots & a_ {1n} \\ a_ {21} & a_ {22} & \ cdots & a_ {2n} \ \ \ vdots & \ vdots & \ ddots & \ vdots \\ a_ {m1} & a_ {m2} & \ cdots & a_ {mn} \ end {array} \ right] \ left [\ begin {array} {c} x_ {1} \\ x_ {2} \\ \ vdots \\ x_ {n} \ end {array} \ right] = \ left [\ begin {array} {c} b_ {1} \\ b_ {2} \\ \ vdots \\ b_ {m} \ end {array} \ right] \]

Выражение \ (AX = B \) также известно как матричная форма соответствующей системы линейных уравнений.Матрица \ (A \) – это просто матрица коэффициентов системы, вектор \ (X \) – это вектор-столбец, построенный из переменных системы, и, наконец, вектор \ (B \) – это вектор-столбец, построенный из константы системы. Важно отметить, что в таком виде можно записать любую систему линейных уравнений.

Обратите внимание, что если мы запишем однородную систему уравнений в матричной форме, она будет иметь вид \ (AX = 0 \) для нулевого вектора \ (0 \).

Из этого определения видно, что вектор \ [X = \ left [\ begin {array} {c} x_ {1} \\ x_ {2} \\ \ vdots \\ x_ {n} \ end {array} \ right] \] удовлетворяет уравнению \ (AX = B \) только тогда, когда элементы \ (x_ {1}, x_ {2}, \ cdots, x_ {n} \) вектора \ (X \) равны решения исходной системы.

Теперь, когда мы изучили, как умножить матрицу на вектор, мы хотим рассмотреть случай, когда мы умножаем две матрицы более общих размеров, хотя эти размеры все еще должны быть подходящими, как мы увидим. Например, в примере [exa: vectormultbymatrix] мы умножили матрицу \ (3 \ times 4 \) на вектор \ (4 \ times 1 \). Мы хотим исследовать, как умножать другие размеры матриц.

Мы еще не дали никаких условий, когда возможно умножение матриц! Для матриц \ (A \) и \ (B \), чтобы сформировать продукт \ (AB \), количество столбцов в \ (A \) должно равняться количеству строк в \ (B.\) Рассмотрим продукт \ (AB \), где \ (A \) имеет размер \ (m \ times n \), а \ (B \) имеет размер \ (n \ times p \). Тогда продукт с точки зрения размера матриц определяется как \ [(m \ times \ overset {\ text {они должны совпадать!}} {\ Widehat {n) \; (n} \ times p}) = m \ раз p \]

Обратите внимание, что два внешних числа указывают размер продукта. Одно из наиболее важных правил умножения матриц заключается в следующем. {th} \) столбец \ (AB \).

Рассмотрим следующий пример.

Пример \ (\ PageIndex {2} \): умножение двух матриц

Найдите \ (AB \), если возможно. \ [A = \ left [\ begin {array} {rrr} 1 & 2 & 1 \\ 0 & 2 & 1 \ end {array} \ right], B = \ left [\ begin {array} {rrr} 1 & 2 & 0 \\ 0 & 3 & 1 \\ -2 & 1 & 1 \ end {array} \ right] \]

Решение

Первое, что вам нужно проверить при вычислении произведения, – это возможность умножения.Первая матрица имеет размер \ (2 \ times 3 \), а вторая матрица имеет размер \ (3 \ times 3 \). Внутренние числа равны, поэтому \ (A \) и \ (B \) – согласованные матрицы. Согласно приведенному выше обсуждению \ (AB \) будет \ (2 \ times 3 \) матрицей. Определение [def: multiplicationoftwomatrices] дает нам способ вычислить каждый столбец \ (AB \) следующим образом.

\ [\ left [\ overset {\ text {Первый столбец}} {\ overbrace {\ left [\ begin {array} {rrr} 1 & 2 & 1 \\ 0 & 2 & 1 \ end {array} \ right ] \ left [\ begin {array} {r} 1 \\ 0 \\ -2 \ end {array} \ right]}}, \ overset {\ text {Второй столбец}} {\ overbrace {\ left [\ begin {array} {rrr} 1 & 2 & 1 \\ 0 & 2 & 1 \ end {array} \ right] \ left [\ begin {array} {r} 2 \\ 3 \\ 1 \ end {array} \ right]}}, \ overset {\ text {Третий столбец}} {\ overbrace {\ left [\ begin {array} {rrr} 1 & 2 & 1 \\ 0 & 2 & 1 \ end {array} \ right] \ left [\ begin {array} {r} 0 \\ 1 \\ 1 \ end {array} \ right]}} \ right] \] Вы знаете, как умножить матрицу на вектор, используя Определение [def: multiplicationvectormatrix ] для каждого из трех столбцов. Таким образом, \ [\ left [\ begin {array} {rrr} 1 & 2 & 1 \\ 0 & 2 & 1 \ end {array} \ right] \ left [\ begin {array} {rrr} 1 & 2 & 0 \\ 0 & 3 & 1 \\ -2 & 1 & 1 \ end {array} \ right] = \ \ left [\ begin {array} {rrr} -1 & 9 & 3 \\ -2 & 7 & 3 \ end {array} \ right] \]

Поскольку векторы – это просто матрицы \ (n \ times 1 \) или \ (1 \ times m \), мы также можем умножить вектор на другой вектор.

Пример \ (\ PageIndex {3} \): умножение вектора на вектор

Если возможно, умножьте \ (\ left [\ begin {array} {r} 1 \\ 2 \\ 1 \ end {array} \ right] \ left [\ begin {array} {rrrr} 1 & 2 & 1 & 0 \ end {array} \ right].\)

Решение

В этом случае мы умножаем матрицу размера \ (3 \ times 1 \) на матрицу размера \ (1 \ times 4. \). Внутренние числа совпадают, поэтому произведение определено. Обратите внимание, что продукт будет матрицей размером \ (3 \ times 4 \). Используя Определение [def: multiplicationoftwomatrices], мы можем вычислить этот продукт следующим образом \ (\: \) \ [\ left [\ begin {array} {r} 1 \\ 2 \\ 1 \ end {array} \ right] \ left [\ begin {array} {rrrr} 1 & 2 & 1 & 0 \ end {array} \ right] = \ left [\ overset {\ text {Первый столбец}} {\ overbrace {\ left [\ begin {array } {r} 1 \\ 2 \\ 1 \ end {array} \ right] \ left [\ begin {array} {r} 1 \ end {array} \ right]}}, \ overset {\ text {Второй столбец }} {\ overbrace {\ left [\ begin {array} {r} 1 \\ 2 \\ 1 \ end {array} \ right] \ left [\ begin {array} {r} 2 \ end {array} \ right]}}, \ overset {\ text {Третий столбец}} {\ overbrace {\ left [\ begin {array} {r} 1 \\ 2 \\ 1 \ end {array} \ right] \ left [\ begin {массив} {r} 1 \ end {array} \ right]}}, \ overset {\ text {Четвертый столбец}} {\ overbrace {\ left [\ begin {array} {r} 1 \\ 2 \\ 1 \ end {array} \ right] \ left [\ begin {array} {r} 0 \ end {array} \ right]}} \ right] \]

Вы можете использовать Определение [def: multiplicationvectormatrix], чтобы убедиться, что этот продукт равен \ [\ left [\ begin {array} {cccc} 1 & 2 & 1 & 0 \\ 2 & 4 & 2 & 0 \\ 1 & 2 & 1 & 0 \ end {array} \ right] \]

Пример \ (\ PageIndex {4} \): умножение, которое не определено

Найдите \ (BA \), если возможно. \ [B = \ left [\ begin {array} {ccc} 1 & 2 & 0 \\ 0 & 3 & 1 \\ -2 & 1 & 1 \ end {array} \ right], A = \ left [\ begin {array} {ccc} 1 & 2 & 1 \\ 0 & 2 & 1 \ end {array} \ right] \]

Решение

Сначала проверьте, возможно ли это. Этот продукт имеет вид \ (\ left (3 \ times 3 \ right) \ left (2 \ times 3 \ right). \) Внутренние числа не совпадают, поэтому вы не можете выполнить это умножение.

В этом случае мы говорим, что умножение не определено.Обратите внимание, что это те же самые матрицы, которые мы использовали в примере [exa: multiplicationoftwomatrices]. В этом примере мы попытались вычислить \ (BA \) вместо \ (AB \). Это демонстрирует еще одно свойство умножения матриц. Хотя продукт \ (AB \) может быть определен, мы не можем предполагать, что продукт \ (BA \) будет возможен. Поэтому важно всегда проверять, определен ли продукт, прежде чем проводить какие-либо расчеты.

Ранее мы определили нулевую матрицу \ (0 \) как матрицу (подходящего размера), содержащую нули во всех элементах. Рассмотрим следующий пример умножения на нулевую матрицу.

Пример \ (\ PageIndex {5} \): умножение на нулевую матрицу

Вычислить произведение \ (A0 \) для матрицы \ [A = \ left [\ begin {array} {rr} 1 & 2 \\ 3 & 4 \ end {array} \ right] \] и \ (2 \ times 2 \) нулевая матрица, заданная как \ [0 = \ left [\ begin {array} {rr} 0 & 0 \\ 0 & 0 \ end {array} \ right] \]

Решение

В этом продукте мы вычисляем \ [\ left [\ begin {array} {rr} 1 & 2 \\ 3 & 4 \ end {array} \ right] \ left [\ begin {array} {rr} 0 & 0 \\ 0 & 0 \ end {array} \ right] = \ left [\ begin {array} {rr} 0 & 0 \\ 0 & 0 \ end {array} \ right] \]

Следовательно, \ (A0 = 0 \).

Обратите внимание, что мы также можем умножить \ (A \) на \ (2 \ times 1 \) нулевой вектор, заданный как \ (\ left [\ begin {array} {r} 0 \\ 0 \ end {array} \ right ] \). Результатом будет нулевой вектор \ (2 \ times 1 \). Следовательно, всегда бывает так, что \ (A0 = 0 \) для нулевой матрицы или вектора подходящего размера.

Умножение матриц

Марко Табога, доктор философии

Эта лекция знакомит с умножением матриц, одним из основных алгебраических методов. операции, которые могут быть выполнены на матрицы.

Точечный продукт

Прежде чем определять умножение матриц, нам нужно ввести понятие точки произведение двух векторов.

Обратите внимание, что в приведенном выше определении имеет значение порядок продуктов, то есть это не то же самое, что , потому что первый вектор () должен быть вектором-строкой, а второй () должен быть вектор-столбец. Кроме того, скалярное произведение определяется только в том случае, если а также иметь одинаковое количество записей ().

Матричный продукт

Теперь мы готовы определить матричный продукт.

Другими словами, -го вход является

Обратите внимание, что порядок товара имеет значение, то есть это не то же самое, что . Кроме того, количество столбцов должно быть равно количеству строк (в этом случае говорят, что две матрицы соответствуют для умножения ).

Следующая диаграмма суммирует размеры, включенные в матрицу. умножение:

Мотивация

Почему умножение матриц определяется таким образом? Есть много возможных ответы на этот вопрос, но самый простой из них связан с необходимостью получение простого матричного представления для систем линейных уравнений. В в следующем примере показано, как это сделать.

Еще одна причина, по которой умножение матриц определяется так, как показано выше. в том, что он позволяет легко работать с системами ввода-вывода, в которых заданные выходы могут быть получены из фиксированных комбинаций входов.

Свойства умножения матриц

Как мы уже говорили, в отличие от умножения действительных чисел матрица умножение не обладает коммутативным свойством, т. е. это не то же самое, что . Однако некоторые из свойств умножения действительных чисел: также пользуется умножением матриц.

Предложение (распределительное имущество) Умножение матриц является дистрибутивным по отношению к сложению матриц, что это для любые матрицы , а также таким образом, чтобы указанные выше умножения и сложения были осмысленно определены.

Проба

Предложение (ассоциативное имущество) Умножение матриц ассоциативно, что это для любые матрицы , а также таким образом, чтобы указанные выше умножения были осмысленно определены.

Проба

Другая недвижимость

Здесь перечислены другие свойства матричных продуктов.

Перенести продукт

Проба

Решенные упражнения

Ниже вы можете найти несколько упражнений с объясненными решениями.

Упражнение 1

Определить матрица а matrixCompute продукт .

Решение

Упражнение 2

Учитывая матрицы а также определено выше, вычислить продукт .

Решение

Упражнение 3

Определить столбец вектор и а ряд векторCompute продукт .

Решение

Как цитировать

Укажите как:

Табога, Марко (2017). «Умножение матриц», Лекции по матричной алгебре. https://www.statlect.com/matrix-algebra/matrix-multiplication.

Объяснитель уроков: сила матрицы

В этом пояснительном материале мы узнаем, как использовать умножение матриц для определить квадрат и куб квадратной матрицы.

Есть много матричных операций, очень похожих на хорошо известные операции из обычной алгебры, такие как сложение, вычитание и масштабирование.Кроме того, хотя умножение матриц существенно больше сложнее, чем его традиционный аналог, он все еще в некоторой степени отражает некоторые алгебраические свойства оригинала.

Одна операция, которая является центральной как для традиционной алгебры, так и для алгебры с использованием матрицы – это возведение в степень, которое обычно называют взятием степень числа или матрицы. В в обычной алгебре можно взять почти любое число 𝑥 и возвести в степень, давая 𝑥.За исключением приведения нуля в отрицательную степень, это не имеет значения. независимо от того, является ли 𝑥 или 𝑦 нулем, отличным от нуля, целым числом, нецелочисленный, рациональный, иррациональный или сложный, поскольку результат всегда может быть рассчитано. То же самое не верно при работе с матрицами, где матрица 𝐴 не всегда можно возвести в степень. Чтобы лучше всего обрисовать эти потенциальные осложнения, давайте сначала определим простейшую форму возведение в степень матрицы: возведение матрицы в квадрат.

Определение: квадрат матрицы

Если 𝐴 – квадратная матрица, определяется как 𝐴 = 𝐴 × 𝐴.

Другими словами, как и для возведения чисел в степень (т. Е. 𝑎 = 𝑎 × 𝑎) квадрат получается умножением матрица сама по себе.

Как можно заметить, самым основным требованием к возведению в степень матрицы должно быть определено, что должно быть квадратным. Это потому, что на двоих общие матрицы 𝐴 и 𝐵, матрица умножение 𝐴𝐵 корректно определено только при одинаковом количестве столбцов в 𝐴, как есть строки в. Если 𝐴 имеет порядок 𝑚 × 𝑛 и Имеет порядок 𝑛 × 𝑝, то Корректно определено и имеет порядок 𝑚 × 𝑛.Если бы мы только рассмотрели матрицу и попытались завершить умножение матриц 𝐴 = 𝐴 × 𝐴, то мы будем попытка умножить матрицу порядка 𝑚 × 𝑛 на другая матрица порядка 𝑚 × 𝑛. Это может быть только хорошо определено, если 𝑚 = 𝑛, что означает, что 𝐴 должно быть матрица порядка 𝑛 × 𝑛 (другими словами квадрат). В порядок 𝐴, следовательно, идентичен исходной матрице 𝐴.

Есть и другие ограничения на принятие степеней матриц, не существуют для действительных чисел.Например, в отличие от обычных чисел, у нас нет способ определения того, что такое 𝐴, и отрицательная сила матрицу вычислить гораздо сложнее. Кроме того, обычные законы возведение в степень не обязательно распространяется на матрицы так же, как они работают с числами, которые мы исследуем позже в этом пояснении.

А пока давайте продемонстрируем, как возведение матрицы в квадрат работает в простом, нетривиальном кейс. Определим матрицу 𝐴 = 1−325.

Для вычисления матрицы 𝐴 мы умножаем матрицу 𝐴 само по себе. Другими словами, у нас есть 𝐴 = 𝐴 × 𝐴 = 1−3251−325.

Как и ожидалось, это умножение хорошо определено, так как у нас есть Матрица 2 × 2, умноженная на 2 × 2 матрица. Теперь осталось завершить умножение матриц, которое мы можем сделать для каждой записи (𝑖, 𝑗) путем умножения элементов в строке 𝑖 левой матрицы элементами столбца 𝑗 правой матрицы и суммируя их.Мы демонстрируем это процесс ниже:

Теперь, когда все записи вычислены, мы можем написать, что 𝐴 =  − 5−181219.

Давайте теперь рассмотрим пример, в котором мы можем применить эту технику возведения в квадрат матрица для решения проблемы.

Пример 1: Нахождение квадрата матрицы

Для 𝐴 = 4−54−5, напишите 𝐴 как кратное 𝐴.

Ответ

Прежде чем пытаться записать 𝐴 как кратное 𝐴, нам нужно вычислить сам.Заполнение необходимой матрицы умножение дает 𝐴 = 𝐴 × 𝐴 = 4−54−54−54−5 =  − 45−45.

Выходная матрица 𝐴 такая же, как исходная матрица 𝐴, за исключением того, что каждая запись была умножена на -1. Мы следовательно, обнаруживаем, что может быть записано в терминах самого себя с помощью выражение 𝐴 = −𝐴.

Увидев простой пример использования мощности матрицы, отметим, что мы часто приходится иметь дело с выражениями, которые потенциально включают несколько матрицы, а также другие матричные операции.К счастью, у нас не должно быть проблемы, связанные с такими вопросами, если мы применяем одни и те же принципы мы только что узнали.

Пример 2: Вычисление матричных выражений, включающих полномочия

Рассмотрим матрицы 𝑋 =  − 3−35−6, 𝑌 = 136−6. Что такое 𝑋 − 𝑌?

Ответ

Мы должны начать с вычисления 𝑋 и 𝑌 обычным способом. Вычисляем, что 𝑋 = 𝑋 × 𝑋 =  − 3−35−6 − 3−35−6 =  − 627−4521.

Также имеем 𝑌 = 𝑌 × 𝑌 = 136−6 136−6 = 19−15−3054.

Теперь, когда у нас есть и 𝑌, это легко вычислить, что 𝑋 − 𝑌 =  − 627−4521 − 19−15−3054 =  − 2542−15−33.

Вероятно, неудивительно, что мы можем легко взять, например, третий мощность матрицы, используя наше понимание того, как мы находим вторую степень матрицы, как мы сделали выше.

Давайте исследуем, как работает третья степень матрицы. По определению третья степень квадратной матрицы 𝐴 задается формулой 𝐴 = 𝐴 × 𝐴 × 𝐴.

Обратите внимание, что использование ассоциативного свойства умножения матриц вместе с определения 𝐴, мы можем записать правую часть это как 𝐴 × 𝐴 × 𝐴 = (𝐴 × 𝐴) × 𝐴 = 𝐴 × 𝐴.

В качестве альтернативы мы можем использовать ассоциативность двух последних членов, чтобы записать это как 𝐴 × 𝐴 × 𝐴 = 𝐴 × (𝐴 × 𝐴) = 𝐴 × 𝐴.

Итак, мы показали, что 𝐴 = 𝐴𝐴 = 𝐴𝐴. В других слов, как только мы вычислили, мы можем найти 𝐴 путем умножения 𝐴 справа (или слева) пользователя 𝐴.

Увидев, как возведение в степень работает для возведения в квадрат и куб, мы могли бы вообразить мы можем применить те же принципы к любой степени.С Следуя определению, это возможно.

Определение: степень матрицы

Если 𝐴 – квадратная матрица, а 𝑘 – положительное целое число, дается 𝑘-я степень числа к 𝐴 = 𝐴 × 𝐴 × ⋯ × 𝐴,  где есть копий матрицы.

В дополнение к этому определению отметим, что, используя ту же логику, что и выше, можно вычислить (для любого положительного целого) сначала вычислив 𝐴 и умножив на дополнительный 𝐴 справа или слева.Так, например, 𝐴 = 𝐴 × 𝐴 = 𝐴 × 𝐴, и так далее.

Давайте теперь рассмотрим пример, в котором нам нужно вычислить третью степень матрица.

Пример 3: Вычисление старших степеней матриц

Учитывая матрицу 𝐴 = 40−37, вычислить 𝐴 − 3𝐴.

Ответ

Мы должны начать с вычисления 𝐴, а затем использовать этот результат для рассчитать 𝐴. Мы находим, что 𝐴 = 𝐴 × 𝐴 = 40−3740−37 = 160−3349.

Теперь у нас есть обе матрицы 𝐴 = 40−37, 𝐴 = 160−3349,  что означает, что мы можем вычислить 𝐴 как матричное умножение между 𝐴 и 𝐴: 𝐴 = 𝐴 × 𝐴 = 40−37160−3349 = 640−279343.

Теперь у нас есть все необходимое для вычисления искомого выражения: 𝐴 − 3𝐴 = 640−279343 − 3160−3349 = 640−279343 − 480−99147 = 160−180196.

. 2 × 2 матрицы, но расширение до более высоких порядков квадратные матрицы очень естественны. Давайте теперь посмотрим на пример того, как мы могли бы найти степень матрицы 3 × 3.

Пример 4: возведение в квадрат матрицы 3 × 3

Рассмотрим 𝐴 = 112101210.

Найдите 𝐴.

Ответ

Матрица 𝐴 имеет порядок 3 × 3, что означает, что 𝐴 также будет иметь этот порядок. Поэтому мы ожидаем найти матрицу вида 𝐴 = 𝐴 × 𝐴 = 112101210112101210 =  ∗∗∗∗∗∗∗∗∗ ,  где необходимо вычислить элементы ∗. Заполним матрицу умножение полностью, полностью иллюстрируя каждый шаг.

Сначала мы вычисляем запись в первой строке и первом столбце самой правой матрицы: 112101210112101210 = 6 ∗∗∗∗∗∗∗∗∗.

Расчет 1 × 1 + 1 × 1 + 2 × 2 = 6. Теперь посчитаем запись в первая строка и второй столбец самой правой матрицы: 112101210112101210 = 63 ∗∗∗∗∗∗∗∗.

Расчет 1 × 1 + 1 × 0 + 2 × 1 = 3. Далее мы сосредотачиваемся на записи в первая строка и третий столбец самой правой матрицы: 112101210112101210 = 633 ∗∗∗∗∗∗∗ .

Расчет 1 × 2 + 1 × 1 + 2 × 0 = 3. Теперь мы переходим ко второму ряду крайняя правая матрица, возвращающаяся к первому столбцу: 112101210112101210 = 6333 ∗∗∗∗∗∗ .

Расчет 1 × 1 + 0 × 1 + 1 × 2 = 3. Затем мы берем запись во втором строка и второй столбец: 112101210112101210 = 63332 ∗∗∗∗ ,

Расчет 1 × 1 + 0 × 0 + 1 × 1 = 2. Последняя запись во второй строке: затем вычислили: 112101210112101210 = 633322 ∗∗∗ .

Расчет 1 × 2 + 0 × 1 + 1 × 0 = 2. Запись в третьей строке и первой столбец рассчитывается: 112101210112101210 = 6333223 ∗∗ .

Расчет 2 × 1 + 1 × 1 + 0 × 2 = 3. Предпоследняя запись тогда завершенный: 112101210112101210 = 63332232 ∗ .

Расчет 2 × 1 + 1 × 0 + 0 × 1 = 2. Затем разрабатывается окончательная запись: 112101210112101210 = 633322325.

Расчет 2 × 2 + 1 × 1 + 0 × 0 = 5. Теперь, когда все записи крайнего правого матрица найдена, ответ можно записать как 𝐴 = 633322325.

Учитывая, что взятие мощности матрицы включает в себя повторяющуюся матрицу умножения, мы могли разумно ожидать, что алгебраические правила матрицы умножение в некоторой степени повлияет на правила возведения в степень матрицы Аналогичным образом.Хотя это до некоторой степени очевидно, опасно обращайтесь к правилам обычной алгебры при ответе на вопросы, включающие матрицы в предположении, что они все еще будут выполняться. В следующих Например, мы будем рассматривать каждое утверждение индивидуально и представим соответствующие свойства матричного умножения в тандеме, объясняя, почему данные утверждения верны или не верны в результате.

Пример 5: Проверка свойств степеней матриц

Какое из следующих утверждений верно для всех 𝑛 × 𝑛 матрицы 𝐴 и 𝐵?

1. 𝐴𝐵 = 𝐴 (𝐴𝐵) 𝐵
2. (𝐴 − 𝐵) = 𝐴 − 2𝐴𝐵 + 𝐵
3. (𝐴𝐵) = 𝐴𝐵
4. (𝐴 + 𝐵) = 𝐴 + 2𝐴𝐵 + 𝐵
5. (𝐴 + 𝐵) (𝐴 − 𝐵) = 𝐴 − 𝐵

Ответ

1. Умножение матриц является ассоциативным, что означает, что 𝐴 (𝐵𝐶) = (𝐴𝐵) 𝐶.Мы могли бы продолжить эту роль, чтобы получить результаты например (𝐴𝐵) (𝐶𝐷) = 𝐴 (𝐵𝐶) 𝐷 = 𝐴𝐵𝐶𝐷 и т. д. В данном уравнения, левая часть равна, что по определению можно записать как 𝐴𝐵 = 𝐴𝐴𝐵𝐵. Учитывая ассоциативность свойство умножения матриц, мы можем написать, что 𝐴𝐵 = 𝐴 (𝐴𝐵) 𝐵 и тем самым подтвердить, что данное утверждение верно.
2. Обычная алгебра коммутативна над умножением. Для двух вещественных чисел 𝑎 и 𝑏, это означает, что 𝑎𝑏 = 𝑏𝑎.Этот результат позволяет нам взять такое выражение, как (𝑎 − 𝑏) = 𝑎 − 𝑎𝑏 − 𝑏𝑎 + 𝑏 и использовать коммутативное свойство собирать два средних члена правой части: (𝑎 − 𝑏) = 𝑎 − 2𝑎𝑏 + 𝑏. Однако умножение матриц, как правило, не коммутативно, что означает, что 𝐴𝐵 ≠ 𝐵𝐴, за исключением особых обстоятельств (таких как диагональные матрицы или одновременно диагональные матрицы). Следовательно, разложение (𝐴 − 𝐵) = 𝐴 − 𝐴𝐵 − 𝐵𝐴 + 𝐵 не может можно упростить в предположении, что 𝐴𝐵 = 𝐵𝐴.Следовательно, данный заявление ложно.
3. Чтобы завершить умножение матриц (𝐴𝐵) , мы можем начать с запись (𝐴𝐵) = (𝐴𝐵) (𝐴𝐵) = 𝐴 (𝐵𝐴) 𝐵,, где мы использовали свойство ассоциативности, чтобы упорядочить последнее выражение. Поскольку матричное умножение не коммутативно, член в квадратных скобках (𝐵𝐴) нельзя переставить как (𝐴𝐵), что означает что мы не можем переписать окончательное выражение как 𝐴𝐴𝐵𝐵, что допустили упрощение 𝐴𝐵.Учитывая, что это не В этом случае утверждение является ложным.
4. Мы имеем, что (𝐴 + 𝐵) = 𝐴 + 𝐴𝐵 + 𝐵𝐴 + 𝐵. Поскольку обычно 𝐴𝐵 ≠, мы не можем получить упрощение, данное в вопросе.
5. Начнем с завершения разложения (𝐴 + 𝐵) (𝐴 − 𝐵) = 𝐴 + 𝐵𝐴 − 𝐴𝐵 − 𝐵. Мы знаем, что, как правило, 𝐵𝐴 ≠ 𝐴𝐵, что означает, что мы не можем записать правую часть в виде 𝐴 − 𝐵 и, следовательно, утверждение в вопросе неверно.

Следовательно, правильный ответ – вариант А.

Несмотря на то, что некоторые общепринятые правила алгебры не выполняются для матриц, есть еще некоторые правила, управляющие степенями матриц, которые мы можем положиться на. В частности, законы показателей для чисел могут быть распространяется на матрицы следующим образом.

Свойство: сложение и умножение степеней матрицы

Если 𝐴 – квадратная матрица, а 𝑟 и 𝑠 – натуральные числа, то 𝐴𝐴 = 𝐴, (𝐴) = 𝐴.

В последнем примере мы рассмотрим преобразование матрицы в гораздо большую степень и посмотрите, как указанные выше свойства можно использовать по касательной к идентификации закономерность поведения матрицы при возведении в степень.

Пример 6: Нахождение старшей степени матрицы путем исследования паттерна своих полномочий

Заполните поле: Если 𝐴 = 403−4, тогда 𝐴 = .

Ответ

Как 𝐴 = 𝐴 × 𝐴 × ⋯ × 𝐴 (пятьдесят раз), очевидно, нам следует избегать попыток вычислить это напрямую. Вместо этого, давайте исследуем эффект, что принятие полномочий Имеет для малых степеней и см. можем ли мы определить закономерность.

Если мы умножим 𝐴 на себя, другими словами, если мы найдем 𝐴 = 𝐴 × 𝐴, имеем 𝐴 = 403−4403−4 = 4004.

Отметим, что, поскольку это диагональная матрица, эта форма может быть полезной для матрица, в которую нужно входить. Продолжая двигаться дальше, если мы вычислим 𝐴 = 𝐴 × 𝐴, имеем 𝐴 = 4004403−4 = 404⋅3−4.

Интересно, что матрица больше не диагональная. Чтобы продолжить расследование паттерн, вычислим 𝐴 = 𝐴 × 𝐴. Это 𝐴 = 404⋅3−4403−4 = 4004.

На этом этапе можно распознать шаблон. Для равных полномочий матрицы мы предполагаем, что матрица диагональна и матрица ненулевыми элементами являются 4, где 𝑛 – мощность матрицы.Для нечетных степеней это не так, поскольку есть ненулевые записи в нижнем левом углу и нижнем правом углу запись становится отрицательной. Однако, поскольку нам нужно только найти 𝐴 где 50 – четная степень, нам нужно только рассмотреть первый случай.

Давайте теперь покажем, как мы можем найти 𝐴, используя четное мощность матрицы. Напомним, что 𝐴 = 4004.

Отметим, что скаляр 4 можно вывести за пределы матрицы, переписав его в виде: 𝐴 = 41001.

Это единичная матрица 2 × 2 𝐼 умножить на константу. Теперь мы знаем, что единичная матрица имеет имущество 𝐼𝑋 = 𝑋𝐼 = 𝑋, где 𝑋 – любая матрица 2 × 2. В частности, если 𝑋 = 𝐼, имеем 𝐼 = 𝐼 × 𝐼 = 𝐼.

Мы можем расширить это до любой степени, т. Е. 𝐼 = 𝐼.

Мы можем использовать это свойство для вычисления 𝐴. Давайте также напомним свойство (𝐴) = 𝐴, что позволяет нам переписать 𝐴 следующим образом: 𝐴 = 𝐴.

Так как = 4𝐼, это означает 𝐴 = 4𝐼 = 4𝐼 = 4𝐼 = 21001.

Так как, 4 = 2.

Тогда, 4 = 2 = 2.

Есть много связанных тем, которые подтверждают обоснованность изучения матричного возведения в степень. При работе с квадратной матрицей ясно, что многократное умножение такой матрицы на себя приведет к обычно приводят к результатам, которые становится все сложнее вычислить с учетом больших чисел вовлечены, как мы видели в нескольких приведенных выше примерах.Поэтому выгодно иметь возможность максимально снизить сложность этих вычислений. При определенных обстоятельства, можно диагонализовать матрицу, что значительно уменьшает сложность вычисления его целочисленных степеней.

Давайте закончим рассмотрением основных вещей, которые мы узнали в этом объяснитель.

Ключевые моменты

• Для квадратной матрицы 𝐴 и положительного целого числа 𝑘, мы определяем степень матрицы повторением матрицы умножение; Например, 𝐴 = 𝐴 × 𝐴 × ⋯ × 𝐴,  где имеется 𝑘 копий матрицы 𝐴 с правой стороны.
• Важно понимать, что мощность матрицы только хорошо определяется, если матрица является квадратной матрицей. Кроме того, если Имеет порядок 𝑛 × 𝑛, то это будет случай для 𝐴, 𝐴 и так далее.
• Высшие степени матрицы могут быть вычислены со ссылкой на нижние степени матрицы. Другими словами, 𝐴 = 𝐴 × 𝐴, 𝐴 = 𝐴 × 𝐴, и так далее.
• Если 𝐴 – квадратная матрица и 𝑟 и 𝑠 – натуральные числа, то 𝐴𝐴 = 𝐴, (𝐴) = 𝐴.

в R – арифметические операции / умножение матриц и разница между операторами * и% *% в

R – важный язык программирования, активно используемый статистиками. Он также используется в машинном обучении, науке о данных, исследованиях и многих других новых областях. Это вычислительная среда, в которой могут быть реализованы статистические данные.

Итак, приступим.

Операторы * И% * % В рэнд

Оператор * – это простой арифметический оператор. Это называется оператором умножения. Оператор% *% – это особый вид оператора умножения. Он используется при умножении матриц в R. Теперь мы увидим, как эти две функции работают по-разному, на примерах.Чтобы увидеть разницу между этими двумя операторами, мы будем использовать оба оператора с двумя числами по отдельности.

1. # Использование оператора простого умножения
2. 2 * 2

> 2 * 2

[1] 4

Как показано выше, мы использовали простой оператор умножения (*). Теперь мы будем использовать оператор умножения матриц% *% с теми же значениями, что и выше.

1. # Использование оператора умножения матриц
2. 2% *% 2

> 2% *% 2

[, 1]

[1,] 4

Теперь мы ясно видим различия, так как у обоих операторов операнды одинаковые, но выходы разные. В простом операторе умножения (*) выходные данные были сгенерированы как вектор, а в операторе умножения матриц выходные данные были созданы как матрица из одной строки и одного столбца.На изображении ниже в R studio показано, как это работает.

Теперь мы увидим и подробно изучим, как умножение матриц работает в R с помощью оператора умножения матриц% *%.

Создание матриц для умножения

Давайте сначала разберемся с постановкой задачи на следующем изображении, где нам нужно найти результат после умножения MatrixA и MatrixB.

Как видно на изображении выше, обе матрицы имеют одинаковые размеры и одинаковые элементы. Итак, чтобы работать с этим, сначала мы создадим матрицу в R. Она была создана с помощью приведенного ниже сценария R в R Studio.

2. Вектор1 <- c (5, 2)
4. MatrixA <- матрица (данные = Vector1, nrow = 1, ncol = 2)
6. MatrixA <- rbind (MatrixA, c (4, 3))
9. Матрица А
11. MatrixB <- MatrixA
13. MatrixB

Выход

> Матрица

[, 1] [, 2]

[1,] 5 2

[2,] 4 3

> MatrixB

[, 1] [, 2]

[1,] 5 2

[2,] 4 3

Здесь мы сначала создали вектор с именем Vector1.Матрица имени MatrixA создана элементами ранее созданного вектора Vector1. Матрица функций используется для создания матрицы в R. Мы снова добавили в эту матрицу дополнительную строку, используя функцию rbind (), как показано выше.

Matrix B была создана путем копирования и назначения всех элементов MatrixA.

Матрицы Умножение С оператором% *%

Теперь перемножим обе матрицы и увидим результат в R studio.Для умножения матриц используется специальный тип оператора умножения матриц% *%. Это было показано ниже с помощью сценария R.

1. # Умножение обеих матриц на% *% Оператор
2. МатрицаA% *% МатрицаB

> МатрицаA% *% МатрицаB

[, 1] [, 2]

[1,] 33 16

[2,] 32 17

Это показано на изображении ниже.

В R Studio это выглядит как на изображении ниже.

Вывод и умножение проиллюстрированы на следующем примере изображения.

Теперь мы уже видели, как умножить две матрицы в R с примерами в R studio на сценарий R, как показано выше. Мы также можем использовать простой оператор умножения, но он будет работать как обычное умножение. Он просто умножит элементы одного индекса.

Итак, для умножения двух матриц в R используется специальный тип оператора, то есть оператор умножения матриц (% *%) в R.

Сводка